Проект по теме» Старинные меры длины»
Фестиваль ученических проектов- 2018
Муниципальное Казенное Общеобразовательное Учреждение
«Средняя
образовательная школы п .Керамкомбинат»
Секция — Точные науки, предмет- Математика
Тип проекта — исследовательский
«Старинные меры длины»
Выполнила:
учащаяся: 9 «А» класса
Шатько Наташа
Руководитель:
Терещенко Светлана
Васильевна
учитель математике
первой квалификационной
категории
2018
Содержание
Введение………………………………………………………………3 — 4
Основная часть……………………………………………………….
Глава 1. Единицы измерения Древней Руси……………………….5-8
Глава 2. Пословицы старинных русских мер длины………………9
Глава 3.Эксперимент…………………………………………………10
Глава 4.………………………………………………..11-12
Заключение. ………………………………………………………… 12
Список использованной литературы….………………………………………………………………13
Математика – это то, посредством чего
люди управляют природой и собой.
(А. Колмогоров)
Введение
При решении различных задач, чтении книг, особенно о старинных
временах, мы постоянно сталкиваемся с различными единицами измерения. Мне стало
интересно узнать об истории возникновения различных единиц измерения, различных
способах измерения. Ведь потребность считать и сравнивать предметы возникла у
людей не сразу, но очень давно, — ещё на ранней ступени развития человечества,
возникла в процессе его трудовой деятельности.
Какие старинные единицы измерения вы знаете? Большинство опрошенных учеников называли старинные единицы измерения. В основном: аршин, сажень, локоть. Некоторые учащиеся добавляли такие единицы, как фут, дюйм, верста. Но, все же некоторые не смогли назвать ни одной старинной единицы измерения.
Почему, по вашему мнению, в современном мире люди используют международную систему единиц (СИ)? Большинство опрошенных – для удобства.
Хотели бы вы узнать о старинных единицах измерения и историю их возникновения? Многим было бы интересно.
Таким образом, я пришла к выводу, что тема «Старинные меры длины» актуальна в настоящее время.
Цели проекта:
1.Узнать какие меры длины существовали в Руси раньше.
2. Где они применялись ?
3.Что означают пословицы старинных русских мер длины?
4.Исследование
Для этого необходимо выполнить следующие задачи:
1. Познакомиться с старинными мерами длины;
Познакомиться с старинными мерами длины;
2. Исследовать где они применялись;
3. Рассмотреть пословицы старинных мер;
. 3. Методы исследования:
Сбор материала, обработка данных, наблюдение, сравнение, анализ,
1. План работы по организации проекта
1. Подготовительно – организационный (1 -4 четверть)
2. Самостоятельная творческая деятельность (сентябрь – январь)
3. Реализация проекта (второе полугодие учебного года февраль-май)
В далекие исторические времена человеку приходилось постепенно постигать не только искусство счета, но и измерений.
Измерения — одно из важнейших дел в современной жизни.
Но не всегда было так. Когда первобытный человек убивал медведя в неравном
поединке, он, конечно, радовался, если тот оказывался достаточно большим. Это
обещало сытую жизнь ему и всему племени на долгое время. Но он не тащил тушу
медведя на весы: в то время никаких весов не было. Не было особой нужды в
измерениях, когда этот человек делал каменный топор: технических условий на
такие топоры не существовало и все определялось размером подходящего камня,
который удавалось найти.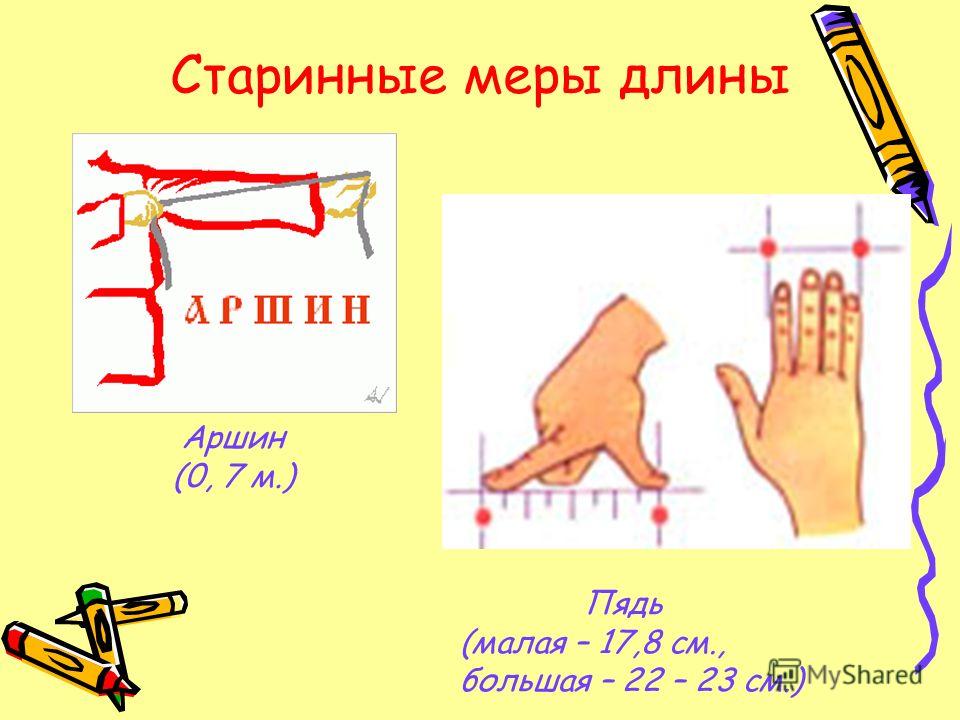 Все делалось на глаз, так, как подсказывало чутье
мастера.
Все делалось на глаз, так, как подсказывало чутье
мастера.
Когда наш предок — древний, но уже мыслящий попытался найти для себя пещеру, он вынужден был соразмерить длину, ширину и высоту своего будущего убежища с собственным ростом. А ведь это и есть измерение. Изготовляя простейшие орудия труда, строя жилища, добывая пищу, возникает необходимость измерять расстояния, а затем площади, емкости, массу, время. Наш предок располагал только собственным ростом, длиной рук и ног. Если при счете человек пользовался пальцами рук и ног, то при измерении расстояний использовались руки и ноги.
Позднее люди стали жить большими группами. Начался обмен
товарами, перешедший потом в торговлю, возникли первые государства. Тогда
появилась нужда в измерениях. Царские писцы должны были знать, какова площадь
поля у каждого крестьянина. Этим определялось, сколько зерна он должен отдать
царю. Надо было измерить урожай с каждого поля, а при продаже льняного масла,
вина и других жидкостей — объем проданного товара. Когда начали строить корабли,
нужно было заранее наметить правильные размеры: иначе корабль затонул бы. И уж,
конечно, не могли обойтись без измерений древние строители пирамид, дворцов и
храмов, до сих пор поражающих нас своей соразмерностью и красотой.
Когда начали строить корабли,
нужно было заранее наметить правильные размеры: иначе корабль затонул бы. И уж,
конечно, не могли обойтись без измерений древние строители пирамид, дворцов и
храмов, до сих пор поражающих нас своей соразмерностью и красотой.
Глава1.
Единицы измерения Древней Руси
Меры длины в Древней Руси измерялись с помощью частей тела человека. Выражение «семь пядей во лбу» используют в разговоре об очень умном человеке. А сколько это в сантиметрах? У наших предков слово «пядь» означало кисть руки. Пядь — это расстояние между вытянутым указательным и большим пальцем, примерно 19 см. Становиться понятным, что «семь пядей во лбу» — это преувеличение.
В Древней Руси о богатырях говорили: «У него косая сажень в плечах».
Косая
сажень — это
расстояние от кончиков пальцев одной руки вытянутой вверх до кончиков пальцев
другой ноги. Была и простая сажень (маховая сажень) — это расстояние между
разведенными в стороны руками.
Для измерения ткани чаще всего использовали длину «локоть» — это расстояние от вытянутого среднего пальца до локтевого сустава.
Все эти меры являются субъективными, так как у каждого человека они свои и зависят от роста. Поэтому, например, купцы, торговавшие тканями, хитрили и нанимали невысоких продавцов: их локти были короче, а значит, ткани отрезалось меньше.
Верста
была самой крупной единицей длины. Она складывалась из саженей. Учитывая, что
сажень у каждого была своя, то в версте было от 500 до 750 саженей . По мнению
многих исследователей, это слово происходит от глагола «верстать»,
означающего «распределять», «уравнивать», «уравнивать
путем сравнения».
Аршин. Это новая, заимствованная с Востока, упоминается в литературных источниках с середины XVI в. Происхождение наименования точно не установлено. Обычно его производят от наименования турецкой меры длины «аршин» (27,9 дюйма = 70,9 см), или от персидского «арши» —длины; на аршин обычно наносили деления в вершках.
С длиной пальца связана и другая старая русская мера длины – вершок, Наименование происходит от слова «верх» («верх перста», т.е. пальца). Вершок упоминается в «Торговой книге» как 1/16 аршина.
Когда-то так называли верхнюю часть чего-либо. Говоря о вершке как о единице длины, имели в виду верх перста. Первоначально вершок определялся длиной двух фаланг указательного пальца, а это приблизительно 4см 5 мм. Повсеместно употреблялись доли вершка: половина, четверть и т.д. Кроме того, в ряде областей в быту использовалась мера длины корх (кулак), равная двум вершкам (ширине сжатой в кулак ладони).
Третьей единицей длины, родственной персту и вершку, так как
также ведет происхождение от пальца, стал дюйм. Такое название
закрепилось за меркой, первоначально равной длине фаланги большого пальца,
примерно 2 см 5 мм. Слово «дюйм» голландского происхождения и появилось в
русском языке благодаря Петру I. Сама же единица длины была заимствована
им у англичан и вскоре вошла в официальное употребление наравне с вершком.
Такое название
закрепилось за меркой, первоначально равной длине фаланги большого пальца,
примерно 2 см 5 мм. Слово «дюйм» голландского происхождения и появилось в
русском языке благодаря Петру I. Сама же единица длины была заимствована
им у англичан и вскоре вошла в официальное употребление наравне с вершком.
В наше время в дюймах измеряют самые разные величины: толщину досок и плитки, длину гвоздей и болтов, диаметр труб и некоторых деталей, размеры автомобильных шин и дисков и др. Также параметры различных устройств и носителей информации, например, диагональ экрана монитора или диаметр жесткого диска. В долях дюйма выражают также высоту шрифта при компьютерном наборе текста (ее измеряют в пунктах, принимая 1 пункт равным одной семьдесят второй).
Повсеместно употреблялись доли вершка: половина, четверть и т.д. Кроме того, в ряде областей в быту использовалась мера длины корх (кулак), равная двум вершкам (ширине сжатой в кулак ладони)
Перст
указующий. В старину палец руки называли перстом. Так же нарекли и самую маленькую единицу
длины. Русский перст был равен ширине указательного пальца, что составляет
примерно 2 см. Хотя перст и не входил в официальную систему мер, долгое время
он использовался для определения размеров мелких предметов.
В старину палец руки называли перстом. Так же нарекли и самую маленькую единицу
длины. Русский перст был равен ширине указательного пальца, что составляет
примерно 2 см. Хотя перст и не входил в официальную систему мер, долгое время
он использовался для определения размеров мелких предметов.
Слово «перст» ныне считается устаревшим, однако в богатом русском языке сохранилось немало порожденных им слов и выражений: перстень, наперсток, перчатки, перст судьбы, один как перст.
Все эти меры длины была крайне неудобны и со временем люди перешли
на метрическую систему. Ведь длина сантиметра никак не зависит от роста
человека. Для измерения больших расстояний в древности была введена мера,
называемая поприще, а затем взамен ее появляется верста. Название это
происходит от слова вертеть, которое в начале означало поворот плуга, а потом
ряд, расстояние от одного до другого поворота плуга при пахоте. Длина версты в
разное время была различной – от 500 до 750 саженей. Да и верст-то было не
одна, а две: путевая – ею измеряли расстояние пути и межевая – ею мерили
земельные участки.
Из вышеизложенного видно, что соотношения между единицами мер были самые разнообразные. У всех народов складывалась сложная и запутанная система мер. Каждое, даже самое маленькое государство, каждый хоть немного самостоятельный народ, каждый город стремились измерять своими мерами. Это вносило большую неразбериху при учете ценностей и особенно в торговле.
Глава 2.
Пословицы старинных русских мер длины. Таким образом, современное общество не только по-прежнему встречаемся со старыми мерами длины в обыденной жизни, но и продолжает использовать их: на словах – в непринужденной беседе или по прямому назначению.
Изучая литературу, мы сделали выборку пословиц старинных русских мер длины.
1. Сам пядь, а борода с локоть.
2. Каждый купец на свой аршин меряет — каждый судит о любом деле односторонне, исходя из собственных интересов.
3.
Сидит, ходит, словно аршин проглотил — о неестественно прямом
человеке.
4. На аршин борода, да ума на пядь.
5. На три аршина в землю видит — о внимательном, прозорливом человеке, от которого ничего невозможно утаить.
6.Умом Россию не понять,
Аршином общим не измерить,
У ней особенная стать —
В Россию можно только верить.
7.Москва верстой далека, а сердцу рядом.
8.Коломенская верста — шутливое прозвище для высокого человека.
9.Все хорошо в меру.
10.Борода с вершок, а слов с мешок.
11.Каждый купец на свой аршин меряет – каждый судит по своему, односторонне, исходя из собственных интересов.
Глава 3.
Эксперимент.
Как мы выяснили, многие единицы длины, которыми пользовались
наши предки, представляют собой измерения различных частей человеческого тела.
Посмотрев определенную литературу по теме, мы узнали, что каждая мера длины
имеет приблизительное значение. Например, перст – старинное название пальца,
его ширина около 2 см, вершок – около 4 см 4 мм, пядь – около 18 см, локоть –
колеблется от 38 до 46 см. Аршин и шаг – величины длиной в 71 см.
Например, перст – старинное название пальца,
его ширина около 2 см, вершок – около 4 см 4 мм, пядь – около 18 см, локоть –
колеблется от 38 до 46 см. Аршин и шаг – величины длиной в 71 см.
Для уточнения собранных нами данных мы решили повести эксперимент – установить опытным путем длины старинных русских мер. Были измерены с помощью сантиметра 8 учеников нашего класса. Мы измеряли вершок, пядь, локоть, аршин и т.д.. Все результаты измерения собраны в таблицу
Имя | пядь | перст | Маховая сажень | локоть | аршин | вершок | дюйм |
Сергей | 23 | 3 | 181 | 49 | 74 | 6 | 3 |
Олег | 24 | 3 | 186 | 50 | 79 | 6 | 3 |
Захар | 19 | 3 | 176 | 48 | 71 | 6 | 3 |
Егор | 20 | 2 | 182 | 50 | 74 | 6 | 3 |
Семен | 20 | 2 | 164 | 43 | 70 | 6 | 4 |
Вадим | 23 | 2 | 169 | 45 | 70 | 6 | 3 |
Настя | 19 | 2 | 150 | 42 | 65 | 5 | 3 |
Катя | 22 | 3 | 164 | 44 | 70 | 6 | 3 |
|
|
|
|
|
|
|
|
Для обоснования и дальнейшего анализа результаты мы начали
работать над их статистической обработкой.
Мы уже знаем, что существует целая наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе – это статистика. Простейшими статистическими характеристиками являются:
- среднее арифметическое – частное от деления суммы чисел на их количество;
- мода – наиболее часто повторяющееся значение в ряду чисел;
- размах – разница между наименьшим и наибольшем значением в ряду чисел.
Простейшие статистические характеристики | Пядь | Перст | Маховая сажень | Локоть | Аршин | Вершок | Дюйм |
Среднее арифметическое |
21,25 |
2,5 |
150,25 |
46,125 |
71,625 |
5,876 |
3,125 |
Размах | 24-19=5 | 3-2=1 | 186-150=36 | 50-42=8 | 79-65=14 | 6-5=1 | 4-3=1 |
Мода | 23 | 3 и 2 | 184 | 50 | 70 | 6 | 3 |
Задача №1.
Перевести маховую сажень Кати 164 см в аршинах и вершках.
Решение:
У Кати аршин = 70см а вершок -6 см. Мы получим ,что 164 см = 2 аршинам и вершкам ( 65*2 + 6*6 )
Задача №2.
Перевести маховую сажень Олега -186 см в локтях и в вершках.
У Олега локоть = 50 см, а вершок = 6 см. Мы получим, что 186 см = 3 локтям и 6 вершкам. ( 50*3 + 6*6 )
Заключение
Была проделана большая, интересная работа. В ходе работы познакомилась с различными старинными единицами измерений.
Каждое, даже самое маленькое государство, каждый хоть немного самостоятельный народ, каждый город стремились измерять своими мерами. Это вносило большую неразбериху при учете ценностей и особенно в торговле.
Опираясь на слова великого русского ученого Дмитрия Ивановича
Менделеева, который сказал, что «Наука начинается с тех пор, как начинают
измерять. Точная наука немыслима без меры» можно смело сказать, что
пользоваться данными мерами длины было весьма и весьма неудобно, т.к. они были
неточны в измерениях и сугубо личными для каждого из нас, даже, несмотря на то,
что эти измерения «были всегда при человеке».
Точная наука немыслима без меры» можно смело сказать, что
пользоваться данными мерами длины было весьма и весьма неудобно, т.к. они были
неточны в измерениях и сугубо личными для каждого из нас, даже, несмотря на то,
что эти измерения «были всегда при человеке».
С развитием торговых отношений между иностранными государствами потребовалось создание эталонов. В разные века предпринимались попытки ввести эталоны. За это время система мер претерпела множество изменений.
В 1960 собралась Генеральная конференция по мерам и весам, на которую прибыли представители 32 стран. Была принята Международная система единиц. С1963 года ею пользуются во всех областях науки, техники и народного хозяйства.
Наша работа актуальна и интересна потому, что заставляет нас не только обратиться к истории языка и освоить простейшие навыки экспериментальной работы, но и использовать полученные знания при изучении не только математики, но и таких предметов как, русский язык, литература, история.
Список литературы
1. Клименченко
Д Величины и их измерения. 1994
Клименченко
Д Величины и их измерения. 1994
2. Шабалин С. А. Измерения для всех. 1990
3. Ермаков Н.Я. Пословицы русского народа. – СПб, 1984.
4. Романова Г.Я. Наименование мер длины в русском языке. – М., 1975
5. Больная Советская Энциклопедия. Электронная версия.
6. Глейзер Г.И. История математики в школе. 1991
7. Интернет ресурсы:
- http://rus-ved-rus.narod.ru/mery.html (Ведическая Русь статья «Старинные русские меры длины, веса, объёма»)
- http://akopyan.ru/s_miru_po_nitke/starinnie_russkie_meri_dlini.html (С миру по нитке. Русская жизнь. Познавательный дневник.)
- http://art.ioso.ru/seminar/2009/projects11/rezim/stat4.html (Статистика, статистические характеристики)
Учебный проект Старинные меры длины | Проект по математике (3 класс):
Старинные меры длины
МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ОБЩЕОБРАЗОВАТЕЛЬНАЯ СРЕДНЯЯ (ПОЛНАЯ) ШКОЛА
С. КАЗЫМ БЕЛОЯРСКОГО РАЙОНА, ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА-ЮГРЫ
КАЗЫМ БЕЛОЯРСКОГО РАЙОНА, ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА-ЮГРЫ
Проект в номинации «Первые шаги»
Тема проекта
«Старинные меры длины»
Автор проекта:
Рандымов Дмитрий Васильевич
3 «А» класс
Руководитель проекта:
Григорьева Любовь Ивановна
МОСШ с. Казым
Учитель начальных классов
с. Казым, 2014 г.
Содержание
Содержание…………………………………………………………………………………… 3
Введение ……………………………………………………………………………………… 4
- Этапы работы……………………………………………………………………… 5
- Результаты работы с литературой и ресурсами ИНТЕРНЕТа ……………… 7
2.1. Из истории возникновения старинных мер длины ………………………………7
2.2. Старинные русские меры длины в литературных произведениях …………… 8
Заключение…………………………………………………………………………………… 10
Ресурсы……………………………………………………………………………………………11
Тезисы…………………………………………………………………………………………. .12
.12
Введение
«Семь раз отмерь, один раз отрежь», — учит нас народная русская пословица. Это означает, что, прежде чем начать какое-либо дело, следует к нему хорошо подготовиться, то есть несколько раз все проверить.
А как родилась эта пословица? Человек какой професии мог её сочинить? Может портной? Вполне возможно, ведь ему важно правильно раскроить ткань, чтобы сшить одежду нужного размера. А может это плотник или столяр? В их работе точность не менее важна.
Впрочем, человек, придумавший эту пословицу, мог быть кем угодно: и кузнецом, и сапожником, и стекольщиком. Потому что люди всех профессий во все времена и во всём мире точности измерений большое значение.
Нам уже хорошо известны слова «метр», «сантиметр», «миллиметр». Всё это привычные для нас меры длины. Но в литературных произведениях часто встречаются непонятные слова, связанные с единицами длины. Чтоба понимать, о чём идёт речь в произведениях, нужно знать значения этих единиц измерения. На уроках математики мы познакомились с некоторыми старинными мерами длины.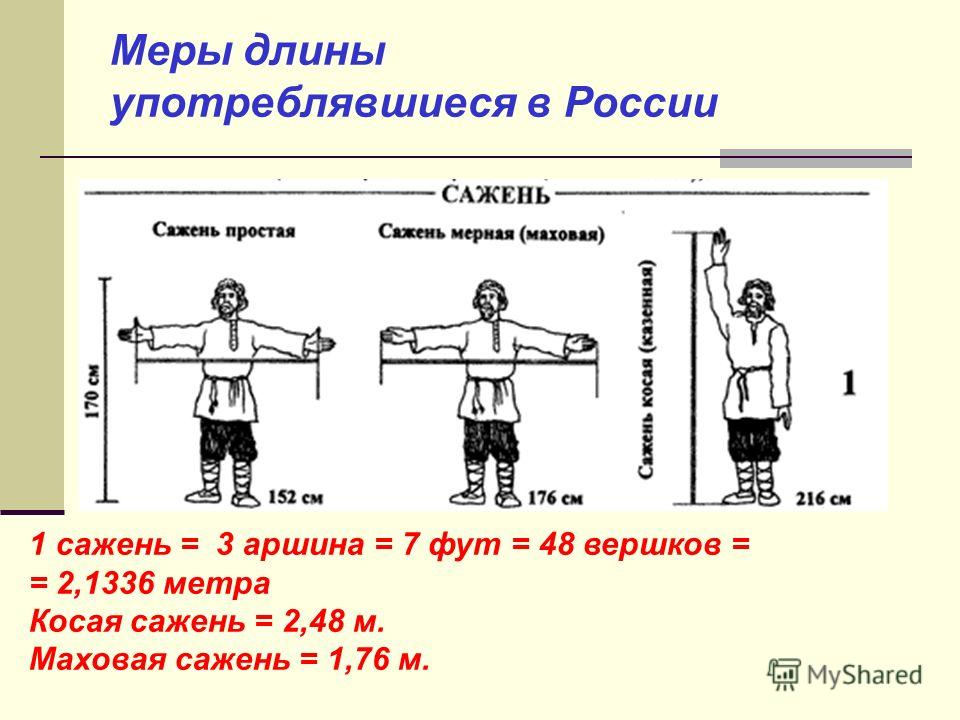 Я решил узнать о них побольше.
Я решил узнать о них побольше.
Цель моего проекта – познакомиться со старинными мерами длины.
Задачи:
- Узнать историю возникновения старинных единиц измерения длины;
- Подобрать литературные произведения, пословицы и поговорки, в которых встречаются старинные единицы измерения длины;
- Описать собранный материал и сделать заключение.
Методы: изучение литературы, описание, обобщение.
Основополагающий вопрос: « Как возникли единицы измерения длины?»
Проблемные вопросы:
1. Как в старину измеряли длину?
2. Используют ли сейчас старинные меры длины?
3. Почему сейчас во всём мире используются одни и теже единицы измерения
длины?
При сборе информации мы воспользовались справочниками, энциклопедиями и учебными пособиями. Из них мы почерпнули информацию об истории развития единиц измерения длины, подобрали пословицы, поговорки, нашли картинки и фотографии.
1. Этапы работы
1.Изучение литературы.
2.Поиск ответа на проблемные вопросы.
3.Составление описания, формулирование вывода — «Как в старину люди измеряли длину?
5.Составление доклада и буклета, подготовка презентации.
6.Защита проекта.
- Результаты работы с литературой и ресурсами ИНТЕРНЕТа
- Из истории возникновения старинных мер длины.
В библиотеке мы нашли много книг, журналов и пособий о старинных мерах длины. В энциклопедиях и справочниках нашли информацию об истории развития единиц измерения, подобрали половицы и поговорки.
Стоит нам только оглянуться по сторонам, и мы сразу увидим, как много людей постоянно что-то измеряют. На стройках, на заводах, в полях, во время спортивных соревнований, у себя дома. Делают это с помощью различных измерительных инструментоав: рулеткой, линейкой, сантиметровой лентой. А как поступали наши далёкие предки?
С древности, мерой длины и веса всегда был сам человек. Во все времена у всех народов собственное тело, свои руки и ноги служили людям «измерительными интрументами». Система древнерусских мер включает в себя следующие основные меры: версту, сажень, аршин, локоть, пядь и вершок.
Во все времена у всех народов собственное тело, свои руки и ноги служили людям «измерительными интрументами». Система древнерусских мер включает в себя следующие основные меры: версту, сажень, аршин, локоть, пядь и вершок.
Аршин – старинная русская мера длины, около 71 сантиметра – длина вытянутой руки взрослого человека. Очень часто в старину аршин использовали купцы, когда итмеряли ткань.
Для мелких мер длины использовалась другая древняя русская мера – пядь.
Это расстояние между растянутых в стороны большого пальца и мизинца.
Существовала «малая пядь» — расстояние от кончиков большого и указа-
тельного пальцев, чуть меньше 18 см. «Большая пядь» — это
расстояние от конца вытянутого мизинца до конца большого пальца,
примерно 22 – 23 см.
Другая русская мера длины, связанная с пальцами, называлась «вершок». Она равнялась длине двух суставов указательного пальца, или ширине двух соседних пальцев – тоже указательного и сренднего, примерно 4см и 5 мм.
Сажень – одна из наиболее распространенных на Руси мер длины. Онии различались по назначению и по длине, и существовало их более десяти.
«Малая сажень» — расстояние от поднятой на уровень плеча руки до пола, примерно 1 м 42 см.
Маховая сажень» — это расстояние между концами пальцев широко расставленных рук взрослового мужчины, приблизительно 1 м 77 см.
«Косая сажень» — самая длинная. Это расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки, примерно 2 м 48 см.
К тому же имелись великая сажень, городовая, греческая, казённая, кладочная, морская, народная, трубная, царская, церковная. Они были разной длины – от 1м 59 см до 2 м 86 см.
Известно, что существовала сажень аршинная, береговая, большая, государева, дворовая, землемерная и другие.
Локоть – исконно древнерусская мера длины, известная уже в 11 веке. Локоть равнялся длине руки от пальцев до локтя. Величина этой меры длины, по разным источникам, составляла от 38 до 47 см. Локоть в старину использовали в торговле, как особенно удобную меру. Им отмеряли сукно, полотно, шерстяные ткани, холст.
Величина этой меры длины, по разным источникам, составляла от 38 до 47 см. Локоть в старину использовали в торговле, как особенно удобную меру. Им отмеряли сукно, полотно, шерстяные ткани, холст.
Самые большие расстояния, например, между городами и сёлами, на Руси измеряли «вёрстами». Верста от слова вертеть. Первоначально это было расстояние от одного поворота плуга до другого во время пахоты. Длина версты равнялась 1060 см.
Фут и дюйм, которыми пользовались в Древней Руси, были заимствованы из Англии. Дюйм означает «большой палец». Равняется дюйм примерно двум с половиной сантиметрам. «Фут» по-английски означает «нога». Равнялась эта мера примерно 30 см 5 см.
Повсюду применялись самые разнообразные меры длины. Использование их было очень неудобным, так как значение их часто отличались. Постепенно старинные меры длины утратили свою значимость по причине своей неточности и неудобства. Они были заменены на единицы измерения, принятые во всё мире.
Выводы
После изучения литературы я узнал:
- В древности для измерения длины человек использовал собственное тело: длину пальцев, рук, ног.

- Первыми русскими мерами длины были: аршин, локоть, вершок, сашень, пядь.
- Использование таких мер длины было очень недобным, так как значение их часто отличались.
- Старинные русские меры длины в литературных произведениях.
Стариые меры длины практически сейчас не применяются, но их нередко можно встретить в рассказах, повестях, книгах по истории, в пословицах и поговрках. Часто мы их встречаем в учебниках литературного чтения.
- А еще рожу конька
Ростом только в три вершка,
На спине с двумя горбами,
Да с аршинными ушами.
«Конек – горбунок»
- Братья сеяли пшеницу,
Да возили в град-столицу.
Знать столица та была
Вёрст 15 от села. «Жар – птица»
3. «Она была маленькая – маленькая, всего с дюйм ростом»
«Она была маленькая – маленькая, всего с дюйм ростом»
Х.К. Андерсен «Дюймовочка»
4. Вырос богатыр большим,
Здоровенным даже.
Голова его с аршин,
В плечах косая сажень «Илья Муромец»
5 «Алиса встала и подошла к зеркалу, чтобы узнать, какого она теперь росту. Судя
по всему в ней было около двух футов»
«Алиса в Зазеркалье» Астрид Лингрен
- Что — то слышится родное
В долгих песнях ямщика:
То разгулье удалое,
То сердечная тоска…
Ни огня, ни чёрной хаты,
Глушь и снег… Навстречу мне
Только вёрсты полосаты
Попадаются одне ….
А.С. Пушкин «Зимняя дорога»
2.3. Старинные меры длины в пословицах и поговорках.
Старинные единицы длины часто встречаются в пословицах и поговорках.
Пословицы и поговорки | Значение. |
От горшка два вершка, а уже указчик. | Молодой человек, не имеющий жизненного опыта, но поучающий всех. |
Не уступить не пяди. | не отдать даже самой малости. |
Семь пядей во лбу. | Об очень умном человеке. |
Косая сажень в плечах. | Человек, высокого роста, широкоплечий. |
На три аршина в землю видит. | Человек очень внимательный, прозорливый, от которого ничего невозможно утаить. |
Коломенская верста | Шутливое прозвище для высокого человека. |
На аршин борода, да ума на пядь. | О взрослом, но глупом человеке. |
Ходит, словно аршин проглотил. | О неестественно прямом человеке. |
Москва верстой далеко, а сердцу рядом. | Так русские люди характеризовали своё отношение к столице. |
Каждый купец на свой аршин меряет. | Каждый судит о любом деле односторонне, исходя из собственных интересов. |
Любовь не вёрстами меряется. | Расстояние не может быть препятсвием для любви. |
Слышно за версту. | Разговаривать очень громко. |
Выводы
- Старинные меры длины практически сейчас не применяются, но их нередко можно встретить в литературных произведениях.
- Во многих русских пословицах и поговорках используются старинные меры длины.
Заключение
Работу над проектом мы выполняли вместе с мамой. Мы искали информацию в разных книгах, журналах, справочниках и энциклопедиях. В ИНТЕРНЕТе мы нашли фотографии и картинки, где показано, как в древности измеряли длину.
С давних времен людям всегда приходилось что-то измерять, чтобы построить избу, спахать землю, сшить одежду. Сейчас это делают с помощью различных измерительных интсрументов. Много лет назад для измерения длины человек использовал собственное тело: длину пальцев, ладони, руки, размах рук. Исконно русскими старинными мерами длины были: верста, сажень, аршин, локоть, пядь и вершок. Много лет именно эти мерки использовал человек.
Много лет именно эти мерки использовал человек.
Постепенно старинные меры утратили свою значимость по причине своей неточности и неудобства. Они были заменены на единицы измерения, принятые во всём мире.
В литературных произведениях часто можно встретить старые русские меры длины. Существует много пословиц, поговорок и фразеологизмов, в которых используются эти единицы измерения.
Работая над проектом, я узнал, как в старину измеряли расстояние. Сейчас, когда я встречаю в сказках, стихах устаревшие меры длины, то могу представить, о каком расстоянии говорится.
Ресурсы
- Багрова Л.А. Я познаю мир. Детская энциклопедия. Меры длины. – М.: АСТ, 2000.
- Кац Э.Э. Литературное чтение: 3 класс: учебник: в 3ч. Ч.2. – М.: АСТ: Астрель,
2012.
- Пегов М. Семь раз отмерь! – М. издательский дом «Фома», 2013.
4. Режим доступа: http: // slovari. Yandex.ru
Yandex.ru
- Режим доступа: http: www. Photodom/ com
Тезисы
Номинация «Первые шаги». Тема проекта: «Старинные меры длины».
Автор: Рандымов Дмитрий. Руководитель: Григорьева Л.И.
Стоит нам только посмотреть по сторонам, и мы увидим, как много людей что-то измеряют. На стройках, на заводах, в полях, во время спортивных соревнований, у себя дома. Делают это с помощью различных измерительных инструментов: линейки, рулетки, сантиметровой ленты. А как измеряли в глубокой древности, когда еще не существовали эти приспособления?
Цель моего проекта – познакомиться со старинными мерами длины.
Задачи:
- Узнать историю возникновения старинных единиц измерения длины;
- Подобрать литературные произведения, пословицы и поговорки, в которых встречаются старинные меры длины;
- Описать собранный материал и сделать заключение.
Главный вопрос: «Как возникли единицы измерения длины?»
Проблемные вопросы
1. Как в старину измеряли длину?
Как в старину измеряли длину?
2. Используют ли сейчас старинные меры длины?
3. Почему сейчас во всём мире используются одни и теже единицы из-
мерения длины?
Этапы работы
1.Изучение литературы.
2.Поиск ответа на проблемные вопросы.
3.Составление описания, формулирование вывода — «Как в старину люди измеряли длину?
Над проектом мы работали вместе с мамой. Из книг, журналов и других источников мы узнали об истори мер длины. В далёком прошлом, когда не было приборов для измерения, собственное тело, свои руки и ноги служили людям «измерительными инструментами».
Старинными русскими мерами длины являются: верста, сажень, аршин, локоть, пядь, вершок.
Аршин – старинная русская мера длины, около 71 сантиметра – длина вытянутой руки взрослого человека. Очень часто аршин использовали купцы, когда итмеряли ткань.
Для мелких мер длины использовалась другая мера – пядь. Это расстояние между растянутых в стороны большого пальца и мизинца. Существовала «малая пядь» — расстояние от кончиков большого и указательного пальцев, чуть меньше 18 см. «Большая пядь» — это расстояние от конца вытянутого мизинца до конца большого пальца, примерно 22 – 23 см.
Существовала «малая пядь» — расстояние от кончиков большого и указательного пальцев, чуть меньше 18 см. «Большая пядь» — это расстояние от конца вытянутого мизинца до конца большого пальца, примерно 22 – 23 см.
Ещё одна мера длины, связанная с пальцами, называлась «вершок». Она равнялась длине двух суставов указательного пальца, примерно 4см и 5 мм.
Сажень – самая распространенная на Руси мера длины.
«Малая сажень» — расстояние от поднятой на уровень плеча руки до пола, примерно 1 м 42 см.
«Маховая сажень» — это расстояние между концами пальцев широко расставленных рук взрослово мужчины, приблизительно 1 м 77 см.
«Косая сажень» — самая длинная. Это расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки, примерно 2 м 48 см.
Локоть – исконно древнерусская мера длины. Локоть использовали в торговле, как особенно удобную меру. Им отмеряли сукно, полотно, шерстяные ткани.
Самые большие расстояния измеряли «вёрстами». Верста от слова вертеть. Сначала это было расстояние от одного поворота плуга до другого во время пахоты. Длина версты равнялась 1060 см.
Верста от слова вертеть. Сначала это было расстояние от одного поворота плуга до другого во время пахоты. Длина версты равнялась 1060 см.
Фут и дюйм были заимствованы из Англии. Дюйм означает «большой палец». Равняется дюйм примерно двум с половиной сантиметрам. «Фут» по-английски означает «нога». Равнялась эта мера примерно 30 см 5 мм.
Старые меры длины сейчас почти не применяются, но их нередко можно встретить в рассказах, повестях, книгах по истории, в пословицах и поговрках. Часто мы их встречаем в учебниках литературного чтения.
Отгадайте, из какого произведения эти строки?
1. Да игрушечку-конька
Ростом только в три вершка,
На спине с двумя горбами
Да с аршинными ушами. Пётр Ершов «Конек – горбунок»
2. Братья сеяли пшеницу,
Да возили в град-столицу.
Знать столица та была
Вёрст пятнадцать от села. «Жар – птица»
- Она была маленькая-маленькая, всего дюйм ростом.

«Дюймовочка»
- Что – то слышится родное
В долгих песнях ямщика:
То разгулье удалое,
То сердечна тоска…
Ни огня, ни чёрной хаты,
Глушь и снег… Навстречу мне
Только вёрсты полосаты
Попадаются одне… А.С. Пушкин «Зимняя дорога»
Старинные единицы длины часто встречаются в пословицах и поговорках.
На уроках математики мы решали задачи со старинными мерами длины.
Решите задачу.
«Отдал царевич приказание, и вскоре явились во дворей 12 добрах молодцев, все на одно лицо и ростом в косую сажень. Какого роста были добры молодцы?»
«Алиса встала и подошла к столу, чтобы выяснить, какого она теперь стала роста. Судя по всему в ней было окло двух футов. Какого роста стала Алиса?»
Заключение
Я узнал, что для измерения длины в старину человек использовал собственное тело: длину пальцев, ладони, руки, размах рук, ноги. Исконно русскими мерами длины были: верста, сажень, аршин, локоть, пядь и вершок. Эти мерки сейчас почти не применяются, они утратили свою значимость потому что неудобны и неточны. Но их нередко можно встретить в рассказах, сказках, книгах по истории, в пословицах и поговорках.
Исконно русскими мерами длины были: верста, сажень, аршин, локоть, пядь и вершок. Эти мерки сейчас почти не применяются, они утратили свою значимость потому что неудобны и неточны. Но их нередко можно встретить в рассказах, сказках, книгах по истории, в пословицах и поговорках.
Спасибо за внимание!
Старинные меры длины — презентация, доклад, проект
Вы можете изучить и скачать доклад-презентацию на тему Старинные меры длины. Презентация на заданную тему содержит 20 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Презентации» Математика» Старинные меры длины
Слайды и текст этой презентации
Слайд 1
Описание слайда:
СТАРИННЫЕ МЕРЫ ДЛИНЫ Выполнила студентка группы НАЛ 15-03 Богданова Светлана
Слайд 2
Описание слайда:
В наше время мы, не задумываясь, производим вычисления в метрах, граммах, литрах и т. д. Это ведь удобно, единая система СИ устраивает почти всех. Но, естественно, так было не всегда. И вот, начиная с древнейших времен язычества, вплоть до 19 века, наши предки пользовались другими мерами и единицами. Нередко мы слышим слова: сажень, верста ,вершок – но, сколько это в переводе, не знаем.
д. Это ведь удобно, единая система СИ устраивает почти всех. Но, естественно, так было не всегда. И вот, начиная с древнейших времен язычества, вплоть до 19 века, наши предки пользовались другими мерами и единицами. Нередко мы слышим слова: сажень, верста ,вершок – но, сколько это в переводе, не знаем.
Слайд 3
Описание слайда:
МЕРЫ ДЛИНЫ
Слайд 4
Описание слайда:
ВЕРСТА
Предположительно слово «верста» произошло от древнерусского «верстать». Звук «в» стерся в разговорной речи.
— Путевая верста = 500 саженей = 1500 аршин = 1066,8м.
— Коломенская верста = 700 саженей. Старая верста.
— Мерная верста = 1000 саженей (1629г.).
С 1649г. 1 верста =1000 саженей
Одновременно существовала верста в 500 саженей «царских». Аналог версты – «поприще» (др.рус.) – чуть более километра.
Поприще = 700 саженей с половиною (XV в.)
или
Поприще = 1000 саженей (1629 г.)
Аналог версты – «поприще» (др.рус.) – чуть более километра.
Поприще = 700 саженей с половиною (XV в.)
или
Поприще = 1000 саженей (1629 г.)
Слайд 5
Описание слайда:
САЖЕНЬ Сажень — встречается с XI в. происходит от слова «сягать» т.е. доставать до чего- либо. Отсюда слово «недосягаемый» — о месте, куда невозможно добраться, о человеке, достоинства которого невозможно повторить. Различали два вида сажени: маховая и косая.
Слайд 6
Описание слайда:
ВИДЫ САЖЕНЕЙ
Маховая сажень
Перехват – расстояние между указательными пальцами разведенных рук = 2,13 – 2,36 см.
Косая сажень
Предположительно расстояние от пальцев вытянутой вверх руки до пальцев отставленной слегка в сторону противоположной ноги. Сажень русская = 3 аршина = 48 вершка.
«Печатная сажень» – точная мера длины с печатью, удостоверяющей ее точность. (Неложное мерило).
Сажень русская = 3 аршина = 48 вершка.
«Печатная сажень» – точная мера длины с печатью, удостоверяющей ее точность. (Неложное мерило).
Слайд 7
Описание слайда:
САЖЕНИ:
Слайд 8
Описание слайда:
АРШИН Аршин — одна из главных русских мер длины, использовалась с XVI в. Происхождение названия : 1.От персидского слова «арш» — локоть. Это длина всей вытянутой руки от плечевого сустава до концевой фаланги среднего пальца. 1 аршин = 71,12 см. 2.От корня «ар» – земля , поверхность земли .
Слайд 9
Описание слайда:
АРШИН
В разных губерниях России были свои единицы измерения длины, поэтому купцы, продавая свой товар, как правило, мерили его своим аршином, обманывая при этом покупателей. Чтобы исключить путаницу, был введен казенный аршин, т.е. эталон аршина, представляющий собой деревянную линейку, на концах которой клепались металлические наконечники с государственным клеймом.
Чтобы исключить путаницу, был введен казенный аршин, т.е. эталон аршина, представляющий собой деревянную линейку, на концах которой клепались металлические наконечники с государственным клеймом.
Слайд 10
Описание слайда:
АРШИН В ПОСЛОВИЦАХ И ПОГОВОРКАХ Писать «аршинными буквами»-писать крупно «Аршин-на кафтан , а два – на заплаты» – починка вещи , дороже самой вещи . Ходит «словно аршин проглотил» – ходит , не сгибаясь «На свой аршин мерить» — судить о чем-то , односторонне ,со своей точки зрения .
Слайд 11
Описание слайда:
ШАГ
Одна из древнейших мер длины.
Использовали шаг для определения расстояния между городами .
В России в шагах определяли длину сторон земельных участков.
Шаг = 71 см .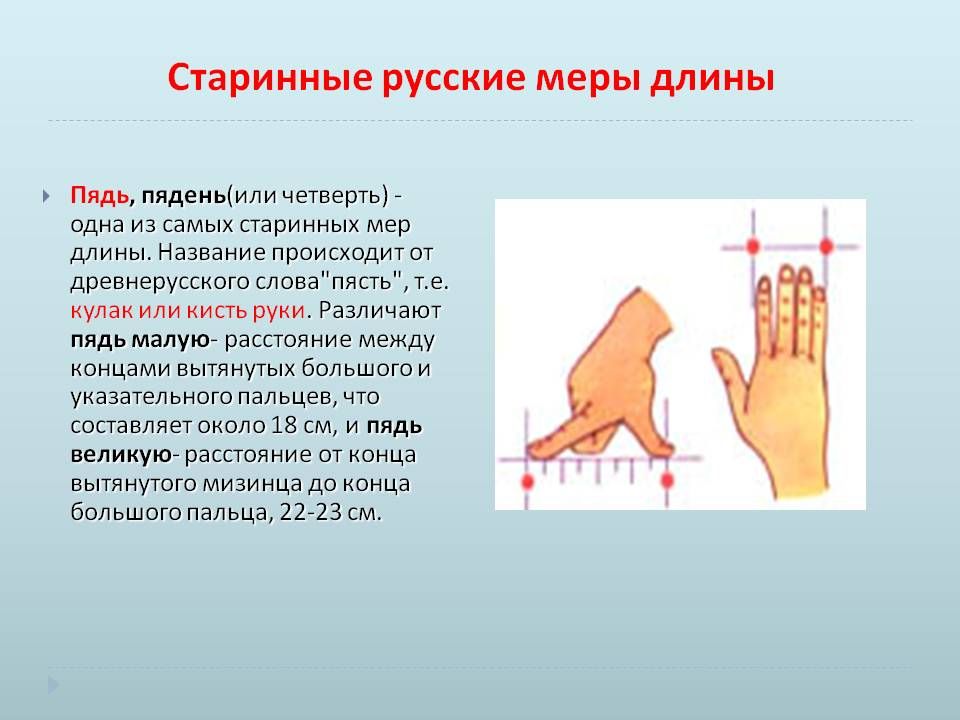 А позднее измеряли расстояние между противниками на дуэлях .
(10 -15 шагов)
А позднее измеряли расстояние между противниками на дуэлях .
(10 -15 шагов)
Слайд 12
Описание слайда:
ЛОКОТЬ Локоть — древнейшая мера длины, которой пользовались многие народы мира. Это расстояние от конца вытянутого среднего пальца руки или сжатого кулака до локтевого сгиба. Его длина колебалась от 38 см до 46 см или 11 – 16 вершков. Как мера длины на Руси встречается с XVI в. Говорят: «Близок локоть да не укусишь», «Сам с ноготок ,а борода-с локоток».
Слайд 13
Описание слайда:
ПЯДЬ Пядь, пядень(или четверть) — одна из самых старинных мер длины. Название происходит от древнерусского слова»пясть», т.е. кулак или кисть руки. Различают пядь: малую — расстояние между концами вытянутых большого и указательного пальцев, что составляет около 18 см великую — расстояние от конца вытянутого мизинца до конца большого пальца, 22-23 см
Слайд 14
Описание слайда:
ВЕРШОК
Вершок — старинная русская мера длины, равная ширине двух пальцев (указательного и среднего) или основной фаланги указательного пальца. старая русская мера длины, употреблявшаяся до введения метрической системы мер.
1 Вершок = 1/16 аршина = 1, 75 дюйма =44, 45 мм = 4, 44 см.
Встречается в пословицах: «Два вершка от горшка, а уже указчик».
старая русская мера длины, употреблявшаяся до введения метрической системы мер.
1 Вершок = 1/16 аршина = 1, 75 дюйма =44, 45 мм = 4, 44 см.
Встречается в пословицах: «Два вершка от горшка, а уже указчик».
Слайд 15
Описание слайда:
Всем известна пословица: «Два вершка от горшка, а уже указчик». А сколько это -2 вершка? 2 вершка = 8,9 см Людей такого роста не бывает . Раньше при определении роста человека или животного счёт велся после двух аршин (обязательных для нормального взрослого человека), т.е. после 142,24 см . Значит от горшка 2 вершка – это 142,24+8,9=151,14 см .
Слайд 16
Описание слайда:
КАК ИЗМЕРЯЛИ РОСТ ЧЕЛОВЕКА НА РУСИ Для человека использовали два способа полного выражения роста: 1 — сочетание «роста *** локтей, *** пядей» 2 — сочетание «рост *** аршина, *** вершков» с 18 века — » *** фута, *** дюйма» Для домашних мелких животных использовали — «рост *** вершков» Для деревьев — «высота *** аршин»
Слайд 17
Описание слайда:
ЛИНИЯ
Линия – ширина пшеничного зерна. 1 линия = 2,54 мм
Этой единицей обозначают и калибр огнестрельного оружия .
Наибольший диаметр пули выражается в линиях или в миллиметрах . Отсюда название для винтовки калибра 7,62 мм (2,54*3=7,62) – калибр знаменитой трехлинейной винтовки Мосева .
1 линия = 2,54 мм
Этой единицей обозначают и калибр огнестрельного оружия .
Наибольший диаметр пули выражается в линиях или в миллиметрах . Отсюда название для винтовки калибра 7,62 мм (2,54*3=7,62) – калибр знаменитой трехлинейной винтовки Мосева .
Слайд 18
Описание слайда:
СИСТЕМА МЕР, УТВЕРЖДЕННАЯ В XVIII ВЕКЕ УКАЗОМ ПЕТРА I 1 сажень = 7 футов = 84 дюйма 1 аршин=28 дюймов 1 вершок=1/16 аршина=1,75 дюймов
Слайд 19
Описание слайда:
ЮНИТ Новое – хорошо забытое старое . Юнит = 1,75 дюйма 1 юнит = 1 вершок
Слайд 20
Описание слайда:
ВЫВОД
Наиболее точно можно измерить рост в современных единицах измерения: в метрах, сантиметрах и миллиметрах.
Tags Старинные меры длины
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
Творческий проект «Старинные меры длины»
Школьная научно-практическая конференция
«Старинные русские меры длины»
(секция естественно-математического цикла)
Работу выполнила: Вьюнкова Вероника,
ученица 5Г класса
Научный руководитель: Дынька А.Н.,
учитель математики МАОУ СОШ№11
Содержание:
- Введение
- Меры длины в Древней Руси (XI.
 -первая половина XV в.)
-первая половина XV в.) - Меры длины в Московском государстве (XV-XVII вв.)
- Меры длины в России (XVIII-XIX вв)
- Старинные русские меры
- Метрическая система мер
- Результаты опроса по выявлению интереса к старинным русским мерам
- Заключение
- Использованная литература
Введение
«Наука начинается там, где начинают измерять».
Д.И.Менделеев
В далекие исторические времена человеку приходилось постепенно постигать не только искусство счета, но и измерений. Когда наш предок — древний, но уже мыслящий, попытался найти для себя пещеру, он вынужден был соразмерить длину, ширину и высоту своего будущего убежища с собственным ростом. А ведь это и есть измерение. Изготовляя простейшие орудия труда, строя жилища, добывая пищу, возникает необходимость измерять расстояния. Многие единицы длины, которыми пользовались наши предки, представляют собой измерения различных частей человеческого тела. Человек как бы всегда носит их с собой и может пользоваться ими в любых условиях.
Человек как бы всегда носит их с собой и может пользоваться ими в любых условиях.
Мне стало интересно, какие меры длины существовали на Руси, и почему сейчас Россия использует такую меру длины как метр. Поэтому я и выбрала эту тему.
Актуальность: Вопрос о значимости единиц измерения всегда актуален, так как метрология всегда находится в центре внимания человеческой деятельности.
Тема: «Старинные русские меры длины».
Объект исследования: История развития старинных русских мер длины.
Предмет исследования: Старинные русские меры длины.
Цель: проследить историю возникновения меры длины на Руси, их совершенствование от времен образования Руси до наших дней.
Задачи исследования:
1) Познакомиться с измерительной системой, которая существовала ранее.
2) Установить взаимосвязь между старой измерительной системой и новой.
3) Проследить отражение старых мер в русском фольклоре.
4) Выяснить, знают и применяют ли в настоящее время жители п. Чкаловска старинные меры длины.
Чкаловска старинные меры длины.
Меры длины в Древней Руси (XI-первая половина XV в.
Система древнерусских мер длины включала в себя следующие основные меры: версту, сажень, локоть, пядь.
Пядь — одна из самых старинных мер длины: от древнерусского слова пясть — кулак или пять — кисть руки. Она удобна тем, что каждый всегда носит её с собой. Ведь пядь — это расстояние между вытянутыми пальцами руки. Пядь составляла одну четверть аршина. Поэтому второе её название — четверть.
Пядь малая — расстояние между концами вытянутых большого и указательного пальцев руки. Длина малой пяди равна примерно 19 см.
Пядь великая — расстояние от конца вытянутого мизинца до конца большого пальца, её длина 22-23 см.
Локоть — древнейшая мера длины, которой пользовались многие народы мира. Это расстояние от конца вытянутого среднего пальца или сжатого кулака до локтевого сгиба. В розничной торговле холстом, сукном, полотном локоть был основной мерой.
Сажень — встречается в летописи с XI века, составленная киевским монахом Нестером. Сажень — русская мера длины. По документам средневековой Руси существовали сажени: косая, прямая, простая, дворовая и лавочная, маховая, большая, или великая, печатная, «писцовая, чем землю мерить». В XVIII веке меры уточнялись, Пётр I указом установил равенство трёхаршинной сажени семи английским футам: сажень = 3 аршинам = 7 футам (= 2,13 м).
Сажень — русская мера длины. По документам средневековой Руси существовали сажени: косая, прямая, простая, дворовая и лавочная, маховая, большая, или великая, печатная, «писцовая, чем землю мерить». В XVIII веке меры уточнялись, Пётр I указом установил равенство трёхаршинной сажени семи английским футам: сажень = 3 аршинам = 7 футам (= 2,13 м).
Верста — от слова вертеть. Первоначально — расстояние от одного поворота плуга до другого во время пахоты. Длина версты — 1060 м. Верста, как мера длины, на Руси встречается с XI века.
Межевая верста — существовала на Руси до XVIII века для определения расстояния между населёнными пунктами и для межевания. Длина такой версты 1000 саженей, или 2,13 км.
Позднее, при Петре I, была введена верста длиной 500 саженей, именно на таком расстоянии друг от друга ставили вдоль дорог столбы. В начале XIX в. вдоль основных дорог России появились чёрно — белые полосатые столбы. Отсюда название — столбовая дорога. Со второй половине XIX столетия на всех столбах, расставленных вдоль железной дороги от Петербурга до Москвы, расстояния стали обозначать в верстах. Верста длиной в 500 саженей, как мера длины, сохранилась в России до введения метрической системы.
Верста длиной в 500 саженей, как мера длины, сохранилась в России до введения метрической системы.
Меры длины в Московском государстве (XV-XVII вв.)
В XV-XVII вв. появились новые меры длины — аршин, с течением времени вытеснивший локоть, и вершок. Были официально узаконены два значения версты.
Версту в 1000 сажен (2,16 км) употребляли широко в качестве межевой меры, а на окраинах России, особенно в Сибири, — и для измерения расстояний между населенными пунктами. 500-саженную версту применяли несколько реже, в основном для измерения расстояния в Европейской части России.
В эпоху Московского государства сажень, равная 152 см, постепенно исчезает и доминирующую роль играет маховая сажень, приравненная к 2,5 аршинам, т.е. 180 см, и казенная сажень — 3 аршина, т.е. 216 см. Соборным уложением 1649 г. была окончательно легализована 3-аршинная сажень как официальная.
Вершок — старинная русская мера длины, равная ширине двух пальцев руки (указательного и среднего). Длина вершка составляет примерно 4,4 см.
Длина вершка составляет примерно 4,4 см.
Аршин — одна из основных русских мер длины использовалась с XVI в. Пришёл аршин на Русь вместе с купцами из далёких восточных стран.
Купцы привозили невиданные ткани. Тончайшие китайские шелка. Сделанную из настоящих золотых и серебреных нитей тяжёлую индийскую парчу. Бархат и тафту, затканную цветами и драконами, — из Персии. Купцы привозили ткани, и их приходилось отмерять. Восточные купцы обходились без всяких метров: ткань они натягивали на собственную руку, до плеча. Это и называлось мерить аршинами. Название аршин происходит от персидского слова «арш» — локоть. Это длина всей вытянутой руки от плечевого сустава до конца фаланги среднего пальца. В аршине 71 см.
Мера была очень удобной — руки всегда при себе, — но был у неё существенный недостаток: руки, к сожалению, у всех разные. У одних они длинные, у других — короче. Хитрые купцы стали искать приказчиков с руками покороче. Но однажды этому пришёл конец. Продавать «на свой аршин» властями было строжайше запрещено. Употреблять разрешалось только «казённый аршин». Этот эталон аршина, представляющий собой металлическую линейку, изготовили в Москве. Деревянные когти такой линейки рассылались по всей территории России.
Употреблять разрешалось только «казённый аршин». Этот эталон аршина, представляющий собой металлическую линейку, изготовили в Москве. Деревянные когти такой линейки рассылались по всей территории России.
Меры длины в России (XVIII-XIX вв)
Система единиц длины, сложившаяся к концу XVII в., увеличилась в XVIII веке введением английских мер — фута, дюйма. Изменение системы мер длины, проведенное Петром I, было вызвано потребностью увязать русские и наиболее распространенные в то время в мире английские меры и упростить соотношения между ними в интересах не только торговли, но и в целях создания русского флота.
Фут — это длина ступни среднего англичанина. 16 англичан выстраивались в цепочку таким образом, что каждый следующий касался концами пальцев своих ног пяток предыдущего. Одна шестнадцатая такой цепочки и составлял один фут.
Дюйм — название происходит от голландского — »большой палец». Равен ширине большого пальца или длине трех сухих зерен ячменя, взятых из средней части колоса.
Старинные русские меры
Единицы длины
Верста́: 1 верста = 500 сажень ≈ 1,0668 км ≈ 1066,8 м
Саже́нь: 1 сажень = 7 футов = 3 аршина ≈ 2,1336 м
Аршин: 1 аршин = 16 вершков = 28 дюймов ≈ 71,12 см
Фут: 1 фут = 12 дюймов ≈ 30,48 см
Вершок ≈ 4,445 см
Дюйм: 1 дюйм = 10 линий = 2,54 см
Локоть≈ 10,667 вершков ≈ 47,415 см
Пядь:1 пядь = 4 вершка ≈ 17,78 см
Метрическая система мер
Применение самых разнообразных мер длины затрудняло развитие науки, торговли между странами. Поэтому назрела необходимость введения единой системы мер, удобной для всех стран. Первыми заговорили о необходимости установить простую, удобную и, главное, единую систему мер не купцы, а ученые, которые также «страдали» от трудностей в сравнении результатов опытов.
Ученые Французской Академии наук во второй половине XVIII века предложили в качестве основной единицы длины взять одну десятимиллионную часть четверти дуги Парижского земного меридиана. Впоследствии эта часть дуги была названа метром. Такую систему назвали метрической системой мер.
Впоследствии эта часть дуги была названа метром. Такую систему назвали метрической системой мер.
Основная единица длины в метрической системе — 1 метр (от греческого слова » метрон»- мера). Первый прототип эталона метра был изготовлен из латуни в 1795 году. В 1889г. был изготовлен более точный международный эталон метра. Этот эталон тоже изготовлен из сплава платины и иридия и имеет поперечное сечение в виде буквы «X». Его копии были переданы на хранение в страны, в которых метр был признан в качестве стандартной единицы длины. Этот эталон всё ещё хранится в Международном бюро мер и весов, хотя больше по своему первоначальному назначению не используется.
Результаты опроса по выявлению интереса к старинным русским мерам длины
Мной был проведен опрос по выявлению сохранения интереса к старинным русским мерам длины. Было опрошено 13 человек, среди них 3 учащихся МАОУ СОШ №11, 6 человек на спортивной секции и 4 человека мои друзья по двору. Каждому из них был задан вопрос: “Вы знакомы со старинными русскими мерами длины? Как например: дюйм, пядь, вершок, аршин, фут и д. р.
р.
На основании анкетирования было выявлено, что нынешнее поколение утратило интерес к старинным русским мерам длины.
Заключение
Проведенная работа интересна в познавательном отношении. Я ближе познакомилась со старинными русскими единицами измерения. Анкетные данные показали, что подрастающее поколение плохо знакомо со старинными единицами измерения.
Большинство старых мер забыто, вышло из употребления. Старинные меры используются редко, но, все же, применяются в нашей современной жизни. Например, сажень применяется до сих пор в сельском хозяйстве.
Закончив работу, я испытала огромное удовольствие от того, что сама впервые написала исследовательскую работу под руководством учителя и думаю, что она у меня получилась!
Использованная литература:
Виленкин, Н.Я., Депман, И.Я. За страницами учебника математики [Текст]/ Н.Я. Виленкин, И.Я. Депман — М., 1981. – 217 с.
История развития метрологии [Электронный ресурс]/ Режим доступа: http://www. metrologie.ru, свободный. Загл с экрана. – Яз.рус.
metrologie.ru, свободный. Загл с экрана. – Яз.рус.
Каменская, Е.Н. Русская метрология [Текст]/ Е.Н. Каменская — М., 1975. – 157 с.
Карпушина, Н.М. Рукотворные мерки[Текст]/ Н.М. Карпушина // Математика в школе. — 2008.- №7. –С.49-61.
Меры длины [Электронный ресурс]/ Режим доступа: http://www.iro.yar.ru, свободный. Загл с экрана. – Яз.рус.
Сравнительная таблица русских и метрических мер [Электронный ресурс]/ Режим доступа: http://trust.narod.ru, свободный. Загл с экрана. – Яз.рус.
Проект «Старинные русские меры длины, объёма, веса»
Санкт-Петербургское государственное бюджетное стационарное учреждение социального обслуживания.
Дом — интернат детей с отклонением в умственном развитии №1
Комитет по социальной политике.
Проект «Старинные русские меры длины, объема, веса»
Выполнила воспитатель:
Пахомова Е.С
г.Петергоф
2014г.
План работы.

Введение.
Решая математические задачи на уроке мы сталкиваемся с такими понятиями, как сантиметр, метр, километр, литр и т.д. И мне стало интересно, а всегда ли меры длины или объема именовались так, как мы привыкли.
Или же они имели другие названия? И что имеют в виду, когда говорят:
Слышно за версту
Косая сажень в плечах
Мерить всех на свой аршин
От горшка два вершка
Сто пудов
Семь пядей во лбу
Мал золотник, да дорог
Старинные русские меры длины.
С глубокой древности наши предки измеряли расстояние собой, своим телом. Это и удобно, и руки с ногами всегда при тебе, их нельзя «забыть дома». Система древнерусских мер длины включала в себя следующие основные меры: версту, сажень, аршин, локоть, пядь и вершок.
Для мелких мер длины базовой величиной была, применяемая испокон на Руси мера — «пядь», из которой глазомерно, легко можно было получить меньшие доли – два вершка (1/2 пяди) или вершок (1/4 пяди).
ПЯДЬ (пядница) — древняя русская мера длины. МАЛАЯ ПЯДЬ — расстояние между концами расставленных большого и указательного (или среднего) пальцев = 17,78 см.
БОЛЬШАЯ ПЯДЬ — расстояние между концами большого пальца и мизинца (22-23 см.).
ПЯДЬ С КУВЫРКОМ («пядень с кувырком», по Далю — ‘пядь с кувыркой’) — пядь с прибавкой двух суставов указательного пальца = 27-31 см
АРШИН — старинная русская мера длины, равная, в современном исчислении 0,7112м.
Есть различные версии происхождения аршинной меры длины. Возможно, первоначально, «аршин» обозначал длину человеческого шага (порядка семидесяти сантиметров, при ходьбе по равнине, в среднем темпе) и являлся базовой величиной для других крупных мер определения длины, расстояний (сажень, верста). Корень «АР» в слове а р ш и н — в древнерусском языке (и в других, соседних) означает «ЗЕМЛЯ», «поверхность земли», и указывает на то, что эта мера могла применяться при определении длины пройденного пешком пути.
Было и другое название этой меры – ШАГ. Практически, счёт мог производиться парами шагов взрослого человека («малыми <простыми> саженями»; раз-два – один, раз-два – два, раз-два – три …), или тройками («казёнными саженями»; раз-два-три – один, раз-два-три – два …), а при измерении шагами небольших расстояний, применялся пошаговый счёт. В дальнейшем, стали так же применять, под этим названием, равную величину – длину руки.
Практически, счёт мог производиться парами шагов взрослого человека («малыми <простыми> саженями»; раз-два – один, раз-два – два, раз-два – три …), или тройками («казёнными саженями»; раз-два-три – один, раз-два-три – два …), а при измерении шагами небольших расстояний, применялся пошаговый счёт. В дальнейшем, стали так же применять, под этим названием, равную величину – длину руки.
ЛОКОТЬ равнялся длине руки от пальцев до локтя (по другим данным — «расстояние по прямой от локтевого сгиба до конца вытянутого среднего пальца руки»). Величина этой древнейшей меры длины, по разным источникам, составляла от 38 до 47 см. С 16-го века постепенно вытесняется аршином и в 19 веке почти не употребляется.
Локоть — исконно древнерусская мера длины, известная уже в 11 веке. Значение древнерусского локтя в 10.25-10.5 вершков (в среднем приблизительно 46-47 см) было получено из сравнения измерений в Иерусалимском храме.
Старинные меры длины можно встретить в произведениях русских поэтов и писателей.
А.С.Пушкин «ЗИМНЯЯ ДОРОГА».
Сквозь волнистые туманы
Пробирается луна,
На печальные поляны
Льет печально свет она.
По дороге зимней, скучной
Тройка борзая бежит,
Колокольчик однозвучный
Утомительно гремит.
Что-то слышится родное
В долгих песнях ямщика:
То разгулье удалое,
То сердечная тоска……
Ни огня, ни черной хаты,
Глушь и снег….
На встречу мне
Только версты полосаты
Попадаются одне…
П.П.Ершов «КОНЕК ГОРБУНОК»
«Да игрушечку-конька
Ростом только в три вершка,
На спине с двумя горбами
Да с аршинными ушами».
ВЕРШОК — мера длины, равная ширине двух пальцев (указательного и среднего). Равнялся 1/16 аршина, 1/4 четверти. В современном исчислении — 4,44см. Наименование «Вершок» происходит от слова «верх».
САЖЕНЬ — одна из наиболее распространенных на Руси мер длины..
Наименование сажень происходит от глагола сягать (досягать) — на сколько можно было дотянуться рукой. Существовали саженные мерные веревки и деревянные «складени», имевшие применение при измерении расстояний и в строительстве.
Существовали саженные мерные веревки и деревянные «складени», имевшие применение при измерении расстояний и в строительстве.
«Маховая сажень» — 1,76м, расстояние между концами пальцев широко расставленных рук взрослого мужчины.
» Косая сажень » — 2,48м ,самая длинная: расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки
По данным историков и архитекторов, саженей было более 10 и они имели свои названия, были несоизмеримы и не кратны одна другой. Сажени: городовая — 284,8 см, без названия — 258,4 см, великая — 244,0 см, греческая — 230,4 см, казённая — 217,6 см, царская — 197,4 см, церковная — 186,4 см, народная — 176,0 см, кладочная — 159,7 см, простая — 150,8 см, малая — 142,4 см и ещё одна без названия — 134,5 см (данные из одного источника), а так же — дворовая, мостовая.
ВЕРСТА — старорусская путевая мера (её раннее название — »поприще»). Этим словом, первоначально называли расстояние, пройденное от одного поворота плуга до другого во время пахоты. Два названия долгое время употреблялись параллельно, как синонимы. «Верстой» также назывался верстовой столб на дороге.
Два названия долгое время употреблялись параллельно, как синонимы. «Верстой» также назывался верстовой столб на дороге.
Величина версты неоднократно менялась в зависимости от числа сажен, входивших в неё, и величины сажени. До царя Алексея Михайловича в 1 версте считали 1000 саженей.
В подмосковном селе Коломенском находилась летняя резиденция царя Алексея Михайловича.
Дорога туда была оживленной, широкой и считалась главной в государстве. А уж когда поставили огромные верстовые столбы, каких в России еще не бывало, слава этой дороги возросла еще более. Смекалистый народ не преминул воспользоваться новинкой и окрестил долговязого человека коломенской верстой. Что означает выражение «Мерить версты»? Ходить на большое расстояние.Про кого говорят «Коломенская верста»? Так называют очень высокого роста, верзилу.
Меры объема.
Ведро = 1/40 бочки = 10 кружек = 30 фунтов воды = 100 чарок = 200 шкаликов = 12 литров. Это железная, деревянная или кожаная посуда, преимущественно цилиндрической формы, с ушками или дужкой для ношения. В обиходе, два ведра на коромысле должны быть в «подъём женщине». Деление на более мелкие меры проводилось по двоичному принципу: ведро делили на 2 полуведра или на 4 четверти ведра или на 8 получетвертей, а также на кружки и чарки. Древнейшая «международная» мера объёма — «горсть».
В обиходе, два ведра на коромысле должны быть в «подъём женщине». Деление на более мелкие меры проводилось по двоичному принципу: ведро делили на 2 полуведра или на 4 четверти ведра или на 8 получетвертей, а также на кружки и чарки. Древнейшая «международная» мера объёма — «горсть».
До середины XVII в. в ведре содержалось 12 кружек, во второй половине XVIIв. так называемое казённое ведро содержало 10 кружек, а в кружке — 10 чарок, так что в ведро входило 100 чарок. Затем, по указу 1652 года чарки сделали втрое больше по сравнению с прежними («чарки в три чарки»). В торговое ведро вмещалось 8 кружек. Значение ведра было переменным, а значение кружки неизменным, в 3 фунта воды (1228,5 грамма). Объем ведра был равен 134,297 кубических вершков.
Бочка, как мера жидкостей применялась в основном в процессе торговли с иностранцами, которым запрещалось вести розничную торговлю вином на малые меры. Равнялась 40 ведрам (492 л)
Чаще всего в крестьянском быту использовались небольшие бочки и бочонки от 5-и до 120-и литров. Большие бочки вмещали до сорока вёдер (сороковки)
Большие бочки вмещали до сорока вёдер (сороковки)
В житейском обиходе и в торговле употребляли разнообразные хозяйственные сосуды: котлы, жбаны, корчаги, братины, ендовы. Значение таких бытовых мер в разных местах было различно: например, емкость котлов колебалась от полуведра до 20 ведер. В XVII в. была введена система кубических единиц на основе 7-футовой сажени, а также введён термин кубический (или «кубичный»). Кубическая сажень содержала 27 кубических аршин или 343 кубических фута; кубический аршин — 4096 кубических вершков или 21952 кубических дюймов.
Кружка (слово означает — ‘для пития по кругу’) = 10 чаркам = 1,23 л.
Современный граненый стакан раньше назывался «досканом» («строганые доски»), состоящим из обвязанных верёвкой ладов-дощечек, вокруг деревянного донца.
Чарка (рус. мера жидкости) = 1/10 штофа = 2 шкаликам = 0,123 л.
Ендова
Деревянная или металлическая утварь (часто, украшенная орнаментом), используемая для подачи к столу напитков. Представляла собой невысокую чашу с носиком. Металлическая ендова изготавливалась из меди или латуни. Деревянные ендовы изготавливали из осины, липы или берёзы.
Представляла собой невысокую чашу с носиком. Металлическая ендова изготавливалась из меди или латуни. Деревянные ендовы изготавливали из осины, липы или берёзы.
Кожаный мешок (бурдюк) – до 60 л
Корчага — 12 л
Насадка — 2,5 ведра (Ногородская мера жидкости, XV век)
Ушат – высота посудины – 30-35 сантиметров, диаметр – 40 сантиметров, объем – 2 ведра или 22-25 л.
Короб — из цельных кусков луба, сшитых полосами лыка. Донце и верхняя крышка — из досок. Размеры – от небольших коробушек до больших «комодов»
Балакирь — долбленая деревянная посудина, объемом в 1/4—1/5, ведра.
Старинные меры объема:
1 куб. сажень = 9,713 куб. метра
1 куб. аршин = 0,3597 куб. метра
1 куб. вершок = 87,82 куб. см
1 куб. фут = 28,32 куб. дециметра (литра)
1 куб. дюйм = 16,39 куб. см
1 куб. линия = 16,39 куб. мм
1 Кварта — немногим больше литра.
Меры веса.
На Руси использовались в торговле следующие меры веса :
• берковец = 10 пудов
• пуд = 40 фунтов = 16,38 кг
• фунт (гривна) = 96 золотников = 0,41 кг
• лот = 3 золотника = 12,797 г
• золотник = 4,27 г
• доля = 0,044 г
БЕРКОВЕЦ — эта большая мера веса, употреблялась в оптовой торговле преимущественно для взвешивания воска, меда и т. д.
д.
Берковец — от названия острова Бьерк. Так на Руси называлась мера веса в 10 пудов, как раз стандартная бочка с воском, которую один человек мог закатить на купеческую ладью, плывущую на этот самый остров. (163,8 кг).
Известно упоминание берковца в XII веке в уставной грамоте князя Всеволода Гавриила Мстиславича новгородскому купечеству.
ЗОЛОТНИК равнялся 4,26 г. Про него говорили: «мал золотник да дорог». Это слово, первоначально обозначало зoлотую монету.
КУЛЬ (ранее Мехъ) – мера сыпучих телъ различного весу (Москва XVII век). Упоминается в летописях.
ГАРНЕЦ («горшок» по-древнерусски).
В Царстве Польском употреблялся до 1849г., разделялся на 4 кварты = 4 литра.
В Галиции употреблялся до 1857г. = 3,85 литра (по Южакову).
Общевосточнославянская мера сыпучих тел.
«Найдется купец и на дырявый гарнец!»
ЧЕТВЕРИК = 26,25 литра.
Мера емкости в России.
В одном четверике 8 гарнцев, 1/8 четверти.
ОСЬМИНА (осьминка).
Мера сыпучих тел равная половине четверти (105 – 125 литра). (по «Библиотеке Фольклора»)
УБОРОК — старинная русская мера небольшой вместимости – около ежедневной порции зерна (по «Русской Правде»).
Я вам рассказала
Про то, как наши предки
Ходили по Руси
Снимав аршином мерки.
Локтями мерить ткань
Купцы тогда умели,
Про версты под ногами
Старинны песни пели!
Литература:
1. «Наименования мер длины, веса и денег в древнерусском языке» И.Н.Гермогенова
2. Седова Л. Н. Вопросы русской метрологии на уроках и внеклассных занятиях по математике. — Ярославль, 1999
3. Федорчук С. В. Метрология древнерусского государства (X — начало XII вв.)
Интернет:
1.KAKRAS.RU
Copyright (С) 2007 – 2009
2.http://www.kapishe.ru
Автор: Пахомова Екатерина Степановна
| Тип | Название материала | Автор | Опубликован |
|---|---|---|---|
| документ | Проект «Старинные русские меры длины, объёма, веса» | Пахомова Екатерина Степановна | 31 Мар 2015 |
| документ | Старинные русские меры длины, веса, объёма | Ащеулова Елена Викторовна | 1 Апр 2015 |
| документ | Учебный проект «Старинные русские меры длины» | Турова Наталья Сегреевна | 13 Мая 2015 |
| документ | Внеклассное мероприятие «Старинные русские меры длины» | Галина Владимировна Разумова | 21 Мар 2015 |
| презентация | презентация «Старинные русские меры длины» | Хисамова Раиса Фаузиевна | 8 Ноя 2015 |
| презентация, документ | Урок в 5 классе. Старинные русские меры длины, веса. Старинные русские деньги. Старинные русские меры длины, веса. Старинные русские деньги. | Жирнова Алеся Григорьевна | 9 Авг 2015 |
| документ | Проект «Старинные русские меры» 5 класс | Богачева Ольга Вениаминовна | 31 Мар 2015 |
| документ | ВНЕКЛАССНОЕ МАТЕМАТИЧЕСКОЕ МЕРОПРИЯТИЕ «Старинные русские меры длины» | Петрова Алла Наумовна | 20 Мар 2015 |
| презентация | Старинные меры длины и веса | Елена Ивановна Кормилина | 1 Апр 2015 |
| презентация | Старинные меры длины и веса | Раевская Валентина Александровна | 16 Дек 2015 |
| презентация, документ | Урок по теме: «Старинные меры длины» | Абраменкова Марина Анатольевна | 21 Мар 2015 |
| презентация | Презентация «Старинные меры длины» | Бондаренко Светлана Семёновна | 30 Мар 2015 |
| разное | Внеклассное занятие по математике «Старинные меры длины» 3 класс. | Савельева Вера Викторовна | 4 Апр 2015 |
| презентация | Презентация по теме «Старинные меры длины» | Кузнецова Ольга Владимировна | 16 Авг 2015 |
| презентация | Презентация «Старинные единицы меры длины» | Засимова Дарья Сергеевна | 14 Ноя 2015 |
| документ | Конспект урока по математике » Старинные меры длины» | Mazunovatata | 8 Фев 2016 |
| разное | Старинные русские меры длины в народных пословицах и поговорках. | Нагибина Надежда Георгиевна | 31 Мар 2015 |
| разное | Старинные русские меры длины в народных пословицах и поговорках. | Нагибина Надежда Георгиевна | 31 Мар 2015 |
| документ | СТАРИННЫЕ РУССКИЕ МЕРЫ ДЛИНЫ 20.12.13 | Шенцева Татьяна Александровна | 31 Мар 2015 |
| презентация | старинные русские меры длины | Орлова Ирина Анатольевна | 1 Апр 2015 |
| документ | Старинные русские меры длины | Журавлева Алена Владимировна | 6 Июн 2015 |
| документ | Старинные русские меры длины | Петрова Алла Наумовна | 11 Апр 2016 |
| презентация | Презентация по математике на тему «Старинные меры длины» 2 класс УМК «Перспектива» | Зудилова Светлана Александровна | 24 Мар 2016 |
| разное | Урок — путешествие в 6 классе «Путешествие в прошлое. Старинные меры длины» Старинные меры длины» | Лилия Геннадьевна Шитикова | 1 Апр 2015 |
| документ | Урок окружающего мира «Старинные меры длины» в технологии МДО | Матвеева Анна Васильевна | 31 Мар 2015 |
| презентация | Математика 4 класс. Проектная работа «Старинные меры длины» | Рожкова Александра Анатольевна | 19 Мар 2016 |
| документ | Учебный проект «Старинные единицы длины» | Дегтярёва Надежда Николаевна | 30 Окт 2015 |
| документ | «Старинные русские меры». Интегрированный урок по математике, русскому языку и литературе. Авторы: Дороженко Ж.Ю., Прищепова И.А. Интегрированный урок по математике, русскому языку и литературе. Авторы: Дороженко Ж.Ю., Прищепова И.А. | Дороженко Жанна Юрьевна | 20 Мар 2015 |
| презентация | Презентация для интегрированного урока по математике и литературе на тему «Старинные русские меры в математике и литературе» | Черемных Вера Борисовна | 31 Мар 2015 |
| презентация | Старинные меры длины | Овечкина Светлана Васильевна | 7 Апр 2015 |
| презентация | Старинные меры длины. | Назаревская Светлана Дмитриевна | 14 Ноя 2015 |
| презентация | Презентация урока математики по теме » Меры длины» | Ерошкина Татьяна Павловна | 30 Мар 2015 |
| презентация, документ | Проектная работа по математике «Меры длины» | iri1969 | 5 Апр 2015 |
| документ | Бинарный урок. Меры площадей, длины и веса Меры площадей, длины и веса | Карпова Ольга Михайловна | 21 Мар 2015 |
| документ | Старинные русские меры | Ерофеева Елена Владимировна | 20 Мар 2015 |
| документ | Старинные русские меры | Паршакова Тамара Алексеевна | 23 Ноя 2015 |
| документ | некоторые старинные меры длины | Лукина Татьяна Анатольевна | 15 Окт 2015 |
| презентация | Презентация Старинные меры длины. | Елена Геннадьевна Соколова | 18 Сен 2015 |
| презентация | Математика 2 кл. Презентация к уроку «Меры длины» УМК «Перспектива» | Кудряшова Светлана | 20 Апр 2015 |
| документ | «Старинные русские меры». | Колесникова Тамара Андреевна | 21 Мар 2016 |
Старинные русские меры длины в современной жизни человека
Образец проекта
Проект:
Старинные русские меры
Актуальность
В этом учебном году я начал изучать новый предмет –
физику. Изучение этой новой для меня науки началось со
знакомства с различными физическими величинами и их
единицами измерения. Я узнал, что с 1963 г. в России и
Я узнал, что с 1963 г. в России и
других странах принимается международная система
единиц СИ (система интернациональная). В этой системе
основной единицей длины является метр, а единицей
массы – килограмм.
При изучении русской литературы мне неоднократно
попадались произведения, в которых часто встречаются
слова, обозначающие единицы измерения длины и массы
Древней Руси, но мы не знаем значения этих слов, поэтому
не всегда правильно понимаем смысл прочитанного.
И я решил побольше узнать об этих мерах единиц
измерения длины и установить взаимосвязь между старой
и новой измерительными системами.
Цели:
установить старинные меры длины,
сравнить их с новой измерительной системой и
найти отражение этих мер в русских пословицах
и поговорках, в литературных произведениях.
Задачи:
• узнать больше о старинных мерах длины;
• исследовать пословицы, поговорки с
упоминанием старинных мер длины;
• подобрать в литературных произведениях
упоминания о старинных мерах длины.
Любопытные способы измерений
• У славян была такая мера длины, как «вержение камня»,
«перестрел» , «бычачий рев» , «пушечный выстрел»
• У эстонских моряков – «три трубки»
• В Испании – «сигара»
• Древние римляне –расстояния измеряли пассами или двойными
шагами (шаг левой ногой, шаг правой). Тысяча двойных шагов
составляла милю (лат. «милле» — тысяча).
Основные единицы
измерения Древней Руси
Перст
Пядь
Сажень
Вершок
Локоть
Аршин
Перст
Вершок
• Русский перст был равен
ширине указательного
пальца, что составляет
• Когда-то так называли
примерно 2 см, самая
верхнюю часть чего-либо.
маленькая единица длины.
Говоря о вершке как о
единице длины, имели в
• Слово «перст» ныне
виду верх перста.
считается устаревшим,
Первоначально вершок
однако в богатом русском
определялся длиной двух
языке сохранилось немало
фаланг указательного
порожденным их слов и
пальца, а это
выражений: перстень,
приблизительно 4см 5 мм.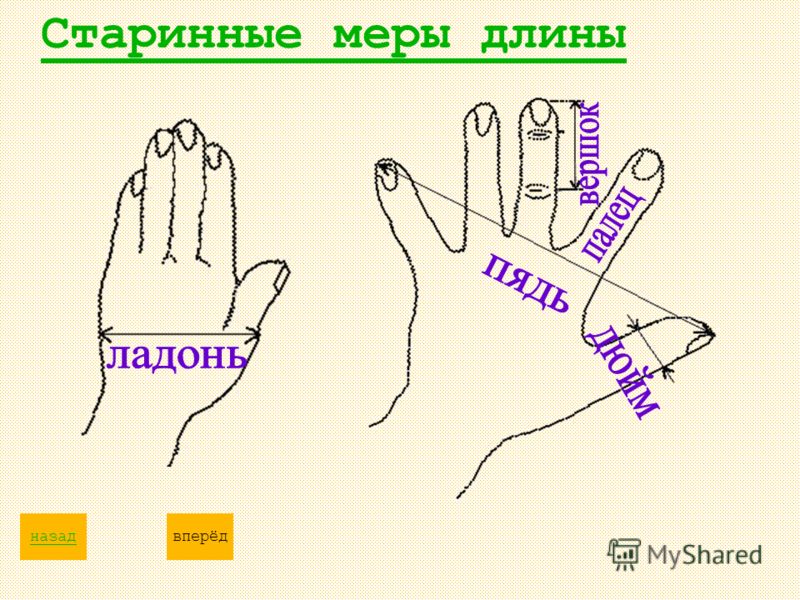
наперсток , перчатки,
перст судьбы , один как
перст.
Пядь
Известно о трех древнерусских пядях
• Малая пядь — расстоянием между концами растянутых
большого и указательного пальцев, примерно 19 см.
• Великая пядь — расстоянию между концами большого
пальца и мизинца, примерно 23 см.
• Пядь с кувырком — малая пядь и две длины сустава
указательного (по некоторым источникам – среднего)
пальца, примерно 27 см.
Локоть
• расстояние от локтевого сгиба до конца вытянутого
среднего пальца или сжатой в кулак кисти руки, что
составляло примерно 46 см и 38 см соответственно.
• большой локоть, равен длине руки от основания плеча
до большого пальца, а это приблизительно 54 см.
• Этой древнейшей мерой длины пользовались многие
народы мира. Локтями купцы измеряли продаваемые
ткани, наматывая их на руку.
Аршин
• Слово «аршин» восходит к персидскому «арш» локоть, которое было некогда заимствованно
тюркскими языками, откуда и попало в русский язык.
Равен длине руки – от основания плеча до кончика
вытянутого среднего пальца, примерно 72см (согласно
«Торговой книге» 2 аршина = 3 локтям)
• Например, ткань мерили, натягивая на собственную
руку до плеча, отсюда пришло выражение «мерить на
свой аршин».
Сажень
• Сажень – древняя мера длины, известная с 10-11 вв.,
применялась главным образом, для измерения земельных
участков и в строительстве.
• Маховая сажень–расстояние между вытянутыми пальцами
раскинутых рук (176 см).
• Сажень косая– расстояние между подошвой левой ноги и
концом среднего пальца вытянутой вверх правой руки (248 см)
.
• Название происходит
от слова «сягать», т.е.
насколько можно было
дотянуться рукой.
Шаг
• Шаг – средняя длина человеческого шага 71см.
Сохранились сведения об использовании шага для
определения расстояния между городами.
• Шагами отмерялось расстояния, на которое должны
были сходиться противники во время дуэли.
• Так, с расстояния 10 шагов на Черной речке под
Петербургом 27 января 1837года на дуэли Дантес
стрелял и ранил смертельно А.С.Пушкина.
• В 1841году 15 июля недалеко от Пятигорска Мартынов
произвел свой роковой выстрел с расстояния 15 шагов и
убил М.Ю.Лермонтова.
Верста
• Верста — от слова вертеть. Первоначально — расстояние от
одного поворота плуга до другого во время пахоты. Длина
версты — 1060 м.
• Межевая верста — существовала на Руси до XVIII века для
определения расстояния между населёнными пунктами и
для межевания (от слова межа — граница земельных
владений в виде узкой полосы). Длина такой версты 1000
саженей или 2,13 км.
• Коломенская верста — «верзила» шутливое название очень высокого
человека.
Миля
• Миля – от латинского слова «милия» – тысяча (шагов)
— русская мера длины. Использовалось как единица для
измерения больших расстояний, равна семи верстам
или ≈7468 м.
• Когда-то были специальные ходоки, которые помогали
составлять карты: они отмеряли расстояние, считая
шаги. Тысяча двойных шагов называлась милей.
Тысяча двойных шагов называлась милей.
• Величина мили была от 1,4 до 1,9 километра. По указу
Петра I русская миля = 7 верстам (≈7,47 км).
Заимственные единицы измерения
Дюйм
• мерка, первоначально равная
длине фаланги большого
пальца, что составляет
примерно 2 см 5 мм.
• Слово «дюйм» голландского
происхождения и появилось в
русском языке благодаря
Петру I.
• Фут (от англ. foot —
ступня) — единица
измерения длины в английс
кой системе мер.
«Международный» фут стал
равняться в точности
0,3048 м.
• Ярд — британская и
американская единица
измерения расстояния,
которая равна 91,44 см.
Старинные русские единицы длины в
произведениях
Старинные русские единицы длины в
литературных произведениях
Петр Ершов «Конек-горбунок»
«Да еще рожу конька
Ростом только 3 вершка,
На спине с двумя горбами
Да аршинными ушами».
• Рост конька: вершок – 4 см
4 см · 3 = 12см.
• Уши конька: аршин – 71 см – длина вытянутой руки от
плеча до конца среднего пальца.
Ганс Христиан Андерсен «Дюймовочка»
• Рост: дюйм = 2 см 5 мм – это ширина
большого пальца
Старинные русские единицы длины в
произведениях
Николай Алексеевич Некрасов «Дедушка Мазай и зайцы»
«…Старый Мазай любит до страсти
Свой низменный край.
За сорок верст в Кострому прямиком
Сбегать лесами ему нипочем.
… С каждой минутой вода подбиралась
К бедным зверькам: уж под ними осталось
Меньше аршина земли в ширину,
Меньше сажени в длину».
-Расстояние, которое проходит Старый Мазай:
40верст • 1 км 668 м = 42 км 672 м.
— Длина островка —2 м 13 см
-Ширина островка меньше 72 см.
Пословицы и поговорки со старинными
мерами длины и их толкование
• Видит на три аршина под землю — об очень проницательном
человеке, на 2,13 м в землю видит.
• Семь пядей во лбу – «189 см во лбу». — об очень умном
человеке.
• Правда – как солнце – ладонью не прикроешь- «Правда – как
солнце – 10,16 см не прикроешь» — всё тайное всегда
становится явным.
• От горшка два вершка, а уже указчик — «От горшка 88 мм, а
уже указчик» -молодой человек, не имеющий жизненного
опыта, но самонадеянно поучающий всех.
Пословицы и поговорки со старинными
мерами длины и их толкование
• На аршин борода, да ума на пядь — «На 71 см борода, а ума
на 27 см» — о знатном, но глупом человеке.
• Любовь не верстами меряется — «Любовь не 1,067км
меряется»-расстояние не может быть препятствием
для любви.
У него косая сажень в плечах – «У него 2,13 м в плечах»
широкоплечий, высокого роста человек.
«Его за версту видно» — о хорошем или плохом человеке,
дела которого заметны далеко, его видно за 1,067 км.
Мои исследования
Установление длины старинных русских
мер опытным путем
Измеряе
мый
Метр
Вершок
Малая
пядь
Дюйм
Локоть
Большой
локоть
Аршин
Мама
1,54
35
8,11
61,6
3,35
2,85
2,39
Папа
1,71
39,86
9
68,4
3,72
3,17
2,17
Я
1,45
32,95
7,63
58
3,15
2,69
2,04
Саша
1,38
31,36
7,26
55,2
3
2,56
1,94
Карина
1,14
25,9
6
45,6
2,48
2,1
1,6
Алина
0,93
21,14
4,89
37,2
2,02
1,72
1,31
Вывод: наиболее точно и удобно можно измерить
рост в современных единицах измерения: в
метрах, сантиметрах, миллиметрах.
Мои наблюдения
• Из проделанной работы я узнал, что в старой Руси меры
зависели от самого человека и видов его практической
деятельности
• В России в разных местностях почти все меры имели
различные значения .
• Без измерений современный человек обходиться не может.
В древности люди тоже не могли обходиться без измерений.
• Старинные единицы длины были неточными.
• С развитием общества возникла
потребность в создании единой
системы мер. Каждая мера должна
была иметь определенную величину
и эталон. Так появился эталон метра.
Мои выводы
• Из проделанной работы я узнал, что в старой Руси
меры зависели от самого человека и видов его
практической деятельности
• Поэтому возникла необходимость отказаться от
установления связей между единицами измерения и
размерами человеческого тела.
• Человек начал искать новые единицы измерения в
окружающей природе.
• Гипотеза подтвердилась: знать старинные меры
длины необходимо для того, чтобы узнать и понять
историю своего народа
• Проведенная работа мне была интересна. Я ближе
Я ближе
познакомился со старинными русскими мерами длины.
Большинство старых мер забыто, вышло из употребления,
но многие из них фигурируют в литературных
произведениях, образной речи.
• История мер – это история торговли, ремесел, сельского
хозяйства и строительства, а это часть истории
человечества.
• Подводя итог работы, я прихожу к выводу, что данная тема
актуальна. Как появились меры, как изменялись, что несли
народам и как влияли на их жизнь интересно и сегодня.
• Я хотел бы продолжить данную работу и исследовать
старинные меры веса, объема, площадей на Руси. Возможно
это станет моей следующей исследовательской работой.
Заключение
«Наука начинается с тех пор, как
начинают измерять. Точная наука
немыслима без меры»
Д.И. Менделеев
В
1960
году
на
Генеральной
конференции по мерам и весам
представители 32 стран
приняли
Международную систему единиц.
С 1963 года этой системой пользуются
во всех областях науки, техники и
народного хозяйства.
Список литературы.
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд
С.И. Математика 5 класс. — М.: Мнемозина, 2008.
2. Глейзер Г.И. История математики в школе. – М.:
Просвещение, 1982.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника
математики — М.: Просвещение, 1989.
4. Нагибин Ф.Ф., Канин Е.Е. Математическая шкатулка. М.:
Просвещение, 1984 .
5. Интернет ресурсы:
— сайт «Фестиваль педагогических идей – открытый урок».
— www. iro. ru /resours/ distant/mant/metrol _3.htm Меры
длины
6.С.И. Ожегов Толковый словарь. Москва, 2002
7. Литературные произведения
Спасибо
за внимание!
Линейки для измерительных стержней, измерительные стержни, измерительные шесты
Покупатели из Канады идут сюда
21 год обслуживания таких клиентов, как вы. Покупайте с уверенностью.
Измерительный стержень можно использовать как для горизонтального, так и для вертикального расстояний. А благодаря телескопической конструкции вы сможете отрегулировать его в соответствии со своими потребностями. Если вам нужно использовать его для измерения высоты или уклона, вы можете подключить лазер, чтобы получать более точные измерения без математических расчетов.
А благодаря телескопической конструкции вы сможете отрегулировать его в соответствии со своими потребностями. Если вам нужно использовать его для измерения высоты или уклона, вы можете подключить лазер, чтобы получать более точные измерения без математических расчетов.
Порядок сортировки DefaultNameПроизводительСамая низкая ценаСамая высокая ценаСамая новая
Seco
— измерительная линейка серии CMR — модель CMR-25
ES215
359,99 $
Seco — измерительная линейка серии CMR — модель CMR-36
ES2213
560,99 $
Nedo — компактная телескопическая линейка Measure Fix 10 футов — от 24 до 119 дюймов (F380213-185)
ES8247
240,99 $
Seco
Шкала высоты на нивелирной рейке SECO основана на телескопической конструкции, которая имеет несколько секций, которые можно поднимать в верхней части. вниз, пока желаемая высота не будет поднята. Этот механизм используется для измерения вертикального расстояния пространства. Сначала нужно поднять верхнюю часть. Затем продолжайте поднимать последующие секции, пока стержень не соприкоснется с другим концом. Убедитесь, что вы держите руку на стержне, когда поднимаете его, потому что он будет удерживать его на месте. Как только он войдет в контакт с другой стороной области, которую вы хотите измерить. Посмотрите на линейку, чтобы определить расстояние между двумя точками.
Использование вехи прямого подъема
Веха прямого подъема SECO основана на системе, которая существует уже более 60 лет и не требует математики. Они предназначены для использования с оптическим устройством, и к ним можно подключить лазер, чтобы вы могли получать более точные показания. Этот тип измерительной штанги имеет два замка — один для торца ленты, а другой — для удлинения штанги. Поскольку вы можете измерить высоту по прямому показанию, вам не нужны математические вычисления. С помощью некоторых простых настроек вы можете измерить высоту. А с помощью нехитрых арифметических действий можно измерить разницу высот. Этот проверенный временем метод измерения штанги можно использовать для определения уклонов любой области или рабочей площадки.
Они предназначены для использования с оптическим устройством, и к ним можно подключить лазер, чтобы вы могли получать более точные показания. Этот тип измерительной штанги имеет два замка — один для торца ленты, а другой — для удлинения штанги. Поскольку вы можете измерить высоту по прямому показанию, вам не нужны математические вычисления. С помощью некоторых простых настроек вы можете измерить высоту. А с помощью нехитрых арифметических действий можно измерить разницу высот. Этот проверенный временем метод измерения штанги можно использовать для определения уклонов любой области или рабочей площадки.
Избранные статьи
Прочтите наши полезные статьи: Лучшие локаторы труб и кабелей
ВАЖНЫЙ ИНСТРУМЕНТ ДЛЯ ОБСЛЕДОВАНИЯ ЛЮБОЙ РАБОЧЕЙ ПЛОЩАДКИ
Когда вы обследуете рабочую площадку, вы хотите иметь в своем распоряжении нужные инструменты. Измерение стержнем является важным способом определения вертикального расстояния и уклона. Вы даже можете использовать его для горизонтальных измерений в определенных ситуациях. А прикрепив лазерный детектор к стержню, вы можете использовать его как уровень, особенно если вы измеряете площадь фундамента, который будет построен позже. Мерная палочка — это удобный инструмент, который может быть выполнен в нескольких разных стилях. Так что независимо от того, какую работу вам нужно провести, такой инструмент должен быть в вашем ящике с инструментами.
А прикрепив лазерный детектор к стержню, вы можете использовать его как уровень, особенно если вы измеряете площадь фундамента, который будет построен позже. Мерная палочка — это удобный инструмент, который может быть выполнен в нескольких разных стилях. Так что независимо от того, какую работу вам нужно провести, такой инструмент должен быть в вашем ящике с инструментами.
УНИВЕРСАЛЬНОЕ УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ РАССТОЯНИЯ И ВЫСОТЫ
Несмотря на простоту конструкции, измерительная рейка может использоваться для определения как расстояния, так и высоты. Благодаря телескопической конструкции его можно отрегулировать под любой рост, а измерительная система в виде линейки упрощает его использование. В то время как некоторые стержни предназначены исключительно для измерения высоты, другие также могут использоваться в качестве нивелиров. Некоторые модели можно даже использовать для измерения уклона земли, что может быть полезно при строительстве фундамента. Независимо от того, какой тип рабочей площадки вам нужно обследовать, измерение штанги считается важной частью процесса.
Линейки, также известные как «измерительные рейки» или «метры», представляют собой удобные инструменты, которые бывают нескольких разных стилей. Некоторые из них могут измерять уровень высот с помощью функции двойного назначения, встроенной в измерительную рейку, в то время как другие предназначены для использования в качестве измерительных линеек без возможностей нивелирующей или нивелирующей рейки. Обычно устройства этого типа используются для измерения мостов и воздушных линий электропередач, поэтому перевозчики широкогрузных автомобилей могут видеть, сможет ли их транспортное средство проехать.
На задней части некоторых стержней уровня или уровня имеется измерительная линейка, которая является дополнительной функцией, которая может пригодиться (особенно если вы ищете оба типа стержней для измерения). Во многих случаях геодезисты могут уменьшить потребность в измерительной рулетке, если у них есть одна из этих измерительных линеек. Затем их можно использовать не только для вертикальных измерений, но и для горизонтальных.
Часто задаваемые вопросы
Что такое мерная рейка?
Измерительный стержень можно использовать для измерения длины участков съемки. Обычно он круглый или разделен на квадраты, но вы также можете найти такой, который выглядит как плоская доска. Не стесняйтесь посмотреть, что у нас есть в Engineer Supply, чтобы вы могли найти измерительную штангу, которая подходит именно вам.
Как можно использовать измерительные стержни?
Измерительная линейка может использоваться для измерения как горизонтальных, так и вертикальных расстояний. А благодаря телескопической конструкции вы можете настроить любую длину или конфигурацию, которые вам нужны. Вы даже можете прикрепить лазер, чтобы измерять высоту или уклон.
Кто изобрел измерительную линейку?
Самая старая мерная палочка пришла из Древнего Шумера и была сделана из медного сплава. Он был найден немецким ассириологом по имени Экхард Унгер во время раскопок в Ниппуре и датируется 2650 годом до нашей эры. Линейка была разделена на шумерские локти (что составляет примерно 20 дюймов), но есть некоторые разногласия относительно того, правда ли это.
Линейка была разделена на шумерские локти (что составляет примерно 20 дюймов), но есть некоторые разногласия относительно того, правда ли это.
Какие существуют типы измерительных инструментов?
Существует много типов измерительных инструментов, но вот некоторые из них, которые нужны каждому строительному профессионалу:
- Рулетка — У него должен быть прочный крюк, который может двигаться. Он также должен иметь возможность легко выдвигаться и втягиваться. Обычно используется 25-футовая измерительная лента, но она должна иметь достаточную длину для измерения протяженных пролетов, но при этом не быть слишком длинной, чтобы быть слишком тяжелой.
- Speed Square — Работает как пять инструментов в одном (как минимум). И маркировка никогда не исчезнет, что позволит вам измерять правильные углы на спилах дерева в течение многих лет.

- Транспортир — Он может сказать вам, какой угол установить торцовочную пилу, прижимая ножки к двум поверхностям и считывая измерение угла.
- Механический карандаш плотника — Обычные карандаши не справятся, если вы будете маркировать дерево, но обычные столярные карандаши требуют постоянной заточки. Вот почему механический столярный карандаш — отличный выбор.
- Лазерный измеритель — он стал стандартным инструментом для большинства дизайнеров, архитекторов и подрядчиков, но также полезен для домовладельцев, если им необходимо измерить расстояния до 50 футов.
Если вы ищете измерительную штангу или любой другой измерительный инструмент, обязательно посмотрите, что у нас есть в Engineer Supply.
Где можно купить качественные измерительные стержни?
Если вам нужна мерная линейка или любой другой измерительный инструмент, вы можете найти его в Engineer Supply. У нас есть широкий выбор измерительных инструментов, которые может использовать любой профессиональный геодезист или строительный подрядчик, и все они поставляются лучшими производителями на рынке. Не стесняйтесь посмотреть, что у нас есть на складе, чтобы вы могли найти измерительную рейку, которая удовлетворит ваши конкретные потребности.
У нас есть широкий выбор измерительных инструментов, которые может использовать любой профессиональный геодезист или строительный подрядчик, и все они поставляются лучшими производителями на рынке. Не стесняйтесь посмотреть, что у нас есть на складе, чтобы вы могли найти измерительную рейку, которая удовлетворит ваши конкретные потребности.
Что такое стержневое измерение?
Штанга, которую иногда называют «жердью» или «шестом», представляет собой тип геодезического инструмента, который можно использовать для измерения длины. И у него будут разные градации, в зависимости от того, для чего он предназначен. Термин «стержень» также относится к старой английской единице измерения, равной 16,5 футам (5,029 метра), но также использовались вариации между 9 и 28 футами (2,743 и 8,534 метра).
Измерение в науке (Стэнфордская философская энциклопедия)
Современные философские дискуссии об измерении, охватывающие
с конца девятнадцатого века до наших дней — можно разделить
на несколько направлений науки. Эти нити отражают разные
точки зрения на характер измерения и условия, которые делают
измерение возможно и надежно. Основные направления математические.
теории измерения, операционализм, конвенционализм, реализм,
теоретико-информационные счета и счета, основанные на моделях. Эти нити
науки не являются, по большей части, непосредственно
конкурирующие взгляды. Вместо этого их лучше всего понимать как выделение
различные и взаимодополняющие аспекты измерения. Ниже приводится
очень грубый обзор этих точек зрения:
Эти нити отражают разные
точки зрения на характер измерения и условия, которые делают
измерение возможно и надежно. Основные направления математические.
теории измерения, операционализм, конвенционализм, реализм,
теоретико-информационные счета и счета, основанные на моделях. Эти нити
науки не являются, по большей части, непосредственно
конкурирующие взгляды. Вместо этого их лучше всего понимать как выделение
различные и взаимодополняющие аспекты измерения. Ниже приводится
очень грубый обзор этих точек зрения:
- Математические теории измерение просмотр измерения как отображение качественного эмпирические отношения к отношениям между числами (или другим математическим сущности).
- Операционалисты и конвенционалисты вид измерение как совокупность операций, формирующих смысл и/или регулируют использование количественного термина.
- Реалисты рассматривают измерение как оценку
независимые от разума свойства и/или отношения.

- Информационно-теоретические счета представление измерений как сбор и интерпретация информации о система.
- Счета на основе модели просмотр измерения как согласованное присвоение значений параметрам в теоретическом и/или статистическая модель процесса.
Эти взгляды в принципе согласуются друг с другом. Пока
математические теории измерения имеют дело с математическими
основы шкал измерения, операционализм и конвенционализм
в первую очередь связаны с семантикой количественных терминов, реализмом
занимается метафизическим статусом измеримых величин,
а теоретико-информационные и основанные на моделях расчеты касаются
эпистемологические аспекты измерения. Тем не менее, предмет
домен не так четко разделен, как предполагает приведенный выше список. вопросы
относительно метафизики, эпистемологии, семантики и математики
основы измерения взаимосвязаны и часто опираются на одно
еще один. Отсюда, например, операционалисты и конвенционалисты
часто придерживались антиреалистических взглядов и сторонников модельного
отчеты выступают против преобладающей эмпиристской интерпретации
математических теорий измерения. Эти тонкости станут
ясно в следующем обсуждении.
Эти тонкости станут
ясно в следующем обсуждении.
Список направлений стипендий не является ни исключительным, ни исчерпывающий. Он отражает историческую траекторию философского дискуссия до сих пор, а не какое-либо принципиальное различие между различные уровни анализа измерений. Некоторые философские работы по измерению принадлежат более чем одной нити, в то время как многие другие работы тоже точно не подходят. Это особенно актуально, поскольку начале 2000-х, когда измерения вернулись на первый план философская дискуссия после нескольких десятилетий относительного забвения. Эту недавнюю группу ученых иногда называют эпистемология измерения» и включает в себя богатый массив работ которые еще не могут быть классифицированы в отдельные школы мысли. Последний раздел этой статьи будет посвящен обзору некоторых эти разработки.
Хотя философия измерения сформировалась как отдельная область
исследования только во второй половине XIX в.
основные понятия измерения, такие как величина и количество
обсуждались с древности. Согласно Евклиду Элементы , величина — например, линия, поверхность или
твердый — измеряет другой, когда последний является целым кратным
первый (Книга V, опр. 1 и 2). Две величины имеют общее
меры, когда они оба являются целыми кратными некоторой величины, и
в противном случае несоизмеримы (Книга X, опр. 1). Открытие
несоизмеримые величины позволили Евклиду и его современникам
развивать понятие отношение величин. Соотношения могут быть
либо рационально, либо иррационально, и поэтому понятие отношения
более общий, чем мера (Michell 2003, 2004a;
Граттан-Гиннесс 1996).
Согласно Евклиду Элементы , величина — например, линия, поверхность или
твердый — измеряет другой, когда последний является целым кратным
первый (Книга V, опр. 1 и 2). Две величины имеют общее
меры, когда они оба являются целыми кратными некоторой величины, и
в противном случае несоизмеримы (Книга X, опр. 1). Открытие
несоизмеримые величины позволили Евклиду и его современникам
развивать понятие отношение величин. Соотношения могут быть
либо рационально, либо иррационально, и поэтому понятие отношения
более общий, чем мера (Michell 2003, 2004a;
Граттан-Гиннесс 1996).
Аристотель различал количество и качество. Примеры
количества – это числа, линии, поверхности, тела, время и место,
тогда как примерами качеств являются справедливость, здоровье, горячность и
бледность ( Категории §6 и §8). Согласно с
Аристотель, количества допускают равенство и неравенство, но не
градусов, так как «одна вещь не более четырех футов, чем другая»
(там же 6.6a19). Качества, наоборот, не допускают равенства или
неравенство, но допускают степени, «ибо одно называется
бледнее или менее бледнее другого» (там же, 8. 10b26). Аристотель
не указал четко, являются ли степени таких качеств, как бледность
соответствуют различным качествам, или одно и то же качество,
бледность, была способна различной интенсивности. Эта тема была на
центр продолжающихся дебатов в тринадцатом и четырнадцатом веках
(Юнг 2011). Дунс Скот поддерживал «теорию сложения».
согласно которому изменение степени качества может быть
объясняется сложением или вычитанием меньших степеней этого
качество (2011: 553). Позже эта теория была уточнена Николь Орем.
которые использовали геометрические фигуры для представления изменений интенсивности
такие качества, как скорость (Клагетт 1968; Силла 1971). Орем
геометрические представления установили подмножество качеств, которые
поддавались количественной обработке, тем самым бросая вызов
строгая аристотелевская дихотомия количества и качества. Эти
развития сделали возможным формулирование количественных законов
движения в шестнадцатом и семнадцатом веках (Грант
1996).
10b26). Аристотель
не указал четко, являются ли степени таких качеств, как бледность
соответствуют различным качествам, или одно и то же качество,
бледность, была способна различной интенсивности. Эта тема была на
центр продолжающихся дебатов в тринадцатом и четырнадцатом веках
(Юнг 2011). Дунс Скот поддерживал «теорию сложения».
согласно которому изменение степени качества может быть
объясняется сложением или вычитанием меньших степеней этого
качество (2011: 553). Позже эта теория была уточнена Николь Орем.
которые использовали геометрические фигуры для представления изменений интенсивности
такие качества, как скорость (Клагетт 1968; Силла 1971). Орем
геометрические представления установили подмножество качеств, которые
поддавались количественной обработке, тем самым бросая вызов
строгая аристотелевская дихотомия количества и качества. Эти
развития сделали возможным формулирование количественных законов
движения в шестнадцатом и семнадцатом веках (Грант
1996).
Концепция качественной интенсивности получила дальнейшее развитие у Лейбница. и Кант. Лейбниц сформулировал «принцип непрерывности».
что все естественные изменения производятся постепенно. Лейбниц утверждал, что
этот принцип применим не только к изменениям протяженных величин, таких как
как длина и продолжительность, но и интенсивность репрезентативного
состояния сознания, такие как звуки (Jorgensen 2009; Диль 2012).
Считается, что Кант опирался на принцип Лейбница.
преемственность, чтобы сформулировать свое различие между экстенсивным и
интенсивные величины. По Канту, экстенсивные величины
те, «в которых изображение частей делает возможным
представление целого» (1787: A162/B203). Пример
длина: линия может быть мысленно представлена только последовательным
синтез, при котором части линии соединяются в единое целое. Для Канта
возможность такого синтеза обосновывалась в формах
интуиция, а именно пространство и время. Интенсивные величины, такие как тепло или
цвета, также приходят в непрерывных степенях, но их понимание занимает
место в одно мгновение, а не посредством последовательного синтеза
части.
и Кант. Лейбниц сформулировал «принцип непрерывности».
что все естественные изменения производятся постепенно. Лейбниц утверждал, что
этот принцип применим не только к изменениям протяженных величин, таких как
как длина и продолжительность, но и интенсивность репрезентативного
состояния сознания, такие как звуки (Jorgensen 2009; Диль 2012).
Считается, что Кант опирался на принцип Лейбница.
преемственность, чтобы сформулировать свое различие между экстенсивным и
интенсивные величины. По Канту, экстенсивные величины
те, «в которых изображение частей делает возможным
представление целого» (1787: A162/B203). Пример
длина: линия может быть мысленно представлена только последовательным
синтез, при котором части линии соединяются в единое целое. Для Канта
возможность такого синтеза обосновывалась в формах
интуиция, а именно пространство и время. Интенсивные величины, такие как тепло или
цвета, также приходят в непрерывных степенях, но их понимание занимает
место в одно мгновение, а не посредством последовательного синтеза
части. Степени интенсивных величин «могут быть только
представлен через приближение к отрицанию» (1787: A
168/B210), то есть воображая их постепенное уменьшение до тех пор, пока
полное отсутствие.
Степени интенсивных величин «могут быть только
представлен через приближение к отрицанию» (1787: A
168/B210), то есть воображая их постепенное уменьшение до тех пор, пока
полное отсутствие.
Научные разработки XIX века поставили под сомнение
Различие между экстенсивными и интенсивными величинами. Термодинамика
и волновая оптика показали, что различия в температуре и оттенке
соответствовали различиям в пространственно-временных величинах, таких как
скорость и длина волны. Электрические величины, такие как сопротивление и
было показано, что проводимость способна к сложению и делению, несмотря на
не являющиеся экстенсивными в кантианском смысле, т. е. не синтезируемыми из
пространственные или временные части. Кроме того, первые эксперименты в
психофизика предположила, что интенсивность ощущений, таких как
яркость и громкость можно представить как сумму «просто
заметные различия» среди стимулов, и поэтому может быть
считать состоящим из частей (см.
Раздел 3.3).
Эти выводы, наряду с достижениями в аксиоматизации ветвей
математики, мотивировало некоторых ведущих ученых позднего
девятнадцатого века, чтобы попытаться прояснить математические основы
измерений (Максвелл 1873; фон Крис 1882; Гельмгольц 1887; Мах
1896; Пуанкаре 1898; Гельдер 1901; для исторических обзоров
см. Darrigol 2003; Мичелл 1993, 2003; Канту и Шлаудт, 2013 г.;
Бьяджоли 2016: гл. 4, 2018). Эти работы сегодня рассматриваются как
предшественники научной группы, известной как «измерение
теория».
Darrigol 2003; Мичелл 1993, 2003; Канту и Шлаудт, 2013 г.;
Бьяджоли 2016: гл. 4, 2018). Эти работы сегодня рассматриваются как
предшественники научной группы, известной как «измерение
теория».
Математические теории измерения (часто называемые собирательно
как «теория измерений») касаются условий
какие отношения между числами (и другими математическими объектами) могут быть
используется для выражения отношений между
объекты. [2] Чтобы понять необходимость математических теорий
измерения, учтите тот факт, что отношения, демонстрируемые
числа, такие как равенство, сумма, разность и отношение, не
всегда соответствуют отношениям между объектами, измеряемыми теми
числа. Например, 60 дважды равно 30, но можно ошибиться, если
думая, что объект, измеренный при температуре 60 градусов по Цельсию, в два раза горячее
как объект при 30 градусах Цельсия. Это связано с тем, что нулевая точка
шкала Цельсия произвольна и не соответствует отсутствию
из
температура. [3] Точно так же числовые интервалы не всегда несут эмпирическую
Информация. Когда испытуемых просят оценить по шкале от 1 до 7
насколько сильно они согласны с данным утверждением, нет примы
facie причина думать, что интервалы между 5 и 6 и
от 6 до 7 соответствуют равным приращениям силы мнения.
Чтобы предоставить третий пример, равенство между числами является транзитивным [если
(a=b & b=c), затем a=c], но эмпирические сравнения между физическими
величины обнаруживают лишь приблизительное равенство, которое не является транзитивным
связь. Эти примеры показывают, что не все математические
отношения между числами, используемыми в измерении, устанавливаются эмпирически
значительным, и что различные виды шкал измерения передают
различные виды эмпирически значимой информации.
Когда испытуемых просят оценить по шкале от 1 до 7
насколько сильно они согласны с данным утверждением, нет примы
facie причина думать, что интервалы между 5 и 6 и
от 6 до 7 соответствуют равным приращениям силы мнения.
Чтобы предоставить третий пример, равенство между числами является транзитивным [если
(a=b & b=c), затем a=c], но эмпирические сравнения между физическими
величины обнаруживают лишь приблизительное равенство, которое не является транзитивным
связь. Эти примеры показывают, что не все математические
отношения между числами, используемыми в измерении, устанавливаются эмпирически
значительным, и что различные виды шкал измерения передают
различные виды эмпирически значимой информации.
Изучение шкал измерений и эмпирической информации, которую они передача является основной задачей математических теорий измерения. В его основополагающее эссе 1887 года «Счет и измерение» Германа фон Гельмгольц сформулировал ключевой вопрос теории измерения как следует:
[Что] является объективным значением выражения через наименования нумерует отношения реальных предметов как величины, и под каким условия мы можем это сделать? (1887: 4)
В широком смысле теория измерения ставит своей целью (i) идентифицировать
предположения, лежащие в основе использования различных математических структур для
описания аспектов эмпирического мира и (ii) извлечения уроков о
адекватность и пределы использования этих математических структур для
описание аспектов эмпирического мира. Вслед за Отто Гёльдером
(1901), теоретики измерения часто решают эти задачи с помощью формальных
доказательства, при этом предположения в (i) служат аксиомами, а уроки
в (ii) следующие как теоремы. Ключевым моментом теории измерения является
что эмпирически значимые аспекты данного математического
структурой являются те, которые отражают соответствующие отношения между
измеряемые объекты. Например, отношение «больше
чем» среди чисел является эмпирически значимым для измерения
длина, поскольку она отражает отношение «длиннее, чем»
среди предметов. Это отражение или отображение отношений между
объекты и математические объекты составляют шкалу измерений. В качестве
будет пояснено ниже, шкалы измерений обычно понимаются как
изоморфизмы или гомоморфизмы между объектами и математическими
сущности.
Вслед за Отто Гёльдером
(1901), теоретики измерения часто решают эти задачи с помощью формальных
доказательства, при этом предположения в (i) служат аксиомами, а уроки
в (ii) следующие как теоремы. Ключевым моментом теории измерения является
что эмпирически значимые аспекты данного математического
структурой являются те, которые отражают соответствующие отношения между
измеряемые объекты. Например, отношение «больше
чем» среди чисел является эмпирически значимым для измерения
длина, поскольку она отражает отношение «длиннее, чем»
среди предметов. Это отражение или отображение отношений между
объекты и математические объекты составляют шкалу измерений. В качестве
будет пояснено ниже, шкалы измерений обычно понимаются как
изоморфизмы или гомоморфизмы между объектами и математическими
сущности.
Помимо этих широких целей и утверждений, теория измерения представляет собой
весьма неоднородный корпус ученых. В него входят произведения, охватывающие
с конца девятнадцатого века до наших дней и поддерживают широкий
множество взглядов на онтологию, эпистемологию и семантику
измерение. Два основных различия между математическими теориями
измерения, заслуживают особого упоминания. Первый касается
природа relata , или «объектов», чьи
числа отношений должны отражать. Эти релята может быть
понимается по крайней мере четырьмя различными способами: как конкретное индивидуальное
объекты, как качественные наблюдения за конкретными отдельными объектами,
как абстрактные представления отдельных объектов или как универсальные
свойства предметов. Какая интерпретация будет принята, зависит от
большая часть на метафизическом и эпистемологическом
обязательства. Этот вопрос будет особенно актуален для обсуждения
реалистичных подходов к измерению
(Раздел 5).
Во-вторых, разные теоретики измерения занимают разные позиции.
о том, какие эмпирические данные необходимы для установления
сопоставления между предметами и числами. В результате измерение
теоретики пришли к разногласиям по поводу необходимых условий для
установление измеримости атрибутов и, в частности, о
поддаются ли измерению психологические атрибуты.
Два основных различия между математическими теориями
измерения, заслуживают особого упоминания. Первый касается
природа relata , или «объектов», чьи
числа отношений должны отражать. Эти релята может быть
понимается по крайней мере четырьмя различными способами: как конкретное индивидуальное
объекты, как качественные наблюдения за конкретными отдельными объектами,
как абстрактные представления отдельных объектов или как универсальные
свойства предметов. Какая интерпретация будет принята, зависит от
большая часть на метафизическом и эпистемологическом
обязательства. Этот вопрос будет особенно актуален для обсуждения
реалистичных подходов к измерению
(Раздел 5).
Во-вторых, разные теоретики измерения занимают разные позиции.
о том, какие эмпирические данные необходимы для установления
сопоставления между предметами и числами. В результате измерение
теоретики пришли к разногласиям по поводу необходимых условий для
установление измеримости атрибутов и, в частности, о
поддаются ли измерению психологические атрибуты. Споры о
измеримости оказались очень плодотворными для развития
теории измерений, а в следующих подразделах будут представлены некоторые
этих дискуссий и основных концепций, разработанных в них.
Споры о
измеримости оказались очень плодотворными для развития
теории измерений, а в следующих подразделах будут представлены некоторые
этих дискуссий и основных концепций, разработанных в них.
3.1 Основные и производные измерения
В конце девятнадцатого и начале двадцатого века несколько были предприняты попытки дать универсальное определение измерения. Хотя подходы к измерениям различались, все согласны с тем, что измерение — это метод присвоения чисел величинам . Например, Гельмгольц (1887: 17) определял измерение как процедуру по которому находят номинальное число, выражающее стоимость величина, где «номинальное число» — это число вместе с единицей, например, 5 метров, а величина есть качество объекты, которые поддаются упорядочению от меньшего к большему, например, длина. Бертран Рассел аналогичным образом заявил, что измерение равно
любой метод, с помощью которого достигается однозначное и взаимное соответствие устанавливается между всеми или некоторыми величинами вида и всеми или некоторые из чисел, целые, рациональные или действительные.
(1903: 176)
Норман Кэмпбелл определял измерение просто как «процесс присвоение чисел для представления качеств», где качество — это свойство, которое допускает непроизвольный порядок (1920: 267).
Определение измерения как числового присвоения поднимает вопрос:
какие задания адекватны и при каких условиях? Рано
теоретики измерения, такие как Гельмгольц (1887 г.), Гельдер (1901) и
Кэмпбелл (1920) утверждал, что чисел достаточно для выражения
величин, поскольку алгебраические операции над числами отражают
эмпирические отношения между величинами. Например, качественный
отношение «длиннее, чем» между жесткими стержнями равно (примерно)
переходный и асимметричный, и в этом отношении имеет общие структурные
функции с отношением «больше чем» между числами.
Более того, сквозное сцепление жестких стержней имеет общие структурные
особенности, такие как ассоциативность и коммутативность, с
математическая операция сложения. Аналогичная ситуация имеет место для
измерение веса с помощью равноплечих весов. Здесь отклонение от
оружие обеспечивает упорядочение гирь и нагромождение гирь на
одна панорама представляет собой конкатенацию.
Здесь отклонение от
оружие обеспечивает упорядочение гирь и нагромождение гирь на
одна панорама представляет собой конкатенацию.
Ранние теоретики измерения сформулировали аксиомы, описывающие эти
качественные эмпирические структуры и использовал эти аксиомы для доказательства
теоремы об адекватности присвоения чисел величинам, которые
демонстрируют такие структуры. В частности, они доказали, что упорядочение и
конкатенации вместе достаточно для построения дополнение числовое представление соответствующих величин.
Аддитивное представление — это представление, в котором сложение производится эмпирически.
осмысленное, а значит, и умножение, деление и т. д. Кэмпбелл
называются измерительными процедурами, удовлетворяющими условиям
аддитивность «фундаментальная», потому что они не включают
измерение любой другой величины (1920: 277). Виды величин
для которых была разработана основная процедура измерения
найдены, такие как длина, площадь, объем, продолжительность, вес и
электрическое сопротивление — Кэмпбелл назвал «фундаментальным
величины». Отличительной чертой таких масштабов является то, что они
их можно сгенерировать, объединив стандартную последовательность
равные единицы, как в примере с рядом равноотстоящих меток на
линейка.
Отличительной чертой таких масштабов является то, что они
их можно сгенерировать, объединив стандартную последовательность
равные единицы, как в примере с рядом равноотстоящих меток на
линейка.
Хотя они считали аддитивность отличительной чертой измерения, большинство первые теоретики измерения признавали, что аддитивность не необходимо для измерения. Существуют и другие величины, допускающие упорядочение от меньшего к большему, но отношения и/или различия которых не могут в настоящее время определяются, кроме как через их отношения к другим, принципиально измеримые величины. Примерами являются температура, которая можно измерить, определив объем ртутного столба, и плотность, которую можно измерить как отношение массы к объему. Такой косвенное определение стало называться «производным». измерение и соответствующие величины, «полученные величины» (Кэмпбелл 1920: 275-7).
На первый взгляд различие между фундаментальным и производным
измерение может показаться напоминающим различие между экстенсивным
и интенсивные величины, и действительно фундаментальное измерение
иногда называют «обширным». Тем не менее важно
отметить, что эти два различия основаны на существенно различающихся
критерии измеримости. Как обсуждалось в
Раздел 2,
экстенсивно-интенсивное различие сосредоточено на внутреннем
структура рассматриваемой величины, т. е. является ли она
состоит из пространственно-временных частей. Фундаментальное производное
различие, напротив, фокусируется на свойствах измерения операции . Принципиально измеримая величина – это величина,
найдена фундаментальная операция измерения.
Следовательно, фундаментальность не является внутренним свойством
величина: производная величина может стать фундаментальной с
открытие новых операций для его измерения. Более того, в
фундаментальное измерение числовое присвоение не обязательно должно отражать
структура пространственно-временных частей. Электрическое сопротивление, для
Например, можно принципиально измерить, подключив резисторы в
сериал (Кэмпбелл 1920: 293). Это считается фундаментальным
операция измерения, потому что она имеет общую структуру с числовыми
Кроме того, даже несмотря на то, что объекты с одинаковым сопротивлением обычно не
равны по размеру.
Тем не менее важно
отметить, что эти два различия основаны на существенно различающихся
критерии измеримости. Как обсуждалось в
Раздел 2,
экстенсивно-интенсивное различие сосредоточено на внутреннем
структура рассматриваемой величины, т. е. является ли она
состоит из пространственно-временных частей. Фундаментальное производное
различие, напротив, фокусируется на свойствах измерения операции . Принципиально измеримая величина – это величина,
найдена фундаментальная операция измерения.
Следовательно, фундаментальность не является внутренним свойством
величина: производная величина может стать фундаментальной с
открытие новых операций для его измерения. Более того, в
фундаментальное измерение числовое присвоение не обязательно должно отражать
структура пространственно-временных частей. Электрическое сопротивление, для
Например, можно принципиально измерить, подключив резисторы в
сериал (Кэмпбелл 1920: 293). Это считается фундаментальным
операция измерения, потому что она имеет общую структуру с числовыми
Кроме того, даже несмотря на то, что объекты с одинаковым сопротивлением обычно не
равны по размеру.
Различие между фундаментальным и производным измерением было
переработаны последующими авторами. Брайан Эллис (1966: главы 5–8)
различают три типа измерений: фундаментальные,
ассоциативный и производный. Фундаментальное измерение требует упорядочения и
операции конкатенации, удовлетворяющие тем же условиям, указанным
Кэмпбелл. Ассоциативные процедуры измерения основаны на
корреляция двух упорядоченных отношений, например, корреляция
между объемом ртутного столбика и его температурой. Полученный
процедуры измерения заключаются в определении значения
постоянным в физическом законе. Константа может быть локальной, как в
определение удельной плотности воды по массе и объему,
или универсальным, как в определении ньютоновского гравитационного
постоянной от силы, массы и расстояния. Генри Кибург (1984: гл.
5–7) предложил несколько иное тройственное различие между
прямое, косвенное и систематическое измерение, которое не полностью
пересекаются с тем, что
Эллис. [4] Более радикальный пересмотр различия между фундаментальными и
производное измерение было предложено Р. Дунканом Люсом и Джоном Тьюки.
(1964) в их работе по совместному измерению, которая будет обсуждаться
в
Раздел 3.4.
Дунканом Люсом и Джоном Тьюки.
(1964) в их работе по совместному измерению, которая будет обсуждаться
в
Раздел 3.4.
3.2 Классификация весов
В предыдущем подразделе обсуждалась аксиоматизация эмпирических
структуры, направление исследований, которое восходит к ранним дням
теория измерений. Дополнительная линия исследования в рамках измерения
теория касается классификации шкал измерений.
психофизик С. С. Стивенс (1946, 1951) выделяется среди четырех
виды шкал: номинальная, порядковая, интервальная и пропорциональная. Номинальные весы
представлять объекты как принадлежащие к классам, не имеющим определенного
порядок, например, мужской и женский. Порядковые шкалы представляют порядок, но не
дальнейшая алгебраическая структура. Например, шкала Мооса минералов.
твердость представляет собой минералы с номерами от 1 (самый мягкий) до
10 (самый сложный), но нет никакого эмпирического значения в равенстве между
интервалы или отношения этих
числа. [5] Цельсия и Фаренгейта являются примерами интервальных шкал: они
представляют равенство или неравенство между интервалами температуры, но
не отношения температур, потому что их нулевые точки произвольны. Шкала Кельвина, напротив, представляет собой шкалу отношений, как и привычные
шкалы, представляющие массу в килограммах, длину в метрах и продолжительность
в секундах. Позднее Стивенс усовершенствовал эту классификацию и
различают линейную и логарифмическую шкалы интервалов (1959:
31–34) и между шкалами отношений с натуральной единицей и без нее.
(1959: 34). Шкалы отношений с натуральными единицами, такие как те, которые используются для
для подсчета дискретных объектов и для представления вероятностей, были
называются «абсолютными» весами.
Шкала Кельвина, напротив, представляет собой шкалу отношений, как и привычные
шкалы, представляющие массу в килограммах, длину в метрах и продолжительность
в секундах. Позднее Стивенс усовершенствовал эту классификацию и
различают линейную и логарифмическую шкалы интервалов (1959:
31–34) и между шкалами отношений с натуральной единицей и без нее.
(1959: 34). Шкалы отношений с натуральными единицами, такие как те, которые используются для
для подсчета дискретных объектов и для представления вероятностей, были
называются «абсолютными» весами.
Как отмечает Стивенс, типы шкал индивидуализируются семействами
преобразования, которые они могут претерпевать без потери эмпирической
Информация. Эмпирические отношения, представленные на шкалах отношений, для
например, инвариантны относительно умножения на положительное число,
например, умножение на 2,54 преобразует дюймы в сантиметры.
Линейные шкалы интервалов допускают умножение на положительное число
и постоянный сдвиг, например, преобразование из градусов Цельсия в градусы Фаренгейта
по формуле °С × 9/5 + 32 = °F. Порядковые шкалы допускают любую функцию преобразования, если она
монотонная и возрастающая, а номинальные шкалы допускают любые взаимно-однозначные
замена. Абсолютные шкалы не допускают никаких преобразований, кроме
личность. Классификация чешуи Стивенса была позже
обобщены Louis Narens (1981, 1985: Ch. 2) и Luce et al. (1990:
Ч. 20) с точки зрения однородности и уникальности соответствующих
группы трансформации.
Порядковые шкалы допускают любую функцию преобразования, если она
монотонная и возрастающая, а номинальные шкалы допускают любые взаимно-однозначные
замена. Абсолютные шкалы не допускают никаких преобразований, кроме
личность. Классификация чешуи Стивенса была позже
обобщены Louis Narens (1981, 1985: Ch. 2) и Luce et al. (1990:
Ч. 20) с точки зрения однородности и уникальности соответствующих
группы трансформации.
В то время как классификация весов Стивенса встречалась с общими
одобрение в научных и философских кругах, его более широкое
последствия для теории измерения стали темой значительного
дебаты. Особенно спорными были два вопроса. Первый был ли
операции классификации и упорядочения заслуживают того, чтобы их называли
операции «измерения» и, соответственно,
представление величин в номинальной и порядковой шкалах должно
считать измерением. Несколько физиков, в том числе Кэмпбелл, утверждали,
что операции классификации и упорядочивания не обеспечивают
достаточно богатая структура, чтобы оправдать использование чисел, и, следовательно,
не должны считаться операциями измерения. Второй спорный вопрос
нужно ли было найти операцию конкатенации для величины
до того, как его можно было фундаментально измерить по шкале отношений. Обсуждение
стал особенно накален, когда он снова разжег более длительную полемику
вокруг измеримости интенсивности ощущения. Это для
этот спор мы сейчас перейдем.
Второй спорный вопрос
нужно ли было найти операцию конкатенации для величины
до того, как его можно было фундаментально измерить по шкале отношений. Обсуждение
стал особенно накален, когда он снова разжег более длительную полемику
вокруг измеримости интенсивности ощущения. Это для
этот спор мы сейчас перейдем.
3.3 Измеримость ощущений
Один из главных катализаторов развития математических теорий
измерения были постоянными дебатами вокруг измеримости в
психология. Споры часто восходят к Густаву Фехнеру.
(1860) Элементы психофизики , в которой он описал
Метод измерения интенсивности ощущений. метод Фехнера
был основан на записи «просто заметных
различия» между ощущениями, связанными с парами
раздражители, например, два звука разной интенсивности. Эти различия
считались равными приращениями интенсивности ощущения. В качестве
Фехнер показал, что при этом предположении устойчивая линейная зависимость имеет вид
между интенсивностью ощущения и логарифмом
интенсивность раздражителя, отношение, которое стало известно как
«Закон Фехнера» (Гейдельбергер 1993а: 203; Люси и
Суппес 2004: 11–2). Этот закон, в свою очередь, обеспечивает метод
косвенно измеряя интенсивность ощущений, измеряя
интенсивность стимула и, следовательно, Фехнер утверждал, обеспечивает
обоснование измерения интенсивности ощущений на реальном
числа.
Этот закон, в свою очередь, обеспечивает метод
косвенно измеряя интенсивность ощущений, измеряя
интенсивность стимула и, следовательно, Фехнер утверждал, обеспечивает
обоснование измерения интенсивности ощущений на реальном
числа.
Утверждения Фехнера об измеримости ощущения
стал предметом ряда дебатов, длившихся почти столетие.
и оказался чрезвычайно плодотворным для философии измерения,
с участием ключевых фигур, таких как Мах, Гельмгольц, Кэмпбелл и Стивенс
(Гейдельбергер 1993а: гл. 6 и 1993b; Мичелл 1999: гл. 6). Те
возражая против измеримости ощущения, такие как Кэмпбелл,
подчеркнул необходимость эмпирической операции конкатенации для
фундаментальное измерение. Поскольку интенсивность ощущений не может быть
соединены друг с другом способом, обеспечиваемым длинами и
веса, не может быть фундаментального измерения ощущения
интенсивность. Более того, Кэмпбелл утверждал, что ни одно из психофизических
открытые к настоящему времени закономерности достаточно универсальны, чтобы считать
как законы в смысле, необходимом для производных измерений (Кэмпбелл в
Фергюсон и др. 1940: 347). Все, что показали психофизики,
что интенсивность ощущений можно последовательно упорядочить, но упорядочить
само по себе еще не гарантирует использование числовых отношений, таких как
суммы и соотношения для выражения эмпирических результатов.
1940: 347). Все, что показали психофизики,
что интенсивность ощущений можно последовательно упорядочить, но упорядочить
само по себе еще не гарантирует использование числовых отношений, таких как
суммы и соотношения для выражения эмпирических результатов.
Центральным оппонентом Кэмпбелла в этих дебатах был Стивенс, чей
Различие между типами шкал измерения обсуждалось выше.
Стивенс определял измерение как «присвоение цифр
объектов или событий в соответствии с правилами» (1951: 1) и утверждал, что
любое последовательное и неслучайное назначение считается измерением в
широкий смысл (1975: 47). В полезных случаях научных исследований Стивенс
заявленное, измерение может быть истолковано несколько более узко как
числовое присвоение, основанное на результатах сопоставления с операции, такие как привязка температуры к объему ртути или
соответствие ощущений друг другу. Стивенс выступал против
считают, что отношения между числами должны отражать качественные эмпирические
структур, утверждая вместо этого, что шкалы измерения должны быть
рассматриваются как произвольные формальные схемы и принимаются в соответствии с
их полезность для описания эмпирических данных. Например, принятие
шкала отношений для измерения ощущений громкости, громкости и
плотность звуков приводит к формулировке простого линейного соотношения
среди отчетов подопытных: громкость = громкость ×
плотность (1975: 57–8). Такое присвоение цифр ощущениям
считается измерением, потому что оно последовательно и неслучайно, потому что
он основан на операциях сопоставления, выполняемых экспериментальными
испытуемых, а также потому, что он фиксирует закономерности в экспериментальных
полученные результаты. По словам Стивенса, эти условия вместе
достаточно, чтобы оправдать использование шкалы отношений для измерения
ощущения, несмотря на то, что «ощущения не могут быть
разделены на составные части или уложены встык, как измерительные
палочки» (1975: 38; см. также Hempel 1952: 68–9).
Например, принятие
шкала отношений для измерения ощущений громкости, громкости и
плотность звуков приводит к формулировке простого линейного соотношения
среди отчетов подопытных: громкость = громкость ×
плотность (1975: 57–8). Такое присвоение цифр ощущениям
считается измерением, потому что оно последовательно и неслучайно, потому что
он основан на операциях сопоставления, выполняемых экспериментальными
испытуемых, а также потому, что он фиксирует закономерности в экспериментальных
полученные результаты. По словам Стивенса, эти условия вместе
достаточно, чтобы оправдать использование шкалы отношений для измерения
ощущения, несмотря на то, что «ощущения не могут быть
разделены на составные части или уложены встык, как измерительные
палочки» (1975: 38; см. также Hempel 1952: 68–9).
3.4 Репрезентативная теория измерений
В середине двадцатого века два основных направления исследований в
теории измерения, посвященной эмпирическим условиям
количественная оценка и классификация весов,
сошлись в работах Патрика Суппеса (1951; Скотт и Суппес, 1958;
исторические обзоры см. в Savage and Ehrlich 1992; Диез, 1997а,б).
Работа Зюппеса заложила основу репрезентативной теории
Измерение (RTM), которое остается самым влиятельным математическим
теории измерения на сегодняшний день (Кранц и др. 1971; Суппес и др. 1989 год;
Люс и др. 1990). RTM определяет измерение как построение
отображения эмпирических реляционных структур в числовые
реляционные структуры (Кранц и др. 1971: 9). Эмпирическое отношение
структура состоит из набора эмпирических объектов (например, жестких стержней)
наряду с определенными качественными отношениями между ними (например, упорядоченность,
конкатенация), в то время как числовая реляционная структура состоит из
набор чисел (например, действительных чисел) и конкретных математических
отношения между ними (например, «равно или больше, чем»,
добавление). Проще говоря, шкала измерения – это отношение «многие к одному».
отображение — гомоморфизм — от эмпирического к числовому
реляционная структура, а измерение есть построение
Весы. [6] RTM уделяет большое внимание разъяснению предположений, лежащих в основе
построение различных типов измерительных шкал.
в Savage and Ehrlich 1992; Диез, 1997а,б).
Работа Зюппеса заложила основу репрезентативной теории
Измерение (RTM), которое остается самым влиятельным математическим
теории измерения на сегодняшний день (Кранц и др. 1971; Суппес и др. 1989 год;
Люс и др. 1990). RTM определяет измерение как построение
отображения эмпирических реляционных структур в числовые
реляционные структуры (Кранц и др. 1971: 9). Эмпирическое отношение
структура состоит из набора эмпирических объектов (например, жестких стержней)
наряду с определенными качественными отношениями между ними (например, упорядоченность,
конкатенация), в то время как числовая реляционная структура состоит из
набор чисел (например, действительных чисел) и конкретных математических
отношения между ними (например, «равно или больше, чем»,
добавление). Проще говоря, шкала измерения – это отношение «многие к одному».
отображение — гомоморфизм — от эмпирического к числовому
реляционная структура, а измерение есть построение
Весы. [6] RTM уделяет большое внимание разъяснению предположений, лежащих в основе
построение различных типов измерительных шкал. Каждый тип
масштаба связано с набором предположений о качественном
отношения, возникающие между объектами, представленными на шкале этого типа.
Из этих предположений или аксиом авторы RTM выводят
репрезентативной адекватности каждого масштабного типа, а также семейства
допустимые преобразования, делающие этот тип шкалы уникальным. В этом
способ, которым RTM обеспечивает концептуальную связь между эмпирической основой
измерение и типология
Весы. [7]
Каждый тип
масштаба связано с набором предположений о качественном
отношения, возникающие между объектами, представленными на шкале этого типа.
Из этих предположений или аксиом авторы RTM выводят
репрезентативной адекватности каждого масштабного типа, а также семейства
допустимые преобразования, делающие этот тип шкалы уникальным. В этом
способ, которым RTM обеспечивает концептуальную связь между эмпирической основой
измерение и типология
Весы. [7]
Что касается измеримости, репрезентативная теория занимает
средний путь между либеральным подходом, принятым Стивенсом, и
строгий акцент на операциях конкатенации, поддерживаемых Кэмпбеллом. Нравиться
Кэмпбелл, RTM признает, что правила количественного определения должны быть основаны на
известных эмпирических структур и не должны выбираться произвольно, чтобы соответствовать
данные. Однако RTM отвергает идею о том, что аддитивные шкалы
подходит только тогда, когда доступны операции конкатенации (Luce и
Суппес 2004: 15). Вместо этого RTM утверждает существование фундаментальных
операции измерения, не связанные с конкатенацией. Центральный
Пример такого типа операции известен как «аддитивный конджойнт».
измерение» (Люс и Тьюки 1964; Кранц и др. 1971:
17–21 и гл. 6–7). Здесь измерения двух или более
различные типы атрибутов, такие как температура и давление
газа, получают путем наблюдения за их совместным действием, например
объем газа. Люс и Тьюки показали, что, устанавливая определенные
качественные отношения между объемами при изменении температуры
и давления можно построить аддитивные представления
температуры и давления, не прибегая к каким-либо предшествующим методам
измерение объема. Такого рода процедура применима к любому
соответственно связанная тройка атрибутов, таких как громкость,
интенсивность и частота чистых тонов или предпочтение вознаграждения,
его размер и задержка с его получением (Luce and Suppes 2004: 17).
открытие аддитивного совместного измерения привело авторов RTM к
разделить фундаментальные измерения на два вида: традиционные измерения
процедуры, основанные на операциях конкатенации, которые они назвали
«обширное измерение» и совместное или
«неэкстенсивное» фундаментальное измерение.
Вместо этого RTM утверждает существование фундаментальных
операции измерения, не связанные с конкатенацией. Центральный
Пример такого типа операции известен как «аддитивный конджойнт».
измерение» (Люс и Тьюки 1964; Кранц и др. 1971:
17–21 и гл. 6–7). Здесь измерения двух или более
различные типы атрибутов, такие как температура и давление
газа, получают путем наблюдения за их совместным действием, например
объем газа. Люс и Тьюки показали, что, устанавливая определенные
качественные отношения между объемами при изменении температуры
и давления можно построить аддитивные представления
температуры и давления, не прибегая к каким-либо предшествующим методам
измерение объема. Такого рода процедура применима к любому
соответственно связанная тройка атрибутов, таких как громкость,
интенсивность и частота чистых тонов или предпочтение вознаграждения,
его размер и задержка с его получением (Luce and Suppes 2004: 17).
открытие аддитивного совместного измерения привело авторов RTM к
разделить фундаментальные измерения на два вида: традиционные измерения
процедуры, основанные на операциях конкатенации, которые они назвали
«обширное измерение» и совместное или
«неэкстенсивное» фундаментальное измерение. Под этим новым
концепция фундаментальности, все традиционные физические атрибуты
могут быть измерены фундаментально, как и многие психологические
атрибуты (Кранц и др. 1971: 502–3).
Под этим новым
концепция фундаментальности, все традиционные физические атрибуты
могут быть измерены фундаментально, как и многие психологические
атрибуты (Кранц и др. 1971: 502–3).
Выше мы видели, что математические теории измерения в первую очередь
связанные с математическими свойствами шкал измерения и
условия их применения. Связанная, но отдельная нить
наука касается значения и использования количественных терминов. Научный
теории и модели обычно выражаются в терминах количественных
отношения между параметрами, носящие имена, такие как
«продолжительность», «уровень безработицы» и
«интроверсия». Реалист в отношении одного из этих терминов
утверждают, что это относится к набору свойств или отношений, которые существуют
независимо от измерения. Операционалист или конвенционалист
утверждал бы, что то, как такие количественные термины применяются к конкретным
детали зависят от нетривиального выбора, сделанного людьми, и
особенно на выбор, который имеет отношение к тому, как соответствующие
измеряется количество. Обратите внимание, что в рамках этой широкой интерпретации реализм
совместим с операционализмом и конвенционализмом. То есть это
возможно, что выбор метода измерения регулирует использование
количество-срок и что, учитывая правильный выбор, этот срок
удается сослаться на независимое от разума свойство или отношение.
Тем не менее, многие операционалисты и конвенционалисты приняли
более сильные взгляды, согласно которым нет никаких фактов по делу, как
какая из нескольких и нетривиально различных операций верна
для применения заданного количественного термина. Эти более сильные варианты
несовместимы с реализмом в отношении измерения. Этот раздел будет
посвященный операционализму и конвенционализму, а рядом
реализм в измерении.
Обратите внимание, что в рамках этой широкой интерпретации реализм
совместим с операционализмом и конвенционализмом. То есть это
возможно, что выбор метода измерения регулирует использование
количество-срок и что, учитывая правильный выбор, этот срок
удается сослаться на независимое от разума свойство или отношение.
Тем не менее, многие операционалисты и конвенционалисты приняли
более сильные взгляды, согласно которым нет никаких фактов по делу, как
какая из нескольких и нетривиально различных операций верна
для применения заданного количественного термина. Эти более сильные варианты
несовместимы с реализмом в отношении измерения. Этот раздел будет
посвященный операционализму и конвенционализму, а рядом
реализм в измерении.
Операционализм (или «операционализм») в отношении измерения точка зрения, согласно которой значение количественных понятий определяется набор операций, используемых для их измерения. Самое сильное выражение операционализма появляется в ранних работах Перси Бриджмена (1927), который утверждал, что
мы подразумеваем под любым понятием не что иное, как совокупность операций; в понятие является синонимом соответствующего набора операций.
(1927: 5)
Длина, например, будет определена как результат операции
соединения жестких стержней. Согласно этой крайней версии
операционализм, разные операции измеряют разные величины.
Длина измеряется линейкой и синхронизацией электромагнитных импульсов.
следует, строго говоря, разделить на два различных
количественные понятия, помеченные как «длина-1» и
«длина-2» соответственно. Этот вывод привел Бриджмена к
утверждают, что принятые в настоящее время концепции количества
«суставы», где различные операции перекрываются в их
область применения. Он предостерег от догматической веры в единство
количественных понятий в этих «стыках», призывая вместо этого
чтобы единство проверялось опытами всякий раз, когда применяется
понятие количества должно быть расширено в новую область. Тем не менее,
Бриджмен признал, что до тех пор, пока результаты различных операций
согласен в пределах ошибки эксперимента, прагматически оправдано маркировать
соответствующие одноименные величины (1927:
16). [8]
[8]
Операционализм стал влиятельным в психологии, где он
хорошо принят такими бихевиористами, как Эдвин Боринг (1945) и Б.Ф.
Скиннер (1945). Действительно, Скиннер утверждал, что бихевиоризм
«не более чем тщательный оперативный анализ
традиционные менталистические концепции» (1945: 271). Стивенс, который был
Ученик Боринга, был ключевым пропагандистом операционализма в
психологии, и утверждал, что психологические понятия имеют эмпирические
значение только в том случае, если они обозначают определенные и конкретные операции (1935:
517; см. также Исаак 2017). Представление о том, что понятия определяются
операции измерения согласуются с либеральными взглядами Стивенса
по измеримости, которые обсуждались выше
(раздел 3.3).
Пока присвоение номеров объектам выполняется в
в соответствии с конкретными и последовательными правилами, Стивенс утверждал, что
такое присвоение имеет эмпирический смысл и не требует выполнения каких-либо
дополнительные ограничения. Тем не менее, Стивенс, вероятно, не принял
антиреалистический взгляд на психологические атрибуты. Вместо этого там
есть веские основания полагать, что он понимал операционализм как
методологическая установка, которая была ценна в той мере, в какой
позволили психологам обосновать выводы, которые они сделали из
эксперименты (Фест, 2005). Например, Стивенс не лечил
рабочие определения как априори , но как поддающийся
улучшение в свете эмпирических открытий, подразумевая, что он принял
психологические атрибуты, чтобы существовать независимо от таких определений
(Стивенс 1935: 527). Это говорит о том, что операционализм Стивенса
был более умеренным разнообразием, чем то, что можно найти в ранних произведениях.
из
Бриджмен. [9]
Вместо этого там
есть веские основания полагать, что он понимал операционализм как
методологическая установка, которая была ценна в той мере, в какой
позволили психологам обосновать выводы, которые они сделали из
эксперименты (Фест, 2005). Например, Стивенс не лечил
рабочие определения как априори , но как поддающийся
улучшение в свете эмпирических открытий, подразумевая, что он принял
психологические атрибуты, чтобы существовать независимо от таких определений
(Стивенс 1935: 527). Это говорит о том, что операционализм Стивенса
был более умеренным разнообразием, чем то, что можно найти в ранних произведениях.
из
Бриджмен. [9]
Поначалу операционализм был встречен с энтузиазмом логическими позитивистами.
рассматривал его как родственное верификационизму. Тем не менее, вскоре
показало, что любая попытка построить теорию значения на
операционалистские принципы были пронизаны проблемами. Среди таких
проблемы заключались в автоматическом операционализме надежности, присущем
измерительные операции, двусмысленность, связанная с понятием
операция, чрезмерно ограничительный операционный критерий
осмысленность, а также тот факт, что многие полезные теоретические концепции
не имеют четких операционных определений (Chang
2009 г. ). [10] В частности, Карл Хемпель (1956, 1966) критиковал операционалистов.
за неспособность определить диспозиционные термины, такие как
«растворимость в воде», и для умножения числа
научных концепций таким образом, который противоречит необходимости
систематические и простые теории. Соответственно, большинство писателей на
семантика количественных терминов избегала поддержки операционного
анализ. [11]
). [10] В частности, Карл Хемпель (1956, 1966) критиковал операционалистов.
за неспособность определить диспозиционные термины, такие как
«растворимость в воде», и для умножения числа
научных концепций таким образом, который противоречит необходимости
систематические и простые теории. Соответственно, большинство писателей на
семантика количественных терминов избегала поддержки операционного
анализ. [11]
Более широко пропагандируемый подход допускал наличие традиционного элемента в
использование количественных терминов, сопротивляясь попыткам уменьшить
значение количественных терминов для операций измерения. Эти аккаунты
классифицируются под общим заголовком
«конвенционализм», хотя они различаются в конкретных
аспекты измерения, которые они считают общепринятыми, и в степени
произвол они приписывают таким
соглашения. [12] Первым предшественником конвенционализма был Эрнст Мах, исследовавший
понятие равенства температурных интервалов (1896: 52). Маха
отметил, что различные типы термометрической жидкости расширяются в разное время.
(и нелинейно связанные) скорости при нагреве, что ставит вопрос:
Какая жидкость наиболее равномерно расширяется при изменении температуры? Согласно с
Мах, нет никакой разницы, какая жидкость расширяется больше
равномерно, поскольку само понятие равенства температур
интервалы не имеют определенного применения до обычного
выбор стандартной термометрической жидкости. Мах ввел термин
«принцип координации» для такого рода
условно выбранный принцип применения величины
концепция. Понятия единообразия времени и пространства получили схожие
процедуры Анри Пуанкаре (1898, 1902: Часть 2).
Пуанкаре утверждал, что процедуры, используемые для определения равенства
среди продолжительностей проистекают из бессознательного предпочтения ученых
описательной простоты, а не от каких-либо фактов о природе.
Точно так же выбор ученых представлять пространство либо
Евклидова или неевклидова геометрия не определяется опытом
а из соображений удобства.
Маха
отметил, что различные типы термометрической жидкости расширяются в разное время.
(и нелинейно связанные) скорости при нагреве, что ставит вопрос:
Какая жидкость наиболее равномерно расширяется при изменении температуры? Согласно с
Мах, нет никакой разницы, какая жидкость расширяется больше
равномерно, поскольку само понятие равенства температур
интервалы не имеют определенного применения до обычного
выбор стандартной термометрической жидкости. Мах ввел термин
«принцип координации» для такого рода
условно выбранный принцип применения величины
концепция. Понятия единообразия времени и пространства получили схожие
процедуры Анри Пуанкаре (1898, 1902: Часть 2).
Пуанкаре утверждал, что процедуры, используемые для определения равенства
среди продолжительностей проистекают из бессознательного предпочтения ученых
описательной простоты, а не от каких-либо фактов о природе.
Точно так же выбор ученых представлять пространство либо
Евклидова или неевклидова геометрия не определяется опытом
а из соображений удобства.
Конвенционализм в отношении измерения достиг своего наибольшего
изощренное выражение в логическом позитивизме. Логические позитивисты
как Ганс Райхенбах и Рудольф Карнап предложили «координационную
определения» или «правила соответствия» в качестве
семантическая связь между теоретическими и наблюдательными терминами. Эти а
Priori , формулировки, подобные определениям, предназначались для регулирования
использование теоретических терминов, связывая их с эмпирическими процедурами
(Reichenbach 1927: 14–19; Carnap 1966: Ch. 24). Пример
координационным определением является утверждение: «измерительная рейка
сохраняет свою длину при транспортировке». Согласно Рейхенбаху,
это утверждение не может быть проверено эмпирически, потому что универсальное и
может существовать экспериментально необнаружимая сила, которая в равной степени искажает
длина каждого объекта при его транспортировке. В соответствии с
верификационизм, утверждения, которые не поддаются проверке, не являются ни истинными, ни
ЛОЖЬ. Наоборот, Рейхенбах воспринял это заявление как выражение
произвольное правило регулирования использования понятия равенства
длина, а именно, для определения того, являются ли конкретные экземпляры длины
равны (Рейхенбах 1927:16). В то же время координационный
определения рассматривались не как замена, а как необходимость
дополнения к привычному виду теоретических определений понятий
с точки зрения других понятий (1927: 14). Под конвенционалистом
точки зрения, то спецификация операций измерения не
исчерпывают смысл таких понятий, как длина или равенство длины,
тем самым избегая многих проблем, связанных с
операционализм. [13]
Наоборот, Рейхенбах воспринял это заявление как выражение
произвольное правило регулирования использования понятия равенства
длина, а именно, для определения того, являются ли конкретные экземпляры длины
равны (Рейхенбах 1927:16). В то же время координационный
определения рассматривались не как замена, а как необходимость
дополнения к привычному виду теоретических определений понятий
с точки зрения других понятий (1927: 14). Под конвенционалистом
точки зрения, то спецификация операций измерения не
исчерпывают смысл таких понятий, как длина или равенство длины,
тем самым избегая многих проблем, связанных с
операционализм. [13]
Реалисты в отношении измерения утверждают, что измерение лучше всего
понимается как эмпирическая оценка объективного свойства или
связь. Необходимо сделать несколько поясняющих замечаний в отношении
это характеристика измерения. Во-первых, термин
«объективный» не означает исключения ментальных свойств или
отношения, являющиеся объектами психологического измерения. Скорее,
измеримые свойства или отношения считаются объективными, поскольку
поскольку они независимы от верований и условностей людей
проведения измерения и методов, используемых для измерения. За
например, реалист утверждал бы, что отношение длины данного
сплошной стержень к эталонному метру имеет объективное значение независимо от
измеряется ли и как. Во-вторых, термин
«оценка» используется реалистами, чтобы подчеркнуть факт
что результаты измерений всего приближения истинного
ценностей (Trout 1998: 46). В-третьих, по мнению реалистов, измерение
направлена на получение знаний о свойствах и отношениях, а не
чем при присвоении значений непосредственно отдельным объектам. Это
важно, потому что наблюдаемые объекты (например, рычаги, химические
решения, люди) часто создают экземпляры измеримых свойств и
отношения, которые не наблюдаются непосредственно (например, количество механических
работа, более кислая, чем интеллект). Знание утверждает о таких
свойства и отношения должны предполагать некоторую фоновую теорию.
Скорее,
измеримые свойства или отношения считаются объективными, поскольку
поскольку они независимы от верований и условностей людей
проведения измерения и методов, используемых для измерения. За
например, реалист утверждал бы, что отношение длины данного
сплошной стержень к эталонному метру имеет объективное значение независимо от
измеряется ли и как. Во-вторых, термин
«оценка» используется реалистами, чтобы подчеркнуть факт
что результаты измерений всего приближения истинного
ценностей (Trout 1998: 46). В-третьих, по мнению реалистов, измерение
направлена на получение знаний о свойствах и отношениях, а не
чем при присвоении значений непосредственно отдельным объектам. Это
важно, потому что наблюдаемые объекты (например, рычаги, химические
решения, люди) часто создают экземпляры измеримых свойств и
отношения, которые не наблюдаются непосредственно (например, количество механических
работа, более кислая, чем интеллект). Знание утверждает о таких
свойства и отношения должны предполагать некоторую фоновую теорию. По
перенос акцента с объектов на свойства и отношения,
реалисты подчеркивают теоретический характер измерений.
По
перенос акцента с объектов на свойства и отношения,
реалисты подчеркивают теоретический характер измерений.
Реализм в отношении измерения не следует путать с реализмом в отношении
объекты (например, электроны). И не реализм в измерении
обязательно влекут за собой реализм в отношении свойств (например, температуры), поскольку
в принципе можно было принять только реальность отношений (например,
отношения между количествами), не принимая во внимание реальность лежащих в основе
характеристики. Тем не менее, большинство философов, защищавших реализм
об измерении сделали это, выступив за некую форму реализма
о свойствах (Байерли и Лазара 1973; Суойер 1987; Манди 1987;
Форель 1998, 2000). Эти реалисты утверждают, что по крайней мере некоторые измеримые
свойства существуют независимо от верований и условностей
людей, которые их измеряют, и что существование и структура этих
properties обеспечивает лучшее объяснение ключевых особенностей
измерения, включая полезность чисел для выражения
результаты измерений и надежность средств измерений.
Например, типичный реалист об измерении длины сказал бы:
что эмпирические закономерности, проявляемые отдельными объектами
длины, когда они упорядочены и соединены, лучше всего объясняются
предполагая, что длина является объективным свойством, имеющим обширную
структура (Свойер 1987: 271-4). То есть отношения между длинами
такие как «длиннее, чем» и «сумма» существуют
независимо от того, являются ли какие-либо объекты упорядоченными и
соединены людьми, и действительно независимо от того, являются ли объекты
некоторая конкретная длина вообще существует. Существование
экстенсивная структура свойств означает, что длины разделяют большую часть своих
структура с положительными действительными числами, и это объясняет
полезность положительных вещественных чисел в представлении длин. Более того, если
измеримые свойства анализируются в терминах диспозиции, становится
легко объяснить, почему некоторые измерительные приборы надежны. За
Например, если предположить, что определенное количество электрического тока в
провод влечет за собой склонность отклонять стрелку амперметра на определенную
угла, следует, что показания амперметра
контрфактически зависят от количества электрического тока в проводе,
и поэтому что амперметр надежен (Форель 1998: 65).
Другой аргумент в пользу реализма в отношении измерения принадлежит Джоэлу. Мичелл (1994, 2005), который предлагает реалистическую теорию чисел, основанную на Евклидово понятие соотношения. По словам Мичелла, цифры отношения между величинами и, следовательно, существуют в пространстве и времени. В частности, 90 323 действительных числа 90 324 являются отношениями между парами бесконечные стандартные последовательности, например последовательность длин обычно обозначаются «1 метр», «2 метра» и т. д., а последовательность целых кратных длины, которую мы пытаемся измерить. Измерение – это обнаружение и оценка таких соотношений. Ан интересным следствием этого эмпирического реализма в отношении чисел является что измерение является не репрезентативной деятельностью, а скорее активность аппроксимации независимых от разума чисел (Мишелл 1994: 400).
Реалистические подходы к измерению в значительной степени сформулированы в оппозиции
к сильным версиям операционализма и конвенционализма, которые
доминировал в философских дискуссиях об измерениях с 1930-х годов. до 1960-х годов. Помимо недостатков операционализма
уже обсуждалось в предыдущем разделе, реалисты отмечают, что
антиреализм в отношении измеримых величин не имеет смысла
научная практика. Если бы величины не имели действительных значений независимо от
выбор процедуры измерения, было бы трудно
объяснить, что ученые подразумевают под «точностью измерения» и
«погрешность измерения», и почему пытаются повысить точность
и уменьшить ошибку. Напротив, реалисты могут легко понять
представления о точности и погрешности с точки зрения расстояния между реальными
и измеренные значения (Байерли и Лазара 1973: 17–8; Свойер 1987:
239; Траут 1998: 57). Тесно связанным моментом является тот факт, что более новые
процедуры измерения, как правило, улучшают точность старых.
Если бы выбор процедуры измерения был просто условным, это было бы
трудно понять смысл такого прогресса. Кроме того, реализм
обеспечивает интуитивно понятное объяснение того, почему различные измерения
процедуры часто дают аналогичные результаты, а именно потому, что они
чувствительны к одним и тем же фактам (Swoyer 1987: 239; Trout 1998: 56).
до 1960-х годов. Помимо недостатков операционализма
уже обсуждалось в предыдущем разделе, реалисты отмечают, что
антиреализм в отношении измеримых величин не имеет смысла
научная практика. Если бы величины не имели действительных значений независимо от
выбор процедуры измерения, было бы трудно
объяснить, что ученые подразумевают под «точностью измерения» и
«погрешность измерения», и почему пытаются повысить точность
и уменьшить ошибку. Напротив, реалисты могут легко понять
представления о точности и погрешности с точки зрения расстояния между реальными
и измеренные значения (Байерли и Лазара 1973: 17–8; Свойер 1987:
239; Траут 1998: 57). Тесно связанным моментом является тот факт, что более новые
процедуры измерения, как правило, улучшают точность старых.
Если бы выбор процедуры измерения был просто условным, это было бы
трудно понять смысл такого прогресса. Кроме того, реализм
обеспечивает интуитивно понятное объяснение того, почему различные измерения
процедуры часто дают аналогичные результаты, а именно потому, что они
чувствительны к одним и тем же фактам (Swoyer 1987: 239; Trout 1998: 56). Наконец, реалисты отмечают, что конструкция измерительной аппаратуры
и при анализе результатов измерений руководствуются теоретическими
предположения о причинно-следственных связях между величинами.
способность таких причинно-следственных предположений направлять измерения предполагает, что
количества онтологически предшествуют процедурам измерения
их. [14]
Наконец, реалисты отмечают, что конструкция измерительной аппаратуры
и при анализе результатов измерений руководствуются теоретическими
предположения о причинно-следственных связях между величинами.
способность таких причинно-следственных предположений направлять измерения предполагает, что
количества онтологически предшествуют процедурам измерения
их. [14]
Хотя их позиция в отношении операционализма и конвенционализма
в значительной степени критичны, реалисты более снисходительны в своих оценках
математические теории измерения. Брент Манди (1987) и Крис
Swoyer (1987) оба принимают аксиоматическую трактовку измерения.
шкалы, но возражают против эмпирической интерпретации, данной
аксиомы выдающихся теоретиков измерения, таких как Кэмпбелл (1920) и
Эрнест Нагель (1931; Коэн и Нагель, 1934: гл. 15). Скорее, чем
интерпретируя аксиомы как относящиеся к конкретным объектам или к
наблюдаемые отношения между такими объектами Манди и Свойер интерпретируют по-новому.
аксиомы, относящиеся к универсальным величинам, например, к
универсальное свойство быть длиной 5 метров, а не бетоном
экземпляры этого свойства. Эта конструкция сохраняет
интуиция, что такие утверждения, как «размер x в два раза больше
размер y ”в первую очередь около двух размеры , и только производные от объектов х и и самих себя (Mundy 1987:
34). [15] Манди и Свойер утверждают, что их интерпретация носит более общий характер.
потому что оно логически влечет за собой все следствия первого порядка
эмпирическая интерпретация вместе с дополнительными утверждениями второго порядка
о вселенских величинах. Более того, в их интерпретации
теория измерения становится подлинно научной теорией,
объясняющие гипотезы и проверяемые предсказания. Опираясь на это
работа, Джо Вольф (2020a) недавно предложил новый реалистический взгляд на
величин, которая опирается на репрезентативную теорию
Измерение. Согласно структуралистской теории Вольфа
количество, количественные признаки являются реляционными структурами.
В частности, атрибут является количественным, если его структура
переводы, образующие архимедову упорядоченную группу.
Эта конструкция сохраняет
интуиция, что такие утверждения, как «размер x в два раза больше
размер y ”в первую очередь около двух размеры , и только производные от объектов х и и самих себя (Mundy 1987:
34). [15] Манди и Свойер утверждают, что их интерпретация носит более общий характер.
потому что оно логически влечет за собой все следствия первого порядка
эмпирическая интерпретация вместе с дополнительными утверждениями второго порядка
о вселенских величинах. Более того, в их интерпретации
теория измерения становится подлинно научной теорией,
объясняющие гипотезы и проверяемые предсказания. Опираясь на это
работа, Джо Вольф (2020a) недавно предложил новый реалистический взгляд на
величин, которая опирается на репрезентативную теорию
Измерение. Согласно структуралистской теории Вольфа
количество, количественные признаки являются реляционными структурами.
В частности, атрибут является количественным, если его структура
переводы, образующие архимедову упорядоченную группу. Вольфа
сосредоточиться на переводах, а не на конкретных отношениях, таких как
конкатенация и упорядочение означает, что количественность может быть
реализуется несколькими способами и не ограничивается экстенсивным
структуры. Это также означает, что количество не имеет ничего
специально для работы с числами, как числовыми, так и нечисловыми
структуры могут быть количественными.
Вольфа
сосредоточиться на переводах, а не на конкретных отношениях, таких как
конкатенация и упорядочение означает, что количественность может быть
реализуется несколькими способами и не ограничивается экстенсивным
структуры. Это также означает, что количество не имеет ничего
специально для работы с числами, как числовыми, так и нечисловыми
структуры могут быть количественными.
Информационно-теоретические подходы к измерению основаны на аналогии
между измерительными системами и системами связи. В простом
системы связи, сообщение (вход) кодируется в сигнал на
стороне передатчика, отправленной стороне получателя, и
затем декодируется обратно (выход). Точность передачи зависит
на особенности системы связи, а также на особенности
окружающей среды, т. е. уровень фонового шума. Аналогично, измерение
инструменты можно рассматривать как «информационные машины».
(Финкельштейн 1977), которые взаимодействуют с объектом в заданном состоянии
(вход), закодировать это состояние во внутренний сигнал и преобразовать его
сигнал в показания (выход). Точность измерения
аналогично зависит от инструмента, а также от уровня шума
в его среде. Задуманный как особый вид информации
передачи, измерение становится доступным для анализа с точки зрения
концептуальный аппарат теории информации (Хартли, 1928; Шеннон
1948 год; Шеннон и Уивер, 1949). Например, информация о том, что
чтение \(y_i\) сообщает о возникновении состояния \(x_k\)
объект можно количественно определить как \(\log \left[\frac{p(x_k \mid
y_i)}{p(x_k)}\right]\), а именно как функцию уменьшения
неопределенность состояния объекта (Финкельштейн 1975: 222; за
альтернативные формулировки см. Brillouin 1962: Ch. 15; Кирпатовский
1974 год; и Мари 1999: 185).
Точность измерения
аналогично зависит от инструмента, а также от уровня шума
в его среде. Задуманный как особый вид информации
передачи, измерение становится доступным для анализа с точки зрения
концептуальный аппарат теории информации (Хартли, 1928; Шеннон
1948 год; Шеннон и Уивер, 1949). Например, информация о том, что
чтение \(y_i\) сообщает о возникновении состояния \(x_k\)
объект можно количественно определить как \(\log \left[\frac{p(x_k \mid
y_i)}{p(x_k)}\right]\), а именно как функцию уменьшения
неопределенность состояния объекта (Финкельштейн 1975: 222; за
альтернативные формулировки см. Brillouin 1962: Ch. 15; Кирпатовский
1974 год; и Мари 1999: 185).
Людвик Финкельштейн (1975, 1977) и Лука Мари (1999) предложили
возможность синтеза теории информации Шеннона-Уивера
и теория измерения. Как они утверждают, обе теории
к идее отображения: теория информации занимается отображением
между символами во входных и выходных сообщениях, а измерение
теория касается отображения между объектами и числами. Если
измерение считается аналогичным манипулированию символами, тогда
Теория Шеннона-Уивера могла бы обеспечить формализацию синтаксиса
измерение, в то время как теория измерения могла бы обеспечить формализацию
его семантика. Тем не менее Мари (1999: 185) также предупреждает, что
аналогия между системами связи и измерения ограничена.
Принимая во внимание, что сообщение отправителя может быть известно с произвольной точностью
независимо от его передачи состояние объекта не может быть
известен с произвольной точностью независимо от его измерения.
Если
измерение считается аналогичным манипулированию символами, тогда
Теория Шеннона-Уивера могла бы обеспечить формализацию синтаксиса
измерение, в то время как теория измерения могла бы обеспечить формализацию
его семантика. Тем не менее Мари (1999: 185) также предупреждает, что
аналогия между системами связи и измерения ограничена.
Принимая во внимание, что сообщение отправителя может быть известно с произвольной точностью
независимо от его передачи состояние объекта не может быть
известен с произвольной точностью независимо от его измерения.
Информационно-теоретические подходы к измерению изначально
разработан метрологами — специалистами в области физических измерений и
стандартизация — при небольшом участии философов.
Независимо от достижений в области метрологии Бас ван Фраассен (2008 г.:
141–185) недавно предложил концепцию измерения в
какая информация играет ключевую роль. Он рассматривает измерение как составленное
двух уровней: на физическом уровне измерительная аппаратура
взаимодействует с объектом и производит чтение, например, указатель
должность. [16] На абстрактном уровне теория фона представляет собой
возможные состояния объекта в пространстве параметров. Измерение
находит объект в подобласти этого абстрактного пространства параметров,
тем самым уменьшая диапазон возможных состояний (2008: 164 и 172).
Это сокращение возможностей сводится к сбору
информацию об измеряемом объекте. Анализ Ван Фраассена
измерения отличается от теоретико-информационного счета, разработанного
в метрологии в ее явной апелляции к фоновой теории и в
тот факт, что он не обращается к символической концепции информации
разработан Шенноном и Уивером.
[16] На абстрактном уровне теория фона представляет собой
возможные состояния объекта в пространстве параметров. Измерение
находит объект в подобласти этого абстрактного пространства параметров,
тем самым уменьшая диапазон возможных состояний (2008: 164 и 172).
Это сокращение возможностей сводится к сбору
информацию об измеряемом объекте. Анализ Ван Фраассена
измерения отличается от теоретико-информационного счета, разработанного
в метрологии в ее явной апелляции к фоновой теории и в
тот факт, что он не обращается к символической концепции информации
разработан Шенноном и Уивером.
С начала 2000-х годов началась новая волна философских исследований.
появился, который подчеркивает взаимосвязь между измерением и
теоретическое и статистическое моделирование (Morgan 2001; Boumans 2005a,
2015 г.; Мари 2005b; Мари и Джордани, 2013 г.; Таль 2016, 2017; Паркер 2017;
Мияке 2017). Согласно модельным счетам, измерение состоит
двух уровней: (i) конкретный процесс взаимодействия между
интересующий объект, инструмент и окружающая среда; и (ii)
теоретическая и/или статистическая модель того процесса, где
«модель» обозначает абстрактное и локальное представление
строится из упрощающих предположений. Центральная цель
измерение в соответствии с этим представлением состоит в том, чтобы присвоить значения одному или нескольким
интересующие параметры модели таким образом, который удовлетворяет определенным
эпистемологические требования, в частности когерентность и последовательность.
Центральная цель
измерение в соответствии с этим представлением состоит в том, чтобы присвоить значения одному или нескольким
интересующие параметры модели таким образом, который удовлетворяет определенным
эпистемологические требования, в частности когерентность и последовательность.
Счета на основе моделей были разработаны путем изучения измерения
практики в науках, и особенно в метрологии. Метрология,
официально определяется как «наука об измерениях и их
применение» (JCGM 2012: 2.2), является областью исследования, касающейся
с проектированием, обслуживанием и усовершенствованием средств измерений
в области естественных и технических наук. Метрологи обычно работают
в бюро стандартизации или в специализированных лабораториях,
ответственный за калибровку измерительного оборудования,
сравнение стандартов и оценка измерений
неопределенности, среди других задач. Вот только недавно
философы начали заниматься богатыми концептуальными проблемами
лежащей в основе метрологической практики, и особенно с выводами
участие в оценке и повышении точности измерений
стандарты (Chang 2004; Boumans 2005a: Глава 5, 2005b, 2007a; Frigerio
и другие. 2010 г.; Теллер 2013, 2018; Риордан 2015; Шлаудт и Хубер, 2015 г.;
Таль 2016а, 2018; Митчелл и др. 2017; Мёсснер и Нордманн
2017; де Куртенэ и др. 2019).
2010 г.; Теллер 2013, 2018; Риордан 2015; Шлаудт и Хубер, 2015 г.;
Таль 2016а, 2018; Митчелл и др. 2017; Мёсснер и Нордманн
2017; де Куртенэ и др. 2019).
Центральным мотивом для разработки счетов на основе моделей является
попытка прояснить эпистемологические принципы, лежащие в основе
аспекты измерительной практики. Например, метрологи используют
различные методы калибровки средств измерений,
стандартизация и отслеживание единиц и оценка
неопределенности (обсуждение метрологии см. в предыдущем
раздел). Традиционные философские объяснения, такие как математические
теории измерения не уточняют допущения, выводы
моделей, доказательных оснований или критериев успеха, связанных с такими
методы. Как Фриджерио и др. (2010) утверждают, что теория измерения
плохо подходит для разъяснения этих аспектов измерения, потому что
абстрагируется от процесса измерения и фокусируется исключительно на
математические свойства весов. Напротив, основанный на модели
учетные записи считают построение масштаба просто одной из нескольких задач
участвуют в измерении, наряду с определением измеряемого
параметры, конструкция прибора и калибровка, отбор проб объекта и
подготовка, обнаружение ошибок и оценка неопределенности, среди прочего
(2010: 145–147).
7.1 Роль моделей в измерении
Согласно основанным на модели счетам, измерение включает взаимодействие между объектом интереса («системой под измерение»), прибор («измерительный система») и окружение, включающее измерительную предметы. Другие, вторичные взаимодействия также могут иметь значение для определение результата измерения, такого как взаимодействие между измерительным прибором и эталонами, используемыми для его калибровка и цепочка сравнений, которые отслеживают эталон вернуться к первичным стандартам измерений (Mari 2003: 25). Измерение происходит путем представления этих взаимодействий набором параметры и присвоение значений подмножеству этих параметров (известные как «измеряемые величины») на основе результатов взаимодействия. Когда измеряемые параметры являются числовыми, они называются «количества». Хотя измеряемые величины не обязательно должны быть количествами, предполагается количественный сценарий измерения, в котором следует.
Два вида выходных данных измерений различаются на основе модели. счета [JCGM 2012: 2.9 и 4.1; Джордани и Мари 2012: 2146; Таль
2013]:
счета [JCGM 2012: 2.9 и 4.1; Джордани и Мари 2012: 2146; Таль
2013]:
- Показания прибора (или «показания»): это свойства измерительного прибор в своем конечном состоянии после процесса измерения полный. Примерами являются цифры на дисплее, метки на множественном выборе. анкеты и биты, хранящиеся в памяти устройства. Показания могут быть представлены числами, но такие числа описывают состояния инструмент, и его не следует путать с результатами измерений, которые касаются состояний измеряемого объекта.
- Результаты измерения (или «результаты»): это утверждения о знаниях о значениях одной или нескольких величин относятся к измеряемому объекту и обычно сопровождаются указанием единицы измерения и масштаба и оценкой неопределенности измерений. Например, результатом измерения может быть выражается предложением «масса объекта a равна 20±1 грамм с вероятностью 68%».
Как подчеркивают сторонники основанных на моделях счетов, выводы из
показания прибора к результатам измерений нетривиальны и
зависит от множества теоретических и статистических предположений о
измеряемый объект, прибор, окружающая среда и
процесс калибровки. Результаты измерения часто получаются с помощью
статистический анализ нескольких показаний, тем самым вовлекая
предположения о форме распределения показаний и
случайность эффектов окружающей среды (Боген и Вудворд 1988:
307–310). Результаты измерения также включают поправки на
систематические эффекты, и такие поправки основаны на теоретических
предположения относительно работы прибора и его
взаимодействия с объектом и окружающей средой. Например, длина
измерения должны быть скорректированы для изменения измерения
длина стержня в зависимости от температуры, поправка, которая выводится
из теоретического уравнения теплового расширения. Систематический
поправки включают в себя собственные неопределенности, например, в
определение значений констант, и эти неопределенности
оценивается с помощью вторичных экспериментов, включающих дальнейшие теоретические
и статистические предположения. Кроме того, неопределенность, связанная с
результат измерения зависит от методов, используемых для
калибровка прибора.
Результаты измерения часто получаются с помощью
статистический анализ нескольких показаний, тем самым вовлекая
предположения о форме распределения показаний и
случайность эффектов окружающей среды (Боген и Вудворд 1988:
307–310). Результаты измерения также включают поправки на
систематические эффекты, и такие поправки основаны на теоретических
предположения относительно работы прибора и его
взаимодействия с объектом и окружающей средой. Например, длина
измерения должны быть скорректированы для изменения измерения
длина стержня в зависимости от температуры, поправка, которая выводится
из теоретического уравнения теплового расширения. Систематический
поправки включают в себя собственные неопределенности, например, в
определение значений констант, и эти неопределенности
оценивается с помощью вторичных экспериментов, включающих дальнейшие теоретические
и статистические предположения. Кроме того, неопределенность, связанная с
результат измерения зависит от методов, используемых для
калибровка прибора. Калибровка требует дополнительных
предположения о приборе, калибровочном аппарате,
измеряемая величина и свойства эталонов
(Ротбарт и Слейден 1994; Франклин 1997; Бэрд 2004: гл. 4; Солер и др.
др. 2013). Другой компонент неопределенности возникает из-за неопределенности
в определении измеряемой величины и называется
«дефиниционная неопределенность» (Mari and Giordani, 2013;
Грежис 2015). Наконец, измерение включает в себя фон
предположения о типе шкалы и используемой системе единиц, и эти
предположения часто связаны с более широкими теоретическими и технологическими
соображения, касающиеся определения и реализации масштабов
и единицы.
Калибровка требует дополнительных
предположения о приборе, калибровочном аппарате,
измеряемая величина и свойства эталонов
(Ротбарт и Слейден 1994; Франклин 1997; Бэрд 2004: гл. 4; Солер и др.
др. 2013). Другой компонент неопределенности возникает из-за неопределенности
в определении измеряемой величины и называется
«дефиниционная неопределенность» (Mari and Giordani, 2013;
Грежис 2015). Наконец, измерение включает в себя фон
предположения о типе шкалы и используемой системе единиц, и эти
предположения часто связаны с более широкими теоретическими и технологическими
соображения, касающиеся определения и реализации масштабов
и единицы.
Эти различные теоретические и статистические предположения составляют основу
для построения одной или нескольких моделей процесса измерения.
В отличие от математических теорий измерения, где термин
«модель» означает теоретико-множественную структуру, которая
интерпретирует формальный язык, здесь термин «модель»
обозначает абстрактное и локальное представление целевой системы, которое
построен на упрощении
предположения. [17] Соответствующей целевой системой в данном случае является процесс измерения,
то есть система, состоящая из измерительного прибора, объектов или
измеряемые события, окружающая среда (включая людей-операторов),
вторичные инструменты и эталоны, эволюция во времени
эти компоненты и их различные взаимодействия друг с другом.
Измерение рассматривается как набор процедур, целью которых является
последовательно присваивать значения параметрам модели на основе инструмента
показания. Таким образом, модели рассматриваются как необходимые предварительные условия для
возможность вывода результатов измерения из прибора
показаний, и как решающее значение для определения содержания измерения
результаты. Как подчеркивают сторонники модельных счетов,
показания, полученные в результате одного и того же процесса измерения, могут использоваться для
установить различные результаты измерения в зависимости от того, как
процесс измерения моделируется, например, в зависимости от того, какая среда
влияния учитываются, какие статистические допущения
используется для анализа шума, и какие приближения используются при применении
фоновая теория.
[17] Соответствующей целевой системой в данном случае является процесс измерения,
то есть система, состоящая из измерительного прибора, объектов или
измеряемые события, окружающая среда (включая людей-операторов),
вторичные инструменты и эталоны, эволюция во времени
эти компоненты и их различные взаимодействия друг с другом.
Измерение рассматривается как набор процедур, целью которых является
последовательно присваивать значения параметрам модели на основе инструмента
показания. Таким образом, модели рассматриваются как необходимые предварительные условия для
возможность вывода результатов измерения из прибора
показаний, и как решающее значение для определения содержания измерения
результаты. Как подчеркивают сторонники модельных счетов,
показания, полученные в результате одного и того же процесса измерения, могут использоваться для
установить различные результаты измерения в зависимости от того, как
процесс измерения моделируется, например, в зависимости от того, какая среда
влияния учитываются, какие статистические допущения
используется для анализа шума, и какие приближения используются при применении
фоновая теория. Как говорит Лука Мари,
Как говорит Лука Мари,
любой результат измерения сообщает информацию, которая имеет смысл только в в контексте метрологической модели, такая модель должна включать спецификацию для всех объектов, которые явно или неявно появляются в выражении результата измерения. (2003: 25)
Точно так же говорят, что модели обеспечивают необходимый контекст для оценка различных аспектов качества результатов измерения, включая точность, прецизионность, ошибку и неопределенность (Боуманс, 2006 г., 2007а, 2009, 2012б; Мари 2005b).
Представления, основанные на моделях, расходятся с эмпирическими интерпретациями
теории измерения в том, что они не требуют соотношений между
результаты измерения должны быть изоморфны или гомоморфны наблюдаемым
отношения между измеряемыми предметами (Mari 2000). Верно,
по модельным счетам отношения между измеряемыми объектами
вовсе не обязательно наблюдать до их измерения (Frigerio et
др. 2010: 125). Вместо этого ключевым нормативным требованием модельного
учетных записей заключается в том, что значения параметров модели присваиваются в согласованной
способ. Критерий согласованности можно рассматривать как совокупность двух
подкритерии: (i) согласованность допущений модели с соответствующими
фоновые теории или другие существенные предположения о
измеряемое количество; и (ii) объективность, т. е. взаимная
непротиворечивость результатов измерений при различных измерениях
инструменты, среда и
модели [18] (Фриджерио и др., 2010; Таль, 2017а; Теллер, 2018). Первый
Подкритерий предназначен для обеспечения того, чтобы предполагаемое количество измеряется, а второй подкритерий предназначен для обеспечения
что результаты измерения могут быть обоснованно отнесены к измеряемому объект , а не какой-то артефакт измерения
инструмент, среда или модель. В совокупности эти два
требования гарантируют, что результаты измерений остаются в силе
независимо от конкретных предположений, связанных с их
производства, и, следовательно, зависимость измерения от контекста
результаты не угрожают их общей применимости.
Критерий согласованности можно рассматривать как совокупность двух
подкритерии: (i) согласованность допущений модели с соответствующими
фоновые теории или другие существенные предположения о
измеряемое количество; и (ii) объективность, т. е. взаимная
непротиворечивость результатов измерений при различных измерениях
инструменты, среда и
модели [18] (Фриджерио и др., 2010; Таль, 2017а; Теллер, 2018). Первый
Подкритерий предназначен для обеспечения того, чтобы предполагаемое количество измеряется, а второй подкритерий предназначен для обеспечения
что результаты измерения могут быть обоснованно отнесены к измеряемому объект , а не какой-то артефакт измерения
инструмент, среда или модель. В совокупности эти два
требования гарантируют, что результаты измерений остаются в силе
независимо от конкретных предположений, связанных с их
производства, и, следовательно, зависимость измерения от контекста
результаты не угрожают их общей применимости.
7.2 Модели и измерения в экономике
Помимо их применимости к физическим измерениям, основанные на моделях
Анализы также проливают свет на измерения в экономике. Как физическое
количества, значения экономических переменных часто невозможно наблюдать
непосредственно и должно быть выведено из наблюдений, основанных на абстрактных и
идеализированные модели. Экономист девятнадцатого века Уильям Джевонс, для
Например, измеряли изменения стоимости золота, постулируя определенные
причинно-следственная связь между стоимостью золота, предложением золота и
общий уровень цен (Hoover and Dowell 2001: 155–159).;
Морган 2001: 239). Как показывает Джулиан Рейсс (2001), Джевонс
измерения стали возможными благодаря использованию двух моделей:
каузально-теоретическая модель экономики, в основе которой лежит
предположение, что количество золота способно увеличить или
снижать цены; и статистическая модель данных, основанная на
предположение о том, что местные колебания цен взаимно
независимы и, следовательно, компенсируют друг друга при усреднении. Взятый
вместе эти модели позволили Джевонсу сделать вывод об изменении значения
золота из данных об исторических ценах различных
товары.
Как физическое
количества, значения экономических переменных часто невозможно наблюдать
непосредственно и должно быть выведено из наблюдений, основанных на абстрактных и
идеализированные модели. Экономист девятнадцатого века Уильям Джевонс, для
Например, измеряли изменения стоимости золота, постулируя определенные
причинно-следственная связь между стоимостью золота, предложением золота и
общий уровень цен (Hoover and Dowell 2001: 155–159).;
Морган 2001: 239). Как показывает Джулиан Рейсс (2001), Джевонс
измерения стали возможными благодаря использованию двух моделей:
каузально-теоретическая модель экономики, в основе которой лежит
предположение, что количество золота способно увеличить или
снижать цены; и статистическая модель данных, основанная на
предположение о том, что местные колебания цен взаимно
независимы и, следовательно, компенсируют друг друга при усреднении. Взятый
вместе эти модели позволили Джевонсу сделать вывод об изменении значения
золота из данных об исторических ценах различных
товары. [19]
[19]
Способы, которыми модели функционируют в экономических измерениях, привели
некоторые философы считают определенные экономические модели мерой
инструменты сами по себе, по аналогии с линейками и весами
(Боуманс, 1999, 2005с, 2006, 2007а, 2009, 2012а, 2015; Морган, 2001).
Марсель Буманс объясняет, как макроэкономисты могут изолировать
интересующая переменная от внешних воздействий путем настройки параметров в
модель макроэкономической системы. Этот метод освобождает экономистов
от невыполнимой задачи управления реальной системой. Как Боуманс
утверждает, что макроэкономические модели функционируют как измерительные инструменты в той мере, в какой
поскольку они производят инвариантные отношения между входами (показаниями) и
выходы (исходы), и поскольку эта инвариантность может быть проверена
калибровка по известным и устойчивым фактам. Когда такая модель на основе
процедуры сочетаются с экспертным заключением, они могут дать
надежные измерения экономических явлений даже вне контролируемых
лабораторных условиях (Boumans 2015: Глава 5).
7.3 Психометрические модели и конструктная валидность
Еще одна область, в которой модели играют центральную роль в измерении, — это
психология. Измерение большинства психологических характеристик, таких как
интеллекта, тревоги и депрессии, не опирается на гомоморфные
отображения, поддерживаемые репрезентативной теорией
Измерение (Уилсон 2013: 3766). Вместо этого психометрическая теория опирается
преимущественно на разработке абстрактных моделей, предназначенных для
прогнозировать эффективность испытуемых в определенных задачах. Эти модели
построены из содержательных и статистических предположений о
измеряемый психологический атрибут и его отношение к каждому
задача измерения. Например, популярная теория отклика на предмет.
подход к психологическим измерениям, использует различные модели для
оценить надежность и валидность анкет. Рассмотрим
анкета, предназначенная для оценки понимания английского языка
(«способность»), предъявляя испытуемым ряд
вопросы «да/нет» («пункты»). Одна из самых простых моделей
Для калибровки таких вопросников используется модель Раша (Rasch 19).60).
Эта модель предполагает прямое алгебраическое соотношение — известное
как «логарифм шансов» — между вероятностью
того, что испытуемый ответит на заданный вопрос правильно, сложность
этот конкретный предмет и способность субъекта. Новый
анкеты калибруются путем проверки соответствия между их
показания и предсказания модели Раша и назначение
уровни сложности для каждого элемента соответственно. Затем модель используется в
в сочетании с анкетой для определения уровня владения английским языком
понимание (результаты) из необработанных баллов анкеты (показания)
(Уилсон, 2013; Мари и Уилсон, 2014).
Одна из самых простых моделей
Для калибровки таких вопросников используется модель Раша (Rasch 19).60).
Эта модель предполагает прямое алгебраическое соотношение — известное
как «логарифм шансов» — между вероятностью
того, что испытуемый ответит на заданный вопрос правильно, сложность
этот конкретный предмет и способность субъекта. Новый
анкеты калибруются путем проверки соответствия между их
показания и предсказания модели Раша и назначение
уровни сложности для каждого элемента соответственно. Затем модель используется в
в сочетании с анкетой для определения уровня владения английским языком
понимание (результаты) из необработанных баллов анкеты (показания)
(Уилсон, 2013; Мари и Уилсон, 2014).
Вид статистической калибровки (или «масштабирования»)
модели Раша дают повторяемые результаты, но часто
только первый шаг к полноценному психологическому измерению.
Психологов обычно интересуют результаты измерения, а не
ради самого себя, а ради оценки некоторых основополагающих и
латентный психологический признак, например, понимание английского языка. Хорошее соответствие между ответами на вопросы и статистической моделью еще не
определить, что измеряет анкета. Процесс
установление того, что процедура измеряет предполагаемое психологическое
атрибут известен как «валидация». Один из способов подтверждения
психометрический инструмент предназначен для проверки различных процедур, которые
предназначены для измерения одного и того же скрытого атрибута, обеспечивают согласованное
полученные результаты. Такое тестирование относится к семейству методов проверки
известная как «проверка конструкции». Конструкция – это
абстрактное представление скрытого атрибута, предназначенного для
измерено, и
Хорошее соответствие между ответами на вопросы и статистической моделью еще не
определить, что измеряет анкета. Процесс
установление того, что процедура измеряет предполагаемое психологическое
атрибут известен как «валидация». Один из способов подтверждения
психометрический инструмент предназначен для проверки различных процедур, которые
предназначены для измерения одного и того же скрытого атрибута, обеспечивают согласованное
полученные результаты. Такое тестирование относится к семейству методов проверки
известная как «проверка конструкции». Конструкция – это
абстрактное представление скрытого атрибута, предназначенного для
измерено, и
отражает гипотезу […] о том, что разнообразие поведения будет коррелируют друг с другом в исследованиях индивидуальных различий и/или будут аналогичным образом затронуты экспериментальными манипуляциями. (обычно и Бернстайн 1994: 85)
Конструкции обозначаются переменными в модели, которая предсказывает, какие
будут наблюдаться корреляции между показаниями различных
меры, если они действительно являются мерами одного и того же атрибута. Такой
модели включают существенные предположения об атрибуте, в том числе
его внутреннюю структуру и его отношения с другими атрибутами, а также
статистические предположения о корреляции между различными показателями
(Кэмпбелл и Фиске 1959; Наннелли и Бернстайн 1994: гл. 3;
Ангнер 2008).
Такой
модели включают существенные предположения об атрибуте, в том числе
его внутреннюю структуру и его отношения с другими атрибутами, а также
статистические предположения о корреляции между различными показателями
(Кэмпбелл и Фиске 1959; Наннелли и Бернстайн 1994: гл. 3;
Ангнер 2008).
В последние годы философы науки все чаще
интересуется психометрией и концепцией валидности. Одна дискуссия
касается онтологического статуса латентных психологических атрибутов.
Денни Борсбум выступал против операционализма в отношении латентных
атрибутов и в пользу определения валидности таким образом, чтобы
охватывает реализм: «тест действителен для измерения атрибута, если
и только если а) атрибут существует и б) вариации в
атрибут причинно порождает вариации результатов
процедура измерения» (2005: 150; см. также Hood 2009)., 2013;
Праздник 2020). Элина Вессонен защитила умеренную форму
операционализм о психологических атрибутах, и утверждал, что
умеренный операционализм совместим с осторожным типом реализма
(2019). Другая недавняя дискуссия посвящена обоснованию
построить процедуры проверки. По словам Анны Александровой,
конструктивная валидация в принципе является оправданной методологией, поскольку
поскольку он устанавливает согласованность с теоретическими предположениями и
фоновые знания о скрытом атрибуте. Тем не менее, Александрова
отмечает, что на практике психометристы, намеревающиеся измерить
счастье и благополучие часто избегают теоретизировать об этих
конструкты, а вместо этого апеллируют к народным верованиям респондентов.
Это противоречит цели валидации конструкции и превращает ее в
узкотехническое упражнение (Александрова и Хайброн 2016; Александрова
2017; см. также McClimans et al. 2017).
Другая недавняя дискуссия посвящена обоснованию
построить процедуры проверки. По словам Анны Александровой,
конструктивная валидация в принципе является оправданной методологией, поскольку
поскольку он устанавливает согласованность с теоретическими предположениями и
фоновые знания о скрытом атрибуте. Тем не менее, Александрова
отмечает, что на практике психометристы, намеревающиеся измерить
счастье и благополучие часто избегают теоретизировать об этих
конструкты, а вместо этого апеллируют к народным верованиям респондентов.
Это противоречит цели валидации конструкции и превращает ее в
узкотехническое упражнение (Александрова и Хайброн 2016; Александрова
2017; см. также McClimans et al. 2017).
Более фундаментальная критика психометрии заключается в том, что она
догматически предполагает, что психологические атрибуты могут быть
количественно. Мичелл (2000, 2004b) утверждает, что психометрия
не предприняли серьезных попыток проверить, являются ли атрибуты, на которые они претендуют,
для измерения имеют количественную структуру, и вместо этого приняли чрезмерно
расплывчатое представление об измерении, скрывающее это пренебрежение. В
ответ, Борсбум и Мелленберг (2004) утверждают, что ответ на предмет
Теория обеспечивает вероятностные тесты количественной оценки
атрибуты. Психометристы, которые строят статистическую модель
сначала предположить, что атрибут является количественным, а затем
подвергнуть модель эмпирическим испытаниям. В случае успеха такие испытания
обеспечить косвенное подтверждение исходной гипотезы, т.е. по
показывая, что атрибут имеет аддитивную совместную структуру (см.
также Вессонен 2020).
В
ответ, Борсбум и Мелленберг (2004) утверждают, что ответ на предмет
Теория обеспечивает вероятностные тесты количественной оценки
атрибуты. Психометристы, которые строят статистическую модель
сначала предположить, что атрибут является количественным, а затем
подвергнуть модель эмпирическим испытаниям. В случае успеха такие испытания
обеспечить косвенное подтверждение исходной гипотезы, т.е. по
показывая, что атрибут имеет аддитивную совместную структуру (см.
также Вессонен 2020).
Несколько ученых указали на сходство между моделями способов
используются для стандартизации измеримых величин в естественных и
социальные науки. Например, Марк Уилсон (2013) утверждает, что
психометрические модели можно рассматривать как инструменты для построения
эталоны измерений в том же смысле, что и «измерительные
стандарт», используемый метрологами. Другие выразили сомнения в
целесообразность и желательность брать пример
естественных наук при стандартизации конструкций в социальных науках.
Нэнси Картрайт и Роза Ранхардт (2014) обсуждают
Концепции Ballung, термин, который они заимствовали у Отто Нейрата. для обозначения понятий с нечеткой и контекстно-зависимой областью применения. Примеры
концепций Баллунга являются раса, бедность, социальная изоляция и
качество докторских программ. Такие понятия слишком многогранны, чтобы
измеряется одной метрикой без потери смысла и должен
представлены либо матрицей индексов, либо несколькими различными
меры в зависимости от того, какие цели и ценности играют роль (см. также
Брэдберн, Картрайт и Фуллер, 2016 г., другие интернет-ресурсы).
Александрова (2008) отмечает, что этические соображения
вопросы об обоснованности мер благосостояния не менее
соображения воспроизводимости. Такие этические соображения
зависит от контекста и может применяться только частично. В подобном
вене, Лия Макклиманс (2010) утверждает, что единообразие не всегда
подходящая цель для разработки вопросников, так как открытость
вопросов часто и неизбежны, и желательны для получения
актуальная информация от
предметы. [20] Переплетение этических и эпистемологических соображений
особенно ясно, когда психометрические опросники используются в медицинских
условия для оценки самочувствия и психического здоровья пациента.
для обозначения понятий с нечеткой и контекстно-зависимой областью применения. Примеры
концепций Баллунга являются раса, бедность, социальная изоляция и
качество докторских программ. Такие понятия слишком многогранны, чтобы
измеряется одной метрикой без потери смысла и должен
представлены либо матрицей индексов, либо несколькими различными
меры в зависимости от того, какие цели и ценности играют роль (см. также
Брэдберн, Картрайт и Фуллер, 2016 г., другие интернет-ресурсы).
Александрова (2008) отмечает, что этические соображения
вопросы об обоснованности мер благосостояния не менее
соображения воспроизводимости. Такие этические соображения
зависит от контекста и может применяться только частично. В подобном
вене, Лия Макклиманс (2010) утверждает, что единообразие не всегда
подходящая цель для разработки вопросников, так как открытость
вопросов часто и неизбежны, и желательны для получения
актуальная информация от
предметы. [20] Переплетение этических и эпистемологических соображений
особенно ясно, когда психометрические опросники используются в медицинских
условия для оценки самочувствия и психического здоровья пациента. В таком
случаи, небольшие изменения в дизайне анкеты или анализа
его результатов может причинить значительный вред или пользу пациентам
(Макклиманс, 2017; Стегенга, 2018, глава 8). Эти выводы подчеркивают
ценностный и контекстуальный характер измерения умственных и
социальные явления.
В таком
случаи, небольшие изменения в дизайне анкеты или анализа
его результатов может причинить значительный вред или пользу пациентам
(Макклиманс, 2017; Стегенга, 2018, глава 8). Эти выводы подчеркивают
ценностный и контекстуальный характер измерения умственных и
социальные явления.
Разработка счетов на основе моделей обсуждалась в предыдущем
раздел является частью более крупного «эпистемического поворота» в
философия измерения, возникшая в начале 2000-х гг. Скорее
чем подчеркивание математических основ, метафизики или
семантика измерения, философская работа в последние годы тяготеет к
сосредоточить внимание на предпосылках и логических выводах, вовлеченных в
конкретные практики измерения, а также исторические, социальные и
материальные размеры измерения. Философское изучение этих
тематика получила название «эпистемология
измерения» (Mari 2003, 2005a; Leplège 2003; Tal 2017a).
В самом широком смысле эпистемология измерения — это изучение
отношения между измерением и знанием. Центральные темы
которые подпадают под сферу эпистемологии измерения, включают
условия, при которых измерение производит знание; в
содержание, объем, обоснование и пределы таких знаний; в
причины, по которым конкретные методологии измерения и
стандартизация преуспела или потерпела неудачу в поддержке конкретных знаний
претензии, а также взаимосвязь между измерением и другими
познавательная деятельность, такая как наблюдение, теоретизирование,
экспериментирование, моделирование и расчет. Преследуя эти
целей, философы опираются на работы историков и
социологи науки, которые исследовали измерение
практики в течение более длительного периода (Уайз и Смит 1986; Латур 1987: гл.
6; Шаффер 1992; Портер 1995, 2007; Мудрый 1995; Ольха 2002; Галисон
2003 г.; Добрый день, 2004 г.; Crease 2011), а также по истории и
философия научных экспериментов (Harré 1981; Hacking
1983 год; Франклин 1986; Картрайт 1999). Следующие подразделы
рассмотреть некоторые из тем, обсуждаемых в этой растущей группе
литература.
Центральные темы
которые подпадают под сферу эпистемологии измерения, включают
условия, при которых измерение производит знание; в
содержание, объем, обоснование и пределы таких знаний; в
причины, по которым конкретные методологии измерения и
стандартизация преуспела или потерпела неудачу в поддержке конкретных знаний
претензии, а также взаимосвязь между измерением и другими
познавательная деятельность, такая как наблюдение, теоретизирование,
экспериментирование, моделирование и расчет. Преследуя эти
целей, философы опираются на работы историков и
социологи науки, которые исследовали измерение
практики в течение более длительного периода (Уайз и Смит 1986; Латур 1987: гл.
6; Шаффер 1992; Портер 1995, 2007; Мудрый 1995; Ольха 2002; Галисон
2003 г.; Добрый день, 2004 г.; Crease 2011), а также по истории и
философия научных экспериментов (Harré 1981; Hacking
1983 год; Франклин 1986; Картрайт 1999). Следующие подразделы
рассмотреть некоторые из тем, обсуждаемых в этой растущей группе
литература.
8.1 Стандартизация и научный прогресс
Тема, которая привлекла значительное внимание философов в
последние годы является выбор и совершенствование измерения
стандарты. Вообще говоря, стандартизировать понятие количества означает
предписывают определенный способ применения этого понятия к
конкретный
подробности. [21] Стандартизировать измерительный прибор означает оценить, насколько хорошо
результаты измерения этим прибором соответствуют заданному режиму
применение соответствующей концепции. [22] Соответственно термин «эталон» имеет по крайней мере
два значения: с одной стороны, оно обычно используется для обозначения
абстрактные правила и определения, регулирующие использование количества
понятия, такие как определение метра. С другой стороны,
Термин «стандарт измерения» также обычно используется для обозначения
к конкретным артефактам и процедурам, которые считаются образцовыми
применение концепции количества, такой как металлический стержень, который
служил стандартным метром до 1960. Эта двойственность смысла
отражает двойственную природу стандартизации, которая включает в себя как
абстрактный и конкретный аспекты.
Эта двойственность смысла
отражает двойственную природу стандартизации, которая включает в себя как
абстрактный и конкретный аспекты.
В
Раздел 4
было отмечено, что стандартизация предполагает выбор среди нетривиальных
альтернативы, такие как выбор среди различных термометрических жидкостей
или среди различных способов маркировки равной продолжительности. Эти варианты
нетривиальны в том смысле, что они влияют на то,
температурные (или временные) интервалы считаются равными и, следовательно, влияют на
независимо от того, содержат ли утверждения естественного права термин
«температура» (или «время») получаются верными.
Обращение к теории, чтобы решить, какой стандарт является более точным, было бы
круговой, так как теория не может быть однозначно применена к
сведения до выбора эталона. Этот
циркулярность по-разному называли «проблемой
координация» (van Fraassen 2008: Ch. 5) и «проблема
номического измерения» (Chang 2004: Ch. 2). Как уже упоминалось,
конвенционалисты попытались избежать циркулярности, постулируя а
априори утверждения, известные как «координационные
определения», которые должны были связать количественные термины с
специальные измерительные операции. Недостатком этого решения является то, что
предполагается, что выбор эталона измерения произволен и
статичны, тогда как в реальной практике стандарты измерения, как правило,
выбираются на основе эмпирических соображений и в конечном итоге улучшаются
или заменены стандартами, которые считаются более точными.
Недостатком этого решения является то, что
предполагается, что выбор эталона измерения произволен и
статичны, тогда как в реальной практике стандарты измерения, как правило,
выбираются на основе эмпирических соображений и в конечном итоге улучшаются
или заменены стандартами, которые считаются более точными.
Новое направление в литературе по проблеме координации появилось в
последние годы, в первую очередь из работ Хасок Чанга
(2001, 2004, 2007; Барвич и Чанг, 2015) и Бас ван Фраассен (2008:
Ч. 5; 2009 г., 2012; см. также Падовани 2015, 2017; Мишель 2019). Эти
работы используют историко-когерентистский подход к проблеме.
Вместо того, чтобы пытаться полностью избежать проблемы цикличности,
как и их предшественники, они намеревались показать, что циркулярность
не порочный. Чанг утверждает, что построение концепции количества и
стандартизация его измерения являются взаимозависимыми и повторяющимися задачами.
Каждая «эпистемическая итерация» в истории
стандартизация уважает существующие традиции и в то же время
исправляя их (Chang 2004: Ch. 5). Донаучная концепция
температура, например, была связана с грубым и неоднозначным
способы упорядочения объектов от горячего к холодному. Термоскопы и
в конечном итоге термометры, помогли изменить первоначальную концепцию и сделали
это точнее. С каждой такой итерацией понятие количества было
пересогласованы с более стабильным набором стандартов, который, в свою очередь,
позволили более точно проверить теоретические предсказания,
облегчение последующего развития теории и построения
более стабильных стандартов и так далее.
5). Донаучная концепция
температура, например, была связана с грубым и неоднозначным
способы упорядочения объектов от горячего к холодному. Термоскопы и
в конечном итоге термометры, помогли изменить первоначальную концепцию и сделали
это точнее. С каждой такой итерацией понятие количества было
пересогласованы с более стабильным набором стандартов, который, в свою очередь,
позволили более точно проверить теоретические предсказания,
облегчение последующего развития теории и построения
более стабильных стандартов и так далее.
Как этот процесс позволяет избежать порочного круга, становится ясно, если мы посмотрим
на него либо «сверху», т. е. задним числом, учитывая наши
современные научные знания, или «изнутри», глядя
на исторические события в их первоначальном контексте (ван Фраассен
2008: 122). С любой точки зрения координация успешна, потому что
это увеличивает согласованность между элементами теории и инструментами.
Вопросы «что считать измерением количества х ?» и «какое количество х ?»,
хотя и неразрешимы независимо друг от друга, адресуются
вместе в процессе взаимного совершенствования. Только когда человек принимает
фундаменталистский взгляд и попытки найти отправную точку для
координация, свободная от предположения, что этот исторический процесс
ошибочно кажется, что ему не хватает эпистемологического обоснования (2008: 137).
Только когда человек принимает
фундаменталистский взгляд и попытки найти отправную точку для
координация, свободная от предположения, что этот исторический процесс
ошибочно кажется, что ему не хватает эпистемологического обоснования (2008: 137).
Новая литература по координации смещает акцент
обсуждение от определений количественных терминов до реализации этих определений. Говоря метрологическим жаргоном,
«реализация» — это физический инструмент или процедура,
приблизительно удовлетворяет данному определению (см. JCGM 2012: 5.1).
Примерами метрологических реализаций являются официальные прототипы
килограмм и цезиевые фонтанные часы, используемые для стандартизации
второй. Недавние исследования показывают, что методы, используемые для проектирования,
поддерживать и сравнивать реализации имеют прямое отношение к
практическое применение понятий количества, единицы и масштаба, не менее
чем определения этих понятий (Riordan 2015; Tal 2016).
связь между определением и реализациями единицы становится
особенно сложно, когда определение сформулировано в теоретических терминах. Некоторые из основных единиц Международной системы (СИ) —
в том числе метр, килограмм, ампер, кельвин и моль — не
больше определяется ссылкой на любой конкретный тип физической системы,
а зафиксировав числовое значение фундаментальной физической константы.
Килограмм, например, был переопределен в 2019 году.как единица массы
так что численное значение постоянной Планка точно
6,62607015 × 10 -34 кг м 2 с -1 (BIPM 2019:131). Понимание килограмма в соответствии с этим определением является
сильно теоретизированная задача. Изучение практической реализации
такие единицы пролили новый свет на развивающиеся отношения между
измерение и теория (Таль, 2018; де Куртенэ и др., 2019; Вольф
2020б).
Некоторые из основных единиц Международной системы (СИ) —
в том числе метр, килограмм, ампер, кельвин и моль — не
больше определяется ссылкой на любой конкретный тип физической системы,
а зафиксировав числовое значение фундаментальной физической константы.
Килограмм, например, был переопределен в 2019 году.как единица массы
так что численное значение постоянной Планка точно
6,62607015 × 10 -34 кг м 2 с -1 (BIPM 2019:131). Понимание килограмма в соответствии с этим определением является
сильно теоретизированная задача. Изучение практической реализации
такие единицы пролили новый свет на развивающиеся отношения между
измерение и теория (Таль, 2018; де Куртенэ и др., 2019; Вольф
2020б).
8.2 Теоретическая нагрузка измерения
Как уже говорилось выше (разделы
7
а также
8.1),
теория и измерение взаимозависимы как исторически, так и
концептуально. С исторической стороны развитие теории и
измерение происходит посредством итеративных и взаимных уточнений. На
концептуальная сторона, спецификация форм процедур измерения
эмпирическое содержание теоретических понятий, а теория дает
систематическая интерпретация показаний измерения
инструменты. Эта взаимозависимость измерения и теории может показаться
как угроза доказательной роли, которую измерение должно
играть в научном предприятии. В конце концов, результаты измерений
считается способным проверять теоретические гипотезы, и это, кажется,
требуют некоторой степени независимости измерения от теории. Этот
угроза особенно очевидна, когда теоретическая гипотеза
уже предполагается как часть модели измерения
инструмент. Чтобы привести пример из работы Франклина и соавт. (1989: 230):
На
концептуальная сторона, спецификация форм процедур измерения
эмпирическое содержание теоретических понятий, а теория дает
систематическая интерпретация показаний измерения
инструменты. Эта взаимозависимость измерения и теории может показаться
как угроза доказательной роли, которую измерение должно
играть в научном предприятии. В конце концов, результаты измерений
считается способным проверять теоретические гипотезы, и это, кажется,
требуют некоторой степени независимости измерения от теории. Этот
угроза особенно очевидна, когда теоретическая гипотеза
уже предполагается как часть модели измерения
инструмент. Чтобы привести пример из работы Франклина и соавт. (1989: 230):
На первый взгляд может показаться, что существует порочный цикл, если использовать ртутный термометр для измерения температуры объекты как часть эксперимента, чтобы проверить, расширяются ли объекты по мере повышения их температуры.
Тем не менее, Франклин и др. сделать вывод, что цикличность не
беспощадный. Ртутный термометр может быть откалиброван по другому
термометр, принцип действия которого не предполагает закона
теплового расширения, например газовый термометр постоянного объема,
тем самым установив надежность ртутного термометра на
независимые основания. Говоря более широко, в контексте
локальной проверки гипотез угроза циркулярности обычно может быть
избегать, обращаясь к другим видам инструментов и другим частям
теория.
Ртутный термометр может быть откалиброван по другому
термометр, принцип действия которого не предполагает закона
теплового расширения, например газовый термометр постоянного объема,
тем самым установив надежность ртутного термометра на
независимые основания. Говоря более широко, в контексте
локальной проверки гипотез угроза циркулярности обычно может быть
избегать, обращаясь к другим видам инструментов и другим частям
теория.
Другой вид беспокойства по поводу доказательной функции измерения
возникает в глобальном масштабе, когда проверка целых теорий
обеспокоенный. Как утверждает Томас Кун (1961), научные теории
обычно принимаются задолго до появления количественных методов их проверки
становятся доступными. Надежность вновь введенного измерения
методы обычно проверяются на соответствие предсказаниям теории
а не наоборот. По словам Куна, «…
Дорога от научного закона к научному измерению редко бывает
ехал в обратном направлении» (1961: 189). Например,
Закон Дальтона, который гласит, что веса элементов в
химические соединения связаны друг с другом целыми числами
пропорции, изначально противоречащие некоторым из наиболее известных
измерения таких пропорций. Это только если предположить
Закон Дальтона, который последующие химики-экспериментаторы смогли
исправить и улучшить свои методы измерения (1961: 173). Следовательно,
Куна, функция измерения в физических науках
не проверять теорию, а применять ее во все возрастающей степени и
точность и, в конечном счете, позволить устойчивым аномалиям всплыть на поверхность
это ускорит следующий кризис и научную революцию. Примечание
что Кун не утверждает, что измерение не имеет доказательной роли для
играть в науку. Вместо этого он утверждает, что измерения не могут проверить
теория изолированно, а только в сравнении с какой-либо альтернативной теорией
это предлагается в попытке объяснить обнаруженные аномалии
за счет все более точных измерений (для наглядного обсуждения
тезиса Куна см. Hacking 1983: 243–5).
Это только если предположить
Закон Дальтона, который последующие химики-экспериментаторы смогли
исправить и улучшить свои методы измерения (1961: 173). Следовательно,
Куна, функция измерения в физических науках
не проверять теорию, а применять ее во все возрастающей степени и
точность и, в конечном счете, позволить устойчивым аномалиям всплыть на поверхность
это ускорит следующий кризис и научную революцию. Примечание
что Кун не утверждает, что измерение не имеет доказательной роли для
играть в науку. Вместо этого он утверждает, что измерения не могут проверить
теория изолированно, а только в сравнении с какой-либо альтернативной теорией
это предлагается в попытке объяснить обнаруженные аномалии
за счет все более точных измерений (для наглядного обсуждения
тезиса Куна см. Hacking 1983: 243–5).
Традиционные рассуждения о перегруженности теорией, как у Куна, были
на фоне логических позитивистов
Различие между теоретическим и наблюдательным языком.
Теоретичность измерений была правильно воспринята как угроза
возможность четкого разграничения между двумя языками. Современных дискуссий, напротив, больше нет.
перегруженность теорией как эпистемологическая угроза, но принимать как должное
что некоторый уровень теоретической нагрузки является предпосылкой для измерений
иметь какую-либо доказательную силу. Без какого-то минимального основного
предположения об измеряемой величине, такие как ее аменабельность
манипулированию и его отношениям к другим величинам, было бы
невозможно интерпретировать показания измерительных приборов и
следовательно, невозможно установить доказательную значимость тех
показания. На это уже обращал внимание Пьер Дюэм (1906:
153–6; см. также Carrier 1994: 9–19). Более того,
современные авторы подчеркивают, что теоретические предположения играют
решающую роль в исправлении ошибок измерения и оценке
неопределенности измерения. Действительно, процедуры физических измерений
становятся 90 323 более 90 324 точными, когда модель, лежащая в их основе,
деидеализированный, процесс, который включает в себя увеличение теоретического
богатство модели (Tal 2011).
Современных дискуссий, напротив, больше нет.
перегруженность теорией как эпистемологическая угроза, но принимать как должное
что некоторый уровень теоретической нагрузки является предпосылкой для измерений
иметь какую-либо доказательную силу. Без какого-то минимального основного
предположения об измеряемой величине, такие как ее аменабельность
манипулированию и его отношениям к другим величинам, было бы
невозможно интерпретировать показания измерительных приборов и
следовательно, невозможно установить доказательную значимость тех
показания. На это уже обращал внимание Пьер Дюэм (1906:
153–6; см. также Carrier 1994: 9–19). Более того,
современные авторы подчеркивают, что теоретические предположения играют
решающую роль в исправлении ошибок измерения и оценке
неопределенности измерения. Действительно, процедуры физических измерений
становятся 90 323 более 90 324 точными, когда модель, лежащая в их основе,
деидеализированный, процесс, который включает в себя увеличение теоретического
богатство модели (Tal 2011).
Признание того, что теория имеет решающее значение для гарантии
доказательная надежность измерения обращает внимание на
«задача наблюдательного заземления», которая является обратной
вызов традиционной угрозе перегруженности теорией (Tal 2016b).
Задача состоит в том, чтобы указать, какая роль наблюдение играет в
измерение, и в частности, какая связь с наблюдением
необходимо и/или достаточно, чтобы измерения могли играть
доказательную роль в науках. Эта проблема особенно очевидна, когда
одна попытка объяснить растущее использование вычислительных
методы выполнения задач, которые традиционно выполнялись
измерительные приборы. В роли Маргарет Моррисон (2009) и Венди Паркер
(2017) утверждают, что есть случаи, когда надежная количественная информация
собирается о целевой системе с помощью компьютера
симуляции, но таким образом, который удовлетворяет некоторым основным
требования к измерению, такие как эмпирическое обоснование и
взгляд назад (см. также Lusk 2016). Такая информация не зависит
по сигналам, передаваемым от интересующего объекта к
инструмента, а на использовании теоретических и статистических моделей для
обрабатывать эмпирические данные о связанных объектах. Например, данные
методы ассимиляции обычно используются для оценки прошлых атмосферных
температуры в регионах, где недоступны показания термометров.
Некоторые методы делают это путем подгонки вычислительной модели
поведение атмосферы в сочетании с доступными данными из
близлежащие регионы и модельный прогноз условий на момент
наблюдение (Паркер, 2017). Затем эти оценки используются в различных
способами, в том числе в качестве данных для оценки перспективных климатических моделей.
Независимо от того, называют ли эти оценки
«измерения», они бросают вызов идее о том, что производство
требуется надежное количественное свидетельство о состоянии объекта
наблюдая за этим объектом, как бы широко ни понимали термин
«наблюдение». [23]
Например, данные
методы ассимиляции обычно используются для оценки прошлых атмосферных
температуры в регионах, где недоступны показания термометров.
Некоторые методы делают это путем подгонки вычислительной модели
поведение атмосферы в сочетании с доступными данными из
близлежащие регионы и модельный прогноз условий на момент
наблюдение (Паркер, 2017). Затем эти оценки используются в различных
способами, в том числе в качестве данных для оценки перспективных климатических моделей.
Независимо от того, называют ли эти оценки
«измерения», они бросают вызов идее о том, что производство
требуется надежное количественное свидетельство о состоянии объекта
наблюдая за этим объектом, как бы широко ни понимали термин
«наблюдение». [23]
8.3 Точность и прецизионность
Два ключевых аспекта надежности результатов измерения:
тщательность и точность. Рассмотрим серию повторных взвешиваний
измерения, выполненные на конкретном объекте равноплечим
остаток средств. С реалистической точки зрения, основанной на ошибках,
результаты этих измерений точны если они близки
истинному значению измеряемой величины — в нашем случае
истинное отношение веса объекта к выбранному
единица — и точное , если они близки друг к другу. Ан
аналогия, часто цитируемая для пояснения основанного на ошибках различия, заключается в том, что
стрелы, выпущенные в цель, с точностью, аналогичной близости
попадания в яблочко и точность, аналогичную герметичности
распространения попаданий (ср. JCGM 2012: 2.13 и 2.15, Teller 2013: 192).
Хотя и интуитивно понятный, основанный на ошибках способ провести различие
вызывает эпистемологическую трудность. Принято считать, что
точные истинные значения большинства величин, представляющих интерес для науки,
непознаваемы, по крайней мере, когда эти величины измеряются на непрерывном
Весы. Если это предположение принимается, то точность, с которой
измеряемые величины не могут быть известны с точностью, а только
оцениваются путем сравнения неточных измерений друг с другом. И все еще
неясно, почему сходимость среди неточных измерений должна быть
воспринимается как указание на истину. Ведь измерения могут быть
страдают от общего предубеждения, которое предотвращает их индивидуальные неточности
от компенсации друг друга при усреднении.
Ан
аналогия, часто цитируемая для пояснения основанного на ошибках различия, заключается в том, что
стрелы, выпущенные в цель, с точностью, аналогичной близости
попадания в яблочко и точность, аналогичную герметичности
распространения попаданий (ср. JCGM 2012: 2.13 и 2.15, Teller 2013: 192).
Хотя и интуитивно понятный, основанный на ошибках способ провести различие
вызывает эпистемологическую трудность. Принято считать, что
точные истинные значения большинства величин, представляющих интерес для науки,
непознаваемы, по крайней мере, когда эти величины измеряются на непрерывном
Весы. Если это предположение принимается, то точность, с которой
измеряемые величины не могут быть известны с точностью, а только
оцениваются путем сравнения неточных измерений друг с другом. И все еще
неясно, почему сходимость среди неточных измерений должна быть
воспринимается как указание на истину. Ведь измерения могут быть
страдают от общего предубеждения, которое предотвращает их индивидуальные неточности
от компенсации друг друга при усреднении. В отсутствие
когнитивный доступ к истинным ценностям, как оценивается измерение
точность возможна?
В отсутствие
когнитивный доступ к истинным ценностям, как оценивается измерение
точность возможна?
Отвечая на этот вопрос, философы извлекли пользу из изучения
различных смыслах термина «точность измерения».
используется практикующими учеными. По крайней мере, пять различных органов чувств
выделяют: метафизический, эпистемологический, операциональный, сравнительный и
прагматичный (Tal 2011: 1084–1085). В частности, эпистемологический или
«основанный на неопределенности» смысл термина метафизически
нейтральна и не предполагает существования истинных ценностей. Вместо,
точность результата измерения принимается за близость
согласие между значениями, разумно приписываемыми данной величине
имеющиеся эмпирические данные и фоновые знания (ср. JCGM 2012: 2.13
Заметка 3; Джордани и Мари, 2012 г .; де Куртенэ и Грежи
2017). Таким образом, точность измерения можно оценить по
установление устойчивости среди последствий моделей, представляющих
различные процессы измерения (Бассо, 2017; Таль, 2017б; Бокулич, 2020;
Стейли 2020).
Согласно концепции, основанной на неопределенности, неточность представляет собой особый вид неточности. Например, погрешность измерения веса широта разброса значений, обоснованно приписываемых вес предмета с учетом показаний весов и имеющиеся базовые знания о том, как работают весы и используются стандартные веса. Неточность этих измерений компонент погрешности, возникающий из-за неконтролируемых изменений в показания баланса по повторным испытаниям. Другие источники неточность помимо неточности включает несовершенные поправки к систематические ошибки, неточно известные физические константы и расплывчатые определения измеряемых величин, среди прочего (см. Раздел 7.1).
Пол Теллер (2018) выдвигает другое возражение против основанного на ошибках
понятие точности измерений. Он возражает против предположения, что
называет «реализмом точности измерений», согласно которому
измеряемые величины имеют в действительности определенные значения. Теллер утверждает
что это предположение неверно, поскольку оно касается величин
обычно измеряется в физике, потому что всякое указание определенного
значений (или диапазонов значений) для таких величин предполагает идеализацию и
следовательно, не может относиться ни к чему в действительности. Например, концепция
обычно понимают под фразой «скорость звука в
воздух» включает в себя множество неявных идеализаций, касающихся
однородность химического состава воздуха, температуры и
давление, а также стабильность единиц измерения. Удаление
эти идеализации полностью потребовали бы добавления бесконечного количества
подробно к каждой спецификации. Как утверждает Теллер, точность измерения
следует понимать как полезную идеализацию, а именно как
концепция, которая позволяет ученым оценивать согласованность и согласованность
среди результатов измерений как будто языковое выражение
эти результаты цеплялись за что угодно в мире. Точность
также идеализированная концепция, основанная на открытом и
неопределенная спецификация того, что считается повторением измерения
при «тех же» обстоятельствах (Teller 2013: 194).
Например, концепция
обычно понимают под фразой «скорость звука в
воздух» включает в себя множество неявных идеализаций, касающихся
однородность химического состава воздуха, температуры и
давление, а также стабильность единиц измерения. Удаление
эти идеализации полностью потребовали бы добавления бесконечного количества
подробно к каждой спецификации. Как утверждает Теллер, точность измерения
следует понимать как полезную идеализацию, а именно как
концепция, которая позволяет ученым оценивать согласованность и согласованность
среди результатов измерений как будто языковое выражение
эти результаты цеплялись за что угодно в мире. Точность
также идеализированная концепция, основанная на открытом и
неопределенная спецификация того, что считается повторением измерения
при «тех же» обстоятельствах (Teller 2013: 194).
Почему лошадей измеряют руками? Традиция или нечто большее?
Любые ссылки на этой странице, которые ведут к продуктам на Amazon, являются партнерскими ссылками, и я получаю комиссию, если вы совершаете покупку. Заранее спасибо — мне очень приятно!
Заранее спасибо — мне очень приятно!
При описании роста лошадей все всегда используют руки в качестве стандартного измерения. Этот уникальный способ измерения лошадей заставил меня задуматься, почему он используется и откуда взялся, поэтому я провел небольшое исследование, чтобы выяснить это.
Лошадей измеряют вручную, потому что в древних обществах не было стандартных измерительных инструментов, поэтому для измерения лошадей обычно использовали руки; эта традиция продолжается и по сей день. Одна рука считается 4 дюйма, поэтому лошадь с 15 руками имеет рост 60 дюймов.
Описание роста лошади вручную имело смысл в прошлом, но по-прежнему ли этот метод применим сегодня? Как только вы узнаете предысторию, я думаю, вы согласитесь, что это стандартное измерение должно быть продолжено.
История измерения лошадей вручную.
Лошади использовались для транспорта, сельского хозяйства и войны на протяжении веков. Для точного измерения лошадей была разработана система измерения лошадей по их росту в руках. Древние египтяне использовали единицу измерения, основанную на частях тела, включая руки.
Для точного измерения лошадей была разработана система измерения лошадей по их росту в руках. Древние египтяне использовали единицу измерения, основанную на частях тела, включая руки.
Они измерили рост лошади как расстояние от земли до вершины ее передней ноги, используя кулаки или открытые ладони в качестве единиц измерения. Эта практика широко использовалась, но не слишком точна. Из-за популярности торговли лошадьми требовалась определенная единица.
Генрих VIII стандартизировал размер руки на уровне 4 дюймов в 1500-х годах. Постоянная ширина позволяла покупателям и продавцам лошадей иметь стандартную ссылку.
Это практичный способ измерения лошадей, который используется до сих пор. После того, как я более подробно объясню, как мы измеряем лошадь, мы рассмотрим, какую роль играет рост у скаковых лошадей? Продолжайте читать, чтобы узнать.
Стандартные ручные измерения появились в 1500-х годах.
В Соединенных Штатах рука остается основной единицей измерения, как и в большинстве англоязычных стран, таких как Великобритания, Канада, Австралия, Ирландия и т. д., в то время как в других европейских странах и Федеральном международном конном спорте (FEI) используются метры.
д., в то время как в других европейских странах и Федеральном международном конном спорте (FEI) используются метры.
Измеряются ли в руках другие животные, кроме лошадей?
Вы знаете, насколько велик бегемот? Как насчет слона? Руки — один из способов, которыми люди измеряют других животных. На самом деле лошади были не первыми существами, которых измеряли таким образом.
Когда дело доходит до измерения других животных, руки являются одной из наиболее распространенных единиц измерения. Эта система, вероятно, вошла в обиход, потому что люди использовали свои тела в качестве эталона для измерения вещей на протяжении всей истории.
Люди обнаружили, что они могут относительно легко оценить рост животных, используя ручные измерения для большинства животных. Есть несколько причин. Во-первых, ручные измерения относительно легко провести, и они дают хорошую оценку размера животного. Кроме того, человеческие руки были относительно похожи по размеру.
Со временем ручные измерения стали чаще ассоциироваться с лошадьми, чем с другими животными. Тем не менее, он по-прежнему используется для пони, и я не уверен, что это приемлемая практика, но мы с друзьями относимся к высоте оленей, лосей и лосей с точки зрения рук.
Тем не менее, он по-прежнему используется для пони, и я не уверен, что это приемлемая практика, но мы с друзьями относимся к высоте оленей, лосей и лосей с точки зрения рук.
Какие другие единицы измерения
основаны на частях тела?- Локоть — расстояние от локтя до кончика среднего пальца. Обычно около 18 дюймов. Эта форма измерения годами использовалась на Ближнем Востоке.
- Ладони: локоть подразделяется на семь ладоней, каждая около 75 см.
- фут: единица измерения фута основана на длине стопы человека.
- Цифра: Ширина пальца, которая обычно составляет около 2 см (около 13/16 дюйма). Если кто-то попросит вас налить ему «пальчик» или два ликера, это высота в коротком стакане.
- Размах : Вытяните руку так, чтобы кончик большого пальца находился как можно дальше от кончика мизинца. Это расстояние называется «пролетом», и для большинства людей оно составляет почти ровно половину локтя.

- Большой палец: Ширина большого пальца, который позже был использован в качестве основы дюйма . https://itotd.com/articles/6165/body-based-units-of-measurement/
Как правильно измерить лошадь.
Лошадей измеряют по холке. Чтобы получить точные ручные измерения, начните с того, что поставьте лошадь на ровную плоскую поверхность и измерьте расстояние от земли до холки.
Холка — самая высокая точка спины лошади. Он находится сразу за плечом у основания шеи. Холка используется в качестве точки измерения, потому что она устойчива.
Было бы непросто измерить голову лошади, потому что она постоянно движется вверх и вниз. Точно так же и спина лошади не идеальна.
Лошадь может выгнуть спину, у нее может быть от природы низкая или высокая спина. Было бы трудно получить точные измерения. Холка является наиболее устойчивым положением для измерения лошади.
Мерки для лошадей просты в использовании.
Рулетка отлично подходит для измерения лошади; однако может быть трудно обращаться с лошадью и при этом получать точные измерения. Мерная палочка является самой простой в использовании и дает пользователю наилучшие возможности точно измерить животное. (щелкните эту ссылку, чтобы проверить цену на ленту роста и веса лошади на Amazon)
Мерная палочка является самой простой в использовании и дает пользователю наилучшие возможности точно измерить животное. (щелкните эту ссылку, чтобы проверить цену на ленту роста и веса лошади на Amazon)
Измерительная линейка представляет собой длинный стержень с маркировкой и горизонтальной полосой, которая скользит вверх и вниз по стержню. Держите более вытянутую часть на земле рядом с лошадью и положите перекладину на холку лошади.
Эти инструменты обеспечивают более точные результаты и имеют маркировку для определения рук, дюймов и сантиметров для облегчения преобразования.
Инструмент для измерения лошадейПреобразовать дюймы в руки очень просто. Однако дробные стрелки не переводятся в десятичные. Другими словами, лошадь ростом 14,2 имеет высоту 14 ладоней плюс 2 дюйма.
Переводить стрелки в дюймы очень просто.
Если бы это было записано с использованием обычной десятичной системы, это было бы записано как 14,5. .5 будет означать 1/2 из 4 дюймов. В нашем примере лошадь имеет рост 58 дюймов. 14×4=56 плюс 2 дюйма равно 58 дюймам.
В нашем примере лошадь имеет рост 58 дюймов. 14×4=56 плюс 2 дюйма равно 58 дюймам.
У средней верховой лошади обычно 15-17 рук. В то время как упряжная лошадь может достигать высоты более 20 рук и миниатюр ниже восьми рук. Чтобы прочитать о размерах жокеев, нажмите здесь.
Какова средняя высота лошади в руках?
У вас есть лошадь? Или вы думаете получить один? Если это так, вам может быть интересно, насколько большими они становятся. Средняя высота лошади составляет около 15 ладоней в холке. Это измерение проводится от самой высокой точки на спине лошади, прямо перед лопатками.
Лошади бывают всех форм и размеров, поэтому не беспокойтесь, если ваша лошадь немного выше или ниже этого размера. Некоторые породы, такие как Шайр, известны своим высоким ростом. А некоторые миниатюрные лошади вырастают только до 36 дюймов в холке.
Итак, каков рост вашей лошади по сравнению со средним показателем? Если вы не уверены, взгляните на нашу таблицу ниже. В нем указан средний рост нескольких популярных пород лошадей.
| Horse Breed | Height in hands |
|---|---|
| Thoroughbred | 16 hands |
| Quarter Horse | 15.1 hands |
| Arabian | 15 hands |
| Shire | 17 руки |
| Friesian | 15.3 hands |
| Morgan | 15 hands |
| Standardbred | 15.5 hands |
| Icelandic | 13 hands |
| Belgian | 16.5 hands |
| Appaloosa | 15 рук |
| Прогулочная лошадь Теннесси | 15,2 руки |
Рост разных типов лошадей: как сравнивать?
В мире существует три основных типа лошадей, и каждая группа по-своему уникальна. Одна из самых интересных вещей в лошадях — это их рост — он сильно варьируется от одного вида к другому.
Одна из самых интересных вещей в лошадях — это их рост — он сильно варьируется от одного вида к другому.
Три основных типа лошадей — это крупные упряжные породы, теплокровные и теплокровные. Крупные упряжные породы — самые большие из всех лошадей, их рост составляет от 16 до 18 ладоней.
Теплокровные в среднем немного ниже, чем рабочие породы, обычно их рост составляет около 15,2-16,2 ладоней. И, наконец, горячая кровь в среднем самая низкая из трех типов лошадей, в среднем около 15,2 руки в высоту.
Весь конный мир использует ручную единицу измерения?
Вот уже много лет меня озадачивает вопрос: все ли мы измеряем лошадей руками или это только в США? Оказывается, в мире существует множество различных способов измерения лошадей, и во многих странах есть свои уникальные системы.
Во всем мире лошадей измеряют по-разному, но наиболее распространенной единицей измерения являются руки. В США, Канаде, Австралии и некоторых частях Европы лошадей чаще всего измеряют в руках, тогда как в других странах, таких как Франция, Испания и Германия, их обычно измеряют в метрах.
Более высокие скаковые лошади бегают быстрее?
Находясь на ипподроме, я всегда поражаюсь росту некоторых чистокровных. С каждым годом они, кажется, становятся выше, чем в предыдущем сезоне; это заставило меня задуматься, разводят ли лошадей по росту и бегают ли более высокие лошади быстрее.
Более высокие скаковые лошади не бегут быстрее. Рост не является определяющим фактором скорости скаковой лошади. Средний рост четвертьхорса ниже, чем у чистокровной лошади, но на некоторых дистанциях они быстрее.
Не было исследований, подтверждающих, что рост влияет на скорость лошади. Что важно, так это длина шага и частота шага .
Длина шага имеет решающее значение для скорости лошади.
Шаг — это длина, которую лошадь преодолевает во время бега с одним прыжком. Другими словами, точка, от которой передняя нога лошади касается земли, до места, где та же самая нога касается земли следующей, называется шагом лошади.
Средний шаг большинства скаковых лошадей составляет 20 футов. Однако у чемпиона Man O’ War длина шага составляла 28 футов.
Скорость шага важна для скорости скаковой лошади.
Частота шагов или коэффициент оборота вычисляет количество шагов, которые скаковая лошадь делает за заданный период времени. Большинство скаковых лошадей имеют скорость шага от 130 до 140 шагов в минуту.
Более быстрые лошади смогут увеличить темп, не уменьшая его. Некоторые лошади-чемпионы имеют шаг более 160 шагов в минуту.
У четвероногих лошадей в среднем более высокая скорость шага, чем у чистокровных. Но чистокровные должны сохранять свой шаг на более длинном расстоянии и во времени. Чтобы совершить этот подвиг, несколько факторов должны работать вместе.
Для эффективного бега скаковой лошади при таком длинном шаге и сохранении высокой частоты шагов необходим идеальный баланс анатомических систем тела.
Лошади потребляют много кислорода во время бега.

Потребление кислорода должно быть максимальным. Когда лошади вытягивают свое тело во время скачек, они вдыхают воздух через нос, а когда сжимают ноги, они выдыхают.
Сердце скаковой лошади тоже должно работать на высоком уровне. Сердце скаковой лошади может циркулировать до 75 галлонов крови в минуту, что увеличивает количество богатых кислородом эритроцитов в кровотоке.
Обеспечивает лошадь необходимым кислородом во время скачек. Сердце средней лошади весит от 9 до 10 фунтов. Другой термин, используемый, когда речь идет о беговой скорости лошади, — угол шага .
Угол шага влияет на скорость лошади.
Угол шага — это расстояние между передней и задней ногой лошади, обычно измеряемое при отталкивании задней ногой.
Другими словами, угол шага — это метод, используемый для определения того, насколько сильно лошадь будет распрямляться во время скачек. Скаковые лошади с более высокими углами шага, в свою очередь, будут иметь более длинный шаг.
Исследование угла шага показало, что у Секретариата самый высокий угол шага среди всех скаковых лошадей — 110 градусов. Сторонники считают, что угол шага является важным фактором, определяющим успех скаковой лошади.
У лошадей с длинным шагом более развита энергетическая система, чем у их собратьев с коротким шагом.
Двумя наиболее важными факторами быстрой скаковой лошади являются длина шага и скорость шага . Высота не показатель.
Интересные факты о лошадях меньшего размера:
Кажется, что большинство людей считают, что чем больше, тем лучше; однако это не обязательно верно, когда речь идет о лошадях.
- Сухарь был маленьким для скаковой лошади. У него была отличная гоночная карьера, и он является предметом многих книг о скаковых лошадях.
- Джон Генри — еще одна маленькая скаковая лошадь. Он стал первой лошадью, выигравшей 4 000 000 долларов. На момент выхода на пенсию его карьерный заработок превысил 6 000 000 долларов.

- Сэр Уолтер Гилби написал книгу под названием «Маленькие лошади на войне». опубликовано в 1900 году. Он приводил пример за примером того, как лошади от 13,2 до 14,3 превосходили крупных лошадей почти во всех начинаниях.
- Во время Крымской войны лошади всех возрастом до 14,3 лет, на которых ездили армяне и башибузуки, постоянно выступали «выше возможностей английской чистокровной кавалерии».
- Д. Пешкоф, казак, выехал из Благовещенска, Сибирь, в ноябре 1889 года. Он и его упряжь весили 180 фунтов, но он ехал на своем пони, который составлял всего 12,3 руки, 5478 миль за 193 дня. Пони по кличке Сери зимой пересекла Сибирь и проходила в среднем 37 миль в день. Невероятный!
http://www.donblazer.com/ahorseofcourse/02_10_big_isnt_better.html
Ниже приведено полезное видео на YouTube, показывающее, как измерить рост лошади.
Часто задаваемые вопросы
Какая лошадь самая высокая? Самой высокой лошадью, которую я нашел, была шайрская лошадь по кличке Сэмпсон, жившая в 1850-х годах. Сэмпсон был 21,2 1/2 руки (7 футов 2-1/2 дюйма в холке) и, как говорят, весил 3300 фунтов. Шайры до сих пор остаются самой крупной породой тяжеловозов.
Сэмпсон был 21,2 1/2 руки (7 футов 2-1/2 дюйма в холке) и, как говорят, весил 3300 фунтов. Шайры до сих пор остаются самой крупной породой тяжеловозов.
Самой маленькой лошадью был крошечный 14-дюймовый пони из Нью-Гэмпшира. Его звали Эйнштейн. Однако оригинальная лошадь была размером с золотистого ретривера.
Какой рост у 16-ручной лошади в футах?
Рост шестнадцатиручной лошади 5 футов 4 дюйма. Измерение руки составляет 4 дюйма, поэтому лошадь с шестнадцатью руками имеет рост 64 дюйма (4 × 16). 64 дюйма, преобразованные в футы, равны пяти футам четырем. дюймы.
| [Индекс] | |
[Введение] [Основы] [Подробнее] [Тест] [Проблемы] | |
Основы | |
| Директор
Размеры
Прочее
Размеры
Флотация
Характеристики
|
Рейтинг сильных форвардов НБА: Яннис, Кевин Дюрант и Леброн Джеймс лидируют в преддверии сезона 2022/23
Тим Дункан. Карл Мэлоун. Кевин Макхейл. Это игроки, о которых мы думаем, когда слышим «мощный форвард». Боже, как все может измениться в течение одного или двух поколений.
Да, четверка спиной к корзине древняя, как телефонная будка, и на самом деле многим из сегодняшних лучших игроков на этой позиции поручено вести нападение в качестве разыгрывающих нападающих. ЛеБрон Джеймс, Яннис Адетокумбо и Кевин Дюрант — плеймейкеры почти в той же степени, что и бомбардиры, и каждый из них зарабатывает деньги, управляя мячом и атакуя с периметра. Тем не менее, в сегодняшней игре они все мощные форварды.
Тем не менее, в сегодняшней игре они все мощные форварды.
Здесь, на CBS Sports, мы попробовали свои силы и составили список из 22 лучших мощных форвардов НБА на сезон 2022–2023 годов с учетом прогнозируемых улучшений и спадов. Это часть выпуска списка 100 лучших игроков НБА, который будет опубликован во вторник.
Мощный форвард — одна из наиболее горячо оспариваемых должностей в лиге, особенно на вершине, где многолетние кандидаты на MVP (и, возможно, будущие) засоряют поле. Совершите круиз по списку и не стесняйтесь сообщить нам, что мы сделали не так. Не то чтобы вы нуждались в нас, чтобы спросить.
Пожалуйста, отметьте поле выбора, чтобы подтвердить, что вы хотели бы подписаться.
Извиняюсь!
При обработке вашей подписки произошла ошибка.
Проведя лето в сборной США, Джонсон провел один из самых результативных атакующих сезонов в лиге в прошлом году для сильного форварда, набирая в среднем 17 очков и 6 подборов за игру при результативности 47/40/76. Он преуспевал в ситуациях типа «брось и поймай», достигнув 87-го процентиля согласно «Синергии», но его атлетизм также позволяет ему эффективно атаковать кольцо. Он может защищать несколько позиций и в прошлом сезоне был на 83-м процентиле в изолированной защите, согласно Synergy. — Колин Уорд-Хеннингер
Он преуспевал в ситуациях типа «брось и поймай», достигнув 87-го процентиля согласно «Синергии», но его атлетизм также позволяет ему эффективно атаковать кольцо. Он может защищать несколько позиций и в прошлом сезоне был на 83-м процентиле в изолированной защите, согласно Synergy. — Колин Уорд-Хеннингер
Ковингтон зарекомендовал себя как сильный форвард в НБА, и он чувствовал себя как дома после того, как его обменяли в «Клипперс» в середине прошлого сезона. Он набирал в среднем 10,4 очка и 5,1 подбора, а также его блестящие 45-процентные трехочковые броски в 23 играх с «Лос-Анджелесом», приземлившись в 93-м процентиле в ситуациях «бросай-бросай», согласно Synergy. Он также продолжает играть роль «игровой машины», совершая 1,5 перехвата и 1,3 блок-шота за игру между «Блэйзерс» и «Клипперс» в прошлом сезоне. Тай Лю иногда использовал Ковингтона в качестве центра смоллбола, и в сезоне 2022/23 у него должно быть больше возможностей. — Колин Уорд-Хеннингер
— Колин Уорд-Хеннингер
Ветеран стал образцом стабильности, набирая не менее 17 очков при 38 процентах попаданий с трехочковых в четырех сезонах подряд. Он не предлагает многого в обороне, но если вы хотите играть в смоллбол и ставить пространство на площадке, он надежный вариант, поэтому он вряд ли останется в Юте надолго. Поскольку «Джаз» продолжают разбирать, Богданович является одним из следующих кандидатов на обмен, на которого будет ориентироваться претендент. — Джек Мэлони
Williams — именно тот игрок, который более ценен в плей-офф. Как и Пи Джей Такер до него, он сильный, умный защитник, который любит травить звезд и преуспевает в схеме «подмени все». Он показал, что заслуживает уважения на периметре — он реализовал 41,1% трехочковых в регулярном сезоне, 46,9% — в углах, 44,6% — на флангах — и может держаться впереди более мелких игроков. После прорыва Уильямса финал показал, что 23-летнему игроку еще есть куда расти с точки зрения его экранной навигации и промежуточной игры. — Джеймс Герберт
После прорыва Уильямса финал показал, что 23-летнему игроку еще есть куда расти с точки зрения его экранной навигации и промежуточной игры. — Джеймс Герберт
Батум превратился в идеального ролевого игрока-ветерана — элитного снайпера (40 процентов трехочковых в прошлом сезоне) и защитника периметра, который также может положить мяч на пол и раздать в крайнем случае. После того, как в течение своей карьеры он несколько раз играл разыгрывающим, Батум теперь обладает длиной, скоростью и силой, чтобы быть идеальной четверкой в системе «Клипперс». — Колин Уорд-Хеннингер
Главными качествами Такера как сильного форварда являются его универсальность и стойкость. Он может защищать обе позиции форварда, а иногда также выступать в роли центра смоллбола. К тому же, он будет лежать на полу. Он финишировал в топ-20 по общему количеству игр, сыгранных пять раз за свою карьеру, и трижды возглавлял лигу в этой категории. Он также финишировал в первой десятке по общему количеству сыгранных минут дважды. Возможность быть доступным для своей команды очень ценна, особенно в сегодняшней НБА. — Майкл Каски-Бломейн
Он также финишировал в первой десятке по общему количеству сыгранных минут дважды. Возможность быть доступным для своей команды очень ценна, особенно в сегодняшней НБА. — Майкл Каски-Бломейн
Кузьма в прошлом сезоне получил значительно больше свободы в Wizards, и в результате мы увидели расцвет его атакующей игры. Он уже был известен как трудолюбивый защитник, который может защищаться на периметре и в нижней стойке, но то, что он лидировал в прорыве в переходе или читал защиту, чтобы сделать своевременную передачу, показало, что есть еще кое-что, что нужно сделать. его игра, чем то, что мы видели с Лейкерс. — Жасмин Уимбиш
Гордон был очень эффективным бомбардиром в прошлом сезоне, но он не в своей тарелке как парень №2. В этом году ему не придется быть с возвращением Джамала Мюррея и Майкла Портера. Когда Гордон вернулся к своей надлежащей роли двустороннего спортсмена, заполняющего пробелы, где он может свободно есть, как резак Николы Йокича, и бегать по площадке, «Наггетс», если они смогут оставаться здоровыми, кажутся одними из лучших в лиге. — Претенденты на звание полки. — Брэд Боткин
— Претенденты на звание полки. — Брэд Боткин
Хотя это был не самый эффективный сезон для Рэндла, он все же набрал 20 и 10 очков, а его универсальность как сильного форварда — вот что отличает его игру. Два сезона назад он доказал, что может растянуть свою игру до трехочковой линии, сбив более 40 процентов своих попыток, а его способность двигаться с мячом и без мяча для кого-то на этой позиции является ценным активом. — Жасмин Уимбиш
В отличие от остальных парней, опережающих Финни-Смита в этом списке, он не собирается набирать кучу очков каждую ночь, но он заставит вас заплатить, если вы оставите его открытым в углу. Он также приложит огромные усилия, чтобы защитить лучшего игрока противоположной команды, и, в конце концов, вы можете посмотреть на боксы и увидеть, что он финишировал с 12 очками и пятью подборами. Это не сногсшибательная статистика, но его роль в «Маверикс» состоит в том, чтобы сбивать его удары, когда это необходимо, жестко защищаться и захватывать несколько досок. Он постоянно ставит все галочки, и это все, что вы можете ожидать от парня, который играет вместе с Дончичем. — Жасмин Уимбиш
Он постоянно ставит все галочки, и это все, что вы можете ожидать от парня, который играет вместе с Дончичем. — Жасмин Уимбиш
Станет ли Коллинз третьим вариантом в новой команде «Ястребов» или, наконец, произойдет долгожданный обмен? Тем не менее, Коллинз уже доказал, что представляет собой серьезную атакующую угрозу. Будь то прыжки к кольцу для переулков или сбивание трехочковых, защита соперника всегда должна быть начеку, когда Коллинз находится на полу. В прошлом сезоне он был одним из девяти игроков, набравших в среднем не менее 15 очков и семи подборов, при этом 35 процентов попаданий с трехочковых. — Джек Мэлони
В начале своей карьеры Харрис некоторое время играл в роли легкого форварда, но в сегодняшней НБА он больше подходит на роль мощного форварда. В прошлом сезоне Харрис был одним из семи мощных форвардов, набравших в среднем более 17 очков, шесть подборов и три передачи за игру при точности более 48 процентов бросков с пола. Он не лучший и даже не второй вариант в Филадельфии, но он надежный ролевой игрок, способный заполнить статистику. — Майкл Каски-Бломейн
Он не лучший и даже не второй вариант в Филадельфии, но он надежный ролевой игрок, способный заполнить статистику. — Майкл Каски-Бломейн
Грант большую часть своей карьеры играл на позиции легкого форварда, но в современной НБА он позиционируется как невероятно универсальная четверка, которая может дотянуться до трехочковой линии, защищаться с нескольких позиций и при необходимости создавать собственную атаку. Теперь, когда он играет с Дэмиана Лилларда в Портленде, ему будет поручено меньше хлопот, и он сможет вернуться к более сложной версии роли, в которой он преуспел в Денвере. Его мастерство в качестве снайпера и изолированного защитника должно хорошо послужить Blazers. — Колин Уорд-Хеннингер
Мобли — настоящий 7-футовый, наделенный ловкостью человека, который намного ниже ростом. Будучи новичком, он был скорее финишером, чем инициатором, но легко увлечься тем, куда может зайти его атакующая игра. В идеале его движения становятся менее механическими, и он чувствует себя более комфортно за пределами дуги. И даже если это займет некоторое время, он может быть звездой в своей оборонительной роли, которая заставляет его бродить повсюду, взрывая действия и прикрывая своих менее универсальных товарищей по команде. Мобли занял третье место в соревнованиях по броскам в прошлом сезоне, уступив только защитникам обода Якобу Поэлтлю и Руди Гоберу. — Джеймс Герберт
В идеале его движения становятся менее механическими, и он чувствует себя более комфортно за пределами дуги. И даже если это займет некоторое время, он может быть звездой в своей оборонительной роли, которая заставляет его бродить повсюду, взрывая действия и прикрывая своих менее универсальных товарищей по команде. Мобли занял третье место в соревнованиях по броскам в прошлом сезоне, уступив только защитникам обода Якобу Поэлтлю и Руди Гоберу. — Джеймс Герберт
Джексон был зверем в обороне в прошлом сезоне – четвертое место в лиге с 2,2 блок-шотами за игру, в то время как бомбардиры наносили только 41,7% бросков, которые Джексон защищал, что является четвертым по точности показателем в лиге. Два сезона назад Джонсон выбился из колеи с 3, но в прошлом году упал до 32 процентов. Если он сможет совместить бросок и защиту в одной кампании и найти способ избежать неприятностей с нарушением правил, вы увидите потенциального игрока Матча звезд даже в переполненной Западной конференции. — Брэд Боткин
— Брэд Боткин
Грина так же сложно отнести к какой-либо позиции, как и любого игрока в баскетболе — в нападении он разыгрывающий, а в обороне он охраняет флангов и центровых так же, как и мощных форвардов. Но как бы вы его ни классифицировали, его величие на обоих концах поля очевидно. Даже несмотря на то, что его результативность уменьшилась практически до нуля, Грин заставляет нападение «Уорриорз» щелкать своими пасами, настройкой экрана и общением. С другой стороны, он был ведущим кандидатом на звание лучшего защитника года в прошлом сезоне, прежде чем из-за травмы выбыл из гонки. Грин, вероятно, способствует победе больше, чем любой другой игрок лиги, не являющийся бомбардиром. — Колин Уорд-Хеннингер
С мячом в руках Сиакам держит оборону в напряжении. Он использует множество нерешительных движений и вращений, чтобы попасть в краску, и как только он доберется туда, он будет искусным финишером, достаточно сильным, чтобы вступить в контакт с кольцом, но с такой же вероятностью сможет поднять его с расстояния флоатинга. В безпозиционной системе «Рэпторс» он может находить катера, делать своевременные разрезы и играть на любой стороне пик-н-ролла. В защите он создан, чтобы переключаться на кого угодно и сеять хаос в верхней части зоны. Теперь, когда ему 28 лет, и начинается его седьмой сезон, речь идет о постепенном улучшении. В прошлом сезоне Сиакам бросал 36,5%, совершая 2,7 точных броска за игру; если это число приблизится к 40, это сильно повлияет на атаку Торонто. — Джеймс Герберт
В безпозиционной системе «Рэпторс» он может находить катера, делать своевременные разрезы и играть на любой стороне пик-н-ролла. В защите он создан, чтобы переключаться на кого угодно и сеять хаос в верхней части зоны. Теперь, когда ему 28 лет, и начинается его седьмой сезон, речь идет о постепенном улучшении. В прошлом сезоне Сиакам бросал 36,5%, совершая 2,7 точных броска за игру; если это число приблизится к 40, это сильно повлияет на атаку Торонто. — Джеймс Герберт
В недавнем интервью CBS Sports Таунс назвал себя «одним из лучших атакующих игроков и талантов, которых когда-либо видела НБА», и у него есть веские доводы, особенно когда речь идет о бигмэнах. Единственный другой игрок в истории лиги, который за несколько сезонов набрал в среднем не менее 24 очков и девять подборов, при этом забивая 41 процент трехочковых, — это Ларри Берд. Теперь в лучшей команде своей карьеры у Таунса будет шанс показать, что его навыки могут привести к успеху в плей-офф. — Джек Мэлони
— Джек Мэлони
Мне кажется несправедливым даже позиционировать Уильямсона, потому что он слишком мал для сильного форварда с показателем всего 6-6, но, учитывая огромную силу, которой он обладает, он способен полностью уничтожить любого крупного защитника, который посмеет встать у него на пути. . Он наносит практически весь свой урон по кольцу, но не в традиционном стиле спиной к корзине. Обычно он действует как разыгрывающий, который подбрасывает мяч к полу и на полной скорости мчится вперед к кольцу. Если вы позволите ему разбежаться у корзины, все кончено. — Жасмин Уимбиш
У нас есть Леброн в качестве сильного форварда. Давайте будем честными: он разыгрывающий «Лейкерс». Когда нужно будет взять на себя управление, поводья возьмут на себя Леброн. Но мне нравится смотреть на него через призму четвертого броска, учитывая все более сильную зависимость Леброна от трехочковых бросков. В прошлом сезоне 34 процента бросков Леброна без лишнего времени были нанесены из-за дуги, что соответствует рекорду в карьере, что равняется восьми попыткам за игру. Он сделал их с отрывом в 36 процентов и набрал более 30 очков за ночь. Делайте более восьми подборов, шесть передач, перехваты и блок-шоты каждую ночь, и подумайте об этих цифрах — не только для 38-летнего игрока, которому скоро исполнится 38 лет; для всех. Всегда. Джеймс, без сомнения, по-прежнему входит в десятку лучших игроков мира, и даже такой уровень квалификации кажется слегка оскорбительным. — Брэд Боткин
В прошлом сезоне 34 процента бросков Леброна без лишнего времени были нанесены из-за дуги, что соответствует рекорду в карьере, что равняется восьми попыткам за игру. Он сделал их с отрывом в 36 процентов и набрал более 30 очков за ночь. Делайте более восьми подборов, шесть передач, перехваты и блок-шоты каждую ночь, и подумайте об этих цифрах — не только для 38-летнего игрока, которому скоро исполнится 38 лет; для всех. Всегда. Джеймс, без сомнения, по-прежнему входит в десятку лучших игроков мира, и даже такой уровень квалификации кажется слегка оскорбительным. — Брэд Боткин
Это не силовой форвард вашего дедушки. Основываясь только на наборе навыков, Дюранта можно было бы назвать атакующим защитником, но его почти 7-футовое телосложение позволяет ему делать вещи вчетвером, что делает его еще большим кошмаром матча, чем он уже был. По данным Synergy, возможно, лучший чистый бомбардир в баскетболе, КД также показал рекордные для карьеры 6,4 передачи за игру в прошлом сезоне и опережает всех нападающих по очкам за владение, включая передачи (минимум 1000 владений). — Колин Уорд-Хеннингер
— Колин Уорд-Хеннингер
Универсальный двукратный MVP может претендовать на ряд позиций, но он зарекомендовал себя как мощный форвард №1. Мощный и безжалостный, он контролирует краску на обоих концах площадки, совершая 80,8% бросков с расстояния в три фута и блокируя 1,4 броска за игру. Но, в соответствии с тенденциями, он также может перемещать пол, но в качестве точки вперед, а не стрелка. — Джек Мэлони
Рыба возвращается в Южную Бразилию после запрета на траловый лов
- Мелкие и крупные рыбаки сообщают об увеличении количества и разнообразия видов рыб в лагуне Патос и на побережье штата Риу-Гранди-ду-Сул.
- Такое изобилие появилось после того, как в 2018 году был принят и подписан закон о запрете моторного траления на побережье штата. Союзники президента Болсонару.
- Назначенный Болсонару в Федеральный верховный суд судья Кассио Нуньес Маркес отменил преобладающее мнение суда и приостановил действие предыдущего решения.
 В дату, которая еще не назначена, последнее слово будет за пленарным заседанием Суда.
В дату, которая еще не назначена, последнее слово будет за пленарным заседанием Суда.
За 22 года работы мелким рыбаком в Риу-Гранди-ду-Сул Вивиан Мачаду Алвес редко видела так много рыбы, прибывающей в бухту, которая открывается в нескольких минутах ходьбы от ее порога. Наизусть она перечисляет невероятное количество кефали, морской камбалы, бразильской атерины и королевской рыбы, а также «несколько видов, которые я никогда не видела и не ела», — говорит она.
Ее муж, проработавший рыбаком 50 лет, даже выбросил морского окуня — рыбу, имеющую промысловое значение и высоко ценимую в местной кухне, — потому что не знал, какое животное поймал его сеть зимой. «Но когда он пришел во второй раз в тот же день, я решил забрать его домой и показать моему дяде, которому за 80. Он был поражен, потому что он был еще ребенком, когда в последний раз увидел морского окуня», — говорит Пауло Матиас.
Он был поражен, потому что он был еще ребенком, когда в последний раз увидел морского окуня», — говорит Пауло Матиас.
Они являются членами старейшей рыбацкой колонии (похожей на профсоюз ассоциации рыбаков из определенного района) в штате Риу-Гранди-ду-Сул, известной как Z1, и расставляют свои сети вокруг острова Маринейрос, в муниципалитете Риу-Гранди, на крайнем юге Бразилии. Они ловят рыбу в районе лагуны Маринейрос — крупнейшей барьерной лагуны в Южной Америке — в 20 километрах (12 миль) по прямой от канала, соединяющего ее с Атлантическим океаном.
Аналогичные сообщения поступают с северного побережья штата, в том числе от рыбаков, которые не пользуются лодками, поскольку ставят сети там, где разбиваются волны. «В том, что мы называем пляжной ловлей троса, мы наблюдаем гораздо более крупные уловы слабой рыбы», — говорит Ана Спинелли. Она возглавляет Палату технического рыболовства Совета Риу-Гранди-ду-Сул по аквакультуре и устойчивому рыболовству.
Рыбный порт в Рио-Гранде, RS. Изображение Marcelo Curia/Mongabay
Изображение Marcelo Curia/MongabayТе, кто занимается крупномасштабным рыболовством в открытом море, также празднуют изобилие. «С 2018 года у нас было два хороших сезона для креветок и белогорлых горбылей», — говорит судовладелец Жоао Гонсалвеш из Рио-Гранде, занимаясь техническим обслуживанием своего судна 9.0323 Yasmin , который может перевозить небольшую рыбацкую команду в течение нескольких дней.
Нынешняя ситуация полностью отличается от той, которую описал в 2018 году тогдашний губернатор Хосе Иво Сартори, когда он представил в парламент штата законопроект о разработке политики устойчивого развития рыболовства: «Он направлен на преодоление нынешнего кризиса в Риу-Гранди-ду- Сула, чтобы избежать ее краха», — написал он в заявлении в парламенте, объясняя причины принятия законопроекта.
Законопроект был принят и достиг своей цели. Но рыбная промышленность подвергла критике запрет на «все траловые сети, вытягиваемые моторными судами в Рио-Гранди-ду-Сул, включая 12-мильную полосу у побережья штата» — 22-километровый (14-мильный) морской район, который использовался в качестве основной зоны траления крупными судами из соседнего штата Санта-Катарина.
Среди пострадавших было несколько членов влиятельной Ассоциации судовладельцев и рыбной промышленности Итажаи (SINDIPI). По данным организации, некоторые суда получали более 70 процентов своего годового дохода от лова креветок (типы santana и ferrinho ) в территориальном море Риу-Гранди-ду-Сул.
Интересы рыбаков стали федеральным вопросом, когда Жаир Болсонару вступил в должность в январе 2019 года и назначил рыбного бизнесмена из Итажаи, крупнейшего порта в штате Санта-Катарина, секретарем по рыболовству в своей администрации.
Под руководством Сейфа Джуниора Министерство сельского хозяйства утвердило план возобновления тралового промысла, ориентированный только на штат Риу-Гранди-ду-Сул. План был одобрен судебным запретом Верховного суда, вынесенным судьей Кассио Маркесом, также назначенным президентом, что противоречило предыдущему постановлению суда и позволяло вновь открывать морские просторы штата для траловых сетей, считающихся хищными.
Прения еще не окончены, потому что окончательное слово по этому вопросу остается за пленарным заседанием Суда. Между тем, судебные запреты, вынесенные Федеральным областным судом 4 -й район (ТРФ-4) не допускать траловые суда на территорию государства.
Но предстоящие выборы добавляют к этой истории новый компонент. Сейф Джуниор будет баллотироваться в Федеральный сенат в Санта-Катарине. Он принадлежит к той же партии, что и президент Болсонару, который будет добиваться переизбрания — Либеральной партии (ЛП) — и эта тема может дать им много голосов в государстве, которое является одним из самых верных президенту, поскольку он сталкивается с изображением кризис.
Жоао Гонсалвеш, судовладелец из Рио-Гранде, РС. Изображение Марсело Куриа/Монгабай Неэффективное рыболовство Траловый лов осуществляется путем волочения сетей по морскому дну. По данным Гринпис, каждое судно вытягивает одну или две сети, в зависимости от цели, а площадь покрытия может достигать 5000 гектаров (12 300 акров) за одну рыбалку. Эта практика гарантирует промышленным предприятиям большие объемы рыбы, но она губительна для окружающей среды и, следовательно, для мелких рыбаков, чьи районы деятельности остаются пустыми после прохода крупных промышленных судов.
Эта практика гарантирует промышленным предприятиям большие объемы рыбы, но она губительна для окружающей среды и, следовательно, для мелких рыбаков, чьи районы деятельности остаются пустыми после прохода крупных промышленных судов.
Траловые сети буквально охватывают дно океана, превращая сложную экосистему в пустыню. Притягиваемая мощными двигателями сетка растягивается и становится меньше, собирая рыбу, ракообразных и все, что появляется. Даже молодь, которая никогда не размножалась, в конечном итоге попадает в ловушку, что ставит под угрозу способность биоразнообразия к восстановлению.
Рыбу меньше промыслового размера выбрасывают в море, но только после того, как она погибнет под тяжестью остальных. Что еще хуже, взбалтывая морские отложения, траловые сети нарушают важное хранилище углекислого газа, что в конечном итоге усугубляет и без того серьезные последствия глобального потепления для океанов.
«После того, как дрифтерные сети были запрещены, траление, безусловно, стало самым вредным и хищническим методом лова», — объясняет профессор Игнасио Морено из Центра прибрежных, лимнологических и морских исследований (CECLIMAR) Федерального университета Риу-Гранди-ду-Сул (UFRGS).
«Он вызывает серьезные изменения в сообществе организмов, которые используют морское дно для кормления, жизни и укрытия, и создает большие выбросы, в том числе исчезающие виды. Это неэффективная эксплуатация», — говорит Луис Густаво Кардосо, руководитель Лаборатории придонных и головоногих рыбных ресурсов Федерального университета Рио-Гранде (FURG).
В любой точке мира картина будет плохой, и по этой причине многие страны сомневаются в долгосрочной жизнеспособности тралового промысла.
Однако у побережья Риу-Гранди-ду-Сул есть две особенности, которые усугубляют ситуацию. Во-первых, тот факт, что 70 процентов тралового лова, практикуемого в штате, используется для ловли креветок, что требует более плотных сетей, которые также ловят более мелких животных. Кроме того, этот район морского дна признан местом размножения и рождения нескольких морских видов, некоторые из которых встречаются только в южной части континента. Из 66 видов, обитающих в этом районе, 22 находятся под угрозой на том или ином уровне.
«Здесь собираются для размножения скаты и акулы, кормятся другие животные, растет молодь. Это действительно питомник», — говорит Мартин Диас, научный руководитель офиса Oceana в Бразилии. Oceana — международная организация по охране морской среды, поддержавшая дебаты о государственном праве.
Геологические особенности, привлекающие животных для размножения – плоское и очень мелкое побережье по сравнению с другими частями страны, с гладким морским дном, состоящим в основном из песка и ила – также делают их более уязвимыми, с небольшим шансом найти укрытие. Тем не менее, он идеально подходит для тралового лова, поскольку в нем нет препятствий, которые могли бы повредить сети.
Район рыбацкой колонии Z3 в Пелотасе, штат RS. Изображение Marcelo Curia/Mongabay Беспрецедентный консенсус Законопроект о государственной политике устойчивого развития рыболовства в Риу-Гранди-ду-Сул был единогласно принят парламентом штата и подписан губернатором 5 сентября 2018 г. (Закон 15223). В результате необычайного единства мелких и крупных рыбаков, ученых и активистов общественных организаций, зачастую находящихся по разные стороны, его отмечали все в штате.
(Закон 15223). В результате необычайного единства мелких и крупных рыбаков, ученых и активистов общественных организаций, зачастую находящихся по разные стороны, его отмечали все в штате.
Помогло и то, что в Риу-Гранди-ду-Сул не было тралового флота: все такие суда, работавшие в его водах, прибыли из других государств. Но эта мера основывалась как на научно-экономических, так и на социальных основаниях.
«Мы собрали всех речных, морских и лагунных рыбаков из Риу-Гранди-ду-Сул. Маленькие и большие, весь рыбный промысел. И мы восемь месяцев работали над законопроектом. Мы обеспечили всю основу», — вспоминает Вивиан Мачадо Алвес, региональный координатор Движения мужчин и женщин-рыбаков (MPP) в Риу-Гранди-ду-Сул и поборник этого единства.
Научная аргументация была предоставлена Федеральным университетом Рио-Гранде, опубликовавшим исследования, свидетельствующие о потенциальных экологических, экономических и социальных последствиях запрета на траловый промысел для штата.
Исследования прогнозировали, что каждая тонна рыбы, выброшенная траулерами (поскольку эти особи слишком молоды и малы для продажи), может превратиться в 10 тонн (11 тонн) всего за два года, если не принимать во внимание естественную гибель и другие факторы, кроме рыболовства.
В результате уловы четырех основных промысловых видов в регионе (белоротый горбыль, слабак, аргентинский горбыль и королевский слабак) вырастут на 709процентов, с 400-процентным увеличением доходов местной рыбной промышленности. Выгода будет достигнута самими траловыми флотами, потому что траление по-прежнему разрешено за пределами 12 морских миль (14 миль), и будет больше рыбы размеров, подходящих для торговли.
С экологической точки зрения, наиболее положительное воздействие ощутят два вида, которые когда-то были многочисленны в этом регионе и теперь находятся под угрозой исчезновения: бразильская рыба-гитара ( Pseudobatos horkelii ) и угловатая акула-ангел ().0323 Squatina guggenheim ), популяция которых за этот период вырастет на 395 и 386 процентов соответственно.
До сих пор нет научной статистики, чтобы узнать, подтвердились ли предсказания, но общее впечатление таково, что они есть.
В дополнение к сообщениям рыбаков, популяция бразильской гитарной рыбы уже демонстрирует признаки восстановления, согласно предварительным данным, собранным Группой по изучению водных млекопитающих Риу-Гранди-ду-Сул, базирующейся в прибрежном городе Торрес.
Исследователи измеряют размер особей, которые случайно попадают в сети мелких рыболовов, и, по словам руководителя исследования Федерико Сукунца, новости «очень положительные». «Девяносто процентов особей старше первой половозрелости, то есть они уже размножились», — говорит он. Они рассчитывают расширить исследование, чтобы подтвердить, повторяется ли это явление в других местах. Лов рыбы-гитары запрещен в Риу-Гранди-ду-Сул, и экземпляры должны быть выброшены, когда они попадают в сети.
«Помимо защиты рыбаков и их средств к существованию, мы также защищаем экосистемы, верно? Мы защищаем океан», — говорит Мачадо Алвес, рыбак с острова.
Бизнесмен Хорхе Сейф Джуниор не имел опыта работы на государственной службе, когда в 2019 году занял пост министра аквакультуры и рыболовства., в первые дни правления Болсонару. В его резюме, опубликованном на правительственном веб-сайте, подчеркивается его 40-летний опыт работы в рыбной промышленности, а также его идеологическое соглашение с президентом, с которым он сблизился до того, что его назвали «06» — отсылка к сыновьям президента Флавио ( 01), Карлос (02), Эдуардо (03) и Ренан (04). У Болсонару также есть дочь по имени Лаура, но она не известна под номером как ее старшие братья.
В должности, представляющей как крупных, так и мелких рыбаков, Сейф Джуниор решил присоединиться к интересам крупных бизнесменов, собравшихся в SINDIPI. Данные, предоставленные ассоциацией, подтверждают решение судьи Нуньеса Маркеса о признании закона штата Риу-Гранди-ду-Сул недействительным. Эти данные также легли в основу «Плана устойчивого возобновления тралового промысла на побережье Риу-Гранди-ду-Сул», который Департамент рыболовства и аквакультуры запустил в марте 2021 года после постановления судьи Маркеса.
Эти данные также легли в основу «Плана устойчивого возобновления тралового промысла на побережье Риу-Гранди-ду-Сул», который Департамент рыболовства и аквакультуры запустил в марте 2021 года после постановления судьи Маркеса.
SINDIPI — крупнейшая ассоциация рыбной промышленности в Бразилии и одна из крупнейших в Латинской Америке. Некоторые из 451 судна, которое она представляет, получали 70 процентов своих доходов от тралового лова в Риу-Гранди-ду-Сул. Таким образом, организация является естественным участником этих дебатов.
Однако SINDIPI также является организацией, защищающей промышленное рыболовство в Итажаи, муниципалитете, где семья Сейф содержит флот судов и их компанию JS Manipulação de Pescados, что вызвало сомнения в мотивах Сейфа Джуниора присоединиться к одной стороне истории. .
«Эти люди из Санта-Катарины обладают властью и политическими связями. Департамент рыболовства был координатором усилий через секретаря Сейфа Джуниора, который имеет прямой контакт с президентом Болсонару», — говорит Диас из Океании.
Дело дошло до Федерального Верховного суда, который рассмотрит оспаривание конституционности запрета Риу-Гранди-ду-Сул на траловый промысел. Конституционный вопрос был подан Либеральной партией президента Болсонару.
Назначенный в Верховный суд Жаиром Болсонару, судья Маркес известен своими решениями, которые нравятся президенту, включая голосование за оправдание конгрессмена, выступающего за Болсонару, который распространял фальшивые новости на выборах, и еще одного осужденного за атакует демократию , которым президент в итоге помиловал.
В декабре 2020 года, через месяц после приведения к присяге в качестве судьи Верховного суда, Нуньес Маркес вынесла судебный запрет в пользу Либеральной партии и интересов SINDIPI. Это позволило провести траление в Риу-Гранди-ду-Сул после того, как его предшественник в суде, бывший судья Селсу де Меллу, вынес решение по тому же вопросу и не усмотрел нарушения Конституции. Болсонару отпраздновал это в прямом эфире вместе со своим протеже: «Поздравляем Кассио Маркеса с этим счастливым судебным запретом. Идите ловить рыбу, ребята».
Идите ловить рыбу, ребята».
До своего решения Нуньес Маркес трижды встречался с секретарем Сейфом Жуниором, чтобы обсудить этот вопрос. Календарь судьи Маркеса, однако, не был открыт для беседы, запрошенной федеральными представителями из Риу-Гранди-ду-Сул, которые призвали к срочному рассмотрению этого вопроса на пленарном заседании Верховного суда. Вместе с мелкими и крупными рыбаками из штата группа просит о встрече как минимум с апреля этого года, но пока им удалось поговорить только с начальником штаба судьи Маркеса.
Судья Маркес держит это дело уже 20 месяцев. На вопрос, когда иск будет рассматриваться на пленарном заседании, суд ответил лишь «нет срока» и проигнорировал другие вопросы, заданные Монгабаем. Секретарь Сейф Джуниор не ответил на письменные вопросы, направленные в его офис. Министерство сельского хозяйства, которому подчиняется Департамент аквакультуры и рыболовства, даже не подтвердило получение электронных писем с запросами по этому поводу.
SINDIPI сообщает Mongabay, что штат Риу-Гранди-ду-Сул политизировал дебаты, сосредоточив запрет «только на методе рыболовства, который не практикуется рыбаками из штата и, следовательно, не ставит под угрозу политический капитал его представителей». Полные комментарии ассоциации можно прочитать здесь.
Полные комментарии ассоциации можно прочитать здесь.
Риу-Гранди-ду-Сул — не единственный штат Бразилии, запретивший траловый промысел на своем побережье в целях защиты окружающей среды и обеспечения устойчивого рыболовства. Закон, запрещающий практику в Амапе, также попал в Верховный суд, который единогласно разрешил штату издавать законы на территории, которая даже больше, чем его территориальное море, и охватывает 30 миль от побережья.
В штате Сан-Паулу ограничение было введено путем создания трех зон охраны окружающей среды, которые следуют собственным правилам управления рыболовством. Десять бразильских штатов имеют местные правила, предотвращающие уничтожение биоразнообразия и рыбных запасов траловым промыслом.
План возобновления тралового промысла, предложенный Департаментом аквакультуры и рыболовства после судебного запрета Маркеса, обещал сделать деятельность устойчивой. Тем не менее, он фокусируется только на Риу-Гранди-ду-Сул, чья запретная для траления зона составляет всего 0,78 процента от 1,7 миллиона квадратных километров (656 000 квадратных миль), на которых разрешена деятельность, согласно Oceana.
Тем не менее, он фокусируется только на Риу-Гранди-ду-Сул, чья запретная для траления зона составляет всего 0,78 процента от 1,7 миллиона квадратных километров (656 000 квадратных миль), на которых разрешена деятельность, согласно Oceana.
«Это не план устойчивого промышленного траления у берегов Бразилии. Это меры, которые нужно применять прямо там, в этом маленьком кусочке моря. На остальном побережье люди могут продолжать работать в том же режиме. Был явный оппортунизм, и вы можете видеть, насколько это была целенаправленная политика», — говорит Диас из Oceana.
Демонстрация рыбаков в защиту Закона штата № 15223, запрещающего траление на расстоянии до 12 миль от берега. Изображение Marcos Jatahy/Oceana Помимо изменения правил только для побережья Риу-Гранди-ду-Сул, организация считает меры департамента недостаточными для обеспечения устойчивости. Их самым большим недостатком является отсутствие разумного объема вылова, способного гарантировать как прибыльность для отрасли, так и пространство для восстановления биоразнообразия, что является возможным балансом.
«Текущая ситуация в Риу-Гранди-ду-Сул связана с чрезмерной эксплуатацией рыбных запасов. Виды выталкиваются на уровни, которые не обеспечивают максимальную урожайность или устойчивое замещение. Это историческая проблема», — говорит Кардосо из FURG.
План повторяет правило, изданное в 2004 году, которое требует, чтобы траулеры устанавливали устройства, исключающие морские черепахи. Но правило никогда не соблюдалось, поэтому такими устройствами никто не пользуется. Другая мера предполагала использование судов с двумя рыболовными сетями для проверки того, будет ли более крупная ячейка обеспечивать хороший улов без поимки исчезающих видов: суда будут ловить рыбу обычной ячейкой с одной стороны и более крупной с другой, а затем сравнивать результаты после каждую рыбалку. Сами экипажи будут отвечать за соблюдение новых правил.
Без обиняков Океана говорит, что план — не что иное, как зеленая промывка. «Включение слова «устойчивый» на самом деле является преднамеренной попыткой замаскировать воздействия, неопределенности и недостатки в рыболовстве и управлении траловым промыслом», — заявляет организация.
По этим причинам в дело вмешался Федеральный суд. Когда правительство Риу-Гранди-ду-Сул потребовало судебного запрета, суд поддержал аргумент о том, что эта мера угрожает работе и доходам местных рыбаков, а также биоразнообразию.
«В целом, постановления департамента нарушают федеральный закон без указания технических причин для их принятия, главным образом потому, что они игнорируют интересы непосредственно затронутого сообщества, и не проводилось никакого специального исследования по эффективной и конкретной устойчивости биомассы Риу-Гранди-ду-Сул. и морское биоразнообразие», — постановил федеральный судья Кларидес Рахмейер, который в апреле 2022 года отклонил возвращение судов из Санта-Катарины к побережью Риу-Гранди-ду-Сул. В июне ее решение было оставлено в силе апелляционным судом.
Судебные запреты возобновили оптимизм рыбаков. «Мы снова увидели, как молодые люди начали заниматься рыболовством, чего больше не видели и что вызывало беспокойство», — говорит Ана Спинелли из Совета Риу-Гранди-ду-Сул по аквакультуре и устойчивому рыболовству.

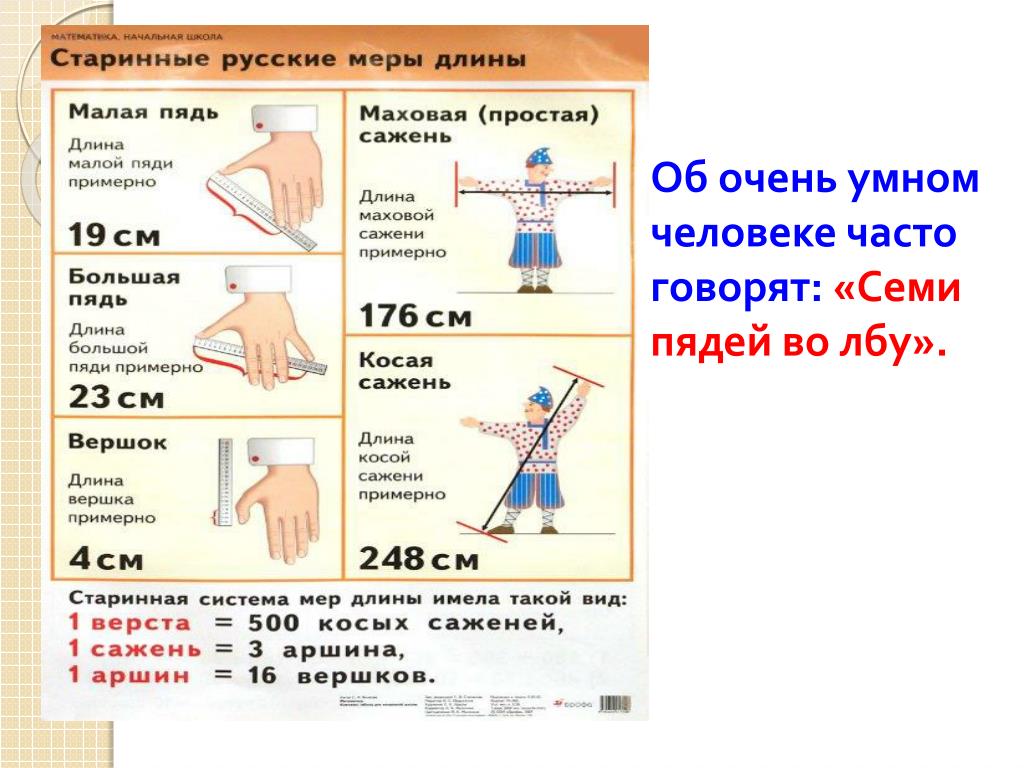
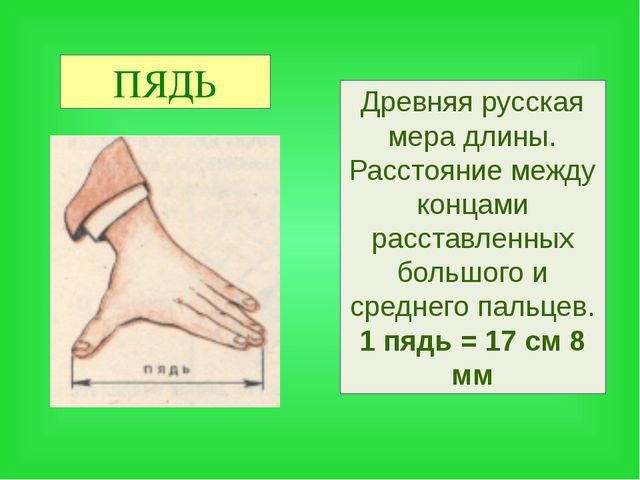


 -первая половина XV в.)
-первая половина XV в.)