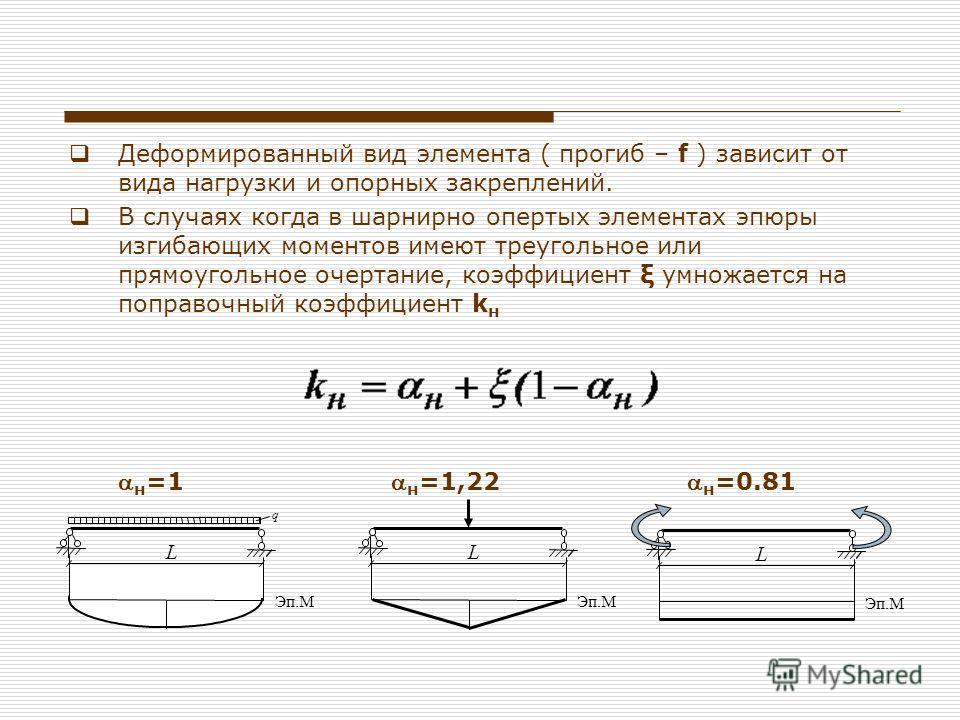
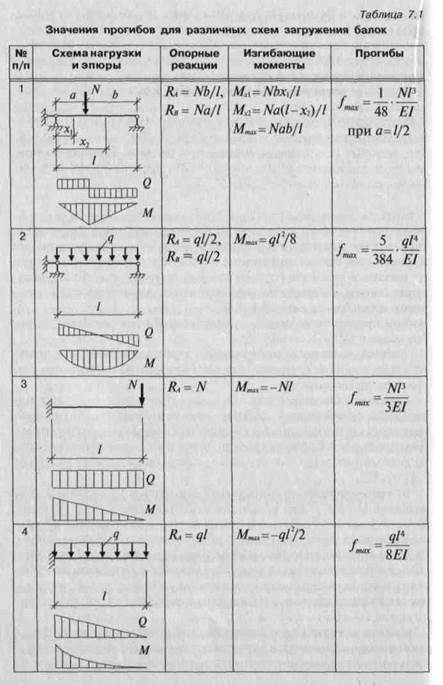
Расчет балок на прогиб. Максимальный прогиб балки: формула расчета
Балка – элемент в инженерии, представляющий собой стержень, который нагружают силы, действующие в направлении, перпендикулярном стержню. Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.
Типы
На сегодняшний день в строительстве могут использоваться балки, изготовленные из разных материалов. Это может быть металл или дерево. Каждый конкретный случай подразумевает под собой разные балки. При этом расчет балок на прогиб может иметь некоторые отличия, которые возникают по принципу разницы в строении и используемых материалов.
Деревянные балки
Сегодняшнее индивидуальное строительство подразумевает под собой широкое применение балок, изготовленных из дерева. Практически каждое строение содержит в себе деревянные перекрытия. Балки из дерева могут использоваться как несущие элементы, их применяют при изготовлении полов, а также в качестве опор для перекрытий между этажами.
Ни для кого не секрет, что деревянная, так же как и стальная балка, имеет свойство прогибаться под воздействием нагрузочных сил. Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.
Допустимый прогиб балки формируется из двух факторов:
- Соответствие прогиба и допустимых значений.
- Возможность эксплуатации здания с учетом прогиба.
Проводимые при строительстве расчеты на прочность и жесткость позволяют максимально эффективно оценить то, какие нагрузки сможет выдерживать здание в ходе эксплуатации. Также эти расчеты позволяют узнать, какой именно будет деформация элементов конструкции в каждом конкретном случае. Пожалуй, никто не будет спорить с тем, что подробные и максимально точные расчеты – это часть обязанностей инженеров-строителей, однако с использованием нескольких формул и навыка математических вычислений можно рассчитать все необходимые величины самостоятельно.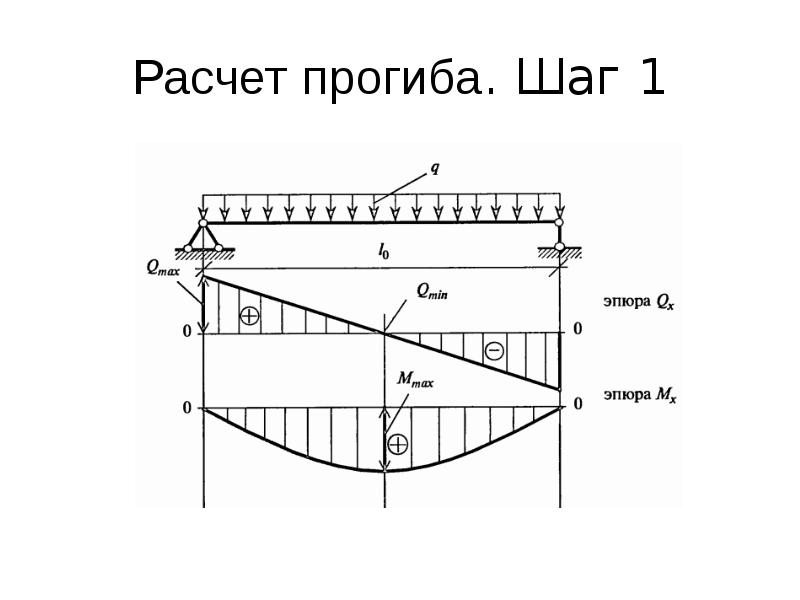
Для того чтобы произвести правильный расчет прогиба балки, нужно также брать во внимание тот факт, что в строительстве понятия жесткости и прочности являются неразрывными. Опираясь на данные расчета прочности, можно приступать к дальнейшим расчетам относительно жесткости. Стоит отметить, что расчет прогиба балки – один из незаменимых элементов расчета жесткости.
Обратите ваше внимание на то, что для проведения таких вычислений самостоятельно лучше всего использовать укрупненные расчеты, прибегая при этом к достаточно простым схемам. При этом также рекомендуется делать небольшой запас в большую сторону. Особенно если расчет касается несущих элементов.
Расчет балок на прогиб. Алгоритм работы
На самом деле алгоритм, по которому делается подобный расчет, достаточно прост. В качестве примера рассмотрим несколько упрощенную схему проведения расчета, при этом опустив некоторые специфические термины и формулы. Для того чтобы произвести расчет балок на прогиб, необходимо выполнить ряд действий в определенном порядке. Алгоритм проведения расчетов следующий:
Алгоритм проведения расчетов следующий:
- Составляется расчетная схема.
- Определяются геометрические характеристики балки.
- Вычисляется максимальную нагрузку на данный элемент.
- В случае возникновения необходимости проверяется прочность бруса по изгибающему моменту.
- Производится вычисление максимального прогиба.
Как видите, все действия достаточно просты и вполне выполнимы.
Составление расчетной схемы балки
Для того чтобы составить расчетную схему, не требуется больших знаний. Для этого достаточно знать размер и форму поперечного сечения элемента, пролет между опорами и способ опирания. Пролетом является расстояние между двумя опорами. К примеру, вы используете балки как опорные брусья перекрытия для несущих стен дома, между которыми 4 м, то величина пролета будет равна 4 м.
Вычисляя прогиб деревянной балки, их считают свободно опертыми элементами конструкции. В случае балки перекрытия для расчета принимается схема с нагрузкой, которая распределена равномерно. Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F. Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.
Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F. Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.
Момент инерции
Геометрическая характеристика, которая получила название момент инерции, важна при проведении расчетов на прогиб балки. Формула позволяет вычислить эту величину, мы приведем ее немного ниже.
При вычислении момента инерции нужно обращать внимание на то, что размер этой характеристики зависит от того, какова ориентация элемента в пространстве. При этом наблюдается обратно пропорциональная зависимость между моментом инерции и величиной прогиба. Чем меньше значение момента инерции, тем больше будет значение прогиба и наоборот. Эту зависимость достаточно легко отследить на практике. Каждый человек знает, что доска, положенная на ребро, прогибается гораздо меньше, чем аналогичная доска, находящаяся в нормальном положении.
Подсчет момента инерции для балки с прямоугольным сечением производится по формуле:
J=b*h^3/12, где:
b – ширина сечения;
h – высота сечения балки.
Вычисления максимального уровня нагрузки
Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей. Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах. Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность. Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м. Также для примера примем расстояние между брусьями перекрытия равным 600 мм. В этом случае нужный нам коэффициент составит 0,6. 3/48*E*J, где:
3/48*E*J, где:
F – сила давления на брус.
Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса. Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.
Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель – установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.
Двутавровая балка
Обратите внимание на то, что балки из двутавра применяются несколько реже в силу их формы. Однако также не стоит забывать, что такой элемент конструкции выдерживает гораздо большие нагрузки, чем уголок или швеллер, альтернативой которых может стать двутавровая балка.
Расчет прогиба двутавровой балки стоит производить в том случае, если вы собираетесь использовать ее в качестве мощного элемента конструкции.
Также обращаем ваше внимание на то, что не для всех типов балок из двутавра можно производить расчет прогиба. В каких же случаях разрешено рассчитать прогиб двутавровой балки? Всего таких случаев 6, которые соответствуют шести типам двутавровых балок. Эти типы следующие:
- Балка однопролетного типа с равномерно распределенной нагрузкой.
- Консоль с жесткой заделкой на одном конце и равномерно распределенной нагрузкой.
- Балка из одного пролета с консолью с одной стороны, к которой прикладывается равномерно распределенная нагрузка.
- Однопролетная балка с шарнирным типом опирания с сосредоточенной силой.
- Однопролетная шарнирно опертая балка с двумя сосредоточенными силами.
- Консоль с жесткой заделкой и сосредоточенной силой.
Металлические балки
Расчет максимального прогиба одинаковый, будь это стальная балка или же элемент из другого материала. Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра. Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа. Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.
Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра. Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа. Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.
Расчет максимального прогиба для балки с двумя опорами
В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.
Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости. В этом случае фактом будет то, что кривая, полученная в результате действия силы, также будет находиться в этой плоскости.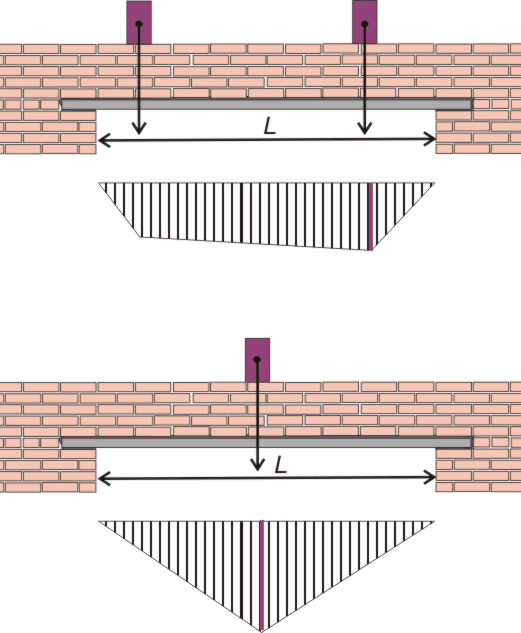 Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.
Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.
Прогиб на расстоянии z от левой опоры балки при 0 ≤ z ≤ a
F(z)=(P*a2*b2)/(6E*J*l)*(2*z/a+z/b-z3/a2*b)
Прогиб балки на двух опорах на расстоянии z от левой опоры при а ≤ z ≤l
f(z)=(-P*a2*b2)/(6E*J*l)*(2*(l-z)/b+(l-z)/a-(l-z)3/a+b2), где Р – прикладываемая сила, Е – модуль упругости материала, J – осевой момент инерции.
В случае балки с двумя опорами момент инерции вычисляется следующим образом:
J=b1h13/12, где b1 и h1 – значения ширины и высоты сечения используемой балки соответственно.
Заключение
В заключение можно сделать вывод о том, что самстоятельно вычислить величину максимального прогиба балки разных типов достаточно просто. Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.
Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.
Прогиб балки | Полный обзор и важные взаимосвязи — Lambda Geeks
Содержание: Отклонение луча- Определение кривой прогиба
- Определение угла отклонения
- Определение отклонения
- Граничные условия прогиба балки
- Взаимосвязь между силами нагрузки, поперечной силой, изгибающим моментом, наклоном и прогибом
- Уравнения и соотношения изгиба балки
- Таблица прогиба балки и формулы для стандартных случаев нагружения
- Отклонение и наклон балки с примерами Случай I: выступающая балка
- Случай II: определение максимального прогиба балки без опоры с точечной нагрузкой в центре.
- Случай III: определение максимального прогиба балки с простой опорой при сосредоточенной точечной нагрузке на расстоянии «а» от опоры А.

- Метод двойной интеграции
- Процедура метода двойного интегрирования
- Метод двойного интегрирования для нахождения прогиба балки на примере консольная балка с равномерно распределенной нагрузкой
- Метод двойного интегрирования для треугольной нагрузки
In инженерия, отклонение — степень смещения элемента конструкции под действием нагрузки (из-за его деформации). Это может относиться к углу или расстоянию. Расстояние прогиба элемента под нагрузкой можно рассчитать путем интегрирования функции, которая математически описывает наклон отклоненной формы элемента под этой нагрузкой. Существуют стандартные формулы для прогиба общих конфигураций балок и загружений в отдельных местах. В противном случае используются такие методы, как виртуальная работа, прямая интеграция, метод Кастильяно, метод Маколея или метод прямой жесткости.
Кривая отклоненияКогда балки нагружены поперечными или продольными нагрузками, начальная прямая продольная ось деформируется в кривую, известную как упругая кривая балки или кривая прогиба. Кривая прогиба — это деформированная ось выбранной балки.
Кривая прогиба — это деформированная ось выбранной балки.
Наклон можно определить как угол между продольной осью балки и касательной, построенной к кривой деформации балки в любом желаемом месте. Это угол поворота нейтральной оси луча. Измеряется в радианах.
прогибОтклонение — это поступление или смещение любой точки на оси балки, измеренное в направлении y от начальной прямой продольной оси до точки на кривой прогиба балки. Измеряется в миллиметрах. Прогиб представляет собой отклонение прямой продольной оси из-за поперечной нагрузки. Напротив, изгиб балки представляет собой отклонение начальной прямой продольной оси из-за осевой сжимающей нагрузки. Обычно он представлен как ‘у»
Если балка изгибается по дуге окружности, это называется изгибом по окружности; в противном случае это называется некруглым изгибом. Предположим, что на призматическую балку действует переменный изгибающий момент. В этом случае это приводит к изгибу некруглого типа, а если он подвергается постоянному изгибающему моменту, приводит к круговому изгибу балки.
В этом случае это приводит к изгибу некруглого типа, а если он подвергается постоянному изгибающему моменту, приводит к круговому изгибу балки.
- y равен нулю на опоре штифта или ролика.
- y равен нулю на встроенной или консольной опоре.
- Предположим, что изгибающий момент и жесткость на изгиб являются разрывными функциями x. В этом случае невозможно написать одно дифференциальное уравнение для всей балки; уравнения кривой для двух соседних сегментов должны удовлетворять данным двум условиям на стыке сегментов:
- 1. y для левой части должен быть равен y для правой части.
- 2. Уклон левого участка должен быть равен уклону правого участка.
Рассмотрим горизонтальную балку AB в ненагруженном состоянии. Если AB отклоняется под нагрузкой, новое положение будет A’B ‘. 4}
4}
- Максимальный наклон и прогиб консольной балки происходит на свободном конце балки, в то время как на зажатом конце консольной балки не наблюдается наклона или прогиба.
- Для балки без опоры с симметричными условиями нагружения максимальный прогиб может быть найден в середине пролета. Максимальный уклон наблюдается у опор балки. Максимальный прогиб возникает при нулевом уклоне.
Рассмотрим выступающую стальную балку, несущую сосредоточенную нагрузку P = 50 кН на конце C.
Для выступающей балки: (a) определить наклон и максимальное отклонение, (b) оценить наклон на расстоянии 7 м от точки A и максимальное отклонение по заданным данным. {- 3} \; m = -8.93 \; мм
{- 3} \; m = -8.93 \; мм
Если жесткость на изгиб EI постоянна, а момент является функцией расстояния x, интегрирование EI (d2 y) / (dx2 ) = M даст наклон
EI \ frac {dy} {dx} = \ int M dx + C_1EIy = \ int \ int Mdxdx + C_1x + C_2
где С1 и C2 являются константами. Они определяются с помощью граничных условий или других условий на балке. Вышеприведенное уравнение дает отклонение y как функцию от x; это называется уравнением кривой упругости или деформации.
Вышеупомянутый метод анализа прогиба и наклона балки известен как метод двойного интегрирования для расчета прогибов балки. Если изгибающий момент и жесткость на изгиб являются непрерывными функциями x, одно дифференциальное уравнение может быть записано для всей балки. Для статически определенной балки существует две опорные реакции; каждая из них накладывает определенный набор ограничений на наклон упругой кривой. Эти ограничения называются граничными условиями и используются для определения двух постоянных интегрирования.
Эти ограничения называются граничными условиями и используются для определения двух постоянных интегрирования.
- y равен нулю на опоре штифта или ролика.
- y равен нулю на встроенной или консольной опоре.
- Предположим, что изгибающий момент и жесткость на изгиб являются разрывными функциями x. В этом случае невозможно написать одно дифференциальное уравнение для всей балки; уравнения кривой для двух соседних сегментов должны удовлетворять данным двум условиям на стыке сегментов:
- 1. y для левой части должен быть равен y для правой части.
- 2. Уклон левого участка должен быть равен уклону правого участка.
- Нарисуйте упругую кривую балки и примите во внимание все необходимые граничные условия, такие как y равен нулю на опоре пальца или ролика и y равен нулю на встроенной или консольной опоре.

- Определите изгибающий момент M на произвольном расстоянии x от опоры методом сечений. Используйте соответствующие правила изгибающего момента при нахождении момента М. для разрывного момента, уравнения кривой для двух соседних сегментов должны удовлетворять данным двум условиям на стыке между сегментами: 1. y для левой части должно быть равно y для правой секции. 2. Уклон левого участка должен быть равен уклону правого участка.
- Проинтегрируйте уравнение дважды, чтобы получить наклон и прогиб, и не забудьте найти постоянное интегрирование для каждого сечения с использованием граничных условий.
Рассмотрим консольную балку длиной L, показанную на рисунке ниже, с равномерно распределенной нагрузкой. В консольной балке один конец зафиксирован, а другой конец может свободно двигаться. Мы выведем уравнение для наклона и изгибающего момента для этой балки, используя метод двойного интегрирования. 4}{120}
4}{120}
у = -0.01758 \; м
Чтобы узнать о прочности материала (нажмите сюда)и метод площади момента Открыть.
Расчет уголка на прогиб
Главная » Разное » Расчет уголка на прогиб
Расчет уголка на прогиб и изгиб
Данный онлайн-калькулятор предназначен для того, чтобы Вы могли легко и быстро подобрать размеры уголка в зависимости от приходящейся на него нагрузки. Особенность его в том, что на одной странице возможно сравнение равнополочных (ГОСТ 8509-93) и неравнополочных (ГОСТ 8510-86) уголков. Последние, в свою очередь, можно подбирать в зависимости от расположения его в пространстве, т.е. в зависимости от того, как он будет ориентирован относительно нагрузки.
Содержание:
1. Калькулятор
2. Инструкция к калькулятору
Расчет уголков производится на изгиб и прогиб (по прочности и по деформациям) для следующих расчетных схем:
- Тип 1 — однопролетная шарнирно-опертая балка с равномерно распределенной нагрузкой.
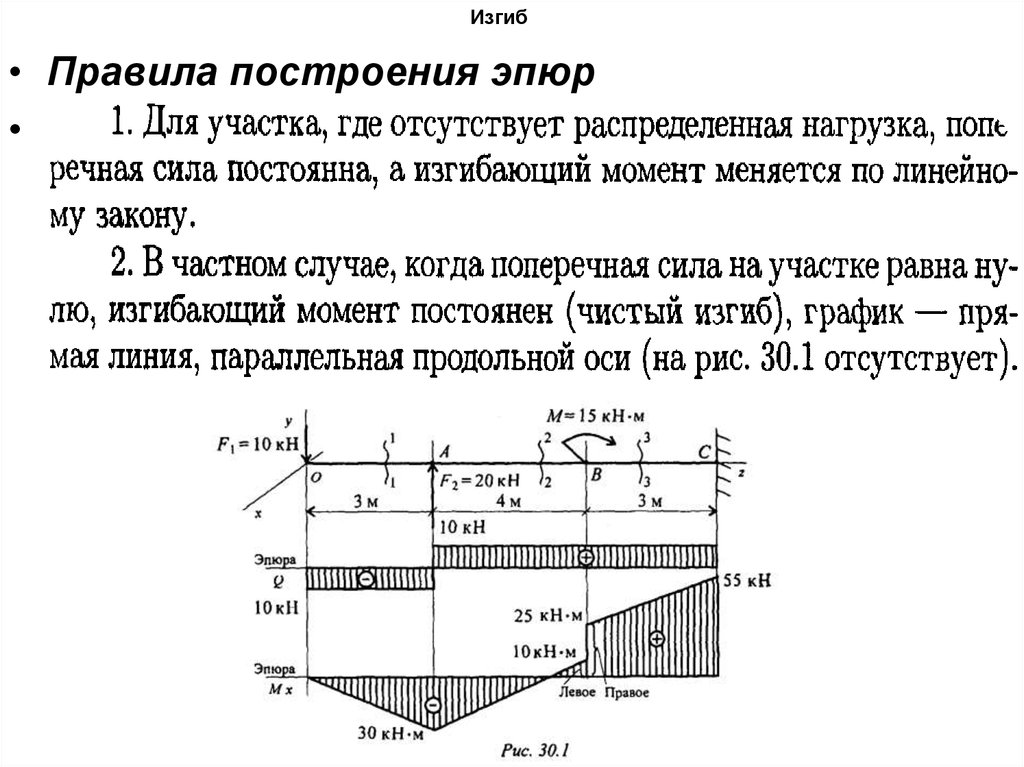 Пример: перемычка из уголка, которая несет плиты перекрытия и небольшую высоту кладки. (Подробнее о расчете перемычек из уголка см. этот калькулятор).
Пример: перемычка из уголка, которая несет плиты перекрытия и небольшую высоту кладки. (Подробнее о расчете перемычек из уголка см. этот калькулятор).
- Тип 2 — консольная балка с жесткой заделкой с равномерно распределенной нагрузкой. Пример: железобетонный козырек, выполненный с применением уголка, который жестко (с применением ребер жесткости, ограничивающих любые повороты) приварен к железобетонной стене.
- Тип 3 — однопролетная шарнирно-опертая балка с консолью с равномерно распределенной нагрузкой. Пример: тот же козырек, что и в предыдущей схеме, только здесь уголок с одной стороны заводится в стену, а с другой опирается на раскос (на рисунке синий).
- Тип 4 — однопролетная шарнирно-опертая балка с одной сосредоточенной силой. Пример: перемычка, на которую опирается одна балка перекрытия.
- Тип 5 — однопролетная шарнирно-опертая балка с двумя сосредоточенными силами.
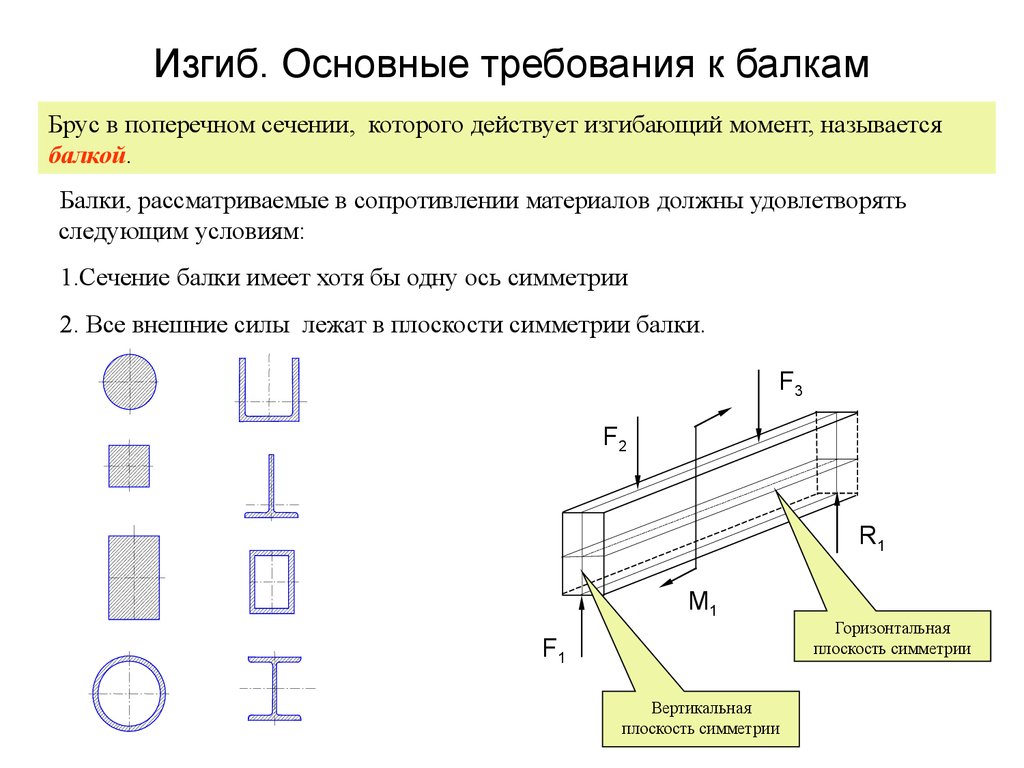 Пример: перемычка, на которую опираются две сосредоточенные силы.
Пример: перемычка, на которую опираются две сосредоточенные силы.
- Тип 6 — консольная балка с одной сосредоточенной силой. Пример: козырек дома с кирпичной стенкой на нем, построенного в африканской республике (где никогда не выпадает снег) по фантазии африканского архитектора. Уголки этого козырька жестко заделаны в стену, так как описано во второй схеме.
Примечание: рассчитываемый уголок на рисунках с примерами окрашен в красный цвет.
КалькуляторРасчет прогиба балки онлайн калькулятор. Площадь поперечного сечения профиля. Расчет на прочность.
Описание
При выборе схемы с распределенной нагрузкой, приложенная «Нагрузка Q» указывается как относительная «килограмм на метр». Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].
Использование калькулятора «Расчет прогиба балки онлайн» значительно сократит время и послужит залогом надежных инженерных конструкций.
Калькулятор разработан исключительно по формулам Сопромата и справочным данным для каждого типа материала и сечения балки. Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий.
Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.
Для быстрого доступа к расчетам необходимого профиля добавьте калькулятор в избранное (CTRL+D на ПК или значек «звездочка» справа вверху браузера)
Пример расчета уголка, швеллера и двутавра на прогиб и изгиб
На данной странице представлен пример расчета швеллера. Что касается расчетов уголка и двутавра, то они производится аналогичным образом. Другими словами, данный пример является полезным для следующих калькуляторов:
В примере будут описаны несколько действий, которые должны выполняться последовательно.
Дано.
Район строительства — Нижний Новгород.
Расчетная схема — Тип 1.
Необходимо подобрать швеллер, который будет воспринимать нагрузку от снега.
Действие 1. Внесение исходных данных.
Расчетная нагрузка = 240 кг/м2 — так как город Н.Новгород находится в IV снеговом районе (в соответствии с табл. 10.1 и картой 1 СП 20.13330.2011 «Нагрузки и воздействия» [1]).
Fmax = 1/200 — так как пролет балки равен 5 м (пункт 2 табл. E1 [1]).
Расположение — по оси Х (швеллер воспринимает нагрузку вертикально).
Расчетное сопротивление Ry=210 МПа — берется как наихудший вариант для стали.
Действие 2. Выбор предполагающих номеров профилей.
Предположим, что мы рассматриваем два вида профилей: с параллельными гранями и с уклоном полок. Поэтому для первоначального расчета выбираются швеллеры размером 8П И 8У.
После произведенного расчета видно, что в графе «Запас» в том и другом случае стоят отрицательные значения.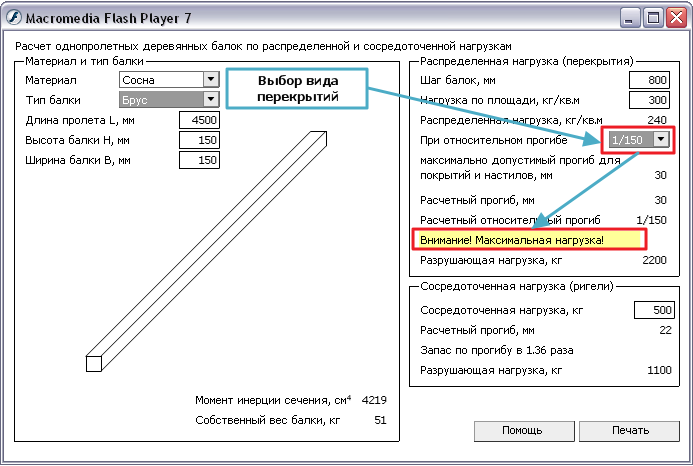 Это означает, что выбранные швеллеры не способны воспринимать приложенную на них нагрузку. Следовательно, необходимо выбирать профили большего размера.
Это означает, что выбранные швеллеры не способны воспринимать приложенную на них нагрузку. Следовательно, необходимо выбирать профили большего размера.
Действие 3. Корректирующий расчет.
При увеличении профилей до 10П и 10У ситуация аналогичная. Но после того, как профили были увеличены до 12П и 12У в графах «Запас» появились положительные значения. Следовательно, в качестве балки перекрытия можно принять тот или иной профиль (имеется в виду 12П или 12У).
| Вид проката Уголок равнополочныйУголок неравнополочныйШвеллер с уклоном полокШвеллер с паралельными гранями полокДвутавр с уклоном полокДвутавр с паралел. гранями полок нормальныйДвутавр с паралел. гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный | Вид и назначение стоек (колонн) Стойки и раскосы передаюшие реакции опорОсновные колонныВторостепенные колонны |
| Сталь С235 (Ст3кп2)Сталь С245 (Ст3пс5,Ст3сп5)Сталь С255 (СтГпс,Ст3Гсп)Сталь С285 (Ст3сп,Ст3Гпс,Ст3Гсп)Сталь С345 (12Г2С,09Г2С)Сталь С345К (10ХНДП)Сталь С375 (12Г2С)Сталь С390 (14Г2АФ)Сталь С390Д (14Г2АФД)Сталь С440 (16ГАФ)Сталь С590 (12Г2СМФ) |
| РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ: |
Размеры проката углового профиля оговариваются ГОСТ 8509-93 и ГОСТ 8510-86; швеллеров ГОСТ 8240-97; двутавров ГОСТ 26020-83; тавров – ТУ 14-2-685-86; (получаемых продольной разрезкой пополам горячекатаных двутавров с параллельными гранями полок по ГОСТ 26020-83).
При проектировании строительных конструкций необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации.
Поэтому стойку,находящуюся под действием сжимающей её нагрузки необходимо проверять:
- на прочность;
- устойчивость;
- допустимую гибкость.
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) расчет на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P/Fp*Ry*Yc <= 1, где
- P – действующая нагрузка,
- Fp – плошадь поперечного сечения стойки,
- Ry – расчётное сопротивление материала (стали стойки), выбирается по таблице В5 Приложения “В” того же СНиПа;
- Yc – коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.

Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi*Fp*Ry*Yc <= 1, где
Fi – коэффициент продольного изгиба центрально-сжатых элементов.
Коэффициент Fi введён в расчёт в качестве компенсации возможности некоторой не прямолинейности стойки, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки. Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г. исходя из гибкости стойки и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет расчёт, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) – некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечного сечения, в частности радиуса инерции:
Lambda = Lr / i; здесь
- Lr – расчётная длина стержня;
- i – радиус инерции поперечного сечения стержня (стойки,колонны).

Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где
- I – момент инерции сечения,
- Fp – его площадь.
Lr (расчётная длина) определяется как MuL;
здесь L- длина стойки,а Mu – коэфф., зависящий от схемы её крепления:
- “заделка-консоль”(свободный конец) – Mu = 2;
- “заделка-заделка”-Mu = 0.5;
- “заделка-шарнир” -Mu = 0.7;
- “шарнир-шарнир”-Mu=1.
Следует иметь ввиду,что при наличии у формы поперечного сечения 2-ух радиусов инерции (например, у швеллера, двутавра, тавра – относительно осей x-x и y-y), при расчёте Lambda используется меньший.
Уголки (как равнополочные так, и неравнополочные) имеют минимальный радиус инерции относительно оси z-z, который и используется в расчётах. Кроме того,сама Lambda (гибкость стойки), рассчитанная по формуле Lambda=Lr/i не должна превышать 220-ти в соответствии с табл. 19.СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально-сжатых стержней.
Для их использования необходимо сделать выбор в таблице калькулятора “Вид, назначение стоек…”. Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэфф. продольного изгиба (Fi), действующей нагрузки(P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
ПРИМЕЧАНИЕ. Размеры выбранного швеллера, двутавра и тавра указываются в строке “РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ”; размеры полок уголков-в их таблицах; толщина уголков выбирается отдельно после появления возможных толщин выбранного номера уголка в вышеуказанной строке.
Расчет металлической балки на прогиб: учимся составлять формулы
Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.
Что такое прогиб балки?
Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).
Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.
ν-прогиб сечения C; θ-угол поворота сечения C.
Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.
Метод начальных параметров
Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)
Под начальными параметрами понимаются уже известные перемещения:
- в опорах прогибы равны нулю;
- в жесткой заделке прогиб и угол поворота сечения равен нулю.
Учитывая эти хитрости, их называют еще граничными условиями, определяются перемещения в других частях балки.
Расчет прогибов балки
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:
Реакции опор
Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.
Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:
Система координат
Далее вводим систему координат, с началом в левой части балки (точка А):
Распределенная нагрузка
Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Если бы нагрузка была приложена вот таким способом:
То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:
Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.
Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:
Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
\[ { V }_{ A }=0\quad при\quad x=0 \]
\[ { V }_{ B }=0\quad при\quad x=8м \]
Записываем уравнение метода начальных параметров для сечения C:
\[ E{ I }_{ z }{ V }_{ C }=… \]
Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:
\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]
Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:
\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+… \]
Учет внешней нагрузки
И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. { 4 } } =-2см \]
{ 4 } } =-2см \]
Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.
На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).
Расчёт балки, рамы бесплатно онлайн
Лимит расчётов:
|
Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки или рамы и
позволит построить эпюры внутренних силовых факторов (изгибающих моментов, поперечных и
осевых или продольных сил), рассчитать реакции в опорах. В итоге формируется отчёт с
готовым решением. |
|
| КАЛЬКУЛЯТОРЫ КОМПРЕССИОННЫХ ЧЛЕНОВ | |
| Калькулятор | Определение |
| Расчет элементов сжатия (продольного изгиба) | |
| ПРОСТО ОПОРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГИБА | |
| Балка с простой опорой и множественными точечными / распределенными нагрузками и моментами | |
| Балка с простой опорой и сосредоточенной нагрузкой в любой точке | |
| Просто поддерживаемая балка с двумя Точечные нагрузки | |
| Балка с простой опорой и частично распределенной промежуточной нагрузкой | |
| Балка с простой опорой и двумя частично распределенными промежуточными нагрузками | |
| Балка с простой опорой и моментом | |
| Балка с простой опорой и двумя моментами | |
| КАНТИЛЬНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГИБА | |
| Консольная балка с множественными точечными / распределенными нагрузками и моментами | |
| Консольная балка с одинарной нагрузкой | |
| Распределенная нагрузка консольной балки | |
.
% PDF-1.6 % 104 0 объект > endobj xref 104 52 0000000016 00000 н. 0000002216 00000 н. 0000002377 00000 н. 0000002421 00000 н. 0000002547 00000 н. 0000002902 00000 н. 0000003045 00000 н. 0000003182 00000 п. 0000003324 00000 н. 0000003351 00000 п. 0000003418 00000 н. 0000003955 00000 н. 0000004444 00000 н. 0000004471 00000 н. 0000005149 00000 п. 0000005176 00000 п. 0000005771 00000 п. 0000006307 00000 н. 0000006764 00000 н. 0000007200 00000 н. 0000007333 00000 н. 0000007360 00000 п. 0000007733 00000 н. 0000008258 00000 н. 0000008758 00000 н. 0000009241 00000 п. 0000009643 00000 п. 0000009713 00000 н. 0000009908 00000 н. 0000046337 00000 п. 0000046548 00000 п. 0000046941 00000 п. 0000047011 00000 п. 0000047272 00000 п. 0000106092 00000 н. 0000106298 00000 п. 0000106421 00000 н. 0000117145 00000 н. 0000117340 00000 н. 0000117547 00000 н. 0000117617 00000 н. 0000117799 00000 н. 0000156281 00000 н. 0000156483 00000 н. 0000156859 00000 н. 0000156929 00000 н. 0000157517 00000 н. 0000157588 00000 н. 0000157704 00000 н. 0000157824 00000 н. 0000157913 00000 н. 0000001336 00000 н. трейлер ] / Назад 1604346 >> startxref 0 %% EOF 155 0 объект > поток hb«`b«ce`c«`f @
0000157588 00000 н. 0000157704 00000 н. 0000157824 00000 н. 0000157913 00000 н. 0000001336 00000 н. трейлер ] / Назад 1604346 >> startxref 0 %% EOF 155 0 объект > поток hb«`b«ce`c«`f @
.
Калькулятор для инженеров — момент инерции площади, центр тяжести, модуль упругости углового сечения
Дополнительные ссылки
Викторина по гражданскому строительству
Проверьте свои знания по различным темам гражданского строительства
Статически неопределенные структуры
Определение и методы решения
Решенных примеров
Расчет сил стержня фермы
методом соединений и методом секций
Сила сдвига и изгибающий момент
Иллюстрированные решенные примеры для построения диаграмм силы сдвига и изгибающего момента
Наклон и прогиб балки и фермы
Иллюстрированные решенные примеры для определения наклона и прогиба балки и фермы
Решение неопределенных конструкций
Отклонение откоса, распределение момента и т. Д.
Д.
Балка железобетонная
Решенные примеры для определения прочности и других параметров
Другие полезные ссылки
Небоскребы мира
Высокие здания мира
Профиль инженеров-строителей
Познакомьтесь с выдающимися инженерами-строителями
Профессиональные общества
Международные профессиональные общества инженеров-строителей
Расскажите о нас друзьям
Поищите на нашем сайте больше…
.
Что такое прогиб? | Программное обеспечение SkyCiv Cloud для структурного анализа
перейти к содержанию
Искать:
- Программное обеспечение
- SkyCiv Structural 3D: Программное обеспечение для структурного анализа
- SkyCiv Beam
- SkyCiv Section Builder
- SkyCiv Connection Design
- SkyCiv RC Design
- SkyCiv Foundation Design
- SkyCiv8 Модуль нагрузки на ветер SkyCiv8 Интеграции и надстройки
.
Угол возвышения Солнца (на год) Калькулятор
- Цель использования
- различные солнечные приложения, конечно, но в основном просто для того, чтобы быть проинформированным о моем физическом окружении.
- Комментарий / запрос
- Я мог бы быть более поучительным, если бы время наблюдения имело вариант местного кажущегося полудня, когда солнце находится на самом высоком уровне. Поскольку вы запрашиваете долготу наблюдателя, это должно быть просто.
[1] 2020/12/20 04:17 Мужчина / 60 лет и старше / Пенсионер / Полезно /
- Цель использования
- Расчет максимальной высоты дерева относительно расположения солнечных панелей.
- Комментарий / запрос
- Вычисление корректировки времени от GMT с использованием долготы было бы полезным и простым.
[2] 2020/12/07 03:31 Мужчина / 60 лет и старше / Инженер / Очень /
- Цель использования
- Размещение солнечных панелей
- Комментарий / запрос
- Arigatou gozaimasu!
[3] 2020/12/07 03:25 Мужской / 40-летний уровень / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Я хочу построить пассивную теплицу на севере ( Северный Квебек), и я хотел знать, под каким углом поставить стену, чтобы максимально эффективно использовать солнце в зимние месяцы
[4] 2020/12/01 22:20 Мужчина / Уровень 50 лет / Офисный работник / Государственный служащий / Полезный /
- Цель использования
- Определение того, в какое время года, в какое время суток и в каком направлении можно видеть радугу в моем местоположении (солнце должно быть ниже 42 градусов над горизонтом).
- Комментарий / запрос
- Я знаю, как узнать мою широту и долготу, поэтому мог бы использовать этот сайт, но если бы была возможность печатать в ближайшем городе, даже если это было бы менее точно, гораздо больше людей уметь его использовать.
[5] 2020/11/16 15:41 Женщина / 60 лет или старше / Пенсионер / Полезно /
- Цель использования
- Анализ выходной мощности солнечной батареи в зависимости от высоты Солнца
- Комментарий / Запрос
- Отличный калькулятор
[6] 2020/11/05 00:16 Мужчина / 60 лет и старше / Учитель / Исследователь / Очень /
- Цель использования
- Проверка тени на крыше для установка PV
- Отчет об ошибке
- По сравнению с диаграммой, углы которой указаны в таблице, азимут и углы возвышения не имеют никакого смысла.Как может полуденное солнце находиться только по азимуту (азимуту) между 39 и 67 градусами? Я мог бы понять эти углы, если бы они были даны от восточной оси.
 Тогда азимут будет в районе 129–157 градусов, то есть примерно в юго-восточном направлении. Кроме того, как солнце может быть выше в зимнее время, чем в летние месяцы? Возможно, если бы эти углы были измерены от вертикальной оси (Зинет), они имели бы больше смысла. Извините, но, на мой взгляд, приведенная здесь информация неверна.
Тогда азимут будет в районе 129–157 градусов, то есть примерно в юго-восточном направлении. Кроме того, как солнце может быть выше в зимнее время, чем в летние месяцы? Возможно, если бы эти углы были измерены от вертикальной оси (Зинет), они имели бы больше смысла. Извините, но, на мой взгляд, приведенная здесь информация неверна.
[7] 2020/11/04 20:42 Мужчина / 60 лет и старше / Инженер / Совсем нет /
- Цель использования
- Я фотограф, выясняю положение солнца в определенные дни в месяц, чтобы я мог делать красивые фотографии в «контролируемой» обстановке.
- Комментарий / запрос
- Спасибо. Продолжайте в том же духе!
[8] 2020/11/04 18:11 Женский / 50-летний уровень / Самозанятые / Полезные /
- Цель использования
- ИСПОЛЬЗОВАНИЕ СОЛНЕЧНОЙ ЭНЕРГИИ
- Комментарий / запрос
- ДУМАЯ О СОЛНЦЕ ПАНЕЛИ
[9] 2020/10/20 04:13 Мужчина / 60 лет и старше / Пенсионер / Очень /
- Цель использования
- Самообразование
[10] 2020/10/19 18:32 Мужчина / 60 лет и старше / Пенсионер / Очень /
.
Таблицы отклонения балки | МеханиКальк
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
В таблицах ниже приведены уравнения для прогиба, наклона, сдвига и момента вдоль прямых балок для различных условий на концах и нагрузок. Вы можете найти исчерпывающие таблицы в таких справочниках, как Gere, Lindeburg и Shigley. Однако приведенные ниже таблицы охватывают большинство распространенных случаев.
Для получения информации об отклонении балки см. наш справочник по напряжениям и отклонениям в балках.
Консольные балки
| Консоль, торцевая нагрузка |
| |||||||||||||||||||
| Консоль, промежуточная нагрузка |
| |||||||||||||||||||
| Консоль, равномерно распределенная нагрузка |
| |||||||||||||||||||
| Консоль, треугольная распределенная нагрузка |
| |||||||||||||||||||
| Консоль, Конечный момент |
|
Просто поддерживаемые балки
| Просто поддерживаемые, промежуточная нагрузка |
Для a ≥ b:
| |||||||||||||||||||||
| Простая опора, центральная нагрузка |
| |||||||||||||||||||||
| Просто поддерживаемый, 2 нагрузки на равном расстоянии от опор |
| |||||||||||||||||||||
| Простая опора, равномерная распределенная нагрузка |
| |||||||||||||||||||||
| Простая опора, момент на каждой опоре |
| |||||||||||||||||||||
| Простая опора, момент в одну опору |
| |||||||||||||||||||||
| Простая опора, центральный момент |
|
Фиксированные-Фиксированные балки
| Фиксированные-Фиксированные, центральная нагрузка |
| |||||||||||||||
| Фиксированная-фиксированная, равномерная распределенная нагрузка |
|
Ознакомьтесь с нашим калькулятором луча, основанным на методологии, описанной здесь.
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
- Будинас-Нисбетт, «Машиностроение Шигли», 8-е изд.
- Гир, Джеймс М., «Механика материалов», 6-е изд.
- Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена PE», 13-е изд.
Формула прогиба балок с диаграммами для всех условий .
Вики
, когда есть вертикальное смещение в любой точке нагруженной балки, говорят, что это отклонение балок . Максимальный прогиб балок происходит там, где уклон равен нулю.
Наклон луча определяется как угол между отклоненным лучом и фактическим лучом в той же точке.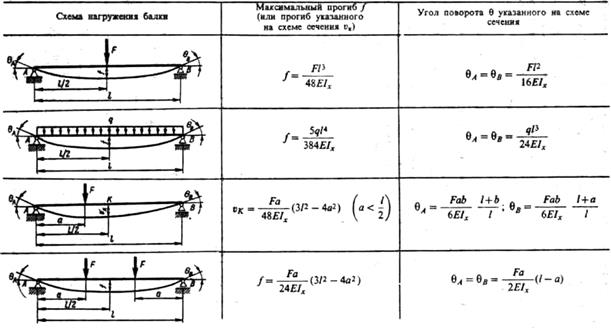
Общие и стандартные уравнения для отклонения лучей приведены ниже:
, где,
M = изгибающий момент,
E = Модуль Янг,
I = 9097 Момент intia of intia of intia of intia of intia of intia of intia of intia of intiam .
Продукт E.I известен как жесткость на изгиб .
Существует много типов балок, и для этих различных типов балок или случаев формула не будет одинаковой. Он должен быть изменен в зависимости от случая или типа луча. Теперь давайте рассмотрим следующие случаи.
1. Свободно опертая балка с центральной точечной нагрузкой:Свободно опертая балка AB длиной l несет точечную нагрузку в центре балки в точке C. Прогиб при точка C будет:
2. Свободно опертая балка с внецентренной точечной нагрузкой: Свободно опертая балка AB длиной l несет нагрузку в центральной точке0994 C , как показано на рис. Отклонение балки определяется следующим образом:
Отклонение балки определяется следующим образом:
Поскольку b > a , поэтому максимальное отклонение происходит в CB , а расстояние от B определяется как:
и определяется как максимальное отклонение :
Свободно опертая балка AB с равномерно распределенной нагрузкой w /единица длины показана на рисунке ,
Максимальное отклонение происходит в средней точке C и определяется как:
4 Постепенно меняющаяся нагрузка:Свободно опертая балка из AB длиной l , несущая постепенно изменяющуюся нагрузку от нуля на B до w/единицы длины на A , показана на рисунке ниже,
The maximum deflection of beam occurs when x = 0. 519 l and its value is given by :
519 l and its value is given by :
A cantilever балка АВ длиной l , несущая на свободном конце точечную нагрузку, показана на рис. Прогиб в любом сечении х на расстоянии х от свободного конца определяется как:
максимальное отклонение происходит на свободном конце (когда x = 0 ), и его значение определяется
6. Кантилеверный луч с равномерно распределенной нагрузкой:AT балка AB длиной l , несущая равномерно распределенную нагрузку на единицу длины, показана на рис. Прогиб в любом сечении х на расстоянии х от В определяется выражением
Максимальное отклонение происходит на свободном конце (когда x = 0), а его значение определяется
, когда консоль частично загружается, как показано на рис.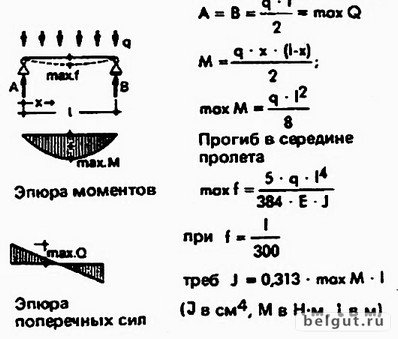 расстояние от фиксированного конца) определяется как:
расстояние от фиксированного конца) определяется как:
и максимальное отклонение происходит на B , чье значение определяется
7. Консольный балок с постепенно изменяющейся нагрузкой:. Кантилеверная луча AB длины L , несущая постепенно, нагрузку на 49444444 гг. на единицу длины при A показан на рис. Прогиб в любом сечении х на расстоянии х от В определяется как
Максимальный прогиб происходит на свободном конце (при х = 0) и его значение определяется как
8. Неподвижная балка, несущая центральную точечную нагрузку:
Неподвижная балка AB длиной l , несущая точечную нагрузку в центре балки C , как показано на рис. Максимальное отклонение балки происходит при C , а его значение определяется формулой
9. Неподвижная балка, несущая эксцентричную нагрузку: Фиксированная балка AB с центральной точкой 909 длиной загрузить в C , как показано на рис.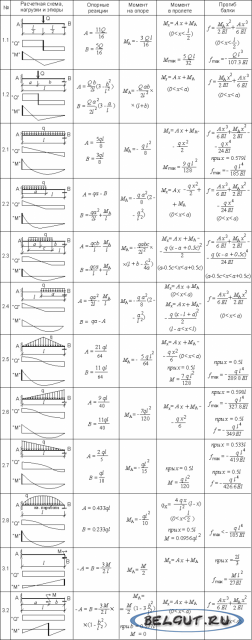 Прогиб в любом сечении X на расстоянии x от A равен
Прогиб в любом сечении X на расстоянии x от A равен
Максимальное расстояние возникает, когда
и прогиб под нагрузкой при C ,
10. Неподвижная балка, несущая равномерно распределенную нагрузку:A94 AB длиной l , несущий равномерно распределенный груз на единицу длины, как показано на рис. Отражение в любом разделе x при A Расстояние x от A дается
. Максимальное отклонение луча происходит в центре луча, и его значение дается
….
Читайте также : Кривая напряжения и деформации для мягкой стали
Читайте также : Анализ скорости строительных работ
Нравится:
Нравится Загрузка…
1.7: Прогиб балок – геометрические методы
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 17613
- Феликс Удойо
- Университет Темпл
Глава 7
Прогиб балок: геометрические методы
7. 1 Введение
1 Введение
Требования к эксплуатационной пригодности ограничивают максимальный прогиб, допустимый для элемента конструкции, подвергающегося внешней нагрузке. Чрезмерный прогиб может привести к дискомфорту при использовании данной конструкции, а также может испортить ее эстетику. Большинство норм и стандартов предусматривают максимально допустимый прогиб для постоянных и временных нагрузок. Чтобы гарантировать, что возможный максимальный прогиб, который может произойти при заданной нагрузке, находится в пределах допустимого значения, конструктивный элемент обычно анализируется на прогиб, а определенное максимальное значение прогиба сравнивается с указанными значениями в нормах и стандартах практики.
Существует несколько методов определения прогиба балки или рамы. Выбор того или иного метода зависит от характера нагрузки и типа решаемой задачи. Некоторые из методов, используемых в этой главе, включают метод двойного интегрирования, метод сингулярной функции, метод момент-площадь, метод удельной нагрузки, метод виртуальной работы и энергетические методы.
7.2 Вывод уравнения кривой упругости балки
Кривая упругости балки является осью отклоненной балки, как показано на рис. 7.1а.
Рис. 7.1. Упругий изгиб балки.
Чтобы вывести уравнение кривой упругости балки, сначала выведите уравнение изгиба.
Рассмотрим часть cdef балки, показанной на рис. 7.1а, на которую действует чистый момент M для вывода уравнения изгиба. Из-за приложенного момента M волокна над нейтральной осью балки будут удлиняться, а волокна ниже нейтральной оси укорачиваются. Пусть O — центр, R — радиус кривизны балки, а ij — ось криволинейной балки. Луч образует угол θ при O . И пусть σ — продольное напряжение в нити гℎ на расстоянии y от нейтральной оси.
Из геометрии длина нейтральной оси луча ij и нити накала gℎ , расположенных на расстоянии y от нейтральной оси луча можно вычислить следующим образом:
Деформация ε в нити может быть рассчитана следующим образом:
Для линейно-упругого материала, к которому применяется закон Гука, уравнение 7. 1 можно записать следующим образом:
1 можно записать следующим образом:
Если элементарная площадь δA на расстоянии y от нейтральной оси балки (см. рис. 7.1c) подвергается изгибающему напряжению σ , элементарная сила на этой площади может быть рассчитана следующим образом:
Сила на всем поперечном сечении балки тогда становится:
Из рассмотрения статического равновесия внешний момент M в балке уравновешивается моментами относительно нейтральной оси внутренних сил, возникающих в сечении балки. Таким образом,
Подстановка из уравнения 7.2 в уравнение 7.5 дает следующее:
Складываем I = ∫ y 2 δA в уравнении 7.6 предполагает следующее:
где
I = момент инерции или второй момент площади сечения.
Объединение уравнений 7.2 и 7.7 дает следующее:
Уравнение кривой упругости балки можно найти следующими способами.
Из дифференциального исчисления кривизна в любой точке кривой может быть выражена следующим образом:
где
— первая и вторая производные функции, представляющей кривую в декартовых координатах x и y .
Поскольку балка на рис. 7.1 предполагается однородной и ведет себя линейно-упругим образом, ее прогиб при изгибе невелик. Поэтому величина, представляющая собой наклон кривой в любой точке деформированной балки, также будет небольшой. Поскольку пренебрежимо мало, уравнение 7.9можно упростить следующим образом:
Объединение уравнений 7.2 и 7.10 дает следующее:
Преобразование уравнения 7.11 дает следующее:
Уравнение 7.12 называют дифференциальным уравнением упругой кривой балки.
7.3 Отклонение методом двойного интегрирования
Прогиб методом двойного интегрирования называют также прогибом методом прямого или постоянного интегрирования. Этот метод заключается в получении прогиба балки путем двойного интегрирования дифференциального уравнения кривой упругости балки и использования граничных условий для определения констант интегрирования. Первое интегрирование дает наклон, а второе интегрирование дает отклонение. Этот метод лучше всего подходит, когда приложенная нагрузка непрерывна.
Первое интегрирование дает наклон, а второе интегрирование дает отклонение. Этот метод лучше всего подходит, когда приложенная нагрузка непрерывна.
Пример 7.1
Консольная балка подвергается комбинированному нагружению, как показано на рис. 7.2а. Методом двойного интегрирования определить наклон и прогиб на свободном конце.
Рис. 7.2. Консольная балка.
Решение
Уравнение для изгибающего момента. Прохождение сечения на расстоянии x от свободного конца балки, как показано на диаграмме свободного тела на рис. 7.2b, и рассмотрение момента справа от сечения предполагает следующее:
Подстановка M в уравнение 7.12 дает следующее:
Уравнение для наклона. Интегрирование по отношению к x предполагает следующее:
Обратите внимание, что на фиксированном конце, где это называется граничным условием. Применение этих граничных условий к уравнению 3 предполагает следующее:
Чтобы получить следующее уравнение наклона, подставьте вычисленное значение C 1 в уравнение 3 следует:
Уравнение для прогиба. Интегрирование уравнения 4 дает следующее:
Интегрирование уравнения 4 дает следующее:
На фиксированном конце x = L , y = 0. Применение этих граничных условий к уравнению 5 дает следующее:
Чтобы получить следующее уравнение упругой кривой, подставьте вычисленное значение C 2 в уравнение 5 следующим образом:
Наклон на свободном конце, т.е. на х = 0
Прогиб на свободном конце, т.е. y на х = 0
3
Пример 7.2
Свободно опертая балка AB несет равномерно распределенную нагрузку в 2 тысячи фунтов на фут по всей своей длине и сосредоточенную нагрузку в 10 тысяч фунтов в середине своего пролета, как показано на рис. 7.3a. Методом двойного интегрирования определить уклон на опоре A и прогиб в средней точке C балки.
Рис. 7.3. Просто поддерживаемая балка.
Решение
Реакции поддержки.
тысячи фунтов по симметрии
Уравнение для изгибающего момента. Момент на участке на расстоянии x от опоры A , как показано на диаграмме свободного тела на рис. 7.3b, записывается следующим образом:
Момент на участке на расстоянии x от опоры A , как показано на диаграмме свободного тела на рис. 7.3b, записывается следующим образом:
. :
Уравнение для наклона. Интегрирование уравнения 2 относительно x предполагает следующее:
Константа интегрирования C 1 оценивается с учетом граничного условия.
Применение вышеуказанных граничных условий к уравнению 3 дает следующее:0004
Уравнение прогиба. Интегрирование уравнения 4 предполагает следующее:
Константа интегрирования C 2 оценивается с учетом граничного условия.
в x = 0, y = 0
0 = 0 — 0 — 0 + C 2
C 2 = 0 0004
Compreting The . 2 обратно в уравнение 5 предлагает следующее уравнение упругой кривой:
Уклон в
Прогиб в средней точке
Пример 7. 3
3
Балка несет распределенную нагрузку, которая изменяется от нуля на опоре A до 50 кН/м на выступающем конце, как показано на рис. 7.4а. Напишите уравнение упругой кривой для отрезка АВ балки, определите уклон на опоре А и определите прогиб в точке балки, расположенной на расстоянии 3 м от опоры А .
Рис. 7.4. Луч.
Решение
Реакции поддержки. Для определения реакции балки применяют уравнения равновесия следующего вида:
Уравнение для изгибающего момента. Момент на участке на расстоянии x от опоры A , как показано на диаграмме свободного тела на рис. 7.4b, равен:
.
Уравнение для наклона. Интегрирование уравнения 2 относительно x дает следующее:
Уравнение для отклонения. Интегрирование уравнения 3 предлагает следующее уравнение отклонения:
Чтобы оценить константы интегрирования, примените следующие граничные условия к уравнению 4:
При x = 0, y = 0 0 – 0 + 0 + С 2
C 2 = 0
в x = 6 м, Y = 0
C 1 = –65. 82
82
Equation of Elastast.
Уравнение упругой кривой теперь можно определить, подставив C 1 и C 2 в уравнение 4.
1 и C 2 обратно в уравнения 3 и 4:
Уравнение наклона.
Уравнение прогиба.
Прогиб на x = 3 м от опоры A .
7.4 Прогибание по методу функции сингулярности
В тех случаях, когда на балку действует комбинация распределенных нагрузок, сосредоточенных нагрузок и моментов, использование метода двойного интегрирования для определения прогибов таких балок действительно требует, так как различные участки балки представляются несколькими функциями моментов, и для нахождения констант интегрирования требуется много вычислительных усилий. Использование в таких случаях метода сингулярных функций для определения прогибов сравнительно проще и относительно быстро. Впервые этот метод анализа был предложен Маколеем в 19 г. 19, и это влечет за собой использование одного уравнения, которое содержит сингулярность или функцию половинного диапазона для описания всей кривой отклонения луча. Функция сингулярности или половинного диапазона определяется следующим образом:
19, и это влечет за собой использование одного уравнения, которое содержит сингулярность или функцию половинного диапазона для описания всей кривой отклонения луча. Функция сингулярности или половинного диапазона определяется следующим образом:
, где
x = координатное положение точки вдоль луча.
a = любое место вдоль балки, где возникает разрыв из-за изгиба.
n = экспоненциальные значения функций; это всегда должно быть больше или равно нулю, чтобы функции были действительными.
Приведенное выше определение подразумевает, что количество ( x – a ) равно нулю или равно нулю, если оно отрицательное, но оно равно ( x – a ), если оно положительное.
Процедура анализа методом функции сингулярности
• Нарисуйте диаграмму свободного тела балки и установите координаты x и y .
• Рассчитайте опорные реакции и напишите уравнение момента как функцию x координат. Соглашение о знаках на данный момент такое же, как и в разделе 4.3.
Соглашение о знаках на данный момент такое же, как и в разделе 4.3.
• Подставьте выражение момента в уравнение упругой кривой и проинтегрируйте один раз, чтобы получить наклон. Интегрируйте снова, чтобы получить отклонение в луче.
•Используя граничные условия, определите константы интегрирования и подставьте их в уравнения, полученные на шаге 3, чтобы получить наклон и прогиб балки. Положительный наклон — против часовой стрелки, отрицательный наклон — по часовой стрелке, положительный — вверх, а отрицательный — вниз.
• При расчете уклона или прогиба в любой точке балки отбрасывайте величину ( x – a ) из уравнения для уклона или прогиба, если оно отрицательное. Если ( x – a ) положительное, оно остается в уравнении.
Пример 7.4
Свободно опертая балка подвергается комбинированной нагрузке, показанной на рис. 7.5а. Методом функции сингулярности определить уклон на опоре А и прогиб на Б .
Рис. 7.5. Просто поддерживаемая балка.
7.5. Просто поддерживаемая балка.
Решение
Реакции поддержки. Чтобы определить реакцию опоры A балки, примените уравнения равновесия следующим образом:
Изгибающий момент. Заменив заданную распределенную нагрузку двумя эквивалентными открытыми нагрузками, как показано на рис. 7.5б, изгибающий момент в сечении, расположенном на расстоянии х от левой опоры А можно выразить следующим образом:
Уравнение упругой кривой. Замена M ( x ) из уравнения 1 в уравнение 7.12 дает следующее:
Интегрирование уравнения 2 дважды дает следующее:
Граничные условия и вычисление констант интегрирования. Применяя граничные условия [ x = 0, y = 0] к уравнению 4 и отмечая, что каждая скобка содержит отрицательную величину и, таким образом, равна нулю по определению сингулярности, можно предположить, что C 2 = 0.
0 = 0 — 0 + 0 — 0 + C 2
C 2 = 0
снова, применяя границы [ x = 0
, применяя граничные условия [ x = 0
, применяя граничные условия [ x = 0
, применяя граничные условия [ x = 0
. 8, y = 0] к уравнению 4 и учитывая, что каждая скобка содержит положительную величину, можно предположить, что значение константы C 1 будет следующим:
8, y = 0] к уравнению 4 и учитывая, что каждая скобка содержит положительную величину, можно предположить, что значение константы C 1 будет следующим:
и С 2 в уравнение 4 предполагает, что выражение для упругой кривой балки будет следующим:
Аналогично, подстановка значений для C 1 в уравнение 3 предполагает, что выражение для наклона будет следующим:
Уклон на
Прогиб на x = 4,5 м от опоры А
Пример 7.5
Консольная балка нагружена равномерно распределенной нагрузкой 4 тысячи фунтов/фут, как показано на рис. 7.6а. Используя метод сингулярной функции, определить уравнение упругой кривой балки, наклон на свободном конце и прогиб на свободном конце.
Рис. 7.6. Консольная балка.
Решение
Реакции поддержки. Чтобы определить реакцию опоры A балки, примените уравнение равновесия следующим образом:
Изгибающий момент. Изгибающий момент в сечении, расположенном на расстоянии х от закрепленного конца балки, показанном на рисунке 7.6б, может быть выражен следующим образом:
Изгибающий момент в сечении, расположенном на расстоянии х от закрепленного конца балки, показанном на рисунке 7.6б, может быть выражен следующим образом:
Уравнение упругой кривой. Замена на M ( x ) из уравнения 1 в уравнение 7.12 дает следующее:
Интегрирование уравнения 2 дважды дает следующее:
Граничные условия и вычисление констант интегрирования. Применяя граничные условия к уравнению 3 и учитывая, что член со скобкой содержит отрицательную величину и, таким образом, равен нулю по определению функции сингулярности, получаем, что C 1 = 0,
Применяя граничные условия [ x = 0, y = 0] к уравнению 4 и отмечая, что член со скобкой содержит отрицательную величину и, таким образом, равен нулю по определению функции сингулярности, находим, что C 2 = 0.
, чтобы найти эластичную кривую луча, замените значения для C 1 и C 2 В КОНСТРУКЦИИ 4, следующим образом:
9 9004 2 . 0003 Аналогичным образом, чтобы найти выражение для наклона, подставьте значения C 1 в уравнение 3 следующим образом:
0003 Аналогичным образом, чтобы найти выражение для наклона, подставьте значения C 1 в уравнение 3 следующим образом:Пример 7.6
Балка с выступом подвергается комбинированной нагрузке, как показано на рис. 7.7а. Методом функции сингулярности определить уклон на опоре А и прогиб на В .
Рис. 7.7. Балка с навесом.
Решение
Реакции поддержки. Чтобы определить реакцию опоры A балки, примените уравнения равновесия следующим образом:
Изгибающий момент. Заменив заданную распределенную нагрузку двумя эквивалентными открытыми нагрузками и изменив момент, как показано на рис. 7.7b, изгибающий момент в сечении, расположенном на расстоянии x от левой опоры A , можно выразить как следует:
Уравнение упругой кривой. Замена на M ( x ) из уравнения 1 в уравнение 7.12 дает следующее:
Интегрирование уравнения 2 дважды дает следующее:
Граничные условия и вычисление констант интегрирования. Применяя граничные условия [ x = 0, y = 0] к уравнению 4 и отмечая, что каждая скобка содержит отрицательную величину и, таким образом, равна нулю по определению сингулярности, получаем, что C 2 = 0.
Применяя граничные условия [ x = 0, y = 0] к уравнению 4 и отмечая, что каждая скобка содержит отрицательную величину и, таким образом, равна нулю по определению сингулярности, получаем, что C 2 = 0.
0 = 0 + 0 – 0 + 0 + 0 + 0 + C 2
C 2 = 0
2 = 0[6 6 6 m 3 граничные условия , y = 0] к уравнению 4 и учитывая, что каждая скобка содержит положительную величину, можно предположить, что значение константы C 1 будет следующим:
и С 2 в уравнении 4 предполагает, что выражение для упругой кривой балки будет следующим:
Уклон на
Прогиб на x = 2 м от опоры А
7.5 Прогиб по методу момент-площадь
В методе момент-площадь используется площадь момента, деленная на изгибную жесткость ( M/EI ) схема балки для определения прогиба и уклона вдоль балки. В этом методе используются две теоремы, которые выводятся ниже.
В этом методе используются две теоремы, которые выводятся ниже.
7.5.1 Теорема о первом моменте-площади
Чтобы вывести первую теорему о моменте-площади, рассмотрим участок AB кривой упругости отклоненной балки, показанной на рис. 7.8b. Луч имеет радиус кривизны R . На рис. 7.8с представлен изгибающий момент этой части. Согласно геометрии длина дуги ds , радиуса R , стягивающий угол dθ , равен произведению радиуса кривизны на стягивающий угол. Следовательно,
Преобразование уравнения 1 предполагает следующее:
Рис. 7.8. Отклоненный луч.
Подстановка уравнения 7.14 в уравнение 7.8 дает следующее:
Поскольку ds бесконечно мал из-за малого бокового отклонения луча, допускаемого в технике, его можно заменить его горизонтальной проекцией дх . Таким образом,
Таким образом, угол θ между касательными в точках A и B может быть получен суммированием стягиваемых углов на бесконечно малую длину, лежащую между этими точками. Таким образом,
Таким образом,
Уравнение 7.17 называют первой теоремой площади момента. Первая теорема о моменте-площади утверждает, что общее изменение наклона между A и B равно площади диаграммы изгибающего момента между этими двумя точками, деленной на изгибную жесткость EI .
7.5.2 Теорема о втором моменте-площади
Снова обращаясь к рисунку 7.8, необходимо определить тангенциальное отклонение точки B относительно точки A , которое является вертикальным расстоянием точки B от касательной, проведенной к кривой упругости в точке A . Для этого сначала вычислите вклад δ ∆ элемента длины dL в расстояние по вертикали. По геометрии
Замена dθ из уравнения 7.15 в уравнение 7.18 дает следующее:
Следовательно,
Уравнение 7.20 называют второй теоремой площади моментов. Вторая теорема момент-площадь утверждает, что вертикальное расстояние точки B на упругой кривой от касательной к кривой в точке A равно моменту относительно вертикали, проходящей через B площади диаграмма изгибающего момента между A и B , разделенные по жесткости на изгиб, EI .
7.5.3 Условные обозначения
Соглашения о знаках для теорем момент-площадь следующие:
(1) Тангенциальное отклонение точки В, относительно касательной, проведенной на кривой упругости в точке А , положительно, если В лежит выше касательной в точке А , и отрицательно, если она лежит ниже касательной (см. рис. 7.9).
(2)Уклон в точке B относительно касательной, проведенной в точке A на кривой упругости, положительно, если касательная, проведенная в точке B , вращается против часовой стрелки относительно касательной в точке A , и отрицательно, если она вращается по часовой стрелке (см. рис. 7.9).
Рис. 7.9. Представление соглашения о подписи.
Процедура анализа методом момент-площадь
• Нарисуйте схему свободного тела балки.
•Нарисуйте M/EI схема балки. Это будет выглядеть как обычная диаграмма изгибающих моментов балки, если балка призматическая (т. е. одинакового поперечного сечения по всей длине).
е. одинакового поперечного сечения по всей длине).
• Чтобы определить наклон в любой точке, найдите угол между касательной, проходящей через эту точку, и касательной, проходящей через другую точку кривой отклонения, разделите диаграмму M/EI на простые геометрические фигуры, а затем примените первую Теорема момент-площадь. Чтобы определить прогиб или тангенциальное отклонение любой точки балки, примените вторую теорему о моменте-площади.
•В тех случаях, когда конфигурация диаграммы M/EI такова, что ее нельзя разделить на простые формы с известными площадями и центроидами, предпочтительно рисовать диаграмму M/EI по частям. Это влечет за собой введение фиксированной опоры в любой удобной точке вдоль балки и построение диаграммы M/EI для каждой из приложенных нагрузок, включая опорные реакции, до применения любой из теорем для определения того, что требуется.
Таблица 7.1. Площади и центроиды геометрических фигур.
Пример 7. 7
7
На свободный конец консольной балки, показанной на рис. 7.10а, действует сосредоточенный момент. Используя метод момент-площадь, определите наклон на свободном конце балки и прогиб на свободном конце балки. EI = константа.
Рис. 7.10. Консольная балка.
Решение
( M/EI ) схема. Сначала начертите диаграмму изгибающего момента балки и разделите ее на изгибную жесткость, EI , чтобы получить диаграмму, показанную на рис. 7.10b.
Наклон на А . Наклон на свободном конце равен площади диаграммы между A и B согласно первой теореме момент-площадь. Используя эту теорему и обращаясь к диаграмме, можно сделать следующее:
Прогиб на A . Прогиб на свободном конце балки равен моменту относительно вертикали через А площади диаграммы между A и B , согласно второй теореме момент-площадь. Используя эту теорему и обращаясь к рисункам 7.10b и 7.10c, можно сделать следующее:
Пример 7. 8
8
Подпираемая консольная балка несет равномерно распределенную нагрузку в 4 тысячи фунтов/фут по всей своей длине, как показано на рис. 7.11a. Используя метод площади момента, определите наклон в точке A и прогиб в точке A .
Рис. 7.11. Подпертая консольная балка.
Решение
( M/EI ) диаграмма. Сначала начертите диаграмму изгибающего момента для балки и разделите ее на изгибную жесткость, EI , чтобы получить диаграмму, показанную на рис. 7.11b.
Наклон на А . Наклон на свободном конце равен площади диаграммы между A и B . Область между этими двумя точками обозначена как A 1 и A 2 на рисунке 7.11b. Используйте Таблицу 7.1, чтобы найти вычисление A 2 , чья дуга является параболической, и расположение ее центроида. Отметив это из таблицы и применив первую теорему о моменте-площади, можно сделать следующее: Прогиб в точке A равен моменту площади диаграммы между A и B относительно A . Таким образом, используя вторую теорему момент-площадь и обращаясь к рисунку 7.11b и рис. 7.11c, можно сделать следующее:0004
Таким образом, используя вторую теорему момент-площадь и обращаясь к рисунку 7.11b и рис. 7.11c, можно сделать следующее:0004
Пример 7.9
Просто опертая деревянная балка длиной 8 футов будет нести распределенную нагрузку на пол в 500 фунтов/фут по всей своей длине, как показано на рис. 7.12а. Используя теорему площади момента, определите наклон на конце B и максимальное отклонение.
Рис. 7.12. Просто поддерживаемая деревянная балка.
Решение
( M/EI ) схема. Сначала начертите диаграмму изгибающего момента балки и разделите ее на изгибную жесткость, EI , чтобы получить диаграмму, показанную на рис. 7.12b.
Уклон на B . Наклон B равен площади диаграммы между B и C . Область между этими двумя точками обозначена как A 2 на рисунке 7.12b. Применение первой теоремы момент-площадь предполагает следующее:
Максимальное отклонение. Максимальный прогиб происходит в центре балки (точка C). Он равен моменту площади диаграммы между B и C о B . Таким образом,
Максимальный прогиб происходит в центре балки (точка C). Он равен моменту площади диаграммы между B и C о B . Таким образом,
Пример 7.10
Призматическая деревянная балка подвергается действию двух сосредоточенных нагрузок одинаковой величины, как показано на рис. 7.13а. Методом момент-площадь определить уклон в точке А и прогиб в точке С.
Рис. 7.13. Призматическая деревянная балка.
Решение
( M/EI ) схема. Сначала начертите диаграмму изгибающего момента балки и разделите ее на изгибную жесткость, EI , чтобы получить диаграмму, показанную на рис. 7.13b.
Наклон на А . Прогиб и поворот балки малы, так как они происходят в пределах упругости. Таким образом, наклон опоры A можно вычислить с помощью теоремы о малом угле следующим образом:
По теореме он равен моменту площади диаграммы между A и B о B . Таким образом,
Таким образом,
Таким образом, наклон в точке A равен
Прогиб в точке C . Прогиб на C можно получить по пропорции.
Аналогично, тангенциальное отклонение С от А можно определить как момент площади диаграммы между А и С относительно С .
Следовательно, прогиб на С это
7.6 Отклонение методом сопряженной балки
Метод сопряженных балок, разработанный Генрихом Мюллером-Бреслау в 1865 году, является одним из методов, используемых для определения наклона и прогиба балки. Метод основан на принципе статики.
Сопряженная балка определяется как фиктивная балка, длина которой такая же, как у реальной балки, но с нагрузкой, равной изгибающему моменту реальной балки, деленному на ее изгибную жесткость, EI .
Метод сопряженных балок использует сходство взаимосвязей между нагрузкой, поперечной силой и изгибающим моментом, а также между кривизной, наклоном и прогибом, полученное в предыдущих главах и представленное в таблице 7. 2.
2.
Таблица 7.2. Взаимосвязь между нагрузкой, сдвигом, изгибающим моментом и кривизной, наклоном, прогибом.
7.6.1 Опоры для сопряженных балок
Опоры для сопряженных балок показаны в Таблице 7.3, а примеры реальных и сопряженных балок показаны на Рисунке 7.4.
Таблица 7.3. Опоры для сопряженных балок.
Таблица 7.4 Реальные балки и их сопряженные.
7.6.2 Соглашение о знаках
Для положительной диаграммы кривизны, где имеется положительная ордината диаграммы, нагрузка в сопряжении должна указывать в положительном направлении y (вверх) и наоборот (см. рис. 7.14).
Рис. 7.14. Диаграмма положительной кривизны.
Если соблюдается соглашение, установленное для диаграмм положительной кривизны, то положительная поперечная сила в сопряженной балке равна положительному наклону в реальной балке, а положительный момент в сопряженной балке равен положительному отклонению (движению вверх) реальной балки. . Это показано на рис. 7.15.
. Это показано на рис. 7.15.
Рис. 7.15. Сдвиг и наклон балки.
Процедура анализа методом сопряженных пучков
• Нарисуйте диаграмму кривизны реальной балки.
• Нарисуйте сопряженную балку для реальной балки. Сопряженный пучок имеет ту же длину, что и реальный пучок. Поворот в любой точке реальной балки соответствует поперечной силе в той же точке сопряженной балки, а смещение в любой точке реальной балки соответствует моменту в сопряженной балке.
•Применить диаграмму кривизны реальной балки в качестве распределенной нагрузки на сопряженную балку.
•Используя уравнения статического равновесия, определить реакции на опорах сопряженной балки.
•Определить поперечную силу и момент в интересующих сечениях сопряженной балки. Эти поперечные силы и моменты равны соответственно наклону и прогибу реальной балки. Положительный сдвиг в сопряженной балке подразумевает наклон реальной балки против часовой стрелки, а положительный момент обозначает отклонение реальной балки вверх.
Пример 7.11
Методом сопряженной балки определите наклон и прогиб в точке A консольной балки, показанной на рис. 7.16а. E = 29 000 тысяч фунтов на квадратный дюйм и I = 280 дюймов 4
Рис. 7.16. Сопряженный пучок.
Решение
( M/EI ) схема. Сначала начертите диаграмму изгибающего момента для балки и разделите ее на изгибную жесткость, EI , чтобы получить диаграмму, показанную на рис. 7.16b.
Сопряженный пучок. Сопряженная балка, нагруженная диаграммой, показана на рис. 7.16в. Обратите внимание, что свободный конец реальной балки фиксируется в сопряженной балке, а фиксированный конец реальной балки становится свободным в сопряженной балке. Диаграмма применяется как направленная вниз нагрузка в сопряженной балке, поскольку на рис. 7.16b она отрицательна.
Наклон на А . Наклон на A в реальной балке является сдвигом на A в сопряженной балке. Стрижка в A в сопряжении выглядит следующим образом:
Стрижка в A в сопряжении выглядит следующим образом:
Здесь используется то же правило знаков для поперечной силы, что и в главе 4.
Таким образом, уклон в реальной балке в точке A будет следующим:
Прогиб в точке A . Прогиб в точке A в реальной балке равен моменту в точке A сопряженной балки. Момент на A сопряженной балки выглядит следующим образом:
Здесь используется то же правило знаков для изгибающего момента, что и в главе 4.
Таким образом, отклонение реального луча в точке А равно:
Пример 7.12
Используя метод сопряженных балок, определите уклон в опоре A и прогиб под действием сосредоточенной нагрузки свободно опертой балки в точке B , как показано на рисунке 7.17a.
E = 29 000 тысяч фунтов на квадратный дюйм и I = 800 дюймов 4
Рис. 7.17. Просто поддерживаемая балка.
Решение
( M/EI ) диаграмма. Сначала начертите диаграмму изгибающего момента для балки и разделите ее на изгибную жесткость, EI , чтобы получить диаграмму кривизны момента (), показанную на рисунке 7.17b.
Сопряженная балка. Сопряженная балка, нагруженная диаграммой, показана на рис. 7.17в. Обратите внимание, что A и C , которые являются простыми опорами в реальной балке, остаются теми же в сопряженной балке. Диаграмма применяется как направленная вверх нагрузка в сопряженной балке, поскольку на рис. 7.17b она положительна.
Реакции на сопряженный пучок. Реакцию на опоры сопряженной балки можно определить следующим образом:
Уклон на A . Наклон в точке A в реальной балке представляет собой поперечную силу в точке A в сопряженной балке. Сдвиг по A в сопряженной балке:
Таким образом, уклон на опоре A реальной балки:
Прогиб по B . Отклонение в B в реальной балке равен моменту B сопряженной балки. Момент в точке В сопряженной балки равен:
Отклонение в B в реальной балке равен моменту B сопряженной балки. Момент в точке В сопряженной балки равен:
Прогиб в точке В реальной балки равен:
Краткое изложение главы
Отклонение балок с помощью геометрических методов: Геометрические методы, рассматриваемые в этой главе, включают метод двойного интегрирования, метод функции сингулярности, метод момент-площадь и метод сопряженной балки. До обсуждения этих методов было получено следующее уравнение кривой упругости балки:
Метод двойного интегрирования: Этот метод включает двойное интегрирование уравнения упругой кривой. Первое интегрирование дает наклон, а второе интегрирование дает отклонение. Константы интегрирования определяются с учетом граничных условий.
Метод функции сингулярности: Этот метод включает использование функции сингулярности или полудиапазона для описания уравнения упругой кривой для всей балки. Функция полудиапазона может быть записана в общем виде следующим образом:
Функция полудиапазона может быть записана в общем виде следующим образом:
Метод сингулярности лучше всего подходит для балок с большим количеством разрывов из-за сосредоточенных нагрузок и моментов. Метод значительно уменьшает количество констант интегрирования, которые необходимо определить, и, таким образом, упрощает расчет по сравнению с методом двойного интегрирования.
Метод момент-площадь : Этот метод использует две теоремы для определения наклона и прогиба в заданных точках на упругой кривой балки. Эти две теоремы заключаются в следующем:
Первая теорема площади момента: Изменение наклона между любыми двумя точками на кривой упругости балки равно площади диаграммы между этими двумя точками.
Вторая теорема площади момента: Вертикальное отклонение точки A от касательной, проведенной к кривой упругости в точке B , равно моменту площади под диаграммой между этими двумя точками относительно точки A .
Метод сопряженной балки: Сопряженная балка определяется как воображаемая балка той же длины, что и реальная балка, но с нагрузкой, равной диаграмме фактической балки. Опоры в реальных балках заменяются фиктивными опорами с граничными условиями, при которых изгибающий момент и поперечная сила в конкретной точке сопряженной балки будут равны соответственно прогибу и наклону в тех же точках реальной балки.
Практические задачи
7.1 Используя метод двойного интегрирования, определите наклоны и прогибы на свободных концах консольных балок, показанных на рис. P7.1–рис. P7.4. EI = константа.
Рис. P7.1. Консольная балка.
Рис. P7.2. Консольная балка.
Рис. P7.3. Консольная балка.
Рис. P7.4. Консольная балка.
7.2 Используя метод двойного интегрирования, определите наклоны в точке A и прогибов в средней точке C балок, показанных на рисунке P7. 5 и рисунке P7.6. EI = константа.
5 и рисунке P7.6. EI = константа.
Рис. P7.5. Луч.
Рис. P7.6. Луч.
7.3 Используя метод сопряженных балок, определите наклон в точке A и прогиб в точке B балки, показанной на рисунках P7.7–P7.10.
Рис. P7.7. Луч.
Рис. P7.8. Луч.
Рис. P7.9. Луч.
Рис. P7.10. Луч.
7.4 Используя метод момент-площадь, определите прогиб в точке A консольной балки, показанной на рисунках с P7.11 по P7.12.
Рис. P7.11. Консольная балка.
Рис. P7.12. Консольная балка.
7.5 Используя метод момент-площадь, определите уклон в точке А и уклон в средней точке С балок, показанных на рисунке P7.13 и рисунке P7.14.
Рис. P7.13. Луч.
Рис. P7.14. Луч.
7.6 Используя метод функции сингулярности, определите наклон и прогиб в точке A консольной балки, показанной на рисунке P7. 15.
15.
Рис. P7.15. Консольная балка.
7.7 Методом функции сингулярности определить наклон в точке В и наклон в точке C балки со свесом, показанным на рисунке П7.16. EI = константа. E = 200 ГПа, I = 500 × 106 мм 4 .
Рис. P7.16. Луч.
7.8 Используя метод функции сингулярности, определить уклон в точке C и прогиб в точке D балки с выступающими концами, как показано на рисунке П7.17. EI = константа.
Рис. P7.17. Луч.
7.9 Используя метод функции сингулярности, определить наклон в точке А и прогиб в точке В балки, показанной на рисунке П7.18. EI = константа.
Рис. P7.18. Луч.
Эта страница под названием 1.7: Отклонение балок — геометрические методы распространяется в соответствии с лицензией CC BY-NC-ND 4.0 и была создана, изменена и/или курирована Феликсом Удойо посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.

 Удачи!
Удачи! = +wL
= +wL = FL / 4
= FL / 4 = wL 2 / 8
= wL 2 / 8 = М 0 / 2
= М 0 / 2