Пятиугольник как построить циркулем: Построение правильного пятиугольника

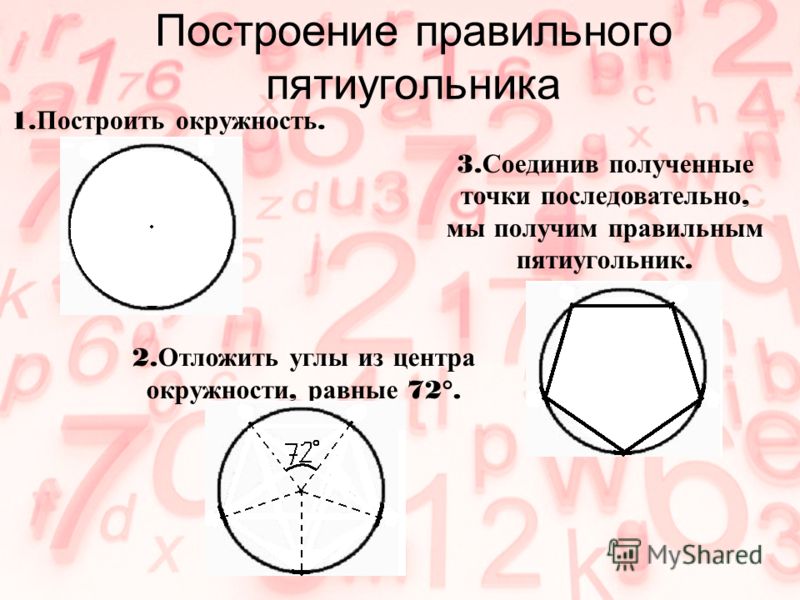
Построение треугольника по трем элементам и правильного пятиугольника

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Гнатко И.В. 1

---

1МБОУ «Лицей №159»

Бутакова В.И. 1

---

1МБОУ «Лицей №159»

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Гипотеза исследования построена на предположении о том, что задачи на построение правильного пятиугольника имеют достаточно широкое распространение в архитектуре, живописи и других, смежных с математикой, науках.

Методы исследования:

Поисковый;

Анализ;

Дедуктивный метод.

Объект исследования — задачи на построение с помощью циркуля и линейки.

Предмет исследования — решение задач повышенной сложности на построение треугольников по трем элементам, построение правильного пятиугольника различными способами.

Проблема — задачи на построение правильного пятиугольника и задачи повышенной сложности на построение треугольника по трем элементам почти не изучаются в школьном курсе математики.

Цель исследования — поиск решения задач на построение правильного пятиугольника, на построение треугольников по трем элементам.
Задачи исследования:

1. Определить в математике понятие задачи на построение с помощью циркуля и линейки, изучить основную литературу по данной теме;

2. Решение задач повышенной сложности на построение треугольников по трем элементам;

3. Исследовать архитектурные сооружения, при проектировании которых использовались правильные пятиугольники;

4.Рассмотреть наиболее интересные способы построения правильных пятиугольников;

5. Создание творческих проектов.

Актуальность исследования — данная тема очень актуальна, так как, выбирая профессию инженера, ученик сталкивается с множеством вопросов, например одним из них: «Где мы можем применить знания математики?» Исследования в данной области приводят к выводу о том, что математика имеет большое практическое применение, как в архитектуре, живописи, дизайне так и в других науках.

История возникновения

Первые задачи на построение возникли в глубокой древности. Уже древними архитекторами и землемерами приходилось решать простейшие задачи на построение, связанные с их профессией.

Самые первые задачи на построение, по-видимому, решались непосредственно на местности и заключались в проведении прямых линий и построения прямого угла.

Древнегреческие математики еще 3000 лет назад проводили свои построения с помощью двух приборов: гладкой дощечки с ровным краем и двух заостренных палок, связанных на одном конце.

К задачам на построение прибегали древние инженеры, когда составляли рабочий чертеж того или иного сооружения. Задачи на построение помогали людям в их хозяйственной жизни, их решения формулировались в виде «практических правил», исходя из наглядных соображений.

Первым греческим ученым, который рассматривал геометрические задачи на построение, был Фалес Милетский. Это он, пользуясь построением треугольника, определил расстояние, недоступное для непосредственного измерения. Это он вычислил и высоту египетской пирамиды по отбрасываемой ею тени.

Задачи на построение интересовали и Пифагора. Пифагор и его ученики потратили много сил, чтобы отдельным геометрическим сведениям, состоящим до того времени из набора интуитивных правил, придать характер настоящей науки. Задачи на построение интересовали Платона. Платон и его ученики считали построение геометрическим, если оно выполнялось при помощи циркуля и линейки. Если же в процессе построения использовались другие чертежные инструменты, то построение не считалось геометрическим. Уже в древности греческие математики встретились с тремя задачами на построение, которые не поддавались решению.

Первая задача. Задача об удвоении куба. Требуется построить ребро куба, который по объему был бы в два раза больше данного куба.

Вторая задача. Задача о трисекции угла. Требуется произвольный угол разделить на три равные части.

Третья задача. Задача о квадратуре круга. Требуется построить квадрат, площадь которого равнялась бы данному кругу. Эти три задачи на построение и носят название «знаменитых геометрических задач древности». Большую роль задачи на построение играют в «Началах» Эвклида , где существование фигур доказывается их построением при помощи циркуля и линейки. В «Началах» Эвклида находятся почти все задачи на построение, которые изучаются в настоящее время в школе.

Теоретическая часть

Что такое задачи на построение?

Задача на построение — это задача, в которой требует­ся построить геометрический объект, пользуясь только двумя инструментами: циркулем и линейкой (односторонней и без де­лений). Решение задач на построение состоит не в том, чтобы проделать «руками» соответствующие построения, а в том, чтобы найти алгоритм решения, то есть описать решение задачи в виде последовательности уже известных стандартных построений, а также рассмотреть различные способы построения правильного пятиугольника. В этом и состоит цель моей работы.

К элементарным задачам на построение, которые рассматривают на начальных этапах изучения в школьном курсе геометрии, как правило, относят следующие:

1. Отложение на прямой отрезка, равного данному.

2. Отложение от заданной полупрямой в заданную полуплоскость угла, равного данному.

3. Построение прямой, проходящей через данную точку и параллельную данной прямой.

4. Построение прямой, проходящей через данную точку и перпендикулярную к данной прямой.

5. Деление отрезка на две равные части.

6. Деление отрезка в заданном отношении.

7. Построение биссектрисы угла.

8. Построение угла, равного данному.

9. Построение треугольника по трём сторонам, по двум сторонам и углу между ними, по стороне и прилежащим к ней углам.

10. Построение прямоугольного треугольника по гипотенузе и катету, по гипотенузе и острому углу, по двум катетам.

11. Нахождение центра построенной окружности.

12. Построение касательной к окружности через заданную на ней точку. Заметим, что представленный перечень элементарных задач является условным, его можно дополнить.

Сколько бывает решений для задач на построение?

Решить задачу на построение — найти все её решения. Покажем на простейших примерах возможные случаи.

З адача имеет одно решение.

Рисунок 1

Пусть требуется построить прямоугольный треугольник по катету и гипотенузе. Таких треугольников на плоскости можно построить множество, и они могут располагаться как угодно, но у всех равны соответственно две стороны два данных отрезка: гипотенуза и катет, а значит, эти треугольники равны. В этом случае говорят, что задача имеет одно решение «с точностью до равенства». Поэтому достаточно построить один треугольник.

Задача имеет конечное число решений.

Рисунок 2

Пусть требуется построить прямоугольный треугольник, катетом которого служит данный отрезок AC, а гипотенуза равна другому данному отрезку L. В этом случае условие задачи требует определённого расположения искомого треугольника относительно катета AC. Треугольник может оказаться в верхней полуплоскости и в нижней полуплоскости относительно отрезка AC. Поэтому задача имеет два решения: Δ и Δ (рис. 2), причём Δ = Δ . Важно отметить, что хотя здесь треугольники и равны, мы считаем их разными решениями (поскольку они расположены по-разному относительно отрезка AC).

Задача имеет бесконечно много решений.

Такого рода задачи называют неопределёнными. Конечно, мы не можем построить все решения неопределённой задачи. Когда же считают неопределённую задачу решённой? В том случае, когда указаны:

1) приём построения одной из искомых фигур задачи;

2) приём получения других искомых фигур.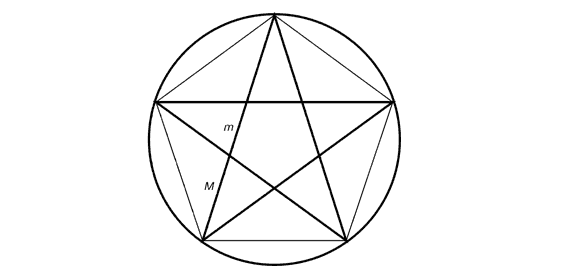

Пример. Построить окружность данного радиуса и касающуюся данной прямой.

Рисунок 3

Р ешение. Через произвольную точку B прямой L проведём прямую L₁⊥L. Отложим на прямой L₁ от точки B, например, в верхнюю полуплоскость отрезок BO = r. Проведём окружность ω(O;OB=r). Через точку O проведём прямую L₂ параллельную L. Заметим, что при всевозможных положениях точки O на прямой L

2 возникают все решения данной задачи. Задача решена.

Задача не имеет решений.

Такие задачи называют переопределёнными.

Пример. Построить окружность, проходящую через три данные точки, лежащие на одной прямой. Если точки лежат на одной прямой, то провести через них окружность нельзя. Следовательно, задача не имеет решения.

О расположении данных в задаче ничего не сказано. В таких случаях задачу считают решённой, если рассмотрены всевозможные случаи расположения данных.

Пример. Провести через данную точку касательную к данной окружности.

Решение. Возможны три случая расположения данных (точки и окружности).

Случай 1. Точка находится вне окружности, но не принадлежит кругу. Здесь можно провести две касательные к окружности (рис. 4).

Случай 2. Точка находится на окружности. Здесь можно провести одну касательную (рис. 5).

Рисунок 4

Рисунок 5

Рисунок 6

С лучай 3. Точка находится вне окружности, но принадлежит кругу. Здесь касательную к окружности провести нельзя (рис. 6).

Что такое правильный пятиугольник? Правильный пятиугольник, или пентагон (от греческого πενταγωνον-пятиугольник) — выпуклая фигура, имеющая пять вершин, все стороны которой равны между собой (рис 7).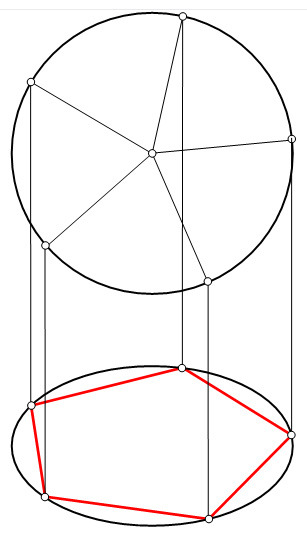

Также, можно заметить, что данная фигура делится в золотом сечении.

Рисунок 7. Правильный пятиугольник

Рисунок 8. Деление правильного пятиугольника в золотом сечении

Архитектурные сооружения, при проектировании которых использовались правильные пятиугольники

Пятиугольный храм (1475-1554) (рис. 10)
Дворец в крепости (1475-1554) (рис. 11)
Театр Советской армии (1934-1940) (рис. 12)
Цитадель в Кортрейке ( III-IV вв.) (рис. 13)
Укреплённая крепость Пиллау (начало XVIIв.) (рис. 14)

Схема типовой крепости из руководства по военному искусству(рис. 15)
Здание министерства обороны США (окончание строительства — январь 1943) (рис. 16)
Дом Советов в Махачкале (1927) (рис. 17)
План типового этажа( 2-9 этаж) 9-этажного дома башенного типа жилого комплекса Слоттсбергет в Гётеборге

Рисунок 9

Рисунок 10

Рисунок 11 Рисунок 12

Рисунок 13 Рисунок 14

Рисунок 15 Рисунок 16

Практическая часть.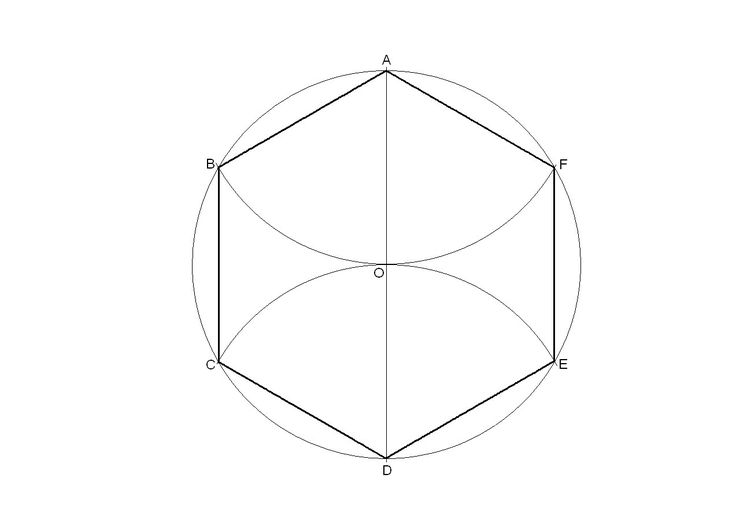 Приложение А

Заключение

Своеобразие геометрии,

выделяющее её среди

других разделов математики,

да и всех наук вообще,

заключается в неразрывном

органическом соединении живого

воображения со строгой логикой.

Геометрия в своей сути и есть

пространственное воображение,

пронизанное и организованное

строгой логикой.

В ходе моей работы цель исследования – поиск решений задач на построение треугольника по трем элементам и правильного пятиугольника была достигнута. В своей работе я рассмотрел архитектурные сооружения различных стилей, построенные в разные эпохи, и выявил, что при проектировании данных сооружений использовались правильные пятиугольники.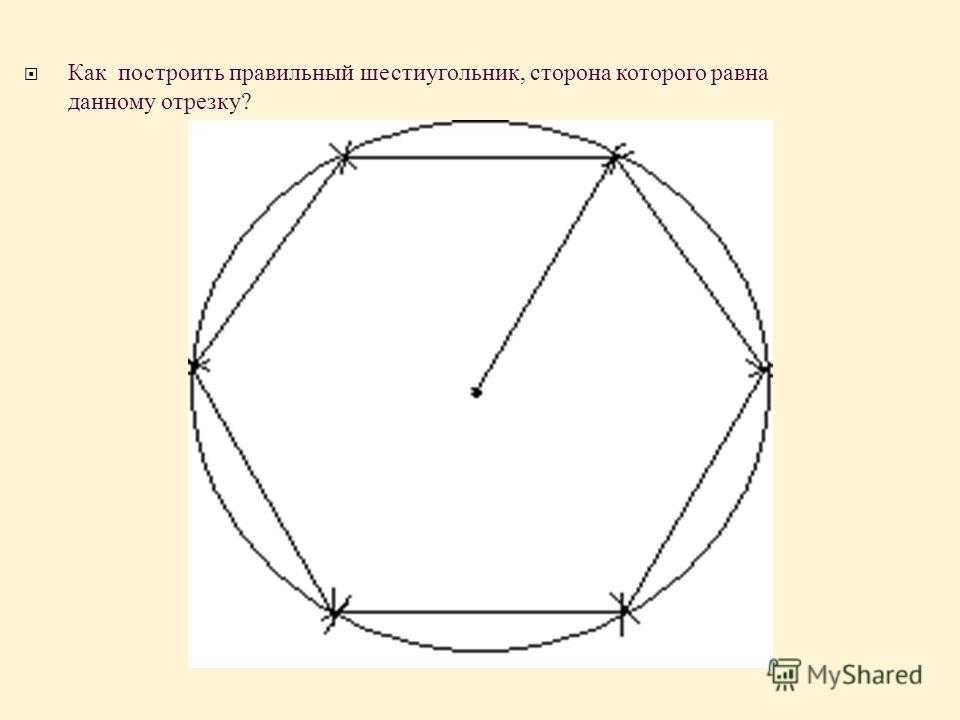 Памятники архитектуры, получившие широкую известность как образцы пропорциональности и гармонии, буквально пронизаны математикой, численными расчетами и геометрией.

Практическая часть моей работы включает в себя различные задачи повышенной сложности на построение с помощью циркуля и линейки треугольника по трем элементам и правильного пятиугольника.

Я выбрал эту тему, так как она имеет большое практическое применение в нашей жизни, например, в архитектуре, геометрии, инженерной графике, проектировании.

Список использованной литературы

1.http://www.psciences.net/main/sciences/mathematics/articles/article-1.html
2.http://poisk-ru.ru/s5188t3.html

3.https://ru.wikipedia.org/wiki/Правильный_пятиугольник

4. В. Н. Литвинов «Правильный пятиугольник» 2012г.

5. Александров И.И. «Сборник геометрических задач на построение», 1950 г

Просмотров работы: 114

Помогите! Внучке задали. С помощью циркуля построить правильный треугольник

В задачах на построение циркуль и линейка считаются идеальными инструментами, в частности линейка не имеет делений и имеет только одну сторону бесконечной длины, а циркуль может иметь сколь угодно большой или сколь угодно малый раствор.

Допустимые построения. В задачах на построение допускаются следующие операции:

1. Отметить точку:

произвольную точку плоскости;

произвольную точку на заданной прямой;

произвольную точку на заданной окружности;

точку пересечения двух заданных прямых;

точки пересечения/касания заданной прямой и заданной окружности;

точки пересечения/касания двух заданных окружностей.

2. С помощью линейки можно построить прямую:

произвольную прямую на плоскости;

произвольную прямую, проходящую через заданную точку;

прямую, проходящую через две заданных точки.

3. С помощью циркуля можно построить окружность:

произвольную окружность на плоскости;

произвольную окружность с центром в заданной точке;

произвольную окружность с радиусом, равным расстоянию между двумя заданными точками;

окружность с центром в заданной точке и радиусом, равным расстоянию между двумя заданными точками.

Решение задач на построение. Решение задачи на построение содержит в себе три существенные части:

Описание способа построения искомого объекта.

Доказательство того, что объект, построенный описанным способом, действительно является искомым.

Анализ описанного способа построения на предмет его применимости к разным вариантам начальных условий, а также на предмет единственности или неединственности решения, получаемого описанным способом.

Построение отрезка, равного данному. Пусть дан луч с началом в точке $O$ и отрезок $AB$. Для построения на луче отрезка $OP = AB$ нужно построить окружность с центром в точке $O$ радиуса $AB$.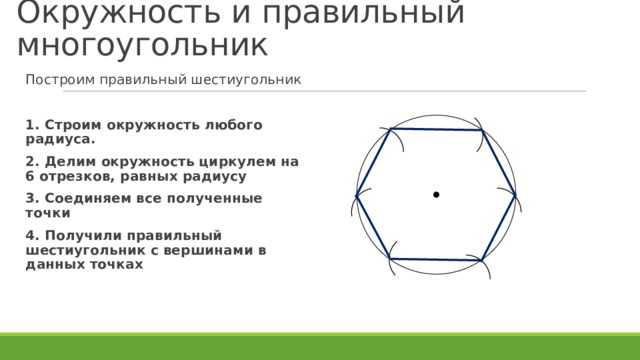 Точка пересечения луча с окружностью будет искомой точкой $P$.

Построение угла, равного данному. Пусть дан луч с началом в точке $O$ и угол $ABC$. C центром в точке $В$ строим окружность с произвольным радиусом $r$. Обозначим точки пересечения окружности с лучами $BA$ и $BC$ соответственно $A»$ и $C»$.

Построим окружность с центром в точке $O$ радиуса $r$. Точку пересечения окружности с лучом обозначим $P$. Построим окружность с центром в точке $P$ радиуса $A»B»$. Точку пересечения окружностей обозначим $Q$. Проведем луч $OQ$.

Получим угол $POQ$, равный углу $ABC$, так как треугольники $POQ$ и $ABC$ равны по трем сторонам.

Построение серединного перпендикуляра к отрезку. Построим две пересекающиеся окружности произвольного радиуса с центрами в концах отрезка. Соединив две точки их пересечения, получим серединный перпендикуляр.

Построение биссектрисы угла. Нарисуем окружность произвольного радиуса с центром в вершине угла.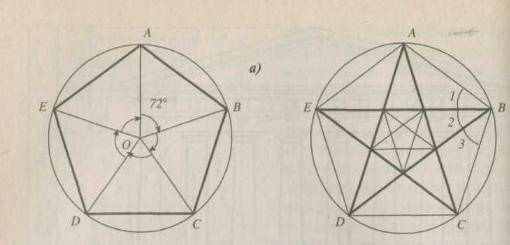 Построим две пересекающиеся окружности произвольного радиуса с центрами в точках пересечения первой окружности со сторонами угла. Соединив вершину угла с любой из точек пересечения этих двух окружностей, получаем биссектрису угла.

Построение суммы двух отрезков. Для построения на данном луче отрезка, равного сумме двух данных отрезков, нужно дважды применить метод построения отрезка, равного данному.

Построение суммы двух углов. Для того чтобы отложить от данного луча угол, равный сумме двух данных углов, нужно дважды применить метод построения угла, равного данному.

Нахождение середины отрезка. Для того чтобы отметить середину данного отрезка, нужно построить серединный перпендикуляр к отрезку и отметить точку пересечения перпендикуляра с самим отрезком.

Построение перпендикулярной прямой через данную точку. Пусть требуется построить прямую, перпендикулярную данной и проходящую через данную точку. Проводим окружность произвольного радиуса с центром в данной точке (независимо от того, лежит она на прямой или нет), пересекающую прямую в двух точках.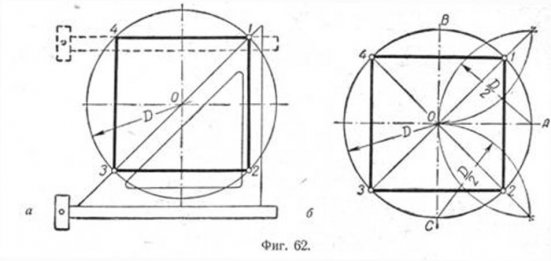 Строим серединный перпендикуляр к отрезку с концами в точках пересечения окружности с прямой. Это и будет искомая перпендикулярная прямая.

Построение параллельной прямой через данную точку. Пусть требуется построить прямую, параллельную данной и проходящую через данную точку вне прямой. Строим прямую, проходящую через данную точку, перпендикулярную данной прямой. Затем строим прямую, проходящую через данную точку, перпендикулярную построенному перпендикуляру. Полученная при этом прямая и будет искомой.

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №34 с углубленным изучением отдельных предметов

МАН, физико-математическая секция

«Геометрические построения с помощью циркуля и линейки»

Выполнила: ученица 7 «А» класса

Батищева Виктория

Руководитель: Колтовская В.В.

Воронеж, 2013

3. Построение угла равного данному.

Проведем произвольную окружность с центром в вершине А данного угла (рис. 3). Пусть В и С — точки пересечения окружности со сторонами угла. Радиусом АВ проведем окружность с центром в точке О-начальной точке данной полупрямой. Точку пересечения этой окружности с данной полупрямой обозначим С 1 . Опишем окружность с центром С 1 и Рис.3

радиусом ВС. Точка В 1 пересечения построенных окружностей в указанной полуплоскости лежит на стороне искомого угла.

6. Построение перпендикулярных прямых.

Проводим окружность с произвольным радиусом r с центром в точке O рис.6. Окружность пересекает прямую в точках A и B. Из точек A и B проводим окружности с радиусом AB. Пусть тоска С – точка пересечения этих окружностей. Точки А и В мы получили на первом шаге, при построении окружности с произвольным радиусом.

Искомая прямая проходит через точки С и О.

Рис.6

1. Задача Брахмагупты

Построить вписанный четырехугольник по четырем его сторонам. Одно из решений использует окружность Аполлония. Решим задачу Аполлония, используя аналогию между трехокружником и треугольником. Как мы находим окружность, вписанную в треугольник: строим точку пересечения биссектрис, опускаем из нее перпендикуляры на стороны треугольника, основания перпендикуляров (точки пересечения перпендикуляра со стороной, на которую он опущен) и дают нам три точки, лежащие на искомой окружности. Проводим окружность через эти три точки – решение готово. Точно также мы поступим с задачей Аполлония.

2. Задача Аполлония

Построить с помощью циркуля и линейки окружность, касающуюся трех данных окружностей. По легенде, задача сформулирована Аполлонием Пергским примерно в 220 г. до н. э. в книге «Касания», которая была потеряна, но была восстановлена в 1600 г. Франсуа Виетом, «галльским Аполлонием», как его называли современники.

Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.

П

равильный (или равносторонний ) треугольник — это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны правильного треугольника равны между собой, а все углы равны 60°. Чтобы построить равносторонний треугольник нужно разделить окружность на 3 равные части. Для этого необходимо провести дугу радиусом R этой окружности лишь из одного конца диаметра, получим первое и второе деление. Третье деление находится на противоположном конце диаметра. Соединив эти точки, получим равносторонний треугольник.

Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения через деление окружности на 6 частей. Используем равенство сторон правильного шестиугольника радиусу описанной окружности. Из противоположных концов одного из диаметров окружности описываем дуги радиусом R. Точки пересечения этих дуг с заданной окружностью разделят её на 6 равных частей. Последовательно соединив найденные точки, получают правильный шестиугольник.

Построение правильного пятиугольника.

П
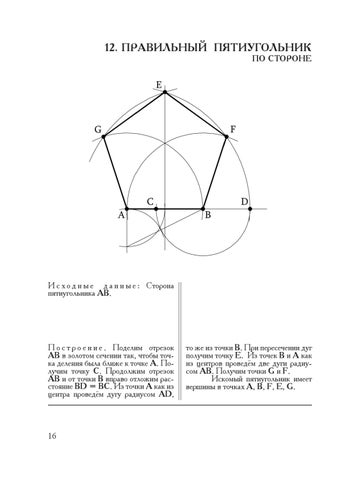
равильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны.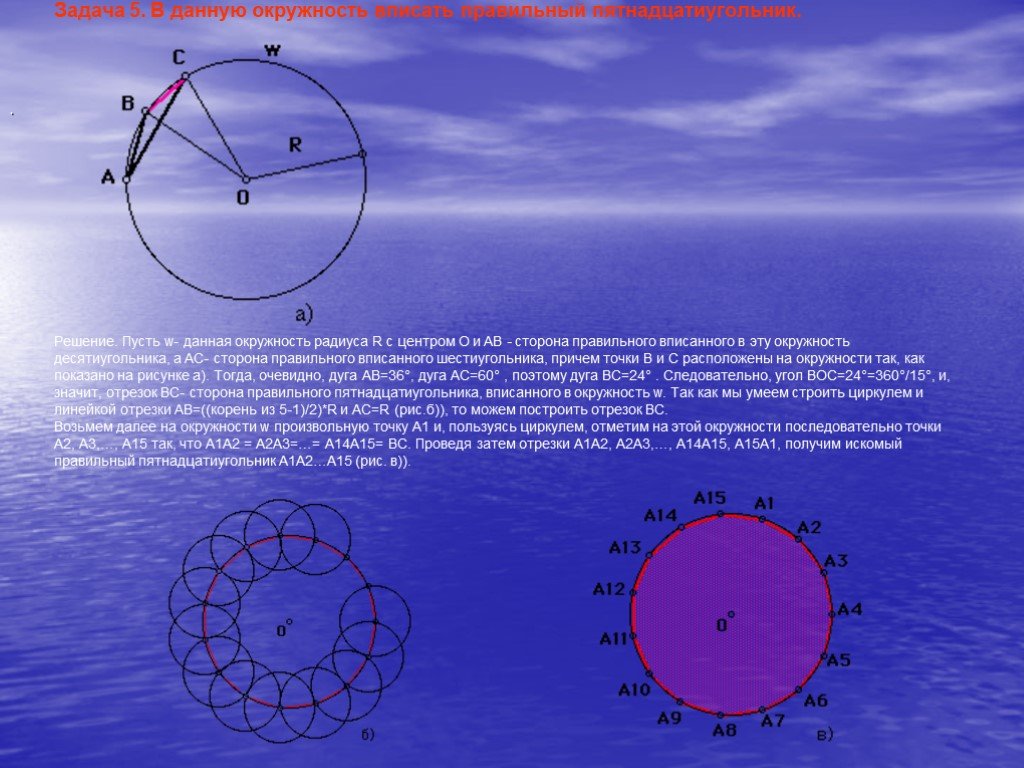 Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

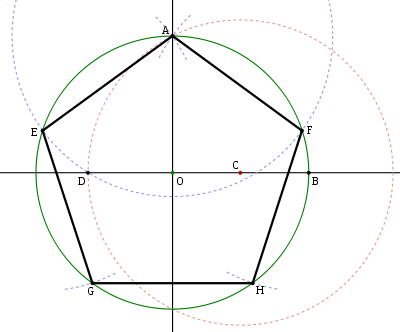
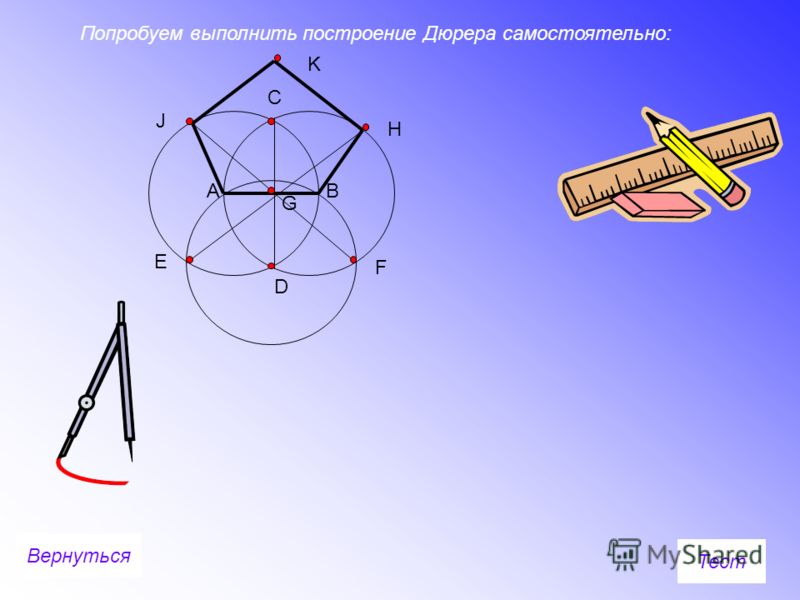
Вот один из методов построения правильного пятиугольника в заданной окружности:

Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O . (Это зелёная окружность на схеме справа).

Выберите на окружности точку A , которая будет одной из вершин пятиугольника. Постройте прямую через O и A .

Постройте прямую перпендикулярно прямой OA , проходящую через точку O . Обозначьте одно её пересечение с окружностью, как точку B .

Постройте точку C посередине между O и B .

C через точку A . Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D .

Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F .

Проведите окружность с центром в E через точку A G .

Проведите окружность с центром в F через точку A . Обозначьте её другое пересечение с первоначальной окружностью как точку H .

Постройте правильный пятиугольник AEGHF .

Следующие три задачи на построение были поставлены ещё в античности:

Иначе говоря, необходимо построить трисектрисы угла — лучи, делящие угол на три равные части. П. Л. Ванцель доказал в 1837 году, что задача разрешима только тогда, когда например, трисекция осуществима для углов α = 360°/n при условии, что целое число n не делится на 3. Тем не менее, в прессе время от времени публикуются (неверные) способы осуществления трисекции угла циркулем и линейкой.

Удвоение куба — классическая античная задача на построение циркулем и линейкой ребра куба, объём которого вдвое больше объёма заданного куба.

В современных обозначениях, задача сводится к решению уравнения . Всё сводится к проблеме построения отрезка длиной . П. Ванцель доказал в 1837 году, что эта задача не может быть решена с помощью циркуля и линейки.

Квадратура круга — задача, заключающаяся в нахождении построения с помощью циркуля и линейки квадрата, равновеликого по площади данному кругу .

Как известно, с помощью циркуля и линейки можно выполнить все 4 арифметических действия и извлечение квадратного корня; отсюда следует, что квадратура круга возможна в том и только в том случае, если с помощью конечного числа таких действий можно построить отрезок длины π. Таким образом, неразрешимость этой задачи следует из неалгебраичности (трансцендентности) числа π, которая была доказана в 1882 году Линдеманом.

Другая известная неразрешимая с помощью циркуля и линейки задача — построение треугольника по трём заданным длинам биссектрис .

Причём эта задача остаётся неразрешимой даже при наличии трисектора.

Только в XIX веке было доказано, что все три задачи неразрешимы при использовании только циркуля и линейки. Вопрос возможности построения полностью решён алгебраическими методами, основанными на теории Галуа.

Когда-то в построение правильных многоугольников вкладывали мистический смысл.

Так, пифагорейцы, последователи религиозно-философского учения, основанного Пифагором, и жившие в древней Греции (V I-I V вв. до н. э.), приняли в качестве знака своего союза звездчатый многоугольник, образованный диагоналями правильного пятиугольника.

Правила строгого геометрического построения некоторых правильных многоугольников изложены в книге «Начала» древнегреческого математика Евклида, жившего в III в. до н.э. Для выполнения этих построений Евклид предлагал пользоваться только линейкой и циркулем, который в то время был без шарнирного устройства соединения ножек (такое ограничение в инструментах было непреложным требованием античной математики).

Правильные многоугольники нашли широкое применение и в античной астрономии. Если Евклида построение этих фигур интересовало с точки зрения математики, то для древнегреческого астронома Клавдия Птолемея (около 90 — 160 г. н. э.) оно оказалось необходимым как вспомогательное средство при решении астрономических задач. Так, в 1-й книге «Альмагесты» вся десятая глава посвящена построению правильных пяти- и десятиугольников.

Однако помимо чисто научных трудов, построение правильных многоугольников было неотъемлемой частью книг для строителей, ремесленников, художников. Умение изображать эти фигуры издавна требовалось и в архитектуре, и в ювелирном деле, и в изобразительном искусстве.

В «Десяти книгах о зодчестве» римского архитектора Витрувия (жившего примерно в 63 -14 гг. до н. э.) говорится, что городские стены должны иметь в плане вид правильного многоугольника, а башни крепости «следует делать круглыми или многоугольными, ибо четырехугольник скорее разрушается осадными орудиями».

Планировка городов очень интересовала Витрувия, который считал, что нужно спланировать улицы так, чтобы вдоль них не дули основные ветры. Предполагалось, что таких ветров восемь и что они дуют в определенных направлениях.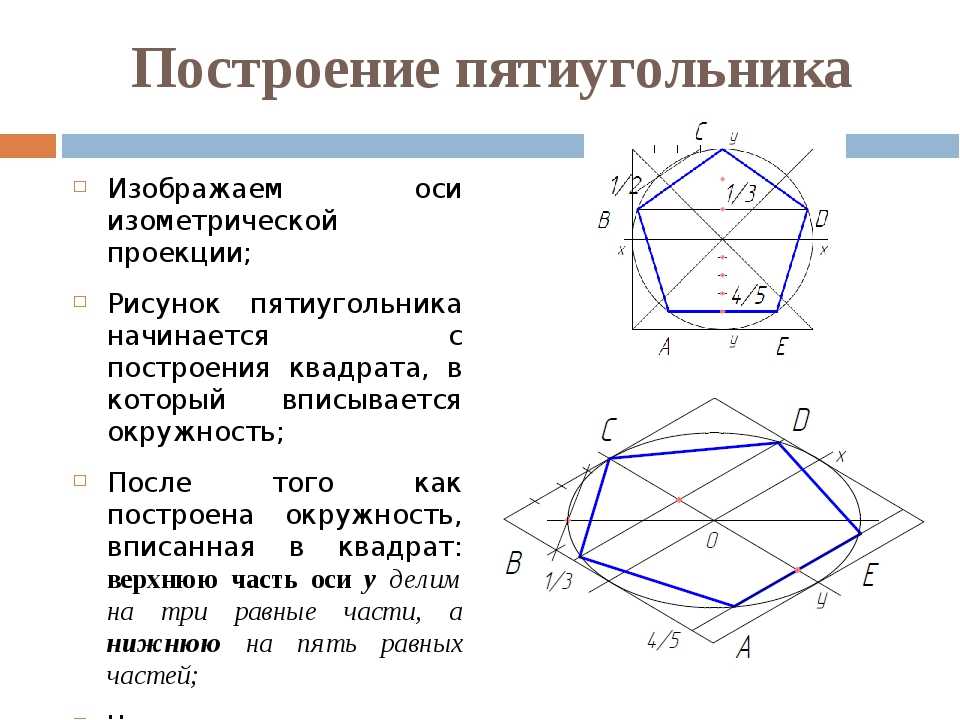

В эпоху Возрождения построение правильных многоугольников, и в частности пятиугольника, представляло не простую математическую игру, а являлось необходимой предпосылкой для построения крепостей.

Правильный шестиугольник явился предметом специального исследования великого немецкого астронома и математика Иоганна Кеплера (1571-1630), о котором он рассказывает в своей книге «Новогодний подарок, или о шестиугольных снежинках». Рассуждал о причинах того, почему снежинки имеют шестиугольную форму, он отмечает, в частности, следующее: «…плоскость можно покрыть без зазоров лишь следующими фигурами: равносторонними треугольниками, квадратами и правильными шестиугольниками. Среди этих фигур правильный шестиугольник покрывает наибольшую площадь»

0дним из наиболее известных ученых, занимавшихся геометрическими построениями, был великий немецкий художник и математик Альбрехт Дюрер (1471 -1528), который посвятил им значительную часть своей книги «Руководства…». Он предложил правила построения правильных многоугольников с 3. 4, 5… 16-ю сторонами. Методы деления окружности, предложенные Дюрером, не универсальны, в каждом конкретном случае используется индивидуальный прием.

Дюрер применял методы построения правильных многоугольников в художественной практике, например, при создании разного рода орнаментов и узоров для паркета. Наброски таких узоров были сделаны им во время поездки в Нидерланды, где паркетные полы встречались во многих домах.

Дюрер составлял орнаменты из правильных многоугольников, которые соединены в кольца (кольца из шести равносторонних треугольников, четырех четырехугольников, трех или шести шестиугольников, четырнадцати семиугольников, четырех восьмиугольников).

Итак, геометрические построения — это способ решения задачи, при котором ответ получают графическим путем. Построения выполняют чертежными инструментами при максимальной точности и аккуратности работы, так как от этого зависит правильность решения.

Благодаря этой работе я познакомилась с историей возникновения циркуля, подробнее познакомилась с правилами выполнения геометрических построений, получила новые знания и применила их на практике.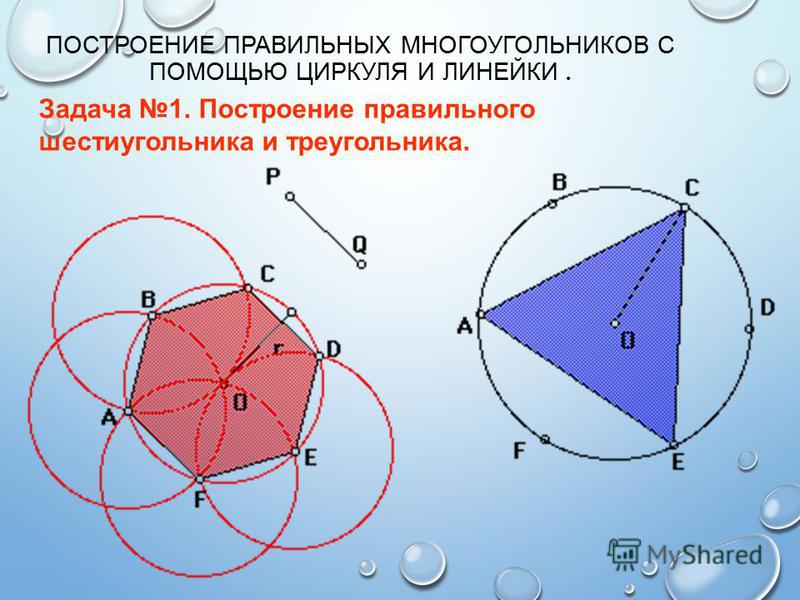
Решение задач на построение циркулем и линейкой – полезное времяпровождение, позволяющее по-новому посмотреть на известные свойства геометрических фигур и их элементов. В данной работе рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями с помощью циркуля и линейки. Рассмотрены основные задачи и даны их решения. Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ.
Таким образом, цель работы достигнута, поставленные задачи выполнены.

Как построить треугольник с помощью циркуля Циркуль – инструмент не только для построения окружности. Он позволяет также отложить равные отрезки заданной длины. Это и поможет нам с его помощью построить треугольник.

Вам понадобится: лист бумаги, циркуль, линейка. Инструкция. 1. возьмите любой листок бумаги. В центре листа поставьте точку. Это будет первая вершина A создаваемого треугольника. A

Инструкция 2.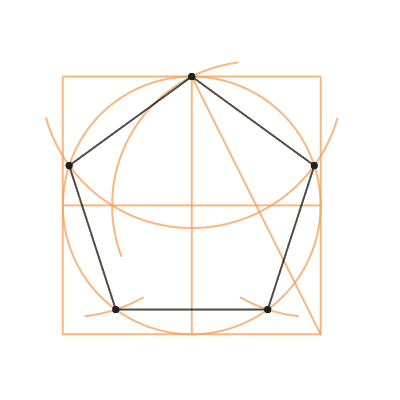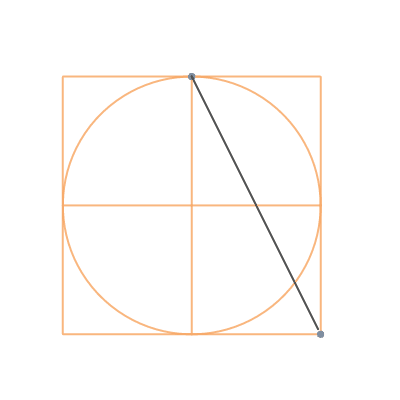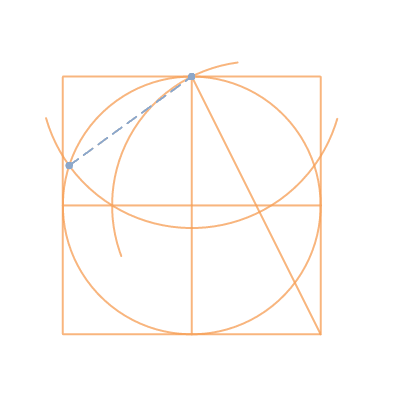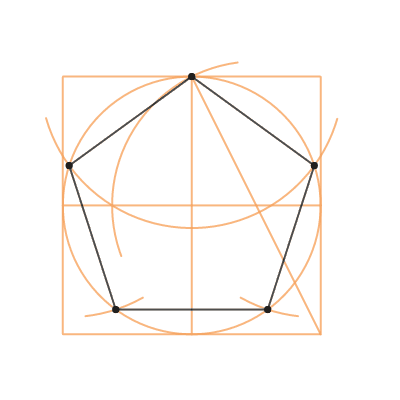 Раскройте циркуль на расстояние, соответствующее требуемой стороне создаваемого треугольника. Жестко зафиксируйте ножки циркуля в данном положении.

Инструкция 3. Поставьте иглу циркуля в отмеченную точку. Нарисуйте ножкой с грифелем дугу окружности отмеренного радиуса.

Инструкция 4. В любом месте по окружности нарисованной дуги поставьте точку. Это будет вторая вершина B создаваемого треугольника.

Инструкция 5. Аналогичным способом поставьте ножку на вторую вершину. Проведите еще одну окружность так, чтобы она пресекалась с первой.

Инструкция 6. В точке пересечения обоих проведенных дуг и находится третья вершина C создаваемого треугольника. Отметьте ее на рисунке.

Как начертить треугольник?

Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.

Треугольники бывают

• разносторонние;
• равнобедренные;
• равносторонние;
• прямоугольные;
• тупоугольные;
• остроугольные;
• вписанные в окружность;
• описанные вокруг окружности.

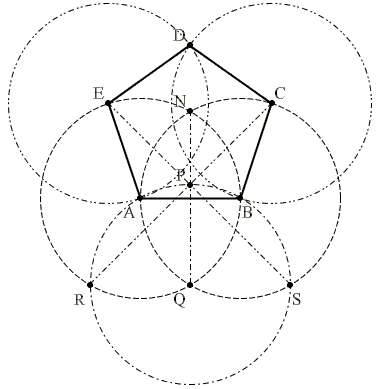
Построение равностороннего треугольника

Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.

1. С помощью линейки начертите одну из сторон, заданной длины.
2. Измерьте ее длину с помощью циркуля.
3. Поместите острие циркуля в один из концов отрезка и проведите окружность.
4. Переставьте острие в другой конец отрезка и проведите окружность.
5. У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.

Построение равнобедренного треугольника

Данный тип треугольников можно построить по основанию и боковым сторонам.

Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:

1. С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
2. Циркулем измеряем необходимую длину боковой стороны.
3. Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
4. Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.

Построение прямоугольного треугольника

Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.

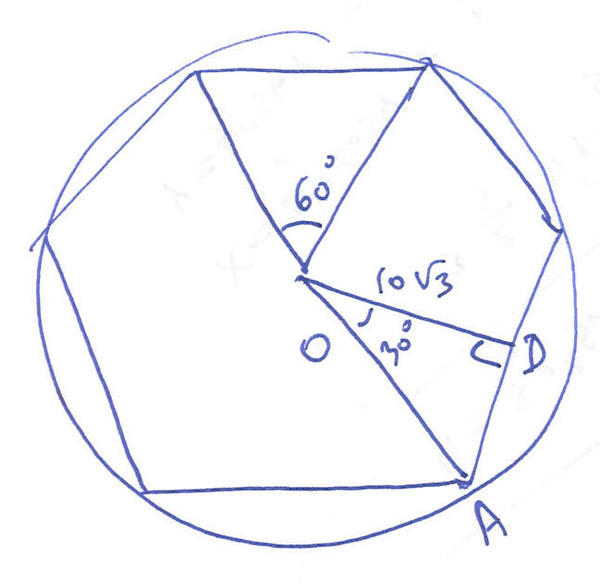
Построение тупоугольного треугольника по углу и двум прилегающим сторонам

Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:

1. С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
2. Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
3. Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.

Построение остроугольного треугольника

Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.

1. Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
2. Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.

Вписанный треугольник

Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:

У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.

Чертим описанный треугольник

Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:

Как построить равнобедренный треугольник? Это легко сделать с помощью линейки, карандаша и клеточек тетради.

Построение равнобедренного треугольника начинаем с основания. Чтобы рисунок получился ровным, количество клеточек в основании должно быть четным числом.

Делим отрезок — основание треугольника — пополам.

Вершину треугольника можно выбрать на любой высоте от основания, но обязательно ровно над срединой.

Как построить остроугольный равнобедренный треугольник?

Углы при основании равнобедренного треугольника могут быть только острыми. Чтобы равнобедренный треугольник получился остроугольным, угол при вершине тоже должен быть острым.

Для этого вершину треугольника выбираем повыше, подальше от основания.

Чем выше вершина, тем меньше угол при вершине. Углы при основании при этом, соответственно, увеличиваются.

Как построить тупоугольный равнобедренный треугольник?

С приближением вершины равнобедренного треугольника к основанию градусная мера угла при вершине увеличивается.

Значит, чтобы построить равнобедренный тупоугольный треугольник, вершину выбираем пониже.

Как построить равнобедренный прямоугольный треугольник?

Чтобы построить равнобедренный прямоугольный треугольник, надо вершину выбрать на расстоянии, равном половине основания (это обусловлено свойствами равнобедренного прямоугольного треугольника).

Например, если длина основания — 6 клеточек, то вершину треугольника располагаем на высоте 3 клеточек над серединой основания. Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.

Построение равнобедренного прямоугольного треугольника можно начать с вершины.

Выбираем вершину, от нее под прямым углом откладываем равные отрезки вверх и вправо. Это — боковые стороны треугольника.

Соединим их и получим равнобедренный прямоугольный треугольник.

Построение равнобедренного треугольника с помощью циркуля и линейки без делений рассмотрим в другой теме.

Как построить правильный пятиугольник с помощью циркуля.

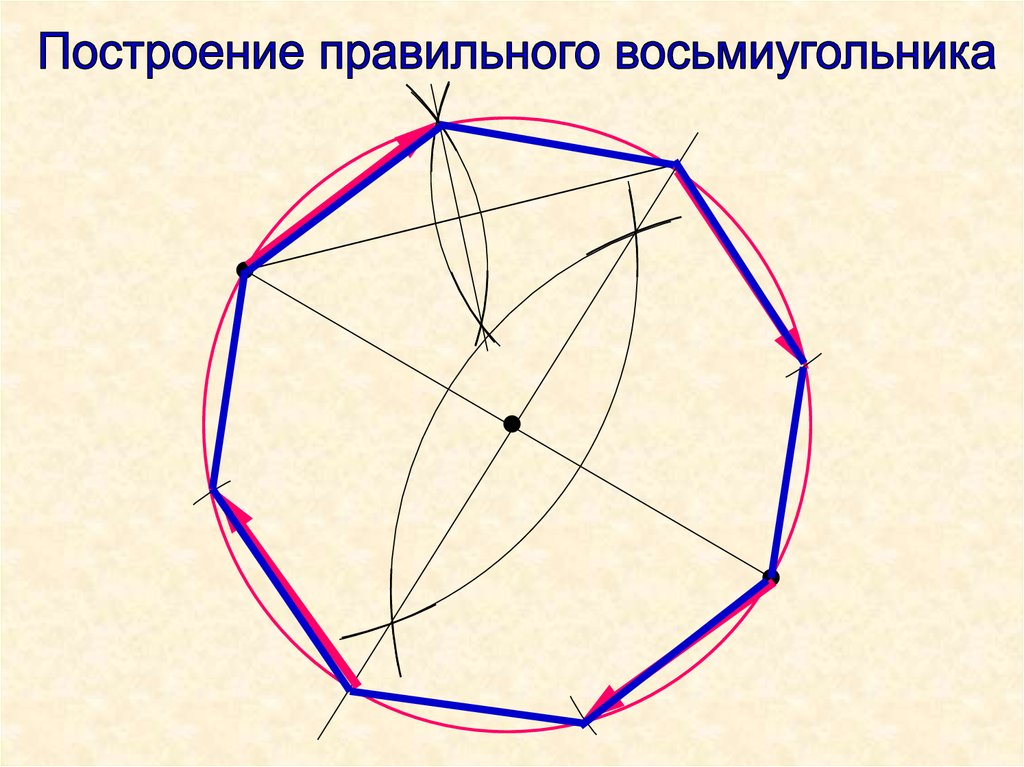Как построить и нарисовать правильный пятиугольник в окружности. Построение правильных многоугольников по заданной стороне

Правильный пятиугольник   — это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать круг. Постройте пятиугольник , и этот конкретный круг поможет.

Инструкция по эксплуатации

Прежде всего необходимо построить круг с помощью циркуля. Пусть центр окружности совпадает с точкой О. Проведите оси симметрии перпендикулярно друг другу. На пересечении одной из этих осей с окружностью поставьте точку V. Эта точка будет вершиной будущей пятиугольник и. На пересечении другой оси с окружностью положение D.

На отрезке OD найдите середину и отметьте в ней точку A. После этого нужно начертить окружность с центром в этой точке циркулем. Кроме того, он должен проходить через точку V, то есть с радиусом CV. Точку пересечения оси симметрии и этой окружности обозначим В.

После этого циркулем нарисуем окружность такого же радиуса, поместив стрелку в точку V. Пересечение этой окружности с исходной обозначим точкой F , Эта точка станет второй вершиной будущей правильной пятиугольник и.

Теперь нужно провести такой же круг через точку Е, но с центром в F. Обозначим пересечение только что нарисованного круга с исходным как G. Эта точка также станет одной из вершин пятиугольника и. Аналогичным образом нужно построить еще один круг. Его центр находится в G. Пусть это будет точка пересечения с исходной окружностью. Это последняя вершина правильного многоугольника.

Должно получиться пять пиков. Остается просто соединить их по линейке. В результате всех этих операций у вас получится правильный вписанный в круг пятиугольник .

Правильное построение пятиугольников   можно с помощью циркуля и линейки. Правда, процесс довольно длительный, как, впрочем, и построение любого правильного многоугольника с нечетным числом сторон. Современные компьютерные программы позволяют сделать это за несколько секунд.

Вам понадобится

• — Компьютер с AutoCAD.

Руководство по эксплуатации

Найдите в AutoCAD верхнее меню и вкладку «Главная» в нем. Щелкните по нему левой кнопкой мыши. Появится панель рисования. Появятся различные типы линий. Выберите замкнутую полилинию. Это полигон, осталось только ввести параметры. AutoCAD Позволяет рисовать различные правильные многоугольники. Количество сторон может достигать 1024. Можно использовать командную строку, в зависимости от версии набрав «_polygon» или «multi-angle».

Независимо от того, используете ли вы командную строку или контекстное меню, на экране появится окно с просьбой ввести количество сторон. Введите туда цифру «5» и нажмите Enter. Вас попросят определить центр пятиугольника. Вбейте в появившееся окно координаты. Вы можете обозначить их как (0,0), но могут быть и любые другие данные.

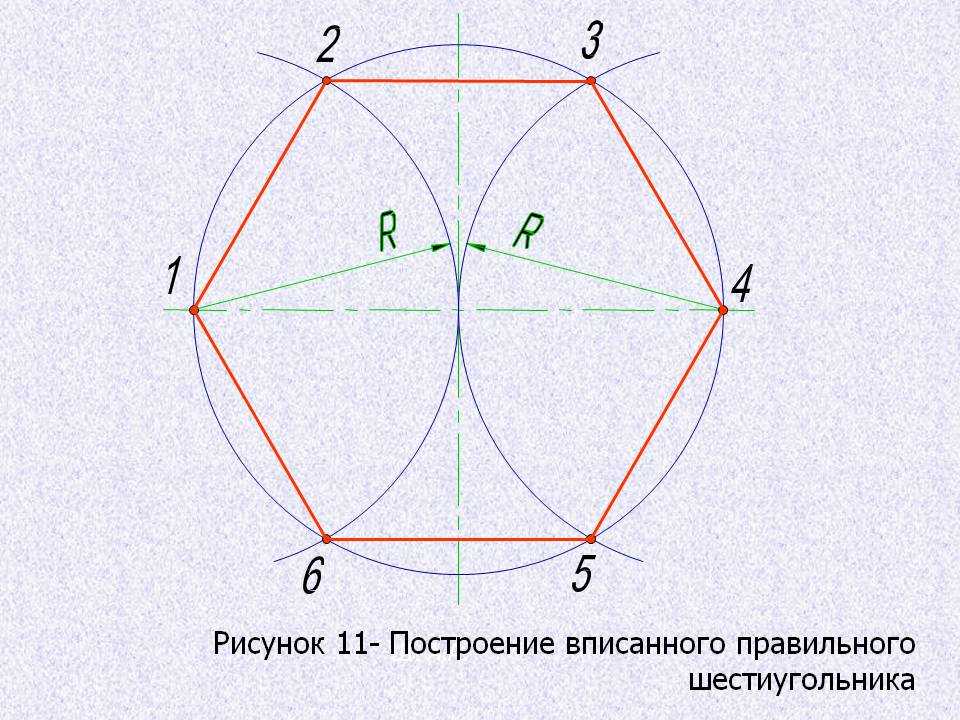Выберите предпочитаемый метод строительства. . AutoCAD предлагает три варианта. Пятиугольник можно описать вокруг или вписать в окружность, но можно также построить его по заданному размеру стороны. Выберите нужный вариант и нажмите Enter. При необходимости укажите радиус окружности и также нажмите ввод.

Точно таким же образом сначала строится пятиугольник на данной стороне. Выберите Нарисовать замкнутую полилинию и введите количество сторон. Щелкните правой кнопкой мыши, чтобы вызвать контекстное меню. Нажмите край или боковую команду. В командной строке введите координаты начальной и конечной точек одной из сторон пятиугольника. После этого на экране появится пятиугольник.

Все операции можно выполнять с помощью командной строки. Например, чтобы построить пятиугольник сбоку в русской версии программы, введите букву «с». В английской версии это будет «_e». Чтобы построить вписанный или описанный пятиугольник, после определения количества сторон введите буквы «o» или «b» (или английские «_c» или «_i»)

Таким простым способом можно построить не только пятиугольник. Для того, чтобы построить треугольник, необходимо развести ножки циркуля на расстояние, равное радиусу окружности. Затем поместите иглу в любую точку. Нарисуйте тонкий опорный круг. Две точки пересечения окружностей, а также точка, в которой находилась катетка циркуля, образуют три вершины правильного треугольника.

Построение правильного шестиугольника, вписанного в окружность.

Построение шестиугольника основано на том, что его сторона равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой.

Правильный шестиугольник можно построить с помощью подступенка и уголка 30X60°. Для выполнения этого построения берем горизонтальный диаметр окружности за биссектрису углов 1 и 4, строим стороны 1 — 6, 4 — 3, 4 — 5 и 7 — 2, после чего проводим стороны 5 — 6 и 3 — 2.

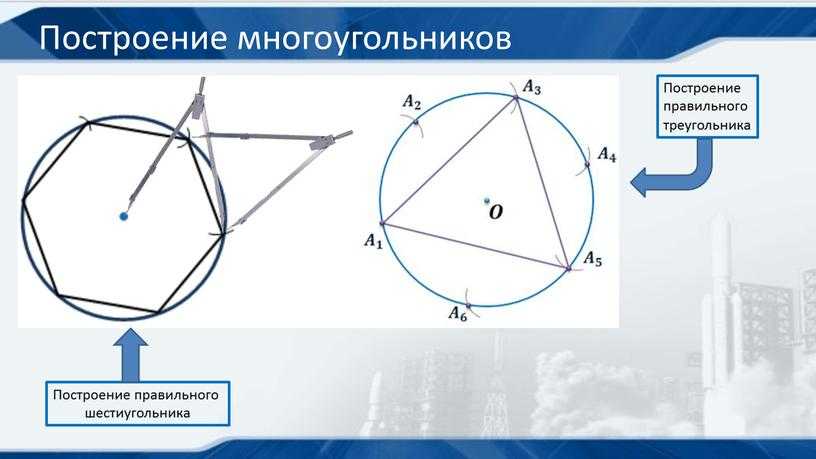Вершины такого треугольника можно построить с помощью циркуля и угольника с углами 30 и 60° или только одного циркуля. Рассмотрим два способа построения равностороннего треугольника, вписанного в окружность.

 Первый способ   (рис. 61, а) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикаль, проведенная через точку 7, является одновременно и высотой, и биссектрисой угла 1. Так как угол 0 — 1 — 2 равен 30°, то для нахождения стороны 1 — 2 достаточно построить угол 30° в точке 1 и стороне 0 — 1. Для этого установите рейку и квадрата, как показано на рисунке, проведите линию 1 – 2, которая будет одной из сторон искомого треугольника. Для построения стороны 2 — 3 устанавливаем траншею в положение, показанное пунктирными линиями, и через точку 2 проводим прямую, определяющую третью вершину треугольника.

  Второй способ   основан на том, что если построить правильный шестиугольник, вписанный в окружность, а затем соединить его вершины через единицу, то получится равносторонний треугольник.

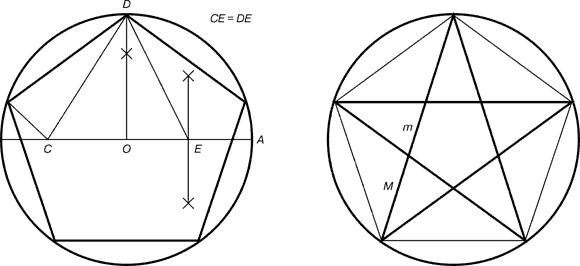Для построения треугольника отметим на диаметре вершину 1 и проведем диаметральную линию 1 — 4. Далее из точки 4 радиусом равным D/2 описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

Эту конструкцию можно построить с помощью угольника и циркуля.

Первый способ  основан на том, что диагонали квадрата пересекаются в центре описанной окружности и наклонены к ее осям под углом 45°. Исходя из этого, устанавливаем стояк и угольник с углами 45°, как показано на рис. 62, а, и отметить точки 1 и 3. Затем через эти точки провести с помощью рейки горизонтальные стороны квадрата 4 — 1 и 3 -2. Затем с помощью рейки по катету квадрата проводим вертикальные стороны квадрата 1 — 2 и 4 — 3.

Второй способ основан на том, что вершины квадрата разделены пополам дугами окружностей, заключенными между концами диаметра. Отметим на концах двух взаимно перпендикулярных диаметров точки А, В и С, а из них радиусом у опишем дуги до их взаимного пересечения.

Далее через точки пересечения дуг провести вспомогательные линии, отмеченные на рисунке сплошными линиями. Точки их пересечения с окружностью определяют вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяются последовательно друг с другом.

Построение правильного пятиугольника, вписанного в окружность.

Чтобы вписать правильный пятиугольник в окружность, делаем следующие построения. Отмечаем на окружности точку 1 и принимаем ее за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках М и В. Соединив эти точки прямой, получим точку К, которую затем соединим с точкой 1. С радиусом, равным отрезку А7, описываем дугу от точки К до пересечения с линией АО в точке Н. Соединив точку 1 с точкой Н, получим сторону пятиугольника. Затем с помощью компаса, равного отрезку 1Н, описав дугу от вершины 1 до пересечения с окружностью, найдем вершины 2 и 5. Сделав таким же решением циркуль надсечки из вершин 2 и 5, найдем получим оставшиеся вершины 3 и 4. 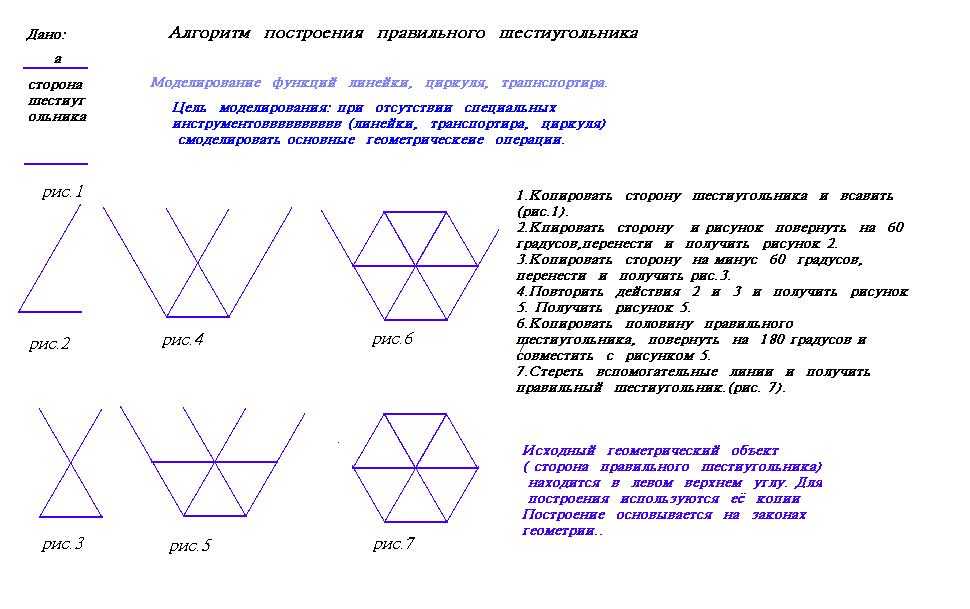Находим соединенные точки последовательно друг с другом.

Построение правильного пятиугольника на заданной стороне.

Чтобы построить правильный пятиугольник с этой стороны от него (рис. 64), разделим отрезок АВ на шесть равных частей. Из точек А и В радиусом АВ описываем дуги, пересечение которых даст точку К. Через эту точку и, разделив 3 линией АВ, провести вертикальную линию. Далее от точки К на этой линии откладываем отрезок, равный 4/6 АВ. Получаем точку 1 — вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, проведенными ранее из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Находим вершины соединяем последовательно друг с другом.

Построение правильного семиугольника, вписанного в окружность.

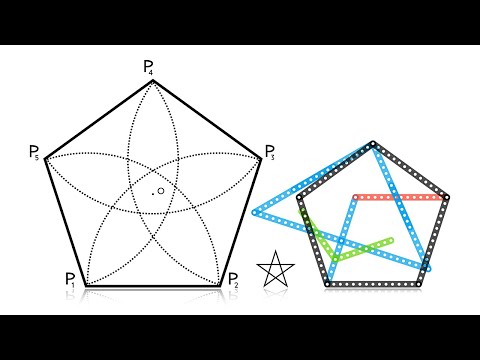Пусть дан круг диаметром D; в него нужно ввести правильный семиугольник (рис. 65). Разделите вертикальный диаметр круга на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точка F называется полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, провести лучи от полюса F через четные деления вертикального диаметра, пересечение которых с окружностью определит вершины VI, V и IV семиугольника. Для получения вершин /-//-// из точек IV, V и VI проводим горизонтальные линии до пересечения с окружностью. Найденные вершины последовательно соединяются друг с другом. Семиугольник можно построить, проведя лучи от полюса F и через нечетные деления вертикального диаметра.

Описанный выше метод подходит для построения правильных многоугольников с любым количеством сторон.

Деление окружности на любое количество равных частей можно также произвести, используя данные табл. 2, где приведены коэффициенты, позволяющие определить размеры сторон правильных вписанных многоугольников.

Длины сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указано количество сторон правильного вписанного многоугольника, а во второй — коэффициенты. Длина стороны данного многоугольника будет получена путем умножения радиуса данной окружности на коэффициент, соответствующий количеству сторон этого многоугольника. 92) (4) \ sqrt (\ frac (5+ \ sqrt (5

{2}};

Правильный пятиугольник   (греч. πενταγωνον ) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства

• Додекаэдр — единственный правильный многогранник, грани которого являются правильными пятиугольниками.
• Pentagon — Здание Министерства обороны США имеет форму правильного пятиугольника.
• Правильный пятиугольник — это правильный многоугольник с наименьшим числом углов из тех, которые нельзя замостить на плоскости.
• В природе не существует кристаллов с гранями в форме правильного пятиугольника.
• Пятиугольник со всеми его диагоналями является проекцией 4-симплекса.

см. также

Написать отзыв о статье «Обычный пятиугольник»

Примечания

Отрывок по поводу обычного пятиугольника

Петя не знал, сколько времени это продолжалось: он наслаждался, все время удивлялся своему удовольствию и желал что некому было сказать ему. Его разбудил ласковый голос Лихачева.
  — Готово, ваш дворянин, на двоих, держите хранителя расплющенным.
  Петя проснулся.
  — Ой, светает, да, светает! Он закричал.
 Невидимые прежде лошади стали видны до хвостов, а сквозь голые ветки просвечивал водянистый свет. Петя встряхнулся, вскочил, вынул из кармана девственницу и подал Лихачеву, помахивая ею, попробовал шашку и вложил ее в ножны. Казаки отвязали лошадей и подтянули подпруги.
 – Вот командир, – сказал Лихачев. Денисов вышел из караульного помещения и, окликнув Петю, приказал собираться.

В темноте быстро разобрали лошадей, подтянули подпруги и разобрались с командами. Денисов стоял у гауптвахты, отдавая последние распоряжения. Пехота партии, шлепнув сотни футов, двинулась вперед по дороге и быстро скрылась между деревьями в предрассветном тумане. Есаул приказал что-то казакам. Петя держал свою лошадь на всякий случай, жадно ожидая приказа сесть. Вымытое холодной водой, лицо его, особенно глаза, горело огнем, по спине пробегал озноб, и что-то быстро и равномерно тряслось по всему телу.
  «Ну что, все готово для тебя?» — сказал Денисов. — Давай, кони.
  Лошадей накормили. Денисов рассердился на казака за то, что подпруга слаба, и, разобрав ее, сел. Петя взялся за стремя. Лошадь по привычке хотела укусить его за ногу, но Петя, не чувствуя своего веса, быстро вскочил в седло и, оглядываясь на шедшего сзади в темноте гусара, подъехал к Денисову.
 — Василий Федорович, вы мне что-нибудь доверите? Пожалуйста… ради бога… — сказал он. Денисов как будто забыл о существовании Пети. Он оглянулся на него.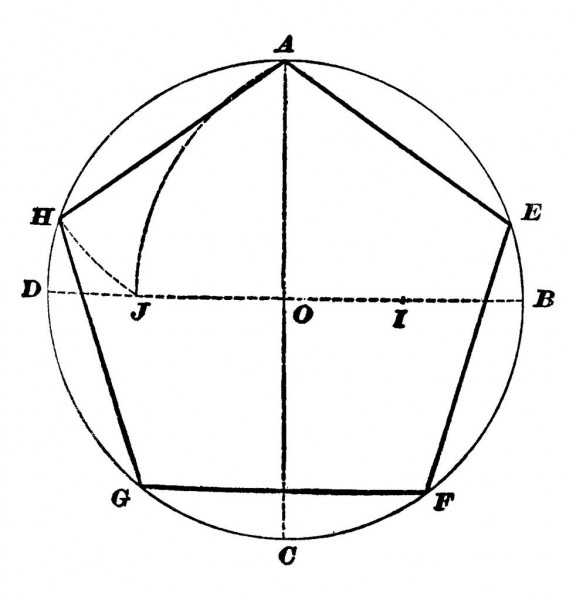
  «Насчет вас г о у о о, он строго сказал,» слушаться меня и никуда не соваться.
  За все время перегона Денисов больше ни слова не сказал с Петей и ехал молча. Когда мы приехали на опушке леса поле уже заметно посветлело.Денисов шепотом заговорил с есаулом, и казаки стали проходить мимо Пети и Денисова.Когда все погнали, Денисов тронул коня и поскакал под гору.Садясь на свои задом и скользя, кони спускались со своими всадниками в лощину. Петя ехал рядом с Денисовым. Дрожь во всем его теле усиливалась. Становилось все светлее и светлее, только туман скрывал далекие предметы. Съехав вниз и оглянувшись, Денисов кивнул головой стоявшему рядом казаку.0133  — Сигнал! Он сказал.
Казак поднял руку, раздался выстрел. И в то же мгновение перед скачущими лошадьми раздался топот, крики с разных сторон и еще выстрелы.
 В ту же минуту, как послышались первые звуки грома и крика, Петя, ударив лошадь и отпустив вожжи, не слушая кричащего на него Денисова, поскакал вперед. Пете показалось, что вдруг, как среди дня, ярко рассвело, как только раздался выстрел. Он прыгнул на мост. Казаки скакали вперед по дороге. На мосту он столкнулся с отсталым казаком и поскакал дальше. Впереди какие-то люди — должно быть, это были французы — бежали с правой стороны дороги налево. Один упал в грязь под ноги Петиной лошади.
  Казаки столпились в одной избе, что-то делали. Из середины толпы раздался страшный крик. Петя подскочил к этой толпе, и первое, что он увидел, было лицо француза, бледное, с трясущейся нижней челюстью, державшегося за направленные на него пики.
  «Ура! .. Ребята… наши… — закричал Петя и, отдав поводья пылающему коню, поскакал вперед по улице.
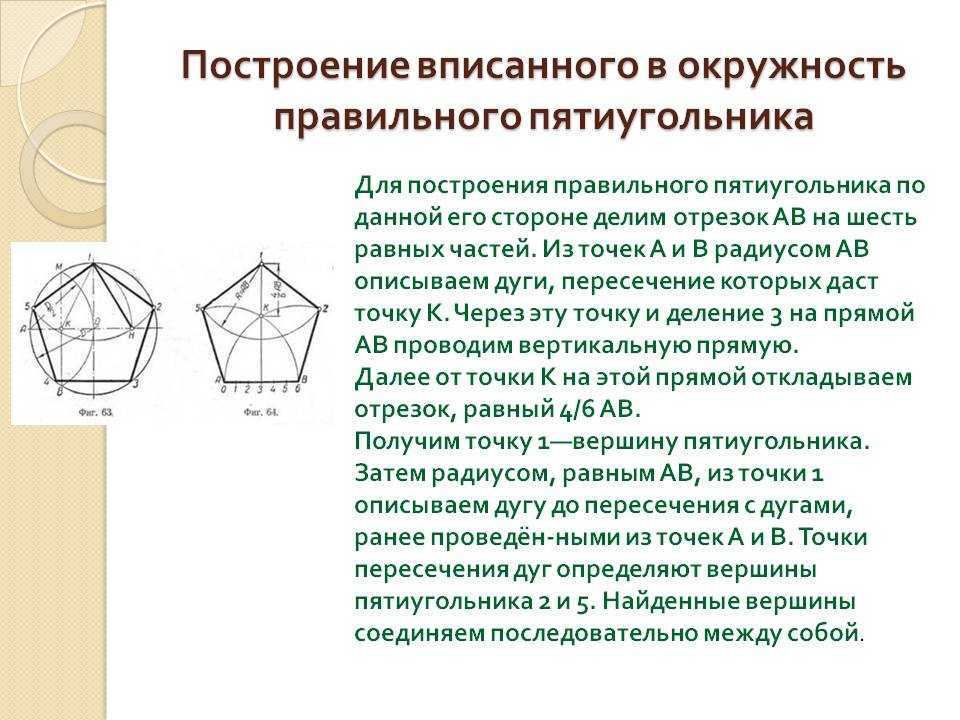  Впереди раздались выстрелы. Казаки, гусары и русские оборванные пленные, бежавшие с обеих сторон дороги, все кричали громко и неловко. Молодой, без шапки, с красным нахмуренным лицом, француз в синей шинели штыком отбивался от гусар. Когда Петя прыгнул, француз уже упал. Опять опоздал, мелькнуло у Пети в голове, и он поскакал обратно туда, откуда слышались частые выстрелы. Во дворе того дворянского дома, где он был с Долоховым прошлой ночью, раздались выстрелы. Французы устроились там за плетнем в густом, заросшем кустарником саду и стреляли по казакам, столпившимся у ворот. Подойдя к воротам, Петя в пороховом дыму увидел Долохова с бледным, зеленоватым лицом, что-то кричавшего людям. «Обход! Подожди пехоту! — кричал он, пока Петя подъезжал к нему.
«Подождать? .. Ураааа! — вскричал Петя и, не медля ни минуты, поскакал к тому месту, откуда были слышны выстрелы и где пороховой дым был гуще. Раздался залп, визг пустых и шлепающие во что-то пули. Казаки и Долохов последовали за Петей в ворота дома. Французы, в колышущемся густом дыму, одни бросали оружие и выбегали из кустов навстречу казакам, другие бежали вниз по склону к пруду. Петя ехал верхом по барскому двору и, вместо того чтобы держать поводья, странно и быстро махал обеими руками и все дальше и дальше отходил от седла в сторону. Лошадь, наткнувшись на тлеющий в утреннем свете костер, отдохнула, и Петя тяжело упал на мокрую землю. Казаки видели, как быстро дергались его руки и ноги, несмотря на то, что голова не двигалась. Пуля пробила ему голову.
 Поговорив со старшим французским офицером, подошедшим к нему из-за дома с шарфом на шпаге и объявившим, что они сдаются, Долохов слез с коня и подошел к распростертому Пете с оружием в руках протянутый.
 — Готово, — сказал он, нахмурившись, и пошел через ворота к шедшему к нему Денисову.
 — Убит?! — вскрикнул Денисов, видя издалека то знакомое, несомненно безжизненное положение, в котором лежало тело Пети.
 — Готов, — повторил Долохов, как будто произношение этого слова ему понравилось, и быстро пошел к арестантам, окруженным спешившимися казаками. — Не возьмем! — крикнул он Денисову.

  8 июня 2011 г.

Первый способ   — по эту сторону S с помощью транспортира.

Нарисуйте линию и установите на ней AB = S; возьмем эту прямую за радиус и этим радиусом из точек А и В описываем дуги:   Далее с помощью транспортира строим в этих точках углы 108°, стороны которых пересекаются с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, пересекающиеся в Е, и соединяем прямые линии точки А, С, Е, D, В.

Получившийся пятиугольник  — желаемый.

Второй способ.   Нарисуйте круг радиусом r. Из точки А проводим циркуль дугой радиуса АМ до пересечения в точках В и С с окружностью. Соединяем В и С линией, пересекающей горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, пересекающую горизонтальную линию в точке О. Наконец, из точки F описываем дугу, пересекающую окружность в точках Н и К. Обведя окружность FO = FH = FK пять раз вокруг окружности и соединив точки деления линиями, получим правильный пятиугольник.

Третий способ. Впишите в этот круг правильный пятиугольник. Проведем два взаимно перпендикулярных диаметра АВ и MS. Разделите радиус АО точкой Е пополам. Из точки Е, как из центра, провести дугу окружности радиуса ЕМ и отрезать ее диаметром АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. При растворе циркуля, равном MF, делаем засечки N 1, P 1, Q 1, K 1 и соединяем их прямыми линиями.

На рисунке с этой стороны построен шестиугольник.

Прямая АВ = 5, как радиус, из точек А и В описывает дуги, пересекающиеся в С; из этой точки с таким же радиусом описываем окружность, на сторону которой АВ откладывается 6 раз.

Шестигранник ADEFGB — желательно.

«Отделка помещений под ремонт»,
Н.П. Краснов

Первый способ сборки. Проведем горизонтальную (АВ) и вертикальную (CD) оси и от точки их пересечения М отложим на соответствующей оси соответствующую ось. Прикладываем малую ось от точки М по большой оси к точке Е. Эллипс, первый способ построения. Разделите БЭ на 2 части и нанесите одну из точки М на большой оси (до F или Н)…

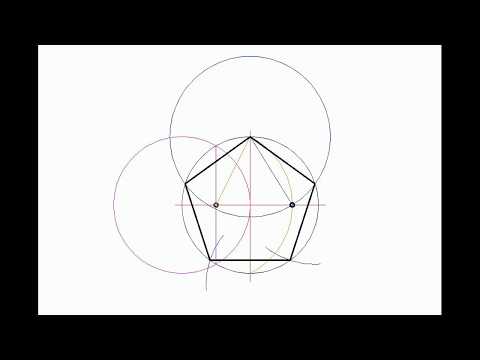
Основанием для нанесения покраски является полностью законченная покраска поверхности стен, потолков и других конструкций; покраска производится по качественному клеевому составу и масляным морилкам, изготовленным под торцовку или флейтц. Приступая к разработке эскиза украшения, мастер должен ясно представить себе всю композицию в бытовой обстановке и ясно понять творческую идею. Только при соблюдении этого основного условия может быть правильным…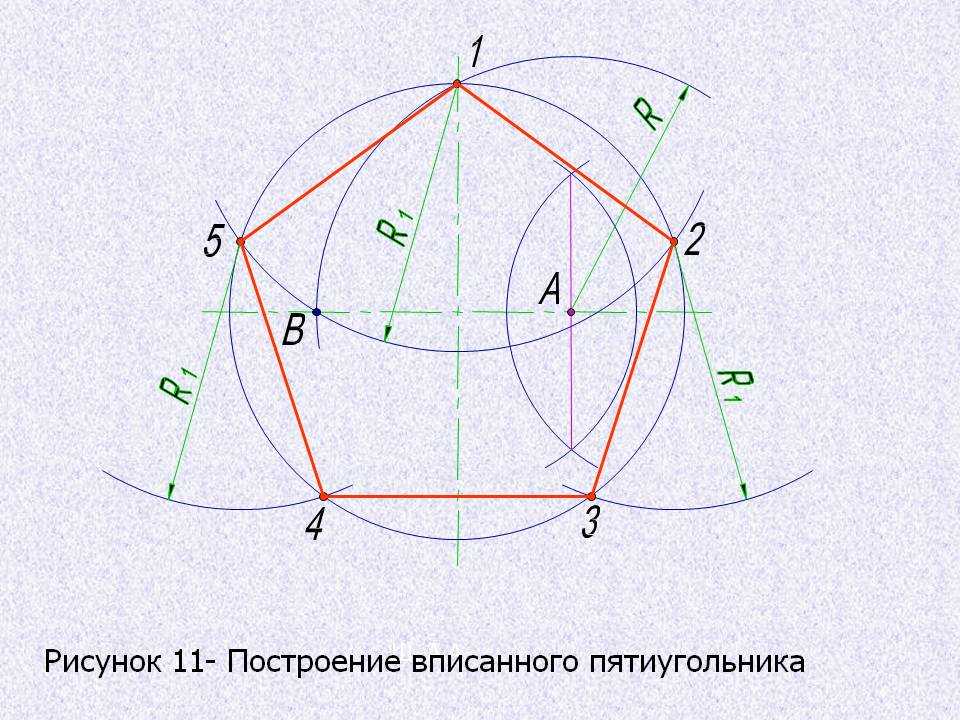

Измерение выполняемых работ, за исключением частных случаев, проводят по площади фактически обрабатываемой поверхности с учетом ее рельефа и минус необработанные места. Для определения реально обрабатываемых поверхностей при покраске следует использовать коэффициенты пересчета, приведенные в таблицах. А. Деревянные оконные устройства (замер производится по площади проемов по наружному контуру коробок) Наименование устройств Коэффициент …

Положительный пятиугольник   Многоугольник, в котором все пять сторон и все пять углов равны друг другу. Вокруг него легко описать круг. Возведите пятиугольника  , и этот конкретный круг поможет.

Руководство по эксплуатации

1.   Прежде всего, вам нужно построить круг с помощью компаса. Пусть центр окружности совпадает с точкой О. Проведите оси симметрии перпендикулярно друг другу. На пересечении одной из этих осей с окружностью поставьте точку V. Эта точка будет вершиной будущей пятиугольник  и. На пересечении другой оси с окружностью позиция D.

2. На отрезке OD найдите середину и отметьте в ней точку А. Позже вам нужно нарисовать круг с центром в этой точке. Кроме того, он должен проходить через точку V, то есть с радиусом CV. Точку пересечения оси симметрии и этой окружности обозначим В.

3.   Далее этим циркулем   начертите окружность такого же радиуса, поместив стрелку в точку V. Обозначьте пересечение этой окружности с исходной точкой F. Эта точка будет 2-й вершиной будущего верного пятиугольник  и.

4.   Теперь нужно провести такой же круг через точку E, но с центром в F. Обозначим пересечение только что начерченного круга с исходным как G. Эта точка также станет одной из вершин пятиугольника   и. Аналогичным образом нужно построить еще один круг. Его центр находится в G. Пусть это будет точка пересечения с исходной окружностью. Это последняя вершина правильного многоугольника.

5.   Должно получиться пять пиков. Осталось легко соединить их в строчку. В результате всех этих операций у вас получится вписанный в круг 9 позитив.0004 пятиугольник .

Построение положительных пятиугольников   Разрешено с поддержкой компаса и линейки. Правда, процесс довольно долгий, как, впрочем, и построение любого положительного многоугольника с нечетным числом сторон. Современные компьютерные программы позволяют сделать это за несколько секунд.

Вам понадобится

• — Компьютер с AutoCAD.

Руководство по эксплуатации

1.   Найдите в AutoCAD верхнее меню и вкладку «Главное». Щелкните по нему левой кнопкой мыши. Появится панель рисования. Появятся различные типы линий. Выберите замкнутую полилинию. Это полигон, осталось только ввести параметры. AutoCAD Позволяет правильно рисовать различные полигоны. Количество сторон может достигать 1024. Разрешается использовать командную строку, в зависимости от версии набрав «_polygon» или «multi-angle».

2.   Независимо от того, используете ли вы командную строку или контекстное меню, на экране появится окно с просьбой ввести количество сторон. Введите туда цифру «5» и нажмите Enter. Вас попросят определить центр пятиугольника. Вбейте в появившееся окно координаты. Допускается их обозначать как (0,0), но могут быть и любые другие данные.

3. Выберите нужный метод построения. . AutoCAD предлагает три варианта. Пятиугольник можно описать вокруг окружности или вписать в нее, но допускается строить его по заданному размеру стороны. Выберите нужный вариант и нажмите Enter. При необходимости укажите радиус окружности и также нажмите ввод.

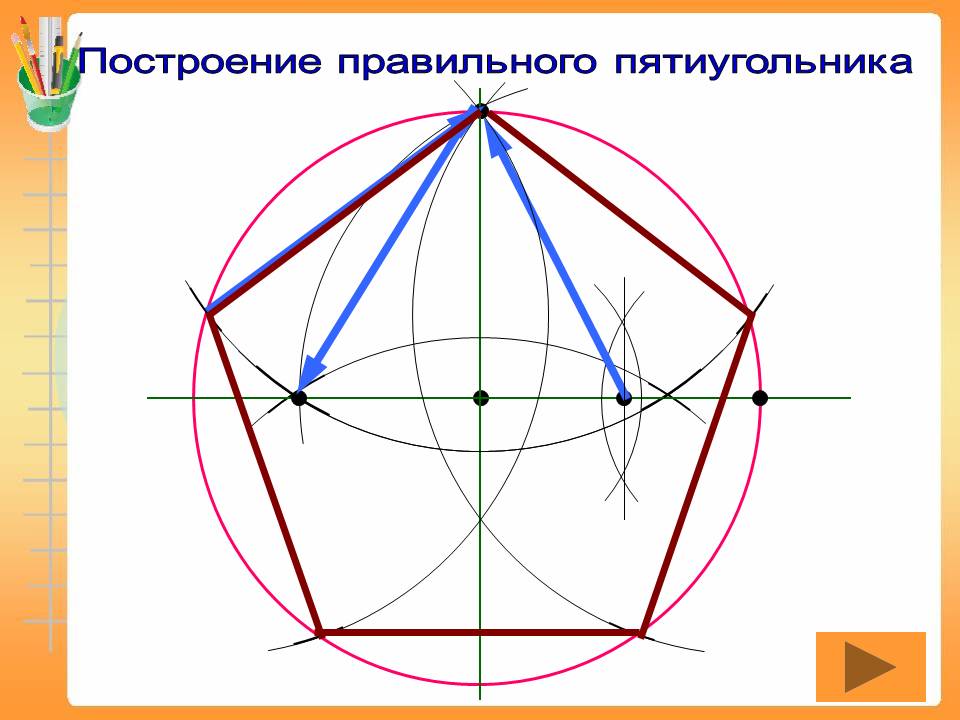4.   Пятиугольник на данной стороне первоначально построен точно так же. Выберите Нарисовать замкнутую полилинию и введите количество сторон. Щелкните правой кнопкой мыши, чтобы вызвать контекстное меню. Нажмите край или боковую команду. В командной строке введите координаты исходной и конечной точек одной из сторон пятиугольника. Позже этот пятиугольник появится на экране.

5.   Все операции можно выполнять с помощью командной строки. Скажем, для построения пятиугольника сбоку в русской версии программы введите букву «с». В английской версии это будет «_e». Чтобы построить вписанный или описанный пятиугольник, введите позже количество сторон буквы «o» или «b» (или английское «_c» или «_i»)

Видео по теме

Видео по теме

Полезный совет
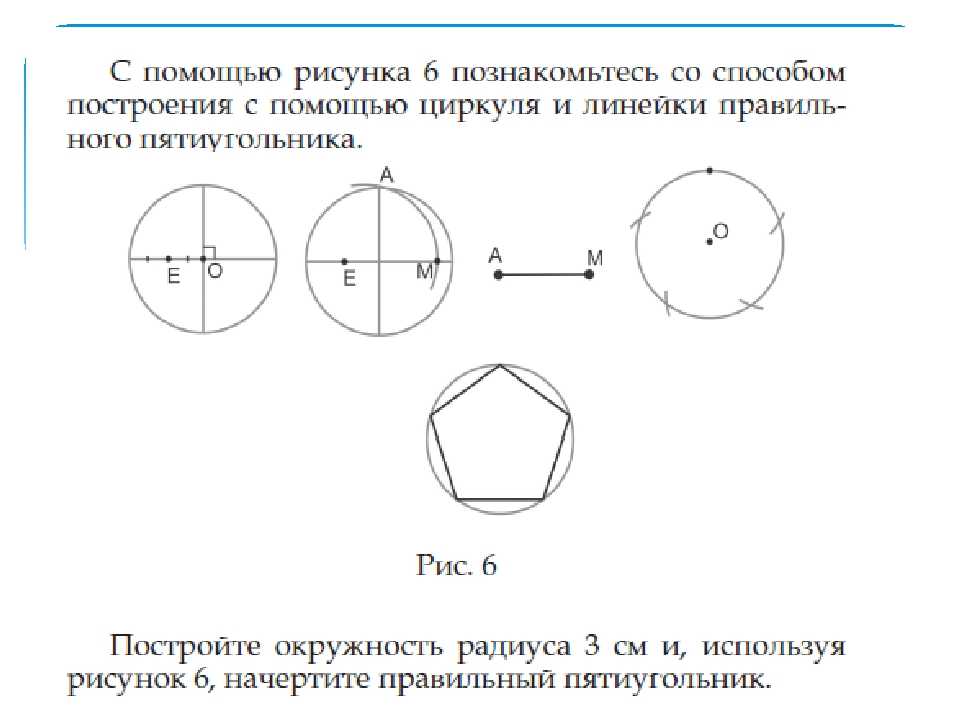  Этот простой метод позволяет построить не только пятиугольник. Для того, чтобы построить треугольник, нужно развести ножки циркуля на расстояние, равное радиусу окружности. После этого установите иглу в любой точке. Нарисуйте тонкий опорный круг. Две точки пересечения окружностей, а также точка, в которой находилась катетка циркуля, образуют три вершины положительного треугольника.

Построение правильных многоугольников

Построение правильных многоугольников

Построение правильных многоугольников Правильный многоугольник проще всего построить в виде шестиугольника. Чтобы построить шестиугольник, используйте циркуль, чтобы нарисовать круг. Теперь (удерживая компас в той же точной настройке), поместите точку компаса на окружность и начертите дугу на окружности. Далее поместите компас точка в только что нарисованной дуге и ударить по другой дуге. Делайте это, пока не нарисуете шесть дуг. (См. рис. 1). Теперь возьмите линейку и проведите линии от одной дуги к другой. 6 линий, которые вы только что нарисовали, — это сторон правильного шестиугольника. (См. рис. 2). Шестиугольник — это только случай, когда стороны многоугольника точно равны радиусу, но с помощью циркуля, линейки и калькулятора ниже можно построить правильные многоугольники с помощью .0146 любое количество сторон. И Н С Т Р У К Ц И Я Допустим, мы хотим построить пятиугольник. Начните с рисования круга с помощью циркуля. (См. рис. 3) Радиус можно не чертить, а измерить его как можно точнее. (Мы измерили радиус 6,70 см.) Используя калькулятор, мы определяем длину каждой стороны пятиугольника (линия AB), введя «стороны многоугольника» 5 , «радиус = 6,70» и затем нажав «РАССЧИТАТЬ». Калькулятор генерирует 3 числа. Для этой конструкции нам нужно число «сторона многоугольника =», равное 7,8765. Теперь как можно точнее установите ширину компаса на 7,8765 см (хорошо, 7,88 см более чем достаточно), поместите компас на точку в точке А и прочертите дугу в точке В. 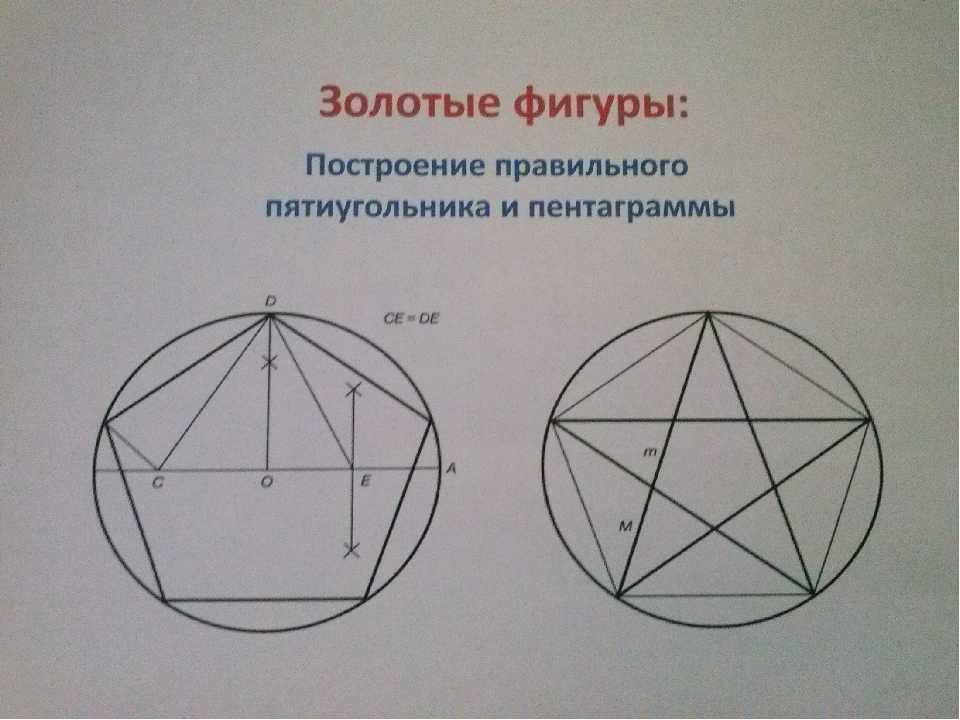Затем, продолжая от точки В, ударить еще 4 дуги. Используя линейку, нарисуйте стороны многоугольника от одной дуги к другой, и вы только что построили правильный пятиугольник! (см. рис. 4) Уравнение, используемое в этом калькуляторе Допустим, вы хотите построить пятиугольник. Начните с рисования круга. Глядя на график, нам нужно рассчитать, какой длины будет каждая сторона (красная линия). Как можно точнее измерьте радиус. (Для этого примера допустим, что это 9,5 см). Из тригонометрии мы знаем, что синус (36°) = ½ стороны ÷ радиус ½ стороны = 0,58779 × 9,5 ½ стороны = 5,5840· Следовательно, каждая сторона = 2 * 5,584 = 11,168 см Итак, уравнение для расчета длины стороны многоугольника: длина = 2 × радиус × синус (n) где n = 180° ÷ количество сторон многоугольника Значимые цифры >>> Для удобства чтения ответы отображаются в формате «значащая цифра», чтобы вы могли , а не см. Prev post Роликовые направляющие для выдвижных ящиков: Мебельные направляющие для выдвижных ящиков. Обзор роликовых, шариковых и скрытых направляющих для кухни и шкафов Next post Домик кровать для девочки: - 10990 mebHOME. 40%. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт