Пятиугольник как построить циркулем: Построение пятиугольника подробно. — Чертежик

Циркуль и линейка

На развитие теории уравнений сильное вли­яние оказали задачи о построениях циркулем и линейкой, в особенности задачи о построении правильных многоугольников. Из школьного курса известно, как строить циркулем и ли­нейкой правильный треугольник, квадрат и шестиугольник. В более подробных курсах рассказано о построении правильного пяти­угольника. А вот о построении правильного семиугольника или девятиугольника ничего не говорится. И это не случайно: ни правиль­ный семиугольник, ни правильный девятиугольник нельзя построить циркулем и линейкой.

Как же это узнали? Ведь доказать разре­шимость задачи сравнительно легко — доста­точно указать путь ее решения. Доказать же, что задачу нельзя решить, очень трудно. Путей решения задачи бесконечно много (мало ли какие построения можно придумать!), и дока­зать, что ни один из них не приведет к цели, на первый взгляд невозможно.

Однако математики справились с этой за­дачей. Для этого они сначала исследовали во­прос, какие отрезки можно построить цир­кулем и линейкой исходя из одного заданного отрезка (в случае построения правильного многоугольника заданным является радиус описанной окружности или сторона искомого правильного многоугольника).

Чтобы ответить на этот вопрос, пришлось ввести понятие квадратичной ирра­циональности. Так назвали числа, которые получаются из единицы с помощью четырех арифметических действий и операции извлечения квадратного корня. Вот для при­мера некоторые числа, являющиеся квадратич­ными иррациональностями:

 

 

 Все квадратичные иррациональности, вместе взятые, образуют числовое поле, при­чем в этом поле всегда выполнима операция извлечения квадратного корня из положитель­ного числа.

Было доказано, что если задан отрезок а, длина которого принимается за единицу, то циркулем и линейкой можно построить любые отрезки, длины которых являются квадратич­ными иррациональностями, и только эти от­резки.

Например, для построения правильного пя­тиугольника с данной стороной достаточно по­строить его диагональ (тогда все вершины можно будет найти с помощью засечек окружности). Расчеты показывают, что если сторона пяти­угольника равна 1, то его диагональ имеет длину

 

Так как это число является квадра­тичной иррациональностью, то построение пра­вильного пятиугольника с помощью циркуля и линейки возможно.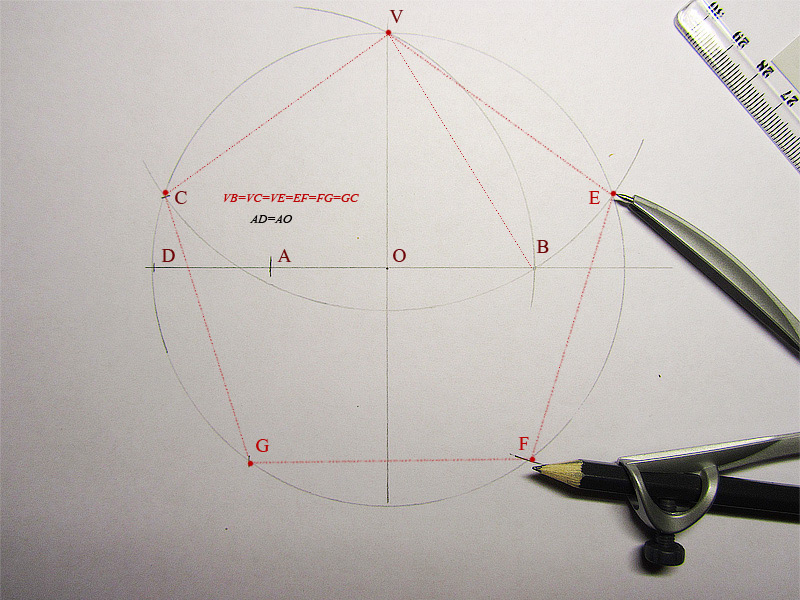
А вот правильный девятиугольник постро­ить нельзя. Его построение сводится к делению угла в 120° на три равные части. По формулам тригонометрии:

то для отыскания cosφ получим кубическое уравнение:

или, полагая 2cosφ=x, получим уравнение:

Было доказано, что если один из корней кубического уравнения с целыми коэффици­ентами является квадратичной иррациональ­ностью, то у него есть и рациональный корень. А легко доказать, что у уравнения (3) раци­ональных корней нет, значит, нет и корней, являющихся квадратичными иррациональностями. Поэтому и нельзя построить правиль­ный девятиугольник циркулем и линейкой. (Поскольку угол в 120° нельзя разделить цир­кулем и линейкой на три равные части, тем более нельзя указать метод деления циркулем и линейкой на три равные части для произ­вольного угла. Для некоторых углов, например 90°, эта задача разрешима.) Точно так же дока­зывается невозможность построения циркулем и линейкой правильного семиугольника.

Окончательное решение вопроса о постро­ении правильных многоугольников циркулем и линейкой дал в 1796 г. Гаусс. Он доказал, что если р — простое число, то правильный р-угольник с данной стороной может быть построен циркулем и линейкой в том, и только в том, случае, когда число

р можно записать в виде р=2²ⁿ +1, где n — целое число. Напри­мер, при n=0 имеем р=3, а при n=1 име­ем р=5. Поэтому правильный треугольник и правильный пятиугольник можно построить циркулем и линейкой. При n=2 получаем р=17. Значит, и правильный семнадцатиугольник строится циркулем и линейкой. Мож­но построить циркулем и линейкой даже правильные многоугольники с 257 и 65536 сторонами. А вот при n=5 число 2²ⁿ+1 оказывается составным. Поэтому правильный

 

 -угольник нельзя построить циркулем и линейкой.

В древности математики потратили много сил на решение следующей задачи об удвое­нии куба: дан куб со стороной а; построить такой куб, объем которого вдвое больше объема данного куба. Подсчитаем, какой отрезок надо построить для решения этой задачи. Примем длину отрезка

а за единицу, а длину ребра иско­мого куба обозначим через х. Тогда объем дан­ного куба будет равен единице, а объем иско­мого куба — двум. По условию задачи должно быть: х³=2. Это уравнение не имеет рациональ­ных корней. Поэтому по упомянутой выше теореме у него нет и корней, являющихся квад­ратичными иррациональностями. Значит, ре­шить задачу удвоения куба циркулем и ли­нейкой невозможно.

Гораздо труднее было доказать, что невоз­можно построить циркулем и линейкой квадрат, равновеликий кругу радиуса 1 (задача о квадратуре круга). Это доказа­тельство было проведено неалгебраи­ческими методами. Было доказано, что сторона такого квадрата не только не являетсяквадратичной иррациональностью, но даже не может быть корнем никакого алгебраического уравнения с целыми коэффициентами (такие числа называют неалгебраическими или тран­сцендентными).

Построение с помощью циркуля и линейки

Построения с помощью циркуля и линейки

 — раздел евклидовой геометрии, известный с античных времён. В задачах на построение циркуль и линейка считаются идеальными инструментами, в частности:

• Линейка не имеет делений и имеет сторону бесконечной длины, но только одну.
• Циркуль может иметь сколь угодно большой или сколь угодно малый раствор (то есть может чертить окружность произвольного радиуса).

Содержание 1 Пример 2 Формальное определение 3 Известные задачи 3.1 Построение правильных многоугольников 3.2 Неразрешимые задачи 4 Возможные и невозможные построения 5 Вариации и обобщения 6 Интересные факты 7 См. также 8 Примечания 9 Литература

Пример

Разбиение отрезка пополам

Задача на бисекцию. С помощью циркуля и линейки разбить данный отрезок

AB на две равные части. Одно из решений показано на рисунке:

• Циркулем проводим окружности с центром в точках A и B радиусом AB.
• Находим точки пересечения P и Q двух построенных окружностей (дуг).
• По линейке проводим отрезок или линию, проходящую через точки P и Q.
• Находим искомую середину отрезка AB — точку пересечения AB и PQ.

Формальное определение

В задачах на построение рассматриваются множество всех точек плоскости, множество всех прямых плоскости и множество всех окружностей плоскости, над которыми допускаются следующие операции:

1. Выделить точку из множества всех точек:
   1. произвольную точку
   2. произвольную точку на заданной прямой
   3. произвольную точку на заданной окружности
   4. точку пересечения двух заданных прямых
   5. точки пересечения/касания заданной прямой и заданной окружности
   6. точки пересечения/касания двух заданных окружностей
2. «С помощью линейки» выделить прямую из множества всех прямых:
   1. произвольную прямую
   2. произвольную прямую, проходящую через заданную точку
   3. прямую, проходящую через две заданных точки
3. «С помощью циркуля» выделить окружность из множества всех окружностей:
   1. произвольную окружность
   2. произвольную окружность с центром в заданной точке
   3. произвольную окружность с радиусом, равным расстоянию между двумя заданными точками
   4. окружность с центром в заданной точке и с радиусом, равным расстоянию между двумя заданными точками

В условиях задачи задается некоторое множество точек.

Требуется с помощью конечного количества операций из числа перечисленных выше допустимых операций построить другое множество точек, находящееся в заданном соотношении с исходным множеством.

Решение задачи на построение содержит в себе три существенные части:

1. Описание способа построения заданного множества.
2. Доказательство того, что множество, построенное описанным способом, действительно находится в заданном соотношении с исходным множеством. Обычно доказательство построения производится как обычное доказательство теоремы, опирающееся на аксиомы и другие доказанные теоремы.
3. Анализ описанного способа построения на предмет его применимости к разным вариантам начальных условий, а также на предмет единственности или неединственности решения, получаемого описанным способом.

Известные задачи

• Задача Аполлония о построении окружности, касающейся трех заданных окружностей. Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.
• Задача Брахмагупты о построении вписанного четырехугольника по четырем его сторонам.

Построение правильных многоугольников

Основная статья: Теорема Гаусса — Ванцеля

Построение правильного пятиугольника

Античным геометрам были известны способы построения правильных n-угольников для , , и .

В 1796 году Гаусс показал возможность построения правильных n-угольников при , где  — различные простые числа Ферма. В 1836 году Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует.

Неразрешимые задачи

Следующие три задачи на построение были поставлены ещё в античности:

• Трисекция угла — разбить произвольный угол на три равные части.
• Удвоение куба — построить ребро куба вдвое большего по объёму, чем данный куб
• Квадратура круга — построить квадрат, равный по площади данному кругу.

Только в XIX веке было доказано, что все три задачи неразрешимы при использовании только циркуля и линейки. Вопрос возможности построения полностью решён алгебраическими методами, основанными на теории Галуа.

• Другая известная неразрешимая с помощью циркуля и линейки задача — построение треугольника по трём заданным длинам биссектрис.^[1] Причём эта задача остаётся неразрешимой даже при наличии трисектора.^[2]

Возможные и невозможные построения

Все построения являются не чем иным, как решениями какого-либо уравнения, причем коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому удобно говорить о построении числа — графического решения уравнения определенного типа. В рамках вышеописанных требований возможны следующие построения:

• Построение решений линейных уравнений.
• Построение решений квадратных уравнений.

Иначе говоря, возможно построить лишь числа равные арифметическим выражениям с использованием квадратного корня из исходных чисел (длин отрезков). Например,

• Если задан только отрезок длины , то невозможно представить в таком виде (отсюда невозможность удвоения куба).
• Возможность построить правильный 17-угольник следует из выражения на косинус угла:

Вариации и обобщения

• Построения с помощью одного циркуля. По теореме Мора — Маскерони с помощью одного циркуля можно построить любую фигуру, которую можно построить циркулем и линейкой. При этом прямая считается построенной, если на ней заданы две точки.
• Построения с помощью одной линейки. Легко заметить, что с помощью одной линейки можно проводить только проективно-инвариантные построения. В частности, невозможно даже разбить отрезок на две равные части, либо найти центр нарисованной окружности. Но при наличии на плоскости заранее проведённой окружности с отмеченным центром с помощью линейки можно провести те же построения, что и циркулем и линейкой (теорема Понселе — Штейнера (англ.)), 1833.

  Если на линейке есть две засечки, то построения с помощью неё эквивалентны построениям с помощью циркуля и линейки (важный шаг в доказательстве этого сделал Наполеон).

• Построения с помощью инструментов с ограниченными возможностями. В задачах такого рода инструменты (в противоположность классической постановке задачи) считаются не идеальными, а ограниченными: прямую через две точки с помощью линейки можно провести только при условии, что расстояние между этими точками не превышает некоторой величины; радиус окружностей, проводимых с помощью циркуля, может быть ограничен сверху, снизу или одновременно и сверху, и снизу.
• Построения с помощью плоского оригами. см. правила Худзита

Интересные факты

• Узор на флаге Ирана описывается как построение с помощью циркуля и линейки^[3].

См. также

• Программы динамической геометрии позволяют выполнять построения с помощью циркуля и линейки на компьютере.

Примечания

1. ↑ Кто и когда доказал невозможность построения треугольника по трем биссектрисам?. Дистанционный консультационный пункт по математике МЦНМО.
2. ↑ Можно ли построить треугольник по трем биссектрисам, если кроме циркуля и линейки разрешается использовать трисектор. Дистанционный консультационный пункт по математике МЦНМО.
3. ↑ Стандарт флага Ирана (перс.)(недоступная ссылка)

Литература

• А. Адлер Теория геометрических построений / Перевод с немецкого Г. М. Фихтенгольца. — Издание третье. — Л.: Учпедгиз, 1940. — 232 с.
• И. И. Александров Сборник геометрических задач на построение. — Издание восемнадцатое. — М.: Учпедгиз, 1950. — 176 с.
• Б. И. Аргунов, М. Б. Балк Геометрические построения на плоскости. Пособие для студентов педагогических институтов. — Издание второе. — М.: Учпедгиз, 1957. — 268 с.
• А. М. Воронец Геометрия циркуля. — М.-Л.: ОНТИ, 1934. — 40 с. — (Популярная библиотека по математике под общей редакцией Л. А. Люстерника).
• В. А. Гейлер Неразрешимые задачи на построение // СОЖ. — 1999. — № 12.  — С. 115—118.
• В. А. Кириченко Построения циркулем и линейкой и теория Галуа // Летняя школа «Современная математика». — Дубна, 2005.
• Ю. И. Манин Книга IV. Геометрия // Энциклопедия элементарной математики. — М.: Физматгиз, 1963. — 568 с.
• Ю. Петерсен Методы и теории решения геометрических задач на построение. — М.: Типография Э. Лисснера и Ю. Романа, 1892. — 114 с.
• В. В. Прасолов Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга. — М.: Наука, 1992. — 80 с. — (Популярные лекции по математике).
• Я. Штейнер Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга. — М.: Учпедгиз, 1939. — 80 с.
• Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 80. — 383 с. — ISBN 5-09-001287-3

Построение пятиугольника

Введение

Геометрическое построение правильного пятиугольника представляет собой интересную задачу. Чтобы иметь возможность построить пятиугольник, нам нужно знать угловые меры вершин и быть в состоянии построить угол вершины или диагонали пятиугольника.

По совпадению, пятиугольник связан с золотым сечением и треугольником 36-72-72. Сначала мы найдем тригонометрические значения треугольника 36-72-72, прежде чем переходить к построению пятиугольника.

Рисунок 1: Равные углыРисунок 2: Равные сегменты

Пентагон

В правильном пятиугольнике, в котором все стороны и углы равны, каждая вершина пятиугольника имеет угловую меру 108°. Так как вершин 5, то сумма всех углов равна 540°. Формула для определения суммы углов S любого правильного многоугольника: \(S = 180n — 360 \), где n — количество сторон. Следовательно, если мы разделим на n , мы получим угловую меру 1 вершины, V : \( V = 180 — \frac{360}{n} \). Для пятиугольника n = 5. Следовательно, мера угла в 1 вершине равна \(V = 180 — \frac{360}{5} = 108 \).

Равнобедренный треугольник 36-72-72 получается, когда мы проводим диагонали пятиугольника. Это особый равнобедренный треугольник, потому что он связан с золотым сечением.

Рисунок 3: Пентагон

Золотое сечение

На рисунке 1 показан равнобедренный треугольник 36-72-72. Если разделить пополам один из тупых углов, равных 72°, то получится такой же меньший треугольник, равнобедренный по подобию. Если мы позволим 92}}{2} \)  (Решение квадратного уравнения для y )

(v) \( y = \frac{x \pm x\sqrt{5}}{2} \)

(vi) \( y = \frac{1 + \sqrt{5}}{2}x \)  (Отбрасывая отрицательную длину и разлагая на множители x )

Значение \( \frac{1 + \sqrt{5}}{ 2} \) — это золотое сечение. В треугольнике 36-72-72 отношение стороны к основанию ( х к х ) является золотым сечением.

Если вместо этого мы найдем x , то получим \( x = \frac{-1 + \sqrt{5}}{2}y \). Значение \( \frac{-1 + \sqrt{5}}{2} \) является обратным значением золотого сечения. 9{\circ} = \frac{\sqrt{10-2\sqrt{5}}}{4} \).

Мы также можем найти значения для 18°, 54° и 72°, которые являются кратными или делителями 36°. Точные значения приведены в таблице здесь: Angle Meausres and Area.

Построение золотого сечения

Мы должны построить треугольник 36-72-72, чтобы построить пятиугольник. Для этого нам нужно построить золотое сечение.

Вот шаги по построению золотого сечения вкратце, прежде чем мы построим пятиугольник:

1. Постройте прямоугольник со сторонами 1 и 2.
2. Постройте диагональ этого прямоугольника. Диагональ будет иметь длину \(\sqrt{5}\).
3. Увеличьте диагональ на 1 единицу, чтобы общая длина была равна \( 1 + \sqrt{5} \).
4. Найдите середину, чтобы отрезок был разделен пополам на длины \(\frac{1+\sqrt{5}}{2} \).

Теперь мы пройдем этапы строительства. Обратите внимание, что вместо настоящего компаса и линейки я буду использовать Geogebra для изображений. Поэтому для построения эквивалентных длин я буду рисовать полные круги. Если бы мы делали это на бумаге, мы бы на самом деле рисовали частичные круги или дуги круга вместо полного круга.

Кроме того, на изображениях не показаны некоторые основные этапы строительства. Подразумевается, что читатель знаком с основами геометрических построений.

Этапы построения

Набор шагов 1: прямоугольник, диагональ и золотое сечение

Набор шагов 1. В первом наборе шагов постройте прямоугольник со сторонами 1 и 2. Затем постройте одну диагональ прямоугольник, OA, который будет иметь длину \(\sqrt{5}\). Затем в одном углу (A на изображении) удлините диагональ на 1 единицу, используя сторону прямоугольника длиной 1 единица. Назовем эту точку B. Следовательно, OB будет иметь длину \(1+\sqrt{5}\). Наконец, разделите отрезок OB пополам, найдя его середину. Мы назовем середину C. Следовательно, OC будет иметь длину \(\frac{1+\sqrt{5}}{2}\), золотое сечение.

Набор шагов 2: Равнобедренный треугольник

Набор шагов 2: В следующем наборе шагов нарисуйте круг с радиусом OC и центром в точке O. Затем нарисуйте еще один круг с радиусом 1 единица и центром в точке C. Вы можете использовать сторона AV ₁ на длину 1. Две окружности пересекутся в точке D. OC и OD будут катетами треугольника 36-72-72, а CD будет основанием.

Шаг 3: Равнобедренный треугольник

Шаг 3: Затем нарисуйте отрезки DC и OD. Затем нарисуйте круг с радиусом DC и центром в D. Этот круг будет пересекать сторону OC в точке E, делая DC и DE равными. В качестве альтернативы вы можете просто разделить угол ODC пополам. В любом случае вы получите два одинаковых треугольника 36-72-72, как на рисунках 1 и 2.

Набор шагов 4: Пятиконечная звезда

Набор шагов 4: Затем нарисуйте окружность с радиусом DO и центром в D. Окружность пересечет линию, содержащую отрезок ED, в точке F. Затем соедините F и H, пересечение окружности D со стороной OD. Он будет пересекать D в точке G. FG будет параллелен CD.

После этого шага вершины пятиугольника должны быть видны. И мы действительно можем нарисовать пятиконечную звезду.

Шаговый набор 5: Завершение Пентагона

Шаговый набор 5: Наконец, чтобы закончить построение, просто соединим отрезки OF, FC, DG и GO. Я показал размеры углов всех вершин с помощью Geogebra, подтверждая, что у нас есть правильный пятиугольник. Набор шагов 5 показывает пятиугольник с исходным прямоугольником, с которого мы начали.

PPT – Построение правильного пятиугольника Презентация PowerPoint | скачать бесплатно

Об этой презентации

Стенограмма и заметки докладчика

Название: Построение правильного пятиугольника

1
Построение правильного пятиугольника
Const. Пент. стр. 1 из 10. A.French 2012

• Dr Andrew French

2
Const. Пент. стр. 2 из 10. A.French 2012
y

• Строительные средства, позволяющие рисовать линии
  с использованием следующего оборудования
• Линейка
• Циркуль

O
x
R
Шаг 1 Нарисуйте круг и разделите это вертикально
и горизонтально, чтобы сформировать оси y и x. Используйте
метод деления линии пополам, чтобы найти ось х,
учитывая ось у.
3
Пост. Пент. стр. 3 из 10. A.French 2012
y
Шаг 2. Постройте круг с половиной радиуса
большего круга. Найдите центр этого круга 90 141, разделив пополам линию OX, как показано.
O
X
x
R
4
Пост. Пент. стр. 4 из 10. A.Французский 2012
y
O
x
R
Шаг 3. Проведите линию от основания большего круга
и через центр меньшего
круг. Найдите, где это пересекает верхний край
меньшего круга.
5
Пост. Пент. стр. 5 из 10. A.French 2012
y
K
O
x
R
Шаг 4. Нарисуйте дугу большого круга с радиусом
от основания первого круга до точки пересечения малого круга
, найденной в шаге 3 , Найдите 90 141 позицию K, где это пересекает исходный круг.
6
Пост. Пент. стр. 6 из 10. A.French 2012
Шаг 5 Проведите прямую линию от
пересечение оси Y и исходной окружности
и точка пересечения K, найденная на шаге 4.
Это ребро правильного пятиугольника! Используйте компас
, чтобы обойти исходный круг и найти
остальные три точки. Чтобы свести к минимуму последствия
ошибок рисования, определите нижние вершины
из пересечения левой и правой большой дуги окружности
, а не обходите с помощью компаса
только с одной стороны.
г
К
О
х
7
Пост. Пент. стр.7 из 10. A.French 2012
y
O
x
R
это решение
8
Const. Пент. стр. 8 из 10. A.French 2012
y
O
x
Теорема о круге
Теперь давайте рассмотрим правильный пятиугольник
отдельно. Чтобы продемонстрировать, почему конструкция
работает, нам нужно выражение для стороны треугольника
k, полученное только из свойств правильного пятиугольника
. то есть независимо от конструкции.
Если все устраивает, то конструкция работает!
9
Пост. Пент. стр.