Пятиугольник рисунок: Правильный пятиугольник или звезда без транспортира.

Содержание

Правильный пятиугольник или звезда без транспортира.



Поделиться:

Правильный пятиугольник.
Давайте попробуем сделать такую форму без транспортира, при помощи складывания определённым образом листа бумаги, линейки , карандаша и ножниц.

Берём квадрат из цветного лста бумаги и складываем его пополам по намеченной линии А А1.

В полученном прямойгольнике на глаз или при помощи линейки делим короткую сторону на три части. Получаем точку В.

Поднимаем угол А и совмещаем с точкой В.
Воспользовавшись краем линейки или просто ногтём проглаживаем получившийся сгиб.

Теперь угол D отводим к центру и приминаем сгиб по линии ВС.

Приподнимаем угол F и совмещаем с отрезком ВС, проглаживаем сгиб.

Для того, чтобы более чётко видеть дальнейшую линию среза, поменяем местами угол F, он будет под углом D.

На глаз или начертив по линейке отрезок D F, отрезаем лишнее. Так мы получим правильный пятиугольник, изображённый на первом фото.
Если же вам нужна звезда, то немного изменяем угол отреза из точки D в точку Н. Получим новую линию отреза — FH.

Правильная плоская звезда готова.
Если вы хотите звезду с ещё более узкими лучами, соответственно придётся ещё немного сместиться к центру в точке С.

А если поверх исходной пятиугольной формы, подобрав округлый предмет, нарисовать полукружия, то такую форму можно тспользовать для создания быстрого шаблона при изготовлении «Шарика на все случаи жизни».
https://stranamasterov.ru/node/91485

Получается вот такая заготовка. Быстро и просто!

Всё, маленький экспресс МК готов!

Такие звёзды можно использовать при изготовлении открыток на 9-ое Мая или 23 февраля, а также, как контурная основа под торцевание на звездочке.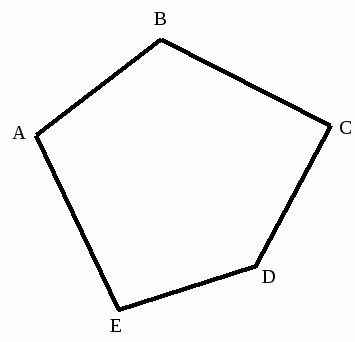

Такой  пятиугольный шаблон пригодится для создание шкатулочек с донышком и крышкой нетрадиционной формы, а также для изначальной формы под некоторые складушки-оригами и заполнения пятиугольной формы в технике изонити.

У Стеллы Филатовой есть вот такой способ вырезания правильного пятиугольника

https://stranamasterov.ru/node/52556?tid=451%2C560

А у Марии — похожий, но немного другой  https://stranamasterov.ru/node/72087

Пятиугольник — Википедия. Что такое Пятиугольник

Пятиугольник — многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы.

Площадь пятиугольника без самопересечений, заданного координатами вершин, определяется по общей для многоугольников формуле.

Выпуклым пятиугольником называется пятиугольник, такой, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. {\circ }}

Любые 9 точек в общем положении содержат вершины выпуклого пятиугольника, и существует множество из 8 точек в общем положении, в котором нет выпуклого пятиугольника[1]. Доказано также, что любые 10 точек на плоскости в общем положении содержат выпуклый пустой пятиугольник, и существует множество из 9 точек в общем положении, в котором нет выпуклого пустого пятиугольника[2].

Правильный пятиугольник

Пентагоном или правильным пятиугольником называется пятиугольник, у которого все стороны и углы равны. Если провести в пентагоне диагонали, то он разобьётся на

[3]:

  • меньший пентагон (образуеся точками пересечения диагоналей) — в центре
  • Вокруг меньшего пентагона — пять равнобедренных треугольников двух видов (с отношением бедра к основанию, равным золотой пропорции):
    • 1) имеют острые углы в 36° при вершине и острые углы в 72° при основании
    • 2) имеют тупой угол в 108° при вершине и острые углы в 36° при основании

При соединении двух первых и двух вторых треугольников их основаниями получатся два «золотых» ромба (первый имеет острый угол в 36° и тупой угол в 144°).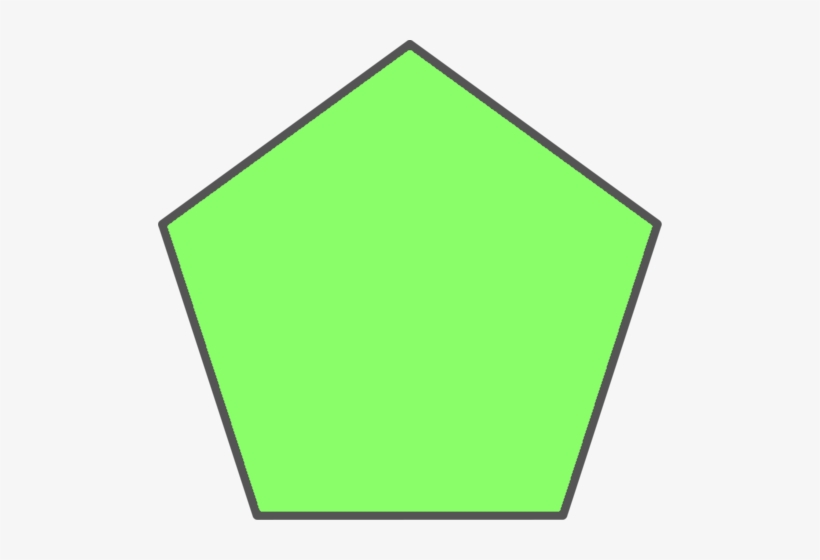 Роджер Пенроуз использовал «золотые» ромбы для конструирования «золотого» паркета (мозаики Пенроуза).

Звездчатые пятиугольники

Многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника называется звёздчатым. Помимо правильного существует ещё один звёздчатый пятиугольник — пентаграмма.

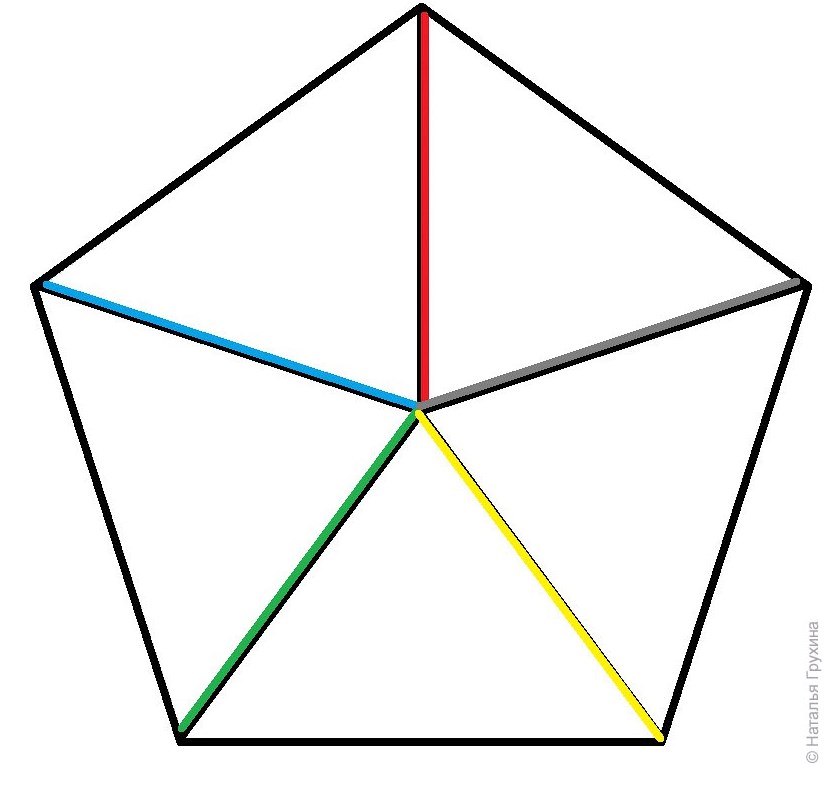
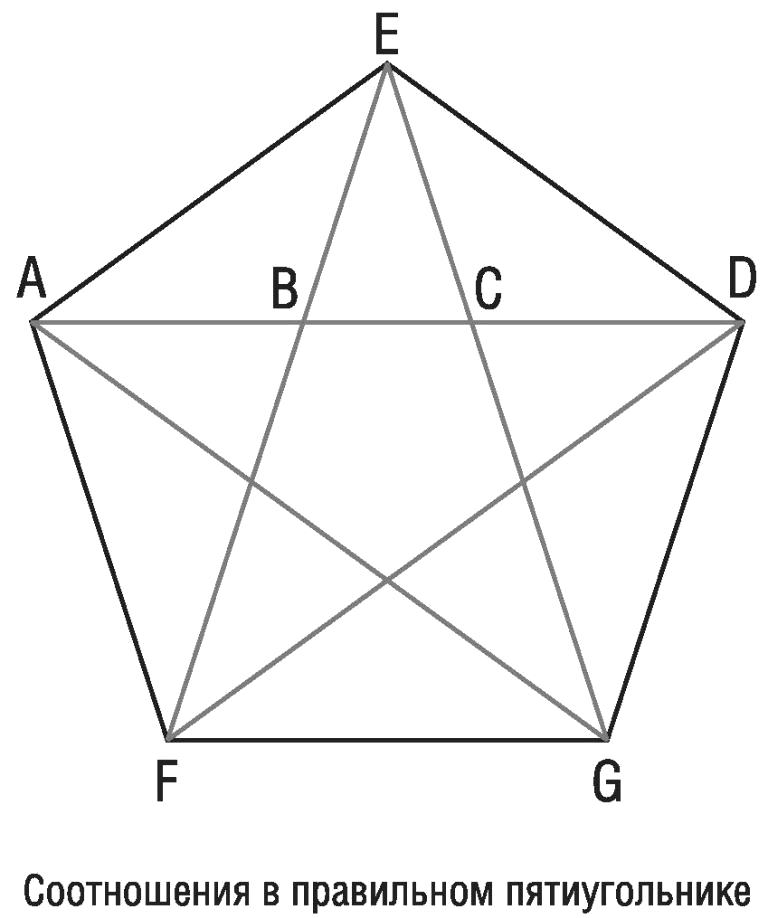
Пентаграмма, как полагал Пифагор, представляет собой математическое совершенство, поскольку демонстрирует золотое сечение (φ = (1+√5)/2 = 1,618…). Если разделить длину любого цветного отрезка на длину самого длинного из оставшихся меньших отрезков, то будет получено золотое сечение φ.

φ=redblue=bluegreen=greenmagenta{\displaystyle \varphi ={\frac {\mathrm {\color {red}red} }{\mathrm {\color {Blue}blue} }}={\frac {\mathrm {\color {Blue}blue} }{\mathrm {\color {Green}green} }}={\frac {\mathrm {\color {Green}green} }{\mathrm {\color {Magenta}magenta} }}}

См. также

Примечания

  1. ↑ Kalbfleisch, J. {\circ }}{2}}t={\frac {\sqrt {5+2{\sqrt {5}}}}{2}}t\approx 1{,}539t}
    • Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
    • Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу 1+52{\displaystyle {\frac {1+{\sqrt {5}}}{2}}}.

    Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

    t=R5−52≈1,17557 R{\displaystyle t=R{\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}17557~R}
    • Радиус вписанной окружности:
    r=55+2510t≈0,688191 t{\displaystyle r={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{10}}t\approx 0{,}688191~t}
    • Радиус описанной окружности:
    R=105+510t=(5−1) r≈0,850651 t≈1,23607 r{\displaystyle R={\frac {{\sqrt {1}}0{\sqrt {5+{\sqrt {5}}}}}{10}}t=({\sqrt {5}}-1)~r\approx 0{,}850651~t\approx 1{,}23607~r}
    d=Φ5R=5+12t≈1,902 R≈1,618 t{\displaystyle d={\sqrt {\Phi {\sqrt {5}}}}R={\frac {{\sqrt {5}}+1}{2}}t\approx 1{,}902~R\approx 1{,}618~t}
    S=55+254t2≈1,72048 t2{\displaystyle S={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}\approx 1{,}72048~t^{2}}
    • Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. {4}=3\Phi +2={\frac {3{\sqrt {5}}+7}{2}}\approx 6{,}8541}
      где Φ{\displaystyle \Phi } — отношение золотого сечения.

      Построение

      Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

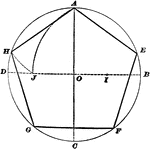
      Вот один из методов построения правильного пятиугольника в заданной окружности:

      1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
      2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
      3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
      4. Постройте точку C посередине между O и B.
      5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
      6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
      7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
      8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
      9. Постройте правильный пятиугольник AEGHF.

      • Построение правильного пятиугольника

      • Построение правильного пятиугольника

      • Построение правильного пятиугольника

      • Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

      Получение с помощью полоски бумаги

      Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

      В природе

      Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.[1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская. Пентасимметрией обладают иглокожие (например морские звёзды) и некоторые растения. См. также Закономерности в природе.

      Интересные факты

      Этот раздел представляет собой неупорядоченный список разнообразных фактов о предмете статьи.

      • Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.
      • Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.
      • Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
      • В природе не существует кристаллов с гранями в форме правильного пятиугольника.
      • Правильный пятиугольник со всеми его диагоналями является проекцией правильного пятиячейника (4-симплекса).

      См. также

      Примечания

      Многоугольники
      Звёздчатые многоугольники
      Паркеты на плоскости
      Правильные многогранники
      и сферические паркеты
      Многогранники Кеплера — Пуансо
      Соты
      Четырёхмерные многогранники
      • {3,3,3}
      • {4,3,3}
      • {3,3,4}
      • {3,4,3}
      • {5,3,3}
      • {3,3,5}

      Итак, вы хотите знать о пятиугольниках?

      В геометрии учащиеся работают с множеством различных форм. Один из самых важных полигонов, с которым нужно познакомиться, — это пятиугольник.

      7 фактов о пятиугольниках, которых вы могли не знать

      1. У всех пятиугольников пять прямых сторон, но стороны не должны быть одинаковой длины.
      2. У правильного пятиугольника пять равных сторон и пять равных углов. В базовой геометрии большинство проблем связано с правильными многоугольниками.
      3. Каждый внутренний угол правильного пятиугольника = 108 градусов.
      4. Каждый внешний угол правильного пятиугольника = 72 градуса.
      5. Сумма внутренних углов правильного пятиугольника = 540 градусов.
      6. Проведение диагональных линий между точками пятиугольника приведет к идеальной форме звезды или пентаграммы.
      7. Если пять сторон фигуры НЕ соединены или у фигуры есть изогнутые стороны, это НЕ пятиугольник.

      Типы пятиугольников

      1. Правильный или равносторонний пятиугольник: пять равных сторон и углов
      2. Неправильный пятиугольник: пять неравных сторон и неравные углы
      3. Выпуклый пятиугольник: внутренний угол не может превышать 180 градусов
      4. Вогнутый пятиугольник: имеет внутренний угол более 180 градусов, из-за чего две стороны «погружаются», как «пещера».

      Части пятиугольника

      1. Сторона: один из пяти отрезков линии
      2. Вершина: две стороны встречаются в точке, называемой вершиной
      3. Диагональ: линия, соединяющая две вершины, которые не являются одной из пяти сторон.
      4. Внутренний угол : внутренний угол, образованный двумя сторонами пятиугольника
      5. Внешний угол : угол на внешней стороне пятиугольника, образованный двумя смежными сторонами

      Как рассчитать площадь пятиугольника

      1. Начало с одной стороны и апофемы *
      2. Разделите пятиугольник на 5 треугольников, проведя 5 линий из центра пятиугольника
      3. Вычислить площадь треугольника **
      4. Умножьте на 5, чтобы найти общую площадь

      * Апофема — это линия от центра пятиугольника к стороне, пересекающая сторону под прямым углом 90º.

      ** Запомните формулу для вычисления площади треугольника: ½ x основание x высота

      Пентагоны — несколько забавных фактов

      Почему Пентагон — это пятиугольник: Штаб-квартира Министерства обороны США в Вашингтоне, округ Колумбия, называется Пентагоном. Это массивное здание из бетона и стали имеет общую площадь почти 7 миллионов квадратных футов и 17,5 миль коридоров. В начале Второй мировой войны в 1941 году президент Рузвельт решил, что для Военного департамента необходимо новое здание.

      Архитектор решил воспользоваться свойствами симметричного пятиугольника. Это сократило расстояние, которое люди должны были бы пройти от одного офиса до другого в этом огромном здании по сравнению с традиционным прямоугольным зданием. Круглое здание также должно было включать более короткие пешеходные расстояния, но построить здание с прямыми сторонами, такими как пятиугольник, было намного проще и быстрее.

      Бамия: В следующий раз, когда вы будете есть жареную бамию или гамбо, взгляните на ломтик бамии. Он имеет форму пятиугольника.

      Морская звезда: Почти все морские звезды имеют пятикратную радиальную симметрию или имеют форму пятиугольника.

      Поэзия: На самом деле существует нечто, известное как поэзия пятиугольника.

      Музыкальные пятиугольники: Если вам нравится музыка 80-х годов, то обратите внимание на группу Pentagon Band Рича Клэра. Для чего-то другого, в Южной Корее есть бойз-бэнд под названием Pentagon.

      Как видите, пятиугольник — очень полезная форма. Мало того, что пятиугольник часто используется в базовой геометрии, это форма, полезная в архитектуре и встречающаяся во всем мире природы.

      чертежей Пентагона на GetDrawings | Бесплатно скачать