Окружности Карлейля, или Как решать квадратные уравнения циркулем и линейкой
Константин Кноп
«Квант» №7, 2020
Казалось бы, какая может быть связь между квадратными уравнениями и геометрическими инструментами — циркулем и линейкой? Однако эта связь есть, и ее исследование с разных сторон — увлекательнейшая задача, тесно связанная и с геометрией, и с алгеброй.
А при чем тут Томас Карлейль? Согласно Википедии, это британский писатель, публицист, историк и философ, автор многотомных сочинений «Французская революция» (1837), «Герои, почитание героев и героическое в истории» (1841), «История жизни Фридриха II Прусского» (1858–1865). О его занятиях математикой практически ничего не известно, и тем не менее, в честь него назван класс окружностей, помогающих решать квадратные уравнения.
А теперь — обо всем по порядку.
Что мы подразумеваем под решением уравнений циркулем и линейкой?
В школьных учебниках геометрии есть какие-то упоминания о возможности построения квадратичных иррациональностей с помощью геометрических инструментов, но в основном не в виде практических алгоритмов построения, а в качестве теоремы существования. 2\).)
2\).)
Обычно после решения этой задачи в школе говорится, что поскольку мы умеем с помощью циркуля и линейки складывать, вычитать, также умножать и делить (пользуясь теоремой Фалеса), а вот теперь умеем и корни извлекать, то этого уже достаточно для того, чтобы по формулам для корней квадратного уравнения научиться строить отрезки соответствующей длины. Действительно, достаточно. Но ведь дико неудобно!
К счастью, есть и нормальный способ «геометрического» решения квадратных уравнений, известный вот уже более двух веков. Этот способ впервые был описан шотландским математиком и физиком Джоном Лесли в его книге «Элементы геометрии и плоской тригонометрии», изданной в 1809 году. В одном из последующих изданий Лесли добавил сноску о том, что идея этого способа принадлежит его бывшему ученику Томасу Карлейлю.
На рисунке 2, заимствованном из книги Лесли, сформулирована задача: «Построить прямоугольник, равновеликий данному прямоугольнику \(CDFE\), полупериметр которого равен данному отрезку \(BC\)».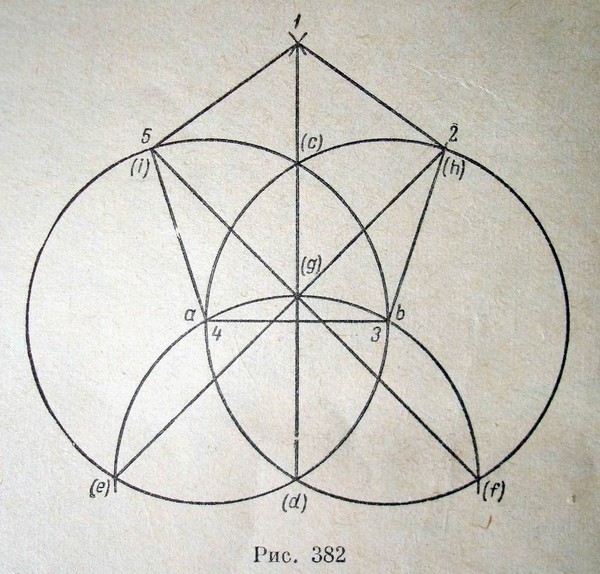 Ее решение, предложенное Карлейлем, показано на рисунке 3. Прокомментируем построение на этом рисунке. Вначале данный отрезок \(BC\) откладывается на продолжении меньшей стороны четырехугольника \((CE)\). Затем на большей его стороне откладывается \(CG=CE\), после чего с помощью параллельных прямых достраивается четвертая вершина прямоугольника \(ABCG\). Теперь достаточно построить окружность на диаметре \(AD\) — точки \(J\) и \(K\) ее пересечения с отрезком \(BC\) и дадут искомые стороны прямоугольника (\(BJ\) и \(JC\) или, как изображено на рисунке, \(BK\) и \(KC=KI\)).
Ее решение, предложенное Карлейлем, показано на рисунке 3. Прокомментируем построение на этом рисунке. Вначале данный отрезок \(BC\) откладывается на продолжении меньшей стороны четырехугольника \((CE)\). Затем на большей его стороне откладывается \(CG=CE\), после чего с помощью параллельных прямых достраивается четвертая вершина прямоугольника \(ABCG\). Теперь достаточно построить окружность на диаметре \(AD\) — точки \(J\) и \(K\) ее пересечения с отрезком \(BC\) и дадут искомые стороны прямоугольника (\(BJ\) и \(JC\) или, как изображено на рисунке, \(BK\) и \(KC=KI\)).
Почему и как это работает? Проще всего ответить на этот вопрос с помощью системы координат. Поместим начало координат в точку \(C\), ось абсцисс направим влево (к \(B\)), а ось ординат вверх (к \(D\)). Кроме того, будем считать, что \(CE=e\), \(CB=b\), \(CD=d\). Тогда координатами точки \(A\) будут \((b;\ e)\), а значит, координатами \(M\) будут \((b/2;\ (d+e)/2)\). Это означает, что окружность с центром \(M\) и радиусом \(MG\ (=MA=MD)\) имеет уравнение
\[\left(x-\frac b2\right)^2+\left(y-\frac{d+e}{2}\right)^2=\left(\frac b2\right)^2+\left(\frac{d-e}{2}\right)^2,\]откуда
\[x^2-bx+\left(\frac b2\right)^2+y^2-(d+e)y+\left(\frac {d+e}2\right)^2=\left(\frac b2\right)^2+\left(\frac{d-e}{2}\right)^2\]и
\[x^2-bx+y^2-(d+e)y+de=0. 2-bx+de=0.\]
2-bx+de=0.\]Как мы знаем из школьной алгебры (теорема Виета), сумма корней этого уравнения равна \(b\), а произведение равно \(de\). Таким образом, если \(K\ (x_1;\ 0)\) и \(J\ (x_2;\ 0)\), то \(CK=CJ=x_1+x_2=b=CB\), а \(CK\cdot CJ=x_1\cdot x_2=de\), т. е. площадь прямоугольника со сторонами \(CK\) и \(BK=CJ\) действительно равна площади исходного прямоугольника \(CDFE\).
То же самое можно было получить и не выписывая уравнения окружности, из чисто геометрических соображений. Ведь \(CK\cdot CJ\) — это произведение длины секущей на ее внешнюю часть, a \(de=CD\cdot CG\) — другое такое же произведение. По теореме о секущих, они равны, т. е. \(CK\cdot CJ=de\). А так как \(ABCD\) — прямоугольная трапеция, а \(M\) — середина ее боковой стороны, то высота в равнобедренном треугольнике \(MJK\) является одновременно средней линией трапеции и медианой в том же треугольнике. Отсюда сразу получаем, что \(CK=BJ\), а значит, \(CK+CJ=CB=b\).
Осмысление того, что способ Карлейля годится не только для одной этой задачи, пришло далеко не сразу.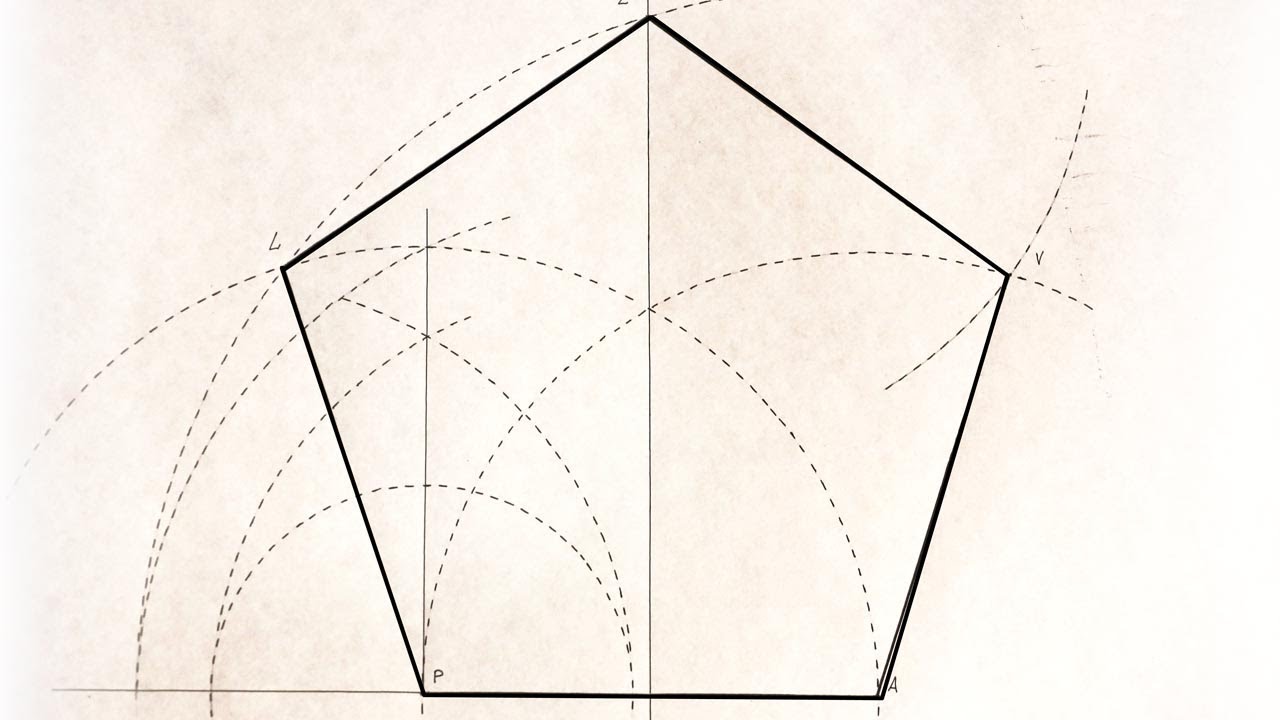 2-sx+p=0\). Тогда мы должны взять на координатной плоскости точки \(A\ (0;\ 1)\) и \(B\ (s;\ p)\), найти середину \(C\) отрезка \(AB\) и построить окружность с центром в \(C\) и радиусом \(CA\) (рис. 4). Точки пересечения этой окружности с осью абсцисс и будут корнями уравнения.
2-sx+p=0\). Тогда мы должны взять на координатной плоскости точки \(A\ (0;\ 1)\) и \(B\ (s;\ p)\), найти середину \(C\) отрезка \(AB\) и построить окружность с центром в \(C\) и радиусом \(CA\) (рис. 4). Точки пересечения этой окружности с осью абсцисс и будут корнями уравнения.
Доказательство практически полностью повторяет решение задачи Лесли, приведенное выше.
Но мы, кажется, собирались что-то строить циркулем и линейкой? А здесь координатная плоскость… Ничего страшного! Все, что нам на самом деле нужно от координат, вполне сводится к двум осям. Действительно, вместо точки \(B\ (s;\ p)\) можно сразу рассмотреть ее проекции на оси \(B_1\ (s;\ 0)\) и \(B_2\ (0;\ p)\). Ведь если мы знаем коэффициенты \(a\) и \(p\), то построить именно эти точки на осях — проще простого. А дальше центр окружности получится пересечением серединных перпендикуляров к \(OB_1\) и \(AB_2\) (постарайтесь разобраться, почему это так, по рисунку 5).
Как видно из рисунка 5, способ с окружностью Карлейля не только простой, но и удивительно легкий для запоминания.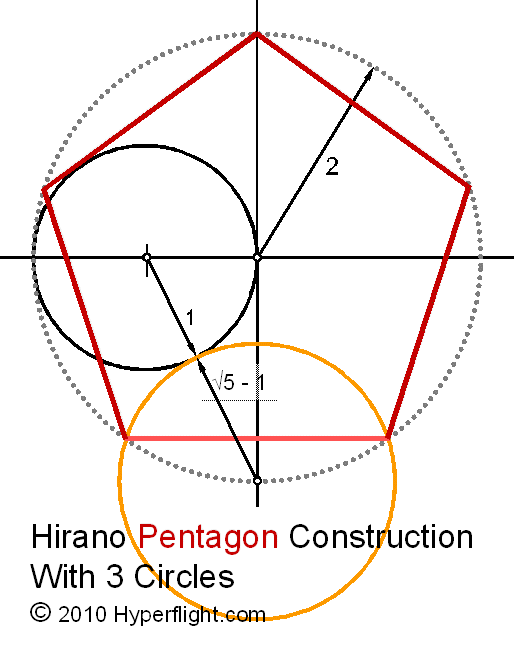 Кроме начала координат, требуются всего три точки — \(B_1\) (абсцисса которой равна коэффициенту \(s\)) откладывается на оси абсцисс, а \(A\ (0;\ 1)\) и \(B_2\) (ордината которой равна \(p\)) — на оси ординат. Два серединных перпендикуляра, одна окружность — вуаля, корни готовы!
Кроме начала координат, требуются всего три точки — \(B_1\) (абсцисса которой равна коэффициенту \(s\)) откладывается на оси абсцисс, а \(A\ (0;\ 1)\) и \(B_2\) (ордината которой равна \(p\)) — на оси ординат. Два серединных перпендикуляра, одна окружность — вуаля, корни готовы!
Как это применять?
Возможно, самое известное применение окружностей Карлейля — построение правильных многоугольников. Многие слышали о том, что построение правильного пятиугольника циркулем и линейкой возможно. (На самом деле — не только возможно, но было дано и полностью обосновано еще Евклидом.) Но многие ли пытались понять, как именно решается эта задача?
Задача 2. Дана окружность с центром \(O\) и точка \(A\) на ней. Постройте правильный пятиугольник \(ABCDE\), вписанный в эту окружность.
Решение. Построение пятиугольника с помощью окружностей Карлейля отличается удивительной простотой. Начнем с координатных осей, проведя через центр круга прямую \(OX\), перпендикулярную \(OA\) (рис. {\circ})\), т. е. углы \(AOB\) и \(AOE\) равны 72 градусам, а углы \(AOC\) и \(AOD\) — 144 градусам. А это и означает, что они являются вершинами правильного пятиугольника. Доказательство правильности построения на этом завершено.
{\circ})\), т. е. углы \(AOB\) и \(AOE\) равны 72 градусам, а углы \(AOC\) и \(AOD\) — 144 градусам. А это и означает, что они являются вершинами правильного пятиугольника. Доказательство правильности построения на этом завершено.
О сложности построений и «геометрографии» Эмиля Лемуана
Француз Эмиль Мишель Гиацинт Лемуан по праву считается одним из отцов современной «геометрии треугольника». Вероятно, вы слышали о точке Лемуана в треугольнике или об окружностях Лемуана. Он же в 1892 году опубликовал работу «Геометрография, или искусство геометрических конструкций» («La Géométrographie ou l’art des constructions géométriques»), в которой впервые предложил сравнивать различные геометрические построения по количеству требуемых элементарных операций (а лучшим построением считать то, на которое тратится меньшее число операций). Оптимальным («геометрографическим») способом Лемуан называет самый экономный из известных алгоритмов построения.
Элементарных операций Лемуан насчитал пять:
\(S_1\) — приложить линейку к определенной точке;
\(S_2\) — провести прямую линию;
\(C_1\) — поставить ножку циркуля в определенную точку;
\(C_2\) — изменить радиус циркуля, поставив ножку с карандашом в определенную точку;
\(C_3\) — провести циркулем окружность.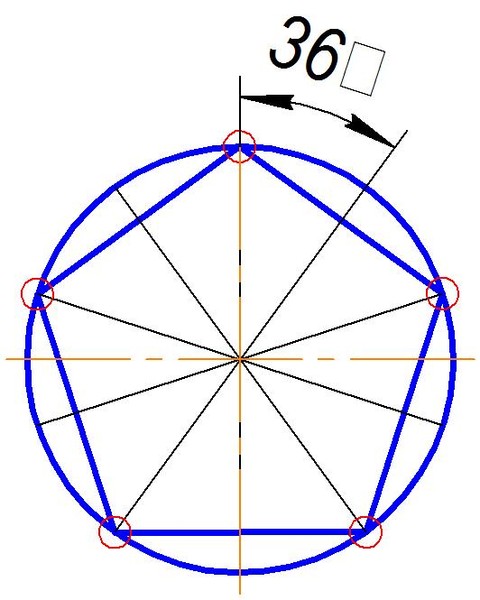
При этом Лемуан считал циркуль устойчивым, т. е. после проведения окружности сохраняющим выставленный радиус. Таким образом, следующая окружность того же радиуса, по Лемуану, требует уже не трех операций: \(C_1+C_2+C_3\), а всего двух: \(C_1+C_3\).
Сосчитаем, например, количество операций в построении корней уравнения с помощью окружности Карлейля, показанном на рисунке 5. Оси координат и точки \(A\), \(B_1\) и \(B_2\) заданы. Построение серединного перпендикуляра к отрезку \(OB_1\) — это две окружности равных радиусов и одна прямая, т. е. \((2C_1+C_2+2C_3)+(2S_1+S_2)\). Следующий серединный перпендикуляр — это \((2C_1+2C_3)+(2S_1+S_2)\), потому что мы строим его, не меняя радиуса циркуля. Тем самым, мы построили центр, затратив 15 элементарных операций. И наконец, сама окружность Карлейля — это еще \(C_1+C_2+C_3\). Итого «сложность» построения \(5C_1+2C_2+5C_3+4S_1+2S_2\) равна 18.
Упражнение 1. Придумайте другой способ построения окружности Карлейля, имеющий сложность 17 или меньше.
Подсказка. Центр этой окружности — середина отрезка, одним из концов которого является \(B_1\). Постройте сначала второй конец этого отрезка.
Современная компьютерная игра-головоломка Euclidea (euclidea.xyz) также требует от решателей задач найти самое экономное построение, но, в отличие от Лемуана, не подсчитывает предварительные операции \(S_1\), \(C_1\) и \(C_2\), а считает только количество проведенных линий (т. е. \(S_2+C_3\) в терминологии Лемуана). С точки зрения Euclidea, построение окружности Карлейля имеет сложность 7.
Можно ли отыскать корни квадратного уравнения с меньшей сложностью?
Когда автор начинал писать эту статью, он предполагал, что этот вопрос будет повешен в качестве финальной улыбки Чеширского Кота и оставлен читателю для самостоятельного решения. Однако планы немножко поменялись, и сейчас я хочу показать более экономный способ, а читателям предложить обдумать, нельзя ли найти еще лучший.
Во-первых, откажемся от оси ординат. Зачем она нужна, если все корни мы ищем на оси абсцисс?
Пусть у нас есть всего одна ось, а на ней — четыре известные точки \(O\ (0)\), \(E\ (1)\), \(S\ (X+Y)\) и \(P\ (XY)\). Последние две точки соответствуют коэффициентам того уравнения, которое мы хотим решить. Рисунок 7 соответствует ситуации, когда \(0<XY<1<X+Y\), но это не очень критично — приведенное ниже построение работает и во многих других случаях, а если оно не будет работать из-за того, что какие-то окружности не пересекутся, то его не очень сложно адаптировать.
Последние две точки соответствуют коэффициентам того уравнения, которое мы хотим решить. Рисунок 7 соответствует ситуации, когда \(0<XY<1<X+Y\), но это не очень критично — приведенное ниже построение работает и во многих других случаях, а если оно не будет работать из-за того, что какие-то окружности не пересекутся, то его не очень сложно адаптировать.
Вначале проведем две окружности равных радиусов с центрами в \(P\ (XY)\) и \(E\ (1)\) (рис. 8) — как будто мы хотим строить середину отрезка между этими точками. Радиус окружностей возьмем таким, чтобы первая окружность прошла через точку \(S\ (X+Y)\). Отметим \(C\) — общую точку этих окружностей.
Затем построим еще две окружности — окружность с центром \(O\ (0)\), проходящую через \(C\), и окружность такого же радиуса с центром \(S\). Их точку пересечения (любую из двух точек) назовем \(D\) (рис. 9).
И (немного неожиданный, как и полагается улыбке Кота) финальный шаг — окружность с центром \(D\), радиус которой точно такой же, как у двух первых (рис. 2\). А поскольку середина этого отрезка имеет координату \((X+Y)/2\), то правый конец отрезка совпадает с большим из чисел \(X\), \(Y\), а левый — с меньшим.
2\). А поскольку середина этого отрезка имеет координату \((X+Y)/2\), то правый конец отрезка совпадает с большим из чисел \(X\), \(Y\), а левый — с меньшим.
Сосчитаем сложность: \(2C_1+C_2+2C_3\) на первую пару окружностей, столько же на вторую и еще \(C_1+C_2+2C_3\) на последнюю окружность — всего \(5+5+3=13\), вместо прежних 17 или 18. Ура!
Дополнение.
Построение правильного 17-угольника
Задача 3. Пусть дана окружность с центром \(O\) и точка \(A\) на ней. Постройте правильный 17-угольник с вершиной \(A\), вписанный в эту окружность.
Эта задача, в отличие от трех неразрешимых задач древности, стала знаменитой после того, как была решена 19-летним Карлом Фридрихом Гауссом. Биографы Гаусса пишут, что только после ее решения Гаусс окончательно выбрал своей будущей профессией математику, а не литературу. Известна также легенда, что Гаусс завещал выбить на своем могильном камне изображение правильного 17-угольника.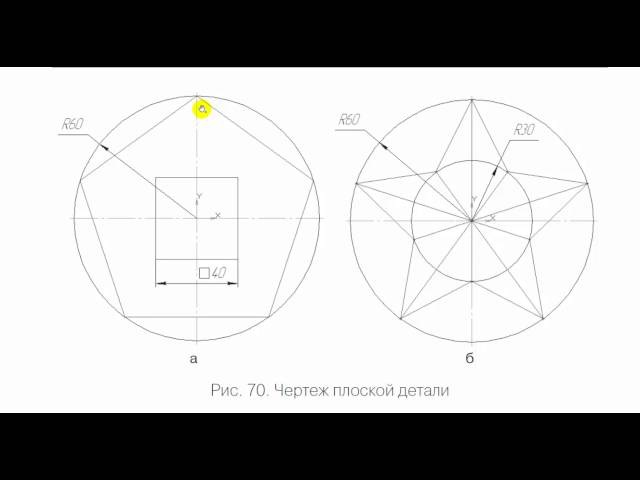 {16}=2\cos(\pi/17)\), так что, зная величину \(\eta_{08}\), мы легко построим вершины правильного 17-угольника, соседние с заданной вершиной \(A\) (аналогично построению вершин по точке \(H_2\) для правильного пятиугольника).
{16}=2\cos(\pi/17)\), так что, зная величину \(\eta_{08}\), мы легко построим вершины правильного 17-угольника, соседние с заданной вершиной \(A\) (аналогично построению вершин по точке \(H_2\) для правильного пятиугольника).
Упражнения
2. Вычислите произведение \(\eta_{08}\eta_{48}\).
3. Дуайн ДиТемпл описал пошаговое построение правильного 17-угольника с помощью окружностей Карлейля (commons.wikimedia.org). Разберитесь в этом построении.
2.2.4 Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника
Деление окружности
на шесть равных частей и построение
правильного вписанного шестиугольника
выполняют с помощью угольника с углами
30, 60 и 90º и/или
циркуля. При
делении окружности на шесть равных
частей циркулем из двух концов одного
диаметра радиусом, равным радиусу данной
окружности, проводят дуги до пересечения
с окружностью в точках 2, 6 и 3, 5 (рис.
2.24). Последовательно
соединив полученные точки, получают
правильный вписанный шестиугольник.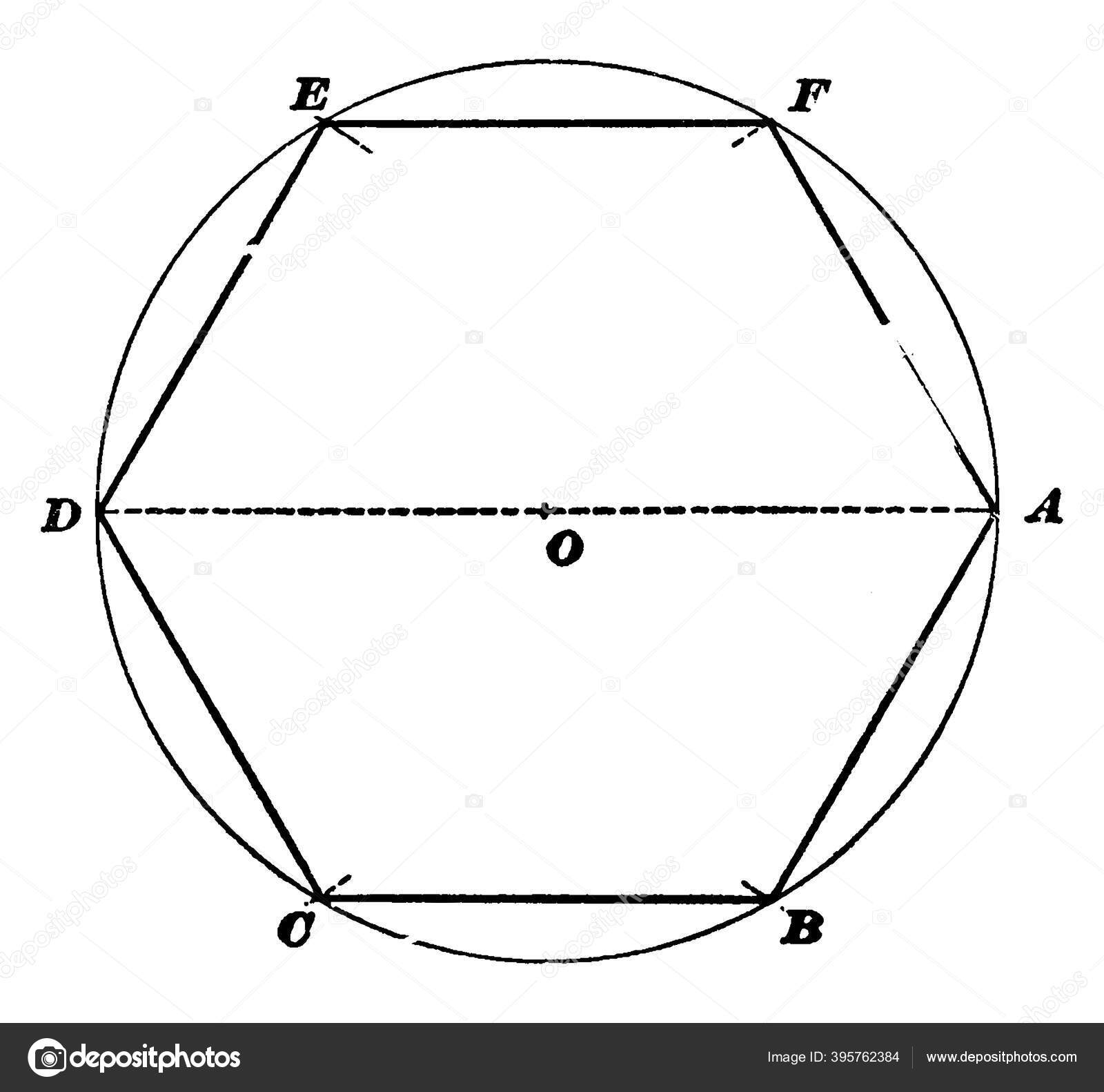
а) б)
Рисунок 2.24
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 2.25). Соединив полученные точки, получают двенадцатиугольник.
а) б)
Рисунок 2.25
2.2.5 Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника
Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис. 2.26.
а) б) в) г)
Рисунок 2.26
Половину любого
диаметра (радиус) делят пополам (рис.
2.26 а), получают точку А. Из точки А, как из центра,
проводят дугу радиусом, равным расстоянию
от точки А до точки 1
до пересечения со второй половиной
этого диаметра, в точке В (рис. 2.26 б). Отрезок 1В равен хорде,
стягивающей дугу, длина которой равна
1/5 длины окружности. Делая засечки на
окружности (рис. 2.26, в) радиусом К, равным
отрезку 1В, делят
окружность на пять равных частей.
Начальную точку 1
выбирают в зависимости от расположения
пятиугольника. Из точки 1 строят точки
2 и 5 (рис. 2.26, в), затем из точки 2
строят точку 3, а из точки 5 строят точку
4. Расстояние от точки 3 до точки 4 проверяют
циркулем. Если расстояние между точками
3 и 4 равно отрезку 1В, то построения были
выполнены точно. Нельзя выполнять
засечки последовательно, в одну сторону,
так как происходит набегание ошибок и
последняя сторона пятиугольника
получается перекошенной. Последовательно
соединив найденные точки, получают
пятиугольник (рис. 2.26, г).
2.26 б). Отрезок 1В равен хорде,
стягивающей дугу, длина которой равна
1/5 длины окружности. Делая засечки на
окружности (рис. 2.26, в) радиусом К, равным
отрезку 1В, делят
окружность на пять равных частей.
Начальную точку 1
выбирают в зависимости от расположения
пятиугольника. Из точки 1 строят точки
2 и 5 (рис. 2.26, в), затем из точки 2
строят точку 3, а из точки 5 строят точку
4. Расстояние от точки 3 до точки 4 проверяют
циркулем. Если расстояние между точками
3 и 4 равно отрезку 1В, то построения были
выполнены точно. Нельзя выполнять
засечки последовательно, в одну сторону,
так как происходит набегание ошибок и
последняя сторона пятиугольника
получается перекошенной. Последовательно
соединив найденные точки, получают
пятиугольник (рис. 2.26, г).
Деление окружности
на десять равных частей выполняют
аналогично делению окружности на пять
равных частей (рис. 2.26), но сначала делят
окружность на пять частей, начиная
построение из точки 1, а затем из точки
6, находящейся на противоположном конце
диаметра (рис.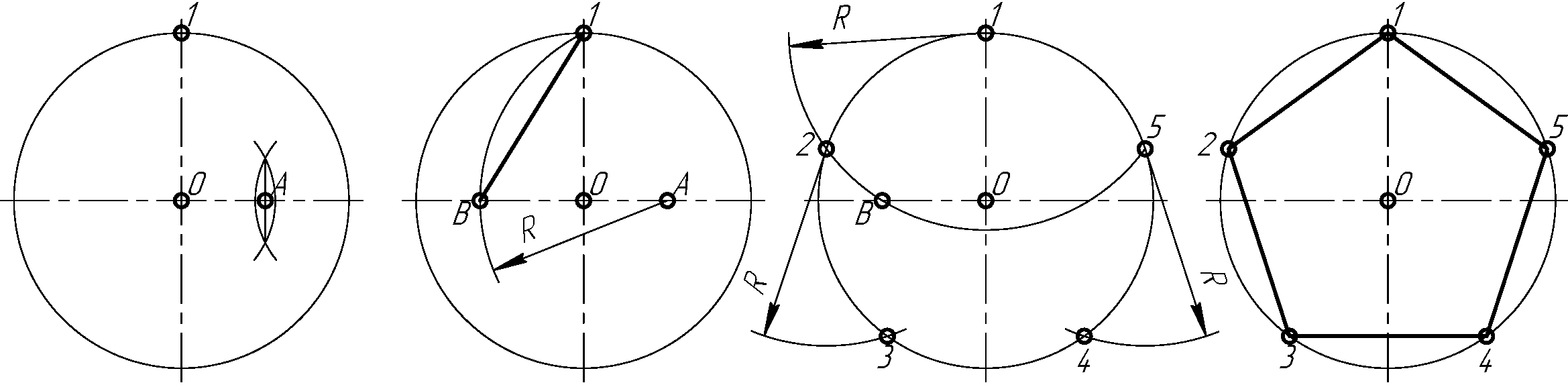 2.27, а).
Соединив последовательно все точки,
получают правильный вписанный
десятиугольник(рис. 2.27, б).
2.27, а).
Соединив последовательно все точки,
получают правильный вписанный
десятиугольник(рис. 2.27, б).
а) б)
Рисунок 2.27
2.2.6 Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и четырнадцатиугольника
Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 2.28 и 2.29.
Из любой точки
окружности, например точки А, радиусом
заданной окружности проводят дугу
(рис. 2.28, а) до пересечения
с окружностью в точках В и D. Соединим
точки В и D прямой.
Половина полученного отрезка (в данном
случае отрезок ВС) будет равна хорде,
которая стягивает дугу, составляющую
1/7 длины окружности. Радиусом, равным
отрезку ВС, делают
засечки на окружности в последовательности,
показанной на рис. 2.28, б. Соединив
последовательно все точки, получают
правильный вписанный семиугольник
(рис. 2.28, в).
2.28, б. Соединив
последовательно все точки, получают
правильный вписанный семиугольник
(рис. 2.28, в).
Деление окружности на четырнадцать равных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 2.29, а).
а) б) в)
Рисунок 2.28
Сначала окружность делится на семь равных частей от точки 1, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырнадцатиугольник (рис. 2.29, б).
а) б)
Рисунок 2.29
| |||||
| | |||||
| ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК В ДАННЫЙ
ОПИСАННАЯ КРУГ На рис. Рисунок 4-25.-Правильный пятиугольник в данной описанной круг. ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК НА ДАННОМ Вписанный круг Построить правильный пятиугольник по заданному вписанный окружность, определить пять равных промежутков на круг таким же образом. Однако вместо соединяя эти точки, нарисуйте каждую сторону фигура, касающаяся окружности в точке пересечения. | |||||
| | |||||
Круг Пятиугольник выпуклый Выпуклый Компас и линейка Правильный многоугольник, круг, угол, текст, симметрия png0075 PNG теги
- угол,
- текст,
- симметрия,
- компас,
- золотое сечение,
- линейка,
- обычный полигон,
- точка,
- пентаграмма,
- пятиугольник,
- математика,
- строка,
- район,
- золотой Пентагон,
- геометрия,
- евклидова геометрия,
- образование Наука,
- схема,
- циркуль и линейка Строительство,
- круг,
- png,
- прозрачный,
- скачать бесплатно
Информация PNG
- Размеры
- 1020x923px
- Размер файла
- 51,56 КБ
- MIME-тип
- Изображение/png
Изменение размера онлайн png
ширина (пкс) высота (пкс)Лицензия
Некоммерческое использование, DMCA Свяжитесь с нами
- org/ImageGallery» align=»middle»>
- иллюстрация желтой линейки, измерение учителя математики, построение компаса и линейки, линейка t, число, умножение, рабочий лист png 1168x1150px 30,4 КБ
- Золотой угол Круг Геометрия Точка Правильный многоугольник, красный круг, угол, белый, сфера png 2785x2525px 86,26 КБ
- Геометрия светового круга, наука и техника, синий механический, синий, угол, электроника png 800x800px 299,43 КБ
- Золотая спираль Золотое сечение Число Фибоначчи Золотой прямоугольник, евклидово, угол, белый, текст png 1600x1012px 42,47 КБ
- Математика Геометрия Формула Евклидово уравнение, Заметки по математике, угол, текст, треугольник png 6354x6354px 911,07 КБ
- org/ImageObject»> иллюстрация треугольника, равносторонний треугольник, форма равнобедренного треугольника, геометрия, треугольник, угол, прямоугольник, треугольник png 600x600px 10,64 КБ
- Правильный многоугольник Hexagon Shape Geometry, шестиугольный, угол, белый, прямоугольник png 2000x2000px 36,48 КБ
- Золотое сечение Круг Золотая спираль Сакральная геометрия, спираль, угол, белый, текст png 1266x2000px 114,08 КБ
- Круг Золотая спираль Золотое сечение Число Фибоначчи, круг, угол, белый, текст png 2000x1237px 40,91 КБ
- Гексагональная мозаика Сотовая гипотеза Геометрия, евклидова, медоносная пчела, угол, белый png 1200x1200px 26,18 КБ
- org/ImageObject»> Равносторонний пятиугольник Правильный многоугольник Правильный многогранник, Goldene, синий, угол, текст png 1200x1142px 29,43 КБ
- Шестиугольник Многоугольник Двумерное пространство Геометрия, граница многоугольника, угол, белый, прямоугольник png 768x768px 11,63 КБ
- Строение циркуля и линейки Математика Транспортир Геометрия, геометрия, угол, техника, треугольник png 650x1528px 276,14 КБ
- Геометрия формы пятиугольника Линия нонагона, геометрические фигуры, угол, прямоугольник, треугольник png 512x512px 7,54 КБ
- Строительный компас и линейка Геометрия, мультипликационный компас, угол, техника, треугольник png 773x955px 59,19 КБ
- org/ImageObject»> Золотое сечение Золотая спираль Число Фибоначчи, Математика, угол, белый, текст png 2000x1268px 390,15 КБ
- 65537-угольник Правильный многоугольник Угол 257-угольник, круговой, белый, текст, другие png 1845x1845px 47,07 КБ
- шестиугольник, шестиугольная плитка, форма многоугольника, шестиугольник, угол, белый, прямоугольник png 1000x866px 20,68 КБ
- Золотая спираль число Фибоначчи Извлечение фолликулярной единицы Золотое сечение, число Фибоначчи, угол, белый, прямоугольник png 800x495px 17,49 КБ
- Правильный многоугольник Пентагон Правильный многогранник Геометрия, геометрические неправильные фигуры, угол, белый, прямоугольник png 1200x1200px 290,77 КБ
- org/ImageObject»> Многоугольник Геометрия Треугольник Евклидов, Многоугольник, текстура, угол, белый png 500x500px 61,81 КБ
- Восьмиугольник Форма Многоугольник Шестиугольник Шаблон, образный, шаблон, угол, белый png 512x512px 2,04 КБ
- Hexagon Bee Honeycomb, соты, угол, прямоугольник, монохромный png 1920x1330px 184,99 КБ
- Золотая спираль Число Фибоначчи Золотое сечение Liber Abaci, Математика, угол, белый, текст png 800x524px 18,2 КБ
- Шестиугольник Многоугольник Настольная форма, шестиугольники, угол, прямоугольник, треугольник png 512x512px 6,57 КБ
- org/ImageObject»> Decagon Правильный многоугольник Геометрия Двумерное пространство, лампочка, угол, белый, прямоугольник png 768x768px 16,92 КБ
- Тесселяция в форме шестиугольника, шестиугольник, угол, белый, прямоугольник png 888x768px 19,57 КБ
- черно-фиолетовая текстовая иллюстрация, бумажная математическая формула науки, фиолетовые математические заметки, угол, текст, симметрия png 4050x4050px 788,52 КБ
- желтая звезда арт, Звездный многоугольник Пентаграмма Золото Желтая, Золотая пятиконечная звезда, угол, звезды, золотая рамка png 1000x1000px 45,31 КБ
- Шестиугольник Треугольник Сакральная геометрия Форма, треугольник, угол, симметрия, многоугольник png 512x512px 16,08 КБ
- org/ImageObject»> Шестиугольник Правильный многоугольник Форма, шестиугольник, угол, прямоугольник, монохромный png 2000x1730px 45,31 КБ
- Геометрическая форма Геометрия, геометрические фигуры, белый, треугольник, симметрия png 800x800px 17,54 КБ
- Символ Пентагона Пентаграмма Правильный многоугольник, золотая пятиконечная звезда, угол, прямоугольник, треугольник png 768x768px 32,84 КБ
- искусство черного шестиугольника, форма шестиугольника, геометрия правильного многоугольника, нарисованные формы синего шестиугольника, угол, белый, прямоугольник png 1024x1024px 22,6 КБ
- Эскиз треугольника, Золотой треугольник Золотая спираль Золотое сечение Число Фибоначчи, треугольник, угол, спираль, треугольник png 2000x2935px 88,53 КБ
- org/ImageObject»> Восьмиугольник Шестиугольник Геометрия Форма, шаблон сертификата, угол, лицо, прямоугольник png 512x512px 1,78 КБ
- Правильный многоугольник Pentagon Shape Правильный многогранник, файл, угол, прямоугольник, треугольник png 1405x1340px 13,95 КБ
- Число Фибоначчи Золотая спираль Золотое сечение Последовательность, спираль, угол, белый, текст png 1600x1012px 47,16 КБ
- иллюстрация списка золотых рамок, золото, край с золотым узором, угол, белый, золотая рамка png 3501x5038px 338,5 КБ
- Правильный многоугольник Восьмиугольник Внутренний угол Равноугольный многоугольник, форма, угол, белый, прямоугольник png 800x800px 5,65 КБ
- org/ImageObject»> Число Фибоначчи Золотая спираль Золотое сечение Математика, Математика, угол, белый, прямоугольник png 1024x633px 12,93 КБ
- Математика Геометрия Точка Пятиугольник Круг, пентаграмма, угол, треугольник, симметрия png 1059x1024px 140,15 КБ
- Кривая преследования Линия Треугольник Парабола, треугольник, угол, спираль, симметрия png 2308x2000px 261,54 КБ
- шестиугольник, форма шестиугольник компьютерные иконки символ, шестиугольник, угол, прямоугольник, геометрическая форма png 512x512px 44,63 КБ
- Правильный многоугольник Octagon Decagon Внутренний угол, джипни, угол, белый, прямоугольник png 2000x2000px 23,45 КБ

 4-25 показан метод построения
а
правильный пятиугольник в данной описанной
4-25 показан метод построения
а
правильный пятиугольник в данной описанной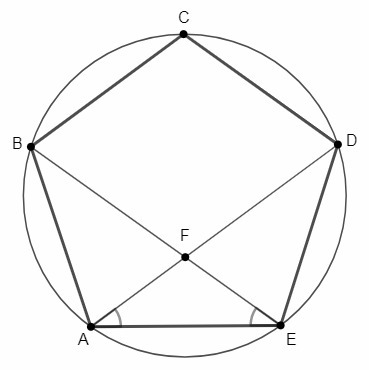 —
—