Пример. Построение многоугольника, вписанного в окружность. AutoCAD 2009. Начали!
Читайте также
Окружность
Окружность Команда CIRCLE, формирующая окружность, вызывается из падающего меню Draw ? Circle или щелчком на пиктограмме Circle на панели инструментов Draw (рис. 9.2). Рис. 9.2. Команда построения окружности в падающем менюОкружности можно строить различными способами. По умолчанию
Окружность
Окружность Команда CIRCLE , формирующая окружность , вызывается из падающего меню Draw ? Circle или щелчком на пиктограмме Circle на панели инструментов Draw (рис. 9.5). Рис. 9.5. Команда построения окружности в падающем менюОкружности можно строить различными способами. По умолчанию
Окружность
Окружность
Окружность является криволинейным примитивом, который часто используется на чертежах самого различного назначения.
Пример. Построение в абсолютных координатах
Пример. Построение в абсолютных координатах Постройте многоугольник, задавая точки в абсолютных координатах (рис. 3.1). Запустите команду формирования отрезка LINE, вызвав ее из падающего меню Draw ? Line или щелкнув на пиктограмме Line на панели инструментов Draw. Ответьте на
Пример. Построение в относительных координатах
Пример. Построение в относительных координатах Постройте многоугольник, задавая точки в относительных координатах (см. рис. 3.1). Запустите команду формирования отрезка LINE, вызвав ее из падающего меню Draw ? Line или щелкнув на пиктограмме Line на панели инструментов Draw.
Пример.
 Построение в полярных координатах
Построение в полярных координатахПример. Построение в полярных координатах Постройте многоугольник, задавая точки в полярных координатах (см. рис. 3.1). Запустите команду формирования отрезка LINE, вызвав ее из падающего меню Draw ? Line или щелкнув на пиктограмме Line на панели инструментов Draw. Ответьте на
Пример. Построение касательной
Пример. Построение касательной Постройте отрезки, нарисованные пунктирной линией, выходящие из точ ки 1 и касательные окружности (рис. 6.6).Запустите команду формирования отрезка LINE, вызвав ее из падающего меню Draw ? Line или щелкнув на пиктограмме Line на панели инструментов Draw.
Пример. Построение нормали
Пример. Построение нормали
Постройте отрезки, нарисованные пунктирной линией, выходящие из точки 1 и перпендикулярные объектам (рис.
Пример. Построение полилинии с установкой толщины
Пример. Построение полилинии с установкой толщины Постройте полилинию, изображенную на рис. 7.2. Рис. 7.2. Построение полилинии с установкой толщиныЗапустите команду PLINE, вызвав ее из падающего меню Draw ? Polyline или щелкнув на пиктограмме Polyline на панели инструментов Draw.
Пример. Построение полилинии в режиме дуг
Пример. Построение полилинии в режиме дуг
Постройте полилинию, изображенную на рис. 7.3.Запустите команду PLINE, вызвав ее из падающего меню Draw ? Polyline или щелкнув на пиктограмме Polyline на панели инструментов Draw.Ответьте на запросы:_PLINESpecify start point: 40,8 – точка 1Current line-width is 0.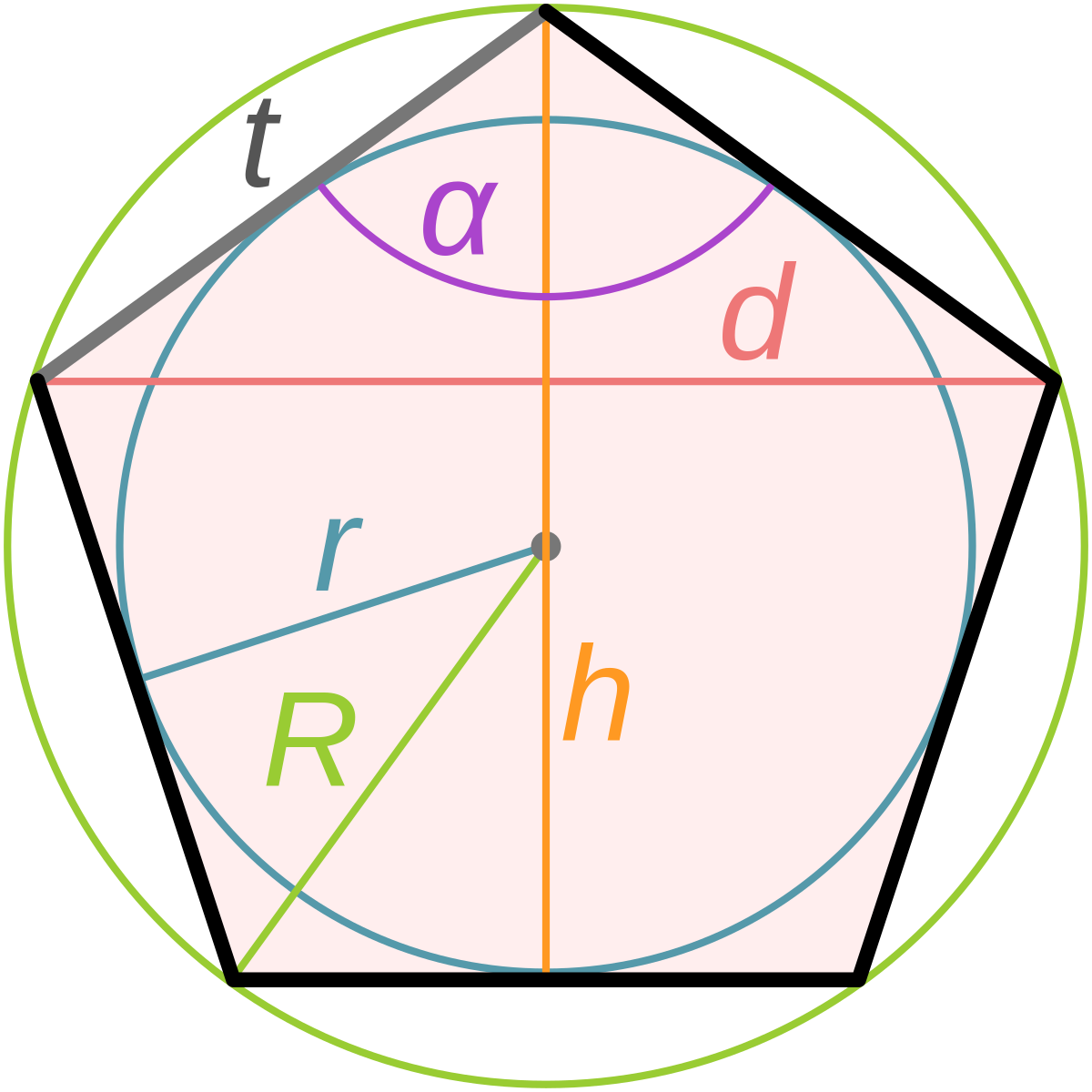
Пример. Построение многоугольника, описанного вокруг окружности
Пример. Построение многоугольника, описанного вокруг окружности Постройте треугольник, описанный вокруг окружности (рис. 7.5).Запустите команду POLYGON, вызвав ее из падающего меню Draw ? Polygon или щелкнув на пиктограмме Polygon на панели инструментов Draw. Ответьте на запросы:_POLYGONEnter
Пример. Построение дуги по трем точкам
Пример. Построение дуги по трем точкам Постройте дугу по варианту 3 Points – рис. 8.2.Запустите команду ARC, вызвав ее из падающего меню Draw ? Arc ? 3 Points или щелкнув на пиктограмме Arc на панели инструментов Draw. Ответьте на запросы:_ARCSpecify start point of arc or [Center]: 50,80 – точка 1Specify second point of arc or
Пример.
 Построение окружности по центру и радиусу
Построение окружности по центру и радиусуПример. Построение окружности по центру и радиусу Постройте окружность по центру и радиусу (рис. 8.4).Запустите команду CIRCLE, вызвав ее из падающего меню Draw ? Circle ? Center, Radius или щелкнув на пиктограмме Circle на панели инструментов Draw. Ответьте на запросы:_CIRCLESpecify center point for circle or
Пример. Построение окружности по двум точкам диаметра
Пример. Построение окружности по двум точкам диаметра Постройте окружность по двум точкам диаметра (рис. 8.5).Запустите команду CIRCLE, вызвав ее из падающего меню Draw ? Circle ? 2 Points или щелкнув на пиктограмме Circle на панели инструментов Draw. Ответьте на запросы:_CIRCLESpecify center point for circle
Пример. Построение эллипса по двум осям
Пример.
Пример. Построение эквидистанты
Пример. Построение эквидистанты Построить несколько вариантов эквидистанты заданной полилинии (рис. 11.5). Рис. 11.5. Построение эквидистантыЗапустите команду OFFSET, вызвав ее из падающего меню Modify ? Offset или щелчком на пиктограмме Offset на панели инструментов Modify. Ответьте на
вписанная в многоугольник или угол
Определения
Окружность \(S\) вписана в угол \(\alpha\), если \(S\) касается сторон угла \(\alpha\).

В этом случае многоугольник \(P\) называется описанным около окружности.
Теорема
Центр вписанной в угол окружности лежит на его биссектрисе.
Доказательство
Пусть \(O\) – центр некоторой окружности, вписанной в угол \(BAC\). Пусть \(B’\) – точка касания окружности и \(AB\), а \(C’\) – точка касания окружности и \(AC\), тогда \(OB’\) и \(OC’\) – радиусы, проведённые в точки касания, следовательно, \(OC’\perp AC\), \(OB’\perp AB\), \(OC’ = OB’\).
Значит, треугольники \(AC’O\) и \(AB’O\) – прямоугольные треугольники, у которых равны катеты и общая гипотенуза, следовательно, они равны, откуда \(\angle CAO = \angle BAO\), что и требовалось доказать.
Теорема
В любой треугольник можно вписать единственную окружность, причём центр этой вписанной окружности есть точка пересечения биссектрис треугольника.
Доказательство
Проведем биссектрисы углов \(\angle A\) и \(\angle B\). Пусть они пересеклись в точке \(O\).
Пусть они пересеклись в точке \(O\).
Т.к. \(O\) лежит на биссектрисе \(\angle A\), то расстояния от точки \(O\) до сторон угла равны: \(ON=OP\).
Т.к. \(O\) также лежит на биссектрисе \(\angle B\), то \(ON=OK\). Таким образом, \(OP=OK\), следовательно, точка \(O\) равноудалена от сторон угла \(\angle C\), следовательно, лежит на его биссектрисе, т.е. \(CO\) – биссектриса \(\angle C\).
Таким образом, точки \(N, K, P\) равноудалены от точки \(O\), то есть лежат на одной окружности. По определению это и есть вписанная в треугольник окружность.
Данная окружность единственна, т.к. если предположить, что существует другая вписанная в \(\triangle ABC\) окружность, то она будет иметь тот же центр и тот же радиус, то есть будет совпадать с первой окружностью.
Таким образом, попутно была доказана следующая теорема:
Следствие
Биссектрисы треугольника пересекаются в одной точке.
Теорема о площади описанного треугольника
Если \(a,b,c\) – стороны треугольника, а \(r\) – радиус вписанной в него окружности, то площадь треугольника \[S_{\triangle}=p\cdot r\] где \(p=\dfrac{a+b+c}2\) – полупериметр треугольника.
Доказательство
\(S_{\triangle ABC}=S_{\triangle AOC}+S_{\triangle AOB}+S_{\triangle BOC}=\frac12OP\cdot AC+\frac12 ON\cdot AB+\frac12 OK\cdot BC\).
Но \(ON=OK=OP=r\) – радиусы вписанной окружности, следовательно,
\[S_{\triangle ABC}=\frac12 r (AC+AB+BC)=p\cdot r\]
Следствие
Если в многоугольник вписана окружность и \(r\) – ее радиус, то площадь многоугольника равна произведению полупериметра многоугольника на \(r\): \[S_{\text{опис.мног-к}}=p\cdot r\]
Теорема
В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.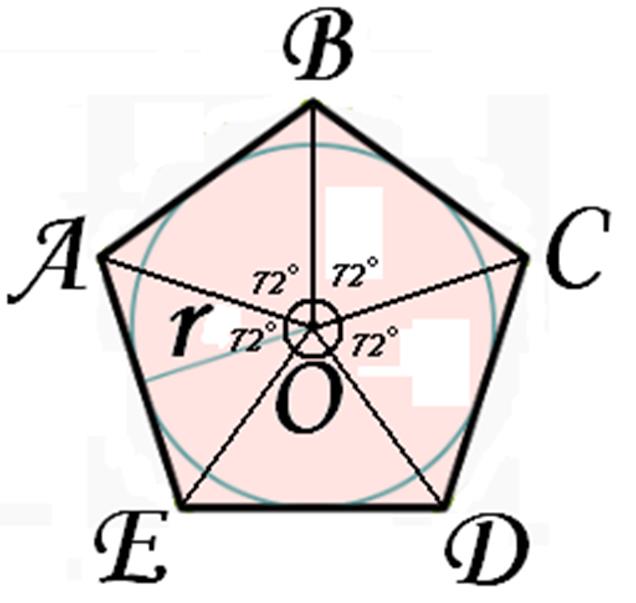
Доказательство
Необходимость. Докажем, что если в \(ABCD\) вписана окружность, то \(AB+CD=BC+AD\).
Пусть \(M,N,K,P\) – точки касания окружности и сторон четырехугольника. Тогда \(AM, AP\) – отрезки касательных к окружности, проведенные из одной точки, следовательно, \(AM=AP=a\). Аналогично, \(BM=BN=b, \ CN=CK=c, \ DK=DP=d\).
Тогда: \(AB+CD=a+b+c+d=BC+AD\).
Проведем биссектрисы углов \(\angle A\) и \(\angle B\), пусть они пересекутся в точке \(O\). Тогда точка \(O\) равноудалена от сторон этих углов, то есть от \(AB, BC, AD\). Впишем окружность в \(\angle A\) и \(\angle B\) с центром в точке \(O\). Докажем, что эта окружность будет касаться и стороны \(CD\).
Предположим, что это не так. Тогда \(CD\) либо является секущей, либо не имеет общих точек с окружностью.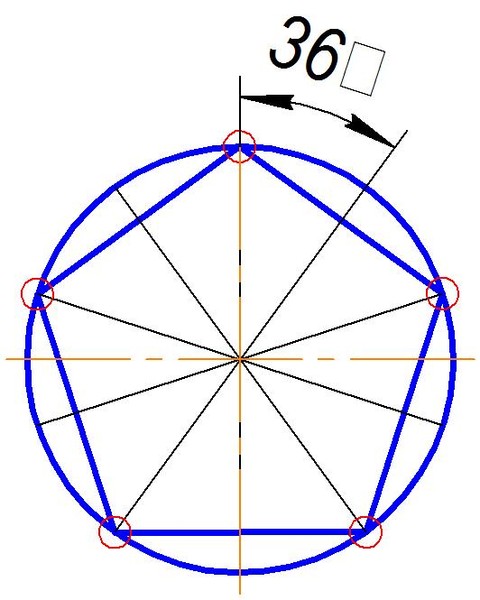 Рассмотрим второй случай (первый будет доказываться аналогично).
Рассмотрим второй случай (первый будет доказываться аналогично).
Проведем касательную прямую \(C’D’ \parallel CD\) (как показано на рисунке). Тогда \(ABC’D’\) – описанный четырехугольник, следовательно, \(AB+C’D’=BC’+AD’\).
Т.к. \(BC’=BC-CC’, \ AD’=AD-DD’\), то:
\[AB+C’D’=BC-CC’+AD-DD’ \Rightarrow C’D’+CC’+DD’=BC+AD-AB=CD\]
Получили, что в четырехугольнике \(C’CDD’\) сумма трех сторон равна четвертой, что невозможно*. Следовательно, предположение ошибочно, значит, \(CD\) касается окружности.
Замечание*. Докажем, что в выпуклом четырехугольнике не может сторона равняться сумме трех других.
Т.к. в любом треугольнике сумма двух сторон всегда больше третьей, то \(a+x>d\) и \(b+c>x\). Складывая данные неравенства, получим: \(a+x+b+c>d+x \Rightarrow a+b+c>d\). Следовательно, сумма любых трех сторон всегда больше четвертой стороны.
Теоремы
1. Если в параллелограмм вписана окружность, то он – ромб (рис. 1).
Если в параллелограмм вписана окружность, то он – ромб (рис. 1).
2. Если в прямоугольник вписана окружность, то он – квадрат (рис. 2).
Верны и обратные утверждения: в любой ромб и квадрат можно вписать окружность, и притом только одну.
Доказательство
1) Рассмотрим параллелограмм \(ABCD\), в который вписана окружность. Тогда \(AB+CD=BC+AD\). Но в параллелограмме противоположные стороны равны, т.е. \(AB=CD, \ BC=AD\). Следовательно, \(2AB=2BC\), а значит, \(AB=BC=CD=AD\), т.е. это ромб.
Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей ромба.
2) Рассмотрим прямоугольник \(QWER\). Т.к. прямоугольник является параллелограммом, то согласно первому пункту \(QW=WE=ER=RQ\), т.е. это ромб. Но т.к. все углы у него прямые, то это квадрат.
Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей квадрата.
Вписанные и описанные многоугольники основные понятия свойства формулы
Вписанные и описанные многоугольники: основные понятия, свойства, формулы
Вписанным в окружность называется многоугольник, вершины которого расположены на окружности (рис.1)
Описанным около окружности называется многоугольник, стороны которого являются касательными к окружности (рис.2)
Соответственно, окружность, проходящая через вершины многоугольника (рис.1), называется описанной около многоугольника; окружность, для которой стороны многоугольника являются касательными (рис.2), называется вписанной в многоугольник. Для произвольного многоугольника невозможно вписать в него и описать около него окружность. Для треугольника это всегда возможно.
Радиус r вписанного круга выражается через стороны a, b, c треугольника:
Радиус R описанного круга выражается формулой:
В четырёхугольник можно
вписать окружность, если суммы его
противоположных сторон равны. Для
параллелограммов это возможно только
для ромба (квадрата).
Для
параллелограммов это возможно только
для ромба (квадрата).
Центр вписанного круга расположен в точке пересечения диагоналей.
Около четырёхугольника можно описать круг, если сумма его противоположных углов равна 180º.Для параллелограммов это возможно только для прямоугольника (квадрата). Центр описанного круга лежит в точке пересечения диагоналей.
Вокруг трапеции можно описать круг, если только она равнобочная.
Правильный многоугольник – это многоугольник с равными сторонами и углами.
На
рис.3 показан правильный
шестиугольник, а на рис.4 – правильный
восьмиугольник. Правильный четырёхугольник
– это квадрат; правильный треугольник
– равносторонний треугольник. Каждый
угол правильного многоугольника равен
180º (n –
2) / n , где n – число его углов. Внутри правильного
многоугольника существует точка O (рис. 3), равноудалённая от всех его вершин
(OA = OB = OC = … = OF), которая называется центром
правильного многоугольника. Центр
правильного многоугольника также
равноудалён от всех его сторон (OP =
OQ = OR = …). Отрезки OP, OQ, OR, … называются апофемами;
отрезки OA, OB, OC, …– радиусы правильного многоугольника. В правильный
многоугольник можно вписать окружность
и около него можно описать окружность.
Центры вписанной и описанной окружностей
совпадают с центром правильного
многоугольника. Радиус описанного круга
— это радиус правильного многоугольника,
a радиус вписанного круга — его апофема.
Соотношения сторон и радиусов правильных
многоугольников:
3), равноудалённая от всех его вершин
(OA = OB = OC = … = OF), которая называется центром
правильного многоугольника. Центр
правильного многоугольника также
равноудалён от всех его сторон (OP =
OQ = OR = …). Отрезки OP, OQ, OR, … называются апофемами;
отрезки OA, OB, OC, …– радиусы правильного многоугольника. В правильный
многоугольник можно вписать окружность
и около него можно описать окружность.
Центры вписанной и описанной окружностей
совпадают с центром правильного
многоугольника. Радиус описанного круга
— это радиус правильного многоугольника,
a радиус вписанного круга — его апофема.
Соотношения сторон и радиусов правильных
многоугольников:
Для большинства правильных многоугольников невозможно выразить посредством алгебраической формулы соотношение между их сторонами и радиусами.
Число сторон | R | r | S |
3 | |||
4 | |||
5 | |||
6 | |||
8 | |||
10 | |||
n |
Теорема Стюарта
Если точка D лежит на стороне ВС треугольника АВС, то AD2=
Дано:
ΔАВС, DВС
Доказать, что:
AD2=
Доказательство:
Применим теорему косинусов к треугольникам АСD и ABD:
(1),
(2).
Умножим первое неравенство на BD, а второе – CD и сложим их:
Так как BD+DC=BC, то
, .
и — смежные, следовательно, cos ADC=cos (180°-)= — cos ADB.
Таким образом,
приобретает вид: .
Разделим обе части равенства на ВС: AD2=
Теорема доказана.
Вывод формулы Герона
Дано:
Δ АВС,
Д
а
в
оказать, что:S
с
=, где а, в, с – длины сторон треугольника, р=Доказательство:
S= a·b·sin, где — угол противолежащий стороне с.
По теореме косинусов:
с2=а2+в2-2а·в·cos.
Отсюда
cos=
Значит,
sin2= 1 – cos2=(1- cos)(1+ cos)=
=
=
Замечая, что
а+в+с=2р, а+в-с=2р-2с, а+с-в=2р-2в, с-а+в=2р-2а,
получаем:
sin=
Таким образом,
S=a·b·sin=
Теорема доказана.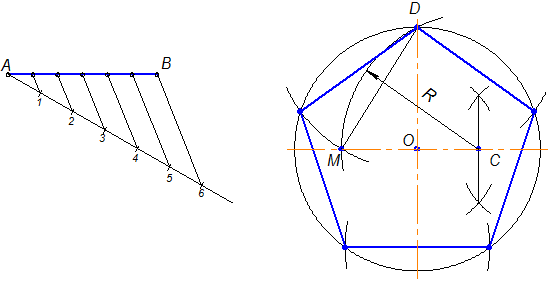
Площадь плоской фигуры. Свойства площадей
Для плоских фигур площадь – это положительная величина, численное значение которой обладает следующими свойствами:
Равные фигуры имеют равные площади;
Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей;
Площадь квадрата со стороной, равной единице измерения, равна единице.
Формулы нахождения площадей:
Треугольник
Обозначения: a, b, c –
стороны; A, B, C – углы;
p
= ( a + b + c ) / 2 — полупериметр; h –
высота; S – площадь; R –
радиус описанной окружности; r –
радиус вписанной окружности.
S=½ah
S=½ab (для прямоугольного треугольника)
S=(для равностороннего треугольника)
S=½ab·sin()= pr =
Трапеция
S=½(AD+ВС)·BH, где AD и ВС– основания, BH –
высота. b)
b)
Квадрат
S= a2=
Прямоугольник
S=ab=
Круга
S= πR2
Кругового сектора
S=
Ромб
S= a2sinα = = аh
Теорема о пропорциональных отрезках в прямоугольном треугольнике
Задача: Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному.
Дано:
ΔАВС- прямоугольный,
CD – высота.
Доказать, что
ΔАВСΔACD,
ΔABCΔCBD,
ΔACDΔCBD
Доказательство:
Пусть АВС – прямоугольный треугольник
с прямым углом С, CD –
высота, проведенная из вершины С к
гипотенузе АВ. Докажем, что ΔАВСΔACD,
ΔABCΔCBD,
ΔACDΔCBD.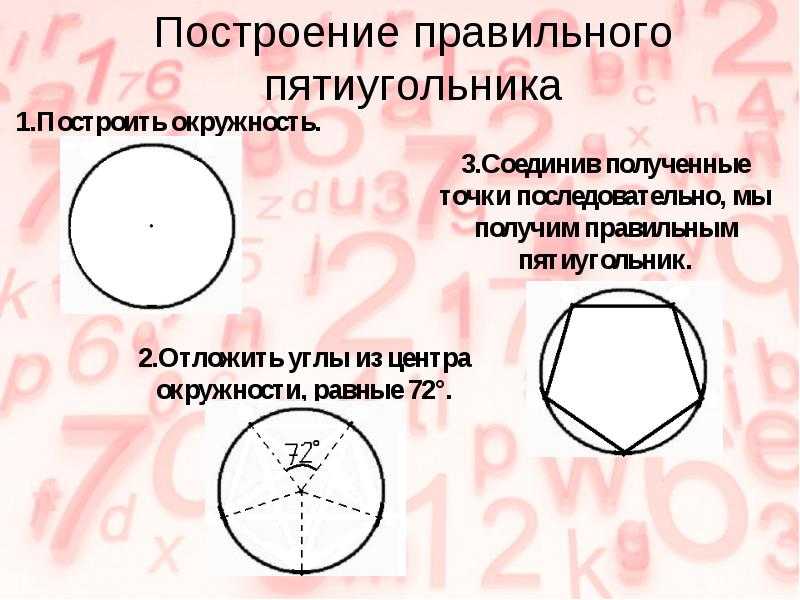
Треугольники ΔАВС и ΔACDподобны по первому признаку подобия треугольников. Точно также подобны треугольники ΔABC и ΔCBD, поэтому . Наконец, треугольники ΔACD и ΔCBD также подобны по первому признаку, что и требовалось доказать.
Отрезки XY называют средним пропорциональным (или средним геометрическим) между отрезками АВ и СD, если XY=.
На основе этой задачи можно доказать следующие два утверждения:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Доказательство:
Действительно, ΔACD ΔCBD, поэтому и, следовательно, СD2=АD·DВ, откуда СD=.
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из вершины прямого угла.
Доказательство:
В самом деле, ΔАВСΔACD,
поэтому и, следовательно, АС=.
Правильные многоугольники. Свойства. Формула для вычисления стороны и площади правильного многоугольника.
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны (рис. 1).
Рис. 1
Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.
Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.
Вид правильного
многоугольникаa
R
r
Сумма углов
Треугольник
60°
180°
Четырехугольник
90°
360°
Шестиугольник
120°
a
720°
Свойства правильных многоугольников
Правильный многоугольник может быть вписанным в окружность и описанным около окружности, при этом центры этих окружностей совпадают.
Центр правильного многоугольника совпадает с центрами вписанной и описанной окружностей.
Сторона an правильного n-угольника связана с радиусом R описанной окружности формулой an=2Rsinn180°=2Rsinn.
Периметры правильных n-угольников относятся как радиусы описанных окружностей.
Основные формулы:
Пусть R — радиус описанной вокруг правильного многоугольника окружности, тогда радиус вписанной окружности равен r=Rcosn, а длина стороны многоугольника равна
Площадь правильного многоугольника с числом сторон n и длиной стороны a составляет S=4na2ctgn .
Площадь правильного многоугольника с числом сторон n, вписанного в окружность радиуса R составляет
Прямоугольник,
ромб, квадрат. Определение, свойства и
признаки, формулы площадей.
Определение, свойства и
признаки, формулы площадей.
П
B
C
а
в
рямоугольником называется параллелограмм, у которого все углы прямые (рис. 1).С
Рис. 1
A
D
войство прямоугольника:Признаки прямоугольника:
Основные формулы:
S=ab=
Ромбом называется параллелограмм, у которого все стороны равны (рис 2).
Свойства ромба
все свойства параллелограмма:
противолежащие стороны равны;
противоположные углы равны;
диагонали точкой пересечения делятся пополам;
сумма углов, прилежащих к одной стороне, равна 180°;
с
Рис. 2
умма квадратов диагоналей равна сумме квадратов всех сторон;диагонали перпендикулярны;
диагонали являются биссектрисами его углов.

Признаки ромба
Если диагонали параллелограмма перпендикулярны, то параллелограмм — ромб.
Если диагональ параллелограмма является биссектрисой его угла, то параллелограмм — ромб.
Основные формулы
S = aha
S = a2sin
S =½d1d2
Прямоугольник, у которого все стороны равны, называется квадратом.
Ромб, у которого есть прямой угол – есть квадрат (рис. 3).
С Рис.3
Если четырехугольник — квадрат, то для него справедливы все следующие утверждения.
Признак квадрата:
Если для четырехугольника справедливо хотя бы одно из следующих утверждений, то он — квадрат.
Утверждения.
Все стороны равны и среди внутренних углов есть прямой угол.
Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
Четырехугольник имеет 4 оси симметрии: прямые, перпендикулярные сторонам и проходящие через их середины; прямые, содержащие диагонали.
Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90 .
Основные формулы:
Р=4а
Построение правильных многоугольников — техническое черчение. Построение правильных многоугольников Начертить 8 угольник с помощью циркуля
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника.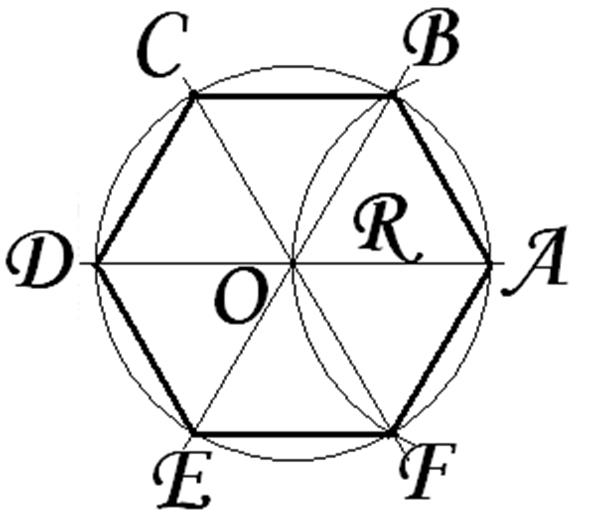 Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
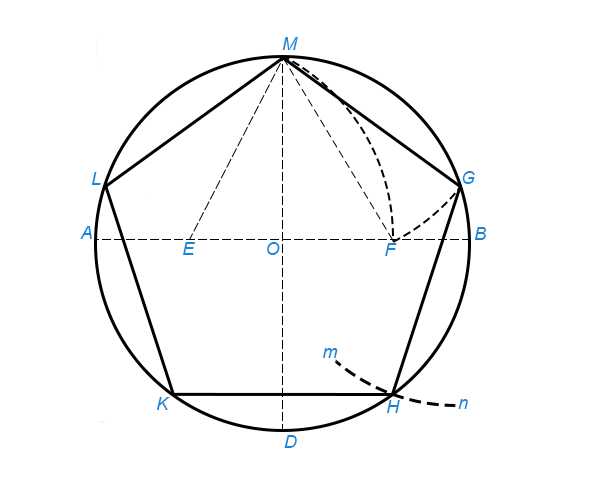
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника.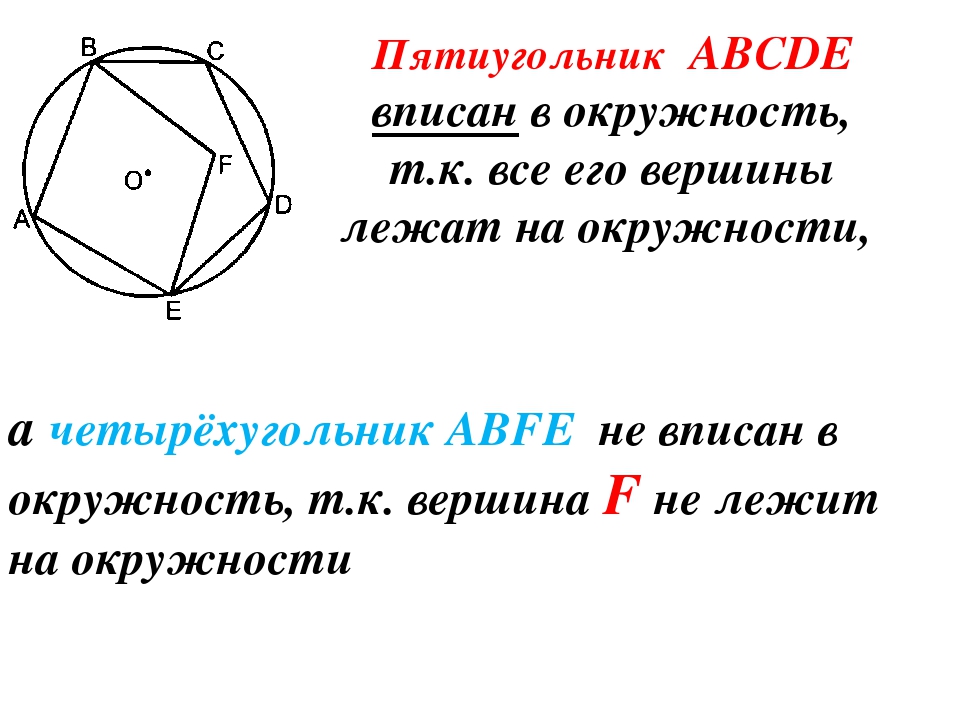 Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника.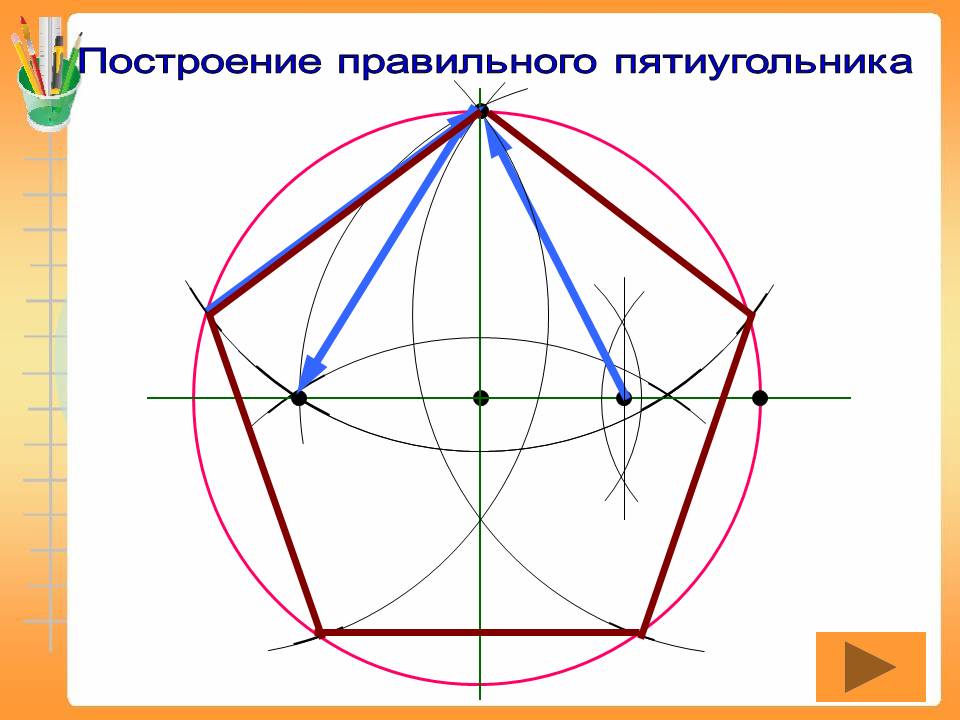 Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В черчении зачастую требуется строить положительные многоугольники. Так, скажем, положительные восьмиугольники применяются на щитах дорожных знаков.
Вам понадобится
- – циркуль
- – линейка
- – карандаш
Инструкция
1. Пускай задан отрезок, равный длине стороны желанного восьмиугольника. Требуется возвести верный восьмиугольник. Первым шагом постройте равнобедренный треугольник на заданном отрезке, применяя отрезок, как основание. Для этого вначале постройте квадрат со стороной, равной отрезку, проведите в нем диагонали. Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.
Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.
2. Постройте окружность с центром в вершине треугольника. Радиус окружности равен стороне треугольника. Сейчас разведите циркуль на расстояние, равное величине заданного отрезка. Отложите это расстояние на окружности, начиная от всякого конца отрезка. Объедините все полученные точки в восьмиугольник.
3. Если же задана окружность, в которую должен быть вписан восьмиугольник, то построения будут еще проще. Постройте две перпендикулярные друг другу осевые линии, проходящие через центр окружности. На пересечении осевых и окружности получатся четыре вершины грядущего восьмиугольника. Осталось поделить расстояние между этими точками на дуге окружности напополам, дабы получить еще четыре вершины.
Верный треугольник – тот, у которого все стороны владеют идентичной длиной. Исходя из этого определения, построение сходственной разновидности треугольник а является нетрудной задачей.
Исходя из этого определения, построение сходственной разновидности треугольник а является нетрудной задачей.
Вам понадобится
- Линейка, лист разлинованной бумаги, карандаш
Инструкция
1. Взять лист чистой бумаги, разлинованной в клеточку, линейку и подметить на бумаге три точки так, дабы они находились на идентичном друг от друга расстоянии (рис.1)
2. С подмогой линейки объединить подмеченные на листе точки ступенчато, друг за ином так, как это показано на рисунке 2.
Обратите внимание!
В верном (равностороннем) треугольнике все углы равны 60 градусам.
Полезный совет
Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это обозначает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Всякий положительный треугольник является равнобедренным, в то время как обратное заявление не правильно.
Восьмиугольник – это, по своей сути, два квадрата, смещенных касательно друг друга на 45° и объединенных на вершинах цельной линией. А потому, для того дабы положительно изобразить такую геометрическую фигуру, нужно твердым карандашом дюже опрятно, по правилам начертить квадрат либо круг, с которыми и проводить последующие действия. Изложение ориентировано на длину стороны, равной 20 см. А значит, при расположении чертежа рассматривайте, дабы вертикальная и горизонтальная линии длиной 20 см умещались на листе бумаги.
А потому, для того дабы положительно изобразить такую геометрическую фигуру, нужно твердым карандашом дюже опрятно, по правилам начертить квадрат либо круг, с которыми и проводить последующие действия. Изложение ориентировано на длину стороны, равной 20 см. А значит, при расположении чертежа рассматривайте, дабы вертикальная и горизонтальная линии длиной 20 см умещались на листе бумаги.
Вам понадобится
- Линейка, прямоугольный треугольник, транспортир, карандаш, циркуль, лист бумаги
Инструкция
1. Метод 1. Начертите внизу горизонтальную линию длиной 20 см. После этого с одной стороны подметьте транспортиром прямой угол, тот, что составляет 90°. То же самое дозволено сделать с поддержкой прямого треугольника. Проведите вертикальную линию и подметьте 20 см. Проделайте те же самые манипуляции с иной стороны. Объедините две полученные точки горизонтальной линией. В итоге получилась геометрическая фигура – квадрат.
2. Для того дабы возвести 2-й (смещенный) квадрат, потребуется центр фигуры.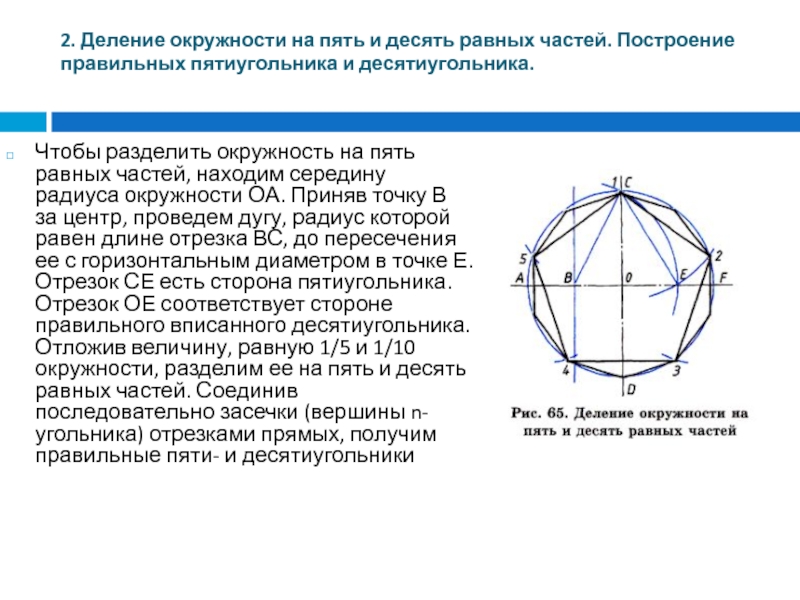 Для этого поделите всякую сторону квадрата на 2 части. Объедините вначале 2 точки параллельных верхней и нижней сторон, а потом точки боковых сторон. Проведите через центр квадрата 2 прямые линии, перпендикулярные касательно друг друга. Начиная от центра, отмерьте на новых прямых длину по 10 см, что в результате даст 4 прямые линии. Объедините 4 полученные наружные точки между собой, в итоге чего получится 2-й квадрат. Сейчас всякую точку из 8 полученных углов объедините между собой. Таким образом, будет начерчен восьмиугольник.
Для этого поделите всякую сторону квадрата на 2 части. Объедините вначале 2 точки параллельных верхней и нижней сторон, а потом точки боковых сторон. Проведите через центр квадрата 2 прямые линии, перпендикулярные касательно друг друга. Начиная от центра, отмерьте на новых прямых длину по 10 см, что в результате даст 4 прямые линии. Объедините 4 полученные наружные точки между собой, в итоге чего получится 2-й квадрат. Сейчас всякую точку из 8 полученных углов объедините между собой. Таким образом, будет начерчен восьмиугольник.
3. Метод 2. Для этого потребуется циркуль, линейка и транспортир. От центра листа с поддержкой циркуля начертите круг диаметром 20 см (радиус 10 см). Через центральную точку проведите прямую линию. После этого начертите вторую перпендикулярную ей линию. То же самое дозволено исполнить с подмогой транспортира либо прямого треугольника. В итоге круг будет поделен на 4 равные части. Дальше всякий из секций поделите еще на 2 части. Для этого также дозволено воспользоваться транспортиром, отмеряя 45° либо прямоугольным треугольником, тот, что приложите острым углом в 45° и проведите лучи. От центра на всякой прямой линии отмерьте по 10 см. В итоге получатся 8 «лучиков», которые объедините между собой. В итоге получится восьмиугольник.
От центра на всякой прямой линии отмерьте по 10 см. В итоге получатся 8 «лучиков», которые объедините между собой. В итоге получится восьмиугольник.
4. Метод 3. Для этого так же начертите круг, проведите через середину линию. После этого возьмите транспортир, поставьте его на центр и отмеряйте углы, рассматривая, что всякий секция восьмиугольника имеет в центре угол 45° . Позже этого на полученных лучах отмерьте длину в 10 см. и объедините их между собой. Восьмиугольник готов.
Полезный совет
Делайте чертеж твердым карандашом, побочные линии на котором после этого легко дозволено будет удалить
Верный восьмиугольник – это геометрическая фигура, у которой всякий угол составляет 135?, и все стороны между собою равны. Эта фигура дюже зачастую используется в архитектуре, к примеру, при постройке колон, а также при изготовлении дорожного знака STOP. Как же нарисовать положительный восьмиугольник?
Вам понадобится
- – альбомный лист;
- – карандаш;
- – линейка;
- – циркуль;
- – ластик.

Инструкция
1. Нарисуйте вначале квадрат. После этого проведите окружность так, дабы квадрат оказался внутри круга. Сейчас проведите две осевые серединные линии квадрата – горизонтальную и вертикальную до пересечения с кругом. Объедините прямыми отрезками точки пересечения осей с кругом и точки прикосновения описанной окружности с квадратом. Таким образом, получите стороны верного восьмиугольника.
2. Нарисуйте верный восьмиугольник иным методом. Вначале начертите окружность. После этого проведите горизонтальную линию через ее центр. Подметьте точку пересечения крайней правой границы окружности с горизонталью. Эта точка будет являться центром еще одной окружности, радиусом равным предыдущей фигуре.
3. Проведите вертикальную линию через точки пересечения 2-й окружности с первой. Поставьте ножку циркуля в точку пересечения вертикали с горизонталью и начертите небольшой круг радиусом, равным расстоянию от центра крошечной окружности до центра начального круга.
4. Начертите прямую линию через две точки – центр начального круга и точку пересечения вертикали и крошечной окружности. Продолжите ее до пересечения с рубежом изначальной фигуры. Это будет точка вершины восьмиугольника. Циркулем подметьте еще одну точку, проведя окружность с центром в точке пересечения крайней правой рубежом начального круга с горизонталью и радиусом, равным расстоянию от центра к теснее имеющейся вершине восьмиугольника.
5. Проведите прямую линию через две точки – центр начального круга и последнюю новообразованную точку. Продолжите прямую линию до пересечения с границами первоначальной фигуры.
6. Объедините прямыми отрезками ступенчато: точку пересечения горизонтали с правой рубежом начальной фигуры, после этого по часовой стрелке все образовавшиеся точки, включая точки пересечения осей с первоначальной окружностью.
Видео по теме
Куклин Алексей
Работа носит реферативный характер с элементами исследовательской деятельности. В ней рассматриваются различные способы построения правильных n-угольников. В работе содержится подробный ответ на вопрос о том, что всегда ли можно построить n-угольник с помощью циркуля и линейки. К работе прилагается презентация, которую можно найти на данном мини-сайте.
В ней рассматриваются различные способы построения правильных n-угольников. В работе содержится подробный ответ на вопрос о том, что всегда ли можно построить n-угольник с помощью циркуля и линейки. К работе прилагается презентация, которую можно найти на данном мини-сайте.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Предварительный просмотр:
https://accounts.google.com
Подписи к слайдам:
Построение правильных многоугольников Работу выполнил: ученик 9 класса «В» МБОУ СОШ № 10 Куклин Алексей
Правильные многоугольники Правильным многоугольником называют выпуклый многоугольник, у которого все стороны и углы равны. Перейти к примерам Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Назад Правильные многоугольники
Основоположниками раздела математики о правильных многоугольниках являлись древнегреческие ученые. Одними из них были Архимед и Евклид.
Одними из них были Архимед и Евклид.
Доказательство существования правильного n-угольника Если n (число углов многоугольника) больше 2, то такой многоугольник существует. Попробуем построить 8ми угольник и доказать это. Доказательство
Возьмем окружность произвольного радиуса с центром в точке О. Разделим её на некоторое число равных дуг, в нашем случае 8. Для этого проведем радиусы так, чтобы получилось 8 дуг, и угол между двумя ближайшими радиусами был равен 360°: количество сторон (в нашем случае 8), соответственно каждый угол будет равен 45°.
3. Получаем точки A1, A2, A3, A4, A5, A6, A7, A8. Поочередно соединяем их и получаем правильный восьмиугольник. Назад
Построение правильного многоугольника по стороне с использованием поворота Правильный многоугольник можно построить, зная его углы. Мы знаем, что сумма углов выпуклого n-угольника равна 180°(n — 2). Из этого можно вычислить угол многоугольника, разделив сумму на n. Углы Построение
Угол правильного: 3-угольника равен 60° 4-угольника равен 90° 5-угольника равен 108° 6-угольника равен 120° 8-угольника равен 135° 9-угольника равен 140° 10-угольника равен 144° 12-угольника равен 150° Градусная мера углов правильных треугольников Назад
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.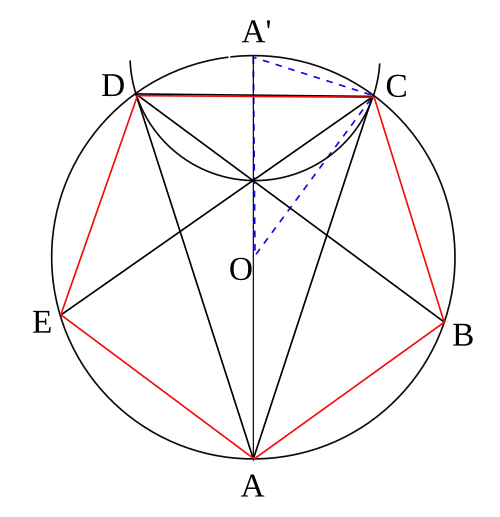 google.com
google.com
Подписи к слайдам:
В 1796 году одним из величайших математиков всех времён Карл Фридрих Гаусс показал возможность построения правильных n-угольников, если выполняется равенство, где n – количество углов, а k-любое натуральное число. Тем самым получилось, что в пределах 30 возможно деление окружности на 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30 равных частей. В 1836 году Ванцель доказал, что правильные многоугольники, не удовлетворяющие данному равенству при помощи линейки и циркуля построить нельзя. Теорема Гаусса
Построение треугольника Построим окружность с центром в точке О. Построим еще одну окружность того же радиуса проходящую через точку О.
3. Соединим центры окружностей и одну из точек их пересечения, получив правильный многоугольник. Назад Построение треугольника
Построение шестиугольника 1. Построим окружность с центром в точке О. 2. Проведем прямую линию через центр окружности. 3. Проведем дугу окружности того же радиуса с центром в точке пересечения прямой с окружностью до пересечения с окружностью.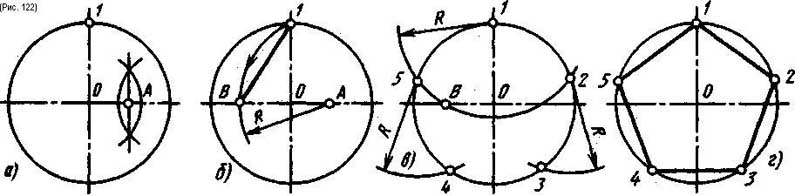
4. Проведем прямые через центр начальной окружности и точки пересечения дуги с этой окружностью. 5. Соединяем точки пересечения всех прямых с исходной окружностью и получаем правильный шестиугольник. Построение шестиугольника
Построение четырёхугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Из точек в которых диаметры касаются окружности проводим другие окружности данного радиуса до их пересечения (окружностей).
Построение четырёхугольника 4. Проводим прямые через точки пересечения окружностей. 5. Соединяем точки пересечения прямых и окружности и получаем правильный четырехугольник.
Построение восьмиугольника Можно построить любой правильный многоугольник у которого в 2 раза больше углов, чем у данного. Построим восьмиугольник при помощи четырехугольника. Соединим противоположные вершины четырехугольника. Проведем биссектрисы углов образованных пересекающимися диагоналями.
4. Соединим точки, лежащие на окружности, получив при этом правильный восьмиугольник.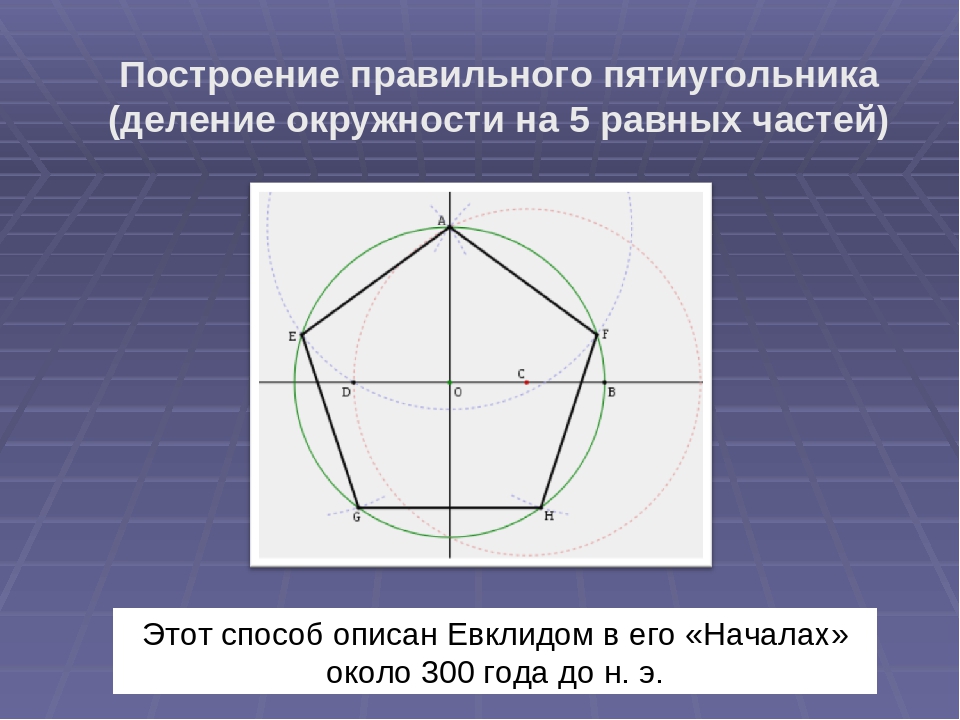 Построение восьмиугольника
Построение восьмиугольника
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Построение десятиугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Разделим радиус окружности пополам и из получившейся на нем точки проведем окружность проходящую через точку О.
Построение десятиугольника 4. Проведем отрезок из центра маленькой окружности к точки в которой большая окружность касается своего радиуса. 5. Из точки соприкосновения большой окружности и её радиуса проведем окружность так, что она будет соприкасаться с маленькой.
Построение десятиугольника 6. Из точек пересечения большой и полученной окружностей проведем окружности построенные в прошлый раз и так будем проводить до тех пор пока соседние окружности не соприкоснутся. 7. Соединим точки и получим десятиугольник.
Построение пятиугольника Для построения правильного пятиугольника нужно во время построения правильного десятиугольника соединить поочередно не все точки, а через одну.
Приблизительное построение правильного пятиугольника методом Дюрера Построим 2 окружности проходящие через центр друг друга. Соединим центры прямой, получив одну из сторон пятиугольника. Соединим точки пересечения окружностей.
Приблизительное построение правильного пятиугольника методом Дюрера 4. Проведем еще одну окружность того же радиуса с центром в точке пересечения двух других окружностей. 5. Проведем 2 отрезка как указано на рисунке.
Приблизительное построение правильного пятиугольника методом Дюрера 6. Соединим точки соприкосновения этих отрезков с окружностями с концами построенной стороны пятиугольника. 7. Достроим до пятиугольника.
Приблизительное построение правильного пятиугольника методами Коваржика, Биона
Об отрезках касательной к окружности
Чаще всего именно геометрические задачи вызывают затруднения у абитуриентов,
выпускников, участников математических олимпиад. Если посмотреть статистику ЕГЭ
2010 года, то видно, что к геометрической задаче С4 приступило около 12%
участников, а получило полный балл только 0,2% участников, а в целом задача
оказалась самой сложной из всех предложенных.
Если посмотреть статистику ЕГЭ
2010 года, то видно, что к геометрической задаче С4 приступило около 12%
участников, а получило полный балл только 0,2% участников, а в целом задача
оказалась самой сложной из всех предложенных.
Очевидно, что чем раньше мы предложим школьникам красивые или неожиданные по
способу решения задачи, тем больше вероятность заинтересовать и увлечь всерьёз и
надолго. Но, как же трудно найти интересные и сложные задачи на уровне 7 класса,
когда только начинается систематическое изучение геометрии. Что можно предложить
интересующемуся математикой школьнику, знающему только признаки равенства
треугольников, свойства смежных и вертикальных углов? Однако, можно ввести
понятие касательной к окружности, как прямой, имеющей с окружностью одну общую
точку; принять, что радиус, проведённый в точку касания, перпендикулярен
касательной. Конечно, стоит рассмотреть все возможные случаи расположения двух
окружностей и общих касательных к ним, которых можно провести от нуля до
четырёх. Доказав ниже предложенные теоремы, можно значительно расширить набор
задач для семиклассников. При этом попутно доказать важные или просто интересные
и занимательные факты. Причём, поскольку многие утверждения не входят в школьный
учебник, то обсуждать их можно и на занятиях кружка и с выпускниками при
повторении планиметрии. Актуальными эти факты оказались в прошлом учебном году.
Так как многие диагностические работы и сама работа ЕГЭ содержали задачу, для
решения которой необходимо было использовать доказываемое ниже свойство отрезка
касательной.
Доказав ниже предложенные теоремы, можно значительно расширить набор
задач для семиклассников. При этом попутно доказать важные или просто интересные
и занимательные факты. Причём, поскольку многие утверждения не входят в школьный
учебник, то обсуждать их можно и на занятиях кружка и с выпускниками при
повторении планиметрии. Актуальными эти факты оказались в прошлом учебном году.
Так как многие диагностические работы и сама работа ЕГЭ содержали задачу, для
решения которой необходимо было использовать доказываемое ниже свойство отрезка
касательной.
Т1Отрезки касательных к окружности,
проведённые из
одной точки равны (рис. 1)
Вот именно с теоремой
можно сначала познакомить семиклассников.
В процессе доказательства
использовали признак равенства прямоугольных треугольников,
сделали
вывод о том, что центр окружности лежит на биссектрисе угла ВСА.
Попутно вспомнили, что биссектриса угла есть геометрическое место точек
внутренней области угла, равноудалённых от его сторон. На этих доступных
даже только начинающим изучать геометрию фактах основывается решение уже
далеко нетривиальной задачи.
1. Биссектрисы углов А, В и С выпуклого
четырёхугольника АВСD
пересекаются в одной точке. Лучи АВ
и DC пересекаются в точке Е, а лучи
ВС и АD
в точке F. Докажите, что у невыпуклого четырёхугольника AECF
суммы длин противоположных сторон равны.
Решение (рис. 2). Пусть О – точка пересечения данных
биссектрис.
Тогда О равноудалена от всех сторон четырёхугольника
АВСD, то есть
является центром окружности вписанной в
четырёхугольник. По теореме 1 верны равенства: AR = AK,
ER = EP, FT = FK. Почленно сложим левые и
правые части, получим верное равенство:
Почленно сложим левые и
правые части, получим верное равенство:
(AR + ER) + FT = (AK +FK) + EP; AE + (FC + CT) = AF + (ЕC + PC). Так как СТ = РС, то АЕ + FC = AF + ЕC, что и требовалось доказать.
Рассмотрим необычную по формулировке задачу, для решения которой достаточно знание теоремы 1.
2. Существует ли n-угольник, стороны которого последовательно 1, 2, 3, …, n, в который можно вписать окружность?
Решение. Допустим, такой n-угольник существует. А1А2 =1,
…, Аn-1Аn = n – 1, АnА1 = n.
B1, …, Bn – соответствующие точки касания.
Тогда по теореме 1 A1B1 = A1Bn < 1,
n – 1 < AnBn < n. По свойству
отрезков касательных AnBn = AnBn-1.
Но, AnBn-1 < An-1Аn = n – 1.
Противоречие. Следовательно, нет n-угольника, удовлетворяющего
условию задачи.
По свойству
отрезков касательных AnBn = AnBn-1.
Но, AnBn-1 < An-1Аn = n – 1.
Противоречие. Следовательно, нет n-угольника, удовлетворяющего
условию задачи.
Т2 Суммы противолежащих сторон
четырёхугольника, описанного около
окружности, равны (рис. 3)
Школьники, как правило, легко доказывают это свойство описанного четырёхугольника. После доказательства теоремы 1, оно является тренировочным упражнением. Можно обобщить этот факт – суммы сторон описанного чётноугольника, взятых через одну, равны. Например, для шестиугольника ABCDEF верно: AB + CD + EF = BC + DE + FА.
3.
 МГУ. В четырёхугольнике ABCD расположены две
окружности:
первая окружность касается сторон AB, BC и AD, а вторая – сторон BC, CD и AD.
На сторонах BC и AD взяты точки E и F соответственно
так, отрезок EF касается обеих
окружностей, а периметр
четырёхугольника ABEF на 2p больше периметра
четырёхугольника ECDF. Найти AB, если CD = a.
МГУ. В четырёхугольнике ABCD расположены две
окружности:
первая окружность касается сторон AB, BC и AD, а вторая – сторон BC, CD и AD.
На сторонах BC и AD взяты точки E и F соответственно
так, отрезок EF касается обеих
окружностей, а периметр
четырёхугольника ABEF на 2p больше периметра
четырёхугольника ECDF. Найти AB, если CD = a.Решение (рис. 1). Так как четырёхугольники ABEF и ECDF вписанные, то по теореме 2 РABEF = 2(AB + EF) и РECDF = 2(CD + EF), по условию
РABEF – РECDF = 2(AB + EF) – 2(CD + EF) = 2p. AB – CD = p. АВ = а + р.
Опорная задача 1. Прямые АВ и АС – касательные в точках В и С к окружности с центром в точке О. Через произвольную точку Х дуги ВС
проведена касательная к окружности, пересекающая отрезки АВ и АС в точках М и Р соответственно.
 Докажите, что периметр
треугольника АМР и
величина угла МОР не зависят от выбора
точки Х.
Докажите, что периметр
треугольника АМР и
величина угла МОР не зависят от выбора
точки Х.Решение (рис. 5). По теореме 1 МВ = МХ и РС = РХ. Поэтому периметр треугольника АМР равен сумме отрезков АВ и АС. Или удвоенной касательной, проведённой к вневписанной окружности для треугольника АМР. Величина угла МОР измеряется половиной величины угла ВОС, который не зависит от выбора точки Х.
Опорная задача 2а. В треугольник со сторонами а, b и c вписана окружность, касающаяся стороны АВ и точке К. Найти длину отрезка АК.
Решение (рис. 6).
Способ первый (алгебраический). Пусть
АК
= АN = x,
тогда
BK = BM = c – x,
CM = CN = a – c + x. АС =
АN + NC,
тогда можем составить уравнение относительно х:
b = x + (a – c + x).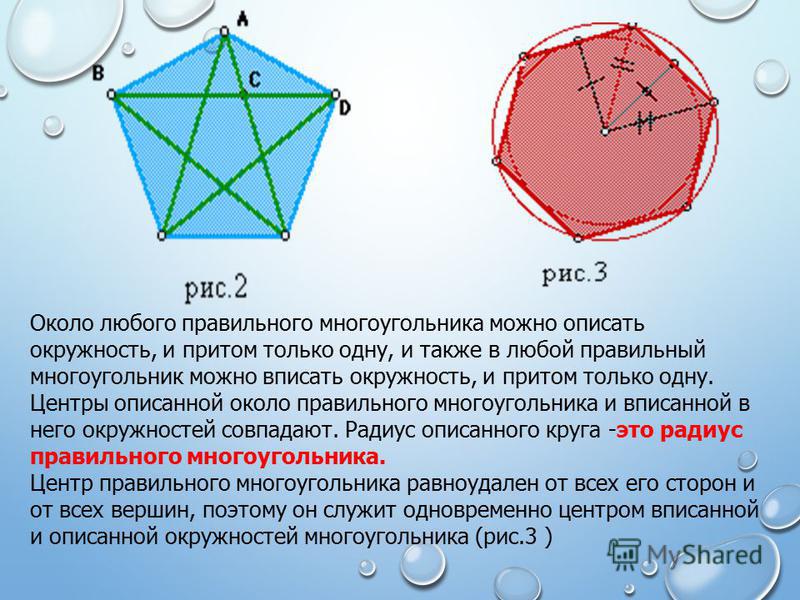 Откуда
.
Откуда
.
Способ второй (геометрический). Обратимся к схеме.
Отрезки
равных касательных, взятые по одному, в сумме дают полупериметр
треугольника. Красный и зелёный составляют сторону а. Тогда
интересующий нас отрезок х = р – а. Безусловно,
полученные результаты совпадают.
Опорная задача 2б. Найти длину отрезка касательной АК, если К – точка касания вневписанной окружности со стороной АВ. Решение (рис. 7). АК = АM = x, тогда BK = BN = c – x, CM = CN. Имеем уравнение b + x = a + (c – x). Откуда . Заметим, что из опорной задачи 1 следует, что СМ = рΔАВС. b + x = p; х = р – b. Полученные формулы имеют применение в следующих задачах.
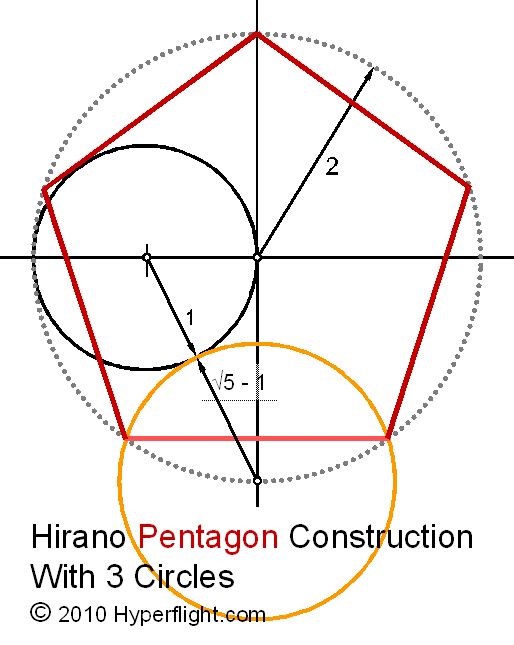
4. Найдите радиус окружности, вписанной в прямоугольный треугольник с катетами а, b и гипотенузой с. Решение (рис. 8). Так как OMCN – квадрат, то радиус вписанной окружности равен отрезку касательной CN. .
5. Докажите, что точки касания вписанной и вневписанной окружности со стороной треугольника симметричны относительно середины этой стороны.
Решение (рис. 9). Заметим, АК – отрезок касательной вневписанной окружности для треугольника АВС. По формуле (2) . ВМ – отрезок касательной вписанной окружности для треугольника АВС. По формуле (1) . АК = ВМ, а это и означает, что точки К и М равноудалены от середины стороны АВ, что и требовалось доказать.
6.
 К двум окружностям проведены две общие внешние касательные
и одна
внутренняя. Внутренняя касательная пересекает внешние в точках А,
В и касается окружностей в точках А1и В1.
Докажите, что АА1 = ВВ1.
К двум окружностям проведены две общие внешние касательные
и одна
внутренняя. Внутренняя касательная пересекает внешние в точках А,
В и касается окружностей в точках А1и В1.
Докажите, что АА1 = ВВ1.
Решение (рис. 10). Стоп… Да что тут решать? Это же просто другая формулировка предыдущей задачи. Очевидно, что одна из окружностей является вписанной, а другая вневписанной для некоего треугольника АВС. А отрезки АА1 и ВВ1соответствуют отрезкам АК и ВМ задачи 5. Примечательно, что задача, предлагавшаяся на Всероссийской олимпиаде школьников по математике, решается столь очевидным образом.
7. Стороны пятиугольника в порядке обхода равны 5, 6, 10, 7, 8. Доказать, что в этот пятиугольник нельзя вписать окружность.
Решение (рис. 11). Предположим, что в пятиугольник АВСDE
можно вписать окружность.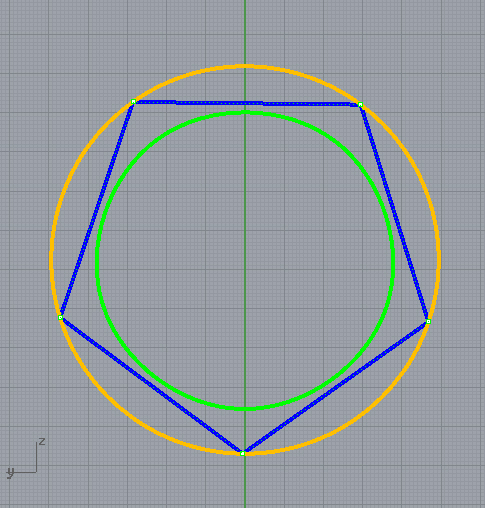 Причём стороны AB, BC, CD,
DE и ЕA равны соответственно 5, 6, 10, 7 и 8. Отметим
последовательно точки касания – F, G, H, M и
N. Пусть длина отрезка AF равна х.
Причём стороны AB, BC, CD,
DE и ЕA равны соответственно 5, 6, 10, 7 и 8. Отметим
последовательно точки касания – F, G, H, M и
N. Пусть длина отрезка AF равна х.
Тогда BF = FD – AF = 5 – x = BG. GC = BC – BG = = 6 – (5 – x) = 1 + x = CH. И так далее: HD = DM = 9 – x; ME = EN = x – 2, AN = 10 – х.
Но, AF = AN. То есть 10 – х = х; х = 5. Однако, отрезок касательной AF не может равняться стороне АВ. Полученное противоречие и доказывает, что в данный пятиугольник нельзя вписать окружность.
8. В шестиугольник вписана окружность, его стороны в порядке обхода равны 1,
2, 3, 4, 5. Найти длину шестой стороны.
Решение. Конечно, можно отрезок касательной обозначить за х, как и в предыдущей задаче, составить уравнение и получить ответ. Но, гораздо эффективнее и эффектнее использовать примечание к теореме 2: суммы сторон описанного шестиугольника, взятых через одну, равны.
Тогда 1 + 3 + 5 = 2 + 4 + х, где х – неизвестная шестая сторона, х = 3.
9. МГУ, 2003 г. химический факультет, № 6(6). В пятиугольник АВСDE вписана окружность, Р – точка касания этой окружности со стороной ВС. Найдите длину отрезка ВР, если известно, что длины всех сторон пятиугольника есть целые числа, АВ = 1, СD = 3.
Решение (рис.12). Так как длины всех сторон являются целыми
числами, то равны дробные
части длин отрезков BT, BP,
DM, DN, AK и AT. Имеем,
АТ + ТВ = 1,
и дробные части длин
отрезков AT и TB равны. Это возможно
только тогда, когда
АТ + ТВ = 0,5.
По теореме 1 ВТ + ВР.
Это возможно
только тогда, когда
АТ + ТВ = 0,5.
По теореме 1 ВТ + ВР.
Значит, ВР = 0,5.
Заметим, что условие СD = 3 оказалось невостребованным.
Очевидно,
авторы задачи предполагали какое-то другое решение. Ответ: 0,5.
10. В четырёхугольнике ABCD AD = DC, AB = 3, BC = 5. Окружности, вписанные в треугольники ABD и CBD касаются отрезка BD в точках M и N соответственно. Найти длину отрезка MN.
Решение (рис. 13). MN = DN – DM. По формуле (1) для треугольников DBA и DBС соответственно, имеем:
11. В четырёхугольник ABCD можно вписать окружность.
Окружности,
вписанные в треугольники ABD и CBD имеют радиусы R и r
соответственно. Найти расстояние между центрами этих окружностей.
Найти расстояние между центрами этих окружностей.
Решение (рис. 13). Так как по условию четырёхугольник ABCD вписанный, по теореме 2 имеем: AB + DC = AD + BC. Воспользуемся идеей решения предыдущей задачи. . Это означает, что точки касания окружностей с отрезком DM совпадают. Расстояние между центрами окружностей равно сумме радиусов. Ответ: R + r.
Фактически доказано, что условие – в четырёхугольник ABCD можно вписать окружность, равносильно условию – в выпуклом четырехугольнике ABCD окружности, вписанные в треугольники ABC и ADC касаются друг друга. Верно обратное.
Доказать эти два взаимно-обратных утверждения предлагается в следующей задаче, которую можно считать обобщением данной.
12. В выпуклом четырехугольнике ABCD
(рис. 14) окружности,
вписанные в треугольники ABC и
ADC касаются друг друга.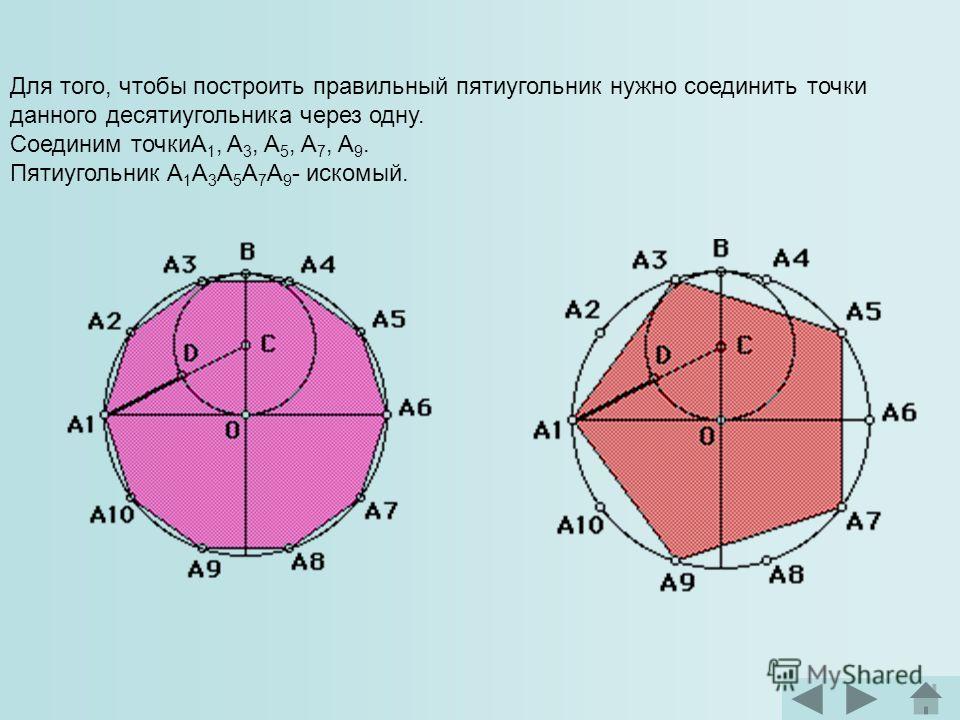 Докажите, что окружности,
вписанные в
треугольники ABD и BDC также касаются друг друга.
Докажите, что окружности,
вписанные в
треугольники ABD и BDC также касаются друг друга.
13. В треугольнике АВС со сторонами а, b и c на стороне ВС отмечена точка D так, что окружности, вписанные в треугольники АВD и ACD касаются отрезка AD в одной точке. Найти длину отрезка BD.
Решение (рис. 15). Применим формулу (1) для треугольников ADC и ADB, вычислив DM двумя
Оказывается, D – точка касания со стороной ВС окружности, вписанной в треугольник АВС. Верно обратное: если вершину треугольника соединить с точкой касания вписанной окружности на противоположной стороне, то окружности, вписанные в получившиеся треугольники, касаются друг друга.
14. Центры О1, О2 и О3 трёх непересекающихся окружностей одинакового радиуса расположены в вершинах треугольника.
 Из точек О1, О2, О3 проведены касательные к
данным окружностям так, как показано на рисунке.
Из точек О1, О2, О3 проведены касательные к
данным окружностям так, как показано на рисунке.Известно, что эти касательные, пересекаясь, образовали выпуклый шестиугольник, стороны которого через одну покрашены в красный и синий цвета. Докажите, что сумма длин красных отрезков равна сумме длин синих.
Решение (рис.
16). Важно понять, как использовать тот
факт, что заданные
окружности имеют одинаковые радиусы. Заметим, что
отрезки ВR и DМ равны, что следует из равенства
прямоугольных треугольников О1ВR и O2BM.
Аналогично DL = DP, FN = FK. Почленно
складываем равенства, затем вычитаем из полученных сумм одинаковые
отрезки касательных, проведенных из вершин А, С, и Е
шестиугольника ABCDEF: АR и AK, CL и CM,
EN и EP. Получаем требуемое.
Получаем требуемое.
Вот пример задачи по стереометрии, предлагавшейся на XII Международном математическом турнире старшеклассников “Кубок памяти А. Н. Колмогорова”.
16. Дана пятиугольная пирамида SA1A2A3A4A5. Существует сфера w , которая касается всех ребер пирамиды и другая сфера w 1, которая касается всех сторон основания A1A2A3A4A5и продолжений боковых рёбер SA1, SA2, SA3, SA4, SA5за вершины основания. Докажите, что вершина пирамиды равноудалена от вершин основания. (Берлов С. Л., Карпов Д. В.)
Решение. Пересечение сферы w с плоскостью любой из граней сферы – это вписанная окружность грани. Пересечение сферы w 1 с каждой из граней SAiAi+1 – вневписанная окружность, касающаяся стороны AiAi+1 треугольника SAiAi+1 и продолжений двух других сторон.
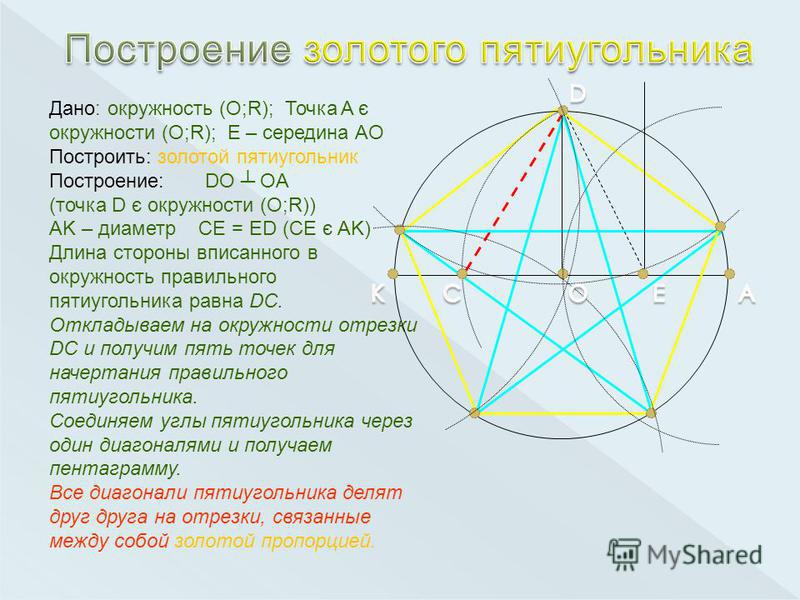 Обозначим точку касания
w 1 с продолжением стороны SAi через Bi. По опорной задаче 1 имеем,
что SBi = SBi+1 = pSAiAi+1
, следовательно, периметры всех боковых граней пирамиды равны.
Обозначим точку касания w со стороной SAi через Сi. Тогда SC1 = SC2 = SC3 = SC4 = SC5= s,
Обозначим точку касания
w 1 с продолжением стороны SAi через Bi. По опорной задаче 1 имеем,
что SBi = SBi+1 = pSAiAi+1
, следовательно, периметры всех боковых граней пирамиды равны.
Обозначим точку касания w со стороной SAi через Сi. Тогда SC1 = SC2 = SC3 = SC4 = SC5= s, так как отрезки касательных равны. Пусть CiAi = ai. Тогда pSAiAi+1 = s+ai+ai+1, и из равенства периметров следует, что a1 = a3 = a5 = a2 = a4, откуда SA1 = SA2 = SA3 = SA4 = SA5.

17. ЕГЭ. Диагностическая работа 8.12.2009 г, С–4. Дана трапеция ABCD, основания которой BC = 44, AD = 100, AB = CD = 35. Окружность, касающаяся прямых AD и AC, касается стороны CD в точке K. Найдите длину отрезка CK.
Решение.
Найдем диагональ AC. Опустим из вершин B и C на сторону AD перпендикуляры BE и CF соответственно. AE = FD, так как трапеция равнобедренная. BCFE – прямоугольник.
Возможны две геометрические конфигурации.
Первый случай (рис. 18): окружность вписана в треугольник ACD.
По формуле (1)
Второй вариант (рис.19): окружность касается продолжений сторон AC и AD за точками C и D соответственно и отрезка CD.
По формуле (2)
Ответ: 5 или 30.
18. ЕГЭ. 4.6. 2010 г. В треугольнике АВС АВ = 13, ВС = 11, СА = 9. Точка D лежит на прямой АС, причём АD : DС = 1 : 9. Окружности, вписанные в каждый из треугольников ВDС и ВDА, касаются стороны ВD в точках Е и F. Найдите длину отрезка EF.
Решение. Возможны два случая (рис. 20 и рис. 21). По формуле (1) найдём длины отрезков DE и DF.
В первом случае AD = 0,1АС, СD = 0,9AC. Во втором – AD = 0,125АС, СD = 1,125AC. Подставляем данные и получаем ответ: 4,6 или 5,5.
Задачи для самостоятельного решения/
1. Периметр равнобедренной трапеции, описанной около окружности равен 2р. Найдите проекцию диагонали трапеции на большее основание.
 (1/2р)
(1/2р)2. Открытый банк задач ЕГЭ по математике. В4. К окружности, вписанной в треугольник ABC (рис. 22), проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника. (24)
3. В треугольник АВС вписана окружность. MN – касательная к окружности, MÎ АС, NÎ ВС, ВС = 13, АС = 14, АВ = 15. Найдите периметр треугольника MNC. (12)
4. К окружности, вписанной в квадрат со стороной а, проведена касательная, пересекающая две его стороны. Найдите периметр отсечённого треугольника. (а)
5. Окружность вписана в пятиугольник со сторонами а, d, c, d и e. Найдите отрезки, на которые точка касания делит сторону, равную а.
Ответ:
6. В треугольник со сторонами 6, 10 и 12 вписана
окружность. К окружности проведена касательная так, что она пересекает две
большие стороны. Найдите периметр отсечённого треугольника. (16)
В треугольник со сторонами 6, 10 и 12 вписана
окружность. К окружности проведена касательная так, что она пересекает две
большие стороны. Найдите периметр отсечённого треугольника. (16)
7. CD – медиана треугольника ABC. Окружности, вписанные в треугольники ACD и BCD, касаются отрезка CD в точках M и N. Найдите MN, если АС – ВС = 2. (1)
8. В треугольнике АВС со сторонами а, b
и c на стороне ВС отмечена точка D. К окружностям,
вписанным в треугольники АВD и ACD, проведена общая касательная,
пересекающая AD в точке М. Найти длину отрезка АМ. (Длина
АМ не зависит от положения точки D и
равна ½ (c + b – a))
9. В прямоугольный треугольник вписана окружность
радиуса а. Радиус окружности, касающейся гипотенузы и продолжений
катетов, равен R. Найдите длину гипотенузы. (R – a)
10. В треугольнике АВС известны длины сторон: АВ = с, АС = b, ВС = а. Вписанная в треугольник окружность касается стороны АВ в точке С1. Вневписанная окружность касается продолжения стороны АВ за точку А в точке С2. Определите длину отрезка С1С2. (b)
11. Найдите длины сторон треугольника, разделённых точкой касания вписанной окружности радиуса 3 см на отрезки 4 см и 3 см. (7, 24 и 25 см в прямоугольном треугольнике)
12.
Соросовская олимпиада 1996 г, 2 тур, 11 класс.
Дан треугольник АВС, на сторонах которого отмечены точки А1,
В1, С1. Радиусы окружностей вписанных в треугольники
АС1В1, ВС1А1, СА1В1
равны по r. Радиус окружности, вписанной в треугольник А1В1С1равен R. Найти радиус окружности, вписанной в треугольник АВС.
(R + r).
Радиус окружности, вписанной в треугольник А1В1С1равен R. Найти радиус окружности, вписанной в треугольник АВС.
(R + r).
Задачи 4–8 взяты из задачника Гордина Р. К. “Геометрия. Планиметрия.” Москва. Издательство МЦНМО. 2004.
Найдите площадь правильного пятиугольника, вписанного в круг
Трейси, у нас для вас три ответа …
Привет, Трейси.
Площадь фигуры всегда равна сумме площадей всех ее частей. Это означает, что мы можем разделить пятиугольник на более мелкие формы, которые легко найти площадь и сложить (или умножить).
Если мы нарисуем радиус ко всем углам зеленым цветом, пятиугольник синим и круг красным, мы получим диаграмму слева.
Я также провел линию от центра круга до середины каждой стороны пятиугольника. Поскольку это середина, она встречается со стороной под прямым углом, поэтому образует конгруэнтные треугольники. Я думаю, вы можете видеть, что по симметрии здесь десять равных прямоугольных треугольников.
Я думаю, вы можете видеть, что по симметрии здесь десять равных прямоугольных треугольников.
Теперь вы можете использовать теорему Пифагора, чтобы найти высоту прямоугольного треугольника. Затем используйте это, чтобы найти площадь прямоугольного треугольника. Наконец, умножьте на количество равных треугольников в пятиугольнике.
Надеюсь, это поможет,
Стивен Ла Рок.
Хай Трейси,
Площадь правильного пятиугольника будет равна сумме площадей пяти одинаковых равнобедренных треугольников, которые вы можете сформировать, проведя радиусы к вершинам пятиугольника.
Теперь вы видите, что вам известны длины всех трех сторон каждого отдельного треугольника.
Формула Герона может использоваться для определения площади треугольника, если известны все три стороны:
где a, b, c — стороны, а s = (1/2) (a + b + c)
Вы также можете определить размер центрального угла (C), который также является углом при вершине каждого образованного треугольника. а затем используйте Area = (1/2) ab * sinC.
а затем используйте Area = (1/2) ab * sinC.
Просто помните, что после того, как вы найдете площадь одного треугольника, вы должны умножить его на 5, чтобы получить площадь всего пятиугольника.
Это всего лишь несколько способов решения данной проблемы.
Надеюсь, это поможет, Лиэнн
Трейси,
Площадь равна 1/2 высоты основания, умноженной на высоту треугольника, который состоит из одной из сторон пятиугольника и радиусов до двух конечных точек этой стороны. Вы умножаете эту площадь на 5, чтобы получить площадь пятиугольника.Я полагаю, что вы можете использовать 6 в качестве длины стороны, но на самом деле сторона имеет длину 10 * sin (36 градусов), что равно примерно 5,8779. Высота (то есть расстояние от центра пятиугольника до стороны) составляет 5 * cos (36 градусов) (что равняется примерно 4,0451). (Если вы используете теорему Пифагора с треугольником, стороны которого равны 5, 5 и 6, высота до основания будет равна 4 вместо более точного 4,0451.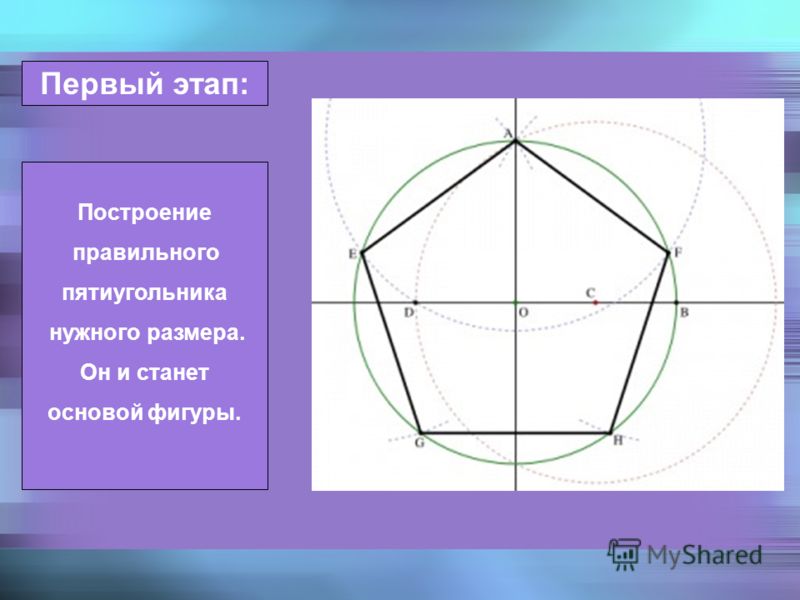 Фактически, треугольник состоит из половины стороны, высоты и радиуса представляет собой прямоугольный треугольник 3-4-5.)
Фактически, треугольник состоит из половины стороны, высоты и радиуса представляет собой прямоугольный треугольник 3-4-5.)
Крис
Генри Х. Ладлоу, геометрическая конструкция правильного десятиугольника и пятиугольника, вписанного в круг.
Страница [без номера]
ЦЕЛЬ БИБЛИОГРАФИЧЕСКОЙ ЗАПИСИ
Библиотека для выпускников
университет Мичигана
Офис консервации
Номер хранилища:
ACR8324
UL FMT B RT a BL m T / C DT 19.07.88 R / DT 19.07.88 CC STAT мм E / L 1
010 :: а 04005550 // r84
035/1 :: a (RLIN) MIUG86-B80566
035/2 :: a (CaOTULAS) 160547486
040 :: Я DLC / ICU c ICU I d MiU
050/1: 0: Я QA482 Jb.L94
100: 1: Ладлоу, Генри Х.I q (Генри Хант), 1854-1926 гг.
245: 00: 1 Геометрическое построение правильного десятиугольника и пятиугольника.
начертано в круге Генри Х. Ладлоу.
260 :: Я — Чикаго, Я — Издательская компания «Открытый суд», | c 1904 г.
300/1 :: | al2p. c 20см.
500/1 :: | a «Отпечатано для автора».
590/2 :: a In [Брошюры. Математика. 1841-1906] v.12.
650/1: 0: | Пентагон
740/1: 0: a [Брошюры.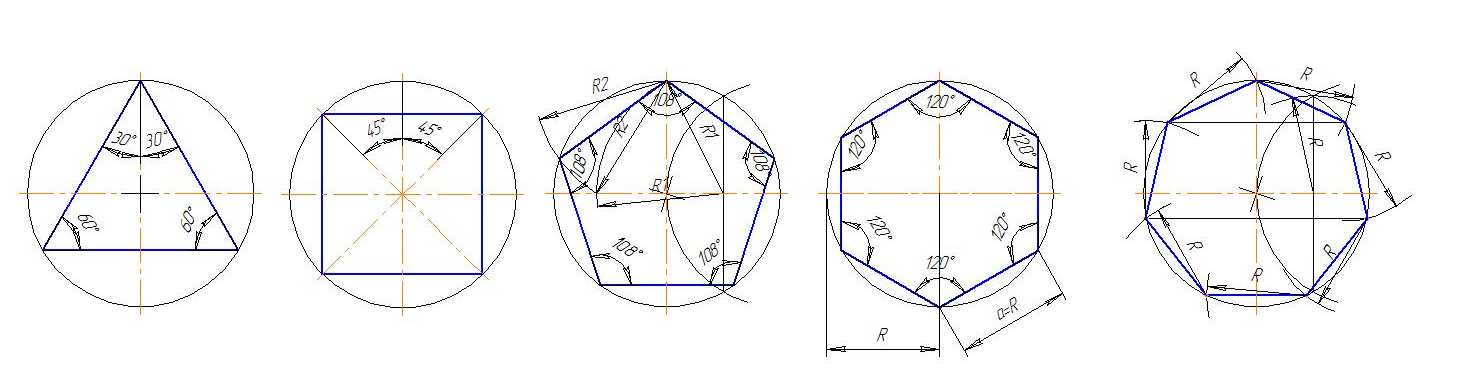 Математика. 1841-1906] | п v.12.
998 :: c РАН | с 9120
Отсканировано Imagenes Digitales
Ногалес, Аризона
От имени
Отдел консервации
Библиотеки Мичиганского университета
Дата начала работы:
Оператор:
Математика. 1841-1906] | п v.12.
998 :: c РАН | с 9120
Отсканировано Imagenes Digitales
Ногалес, Аризона
От имени
Отдел консервации
Библиотеки Мичиганского университета
Дата начала работы:
Оператор:
Страница [без номера] ГЕОМЕТРИЧЕСКОЕ СТРОИТЕЛЬСТВО ПРИНАДЛЕЖАЩИЙ ОБЫЧНЫЙ ДЕКАГОН И ПЕНТАГОН ЗАПИСАНО ПО КРУГУ ОТ ГЕНРИ Х.LUDLOW ОСНОВНОЙ В АРТИЛЛЕРИЙСКОМ КОРПУСЕ АРМИИ США НАПЕЧАТАНО ДЛЯ ITHE A U’HOR ОТКРЫТО ЧИКАГО COUR; T PUBLISHING CO. 1904 г.
Страница [без номера] АВТОРСКОЕ ПРАВО, 1904 г. ЭНРИ Х. ЛАДЛОУ СТАРКВИЛЛ, мисс.
Страница [без номера] СОДЕРЖАНИЕ. СТРАНИЦА Теорема I …………….. 7 Теорема II ……………. 8 Теорема III …………… 9 Проблема I ……………. 9 Проблема II ……………. 11 Проблема III …………… 11
Страница [без номера]
Стр. 5
ПРЕДИСЛОВИЕ.Весной 1873 года в Вест-Пойнте, штат Нью-Йорк,
внимание автора было обращено на построение в последнем абзаце этой статьи
покойный Альберт Э.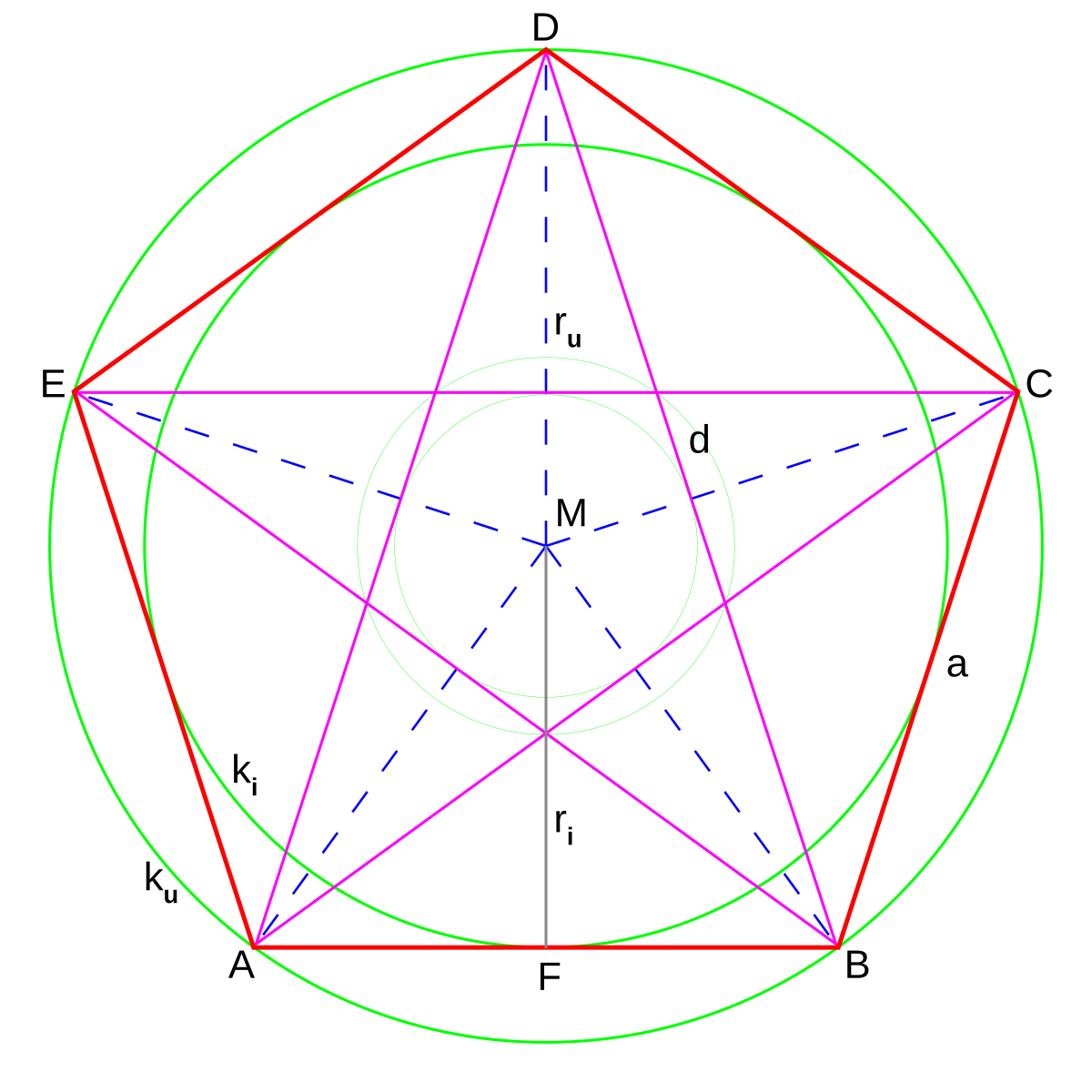 Черч, затем профессор математики в Военной академии США, Запад
Пойнт, Н. Я. Он заявил классу писателя:
затем изучая геометрию как кадеты, это
древнее сооружение, вероятно, китайского
источник; что он проверил это тригонометрическим
вычисление с небольшим расхождением, которое
может быть связано с неточностью таблиц.Он
выразил сомнение в его геометрической истинности и
предложил классу как задачу «Доказать
или опровергнуть его истинность ». * В результате были найдены два решения:
один покойным Эдвардом С. Фэрроу, другой —
писатель.
Случайно к решению писателя пришло
конструкция в пункте 4, который действительно
часть старинного сооружения. Это так много
проще, чем конструкция, обычно приводимая в
элементарная геометрия, которой учил писатель
кадетам в Вест-Пойнт, штат Нью-Йорк, в 1880 году, а затем и в других местах с этим доказательством.* Конструкция без доказательств может быть найдена у Дэвиса.
и Математический словарь Пека.
Черч, затем профессор математики в Военной академии США, Запад
Пойнт, Н. Я. Он заявил классу писателя:
затем изучая геометрию как кадеты, это
древнее сооружение, вероятно, китайского
источник; что он проверил это тригонометрическим
вычисление с небольшим расхождением, которое
может быть связано с неточностью таблиц.Он
выразил сомнение в его геометрической истинности и
предложил классу как задачу «Доказать
или опровергнуть его истинность ». * В результате были найдены два решения:
один покойным Эдвардом С. Фэрроу, другой —
писатель.
Случайно к решению писателя пришло
конструкция в пункте 4, который действительно
часть старинного сооружения. Это так много
проще, чем конструкция, обычно приводимая в
элементарная геометрия, которой учил писатель
кадетам в Вест-Пойнт, штат Нью-Йорк, в 1880 году, а затем и в других местах с этим доказательством.* Конструкция без доказательств может быть найдена у Дэвиса.
и Математический словарь Пека.
Стр. 6
6 ПРЕДИСЛОВИЕ.
Вопрос был недавно поднят
будут ли геометрические доказательства этих построений
опубликованы, писатель предлагает их
общественность, считая их достойными включения в учебники элементарной геометрии. Вступительные параграфы были помещены в
максимально просто довести до этих построек. Х. Х. Л.СЕЛЬСКОХОЗЯЙСТВЕННЫЙ КОЛЛЕДЖ MISSISSIPPI,
Декабрь 1903 г.
Вступительные параграфы были помещены в
максимально просто довести до этих построек. Х. Х. Л.СЕЛЬСКОХОЗЯЙСТВЕННЫЙ КОЛЛЕДЖ MISSISSIPPI,
Декабрь 1903 г.
Стр. 7
ГЕОМЕТРИЧЕСКОЕ ПОСТРОЕНИЕ
ОБЫЧНЫЙ ДЕКАГОН И ПЕНТАГОН
ЗАПИСАНО ПО КРУГУ.
1. ТЕОРЕМА I. Сторона правильного десятиугольника, вписанного в окружность, равна стороне
средний сегмент радиуса, деленный на
крайнее и среднее соотношение.
А
21 год
C
Пусть AB представляет собой сторону правильного десятиугольника.
вписаны в круг с центром C. Нарисуйте
радиусов CA, CB и разделим угол ABC пополам на
BD, встреча AC в D.
Поскольку AB — сторона правильной вписанной
десятиугольник, это хорда, составляющая одну десятую окружности, а угол ACB составляет одну десятую четвертой.
прямые углы, или две пятых прямого угла.В
сумма внутренних углов равнобедренного треугольника ABC составляет два прямых угла, причем углы
Каждый из A и B равен — (2 — -) —
прямой угол, и половина B равна C. Следовательно
треугольник BCD равнобедренный, что дает BD = CD.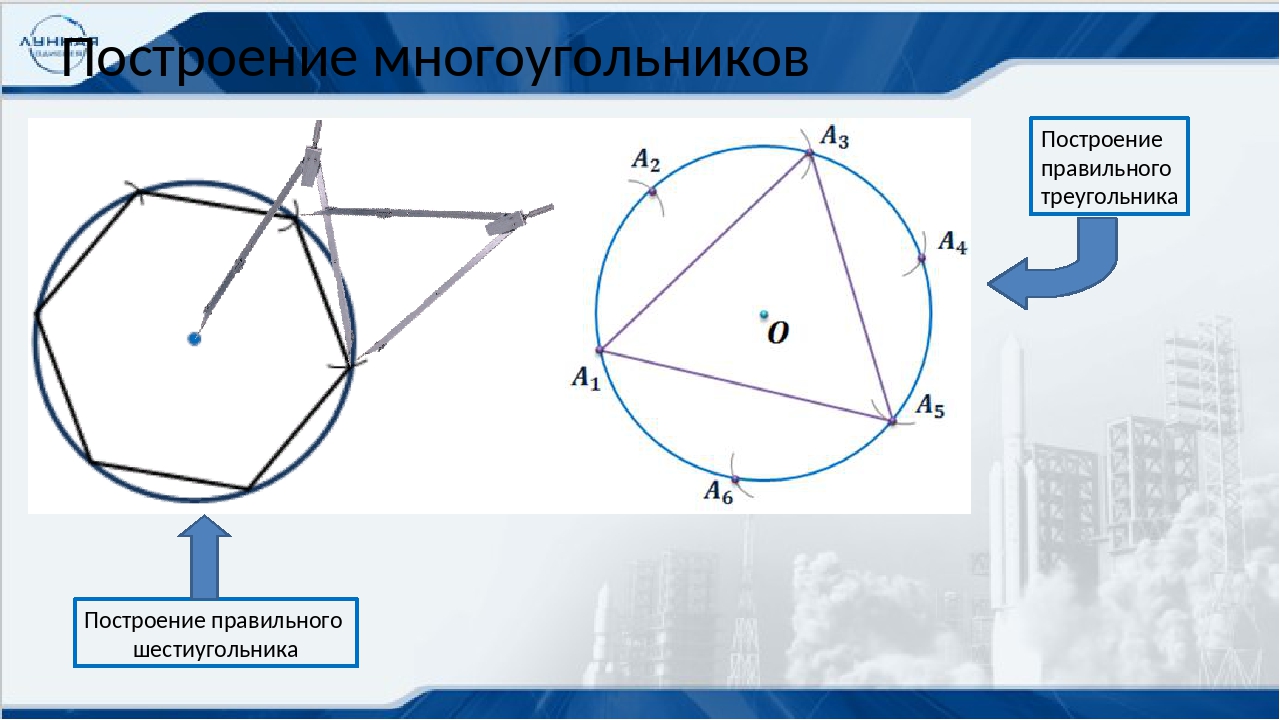 Треугольники CBA и BDA, имеющие угол
Треугольники CBA и BDA, имеющие угол
Стр. 8 8 КОНСТРУКЦИЯ ДЕКАГОНА И ПЕНТАГОНА. А в общем и угол BCA, равный угол DBA, равноугольны и похожи друг на друга. Но треугольник CBA равнобедренный, поэтому BDA тоже равнобедренный, а AB = BD — CD.Поскольку треугольники CBA и BDA подобны, у нас есть CA: AB :: AB: DA, или CA: CD :: CD: CA, в котором AB = CD. К. Э. Д. 2. ТЕОРЕМА II. Высота дуги, образуемой стороной правильного пятиугольника. вписанный в круг равен половине крайний отрезок радиуса делится на крайнее и среднее соотношение. А t4 Возобновим построение ~ 1. Из B ничья BE перпендикулярно CA, встречая его в точке E и дуга, образованная в F. Поскольку BF перпендикулярна радиусу CA, хорда BF и ее дуга Оба BAF делятся пополам CA.Следовательно, BF является сторона правильного вписанного пятиугольника. Поскольку BE перпендикуляр из вершины B к основанию DA равнобедренного треугольника BDA, он делит основание пополам в точке E, и EA — — DA. К. Э. Д.
Стр. 9
КОНСТРУКЦИЯ ДЕКАГОНА И ПЕНТАГОНА.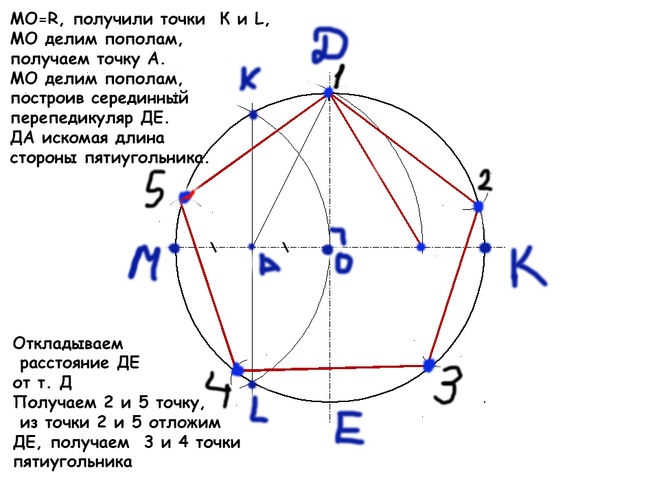 9
3. ТЕОРЕМА III. В любом круге квадрат
стороны правильного вписанного пятиугольника
превышает квадрат стороны обычного
вписанный десятиугольник квадратом
радиус.
Возобновим построение ~ 2. Начиная с FB- 2
А
E 2
C
EB, у нас FB2 4 EB2.Правый треугольник
AEB дает EB2 = AB2 — EA2. Следовательно,
FB2 = 4 AB — 4EA2.
Поскольку AB = CD = CA- DA, имеем FB2
3 AB2 + (CA2 — 2 CA x DA + DA2) — 4 EA2.
Но СА делится на крайнее и среднее соотношение.
atD, ~ 1, что дает CA x DA = CD2 = AB2, и по
~ 2, DA2 4 EA2, что сводит указанное выше к
FB2 = AB2 + CA2.
К. Э. Д.
4. ПРОБЛЕМА I. Разделить данную прямую.
линия в крайнем и среднем соотношении.
Пусть AB представляет данную линию. В B возвести
перпендикуляр BC = AB и производим AB до
D, что делает BD = I AB. Присоединяйтесь к CD. От D как
9
3. ТЕОРЕМА III. В любом круге квадрат
стороны правильного вписанного пятиугольника
превышает квадрат стороны обычного
вписанный десятиугольник квадратом
радиус.
Возобновим построение ~ 2. Начиная с FB- 2
А
E 2
C
EB, у нас FB2 4 EB2.Правый треугольник
AEB дает EB2 = AB2 — EA2. Следовательно,
FB2 = 4 AB — 4EA2.
Поскольку AB = CD = CA- DA, имеем FB2
3 AB2 + (CA2 — 2 CA x DA + DA2) — 4 EA2.
Но СА делится на крайнее и среднее соотношение.
atD, ~ 1, что дает CA x DA = CD2 = AB2, и по
~ 2, DA2 4 EA2, что сводит указанное выше к
FB2 = AB2 + CA2.
К. Э. Д.
4. ПРОБЛЕМА I. Разделить данную прямую.
линия в крайнем и среднем соотношении.
Пусть AB представляет данную линию. В B возвести
перпендикуляр BC = AB и производим AB до
D, что делает BD = I AB. Присоединяйтесь к CD. От D как
Стр.10
10 КОНСТРУКЦИЯ ДЕКАГОНА И ПЕНТАГОНА.центр с DC в качестве радиуса, нарисуйте дугу AB в точке E.
Тогда будет AB: EB :: EB: AE.
Для, создайте дугу EC до тех пор, пока она не прорежет AB proA E P
в точке G.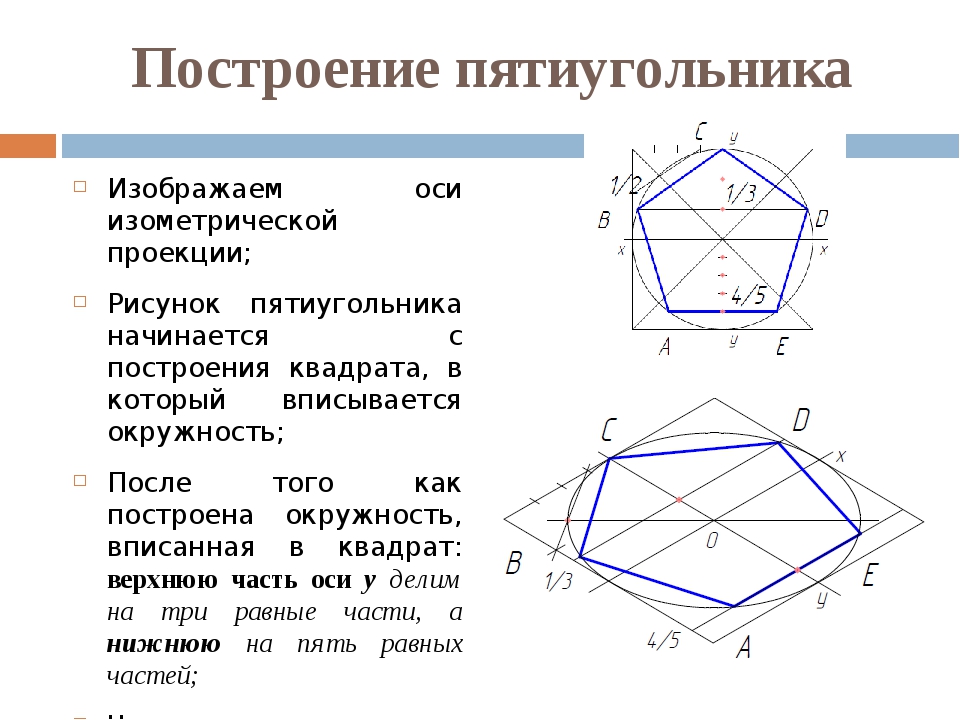 Поскольку BC — перпендикуляр из
точка полуокружности к диаметру,
это среднее значение, пропорциональное сегментам
диаметра, давая
EB: BC :: BC: BG.
По делению мы имеем
BC-EB: EB :: BG- BC: BC,
но
BC — 4B EBAB EB AE, BG — BC BGAB = BG — 2BD = EB,
и
BC = AB,
давая
AE: EB :: EB: AB.
К. Э. Д.
5. Если требуется внешняя точка разделения,
он будет находиться во второй точке пересечения G.Поскольку, как указано выше,
BG: BC :: BC: EB.
По составу
BG + BC BG :: BC: + EB: BC.
Поскольку BC — перпендикуляр из
точка полуокружности к диаметру,
это среднее значение, пропорциональное сегментам
диаметра, давая
EB: BC :: BC: BG.
По делению мы имеем
BC-EB: EB :: BG- BC: BC,
но
BC — 4B EBAB EB AE, BG — BC BGAB = BG — 2BD = EB,
и
BC = AB,
давая
AE: EB :: EB: AB.
К. Э. Д.
5. Если требуется внешняя точка разделения,
он будет находиться во второй точке пересечения G.Поскольку, как указано выше,
BG: BC :: BC: EB.
По составу
BG + BC BG :: BC: + EB: BC.
Стр.
КОНСТРУКЦИЯ ДЕКАГОНА И ПЕНТАГОНА. 11 Но
BG + BC BG + AB = AG, BC + EB = AB +
EB = 2 BD EB = BG,
и
BC = AB,
давая
АГ: БГ :: БГ: АВ.
К. Э. Д.
6. ПРОБЛЕМА II. Вписать правильный десятиугольник в заданный круг.
А
Пусть C — центр, а CA — любой радиус. В
A проведите касательную AB и отложите AB
AC. Присоединяйтесь к CB. Из B как центр с BC
в качестве радиуса описать дуговую резку BA, произведенную
в Д.
Тогда ~~ 4, 1, DA — искомая сторона.От
Отсрочка следующих друг за другом аккордов, каждая равная AD.
7. ПРОБЛЕМА III. Чтобы вписать правильный пятиугольник в заданный круг.
Первый способ. Пусть C — центр
заданный круг, АС любого радиуса. Нарисуйте радиус
Чтобы вписать правильный пятиугольник в заданный круг.
Первый способ. Пусть C — центр
заданный круг, АС любого радиуса. Нарисуйте радиус
Стр. 12
12 КОНСТРУКЦИЯ ДЕКАГОНА И ПЕНТАГОНА. CB перпендикулярно AC. Произвести от AC до D,
создание CD -i AC. Присоединяйтесь к BD. От D как
A C JP
центр, радиусом DB проведите дуговую резку
AC в E. Нарисуйте аккорд BE. Это будет
сторона требуемого пятиугольника.Ведь на ~ 4 АС делится на крайнюю и
среднее отношение в E, а EC равно стороне
правильного вписанного десятиугольника, ~~ 1, 6. Но
в прямоугольном треугольнике BCE BE2 = EC2 + CB2.
Следовательно, ~ 3, BE равна стороне
правильный вписанный пятиугольник.
От B отложите последовательные аккорды, каждый равный
быть.
Второй способ. Нарисуйте перпендикуляр
биссектриса AE. Это будет нужная сторона.
Ведь его высота дуги от хорды такая же.
как и сторона правильного вписанного пятиугольника ~ 2, обе хорды равны
далеки от центра и равны.Третий способ. Впишите правильный десятиугольник,
~ 6, и соединим альтернативные вершины.
вписанных и описанных окружностей и многоугольников в GMAT
вписанных и описанных
Еще один сложный тип геометрической диаграммы включает многоугольники «внутри» окружностей или окружности «внутри» многоугольников. Когда многоугольник находится «внутри» круга, каждая вершина должна лежать на нем:
На этой диаграмме неправильный пятиугольник ABCDE равен , вписанному в круг , а круг — , описанному вокруг пятиугольника, .Мы также можем сказать: круг ограничивает пятиугольник. Слово «вписанный» описывает внутреннюю форму, а слово «описанный» описывает внешнюю форму. Вот еще одна диаграмма с многоугольником снаружи.
Обратите внимание, что каждая сторона этого неправильного пятиугольника составляет касательную к окружности. Итак, пятиугольник — это , описанный на по окружности, и круг — это , вписанный в , вписанный в пятиугольник .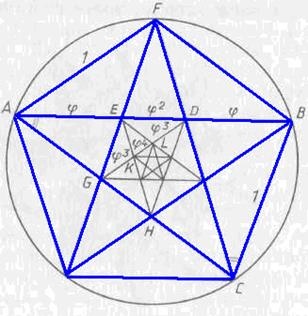 В обоих случаях внешняя форма описывается, а внутренняя форма вписывается.
В обоих случаях внешняя форма описывается, а внутренняя форма вписывается.
Треугольники
Как это часто бывает при обсуждении многоугольников, треугольники — это особый случай в обсуждении вписанных и описанных. Каждый возможный треугольник можно вписать в один круг и описать другой круг. . Это «универсальное двойное членство» верно ни для каких других многоугольников более высокого порядка — оно верно только для треугольников. Вот небольшая галерея треугольников, каждый из которых вписан в один круг и описывает другой.
Обратите внимание, что, когда один угол особенно тупой, близкий к 180 °, разница в размерах между описанной окружностью и вписанной окружностью становится довольно большой. Также обратите внимание: в случае прямоугольного треугольника, второго изображения, гипотенуза треугольника равна диаметру описанной окружности. Мы вернемся к этому моменту.
Четырехугольники
Многие четырехугольники нельзя ни вписать в круг, ни описать кругом: то есть невозможно построить круг, проходящий через все четыре вершины, а также невозможно построить круг, к которому все четыре стороны касаются друг друга.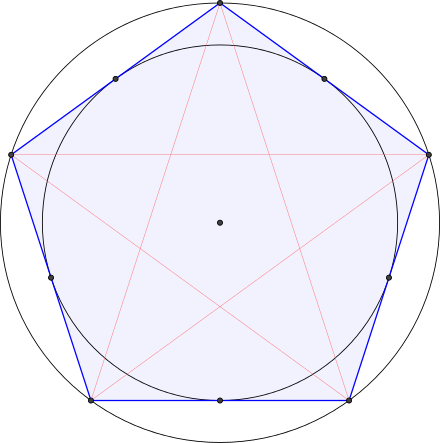
Некоторые четырехугольники, например продолговатый прямоугольник, можно вписать в круг, но нельзя описать круг. Другие четырехугольники, такие как наклонный ромб, описывают круг, но не могут быть вписаны в круг.
Несколько элитных четырехугольников могут описывать один круг и вписываться в другой круг. Конечно, квадрат (внизу слева), самый элитный из четырехугольников, обладает этим свойством. Другой пример — «правый воздушный змей» (внизу справа), воздушный змей с парой противоположных прямых углов:
Хотя это «двойное членство» верно для всех треугольников, оно ограничено некоторыми частными случаями с четырехугольниками.
Высшие многоугольники
То, что было верно для четырехугольников, также верно и для всех высших многоугольников.
а. Большинство, подавляющее большинство, не могут ни описать круг, ни вписать круг.
г. Некоторые можно вписать в круг, но нельзя описать круг.
г. Некоторые могут описать круг, но не могут быть вписаны в круг.
г. Некоторые избранные могут как описать круг, так и вписаться в него.
Последняя категория, элитные члены, всегда включает правильный многоугольник.Подобно тому, как все треугольники имеют это «двойное членство», так и все правильные многоугольники. Вот галерея правильных многоугольников, как с вписанной, так и с описанной окружностью.
Очевидно, что с увеличением количества сторон размеры двух окружностей становятся все ближе и ближе.
Вопросы GMAT о вписанных и описанных многоугольниках встречаются редко и могут проверить как ваше понимание терминологии, так и ваши навыки визуализации, описывая геометрическую ситуацию (например,г. «Прямоугольник JKLM вписан в круг») и , а не , дающий вам диаграмму.
Особый случай: треугольник, вписанный в полукруг.
Это особый случай, который нравится GMAT. Он появляется в OG13 (DS # 118) и может легко появиться где-нибудь в разделе Quant вашего настоящего GMAT.
Если все, что вы знаете, это то, что KL — это диаметр окружности, этого достаточно, чтобы установить, что ∠J = 90 ° и что треугольник JKL является прямоугольным треугольником с KL в качестве гипотенузы.С другой стороны, если все, что вам известно, это то, что треугольник JKL является прямоугольным с KL в качестве гипотенузы, этого достаточно, чтобы установить, что дуга KJL является полукругом, а KL — диаметром. Это мощный набор идей, потому что выводы работают в обоих направлениях и потому, что он неразрывно связывает две, казалось бы, несопоставимые идеи.
Кстати, этот пост — четвертый в серии из пяти статей. Вот вся серия.
1) Введение в круги в GMAT
2) Геометрия GMAT: круги и углы
3) Круговые и линейные диаграммы в GMAT
4) Вписанные и описанные круги и многоугольники в GMAT
5) Разрезание на части GMAT Circles: Arclengths, Sectors, and Pi
Практический вопрос
1) На диаграмме выше S — центр круга.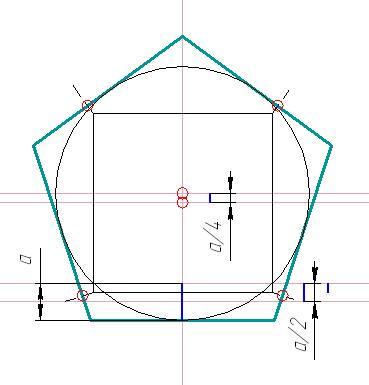 Если QS = 5 и QR = 6, что такое PQ?
Если QS = 5 и QR = 6, что такое PQ?
A. 7
B. 8
C. 9
D. 10
E. 11
Практическое объяснение вопроса
1) Прежде всего, QS — это радиус, поэтому если QS = 5 , это означает, что PS = SR = 5 и диаметр PR = 10. Кроме того, поскольку PR — это диаметр, это означает, что треугольник PQR является прямоугольным с ∠PQR = 90 °. Нам известны две стороны этого прямоугольного треугольника: QR = 6 и PR = 10, поэтому мы можем использовать теорему Пифагора, чтобы найти третью сторону.2 = 100 — 36 = 64
PQ = sqrt {64} = 8
Ответ = B
Готовы получить отличный результат GMAT? Начало здесь.
Самые популярные ресурсы
Майк работал экспертом по GMAT в Magoosh, помогая создавать сотни видеоуроков и практических вопросов, чтобы помочь студентам GMAT добиться успеха. Он также был отмечен как «участник месяца» более двух лет в клубе GMAT. Майк имеет степень бакалавра гуманитарных наук.
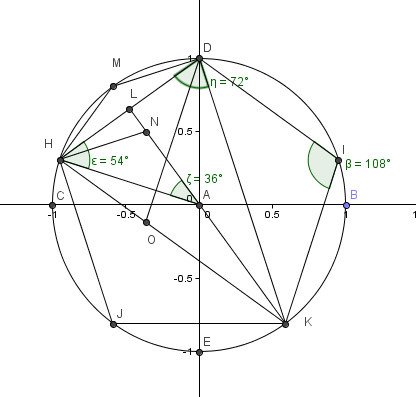 Магистр физики (выпуск с отличием, ) и M.Т.С. в «Религиях мира», оба из Гарварда. Помимо стандартизированного тестирования, у Майка более 20 лет опыта преподавания как в частных, так и в государственных школах, специализирующихся на математике и физике. В свободное время Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидной черепно-мозговой недостаточности, он настаивает на том, чтобы болеть за Нью-Йорк Метс. Узнайте больше о GMAT из видеообъяснений Майка на YouTube и из таких ресурсов, как «Каков хороший результат GMAT?» и диагностический тест GMAT.
Магистр физики (выпуск с отличием, ) и M.Т.С. в «Религиях мира», оба из Гарварда. Помимо стандартизированного тестирования, у Майка более 20 лет опыта преподавания как в частных, так и в государственных школах, специализирующихся на математике и физике. В свободное время Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидной черепно-мозговой недостаточности, он настаивает на том, чтобы болеть за Нью-Йорк Метс. Узнайте больше о GMAT из видеообъяснений Майка на YouTube и из таких ресурсов, как «Каков хороший результат GMAT?» и диагностический тест GMAT.Посмотреть все сообщения
Пентагон с компасом и линейкой.Как построить и нарисовать правильный пятиугольник вокруг круга
Эта форма представляет собой многоугольник с минимальным количеством углов, которые нельзя вымощать площадкой. Только у пятиугольника количество диагоналей равно количеству его сторон. Используя формулы для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пятиугольник.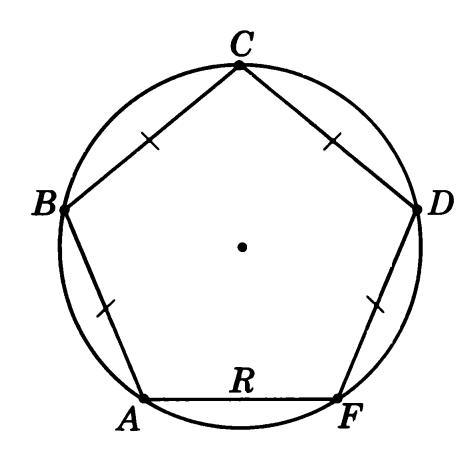 Например, впишите его в круг с заданным радиусом или постройте по заданной боковой стороне.
Например, впишите его в круг с заданным радиусом или постройте по заданной боковой стороне.
Как правильно нарисовать луч и какие аксессуары для рисования вам понадобятся? Возьмите лист бумаги и отметьте точку в произвольном месте.Затем прикрепите линейку и проведите линию от указанной точки до бесконечности. Чтобы нарисовать прямую линию, нажмите клавишу Shift и перетащите линию нужной длины. Сразу после рисования открывается вкладка Формат. Удалите выделение из строки, и вы увидите точку, появившуюся в начале строки. Чтобы создать подпись, нажмите кнопку «Нарисовать подпись» и создайте поле, в котором будет располагаться подпись.
Первый способ построения пятиугольника считается более «классическим». В результате получится правильный пятиугольник.Двенадцатьугольник — не исключение, поэтому его построение будет невозможно без использования компаса. Задача построения правильного пятиугольника сводится к задаче разделить круг на пять равных частей. Нарисовать пентаграмму можно простейшими инструментами.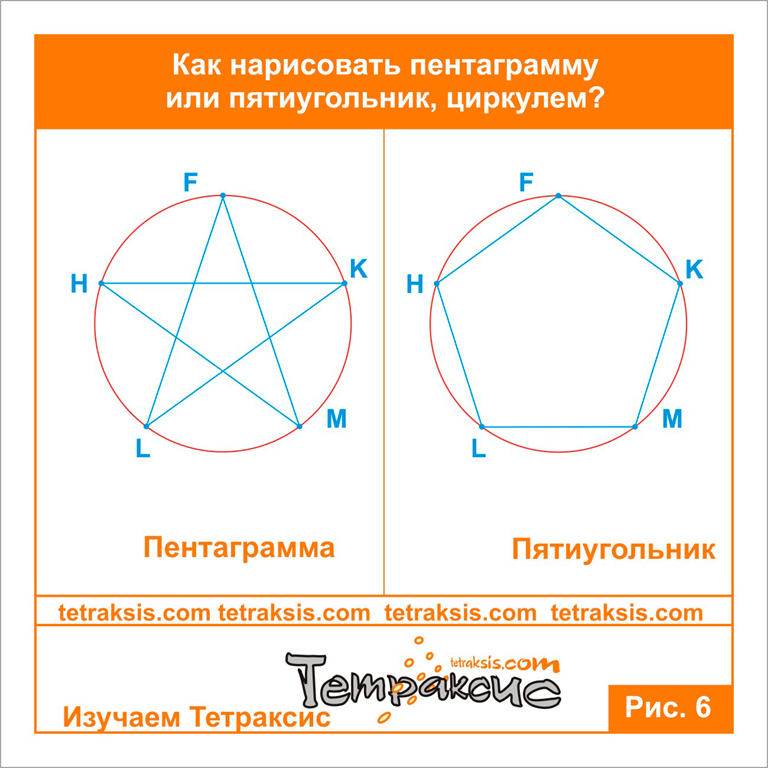
Я долго боролся, пытаясь добиться этого и самостоятельно находить пропорции и зависимости, но у меня ничего не получалось. Оказалось, что существует несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками.Интересен тот факт, что эту задачу можно решить арифметически только приблизительно точно, так как вам придется использовать иррациональные числа. Но ее можно решить геометрически.
Деление кружков. Точки пересечения этих прямых с кругом являются вершинами квадрата. Вертикальный диаметр следует нарисовать в окружности радиуса R (шаг 1). В точке сопряжения N прямой и окружности прямая линия касается окружности.
Получение с полоской бумаги
Правильный шестиугольник можно построить с помощью направляющей и квадрата 30X60 °. Вершины такого треугольника можно построить с помощью циркуля и квадрата с углами 30 и 60 ° или всего одного циркуля. Чтобы построить сторону 2-3, установите дорожку качения в положение, показанное пунктирными линиями, и проведите прямую линию через точку 2, которая определит третью вершину треугольника. Отметим на окружности точку 1 и примем ее за одну из вершин пятиугольника.Соединяем найденные вершины последовательно между собой. Семиугольник можно построить, проведя лучи от полюса F через нечетные части вертикального диаметра.
Отметим на окружности точку 1 и примем ее за одну из вершин пятиугольника.Соединяем найденные вершины последовательно между собой. Семиугольник можно построить, проведя лучи от полюса F через нечетные части вертикального диаметра.
А на другой конец нитки поставил карандаш и зациклился. Если вы умеете рисовать звезду, но не знаете, как нарисовать пятиугольник, нарисуйте звезду карандашом, затем соедините смежные концы звезды вместе, а затем сотрите саму звезду. Затем кладем лист бумаги (лучше закрепить на столе четырьмя пуговицами или иголками).Используйте пуговицы или иголки, чтобы прикрепить эти 5 полосок к листу бумаги, чтобы они оставались неподвижными. Затем обведите получившийся пятиугольник и уберите эти полосы с листа.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для изображения советского прошлого или настоящего Китая. Правда, для этого нужно уметь создать рисунок звезды в перспективе. Таким же образом можно нарисовать фигуру карандашом на бумаге.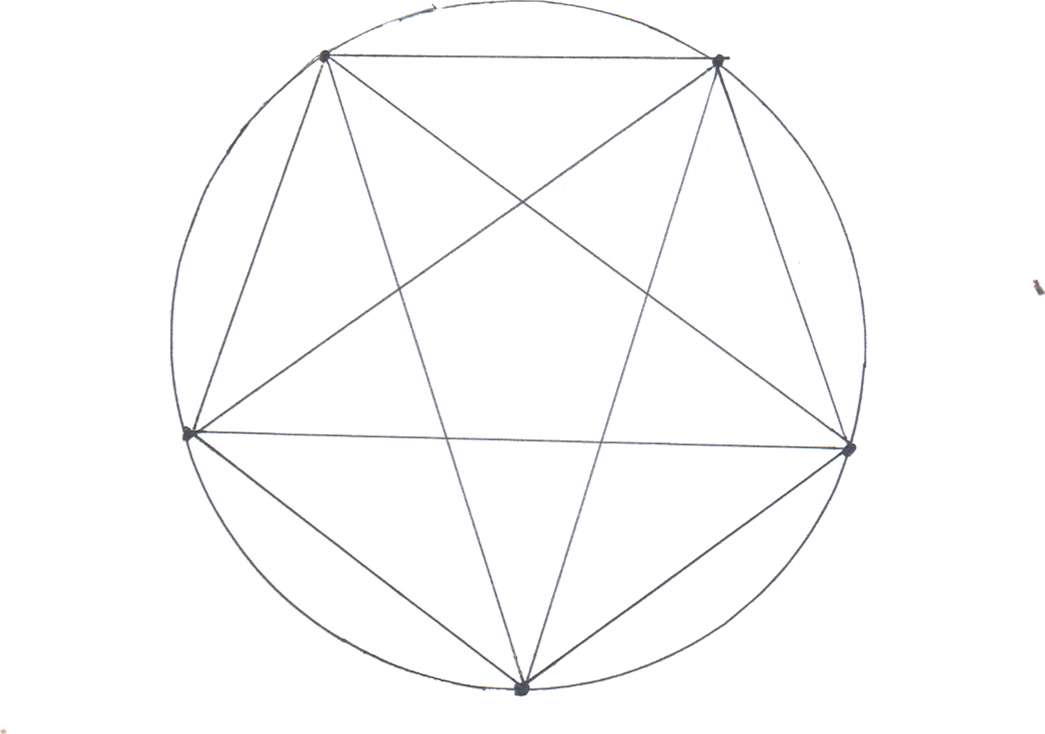 Как правильно нарисовать звезду, чтобы она выглядела гладко и красиво, сразу ответить нельзя.
Как правильно нарисовать звезду, чтобы она выглядела гладко и красиво, сразу ответить нельзя.
От центра опустите 2 луча до окружности так, чтобы угол между ними составлял 72 градуса (транспортир). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — одна из фигур, содержащих пропорции золотого сечения, художники и математики давно интересовались его построением. Эти принципы построения с использованием циркуля и линейки были изложены в Евклидовых принципах.
Задача построения истинного пятиугольника сводится к задаче разделить круг на пять равных частей. Поскольку правильный пятиугольник — одна из фигур, содержащих пропорции золотого сечения, художники и математики давно интересовались его построением. В настоящее время открыто несколько методов построения правильного многоугольника, вписанного в заданный круг.
Вам понадобится
Инструкции
1. По-видимому, если вы построите правильный десятиугольник, а затем соедините его вершины через одну, вы получите пятиугольник.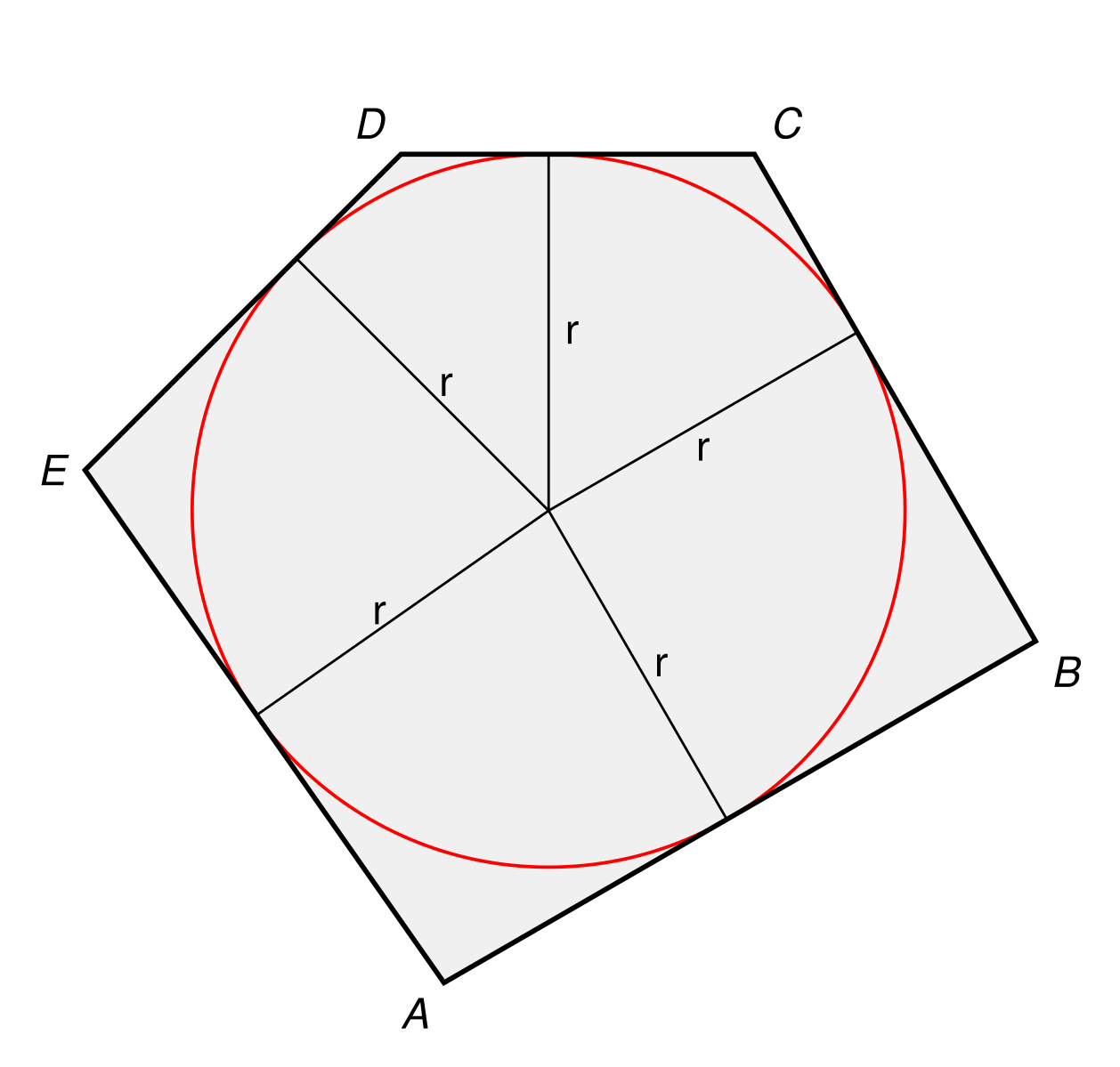 Чтобы нарисовать десятиугольник, нарисуйте круг с заданным радиусом. Обозначьте его центр буквой O. Нарисуйте два перпендикулярных радиуса, на рисунке они обозначены как OA1 и OB. Разделите радиус OB пополам с помощью линейки или разделив отрезок пополам с помощью циркуля. Нарисуйте небольшой круг с центром C в середине OB с радиусом, равным половине OB. Соедините точку C с точкой A1 на начальном круге с помощью линейки.Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне истинного десятиугольника, вписанного в эту окружность. С помощью циркуля проведите этот сегмент по окружности, затем объедините точки пересечения через одну, и вы получите положительный пятиугольник.
Чтобы нарисовать десятиугольник, нарисуйте круг с заданным радиусом. Обозначьте его центр буквой O. Нарисуйте два перпендикулярных радиуса, на рисунке они обозначены как OA1 и OB. Разделите радиус OB пополам с помощью линейки или разделив отрезок пополам с помощью циркуля. Нарисуйте небольшой круг с центром C в середине OB с радиусом, равным половине OB. Соедините точку C с точкой A1 на начальном круге с помощью линейки.Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне истинного десятиугольника, вписанного в эту окружность. С помощью циркуля проведите этот сегмент по окружности, затем объедините точки пересечения через одну, и вы получите положительный пятиугольник.
2. Другой метод был открыт немецким художником Альбрехтом Дюрером. Чтобы построить пятиугольник по его методу, начните снова с рисования круга. Заново проведите его центр O и нарисуйте два перпендикулярных радиуса OA и OB.Разделите радиус OA пополам и проведите по центру буквой C.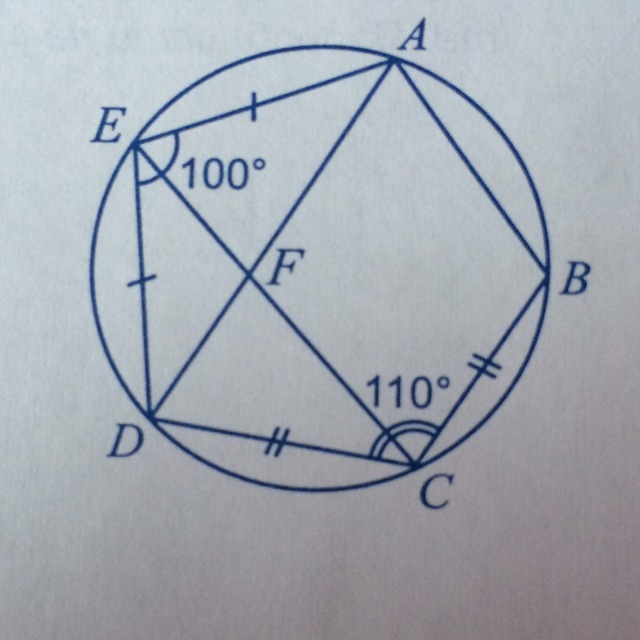 Поместите стрелку циркуля в точку C и откройте ее до точки B. Нарисуйте круг радиуса BC, пока он не пересечет диаметр начальной окружности, на которой лежит радиус OA. . Обозначьте точку пересечения D. Отрезок BD — это сторона положительного пятиугольника. Отступите от этого отрезка пять раз по начальному кругу и совместите точки пересечения.
Поместите стрелку циркуля в точку C и откройте ее до точки B. Нарисуйте круг радиуса BC, пока он не пересечет диаметр начальной окружности, на которой лежит радиус OA. . Обозначьте точку пересечения D. Отрезок BD — это сторона положительного пятиугольника. Отступите от этого отрезка пять раз по начальному кругу и совместите точки пересечения.
3. Если вам нужно построить пятиугольник по заданной стороне, то вам понадобится 3-й способ.Нарисуйте сторону пятиугольника по линейке, отметьте этот отрезок буквами A и B. Разделите его на 6 равных частей. Из середины отрезка AB проведите луч перпендикулярно отрезку. Постройте два круга с радиусом AB и центрами в точках A и B, как если бы вы собирались разрезать сегмент пополам. Эти окружности пересекаются в точке C. Точка C в этом случае лежит на луче, исходящем перпендикулярно вверх из середины AB. Отойдите от C вверх по этому лучу на расстояние, равное 4/6 длины AB, обозначьте эту точку D.Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя построенными ранее вспомогательными даст две последние вершины пятиугольника.
Пересечение этой окружности с двумя построенными ранее вспомогательными даст две последние вершины пятиугольника.
Тема разделения круга на равные части для построения правильных вписанных многоугольников давно занимала умы древних ученых. Эти тезисы построения с помощью циркуля и линейки были выражены в Евклидовых «Принципах». Однако всего через два тысячелетия эта задача была полностью решена не только графически, но и математически.
Инструкции
1. Примерное построение положительного пятиугольника по методу А. Дюрера с помощью циркуля и линейки (через две окружности с общим радиусом, равным стороне пятиугольника ).
2. Построение верного пятиугольника на основе положительного десятиугольника, вписанного в круг (объединение вершин десятиугольника через одну).
3. График через рассчитанный внутренний угол пятиугольник с опорой транспортиром и линейкой (сумма углов выпуклого n-угольника равна Sn = 180 ° (n — 2), так как все углы положительного многоугольника равны равный). При n = 5, S5 = 5400 значение угла 1080; (36005 = 720). Их пересечение с кругом даст отрезок, равный стороне пятиугольника .
При n = 5, S5 = 5400 значение угла 1080; (36005 = 720). Их пересечение с кругом даст отрезок, равный стороне пятиугольника .
4. Другой простой графический метод: разделите диаметр данной окружности AB на три части (AC = CD = DE). Из точки D опускаем перпендикуляр до пересечения с окружностью в точках E, F. Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.Точки G, E, B, F, H являются вершинами положительного пятиугольника .
5. Конструкция с поддержкой техники Биона (которая позволяет нам построить настоящий многоугольник, вписанный в круг с любым числом сторон n в соответствии с заданным соотношением). Скажем: для n = 5. Построим положительный треугольник ABC, где AB — диаметр данной окружности. Найдите точку D на AB согласно дальнейшему соотношению: AD: AB = 2: n. Для n = 5 AD = 25 * AB. Проведем прямую через CD до пересечения с окружностью в точке E.Отрезок AE — это сторона правильного вписанного пятиугольника .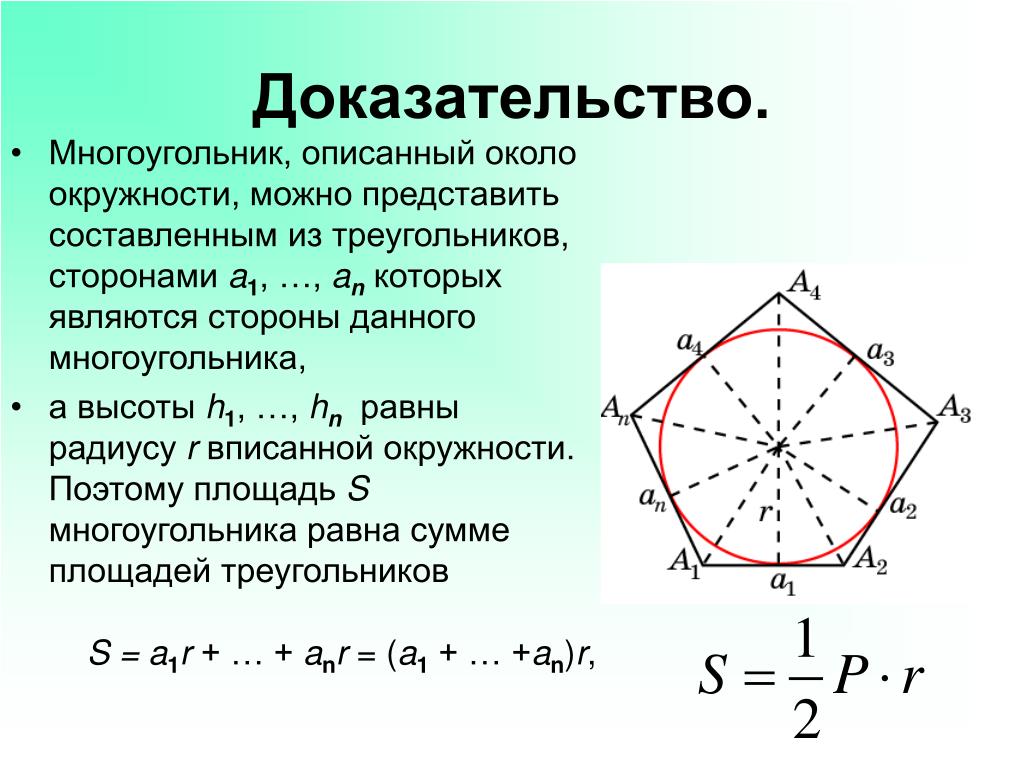 При n = 5,7,9,10 погрешность построения не превышает 1%. С увеличением n ошибка аппроксимации растет, но остается менее 10,3%.
При n = 5,7,9,10 погрешность построения не превышает 1%. С увеличением n ошибка аппроксимации растет, но остается менее 10,3%.
6. Построение заданной стороны по методу Л. Да Винчи (с использованием соотношения сторон многоугольника (аn) и апофемы (ha): ан / 2: ha = 3 / (n-1), которое может быть выражается следующим образом: tg180 ° / n = 3 / (n-1)).
7. Общий метод построения положительных многоугольников на заданной стороне по методу Ф.Коваржик (1888), основанный на правиле Л. да Винчи. Интегральный метод построения положительного n-угольника, основанный на теореме Фалеса. Можно только добавить, что приблизительные методы построения полигонов подлинные, примитивные и красивые.
Есть два основных метода построения истинного пятистороннего многоугольника. Оба предлагают использовать циркуль, линейку и карандаш. 1-й способ заключается в установке пятиугольника в круг, а 2-й метод основан на заданной длине стороны вашей будущей геометрической фигуры.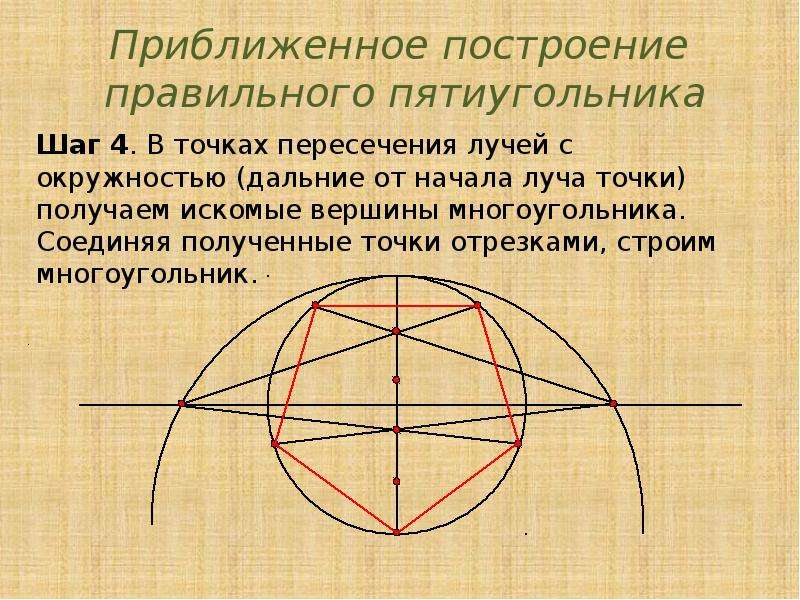
Вам понадобится
Инструкции
1. 1-й способ построения пятиугольник считается более «типовым». Сначала нарисуйте круг и как-нибудь обозначьте его центр (обычно для этого используется буква О). После этого нарисуйте диаметр этого круга (назовем его AB) и разделите один из двух полученных радиусов (скажем, OA) ровно пополам. Середина этого радиуса будет обозначена буквой C.
2. Из точки O (центр начальной окружности) нарисуйте другой радиус (OD), который будет строго перпендикулярен ранее нарисованному диаметру (AB).После этого возьмите циркуль, поместите его в точку C и измерьте расстояние до пересечения нового радиуса с окружностью (CD). Установите такое же расстояние для диаметра AB. Вы получите новую точку (назовем ее E). Измерьте циркулем расстояние от точки D до точки E — оно будет равно длине стороны вашего будущего пятиугольника .
3. Поместите циркуль в точку D и отметьте расстояние, равное отрезку DE на окружности. Повторите эту процедуру еще 3 раза, а затем объедините точку D и 4 новые точки на начальном круге.Получившаяся форма будет настоящим пятиугольником.
Повторите эту процедуру еще 3 раза, а затем объедините точку D и 4 новые точки на начальном круге.Получившаяся форма будет настоящим пятиугольником.
4. Чтобы построить пятиугольник другим способом, сначала нарисуйте отрезок прямой. Допустим, это будет отрезок AB длиной 9 см. Затем разделите свой отрезок на 6 равных частей. В нашем случае длина любой детали составит 1,5 см. Теперь возьмите циркуль, поместите его на один из концов отрезка и нарисуйте окружность или дугу с радиусом, равным длине отрезка (AB). После этого переместите компас на другой конец и повторите операцию.Полученные круги (или дуги) будут пересекаться в одной точке. Назовем его C.
5. Теперь возьмите линейку и проведите прямую линию через точку C и центр отрезка AB. После этого, начиная с точки C, отложите на этой прямой отрезок, составляющий 4/6 отрезка AB. Второй конец отрезка будет обозначен буквой D. Точка D будет одной из вершин приближающегося пятиугольника … Из этой точки нарисуйте окружность или дугу с радиусом, равным AB.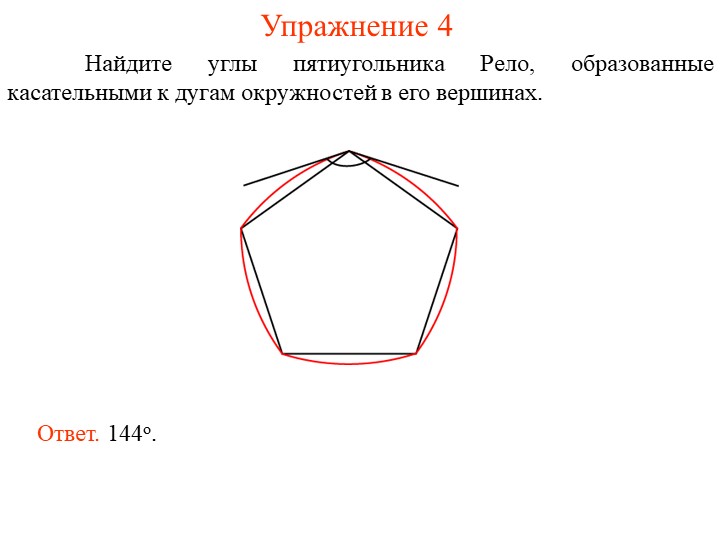 Эта окружность (дуга) будет пересекать ранее построенные окружности (дуги) в точках, которые являются двумя недостающими вершинами пятиугольник … Объедините эти точки с вершинами D, A и B, и построение положительного пятиугольника будет завершено.
Эта окружность (дуга) будет пересекать ранее построенные окружности (дуги) в точках, которые являются двумя недостающими вершинами пятиугольник … Объедините эти точки с вершинами D, A и B, и построение положительного пятиугольника будет завершено.
Похожие видео
Луч — это прямая линия, проведенная из точки и не имеющая конца. Есть и другие определения луча: скажем, «… это прямая линия, ограниченная точкой с одной стороны». Как правильно проследить луч и какие принадлежности для рисования вам понадобятся?
Вам понадобится
- Лист бумаги, карандаш и линейка.
Инструкции
1. Возьмите лист бумаги и отметьте точку в любом месте. После этого прикрепите линейку и проведите линию от указанной точки до бесконечности. Эта нарисованная линия называется лучом. Теперь отметьте другую точку на луче, например букву C. Линия от начала координат до точки C будет называться отрезком. Если вы рисуете линию примитивно и на самом деле не протягиваете одну точку, то эта линия не будет лучом.
Если вы рисуете линию примитивно и на самом деле не протягиваете одну точку, то эта линия не будет лучом.
2. Нарисовать луч в любом графическом редакторе или в том же MSOffice не сложнее, чем вручную.Возьмем, к примеру, Microsoft Office 2010. Перейдите в Insert и выберите Shapes. Выберите фигуру линии из раскрывающегося списка. Далее курсор примет форму креста. Чтобы нарисовать прямую линию, нажмите клавишу Shift и проведите линию необходимой длины. Вкладка «Формат» откроется сразу после стиля. Теперь вы нарисовали примитивную прямую линию без фиксированной точки, и, исходя из определения, луч должен быть ограничен точкой с одной стороны.
3. Чтобы поставить точку в начале линии, сделайте следующее: выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.
4. Выберите формат фигуры. В меню слева выберите «Тип линии». Затем найдите заголовок «Параметры линии» и выберите «Тип начала» в виде круга. Там же вы можете настроить толщину начальной и конечной линий.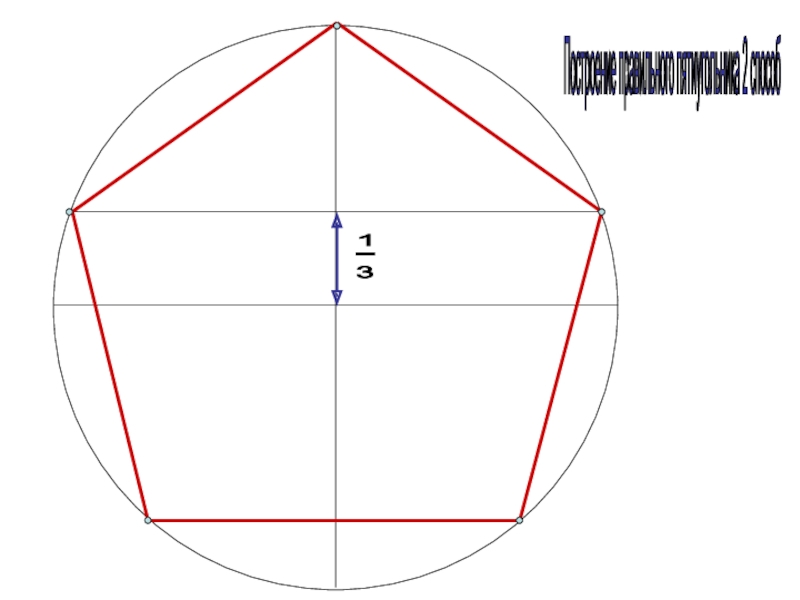
5. Удалите выделение из линии, и вы увидите, что в начале строки появится точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, в котором она будет располагаться.После написания надписи нажмите на свободное место и оно будет активировано.
6. Луч безопасно нарисован, и это происходило каждые несколько минут. Рисование луча в других редакторах осуществляется по тому же тезису. Удерживая нажатой клавишу Shift, неизменно будут рисоваться пропорциональные формы. Славное использование.
Похожие видео
Примечание!
Отношение диагонали истинного пятиугольника к его стороне — это золотое сечение (иррациональное число (1 + √5) / 2).Все пять внутренних углов пятиугольника равны 108 °.
Полезный совет
Если совместить вершины настоящего пятиугольника с диагоналями, получится пентаграмма.
Правильный пятиугольник можно построить с помощью циркуля и линейки, или вписав его в заданный круг, или построив его на заданной стороне. Этот процесс описан Евклидом в его «Началах» около 300 г. до н.э. NS.
Этот процесс описан Евклидом в его «Началах» около 300 г. до н.э. NS.
Вот один из методов построения правильного пятиугольника в данном круге:
1.Постройте круг, в который будет вписан пятиугольник, и отметьте его центр как O … (это зеленый круг на диаграмме справа).
- Выберите точку на окружности A , которая будет одной из вершин пятиугольника. Постройте прямую линию через O и A .
- Постройте прямую, перпендикулярную прямой OA , проходящую через точку O … Обозначьте одно из ее пересечений окружностью как точку B .
- Постройте точку C посередине между O и B .
- C через точку A … Отметьте его пересечение прямой линией OB (внутри исходной окружности) как точку D .
- Нарисуйте круг с центром A через точку D … Отметьте его пересечения с оригиналом (зеленый кружок) как точки E и F .
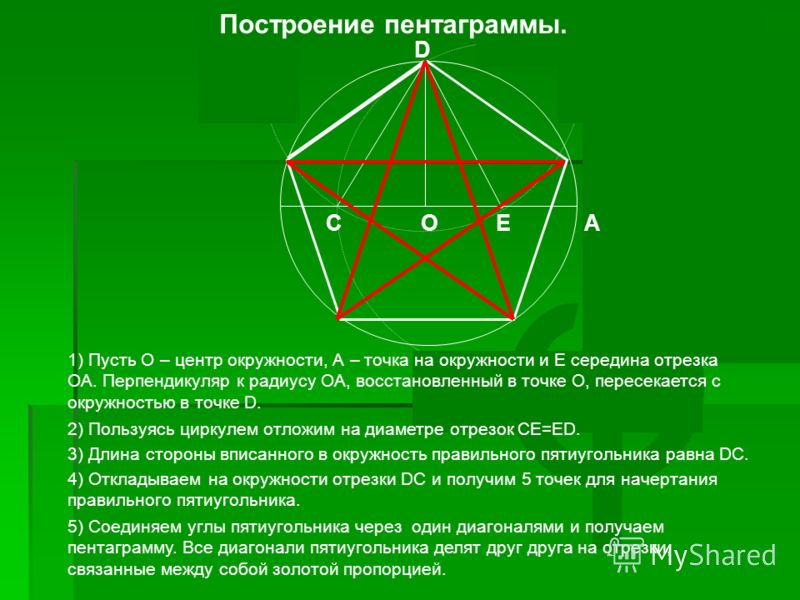
- Нарисуйте круг с центром E через точку A G .
- Нарисуйте круг с центром F через точку A … Обозначьте его другое пересечение с исходной окружностью точкой H .
- Постройте правильный пятиугольник AEGHF .
Икосаэдр
Икосаэдр — одно из пяти Платоновых тел, в простоте следующих за тетраэдром и октаэдром. Их объединяет то, что грани каждого представляют собой равносторонние треугольники.При создании модели икосаэдра вы можете выбрать один из двух впечатляющих вариантов распределения пяти цветов.
Во-первых, икосаэдр можно раскрасить так, чтобы каждая вершина имела все пять цветов (однако в этом случае противоположные грани не будут окрашены одинаково).
Другой метод обеспечивает противоположные цвета с одинаковыми цветами, но в каждой вершине, кроме двух полярных, один и тот же цвет будет повторяться в круге.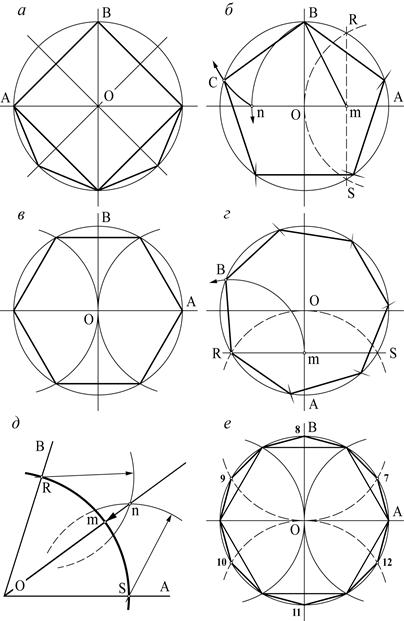 Обе раскраски очень интересны и полезны для наших целей, потому что многие из описанных ниже однородных многогранников обладают икосаэдрической симметрией.
Обе раскраски очень интересны и полезны для наших целей, потому что многие из описанных ниже однородных многогранников обладают икосаэдрической симметрией.
Невозможно обойтись без изучения техники этого процесса. Есть несколько вариантов выполнения работы. Как нарисовать звезду с помощью линейки, поможет разобраться в самых известных приемах этого процесса.
Разновидности звезд
Существует множество вариантов внешнего вида такой формы, как звезда.
С давних времен его пятиконечная разновидность использовалась для рисования пентаграмм. Это связано с его свойством, которое позволяет рисовать рисунок, не отрывая ручку от бумаги.
Есть еще шестиконечные хвостатые кометы.
У морской звезды традиционно пять вершин. Часто встречаются изображения рождественской версии такой же формы.
В любом случае, чтобы нарисовать пятиконечную звезду поэтапно, нужно прибегать к использованию специальных инструментов, так как изображение от руки вряд ли будет выглядеть симметричным и красивым.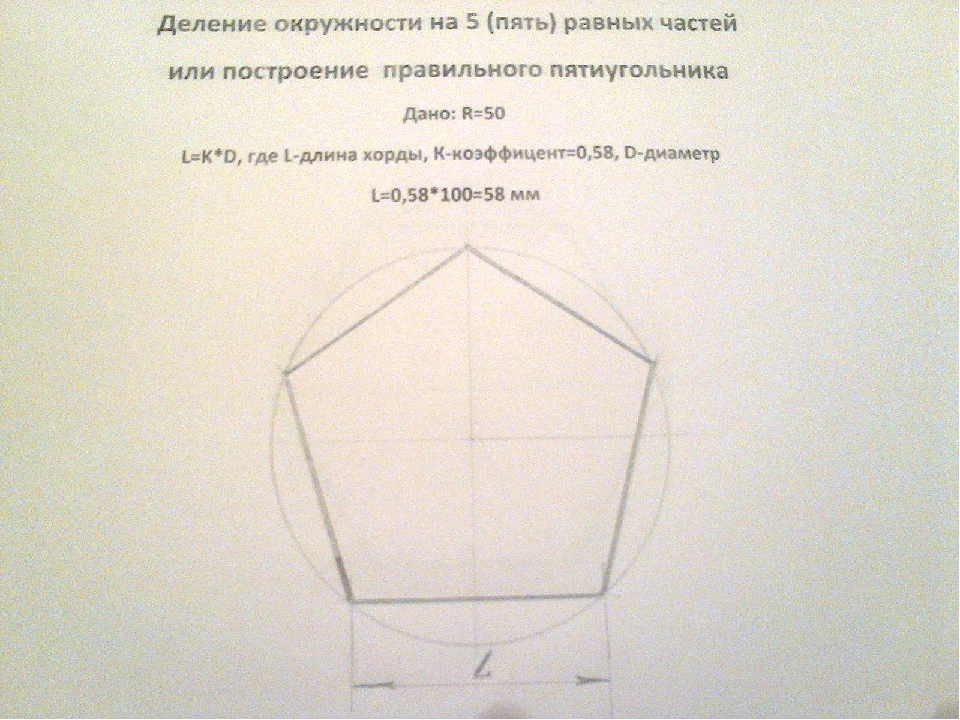
Выполнение рисунка
Чтобы понять, как нарисовать четную звезду, необходимо разобраться в сути этого рисунка.
Основа его контура — ломаная линия, концы которой сходятся в начальной точке. Он образует правильный пятиугольник — пятиугольник.
Отличительными свойствами такой фигуры являются способность вписать ее в круг, а также окружность в этот многоугольник.
Все стороны пятиугольника равны. Разобравшись, как правильно выполнить чертеж, можно понять суть процесса построения всех фигур, а также различных схем деталей и узлов.
Чтобы достичь такой цели, как нарисовать звезду с помощью линейки, вы должны знать простейшие математические формулы, которые являются фундаментальными в геометрии. Вам также нужно будет уметь рассчитывать на калькулятор. Но самое главное — логическое мышление.
Работа несложная, но потребует точности и кропотливости. Затраченные усилия будут вознаграждены хорошим симметричным, а потому красивым изображением пятиконечной звезды.
Классическая техника
Самый известный способ нарисовать звезду с помощью циркуля, линейки и транспортира довольно прост.
Для этой техники вам понадобится несколько инструментов: циркуль или транспортир, линейка, простой карандаш, ластик и лист белой бумаги.
Чтобы понять, как красиво нарисовать звезду, следует действовать последовательно, поэтапно.
Вы можете использовать в своей работе специальные расчеты.
Расчет фигуры
На этом этапе рисования правильной звезды просвечивают контуры готовой фигуры.
Если все сделано правильно, результирующее изображение будет плоским.Это можно проверить визуально, повернув лист бумаги и оценив форму. Так будет на каждом шагу.
Основные контуры более четко ведутся линейкой и простым карандашом. Все вспомогательные линии удалены.
Чтобы понять, как нарисовать звезду поэтапно, следует выполнять все действия вдумчиво. В случае ошибки можно поправить рисунок ластиком или провести все манипуляции заново.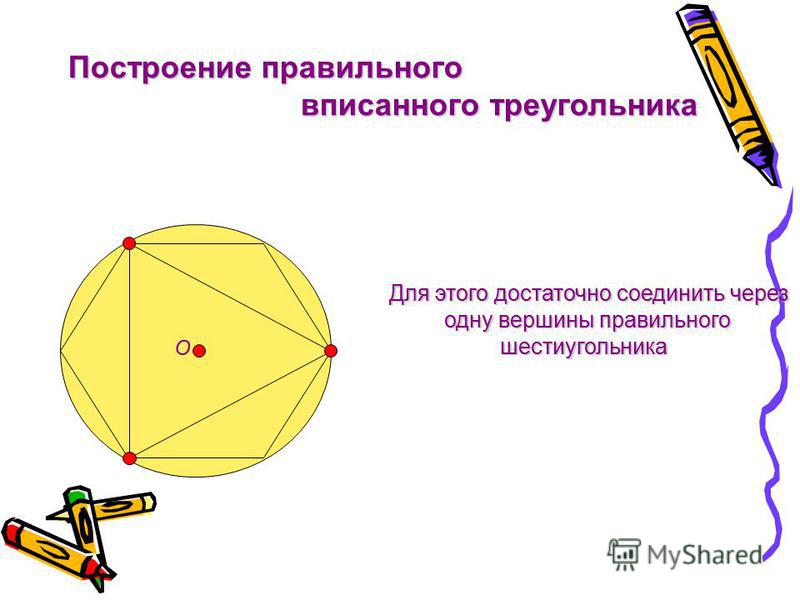
Оформление работы
Готовую форму можно декорировать самыми разными способами.Главное — не бояться экспериментов. Фантазия подскажет оригинальный и красивый образ.
Вы можете нарисовать нарисованную ровную звезду простым карандашом или использовать самые разные цвета и оттенки.
Чтобы понять, как нарисовать правильную звезду, вам нужно придерживаться идеальных линий на всем протяжении. Поэтому самый популярный вариант дизайна — разделить каждый луч фигуры на две равные части линией, идущей от вершины к центру.
Не обязательно разделять стороны звезды линиями.Допускается просто закрашивать каждый луч фигуры более темным оттенком с одной стороны.
Этот вариант также будет ответом на вопрос, как правильно нарисовать звезду, ведь все ее линии будут симметричными.
При желании к эстетичному оформлению фигурки можно добавить орнамент или другие различные элементы. Добавляя кружочки к вершинам, можно получить звезду шерифа. Применяя плавную растушевку теневых сторон, можно получить морскую звезду.
Этот прием является наиболее распространенным, так как позволяет без труда понять, как нарисовать пятиконечную звезду поэтапно.Не прибегая к сложным математическим расчетам, можно получить правильное красивое изображение.
Обдумав все способы, как нарисовать звезду с помощью линейки, вы можете выбрать тот, который вам больше всего подходит. Наибольшей популярностью пользуется геометрический ступенчатый метод. Это довольно просто и эффективно. Используя фантазию и фантазию, из полученной правильной красивой формы можно создать оригинальную композицию. Вариантов оформления картины великое множество. Но всегда можно придумать свой, самый необычный и запоминающийся сюжет.Главное — не бояться экспериментов!
Уровень сложности: Легкий
Шаг 1
Сначала выберите, где разместить центр круга. Там нужно поставить точку отсчета, пусть она будет называться О. С помощью циркуля начертите вокруг нее окружность заданного диаметра или радиуса.
Шаг 2
Затем проводим две оси через точку O, центр круга, одну горизонтальную, другую под углом 90 градусов по отношению к ней — вертикальную. Точки пересечения по горизонтали назовем слева направо A и B, по вертикали, сверху вниз — M и N.Радиус, лежащий на любой оси, например, по горизонтали справа, уменьшается вдвое. Сделать это можно следующим образом: устанавливаем циркуль с известным нам радиусом окружности острием на пересечении горизонтальной оси и окружности — B, очерчиваем пересечения окружностью, называем получившиеся точки, соответственно сверху вниз — C и P, соединить их отрезком, который будет пересекать ось OB, точка пересечения называется K.
Точки пересечения по горизонтали назовем слева направо A и B, по вертикали, сверху вниз — M и N.Радиус, лежащий на любой оси, например, по горизонтали справа, уменьшается вдвое. Сделать это можно следующим образом: устанавливаем циркуль с известным нам радиусом окружности острием на пересечении горизонтальной оси и окружности — B, очерчиваем пересечения окружностью, называем получившиеся точки, соответственно сверху вниз — C и P, соединить их отрезком, который будет пересекать ось OB, точка пересечения называется K.
Шаг 3
Мы соединяем точки K и M и получаем отрезок KM, устанавливаем циркуль в точке M, устанавливаем расстояние до точки K на ней и очерчиваем отметки на радиусе OA, называем эту точку E, затем рисуем компас, пока он не пересечется с верхняя левая часть круга ОМ.Эта точка пересечения называется F. Расстояние, равное отрезку ME, является желаемой стороной равностороннего пятиугольника. В этом случае точка M будет одной вершиной пятиугольника, вложенного в окружность, а точка F — другой.
Шаг 4
Далее из полученных точек по всей окружности проводим циркулем расстояния, равные отрезку МЕ, всего точек должно быть 5. Соединяем все точки отрезками — получаем вписанный в окружность пятиугольник.
- При рисовании осторожно измеряйте расстояния, не допускайте ошибок, чтобы пятиугольник действительно получился равносторонним
Видео с вопросом: вычисление длины стороны правильного ограниченного пятиугольника с учетом радиуса окружности
Стенограмма видео
Правильный пятиугольник описан вокруг круга радиусом два сантиметра. Найдите длину одной стороны пятиугольника.Ответьте правильно с точностью до одного десятичного знака.
Вот круг. Во-первых, мы можем добавить центр к этому кругу. И затем у нас есть пять мест, где пятиугольник касается этой окружности. Мы знаем, что расстояние от центра до любой точки внешнего круга — это радиус. А мы знаем, что радиус составляет два сантиметра.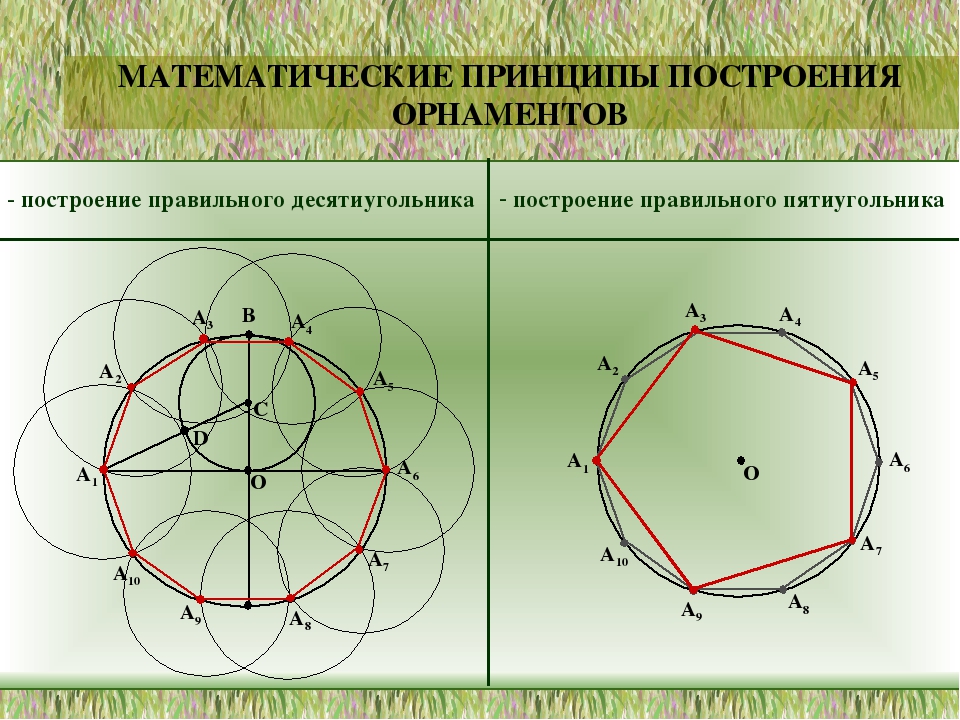 Мы замечаем, что вершина пятиугольника — это пересечение двух касательных, что говорит нам о том, что каждая из этих касательных имеет одинаковую длину.Мы также должны помнить, что когда касательная пересекает радиус, пересечение составляет 90 градусов.
Мы замечаем, что вершина пятиугольника — это пересечение двух касательных, что говорит нам о том, что каждая из этих касательных имеет одинаковую длину.Мы также должны помнить, что когда касательная пересекает радиус, пересечение составляет 90 градусов.
На данный момент может показаться, что мы больше ничего не можем добавить. Но мы знаем, что это правильный пятиугольник. А это значит, что мы можем либо запомнить каждый из этих углов, либо знать, как их вычислить. Если вы не помните, каковы внутренние углы правильного многоугольника, вы можете вычислить внутренние углы любого многоугольника по формуле: 𝑠 равно 𝑛 минус два раза на 180 градусов.Где 𝑠 представляет собой сумму внутренних углов, а 𝑛 — количество сторон многоугольника.
У пятиугольника пять сторон. Итак, нам нужно пять минус два раза по 180 градусов. Пять минус два — три. Трижды 180 равно 540. Но помните, что это сумма всех пяти углов. Но поскольку это правильный пятиугольник, все пять углов равны. А это означает, что если мы разделим 540 на пять, мы сможем найти меру каждого из этих углов.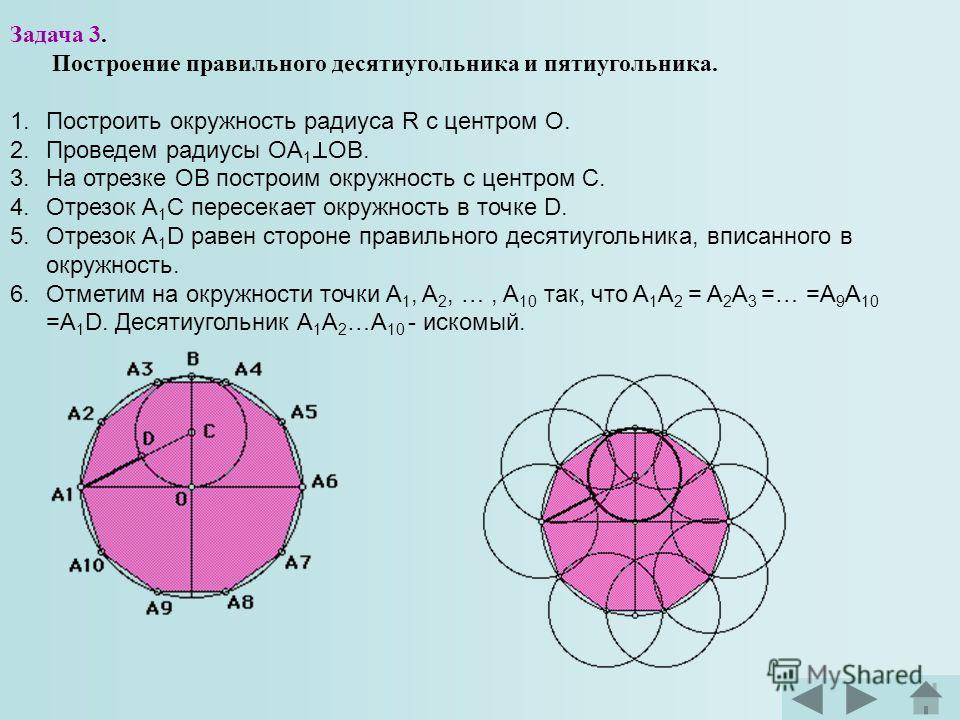 540, разделенное на пять, дает 108. В правильном пятиугольнике все углы составляют 108 градусов.Но это все равно нам не совсем помогает.
540, разделенное на пять, дает 108. В правильном пятиугольнике все углы составляют 108 градусов.Но это все равно нам не совсем помогает.
Но что произойдет, если мы проведем линию между одной из вершин и центром круга? Эта линия делит эти углы пополам. Вместо 108 каждый из них был бы 54 градуса. На этом этапе, вероятно, будет полезно увеличить масштаб того, о чем мы говорим.
У нас есть радиус в два сантиметра, одна часть пятиугольника и линия, которую мы только что провели от вершины пятиугольника к центру круга. Мы знаем, что радиус и касательная пересекаются под прямым углом, и что этот угол составляет 54 градуса.В любом треугольнике все углы нужно складывать до 180 градусов. Это означает, что 90 градусов плюс 54 градуса плюс некоторый угол должны равняться 180 градусам. Когда мы складываем 90 и 54, мы получаем 144. И если мы вычитаем 144 из 180, мы обнаруживаем, что наш недостающий угол составляет 36 градусов.
Помните, наша цель — найти длину одной стороны этого правильного многоугольника. Поскольку это правильный многоугольник, мы знаем, что все стороны имеют одинаковую длину. А это означает, что если мы найдем длину одной стороны, мы найдем длину всех сторон.Если мы добавим еще один радиус, мы снова увидим, что у нас есть две касательные, которые будут равной длины. А это означает, что если мы можем найти это расстояние, нам нужно умножить его на два, чтобы найти длину одной стороны пятиугольника. А это значит, что нам нужно рассмотреть этот прямоугольный треугольник. И нам нужно найти эту недостающую длину стороны.
Поскольку это правильный многоугольник, мы знаем, что все стороны имеют одинаковую длину. А это означает, что если мы найдем длину одной стороны, мы найдем длину всех сторон.Если мы добавим еще один радиус, мы снова увидим, что у нас есть две касательные, которые будут равной длины. А это означает, что если мы можем найти это расстояние, нам нужно умножить его на два, чтобы найти длину одной стороны пятиугольника. А это значит, что нам нужно рассмотреть этот прямоугольный треугольник. И нам нужно найти эту недостающую длину стороны.
Поскольку теперь мы имеем дело с прямоугольными треугольниками, мы можем использовать нашу тригонометрию прямоугольного треугольника. Если мы подумаем о трех тригонометрических отношениях, у нас есть синус, косинус и тангенс.Синус противоположен гипотенузе. Косинус является смежным по гипотенузе. А касательная равна противоположной по соседней. Длина желтой стороны — это гипотенуза, и мы не знаем, какова ее длина. Мы знаем радиус розовой стороны и хотим знать длину другой стороны.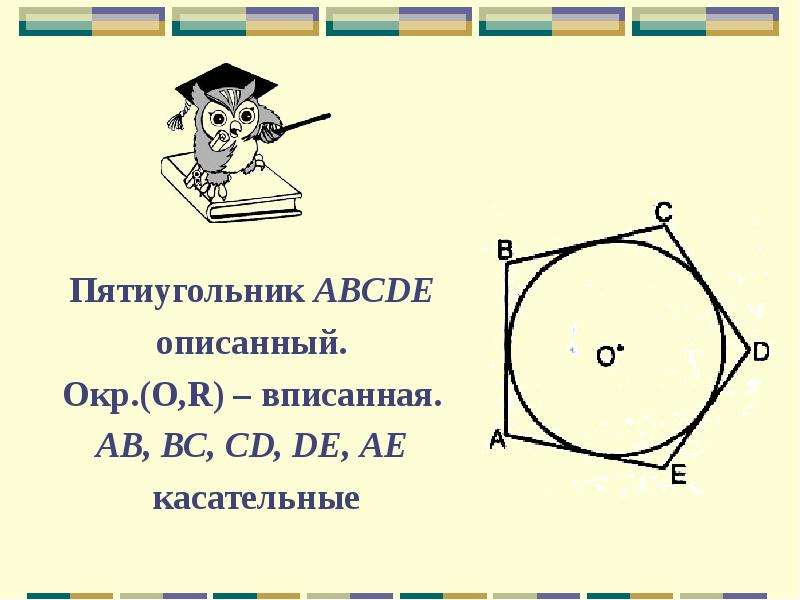 Нас не интересует гипотенуза. А это значит, что лучше всего использовать касательную связь.
Нас не интересует гипотенуза. А это значит, что лучше всего использовать касательную связь.
Если мы начнем с угла в 54 градуса, мы можем сказать, что тангенс 54 градуса равен длине противоположной стороны, два сантиметра.А длина соседней стороны — это наша недостающая сторона 𝑠. Но это не единственный вариант. Мы также могли бы взять тангенс 36 градусов, где противоположная сторона равна длине стороны 𝑠, а длина смежной стороны равна радиусу двух сантиметров. Любой из них будет работать. Но я собираюсь выбрать тангенс 36 градусов, поскольку математика будет немного проще, потому что длина стороны находится в числителе дроби, а не в знаменателе. Таким образом, у нас будет на один шаг меньше, чем при использовании тангенса в 54 градуса.
В этом случае нам просто нужно умножить обе части уравнения на два сантиметра. И у нас получится, что два сантиметра, умноженные на тангенс 36 градусов, равны длине стороны. Когда мы умножаем тангенс 36 градусов на два раза, получаем 1.45308.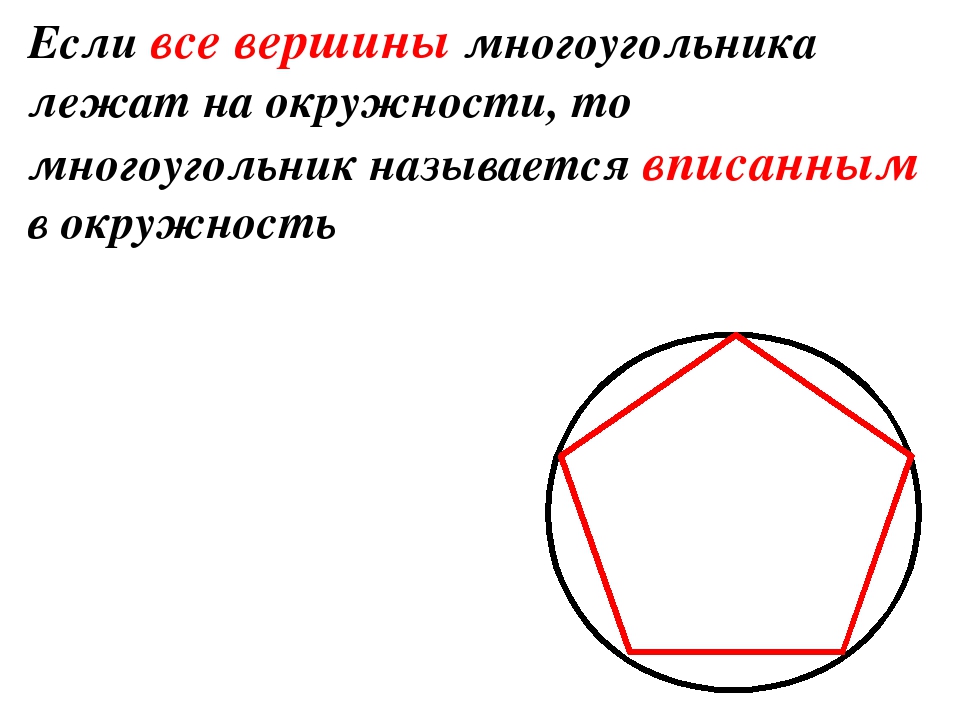 Если вы этого не понимаете, убедитесь, что на калькуляторе, который вы используете, установлены градусы, а не радианы.
Если вы этого не понимаете, убедитесь, что на калькуляторе, который вы используете, установлены градусы, а не радианы.
Здесь нам нужно быть осторожными, потому что это продолжение 1.45308 составляет только половину этой стороны пятиугольника. Оба эти расстояния равны 1.45308 продолжающихся сантиметров. И вместе они образуют длину одной стороны этого правильного пятиугольника. Таким образом, длина одной стороны этого пятиугольника равна двум умноженным на два сантиметра тангенсу 36 градусов, или двум умноженным на 1,45308 сантиметрам продолжительности. Когда мы проделаем это умножение, мы получим 2,.
Мы округляем до первого десятичного знака. Это означает, что нам нужно смотреть вправо, на сотню. Поскольку в разряде сотен стоит ноль, мы округляем до 2.9 сантиметров.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings. ADD_COLLECTION_DESCRIPTION}}
ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.ЯЗЫК}} {{$ select.selected.display}} {{article.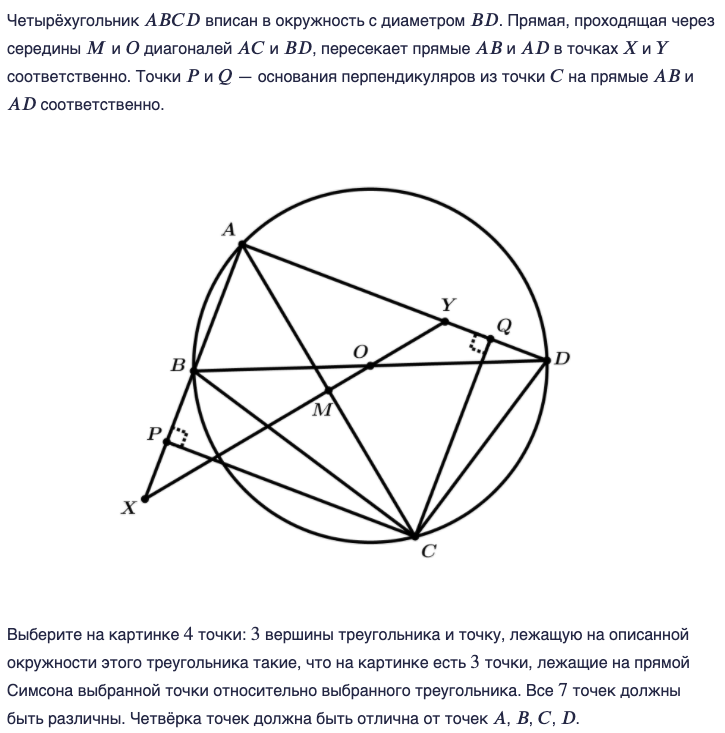 content_lang.display}}
content_lang.display}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Средняя школа: Геометрия — Общее ядро: Средняя школа
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.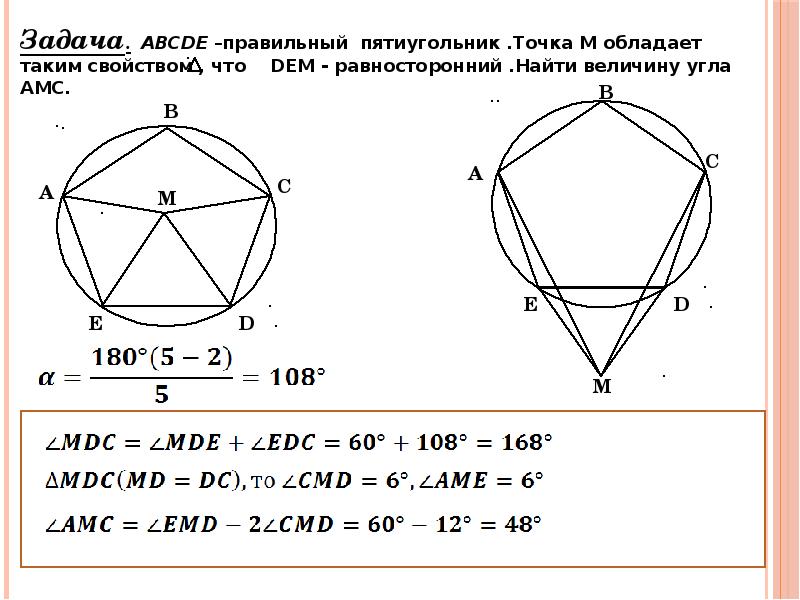 Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.
