Равномерно распределенная нагрузка на балку: Расчет балки на действие наклонной равномерно распределенной нагрузки

Расчет балки на действие наклонной равномерно распределенной нагрузки

Тут, впрочем, могут рассматриваться и другие варианты. Например, наклонную балку, к которой приложена вертикальная равномерно распределенная нагрузка, вполне можно рассматривать как горизонтальную балку, к которой приложена все та же вертикальная нагрузка, вот только расчетная длина балки будет при этом меньше и будет равна длине балки, умноженной на косинус угла наклона.

Кроме того, если обрешетка — не сплошной настил, то более правильно рассчитывать такую балку не на равномерно распределенную нагрузку, а на несколько сосредоточенных, количество которых равно количеству балок обрешетки. Впрочем, если количество балок обрешетки больше 4-5 то проще заменить несколько сосредоточенных нагрузок, на эквивалентную, равномерно распределенную. Да и вообще, расчет балки на наклонную нагрузку почти ничем не отличается от расчета балки, к которой нагрузка приложена перпендикулярно. Но обо всем по порядку.

Дано:

1.

Однопролетная балка постоянного по длине сечения на двух шарнирных опорах А и В, без консолей, длиной l = 4.6 м. Балка расположена горизонтально.

2. Равномерно распределенная нагрузка q = 3.2 кН приложена под углом 60 градусов к нейтральной оси балки по всей длине балки.

Примечание: Еще раз обращаю внимание на то, что в данном примере рассматривается горизонтальная балка на действие наклонной нагрузки, а не наклонная балка на действие вертикальной нагрузки. Т.е. если вам известна длина пролета наклонной балки, то длина наклонной балки будет равна длине пролета, деленной на косинус угла наклона балки.

Если теоретические основы расчета вас не интересуют, а вы просто хотите рассчитать свою балку, то можете воспользоваться калькулятором для данной расчетной схемы (впрочем этот калькулятор в части определения требуемых размеров сечения — только для деревянных балок, со временем возможно будет и для стальных, а может и для железобетонных).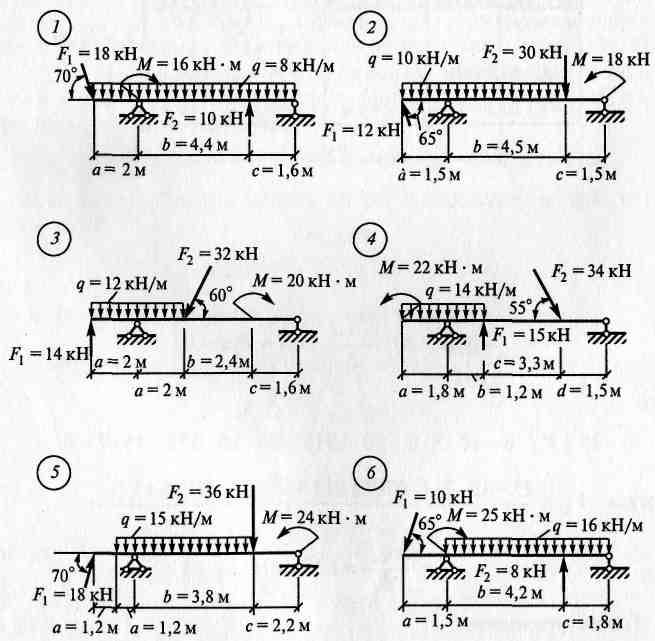

1 Определение опорных реакций (вертикальных и горизонтальных):

А_в = B_в = qlsina/2 = 3.2·4.6·0.866/2 = 6.37395 кН (679.1.1)

Соответственно максимальная поперечная сила, действующая в поперечных сечениях балки будет «Q» = 6.37395 кН. Действовать эта поперечная сила будет на опорах балки.

А_г = qlcosa = 3.2·4.6·0.5 = 7.36 кН (679.1.2)

В_г = 0 (679.1.3)

Примечание: при выбранной расчетной схеме (статически определимая балка с тремя стрежнями опоры, двумя вертикальными и одним горизонтальным) горизонтальная опорная реакция возникает на опоре А. На опоре В горизонтального опорного стержня нет, потому и горизонтальная опорная реакция на опоре В равна нулю. На расчетной схеме (см. рис.679.1) показаны опорные стержни в «классическом» варианте — так как рисуют преподы. Более правильно изображать опоры так:

Рисунок 145. 2.3

2. Определение максимального изгибающего момента: 

Максимальный изгибающий момент будет действовать посредине пролета балки и он составит:

М = ql²sina/8 = 3.2·4.6²·sina/8 = 7.33 кНм (679.2)

3. Подбор сечения балки:

3.1 Для деревянной балки с расчетным сопротивлением R = 13 МПа (13000 кПа) требуемый момент сопротивления составит:

W_тр = M/R = 7.33/13000 = 0.00056385 м³ (563.85 см³) (679.3.1)

Как правило поперечные сечения деревянных балок имеют прямоугольную форму. Момент сопротивления прямоугольного сечения определяется по следующей формуле:

W = bh²/6 (679.3.2)

Дальше возможны различные варианты, например при высоте сечения балки h = 20 см требуемая ширина сечения составит не менее:

b = 6W/h² = 6·563.85/20² = 8.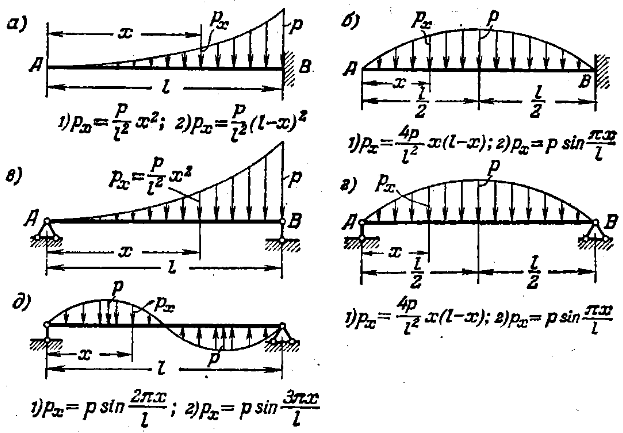 46 см (679.3.3)

По сортаменту таким требованиям удовлетворяет балка с сечением 20х10 см.

Если поперечное сечение деревянной балки имеет форму, отличную от прямоугольной или квадратной, то для определения момента сопротивления можно воспользоваться одной из следующих формул, а при особо сложной форме сечения сначала определить момент инерции, а потом уже момент сопротивления.

3.2 Для стальной балки с расчетным сопротивлением R = 245 Мпа (245000) кПа) требуемый момент сопротивления составляет:

W_тр = M/R = 7.33/245000 = 2.99·10^-5 м³ (29.9 см³) (679.3.4)

Далее требуемое сечение подбирается по одному из сортаментов.

Ну а подбор сечения ж/б балки — это отдельная большая тема.

4. Проверка по касательным напряжениям (для деревянной балки):

Расчетное сопротивление скалыванию вдоль волокон (для древесины второго сорта) R_ск = 1. 6 МПа.

Для прямоугольного сечения максимальные касательные напряжения определяются по следующей формуле:

т = 1.5″Q»/bh = 1.5·6.374/(0.1·0.2) = 452.052 кПа (0.452 МПа) < 1.6 МПа (679.4)

Требование по касательным напряжениям соблюдено.

Для сечений другой формы значение касательных напряжений определяется по формуле Журавского.

Стандартные стальные профили в дополнительной проверке по касательным напряжениям как правило не нуждаются.

5. Определение прогиба:

Для деревянной балки сечением 20х10 см момент инерции составит:

I = Wh/2 = 666.66·20/2 = 6666.6 см⁴ (0.00006666 м⁴

) (679.5.1)

Модуль упругости древесины составляет Е = 1·10⁴ МПа (10⁷ кПа)

f = sina5Ql⁴/(384EI) = 0.0242 м (2.42 см) (671.5.2)

В данном случае прогиб составляет 1/190 от длины пролета балки.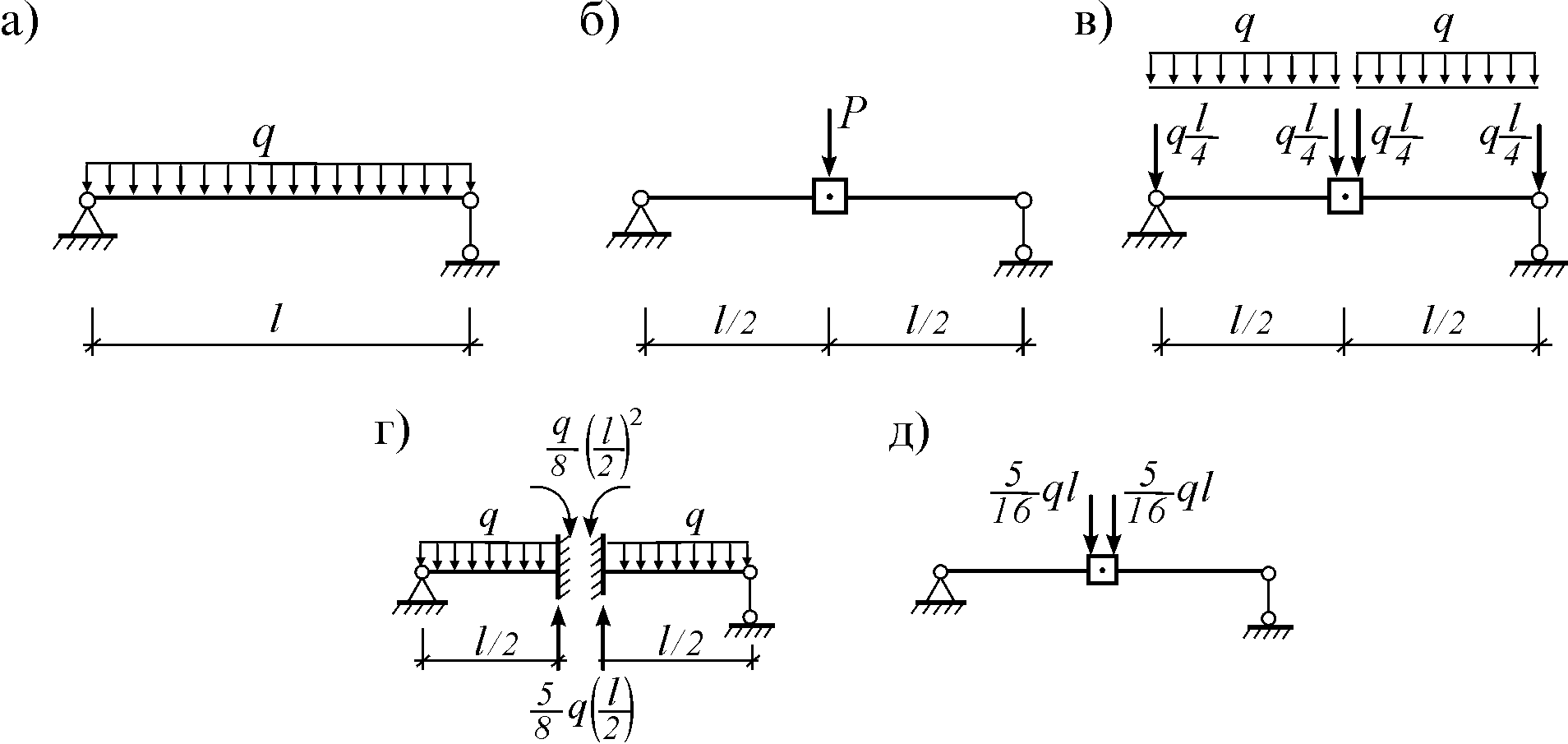

6. Определение углов поворота поперечного сечения.

θ_A = θ_B = ql³sina/24EI = 11.24/EI (671.8.6)

7. Построение эпюр поперечных сил и изгибающих моментов:

На основании полученных ранее данных строим эпюры:

 

<

Рисунок 679.1. Расчетная схема (а), замена опор на реактивные силы (б), эпюра поперечных сил (в), эпюра нормальных сил (г), эпюра изгибающих моментов (д), эпюра углов поворота (е), эпюра прогибов (ж).

Вот собственно и весь расчет.

Распределенные нагрузки.

Теоретическая механика



Распределенные нагрузки

Как мы уже знаем, любая сила характеризуется тремя свойствами: модулем (скалярной размерностью), вектором (направлением в пространстве) и точкой приложения. Для того, чтобы иметь полное представление о характере и последствиях воздействия любой силы на тело или элемент конструкции, необходимо знать — какова величина этой силы, куда она направлена и к какой точке приложена.

В действительности сила не может быть приложена к точке, поскольку точка — безразмерная, бесконечно малая единица пространства, поэтому фактически силы воздействуют на очень малую площадку, размерами которой пренебрегают. Такие силы (приложенные к ничтожно малой площадке тела) называют сосредоточенными.

В реальности часто встречаются силы, приложенные не к точке, а к объему или поверхности тела, например сила тяжести, давления ветра, воды и т. п., т. е. нагрузку воспринимает не бесконечно малая площадка, а значительная площадь или объем тела. Такие силы называют распределенными.

Примером распределенной силы (обычно употребляют выражение «распределенная нагрузка») может послужить выпавший на крышу дома снег. Сила тяжести снежного покрова давит на всю поверхность крыши, нагружая одинаково (или неодинаково) каждую единицу ее площади, а не какую-либо точку.

Плоская система распределенных сил характеризуется ее интенсивностью, обычно обозначаемой латинской буквой q.
Интенсивность — это сила, приходящаяся на единицу длины (или площади) нагруженного участка.
Интенсивность в системе единиц СИ выражается в ньютонах на метр (Н/м) или, соответственно, в ньютонах на квадратный метр (для нагрузки, действующей на площадь).

Интенсивность воздействия силы на площадь характеризует такие физические понятия, как давление и напряжение. В плоской системе рассматривается интенсивность действия силы на единицу длины.



Распределенная нагрузка, имеющая постоянную интенсивность по всей длине участка называется равномерно распределенной (см. рисунок 1).

При решении задач статики распределенную нагрузку заменяют ее равнодействующей. Модуль равнодействующей равномерно распределенной нагрузки равен Q = ql (см. рисунок).
Равнодействующая равномерно распределенной нагрузки Q прикладывается в середине отрезка АВ.

Распределенная нагрузка, имеющая переменную интенсивность, называется неравномерно распределенной (рис. 2).
Примером такой нагрузки может служить меняющееся по высоте давление воды на плотину или снег, лежащий на крыше неровным слоем.
Определение точки С приложения равнодействующей неравномерно распределенной нагрузки производится путем геометрических расчетов и построений. Равнодействующая сила Q при таких нагрузках равна площади фигуры, охватываемой эпюрой нагрузки, а точка С приложения равнодействующей расположена в центре тяжести этой фигуры.

Нагрузки, распределенные по поверхности (по площади), характеризуются давлением, т. е. силой, приходящейся на единицу площади. В системе единиц СИ давление измеряется в Паскалях (Па) или ньютонах на квадратный метр (Н/м²).

***

Пример решения задачи с распределенной нагрузкой

Задача: Балка находится в равновесии под действием сосредоточенной силы F = 100 Н и равномерно распределенной нагрузки q = 60 Н/м (см. схему 3).
Необходимо определить реакцию R_В опоры В.

Решение.
Поскольку по условию задачи необходимо определить реакцию опоры В, составим уравнение моментов сил относительно опоры А, учитывая, что равномерно распределенную нагрузку можно заменить сосредоточенной силой:
Q = ql,    где l = (10 — 5) метров — часть балки, к которой приложена распределенная нагрузка.

Точка приложения сосредоточенной силы Q расположена в середине той части балки, к которой приложена распределенная нагрузка; плечо этой силы относительно опоры А будет равно: h = (10 — 5)/2 = 2,5 м.
Cоставляем уравнение моментов сил относительно опоры А из условия, что балка находится в состоянии равновесия (уравнение равновесия).

Учитываем знаки:

• сила R_В создает относительно точки А положительный момент, плечо которого равно 10м;
• сила F создает относительно точки А отрицательный момент, плечо которого равно 5 м;
• распределенная нагрузка q создает (посредством силы Q и плеча h) относительно точки А отрицательный момент.

Получаем уравнение равновесия балки, в котором лишь одна неизвестная величина (R_В):

ΣM = 10R_В — qlh — 5F = 10R_В — q(10-5)(10-5)/2 — 5F = 0, откуда находим искомую реакцию опоры R_В:

R_В = {q(10-5)(10-5)/2 + 5F}/10 = 125 Н

Задача решена.

***

Условия равновесия плоской системы сходящихся сил



Главная страница

Дистанционное образование

Специальности

Учебные дисциплины

Олимпиады и тесты

Распределенная нагрузка — Теория и решение задач

Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.

Размерность для линейной нагрузки — Н/м, для нагрузки распределенной по площади — Н/м², для объемной (например при учете собственного веса элементов конструкции) — Н/м³.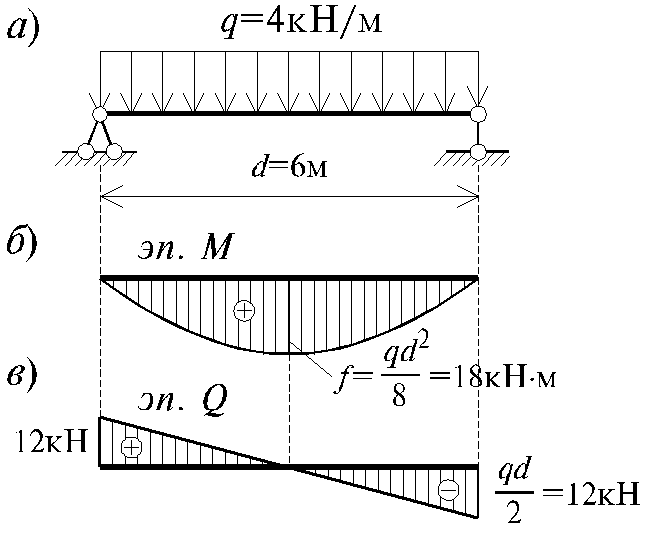

Например, на рисунке 1.23, а приведена равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой

Q = q ∙ AB [Н],

приложенной в середине отрезка AB.

На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой

Q = q_max∙AB/2,

приложенной в точке C, причем AC = 2/3AB.

В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу

Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).

Рисунок 1.23

Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1. 24).

Выделим элемент сектора с углом ∆φ и определим силу ∆Q, действующую на плоский элемент дуги:

∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ. (1.14)

Рисунок 1.24

Проекция этой силы на ось Ox будет

∆Q_x = q ∙ R ∙ ∆φ∙ cosφ. (1.15)

В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:

Q_y = 0, т.е. Q = Q_x, (1.16)

где АВ – хорда, стягивающая концы дуги.

Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м,²]. Если цилиндр рассечен по диаметру (рисунок 1.25), то равнодействующая этих сил равна F = q ∙ d ∙ h (d – внутренний диаметр) или

F = p ∙ 2R ∙ h.

Разрывающие баллон по диаметру усилия:

S₁ = S₂ = S;
2S = F;
S = p∙h∙R. (1.18)

Рисунок 1.25

Если принять a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно

>> Уравнения равновесия системы сил

1.12.Распределенная нагрузка

При решении практических задач далеко не всегда можно считать, что действующая на тело сила приложена в одной точке. Часто силы бывают приложены на целом участке тела (например снеговая нагрузка, ветровая и т.д.). Такая нагрузка называется распределенной. Равномерно распределенная нагрузка характеризуется интенсивностью q (рис.1.29). Интенсивность — это суммарная нагрузка, приходящаяся на единицу длины конструкции.

Единица измерения интенсивности [H/м], [кН/м]. При решении задач статики распределенную нагрузку можно заменить ее равнодействующей, которая равна произведению интенсивности на длину участка, на который действует распределенная нагрузка, и которая приложена в середине этого участка.

1.13. Решение задач на плоскую систему сил

Пример (рис.1.30). Определить реакции шарнирно опертой балки, нагруженной силой и парой сил с моментом М.

Решение. Воспользуемся тем же планом, который применялся для решение задач на сходящуюся систему сил. Объектом равновесия является вся балка, нагрузка на которую показана на чертеже. Отбросим связи — шарниры А и В. Реакцию неподвижного шарнира А разложим на две составляющих — и, а реакция подвижного шарнира В направлена перпендикулярно опорной плоскости. Таким образом, на балку действует плоская произвольная система сил, для которой можно составить три уравнения равновесия. Выберем оси координат и составим эти уравнения. Уравнения проекций:

1. F_kx = 0; R_ax -Fcos(60) = 0;

2. F_ky = 0; R_ay + R_B — Fcos(30) = 0;

(пара в уравнение проекций не входит, так как сумма проекций сил пары на любую ось равна нулю).

Уравнение моментов составляем относительно точки А, поскольку в ней пересекаются две неизвестных силы. При нахождении момента пары относительно точки А помним, что сумма моментов сил пары относительно любой точки равен моменту пары, а знак момента будет положительным, поскольку пара стремится повернуть тело против часовой стрелки. Для нахождения момента силы удобно разложить ее на вертикальную и горизонтальную составляющие:

F_x=Fcos(60), F_y=Fcos(30)

и воспользоваться теоремой Вариньона, причем следует учесть, что момент от силы относительно точки А равен нулю, поскольку ее линия действия проходит через эту точку. Тогда уравнение моментов примет вид:

3. ; R_в^. 3-F_Bcos(30)2 + M = 0.

Решая это уравнение получим:

Из уравнения (2) находим:

R_ay = Fcos(30) — R_B = 20,867 — 4=-2,67 кН,

а из уравнения (1) R_ax = Fcos(60) = 20,5 = 1 кН.

Пример (рис.1.31). Определить реакции жестко защемленной балки длиной 3 м, нагруженной равномерно распределенной нагрузкой итенсивностью q=10кН/м.

Решение. Заменим равномерно распределенную нагрузку ее равнодействующей Q = 3q = 310 = 30 кН. Она будет приложена в середине пролета, то есть на расстоянии АС = 1,5 м. Рассматриваем равновесие балки АВ. Отбрасываем связь — жесткую заделку, а вместо нее прикладываем две составляющие реакции R_ах и R_ау и реактивный момент M_а.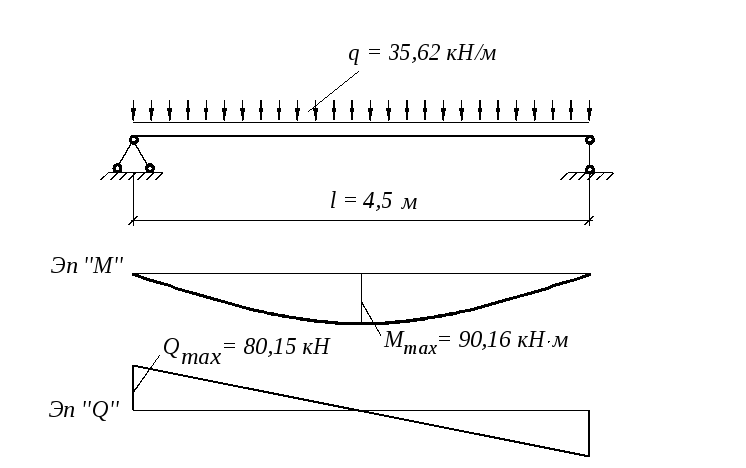 На балку будет действовать плоская произвольная система сил, для которой можно составить три уравнения равновесия, из которых можно найти искомые неизвестные.

F_кх = 0; R_ах = 0;

F_ку = 0; R_ау — Q = 0; R_ау = Q = 30 кН;

M_а(F_к) = 0; M_а — 1,5Q = 0; M_а = 1,5Q = 1,530 = 45 кHм.

Нагрузка равномерно распределенная — Энциклопедия по машиностроению XXL

Определим теперь удлинение стержня постоянного сечения под действием силы тяжести, представляющей собой нагрузку, равномерно распределенную вдоль стержня (рис. 11.5, а). Удельный вес материала бруса обозначим у- Рассмотрим деформацию элемента ба, выделенного на расстоянии а от нижнего конца. Он растягивается силой уЛа, равной силе тяжести части стержня, расположенной ниже сечения т — п. Удлинение элемента равно  [c.27]
Параболическая нить. Пу ть нить находится под действием непрерывной вертикальной нагрузки, равномерно распределенной по длине проекции нити на горизонтальную ось аЬ и приложенной во всех точках нити. Такой случай нагрузки встречается в висячих мостах. Найдем форму кривой, по которой расположится нить при этой нагрузке (рис. 311).  [c.317]

В плоскости верхней грани на раму действует горизонтальная нагрузка, равномерно распределенная по пролету I, интенсивностью q (рис. 120) [65].  [c.335]

При расчете разбиваем основание фундамента на 25 квадратов со сторонами с = 0,5 м в центре каждого квадрата помещаем абсолютно жесткий опорный стержень с шарнирами по краям, соединяющий фундамент с полупространством, и по площади прямоугольника сХ с принимаем нагрузку равномерно распределенной  [c.370]

Указание. Инерционная нагрузка равномерно распределенная по длине I, вычисляется из условия (q p + 9и) = Од, где — вес 1 м трубы. Скорость V найдем из равенства кинетической энергии трубы Т и потенциальной энергии ее деформации U от нагрузки в момент удара трубы об -опоры Т = и.  [c.286]

Найти, как изменится величина угловых и линейных перемещений концевого сечения балки, изображенной на рисунке, если сплошную нагрузку, равномерно распределенную по длине АВ = а, переместить на участок ВС.  [c.175]

Возможна расчетная схема, при которой сила, передающаяся от колеса на ось, рассматривается как нагрузка, равномерно распределенная по длине ступицы колеса (на участке длиной 140 мм).  [c.309]

Пример 95, Дано q — интенсивность нагрузки, равномерно распределенной по горизонтали, р, P=2q , Е, /, (рис. 173, а). Определить 8 — перемещение подвижной опоры.  [c.300]

Так как С является постоянной величиной, то и должно быть постоянным. Следовательно, функция (б) является решением дифференциального уравнения (7.16) при поперечной нагрузке равномерно распределенной по поверхности пластинки.  [c.129]

Нагрузка, равномерно распределенная по всей поверхности пластинки.  [c.135]

И общее решение неоднородного дифференциального уравнения (7.39) для нагрузки, равномерно распределенной по поверхности пластинки, будет  [c.149]

Чтобы получить напряжения, вызываемые всей нагрузкой, равномерно распределенной по площади круга радиуса а, проинтегрируем выражение (д) по ф в пределах от О до я/2 и по г от О до а. Отсюда  [c.408]

Это означает, что нагрузка, равномерно распределенная по площади отверстия 1), уравновешивается растягивающими усилиями  [c.536]

Поэтому арку с заданными нагрузками pi и можно дополнительно нагрузить по всему пролету равномерной нагрузкой р = (Р1 + Рз)/2, что не отразится на изгибающих моментах. Задача сведется к расчету арки на антисимметричную нагрузку (pi — Рз)/2. Аналогичные рассуждения применимы и для параболической арки при вертикальной нагрузке, равномерно распределенной 110 горизонтальной проекции.  [c.374]

Круглая пластинка, защемленная по контуру, нагрузка, равномерно распределенная по всей площади  [c.409]

Построим эпюры для балки с защемленным концом, к которой приложена нагрузка, равномерно распределенная по всей длине I (рис. 91, а). Пусть на единицу длины приходится нагрузка q, тогда вся нагрузка, действующая на балку, равна ql.  [c.100]

Нагрузка равномерно распределенная по всей длине двухопорной балки.  [c.133]

Проф. Н. Е. Жуковский показал, что нагрузка по виткам гайки распределяется неравномерно наиболее нагруженными оказываются витки, расположенные со стороны приложенной силы. Однако в первом приближении с достаточной точностью можно принять нагрузку равномерно распределенной, причем удельное давление при наличии между витками гайки и винта смазки можно определить  [c.483]

Таким образом, односторонняя нагрузка, расположенная вдоль средней диафрагмы, вызывает в ряде случаев большие усилия, чем нагрузка, равномерно распределенная по всей поверхности. Изменение жесткости контура влияет на распределение усилий в оболочке при односторонней нагрузке вдоль средней диафрагмы примерно так же, как и при нагрузке по всему покрытию.  [c.118]

Расчетное сочетание нагрузок. При испытании конструкции нагружали равномерно распределенными по всей поверхности и односторонними нагрузками, а также сосредоточенными нагрузками по диафрагмам в виде арок большого пролета и в местах пересечения ребер панелей. Первоначально все нагружения осуществляли в пределах упругой работы покрытия. До разрушения конструкция была доведена пропорциональным увеличением расчетного сочетания нагрузок (равномерно распределенная — постоянная и снеговая, снеговая с учетом перераспределения по покрытию, сосредоточенная нагрузка от крана по средней диафрагме). При этом нагрузка, равномерно распределенная по покрытию, составляла 6650 Н/м , нагрузка в пределах снегового мешка (в зоне сопряжения оболочек) — 8820 Н/м и сосредоточенная, приложенная к средней диафрагме, 196 кН (рис. 3.48). Конструкция разрушилась от нарушения анкеровки арматуры затяжек 12-метрового пролета в двух опорных узлах. При этом она опустилась на страховочные леса. Наметилось также разрушение оболочки в месте приложения сосредоточенной силы к промежуточной диафрагме — отрыв участка верхнего пояса средней диафрагмы от примыкающих к ней оболочек (рис. 3.48, б).  [c.268]

При действии па цилиндр сосредоточенной кольцевой нагрузки последнюю можно рассматривать как нагрузку, равномерно распределенную на участке бесконечно малой длины.  [c.226]

При действии на цилиндр сосредоточенной кольцевой нагрузки (см. фиг. 10) последнюю можно рассматривать как нагрузку, равномерно распределенную на участке бесконечно малой длины, В этом случае постоянные интегрирования имеют следующие значения  [c.218]

Прямоугольные резервуары и сосуды позволяют более рационально использовать производственные площади, что является важным фактором. В прямоугольных сосудах удобно размещать рабочие устройства. Они конструктивно просты при их изготовлении количество отходов металла незначительно. Прямоугольные сосуды могут быть без укрепляющих элементов (баки), с внутренними и наружными укрепляющими элементами. Сверху открытых сосудов обычно приваривается уголковый фланец для усиления бортов. Листы корпусов прямоугольных аппаратов соединяются встык, листы днищ — встык с подкладкой снизу. Стенки прямоугольных аппаратов можно рассчитывать как пластинки, нагруженные давлением. Заделку краев пластинок (стенок) можно считать шарнирной. Среднее давление жидкости можно принимать в качестве расчетной нагрузки, равномерно распределенной по всей площади пластинки.  [c.146]

Таким образом, хотя нечувствительные скорости ступенчатых роторов современных турбогенераторов при нагрузке, равномерно распределенной по бочке , лежат выше их рабочей скорости, тенденция к повышению мощности генераторов и связанное с этим снижение изгибной жесткости их роторов может привести к появлению в их рабочих диапазонах нечувствительных скоростей не только от сосредоточенных, но и от распределенных грузов. Результаты нашего исследования намечают некоторые пути для своевременного учета этого обстоятельства и дают возможность выбрать длину участка, на котором устанавливаются распределенные грузы так, чтобы избежать появления в рабочем диапазоне нечувствительных скоростей.  [c.163]

Высокие скорости циркуляции в горизонтальных трубах ограничивают осаждение солей на их стенках при повышенных удельных тепловых нагрузках. Равномерное распределение пароводяной смеси по циклонам при равном паросодержании потоков и высоком сопротивлении циклонов обеспечивает их равномерную нагрузку при значительных скоростях пароводяной смеси. В результате увеличивается интенсивность работы циклонов и повышается качество пара.  [c.177]

Рассматривая лопатку как консольную балку, защемленную в корне, определяем изгибающие моменты, действующие в плоскостях главных осей инерции. Для небольших лопаток с отношением D p// 15 обычно пренебрегают переменными усилиями по высоте лопаток и принимают нагрузку равномерно распределенной. Интенсивность такой нагрузки  [c.43]

На фиг. 230, а показаны совмещенные таким образом характеристики, обеспечивающие равномерное распределение нагрузки (при одинаковых двигателях) только при полной нагрузке на выбранном скоростном режиме Пу. По мере сброса нагрузки равномерность распределения ее резко нарушается, и при п = Пу  [c.309]

Частичное нагружение пластины. Рассмотрим действие нагрузки, равномерно распределенной по площади прямоугольника со сторонами с W d (рис. 20.26).  [c.441]

Распределенными нагрузками называются силы, приложенные непрерывно на протяжении некоторой длины или площади конструкции. Слой песка одинаковой толщины, насыпанный на тротуар моста, представляет собой нагрузку, равномерно распределенную по некоторой площади при неодинаковой толщине слоя мы получим неравномерно распределенную сплошную нагрузку. Собственный вес балки какого-либо перекрытия представляет собой нагрузку, распределенную по длине элемента.  [c.17]

На круглую пластину радиусом 1 м действуют сжимающие радиалшые нагрузки, равномерно распределенные по контуру, которые представляют собой случайную величину с нормальным законом распределения. Края пластины свободно оперты по контуру. Надо так подобрать толщину пластины й,то)бы ее надежность по устойчивости Язад = 0,9958. Кроме того, известно, что т = 2 10 Н/м а = = 2 10 Н/м 11 = 0,3 с вероятностью Hg = 0,9986 Е>2 — 10 Па. Учет случайного разброса толщины пластины следует проводить с доверительной вероятностью Ял = 0,9986, т.е. Язад/Я -Я = 0,9986. Для Я = 0,9986 7 = 3. По (1.23)  [c.12]

Пример 2. Рассмотрим задачу о сжатии двух цилиндров радиусами Ri и (рис. 5.13), загруженных нагрузкой, равномерно распределенной по длине цилиндра, ннтенсивностью р.  [c.145]

Балка, лежащая на двух опорах, составлена из двух дюралевых бульбуголков Пр. 105 № 11 (момент инерции сечения одного уголка относительно горизонтальной оси У=3,75 см ). К концам балки жестко прикреплены стойки высотой h=l м. Определить сближение б концов тип стоек под влиянием нагрузки, равномерно распределенной по балке, интенсивностью р=150 кГ/м, Пролет балки /=1,5 м. Модуль упругости =7,5-10 кГ/см .  [c.128]

Цилиндрический поплавок осажен в воду на половину своей высоты нагрузкой, равномерно распределенной вдоль верхнего стрингера (в вертикательной диаметральной плоскости). Диаметр поплавка с1 = 2г — 0,6м, объемный вес воды у 1 Т/м . На взаимном расстоянии а = 0,4 ж расположены кольцевые шпангоуты /- onst. Построить эпюры М, N, Q ъ шпангоуте, пренебрегая разницей между диаметрами поплавка и оси шпангоута.  [c.186]

Пусть брусья А и В, имеющие поперечное сечение Р (рис. 2.5), находятся под действием нагрузок, приложенных к их торцам брус А нагружен равномерно распределенными нагрузками интенсивности д, а брус В —самоуравновешенными системами сил, состоящими из сосредоточенных сил Р и распределенных нагрузок интенсивности д, причем дР = Р. Воспользовавшись принципом суперпозиции и наложив одно напряженное состояние (Л) на другое (В), получим новое состояние (С) напряжение в стержне, растягиваемом сосредоточенными силами. Как и в случае растяжения нагрузками, равномерно распределенными по торцам, нормальные напряжения по поперечному сечению определяются по формуле  [c.129]

Допустим, что поллс кит расчету свободно лежащая балка пролетом / = 4 м. несущая постоянную нагрузку ([равномерно распределенную по всему пролету) интенсивностью 7 = 0,5 7 /,1г и временную (сосредоточенную в середине полета) нагрузку Р весом 10 Т. Расчетные коэффициенты имеют значения а, = 1,1 п =, 3 k — =т=0,9. Нормативное сопротивление стали Ra 2,5 Т/см . Требуется установить потребный номер двутавра по ГОСТу.  [c.245]

Поведение оболочки под нагрузкой рассмотрим на примере кругового тонкостенного цилиндра, сжатого вдоль образующей (рис. 18.78, а). Если конструкция имеет строго правильную поверхность и радиальные перемещения на торцах ничем не стеснены, то при любой нагрузке, равномерно распределенной по торцу, безызгибная форма будет равновесной (ось ординат на диаграмме рис. 18.78,6). Наряду с этим, как показывает нелинейный анализ, возможны различные изгибные формы равновесия 2). Естественно, что в первую очередь представляет интерес та форма искривления поверхности, которая является равновесной для наиболее низкой нагрузки. Такими оказываются искривления поверхности в форме ромбовидных вмятин (см. рис. 18.78, а). Пусть под / по-прежнему понимается характерное перемещение изгибной формы равновесия (например, глубина вмятины). Обозначим через О отношение размеров вмятины по направляющей и образующей поверхности. Каждой фиксированной форме вмятины отвечает своя равновесная кривая  [c.418]

У хрома НВ 5—25. Хромированная поверхность в 1,5—2,5 раза более износоустойчива, чем нехроиирован-пая. Хром хорошо выдерживает динамическую нагрузку, равномерно распределенную по рабочей поверхности, и разрушается под действием сосредоточенных ударов или при больших давле-  [c.197]

Расчет оболочек без учета влияния деформативноети диафрагм, как было показано выше, дает респределение усилий, значительно отличающееся от опыта. Разработано несколько методов расчета отдельно стоящих и многоволновых оболочек положительной кривизны, учитывающих жесткость диафрагм. В настоящем разделе даются основные положения расчета оболочек методом В. С. Бартенева [49], позволяющим рассчитывать отдельно стоящие и многоволновые ОПГК на действие равномерно распределенной по всей поверхности покрытия и односторонней снеговых нагрузок при диафрагмах в виде балок, арок, ферм, рам и т. д. Расчет разработан для трех вариантов воздействия равномерно распределенной нагрузки (равномерное распределение нагрузки по всему покрытию, кососимметричное загружение в продольном сечении и кососимметричное загружение в поперечном сечении). Последние два варианта позволяют учитывать нагрузку от снеговых мешков.  [c.141]

При составлении дифференциального уравнения для второго участка (при a x l) необходимо согласно изложенному выше второму правилу сохранить все слагаемые первого участка. В данном случае слагаемое (—qxy2), сохраненное для второго участка, соответствует нагрузке, равномерно распределенной по всей длине балки. Но такой нагрузки на самом деле нет. Выходом из создавшегося противоречия будет следующее. Нагрузим балку равномерно распределенной нагрузкой интенсивности q сверху по всей длине, а также равномерно распределенной нагрузкой такой же интенсивности снизу, но только на длине второго участка (рис. 11.56). Верхняя нагрузка на первом и втором участках будет описываться одним и тем же слагаемым -qxV2), нижняя — слагаемым (q x—af/2) только на втором участке. Таким образом, при а х 1. имеем следующую цепочку равенств  [c.194]

Такая балка-стенка изображена на рис. 27 Она опирается на ряд колонн, расположенных с одинаковым шагом 21, и несет нагрузку, равномерно распределенную по верхней гранн. Собственный вес балки-стенкн при расчете во внимание не принимается.  [c.80]

НИИ. перпендикулярном плоскости чертежа, весьма мала, то возникает сбсбщенное плоское напряженное состояние. Если же протяженность среды в указанном направлении велика, то имеем дело с плоской деформацией и в этом случае сила Р представляет собой нагрузку, равномерно распределенную вдоль прямой, перпендикулярной плоскости чертежа.  [c.99]

Нить имеет постоянное сечение, следовательно, вес ее распределен равномерно по ее длине. Обычно провисание нити невелико по сравнению с ее пролетом, а длина кривой АОВ мало отличается (не более чем на 10%) от длины хорды Л В. В этом случае с достаточной степенью точности можно считать, что вес нити равномерно распределен по длине ее проекции на горизонтальную ось, т. е. вдоль пролета I. Эту категорию гйбких нитей мы и рассмотрим. Примем, что интенсивность нагрузки, равномерно распределенной по пролету нити, равна д. Эта нагрузка, имеющая размерность сила/длина, может быть не только собственным весом нити, приходящимся на  [c.89]

---

И распределяет равномерную нагрузку на. Распределенная нагрузка. Расчет составных систем

Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно расстоянию между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки также попадают на начало и на конец пролета, но при этом вызывают только увеличение опорной реакции, на значение изгибающих моментов и на прогиб крайние сосредоточенные нагрузки никак не влияют, а потому при расчетах несущей способности конструкции не учитываются. Рассмотрим это на примере балок перекрытия опирающихся на перемычку. Кирпичная кладка, которая может быть между перемычкой и балками перекрытия, и создавать при этом равномерно распределенную нагрузку, для простоты восприятия не показана.

Рисунок 1 . Приведение сосредоточенных нагрузок к эквивалентной равномерно распределенной нагрузке.

Как видно из рисунка 1, определяющим является изгибающий момент, который используется при расчетах конструкций на прочность. Таким образом, чтобы равномерно распределенная нагрузка создавала такой же изгибающий момент, как и сосредоточенная нагрузка, ее нужно умножить на соответствующий коэффициент перехода (коэффициент эквивалентности). А определяется этот коэффициент из условий равенства моментов. Думаю, рисунок 1 это очень хорошо иллюстрирует. А еще, анализируя полученные зависимости, можно вывести общую формулу для определения коэффициента перехода. Так, если количество приложенных сосредоточенных нагрузок является нечетным, т.е. одна из сосредоточенных нагрузок обязательно попадает на середину пролета, то для определения коэффициента эквивалентности можно использовать формулу:

γ = n/(n — 1) (305.1.1)

где n — количество пролетов между сосредоточенными нагрузками.

q экв = γ(n-1)Q/l (305.1.2)

где (n-1) — количество сосредоточенных нагрузок.

Впрочем, иногда удобнее производить расчеты, исходя из количества сосредоточенных нагрузок. Если это количество выразить переменной m, то тогда

γ = (m +1)/m (305.1.3)

При этом эквивалентная равномерно распределенная нагрузка будет равна:

q экв = γmQ/l (305.1.4)

Когда количество сосредоточенных нагрузок является четным, т.е. ни одна из сосредоточенных нагрузок не попадает на середину пролета, то значение коэффициента можно принимать, как для следующего нечетного значения количества сосредоточенных нагрузок. В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:

γ = 2 — если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки.

γ = 1.33 — для балки, на которую действуют 2 или 3 сосредоточенные нагрузки;

γ = 1.2 — для балки, на которую действуют 4 или 5 сосредоточенных нагрузок;

γ = 1.142 — для балки, на которую действуют 6 или 7 сосредоточенных нагрузок;

γ = 1.11 — для балки, на которую действуют 8 или 9 сосредоточенных нагрузок.

2 вариант

Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно половине расстояния между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки не попадают на начало и на конец пролета.

Рисунок 2 . Значения коэффициентов перехода при 2 варианте приложения сосредоточенных нагрузок.

Как видно из рисунка 2, при таком варианте загружения значение коэффициента перехода будет значительно меньше. Так, например, при четном количестве сосредоточенных нагрузок, коэффициент перехода вообще можно принимать равным единице. При нечетном количестве сосредоточенных нагрузок для определения коэффициента эквивалентности можно использовать формулу:

γ = (m +7)/(m +6) (305.2.1)

где m — количество сосредоточенных нагрузок.

При этом эквивалентная равномерно распределенная нагрузка все также будет равна:

q экв = γmQ/l (305.1.4)

В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:

γ = 2 — если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки, а попадают ли балки перекрытия на начало или конец пролета или расположены сколь угодно далеко от начала и конца пролета, в данном случае значения не имеет. А значение это имеет при определении сосредоточенной нагрузки.

γ = 1 — если на рассматриваемую конструкцию, действует четное количество нагрузок.

γ = 1.11 — для балки, на которую действуют 3 сосредоточенные нагрузки;

γ = 1.091 — для балки, на которую действуют 5 сосредоточенных нагрузок;

γ = 1.076 — для балки, на которую действуют 7 сосредоточенных нагрузок;

γ = 1.067 — для балки, на которую действуют 9 сосредоточенных нагрузок.

Не смотря на некоторую заковыристость определения, коэффициенты эквивалентности очень просты и удобны. Так как при расчетах очень часто известна распределенная нагрузка, действующая на квадратный или погонный метр, то чтобы не переводить распределенную нагрузку сначала в сосредоточенную, а потом снова в эквивалентную распределенную, достаточно просто умножить значение распределенной нагрузки на соответствующий коэффициент. Например, на перекрытие будет действовать нормативная распределенная нагрузка 400 кг/м 2 , при этом собственный вес перекрытия составит еще 300 кг/м 2 . Тогда при длине балок перекрытия 6 м на перемычку могла бы действовать равномерно распределенная нагрузка q = 6(400 + 300)/2 = 2100 кг/м. А дальше, если будет только одна балка перекрытия посредине пролета, то γ = 2, а

q экв = γq = 2q (305.2.2)

Если ни одно из двух вышеприведенных условий не соблюдается, то использовать коэффициенты перехода в чистом виде нельзя, нужно добавить еще пару дополнительных коэффициентов, учитывающих расстояние до балок, не попадающих на начало и конец пролета перемычки, а также возможную несимметричность приложения сосредоточенных нагрузок. Вывести такие коэффициенты в принципе можно, однако в любом случае они будут понижающими во всех случаях, если рассматривать 1 вариант загружения и в 50% случаев, если рассматривать 2 вариант загружения, т.е. значения таких коэффициентов будут

Наряду с рассмотренными выше сосредоточенными силами строительные конструкции и сооружения могут подвергаться воздействию распределенных нагрузок – по объему, по поверхности или вдоль некоторой линии – и определяемых ее интенсивностью.

Примером нагрузки, распределенной по площади , является снеговая нагрузка, давление ветра, жидкости или грунта. Интенсивность такой поверхностной нагрузки имеет размерность давления и измеряется в кН/м 2 или килопаскалях (кПа = кН/м 2).

При решении задач очень часто встречается нагрузка, распределенная по длине балки . Интенсивность q такой нагрузки измеряется в кН/м.

Рассмотрим балку, загруженную на участке [a , b ] распределенной нагрузкой, интенсивность которой изменяется по закону q = q (x ). Для определения опорных реакций такой балки нужно заменить распределенную нагрузку эквивалентной сосредоточенной. Это можно сделать по следующему правилу:

Рассмотрим частные случаи распределенной нагрузки.

а) общий случай распределенной нагрузки (рис.24)

Рис.24

q(x) — интенсивность распределенной силы [Н/м],

Элементарная сила.

l – длина отрезка

Распределенная по отрезку прямой сила интенсивности q(x) эквивалентна сосредоточенной силе

Сосредоточенная сила прикладывается в точке С (центре параллельных сил) с координатой

б) постоянная интенсивность распределенной нагрузки (рис.25)

Рис.25

в) интенсивность распределенной нагрузки, меняющаяся по линейному закону (рис.26)

Рис.26

Расчет составных систем.

Под составными системами будем понимать конструкции, состоящие из нескольких тел, соединенных друг с другом.

Прежде, чем переходить к рассмотрению особенностей расчета таких систем, введем следующее определение.

Статически определимыми называются такие задачи и системы статики, для которых число неизвестных реакций связей не превышает максимально допустимого числа уравнений.

Если число неизвестных больше числа уравнений, соответствующие задачи и системы называются статически неопределимыми . При этом разность между числом неизвестных и числом уравнений называется степенью статической неопределимости системы.

Для любой плоской системы сил, действующих на твердое тело, имеется три независимых условия равновесия. Следовательно, для любой плоской системы сил из условий равновесия можно найти не более трех неизвестных реакций связи.

В случае пространственной системы сил, действующих на твердое тело, имеется шесть независимых условия равновесия. Следовательно, для любой пространственной системы сил из условий равновесия можно найти не более шести неизвестных реакций связи.

Поясним это на следующих примерах.

1. Пусть центр невесомого идеального блока (пример 4) удерживается при помощи не двух, а трех стержней: АВ , ВС и BD и нужно определить реакции стержней, пренебрегая размерами блока.

С учетом условий задачи мы получим систему сходящихся сил, где для определения трех неизвестных: S A , S C и S D можно составить по-прежнему систему только двух уравнений: ΣX = 0, ΣY =0. Очевидно, поставленная задача и соответствующая ей система будут статически неопределимыми.

2. Балка, жестко защемленная на левом конце и имеющая на правом конце шарнирно-неподвижную опору, загружена произвольной плоской системой сил (рис.27).

Для определения опорных реакций можно составить только три уравнения равновесия, куда войдут 5 неизвестных опорных реакций: X A , Y A , M A , X B и Y B . Поставленная задача будет дважды статически неопределимой.

Такую задачу нельзя решить в рамках теоретической механики, предполагая рассматриваемое тело абсолютно твердым.

Рис.27

Вернемся к изучению составных систем, типичным представителем которых является трехшарнирная рама (рис. 28,а ). Она состоит из двух тел: AC и BC , соединенным ключевым шарниром C . На примере этой рамы рассмотрим два способа определения опорных реакций составных систем.

1 способ. Рассмотрим тело AC , загруженное заданной силой Р , отбросив в соответствии с аксиомой 7 все связи и заменив их соответственно реакциями внешних (X A , Y A ) и внутренних (X C , Y C ) связей (рис. 28,б ).

Аналогично можно рассмотреть равновесие тела BC под действием реакций опоры В — (X B , Y B ) и реакций в соединительном шарнире C — (X C ’ , Y C ’) , где в соответствии с аксиомой 5: X C = X C ’ , Y C = Y C ’.

Для каждого из этих тел можно составить три уравнения равновесия, таким образом, общее число неизвестных: X A , Y A , X C =X C ’ , Y C =Y C ’, X B , Y B равняется суммарному числу уравнений, и задача является статически определимой.

Напомним, что по условию задачи требовалось определить только 4 опорные реакции, нам же пришлось проделать дополнительную работу, определяя реакции в соединительном шарнире. В этом и заключается недостаток данного способа определения опорных реакций.

2 способ. Рассмотрим равновесие всей рамы АВС , отбросив только внешние связи и заменив их неизвестными опорными реакциями X A , Y A , X B , Y B .

Полученная система состоит из двух тел и не является абсолютно твердым телом, поскольку расстояние между точками А и В может изменяться вследствие взаимного поворота обеих частей относительно шарнира С . Тем не менее можно считать, что совокупность сил, приложенных к раме АВС образует систему, если воспользоваться аксиомой отвердевания (рис.28,в ).

Рис.28

Итак, для тела АВС можно составить три уравнения равновесия. Например:

ΣM A = 0;

ΣX = 0;

В эти три уравнения войдут 4 неизвестных опорных реакции X A , Y A , X B и Y B . Отметим, что попытка использовать в качестве недостающего уравнения, например такое: ΣM В = 0 к успеху не приведет, поскольку это уравнение будет линейно зависимым с предыдущими. Для получения линейно независимого четвертого уравнения необходимо рассмотреть равновесие другого тела. В качестве него можно взять одну из частей рамы, например — ВС . При этом нужно составить такое уравнение, которое содержало бы «старые» неизвестные X A , Y A , X B , Y B и не содержало новых. Например, уравнение: ΣX (ВС ) = 0 или подробнее: —X С ’ + X B = 0 для этих целей не подходит, поскольку содержит «новое» неизвестное X С ’, а вот уравнение ΣM С (ВС ) = 0 отвечает всем необходимым условиям. Таким образом, искомые опорные реакции можно найти в следующей последовательности:

ΣM A = 0; → Y B = Р /4;

ΣM В = 0; → Y А = —Р /4;

ΣM С (ВС ) = 0; → X B = —Р /4;

ΣX = 0; → X А = -3Р /4.

Для проверки можно использовать уравнение: ΣM С (АС ) = 0 или, подробнее: —Y А ∙2 + X А ∙2 + Р ∙1 = Р /4∙2 -3Р /4∙2 + Р ∙1 = Р /2 — 3Р /2 + Р = 0.

Отметим, что в это уравнение входят все 4 найденные опорные реакции: X А и Y А — в явной форме, а X B и Y B — в неявной, поскольку они были использованы при определении двух первых реакций.

Графическое определение опорных реакций.

Во многих случаях решение задач можно упростить, если вместо уравнений равновесия или в дополнение к ним непосредственно использовать условия равновесия, аксиомы и теоремы статики. Соответствующий подход и получил название графического определения опорных реакций.

Прежде чем перейти к рассмотрению графического метода отметим, что, как и для системы сходящихся сил, графически можно решить только те задачи, которые допускают аналитическое решение. При этом графический метод определения опорных реакций удобен при небольшом числе нагрузок.

Итак, графический метод определения опорных реакций основан главным образом на использовании:

Аксиомы о равновесии системы двух сил;

Аксиомы о действии и противодействии;

Теоремы о трех силах;

Условия равновесия плоской системы сил.

При графическом определении реакций составных систем рекомендуется следующая последовательность рассмотрения :

Выбрать тело с минимальным числом алгебраических неизвестных реакций связей;

Если таких тел два или больше, то начать решение с рассмотрения тела, к которому приложено меньшее число сил;

Если таких тел два или больше, то выбрать тело, для которого большее число сил известно по направлению.

Решение задач.

При решения задач этого раздела сле­дует иметь в виду все те общие указания, которые были сделаны ранее.

Приступая к решению, надо, прежде всего, установить, равновесие какого именно тела следует в данной задаче рассмотреть. Затем, выделив это тело и рассматривая его как свободное, следует изобразить все действующие на тело заданные силы и реакции отброшенных связей.

Далее следует составить условия равновесия, применяя ту из форм этих условий, которая приводит к более простой системе урав­нений (наиболее простой будет система уравнений, в каждое из ко­торых входит по одному неизвестному).

Для получения более простых уравнений следует (если это только не усложняет ход расчета):

1) составляя уравнения проекций, проводить координатную ось, перпендикулярно какой-нибудь неиз­вестной силе;

2) при составлении моментного уравнения в качестве моментной целесообразно выбирать точку, где пересекаются линии действия двух неизвестных опорных реакций из трех – в этом случае они не войдут в уравнение, и оно будет содержать только одно неизвестное;

3) если две неизвестных опорных реакции из трех параллельны, то при составлении уравнения в проекциях на ось последнюю следует направить так, чтобы она была перпендикулярна к двум первым реакциям – в этом случае уравнение будет содержать только последнее неизвестное;

4) при решении задачи систему координат надо выбирать так, чтобы ее оси были ориентированы так же, как большинство приложенных к телу сил системы.

При вычислении моментов иногда бывает удобно разла­гать данную силу на две составляющие и, пользуясь теоремой Вариньона, находить момент силы как сумму моментов этих соста­вляющих.

Решение многих задач статики сводится к определению реакций опор, с помощью которых закрепляются балки, мостовые фермы и т. п.

Пример 7. К кронштейну, изображенному на рис.29, а, в узле В подвешен груз весом 36 кН. Соединения элементов кронштейна шарнирные. Определить усилия, возникающие в стержнях АВ и ВС , считая их невесомыми.

Решение. Рассмотрим равновесие узла В , в котором сходятся стержни АВ и ВС . Узел В представляет собой точку на чертеже. Так как груз подвешен к узлу В , то в точке В прикладываем силу F, равную весу подвешенного груза. Стержни ВА и ВС , шарнирно соединенные в узле В, ограничивают возможность любого его линейного перемещения в вертикальной плоскости, т.е. являются связями по отношению к узлу В .

Рис. 29. Расчетная схема кронштейна к примеру 7:

а – расчетная схема; б – система сил в узле B

Мысленно отбрасываем связи и заменяем их действия силами — реакциями связей R А и R С . Так как стержни невесомые, то реакции этих стержней (усилия в стержнях) направлены вдоль оси стержней. Предположим, что оба стержня растянуты, т.е. их реакции направлены от шарнира внутрь стержней. Тогда, если после расчета реакция получится со знаком минус, то это будет означать, что на самом деле реакция направлена в сторону, противоположную указанной на чертеже, т.е. стержень будет сжат.

На рис. 29, б показано, что в точке В приложены активная сила F и реакции связей R А и R С. Видно, что изображенная система сил представляет плоскую систему сил, сходящихся в одной точке. Выбираем произвольно оси координат OX и OY и составляем уравнения равновесия вида:

ΣF x = 0; -R a — R c cos 𝛼 = 0;

ΣF y = 0; -F — R c cos (90 — α) = 0.

Учитывая, что cos (90 — α) = sin α, из второго уравнения находим

R c = -F/sin α = — 36/0,5 = -72 кН.

Подставив значение R c в первое уравнение, получим

R a = -R c cos α= — (-72) ∙0,866 = 62,35 кН.

Таким образом, стержень АВ — растянут, а стержень ВС — сжат.

Для проверки правильности найденных усилий в стержнях спроектируем все силы на любую ось, не совпадающую с осями X и Y , например, ось U :

ΣF u = 0; —R c — R a cos α — F cos (90- α) = 0.

После подстановки значений найденных усилий в стержнях (размерность в килоньютонах) получим

— (-72) – 62,35∙0,866 — 36∙0,5 = 0; 0 = 0.

Условие равновесия выполняется, таким образом, найденные усилия в стержнях верны.

Пример 8. Балка строительных подмостей, весом которой можно пренебречь удерживается в горизонтальном положении гибкой тягой СD и шарнирно опирается на стену в точке А . Найти усилие в тяге СD , если на край подмостей встанет рабочий весом 80 кг ≈0,8 кН (рис.30, а ).

Рис. 30. Расчетная схема подмостей к примеру 8:

а – расчетная схема; б – система сил действующих на подмости

Решение. Выделяем объект равновесия. В данном примере объектом равновесия является балка подмостей. В точке В на балку действует активная сила F , равная весу человека. Связями в данном случае являются неподвижный опорный шарнир А и тяга CD . Мысленно отбросим связи, заменив их действие на балку, реакциями связей (рис. 30, б ). Реакцию неподвижной шарнирной опоры по условию задачи определять не нужно. Реакция в тяге CD направлена вдоль тяги. Предположим, что стержень CD растянут, т.е. реакция R D направлена от шарнира С внутрь стержня. Разложим реакцию R D , по правилу параллелограмма, на горизонтальную и вертикальную составляющие:

R Dx гор =R D cos α;

R Dy верт = R D cos (90-α) =R D sin α.

В результате получили произвольную плоскую систему сил, необходимым условием равновесия которой является равенство нулю трех независимых условий равновесия,.

В нашем случае удобно первым записать условие равновесия в виде суммы моментов относительно моментной точки А , так как момент опорной реакции R A относительно этой точки равен нулю:

Σm A = 0; F ∙3a — R dy ∙a = 0

F ∙3a — R D sin α= 0.

Значение тригонометрических функций определим из треугольника АСD:

cosα = АC/CD = 0,89,

sinα = AD/CD = 0,446.

Решая уравнение равновесия, получим R D = 5,38 кH. (Тяж СD — растянут).

Для проверки правильности вычисления усилия в тяже CD необходимо вычислить хотя бы одну из составляющих опорной реакции R A . Воспользуемся уравнением равновесия в виде

ΣF y = 0; V A + R Dy — F = 0

V A = F — R dy .

Отсюда V A = -1,6 кН.

Знак минус означает, что вертикальная составляющая реакции R A на опоре направлена вниз.

Проверим правильность вычисления усилия в тяже. Используем еще одно условие равновесия в виде уравнений моментов относительно точки В .

Σm B = 0; V A ∙3а + R Dy ∙ 2a = 0;

1,6∙3а + 5,38∙0,446∙2а = 0; 0 = 0.

Условия равновесия соблюдаются, таким образом, усилие в тяже найдено верно.

Пример 9. Вертикальный бетонный столб забетонирован нижним концом в горизонтальное основание. Сверху на столб передается нагрузка от стены здания весом 143 кН. Столб изготовлен из бетона плотностью γ= 25 кН/м 3 . Размеры столба показаны на рис. 31, а . Определить реакции в жесткой заделке.

Рис. 31. Расчетная схема столба к примеру 9:

а – схема загрузки и размеры столба; б – расчетная схема

Решение. В данном примере объектом равновесия является столб. Столб загружен следующими типами активных нагрузок: в точке А сосредоточенной силой F, равной весу стены здания, и собственным весом столба в виде равномерно распределенной по длине бруса нагрузки интенсивностью q на каждый метр длины столба: q = 𝛾А , где А — площадь поперечного сечения столба.

q = 25∙0,51∙0.51 = 6,5 кН/м.

Связями в данном примере является жесткая заделка в основании столба. Мысленно отбросим заделку и заменим ее действие реакциями связей (рис. 31, б ).

В нашем примере рассматривается частный случай действия системы сил, перпендикулярных заделке и проходящих по одной оси через точку приложения опорных реакций. Тогда две опорные реакции: горизонтальная составляющая и реактивный момент будут равны нулю. Для определения вертикальной составляющей опорной реакции спроектируем все силы на ось элемента. Совместим эту ось с осью Z, тогда условие равновесия запишется в следующем виде:

ΣF Z = 0; V B — F — ql = 0,

где ql — равнодействующая распределенной нагрузки.

V B = F +ql= 143 + 6,5∙4 = 169 кН.

Знак плюс указывает, что реакция V B направлена вверх.

Для проверки правильности вычисления опорной реакции остается еще одно условие равновесия — в виде алгебраической суммы моментов всех сил относительно любой точки, не проходящей через ось элемента. Предлагаем выполнить эту проверку самостоятельно.

Пример 10. Для балки, изображенной на рис.32, а , требуется определить опорные реакции. Дано: F = 60 кН, q = 24 кН/м, М = 28 кН∙м.

Рис. 32. Расчетная схема и размеры балки к примеру 10:

Решение. Рассмотрим равновесие балки. Балка загружена активной нагрузкой в виде плоской системы параллельных вертикальных сил, состоящих из сосредоточенной силы F , равномерно распределенной нагрузки интенсивностью q с равнодействующей Q , приложенной в центре тяжести грузовой площади (рис. 32, б ), и сосредоточенного момента М , который можно представить в виде пары сил.

Связями в данной балке являются шарнирно-неподвижная опора А и шарнирно-подвижная опора В . Выделим объект равновесия, для этого отбросим опорные связи и заменим их действия реакциями в этих связях (рис. 32, б ). Реакция подвижной опоры R B направлена вертикально, а реакция шарнирно-неподвижной опоры R A будет параллельна активной системе действующих сил и направлена также вертикально. Предположим, что они направлены вверх. Равнодействующая распределенной нагрузки Q = 4,8∙q приложена в центре симметрии грузовой площади.

При определении опорных реакций в балках необходимо стремиться так составлять уравнения равновесия, чтобы в каждое из них входило только одно неизвестное. Этого можно добиться, составляя два уравнения моментов относительно опорных точек. Проверку опорных реакций обычно проводят, составляя уравнение в виде суммы проекций всех сил на ось, перпендикулярную оси элемента.

Примем условно направление вращения момента опорных реакций вокруг моментных точек за положительное, тогда противоположное направление вращения сил будем считать отрицательным.

Необходимым и достаточным условием равновесия в данном случае является равенство нулю независимых условий равновесия в виде:

Σm A = 0; V B ∙6 — q ∙4,8∙4,8 + M + F ∙2,4 = 0;

Σm B = 0; V A ∙6 — q ∙4,8∙1,2 — M — F ∙8,4 = 0.

Подставляя численные значения величин, находим

V B = 14,4 кН, V A = 15,6 кН.

Для проверки правильности найденных реакций используем условие равновесия в виде:

ΣF y = 0; V A + V B — F -q ∙4,8 =0.

После подстановки численных значений в это уравнение получаем тождество типа 0=0. Отсюда делаем выводы, что расчет выполнен верно и реакции на обеих опорах направлены вверх.

Пример 11. Определить опорные реакции для балки, изображенной на рис.33, а . Дано: F = 2,4 кН, M = 12 кН∙м, q = 0,6 кН/м, a = 60°.

Рис. 33. Расчетная схема и размеры балки к примеру 11:

а – расчетная схема; б – объект равновесия

Решение. Рассмотрим равновесие балки. Мысленно освобождаем балку от связей на опорах и выделяем объект равновесия (рис. 33, б ). Балка загружена активной нагрузкой в виде произвольной плоской системы сил. Равнодействующая распределенной нагрузки Q = q ∙3 приложена в центре симметрии грузовой площади. Силу F разложим по правилу параллелограмма на составляющие – горизонтальную и вертикальную

F z = F cosα= 2,4 cos60° = 1,2 кН;

F y =F cos(90-α) = F sin60° = 2,08 кН.

Прикладываем к объекту равновесия вместо отброшенных связей реакции. Предположим, вертикальная реакция V A шарнирно подвижной опоры А направлена вверх, вертикальная реакция V B шарнирно неподвижной опоры B направлена также вверх, а горизонтальная реакция H В — вправо.

Таким образом, на рис. 33, б изображена произвольная плоская система сил, необходимым условием равновесия которой является равенство нулю трех независимых условий равновесия для плоской системы сил. Напомним, что, согласно теореме Вариньона, момент силы F относительно любой точки равен сумме моментов составляющих F z и F y относительно этой же точки. Примем условно, направление вращения момента опорных реакций вокруг моментных точек за положительное, тогда противоположное направление вращение сил будем считать отрицательным.

Тогда условия равновесия удобно составить в следующем виде:

ΣFz = 0; — F z + H B = 0; отсюда H B = 1,2 кН;

Σm A = 0; V B ∙6 + M — F y ∙2 + 3q ∙0.5 = 0; отсюда V B = — 1,456 кН;

Σm B = 0; V A ∙6 — 3q ∙6,5 — F y ∙4 — M = 0; отсюда V A = 5,336 кН.

Для проверки правильности вычисленных реакций используем еще одно условие равновесия, которое не использовали, например:

ΣF y = 0; V A + V B — 3q — F y = 0.

Вертикальная опорной реакции V B получилась со знаком минус, это показывает, что в данной балке она направлена не вверх, а вниз.

Пример 12. Определить опорные реакции для балки, жестко заделанной с одной стороны и изображенной на рис. 34, а . Дано: q =20 кН/м.

Рис. 34. Расчетная схема и размеры балки к примеру 12:

а – расчетная схема; б – объект равновесия

Решение. Выделим объект равновесия. Балка загружена активной нагрузкой в виде плоской системы параллельных сил, расположенных вертикально. Мысленно освобождаем балку от связей в заделке и заменяем их реакциями в виде сосредоточенной силы V B и пары сил с искомым реактивным моментом М B (см. рис.34, б ). Так как активные силы действуют только в вертикальном направлении, то горизонтальная реакция Н B равна нулю. Примем условно направление вращения момента опорных реакций вокруг моментных точек по часовой стрелке за положительное, тогда противоположное направление вращения сил будем считать отрицательным.

Составляем условия равновесия в виде

ΣF y = 0; V B — q ∙1,6 = 0;

Σm B = 0; M B — q ∙1,6∙1,2 = 0.

Здесь q ∙1,6 – равнодействующая распределенной нагрузки.

Подставив численные значения распределенной нагрузки q , находим

V В = 32 кН, М B = 38,4 кН∙м.

Для проверки правильности найденных реакций составим еще одно условие равновесия. Теперь возьмем за моментную точку какую-нибудь другую точку, например правый конец балки, тогда:

Σm A = 0; M B – V B ∙2 + q ∙1,6∙0,8 = 0 .

После подстановки численных значений получаем тождество 0=0.

Окончательно делаем выводы, что опорные реакции найдены верно. Вертикальная реакция V B направлена вверх, а реактивный момент М В — по часовой стрелке.

Пример 13. Определить опорные реакции балки (рис.35, а ).

Решение. В качестве активной нагрузки выступает равнодействующая распределенной нагрузки Q =(1/2)∙aq =(1/2)∙3∙2=3кН, линия действия которой проходит на расстоянии 1 м от левой опоры, сила натяжения нити Т = Р = 2 кН, приложенная на правом конце балки и сосредоточенный момент.

Поскольку последний можно заменить парой вертикальных сил, то действующая на балку нагрузка вместе с реакцией подвижной опоры В образует систему параллельных сил, поэтому реакция R A будет также направлена вертикально (рис.35, б ).

Для определения этих реакций воспользуемся уравнениями равновесия.

ΣM A = 0; —Q ∙1 + R В ∙3 — M + Т ∙5 = 0,

R В = (1/3) (Q + M — Р ∙5) = (1/3) (3 + 4 — 2∙5) = -1 кН.

ΣM B = 0; — R A ∙3 + Q ∙2 — M + Т ∙2 = 0,

R A = (1/3) (Q ∙2 — M + Р ∙2) = (1/3) (3∙2 — 4 + 2∙2) = 2 кН.

Рис.35

Чтобы проверить правильность полученного решения, воспользуемся дополнительным уравнением равновесия:

ΣY i = R A — Q + R В + Т = 2 — 3 — 1 + 2 = 0,

то есть, задача решена правильно.

Пример 14. Найти опорные реакции консольной балки, загруженной распределенной нагрузкой (рис.36, а ).

Решение. Равнодействующая распределенной нагрузки приложена в центре тяжести грузовой эпюры. Чтобы не искать положение центра тяжести трапеции, представим ее в виде суммы двух треугольников. Тогда заданная нагрузка будет эквивалентна двум силам: Q 1 = (1/2)∙3∙2 = 3 кН и Q 2 = (1/2)∙3∙4 = 6 кН, которые приложены в центре тяжести каждого из треугольников (рис.36,б ).

Рис.36

Опорные реакции жесткого защемления представлены силой R A и моментом M A , для определения которых удобнее использовать уравнения равновесия системы параллельных сил, то есть:

ΣM A = 0; M A = 15 кН∙м;

ΣY = 0, R A = 9 кН.

Для проверки воспользуемся дополнительным уравнением ΣM В = 0, где точка В находится на правом конце балки:

ΣM В = M A — R A ∙3 + Q 1 ∙2 + Q 2 ∙1 = 15 — 27 + 6 +6 = 0.

Пример 15. Однородная балка весом Q = 600 Н и длиной l = 4 м опирается одним концом на гладкий пол, а промежуточной точкой В на столб высотой h = 3 м, образуя с вертикалью угол 30°. В таком положении балка удерживается веревкой, протянутой по полу. Определить натяжение веревки T и реакции столба — R B и пола — R A (рис.37,а ).

Решение. Под балкой или стержнем в теоретической механике понимают тело, у которого поперечными размерами в сравнении с его длиной можно пренебречь. Таким образом, вес Q однородной балки приложен в точке С , где АС = 2 м.

Рис.37

1) Поскольку две неизвестных реакции из трех приложены в точке А , первым следует составить уравнение ΣM A = 0, так как туда войдет только реакция R B :

— R B ∙АВ + Q ∙(l /2)∙sin30° = 0,

где АВ = h /cos30°= 2 м.

Подставляя в уравнение, получим:

R B ∙2 = 600∙2∙(1/2) = 600,

R B = 600/ (2 ) = 100 ≅ 173 Н.

Аналогично из моментного уравнения можно было бы найти и реакцию R A , выбрав в качестве моментной точку, где пересекаются линии действия R B и Т . Однако это потребует дополнительных построений, поэтому проще воспользоваться другими уравнениями равновесия:

2) ΣX = 0; R B ∙cos30° — Т = 0; → Т = R B ∙cos30°= 100 ∙( /2) = 150 Н;

3) ΣY = 0, R B ∙sin30°- Q + R A = 0; → R A = Q — R B ∙sin30°= 600 — 50 ≅ 513 Н.

Таким образом, мы нашли Т и R A через R B , поэтому проверить правильность полученного решения можно с помощью уравнения: ΣM B = 0, куда в явном или неявном виде войдут все найденные реакции:

R A ∙АВ sin30°- Т ∙АВ cos30° — Q ∙(АВ — l /2)∙sin30°= 513∙2 ∙(1/2) — 150∙2 ∙( /2) — 600∙ (2 — 2)∙(1/2) = 513∙ — 150∙3 — 600∙( -1) ≅ 513∙1,73 — 450 — 600∙0,73 = 887,5 — 888 = -0,5.

Полученная в результате округления невязка ∆= -0,5 называется абсолютной погрешностью вычисления.

Для того чтобы ответить на вопрос насколько точным является полученный результат, вычисляют относительную погрешность , которая определяется по формуле:

ε=[|∆| / min(|Σ + |, |Σ — |)]∙100% =[|-0,5| / min(|887,5|, |-888|)]∙100% = (0,5/887,5)∙100% = 0,06%.

Пример 16. Определить опорные реакции рамы (рис.38). Здесь и в дальнейшем, если не оговорено специально, все размеры на рисунках будем считать указанными в метрах, а силы — в килоньютонах.

Рис.38

Решение. Рассмотрим равновесие рамы, к которой в качестве активной приложена сила натяжения нити Т , равная весу груза Q .

1) Реакцию подвижной опоры R B найдем из уравнения ΣM A = 0. Чтобы при этом не вычислять плечо силы Т , воспользуемся теоремой Вариньона, разложив эту силу на горизонтальную и вертикальную составляющие:

R B ∙2 + Т sin30°∙3 — Т cos30°∙4 = 0; → R B = (1/2)∙ Q (cos30°∙4 — sin30°∙3) = (5/4) ∙ (4 — 3) кН.

2) Для вычисления Y A составим уравнение ΣM С = 0, где точка С лежит на пересечении линий действия реакций R B и Х A :

— Y A ∙2 + Т sin30°∙3 — Т cos30°∙2 = 0; → Y A = (1/2)∙ Q (sin30°∙3 -cos30°∙2) = (5/4) ∙ (3 -2 ) кН.

3) Наконец, находим реакцию Х A :

ΣX = 0; Х A — Т sin30° = 0; → Х A = Q sin30° = 5/2 кН.

Поскольку все три реакции были найдены независимо друг от друга, для проверки нужно взять уравнение, в которое входит каждая из них:

ΣM D = Х A ∙3 — Y A ∙4 — R B ∙2 = 15/2 — 5∙(3 -2 ) — (5/2)∙ (4 — 3) = 15/2 — 15 + 10 -10 +15/2 = 0.

Пример 17. Определить опорные реакции стержня, имеющего ломаное очертание (рис.39,а ).

Решение. Заменяем распределенную нагрузку на каждом участке стержня сосредоточенными силами Q 1 = 5 кН и Q 2 = 3 кН, а действие отброшенного жесткого защемления — реакциями Х A ,Y A и M А (рис.39,б ).

Рис.39

1) ΣM А = 0; M А —Q 1 ∙2,5 — Q 2 ∙5,5 = 0; → M А = 5∙2,5 + 3∙5,5 = 12,5 + 16,5 = 29 кНм.

2) ΣX = 0; Х A + Q 1 ∙sina = 0; → Х A = -5∙(3/5) = -3 кН.

3) ΣY = 0; Y A — Q 1 cosa — Q 2 = 0; → Y A = 5∙(4/5) + 3 = 4 + 3 = 7 кН, так как sinα = 3/5, cosα = 4/5.

Проверка: ΣM В = 0; M А + Х A ∙3 — Y A ∙7 + Q 1 cosα∙4,5 + Q 1 sinα∙1,5 + Q 2 ∙1,5 = 29 -3∙3 — 7∙7 + 5∙(4/5)∙5 + 5∙(3/5)∙1,5 + 3∙1,5 = 29 — 9 — 49 + 20 + 4,5 + 4,5 = 58 — 58 = 0.

Пример 18. Для рамы изображенной на рис.40, а, требуется определить опорные реакции. Дано: F = 50 кН, М = 60 кН∙м, q = 20 кН/м.

Решение . Рассмотрим равновесие рамы. Мысленно освобождаем раму от связей на опорах (рис.40, б ) и выделяем объект равновесия. Рама загружена активной нагрузкой в виде произвольной плоской системы сил. Вместо отброшенных связей прикладываем к объекту равновесия реакции: на шарнирно-неподвижной опоре А — вертикальную V A и горизонтальную H A , а на шарнирно-подвижной опоре В — вертикальную реакцию V B Предполагаемое направление реакций показано на рис.40, б .

Рис.40. Расчетная схема рамы и объект равновесия к примеру 18:

а – расчетная схема; б – объект равновесия

Составляем следующие условия равновесия:

ΣF x = 0; —H A + F = 0; H A = 50 кН.

Σm A = 0; V B ∙6 + M — q ∙6∙3 — F ∙6 = 0; V B = 100 кН.

ΣF y = 0; V A + V B — q ∙6 = 0; V A = 20 кН.

Здесь условно принято направление вращения вокруг моментных точек против движения часовой стрелки за положительное.

Для проверки правильности вычисления реакций используем условие равновесия, в которое входили бы все опорные реакции, например:

Σm C = 0; V B ∙3 + M – H A ∙6 – V A ∙3 = 0.

После подстановки численных значений получаем тождество 0=0.

Таким образом, направления и величины опорных реакций определены верно.

Пример 19. Определить опорные реакции рамы (рис.41,а ).

Рис.41

Решение. Как и в предыдущем примере, рама состоит из двух частей, соединенных ключевым шарниром С. Распределенную нагрузку, приложенную к левой части рамы, заменяем равнодействующей Q 1 , а к правой — равнодействующей Q 2 , где Q 1 = Q 2 = 2кН.

1) Находим реакцию R B из уравнения ΣM С (ВС ) = 0; → R B = 1кН;

В инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности по тому или иному закону. Рассмотрим некоторые простейшие примеры распределенных сил, лежащих в одной плоскости.

Плоская система распределенных сил характеризуется ее интенсивностью q, т. е. значением силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в ньютонах, деленных на метры

1) Силы, равномерно распределенные вдоль отрезка прямой (рис. 69, а). Для такой системы сил интенсивность q имеет постоянное значение. При статических расчетах эту систему сил можно заменить равнодействующей

По модулю,

Приложена сила Q в середине отрезка АВ.

2) Силы, распределенные вдоль отрезка прямой по линейному закону (рис. 69, б). Примером такой нагрузки могут служить силы давления воды на плотину, имеющие наибольшее значение у дна и падающие до нуля у поверхности воды. Для этих сил интенсивность q является величиной переменной, растущей от нуля до максимального значения Равнодействующая Q таких сил определяется аналогично равнодействующей сил тяжести, действующих на однородную треугольную пластину ABC. Так как вес однородной пластины пропорционален ее площади, то, по модулю,

Приложена сила Q на расстоянии от стороны ВС треугольника ABC (см. § 35, п. 2).

3) Силы, распределенные вдоль отрезка прямой по произвольному закону (рис. 69, в). Равнодействующая Q таких сил, по аналогии с силой тяжести, по модулю равна площади фигуры ABDE, измеренной в соответствующем масштабе, и проходит через центр тяжести этой площади (вопрос об определении центров тяжести площадей будет рассмотрен в § 33).

4) Силы, равномерно распределенные по дуге окружности (рис. 70). Примером таких сил могут служить силы гидростатического давления на боковые стенки цилиндрического сосуда.

Пусть радиус дуги равен , где — ось симметрии, вдоль которой направим ось Действующая на дугу система сходящихся сил имеет равнодействующую Q, направленную в силу симметрии вдоль оси при этом численно

Для определения величины Q выделим на дуге элемент, положение которого определяется углом а длина Действующая на этот элемент сила численно равна а проекция этой силы на ось будет Тогда

Но из рис. 70 видно, что Следовательно, так как то

где — длина хорды, стягивающей дугу АВ; q — интенсивность.

Задача 27. На консольную балку А В, размеры которой указаны на чертеже (рис. 71), действует равномерно распределенная нагрузка интенсивностью Пренебрегая весом балки и считая, что силы давления на заделанный конец — определены по линейному закону, определить значения наибольших интенсивностей этих сил, если

Решение. Заменяем распределенные силы их равнодействующими Q, R и R, где согласно формулам (35) и (36)

и составляем условия равновесия (33) для действующих на балку параллельны сил

Подставляя сюда вместо Q, R я R их значения и решая полученные уравнения, найдем окончательно

Например, при получим а при

Задача 28. Цилиндрический баллон, высота которого равна Н, а внутренний диаметр d, наполнен газом под давлением Толщина цилиндрических стенок баллона а. Определить испытываемые этими стенками растягивающие напряжения в направлениях: 1) продольном и 2) поперечном (напряжение равно отношению растягивающей силы к площади поперечного сечения), считая малым.

Решение. 1) Рассечем цилиндр плоскостью, перпендикулярной его оси, на две части и рассмотрим равновесие одной из них (рис.

72, а). На нее в направлении оси цилиндра действуют сила давления на дно и распределенные по площади сечения силы (действие отброшенной половины), равнодействующую которых обозначим Q. При равновесии

Считая приближенно площадь поперечного сечения равной получим для растягивающего напряжения значение

В инженерных расчетах наряду с сосредоточенными силами, которые прилагаются к твердому телу в некоторой точке, встречаются силы, действие которых распределено по определенным участкам объема тела, его поверхности или линии.

Поскольку все аксиомы и теоремы статики формулируются для сосредоточенных сил, то необходимо рассмотреть способы перехода от распределенной нагрузки к сосредоточенным силам.

Рассмотрим некоторые простые случаи распределенной нагрузки тела параллельными силами, которые лежат в одной плоскости вдоль отрезка прямой.

Плоская система распределенных сил характеризуется ее интенсивностью q , то есть величиной силы, которая приходится на единицу длины нагруженного отрезка. Единицей измерения интенсивности является Ньютон, поделенный на метр (Н/м). Интенсивность может быть постоянной (равномерно распределенная нагрузка) или изменяться по линейным и произвольным законам.

Равномерно распределенная нагрузка (рис. 2.5, а), интенсивность которой q является постоянной величиной, при статических расчетах заменяется одной сосредоточенной силой, модуль которой

где – длина нагруженного отрезка.

а) б) в)

Рисунок 2.5

Эта равнодействующая сила , параллельная силам распределенной нагрузки, направлена в направлении распределенных сил и прикладывается посредине нагруженного отрезка АВ .

Такая нагрузка имеет место при размещении на теле однородной балки длиной l с удельным весом q .

Распределенная нагрузка с интенсивностью, изменяющейся по линейному закону (рис. 2.5, б), появляется, например, под действием давления воды на дамбу, когда нагружение на дамбу будет наибольшим возле дна водоема и является нулевым возле поверхности воды. При этом величина q интенсивности растет от нулевого значения к наибольшему значению q max . Равнодействующая Q такой нагрузки определяется как вес однородной треугольной пластинки АВС , который пропорционален ее площади. Тогда величина этой равнодействующей:

Линия действия равнодействующей силы проходит через центр треугольника АВС на расстоянии от его вершины А .

Примером действия сил, распределенных вдоль отрезка прямой по произвольному закону (рис. 2.5, в), является нагрузка плоского перекрытия сугробом снега. Равнодействующая таких сил по аналогии с силой веса численно будет равняться площади фигуры, измеренной в соответствующем масштабе, а линия действия этой равнодействующей будет проходить через центр площади этой фигуры.

Каждый владелец трехфазного ввода (380 В) обязан позаботиться о равномерной нагрузке на фазы, дабы избежать перегрузки одной из них. При неравномерном распределении на трехфазном вводе, при отгорании нуля или его плохом контакте, напряжения на фазных проводах начинают различаться друг от друга, как в большую так и в меньшую сторону. На уровне однофазного питания (220 Вольт) это может повлечь за собой поломку электрических приборов, из-за повышенного напряжения 250-280 Вольт, или же пониженного 180-150 Вольт. Помимо этого в данном случае наблюдается завышенное потребление электроэнергии у нечувствительных к перекосу напряжений электрических приборов. В этой статье мы расскажем вам, как выполняется распределение нагрузки по фазам, предоставив краткую инструкцию со схемой и видео примером.

Что важно знать

Данная диаграмма условно иллюстрирует трехфазную сеть:

Напряжение между фазами 380 вольт обозначено синим цветом. Зеленым цветом обозначено равномерное распределенное линейное напряжение. Красным — перекос напряжений.

Новым, трехфазным абонентам электросети в частном доме или квартире, при первом подключении, не стоит сильно надеяться на изначально равномерно распределенную нагрузку на вводной линии. Поскольку от одной линии могут быть запитаны несколько потребителей, а у них с распределением могут возникать проблемы.

Если после измерений вы увидели, что есть (более 10%, согласно ГОСТ 29322-92), необходимо обратиться в электроснабжающую организацию для принятия соответствующих мероприятий по восстановлению симметрии фаз. Более подробно о том, можете узнать из нашей статьи.

Согласно договору между абонентом и РЭС (о пользовании электроэнергией), последние должны поставлять качественную электроэнергию в дома, с указанным . Частота также должна соответствовать 50 Герц.

Правила распределения

При проектировании схемы проводки необходимо максимально одинаково подбирать предполагаемые группы потребителей и распределить их по фазам. К примеру, каждая группа розеток по комнатам в доме подключена к своему фазному проводу и сгруппирована таким образом, чтобы нагрузка на сеть была оптимальна. Таким же образом организовывают линии освещения, выполняя их распределение по разным фазным проводника и так далее: стиральная машина, печь, духовка, котел, бойлер.

Расчет равномерно распределенной нагрузки

Теоретическая механика

Распределенные нагрузки

Как мы уже знаем, любая сила характеризуется тремя свойствами: модулем (скалярной размерностью), вектором (направлением в пространстве) и точкой приложения. Для того, чтобы иметь полное представление о характере и последствиях воздействия любой силы на тело или элемент конструкции, необходимо знать — какова величина этой силы, куда она направлена и к какой точке приложена.
В действительности сила не может быть приложена к точке, поскольку точка — безразмерная, бесконечно малая единица пространства, поэтому фактически силы воздействуют на очень малую площадку, размерами которой пренебрегают. Такие силы (приложенные к ничтожно малой площадке тела) называют сосредоточенными .

В реальности часто встречаются силы, приложенные не к точке, а к объему или поверхности тела, например сила тяжести, давления ветра, воды и т. п., т. е. нагрузку воспринимает не бесконечно малая площадка, а значительная площадь или объем тела. Такие силы называют распределенными .
Примером распределенной силы (обычно употребляют выражение «распределенная нагрузка») может послужить выпавший на крышу дома снег. Сила тяжести снежного покрова давит на всю поверхность крыши, нагружая одинаково (или неодинаково) каждую единицу ее площади, а не какую-либо точку.

Плоская система распределенных сил характеризуется ее интенсивностью, обычно обозначаемой латинской буквой q .
Интенсивность — это сила, приходящаяся на единицу длины (или площади) нагруженного участка.
Интенсивность в системе единиц СИ выражается в ньютонах на метр (Н/м) или, соответственно, в ньютонах на квадратный метр (для нагрузки, действующей на площадь).

Интенсивность воздействия силы на площадь характеризует такие физические понятия, как давление и напряжение. В плоской системе рассматривается интенсивность действия силы на единицу длины.

Распределенная нагрузка, имеющая постоянную интенсивность по всей длине участка называется равномерно распределенной (см. рисунок 1) .

При решении задач статики распределенную нагрузку заменяют ее равнодействующей. Модуль равнодействующей равномерно распределенной нагрузки равен Q = ql (см. рисунок) .
Равнодействующая равномерно распределенной нагрузки Q прикладывается в середине отрезка АВ .

Распределенная нагрузка, имеющая переменную интенсивность, называется неравномерно распределенной (рис. 2) .
Примером такой нагрузки может служить меняющееся по высоте давление воды на плотину или снег, лежащий на крыше неровным слоем.
Определение точки С приложения равнодействующей неравномерно распределенной нагрузки производится путем геометрических расчетов и построений. Равнодействующая сила Q при таких нагрузках равна площади фигуры, охватываемой эпюрой нагрузки, а точка С приложения равнодействующей расположена в центре тяжести этой фигуры.

Нагрузки, распределенные по поверхности (по площади), характеризуются давлением, т. е. силой, приходящейся на единицу площади. В системе единиц СИ давление измеряется в Паскалях (Па) или ньютонах на квадратный метр (Н/м 2 ).

Пример решения задачи с распределенной нагрузкой

Задача: Балка находится в равновесии под действием сосредоточенной силы F = 100 Н и равномерно распределенной нагрузки q = 60 Н/м (см. схему 3) .
Необходимо определить реакцию R_В опоры В .

Решение .
Поскольку по условию задачи необходимо определить реакцию опоры В , составим уравнение моментов сил относительно опоры А , учитывая, что равномерно распределенную нагрузку можно заменить сосредоточенной силой:
Q = ql , где l = (10 — 5) метров — часть балки, к которой приложена распределенная нагрузка .
Точка приложения сосредоточенной силы Q расположена в середине той части балки, к которой приложена распределенная нагрузка; плечо этой силы относительно опоры А будет равно: h = (10 — 5)/2 = 2,5 м.
Cоставляем уравнение моментов сил относительно опоры А из условия, что балка находится в состоянии равновесия (уравнение равновесия) .

• сила R_В создает относительно точки А положительный момент, плечо которого равно 10м;
• сила F создает относительно точки А отрицательный момент, плечо которого равно 5 м;
• распределенная нагрузка q создает (посредством силы Q и плеча h ) относительно точки А отрицательный момент.

Получаем уравнение равновесия балки, в котором лишь одна неизвестная величина ( R_В ) :

ΣM = 10R_В — qlh — 5F = 10R_В — q(10-5)(10-5)/2 — 5F = 0 , откуда находим искомую реакцию опоры R_В :

Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.

Размерность для линейной нагрузки — Н/м, для нагрузки распределенной по площади — Н/м 2 , для объемной (например при учете собственного веса элементов конструкции) — Н/м 3 .

Например, на рисунке 1.23, а приведена равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой

приложенной в середине отрезка AB.

На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой

приложенной в точке C, причем AC = 2/3AB.

В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу

Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).

Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1.24).

Выделим элемент сектора с углом ∆φ и определим силу ∆Q, действующую на плоский элемент дуги:

В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:

где АВ – хорда, стягивающая концы дуги.

Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м, 2 ]. Если цилиндр рассечен по диаметру (рисунок 1.25), то равнодействующая этих сил равна F = q ∙ d ∙ h ( d – внутренний диаметр) или

Разрывающие баллон по диаметру усилия:

Если принять a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно

В практике расчета строительных конструкций часто встречаются случаи неравномерно распределенной нагрузки (отдельные случаи ветровой и снеговой нагрузки, нагрузки от собственного веса балок переменного сечения и др.). Как правило, строительные нормы допускают замену неравномерно распределенной нагрузки приближенным нагрузкой, распределенной по линейной зависимости (по треугольнику или трапеции).

Рассмотрим простейшие случаи неравномерно распределенной нагрузки.

Примеры построения эпюр в стержнях с ломаной осью

Стержень с ломаной осью считается система прямых стержней, жестко с ’ объединенных между собой в узлах. В данном курсе будем рассматривать только плоские системы, т. е. такие, в которых оси всех стержней лежат в одной плоскости. Внешняя нагрузка также должна быть приложена в этой плоскости. В каждом стержни этой системы могут возникать поперечная и продольная силы $N$, $Q$ и изгибающий момент $M$. Рассмотрим простейшие примеры построения эпюр в стержнях с ломаной осью.

Проверка равновесия узлов

Аналогично проверка проводится и для узла С.

Проверка равновесия узлов

Аналогично проверка проводится и для узла B.

Наша группа

Новости сайта:

Добавлен , теперь намного проще и быстрее можно построить расчетную схему для стандартных ферм.

В расчете балок исправлена ошибка при длинах балки больше 10м. была неверная прорисовка балки.

Расчет рам методом сил стал проще. В расчете рам реализована возможность получения развернутого решения методом сил.

В расчете геометрических характеристик сечения добавлен полукруг.

РАСЧЕТ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК СЕЧЕНИЙ теперь адаптирован под мобильные устройства . Теперь моменты инерции и центр тяжести можно вычислить на смартфоне.

Существенно переработан РАСЧЕТ БАЛОК . Добавлена возможность учета треугольной и трапециевидной нагрузки . Оптимизировано для использования на смартфонах .

Очередные улучшения расчета рам — теперь сервис автоматически определяет степень статической неопределимости системы и позволяет упростить Вам ход расчета статически неопределимой рамы методом сил или перемещений.

Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.

Размерность для линейной нагрузки — Н/м, для нагрузки распределенной по площади — Н/м 2 , для объемной (например при учете собственного веса элементов конструкции) — Н/м 3 .

Например, на рисунке 1.23, а приведена равномерно распределенная по длине , измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой

приложенной в середине отрезка AB .

На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой

приложенной в точке C , причем AC = 2/3AB .

В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу

Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x) .

Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1.24).

Выделим элемент сектора с углом ∆φ и определим силу ∆Q , действующую на плоский элемент дуги:

∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ . (1.14)

∆Q x = q ∙ R ∙ ∆φ∙ cosφ . (1.15)

В силу симметрии элемента трубы (с дугой AB ) относительно оси Ox проекция результирующей силы на ось Oy :

Q y = 0 , т.е. Q = Q x , (1.16)

где АВ – хорда, стягивающая концы дуги.

Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м, 2 ] . Если цилиндр рассечен по диаметру (рисунок 1.25), то равна F = q ∙ d ∙ h (d – внутренний диаметр) или

Разрывающие баллон по диаметру усилия:

S 1 = S 2 = S;
2S = F;
S = p∙h∙R . (1.18)

Поверхностные и объёмные силы представляют собой нагрузку, распределённую по некоторой поверхности или объёму. Такая нагрузка задаётся интенсивностью , которая представляет собой силу, приходящуюся на единицу некоторого объёма, или некоторой площади, или некоторой длины.

Особое место при решении ряда практически интересных задач занимает случай плоской распределённой нагрузки, приложенной по нормали к некоторой балке. Если вдоль балки направить ось , то интенсивность будет функцией координаты и измеряется в Н/м. Интенсивность представляет собой силу, приходящуюся на единицу длины.

Плоская фигура, ограниченная балкой и графиком интенсивности нагрузки, называется эпюрой распределённой нагрузки (Рис. 1.28). Если по характеру решаемой задачи можно не учитывать деформации, т.е. можно считать тело абсолютно твёрдым, то распределённую нагрузку можно (и нужно) заменить равнодействующей.

Разобьём балку на отрезков длиной

, на каждом из которых будем считать интенсивность постоянной и равной

, где –координата отрезка

. При этом кривая интенсивности заменяется ломаной линией, а нагрузка, приходящаяся на отрезок

, заменяется сосредоточенной силой

, приложенной в точке (Рис. 1.29). Полученная система параллельных сил имеет равнодействующую, равную сумме сил, действующих на каждый из отрезков, приложенную в центре параллельных сил.

Понятно, что такое представление тем точнее описывает реальную ситуацию, чем меньше отрезок

, т.е. чем больше число отрезков . Точный результат получаем, переходя к пределу при длине отрезка

, стремящейся к нулю. Предел, получаемый в результате описанной процедуры, представляет собой интеграл. Таким образом, для модуля равнодействующей получаем:

Для определения координаты точки приложения равнодействующей используем теорему Вариньона:

если система сил имеет равнодействующую, то момент равнодействующей относительно любого центра (любой оси) равен сумме моментов всех сил системы относительно этого центра (этой оси)

Записывая эту теорему для системы сил

в проекциях на ось и переходя к пределу при длине отрезков, стремящейся к нулю, получаем:

Очевидно, модуль равнодействующей численно равен площади эпюры распределённой нагрузки, а точка её приложения совпадает с центром тяжести однородной пластины, имеющей форму эпюры распределённой нагрузки.

Отметим два часто встречающихся случая.

(Рис. 1.30). Модуль равнодействующей и координата её точки приложения определяются по формулам:

В инженерной практике такая нагрузка встречается довольно часто. Равномерно распределённой в большинстве случаев можно считать весовую и ветровую нагрузку.

(Рис. 1.31). В этом случае:

В частности, давление воды на вертикальную стенку прямо пропорционально глубине .

Определить реакции опор ибалки, находящейся под действием двух сосредоточенных сил и равномерно распределённой нагрузки. Дано:

Найдём равнодействующую распределённой нагрузки. Модуль равнодействующей равен

плечо силы относительно точкиравно

Рассмотрим равновесие балки. Силовая схема представлена на Рис. 1.33.

Определить реакцию заделки консольной балки, находящейся под действием сосредоточенной силы, пары сил и распределённой нагрузки (Рис. 1.34).

Заменим распределённую нагрузку тремя сосредоточенными силами. Для этого разобъём эпюру распределённой нагрузки на два треугольника и прямоугольник. Находим

Силовая схема представлена на Рис. 1.35.

Вычислим плечи равнодействующих относительно оси

Условия равновесия в рассматриваемом случае имеют вид:

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Что называется интенсивностью распределённой нагрузки?

2. Как вычислить модуль равнодействующей распределённой нагрузки?

3. Как вычислить координату точки приложения равнодействующей распределённой

4. Чему равен модуль и какова координата точки приложения равномерно распределённой нагрузки?

5. Чему равен модуль и какова координата точки приложения линейно распределённой нагрузки?

Из сборника задач И.В.Мещерского: 4.28; 4.29; 4.30; 4.33; 4.34.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА — теория и практика»: комплекты СР-2; СР-3.

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 4-5

Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно расстоянию между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки также попадают на начало и на конец пролета, но при этом вызывают только увеличение опорной реакции, на значение изгибающих моментов и на прогиб крайние сосредоточенные нагрузки никак не влияют, а потому при расчетах несущей способности конструкции не учитываются. Рассмотрим это на примере балок перекрытия опирающихся на перемычку. Кирпичная кладка, которая может быть между перемычкой и балками перекрытия, и создавать при этом равномерно распределенную нагрузку, для простоты восприятия не показана.

Рисунок 1 . Приведение сосредоточенных нагрузок к эквивалентной равномерно распределенной нагрузке.

Как видно из рисунка 1, определяющим является изгибающий момент, который используется при расчетах конструкций на прочность. Таким образом, чтобы равномерно распределенная нагрузка создавала такой же изгибающий момент, как и сосредоточенная нагрузка, ее нужно умножить на соответствующий коэффициент перехода (коэффициент эквивалентности). А определяется этот коэффициент из условий равенства моментов. Думаю, рисунок 1 это очень хорошо иллюстрирует. А еще, анализируя полученные зависимости, можно вывести общую формулу для определения коэффициента перехода. Так, если количество приложенных сосредоточенных нагрузок является нечетным, т.е. одна из сосредоточенных нагрузок обязательно попадает на середину пролета, то для определения коэффициента эквивалентности можно использовать формулу:

где n — количество пролетов между сосредоточенными нагрузками.

где (n-1) — количество сосредоточенных нагрузок.

Впрочем, иногда удобнее производить расчеты, исходя из количества сосредоточенных нагрузок. Если это количество выразить переменной m, то тогда

При этом эквивалентная равномерно распределенная нагрузка будет равна:

q экв = γmQ/l (305.1.4)

Когда количество сосредоточенных нагрузок является четным, т.е. ни одна из сосредоточенных нагрузок не попадает на середину пролета, то значение коэффициента можно принимать, как для следующего нечетного значения количества сосредоточенных нагрузок. В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:

γ = 2 — если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки.

γ = 1.33 — для балки, на которую действуют 2 или 3 сосредоточенные нагрузки;

γ = 1.2 — для балки, на которую действуют 4 или 5 сосредоточенных нагрузок;

γ = 1.142 — для балки, на которую действуют 6 или 7 сосредоточенных нагрузок;

γ = 1.11 — для балки, на которую действуют 8 или 9 сосредоточенных нагрузок.

2 вариант

Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно половине расстояния между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки не попадают на начало и на конец пролета.

Рисунок 2 . Значения коэффициентов перехода при 2 варианте приложения сосредоточенных нагрузок.

Как видно из рисунка 2, при таком варианте загружения значение коэффициента перехода будет значительно меньше. Так, например, при четном количестве сосредоточенных нагрузок, коэффициент перехода вообще можно принимать равным единице. При нечетном количестве сосредоточенных нагрузок для определения коэффициента эквивалентности можно использовать формулу:

где m — количество сосредоточенных нагрузок.

При этом эквивалентная равномерно распределенная нагрузка все также будет равна:

q экв = γmQ/l (305.1.4)

В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:

γ = 2 — если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки, а попадают ли балки перекрытия на начало или конец пролета или расположены сколь угодно далеко от начала и конца пролета, в данном случае значения не имеет. А значение это имеет при определении сосредоточенной нагрузки.

γ = 1 — если на рассматриваемую конструкцию, действует четное количество нагрузок.

γ = 1.11 — для балки, на которую действуют 3 сосредоточенные нагрузки;

γ = 1.091 — для балки, на которую действуют 5 сосредоточенных нагрузок;

γ = 1.076 — для балки, на которую действуют 7 сосредоточенных нагрузок;

γ = 1.067 — для балки, на которую действуют 9 сосредоточенных нагрузок.

Не смотря на некоторую заковыристость определения, коэффициенты эквивалентности очень просты и удобны. Так как при расчетах очень часто известна распределенная нагрузка, действующая на квадратный или погонный метр, то чтобы не переводить распределенную нагрузку сначала в сосредоточенную, а потом снова в эквивалентную распределенную, достаточно просто умножить значение распределенной нагрузки на соответствующий коэффициент. Например, на перекрытие будет действовать нормативная распределенная нагрузка 400 кг/м 2 , при этом собственный вес перекрытия составит еще 300 кг/м 2 . Тогда при длине балок перекрытия 6 м на перемычку могла бы действовать равномерно распределенная нагрузка q = 6(400 + 300)/2 = 2100 кг/м. А дальше, если будет только одна балка перекрытия посредине пролета, то γ = 2, а

q экв = γq = 2q (305.2.2)

Если ни одно из двух вышеприведенных условий не соблюдается, то использовать коэффициенты перехода в чистом виде нельзя, нужно добавить еще пару дополнительных коэффициентов, учитывающих расстояние до балок, не попадающих на начало и конец пролета перемычки, а также возможную несимметричность приложения сосредоточенных нагрузок. Вывести такие коэффициенты в принципе можно, однако в любом случае они будут понижающими во всех случаях, если рассматривать 1 вариант загружения и в 50% случаев, если рассматривать 2 вариант загружения, т.е. значения таких коэффициентов будут

ФОРМУЛА БАЛКИ С СДВИГОМ И МАШИНОЙ

Равномерно распределенная нагрузка
@
Частично распределенная равномерная нагрузка
@
Равномерная нагрузка, частично распределенная на одном конце
@
Равномерная нагрузка, частично распределенная на каждом конце
@
Равномерное увеличение нагрузки на один конец
@
Равномерное увеличение нагрузки до центра
@
Сосредоточенная нагрузка в центре
@
Концентрированная нагрузка в любой точке
@
Две равные сосредоточенные нагрузки, расположенные симметрично
@
Две равные сосредоточенные нагрузки размещены несимметрично
@
Две неравные сосредоточенные нагрузки размещены несимметрично
@
Равномерно распределенная нагрузка
@
Концентрированная нагрузка на свободном конце
@
Концентрированная нагрузка в любой точке
@
Балка закреплена на одном конце, равномерно поддерживается на другом V Распределенная нагрузка
@
Луч закреплен на одном конце, поддерживается на другом V Сосредоточенная нагрузка в центре
@
Луч закреплен на одном конце, поддерживается на другом V Сосредоточенная нагрузка в любой точке
@
Балка, нависающая над одной опорой V, равномерно распределена Нагрузка
@
Балка, нависающая над одной опорой V, равномерно распределена Нагрузка на свес
@
Балка нависает над одной опорой V Концентрированная нагрузка при Конец свеса
@
Балка нависает над одной опорой V Концентрированная нагрузка в любом месте Точка между опорами
@
Балка нависает над обеими опорами V Неравные вылеты V Равномерно распределенная нагрузка
@
Балка, закрепленная на обоих концах V Равномерно распределенная нагрузка
@
Балка, закрепленная на обоих концах V Концентрированная нагрузка в центре
@
Балка, закрепленная на обоих концах V Концентрированная нагрузка в любом месте Путевая точка
@
Непрерывная балка V Два равных пролета V Равномерная нагрузка на Один пролет
@
Непрерывная балка V, два равных пролета, V, сосредоточенная нагрузка в центре одного пролета
@
Непрерывная балка V, два равных пролета, V, сосредоточенная нагрузка в любой точке
@
Непрерывная балка V, два равных пролета, V, равномерно Распределенная нагрузка
@
Непрерывная балка V два равных пролета V два равных Сосредоточенные нагрузки симметрично размещены
@
Непрерывная балка V, два неравных пролета, V, равномерно Распределенная нагрузка
@
Непрерывная балка V, два неравных пролета, V, сосредоточенная нагрузка симметрично размещены на каждом пролете

Диаграмма изгибающего момента — форма и кривизна

Изгибающий момент необходим для конструкции балки и также для расчета наклон и прогиб луча.Следующие ниже примеры будут проиллюстрировать, как написать уравнение изгибающего момента для разных типов нагрузки, а затем нарисуйте диаграммы изгибающего момента.

Корпус I Изгибающий момент из-за точечная нагрузка

Изгибающий момент от точки нагрузка — это произведение нагрузки на перпендикулярное расстояние от момент момента. как показано ниже.

Рассмотрим кантилевер, подверженный точечная нагрузка на свободном конце.

Изгибающий момент на закрепленном конце = W х L = WL

Изгибающий момент M _x при расстояние x от свободного конца = W x х = Ш х

Это уравнение прямой и диаграмма изгибающего момента на приведенном выше рисунке показывает, что изменение изгибающий момент по пролету кантилевера — прямая линия.

Корпус II Изгибающий момент из-за равномерно распределенная нагрузка

Изгибающий момент из-за равномерного распределенная нагрузка (udl) равняется интенсивности нагрузки x длина груза Икс расстояние его центра от точки момента, как показано на следующие примеры.

Изгибающий момент на закрепленном конце = 10 х 2 x 1 = 20 кНм

Изгибающий момент M _x при расстояние «x» от свободного конца = 10 x (х) х (х / 2) = 0.5 х ²

которая является функцией второй степени от «x» и, следовательно, параболический.

Корпус III Изгибающий момент из-за равномерно меняющаяся нагрузка

Изгибающий момент из-за переменной нагрузки составляет равна площади диаграммы нагрузки x расстояние его центроида с момента.

Форма диаграммы изгибающего момента из-за к равномерно изменяющейся нагрузке — кубическая парабола.

Случай IV Изгибающий момент из-за пара

Изгибающий момент на участке из-за пара равна величине пары и в том же смысле как пара.

Следующие ниже примеры будут очень полезны для объяснения того, как напишите уравнения для поперечной силы и расчет изгибающего момента и построить диаграммы для консольные, свободно опертые и нависающие балки.

Калькулятор пучка с простой опорой | calcresource

Предпосылки

Оглавление

Введение

Балка с простой опорой — одна из самых простых конструкций.У него всего две опоры, по одной с каждой стороны. Одна штифтовая опора и роликовая опора. Оба они препятствуют любому вертикальному движению, позволяя, с другой стороны, свободное вращение вокруг них. Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя свободному горизонтальному перемещению препятствует другая опора.

Удаление любой из опор или установка внутреннего шарнира приведет к превращению балки с простой опорой в механизм, то есть без ограничений перемещается в одном или нескольких направлениях.Очевидно, это нежелательно для несущей конструкции. Следовательно, балка с простой опорой не обеспечивает избыточности с точки зрения опор. Если произойдет локальный сбой, вся конструкция рухнет. Эти типы структур, которые не предлагают избыточности, называются критическими или детерминантными структурами. Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией .

Допущения

Статический анализ любой несущей конструкции включает оценку ее внутренних сил и моментов, а также ее прогибов. Обычно для плоской конструкции с плоской нагрузкой интересующими внутренними действиями являются осевая сила N, поперечная поперечная сила V и изгибающий момент M. Для балки с простой опорой, которая несет только поперечные нагрузки, осевая сила всегда равна ноль, поэтому им часто пренебрегают. Результаты расчетов на странице основаны на следующих предположениях:

• Материал однороден и изотропен (другими словами, его характеристики одинаковы во всех точках и в любом направлении)
• Материал линейно эластичный
• Нагрузки прикладываются статично (они не меняются со временем)
• Поперечное сечение одинаково по всей длине балки
• Прогибы небольшие
• Каждое поперечное сечение, которое изначально является плоским, а также перпендикулярно продольной оси, остается плоской и перпендикулярно отклоненной оси.Это тот случай, когда высота поперечного сечения значительно меньше длины балки (в 10 и более раз), а также поперечное сечение не является многослойным (не сечение сэндвич-типа).

Последние два предположения удовлетворяют кинематическим требованиям теории пучка Эйлера-Бернулли, которая здесь также принята.

Условные обозначения

Для расчета внутренних сил и моментов при любом разрезе сечения балки необходимо условное обозначение. Здесь приняты следующие значения:

1. Осевая сила считается положительной, когда она вызывает натяжение детали.
2. Сдвигающая сила является положительной, когда она вызывает вращение детали по часовой стрелке.
3. Изгибающий момент является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.

Эти правила хотя и не являются обязательными, но достаточно универсальны. Другой набор правил, если следовать им последовательно, также даст те же физические результаты.

Обозначения

• E: модуль упругости материала (модуль Юнга)
• I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
• L: общий пролет балки
• R: опора реакция
• d: прогиб
• M: изгибающий момент
• V: поперечная поперечная сила
• \ theta: slope

Балка с простой опорой и равномерно распределенной нагрузкой

Нагрузка w распределяется по всему пролету балки с постоянной величиной и направление.Его размеры — сила на длину. Общее количество силы, приложенной к балке, равно W = w L, где L — длина пролета. В зависимости от обстоятельств может быть задана либо общая сила W, либо распределенная сила на длину w.

В следующей таблице представлены формулы, описывающие статический отклик простой балки при равномерно распределенной нагрузке w.

96) wL уклоны: 90 725

Балка с простой опорой и равномерной распределенной нагрузкой (UDL)
Количество	Формула
Реакции:	R_A = R_B000 = {	\ theta_B = — \ theta_A = \ frac {wL ^ 3} {24E I}
Предельный изгибающий момент:	M_u = {1 \ over8} w L ^ 2
Предельное усилие сдвига :	V_u = {1 \ over2} w L
Максимальный прогиб:	d_u = \ frac {5w L ^ 4} {384 EI}
Изгибающий момент при x:	M (x) = {1 \ over2} wx \ left (L — x \ right)
Сила сдвига в x:	V (x) = {1 \ over2} w \ left (L -2 x \ right)
Прогиб при x:	d (x) = \ frac {wx (L ^ 3 — 2 L x ^ 2 + x ^ 3)} {24 EI}
Наклон при x:	\ theta ( x) = — \ frac {w (L ^ 3-6 L x ^ 2 + 4 x ^ 3)} {24 EI}

Балка с простой опорой и точечной силой в середине

Сила сосредоточена в одной точке, расположенной в середине балки.Однако на практике сила может распространяться на небольшую площадь, хотя размеры этой области должны быть существенно меньше длины пролета балки. В непосредственной близости от приложения силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией балки, может быть неточным. Однако это только местное явление. По мере удаления от места расположения силы результаты становятся действительными в силу принципа Сен-Венана.

В следующей таблице представлены формулы, описывающие статический отклик простой балки под действием сосредоточенной точечной силы P, приложенной посередине.2)} {16 E I} &, x> L / 2 \ end {align} \ right.

где:

\ острый {x} = L-x

Балка с простой опорой и точечной силой в произвольном положении

Сила сосредоточена в одной точке, в любом месте пролета. Однако на практике сила может распространяться на небольшую площадь. Однако, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. 3} {6EI} &, x> a \ end {align} \ right.2} {2 E I} &, x> a \ end {align} \ right.

где:

b = La

\ строго {x} = Lx

Балка с простой опорой с точечным моментом

В этом случае момент накладывается на одну точку балки в любом месте пролета балки. С практической точки зрения, это может быть пара сил или элемент на кручение, соединенный из плоскости и перпендикулярно балке.

В любом случае область приложения момента должна распространяться на небольшую длину луча, чтобы ее можно было успешно идеализировать как сосредоточенный момент в точке.Хотя в непосредственной близости от области применения ожидается, что результаты, предсказанные с помощью классической теории пучка, будут неточными (из-за концентраций напряжений и других локализованных эффектов), по мере того, как мы удаляемся, предсказанные результаты полностью верны, как заявил Святой -Венантный принцип.

В следующей таблице представлены формулы, описывающие статический отклик простой балки на концентрированный момент M точки, приложенный на расстоянии a от левого конца. 2 )} {6E IL}

Предельный изгибающий момент: M_u = \ left \ {\ begin {align} & {Mb \ over L} &, \ textrm {if:} a \ le L / 2 \ \ — & {Ma \ over L} &, \ textrm {if:} a> L / 2 \ end {align} \ right.2} {2 E I} &, x> a \ end {align} \ right.

где:

b = La

\ строго {x} = Lx

Балка с простой опорой и треугольной нагрузкой

Нагрузка распределяется по всему пролету балки, однако ее величина не константа, но изменяется линейно, начиная от нуля на левом конце до своего пикового значения w_1 на правом конце. Размеры w_1 — сила на длину. Общее количество силы, приложенной к балке, равно W = {1 \ over2} w L, где L — длина пролета.

Ориентация треугольной нагрузки важна! Формулы, представленные в этом разделе, были подготовлены для случая восходящей нагрузки (слева направо), как показано на схеме. Для нисходящей нагрузки вы можете отразить балку так, чтобы ее левый конец (точка A) был наименее загруженным. Ось x и все результаты также будут отражены.

В следующей таблице представлены формулы, описывающие статический отклик простой балки при линейно изменяющейся (треугольной) распределенной нагрузке, восходящей слева направо.4} {24EIL}

где:

C = \ sqrt {15- \ sqrt {120}} \ left (\ sqrt {15} + \ sqrt {50} \ right) \ приблизительно 22.01237

Балка с простой опорой и трапецеидальной нагрузкой

Нагрузка распределяется по всему пролету балки, имея линейно изменяющуюся величину, начиная с w_1 на левом конце и заканчивая w_2 на правом конце. Размеры w_1 и w_2 — сила на длину. Общее количество силы, приложенной к балке, равно W = {L \ over2} (w_1 + w_2), где L — длина пролета.

Значения w_1 и w_2 могут быть присвоены произвольно. Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба).

В следующей таблице представлены формулы, описывающие статический отклик простой балки при изменяющейся распределенной нагрузке трапециевидной формы. 3} {24EI}

где:

w_x = w_1 + {(w_2-w_1) x \ over L}

900 05

Балка с простой опорой и трапециевидным распределением нагрузки типа плиты

Такое распределение нагрузки типично для балок по периметру плиты.Распределение имеет трапециевидную форму с максимальной величиной w внутри балки, а на двух ее концах становится равной нулю. Размеры (\ w \) — сила на длину. Общее количество силы, приложенной к балке, равно W = w (La / 2-b / 2), где L — длина пролета, а a, b — длины с левой и правой стороны балки соответственно, где распределение нагрузки равно разная (треугольная).

В следующей таблице представлены формулы, описывающие статический отклик простой балки при трапецеидальном распределении нагрузки, как показано на схеме выше.3

Балка с простой опорой и частично распределенной равномерной нагрузкой

Нагрузка распределяется на часть пролета балки с постоянной величиной w, в то время как оставшийся пролет разгружен. Размеры w — сила на длину. Общее количество силы, приложенной к балке, равно W = \ left (L-a-b \ right) w, где L — длина пролета, а a, b — длины без нагрузки с левой и правой стороны балки, соответственно.

В следующей таблице представлены формулы, описывающие статический отклик простой балки при частично распределенной равномерной нагрузке.2} {2 E I} &, x \ ge L-b \ end {align} \ right.

где:

\ острый {x} = Lx

x_a = xa

L_w = Lab

Балка с простой опорой и частично распределенной трапециевидной нагрузкой

Нагрузка распределяется на часть пролет балки, имеющий линейно изменяющуюся величину от w_1 до w_2, а оставшийся пролет не нагружен. Размеры w_1 и w_2 — сила на длину. Общее количество силы, приложенной к балке, равно W = {L-a-b \ over2} (w_1 + w_2), где L — длина пролета, а a, b — длины без нагрузки с левой и правой стороны балки соответственно.

Значения w_1 и w_2 могут быть присвоены произвольно. Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба).

Это самый общий случай. Формулы для частично распределенных равномерных и треугольных нагрузок можно получить, соответствующим образом задав значения w_1 и w_2. Кроме того, соответствующие случаи для полностью нагруженного пролета можно получить, установив a и b равными нулю.

В следующей таблице представлены формулы, описывающие статический отклик простой балки при частично распределенной трапециевидной нагрузке.3

Статьи по теме

Понравилась эта страница? Поделись с друзьями!

Просто поддерживаемые формулы пучка UDL

• Ниже приведены формулы балок и соответствующие им SFD и BMD

Балка с простой опорой — это наиболее простая конструкция конструкции. Балка поддерживается на каждом конце, и нагрузка распределяется по ее длине.Балка с простой опорой не может иметь никаких поступательных смещений в точках опоры, но никаких ограничений на вращение опор не накладывается.

Рис. 1 Справа показаны формулы для расчета балок с простой опорой, имеющей равномерно распределенную нагрузку.

Рис. 2 Диаграмма поперечной силы и изгибающего момента для равномерно распределенной нагрузки на свободно опертой балке

Рисунок 2	Рисунок 1

Рис. 3 Формулы для расчета балок со свободно опертой опорой, имеющей равномерно распределенную нагрузку в среднем пролете

Рис. 4 SFD и BMD для несущей балки UDL с простой опорой в середине пролета

Рисунок 4	Рисунок 3

Рис. 5 Диаграмма поперечного усилия и изгибающего момента для легко поддерживаемой равномерно распределенной нагрузки на левой опоре

Рис. 6 Формулы для определения моментов и реакций на различных участках балки с простой опорой, имеющей UDL на правой опоре

Рисунок 5	Рисунок 6

Рис. 7 SFD и BMD для UDL на обоих концах

Рис. 8 Формулы для расчета балки с SFD и BMD на обоих концах

Рисунок 7	Рисунок 8

Рис. 9 Сборник формул для анализа свободно опертой балки, имеющей равномерно изменяющуюся нагрузку по всей ее длине

Рис. 10 Диаграмма поперечного усилия и диаграмма изгибающего момента для балки с простой опорой, имеющей UVL вдоль пролета

Рисунок 10	Рисунок 9

Рис. 11 SFD и BMD для балки с простой опорой, имеющей UVL от середины пролета до обоих концов

Рис. 12 Формулы для расчета моментов и реакций на балке с прямой опорой, имеющей UVL от середины пролета до обоих концов

Рисунок 11	Рисунок 12

Сообщите нам в комментариях, что вы думаете о концепциях в этой статье!

Балка — фиксированная на обоих концах

Балка, фиксированная на обоих концах — одноточечная нагрузка

Изгибающий момент

M _A = — F ab ² / L ² (1a)

где

M _A = момент на неподвижном конце A (Нм, фунт _f футов)

F = нагрузка (Н, фунт _f )

M _B = — F a ² b / L ² (1b)

где

M _B = момент на неподвижном конце B (Нм, фунт _f футов)

M _F = 2 F a ² b ² / L ³ (1c)

где

M _F = момент при точечной нагрузке (Нм, фунт _f футов)

Deflecti на

δ _F = F a ³ b ³ / (3 L ³ EI) (1d)

где

δ _F = прогиб при точечной нагрузке (м, фут)

E = Модуль упругости (Па (Н / м ² ), Н / мм ² , psi)

I = Момент площади инерции (м ⁴ , мм ⁴ , дюйм ⁴ )

Реакции опоры

R _A = F (3 a + b) b ² / L ³ (1f)

где

R _A = сила опоры на неподвижном конце A (Н, фунт _f )

R _B = F (a + 3 b) a ² / L ³ (1 г)

где

R _B = усилие опоры на фиксированном конце B (Н, фунт _f )

Балка, закрепленная на обоих концах — равномерная непрерывная распределенная нагрузка

Изгибающий момент

M _{M A = M B}

= — q L ² /12 (2a)

где

M = моменты на неподвижных концах (Нм, фунт _f футов)

q = равномерная нагрузка (Н / м, фунт _f / фут)

M ₁ = q L ² /24 (2b)

где

M ₁ = момент в центре (Нм, фунт _на футов)

Прогиб

δ _макс = q L ⁴ / (384 EI) (2c)

91 715 где

δ _max = максимальный прогиб в центре (м, фут)

E = Модуль упругости (Па (Н / м ² ), Н / мм ² , psi)

I = Момент инерции площади (м ⁴ , мм ⁴ , дюйм ⁴ )

Реакции опоры

916 R _B

= q L / 2 (2d)

, где

R = опорные силы на неподвижных концах (Н, фунты _f )

Балка, закрепленная на обоих концах — Равномерно уменьшающаяся распределенная нагрузка

Изгибающий момент

M _A = — q L ² /20 (3a)

где

M _A = моменты на неподвижном конце A (Нм, фунт _на футов)

q = равномерная падающая нагрузка (Н / м, фунт _на / фут)

M _B = — q L ² / 30 (3b)

где

M _B = моменты на неподвижном конце B (Нм, фунт _на футов)

M ₁ = q L ² /46 .6 (3c)

где

M ₁ = момент при x = 0,475 L (Нм, фунт _на футов)

Прогиб

δ _max = q L ⁴ / (764 EI) (3d)

где

δ _макс. = максимальный прогиб при x = 0,475 L (м, фут)

E = Модуль упругости (Па (Н / м ² ), Н / мм ² , psi)

I = Момент инерции площади (м ⁴ , мм ⁴ , дюйм ⁴ )

δ _1/2 = q L ⁴ / (768 EI) (3e)

где

δ _1/2 = прогиб при x = 0.5 л (м, фут)

Реакции опоры

R _A = 7 q L / 20 (3f)

где

R _A = сила опоры на неподвижном конце A (Н, фунт _на )

R _B = 3 q L / 20 (3g)

где

R _B = сила опоры на фиксированном конце B (Н, фунт _f )

Балка, закрепленная на обоих концах — частично равномерная непрерывная распределенная нагрузка

Изгибающий момент

M _A = — (qa ² /6) (3-4 a / l + 1.5 (a / L) ² ) (4a)

где

M _A = момент на неподвижном конце A (Нм, фунт _f футов)

q = частично однородный нагрузка (Н / м, фунт _f / фут)

M _B = — (qa ² /3) (a / L — 0,75 (a / L) ² ) (4b)

где

M _B = момент на неподвижном конце B (Нм, фунт _f футов)

Реакции опоры

R _A = qa (L — 0.5 a) / L — (M _A — M _B ) / L (4c)

где

R _A = сила опоры на неподвижном конце A (Н, фунт _f )

R _B = qa ² / (2 л) + (M _A — M _B ) / L (4d)

где

R _B = опорная сила на фиксированном конце B (Н, фунт _f )

Точка в сравнении с равномерно распределенной нагрузкой: понимание разницы

При размещении грузов одинакового веса на стеллаже для хранения важно помнить, что не все поддоны или грузы созданы одинаковыми.Некоторые поддоны имеют несколько досок или стрингеров, охватывающих нижнюю поверхность; у других по ноге в каждом углу. Грузы необычной формы, такие как рулоны стали или рулоны бумаги, также могут создавать проблемы. Конструкция днища поддона в значительной степени определяет, равномерно ли распределяется нагрузка или лежит на определенных точках. Это означает, что распределение веса груза может быть разным, в зависимости от типа поддона под ним или конкретного типа продукта, хранящегося на стеллажной системе.

При размещении в стальных стеллажах для хранения равномерно распределенная нагрузка — это нагрузка, вес которой равномерно распределяется по всей поверхности балок или настила стеллажа. Точечная нагрузка — это нагрузка, вес которой значительно сконцентрирован в одном (или нескольких) местах балок или настилов стеллажа. Например, стальной рулон, хранящийся непосредственно на балке стеллажа, может создавать очень концентрированную точечную нагрузку; даже если стальной рулон весит столько же, сколько груз на поддоне, грузовая балка, вероятно, будет более тяжелой.(Существует также третий тип распределения нагрузки: линейная нагрузка, у которой есть только две или три доски на дне, что создает более равномерное распределение веса, чем точечная нагрузка, но менее равномерное, чем равномерно распределенная нагрузка).

Итак, что это означает для безопасности стойки? Размещение точечной нагрузки в стальном стеллаже для хранения, который был разработан исключительно для поддержки равномерно распределенных нагрузок, может вызвать одну из двух ситуаций: чрезмерный прогиб и / или отказ балки или настила.

Отклонение балки: Когда инженер-проектировщик стеллажей определяет спецификации для опорной балки поддонов, максимальная величина допустимого прогиба — или изгиба — включается в расчеты, как указано в разделе 5.3 ANSI Mh26.1-2012 RMI: Спецификация по проектированию, испытанию и использованию промышленных стальных стеллажей для хранения. Предел отклонения равен длине балки по горизонтали, деленной на 180 (т. Е. L / 180). Риск безопасности возникает, если точечная нагрузка помещается на балку, которая рассчитана только на то, чтобы выдерживать вес равномерно распределенных нагрузок.Это связано с тем, что концентрация может привести к отклонению луча за пределы максимально допустимой величины, что приведет к возможному отказу и потенциально может привести к падению груза.

Отказ настила: Обычно настил из сварной проволоки с армирующими швеллерами или гофрированной стали часто помещается на балки стеллажа для поддонов, чтобы перекрыть расстояние между ними. Хотя это обеспечивает дополнительную поддержку груза поддона, если настил не был должным образом спроектирован для восприятия точечных нагрузок, как указано в стандарте ANSI Mh36 RMI.2-2017: Проектирование, изготовление, испытания и использование сварного настила стеллажа из проволоки — сосредоточенная точечная нагрузка может привести к его выходу из строя и падению нагрузки.

Таким образом, чтобы обеспечить наиболее безопасную конструкцию стеллажа для поддонов, квалифицированный инженер-конструктор должен быть проинформирован о типах грузов и поддонах, на которые они будут помещены для хранения. В приложениях, где несколько типов поддонов могут храниться в одной стеллажной конструкции, система должна быть спроектирована так, чтобы выдерживать точечные нагрузки, что является наиболее консервативным и самым безопасным подходом.

Есть еще вопросы о стальных стеллажах? Получите ответы из списка часто задаваемых вопросов RMI.

4.2 Общие типы нагрузок для балок и рам

>> Когда вы закончите читать этот раздел, проверьте свое понимание с помощью интерактивной викторины внизу страницы.

Ряд распространенных типов нагрузки для балок и рам показан на рисунке 4.1. Это не исчерпывающий список, но он показывает все типы нагрузок, с которыми мы будем иметь дело в этой книге.Из них наиболее распространенными являются две верхние, точечная нагрузка и равномерно распределенная нагрузка . Точечная нагрузка — это всего лишь единичная сила, действующая на одну точку на балке или элементе рамы. Равномерно распределенная нагрузка, также называемая равномерной нагрузкой — это нагрузка, которая равномерно распределена по некоторой длине балки или элемента рамы. В конструкциях эти равномерные нагрузки обычно возникают из-за поверхностных нагрузок, действующих на поверхность пола или стены, которым должна противостоять соединенная балка или колонна.Эта нагрузка на площадь умножается на шириной притока, обычно это расстояние между соседними балками или колоннами, чтобы преобразовать нагрузку на площадь в равномерную линейную нагрузку, как показано на рисунке. Эти равномерные нагрузки даны в единицах силы на единицу расстояния (например, кН / м). В дополнение к равномерной нагрузке, нагрузка может распределяться по элементам конструкции другими способами, такими как треугольные или трапециевидные распределенные нагрузки, показанные на рисунке 4.1 (среди прочего). Мы также встретим точечные моменты, как показано на рисунке.Эти точечные моменты часто могут быть вызваны другими элементами или элементами, которые соединены с балкой или элементом рамы, которые не включены непосредственно в схему свободного тела. Чаще вы будете сталкиваться с точечными моментами в фиксированных конечных точках реакции.

Рисунок 4.1: Распространенные типы нагрузки

Как мы можем работать с этими типами однородных или других распределенных нагрузок при выполнении расчетов равновесия? Способ сделать это — рассмотреть эквивалентную общую нагрузку или действующую силу , вызванную распределенной нагрузкой, которая действует в центре тяжести распределения.Расположение этого центроида различается в зависимости от типа распределения нагрузки, как показано в правой части рисунка 4.1. Для равномерной нагрузки эффективная сила равна общей нагрузке, полученной путем умножения нагрузки на единицу длины на общую длину (или $ wL $). Это также равно площади под диаграммой распределенной нагрузки, в данном случае прямоугольной. Для равномерной нагрузки центр тяжести находится в центре распределения ($ L / 2 $). Это место, куда вы поместите эффективную силу, чтобы использовать ее в расчетах равновесия.