Сетка прямых координатных осей в компасе где находится: Сетка и системы координат в КОМПАС-3D

Страница не найдена

2023. — Т 15. — № 3, Статьи →

Разов Игорь Олегович ФГБОУ ВО «Тюменский индустриальный университет», Тюмень, Россия Доцент базовой кафедры АО «Мостострой-11» Кандидат технических наук E-mail: [email protected] ORCID: https://orcid.org/0000-0002-4829-7080 Комзюк Леонид Викторович ФГБОУ ВО «Тюменский индустриальный университет», Тюмень, Россия E-mail: [email protected] Шелудков Юрий Николаевич ФГБОУ ВО «Тюменский …

18.07.2023

Читать далее…

2023. — Т 15. — № 3, Статьи →

Панова Валентина Феодосьевна ФГБОУ ВО «Сибирский государственный индустриальный университет», Новокузнецк, Россия Доцент кафедры «Инженерных конструкций, строительных технологий и материалов» Кандидат технических наук, доцент E-mail: [email protected] Панов Сергей Александрович ФГБОУ ВО «Сибирский государственный индустриальный университет», Новокузнецк, Россия Доцент кафедры «Инженерных конструкций, …

18.

07.2023

Читать далее…

2023. — Т 15. — № 3, Статьи →

Агапов Глеб Александрович ФГОБУ ВО «Финансовый университет при Правительстве Российской Федерации» Филиал в г. Смоленск, Смоленск, Россия Доцент Кандидат исторических наук E-mail: [email protected] Аннотация. В статье проанализированы некоторые аспекты одной из самых заметных теорий, описывающих возможные сценарии развития наиболее развитых …

18.07.2023

Читать далее…

2023. — Т 15. — № 3, Статьи →

Зиганшин Раис Шамильевич ФГБОУ ВО «Самарский государственный технический университет», Самара, Россия Аспирант E-mail: [email protected] РИНЦ: https://elibrary.ru/author_profile.asp?id=1134747 Маргачев Данила Андреевич ФГБОУ ВО «Самарский государственный технический университет», Самара, Россия E-mail: [email protected] Зиновьев Алексей Михайлович ФГБОУ ВО «Самарский государственный технический университет», Самара, Россия …

18. 07.2023

Читать далее…

2023. — Т 15. — № 3, Статьи →

Рубин Олег Дмитриевич АО «Проектно-изыскательский и научно-исследовательский институт «Гидропроект» имени С.Я. Жука», Москва, Россия Научно-исследовательский институт энергетических сооружений Директор филиала Доктор технических наук E-mail: [email protected] РИНЦ: https://www.elibrary.ru/author_profile.asp?id=423001 Антонов Антон Сергеевич АО «Проектно-изыскательский и научно-исследовательский институт «Гидропроект» имени С.Я. Жука», Москва, …

18.07.2023

Читать далее…

2023. — Т 15. — № 3, Статьи →

Фетисов Валерий Андреевич ФГОБУ ВО «Финансовый университет при Правительстве Российской Федерации», Москва, Россия Старший преподаватель Кандидат экономических наук E-mail: [email protected] ORCID: https://orcid.org/0000-0002-1626-7936 РИНЦ: https://elibrary.ru/author_profile.asp?id=780210 Аннотация. На протяжении всей истории человек стремился к повышению своего положения и благосостояния всеми возможными средствами.

…

18.07.2023

Читать далее…

2023. — Т 15. — № 3, Статьи →

Купрейшвили Екатерина Тенгизовна ФАУ «Российский дорожный научно-исследовательский институт», Москва, Россия Заместитель начальника экспертно-аналитического управления E-mail: [email protected] Соловьёв Богдан Анатольевич ФГАОУ ВО «Российский университет транспорта», Москва, Россия Доцент кафедры «Экономическая теория и менеджмент» Кандидат экономических наук, доцент E-mail: [email protected] РИНЦ: https://elibrary.ru/author_profile.asp?id=207528 …

17.07.2023

Читать далее…

2023. — Т 15. — № 3, Статьи →

Митенков Алексей Владимирович ПАО «Криогенмаш», Балашиха, Россия Директор по цифровой трансформации ФГАОУ ВО «Национальный исследовательский технологический университет «МИСИС», Москва, Россия Институт экономики и управления промышленными предприятиями Директор Кандидат философских наук E-mail: amit-77@mail. ru ORCID: https://orcid.org/0000-0003-3146-621X РИНЦ: https://www.elibrary.ru/author_profile.asp?id=385126 Аннотация. В статье рассматривается …

17.07.2023

Читать далее…

2023. — Т 15. — № 3, Статьи →

Булекбаев Берик Раимбекович ОЮЛ «Партнерство по транспорту и логистике в Центральной Азии», Алматы, Казахстан Президент E-mail: [email protected] Сербаева Наталья Яковлевна ТОО «Научно-исследовательский институт транспорта и коммуникаций», Алматы, Казахстан Учёный секретарь E-mail: [email protected] Бекмагамбетова Гульнара Муратовна ОЮЛ «Ассоциация научно-исследовательских и проектных …

17.07.2023

Читать далее…

2023. — Т 15. — № 3, Статьи →

Купрейшвили Екатерина Тенгизовна ФАУ «Российский дорожный научно-исследовательский институт», Москва, Россия Заместитель начальника экспертно-аналитического управления E-mail: [email protected] Соловьёв Богдан Анатольевич ФГАОУ ВО «Российский университет транспорта», Москва, Россия Доцент кафедры «Экономическая теория и менеджмент» Кандидат экономических наук, доцент E-mail: bsolovev@gmail. com РИНЦ: https://elibrary.ru/author_profile.asp?id=207528 …

17.07.2023

Читать далее…

Компьютерная графика | Уроки по КОМПАС-3D | Основные приемы черчения в КОМПАС-График

По вопросам репетиторства по компьютерной графике (Autocad, Solidworks, Inventor, Компас), вы можете связаться любым удобным для вас способом в разделе Контакты. Подробное описание программ обучения и стоимость, вы можете посмотреть выбрав соответствующий курс. Обучение возможно очно и дистанционно.

1.1 Цель

Получить навыки построения изображения детали в приложении «КОМПАС-График».

1.2 Содержание

• ознакомиться с интерфейсом приложения «КОМПАС-График» и основными командами по выполнению чертежа;
• получить навыки: настройки системы; создания и сохранения чертежа; управления чертежом; работы с Менеджером документа; выполнения настроек чертежа;
• выполнить один вид детали «Крышка» по описанию в лабораторном практикуме;
• ознакомиться с вариантом задания, предложенного преподавателем;
• определиться с форматом и масштабом чертежа;
• выполнить изображение детали с простановкой необходимых размеров, заполнить основную надпись.

1.3 Последовательность и пример выполнения

Рассмотрим построение изображения, представленного на Рисунке 1.1.

Рисунок 1.1 — Задание для выполнения чертежа крышки

Построение двухмерного изображения крышки

1. Проанализируйте деталь: изображение симметричное, состоит из трех контуров; в каждом контуре есть повторяющиеся элементы, которые можно построит либо зеркальным отображением, либо круговым массивом. Выберите команду Файл⇒Создать⇒Чертеж

2. Войдите в режим редактирования основной надписи (по ПКМ на основной надписи, выбрав команду из контекстного меню Заполнить основную надпись), заполните графы Обозначение – КГ.0001ХХ.001 и Наименование – Крышка. Сохраните файл.

3. Для удобства, вставьте рисунок на рабочую область, для чего, вызовите команду из списка наборов Черчение⇒Вставка и макроэлементы⇒Рисунок , выберите файл рисунка задания и укажите его местоположение на рабочей области.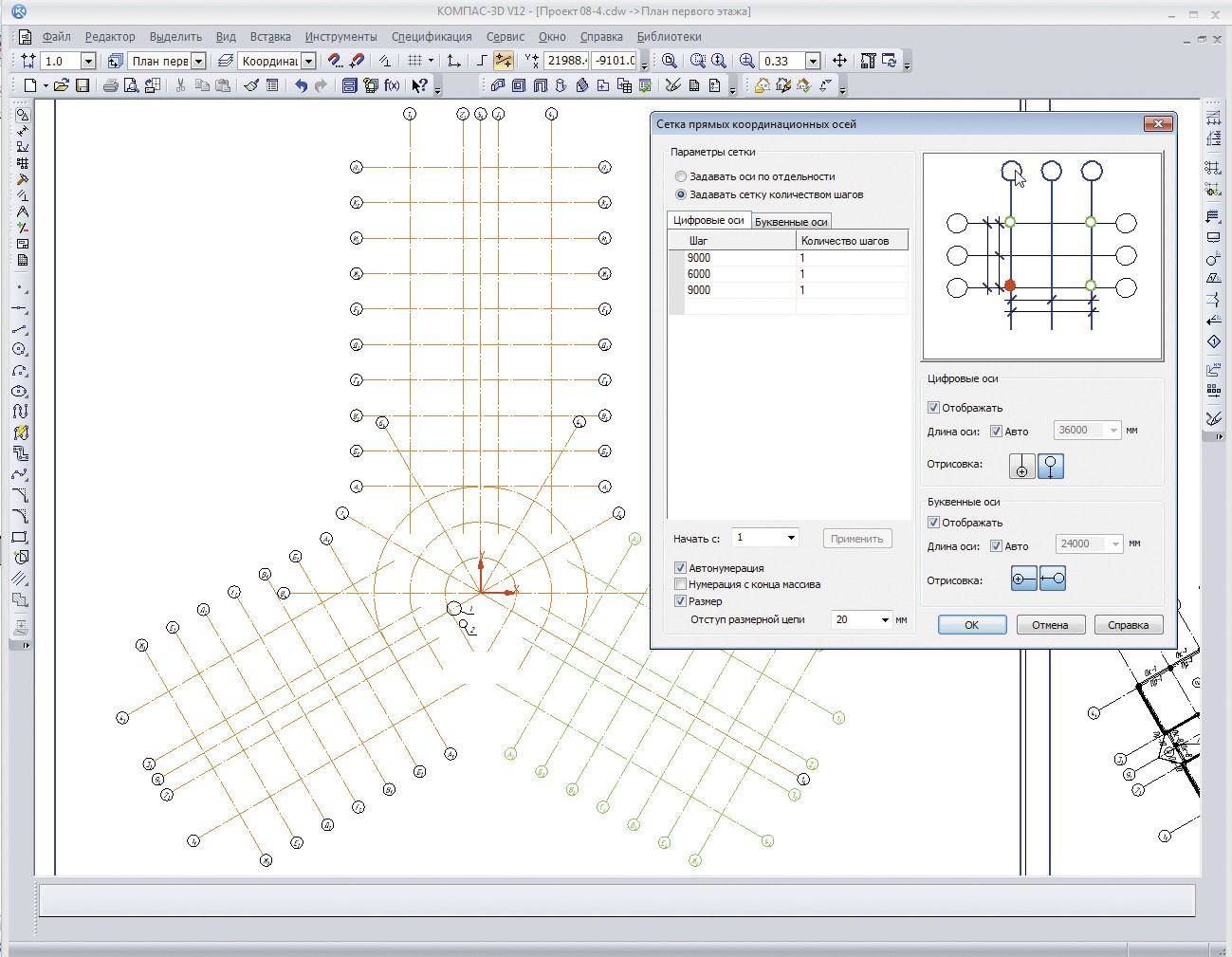

Для построения внешнего контура, постройте окружность диаметром 130 мм. Для чего, вызовите команду либо из списка наборов Черчение⇒Геометрия⇒Окружность , либо в меню Черчение⇒Окружности⇒Окружность.
Постройте еще две окружности диаметрами 30 мм и 16 мм.

4. Для обрезки лишних линий вызовите команду либо из списка наборов Черчение⇒Правка⇒Усечь кривую  , либо в меню Черчение⇒Усечь⇒Усечь кривую и укажите обрезаемые части кривых.

5. Для копирования одинаковых элементов выделите дугу и маленькую окружность, вызовите команду из списка наборов Черчение⇒Правка⇒Копия по окружности  . На Панели свойств задайте количество элементов массива – 6, нажмите кнопку в области Размещение копий⇒Вдоль всей окружности для равномерного распределения элементов массива по окружности, укажите центр массива – центр большой окружности и нажмите кнопку Создать объект .

    

6. Используя команду Усечь кривую  обрежьте лишние фрагменты кривых.

7. Перейдем к построению следующего контура. Создайте окружность диаметром 92 мм и еще две концентрические с диаметрами 14 мм и 28 мм.

8. Используя команду Усечь кривую  обрежьте лишние фрагменты кривых.

9. Выделите дугу и маленькую окружность. Выберите команду Правка⇒Зеркально отразить . С помощью двух точек (обязательно с привязкой, например, Центр ), расположенных на вертикальной оси больших окружностей, укажите ось симметрии. Используя команду Усечь кривую   обрежьте лишние фрагменты кривых.

10. Для построения внутреннего контура, постройте две окружности диаметрами 64 мм и 40 мм.

11. Для построения лепестков, постройте три вспомогательные прямые под углом 45° и на расстоянии от средней линии по 8 мм, используя команды Геометрия⇒Вспомогательная прямая  и Параллельная прямая .

   

12. Через точки пересечения вспомогательных прямых с окружностью диаметром 64 мм, постройте два отрезка, пересекающихся в центре больших окружностей, используя команду Отрезок .

13. Используя команду Усечь кривую обрежьте лишние фрагменты отрезков.

14. Выделите четыре полученных отрезка. Выберите команду Правка⇒Зеркально отразить . С помощью двух точек (обязательно с привязкой, например,  Центр  ), расположенных на вертикальной оси больших окружностей, укажите ось симметрии. Используя команду Усечь кривую   обрежьте лишние фрагменты окружностей.

15. Постройте осевые линии, используя команду из списка наборов Черчение⇒Обозначения⇒Обозначение центра  . Для построения радиальных осевых линий используйте опцию в области Тип⇒Одна ось  . Для построения диаметральных осевых линий, используйте команду Геометрия⇒Дуга  , со стилем линии Осевая.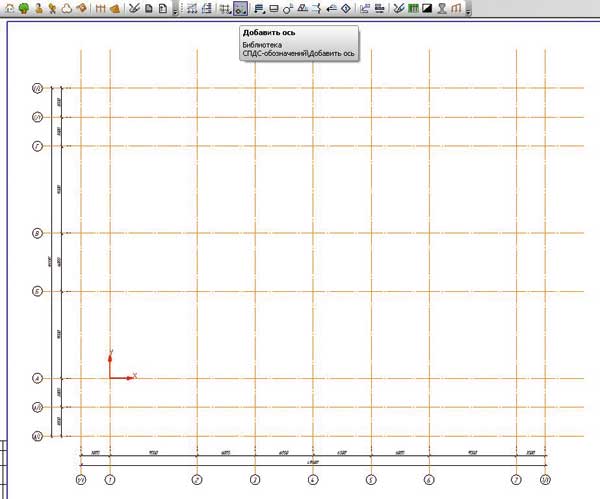

Используя команды списка наборов Черчение⇒Размеры⇒Линейный размер  , Диаметральный размер  , Радиальный размер  , Угловой размер , нанесите необходимые размеры согласно ГОСТ 2.307-68. Законченный чертеж представлен на Рисунке 1.2.

Рисунок 1.2 – Пример выполнения задания – чертеж Крышки

По вопросам репетиторства по компьютерной графике (Autocad, Solidworks, Inventor, Компас), вы можете связаться любым удобным для вас способом в разделе Контакты. Подробное описание программ обучения и стоимость, вы можете посмотреть выбрав соответствующий курс. Обучение возможно очно и дистанционно.

Система координат

— Меридиональная конвергенция. Истинный север, магнитный север и север сетки

спросил 9 лет, 9 месяцев назад

Изменено 8 лет, 7 месяцев назад

Просмотрено 15 тысяч раз

Мне трудно уловить схождение меридианов, горизонтальное угловое расстояние между истинным севером и севером по координатной сетке.

Скажем, я хочу определить, лежит ли объект к востоку или западу от центрального меридиана (ЦМ), используя обозначения истинного севера и севера сетки на топографической карте.

Я понимаю, что север сетки параллелен ЦМ, в то время как истинный север указывает на полюса, а магнитный север — это направление, которое указывает компас, и оно постоянно меняется.

Глядя на рисунок ниже, я вижу северные точки сетки к востоку от истинного севера. Значит ли это, что сам по себе этот факт означает, что все в сетке находится к востоку от истинного севера и, следовательно, от ЦМ? Означает ли этот простой факт, что объекты в этой сетке лежат к востоку от ЦМ, или я что-то упускаю?

Кроме того, я понимаю, что могу просто посмотреть на метки и увидеть, что эта сетка, в частности, покрывает от -80°22’ до -80°15, а ЦМ для зоны 17R лежит на 81°. Но если бы я этого не знал и хотел использовать стрелки на север. Пожалуйста, объясни.

• система координат
• utm
• стрелка на север

2

Представьте, что вы находитесь где-то на Земле (легко представить, я думаю), и у вас есть одна карта мира в одной руке и компас в другой.

СЕТКА СЕВЕР: карта, которую вы держите в руках, вероятно, имеет несколько горизонтальных и вертикальных линий. Направление каждой вертикальной линии указывает на север сетки. Таким образом, для каждой точки на карте вертикальная линия, проходящая через эту точку, указывает на север сетки. Но это не настоящий север, потому что он не указывает на северный полюс, потому что карты — это изображения круглой Земли на плоской бумаге — они всегда содержат ошибки.

ИСТИННЫЙ СЕВЕР: Теперь, поскольку у вас очень острый слух, вы можете слышать голос, исходящий с северного полюса. Вы следуете за этим голосом, идя по прямой линии. Направление, в котором вы идете, является истинным севером, потому что оно указывает вам на северный полюс.

МАГНИТНЫЙ СЕВЕР: первые два типа севера имели геометрическое значение. Это имеет физический смысл. Магнитный север — это направление, куда указывает стрелка вашего компаса. Стрелка указывает на магнитный полюс, который немного смещен от истинного севера, потому что масса Земли неоднородна и, следовательно, не соответствует геометрическому полюсу.

Северная сетка похожа на тангенс истинного севера в интересующей точке. Если предположить, что центральный меридиан проходит посередине карты, то в половине левой (западной) части карты (разделенной центральным меридианом) север сетки всегда находится на западе. В самом центре север сетки и истинный север совпадают. Затем, в восточной части, север сетки всегда находится на востоке от истинного севера. Однако это только случай карты, где меридианы являются прямыми линиями. Если мы говорим о других проекциях, таких как синусоидальная:

Северная сетка — это не просто линия, идущая прямо вверх.

5

Короткий ответ: центр сетки UTM всегда равен 500 000, маленькие 5, большие 65 (5|65) на картах USNG обозначают 565 000. Это больше 500 000, поэтому карта находится к востоку от меридиана 65 000 метров. X, Y или восток, север сетки UTM расположены следующим образом. Y, Northing, 0 находится на экваторе и используется для полной зоны севера и юга.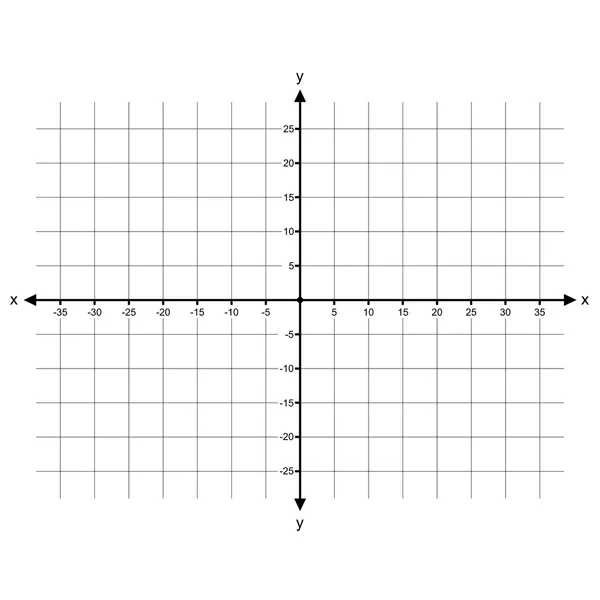 X дан «ложный восток» на центральном меридиане 500 000. Зона 6° всегда меньше 1 миллиона метров. На экваторе диапазон составляет чуть менее 166 000–834 000 и уменьшается на севере и юге. Обратите внимание на вашу цифру (5 | 65, 5 | 66 и 5 | 67) = X или на восток, 565 000, 566 000 и 567 000 или расстояние в 1 километр. Метры на запад вычитаются, а метры на восток добавляются, поэтому 565 000 составляют 65 000 метров к востоку от CM или истинного севера. Следовательно, если бы на вашей карте было 4|65, это было бы к западу от 81° (500 000 — 465 000 = 55 000 м).

Мы знаем, что линии долготы сходятся на полюсах, как дольки апельсина. Мы называем линии восток-запад параллелями широты, а те, что на карте, а на земном шаре — кругом. Представьте столб в поле. Затем привяжите веревку к шесту, возьмитесь за конец и идите. Вы ходите вокруг шеста, и во время ходьбы вы постоянно меняетесь, но на какой бы длине вы ни держали веревку, вы ходите по параллельным кругам. Веревка — это Логитюд, а ваш путь — Широта.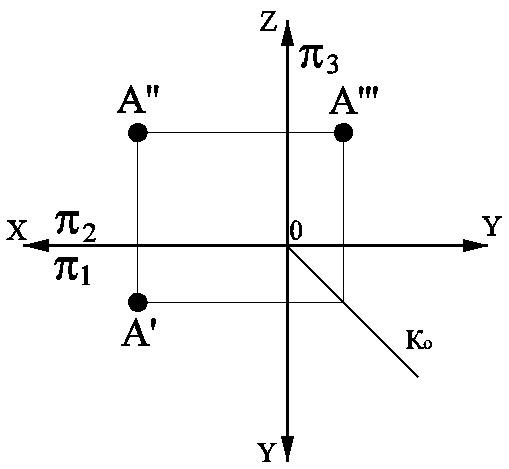 В любой точке создайте сетку и сделайте центр этой сетки параллельным веревке. Теперь начните ходить. Вскоре веревка не параллельна сетке, как и ваш путь. Угол между канатом и сеткой называется углом схождения. Сетка отклоняется не только с севера на юг, но и с востока на запад. Расстояние 3° ограничивает отклонение примерно до 2°. Читайте: Федеральный комитет по географическим данным (FGDC), стандарты, публикации, [Стандарт для национальной сети США, FGDC-STD-011-2001] http://www.fgdc.gov/standards/projects/FGDC-standards-projects/usng/fgdc_std_011_2001_usng.pdf

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.

Меркатор—ArcGIS Pro | Документация

Описание

Меркатор — это конформная цилиндрическая картографическая проекция, которая изначально была создана для отображения точных направлений по компасу при морских путешествиях. Дополнительной особенностью этой проекции является то, что все локальные формы точны и правильно определены в бесконечно малом масштабе.

Он был представлен Герардусом Меркатором в 1569 году. Вариант проекции Web Mercator является стандартом де-факто для веб-карт и онлайн-сервисов. Он доступен в ArcGIS Pro 1.0 и более поздних версиях, а также в ArcGIS Desktop 8.0 и более поздних версиях.

Цилиндрическая картографическая проекция Меркатора показана с центром в Гринвиче.

Свойства проекции

В подразделах ниже описываются свойства проекции Меркатора.

Гратикула

Меркатор — цилиндрическая проекция. Меридианы представляют собой вертикальные линии, параллельные друг другу и расположенные на равном расстоянии друг от друга, и они уходят в бесконечность при приближении к полюсам.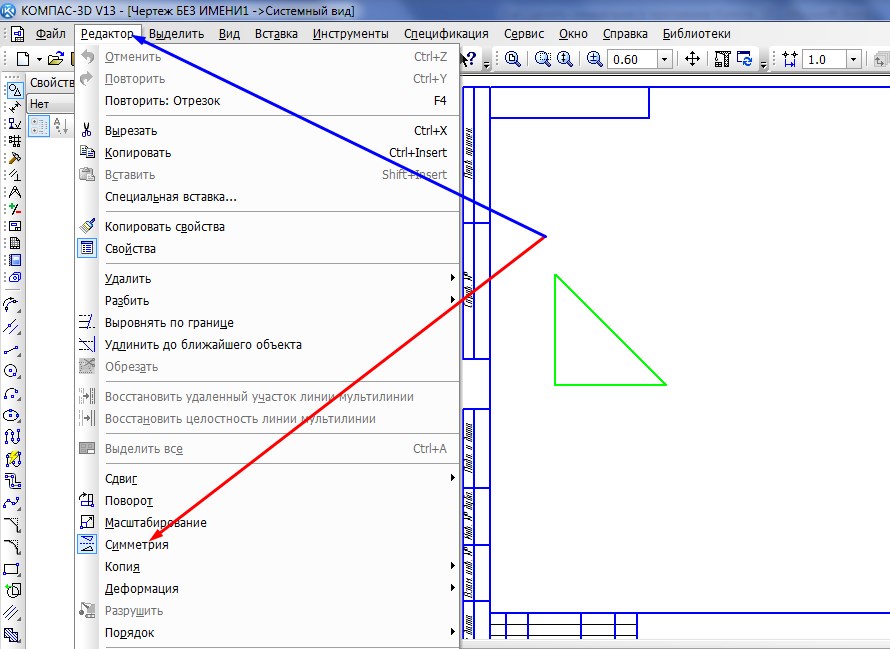 Линии широты представляют собой горизонтальные прямые линии, перпендикулярные меридианам и имеющие ту же длину, что и экватор, но они отдаляются друг от друга по направлению к полюсам. Полюса проецируются в бесконечность и не могут быть показаны на карте. Гратикула симметрична относительно экватора и центрального меридиана.

Искажение

Меркатор — конформная картографическая проекция. Направления, углы и формы поддерживаются в бесконечно малом масштабе.

Любая прямая линия, проведенная на этой проекции, представляет собой фактический компасный азимут. Эти линии истинного направления являются прямыми линиями и обычно не описывают кратчайшее расстояние между точками.

Расстояния истинны по экватору или по секущим широтам (стандартные параллели).

Площадь все больше искажается в сторону полярных регионов. Например, хотя Гренландия составляет лишь одну восьмую размера Южной Америки, Гренландия кажется больше Южной Америки в проекции Меркатора. Значения искажений одинаковы вдоль определенной параллели и симметричны относительно экватора и центрального меридиана.

Использование

Проекция подходит для крупномасштабного картографирования областей вблизи экватора, таких как Индонезия и части Тихого океана. Из-за свойства прямых румбов рекомендуется для стандартных морских навигационных карт. Его вариант, веб-проекция Меркатора, является стандартным для веб-карт и онлайн-сервисов. Проекция часто неправильно используется для карт мира, настенных диаграмм и тематических карт на веб-картах.

Варианты

В ArcGIS доступны четыре варианта:

• Mercator также известен как вариант Mercator B. Он доступен в ArcGIS Pro 1.0 и более поздних версиях, а также в ArcGIS Desktop 8.0 и более поздних версиях.
• Вспомогательная сфера Меркатора не поддерживает эллипсоид и использует уравнения на основе сферы со сферой, заданной параметром Тип вспомогательной сферы. При использовании эллипсоида в этом варианте свойства конформной и прямой локсодромии не сохраняются. Он доступен в ArcGIS Pro 1. 0 и более поздних версиях, а также в ArcGIS Desktop 9.3 и более поздних версиях.
• Меркатор вариант А отличается от варианта В только параметрами проекции. У них один и тот же алгоритм. Он доступен в ArcGIS Pro 1.2 и более поздних версиях, а также в ArcGIS Desktop 10.4 и более поздних версиях.
• Меркатор вариант С отличается от варианта В только параметрами проекции. У них один и тот же алгоритм. Он доступен в ArcGIS Pro 1.2 и более поздних версиях, а также в ArcGIS Desktop 10.4 и более поздних версиях.

Ограничения

Полюса не могут быть представлены в проекции Меркатора. Можно проецировать все меридианы, но верхний и нижний пределы широты находятся на 89°.° северной широты и 89 ° южной широты. При использовании для веб-картографирования с EPSG:3857 верхний и нижний пределы широты находятся приблизительно на 85°03’04,0636″ северной и южной широты. Большие искажения площади делают проекцию Меркатора непригодной для общих географических карт мира и тематических карт.

Параметры

Параметры Меркатора следующие: alse Easting

False Northing

Central Meridian

Standard Parallel 1

Параметры вспомогательной сферы Меркатора:

• Ложное восточное направление
• Ложное северное направление
• Центральный меридиан
• Стандартная параллель 1
• Тип вспомогательной сферы со следующими значениями:
  • 0 = использовать большую полуось или радиус географическая система координат
  • 1 = использовать малую полуось или радиус
  • 2 = вычислить и использовать аутентичный радиус
  • 3 = использовать аутентичный радиус и преобразовать геодезические широты в аутентичные широты

Вариант Меркатора A параметры следующие:

• Ложное восточное направление
• Ложное северное направление
• Центральный меридиан
• Масштабный коэффициент

Параметры варианта Меркатора C следующие:

• Ложное восточное направление
• Ложное северное направление
• Центральный меридиан
• Стандартная параллель 1
• Широта начала координат

Система координат Web Mercator

Система координат Web Mercator также известна как Google Web Mercator, Spher ical Mercator, WGS 84 Web Mercator и Pseudo-Mercator. Это стандарт де-факто для веб-карт и онлайн-сервисов. В этой системе координат геодезические координаты, определенные в датуме WGS 84, проецируются так, как если бы они были определены на сфере, с использованием основанной на сфере версии проекции Меркатора. Радиус сферы равен WGS 1984 большая полуось, 6378137,0 метров. Сочетание геодезических координат на эллипсоиде со сферическими уравнениями, следовательно, приводит к системе координат, которая не сохраняет масштабный коэффициент во всех направлениях. Таким образом, система координат Веб-Меркатора не является конформной и, помимо огромных искажений площади и расстояния от экватора, также не проецирует локсодромии как прямые.

Существует два метода имитации проекции Меркатора, используемой веб-сервисы. Если реализация Меркатора поддерживает сфероиды (эллипсоиды), система координат проекции должна быть основана на сферическая географическая система координат. Это заставит использовать уравнений сферы. Реализация Меркатора вспомогательного Сфера имеет только уравнения сферы.