Система жертва хищник: Я догоняю, ты убегаешь

Моделирование инновационной экосистемы на основе модели «хищник–жертва» : Бизнес-информатика

Моделирование инновационной экосистемы на основе модели «хищник–жертва»

Романов Виктор Петрович — доктор технических наук, профессор кафедры информационных систем в экономике и менеджменте, факультет математической экономики и информатики, Российский экономический университет им. Г.В.Плеханова
Адрес: 117997, Москва, Стремянный пер., д. 36.  
E-mail: [email protected]

Ахмадеев Булат Анасович — аспирант кафедры информационных систем в экономике и менеджменте, факультет математической экономики и информатики, Российский экономический университет им. Г.В.Плеханова
Адрес: 117997, Москва, Стремянный пер., д. 36.  
E-mail: [email protected]

      В работе анализируется понятие и сущность процессов слияний и поглощений компаний, приводится аналитический обзор имеющейся в научной и специальной литературе информации об этих процессах. Выявлены мотивы и цели участников данных сделок, а также их виды. Рассмотрены наиболее значимые слияния и поглощения компаний в сфере информационных технологий за последнее десятилетие, показан синергетический эффект от этих процессов в их деятельности, проявляющийся в случае, когда цель поглощения – доступ к новым технологиям или погоня за талантливыми кадрами. Показаны последствия слияний и поглощений компаний с позиции процессов развития природных экосистем, проводятся аналогии с биологическими отношениями, имеющими характер поглощения типа «хищник-жертва». Выявлено, что объекты в экономических системах имеют схожее поведение с поведением объектов в биологических системах. Показано, что биологическая экосистема в определенном виде может иметь инновационный характер, формируясь за счет построения эффективных финансовых, информационных и других видов обратных связей между хозяйствующими субъектами. Анализируется понятие инновационной экосистемы и разбираются основные факторы, приводящие к ее росту. Предлагается авторская модель динамического развития инновационной экосистемы на основе модели Лотки-Вольтерры (модель «хищник-жертва»), где хищники представлены корпорациями, а жертвы – малыми инновационными предприятиями (МИП). Модель, реализованная в авторской компьютерной программе, при определенных параметрах системы дает монотонный экспоненциальный рост популяций. Сделаны выводы о том, что рост инновационной экосистемы возможен за счет правильного регулирования параметров налогообложения корпораций, дотаций малым инновационным предприятиям, регулированию внутривидовой конкуренции и коэффициента поглощения малых инновационных предприятий корпорациями.

Динамические режимы стохастической модели «хищник – жертва» с учетом конкуренции и насыщения

TY — JOUR

T1 — Динамические режимы стохастической модели «хищник – жертва» с учетом конкуренции и насыщения

AU — Abramova, E. P.

AU — Ryazanova, T. V.

PY — 2019/1/1

Y1 — 2019/1/1

N2 — В работе рассматривается модель «хищник – жертва» с учетом конкуренции жертв, хищников за отличные от жертвы ресурсы и их взаимодействия, описываемого трофической функцией Холлинга второго типа.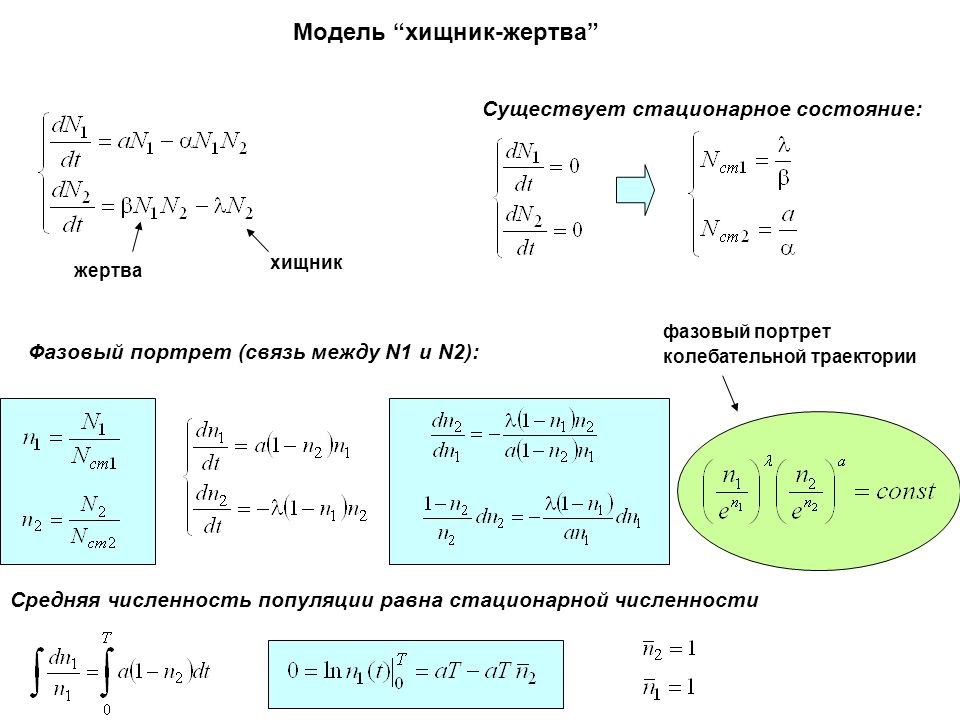 Проводится анализ аттракторов модели в зависимости от коэффициента конкуренции хищников. В детерминированном случае данная модель демонстрирует сложное поведение, связанное с локальными (Андронова–Хопфа и седлоузловая) и глобальной (рождение цикла из петли сепаратрисы) бифуркациями. Важной особенностью этой модели является исчезновение устойчивого цикла вследствие седлоузловой бифуркации. В силу наличия внутривидовой конкуренции в обеих популяциях возникают параметрические зоны моно- и бистабильности. В зоне параметров бистабильности система имеет сосуществующие аттракторы: два равновесия или цикл и равновесие. Проводится исследование геометрического расположения аттракторов и сепаратрис, разделяющих их бассейны притяжения. Понимание взаимного расположения аттракторов и сепаратрис, в совокупности с чувствительностью аттракторов к случайным воздействиям, является важной составляющей в изучении стохастических явлений. В рассматриваемой модели сочетание нелинейности и случайных возмущений приводит к появлению новых феноменов, не имеющих аналогов в детерминированном случае, таких как индуцированные шумом переходы через сепаратрису, стохастическая возбудимость и генерация осцилляций смешанных мод. Для параметрического исследования этих феноменов используются аппарат функции стохастической чувствительности и метод доверительных областей, эффективность которых проверялась на широком круге моделей нелинейной динамики. В зонах бистабильности проводится исследование деформации равновесного или осцилляционного режимов под действием шума. Геометрическим критерием возникновения такого рода качественных изменений служит пересечение доверительных областей с сепаратрисой детерминированной модели. В зоне моностабильности изучаются феномены резкого изменения численности и вымирания одной или обеих популяций при малых изменениях внешних условий. С помощью аппарата доверительных областей решается задача оценки близости стохастической популяции к опасным границам, при достижении которых сосуществование популяций разрушается и наблюдается их вымирание.

AB — В работе рассматривается модель «хищник – жертва» с учетом конкуренции жертв, хищников за отличные от жертвы ресурсы и их взаимодействия, описываемого трофической функцией Холлинга второго типа. Проводится анализ аттракторов модели в зависимости от коэффициента конкуренции хищников. В детерминированном случае данная модель демонстрирует сложное поведение, связанное с локальными (Андронова–Хопфа и седлоузловая) и глобальной (рождение цикла из петли сепаратрисы) бифуркациями. Важной особенностью этой модели является исчезновение устойчивого цикла вследствие седлоузловой бифуркации. В силу наличия внутривидовой конкуренции в обеих популяциях возникают параметрические зоны моно- и бистабильности. В зоне параметров бистабильности система имеет сосуществующие аттракторы: два равновесия или цикл и равновесие. Проводится исследование геометрического расположения аттракторов и сепаратрис, разделяющих их бассейны притяжения. Понимание взаимного расположения аттракторов и сепаратрис, в совокупности с чувствительностью аттракторов к случайным воздействиям, является важной составляющей в изучении стохастических явлений. В рассматриваемой модели сочетание нелинейности и случайных возмущений приводит к появлению новых феноменов, не имеющих аналогов в детерминированном случае, таких как индуцированные шумом переходы через сепаратрису, стохастическая возбудимость и генерация осцилляций смешанных мод. Для параметрического исследования этих феноменов используются аппарат функции стохастической чувствительности и метод доверительных областей, эффективность которых проверялась на широком круге моделей нелинейной динамики. В зонах бистабильности проводится исследование деформации равновесного или осцилляционного режимов под действием шума. Геометрическим критерием возникновения такого рода качественных изменений служит пересечение доверительных областей с сепаратрисой детерминированной модели. В зоне моностабильности изучаются феномены резкого изменения численности и вымирания одной или обеих популяций при малых изменениях внешних условий. С помощью аппарата доверительных областей решается задача оценки близости стохастической популяции к опасным границам, при достижении которых сосуществование популяций разрушается и наблюдается их вымирание.

KW — Bistability

KW — Population dynamics

KW — Stochastic phenomena

UR — http://www.scopus.com/inward/record.url?scp=85071313362&partnerID=8YFLogxK

UR — https://elibrary. ru/item.asp?id=39452780

U2 — 10.20537/2076-7633-2019-11-3-515-531

DO — 10.20537/2076-7633-2019-11-3-515-531

M3 — Статья

AN — SCOPUS:85071313362

VL — 11

SP — 515

EP — 531

JO — Компьютерные исследования и моделирование

JF — Компьютерные исследования и моделирование

SN — 2076-7633

IS — 3

ER —

Анализ системы уравнений «хищник — жертва» и доказательство первого и второго законов Вольтерры

Библиографическое описание:

Сауленко, Е. П. Анализ системы уравнений «хищник — жертва» и доказательство первого и второго законов Вольтерры / Е. П. Сауленко. — Текст : непосредственный // Молодой ученый. — 2020. — № 2 (292). — С. 1-5. — URL: https://moluch.ru/archive/292/66101/ (дата обращения: 08.05.2021).



В данной статье рассмотрена система дифференциальных уравнений Лотки — Вольтерры, а также приведены формулировки доказательства первого и второго законов Вольтерры.

Ключевые слова: математика, дифференциальные уравнения, система Лотки — Вольтерры.

Существует множество практических приложений теории дифференциальных уравнений, одним из таковых является исследование конкуренции двух некоторых групп, называемых условно «хищниками» и «жертвами». Модель, описывающая данные взаимоотношения, была предложена в начале XX века Альфредом Лоткой и Вито Вольтеррой, работавшими независимо друг от друга.

Модель Лотки — Вольтерры представляет собой систему дифференциальных уравнений вида:

Где и — количество жертв и хищников соответственно,

— коэффициент рождаемости жертв, — коэффициент убыли хищников. При встречах хищников и жертв происходит убийство жертв с коэффициентом β, сытые хищники способны к воспроизводству с коэффициентом .

Для данной модели Вито Вольтерра вывел три закона [1], в данной статье мы рассмотрим и приведем доказательства для первого и второго закона Вольтерры.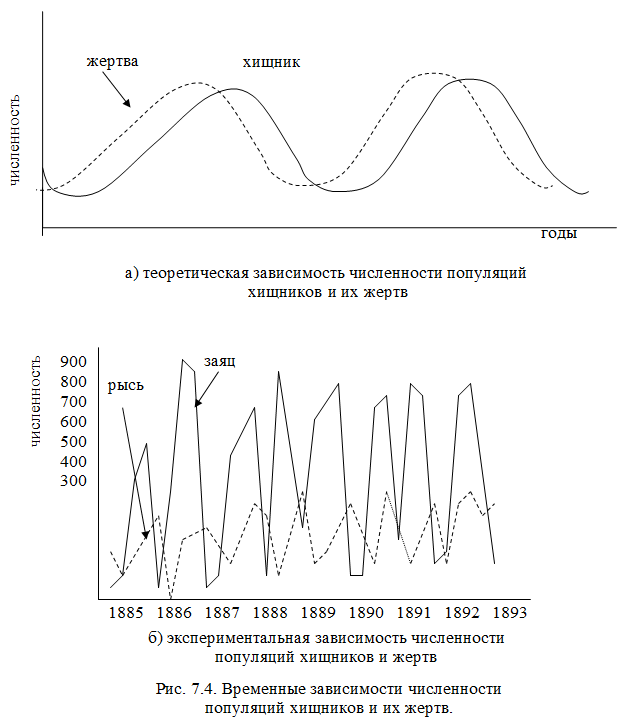 Все законы приведены в формулировке, представленной в учебном пособии «Модели динамики популяций» С. В. Соколова [2]δ

Первый закон Вольтерры сформулирован следующим образом: «Процесс уничтожения жертвы хищником нередко приводит к периодическим колебаниям численности популяций обоих видов, зависящим только от скорости роста популяций хищника и жертвы и от исходного соотношения их численности. Колебания численности двух видов периодическое, с периодом, зависящим как от начальной численности, так и от коэффициентов системы».

Докажем его, основываясь на методе В. И. Арнольда [3].

Теорема: Фазовые кривые системы замкнуты

Доказательство: Приведем данную систему к уравнению с разделяющимися переменными вида

Его интегральные кривые совпадают с фазовыми кривыми исходной системы в области, где x, y, bx-l и k-ay отличны от 0.

Следовательно,

Аналогично можем записать , где , и . Графики функций p и q имеют вид ям (рисунок 1 и 2), тогда и график функции p+q имеет такой же вид.

Рис. 1. Эскиз графика функции p(x)

Рис. 2. Эскиз графика функции q(y)

Следовательно, линии уровня функции p+q являются замкнутыми кривыми (Рисунок 3), совпадающими с фазовыми кривыми исходной системы (Рисунок 4). Теорема доказана.

Рис. 3. Линии уровня функции p+q

Рис. 4. Фазовые кривые системы Лотки-Вольтерра

Из замкнутости фазовых кривых следует, что x и y меняются со временем периодически. Первый закон Вольтерры доказан.

Второй закон Вольтерры: «Средняя численность популяции для каждого вида постоянна, независимо от начального уровня, при условии, что специфические скорости увеличения численности популяций, а также эффективность хищничества постоянны. Средняя численность популяции не зависит от начальной численности, но зависит от коэффициентов системы» [2].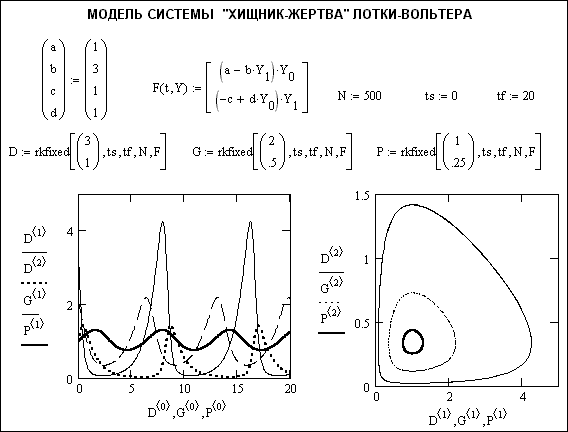

Докажем второй закон, основываясь на методе из [2], для этого вычислим среднее значение количества хищников и жертв для произвольной фазовой кривой в положительном квадранте.

Произведем для удобства замену . Перепишем исходную систему в виде:

Проинтегрируем первое уравнение на промежутке [0;T], где T –период колебаний.

Учитывая формулу Ньютона — Лейбница, свойства интеграла [4] и свойства периодических функций:

Получаем:

Аналогично, интегрируя второе уравнение:

Второй закон Вольтерры доказан.

Выводы:

1. Фазовые кривые системы уравнений Лотки-Вольтерра замкнуты
2. Численность популяций хищников и жертв меняется периодически
3. Период колебаний зависит от начальной численности популяций и коэффициентов системы
4. Средняя численность популяции не зависит от начального значения, но зависит от коэффициентов системы

Литература:

1. Вольтерра В. Математическая теория борьбы за существование. М.: Наука, 1976. 228 с.
2. Соколов С. В. Модели динамики популяций: учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2018. 61 с.
3. Арнольд В. И. Обыкновенные дифференциальные уравнения. –– Новое издание, исправл. –– М.: МЦНМО, 2012. 344 с.: ил.
4. Зорич В. А. Математический анализ. Часть I. — 6-е изд, дополн.— М.: МЦНМО, 2012. — XVIII + 702 с. Библ.: 55 назв. Илл.: 65.

Основные термины (генерируются автоматически): исходная система, кривой, численность популяции, вид, жертва, коэффициент системы, линия уровня функции, начальная численность, период колебаний, система, уравнение, эскиз графика функции.

90 years of evolving trophic functions (in Russian)]

ЖУРНАЛ ОБЩЕЙ БИОЛОГИИ том 79 № 6 2018

ОТ ЛОТКИ–ВОЛЬТЕРРА К АРДИТИ–ГИНЗБУРГУ 433

Lenski, 1997; Haydon, Lloyd, 1999; Jeschke et al.,

2004; Tully et al., 2005). С другой стороны, попыт-

ки приложения классических моделей к описа-

нию динамики крупномасштабных экологиче-

ских систем часто оказывались несостоятельны-

ми.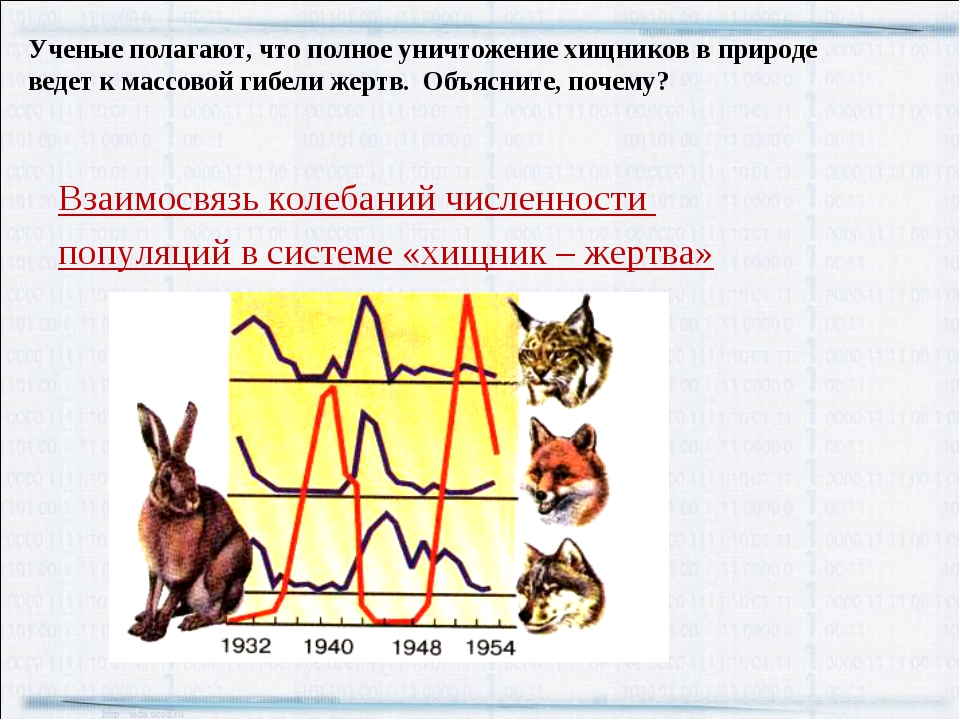 Данное противоречие выходит за рамки чисто

теоретической проблемы, поскольку использова-

ние того или иного вида трофической функции в

моделях трофических систем способно полно-

стью изменить их динамические свойства (Базы-

кин, 1985; Arditi et al., 2004; Svirezhev, 2008; Arditi,

Ginzburg, 2012), а стало быть, и модельный про-

гноз реакции экосистемы на управляющие воз-

действия при решении таких прикладных задач,

как биологический контроль насекомых-вреди-

телей и сорных растений, выращивание в аква-

культуре ценных пород рыб, охрана редких видов

растений и животных.

Так, при использовании наиболее популярной

функции Холлинга типа II (6) и функции логи-

стического роста популяции жертв модель (1), из-

вестная в этом случае как модель Розенцвейга –

МакАртура (Rosenzweig, MacArthur, 1963), демон-

стрирует такие абсурдные, противоречащие на-

блюдениям свойства, как “парадокс обогаще-

ния” (paradox of enrichment) (Rosenzweig, 1971) и

тесно связанный с ним “парадокс биологическо-

го контроля” (paradox of biological control) (Luck,

1990; Berryman, 1999; Arditi, Berryman, 1991). Па-

радокс обогащения состоит в том, что в ответ на

увеличение первичной продукции происходит

дестабилизация динамики модели и, как след-

ствие роста амплитуды колебаний численностей,

повышение риска вымирания либо хищников,

либо обеих популяций. Однако нет убедительных

свидетельств проявления подобного эффекта в

природных условиях (Jensen, Ginzburg, 2005;

Arditi, Ginzburg, 2012). Парадокс биологического

контроля заключается в невозможности при по-

мощи общепринятой модели Розенцвейга–Мак-

Артура воспроизвести стабильную динамику с

низкой численностью вредителя, соответствую-

щую ситуации успешного подавления вредителя

агентом биометода (Arditi, Berryman, 1991;

Sapoukhina et al., 2003). Использование этой же

трофической функции H-II при моделировании

пищевой цепи ведет к еще одному парадоксаль-

ному несоответствию свойств математической

модели наблюдениям за природными трофиче-

скими сообществами: модель предсказывает

нереалистичную разнонаправленную реакцию

уровней трофического каскада на биоманипуля-

ции “снизу–вверх” (enrichment response) (Jensen,

Ginzburg, 2005; Arditi, Ginzburg, 2012). А именно,

если пронумеровать уровни, начиная с вершины

цепи, то в ответ на повышение продуктивности

нижнего уровня осредненная по времени числен-

ность популяции первого (самого верхнего уров-

ня) увеличится, второго останется неизменной, а

реакция других уровней будет зависеть от четно-

сти их номеров: для уровней с нечетными номе-

рами (1, 3,…) имеет место увеличение, а с четны-

ми (4, 6,…) – уменьшение, либо сохранение чис-

ленности при трофической функции H-I (Arditi,

Ginzburg, 2012). Дженсен и Гинзбург (Jensen,

Ginzburg, 2005) отмечают, что для цепи, включа-

ющей более трех уровней, такая реакция на рост

первичной продукции представляется патологи-

ческой, а все известные попытки предоставить

натурные наблюдения, демонстрирующие подоб-

ную динамику, связаны либо с неаккуратной об-

работкой, либо с ошибочной интерпретацией

данных (см. также Akcakaya et al., 1995; Arditi,

Ginzburg, 2012).

Те же самые проблемы возникают при исполь-

зовании и любой другой трофической функции,

зависящей только от численности популяции

жертв, (Arditi, Ginzburg, 1989; 2012). Фунда-

ментальная причина вышеупомянутых противо-

речий заключается в том, что нулевая изоклина

второго уравнения системы (1), описываю-

щего динамику популяции хищников, которая

определяется как решение уравнения ,

проходит вертикально (рис. 2, а, б). Вертикаль-

ность изоклины означает, что для поддержания

любой численности хищников в системе доста-

точно только постоянной численности жертв. Бо-

лее реалистичной является гипотеза, требующая

учета взаимной интерференции хищников (Begon

et al., 1986): “для поддержания более многочис-

ленной популяции хищников требуется большее

количество жертв”. Тогда нуль-изоклина

представляет собой наклонную линию, что ока-

зывает стабилизирующее влияние на динамику

системы, причем наклон изоклины тем больше,

чем выше взаимная интерференция хищников.

Таким образом, противоречия классической тео-

рии устраняются путем включения в модель ин-

терференции хищников, проявляющейся на по-

пуляционном уровне как зависимость трофиче-

ской функции от плотности хищников,

(Begon et al., 1986; Ильичев, 1986, 2009; Бигон и др.,

1989; Arditi, Ginzburg, 1989, 2012; Abrams, Ginz-

burg, 2000; DeAngelis et al., 1975; Berdnikov et al.,

1999; Cosner et al., 1999).

В своей статье Ардити и Гинзбург (Arditi, Ginz-

burg, 1989) не только привлекли внимание к про-

блемам классической теории трофических си-

стем, но и предложили наиболее простой способ

учета взаимной интерференции хищников в мо-

дели (1), AGС:

(8)

Поскольку трофическая функция (8) по форме

совпадает с формулой Контуа (Contois, 1959), ис-

пользуемой в микробиологии для описания зави-

Система «хищник — жертва» — Вики

Система «хищник-жертва» — сложная экосистема, для которой реализованы долговременные отношения между видами хищника и жертвы, типичный пример коэволюции.

Отношения между хищниками и их жертвами развиваются циклически, являясь иллюстрацией нейтрального равновесия ^[1]

Биологическая система

Приспособления, вырабатываемые жертвами для противодействия хищникам, способствуют выработке у хищников механизмов преодоления этих приспособлений. Длительное совместное существование хищников и жертв приводит к формированию системы взаимодействия, при которой обе группы устойчиво сохраняются на изучаемой территории. Нарушение такой системы часто приводит к отрицательным экологическим последствиям.

Негативное влияние нарушения коэволюционных связей наблюдается при интродукции видов. В частности, козы и кролики, интродуцированные в Австралии, не имеют на этом материке эффективных механизмов регуляции численности, что приводит к разрушению природных экосистем.

Допустим, что на некоторой территории обитают два вида животных: кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов x{\displaystyle x}, число лис y{\displaystyle y}. Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имя модели Вольтерра — Лотки:

{x˙=(α−cy)x;y˙=(−β+dx)y.{\displaystyle {\begin{cases}{\dot {x}}=(\alpha -cy)x;\\{\dot {y}}=(-\beta +dx)y.\end{cases}}}

Эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора. Как и в случае гармонического осциллятора, это поведение не является структурно устойчивым: малое изменение модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения. Например, равновесное состояние может стать устойчивым, и колебания численности будут затухать. Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов.

На вопрос о том, какой из этих сценариев реализуется, модель Вольтерра — Лотки ответа не дает: здесь требуются дополнительные исследования.

Поведение модели

Групповой образ жизни хищников и их жертв радикально меняет поведение модели, придает ей повышенную устойчивость.

Обоснование: при групповом образе жизни снижается частота случайных встреч хищников с потенциальными жертвами, что подтверждается наблюдениями за динамикой численности львов и антилоп гну в парке Серенгети

[2]

История

Модель совместного существования двух биологических видов (популяций) типа «хищник — жертва» называется также моделью Вольтерра — Лотки.

Была впервые получена А. Лоткой в 1925 году (использовал для описания динамики взаимодействующих биологических популяций).

В 1926 году (независимо от Лотки) аналогичные (и более сложные) модели были разработаны итальянским математиком В. Вольтерра. Его глубокие исследования в области экологических проблем создали основу математической теории биологических сообществ (математической экологии). ^[3]

Литература

• В. Вольтерра, Математическая теория борьбы за существование. М.: Наука, 1976. ISBN: 5-93972-312-8
• Eusebius Doedel. Lecture notes on Numerical analysis of bifurcation problems. Hamburg, march, 1997
• П. В. Турчин, Популяционная динамика

Примечания

См. также

Новая математическая модель уточнит прогнозы популяции хищников и травоядных

Математик из РУДН уточнил модель взаимодействия «хищник-жертва» для более верных прогнозов природных систем. Он ввел косвенные факторы, которые влияют на популяцию

Традиционная математическая модель отношений между хищником и жертвой в дикой природе учитывает только непосредственное взаимодействие животных в каждой заданной точке системы. Математик РУДН Сергей Петровский показал, что на численность влияют и косвенные, так называемые нелокальные взаимодействия.

Математические модели экосистем позволяют экологам понять, как они устроены и составить прогнозы. С помощью модели «хищник-жертва» рассчитывают, как в системе меняется численность хищников и травоядных в зависимости от условий: размножения травоядных, смертей хищников от голода, поедания хищниками травоядных, миграции животных. Новая математическая модель предлагает, кроме непосредственного взаимодействия, учитывать влияние косвенных факторов.

Пример нелокального взаимодействия в природе — засушливые регионы, где растения развивают широкую корневую систему и собирают влагу с большей, чем обычно территории. Математически эта нелокальность выражается с помощью интеграла — он «суммирует» влияние всей системы на каждую заданную точку. Математики показали, что, например, конкуренция за пищу среди травоядных нелокальна, то есть учитывать нужно количество пищи не в каждой конкретной точке, а «интегрально» — во всей системе в совокупности.

«Нелокальные свойства движения рассматриваются все чаще, но вот вопрос о нелокальном происхождении этой динамики редко принимается во внимание. Однако системы, в которых взаимодействие не локально, изобилуют в природе. Может быть, самым известным таким примером будет система „растительность-вода“, особенно в полузасушливых регионах, где нелокальность — непосредственный результат широкой (иногда чрезмерно большой) системы корней растений. Мы показали, что в модели „хищник-жертва“ нелокальность внутривидовых взаимодействий приводит к различным механизмам динамики всей системы», — рассказал профессор РУДН Сергей Петровский.

С помощью компьютерного моделирования ученые выяснили, что в системе с изначально равной численностью хищников и травоядных со временем их количество начинает различаться в разных точках.

Изучение систем типа «Хищник-жертва» средствами мультиагентного моделирования

В работе рассматривается эволюция биологической системы, состоящей из двух популяций рыб (хищники – акулы и жертвы – мелкие рыбы). Моделирование системы проведено на основе компьютерной модели, использующей мультиагентный подход.

Математические модели позволяют c достаточно высокой степенью точности описать некоторые явления или процессы, ранее неизвестные исследователю, а результаты моделирования могут быть использованы впоследствии для управления процессами любой природы. Очень часто при моделировании отдельных процессов, происходящих как в живой, так и неживой природе, используют имитационное мультиагентное моделирование, основанное на определенных правилах, которым подчиняются все элементы изучаемой системы (например, в [8, 9] оно используется для исследования транспортных потоков).

Моделирование живых систем сегодня является одной из ключевых научных и практических дисциплин в области информационных технологий. Особенное развитие получило мультиагентное моделирование для качественного описания закономерностей некоторых биологических процессов (в отличие от других видов моделирования оно позволяет достаточно легко учитывать пространственное распределение агентов).

В представленной работе проведено моделирование биологической системы, представляющей собой две популяции рыб, одна из которых выступает в роли хищника (акулы), а вторая – в роли жертвы (мелкие рыбы). Основные задачи работы – рассмотрение различных взаимодействий между элементами живой системы, исследование совместного сосуществования мелких рыб и акул на одной территории при различных параметрах рассматриваемой системы на основе мультиагентной компьютерной модели.

Работа выполнена в программе математического моделирования биологических систем типа «хищник-жертва» [13], описанной в работе [7]. Стоит отметить, что рассмотрению вопросов математического моделирования систем типа «хищник-жертва» посвящено большое количество работ, например [1-6, 10-12, 14].

Используемая для моделирования системы программа имеет достаточно большое количество настраиваемых параметров, позволяющих учитывать продолжительность жизни (как хищников, так и жертв), вероятность рождения особей определенного пола, учет внутривидовой конкуренции (состояние перенаселения), интервалы появления потомства, область поиска потенциального партнера. Для хищника также возможно задать умное поведение, при котором он чувствует добычу на определенном расстоянии от себя и начинает ее преследование.

Рассмотрим некоторые результаты, полученные в ходе моделирования.

На рис. 1-8 показано пространственное распределение особей популяций на определенных этапах моделирования. Рис. 1-4 соответствуют случайному блужданию хищников и появлению потомства от одного родителя (потомство от одного родителя в данном случае лишь означает, что размножение происходит всегда, как только особь становится к нему готова – при этом партнер для особи всегда предполагается в наличии). Рис. 1 соответствует начальному распределению хищников и жертв (итерация 0), рис. 2-4 соответствуют отдельным последовательным этапам моделирования. Текущее количество особей отдельной популяции на каждом конкретном этапе моделирования можно видеть в строке статуса программы.

Рис. 1. Случайное блуждание хищников: начальное распределение

Рис. 2. Случайное блуждание хищников: итерация 16

Рис. 3. Случайное блуждание хищников: итерация 112

Рис. 4. Случайное блуждание хищников: итерация 461

На рис. 5-8 показаны случаи, когда акулам свойственно умное движение и они способны к преследованию жертв. При этом в процессе размножения участвуют оба родителя и для появления потомства необходимо одновременное выполнение двух условий: наличие в области (на некотором расстоянии) от самки особи мужского пола, способность и готовность самки к процессу воспроизводства.

По сравнению со случайным блужданием отчетливо видно, что хищники разделяют исходную популяцию жертв на более мелкие популяции (рис. 8), которые в течение некоторого времени будут развиваться по отдельности. Это вполне соответствует реальной ситуации, когда со временем накапливаются различия между особями одной и той же популяции (конечно, в используемой версии программы накопление различий между особями не учитывается, но оно может быть учтено в новых версиях программы).

Рис. 5. Умное поведение акул: начальное распределение

Рис. 6. Умное поведение акул: итерация 26

Рис. 7. Умное поведение акул: итерация 101

Рис. 8. Умное поведение акул: итерация 771

Из рис. 7 отчетливо видны еще некоторые свойства, присущие реальным взаимодействующим популяциям: хищник всегда следует за жертвой (по крайней мере, большая их часть), а жертвы очень быстро распространяются и развиваются на территориях, свободных от хищников. При этом хищник, оказавшийся вдали от потенциальных жертв (и, соответственно, оставшийся без пищи), будет обречен на гибель, что также хорошо согласуется с действительностью.

Рассмотрим теперь графические зависимости, иллюстрирующие эволюцию изучаемой системы со временем (в качестве времени выступают итерации программы).

На рис. 9 показана эволюция системы для случая, когда для прироста популяции акул необходимы оба родителя. Линии 1 описывают колебания численности акул, а линии 2 – мелких рыб. При описании движения акул принята модель умного поведения, вероятность рождения особи мужского пола принята равной 50%, за время жизни акула может дать потомство до 8 раз, радиус обнаружения равен 10, радиус взаимодействия с особью противоположного пола равен 15. Первоначальная численность акул 50, мелких рыб – 3000. При этом в системе устанавливается циклическое равновесие.

Рис. 9. Эволюция системы: потомство от двух родителей для акул

На рис. 10 показана эволюция изучаемой системы для случая появления потомства от двух родителей для обоих популяций рыб. При этом вероятность рождения мужских особей для акул принята равной 40%, для мелких рыб – 20 % (увеличение процента мужских особей при значениях других параметров, принятых в модели при получении рис. 10, приводит к гибели обоих популяций). Линии 1 описывают колебания численности акул, а линии 2 – мелких рыб.

Рис. 10. Эволюция системы: потомство от двух родителей

Проведенное моделирование на основе [13] показало, что при определенных параметрах модели между численностями популяций устанавливается вполне определенное равновесие, при котором происходит циклическое изменение численности особей обоих популяций. Такое поведение системы вполне соответствует решению, получаемому из рассмотрения системы Лотки-Вольтерры, что говорит о возможности применения мультиагентного моделирования к описанию рассмотренного в работе процесса.

Также на основе компьютерной модели [13] можно изучать влияние вероятности появления особей определенного пола на эволюцию обоих популяций в целом.

Модель хищник-жертва — Scholarpedia

Рис. 1: Периодическая активность, генерируемая моделью хищник-жертва.

Модели хищник-жертва, возможно, являются строительными блоками био- и экосистем, поскольку биомассы выросли на из их ресурсных масс. Виды соревнуются, развиваются и рассеиваются просто с целью поиска ресурсов для поддержания своей борьбы за само свое существование. В зависимости от конкретных настроек приложений они могут принимать формы взаимодействий между потребителями ресурсов, растениями-травоядными, паразитами-хозяевами, опухолевыми клетками (вирусами) и иммунной системой, восприимчиво-инфекционными взаимодействиями и т.Они имеют дело с общими взаимозависимостями между проигрышами и выигрышами и, следовательно, могут иметь приложения вне экосистем. При тщательном изучении кажущихся конкурентных взаимодействий часто оказывается, что на самом деле они представляют собой некие скрытые формы взаимодействия хищника и жертвы.

Модель общего хищника-жертвы

Рассмотрим две популяции, размеры которых в контрольный момент времени \ (t \) равны обозначается как \ (x (t) \, \) \ (y (t) \, \) соответственно. Функции \ (x \) и \ (y \) могут обозначать численность населения или концентрацию (число на площадь) или некоторая другая масштабная мера размеров популяций, но быть непрерывными функциями.Изменения численности популяции со временем описывается производными по времени \ (\ dot x \ Equiv dx / dt \) и \ (\ dot y \ Equiv dy / dt \, \) соответственно, и общая модель взаимодействующих популяции записывается в терминах двух автономных дифференциальных уравнений \ [\ точка x = x f (x, y) \] \ [\ точка y = y g (x, y) \] (т.е. время \ (t \) не появляется явно в функции \ (x f (x, y) \) и \ (y g (x, y) \)). Функции \ (f \) и \ (g \) обозначают соответствующие темпов роста на душу населения двух видов.Предполагается, что \ (df (x, y) / dy <0 \) и \ (dg (x, y) / dx> 0. \) Эту общую модель часто называют моделью хищник-жертва Колмогорова (Freedman 1980, Brauer and Castillo-Chavez 2000).

Lotka-Volterra Модель

В 1926 году известный итальянский математик Вито Вольтерра предложил дифференциальное уравнение модели для объяснения наблюдаемого увеличения численности хищных рыб (и соответствующих уменьшение добычи рыбы) в Адриатическом море во время Первой мировой войны. В то же время в США уравнения, изученные Вольтеррой, были независимо выведенный Альфредом Лоткой (1925) для описания гипотетической химической реакции, в которой химические концентрации колеблются.Модель Лотки-Вольтерра — это простейшая модель взаимодействия хищник-жертва. Он основан на линейном росте на душу населения ставки, которые записываются как \ [f = b-p y \] и \ (g = r x-d \. \)

• Параметр \ (b \) — это скорость роста вида \ (x \) (жертва) при отсутствии взаимодействия с видами \ (y \) (хищниками). Эти взаимодействия уменьшают количество жертв: темп роста на душу населения уменьшается (здесь линейно) с увеличением \ (y \, \), возможно, становясь отрицательным.
• Параметр \ (p \) измеряет влияние хищничества на \ (\ dot x / x \.\)
• Параметр \ (d \) — скорость гибели (или эмиграции) видов \ (y \) при отсутствии взаимодействия с видами \ (x \. \)
• Термин \ (r x \) обозначает чистую скорость роста (или иммиграции) популяции хищников в зависимости от размера популяции жертвы.

Модель Prey-Predator с линейными темпами роста на душу населения \ [\ точка x = (b — p y) x \] (Добыча) \ [\ dot y = (r x — d) y \] (Хищники) Эта система упоминается как модель Лотка-Вольтерра : она представляет собой одну из самых ранних моделей в математической экологии.

Рисунок 2: Динамика Prey-Predator, описанная кривыми уровня сохраняемого количества. Стрелки указывают скорость и направление решений. В этом моделировании данные следующие: \ (d = r = b = d = 1 \. \) Имеются состояния равновесия в \ (x = 1, y = 1 \) и в \ (x = 0, y = 0 \. \)

Система может быть интегрирована напрямую. В частности, любое решение \ ((x (t), y (t)) \) системы удовлетворяет тождеству \ [C = b \ ln y (t) — p y (t) — r x (t) + d \ ln x (t) \] для всех \ (t \, \), где постоянная \ (C = b \ ln y (0) — p y (0) — r x (0) + d \ ln x (0) \) определяется начальными условиями и параметрами системы.(Здесь \ (\ ln x \) обозначает натуральный логарифм \ (x \, \) и т. Д.) количество в правой части тождества выше упоминается как закон сохранения , так как он постоянен вдоль любого решение. Сохранение количества облегчает визуализацию решения. На рисунке нанесены горизонтальные контуры поверхность \ [z = b \ ln y — p y — r x + d \ ln x \] в первом квадранте плоскости \ (xy \). Контуры описывают решения системы определяются их начальными данными, и, поскольку они представляют собой замкнутые кривые, решения представляют собой периодические колебания.

Если \ (b> 0 \, \) есть два состояния равновесия, \ (x = 0, y = 0 \) (вымирание) и \ (x = d / r, y = b / p \) (сосуществование), а поверхность \ [z = b \ ln y — p y — r x + d \ ln x \] имеет единственный пик в последнем равновесии. В контурные линии на рисунке описывают классический циклы «жертва-хищник», наблюдаемые в экологических системах.

Приведенная выше модель была получена независимо в следующих областях:

• эпидемии (Кермак и МакКендрик 1927, 1932, 1933) (\ (b = 0 \))
  • \ (x \) — восприимчивые люди и
  • \ (y \) — инфекционные особи,
• экология (Лотка 1925, Вольтерра 1926)
  • \ (x \) являются добычей и
  • \ (y \) хищники,
• теория горения (Семенов 1935)
  • \ (x \) и \ (y \) — химические радикалы, образующиеся при горении H ₂ O ₂ ,
• экономика (Гэлбрейт, 2006)
  • \ (x \) — население и
  • \ (у \) — хищническое учреждение,

и множество других исследований из разных дисциплин.

Альфред Джеймс Лотка (1880-1949, США, химик, демограф, эколог и математик) родился во Львове (Лемберг), в то время находившемся в Австрии, ныне в Украине. Он приехал в Соединенные Штаты в 1902 году и написал ряд теоретических статей о химических колебаниях в первые десятилетия двадцатого века, а также написал книгу по теоретической биологии (1925). Затем он оставил (академическую) науку и провел большую часть своей трудовой жизни в страховой компании (Metropolitan Life).В этом качестве он стал президентом PAA (Ассоциации народонаселения Америки).

Вито Вольтерра (3 мая 1860 — 11 октября 1940, итальянец, математик и физик, наиболее известный своим вкладом в математическую биологию) родился в Анконе в очень бедной семье. Вольтерра рано проявил себя в математике еще до поступления в Пизанский университет. Его работа кратко изложена в его книге «Теория функционалов, интегральных и интегродифференциальных уравнений» (1930).После Первой мировой войны Вольтерра обратил свое внимание на применение своих математических идей в биологии, в основном повторяя и развивая работы Пьера Франсуа Ферхюльста. Самый известный результат этого периода — модель Лотки-Вольтерры. В 1922 году он присоединился к оппозиции фашистскому режиму Бенито Муссолини, а в 1931 году отказался принять обязательную присягу на верность. Он был вынужден оставить свой университетский пост и членство в академиях наук, и в последующие годы он жил в основном за границей, вернувшись в Рим незадолго до своей смерти.

Модель Kermack-McKendrick

При хищничестве и эпидемиях существует коллективный иммунитет. это удобно сформулировать это с точки зрения эпидемиологии, где теперь мы говорим для жертвы как восприимчивые, а для хищников как инфекционные. Динамика заражения отображена графиком \ (x \ to y \ to \, \), что указывает на то, что восприимчивые люди могут стать заразными и что инфекционные заболевания могут быть удалены из процесса (например, через смерть, карантин, или прививка). Рассмотрим короткий промежуток времени. по сравнению с воспроизводством восприимчивой популяции, т.е.э., пусть \ (b = 0 \. \) Если начальная восприимчивая популяция настолько велика, что \ (x (0)> d / r \, \) то из второго уравнения модели хищник-жертва мы видим, что первоначально \ (\ dot y> 0 \, \), что указывает на то, что инфекция изначально будет больше чем заменить себя, передав инфекцию. Однако если это условие не выполняется, инфекционная популяция будет снижаться. Критическое значение \ (R \ Equiv rx (0) / d = 1 \) называется быть эпидемическим порогом или переломным моментом в этом процессе.

Рисунок 3: Модель распространения инфекционного заболевания Кермака-Маккендрика. Переломный момент находится в \ (x = 1.0 \. \). Если \ (x (0) \) выше этого значения, разовьется эпидемия. Степень серьезности можно оценить, проследив кривую, исходящую от \ (x (0) \), пока она не сходится к горизонтальной оси. Это указывает на размер восприимчивой популяции, которая избегает инфекции. Обратите внимание, что горизонтальная ось, как показано здесь, начинается с x = 0,1, чтобы избежать логарифмической сингулярности. * \, \), как показано на рисунке.Удивительно, но это число всегда больше нуля, что показывает, что некоторые восприимчивые всегда выживут!

Это явление, о котором говорится to as на практике соблюдается коллективный иммунитет ; на самом деле номер \ (R \) регулярно публикуется для различных болезней и регионов. в качестве меры борьбы с эпидемией. Это отражает тот факт, что восприимчивое население может быть уменьшено до уровня, ниже которого инфекционные заболевания не увеличиваются. Модель в этом случае называется как модель Кермака-МакКендрика восприимчиво-инфекционных взаимодействий в эпидемиологии.

Jacob-Monod Модель

Другой подход к моделированию взаимодействия между добычей и хищники были разработаны для учета организмов (таких как бактерии), поглощающие питательные вещества. Существует ограниченная скорость приема, которая такие организмы способны, и следующая модель учитывает ограниченная скорость приема. Предположим теперь, что \ (x \) обозначает размер популяции кормушек и что они питаются химическими веществами. вид концентрации \ (y \. \) Обычно они используются для обозначения концентрации питательных веществ и питательных веществ в растворе, а не «подсчет головы».Модель Jacob-Monod — это \ [\ dot x = \ frac {V y} {K + y} x \] \ [\ dot y = — \ frac 1Y \ frac {V y} {K + y} x \] где

• \ (V \) — скорость поглощения,
• \ (K \) — постоянная насыщения, а
• \ (Y \) — это доходность \ (x \) на единицу \ (y \) занятого.

Обратите внимание, что когда \ (y = K \, \) скорость поглощения составляет \ (V / 2 \, \) половину максимальной; на практике \ (y = K \) считается переломным моментом: Если \ (y

Величина \ (C = x + Y y \) сохраняется (так как производная с по времени правой части равна нулю) где \ (С = х (0) + Уу (0) \.\) Подставляя это в первое уравнение, получаем \ [\ dot x = \ frac {V (C-x)} {Y K + (C-x)} x \. \] Решения можно найти с помощью квадратур, и они показывают, что если \ (x (0)> 0 \, \), затем \ (x (t) \ to C \) как \ (t \ to \ infty \, \), в этот момент питательное вещество было истощено.

Типичное использование этой модели — описание непрерывного роста потока устройство, такое как хемостат, где происходит непрерывное удаление питательных веществ и кормушек и постоянный приток свежих питательных веществ. Модель Якоба-Монода используется для описания такого устройства для роста бактерий, например, для определения условий существования устойчивого динамического равновесия путем уравновешивания роста за счет поглощения питательного вещества с вымыванием из кормушек.

В некоторых моделях хищник-жертва используются термины, аналогичные тем, которые используются в модели Якоба-Монода, для описания скорости, с которой хищники поедают добычу. В более общем смысле, любые данные в модели Лотки-Вольтерры можно считать зависящими от плотности добычи в зависимости от изучаемой системы. Это называется функциональной реакцией, идея, которую представил и обсудил К. С. Холлинг (1959). В популяционных моделях использовалось несколько различных форм функциональной реакции, но форма Якоба-Моно, также называемая экологами формой Холлинга 2, является одной из наиболее распространенных.g-1 \ ​​right) \) с \ (0

Логистическое уравнение

Интересный футляр для \ [\ dot x = \ frac {V (C-x)} {Y K + (C-x)} x \] это когда \ (V \) и \ (YK \) очень велики по сравнению с другими данными в модели, но с их соотношение среднего размера, скажем \ (V / (YK) \ приблизительно r \.\) Тогда мы можно игнорировать второй член в знаменателе и получить \ [\ точка x = r (C-x) x \. \] Это называется логистическим уравнением . Это тоже возникло в различных дисциплин, но одно из первых его появление было связано с Ферхюльстом в середине 19 века, который использовал его для исправления некоторых отклонения модели Мальтуса (\ (\ dot x = r x \)) от некоторых человеческих данные о населении. Число \ (C \) теперь упоминается как грузоподъемность для населения; это соответствует в модели Якоба-Моно не осталось питательных веществ.

Логистическое уравнение может быть решено в замкнутая форма по квадратурам. Это показывает, что \ (x (t) \ to C \) при \ (t \ to \ infty \, \), если \ (x (0)> 0 \. \)

Хищничество с задержками: хаос в уравнении воспроизведения Риккера

Задержки во времени возникают в биологических системах, и они могут производить сложная динамика. Для моделирования возрастной структуры (и других временных задержек) в системе мы воспользуемся подходом, который был введен Эйлером в 18 век. Пусть \ (x (t) \) обозначает число, рожденное в момент \ (т \.\) Тогда \ (x (t-a) \) обозначает число, которое родилось \ (a \) единицы назад. Предположим, что существует такой нелинейный эффект, что количество новорожденные \ (a \) единицы назад, которые могут участвовать в воспроизводстве на время \ (t \) есть \ (h (x (t-a)) \), где функция \ (h \) называется функция воспроизведения . Эта нелинейность может быть связана с хищниками или факторами окружающей среды, как обсуждалось ранее. Предположим, что у людей возраста \ (a \) есть фертильность \ (m (a) \. \) Тогда уравнение ниже показывает, сколько родится в момент \ (t \.t m (a) h (x (t-a)) \, da \, \] где \ (x_0 (t) \) обозначает затяжной вклад в более поздние роды исходной популяции. В случае, когда \ (h (x) = x \) — линейная функция, это уравнение называется Уравнение обновления , которое широко используется в демографии. Его Решение может быть найдено с помощью преобразований Лапласа (Keyfitz, Flieger, 1971). Однако, если \ (h \) — нелинейная функция, то этот метод решение недоступно.

Функция фертильности \ (m (a) \) описывает фертильность возраст \ (а \.n x_0 \. \) Однако, если \ (h \) имеет вид в случае Ферхюльста, где \ (h (x) = x (C — x) _ + \ Equiv \ max (C-x, 0), \) рекурсия становится \ [x_ {n + 1} = r x_n (C-x_n) _ + \, \] чьи итерации могут демонстрировать довольно дикое поведение. Это было первое заметил эколог У. Рикер в 1950-х годах, который использовал функция \ (h (x) = x \ exp {(- x)} \) в исследованиях динамики рыболовства, хотя в то время его работы в значительной степени игнорировались. Это воспроизведение функция учитывает каннибализм (самохищение) в том случае, если численность населения мала, модель похожа на модель Мальтуса, но для больших популяций размножение сильно подавлено. {- x_n} \.\] Начиная с \ (x_1 = 1 \, \) определяем последовательность \ (\ {x_ {50}, x_ {51}, x_ {52}, x_ {53}, \ dots, x_ {300} \} \) и записать в массив, скажем \ (D (r, x) \, \) количество элементов последовательности, которые находятся в каждая корзина. Мы начинаем отсчет только после 50 начальных повторяется, чтобы избежать переходных процессов. Результатом является поверхность \ (D (r, x) \), которая описывает динамику. Мы строим эту запись, глядя сверху, так как показано на рисунке (Hoppensteadt and Hyman 1977). Решение всегда укладывается в некую структуру, которая может быть очень сложной.Во-первых, это уникальное стабильное состояние. Около \ (г = 8 \) этого состояния раздваивается в колебание периода 2. Около \ (г = 12 \) период 2 решение распадается на решение периода 4 и т. д. При \ (r = 18 \) набор решений довольно сложен. Это в диапазоне хаотических динамика. Когда функция фертильности \ (m \) пользуется более широкой поддержкой, решение набор еще сложнее.

Список литературы

• Ф. Брауэр и К. Кастильо-Чавес, Математические модели в популяционной биологии и эпидемиологии, Springer-Verlag, Heidelberg, 2000.
• Х. И. Фридман, Детерминированные математические модели в популяционной экологии. Нью-Йорк: Марсель Деккер, 1980.
• J.K. Гэлбрейт, The Predator State, Mother Jones, май / июнь 2006 г.
• Дж. Глейк, Хаос: создание новой науки, Viking Press, Нью-Йорк, 1987.
• К. С. Холлинг, Характеристики простого типа хищничества и паразитизма, Канадский энтомолог 91 (1959), 385-398.
• F.C. Хоппенстедт, Дж.М. Хайман, Периодические решения разностного логистического уравнения, SIAM J.Прил. Математика. 58 (1977) 73-81.
• O. Kermack, A.G. McKendrick, Proc. Рой. Soc. А, 115 (1927) 700-721, 138 (1932) 55-83, 141 (1933) 94-122.
• Н. Кейфиц, В. Флигер, Население: факты и методы демографии, У. Х. Фриман, Сан-Франциско, 1971.
• М. Кот, Элементы математической экологии, Издательство Кембриджского университета, 2001 г.
• А.Дж. Лотка, Элементы физической биологии. Уильямс и Уилкинс, Балтимор, 1925 г.
• Р. М. Мэй, Стабильность и сложность модельных экосистем, Princeton U.Press, NJ, 1974.
• Н.Н. Семенов, Химическая кинетика и цепные реакции, Кларендон, Оксфорд, 1935.
• Х. Смит, П. Уолтман, Математическая теория хемостатов, Cambridge U. Press, 1997.
• V. Volterra, Variazioni e fluttuazioni del numero d’individui in specie animali conviventi. Mem. R. Accad. Наз. дей Линчеи 2 (1926) 31,13

Внутренние ссылки

• Джефф Мохлис, Кресимир Йосич, Эрик Т. Ши-Браун (2006) Периодическая орбита.Академия наук, 1 (7): 1358.
• Филип Холмс и Эрик Т. Ши-Браун (2006) Стабильность. Академия наук, 1 (10): 1838.

Внешние ссылки

См. Также

Динамические системы, Периодическая орбита, Динамика населения, Фазовое пространство, Стабильность

Модель хищник-жертва — Scholarpedia

Рис. 1: Периодическая активность, генерируемая моделью хищник-жертва.

Модели хищник-жертва, возможно, являются строительными блоками био- и экосистем, поскольку биомассы выросли на из их ресурсных масс.Виды соревнуются, развиваются и рассеиваются просто с целью поиска ресурсов для поддержания своей борьбы за само свое существование. В зависимости от конкретных настроек приложений они могут принимать формы: ресурс-потребитель, растение-травоядное, паразит-хозяин, опухолевые клетки (вирус) -иммунная система, восприимчивые-инфекционные взаимодействия и т. Д. взаимодействия и, следовательно, могут иметь приложения за пределами экосистем. При тщательном изучении кажущихся конкурентных взаимодействий часто оказывается, что на самом деле они представляют собой некие скрытые формы взаимодействия хищника и жертвы.

Модель общего хищника-жертвы

Рассмотрим две популяции, размеры которых в контрольный момент времени \ (t \) равны обозначается как \ (x (t) \, \) \ (y (t) \, \) соответственно. Функции \ (x \) и \ (y \) могут обозначать численность населения или концентрацию (число на площадь) или некоторая другая масштабная мера размеров популяций, но быть непрерывными функциями. Изменения численности популяции со временем описывается производными по времени \ (\ dot x \ Equiv dx / dt \) и \ (\ dot y \ Equiv dy / dt \, \) соответственно, и общая модель взаимодействующих популяции записывается в терминах двух автономных дифференциальных уравнений \ [\ точка x = x f (x, y) \] \ [\ точка y = y g (x, y) \] (я.е. время \ (t \) явно не фигурирует в функции \ (x f (x, y) \) и \ (y g (x, y) \)). Функции \ (f \) и \ (g \) обозначают соответствующие темпов роста на душу населения двух видов. Предполагается, что \ (df (x, y) / dy <0 \) и \ (dg (x, y) / dx> 0. \) Эту общую модель часто называют моделью хищник-жертва Колмогорова (Freedman 1980, Brauer and Castillo-Chavez 2000).

Lotka-Volterra Модель

В 1926 году известный итальянский математик Вито Вольтерра предложил дифференциальное уравнение модели для объяснения наблюдаемого увеличения численности хищных рыб (и соответствующих уменьшение добычи рыбы) в Адриатическом море во время Первой мировой войны.В то же время в США уравнения, изученные Вольтеррой, были независимо выведенный Альфредом Лоткой (1925) для описания гипотетической химической реакции, в которой химические концентрации колеблются. Модель Лотки-Вольтерра — это простейшая модель взаимодействия хищник-жертва. Он основан на линейном росте на душу населения ставки, которые записываются как \ [f = b-p y \] и \ (g = r x-d \. \)

• Параметр \ (b \) — это скорость роста вида \ (x \) (жертва) при отсутствии взаимодействия с видами \ (y \) (хищниками).Эти взаимодействия уменьшают количество жертв: темп роста на душу населения уменьшается (здесь линейно) с увеличением \ (y \, \), возможно, становясь отрицательным.
• Параметр \ (p \) измеряет влияние хищничества на \ (\ dot x / x \. \)
• Параметр \ (d \) — скорость гибели (или эмиграции) видов \ (y \) при отсутствии взаимодействия с видами \ (x \. \)
• Термин \ (r x \) обозначает чистую скорость роста (или иммиграции) популяции хищников в зависимости от размера популяции жертвы.

Модель Prey-Predator с линейными темпами роста на душу населения \ [\ точка x = (b — p y) x \] (Добыча) \ [\ dot y = (r x — d) y \] (Хищники) Эта система упоминается как модель Лотка-Вольтерра : она представляет собой одну из самых ранних моделей в математической экологии.

Рисунок 2: Динамика Prey-Predator, описанная кривыми уровня сохраняемого количества. Стрелки указывают скорость и направление решений. В этом моделировании данные равны \ (d = r = b = d = 1 \.\) Есть положения равновесия в \ (x = 1, y = 1 \) и в \ (x = 0, y = 0 \. \)

Система может быть интегрирована напрямую. В частности, любое решение \ ((x (t), y (t)) \) системы удовлетворяет тождеству \ [C = b \ ln y (t) — p y (t) — r x (t) + d \ ln x (t) \] для всех \ (t \, \), где постоянная \ (C = b \ ln y (0) — p y (0) — r x (0) + d \ ln x (0) \) определяется начальными условиями и параметрами системы. (Здесь \ (\ ln x \) обозначает натуральный логарифм \ (x \, \) и т. Д.) количество в правой части тождества выше упоминается как закон сохранения , так как он постоянен вдоль любого решение.Сохранение количества облегчает визуализацию решения. На рисунке нанесены горизонтальные контуры поверхность \ [z = b \ ln y — p y — r x + d \ ln x \] в первом квадранте плоскости \ (xy \). Контуры описывают решения системы определяются их начальными данными, и, поскольку они представляют собой замкнутые кривые, решения представляют собой периодические колебания.

Если \ (b> 0 \, \) есть два состояния равновесия, \ (x = 0, y = 0 \) (вымирание) и \ (x = d / r, y = b / p \) (сосуществование), а поверхность \ [z = b \ ln y — p y — r x + d \ ln x \] имеет единственный пик в последнем равновесии.В контурные линии на рисунке описывают классический циклы «жертва-хищник», наблюдаемые в экологических системах.

Приведенная выше модель была получена независимо в следующих областях:

• эпидемии (Кермак и МакКендрик 1927, 1932, 1933) (\ (b = 0 \))
  • \ (x \) — восприимчивые люди и
  • \ (y \) — инфекционные особи,
• экология (Лотка 1925, Вольтерра 1926)
  • \ (x \) являются добычей и
  • \ (y \) хищники,
• теория горения (Семенов 1935)
  • \ (x \) и \ (y \) — химические радикалы, образующиеся при горении H ₂ O ₂ ,
• экономика (Гэлбрейт, 2006)
  • \ (x \) — население и
  • \ (у \) — хищническое учреждение,

и множество других исследований из разных дисциплин.

Альфред Джеймс Лотка (1880-1949, США, химик, демограф, эколог и математик) родился во Львове (Лемберг), в то время находившемся в Австрии, ныне в Украине. Он приехал в Соединенные Штаты в 1902 году и написал ряд теоретических статей о химических колебаниях в первые десятилетия двадцатого века, а также написал книгу по теоретической биологии (1925). Затем он оставил (академическую) науку и провел большую часть своей трудовой жизни в страховой компании (Metropolitan Life).В этом качестве он стал президентом PAA (Ассоциации народонаселения Америки).

Вито Вольтерра (3 мая 1860 — 11 октября 1940, итальянец, математик и физик, наиболее известный своим вкладом в математическую биологию) родился в Анконе в очень бедной семье. Вольтерра рано проявил себя в математике еще до поступления в Пизанский университет. Его работа кратко изложена в его книге «Теория функционалов, интегральных и интегродифференциальных уравнений» (1930).После Первой мировой войны Вольтерра обратил свое внимание на применение своих математических идей в биологии, в основном повторяя и развивая работы Пьера Франсуа Ферхюльста. Самый известный результат этого периода — модель Лотки-Вольтерры. В 1922 году он присоединился к оппозиции фашистскому режиму Бенито Муссолини, а в 1931 году отказался принять обязательную присягу на верность. Он был вынужден оставить свой университетский пост и членство в академиях наук, и в последующие годы он жил в основном за границей, вернувшись в Рим незадолго до своей смерти.

Модель Kermack-McKendrick

При хищничестве и эпидемиях существует коллективный иммунитет. это удобно сформулировать это с точки зрения эпидемиологии, где теперь мы говорим для жертвы как восприимчивые, а для хищников как инфекционные. Динамика заражения отображена графиком \ (x \ to y \ to \, \), что указывает на то, что восприимчивые люди могут стать заразными и что инфекционные заболевания могут быть удалены из процесса (например, через смерть, карантин, или прививка). Рассмотрим короткий промежуток времени. по сравнению с воспроизводством восприимчивой популяции, т.е.э., пусть \ (b = 0 \. \) Если начальная восприимчивая популяция настолько велика, что \ (x (0)> d / r \, \) то из второго уравнения модели хищник-жертва мы видим, что первоначально \ (\ dot y> 0 \, \), что указывает на то, что инфекция изначально будет больше чем заменить себя, передав инфекцию. Однако если это условие не выполняется, инфекционная популяция будет снижаться. Критическое значение \ (R \ Equiv rx (0) / d = 1 \) называется быть эпидемическим порогом или переломным моментом в этом процессе.

Рисунок 3: Модель распространения инфекционного заболевания Кермака-Маккендрика. Переломный момент находится в \ (x = 1.0 \. \). Если \ (x (0) \) выше этого значения, разовьется эпидемия. Степень серьезности можно оценить, проследив кривую, исходящую от \ (x (0) \), пока она не сходится к горизонтальной оси. Это указывает на размер восприимчивой популяции, которая избегает инфекции. Обратите внимание, что горизонтальная ось, как показано здесь, начинается с x = 0,1, чтобы избежать логарифмической сингулярности. * \, \), как показано на рисунке.Удивительно, но это число всегда больше нуля, что показывает, что некоторые восприимчивые всегда выживут!

Это явление, о котором говорится to as на практике соблюдается коллективный иммунитет ; на самом деле номер \ (R \) регулярно публикуется для различных болезней и регионов. в качестве меры борьбы с эпидемией. Это отражает тот факт, что восприимчивое население может быть уменьшено до уровня, ниже которого инфекционные заболевания не увеличиваются. Модель в этом случае называется как модель Кермака-МакКендрика восприимчиво-инфекционных взаимодействий в эпидемиологии.

Jacob-Monod Модель

Другой подход к моделированию взаимодействия между добычей и хищники были разработаны для учета организмов (таких как бактерии), поглощающие питательные вещества. Существует ограниченная скорость приема, которая такие организмы способны, и следующая модель учитывает ограниченная скорость приема. Предположим теперь, что \ (x \) обозначает размер популяции кормушек и что они питаются химическими веществами. вид концентрации \ (y \. \) Обычно они используются для обозначения концентрации питательных веществ и питательных веществ в растворе, а не «подсчет головы».Модель Jacob-Monod — это \ [\ dot x = \ frac {V y} {K + y} x \] \ [\ dot y = — \ frac 1Y \ frac {V y} {K + y} x \] где

• \ (V \) — скорость поглощения,
• \ (K \) — постоянная насыщения, а
• \ (Y \) — это доходность \ (x \) на единицу \ (y \) занятого.

Обратите внимание, что когда \ (y = K \, \) скорость поглощения составляет \ (V / 2 \, \) половину максимальной; на практике \ (y = K \) считается переломным моментом: Если \ (y

Величина \ (C = x + Y y \) сохраняется (так как производная с по времени правой части равна нулю) где \ (С = х (0) + Уу (0) \.\) Подставляя это в первое уравнение, получаем \ [\ dot x = \ frac {V (C-x)} {Y K + (C-x)} x \. \] Решения можно найти с помощью квадратур, и они показывают, что если \ (x (0)> 0 \, \), затем \ (x (t) \ to C \) как \ (t \ to \ infty \, \), в этот момент питательное вещество было истощено.

Типичное использование этой модели — описание непрерывного роста потока устройство, такое как хемостат, где происходит непрерывное удаление питательных веществ и кормушек и постоянный приток свежих питательных веществ. Модель Якоба-Монода используется для описания такого устройства для роста бактерий, например, для определения условий существования устойчивого динамического равновесия путем уравновешивания роста за счет поглощения питательного вещества с вымыванием из кормушек.

В некоторых моделях хищник-жертва используются термины, аналогичные тем, которые используются в модели Якоба-Монода, для описания скорости, с которой хищники поедают добычу. В более общем смысле, любые данные в модели Лотки-Вольтерры можно считать зависящими от плотности добычи в зависимости от изучаемой системы. Это называется функциональной реакцией, идея, которую представил и обсудил К. С. Холлинг (1959). В популяционных моделях использовалось несколько различных форм функциональной реакции, но форма Якоба-Моно, также называемая экологами формой Холлинга 2, является одной из наиболее распространенных.g-1 \ ​​right) \) с \ (0

Логистическое уравнение

Интересный футляр для \ [\ dot x = \ frac {V (C-x)} {Y K + (C-x)} x \] это когда \ (V \) и \ (YK \) очень велики по сравнению с другими данными в модели, но с их соотношение среднего размера, скажем \ (V / (YK) \ приблизительно r \.\) Тогда мы можно игнорировать второй член в знаменателе и получить \ [\ точка x = r (C-x) x \. \] Это называется логистическим уравнением . Это тоже возникло в различных дисциплин, но одно из первых его появление было связано с Ферхюльстом в середине 19 века, который использовал его для исправления некоторых отклонения модели Мальтуса (\ (\ dot x = r x \)) от некоторых человеческих данные о населении. Число \ (C \) теперь упоминается как грузоподъемность для населения; это соответствует в модели Якоба-Моно не осталось питательных веществ.

Логистическое уравнение может быть решено в замкнутая форма по квадратурам. Это показывает, что \ (x (t) \ to C \) при \ (t \ to \ infty \, \), если \ (x (0)> 0 \. \)

Хищничество с задержками: хаос в уравнении воспроизведения Риккера

Задержки во времени возникают в биологических системах, и они могут производить сложная динамика. Для моделирования возрастной структуры (и других временных задержек) в системе мы воспользуемся подходом, который был введен Эйлером в 18 век. Пусть \ (x (t) \) обозначает число, рожденное в момент \ (т \.\) Тогда \ (x (t-a) \) обозначает число, которое родилось \ (a \) единицы назад. Предположим, что существует такой нелинейный эффект, что количество новорожденные \ (a \) единицы назад, которые могут участвовать в воспроизводстве на время \ (t \) есть \ (h (x (t-a)) \), где функция \ (h \) называется функция воспроизведения . Эта нелинейность может быть связана с хищниками или факторами окружающей среды, как обсуждалось ранее. Предположим, что у людей возраста \ (a \) есть фертильность \ (m (a) \. \) Тогда уравнение ниже показывает, сколько родится в момент \ (t \.t m (a) h (x (t-a)) \, da \, \] где \ (x_0 (t) \) обозначает затяжной вклад в более поздние роды исходной популяции. В случае, когда \ (h (x) = x \) — линейная функция, это уравнение называется Уравнение обновления , которое широко используется в демографии. Его Решение может быть найдено с помощью преобразований Лапласа (Keyfitz, Flieger, 1971). Однако, если \ (h \) — нелинейная функция, то этот метод решение недоступно.

Функция фертильности \ (m (a) \) описывает фертильность возраст \ (а \.n x_0 \. \) Однако, если \ (h \) имеет вид в случае Ферхюльста, где \ (h (x) = x (C — x) _ + \ Equiv \ max (C-x, 0), \) рекурсия становится \ [x_ {n + 1} = r x_n (C-x_n) _ + \, \] чьи итерации могут демонстрировать довольно дикое поведение. Это было первое заметил эколог У. Рикер в 1950-х годах, который использовал функция \ (h (x) = x \ exp {(- x)} \) в исследованиях динамики рыболовства, хотя в то время его работы в значительной степени игнорировались. Это воспроизведение функция учитывает каннибализм (самохищение) в том случае, если численность населения мала, модель похожа на модель Мальтуса, но для больших популяций размножение сильно подавлено. {- x_n} \.\] Начиная с \ (x_1 = 1 \, \) определяем последовательность \ (\ {x_ {50}, x_ {51}, x_ {52}, x_ {53}, \ dots, x_ {300} \} \) и записать в массив, скажем \ (D (r, x) \, \) количество элементов последовательности, которые находятся в каждая корзина. Мы начинаем отсчет только после 50 начальных повторяется, чтобы избежать переходных процессов. Результатом является поверхность \ (D (r, x) \), которая описывает динамику. Мы строим эту запись, глядя сверху, так как показано на рисунке (Hoppensteadt and Hyman 1977). Решение всегда укладывается в некую структуру, которая может быть очень сложной.Во-первых, это уникальное стабильное состояние. Около \ (г = 8 \) этого состояния раздваивается в колебание периода 2. Около \ (г = 12 \) период 2 решение распадается на решение периода 4 и т. д. При \ (r = 18 \) набор решений довольно сложен. Это в диапазоне хаотических динамика. Когда функция фертильности \ (m \) пользуется более широкой поддержкой, решение набор еще сложнее.

Список литературы

• Ф. Брауэр и К. Кастильо-Чавес, Математические модели в популяционной биологии и эпидемиологии, Springer-Verlag, Heidelberg, 2000.
• Х. И. Фридман, Детерминированные математические модели в популяционной экологии. Нью-Йорк: Марсель Деккер, 1980.
• J.K. Гэлбрейт, The Predator State, Mother Jones, май / июнь 2006 г.
• Дж. Глейк, Хаос: создание новой науки, Viking Press, Нью-Йорк, 1987.
• К. С. Холлинг, Характеристики простого типа хищничества и паразитизма, Канадский энтомолог 91 (1959), 385-398.
• F.C. Хоппенстедт, Дж.М. Хайман, Периодические решения разностного логистического уравнения, SIAM J.Прил. Математика. 58 (1977) 73-81.
• O. Kermack, A.G. McKendrick, Proc. Рой. Soc. А, 115 (1927) 700-721, 138 (1932) 55-83, 141 (1933) 94-122.
• Н. Кейфиц, В. Флигер, Население: факты и методы демографии, У. Х. Фриман, Сан-Франциско, 1971.
• М. Кот, Элементы математической экологии, Издательство Кембриджского университета, 2001 г.
• А.Дж. Лотка, Элементы физической биологии. Уильямс и Уилкинс, Балтимор, 1925 г.
• Р. М. Мэй, Стабильность и сложность модельных экосистем, Princeton U.Press, NJ, 1974.
• Н.Н. Семенов, Химическая кинетика и цепные реакции, Кларендон, Оксфорд, 1935.
• Х. Смит, П. Уолтман, Математическая теория хемостатов, Cambridge U. Press, 1997.
• V. Volterra, Variazioni e fluttuazioni del numero d’individui in specie animali conviventi. Mem. R. Accad. Наз. дей Линчеи 2 (1926) 31,13

Внутренние ссылки

• Джефф Мохлис, Кресимир Йосич, Эрик Т. Ши-Браун (2006) Периодическая орбита.Академия наук, 1 (7): 1358.
• Филип Холмс и Эрик Т. Ши-Браун (2006) Стабильность. Академия наук, 1 (10): 1838.

Внешние ссылки

См. Также

Динамические системы, Периодическая орбита, Динамика населения, Фазовое пространство, Стабильность

Модель хищник-жертва — Scholarpedia

Рис. 1: Периодическая активность, генерируемая моделью хищник-жертва.

Модели хищник-жертва, возможно, являются строительными блоками био- и экосистем, поскольку биомассы выросли на из их ресурсных масс.Виды соревнуются, развиваются и рассеиваются просто с целью поиска ресурсов для поддержания своей борьбы за само свое существование. В зависимости от конкретных настроек приложений они могут принимать формы: ресурс-потребитель, растение-травоядное, паразит-хозяин, опухолевые клетки (вирус) -иммунная система, восприимчивые-инфекционные взаимодействия и т. Д. взаимодействия и, следовательно, могут иметь приложения за пределами экосистем. При тщательном изучении кажущихся конкурентных взаимодействий часто оказывается, что на самом деле они представляют собой некие скрытые формы взаимодействия хищника и жертвы.

Модель общего хищника-жертвы

Рассмотрим две популяции, размеры которых в контрольный момент времени \ (t \) равны обозначается как \ (x (t) \, \) \ (y (t) \, \) соответственно. Функции \ (x \) и \ (y \) могут обозначать численность населения или концентрацию (число на площадь) или некоторая другая масштабная мера размеров популяций, но быть непрерывными функциями. Изменения численности популяции со временем описывается производными по времени \ (\ dot x \ Equiv dx / dt \) и \ (\ dot y \ Equiv dy / dt \, \) соответственно, и общая модель взаимодействующих популяции записывается в терминах двух автономных дифференциальных уравнений \ [\ точка x = x f (x, y) \] \ [\ точка y = y g (x, y) \] (я.е. время \ (t \) явно не фигурирует в функции \ (x f (x, y) \) и \ (y g (x, y) \)). Функции \ (f \) и \ (g \) обозначают соответствующие темпов роста на душу населения двух видов. Предполагается, что \ (df (x, y) / dy <0 \) и \ (dg (x, y) / dx> 0. \) Эту общую модель часто называют моделью хищник-жертва Колмогорова (Freedman 1980, Brauer and Castillo-Chavez 2000).

Lotka-Volterra Модель

В 1926 году известный итальянский математик Вито Вольтерра предложил дифференциальное уравнение модели для объяснения наблюдаемого увеличения численности хищных рыб (и соответствующих уменьшение добычи рыбы) в Адриатическом море во время Первой мировой войны.В то же время в США уравнения, изученные Вольтеррой, были независимо выведенный Альфредом Лоткой (1925) для описания гипотетической химической реакции, в которой химические концентрации колеблются. Модель Лотки-Вольтерра — это простейшая модель взаимодействия хищник-жертва. Он основан на линейном росте на душу населения ставки, которые записываются как \ [f = b-p y \] и \ (g = r x-d \. \)

• Параметр \ (b \) — это скорость роста вида \ (x \) (жертва) при отсутствии взаимодействия с видами \ (y \) (хищниками).Эти взаимодействия уменьшают количество жертв: темп роста на душу населения уменьшается (здесь линейно) с увеличением \ (y \, \), возможно, становясь отрицательным.
• Параметр \ (p \) измеряет влияние хищничества на \ (\ dot x / x \. \)
• Параметр \ (d \) — скорость гибели (или эмиграции) видов \ (y \) при отсутствии взаимодействия с видами \ (x \. \)
• Термин \ (r x \) обозначает чистую скорость роста (или иммиграции) популяции хищников в зависимости от размера популяции жертвы.

Модель Prey-Predator с линейными темпами роста на душу населения \ [\ точка x = (b — p y) x \] (Добыча) \ [\ dot y = (r x — d) y \] (Хищники) Эта система упоминается как модель Лотка-Вольтерра : она представляет собой одну из самых ранних моделей в математической экологии.

Рисунок 2: Динамика Prey-Predator, описанная кривыми уровня сохраняемого количества. Стрелки указывают скорость и направление решений. В этом моделировании данные равны \ (d = r = b = d = 1 \.\) Есть положения равновесия в \ (x = 1, y = 1 \) и в \ (x = 0, y = 0 \. \)

Система может быть интегрирована напрямую. В частности, любое решение \ ((x (t), y (t)) \) системы удовлетворяет тождеству \ [C = b \ ln y (t) — p y (t) — r x (t) + d \ ln x (t) \] для всех \ (t \, \), где постоянная \ (C = b \ ln y (0) — p y (0) — r x (0) + d \ ln x (0) \) определяется начальными условиями и параметрами системы. (Здесь \ (\ ln x \) обозначает натуральный логарифм \ (x \, \) и т. Д.) количество в правой части тождества выше упоминается как закон сохранения , так как он постоянен вдоль любого решение.Сохранение количества облегчает визуализацию решения. На рисунке нанесены горизонтальные контуры поверхность \ [z = b \ ln y — p y — r x + d \ ln x \] в первом квадранте плоскости \ (xy \). Контуры описывают решения системы определяются их начальными данными, и, поскольку они представляют собой замкнутые кривые, решения представляют собой периодические колебания.

Если \ (b> 0 \, \) есть два состояния равновесия, \ (x = 0, y = 0 \) (вымирание) и \ (x = d / r, y = b / p \) (сосуществование), а поверхность \ [z = b \ ln y — p y — r x + d \ ln x \] имеет единственный пик в последнем равновесии.В контурные линии на рисунке описывают классический циклы «жертва-хищник», наблюдаемые в экологических системах.

Приведенная выше модель была получена независимо в следующих областях:

• эпидемии (Кермак и МакКендрик 1927, 1932, 1933) (\ (b = 0 \))
  • \ (x \) — восприимчивые люди и
  • \ (y \) — инфекционные особи,
• экология (Лотка 1925, Вольтерра 1926)
  • \ (x \) являются добычей и
  • \ (y \) хищники,
• теория горения (Семенов 1935)
  • \ (x \) и \ (y \) — химические радикалы, образующиеся при горении H ₂ O ₂ ,
• экономика (Гэлбрейт, 2006)
  • \ (x \) — население и
  • \ (у \) — хищническое учреждение,

и множество других исследований из разных дисциплин.

Альфред Джеймс Лотка (1880-1949, США, химик, демограф, эколог и математик) родился во Львове (Лемберг), в то время находившемся в Австрии, ныне в Украине. Он приехал в Соединенные Штаты в 1902 году и написал ряд теоретических статей о химических колебаниях в первые десятилетия двадцатого века, а также написал книгу по теоретической биологии (1925). Затем он оставил (академическую) науку и провел большую часть своей трудовой жизни в страховой компании (Metropolitan Life).В этом качестве он стал президентом PAA (Ассоциации народонаселения Америки).

Вито Вольтерра (3 мая 1860 — 11 октября 1940, итальянец, математик и физик, наиболее известный своим вкладом в математическую биологию) родился в Анконе в очень бедной семье. Вольтерра рано проявил себя в математике еще до поступления в Пизанский университет. Его работа кратко изложена в его книге «Теория функционалов, интегральных и интегродифференциальных уравнений» (1930).После Первой мировой войны Вольтерра обратил свое внимание на применение своих математических идей в биологии, в основном повторяя и развивая работы Пьера Франсуа Ферхюльста. Самый известный результат этого периода — модель Лотки-Вольтерры. В 1922 году он присоединился к оппозиции фашистскому режиму Бенито Муссолини, а в 1931 году отказался принять обязательную присягу на верность. Он был вынужден оставить свой университетский пост и членство в академиях наук, и в последующие годы он жил в основном за границей, вернувшись в Рим незадолго до своей смерти.

Модель Kermack-McKendrick

При хищничестве и эпидемиях существует коллективный иммунитет. это удобно сформулировать это с точки зрения эпидемиологии, где теперь мы говорим для жертвы как восприимчивые, а для хищников как инфекционные. Динамика заражения отображена графиком \ (x \ to y \ to \, \), что указывает на то, что восприимчивые люди могут стать заразными и что инфекционные заболевания могут быть удалены из процесса (например, через смерть, карантин, или прививка). Рассмотрим короткий промежуток времени. по сравнению с воспроизводством восприимчивой популяции, т.е.э., пусть \ (b = 0 \. \) Если начальная восприимчивая популяция настолько велика, что \ (x (0)> d / r \, \) то из второго уравнения модели хищник-жертва мы видим, что первоначально \ (\ dot y> 0 \, \), что указывает на то, что инфекция изначально будет больше чем заменить себя, передав инфекцию. Однако если это условие не выполняется, инфекционная популяция будет снижаться. Критическое значение \ (R \ Equiv rx (0) / d = 1 \) называется быть эпидемическим порогом или переломным моментом в этом процессе.

Рисунок 3: Модель распространения инфекционного заболевания Кермака-Маккендрика. Переломный момент находится в \ (x = 1.0 \. \). Если \ (x (0) \) выше этого значения, разовьется эпидемия. Степень серьезности можно оценить, проследив кривую, исходящую от \ (x (0) \), пока она не сходится к горизонтальной оси. Это указывает на размер восприимчивой популяции, которая избегает инфекции. Обратите внимание, что горизонтальная ось, как показано здесь, начинается с x = 0,1, чтобы избежать логарифмической сингулярности. * \, \), как показано на рисунке.Удивительно, но это число всегда больше нуля, что показывает, что некоторые восприимчивые всегда выживут!

Это явление, о котором говорится to as на практике соблюдается коллективный иммунитет ; на самом деле номер \ (R \) регулярно публикуется для различных болезней и регионов. в качестве меры борьбы с эпидемией. Это отражает тот факт, что восприимчивое население может быть уменьшено до уровня, ниже которого инфекционные заболевания не увеличиваются. Модель в этом случае называется как модель Кермака-МакКендрика восприимчиво-инфекционных взаимодействий в эпидемиологии.

Jacob-Monod Модель

Другой подход к моделированию взаимодействия между добычей и хищники были разработаны для учета организмов (таких как бактерии), поглощающие питательные вещества. Существует ограниченная скорость приема, которая такие организмы способны, и следующая модель учитывает ограниченная скорость приема. Предположим теперь, что \ (x \) обозначает размер популяции кормушек и что они питаются химическими веществами. вид концентрации \ (y \. \) Обычно они используются для обозначения концентрации питательных веществ и питательных веществ в растворе, а не «подсчет головы».Модель Jacob-Monod — это \ [\ dot x = \ frac {V y} {K + y} x \] \ [\ dot y = — \ frac 1Y \ frac {V y} {K + y} x \] где

• \ (V \) — скорость поглощения,
• \ (K \) — постоянная насыщения, а
• \ (Y \) — это доходность \ (x \) на единицу \ (y \) занятого.

Обратите внимание, что когда \ (y = K \, \) скорость поглощения составляет \ (V / 2 \, \) половину максимальной; на практике \ (y = K \) считается переломным моментом: Если \ (y

Величина \ (C = x + Y y \) сохраняется (так как производная с по времени правой части равна нулю) где \ (С = х (0) + Уу (0) \.\) Подставляя это в первое уравнение, получаем \ [\ dot x = \ frac {V (C-x)} {Y K + (C-x)} x \. \] Решения можно найти с помощью квадратур, и они показывают, что если \ (x (0)> 0 \, \), затем \ (x (t) \ to C \) как \ (t \ to \ infty \, \), в этот момент питательное вещество было истощено.

Типичное использование этой модели — описание непрерывного роста потока устройство, такое как хемостат, где происходит непрерывное удаление питательных веществ и кормушек и постоянный приток свежих питательных веществ. Модель Якоба-Монода используется для описания такого устройства для роста бактерий, например, для определения условий существования устойчивого динамического равновесия путем уравновешивания роста за счет поглощения питательного вещества с вымыванием из кормушек.

В некоторых моделях хищник-жертва используются термины, аналогичные тем, которые используются в модели Якоба-Монода, для описания скорости, с которой хищники поедают добычу. В более общем смысле, любые данные в модели Лотки-Вольтерры можно считать зависящими от плотности добычи в зависимости от изучаемой системы. Это называется функциональной реакцией, идея, которую представил и обсудил К. С. Холлинг (1959). В популяционных моделях использовалось несколько различных форм функциональной реакции, но форма Якоба-Моно, также называемая экологами формой Холлинга 2, является одной из наиболее распространенных.g-1 \ ​​right) \) с \ (0

Логистическое уравнение

Интересный футляр для \ [\ dot x = \ frac {V (C-x)} {Y K + (C-x)} x \] это когда \ (V \) и \ (YK \) очень велики по сравнению с другими данными в модели, но с их соотношение среднего размера, скажем \ (V / (YK) \ приблизительно r \.\) Тогда мы можно игнорировать второй член в знаменателе и получить \ [\ точка x = r (C-x) x \. \] Это называется логистическим уравнением . Это тоже возникло в различных дисциплин, но одно из первых его появление было связано с Ферхюльстом в середине 19 века, который использовал его для исправления некоторых отклонения модели Мальтуса (\ (\ dot x = r x \)) от некоторых человеческих данные о населении. Число \ (C \) теперь упоминается как грузоподъемность для населения; это соответствует в модели Якоба-Моно не осталось питательных веществ.

Логистическое уравнение может быть решено в замкнутая форма по квадратурам. Это показывает, что \ (x (t) \ to C \) при \ (t \ to \ infty \, \), если \ (x (0)> 0 \. \)

Хищничество с задержками: хаос в уравнении воспроизведения Риккера

Задержки во времени возникают в биологических системах, и они могут производить сложная динамика. Для моделирования возрастной структуры (и других временных задержек) в системе мы воспользуемся подходом, который был введен Эйлером в 18 век. Пусть \ (x (t) \) обозначает число, рожденное в момент \ (т \.\) Тогда \ (x (t-a) \) обозначает число, которое родилось \ (a \) единицы назад. Предположим, что существует такой нелинейный эффект, что количество новорожденные \ (a \) единицы назад, которые могут участвовать в воспроизводстве на время \ (t \) есть \ (h (x (t-a)) \), где функция \ (h \) называется функция воспроизведения . Эта нелинейность может быть связана с хищниками или факторами окружающей среды, как обсуждалось ранее. Предположим, что у людей возраста \ (a \) есть фертильность \ (m (a) \. \) Тогда уравнение ниже показывает, сколько родится в момент \ (t \.t m (a) h (x (t-a)) \, da \, \] где \ (x_0 (t) \) обозначает затяжной вклад в более поздние роды исходной популяции. В случае, когда \ (h (x) = x \) — линейная функция, это уравнение называется Уравнение обновления , которое широко используется в демографии. Его Решение может быть найдено с помощью преобразований Лапласа (Keyfitz, Flieger, 1971). Однако, если \ (h \) — нелинейная функция, то этот метод решение недоступно.

Функция фертильности \ (m (a) \) описывает фертильность возраст \ (а \.n x_0 \. \) Однако, если \ (h \) имеет вид в случае Ферхюльста, где \ (h (x) = x (C — x) _ + \ Equiv \ max (C-x, 0), \) рекурсия становится \ [x_ {n + 1} = r x_n (C-x_n) _ + \, \] чьи итерации могут демонстрировать довольно дикое поведение. Это было первое заметил эколог У. Рикер в 1950-х годах, который использовал функция \ (h (x) = x \ exp {(- x)} \) в исследованиях динамики рыболовства, хотя в то время его работы в значительной степени игнорировались. Это воспроизведение функция учитывает каннибализм (самохищение) в том случае, если численность населения мала, модель похожа на модель Мальтуса, но для больших популяций размножение сильно подавлено. {- x_n} \.\] Начиная с \ (x_1 = 1 \, \) определяем последовательность \ (\ {x_ {50}, x_ {51}, x_ {52}, x_ {53}, \ dots, x_ {300} \} \) и записать в массив, скажем \ (D (r, x) \, \) количество элементов последовательности, которые находятся в каждая корзина. Мы начинаем отсчет только после 50 начальных повторяется, чтобы избежать переходных процессов. Результатом является поверхность \ (D (r, x) \), которая описывает динамику. Мы строим эту запись, глядя сверху, так как показано на рисунке (Hoppensteadt and Hyman 1977). Решение всегда укладывается в некую структуру, которая может быть очень сложной.Во-первых, это уникальное стабильное состояние. Около \ (г = 8 \) этого состояния раздваивается в колебание периода 2. Около \ (г = 12 \) период 2 решение распадается на решение периода 4 и т. д. При \ (r = 18 \) набор решений довольно сложен. Это в диапазоне хаотических динамика. Когда функция фертильности \ (m \) пользуется более широкой поддержкой, решение набор еще сложнее.

Список литературы

• Ф. Брауэр и К. Кастильо-Чавес, Математические модели в популяционной биологии и эпидемиологии, Springer-Verlag, Heidelberg, 2000.
• Х. И. Фридман, Детерминированные математические модели в популяционной экологии. Нью-Йорк: Марсель Деккер, 1980.
• J.K. Гэлбрейт, The Predator State, Mother Jones, май / июнь 2006 г.
• Дж. Глейк, Хаос: создание новой науки, Viking Press, Нью-Йорк, 1987.
• К. С. Холлинг, Характеристики простого типа хищничества и паразитизма, Канадский энтомолог 91 (1959), 385-398.
• F.C. Хоппенстедт, Дж.М. Хайман, Периодические решения разностного логистического уравнения, SIAM J.Прил. Математика. 58 (1977) 73-81.
• O. Kermack, A.G. McKendrick, Proc. Рой. Soc. А, 115 (1927) 700-721, 138 (1932) 55-83, 141 (1933) 94-122.
• Н. Кейфиц, В. Флигер, Население: факты и методы демографии, У. Х. Фриман, Сан-Франциско, 1971.
• М. Кот, Элементы математической экологии, Издательство Кембриджского университета, 2001 г.
• А.Дж. Лотка, Элементы физической биологии. Уильямс и Уилкинс, Балтимор, 1925 г.
• Р. М. Мэй, Стабильность и сложность модельных экосистем, Princeton U.Press, NJ, 1974.
• Н.Н. Семенов, Химическая кинетика и цепные реакции, Кларендон, Оксфорд, 1935.
• Х. Смит, П. Уолтман, Математическая теория хемостатов, Cambridge U. Press, 1997.
• V. Volterra, Variazioni e fluttuazioni del numero d’individui in specie animali conviventi. Mem. R. Accad. Наз. дей Линчеи 2 (1926) 31,13

Внутренние ссылки

• Джефф Мохлис, Кресимир Йосич, Эрик Т. Ши-Браун (2006) Периодическая орбита.Академия наук, 1 (7): 1358.
• Филип Холмс и Эрик Т. Ши-Браун (2006) Стабильность. Академия наук, 1 (10): 1838.

Внешние ссылки

См. Также

Динамические системы, Периодическая орбита, Динамика населения, Фазовое пространство, Стабильность

В системе хищник-жертва с задержкой пищеварения и стратегией борьбы с хищниками

Абрамс П.А., Гинзбург Л.Р .: Природа хищничества: зависит от жертвы, зависит от соотношения или нет? Trends Ecol.Evol. 15 , 337–341 (2000)

Артикул Google Scholar

Ардити, Р., Гинзбург, Л.Р .: Взаимодействие в динамике хищник-жертва: зависимость отношения. J. Theor. Биол. 139 , 311–326 (1989)

Артикул Google Scholar

Кастильо-Чавес, К., Тим, Х.Р .: Асимптотически автономные модели эпидемий. В: Arino, O., et al. (ред.) Математическая динамика населения: анализ неоднородности, I.Теория эпидемий, стр. 33–50. Вюрц, Виннипег (1995)

Google Scholar

Крил, С., Кристиансон, Д .: Взаимосвязь между прямым хищничеством и эффектами риска. Trends Ecol. Evol. 23 , 194–201 (2008)

Артикул Google Scholar

Cresswell, W .: Хищничество в популяциях птиц. J. Ornithol. 152 , 251–263 (2011)

Статья Google Scholar

Кушинг, Дж.М .: Интегро-дифференциальные уравнения и модели с запаздыванием в динамике населения. Конспект лекций по биоматематике, т. 20. Springer, Berlin (1977)

Книга Google Scholar

Дас А., Саманта Г.П .: Моделирование эффекта страха на стохастическую систему «жертва – хищник» с дополнительной пищей для хищника. J. Phys. Математика. Теор. 51 , 465601 (2018)

MathSciNet Статья Google Scholar

Хейл, Дж.К., Люнель С.М.В .: Введение в функционально-дифференциальные уравнения. Спрингер, Нью-Йорк (1993)

Книга Google Scholar

Хейс, Н.Д .: Корни трансцендентных уравнений, связанных с определенным дифференциально-разностным уравнением. J. Lond. Математика. Soc. 25 , 226–232 (1950)

Артикул Google Scholar

Холлинг, К.С.: Функциональный ответ хищника на плотность добычи и его роль в мимикрии и регулировании популяции.Mem. Энтомол. Soc. Может. 45 , 1–60 (1965)

Google Scholar

Йешке, Дж. М., Копп, М., Толлриан, Р .: Функции хищника: различение между обработкой и перевариванием добычи. Ecol. Monogr. 72 (1), 95–112 (2002)

Статья Google Scholar

Ли, Ф., Ли, Х .: Бифуркация Хопфа модели хищник-жертва с временной задержкой и стадийной структурой жертвы.Математика. Comput. Модель. 55 , 672–679 (2012)

MathSciNet Статья Google Scholar

Лима, С.Л .: Несмертельные эффекты в экологии взаимодействий хищник – жертва. Bioscience 48 , 25–34 (1998)

Статья Google Scholar

Лима, С.Л .: Хищники и гнездящиеся птицы: поведенческая и репродуктивная гибкость в условиях риска нападения хищников.Биол. Ред. 84 , 85–513 (2009)

Статья Google Scholar

Лотка А.Дж .: Аналитическая записка об определенных ритмических отношениях в органических системах. Proc. Natl. Акад. Sci. США 6 , 410–415 (1920)

Статья Google Scholar

Лотка А.Дж .: Элементы физической биологии. Уильямс и Уилкинс, Филадельфия (1925)

MATH Google Scholar

Мондаль, С., Маити, А., Саманта, Г.П .: Эффекты страха и дополнительной пищи в модели отложенного хищника-жертвы. Биофиз. Rev. Lett. 13 , 157–177 (2018)

Статья Google Scholar

Розенцвейг, М.Л., Макартур, Р.Х .: Графическое представление и условия устойчивости взаимодействий хищник-жертва. Являюсь. Nat. 97 , 209–223 (1963)

Артикул Google Scholar

Скальски, Г.Т., Гиллиам, Дж. Ф .: Функциональные реакции на вмешательство хищников: жизнеспособные альтернативы модели Холлинга типа II. Экология 82 , 3083–3092 (2001)

Статья Google Scholar

Смит, Х .: Монотонные динамические системы: Введение в теорию конкурентных и кооперативных систем. Математические обзоры и монографии, т. 41. Американское математическое общество, Провиденс (1995)

MATH. Google Scholar

Смит, Х.: Введение в дифференциальные уравнения с запаздыванием в приложениях к наукам о жизни. Спрингер, Нью-Йорк (2010)

Google Scholar

Volterra, V .: Variazioni e fluttuazioni del numero d’individui in specie animali conviventi. Mem. Акад. Линчеи Рома 2 , 31–113 (1926)

MATH Google Scholar

Вольтерра, В .: Вариации и колебания количества особей у видов животных, живущих вместе.В: Chapman, R.N. (ред.) Экология животных. Макгроу-Хилл, Нью-Йорк (1931)

Google Scholar

Ван, X., Zou, X .: Моделирование эффекта страха во взаимодействиях хищник-жертва с адаптивным избеганием хищников. Бык. Математика. Биол. 79 , 1325–1359 (2017)

MathSciNet Статья Google Scholar

Ван, X., Zou, X .: Формирование паттерна модели хищник-жертва со стоимостью поведения антихищника.Математика. Biosci. Англ. 15 , 775–805 (2018)

MathSciNet Статья Google Scholar

Ван, X., Zanette, L.Y., Zou, X .: Моделирование эффекта страха при взаимодействии хищника и жертвы. J. Math. Биол. 73 , 1179–1204 (2016)

MathSciNet Статья Google Scholar

Вангерски П.Дж., Каннингем У.Дж .: Временной лаг в моделях популяций жертва – хищник.Экология 38 , 136–139 (1957)

Статья Google Scholar

Сюй, Р .: Глобальная динамика модели хищник-жертва с временной задержкой и стадийной структурой жертвы. Нелинейный анал. RWA 12 , 2151–2162 (2011)

MathSciNet Статья Google Scholar

Занетт, Л.Ю., Уайт, А.Ф., Аллен, М.К., Клинчи, М.: Воспринимаемый риск хищничества снижает количество потомства певчих птиц, производимых ежегодно.Наука 334 (6061), 1398–1401 (2011)

Статья Google Scholar

Динамика зависимой от отношения системы жертва-хищник с выборочной добычей хищников

1.

П. Абрамс, Ошибки зависимости отношения хищников , Экология 75 (1994), 1842–1850.

Артикул Google Scholar

2.

Ф. Брауэр и А.C. Soudack, Области стабильности и переходные явления для системы добытый хищник-жертва , J. Math. Биол. 7 (1979), 319–337.

МАТЕМАТИКА Статья MathSciNet Google Scholar

3.

Дж. Чаттопадхай, Г. Гошал и К. С. Чаудхури, Неселективный отлов сообщества хищников с инфицированной добычей , J. Appl. Математика. and Computing (старый: KJCAM) 6 (3) (1999), 601.

MATH Google Scholar

4.

C. W. Clark, Mathematical Bioeconomics, The Optimal Management of Renewable Resources , 2nd Eds., John Wiley & Sons., New York, 1990.

MATH Google Scholar

5.

Дж. М. Кушинг, Интегро-дифференциальные уравнения и модели запаздывания в динамике населения , Springer-verlag, Heidelber, 1977.

Google Scholar

6.

Дж. М. Кушинг и М.Saleem, Модель хищник-жертва с возрастной структурой , J. Math. Биол. 14 (1982), 231–250.

МАТЕМАТИКА Статья MathSciNet Google Scholar

7.

Р. Драйвер, Обыкновенные уравнения и дифференциальные уравнения с запаздыванием , Нью-Йорк, Спрингер, 1977 г.

MATH Google Scholar

8.

М. Фан, Ю. Куанг, Динамика неавтономной системы хищник-жертва с функциональным ответом Беддингтона-ДеАнгелиса , J.Математика. Анальный. Прил. 295 (2004), 15–39.

МАТЕМАТИКА Статья MathSciNet Google Scholar

9.

М. Фан, К. Ван и Х. Цзоу, Дианамика неавтономной системы «хищник-добыча», зависящей от отношения , Труды Королевского общества Эдинбурга A 133 (2003), 97–118.

МАТЕМАТИКА Статья MathSciNet Google Scholar

10.

М.Фан и К. Ван, Периодические решения дискретной временной неавтономной системы хищник-жертва, зависящей от соотношений , Математическое и компьютерное моделирование 35 (2002), 951–961.

МАТЕМАТИКА Статья MathSciNet Google Scholar

11.

М. Фан и К. Ван, Периодичность в системах добычи хищников, зависящих от отсроченного отношения , J. Math. Анальный. Прил. 262 (1) (2001), 179–190.

МАТЕМАТИКА Статья MathSciNet Google Scholar

12.

Р. Гамбелл, В. Н. Ин, Д. В. Х. Уолтон, (ред.), Птицы и млекопитающие — антарктические киты в Антарктиде . Pergamon Press, Нью-Йорк, 1985.

Google Scholar

13.

К. Гопалсвами, Стабильность и колебания в дифференциальных уравнениях динамики населения с запаздыванием , Kluwer Academic, Dordrecht, 1992.

Google Scholar

14.

Дж. К. Хейл, Обыкновенные дифференциальные уравнения, , Уайли, Нью-Йорк, 1969.

МАТЕМАТИКА Google Scholar

15.

Кар Т.К., Селективная добыча у хищника-хищника с задержкой по времени , Матем. Комп. Модель 38 (3/4) (2003), 449–458.

МАТЕМАТИКА Статья MathSciNet Google Scholar

16.

Т. К. Кар, Анализ устойчивости модели жертва-хищник с задержкой и промыслом , J. Biol. Syst. 12 (1) (2004), 61–72.

МАТЕМАТИКА Статья MathSciNet Google Scholar

17.

Т. К. Кар, Влияние шумов окружающей среды на модель Гомпертца двух видов промысла , Экологическое моделирование 173 (2-3) (2004), 283–293.

Артикул Google Scholar

18.

Т. К. Кар, Оптимальная добыча и стабильность для системы «добыча-хищник» со ступенчатой ​​структурой .Успехи в моделировании, серия D, AMSE Periodicals 8 (3) (2003), 61.

Google Scholar

19.

Ю. Куанг и Э. Беретта, Глобальный качественный анализ системы хищник-жертва, зависящей от отношения , J. Math. Биол. 36 (1998), 389–406.

МАТЕМАТИКА Статья MathSciNet Google Scholar

20.

Ю. Куанг, Богатая динамика системы хищник-жертва, зависящая от отношения типа Гаузе , Коммуникации полевого института 21 (1999), 325–337.

MathSciNet Google Scholar

21.

Н. Макдональд, Запаздывание во времени в биологических моделях , Springer-Verlag, Heidelberg, 1978.

MATH Google Scholar

22.

А. Мукхопадхьяй, Дж. Чаттопадхьяй и П. К. Тапасви, Селективный промысел на двухвидовой модели рыболова , Ecol. Модель 94 (1997), 243–253.

Артикул Google Scholar

23.

G. P. Samanta, D. Manna and A. Maiti, Биоэкономическое моделирование промысла трех видов с эффектом переключения , J. Appl. Математика. & Вычислительная техника 12 (2003), 219.

MATH MathSciNet Статья Google Scholar

24.

X. Сонг и Л. Чен, Оптимальный сбор урожая и стабильность для двухвидовой конкурентной системы со ступенчатой ​​структурой , Math. Biosci. 170 (2001), 173–186.

МАТЕМАТИКА Статья MathSciNet Google Scholar

25.

К. Чжан, М. Лю и Б. Чжэн, Бифуркация Хофта в численном приближении для дифференциальных уравнений с запаздыванием , J. Appl. Математика. & Вычислительная техника 14 (2004), 319.

MathSciNet Google Scholar

Произошла ошибка при настройке вашего пользовательского файла cookie

Произошла ошибка при настройке вашего пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка вашего браузера для приема файлов cookie

Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:

• В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
• Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
• Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
• Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
• Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файлах cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.

Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.

Динамика и пространственно-временные закономерности в системе жертва-хищник с апосематической добычей

[1]	Р. М. Мэй, Биологические популяции с неперекрывающимися поколениями: стабильные точки, стабильные циклы и хаос, Science, 186 (1974), 645–647.
[2]	Дж.Банерджи, С.К. Сасмал и Р.К. Лайек, Сверхкритические и подкритические бифуркации Хопфа в системе «добыча-хищник с двумя отсрочками» с зависимой от плотности смертностью хищников и сильным эффектом Аллее на добычу, BioSystems, 180 (2019), 19–37.
[3]	С. К. Сасмал, Динамика популяции с множественными эффектами Аллее, вызванными факторами страха — математическое исследование взаимодействий жертва-хищник, Appl.Математика. Модели., 64 (2018), 1–14.
[4]	Дж. Банерджи, Т. Ранджан и Р.К. Лайек, Динамика прогрессирования и подавления рака: новый подход, основанный на эволюционной теории игр, 37-я ежегодная международная конференция Общества инженеров IEEE в медицине и биологии (EMBC), (2015), 5367 –5371.
[5]	Дж.Банерджи, Т. Ранджан, Р. К. Лайек, Анализ устойчивости модели динамики населения в
[6]	Микробные биопленки с неучаствующими штаммами, 7-я Международная конференция ACM по биоинформатике, компьютерной биологии и информатике здравоохранения, (201, 220–230.
[7]	6.М. Ван, А. Л. Шефер, А. А. Дандекар и др., Распознавание кворума и контроль социальных мошенников Pseudomonas aeruginosa, Proceed. Nat. Aca. Наук, 112 (2015), 2182191.
[8]	7. Дж. Банерджи, Р. К. Лайек, С. К. Сасмал и др., Отложенная эволюционная модель конкуренции за общественные блага с политикой в ​​фенотипически измененных бактериальных биопленках, Europhys.Let., (2019) (в печати).
[9]	8. М. Стивенс и Г. Д. Ракстон, Связывание эволюции и формы предупреждающей окраски в природе, Proceed. Royal Soc. B Biol. Наук, 27 (2011), 417–426.
[10]	9.Дж. Скелхорн, К. Г. Халпин и К. Роу, Изучение апосематической добычи, Behav. Экол., 27 (2016), 955–964.
[11]	10. Дж. Скелхорн и К. Роу, Бремя токсинов хищников влияет на их стратегические решения поедать токсичную добычу, Curr. Биол., 17 (2007), 1479–1483.
[12]	11.К. Г. Халпин, Дж. Скелхорн и К. Роу, Решение хищников съесть защищенную добычу зависит от размера незащищенной добычи, Animal Behav., 85 (2013), 1315–1321.
[13]	12. К. Е. Смит, К. Г. Халпин и К. Роу, Размер тела имеет значение для апосематической добычи во время обучения отвращению хищников, Behav. Процесс., 109 (2014), 173–179.
[14]	13. J. E. Huheey, Математические модели мимикрии, Am. Nat., 131 (1988), S22 – S41.
[15]	14. Дж. С. Сантос, Л. А. Колома и Д. К. Каннателла, Множественные, повторяющиеся истоки апосематизма и специализация диеты у ядовитых лягушек, Proceed.Nat. Aca. Sci., 100 (2003), 12792–12797.
[16]	15. Р. А. Сапорито, Р. Цуэрчер, М. Робертс и др., Экспериментальные доказательства апосематизма у дендробатидных ядовитых лягушек Oophaga pumilio, Copeia, 2007 (2007), 1006–1011.
[17]	16.J. C. Santos и D. C. Cannatella, Фенотипическая интеграция возникает из апосематизма и масштабов у ядовитых лягушек, Proceed. Nat. Aca. Наук, 108 (2011), 6-6180.
[18]	17. Э. Д. Броди III, Дифференциальное избегание полосатых полос коралловых змей свободными птичьими хищниками в Коста-Рике, Evolution, 47 (1993), 227–235.
[19]	18. Такеучи Ю., Ван В., Накаока С. и др., Динамическая адаптация родительской заботы, Bull. Математика. Биол., 71 (2009), 931–951.
[20]	19. С. Чакраборти, П.К. Тивари, С. К. Сасмал и др., Интерактивные эффекты убежища жертвы и дополнительной пищи для хищника в диффузной системе хищник-жертва, Appl. Математика. Модель., 47 (7), 128–140.
[21]	20. Д. Алонсо, Ф. Бартумеус и Дж. Каталан, Взаимное вмешательство между хищниками может привести к пространственным структурам Тьюринга, Ecology, 83 (2002), 28–34.
[22]	21. Дж. Р. Мейер, С. П. Элльнер, Н. Г. Хейрстон и др., Эволюция жертвы на временной шкале динамики хищник-жертва, выявленная с помощью аллель-специфической количественной ПЦР, Proceed. Nat. Aca. Sci., 103 (2006), 10690–10695.
[23]	22.Л. Линдстрем, Р. Prev post Как сделать для кукол канцтовары: Канцтовары для кукол (готовимся к школе) Next post Коническая резьба обозначение на чертеже: Страница не найдена - IPMET.RU Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт