Сидак-СП — о компании
СЕВЕРО-ЗАПАДНЫЙ ФО| Архангельск | ул. Лермонтова, 23, строение 20 | ИП Степанян В.Г. | +7 (8182) 49-40-44, +7 (911) 551-71-88 [email protected] |
| Архангельск | пр. Московский, 25, корп.4 | ИП Степанян В.Г. | +7 (8182) 420-420 [email protected] |
| Вологда | ул. Новгородская, д.7 | ИП Кузьмина И.В. (ТОРГОВЫЙ ПАРТНЕР) | +7 909 594-29-14 [email protected] |
| Калининград | Советский пр., д.125 | ООО «Компания Балтламинат» | +7 (4012) 777-001 [email protected] |
| Мурманск | ул. Домостроительная, 16 | ИП Курьян М. | +7 (8152) 41-27-02, 41-27-41 [email protected] |
| Псков | ул. Ипподромная, 108б | ИП Лашкин Д.Н. (ТОРГОВЫЙ ПАРТНЕР) | +7 (8112) 75-82-38 [email protected] |
| Петрозаводск | ул. Кооперативная, 6 | ИП Курьян М.Е. (ТОРГОВЫЙ ПАРТНЕР) | +7 (8142) 73-33-47 [email protected] |
| Псков | ул. Леона Поземского, 108 | ООО «ЛАМИНАТ-МОНЗА» (ТОРГОВЫЙ ПАРТНЕР) | +7 (921) 211-01-00, +7 (921) 211-04-44 [email protected] |
| Северодвинск | ул. Ломоносова 85 кор.2 | ИП Степанян В.Г. | +7 (8184) 50-05-22, +7 (911) 557-84-70 [email protected] |
| Сыктывкар | ул. Первомайская, д. 40 | ООО «АДМ Трейд» (представитель ООО «Домфорт») | +7 (8212) 25-55-25 adm_trade@inbox.  ru ru |
| Череповец | ул. Наседкина, 8 | ИП Нечаева Е.Г. (ТОРГОВЫЙ ПАРТНЕР) | +7 (921) 253-57-74, +7 (921) 231-72-96 [email protected] |
| Брянск | ул. Красноармейская, д. 128 (2-я линия) | ИП Шешин А.А. | +7(910) 333-30-39, +7 (903) 869-59-06 [email protected] |
| Владимир | ул. Промышленный проезд, д. 5 «В» | ООО «Андрия» | +7 (4922) 49-41-91 [email protected] |
| Владимир | с. Суходол, ул. Н. Андрианова, д. 34 | ИП Гулевская И.А. | +7 (4922) 778-778 [email protected] |
| Воронеж | ул. Свободы 75з | ООО «ПлитСтройСервис», (Торговый партнер) | +7 (473) 251-41-01 goncharova.  [email protected] [email protected] |
| Иваново | ул. Калашникова, 28Ж | ИП Гулевская И.А. | +7(4932)590-915 [email protected] |
| Кострома | ул. 2-ая Волжская, д.19, стр.2 | ООО «Мебельные Технологии» | +7 (4942) 64-11-26 |
| Рыбинск | ул. Крестовая, 101 | ООО «Мебельный Приклад» (Торговый партнер) | +7 (910) 644-20-15, +7 (915) 968-12-12 [email protected] |
| Тверь | бул. Шмидта, 20 | ООО «МЕБЕЛЬНЫЕ КОМПЛЕКТУЮЩИЕ» | +7 (905) 602-27-77 [email protected] |
| Тула | Клары Цеткин, д.20 (Территория фабрики ТулаМебель) | ООО «КОМПЛЕКТ СЕРВИС» | +7 (4872) 74-02-66 [email protected] |
| Ярославль | ул. Промышленная , 16А Промышленная , 16А | ИП Гулевская И.А. | +7(4852)770-770, +7(4852)772-772 [email protected] |
| Ижевск (обслуживается ООО «СИДЭЯ-ЕКАТЕРИНБУРГ») | ул. Ключевой поселок, 39а | ИП Патрушев А.В. (Торговый партнер) | +7 (3412) 55-37-28 [email protected] |
| Киров (обслуживается ООО «СИДЭЯ-СПБ-ЦЕНТР») | ул. Базовая, 3 | ООО «Домфорт» | +7 (8332) 755-769, +7 (953) 945-57-69 [email protected] |
| Казань (обслуживается ООО «СИДЭЯ-СПБ-ЦЕНТР») | ул. Белинского, 21Б | ИП Секарина Н.В. (представитель ООО «Домфорт») | +7 (843) 210-21-18 [email protected] |
| Казань | ул. Рахимова, 8, корп. 30, 3-й этаж, правое крыло Рахимова, 8, корп. 30, 3-й этаж, правое крыло | ООО «Аметист» | +7 (843) 511-97-46 [email protected] |
| Ижевск | ул. Маяковского 41, 1 этаж, 103 офис | ООО «Тексима» (Торговый партнер) | +7 (3412) 97-09-60 [email protected] |
| Нижний Новгород | ул. Гордеевская, д. 59Е, 2-й этаж | ООО «Мебель Сервис» | +7 (908) 762-71-05 [email protected] |
| Пермь (обслуживается ООО «СИДЭЯ-ЕКАТЕРИНБУРГ») | ул. Верхнемуллинская, 103 | ИП Патрушев А.В. (Торговый партнер) | +7 (342) 291-93-00, +7 (919) 460-41-21 [email protected] |
| Самара | Циолковского, 1А (1 этаж) | ООО «КОНСТАНТИН» (Торговый партнер) | +7 (939) 753-40-41 mail@ooo-konstantin.  ru ru |
| Саратов | ул. Большая Горная, 324 | ООО «Мир фасадов и столешниц» | +7 (8452) 65-08-60 |
| Тольятти | ТЦ «Самара», Ст. Разина 36а, 3 этаж, офис 329 | ООО «Про-Стиль» (Торговый партнер) | +7 (927) 898-27-09, +7 (937) 667-65-79 [email protected] |
| Уфа (обслуживается ООО «СИДЭЯ-ЕКАТЕРИНБУРГ») | Базисный пр., 4/1 | ИП Журавлев А.А (Торговый партнер) | +7 922 23 83 183 [email protected] |
| Уфа (обслуживается ООО «СИДЭЯ-ЕКАТЕРИНБУРГ») | ул. Менделеева, 219/3, офис 1, 2-й этаж | ООО «Фасадовъ» (Авторизованный продавец) | +7 (347) 266-62-61 [email protected] |
| Волгоград (обслуживается ООО «СИДЭЯ-МСК») | ул. Песчанокопская, 2А Песчанокопская, 2А | ООО «ПлитКом Плюс» | +7 (927) 500-07-01, +7 (999) 629-88-45 [email protected] |
| Симферополь | ул. Коммунальная, 38 | ООО «Хиндустан-Крым» | +7 (978) 783-51-01 [email protected] |
| Сочи | с. Сергей-Поле, ул. Славы, 2/2 | ООО «Прима» | +7 (918) 403-80-32 [email protected] |
| Ессентуки | ул. Пятигорская, д.129 | «ИП Казанчиев Л.А.» (Торговый партнер) | +7 (928) 008-45-45, +7 (928) 008-38-88, +7 (938) 302-22-05 [email protected] |
| Курган | ул. Омская, 179Б, стр.4 | ИП Аристов В.А. (Авторизованный продавец) | +7 (3522) 555-001, +7 (912) 064-50-01 ip_aristov@mail.  ru ru |
| Тюмень | ул. 30 лет Победы, д. 7/5, ТЦ «Новый Магнат», 3 этаж | ИП Байрамгулова Э.Н. (Торговый партнер) | +7 (950) 495-13-37 [email protected] |
| Челябинск | ул. Шарова, 73А, (этаж 2) | ИП Журавлев А.А (Торговый партнер) | +7 (922) 23-83-183 [email protected] |
| Абакан | ул. Дружбы народов, 52 | ИП Караваев Д.С. (ТОРГОВЫЙ ПАРТНЕР) | +7 (983) 195-33-33, +7 (983) 195-11-11 [email protected] |
| Иркутск | ул. Октябрьской Революции, 12/2 | ИП Муравьев Р.Р. | +7 (3952) 78-19-69 [email protected] |
| Иркутск | ул. Челябинская, 26, корп. 5 Челябинская, 26, корп. 5 | ИП Муравьев Р.Р. | +7 (3952) 43-19-74 [email protected] |
| Кемерово | ул. Карболитовская, 1/1 | ООО «АВИДА» (ТОРГОВЫЙ ПАРТНЕР) | +7 (3842) 39-61-86, +7 (3842) 39-61-87 [email protected] |
| Красноярск | ул. Кутузова, 1, стр. 9 | ООО «М-ПРОФИЛЬ», ООО «М-КОМПЛЕКТ» (АВТОРИЗОВАННЫЙ ПРОДАВЕЦ) | +7 (391) 226-65-55 [email protected] |
| Омск | ул. 70 лет Октября, 25/1 | ООО «ТОРГОВАЯ КОМПАНИЯ ВАЖНЫЙ ВЫБОР 55» (АВТОРИЗОВАННЫЙ ПРОДАВЕЦ) | +7 (904) 585-13-14, +7 (904) 587-72-16 [email protected] |
| Омск | ул. 22 Декабря, 94 | ООО «ТОРГОВАЯ КОМПАНИЯ ВАЖНЫЙ ВЫБОР 55» (АВТОРИЗОВАННЫЙ ПРОДАВЕЦ) | +7 (3812) 27-30-18, +7 (3812) 27-30-94, +7 (904) 585-13-14 neta78@bk.  ru ru |
| Томск | Комсомольский просп., 37 | ИП Кравченко И.С. (ТОРГОВЫЙ ПАРТНЕР) | +7 (3822) 21-31-45 [email protected] |
| Томск | ул. Пушкина, 59/1, ТЦ Мебельпарк | ООО «СК Строитель» | +7 913-884-23-27, +7 (3822) 901-065 [email protected] |
| Улан-Удэ | пр. Автомобилистов, 1, строение 3 | ИП Муравьев Р.Р. | +7 (3012) 480-126, +7 (3012) 372-151, +7 (908) 653-50-27 [email protected] |
| Хабаровск | Восточное шоссе, 16Б | ИП Муравьев Р.Р. | +7 (4212) 655-190, +7 (4212) 260-440, +7 (914) 158-77-68 [email protected] |
| Южно-Сахалинск | ул. Железнодорожная, 128А, офис В5 Железнодорожная, 128А, офис В5 | ООО «ГЛЕЛ» | +7 (4242) 630-042, +7 (4242) 468-333 [email protected] |
| Якутск | ул. Чусовского, д. 79 | ИП Саакян С.С. (ТОРГОВЫЙ ПАРТНЕР) | +7 (924) 169-99-41, +7 (914) 273-33-90 [email protected] |
| Барановичи | ул. Куйбышева, 42 | Авитак, ТОРГОВЫЙ ПАРТНЕР | +375 29 848-41-69 [email protected] |
| Брест | ул.Янки Купалы, 15 | ИП Назаров А.Н. | +375 (29) 629-32-62 [email protected] |
| Витебск | ул. Баграмяна, 12 | ООО «БыстроМебель» (Авторизованный продавец) | +375 33 307-70-07 artellux@mail.  ru ru |
| Витебск | ТЦ «Мега», пр Победы 15, 4 этаж, 268 пав. | ООО «БыстроМебель» (Авторизованный продавец) | +375 33 307-70-07 [email protected] |
| Минск | ул. Янки Мавра, 47/40 | ООО «Бами Мебель» | +375 29 882 84 60 [email protected] |
| Гомель | ул. Троллейбусная, 10 | «Тимберлэнд» (Торговый партнер) | +375336140268 [email protected] |
| Орша | ул. Мира, ТЦ «Центрум», пав 22 | ООО «БыстроМебель» (Авторизованный продавец) | +375 33 307-70-07 [email protected] |
| Орша | пр-т Текстильщиков, 35 | ООО «БыстроМебель» (Авторизованный продавец) | +375 33 307-70-07 [email protected] |
| Астана | пр. Республики 58/2, Технопарк, цех №6 Республики 58/2, Технопарк, цех №6 | ИП Кулмаганбетова К.О. | +7 (7172) 311-249, +7 (701) 068-88-28 [email protected] |
| Астана | район Есиль, пр. Кабанбай батыра, 42, н.п. 28б | ТОО «Amonte» (Авторизованный продавец) | +7 (705) 509-88-99 [email protected] |
| Костанай | ул. Карбышева 8/1 | ИП «Фурнитех» | +7 (7142) 39-20-30 [email protected] |
| Костанай | ул. О. Дощанова, 130 | ИП Абдулов Р. М. (Авторизованный продавец) | +7 (7142) 50-36-30 [email protected] |
| Усть-Каменогорск | ул. Потанина 15 Б, офис 8 | ТОО «75 квадратов» (Авторизованный продавец) | +7 (777) 014-40-22 [email protected] |
| Ереван | ул. Давида Анахта, 8 Давида Анахта, 8 | ООО «Гроссмейстер» | +37499040110 [email protected] |
| Ереван –Таиров | ул. Майракахакаин, 145 | ООО «Гроссмейстер» | +37443084480 [email protected] |
Производители фасадов и компонентов для кухонной мебели
Российские фабрики мебельных компонентов ищут дилеров и оптовых покупателей из России. Смотрите ассортимент, цены, рейтинг брендов и контакты производителей в каталоге. Производство компонентов, фасадов для кухни и мебели, столешниц и пр.
Фасады для кухни в алюминиевых рамках
- 15 Марта 2021
- 679
Идеальный фасад для кухонного гарнитура должен быть прочным, легким в уходе, гигиеничным, безопасным и, желательно, красивым. И при всех своих достоинствах — недорогим. Найти подобный вариант…
Найти подобный вариант…
Фасады Fenix
- 15 Марта 2021
- 474
Фасады FENIX NTM Откройте для себя FENIX, инновационные материалы для дизайна интерьера, созданные Arpa Industriale для широкого спектра вертикальных и горизонтальных применений дизайна интерьера:…
ПодробнееКомпания Rehau
- 15 Марта 2021
- 480
Фасады REHAU — это инновационный дизайн и немецкое качество! МОНОЛИТНАЯ ПОВЕРХНОСТЬ ВСЕГО ФАСАДА Использование бесшовной технологии присоединения кромки к фасаду придает изделию эффект…
ПодробнееКомпания Sidak
- 15 Марта 2021
- 453
ФАСАДЫ ФАБРИКИ «СИДАК» (Санкт-Петербург):
Компания Сидак выпускает широкий ассортимент высококачественных мебельных фасадов, изготавливаемых в технологиях 1-D, 2-D и 3-D. В предложении…
В предложении…
Компания WIECH
- 15 Марта 2021
- 391
Компания WIECH занимается изготовлением мебельных фасадов по индивидуальным заказам клиентов. Основным сырьем является плита МДФ, которая обрабатывается для фрезеровки и обертывания пленками ПВХ и…
ПодробнееКомпания ВХЦ
- 15 Марта 2021
- 412
ВХЦ ведущий производитель фасадов и мебельных дверей Санкт-Петербурга и входит в ТОП-10 компаний России на этом рынке. Компании ВХЦ 20 лет, и она специализируемся на производстве МДФ фасадов в пленке…
ПодробнееКомпания Stolzen
- 15 Марта 2021
- 395
Компания Stolzen была основана в 1994 году. Динамично развиваясь на протяжении всех этих лет мы стали одним из ведущих польских производителей мебельных фасадов и кухонных гарнитуров.
Продукцию…
Динамично развиваясь на протяжении всех этих лет мы стали одним из ведущих польских производителей мебельных фасадов и кухонных гарнитуров.
Продукцию…
Стеновые панели для кухни
- 27 Февраля 2015
- 5873
Стеновые панели (фартуки) для кухни из МДФ, ЛДСП и стекла В нашей компании при заказе кухни, Вы можете заказать фартук для кухни из различных материалов. Стеклянная стеновая панель для кухни…
ПодробнееСтолешницы — производители, выбор замена, монтаж
- 16 Марта 2014
- 487
Профессиональная замена кухонных столешниц
Распилим в размер. Семь раз отмерим — один раз отрежем! Профессиональное оборудование. Высококвалифицированный персонал.
Доставим. Доставим в самом…
Высококвалифицированный персонал.
Доставим. Доставим в самом…
Показано 1 — 9 (всего 9 статей)
Хэштеги — теги — ключевые слова для поиска статей нашего мебельного сайта
обмен ссылками шкаф купе гардеробная кухня спб на заказ водогрей на кухне газовый котел на кухне Akrilika кухня модерн фартук стеновая панель Stolzen вхц Компания WIECH Sidak Rehau Fenix алюминиевые рамки фасад столешницы замена монтаж кухни на заказ замена столешницы мебель в прихожую
3.
 3 — Множественные сравнения | СТАТ 503
3 — Множественные сравнения | СТАТ 503Метод Шеффе
Метод Шеффе для исследования всех возможных контрастов средних точно соответствует F -критерию в следующем смысле. Если F -критерий отвергает нулевую гипотезу на уровне \(\alpha\), то существует по крайней мере одно отличие, которое было бы отвергнуто с помощью процедуры Шеффе на уровне \(\alpha\). Таким образом, Шеффе обеспечивает защиту на уровне \(\альфа\) от отклонения нулевой гипотезы, когда она верна, независимо от того, сколько контрастов средств проверяется.
LSD Фишера
LSD Фишера, который представляет собой тест F , за которым следуют обычные тесты t- среди всех пар средних значений, но только если тест F отвергает нулевую гипотезу. Тест F обеспечивает общую защиту от отклонения \(H_0\), когда оно истинно. Каждый тест t выполняется на уровне \(\альфа\) и поэтому, вероятно, будет отбраковывать больше, чем следует, когда тест F отклоняется. Это утверждение можно объяснить на простом примере: предположим, что есть восемь групп лечения, и одно лечение имеет среднее значение выше, чем у других семи, которые все имеют одинаковое значение, и 9{\ простое} \) в \ (\ альфа = 0,05 \). Несмотря на этот недостаток, ЛСД Фишера остается любимым методом, поскольку он имеет общую защиту на \(\альфа\) уровне и предлагает простоту для понимания и интерпретации.
Это утверждение можно объяснить на простом примере: предположим, что есть восемь групп лечения, и одно лечение имеет среднее значение выше, чем у других семи, которые все имеют одинаковое значение, и 9{\ простое} \) в \ (\ альфа = 0,05 \). Несмотря на этот недостаток, ЛСД Фишера остается любимым методом, поскольку он имеет общую защиту на \(\альфа\) уровне и предлагает простоту для понимания и интерпретации.
Метод Бонферрони
Метод Бонферрони для \(g\) сравнений – используйте \(\alpha / g\) вместо \(\alpha\) для проверки каждого из \(g\) сравнений.
Сравнение процедуры Бонферрони с LSD Фишера
Метод LSD Фишера является альтернативой другим методам попарных сравнений (для последующего анализа ANOVA). Этот метод управляет частотой ошибок \(\alpha\text{-level}\) для каждого попарного сравнения, поэтому он не контролирует частоту ошибок семейства. Эта процедура использует t статистика для тестирования \(H_0 \двоеточие \mu_i = \mu_j\) для всех пар i и j .
\(t=\dfrac{\bar{y}_i-\bar{y}_j}{\sqrt{MSE(\frac{1}{n_i}+\frac{1}{n_j})}}\ )
В качестве альтернативы, метод Бонферрони контролирует частоту ошибок семейства, выполняя тесты парных сравнений с использованием уровня значимости \(_{\alpha/g}\), где g — количество парных сравнений. Следовательно, доверительные интервалы Бонферрони для различий средних шире, чем у LSD Фишера. Кроме того, легко показать, что p -значение каждого попарного сравнения, рассчитанное методом Бонферрони, равно g, умноженному на p -значение, рассчитанное методом LSD Фишера.
Стьюдентизированный диапазон Тьюки
Стьюдентизированный диапазон Тьюки рассматривает различия между всеми парами средних значений, разделенные на оценочное стандартное отклонение среднего, и сравнивает их с табличными критическими значениями, представленными в Приложении VII. Почему он называется студенческим диапазоном? В знаменателе используется оценочное стандартное отклонение, следовательно, статистика студенческая, как у студента 9.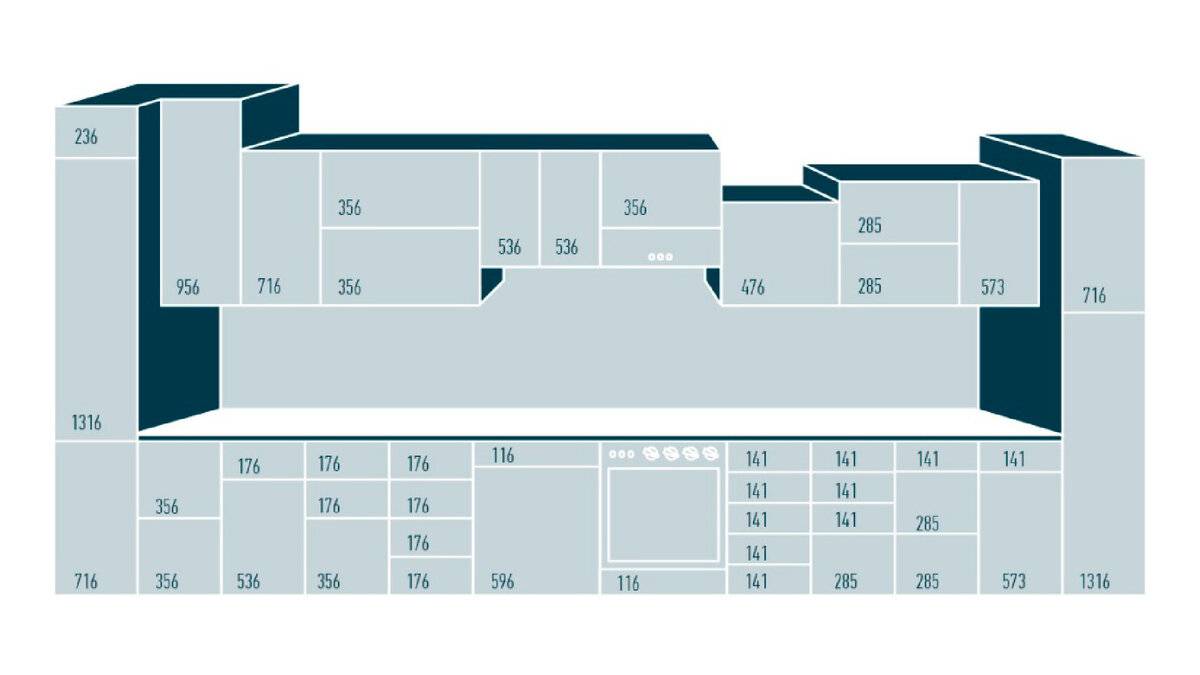 0005 т -тест. Процедура Тьюки предполагает, что все \(n_i\) равны, скажем, \(n\).
0005 т -тест. Процедура Тьюки предполагает, что все \(n_i\) равны, скажем, \(n\).
\(q=\dfrac{\bar{y}_i-\bar{y}_j}{\sqrt{MSE(\frac{1}{n})}}\)
Сравнение процедуры Тьюки с процедурой Бонферрони Раздел
Процедура Бонферрони является хорошим универсальным инструментом, но для всех попарных сравнений процедура студенческого диапазона Тьюки немного лучше, как показано здесь.
Стьюдентский диапазон — это распределение разницы между максимумом и минимумом по стандартной ошибке среднего. Когда мы вычисляем t -тест, или когда мы используем поправку Бонферрони, где г — количество сравнений, мы не сравниваем яблоки и апельсины. В одном случае (Тьюки) статистика имеет знаменатель со стандартной ошибкой одного среднего, а в другом случае ( t — тест) со стандартной ошибкой разницы между средними, как видно из уравнения для t и q выше.
Пример 3.3: подходы Тьюки против Бонферрони Раздел
Вот пример, который мы можем разработать. Допустим, у нас есть 5 средних значений, поэтому a = 5, мы допустим \(\alpha = 0,05\), а общее количество наблюдений N = 35, поэтому каждая группа имеет семь наблюдений и df = 30
Если мы посмотрим на студенческое распределение диапазона для 5, 30 степеней свободы, мы найдем критическое значение 4,11.
Если бы мы использовали подход Бонферрони, мы бы использовали \(g = 5 × 4/2 = 10\) попарных сравнений, поскольку a = 5. Таким образом, снова для теста α = 0,05 все, что нам нужно посмотреть, это t -распределение для \(\alpha / 2g = 0,0025\) и N — a =30 дф . Глядя на таблицу t , мы получаем значение 3,03. Однако для сравнения со статистикой студенческого диапазона Тьюки нам нужно умножить табличное критическое значение на \(\sqrt{2} = 1,414\), поэтому 3,03 x 1,414 = 4,28 , , что немного больше, чем полученное 4,11. для таблицы Тьюки.
для таблицы Тьюки.
Мы хотим подчеркнуть, что процедура Бонферрони несколько более консервативна, чем результат Тьюки, поскольку процедура Тьюки в этой ситуации является точной, а процедура Бонферрони лишь приближенной.
Процедура Тьюки является точной для образцов одинакового размера. Однако существует приблизительная процедура, называемая тестом Тьюки-Крамера для неравных \(n_i\).
Если вы просматриваете все попарные сравнения, то точная процедура Тьюки, вероятно, является наилучшей для использования. Однако Бонферрони — хорошая общая процедура.
Сравнение средних
Попарное сравнение — это только один пример сравнения средних. Общий контраст может быть записан как набор коэффициентов средних, которые в сумме равны нулю. Это часто будет включать больше, чем просто пару процедур. В общем, мы можем написать контраст, чтобы сделать любое сравнение, которое нам нравится. Мы также будем рассматривать множества ортогональных контрастов.
Пример 3.
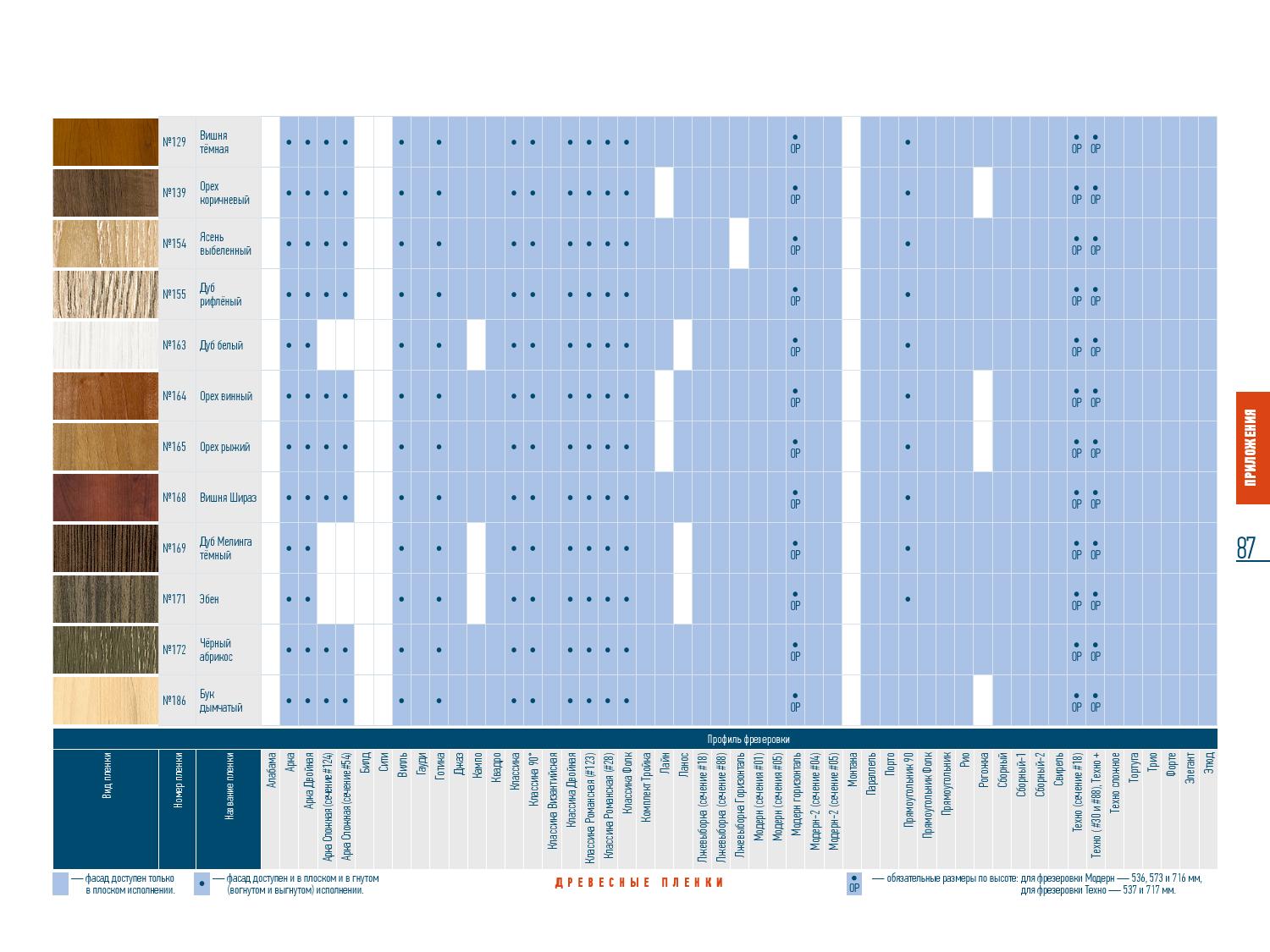 4: Расход бензина
Раздел
4: Расход бензина
Раздел Мы хотим сравнить расход бензина на нескольких автомобилях: Ford Escape (гибрид), Toyota Camry, Toyota Prius (гибрид), Honda Accord и Honda Civic (гибрид). Группа тестирования потребителей хочет проверить каждый из этих автомобилей на расход бензина при определенных условиях. Они берут н предписаны пробные заезды и запись пробега для каждого автомобиля.
Теперь им сначала нужно определить некоторые различия между этими средствами. Контрасты — это коэффициенты, обеспечивающие значимое сравнение. Затем они могут проверить и оценить эти контрасты. Для первого сравнения, \(C_1\), они могли сравнить американский бренд с иностранными брендами. Нам нужно, чтобы каждый контраст суммировался с 0, и для удобства используйте только целые числа. Как насчет сравнения Toyota с Honda (то есть \(C_2\)), или гибрида с негибридом (то есть \(C_3\)).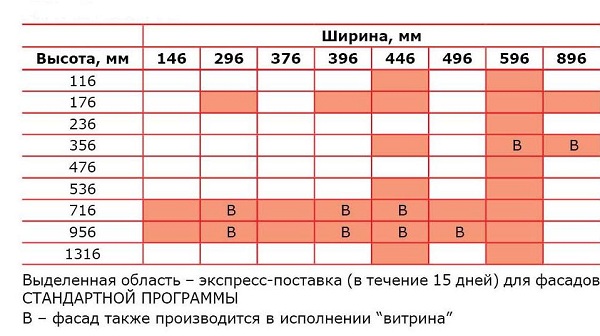
| Форд Эскейп | Тойота Камри | Тойота Приус | Хонда Аккорд | Хонда Сивик | |
|---|---|---|---|---|---|
| \(Y_{1.}\) | \(Y_{2.}\) | \(Y_{3.}\) | \(Y_{4.}\) | \(Y_{5.}\) | |
| \(С_1\) | 4 | -1 | -1 | -1 | -1 |
| \(С_2\) | 0 | -1 | -1 | 1 | 1 |
| \(С_3\) | 2 | -3 | 2 | -3 | 2 |
| \(С_4\) | 0 | -1 | 1 | 0 | 0 |
| \(С_5\) | 0 | 0 | 0 | -1 | 1 |
Таким образом, первые три коэффициента контрастности определяют описанные сравнения, а \(C_4\) и \(C_5\) представляют собой сравнения внутри брендов с двумя моделями.
После того, как мы разработаем набор контрастов, мы можем протестировать эти контрасты или оценить их.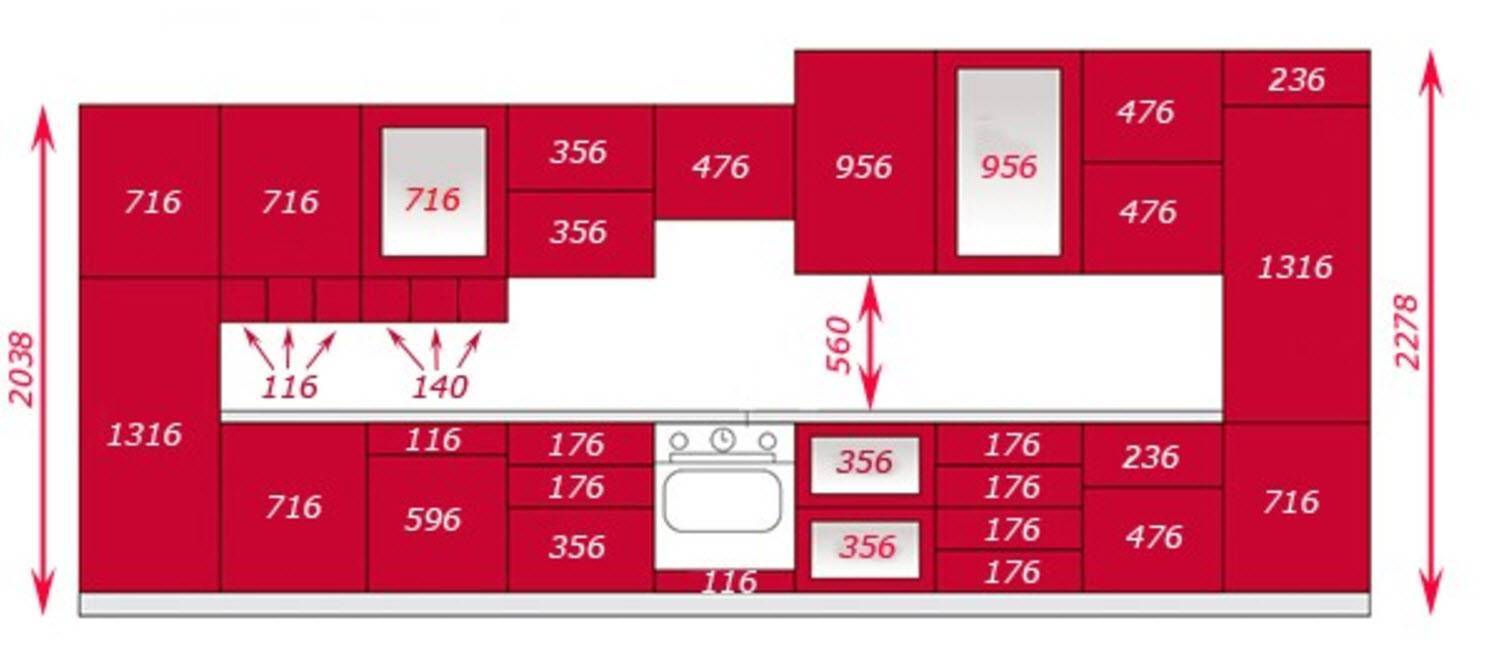 Мы также можем рассчитать доверительные интервалы вокруг истинного контраста средних значений, используя расчетный контраст ± распределение t , умноженное на расчетное стандартное отклонение контраста. См. уравнение 3-30 в тексте.
Мы также можем рассчитать доверительные интервалы вокруг истинного контраста средних значений, используя расчетный контраст ± распределение t , умноженное на расчетное стандартное отклонение контраста. См. уравнение 3-30 в тексте.
О наборах множественных контрастов Раздел
Метод Шеффе обеспечивает защиту \(\alpha\text{-level}\) для всех возможных контрастов, что особенно полезно, когда мы заранее не знаем, сколько контрастов у нас будет. Этот тест достаточно консервативен, потому что он действителен для всех возможных контрастов средств. Следовательно, процедура Шеффе эквивалентна тесту F-, и если тест F- отклонен, будет некоторый контраст, который не будет содержать ноль в своем доверительном интервале.
Что такое ортогональный контраст?
Два контраста ортогональны, если сумма произведения коэффициентов двух контрастов равна нулю. Ортогональный набор контрастов также ортогонален общему среднему, поскольку сумма коэффициентов равна нулю.
Ортогональный набор контрастов также ортогонален общему среднему, поскольку сумма коэффициентов равна нулю.
Посмотрите на таблицу выше и определите, какие контрасты ортогональны.
Всегда существует a -1 ортогональных противоположностей средства. Когда размеры выборки равны, сумма квадратов этих контрастов при суммировании дает общую сумму квадратов из-за лечения. Любой набор ортогональных контрастов разбивает вариацию так, что полная вариация, соответствующая этим a -1 контрасты равны общей сумме квадратов между обработками. Когда размеры выборки не равны, определение ортогональных контрастов включает размеры выборки.
Процедура Даннета
Процедура Даннета — это еще одна процедура множественного сравнения, специально разработанная для сравнения каждой обработки с контролем. Если у нас есть и групп, пусть последняя будет контрольной группой, а первые и -1 будут лечебными группами. Мы хотим сравнить каждую из этих лечебных групп с этой контрольной группой. Следовательно, у нас будет a — 1 контраст или a — 1 парное сравнение. Для проведения множественных сравнений этих и — 1 противопоставлений мы используем специальные таблицы для нахождения критических значений проверки гипотез, выведенные Даннеттом.
Следовательно, у нас будет a — 1 контраст или a — 1 парное сравнение. Для проведения множественных сравнений этих и — 1 противопоставлений мы используем специальные таблицы для нахождения критических значений проверки гипотез, выведенные Даннеттом.
Сравнение процедуры Даннета с процедурой Бонферрони Раздел
Мы можем сравнить подход Бонферрони с процедурой Даннета. Процедура Даннета вычисляет разницу средних значений для контроля и лечения один, контроля и лечения два и т. д. до a — 1. Что обеспечивает a — 1 парных сравнений.
Итак, теперь мы рассмотрим пример, где у нас есть шесть групп, a = 6, и t = 5 и n = 6 наблюдений в группе. Тогда процедура Даннета даст критическую точку для сравнения разности средних. Из таблицы получаем \(\alpha =0,05\) двустороннего сравнения d ( a -1, f ) = 2,66, где a — 1 = 5 и f = df = 30.
Используя подход Бонферрони, если мы посмотрим на t -распределение для г = 5 сравнений и двусторонний тест с 30 степенями свободы для ошибки, мы получим 2,75.
Сравнивая их, мы видим, что подход Бонферрони немного более консервативен. Метод Даннета представляет собой точную процедуру сравнения контроля с и -1 обработками. Бонферрони — это общий инструмент, но не точный. Тем не менее, в этом примере нет большой разницы
ЛСД Фишера удобен тем, что всегда используется одна и та же измерительная линейка, нескорректированный тест t-. Всем известно, что если вы проводите много таких тестов, то из каждых 20 тестов один из них может быть ошибочным случайно. Это еще один способ справиться с этой неопределенностью. Все эти методы защищают вас от слишком большого количества ошибок типа I, независимо от того, выполняете ли вы проверку гипотез или доверительные интервалы. За свою жизнь сколько тестов вы собираетесь сделать?
Таким образом, в некотором смысле вы должны задать себе вопрос о том, какой набор тестов я хочу защитить от ошибок типа I. Таким образом, в процедуре LSD Фишера каждый тест стоит сам по себе и на самом деле не является тестом множественных сравнений. Если вы ищете какие-либо различия и не знаете, сколько из них вы в конечном итоге сделаете, вам, вероятно, следует использовать Scheffé, чтобы защитить себя от всех них. Но если вы знаете, что все попарно, и это все, то вариант Тьюки будет лучшим. Если вы сравниваете несколько вариантов лечения с контролем, то метод Даннетта будет лучшим.
Таким образом, в процедуре LSD Фишера каждый тест стоит сам по себе и на самом деле не является тестом множественных сравнений. Если вы ищете какие-либо различия и не знаете, сколько из них вы в конечном итоге сделаете, вам, вероятно, следует использовать Scheffé, чтобы защитить себя от всех них. Но если вы знаете, что все попарно, и это все, то вариант Тьюки будет лучшим. Если вы сравниваете несколько вариантов лечения с контролем, то метод Даннетта будет лучшим.
Сейчас доступно целое семейство пошаговых процедур, но мы их здесь рассматривать не будем. Можно показать, что каждый из них лучше в определенных ситуациях. Другой подход к этой проблеме называется контролем частоты ложных открытий. Он используется, когда существуют сотни гипотез — ситуация, возникающая, например, при тестировании экспрессии всех генов в организме или различия в интенсивности пикселей для пикселей в наборе изображений. Рассмотренные выше процедуры множественного сравнения защищают от вероятности одного ложного значимого вызова. Но когда есть сотни тестов, мы могли бы предпочесть сделать несколько ложных значимых вызовов, если это значительно увеличивает нашу способность обнаруживать истинное различие. Методы False Discovery Rate пытаются контролировать ожидаемый процент ложных значимых вызовов среди тестов, объявленных значимыми.
Но когда есть сотни тестов, мы могли бы предпочесть сделать несколько ложных значимых вызовов, если это значительно увеличивает нашу способность обнаруживать истинное различие. Методы False Discovery Rate пытаются контролировать ожидаемый процент ложных значимых вызовов среди тестов, объявленных значимыми.
Что такое тест Бонферрони (коррекция) и как его использовать?
К Адам Хейс Полная биография Адам Хейс, доктор философии, CFA, финансовый писатель с более чем 15-летним опытом работы на Уолл-стрит в качестве трейдера деривативов. Помимо своего обширного опыта торговли деривативами, Адам является экспертом в области экономики и поведенческих финансов. Адам получил степень магистра экономики в Новой школе социальных исследований и докторскую степень. из Университета Висконсин-Мэдисон по социологии. Он является обладателем сертификата CFA, а также лицензий FINRA Series 7, 55 и 63. В настоящее время он занимается исследованиями и преподает экономическую социологию и социальные исследования финансов в Еврейском университете в Иерусалиме.
Узнайте о нашем редакционная политика
Обновлено 29 ноября 2021 г.
Рассмотрено Хадиджа ХартитРассмотрено Хадиджа Хартит
Полная биографияХадиджа Хартит — эксперт по стратегии, инвестициям и финансированию, а также преподаватель финансовых технологий и стратегических финансов в ведущих университетах. Она была инвестором, предпринимателем и консультантом более 25 лет. Она является держателем лицензий FINRA Series 7, 63 и 66.
Узнайте о нашем Совет по финансовому обзору
Факт проверен Ярилет ПересФакт проверен Ярилет Перес
Полная биографияЯрилет Перес — опытный мультимедийный журналист и специалист по проверке фактов со степенью магистра журналистики. Она работала в нескольких городах, освещая последние новости, политику, образование и многое другое. Она специализируется в личных финансах и инвестициях, а также в сфере недвижимости.
Узнайте о нашем редакционная политика
Что такое тест Бонферрони?
Тест Бонферрони — это тип теста множественных сравнений, используемый в статистическом анализе. При выполнении проверки гипотезы с множественными сравнениями в конечном итоге может получиться результат, демонстрирующий статистическую значимость зависимой переменной, даже если ее нет.
При выполнении проверки гипотезы с множественными сравнениями в конечном итоге может получиться результат, демонстрирующий статистическую значимость зависимой переменной, даже если ее нет.
Если конкретный тест, такой как линейная регрессия, таким образом, дает правильные результаты в 99% случаев, запуск одной и той же регрессии на 100 различных выборках может привести как минимум к одному ложноположительному результату в какой-то момент. Тест Бонферрони пытается предотвратить ошибочное представление данных как статистически значимых, как это, путем внесения корректировок во время сравнительного тестирования.
Ключевые выводы
- Тест Бонферрони – это статистический тест, используемый для уменьшения количества ложноположительных результатов.
- В частности, Бонферрони разработал корректировку для предотвращения ошибочного представления данных как статистически значимых.
- Важным ограничением поправки Бонферрони является то, что она может привести к тому, что аналитики будут смешивать фактические результаты с истинными.
Понимание теста Бонферрони
Тест Бонферрони, также известный как «коррекция Бонферрони» или «корректировка Бонферрони», предполагает, что p-значение для каждого теста должно быть равно его альфа, деленному на количество выполненных тестов.
Тест Бонферрони представляет собой поправку множественного сравнения, используемую при одновременном выполнении нескольких зависимых или независимых статистических тестов. Причина в том, что, хотя данное значение альфа-канала может подходить для каждого отдельного сравнения, оно не подходит для набора всех сравнений. Чтобы исключить множественные ложные положительные результаты, значение альфа необходимо снизить, чтобы учесть количество выполняемых сравнений.
Тест назван в честь разработавшего его итальянского математика Карло Эмилио Бонферрони (189 г.2–1960). Другие типы тестов множественного сравнения включают тест Шеффе и тест метода Тьюки-Крамера. Критика теста Бонферрони заключается в том, что он слишком консервативен и может не дать некоторых важных результатов.
В статистике нулевая гипотеза — это, по сути, убеждение в отсутствии статистической разницы между двумя сравниваемыми наборами данных. Проверка гипотезы включает проверку статистической выборки для подтверждения или отклонения нулевой гипотезы. Тест проводится путем взятия случайной выборки из населения или группы. В то время как проверяется нулевая гипотеза, также проверяется альтернативная гипотеза, в результате чего два результата являются взаимоисключающими.
Однако при любой проверке нулевой гипотезы можно ожидать ложноположительного результата. Формально это называется ошибкой типа I, и в результате тесту присваивается частота ошибок, отражающая вероятность ошибки типа I. Другими словами, определенный процент результатов, скорее всего, даст ложноположительный результат.
Использование поправки Бонферрони
Например, статистическому тесту обычно может быть назначена частота ошибок 5%, что означает, что 5% времени, вероятно, будут ложноположительными. Этот уровень ошибок в 5% называется альфа-уровнем. Однако, когда в анализе выполняется много сравнений, частота ошибок для каждого сравнения может повлиять на другие результаты, создавая множество ложных срабатываний.
Этот уровень ошибок в 5% называется альфа-уровнем. Однако, когда в анализе выполняется много сравнений, частота ошибок для каждого сравнения может повлиять на другие результаты, создавая множество ложных срабатываний.
Бонферрони разработал свой метод коррекции повышенного уровня ошибок при проверке гипотез с множественными сравнениями. Поправка Бонферрони рассчитывается путем деления количества тестов на альфа-значение. Используя коэффициент ошибок 5% из нашего примера, два теста дадут коэффициент ошибок 0,025 или (0,05/2), а четыре теста, следовательно, будут иметь коэффициент ошибок 0,0125 или (0,05/4). Обратите внимание, что частота ошибок уменьшается по мере увеличения размера выборки.
Статья Источники
Investopedia требует, чтобы авторы использовали первоисточники для поддержки своей работы. К ним относятся официальные документы, правительственные данные, оригинальные отчеты и интервью с отраслевыми экспертами. Мы также при необходимости ссылаемся на оригинальные исследования других авторитетных издателей.
