Виды углов. Измерение углов
На каждом из рисунков 82, a − г изображены два луча. На каком из рисунков пара лучей образует угол, сторонами которого являются эти лучи?
Поскольку на рисунках 82, а − в начала лучей не совпадают, то они не могут служить сторонами угла. Лучи на рисунке 82, г образуют прямую. При этом начала лучей совпадают, а следовательно, они образуют угол. Такой угол называт развернутым.
Угол, стороны которого образуют прямую, нахывают развернутым.
Углы, как и отрезки, можно измерять. Напомним, что для измерения отрезков мы использовали единичный отрезок (1 мм, 1 см и т.п.).
Однако для измерения углов мы пока не имеем такого единичного угла.
Создать его можно, например, так. Разделим развернутый угол на 180 равных углов (рис. 83). Угол, образованный двумя соседними лучами, выбирают за единицу измерения. Его величину называют градусом (от лат.
gradus − «шаг», «ступенька») и записывают 1°.
Измерить угол − значит подсчитать, сколько единичных углов в нем помещается.
Тогда величина или, как еще принято говорить, градусная мера развернутого угла равна 180°.
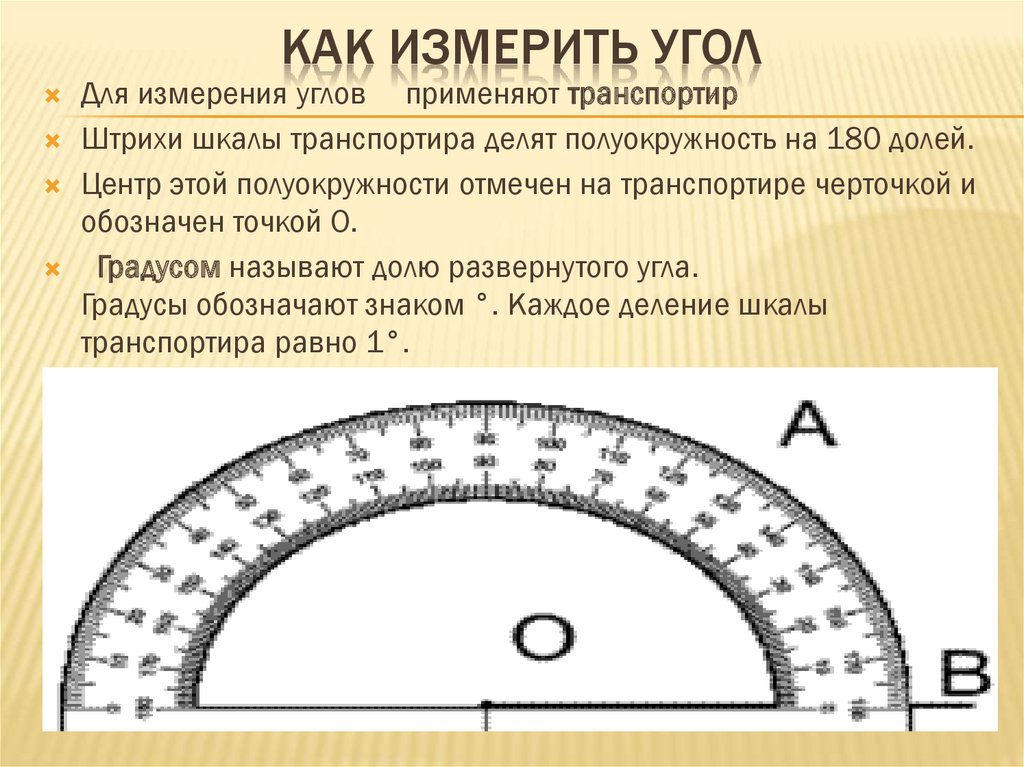
Для измерения углов используют специальный прибор − транспортир (рис. 84). Он состоит, как правило, из полукольца, соединенного с линейкой. Его шкала содержит 180 делений.
Чтобы измерить угол, совместим его вершину с центром транспортира таким образом, чтобы одна из сторон угла прошла по линейке (рис. 85).
Тогда штрих на шкале, через который пройдет вторая сторона, укажет градусная (величину) этого угла.
Так, на рисунке 85 градусная мера угла AOB равна 55°. Пишут: ∠AOB = 55°. На рисунке 86 имеем: ∠MON = 134°.
Равные углы имеют равные градусные меры. Из двух неравных углов бОльшим будем считать тот, градусная мера которого больше. Например, из трех углов, изображенных на рисунке 87, ∠MON − наибольший.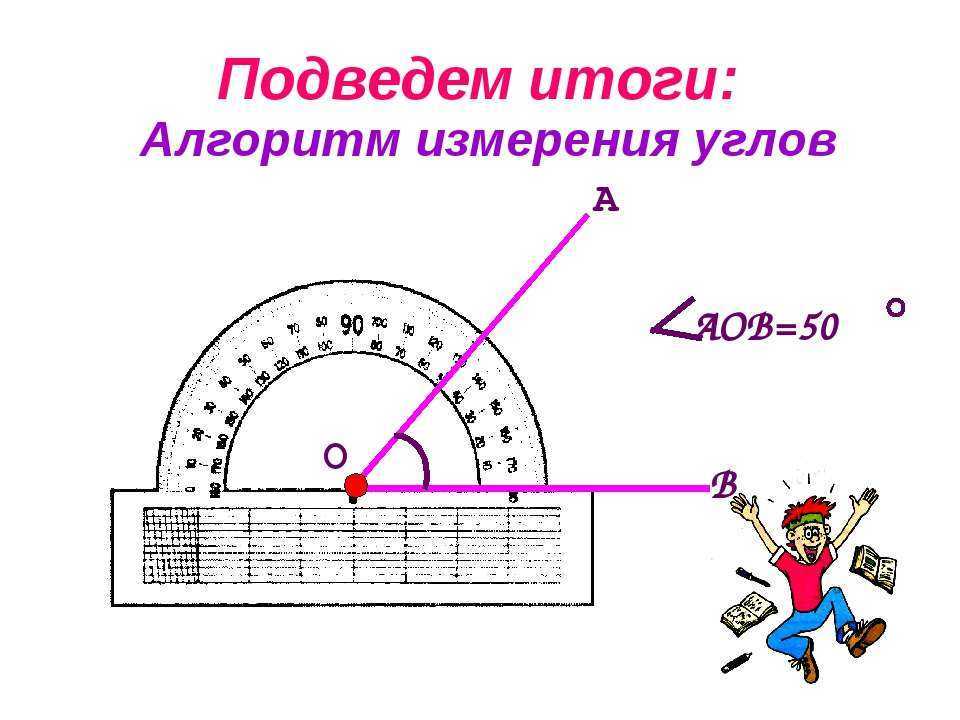
В этом легко убедиться, измерив углы транспортиром.
Величина угла обладает следующим свойством.
Если между сторонами угла ABC провести луч BD, то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC (рис. 88), т.е.
∠ABC = ∠ABD + ∠DBC.
Угол, градусная мера которого меньше 90°, называют острым (рис. 89, a).
Угол, градусная мера которого равна 90°, называют прямым (рис. 89, б).
На рисунке прямой угол обозначает так: ∟.
Угол, градусная мера которого больше 90°, но меньше 180° называют тупым (рис. 89, в).
Отметим, что биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90°. Следовательно, биссектриса развернутого угла делит его на два прямых угла (рис. 90).
Пример 1. Дан луч OA. Постройте угол BOA, равный 72°.
Решение.
Совместим центр транспортира с точкой O так, чтобы луч OA прошел по линейке.
Выберем на кольце транспортира штрих, который соответствует 72°. Возле этого штриха отметим точку B (рис. 91). Проведем луч OB. Угол BOA − искомый.
Если дан луч OA и построен угол BOA, то говорят, что от луча OA отложен угол BOA.
Пример 2. Из вершины угла ABC проведены два луча BK и BM так, что ∠ABK = 48°, ∠CBM = 72° (рис. 92).
Вычислите величину угла ABC, если ∠MBK = 16°.
Решение.
Имеем: ∠ABM = ∠ABK − ∠MBK, ∠ABM = 48° − 16° = 32°;
∠ABC = ∠ABM + ∠СBM, ∠ABC = 32° + 72° = 104°.
Ответ: 104°.
Углы и измерение углов — Студопедия
Поделись
Угловые размеры определяют положение плоскостей, осей, линий, центров отверстий и т. д. Угловые размеры бывают зависимые и назависимые.
Независимые углы не связаны с другими параметрами изделия; зависимые углы определяются основными параметрами изделий, к которым они относятся.
В качестве единицы измерения плоских углов Международной системой единиц (СИ) принят радиан — угол между двумя радиусами круга, вырезающими на его окружности дугу, длина которой равна радиусу данного круга.
Измерение углов в радианах на практике связано с значительными трудностями, так как ни один из современных угломерных приборов не имеет градуировки в радианах.
По этой причине в машиностроении для угловых измерений в основном применяются внесистемные единицы: градус, минута и секунда. Эти единицы связаны между собой следующими соотношениями:
- 1° = π/180 рад = 1,745329 × 10-2 рад;
- 1‘ = π /10800 рад = 2,908882 × 10-1 рад;
- 1” = π/648000 рад = 4,848137 × 10-6 рад.
Значение угла при измерении определяют сравнением его с известным углом. Известный угол может быть задан так называемыми жесткими (с постоянным значением угла) мерами — аналогами формы элементов детали: угловыми мерами, угольниками, угловыми шаблонами, коническими калибрами, многогранными призмами.
Измеряемый угол можно сравнивать также с многозначными угломерными штриховыми мерами и различными видами круговых и секторных шкал.
Еще одним методом получения известного угла является его расчет по значениям линейных размеров на основании тригонометрических зависимостей.
В соответствии с этим классификацию методов измерений углов производят в первую очередь по виду создания известного угла: сравнением с жесткой мерой, сравнением с штриховой мерой (гониометрические методы) и тригонометрическими методами (по значениям линейных размеров).
При сравнении углов с жесткой мерой отклонение измеряемого угла от угла меры определяют по просвету между соответствующими сторонами углов детали и меры, по отклонению показаний прибора линейных размеров, измеряющих несовпадение этих сторон или при контроле «по краске», т.е. по характеру тонкого, слоя краски, перенесенного с одной поверхности на другую.
В приборах для гониометрических измерений имеются штриховая угломерная шкала, указатель и устройство для определения положения сторон угла. Это устройство связано с указателем или шкалой, а измеряемая деталь — соответственно со шкалой или указателем.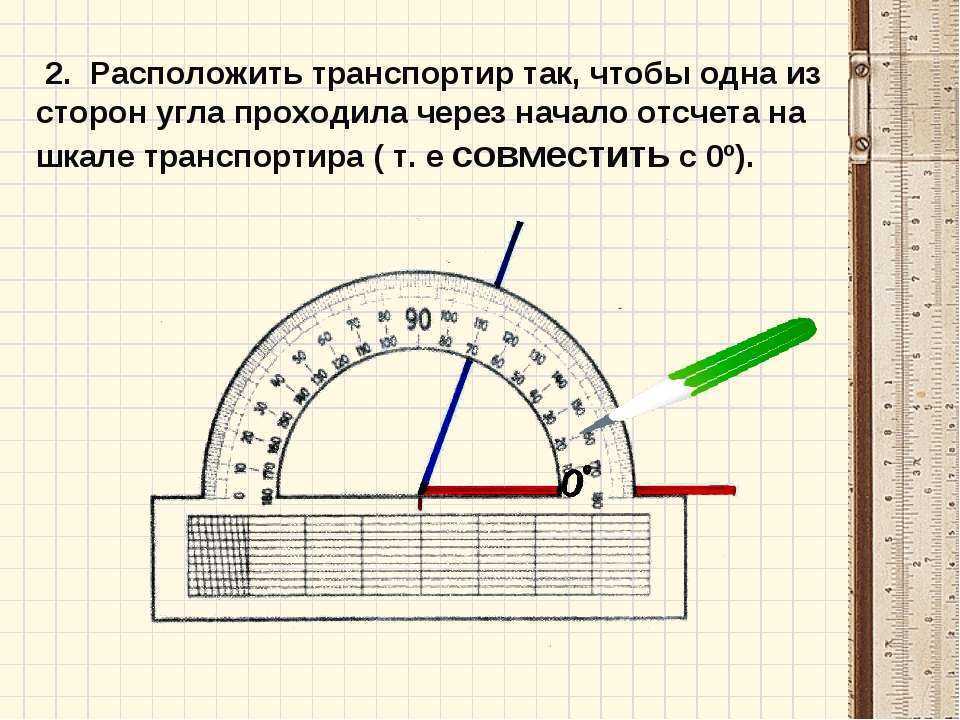
Определение положения сторон угла можно производить как контактным, так и бесконтактным (оптическим) способом. При соответствующих измеряемому углу положениях узлов прибора определяют угол относительного поворота шкалы и указателя.
При косвенных тригонометрических методах определяют линейные размеры сторон прямоугольного треугольника, соответствующего измеряемому углу, и по ним находят синус или тангенс этого угла (координатные измерения). В других случаях (измерение с помощью синусных или тангенсных линеек) воспроизводят прямоугольный треугольник с углом, номинально равным измеряемому, и устанавливая его как накрест лежащий с измеряемым углом, определяют линейные отклонения от параллельности стороны измеряемого угла основанию прямоугольного треугольника.
При всех методах измерений углов должно быть обеспечено измерение угла в плоскости, перпендикулярной к ребру двугранного угла. Перекосы приводят к погрешности измерения.
При наличии наклона плоскости измерения в двух направлениях погрешность измерения угла может быть и положительной и отрицательной.
Угол наклона плоскостей обычно определяется уклоном, численно равным тангенсу угла наклона.
Малые значения уклонов часто указывают в микрометрах на 100 мм длины, в промилле или миллиметрах на метр длины (мм/м).
Например, в мм/м указывается цена деления уровней. Пересчет уклонов в угол обычно производится по приближенной зависимости: уклон
Как было показано выше в машиностроении в зависимости от используемых средств и методов различают три основных способа измерения углов:
Сравнительный метод измерения углов с помощью жестких угловых мер. При этом измерении определяется отклонение измеряемого угла от угла меры.
Абсолютный гониометрический метод измерения углов, при котором измеряемый угол определяется непосредственно по угломерной шкале прибора.
Косвенный тригонометрический метод: угол определяется расчетным путем по результатам измерения линейных размеров (катетов, гипотенузы), связанных с измеряемым углом тригонометрической функцией (синусом или тангенсом).
Сравнительный метод измерения углов обычно сочетается с косвенным тригонометрическим методом, последним определяется разница сравниваемых углов в линейных величинах на определенной длине стороны угла.
App Store: Measure Angles — Bubble Level
Описание
.
..точность благодаря более чем 10-летнему опыту работы с цифровыми инструментами.
Измерение углов и наклонов: самый точный клинометр и цифровой пузырьковый уровень в вашем кармане. В том числе фонарик + компас + линейка + измерение камеры — все в одном удобном приложении.
◉ Транспортир 360°, клинометр с пузырьковым уровнем, прибор для измерения уровня
◉ Автоматические пузырьковые уровни / спиртовые уровни для 90°/180°/270°/360°
◉ Уровень поверхности, отвес со звуковым предупреждением
◉ Автоматический переход от транспортира к отвесу
◉ Акустический сигнал, показывающий угловую разницу между фактическим и целевым углом
◉ 6-этапный помощник по калибровке
◉ Память для нескольких значений угла
◉ Дополнительная память целевого угла
◉ Ввод целевого угла вручную
На этом ваш поиск идеального мобильного клинометра, транспортира для измерения углов и выравнивания поверхностей заканчивается.
Наш клинометр, спиртовой уровень, транспортир, пузырьковый уровень — мультитул чрезвычайно точен и интуитивно понятен в обращении.
Эти интуитивно понятные функции объединены в инструменте уровня приложения «Измерение» с простыми пользовательскими элементами управления и интуитивно понятным управлением.
■ Клинометр 360° ■
С помощью клинометра измерьте углы по всем краям телефона. Вы можете установить целевой угол, перемещая палец по дисплею. Кроме того, вы можете сохранить до 5 ракурсов в списке ракурсов и быстро вызывать их как целевые ракурсы.
Protractor-Multitool также имеет индикатор стабильности, показывающий скорость изменения.
■ Ватерпас ■
При приближении к 0°/90°/180°/270° отображается спиртовой уровень. Это позволяет точно выравнивать предметы.
■ Уровень поверхности ■
Инструмент поверхности позволяет выравнивать поверхности. Разница уровней будет отображаться в градусах.
■ Интуитивно понятный ■
В зависимости от ориентации вашего iPhone вид переходит с уровня поверхности на 360°-транспортир.
■ Высочайшая точность ■
Помощник по 6-точечной калибровке гарантирует высокую точность до 0,01°.
Уровень поверхности и калибровка транспортира полностью независимы друг от друга, что обеспечивает еще более высокую точность.
■ Утонченный дизайн ■
Приложение Measure App имеет встроенные возможности рисования вашего телефона для чрезвычайно четкого и плавного отображения.
Цифровой уровень (нивелир, мишень, индикатор тангажа и крена, уровень поверхности)!
Версия 3.
99.82
Новый индикатор показывает разницу между текущим и опорным углом (внутри основного диска).
Улучшенный дизайн.
Теперь в инструмент уровня поверхности включен настоящий транспортир, который позволяет измерять углы на ровной поверхности.
Дополнительно улучшено отображение транспортира с плоской поверхностью.
Проверьте это и сообщите нам, нравится ли вам новая функция.
Рейтинги и обзоры
1 Рейтинг
Покупки в приложении
Professional Edition
Удалить рекламу и разблокировать все инструменты.
4,49 доллара США
Разработчик, Йенс Рикхоф, указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Данные, используемые для отслеживания вас
- Идентификаторы
- Данные об использовании
Данные, связанные с вами
Следующие данные могут быть собраны и связаны с вашей личностью:
Данные, не связанные с вами
Следующие данные могут быть собраны, но они не связаны с вашей личностью:
- Идентификаторы
- Данные об использовании
- Диагностика
Методы обеспечения конфиденциальности могут различаться в зависимости, например, от используемых вами функций или вашего возраста.
Узнать больше
Информация
- Поставщик
- Йенс Рикхоф
- Размер
- 40,3 МБ
- Категория
- Утилиты
- Возрастной рейтинг
- 4+
- Авторское право
- © 2022 — JRSoftWorx
- Цена
- Бесплатно
- Сайт разработчика
- Тех. поддержка
- Политика конфиденциальности
Еще от этого разработчика
Вам также может понравиться
измерений углов в любом месте | Американская типография
Автор: Ли Чжоу 24 апреля 2020 г.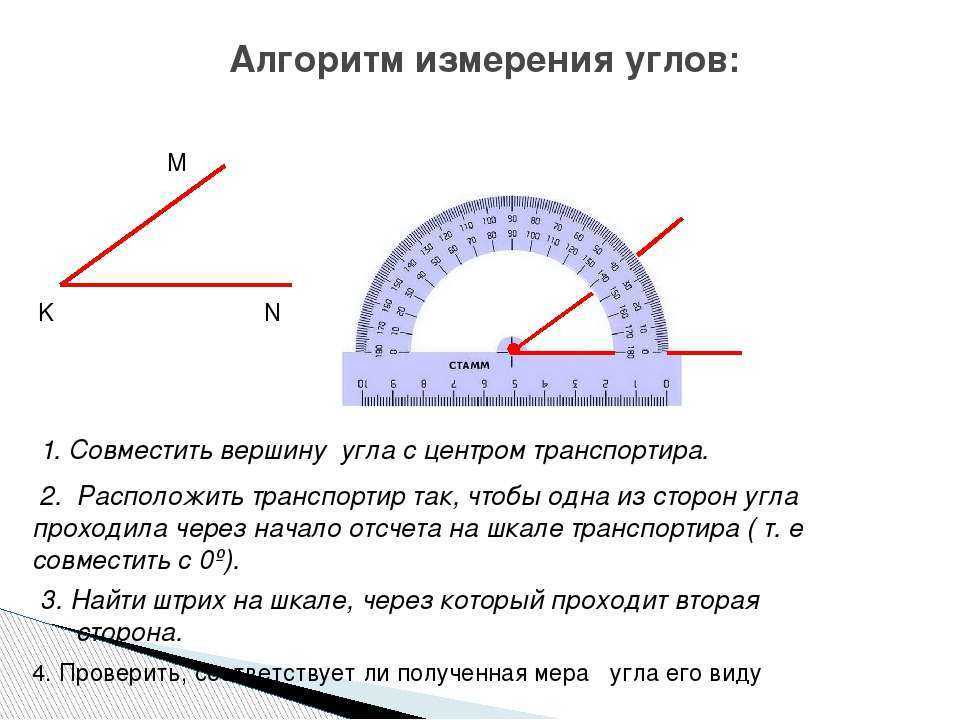
Ищете интересный способ для вашего ребенка младшего школьного возраста попрактиковаться в математических навыках? Как насчет измерения углов с помощью iPad или iPhone? Попробуйте приложение Draw2Measure Protractor от American Printing House for the Blind. Учащиеся старших классов, если вы хотите бросить вызов своим знаниям в области тригонометрии и увидеть пример того, как математика используется в разработке приложений, вам также будет очень интересно это маленькое приложение!
Draw2Measure Protractor предоставляет учащимся с нарушениями зрения альтернативный способ измерения углов. Это бесплатное приложение, предназначенное для iPad, iPhone или iPod Touch. Загрузите приложение из App Store на свое устройство.
Задание для учащихся начальной школы: Измерьте углы вокруг себя.
Какие предметы в вашей комнате имеют острые углы? Можете ли вы найти вокруг себя что-нибудь, что имеет тупой угол?
Приложение Draw2Measure Protractor позволяет учащимся измерять углы двумя способами.
Во-первых, учащиеся могут расположить угол над экраном устройства, например телефона или планшета, и провести по сторонам угла кончиком пальца или стилусом. Приложение записывает расположение сторон, а затем вычисляет угол.
Для объектов, которые не помещаются на экране, учащиеся могут найти измерения, вращая само устройство, которое использует встроенный датчик гироскопа для измерения угла. Перейдите к разделу «Как использовать » для получения пошаговых инструкций, а также демонстрационного видео.
Задание для старшеклассников: сможете ли вы понять, как вычисляются углы?
С точки зрения разработчика приложений экран устройства подобен координатной плоскости в математике. Каждая точка на экране имеет уникальную комбинацию координат x и y (x, y). После того, как пользователь этого приложения нарисует линию вдоль одной стороны угла, приложение получит координаты многих точек на этой же линии (например, от 60 до 70 точек, в зависимости от того, как долго нарисована линия).
Приложение выберет только две точки: одну ближе к началу линии (назовем ее точкой А), а другую — ближе к концу линии (точка Б). Затем из второй строки приложение также получит две точки C и D. Зная координаты точек A, B, C и D, знаете ли вы, как приложение вычисляет угол между линией AB и линией CD? Сколько существует способов сделать это? Просто подсказка, вам нужно будет использовать свои знания тригонометрии. Поделитесь со своим учителем математики тем, что вы узнали.
Приятного обучения!
Чтобы получить дополнительные ресурсы, ознакомьтесь с нашим списком ресурсов #AtHomeWithAPH , где вы найдете бесплатные и доступные мероприятия, советы, вебинары и многое другое от APH, наших партнеров и других специалистов. У вас есть бесплатный и доступный ресурс, который вы хотели бы, чтобы мы включили? Напишите нам по адресу [email protected] , чтобы рассказать нам об этом!
Поделитесь этой статьей.
Связанные статьи
Мы используем приложения каждый день, чтобы проверять электронную почту, слушать музыку, играть в игры и общаться с друзьями.