Правильный шестиугольник. Правильный шестиугольник свойства.
- Альфашкола
- Статьи
- Правильный шестиугольник
Дарим в подарок бесплатный вводный урок!
Предметы
- Репетитор по математике
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ОГЭ по математике
- Репетитор по алгебре
- Репетитор по химии для подготовки к ЕГЭ
- Репетитор по русскому языку для подготовки к ЕГЭ
- Репетитор по русскому языку для подготовки к ОГЭ
- Подготовка к олимпиадам по английскому языку
- ВПР по математике
- Репетитор для подготовки к ВПР по обществознанию
- Репетитор по биологии для подготовки к ЕГЭ
- Репетитор по информатике для подготовки к ЕГЭ
Правильный шестиугольник — это многоугольник, состоящий из шести равных сторон и шести равных углов.
Свойства правильного шестиугольника
Вот некоторые свойства правильного шестиугольника:
-
Равные стороны: Все стороны правильного шестиугольника имеют одинаковую длину. Это означает, что каждая сторона равна другим сторонам в шестиугольнике.
-
Равные углы: Углы в правильном шестиугольнике равны между собой. Каждый угол равен 120 градусам.
-
Сумма углов: Сумма всех углов в правильном шестиугольнике равна 720 градусам. Это можно получить, умножив число углов (6) на величину каждого угла (120 градусов).
-
Центральная симметрия: У правильного шестиугольника есть центр симметрии, что означает, что при вращении шестиугольника вокруг этого центра на угол 60 градусов он будет выглядеть так же, как и до вращения.
-
Радиус окружности: В правильном шестиугольнике можно описать окружность, в которую все вершины шестиугольника попадают на окружность.
2, где сторона — длина стороны шестиугольника.
Эти свойства помогают определить и описать основные характеристики и свойства правильного шестиугольника.
Часто задаваемые вопросы:
✅ Можно ли вписать правильный шестиугольник в окружность?
↪ Да, правильный шестиугольник можно вписать в окружность таким образом, чтобы все его вершины лежали на окружности.
✅ Какие свойства имеют стороны в правильном шестиугольнике?
↪ В правильном шестиугольнике все стороны равны между собой.
✅ Какова сумма углов в правильном шестиугольнике?
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Александр Дмитриевич Родин
Репетитор по математике
Стаж (лет)
Образование:
Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА – Российский технологический университет»
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Ольга Николаевна Федорова
Репетитор по математике
Стаж (лет)
Образование:
Саратовский национальный исследовательский государственный университет имени Н.
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Роман Михайлович Мясников
Репетитор по математике
Стаж (лет)
Образование:
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Похожие статьи
- Признаки делимости (Часть 1)
- Периметр параллелограмма
- Как решать уравнения с помощью пропорции?
- НИЯУ МИФИ: Факультет Экономики
- Подготовка к контрольной работе по геометрии
- Как вычислить площадь квадрата стороны которого лежат на прямых
- 15 советов по воспитанию ребенка от Медведя из мультика Маша и Медведь
- Как создать лето зимой: растим огород на подоконнике
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Шестиугольник, виды, свойства и формулы
Шестиугольник, виды, свойства и формулы.

Поделиться в:
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник, выпуклый и невыпуклый шестиугольник
Правильный шестиугольник (понятие и определение)
Свойства правильного шестиугольника
Формулы правильного шестиугольника
Правильный шестиугольник в природе, технике и культуре
Звездчатый шестиугольник
Восьмиугольник
Шестиугольник, выпуклый и невыпуклый шестиугольник:
Шестиугольник – это многоугольник с шестью углами.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый шестиугольник
Рис. 2. Невыпуклый шестиугольник
Сумма внутренних углов любого выпуклого шестиугольника равна 720°.
.
Правильный шестиугольник (понятие и определение):
Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
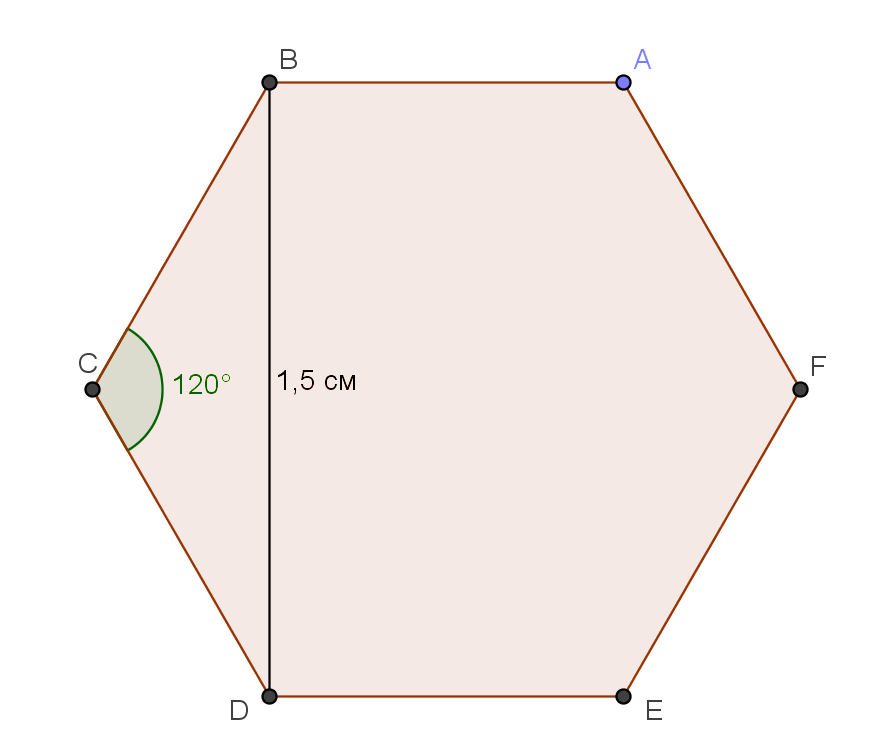
Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.
Рис. 3. Правильный шестиугольник
Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.
Углы правильного шестиугольника образуют шесть равносторонних треугольников.
Правильный шестиугольник можно построить с помощью циркуля и линейки.
Свойства правильного шестиугольника:
1. Все стороны правильного шестиугольника равны между собой.
Все стороны правильного шестиугольника равны между собой.
a1 = a2 = a3 = a4= a5= a6.
2. Все углы равны между собой и составляют 120°.
α1 = α2 = α3 = α4 = α5 = α6 = 120°.
Рис. 4. Правильный шестиугольник
3. Сумма внутренних углов любого правильного шестиугольника равна 720°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.
Рис. 5. Правильный шестиугольник
5. Количество диагоналей правильного шестиугольника равно 9.
Рис. 6. Правильный шестиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.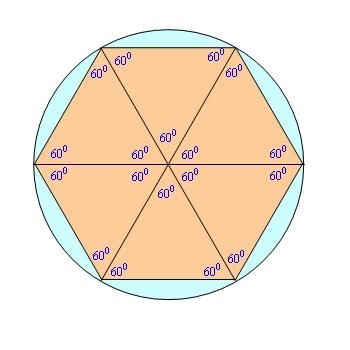
Рис. 7. Правильный шестиугольник
7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
8. Радиус описанной окружности правильного шестиугольника и его сторона равны.
Рис. 8. Правильный шестиугольник
R = a
Правильный шестиугольник в природе, технике и культуре:
Пчелиные соты имеют форму правильного шестиугольника.
Графит, графен имеют гексагональную кристаллическую решетку.
Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.
Рис. 9. Гигантский гексагон на Сатурне
Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
Панцирь черепахи состоит из шестиугольников.
Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.
Рис. 10. Материковая часть Франции
Формулы правильного шестиугольника:
Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.
Формулы периметра правильного шестиугольника:
Формулы площади правильного шестиугольника:
Формула радиуса окружности, вписанной в правильный шестиугольник:
Формула радиуса окружности, описанной вокруг правильного шестиугольника:
R = a
Звездчатый шестиугольник:
Звездчатый шестиугольник (гексаграмма) – это многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника.
Гексаграмма (др.-греч. ἕξ – «шесть» и γραμμή – «черта, линия») – это звезда с шестью углами, которая образуется из двух наложенных друг на друга равносторонних треугольников.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности 7 696
Как найти угол в шестиугольнике
Все математические ресурсы PSAT
10 диагностических тестов 421 практический тест Вопрос дня Карточки Learn by Concept
PSAT Math Help » Геометрия » Плоская геометрия » Шестиугольники » Как найти угол в шестигранке
Возможные ответы:170
210
190
200
180
Правильный ответ:190
Пояснение:Сообщить об ошибке
Если треугольник имеет 180 градусов, какова сумма внутренних углов правильного восьмиугольника?
Возможные ответы: Правильный ответ: Объяснение: Сумма внутренних углов многоугольника определяется как где = количество сторон многоугольника.
Сообщить об ошибке
Какова величина каждого внутреннего угла в прямоугольном шестиугольнике?
Возможные ответы:120 градусов
72 градуса
90 градусов
105 градусов
150 градусов
9001 0 Правильный ответ:120 градусов
Пояснение:Сумма внутренних углов шестиугольника должна равняться 720 градусам. Поскольку шестиугольник правильный, все внутренние углы будут иметь одинаковую величину. Шестиугольник имеет шесть сторон и шесть внутренних углов. Следовательно, каждый угол измеряет.
Сообщить об ошибке
Примечание. Рисунок выполнен НЕ в масштабе.
См. рисунок выше. Оценивать .
Возможные ответы: Правильный ответ: Объяснение:Сумма градусных мер углов (шестистороннего) шестиугольника равна
. Мы можем решить в уравнении Ошибка
Мы можем решить в уравнении Ошибка
Примечание: Рисунок выполнен НЕ в масштабе.
См. рисунок выше. Оценивать .
Возможные ответы: Правильный ответ: Объяснение:Сумма градусных мер углов (шестистороннего) шестиугольника равна
. Мы можем найти в уравнении
9 0005
Сообщить об ошибке
Три угла шестиугольника. Остальные три угла равны между собой. Какова мера каждого из последних трех углов?
Возможные ответы:Этот шестиугольник не может существовать.
Правильный ответ: Объяснение:Сумма градусных мер углов (шестистороннего) шестиугольника равна
Позвольте быть общей мерой трех рассматриваемых конгруэнтных углов. Мы можем найти в уравнении
Сообщить об ошибке
Какова величина одного из внутренних углов правильного шестиугольника?
Возможные ответы: Правильный ответ: Объяснение: Чтобы найти сумму внутренних углов любого правильного многоугольника, используйте формулу , где представляет количество сторон правильного многоугольника.
Сумма внутренних углов правильного шестиугольника равна 720 градусов. Чтобы найти величину одного угла, разделите его на количество внутренних углов (или сторон):
Размер одного угла в правильном шестиугольнике равен 120 градусам.
Сообщить об ошибке
Уведомление об авторских правах
Все математические ресурсы PSAT
10 диагностических тестов 421 практический тест Вопрос дня Карточки Учитесь по концепции
Как найти угол в шестиугольнике
Все ресурсы по геометрии среднего уровня
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept
Intermediate Geometry Help » Плоская геометрия » Шестиугольники » Как найти угол в шестиугольнике
Существует правильный шестиугольник с длиной стороны . Чему равен внутренний угол?
Чему равен внутренний угол?
невозможно определить
Правильный ответ: Пояснение:Учитывая, что шестиугольник является правильным шестиугольником, это означает, что длины всех сторон равны и все внутренние углы равны. Вопрос требует от нас решения для меры внутреннего угла. Учитывая вышеупомянутое определение правильного многоугольника, это означает, что должен быть только один правильный ответ.
Чтобы найти ответ, вопрос предоставляет дополнительную информацию, которая не обязательно требуется. Меру внутреннего угла можно решить с помощью уравнения:
где количество сторон многоугольника.
В этом случае .
Для этой задачи информация о длине стороны может быть инвертирована.
Сообщить об ошибке
Каков внутренний угол правильного шестиугольника, если его площадь равна 15?
Возможные ответы: Правильный ответ: Пояснение: Площадь не имеет отношения к нахождению угла правильного шестиугольника.
В правильном шестиугольнике 6 сторон. Используйте следующую формулу для определения внутреннего угла.
Подставьте стороны, чтобы определить сумму всех внутренних углов шестиугольника в градусах.
Поскольку сторон 6, разделите это число на 6, чтобы определить величину каждого внутреннего угла.
Сообщить об ошибке
Дано: правильный шестиугольник с центром . Постройте сегменты и , чтобы сформировать четырехугольник .
Верно или неверно: Четырехугольник — это прямоугольник.
Возможные ответы:Верно
Неверно
Правильный ответ:Неверно
Объяснение:Ниже показан правильный Шестиугольник с центром – отрезок, проведенный из к каждой вершине, то есть к каждой из его радиусов нарисовано.
Каждый угол правильного шестиугольника измеряет ; по симметрии каждый радиус делит угол шестиугольника пополам, поэтому
.
Углы прямоугольника должны измеряться , поэтому было опровергнуто, что Четырехугольник является прямоугольником.
Сообщить об ошибке
Верно или неверно: измеряется каждый из шести углов правильного шестиугольника.
Возможные ответы:Неверно
Верно
Правильный ответ:Правда
Объяснение:Правильный многоугольник со сторонами имеет конгруэнтные углы, каждый из которых измеряет
При установке , общая мера угла может быть вычислена как
Таким образом, утверждение верно.
Сообщить об ошибке
Верно или неверно: каждый из внешних углов правильного шестиугольника измеряет .
Возможные ответы:Неверно
Верно
Правильный ответ:Неверно
Объяснение: Если в каждой вершине любого многоугольника взять один внешний угол и сложить их меры, то сумма будет равна . Каждый внешний угол правильного шестиугольника имеет одинаковую меру, поэтому, если мы допустим эту общую меру, то
Каждый внешний угол правильного шестиугольника имеет одинаковую меру, поэтому, если мы допустим эту общую меру, то
Решите для:
Утверждение неверно.
Сообщить об ошибке
Дано: Шестиугольник .
Верно, ложно или неопределенно: шестиугольник правильный.
Возможные ответы:Не определено
Неверно
Верно
Правильный ответ:Неверно
Объяснение:Предположим, что шестиугольник правильный. Каждый угол правильного многоугольника со сторонами имеет размер
У шестиугольника 6 сторон, поэтому установите ; каждый угол правильного шестиугольника имеет меру
Поскольку для измерения задан один угол, шестиугольник не может быть правильным.
Сообщить об ошибке
Какова мера одного внешнего угла правильного двадцатистороннего многоугольника?
Возможные ответы: Правильный ответ: Объяснение: Сумма внешних углов любого многоугольника, по одному в каждой вершине, равна .