Углы в шестиугольнике правильном: Обучение — учебные курсы и тесты

Шестиугольная призма — геометрическое тело

Шестиугольная призма — геометрическое тело — Mnogogranniki.ru

Вы здесь:
• Главная
• Правильная шестиугольная призма

Правильная шестиугольная призма — это шестиугольная призма у которой основания правильные шестиугольники (все стороны которых равны, углы между сторонами основания составляют 120 градусов), а боковые грани прямоугольники.

Основания призмы являются равными правильными шестиугольниками.

Боковые грани призмы являются прямоугольниками.

Боковые рёбра призмы параллельны и равны.

Размеры призмы можно выразить через длину стороны a и высоту h.

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Формула площади поверхности шестиугольной призмы:

Объём призмы равен произведению её высоты на площадь основания.

Формула объема правильной шестиугольной призмы:

Правильная шестиугольная призма может быть вписана в цилиндр.

Формула радиуса цилиндра вписанной шестиугольной призмы:

Двойственным многогранником прямой призмы является бипирамида.

Исторически понятие «призма» возникло из латыни и означало — нечто отпиленное.

Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.

Скачать развертку правильной шестиугольной призмы для печати на листе А4

 

Геометрические размеры готовой призмы (мм):

Длина = 90

Ширина = 78

Высота = 45

 

Скачать развертку правильной шестиугольной призмы для печати на листе А4

 

Геометрические размеры готовой призмы (мм):

Длина = 73

Ширина = 64

Высота = 73

Скачать развертку правильной шестиугольной призмы для печати на листе А4

 

Геометрические размеры готовой призмы (мм):

Длина = 62

Ширина = 54

Высота = 93

 

 

посмотреть другие призмы

Популярное

Отличие выпусков № 12 и № 36 Волшебных граней

Когда мы готовили 36-ой выпуск «Волшебные грани», у наших коллег возник вопрос: «Почему мы опять собираемся говорить о правильных многогранниках,…

Что такое многогранник? Примеры

Многогранник — (определение) геометрическое тело, ограниченное со всех сторон плоскими многоугольниками — гранями.

Звезда Кеплера

Монумент «Звезда Кеплера» (норв. Keplerstjernen), высотой 45 метров, расположен недалеко от города Осло (Норвегия) в окрестностях аэропорта…

Новоталицкая школа

Под руководством учителя математики Тимофеевой Татьяны Юрьевны ребята работали над проектом «Удивительный мир многогранников». Делали свои развертки и использовали развертки из…

Миры Ричарда Суини

Молодой британский дизайнер Ричард Суини (Richard Sweeney) создает удивительные скульптуры из. ..

Правильные многогранники

Правильные многогранники, их всего пять: тетраэдр, октаэдр, куб (другое название гексаэдр),…

Выбрать один продукт

В настоящее время покупатель столкнулся с настолько широким ассортиментом товаров, что сил на то чтобы сделать рациональный выбор уже не хватает. И реклама иногда только усиливает…

Площадь правильного шестиугольника онлайн

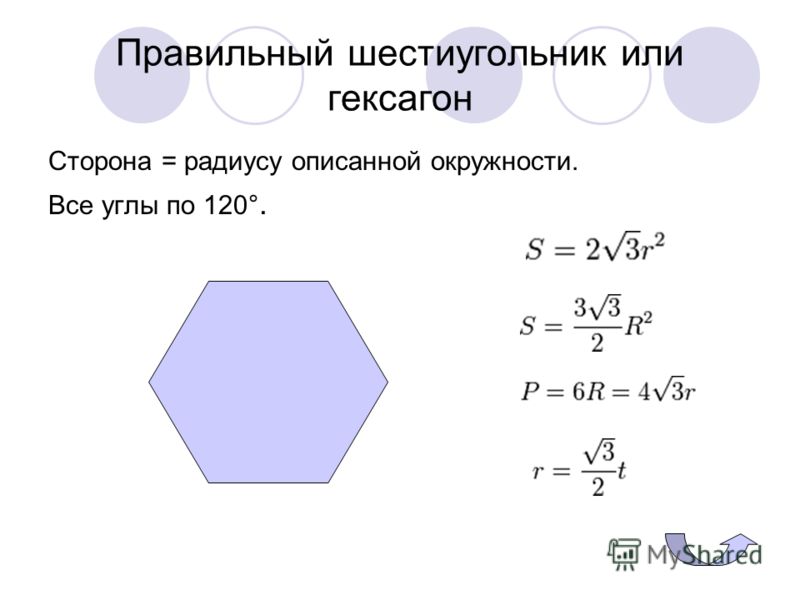
Шестиугольник — многоугольник, у которого есть шесть сторон и шесть углов. В правильном заданном многоугольном геометрическом объекте все стороны равняются друг другу, а углы формируют шесть равносторонних треугольников.

Площадь правильной фигуры с шестью углами — положительная величина некоторой области плоскости, занимаемой данным многоугольным геометрическим объектом.

Выделяют ряд методов нахождения площади этого многоугольника, зависимо от его типа.

• Площадь правильного шестиугольника через длину стороны
• Площадь правильного шестиугольника через радиус описаной окружности
• Площадь правильного шестиугольника через радиус вписаной окружности
• Площадь правильного шестиугольника через длинную диагональ
• Площадь правильного шестиугольника через короткую диагональ
• Площадь правильного шестиугольника через периметр

Через длину стороны

По той причине, что выпуклый шестиугольник включает в себя шесть равносторонних треугольников, тогда формула нахождения требуемой величины через длину стороны выглядит следующим образом:

S = (3√3*a²)/2

где a — это продолжительность стороны.

Сторона (a):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

Рассмотрим пример. Пусть длина стороны эквивалентна 8. Тогда, согласно этой формуле, заданную характеристику замкнутого выпуклого шестиугольника будет примерно равна 166.

Всё достаточно просто, если сторона заранее известна. Если же эта величина нам не дана, но известен периметр или апофема — высота одного из шести равносторонних треугольников — тогда длину стороны можно высчитать.

В случае, если известен периметр, его необходимо поделить на шесть, таким образом получается длина стороны. К примеру, если периметр равен 36, то, поделив 36 на 6, получается 6 — это и есть протяжённость стороны.

Если известна лишь апофема, тогда можно посчитать длину стороны, подставив апофему в формулу b = x√3 и умножив ответ на 2. Всё это потому, что апофема — это сторона x√3 составляемого ей треугольника с углами 30, 60 и 90 градусов. К примеру, если апофема 11√3, то x = 11, а протяжённость стороны будет эквивалентна 22.

Через периметр

Если при изучении правильной фигуры с шестью углами нам известен только его периметр, несложно рассчитать площадь этой фигуры по такой формуле:

Периметр (P):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

S = (3√3*(p/6)²)/2

где p — это периметр фигуры.

Допустим, если периметр будет равняться 24, тогда площадь будет примерно эквивалентна 42. Если в качестве периметра возьмём число 50, тогда площадь фигуры окажется 180.

Через длинную диагональ

Длинная или большая диагональ шестиугольника — это диаметр описанной вокруг него плоской кривой, как правило, она равняется двум его сторонам.

Диагональ (D):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

Используем такое выражение для подсчёта площади подобного правильного многоугольного геометрического объекта через длинную диагональ этого множества точек:

S = (3√3*D²)/8

где D — это длинный отрезок, соединяющий несмежные вершины.

К примеру, если D = 6, тогда заданная характеристика замкнутого выпуклого многоугольника будет приблизительно равна 23. Если в качестве длинной диагонали возьмём 8, тогда величина будет примерно эквивалентна 42.

Через короткую диагональ

Меньшая или короткая диагональ правильного шестиугольника в √3 раз длиннее его стороны, также она образует с ней прямой угол.

Диагональ (D):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

Если известна короткая диагональ такого выпуклого многоугольника, то с её помощью можно найти площадь этой фигуры следующим образом:

S = (√3*D²)/2

где D — это протяжённость короткого отрезка, соединяющего несмежные вершины.

К примеру, если длина такой диагонали будет равна 14, тогда необходимая характеристика фигуры будет примерно равняться 170. Если же в качестве D мы возьмём 2, тогда величина окажется всего лишь 3.

Через радиус описанной окружности

Шестиугольник считается правильным многоугольником, ведь все его стороны и углы эквивалентны друг другу. Соответственно, около такого многоугольника можно описать окружность.

Чтобы найти площадь выпуклого многоугольника через радиус описанной окружности, необходимо воспользоваться такой формулой:

S = (3√3*R²)/2

где R — это отрезок, соединяющий центр и любую точку описанной замкнутой плоской кривой.

Радиус (R):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

К примеру, если отрезок, соединяющий центр и любую точку, равняется 5, тогда заданная характеристика замкнутой фигуры будет примерно равна 65. Если же в качестве радиуса возьмём число 12, соответственно, заданная характеристика замкнутой фигуры получится примерно 374.

Через радиус вписанной окружности

Шестиугольник считается правильным многоугольником, ведь все его стороны и углы равны друг другу.

Соответственно, во всякий шестиугольник можно вписать окружность.

Формула для расчёта площади следующего выпуклой фигуры с шестью углами через радиус вписанной окружности будет выглядеть следующим образом:

S = √3*r²

где r — это отрезок, соединяющий центр и любую точку вписанной замкнутой плоской кривой.

Радиус (R):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

К примеру, если этот отрезок, соединяющий центр и любую точку, равен 14, тогда необходимая величина этого множества точек будет примерно равна 679. Если в качестве отрезка, соединяющего центр и любую точку, возьмем 4, тогда площадь будет приблизительно равна 55.

Что такое правильный шестиугольник

Этот многоугольный геометрический объект имеет определённые свойства:

• Каждый угол этой фигуры равняется 120 градусам;
• Вокруг правильного шестиугольника можно описать окружность, причем единственную, а её радиус равняется его стороне;
• Большие диагонали такого выпуклого многоугольника разделяют его на шесть равносторонних треугольников, высота каждого равняется радиусу вписанной в выпуклый многоугольник окружности;
• Центры вписанной и описанной окружностей около подобного выпуклого многоугольника — это точка пересечения больших диагоналей этого множества точек.

Эта фигура очень часто встречается в природе, технике и культуре. К примеру:

• Пчелиные соты изображают разделение плоскости на выпуклые шестиугольники;
• Некоторые сложные молекулы углерода имеют гексагональную кристаллическую решётку;
• Сечение гайки и большинства карандашей описывается таким выпуклым многоугольником;
• Гексаграмма — это шестиконечная звезда, сформированная двумя правильными треугольниками. Также её называют звездой Давида, она считается символом иудаизма.

Шестиугольник | Площадь шестиугольника | Правильный шестиугольник

Многоугольник – это двумерная (2-D) замкнутая фигура, состоящая из отрезков прямых линий. В геометрии шестиугольник — это многоугольник с 6 сторонами. Если длины всех сторон и измерения всех углов равны, такой шестиугольник называется правильным шестиугольником. Другими словами, стороны правильного шестиугольника равны.

Существует предопределенный набор формул для расчета периметра и площади правильного шестиугольника, которые в совокупности называются формулой шестиугольника. Формула шестиугольника для шестиугольника со стороной a задается как: 9{2}\end{array} \)

Формула шестиугольника помогает нам вычислить площадь и периметр шестиугольных объектов. Соты, кварцевый кристалл, головка болта, колесная гайка, шестигранный ключ, напольная плитка и т. д. — вот несколько вещей, которые можно найти в шестиграннике.

Свойства правильного шестиугольника:

• Шесть сторон и шесть углов.
• Длины всех сторон и размеры всех углов равны.
• Общее количество диагоналей в правильном шестиугольнике равно 9.
• Сумма всех внутренних углов равна 720 градусам, где каждый внутренний угол равен 120 градусам.
• Сумма всех внешних углов равна 360 градусам, где каждый внешний угол равен 60 градусам.

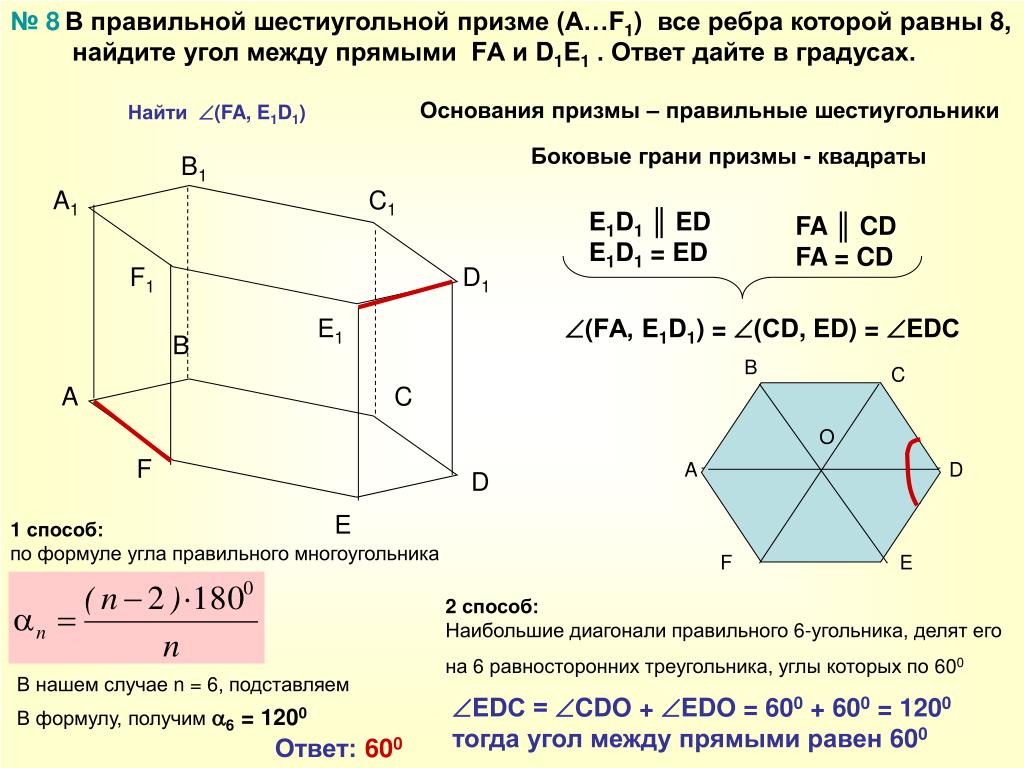
Вывод:

Рассмотрим правильный шестиугольник, каждая сторона которого равна a единиц.

Формула площади шестиугольника: Площадь шестиугольника определяется как область, занимаемая внутри границы шестиугольника.

Чтобы вычислить площадь шестиугольника, мы разделим его на шесть маленьких равнобедренных треугольников. Вычислите площадь одного из треугольников, а затем умножьте на 6, чтобы найти общую площадь многоугольника.

Возьмите один из треугольников и проведите линию от вершины до середины основания, чтобы получился прямой угол. Основание треугольника a , длина стороны многоугольника. Пусть длина этой линии будет ч .

Сумма всех внешних углов равна 360 градусам. Здесь ∠AOB = 360/6 = 60°

∴ θ = 30°

Мы знаем, что тангенс угла находится напротив смежной стороны,

Следовательно,

\(\begin{array}{l } tan\theta = \frac{\left ( a/2 \right )}{h}\end{array} \)

\(\begin{array}{l}tan30 = \frac{\left ( a/ 2 \right )}{h}\end{array} \)

\(\begin{array}{l}\frac{\sqrt{3}}{3}= \frac{\left ( a/2 \ справа )}{h}\end{массив} \)

\(\begin{array}{l}h= \frac{a}{2}\times \frac{3}{\sqrt{3}}\ конец {массив} \) 9{2}\end{array} \)

Формула для периметра шестиугольника: Периметр шестиугольника определяется как длина границы шестиугольника. {2}\end{массив} \)

= 41,57 см²

Чтобы решить другие задачи по этой теме, загрузите BYJU’S-The Learning App.

Углов в шестиугольнике — Математика GCSE

Введение

Как решать задачи на углы в шестиугольнике

Углы в рабочем листе шестиугольника

Распространенные заблуждения

Практика углов в шестиугольнике вопросы

Углы в шестиугольнике GCSE вопросы

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Как решать задачи на углы в шестиугольнике

Углы в рабочем листе шестиугольника

Распространенные заблуждения

Практика углов в шестиугольнике вопросы

Углы в шестиугольнике GCSE вопросы

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем об углах шестиугольника, включая нахождение суммы внутренних углов и решение задач на внутренние и внешние углы.

В рабочих листах также есть углы в виде шестиугольника , основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.

Какие углы в шестиугольнике?

Углы шестиугольника — это углы шестигранного многоугольника (двумерная форма).

• A правильный шестиугольник имеет шесть равных длин сторон, шесть вершин и шесть равных внутренних углов .
9{\circ}, потому что они образуют прямую линию. Это дополнительные углы.
• Внутренние углы шестиугольника — это углы внутри двумерной формы, образованные при встрече двух сторон формы.

  Мы можем найти сумму внутренних углов шестиугольника по формуле

  \text{Сумма внутренних углов}=(n-2) \times 180, где n — количество сторон.

  У шестиугольника 6 сторон, поэтому n=6. {\circ} \end{выровнено}

  В приведенной выше формуле используется соотношение между углами треугольника и количеством треугольников, на которые можно разделить многоугольник.

  
  Чтобы найти внутренний угол правильного шестиугольника , мы можем разделить сумму внутренних углов на количество сторон, в данном случае 6.

Пошаговое руководство: Внутренние углы многоугольника

• Внешние углы шестиугольника 9{\ круг}.

  Чтобы найти каждый из внешних углов правильного шестиугольника , мы можем использовать формулу

  \text{Внешний угол правильного многоугольника}=\frac{360}{n}, где n — число сторон.

  В качестве альтернативы, если мы знаем размер внешнего угла многоугольника, мы можем использовать преобразование приведенной выше формулы для определения количества сторон многоугольника.

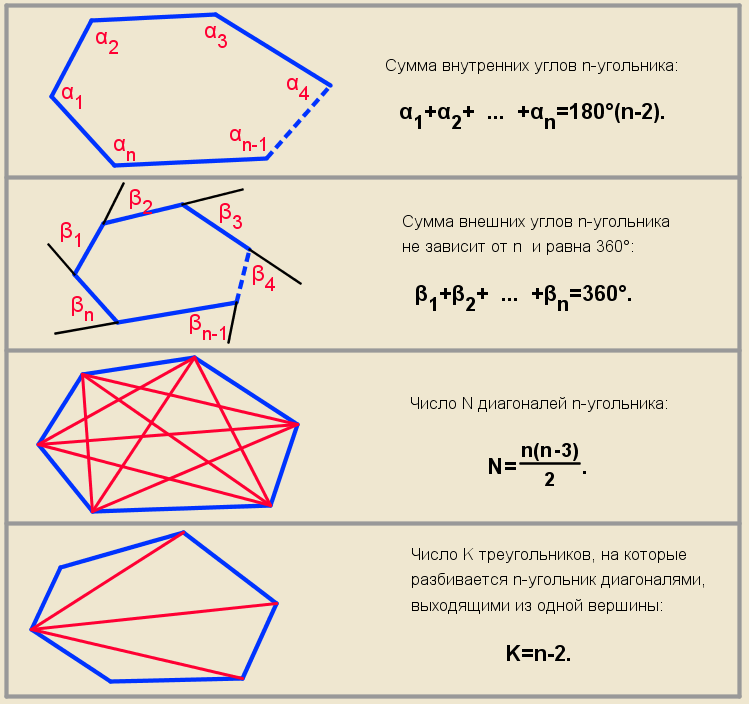
  \text{Число сторон}=\frac{360}{\text { внешний угол }}

Пошаговое руководство: Внешние углы многоугольника

Как решать задачи на углы в шестиугольнике

шестиугольник регулярный или нерегулярный.

• Определите, к чему относится вопрос.
• Решите проблему, используя собранную информацию.

Как решать задачи на углы в шестиугольнике

Рабочий лист углов в многоугольниках (включает углы в шестиугольнике)

Получите свободные углы в рабочем листе шестиугольника из 20+ углов в многоугольниках, вопросы и ответы. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО
Икс

Рабочий лист углов в многоугольниках (включает углы в шестиугольнике)

Получите свободные углы в рабочем листе шестиугольника из 20+ углов в многоугольниках, вопросы и ответы. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Связанные уроки по углам в многоугольниках

Углы в четырехугольнике  являются частью нашей серии уроков, посвященных пересмотру углов в многоугольниках . Возможно, вам будет полезно начать с урока по основным углам в многоугольниках, чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства ниже для получения дополнительной информации по отдельным темам. Другие уроки этой серии включают:

• Углы в многоугольниках
• Углы в треугольнике
• Углы пятиугольника
• Углы четырехугольника

Углы в шестиугольнике примеры

Пример 1: нахождение внешнего угла правильного шестиугольника

Ниже приведен правильный шестиугольник. Найдите угол, отмеченный х.

1. Определите, является ли шестиугольник правильным или неправильным.

Вопрос говорит нам, что это правильный шестиугольник. Это означает, что стороны шестиугольника равны, а внутренние углы равны.

2 Определите, к чему относится вопрос.

Задача состоит в том, чтобы мы нашли угол x, который является одним из шести внешних углов этого шестиугольника.

3 Решите проблему, используя собранную информацию.

Чтобы найти размер внешних углов правильного шестиугольника, мы можем использовать формулу

\text{Внешний угол правильного многоугольника}=\frac{360}{n}, где n — количество сторон .

Итак, недостающий угол можно вычислить как 9{\ круг}.

Пример 2: нахождение суммы внутренних углов шестиугольника

Чему равна сумма внутренних углов шестиугольника?

Определите, является ли шестиугольник правильным или неправильным.

Вопрос не уточняет, правильный или неправильный шестиугольник, однако в контексте вопроса это не имеет значения. Сумма внутренних углов шестиугольника будет одинаковой независимо от того, правильный он или неправильный.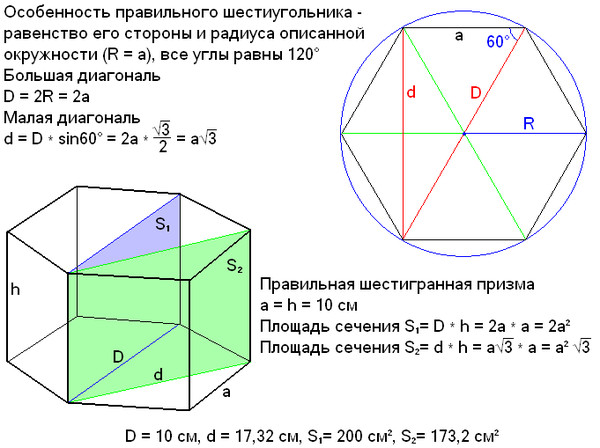 {\ circ} \end{выровнено}

Пример 3: нахождение внутреннего угла правильного шестиугольника

Ниже показана форма правильного шестиугольника. Найдите угол, отмеченный х.

Определите, является ли шестиугольник правильным или неправильным.

Вопрос говорит нам, что это правильный шестиугольник.

Определите, к чему относится вопрос.

Задача состоит в том, чтобы мы нашли угол x, который является одним из шести внутренних углов этого шестиугольника.

Решите проблему, используя собранную информацию.

Чтобы найти размер внутреннего угла любого шестиугольника, нам нужно сначала вычислить сумму внутренних углов.


Чтобы вычислить сумму внутренних углов любого многоугольника, мы можем использовать формулу


\text{Сумма внутренних углов}=(n-2) \times 180, где n — количество сторон.


Итак, внутренний угол шестиугольника можно рассчитать как


\begin{aligned} & =(n-2) \times 180 \\\\ & =(6-2) \times 180 \\ \\ & =4 \times 180 \\\\ & =720^{\circ} \end{align} 9{\ круг}.

Пример 4: нахождение внутреннего угла неправильного шестиугольника

Ниже приведен многоугольник. Найдите величину недостающего угла х.

Определите, является ли шестиугольник правильным или неправильным.

В вопросе не указано, является ли многоугольник правильным или неправильным, однако внутренние углы шестиугольника не равны, поэтому он должен быть неправильным.

Определите, к чему относится вопрос.

Вопрос просит нас вычислить сумму внутренних углов шестиугольника.

Решите проблему, используя собранную информацию.

Чтобы найти размер внутреннего угла любого шестиугольника, нам нужно сначала вычислить сумму внутренних углов.


Чтобы вычислить сумму внутренних углов любого многоугольника, мы можем использовать формулу


\text{Сумма внутренних углов}=(n-2) \times 180, где n — количество сторон.


Итак, внутренний угол шестиугольника можно рассчитать как

9{\circ}

Пример 5: нахождение внешнего угла неправильного шестиугольника

Ниже показан неправильный многоугольник. Найдите величину недостающего угла х.

Определите, является ли шестиугольник правильным или неправильным.

В вопросе говорится, что многоугольник неправильный.

Определите, к чему относится вопрос.

Задача состоит в том, чтобы найти недостающий внешний угол.

Решите проблему, используя собранную информацию.

Чтобы найти размер внешнего угла x, нам нужно найти соответствующий ему отсутствующий внутренний угол, обозначенный y на диаграмме ниже.


Чтобы найти размер внутреннего угла любого шестиугольника, нам нужно сначала вычислить сумму внутренних углов.


Чтобы вычислить сумму внутренних углов любого многоугольника, мы можем использовать формулу


\text{Сумма внутренних углов}=(n-2) \times 180, где n — количество сторон. 9{\ круг}.

Пример 6: решение угловых задач с использованием шестиугольников

На схеме показана мозаика из фрагмента напольной плитки.

Фигура состоит из двух правильных многоугольников.

Найдите величину угла, обозначенного x.

Определите, является ли шестиугольник правильным или неправильным.

В вопросе говорится, что оба многоугольника на диаграмме являются правильными многоугольниками.

Определите, к чему относится вопрос.

Вопросы просят нас найти размер угла x, который образован снаружи двух правильных шестиугольников.

Решите проблему, используя собранную информацию.

Чтобы найти размер угла x, нам нужно найти недостающие внутренние углы, которые пересекаются с ним в этой точке.


Чтобы найти размер внутреннего угла любого шестиугольника, нам нужно сначала вычислить сумму внутренних углов.


Чтобы вычислить сумму внутренних углов любого многоугольника, мы можем использовать формулу 9{\ круг}.

Распространенные заблуждения

• Правильные и неправильные многоугольники

Важно правильно определить, является ли многоугольник правильным или неправильным, используя информацию, указанную в вопросе или на диаграмме. Не предполагайте ни того, ни другого.

• Неправильное использование формул

Правильный или неправильный многоугольник определяет, как можно использовать формулы для работы с внутренними и внешними углами. Например, формула 9{\circ}

Чтобы найти значение одного внутреннего угла неправильного многоугольника, нам сначала нужно вычислить сумму внутренних углов многоугольника.

 

Сумму внутренних углов любого многоугольника можно найти по формуле

 

\text{Сумма внутренних углов}=(n-2) \times 180, где n — количество сторон.

 

Таким образом, сумма внутренних углов шестиугольника может быть рассчитана как

 

9019{\circ}

Чтобы найти величину внешнего угла x, нам нужно найти соответствующий ему недостающий внутренний угол. Чтобы найти размер внутреннего угла любого шестиугольника, нам нужно сначала вычислить сумму внутренних углов.

 

Чтобы вычислить сумму внутренних углов любого многоугольника, мы можем использовать формулу

 

\text{Сумма внутренних углов}=(n-2) \times 180, где n — количество сторон .

 

Итак, внутренний угол шестиугольника можно рассчитать как 9{\ круг}. Найдите количество сторон многоугольника и, следовательно, назовите фигуру.

 

(2 балла)

Показать ответ

\frac{360}{60}=6

(1)

Шестиугольник

(1)

Контрольный список

Теперь вы знаете, как:

• Найти внешний угол шестигранника
• Найдите сумму внутренних углов шестиугольника
• Найдите значение внутреннего угла шестиугольника
• Решить задачи с углами в шестиугольниках

Все еще зависает?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.

Узнайте больше о нашей программе обучения математике GCSE.

Мы используем необходимые и необязательные файлы cookie, чтобы улучшить работу нашего веб-сайта.