Углы в правильной шестиугольной призме — Dudom
Изучением призм занимается пространственная геометрия. Важными их характеристиками являются заключенный в них объем, площадь поверхности и число составляющих элементов. В статье рассмотрим все эти свойства для шестиугольной призмы.
О какой призме пойдет речь?
Призма шестиугольная — это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.
На рисунке изображен пример этой призмы.
Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.
Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90 o . Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
Элементы
Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).
В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:
число ребер = число граней + число вершин — 2.
Указанные выше цифры удовлетворяют этой формуле.
Диагонали призмы
Все диагонали шестиугольной призмы можно разделить на два типа:
- те, которые лежат в плоскостях ее граней;
Рисунок ниже показывает все эти диагонали.
Видно, что D1 — это диагональ боковой стороны, D2 и D3 — диагонали всей призмы, D4 и D5 — диагонали основания.
Длины диагоналей боковых сторон между собой равны. Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b — длину бокового ребра. Тогда диагональ имеет длину:
Диагональ D4 также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D4 является диаметром этой окружности, то есть получим следующую формулу:
Диагональ D5 основания найти несколько сложнее.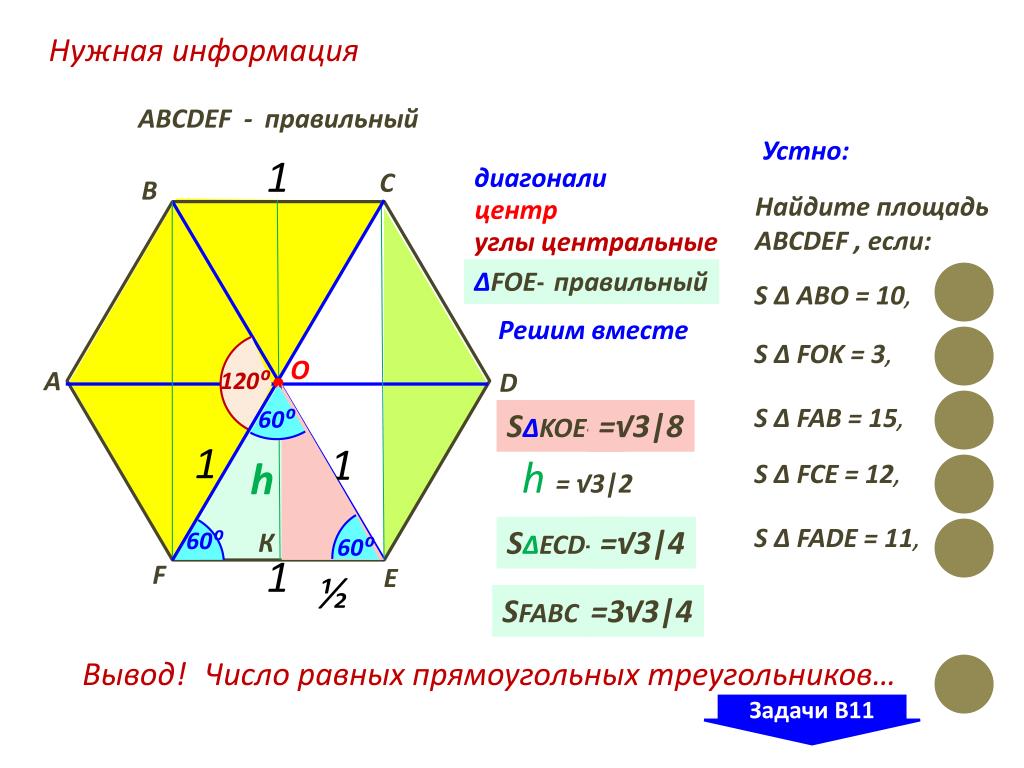 Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120 o . Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:
Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120 o . Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:
Сторона AC является диагональю D5, поэтому получаем:
Теперь остается найти диагонали D2 и D3 правильной шестиугольной призмы. Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:
Таким образом, самой большой диагональю для любых значений a и b является D2.
Площадь поверхности
Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.
Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты.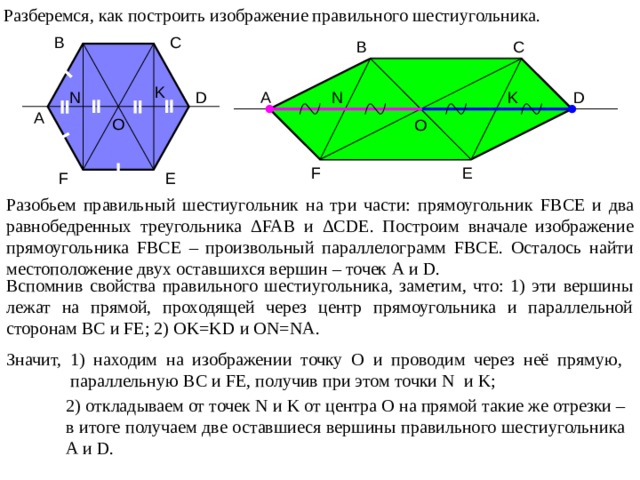 Шестиугольников 2, прямоугольников 6.
Шестиугольников 2, прямоугольников 6.
Для площади прямоугольника получаем:
Тогда площадь боковой поверхности равна:
Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:
Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:
Это выражение следует умножить на два, чтобы получить площадь оснований призмы:
Остается сложить Sos и S2, чтобы получить полную площадь поверхности фигуры:
Объем призмы
После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого. Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:
Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра.
На сайте уже были рассмотрены некоторые типы задач по стереометрии, которые входят в единый банк заданий экзамена по математике. Например, задания про составные многогранники .
Призма называется правильной если её боковые перпендикулярны основаниям и в основаниях лежит правильный многоугольник. То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.
В этой статье для вас задачи на решение призмы, в основании которой лежит правильный шестиугольник . Особенностей и сложностей в решении нет никаких. В чём суть? Дана правильная шестиугольная призма, требуется вычислить расстояние между двумя вершинами или найти заданный угол. Задачи на самом деле простые, в итоге решение сводится к нахождению элемента в прямоугольном треугольнике.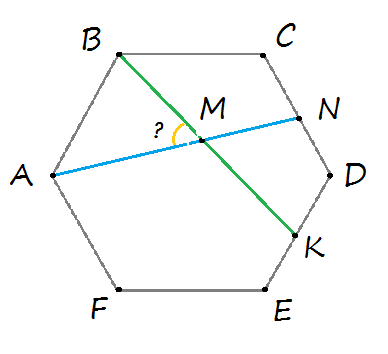
Используется теорема Пифагора и теорема косинусов . Необходимо знание определений тригонометрических функций в прямоугольном треугольнике.
Обязательно посмотрите информацию о правильном шестиугольнике в этой статье (пункт 6) . Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.
Кратко: что представляет собой правильный шестиугольник?
Известно, что в правильном шестиугольнике стороны равны. Кроме этого, углы между сторонами тоже равны .
*Противолежащие стороны параллельны.
Радиус окружности описанной около правильного шестиугольника равен его стороне. *Это подтверждается очень просто: если мы соединим противоположные вершины шестиугольника, то получим шесть равных равносторонних треугольников. Почему равносторонних?
У каждого треугольника угол при его вершине лежащей в центре равен 60 0 (360:6=60).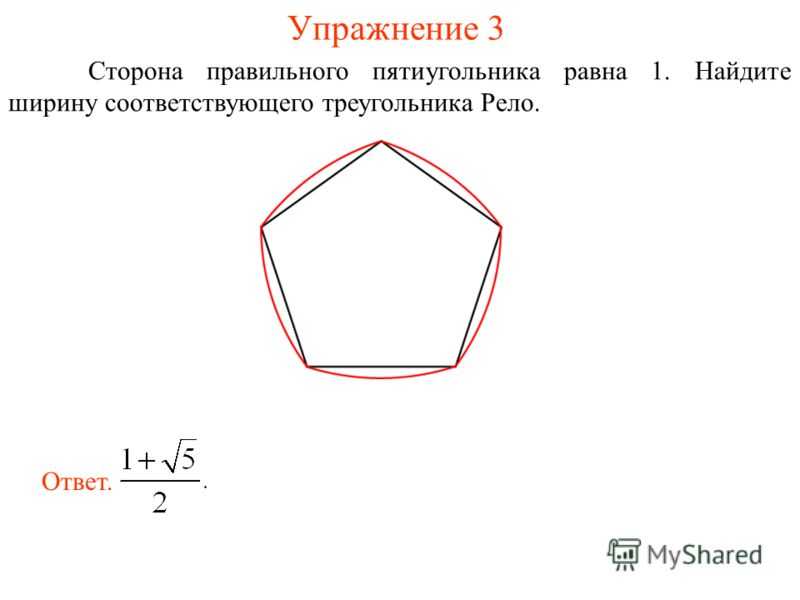 Так как у треугольника две стороны имеющие общую вершину в центре равны (это радиусы описанной окружности), то каждый угол при основании такого равнобедренного треугольника так же равен 60 градусам.
Так как у треугольника две стороны имеющие общую вершину в центре равны (это радиусы описанной окружности), то каждый угол при основании такого равнобедренного треугольника так же равен 60 градусам.
То есть правильный шестиугольник, образно говоря, состоит как бы из шести равных равносторонних треугольников.
Какой полезный для решения задач факт ещё следует отметить? Угол при вершине шестиугольника (угол между его соседними сторонами) равен 120 градусам.
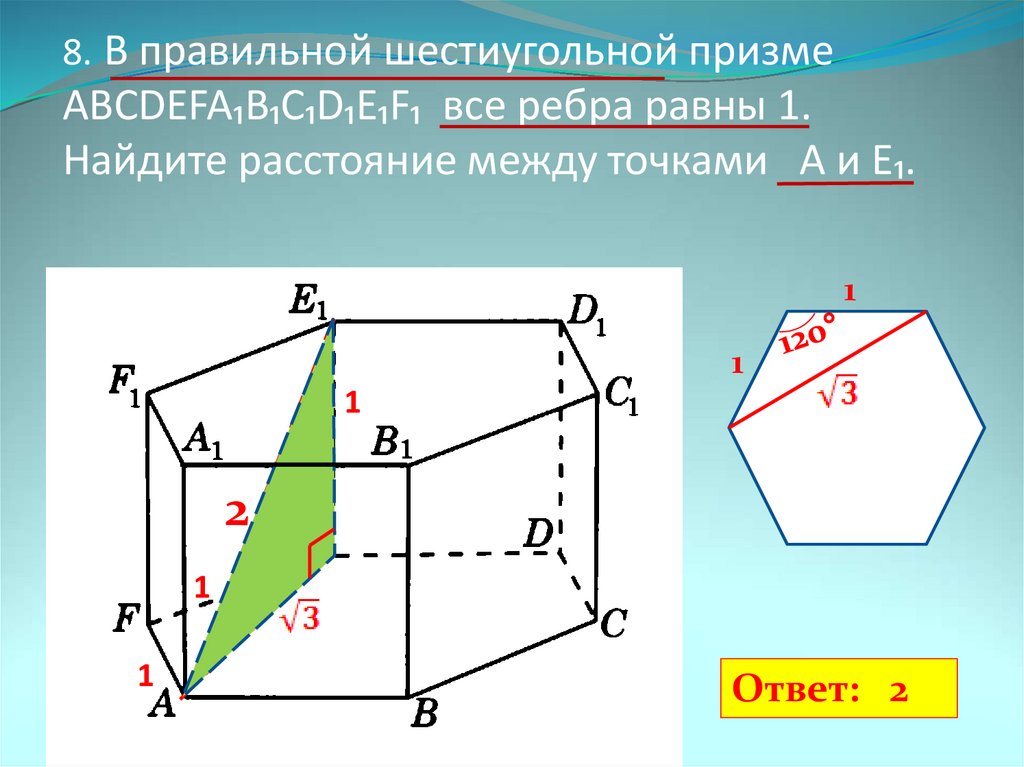
*Умышленно не коснулись формул правильного N-угольника. Данные формулы мы подробно рассмотрим в будущем, здесь они просто не нужны.272533. В правильной шестиугольной призме ABCDEFA 1B 1C 1D 1E 1F 1 все ребра равны 48. Найдите расстояние между точками A и E1.
Рассмотрим прямоугольный треугольник AA 1 E 1 . По теореме Пифагора:
*Угол между сторонами правильного шестиугольника равен 120 градусам.
Отрезок АЕ 1 является гипотенузой, АА 1 и А 1 Е 1 катеты.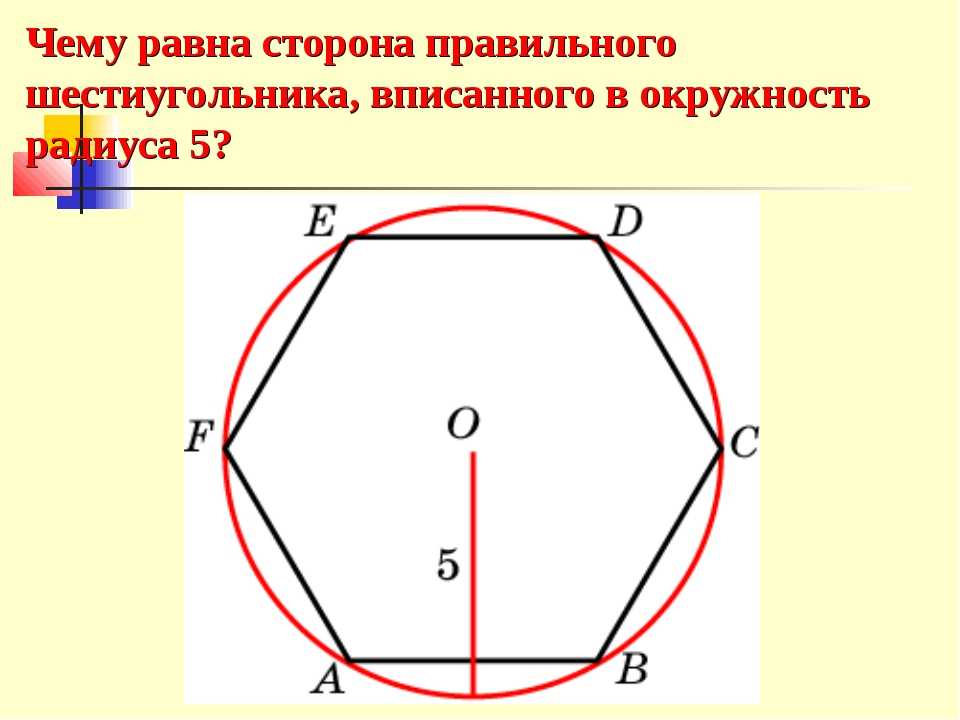 Ребро АА 1 нам известно. Катет А 1 Е 1 мы можем найти используя используя теорему косинусов.
Ребро АА 1 нам известно. Катет А 1 Е 1 мы можем найти используя используя теорему косинусов.
Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
По теореме Пифагора:
*Обратите внимание, что 48 возводить в квадрат совсем не обязательно.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 35. Найдите расстояние между точками B и E.
Рассмотрим правильный шестиугольник:
Сказано, что все рёбра равны 35, то есть сторона шестиугольника лежащего в основании равна 35. А так же, как уже сказано, радиус описанной около него окружности равен этому же числу.
273353. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны сорока корням из пяти.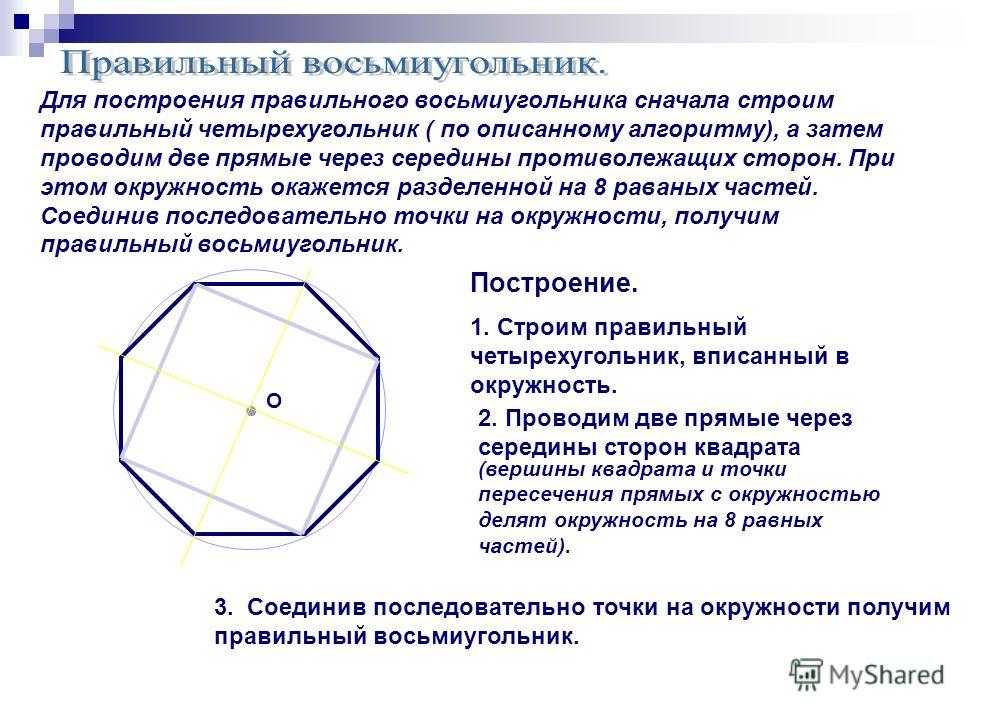 Найдите расстояние между точками B и E1.
Найдите расстояние между точками B и E1.
Рассмотрим прямоугольный треугольник BB 1 E 1 . По теореме Пифагора:
Отрезок B 1 E 1 равен двум радиусам описанной около правильного шестиугольника окружности, а её радиус равен стороне шестиугольника, то есть
273683. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 45. Найдите тангенс угла AD1D.
Рассмотрим прямоугольный треугольник ADD1, в котором AD равно диаметру окружности, описанной вокруг основания. Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 23. Найдите угол DAB. Ответ дайте в градусах.
Рассмотрим правильный шестиугольник:
В нём углы между сторонами равны 120°.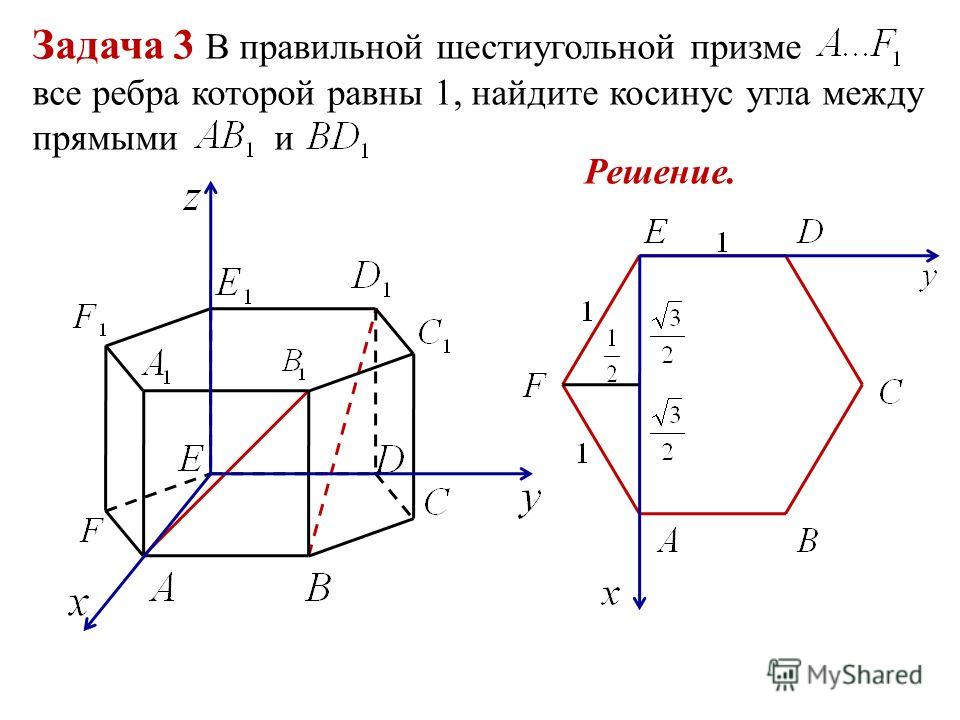
Сама длина ребра не имеет значения, на величину угла она не влияет.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
Рассмотрим прямоугольный треугольник AC1C:
Найдём AC . В правильном шестиугольнике углы между его сторонами равны 120 градусам, тогда по теореме косинусов для треугольника АВС :
Значит, угол AC 1 C равен 60 градусам.
274453. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
Рассмотрим треугольник AС 1 С, он прямоугольный. Вычислим тангенс указанного в условии угла и определим угол. Известно, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть
Катет С1С = 10.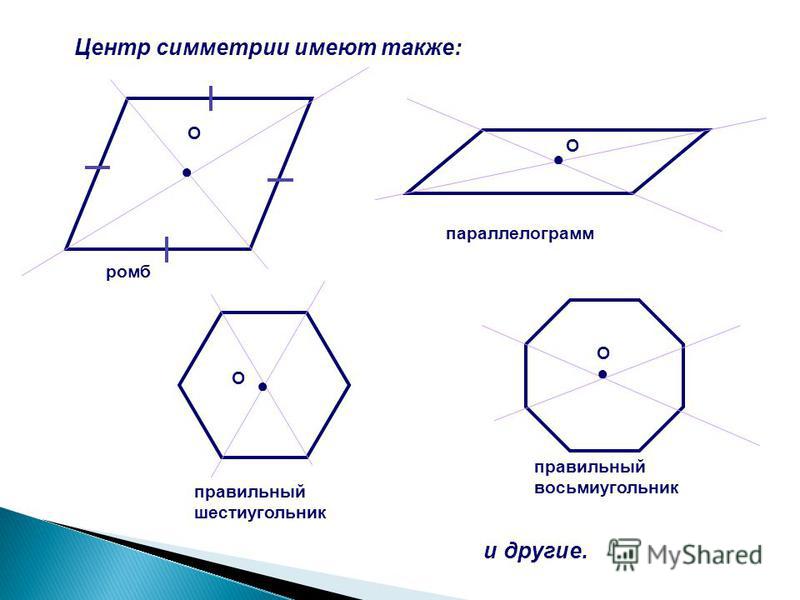 Отрезок АС вычислим по теореме косинусов (это мы уже делали в первой задаче, запишем ещё раз):
Отрезок АС вычислим по теореме косинусов (это мы уже делали в первой задаче, запишем ещё раз):
В правильном шестиугольнике углы при вершинах равны 120 градусам, то есть
245364. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками А и Е1.
245365. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками В и Е.
245366. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1все ребра равны корню из пяти. Найдите расстояние между точками В и Е
245367. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1.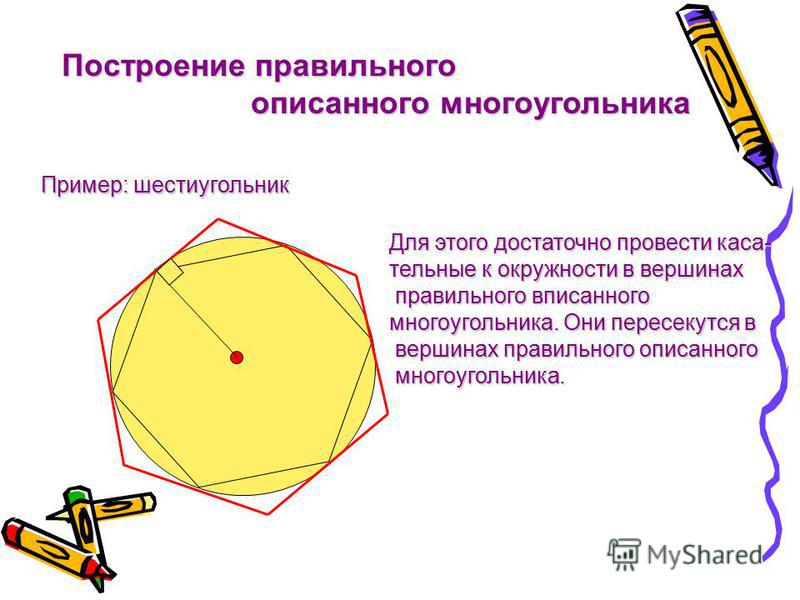 Найдите тангенс угла AD1D.
Найдите тангенс угла AD1D.
245368. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.
245369. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол AC1C. Ответ дайте в градусах.
На этом всё! Успеха Вам!
В состав ЕГЭ включены и другие задачи по стереометрии, и они довольно разнообразны. Обязательно будем их рассматривать, не пропустите! Успехов вам!
Что ты хочешь узнать?
Ответ
Проверено экспертом
Найдите угол DAB — угол правильного шестиугольника ( основания призмы)
Сумма углов многоугольника находится по формуле
180(n-2)
180*(6-2)=720°
Величина одного угла правильного шестиугольника
720:6=120°
Вопрос задан полностью? Иначе призма и ее ребра здесь как будто ни при чем.
«>
Шестиугольник, виды, свойства и формулы
Шестиугольник, виды, свойства и формулы.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник, выпуклый и невыпуклый шестиугольник
Правильный шестиугольник (понятие и определение)
Свойства правильного шестиугольника
Формулы правильного шестиугольника
Правильный шестиугольник в природе, технике и культуре
Звездчатый шестиугольник
Восьмиугольник
Шестиугольник, выпуклый и невыпуклый шестиугольник:
Шестиугольник – это многоугольник с шестью углами.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый шестиугольник
Рис. 2. Невыпуклый шестиугольник
Сумма внутренних углов любого выпуклого шестиугольника равна 720°.
.
Правильный шестиугольник (понятие и определение):
Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.
Рис. 3. Правильный шестиугольник
Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.
Углы правильного шестиугольника образуют шесть равносторонних треугольников.
Правильный шестиугольник можно построить с помощью циркуля и линейки.
Свойства правильного шестиугольника:
1. Все стороны правильного шестиугольника равны между собой.
a1 = a2 = a3 = a4= a5= a6.
2. Все углы равны между собой и составляют 120°.
α1 = α2 = α3 = α4 = α5 = α6 = 120°.
Рис. 4. Правильный шестиугольник
3. Сумма внутренних углов любого правильного шестиугольника равна 720°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.
Рис. 5. Правильный шестиугольник
5. Количество диагоналей правильного шестиугольника равно 9.
Количество диагоналей правильного шестиугольника равно 9.
Рис. 6. Правильный шестиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный шестиугольник
7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
8. Радиус описанной окружности правильного шестиугольника и его сторона равны.
Рис. 8. Правильный шестиугольник
R = a
Правильный шестиугольник в природе, технике и культуре:
Пчелиные соты имеют форму правильного шестиугольника.
Графит, графен имеют гексагональную кристаллическую решетку.
Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.
Рис. 9. Гигантский гексагон на Сатурне
9. Гигантский гексагон на Сатурне
Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
Панцирь черепахи состоит из шестиугольников.
Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.
Рис. 10. Материковая часть Франции
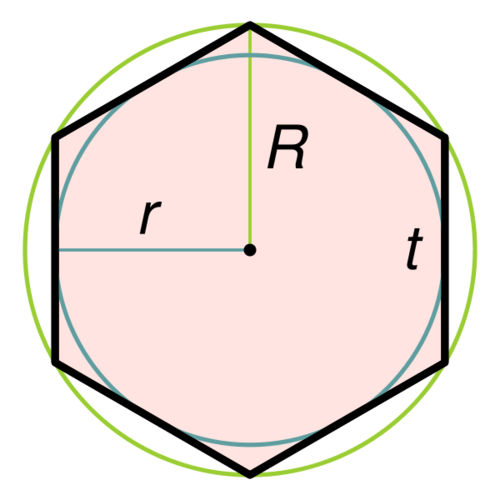
Формулы правильного шестиугольника:
Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.
Формулы периметра правильного шестиугольника:
Формулы площади правильного шестиугольника:
Формула радиуса окружности, вписанной в правильный шестиугольник:
Формула радиуса окружности, описанной вокруг правильного шестиугольника:
R = a
Звездчатый шестиугольник:
Звездчатый шестиугольник (гексаграмма) – это многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника.
Гексаграмма (др.-греч. ἕξ – «шесть» и γραμμή – «черта, линия») – это звезда с шестью углами, которая образуется из двух наложенных друг на друга равносторонних треугольников.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности 5 837
Правильные многоугольники — Свойства
Многоугольник
Многоугольник представляет собой плоскую фигуру (двумерную) с прямыми сторонами. Примеры включают треугольники, четырехугольники, пятиугольники, шестиугольники и так далее.
Обычный
«Правильный многоугольник» имеет:
В противном случае неправильный . |
|
Здесь мы рассматриваем только правильных многоугольников .
Свойства
Итак, что мы можем знать о правильных многоугольниках? Прежде всего, мы можем работать с углами.
Внешний уголок Внешний угол — это угол между любой стороной фигуры, |
Все внешние углы многоугольника в сумме дают 360°, поэтому:
Каждый внешний угол должен быть равен 360°/n
(где n — количество сторон)
кнопку, чтобы увидеть.
Внешний угол
(правильного восьмиугольника)
Пример: Каков внешний угол правильного восьмиугольника?
Восьмиугольник имеет 8 сторон, поэтому:
Внешний угол =360°/n
=360°/8
=45°
Внутренние углыВнутренний угол и Внешний угол измеряются от одной линии, поэтому их в сумме дают 180° . |
Внутренний угол = 180° − Внешний угол
Мы знаем, что Внешний угол = 360°/n , поэтому:
Внутренний угол = 180° − 360°/n
Которые можно переставить следующим образом:
Внутренний угол = 180° − 360°/n
= (n × 180° / n) − (2 × 180° / n)
= (n−2) × 180°/n
Итак, у нас также есть это:
Внутренний угол = (n−2 ) × 180° / n
Пример.
 Каков внутренний угол правильного восьмиугольника?
Каков внутренний угол правильного восьмиугольника?У правильного восьмиугольника 8 сторон, поэтому:
Внешний угол = 360 ° / 8 = 45°
Внутренний угол = 180° − 45° = 135°
Внутренний угол = (n−2) × 180° / n = (8−2) × 180° / 8 = 6 × 180° / 8 = 135° Правильный шестиугольник имеет 6 сторон, значит: Внешний угол = 360 ° / 6 = 60° Внутренний угол = 180 ° − 60° = 120° ..» Звучит довольно музыкально, если повторить несколько раз, но это всего лишь названия «внешней» и «внутренней» окружностей (и каждого радиуса), которые можно нарисовать на многоугольнике вот так: «Внешний» круг называется описывает окружность и соединяет все вершины (угловые точки) многоугольника. Радиус описанной окружности также равен радиусу многоугольника. «Внутренняя» окружность называется вписанной окружностью , и она просто касается каждой стороны многоугольника в своей средней точке. Радиус вписанной окружности равен апофеме многоугольника. (этими свойствами обладают не все многоугольники, но треугольники и правильные многоугольники). Мы можем многое узнать о правильных многоугольниках, разбив их на треугольники следующим образом: Обратите внимание, что: Теперь площадь треугольника равна половине основания, умноженному на высоту, поэтому: Площадь одного треугольника = основание × высота / 2 = сторона × апофема / 2 Чтобы получить площадь всего многоугольника, просто добавьте площади всех маленьких треугольников (n из них): Площадь многоугольника = n × сторона × апофема / 2 А поскольку периметр равен всем сторонам = n × сторона, мы получаем: Площадь многоугольника = периметр × апофема / 2 Разрезав треугольник пополам, мы получим: (Примечание: углы даны в радианах, а не в градусах) Маленький треугольник прямоугольный, поэтому мы можем использовать найти как стороны , радиус , апофема и n (количество сторон) связаны: Таких отношений намного больше (большинство из них просто «перестановки»), но пока что хватит и этих. Мы можем использовать это для вычисления площади, когда мы знаем только Апофему: Площадь малого треугольника = ½ × Апофема × (Сторона/2) Формула выше), что: Сторона = 2 × Апофема × тангенс (π/n) Итак: Площадь малого треугольника = ½ × Apothem × (Apothem × tan(π/n)) = ½ × Apothem 2 × tan(π/n) весь многоугольник : Площадь многоугольника = n × Apothem 2 × tan(π/n) Когда мы не знаем Apothem, мы можем использовать ту же формулу, но переработанную для радиуса или для Сторона: Площадь многоугольника = ½ × n × радиус 2 × sin(2 × π/n) Площадь многоугольника = ¼ × n × сторона 2 / tan(π/n) А вот таблица сторон, апофем и площадей в сравнении с радиусом «1», используя формулы, которые мы разработали: А вот график таблицы выше, но с числом сторон («n») от 3 до 30. Обратите внимание, что чем больше «n», тем больше апофема к 1 (равному Радиусу) и что Площадь стремится к π = 3,14159…, как круг. К чему стремится длина стороны? Шестиугольник – это многоугольник с 6 сторонами и 6 углами (шестиугольник означает шесть). На рисунке ниже показаны 3 различных типа шестиугольников. Шестиугольник — форма, часто встречающаяся в повседневной жизни. Как и другие многоугольники, шестиугольник может быть правильным или неправильным. Если все стороны и внутренние углы шестиугольника равны, то это правильный шестиугольник. В противном случае это неправильный шестиугольник. Шестиугольники или другие многоугольники также могут быть классифицированы как выпуклые или вогнутые. Если все внутренние углы шестиугольника или многоугольника меньше 180°, то он выпуклый. Если один или несколько внутренних углов больше 180 °, он вогнутый. Правильный шестиугольник всегда является выпуклым шестиугольником. Диагональ — это отрезок, соединяющий две непоследовательные вершины. Из каждой вершины можно провести три диагонали. Всего у шестиугольника можно провести девять диагоналей. Следующий рисунок является примером. Сумма внутренних углов шестиугольника равна 720°. Как показано на рисунке выше, можно провести три диагонали, чтобы разделить шестиугольник на четыре треугольника. Синие линии выше показывают только один способ разделить шестиугольник на треугольники; есть другие. Сумма внутренних углов четырех треугольников равна сумме внутренних углов шестиугольника. Поскольку сумма внутренних углов треугольника равна 180°, сумма внутренних углов шестиугольника равна 4 × 180° = 720°. Правильный шестиугольник — это шестиугольник, у которого все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую величину. Поскольку все шесть внутренних углов правильного шестиугольника равны по размеру, каждый внутренний угол равен 720°/6 = 120°, как показано ниже. Каждый внешний угол правильного шестиугольника равен 60°. Стороны правильного шестиугольника равны по длине, а противоположные стороны параллельны. AB = BC = CD = DE = EF = FA и AB//DE, BC//EF, CD//FA Правильный шестиугольник имеет 6 линий симметрии и вращательную симметрию 6-го порядка, что означает, что его можно повернуть таким образом, что он будет выглядеть так же, как исходная форма 6 раз на 360° . Площадь правильного шестиугольника со стороной s: Из центра правильный шестиугольник можно разделить на шесть равносторонних треугольников, каждый из которых имеет длину стороны s, как показано ниже.
Внутренний угол
(обычного восьмиугольника, который можно использовать)5 5 9 Пример. внешние углы правильного шестиугольника?

Разбиение на треугольники
Меньший треугольник
sin(π/n) = (сторона/2) / радиус Сторона = 2 × радиус × sin(π/n) cos(π/n) = Апофема / Радиус Апофема = радиус × cos(π/n) tan(π/n) = (Сторона/2) / Апофема Сторона = 2 × Апофема × тангенс (π/n) 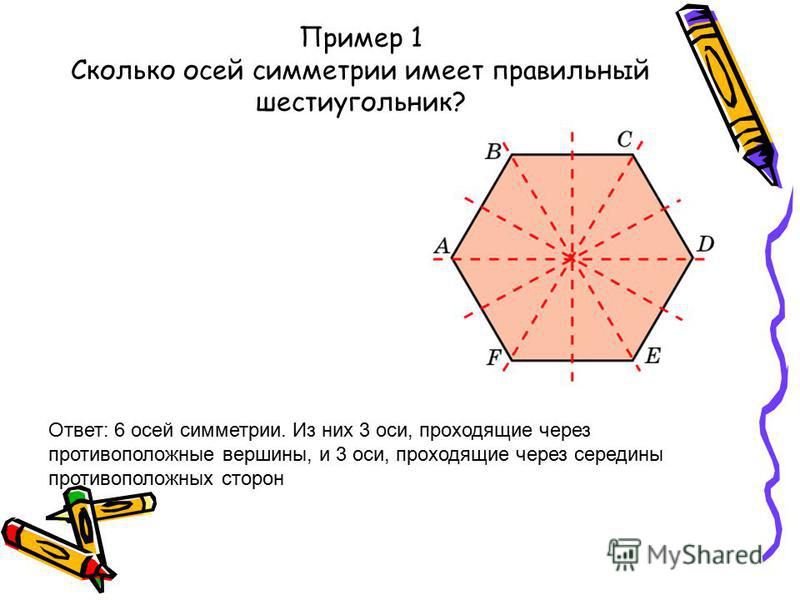
Другие формулы площади
Таблица значений
Тип Имя, когда
Обычный сторон
(н) Форма Внутренний уголок Радиус Боковой Апофема Район Треугольник
(или Тригон) Равносторонний
Треугольник 3 60° 1 1,732
(√3) 0,5 1,299
(¾√3) Четырехугольник
(или Тетрагон) Квадрат 4 90° 1 1,414
(√2) 0,707
(1/√2) 2 Пентагон Обычный
Пентагон 5 108° 1 1,176 0,809 2,378 Шестигранник Обычный
Шестигранник 6 120° 1 1 0,866
(½√3) 2,598
((3/2)√3) Семиугольник
(или септагон) Обычный
Гептагон 7 128,571° 1 0,868 0,901 2,736 Октагон Обычный
Октагон 8 135° 1 0,765 0,924 2,828
(2√2) . 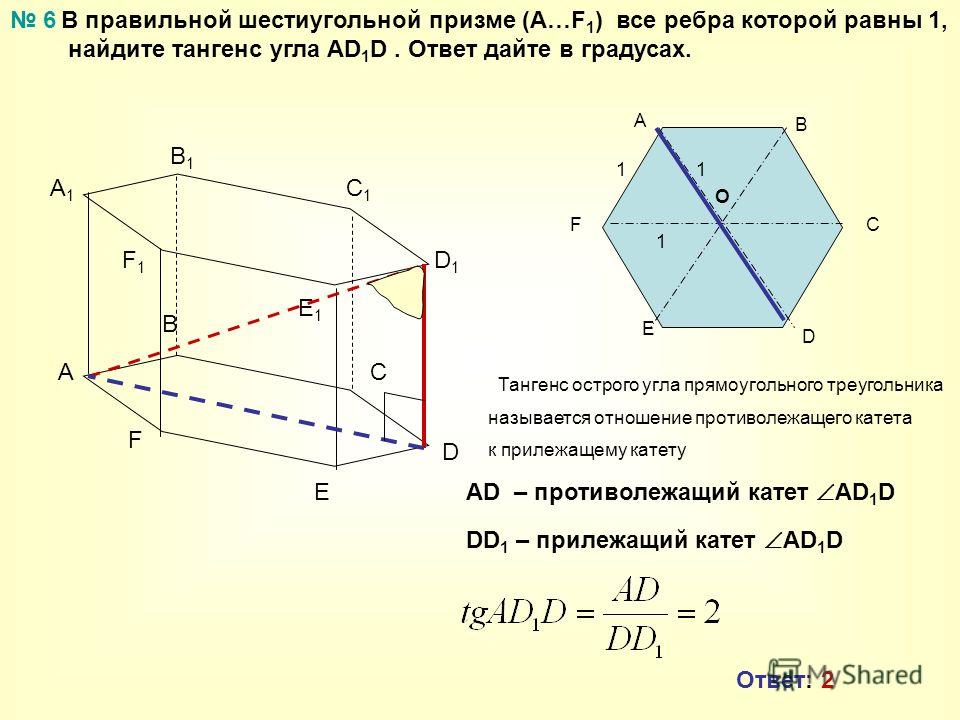 ..
.. … Пятиугольник Обычный
Пентаконтагон 50 172,8° 1 0,126 0,998 3.133 (Примечание: значения верны только до 3 знаков после запятой) График
Шестиугольник
 Формы, из которых состоят соты, гайки и болты, — все это примеры реальных объектов в форме шестиугольника.
Формы, из которых состоят соты, гайки и болты, — все это примеры реальных объектов в форме шестиугольника. Классификация шестиугольников
Правильный шестигранник Неправильный шестигранник Все стороны и внутренние углы равны Не все стороны и углы равны 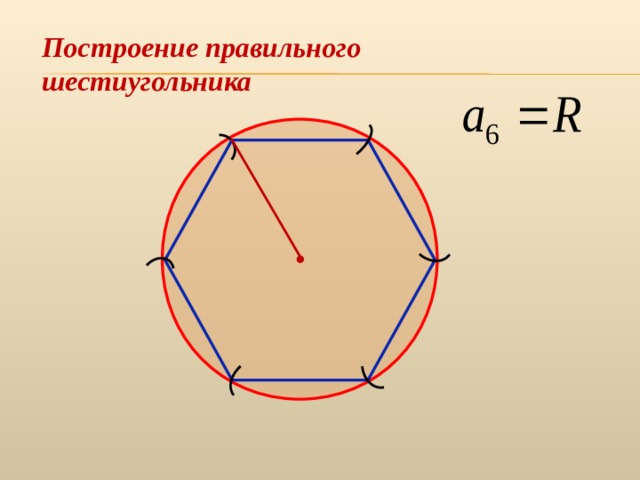
Выпуклый шестигранник Вогнутый шестигранник Все внутренние углы < 180° Один или несколько внутренних углов > 180° Диагонали шестиугольника
Внутренние углы шестиугольника

Правильный шестиугольник
Углы и стороны правильного шестиугольника
Симметрия в правильном шестиугольнике
Линии симметрии Вращательная симметрия 6 линий симметрии Шесть углов поворота 60° Площадь правильного шестиугольника