Вершина пятиугольника это: Сколько вершин у пятиугольника?

Многоугольники /qualihelpy

Многоугольником  на плоскости называют фигуру, состоящую из точек  и соединяющих их непересекающихся отрезков . Точки  называют вершинами многоугольника, а отрезки  – его сторонами. 

Две вершины многоугольника называются смежными, если они соединяются стороной многоугольника. Две стороны многоугольника называются смежными, если они имеют общую вершину.

Диагональю многоугольника называют отрезок, соединяющий две несмежные вершины. 

Например, на рисунке 8.22 из вершины  многоугольника  проведены диагонали  и .

Многоугольник называют выпуклым, если он расположен в одной полуплоскости относительно прямой, содержащей любую его сторону. 

Например, на рисунке 8.22 изображен выпуклый многоугольник, а на рисунке 8.23 – невыпуклый.

Вершины многоугольника являются вершинами его углов. Различают внутренние и внешние углы многоугольника. 

Например, пятиугольник , изображенный на рисунке 8. 21 имеет пять внутренних углов, которые можно обозначать тремя буквами или одной буквой. Это углы:  и . 

Внешним углом многоугольника называют угол, смежный с его внутренним углом. 

Например, на рисунке 8.22 угол  внешний угол при вершине  многоугольника . 

Сумму внутренних углов выпуклого многоугольника находят по формуле:

, (8.1)

где n – число сторон (углов) многоугольника. 

Периметром многоугольника называют сумму длин всех его сторон. 

Многоугольник называют правильным, если все его стороны и все его углы равны. 

Например, на рисунке 8.24 изображен правильный треугольник, на рисунке 8.25 – правильный четырехугольник, а на рисунке 8.26 – правильный шестиугольник.

Внутренние углы правильного n-угольника находят по формуле: 

. (8.2)

В дальнейшем мы будем рассматривать только выпуклые многоугольники.

Многоугольника зависит от количества вершин

МНОГОУГОЛЬНИКИ.

1. У многоугольника стороны могут пересекаться, а могут не пересекаться.

2. Смежные отрезки многоугольника лежат на одной прямой.

3. Две смежные стороны многоугольника имеют одну общую вершину.

4. Название многоугольника зависит от количества вершин.

5. Количество сторон многоугольника не зависит от количества его вершин.

6. Периметр многоугольника – это сумма длин всех его сторон.

7. Соседние вершины многоугольника лежат на разных сторонах.

8. Отрезок, соединяющий любые две соседние вершины, называют диагональю многоугольника.

9. Любой многоугольник разделяет плоскость на внешнюю и внутреннюю области.

10. Многоугольник состоит из сторон многоугольника и его внутренней области.

11. Верно ли, что многоугольники бывают выпуклые и невыпуклые.

12. Прямая, проходящая через любую сторону выпуклого многоугольника разделяет его на две части.

13. Невыпуклый многоугольник находится по одну строну от прямой, проходящей через любую его сторону.

14. Верно ли, что у многоугольника углов столько же, сколько и сторон.

15. У четырехугольника и сторон, и углов, и вершин – четыре.

16. Соседние стороны четырехугольника называют противоположными.

17. Противоположные вершины четырехугольника не являются соседними.

18. Четырехугольники бывают только выпуклые.

19. У четырехугольника можно провести четыре диагонали.

20. Каждая диагональ разбивает четырехугольник на два треугольника.

21. Сумма углов любого выпуклого четырехугольника, параллелограмма и трапеции равна 360⁰.

22. У параллелограмма соседние стороны параллельны и равны.

23. У параллелограмма противоположные углы равны.

24. Диагонали параллелограмма точкой пересечения не делятся пополам.

25. У трапеции противоположные стороны параллельны.

26. Основания трапеции между собой равны.

27. Боковые стороны равнобедренной трапеции между собой равны.

28. У прямоугольной трапеции три угла прямые.

КЛЮЧ:

«+» — 3; 4; 6; 9; 10; 11; 14; 15; 17; 20; 21; 23; 27;

«-» — 1; 2; 5; 7; 8; 12; 13; 16; 18; 19; 22; 24; 25; 26; 28

ОЦЕНКИ:

«3» — 15 – 19

«4» — 20 – 25

«»5 – 26 – 28

ТЕМА: Площадь.

1. Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.

2. За единицу измерения площадей принимают только квадрат со стороной 1 см.

3. Площадь многоугольника выражается только положительной величиной.

4. Верно ли, что равные многоугольники имеют равные площади?

5. Если многоугольник разбит на части, то его площадь равна сумме площадей этих частей.

6. Площадь квадрата равна кубу его стороны.

7. Площадь прямоугольника равна половине произведения его противоположных сторон.

8. Площадь прямоугольника равна произведению его соседних сторон.

9. Основание – это одна из сторон параллелограмма.

10. Высота треугольника – это перпендикуляр, опущенный из любой точки противоположной стороны к прямой, содержащей основание.

11. Площадь параллелограмма равна половине произведения высоты на основание.

12. Одну из сторон треугольника называют основанием.

13. Площадь треугольника равна половине произведения его основания на высоту.

14. Площадь прямоугольного треугольника равна произведению его катетов.

15. Если основания двух треугольников равны, то их площади относятся как высоты.

16. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

17. Высота трапеции – это перпендикуляр, проведенный к боковой стороне.

18. Площадь трапеции равна произведению полусуммы ее оснований на высоту.

19. Площадь ромба равна произведению его диагоналей.

20. Площадь ромба можно найти по той же формуле, что и параллелограмм.

21. Теорема Пифагора используется в любых треугольниках.

22. В прямоугольном треугольнике квадрат любого катета равен сумме квадратов гипотенузы и другого катета.

23. Пифагоровы треугольники те, у которых длины сторон выражаются целыми числами.

24. Треугольник со сторонами 3, 4, 5 называют египетским треугольником.

КЛЮЧ:

«+» — 1; 3; 4; 5; 8; 9; 10; 12; 13; 16; 18; 20; 23; 24

«-» — 2; 6; 7; 11; 14; 15; 17; 19; 21; 22;

ОЦЕНКИ:

«3» — 12 – 16

«4» — 17 – 21

«5»– 22 – 24

ТЕМА: «Определение подобных треугольников. Признаки подобия треугольников»

1. Верно ли, что отношение двух отрезков – это деление одного отрезка на другой?

2. Если одна пара отрезков пропорциональна другой паре отрезков, то их отношения не равны.

3. Понятие пропорциональность рассматривается только на примере двух отрезков.

4. В геометрии фигуры одинаковой формы принято называть подобными.

5. Если у двух треугольников MNK и M₁N₁K₁ соответствующие углы равны, то стороны MK и N₁K₁ называют сходственными.

6. Два треугольника называют подобными, если их углы соответственно равны, а стороны одного треугольника соответственно пропорциональны сторонам другого.

7. Коэффициент подобия – это число, равное отношению сходственных сторон подобных треугольников.

8. Подобие треугольников нельзя установить, если известно, что некоторые углы соответственно равны или некоторые стороны пропорциональны.

9. Площади двух подобных треугольников относятся как коэффициент подобия в квадрате.

10. Отношение периметров двух подобных треугольников равно коэффициенту подобия в квадрате.

11. По первому признаку подобия треугольников необходимо указать две пропорциональные стороны и угол между ними.

12. По второму признаку подобия треугольников необходимо указать два равных угла в каждом треугольнике.

13. По третьему признаку подобия треугольников необходимо указать пропорциональность трех сторон.

14. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

КЛЮЧ:

«+» — 1; 4; 6; 7; 9; 13; 14

«-» — 2; 3; 5; 8; 10; 11; 12

ОЦЕНКИ:

«3» — 7 – 9

«4» — 10 – 12

«5»– 13 – 14

ТЕМА : «Применение подобия к доказательству теорем и решению задач»

1) Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.

2) В любом треугольнике можно провести только одну среднюю линию.

3) Средняя линия треугольника параллельна одной из его сторон и равна ее половине.

4) Средняя линия треугольника отсекает от первоначального треугольника подобный ему треугольник.

5) Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от конца медианы.

6) Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет его на два прямоугольных треугольника не подобных данному треугольнику.

7) Отрезок MN называют средним пропорциональным для двух отрезков АВ и CD, если он равен квадратному корню из суммы этих отрезков.

8) Высота прямоугольного треугольника, проведенная из любой вершины, есть среднее пропорциональное для отрезков, на которые делится катет.

9) Катет прямоугольного треугольника, проведенный из вершины прямого угла, есть среднее пропорциональное для гипотенузы и проекции этого катета на гипотенузу.

10) Метод подобия нельзя применить для решения задач на построение треугольников.

11) Измерительные работы на местности можно провести с помощью подобия двух прямоугольных треугольников.

12) Фигуры F и F₁ называют подобными, если для любых двух точек этих фигур выполняется равенство .

13) Коэффициент подобия – это число, равное отношению сходственных сторон подобных фигур.

14) Верно ли, что если ширина одного прямоугольника больше в 2 раза ширины подобного ему прямоугольника, то длина может быть в 3 раза.

КЛЮЧ:

«+» — 1; 3; 4; 9; 11; 12: 13;

«-» — 2; 5; 6; 7; 8; 10; 14

ОЦЕНКИ:

«3» — 7 – 9

«4» — 10 – 12

«5»– 13 – 14

ТЕМА: «Окружность»

1) Верно ли, что возможны три случая взаимного расположения прямой и окружности.

2) Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность имеют две общих точки.

3) Прямая называется касательной, если расстояние от центра окружности до прямой равно радиусу окружности.

4) По свойству: радиус окружности, проведенный в точку касания перпендикулярен к касательной.

5) Отрезки касательных к окружности, проведенные из одной точки равны.

6) Верно ли, что прямая проходящая через конец диаметра, лежащий на окружности и перпендикулярна к этому диаметру, то она является касательной.

7) На окружности можно построить дугу любой градусной меры.

8) Центральный угол – это угол, одна сторона которого является диаметром.

9) Если центральный угол развернутый, то его соответствующая дуга называется полуокружностью.

10) Если центральный угол больше развернутого, то соответствующая дуга меньше полуокружности.

11) Градусная мера дуги – это градусная мера соответствующего центрального угла.

12) Вписанный угол – это угол, вершиной которого является центр окружности.

13) Говорят, что вписанный угол опирается на дугу, если она не лежит внутри вписанного угла.

14) Вписанный угол равен половине дуги, на которую он опирается.

15) Вписанный угол равен центральному углу.

16) Вписанные углы, опирающиеся на одну и ту же дугу не равны.

17) Вписанный угол, опирающийся на диаметр – прямой.

18) Каждая точка биссектрисы неразвернутого угла находится на разном расстоянии от его сторон.

19) Всего существует четыре замечательных точки треугольника.

20) Вписанная окружность касается всех сторон многоугольника.

21) Все вершины вписанного многоугольника лежат внутри окружности.

22) В любой четырехугольник можно вписать окружность и описать около него окружность.

23) Центры вписанной и описанной окружности треугольника не являются замечательными точками.

Ключ:

«+»: 1; 3; 4; 5; 6; 7; 9; 11; 13; 14; 17; 19; 20;

«-»: 2; 8; 10; 12; 15; 16; 18; 21; 22; 23.

Оценки:

«3» — 11 – 14;

«4» — 15 – 21;

«5» — 22 — 23

ТЕМА: «Понятие вектора. Сложение и вычитание векторов»

1) Величины, которые задаются не только числовым значением, но и направлением называют векторными величинами.

2) Вектор – это направленный отрезок.

3) У вектора неважно, какая точка является началом, а какая концом.

4) Любую точку можно назвать вектором.

5) Длина вектора – это обязательно расстояние от начала до конца вектора.

6) У нулевого вектора нельзя найти длину.

7) Коллинеарные векторы лежат только на параллельных прямых.

8) Нулевой вектор не может быть коллинеарен произвольному вектору.

9) Коллинеарные векторы делятся на сонаправленные и противоположно направленные.

10) Нулевой вектор имеет любое направление.

11) Векторы называют равными, если их длины равны.

12) От любой точки можно отложить несколько векторов, равных данному.

13) При сложении двух векторов по правилу треугольника необходимо, чтобы начало одного вектора, совпадало с началом другого.

14) При сложении векторов можно пользоваться сочетательным или переместительным законом.

15) При сложении векторов по правилу параллелограмма суммой будет являться диагональ, исходящая из их общего начала.

16) При вычитании векторов результатом будет вектор с началом в конце первого и концом в конце второго.

17) По правилу многоугольника можно сложить любое количество векторов.

18) При сложении по правилу многоугольника все векторы должны иметь общее начало.

Ключ:

«+»: 1; 2; 4; 9; 10; 14; 15; 17

«-»: 3; 5; 6; 7; 8; 11; 12; 13; 16; 18

Оценки:

«3» — 8 – 11;

«4» — 12 – 16;

«5» — 17 — 18

Многоугольники — урок. Геометрия, 8 класс.

Ломаной называется фигура, которая состоит из точек и соединяющих их отрезков.

 

Точки называются вершинами ломаной, а отрезки — звеньями ломаной.

Виды ломаных

Ломаная называется замкнутой, если у неё концы совпадают.

 

Если концы ломаной не совпадают, то она называется незамкнутой.

  

Ломаная называется простой, если она не имеет самопересечений. Обе ломаные выше являются простыми.

 

На следующем рисунке — ломаная с самопересечением.

 

 

Многоугольник

Многоугольник — это простая замкнутая ломаная линия и конечная часть

плоскости, которую она ограничивает.

 

Вершины ломаной линии называются вершинами многоугольника, а её звенья — сторонами многоугольника.

 

Отрезок, соединяющий две вершины, не лежащие на одной стороне, называется диагональю многоугольника.

 

 

\(A\), \(B\), \(C\), \(D\), \(E\) — вершины;
\(AB\), \(BC\), \(CD\), \(DE\), \(AE\) — стороны;
\(AC\), \(AD\), \(BE\), \(BD\), \(CE\) — диагонали.

 

Многоугольник, у которого все углы меньше 180°, называется выпуклым многоугольником.

 

Пятиугольник \(ABCDE\) является выпуклым многоугольником. 

Сумма углов выпуклого \(n\)-угольника

В общем случае многоугольник можно назвать \(n\)-угольником, это означает, что у данного многоугольника \(n\) сторон и \(n\) вершин.

Сумма углов выпуклого \(n\)-угольника равна 180°⋅n−2.

Любой выпуклый многоугольник можно разделить на треугольники. Количество треугольников на \(2\) меньше, чем количество сторон в многоугольнике.

 

Сумма внутренних углов любого треугольника равна 180°.

Поэтому сумма углов выпуклого \(n\)-угольника равна 180°⋅n−2.

Пример:

вычисли сумму внутренних углов выпуклого одиннадцатиугольника.

Можно нарисовать рисунок, но это не обязательно для решения задачи.
Используем формулу:
180°⋅n−2=180°⋅11−2=180°⋅9=1620°.

Урок 1. многоугольники. четырёхугольник — Геометрия — 8 класс

Рассмотрим фигуру, составленную из отрезков AB, BC, CD, DE, EF, FA так, что смежные отрезки (имеющие общую точку) лежат на одной прямой, а не смежные отрезки не имеют общих точек. Такая фигура называется многоугольником.
Точки A, B, C, D, E, F называются вершинами многоугольника, а отрезки AB, BC, CD, DE, EF, FA – сторонами многоугольника.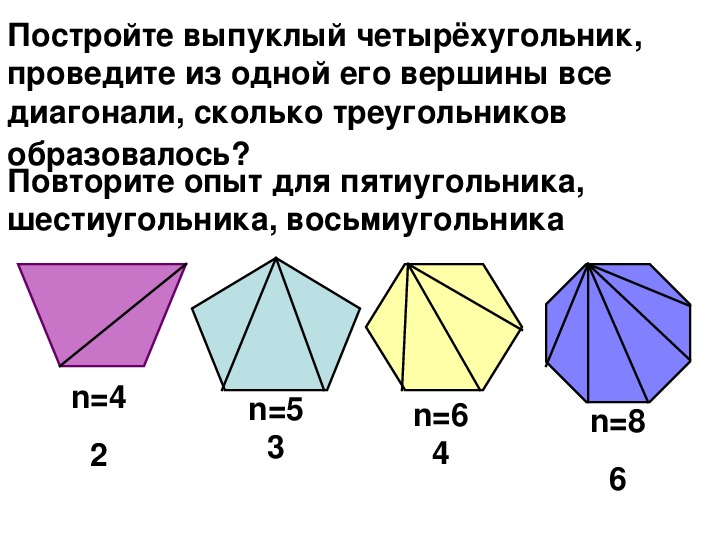
Многоугольник с n вершинами имеет n сторон и называется n-угольником.
Сумма длин всех сторон называется периметром многоугольника.
Две вершины многоугольника, принадлежащие одной стороне называются соседними. Отрезок, соединяющий любые не соседние вершины многоугольника, называется диагональю многоугольника.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю.
Фигуру, состоящую из многоугольника и его внутренней области, также называют многоугольником. Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Примером выпуклого многоугольника является четырехугольник. У него 4 вершины, 4 угла, 4 стороны, 2 диагонали.
Треугольник является многоугольником. Мы знаем, что сумма углов треугольника равна 180 градусов. Возникает вопрос: можно ли найти сумму углов произвольного n-угольника?
Рассмотрим поочередно четырехугольник, пятиугольник и шестиугольник. Одну из вершин этих многоугольников соединим диагоналями с другими вершинами так, чтобы получились треугольники. Первый множитель в формуле для вычисления суммы углов выпуклого многоугольника равен 180°, так как мы разбивали на треугольники. А второй множитель на 2 меньше числа сторон многоугольника, то есть равен n – 2
Получается формула для вычисления суммы углов выпуклого многоугольника: (n – 2) * 180º

О звездах / Хабр

Иногда мне в голову попадают задачи, не имеющие какой-то очевидной практической ценности, но, тем не менее, они захватывают так или иначе мое воображение, по крайней мере, пока не решу. Практическая ценность задачи, как правило, нулевая, но в процессе решаются другие, которые могут иметь бОльшую ценность, чем решенная.

Все началось с желания изучить свойства правильных октагонов и октаграмм, но результаты оказались применимы ко всем выпуклым многоугольникам (полигонам) и звездам, построенным в них (по аналогии назову их полиграммами — пентаграмма, гексаграмма, септаграмма, октаграмма и т. д. — хотя этот термин имеет и иные значения).

Для начала терминология. Пентаграммой называют совокупность всех диагоналей пятиугольника, в случае гексаграммы — это уже не все диагонали, а только те, которые соединяют непротивоположные вершины шестиугольника. Во обоих случаях эти вершины идут через одну друг от друга. Например, если вершины пятиугольника перенумеровать (0, 1, 2, 3, 4), то пентаграмма — совокупность линий (0, 2), (1, 3), (2, 4), (3, 0), (4, 1). Гексаграмма (0, 1, 2, 3, 4, 5), соответственно, является совокупностью линий (0, 2), (1, 3), (2, 4), (3, 5), (4, 0), (5, 1). Нули в качестве начальной точки взяты не случайно и не как дань програмистскому мышлению, удобство этого обозначения я опишу ниже. Линии, образующие полиграмму, я буду называть ребрами. Вершинами полиграммы я буду называть вершины исходного полигона, а не все точки пересечения ребер.

Определение можно обобщить, введя понятие «порядок полиграммы» как некоторое целое число k, имеющее диапазон значений между 1 и n / 2, где n — количество углов исходного полигона. Верхняя граница k (равная целой части n / 2) определят количество разных обобщенных полиграмм. Сам же порядок обозначает, какая по счету вершина от исходной должна быть соединена диагональю, входящей в полиграмму. Что это значит? Если рассматривать номера вершин полиграммы, начиная с нуля, то они образуют аддитивную группу вычетов по модулю n. Пусть m — это номер вершины полиграммы. Тогда отрезок, соединяющий вершину m и m + k (где k — порядок полиграммы) в данной группе, будет являться частью полиграммы порядка k. В этом обобщении полиграмма порядка 1 совпадет с исходным многоугольником.

В случае пентагона согласно формуле существует две обобщенные пентаграммы — сам пентагон и пентаграмма в классическом смысле.

В случае гексагона есть три обобщенные гексаграммы: сам гексагон, классическая гексаграмма и диагонали, соединяющие противоположенные вершины (вырожденный случай).

Для лучше иллюстрации разберу полиграмм для септагона и октагона. По формуле количество септаграмм будет равно трем, количество октаграмм четырем.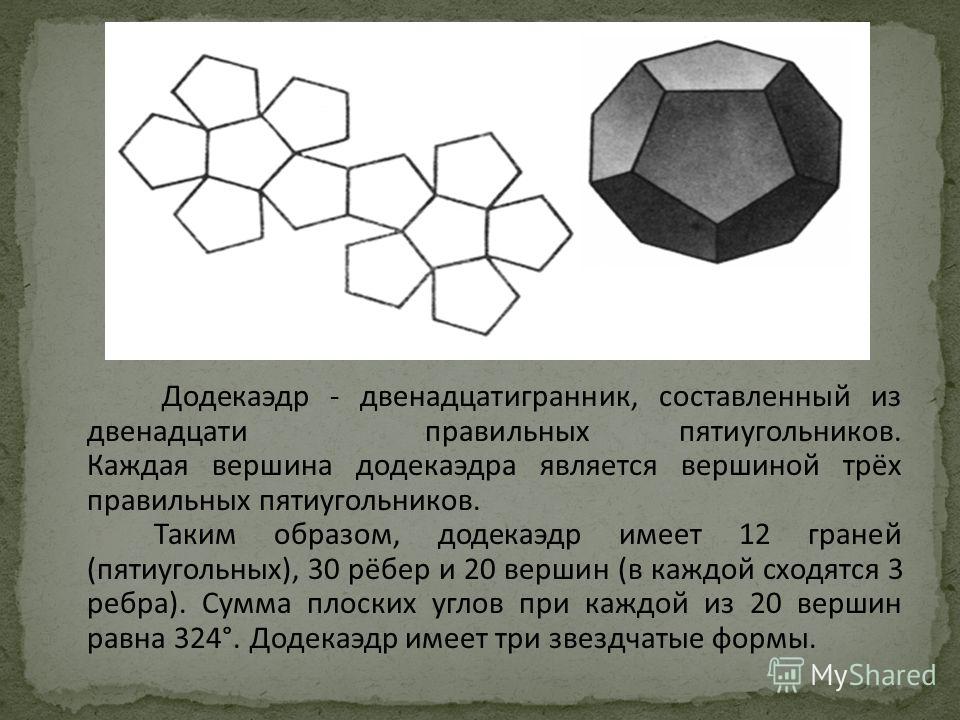

В качестве побочного эффекта можно увидеть, что полиграммы естественным образом делятся на связные и несвязные. Связные полиграммы — это полиграммы, между любой парой вершин которых существует путь по ребрам (перескакивать с ребра на ребро можно только в вершинах многоугольника). Воспользовавшись теорией чисел, можно заметить, что полиграммы связны тогда и только тогда, когда количество углов исходного полигона и порядок полиграммы — взаимно простые числа.

На картинке ниже приведены примеры несвязных полиграмм, их отдельные части выделены разными цветами. Нонаграмма (n = 9, k = 3) распадается на три треугольника, декаграмма (n = 10, k = 4) — на две пентаграммы:

Теперь полиграммы с тем же количеством углов (n = 9, k = 2 и n = 10, k = 3), но уже связные:

Кроме того, в случае четных n и максимальных для такого случая k (k = n / 2) полиграммы вырождаются в набор диагоналей, соединяющих противоположные вершины.

Довольно неожиданным для меня результатом оказалось то, что сумма углов при вершинах полиграмм (в случае выпуклых полигонов) является довольно просто вычислимая величина: π(n — 2k).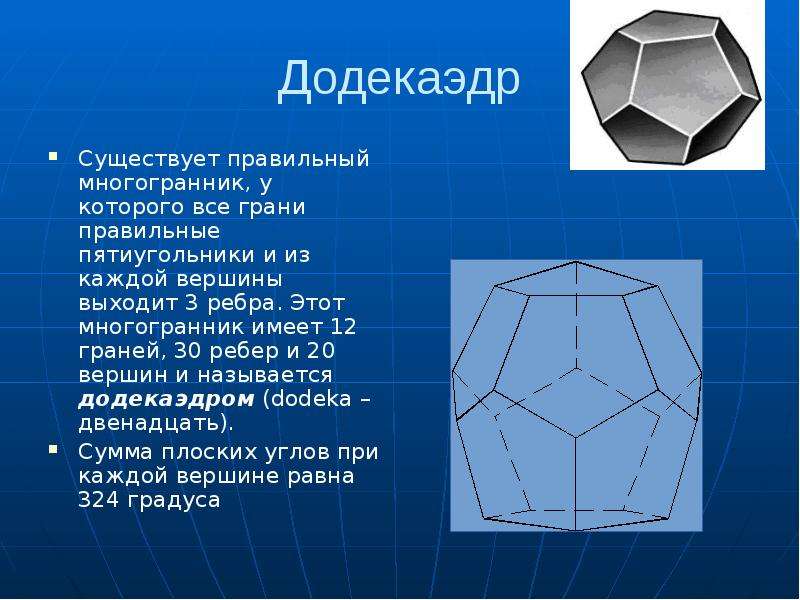 В случае полиграмм первого порядка (которые совпадают с исходным полигоном) формула сводится к известной формуле вычисления углов многоугольника, в случае же вырожденной полиграммы сумма углов оказывается равной нулю (что естественно). Доказательство этого факта заключается в следующем: каждое ребро полиграммы (при 1 < k < n / 2 — отброшен случай вырожденной полиграммы и совпадающей с исходным полигоном) делит многоугольник на два: один c k + 1 углом, другой с n — k + 1. просуммировав суммы углов всех меньших по количеству углов частей (которые с k + 1 углом), получится результат π(k — 1)n (на каждую вершину полигона по одному (k + 1)-угольнику). Каждый целый угол исходного полигона присутствует k — 1 раз. Плюс к этому по одному разу присутствуют смежные с углами полиграммы углы, Если из первой суммы вычесть присутствующую в ней сумму целых углов полиграммы (которая равна π(n — 2)(k — 1), так как каждый целый угол встречается k — 1 раз), получится сумма смежных с углами полиграммы углов π(k — 1)n — π(n — 2)(k — 1). 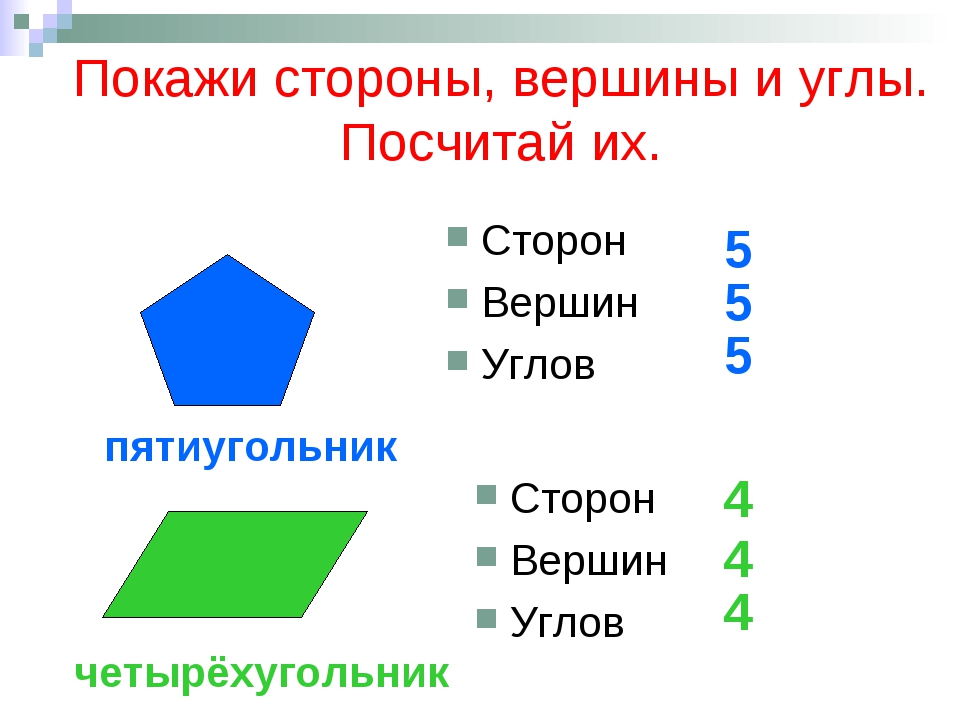Если теперь из суммы углов исходного полигона вычесть эту сумму углов, получится сумма углов полиграммы:

π(n — 2) — (π(k — 1)n — π(n — 2)(k — 1)) =π(n — 2) — π(k — 1)n + π(n — 2)(k — 1) = π(n — 2)k — π(k — 1)n = π(n — 2k)

Все иллюстрации и рассуждения выше относились к любым полиграммам, построенным на выпуклых многоугольниках. На рисунках я изобразил случаи правильных полиграмм исключительно из собственной лени — так было проще написать рисующую программу. Далее речь пойдет только о правильных полиграммах.

Исходя из формулы выше, угол при вершине правильной полиграммы равен π — 2πk / n.

Если взять горизонт (множество внешних точек) правильной полиграммы, то данная фигура будет представлять собой невыпуклый 2n-угольник (n — количество вершин полиграммы. Границы фигур справа иллюстрируют это:

Таким образом появляется еще n «лишних» углов, которые я буду называть внутренними углами полиграммы. Эти углы невыпуклы, из формулы суммы углов многоугольника для правильной полиграммы они равны (π(2n — 2) — π(n — 2k)) / n =π(n + 2k — 2) / n =π + 2π(k — 1) / n.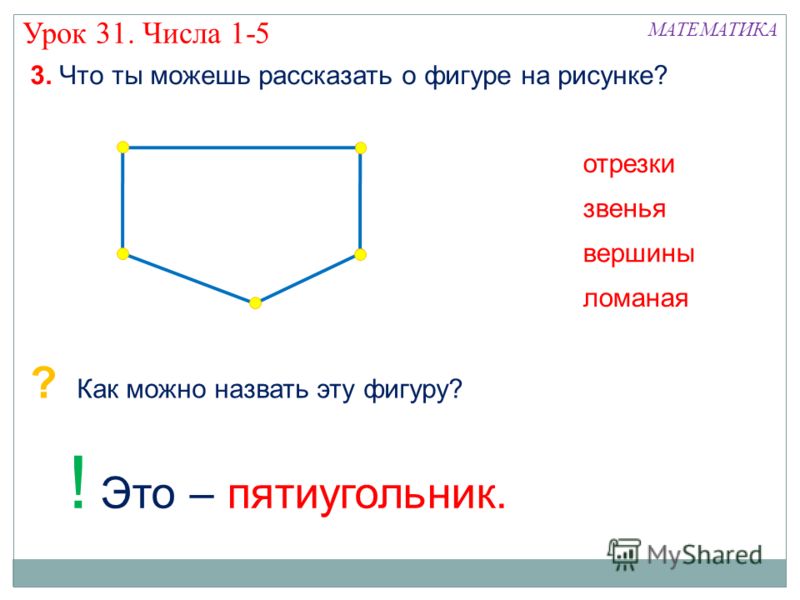 Обратные по отношению к ним углы равны, соответственно π — 2π(k — 1) / n. Этот угол я буду называть углом между лучами.

Данные вычисления могут пригодиться для построения узоров и забавных орнаментов, что будет проиллюстрировано ниже для терпеливых читателей.

Далее идет достаточно бесполезная часть, которая доставила мне в свое время эстетическое удовольствие, но результатом которой может быть лишь потерянное время читателя, что и послужило причиной добавления в хабр «Забавные задачки».

Узор с октаграммойПри k = 2 угол между лучами будет равен π — 2π / n, что в точности равно углу исходного многоугольника, в котором построена полиграмма. В каких случах такие многоугольники будут плотно примыкать друг к другу, образуя подобие мозаики? иними словами, сумма угла при вершине полиграммы плюс удвоенный угол при вершине многоугольника должны быть равны 2π. Угол при вершине правильной полиграммы в данном случае равен π — 4π / n. Таким образом, получается уравнение:

π — 4π / n + 2(π — 2π / n) = 2π
3π — 8π / n = 2π
8π / n = pi;
n = 8

Таким образом, октаграмму при k = 2 можно получить, нарисовав 8 восьмиугольников, соседние из которых имеют общую сторону — внутренние стороны таких многоугольников образуют горизонт такой октаграммы.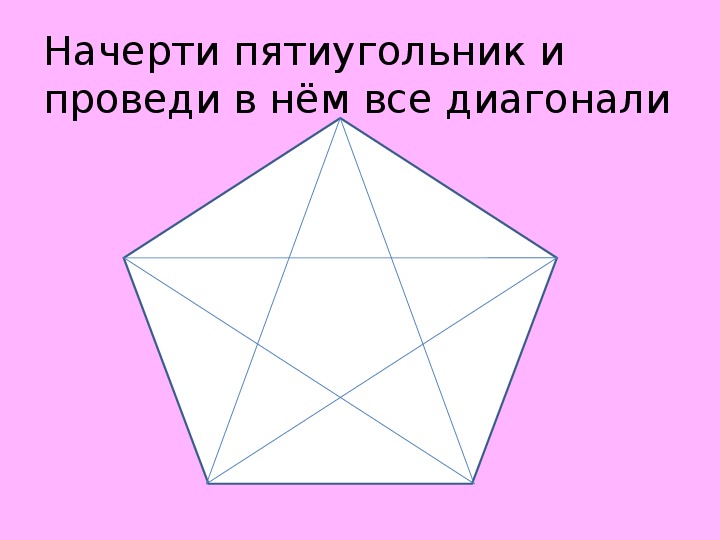

Октаграмма (n = 8, k = 2) является несвязной и состоит из двух квадратов (углы во всех вершинах прямые: π — 4 π / 8 = π / 2). На лучах такой октаграммы можно построить квадраты со стороной, равной стороне луча.

Внутренний угол этой октаграммы равен 5π / 4. Вычитая из внутреннего угла сумму углов квадратов, построенных на лучах, получится угол между сторонами соседних квадратов, находящихся внутри октограммы. Этот угол равен π / 4. Итак, внутренние стороны квадратов образуют звездообразную фигуру с углами при восьми вершинах π / 4 и углами между лучами π / 2 (угол при вершине квадрата). Таким образом, внутренние углы этой фигуры будут равны 3π / 2.

Если теперь рассмотреть углы октаграммы (n = 8, k = 3), обнаруживается, что угол при вершине равен π — 2πk / n = π / 4, а внутренние углы π + 2π(k — 1) / n = 3π / 2, что в точности соответсвует фигуре, ограниченной квадратами, описанными выше.

Иллюстрацией этих вычислений может послужить симпатичная картинка:

Гексагоно-гексаграммная мозаикаРассмотрю опять случай k = 2. Как было описано выше в случае с октаграммой, в угол между лучами правильной полиграммы в таком случае может быть вписан правильный многоугольник с числом углов, равным числу вершин полиграммы. При этом сумма углов двух многоугольников и луча полиграммы, к которому они прилегают, в случае n > 8 будет превышать 2π, в случае n < 8 будет менее 2π. В первом случае построить что-то на данный момент интересное не удастся, а во втором в оставшееся место можно вписать что-то еще. Это может быть еще один многоугольник либо луч полиграммы.

Если это третий многоугольник, то количество сторон можно вычислить уравнением:
π — 4π / n + 3(π — 2π / n) = 2π
2π — 10π / n = 0
n = 5
Таким образом, вокруг луча пятиконечной звезды можно нарисовать три пятиугольника с общей вершиной в вершине пентаграммы. К сожалению, в данном случае мозаики не получится, разве что узор, подобный описанному выше, где вокруг вершины каждого луча группируется три пятиугольника:

Рассматривая случай с двумя многоугольниками и двумя лучами, можно придти к следующему уравнению:
2(π — 4π / n) + 2(π — 2π / n) = 2π
2π — 12π / n = 0
n = 6

Результатом получается вот такая мозаика:

геометрия / Кратчайшее растояние до вершин многоугольника / Математика

Я раньше не видела этой задачи, но меня заинтересовала рекуррентная формула, приведенная Вами. 2}}}.$$

Из этого равенства можно сделать рекуррентное соотношение.

Многоугольники. Выпуклый многоугольник. Четырехугольник 8 класс онлайн-подготовка на Ростелеком Лицей

Многоугольники. Выпуклый многоугольник. Четырехугольник.

Треугольник – это частный случай многоугольника.

 

 

В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник – фигуру с пятью углами.

Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.

Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю.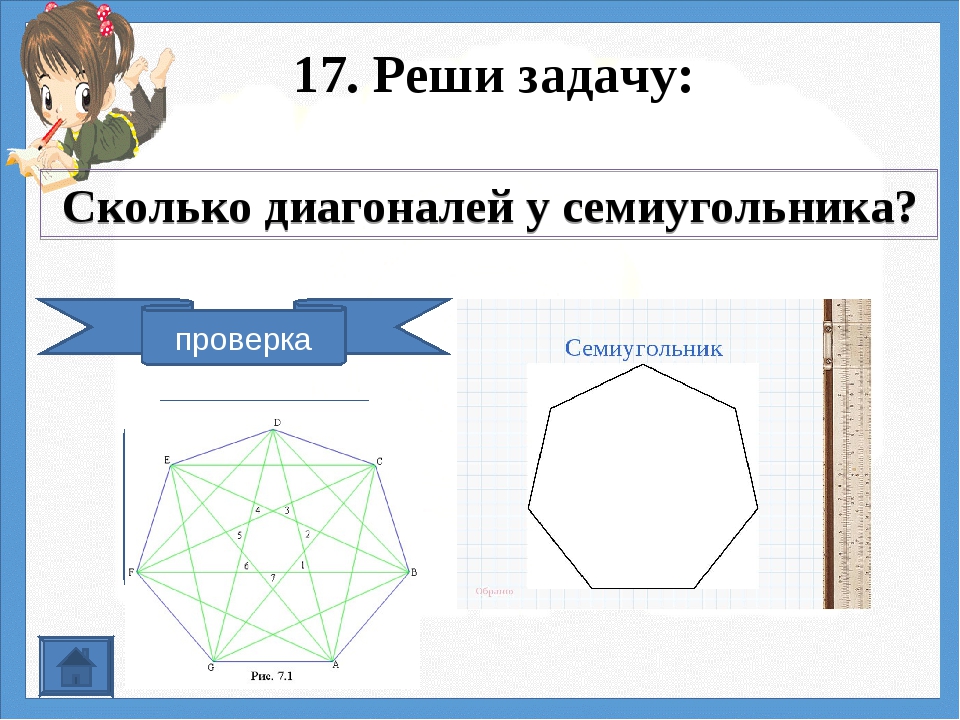 Внутреннюю область также относят к многоугольнику.

Иными словами, например, когда говорят о пятиугольнике А₁А₂А₃А₄А₅, имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника.

 

 

Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).

Периметр многоугольника – сумма длин сторон многоугольника.

Отрезок, соединяющий любые две противоположные вершины, называется диагональю многоугольника.

 

 

Многоугольники делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на рисунке выше, является выпуклым, а на рисунке ниже – невыпуклым.

 

 

Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой. Невыпуклыми являются все остальные многоугольники.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны.

Существенное отличие четырехугольника от треугольника в том, что он может быть выпуклым или невыпуклым.

 

 

 

Очень важное различие, о котором знает каждый плотник, состоит в том, что треугольник – «жесткая» фигура, а четырехугольник (как и все остальные многоугольники) – «нежесткая».

У треугольника невозможно изменить его форму, не изменив длин сторон. При этом у любого четырехугольника можно изменить его форму, не меняя длины сторон. На практике это будет означать, что треугольник, сколоченный из трех дощечек, будет жестким, не будет сминаться даже при сильных воздействиях, а четырехугольник при достаточной нагрузке со стороны изменит свою форму.

Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольникаитеорема о сумме внешних углов выпуклого многоугольника.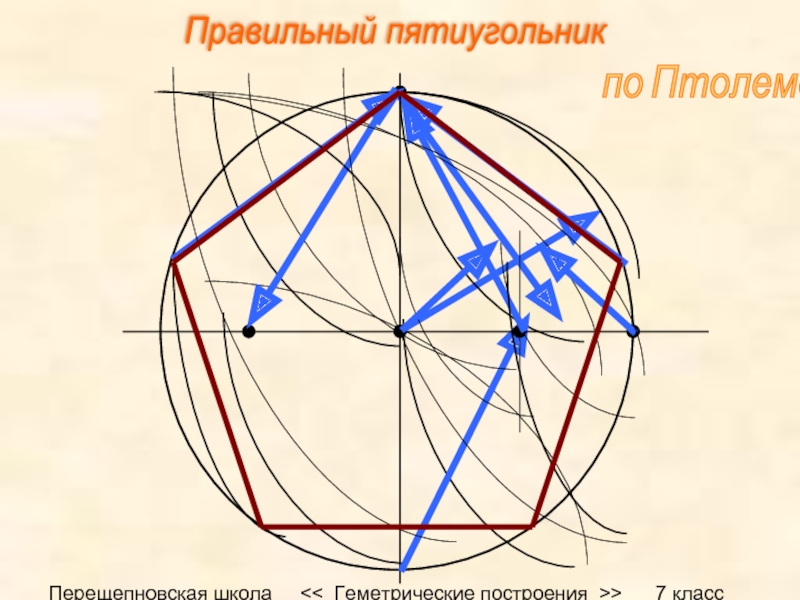

Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).

Сумма углов n-угольника равна 180°·(n-2).

Математическая запись: ∠A1+∠A2+…+∠An=180°(n-2), где n – количество его углов (сторон).

Вспомним, что любой четырехугольник состоит из двух треугольников (достаточно провести диагональ). Но сумма углов каждого из них одинакова и равна 180⁰, значит, сумма углов четырехугольника 360⁰.

Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).

∠1’+∠2’+…+∠n’=360°, где n – количество его углов (сторон), а ∠1′,…,∠n’ – внешние углы, по одному от каждой вершины.

Некоторые ответы о пятиугольниках

Некоторые ответы о пятиугольниках

Некоторые отношения в правильных пятиугольниках

Сумма углов -> Угол при вершине

Общая сумма углов пятиугольника = 3 * 180 = 540 градусов. Таким образом, каждый угол при вершине = 540/5 = 108 градусов.

Равнобедренные треугольники

<-> Углы

Две стороны и вершина образуют тупой равнобедренный треугольник, две такие заштрихованные. здесь.

Так как угол тупой вершины EAB = 108 и два равных угла при основании имеют сумму = 180 108 = 72, острые углы основания, такие как CAB = 36 градусов.

Кроме того, угол CAD = угол EAB — 2 * 36 = 36 градусов, поэтому 2 диагонали от вершина, такая как A, делит угол при вершине пополам; то есть делят угол при вершине на 3 равных угла по 36 градусов.

Наконец, треугольник DAC равнобедренный, поскольку каждый из углов основания ACD и ADC равны 108 36 = 72 градусам.

Пентаграмма (5 звезд)

Если все 5 диагоналей нарисованы в правильном пятиугольнике, эти 5 сегментов образуют форму звезды, называемую правильной пентаграммой.

Объединив то, что теперь известно о равных углах при вершинах, получим Легко видеть, что пятиугольник ABCDE разделен на 5 равнобедренных треугольников, похожих на к треугольнику ABC 36-108-36 градусов, 5 равнобедренных треугольников, подобных 72-36-72 градусный треугольник DAC и один правильный пятиугольник в центре.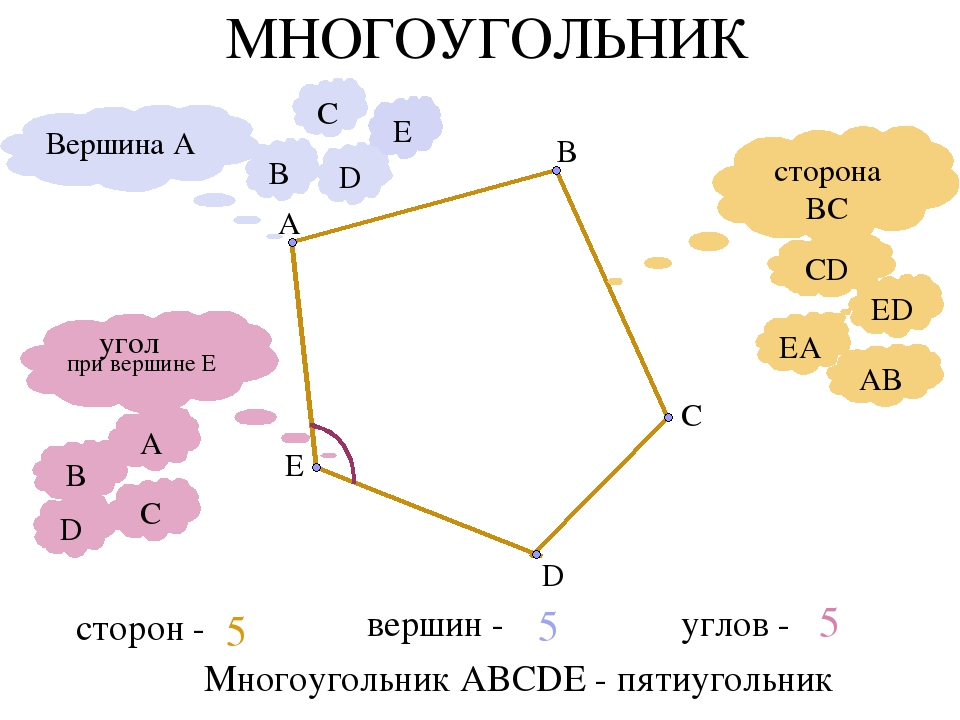

Равнобедренная трапеция и параллельные линии

Есть несколько способов увидеть, что диагональ BE параллельна CD и что CDEB — равнобедренная трапеция.Если предположить, что знания об углах Как описано выше, есть несколько быстрых способов убедиться в этом.

Метод поперечного и дополнительного угла: Линия BC является поперечной CD и BE. Угол DCB = 3 * 36 и угол CBE = 2 * 36, поэтому сумма углов = 5 * 36 = 180. Поскольку углы дополнительные, прямые CD и BE параллельны.

Метод поперечных и равных углов: Линия BD является поперечной CD и BE.Угол BDC = 36 и угол DBE = 36. Эти совпадающие чередующиеся внутренние углы означают, что прямые CD и BE параллельны.

Метод симметрии линии равнобедренного треугольника: Поскольку треугольник EAB равнобедренный, биссектриса угла EAB является серединным перпендикуляром отрезка БЫТЬ. Поскольку треугольник DAC равнобедренный, биссектриса угла DAC — серединный перпендикуляр к CD. Но биссектрисы углов двух углы — это одна и та же линия (так как биссектриса DAC делит угол EAB на два углы размером 18 + 36 градусов).Но это значит, что у CD и BE одинаковые серединный перпендикуляр. Таким образом, эти линии параллельны. Кроме того, поскольку BC является При отражении DE отрезки имеют одинаковую длину.

Ромбики одинаковой длины

Теперь мы знаем, что каждая диагональ параллельна одной из сторон. Итак, если мы нарисуем две диагонали, они образуют параллелограмм параллелограммом. Но с тех пор стороны правильного пятиугольника равны, параллелограмм представляет собой ромб.(Противоположные стороны равны в любом параллелограмме; если две соседние стороны равны, тогда все четыре стороны равны.)

Это означает, что определенные длины внутри звездообразной формы равны сторонам пятиугольника.

Золотое сечение в регулярном пентагоне

Теперь у нас есть много способов найти вложенные похожие равнобедренные треугольники в пентаграмме.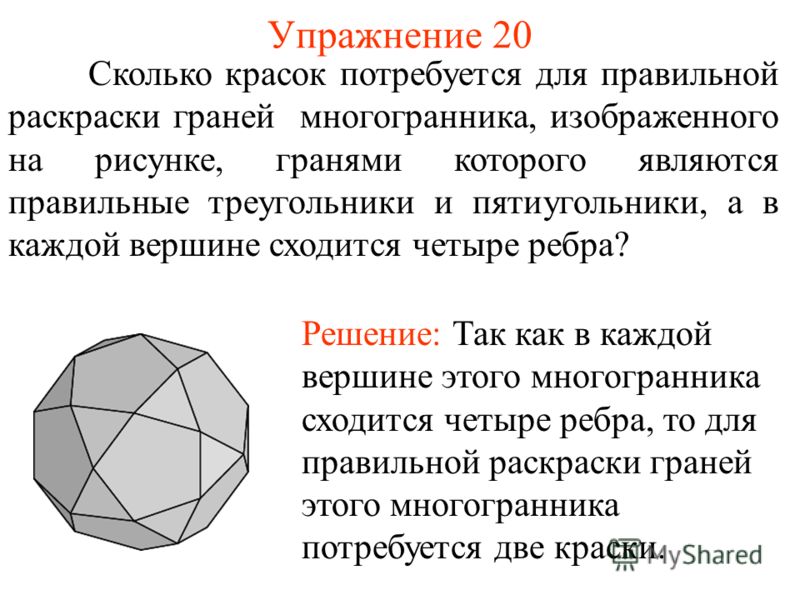 2 d 1 = 0.

Положительный корень этого квадратного уравнения равен (1/2) * (1 + sqrt 5). Это называется золотым сечением .

Для любого правильного пятиугольника со стороной s и длиной диагонали d отношение d / s = золотое сечение.

Построение правильного пятиугольника со стороны

Мы узнали, как по единице длины s построить длину sqrt 5, так что это можно использовать для построения длины d, которая является золотым сечением * s.

Затем с помощью s и d можно начать с отрезка AB и построить все треугольники. ABC, ABD, ABE и таким образом построить правильный пятиугольник со стороной AB.

Этот метод также создает случайные углы, равные 36 градусам и целым числам. кратные 36 градусам.

Построение правильного пятиугольника из центра и вершины

Дан центр O и точка A, можно построить правильный пятиугольник ABCDE нарисовав круг с центром О через А, а затем построив углы необходимы (либо центральные углы, такие как AOB, либо углы при вершинах).

Но построение золотого сечения также создает необходимые углы, как было отмечено в предыдущем разделе.

полигонов — Основы работы с полигонами — Подробно

Слово многоугольник представляет собой сочетание двух греческих слов: «поли» означает «много» и «гон». означает угол. У многоугольника помимо углов есть стороны и вершины. «Три» означает «три», поэтому самый простой многоугольник называется треугольник, потому что у него три угла.Он также имеет три стороны и три вершины. Треугольник всегда компланарен, чего нельзя сказать о многих из них. другие полигоны.

Правильный многоугольник — многоугольник, все углы и стороны которого совпадают или равны. Вот некоторые правильные многоугольники.

Мы можем использовать формула, чтобы найти сумму внутренних углов любого многоугольника. В этой формуле буква n обозначает количество сторон или углов многоугольника.

сум углов = (n — 2) 180 °

Давайте использовать формула, чтобы найти сумму внутренних углов треугольника. Запасной 3 для п. Получаем, что сумма равна 180 градусам. Это важный факт, о котором следует помнить.

сум углов = (n — 2) 180 ° 90 · 106 = (3 — 2) 180 ° = (1) 180 ° = 180 °

Чтобы найти сумма внутренних углов четырехугольника, мы можем снова использовать формулу.На этот раз замените n на 4. Мы находим, что сумма внутренних углов четырехугольника 360 градусов.

сум углов = (n — 2) 180 ° 90 · 106 = (4-2) 180 ° = (2) 180 ° = 360 °

Полигоны могут быть разделенными на треугольники, нарисовав все диагонали, которые можно нарисовать из одной единственной вершины. Давайте попробуем это с четырехугольником, показанным здесь. Из вершине A мы можем провести только одну диагональ, к вершине D.Четырехугольник может поэтому разделим на два треугольника.

Если вы посмотрите вернувшись к формуле, вы увидите, что n — 2 дает количество треугольников в многоугольнике, и это число умножается на 180, сумма мер всех внутренних углов в треугольнике. Вы видите, где «н — 2 «? Это дает нам количество треугольников в многоугольнике. Как Как вы думаете, много ли треугольников будет у 5-стороннего многоугольника?

Вот пятиугольник, 5-сторонний многоугольник.Из вершины A можно провести две диагонали, разделяющие пятиугольник на три треугольника. Умножаем 3 раза на 180 градусов, чтобы найти сумма всех внутренних углов пятиугольника, составляющая 540 градусов.

сум углов = (n — 2) 180 ° 90 · 106 = (5-2) 180 ° = (3) 180 ° = 540 °

Ссылки по теме:
Определения многоугольников, формулы полигонов (площадь, периметр) и имена полигонов (таблицы и формулы)

Полигоны средней точки

Проблема

Решение

Оригинал Обсуждение

Педагогика

Демонстрации

Библиография

Выпуклые пятиугольники Периметр А как насчет периметров средних пятиугольников? Для правильного пятиугольника многоугольник в средней точке — это еще один правильный пятиугольник со сторонами, равными половине длины каждой диагонали. Отношение периметра средней точки к оригиналу тогда составляет половину отношения стороны к диагонали, то есть половину обратной величины золотого сечения, = 1 / (2t), около 0,806. Тот же анализ показывает, что для общий выпуклый пятиугольник, периметр многоугольника средней точки составляет половину суммы длин диагоналей, и это определенно не является константой. Площадь А как насчет площадей средних пятиугольников для выпуклых пятиугольников? Для правильного пятиугольника площадь среднего пятиугольника, деленная на площадь исходной фигуры, равна 1 / (4t 2 ).Однако для пятиугольника, близкого к треугольнику, с двумя вершинами, близкими к одной вершине внизу и двум близким к другой вершине внизу, площадь средней точки фигуры настолько близка к 3/4, насколько нам угодно. Это, по-видимому, максимальное соотношение, достижимое для пятиугольников. Демонстрация 4. Площадь средних пятиугольников Обратите внимание, что для выпуклых многоугольников с шестью или более сторонами отношение площади среднего пятиугольника к площади оригинала настолько близко к 1, насколько нам угодно.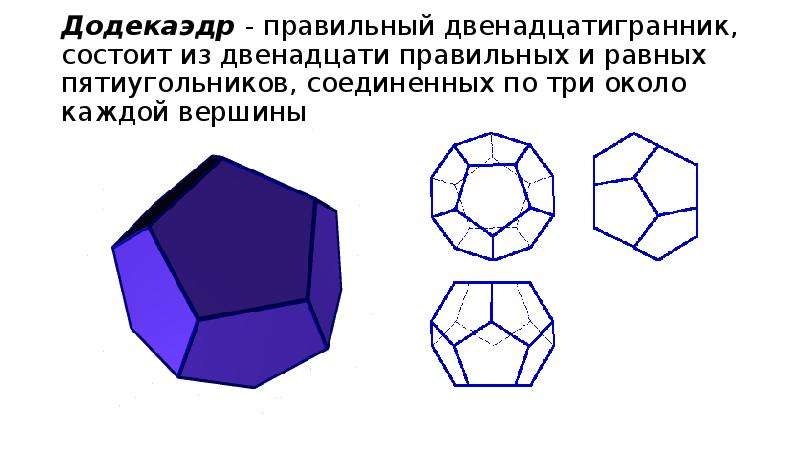 Этого можно добиться, разместив первые две вершины около одной вершины треугольника, следующие две — около второй, а все остальные — около третьей. Отношение не может быть больше 1, поскольку многоугольник средней точки лежит внутри исходного выпуклого многоугольника. Рис. 4. Отношение площадей, приближающееся к 1 для среднего шестиугольника Удивительно, хотя соотношение площадей для пятиугольника не является постоянным, мы все же можем найти взаимосвязь между площадью оригинала, площадью многоугольника средней точки и площадью другой фигуры.Сначала это видно аналитически, а затем с помощью прямого геометрического аргумента. Напомним, что для выпуклого многоугольника с центром внутри, мы можем найти площадь, сложив площади треугольников с началом координат как одной вершиной и стороной многоугольника как противоположным знаком. Если координаты вершины i равны ( x i , y i ), то площадь треугольника i с вершинами (0,0), ( x i , y i ), ( x i + 1 , y i + 1 ) является В векторной записи, если ( x i , y i ) = X i , то площадь равна С другой стороны, вершины многоугольника средней точки равны Y i = ( X i + X i +1 ) / 2, поэтому площадь многоугольника средней точки является Что означает дополнительный термин? Формально в случае пятиугольника он представляет собой 1/4 площади многоугольника с вершинами X 1 , X 3 , X 5 , X 2 , Х 4 . Это так называемый «звездный пятиугольник», образованный последовательностью пяти диагоналей, самопересекающийся многоугольник. Сумма пяти треугольников даст площадь звезды, но средний пятиугольник в звезде считается дважды.

Координаты вершин правильного многоугольника с калькулятором

Координаты вершин правильного многоугольника с калькулятором

Этот калькулятор берет параметры правильного многоугольника и вычисляет его координаты.Он производит как координаты вершины и координаты отрезков, составляющих стороны многоугольника.

Пригодится слепым пользователям и тем, кто производит материалы для слабовидящих. Программы для тиснения фигур на страницах для слепых нужны координаты линий, составляющих фигуру. Эта страница была разработана, чтобы упростить создание данных, необходимых этим программам (например, SVG Draw) для «рисования» правильных многоугольников.

Инструкции

На этой странице четыре заголовка:

1. Инструкции
2. Входы
3. Список сторон
4. Список вершин

Входы следующие:

• Центр X и центр Y — координаты центральной точки многоугольника. 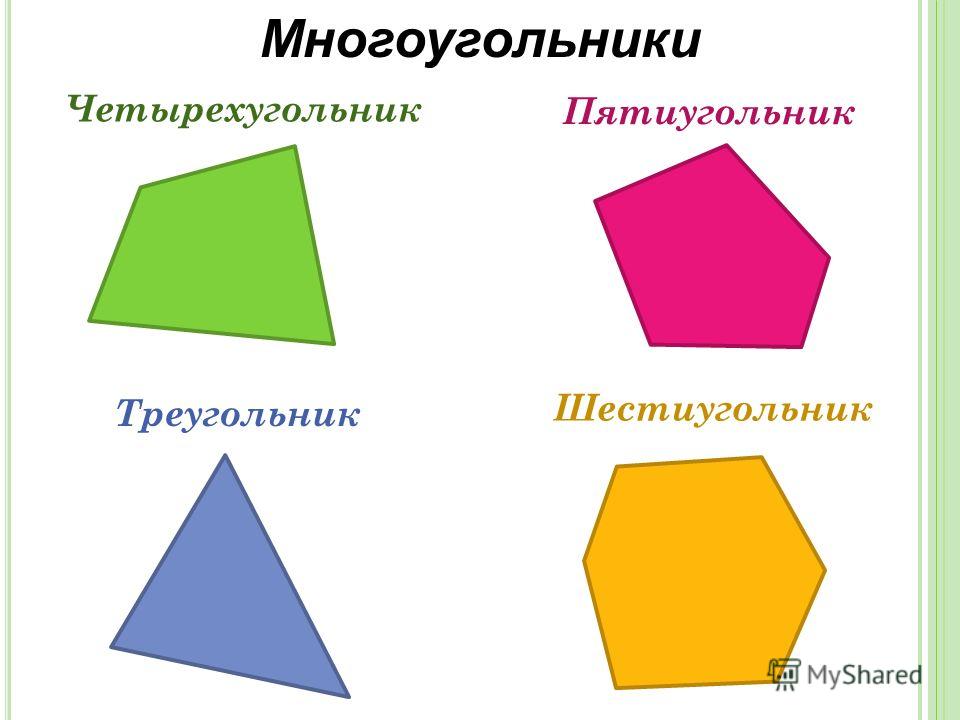Первоначально установите значения 550, 550. Обратите внимание, что координата y положительна вниз, чтобы соответствовать соглашениям в большинстве компьютерных программ. Положительный x находится справа.
• Количество сторон. Должно быть больше 2. Изначально установить на 5.
• Радиус — это расстояние от центра до вершины. Первоначально установлен на 100.
• Начальный угол — это положение первой вершины.

  Этот угол выражается в градусах и представляет собой угол, начинающийся с 3 часов против часовой стрелки.Так, например, если вы хотите, чтобы первая вершина находилась в положении «12 часов», установите значение 90. Изначально установите пустое значение (авто).

  Если вы оставите это поле пустым, оно будет установлено автоматически: если количество сторон нечетное, (например, пятиугольник), первая вершина будет на 12 часах. Если даже, например восьмиугольник, верхняя и нижняя стороны будут горизонтальными на странице.

Нажмите кнопку «Рассчитать», чтобы обновить результаты. Обратите внимание, что координаты y положительны вниз, чтобы соответствовать соглашениям в большинстве компьютерных программ.Положительный x находится справа.

Выходными данными сторон является таблица, содержащая начальные и конечные координаты x, y каждой стороны многоугольника, идущий против часовой стрелки от первого. Ниже представлены те же данные в формате CSV.

Выходные данные вершины — это таблица, содержащая координаты x и y каждой вершины многоугольника, идущие против часовой стрелки от первой. Ниже представлены те же данные в формате CSV.

Входы

Рассчитать

Стороны

В виде таблицы

Как CSV

Вершины

В виде таблицы

Как CSV

Другие темы о координатной геометрии

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

Пентагон | Math Wiki | Fandom

Эта статья требует дополнительных ссылок для проверки . Пожалуйста, помогите улучшить эту статью, добавив цитаты из надежных источников. Материал, не полученный от источника, может быть оспорен и удален.

Правильный пятиугольник
Правильный пятиугольник, {5}
Ребра и вершины	5
Символ Шлефли	{5}
Диаграмма Кокстера – Дынкина
Группа симметрии	Двугранный (D 5 )
Площадь (с = длина кромки)
Внутренний угол (градусы)	108 °

Шаблон: WiktionaryparTemplate: Два других использования

В геометрии пятиугольник — это любой пятиугольник. Пятиугольник может быть простым или самопересекающимся. Внутренние углы в простом пятиугольнике всего.

Содержание

• 1 Правильные пятиугольники
  • 1,1 Строительство
• 2 графика
• 3 Пентагона в природе
  • 3.1 Растения
  • 3,2 Животные
• 4 См. Также
• 5 Внешние ссылки

Правильные пятиугольники

Термин пятиугольник обычно используется для обозначения правильного выпуклого пятиугольника , у которого все стороны равны и все внутренние углы равны (108 °).Его символ Шлефли — {5}. Хорды ​​этого пятиугольника находятся в золотой пропорции к его сторонам.

Площадь правильного выпуклого пятиугольника с длиной стороны определяется выражением

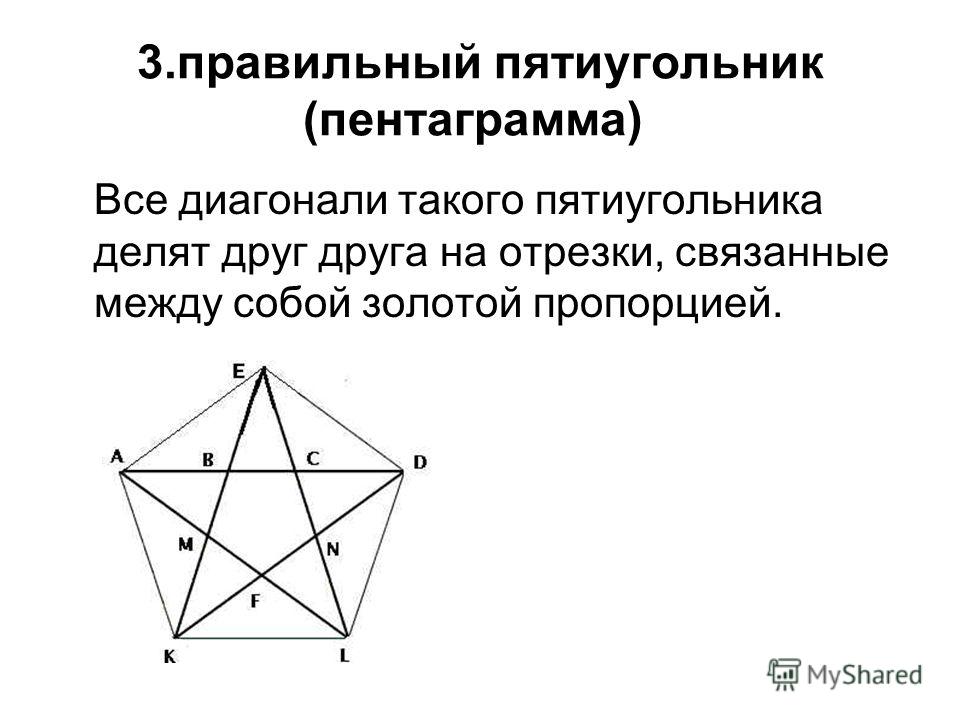
Пентаграмма или пятиугольник — это правильный пятиугольник звезды . Его символ Шлефли — {5/2}. Его стороны образуют диагонали правильного выпуклого пятиугольника — в этом расположении стороны двух пятиугольников находятся в золотом сечении.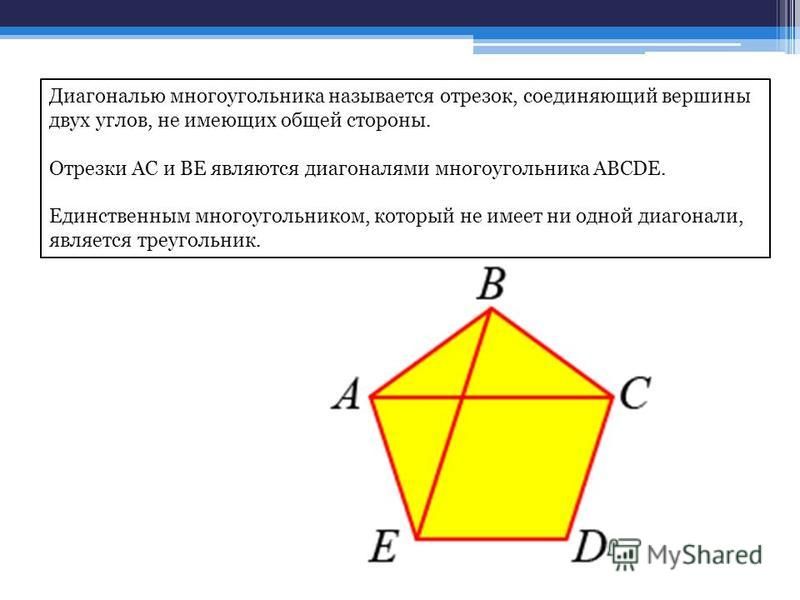

Когда правильный пятиугольник вписан в круг с радиусом, длина его ребра определяется выражением

Строительство

Правильный пятиугольник можно построить с помощью циркуля и линейки, вписав один в заданный круг или построив один на заданном крае.Этот процесс был описан Евклидом в его Elements около 300 г. до н.э.

Один из методов построения правильного пятиугольника в данном круге заключается в следующем:

Построение правильного пятиугольника

Альтернативный метод:

Построение пятиугольника

1. Нарисуйте круг, в который нужно вписать пятиугольник, и отметьте его центральную точку. (Это зеленый кружок на диаграмме справа).
2. Выберите точку на окружности, которая будет одной из вершин пятиугольника. Проведите линию через и.
3. Постройте линию, перпендикулярную проходящей через нее линии. Отметьте его пересечение с одной стороной круга в качестве точки.
4. Постройте точку как середину.
5. Нарисуйте круг с центром в точке. Отметьте его пересечение с линией (внутри исходного круга) как точку.
6. Нарисуйте круг с центром в точке.Отметьте его пересечения с исходным (зеленым) кружком точками и.
7. Нарисуйте круг с центром в точке. Отметьте его другое пересечение с исходной окружностью как точку.
8. Нарисуйте круг с центром в точке. Отметьте его другое пересечение с исходной окружностью как точку.
9. Постройте правильный пятиугольник.

После образования правильного выпуклого пятиугольника, если вы соедините несмежные углы (рисуя диагонали пятиугольника), вы получите пентаграмму с меньшим правильным пятиугольником в центре.Или, если вы вытянете стороны, пока не встретятся несмежные, вы получите пентаграмму большего размера.

Простой метод создания правильного пятиугольника из полоски бумаги состоит в том, чтобы завязать узел сверху на полоске и аккуратно распрямить узел, потянув за концы полоски бумаги. Если загнуть один из концов над пятиугольником, вы увидите пентаграмму при контровом свете.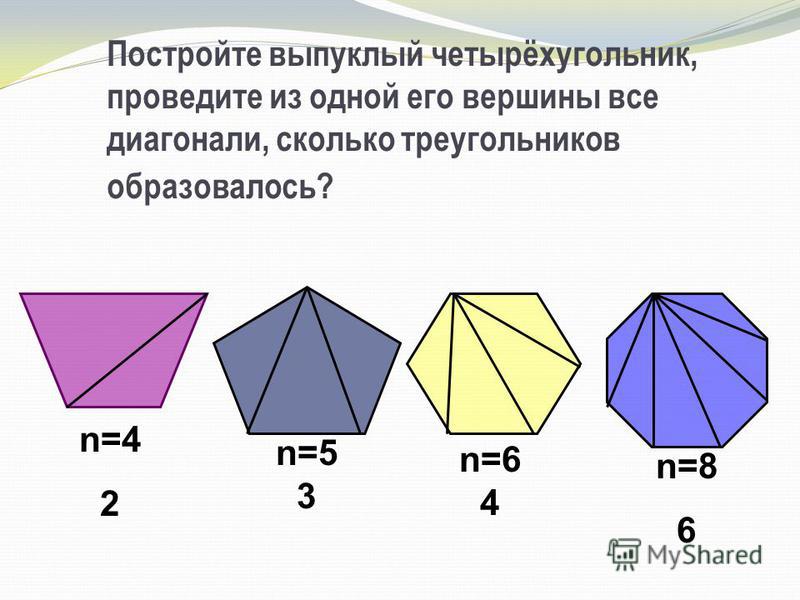

Графики

Полный граф часто изображают в виде правильного пятиугольника со всеми 10 соединенными ребрами.Этот граф также представляет собой ортогональную проекцию 5 вершин и 10 ребер 5-ячейки. Выпрямленная 5-ячеечная с вершинами на средних краях 5-ячеечной проекции проецируется внутри пятиугольника.

5-элементный (4D)

Выпрямленный 5-элементный (4D)

Пентагоны в природе

Растения

Пятиугольное поперечное сечение бамии. Утренняя слава, как и многие другие цветы, имеет пятиугольную форму. Гинецей яблока состоит из пяти плодолистиков, расположенных в форме пятиконечной звезды. Звездный фрукт — еще один фрукт с пятикратной симметрией.
Добавить фото в эту галерею

Животные

Морская звезда. Многие иглокожие имеют пятикратную радиальную симметрию. Иллюстрация хрупких звезд, а также иглокожих пятиугольной формы.
Добавить фото в эту галерею

См.

Также

• Пентагон, штаб-квартира Министерства обороны США
• Додекаэдр, многогранник правильной формы, состоящий из 12 пятиугольных граней
• Тригонометрические константы пятиугольника
• Пятиугольные числа
• Ассоциаэдр — пятиугольник — это ассоциаэдр четвертого порядка
• Пентаграмма
• Pentastar, логотип Chrysler

Внешние ссылки

• Weisstein, Eric W., «Пентагон» от MathWorld.
• Как построить правильный пятиугольник, используя только циркуль и линейку.
• Как сложить правильный пятиугольник, используя только полоску бумаги
• Определение и свойства пятиугольника с интерактивной анимацией
• Девять конструкций правильного пятиугольника Робина Ху
• Примерное построение художниками эпохи Возрождения правильных пятиугольников на Конвергенции

v t e Правильные многоугольники Перечисляется по количеству сторон 1–10 сторон Henagon (Моногон) Дигон Равносторонний треугольник Квадрат Пентагон Шестигранник семиугольник восьмиугольник Нонагон (Эннеагон) Десятиугольник 11–20 сторон Hendecagon Додекагон Tridecagon Тетрадекагон Пентадекагон (Quindecagon) Шестигранник Гептадекагон восьмиугольник Эннеадекагон (Nonadecagon) Икосагон 30-90 Триаконтагон Тетрактагон Пентаконтагон (Quincontagon) Шестигранник Гептаконтагон Octacontagon Enneacontagon (Nonacontagon) Прочие Гектогон (Hecatontagon) Чилигон Мириагон Мегагон Апейрогон Звездообразные многоугольники Пентаграмма Гексаграмма Гептаграмма Октаграмма Эннеаграмма Декаграмма Хендекаграмма Додекаграмма

полигонов

полигонов

Многоугольники: имена, диагонали и углы

Полигоны: термины и описания

Определение: многоугольник — мертвый попугай!

В шутку возможно, но в геометрии,

Многоугольник — плоская фигура, образованная 3 или
более пересекающихся отрезков прямых .

Линии называются сторонами , а точка или угол , где встречаются 2 стороны, называется вершиной (множественное число — вершина — произносится vur — tih — видит ). Мы помечаем вершины заглавными (заглавными) буквами (см. Зеленый пятиугольник ниже). Линия, соединяющая последовательные вершины, является стороной.

Диагональ — это отрезок линии , который соединяет любые две непоследовательных вершин многоугольника (показано розовым шестиугольником ниже).

Многоугольник со сторонами n имеет внутренние углы n и внешние углы n .
внешний угол образован стороной и продолжением смежной стороной .

В многоугольнике Regular все стороны , все внутренние и внешние углы равны .

Правильные треугольники и четырехугольники имеют особые названия.
Правильный треугольник называется равносторонним треугольником .
Правильный четырехугольник называется квадрат .

Именование полигонов

Почти в каждой книге по математике, в которой обсуждается многоугольник, мы встретим это утверждение:

многоугольников названы по количеству сторон.

Это не совсем так. Единственный многоугольник, который правильно назван по количеству сторон, — это четырехугольник, поскольку quad в качестве префикса означает четыре , а lateral означает сторону .Боковой пас в футболе — это пас в сторону , а не вперед. Односторонний означает односторонний, а двусторонний — двусторонний.

Все остальные многоугольников , такие как пента угольник , шестигранник угольник и окта угольник , названы по количеству их вершин или углов . Суффикс « гон » происходит от греческого слова « гония », что означает «угол » или «угол».Однако, поскольку количество углов в многоугольнике всегда равно количеству сторон , мы можем продолжать делать вид, что многоугольники названы по количеству сторон.

Но на самом деле мы называем полигона по количеству вершин или углов в них .
Треугольник имеет 3 угла , о которых говорится в его названии.
пент агон имеет 5 углов и 5 сторон, а дека уголь имеет 10 и т. д.

Знак остановки на углу — это обычный окт агон — с 8 равными углам и сторонам. Стены и полы, выложенные плиткой в ​​наших зданиях и домах, состоят из правильных многоугольников, образующих узоры. Наши дворы, здания, мебель и одежда имеют форму различных многоугольников, поэтому они встречаются повсюду вокруг нас — даже в некоторых из самых приятных мест на природе.

Посмотрите на этот узор из правильных шестиугольников!

Диагонали в многоугольнике

Как мы уже говорили, диагональ многоугольника — это отрезок линии , который соединяет любые две непоследовательных вершин многоугольника.Мы видим их как линии, пересекающие внутреннее пространство многоугольника. Теперь мы придумаем формулу, чтобы найти общее количество диагоналей в многоугольнике, когда мы знаем, сколько сторон — ой! — вершины есть.

Давайте исследуем, что происходит, когда мы соединяем диагонали вокруг вершин пятиугольника.

Поскольку вершина A соединена с двумя другими вершинами — B и E — сторонами, а вершина A не может быть соединена сама с собой для образования диагонали, мы определили 3 вершины, которые не могут быть концом диагональ от А.Итак, поскольку у нашего пятиугольника 5 вершин, у нас остается 5–3 или 2 вершины, которые нужно соединить диагональной линией.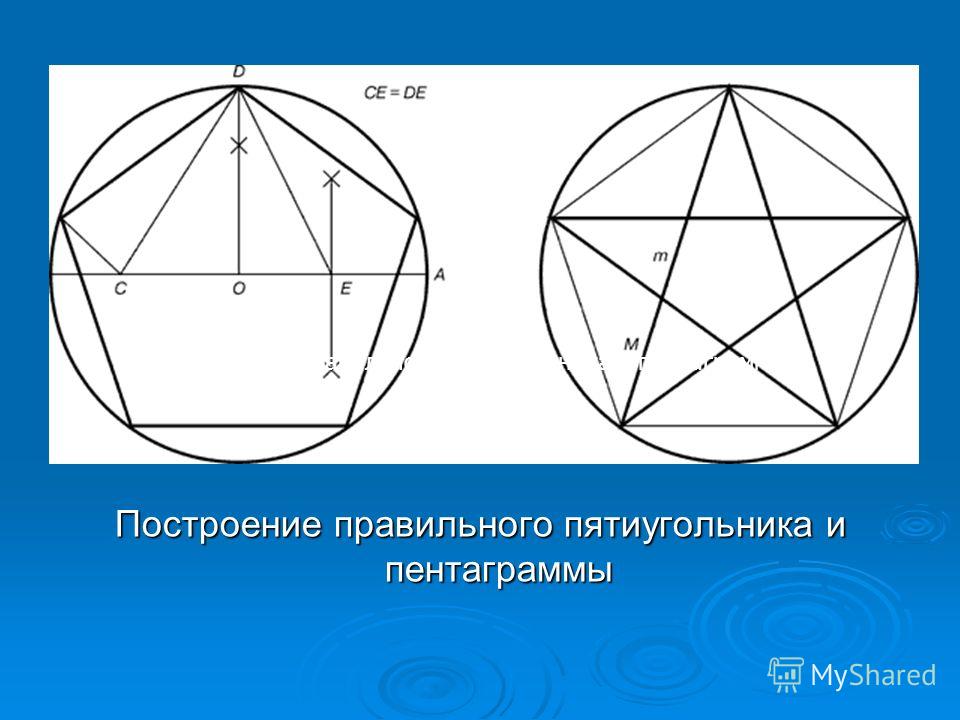
То же самое и с вершиной E. Ее можно соединить только с B и C диагональными линиями. Затем мы переходим к D, который уже соединен с A, поэтому мы можем провести только одну диагональ, DB, из этой вершины.

То же и для шестигранника LMNOPQ. У Q и P по 3 диагонали, у O — 2, а у N — осталась только одна диагональ.

Формула, которую мы используем, чтобы найти общее количество диагоналей в многоугольнике из n сторон, выглядит следующим образом:

Часть ( n — 3 ) указывает, что каждую вершину можно соединить диагональю на 3 меньше, чем общее количество вершин.А часть n /2 говорит, что каждая диагональ использует 2 вершины.
Для нашего шестиугольника с 6 вершинами количество диагоналей равно

Для восьмиугольника с 8 вершинами количество диагоналей равно

.

Сумма внутреннего и внешнего углов многоугольника

Давайте посмотрим на изображение, чтобы увидеть логику теоремы, которая гласит:

Сумма внутренних углов многоугольника со сторонами n равна
(n — 2) прямых угла ; или (n — 2) 180 °

Поскольку каждая вершина соединена с двумя другими вершинами сторонами,
мы всегда будем получать ( n — 2) треугольника из многоугольника со сторонами n .
А поскольку сумма трех углов в треугольнике равна 180 °,
сумма внутренних углов многоугольника из n сторон составляет ( n — 2) × 180 °.
В правильном многоугольнике, поскольку внутренние углы n равны,
каждая измеряет ( n — 2) × 180 ° ÷ n

Градусная мера каждого внутреннего угла в ОБЫЧНОМ ПОЛИГОНЕ из n сторон составляет

С этой формулой, как и со всеми формулами, мы можем работать в обратном направлении.Скажем, мы знаем, что каждый внутренний угол правильного многоугольника составляет 144 ° , и мы хотим знать , сколько у него сторон . Устанавливаем
формулу, равную 144, и решите ее для n следующим образом:

затем решаем так: 180 n — 360 = 144 n , чтобы получить 36 n = 360, поэтому n = 10

Теперь, когда мы знаем, что сумма внутренних углов всегда ( n -2) 180 °, мы можем найти сумму внешних углов . Из шестиугольника на диаграмме мы видим, что сумма всех прямых углов в 6 вершинах будет 6 (180 °). Но сумма интерьеров — 4 (180 °). Следовательно, сумма внешних углов должна быть 2 (180 °) или 360 ° . Это верно для всех полигонов , правильных или нет.
В правильном многоугольнике все внешние углы равны ( 360 ° / n ).

Сумма внешних углов любого многоугольника составляет 360 ° Градус каждого внешнего угла в ОБЫЧНОМ ПОЛИГОНЕ из n сторон

Примечание: Так как внешние и внутренние углы в любой вершине равны , дополнительные ,
(они складываются до 180 °,) внешний угол равен 180 ° — (внутренний угол).

.

Пример 1 : Для правильного двенадцатиугольника (12 сторон) найдите:

a) Сумма 12 внутренних углов.

б) Измерение каждого внутреннего угла.

c) Измерение каждого внешнего угла.

Решение : n = 12

a) Сумма 12 внутренних углов = ( n — 2) 180 ° = 10 (180 °) = 1800 °.

b) Размер каждого внутреннего угла = (1800 °) / 12 = 150 °.

c) Размер каждого внешнего угла = (360 °) / 12 = 30 ° или (180 ° — 150 °) = 30 °.

Пример 2:

Найдите количество сторон правильного многоугольника, если каждый внутренний угол равен:

a) 140 ° Решение: 180 (n — 2) = 140 n 40n = 360, поэтому n = 9 сторон.

b) 157,5 ° Решение: 180 (n — 2) = 157,5 n 22.5n = 360, поэтому n = 16 сторон.

c) 108 ° Решение: 180 (n — 2) = 108 n 72n = 360, поэтому n = 5 сторон.

.

Формулы для многоугольника с n вершинами
Формула для	Формула
количество диагоналей	.
количество треугольников	n -2
сумма внутренних углов	( n -2) 180 °
сумма внешних углов	360 °
каждый внутренний угол правильного многоугольника
каждый внешний угол правильного многоугольника

Теперь возьмите карандаш, ластик и записную книжку, скопируйте вопросы,
выполните практические упражнения, а затем проверьте свою работу с решениями.
Если вы застряли, просмотрите примеры в уроке, а затем попробуйте еще раз.

Практические упражнения

1) Сопоставьте каждое слово в списке слева со всеми буквами всех цифр, которые оно описывает.
(для одного слова может быть более одного совпадения)

( раствор )

2) Подсчитайте количество диагоналей для каждой цифры в №1.

( раствор )

3) Объясните, как вы можете использовать линейку и транспортир, чтобы построить
правильный шестиугольник со стороной 7 см.

( раствор )

4) Найдите размер каждого внутреннего и внешнего угла для:

а) Правильный десятиугольник.

б) Правильный двенадцатигранник (12 сторон)

в) Правильный семиугольник.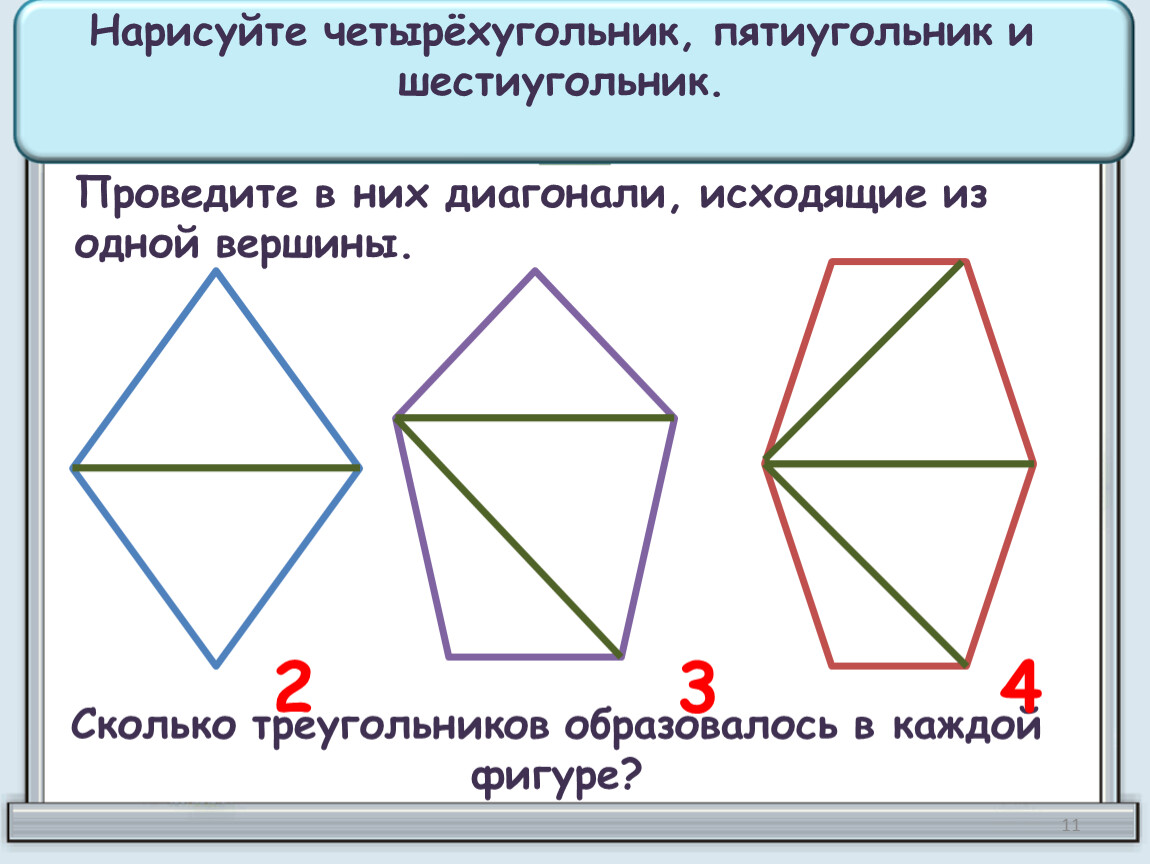

( раствор )

5) Найдите количество сторон правильного многоугольника, если каждый внутренний угол равен 156 °.

( раствор )

.

Решения

1)

2) Вычислите количество диагоналей для каждой цифры в # 1.

a) n = 3, поэтому 0 диагоналей	b) n = 4, поэтому ½ n ( n — 3) = 2 × 1 = 2	c) n = 3, значит, 0 диагоналей
d) n = 7, значит, 14 диагоналей	e) n = 5, значит, 5 диагоналей	f) n = 5, значит, 5 диагоналей
g) n = 6, так что 9 диагоналей	h) n = 8 итак 20 диагоналей

3) Шестигранник имеет 6 сторон. Рисуем отрезок линии и отмечаем АВ = 7 см.
Поскольку каждый внутренний угол правильного шестиугольника = 120 °, мы строим угол 120 °
на обоих A и B. Затем мы измеряем 7 см до C справа и F слева. Мы продолжаем
процесс, пока не завершим шестиугольник.

.

4) Найдите размер каждого внутреннего и внешнего угла для:

а) Правильный десятиугольник. внутри = 144 ° внешний = 36 °

b) Правильный двенадцатигранник (12 сторон) внутренний = 150 ° внешний = 30 °

в) Правильный семиугольник. внутри = 128,57 ° external = 51,43 °

5) Мы знаем, что 156 n = ( n — 2) 180 , что дает нам 156 n = 180 n — 360
когда мы решаем для n , мы получаем 15 сторон .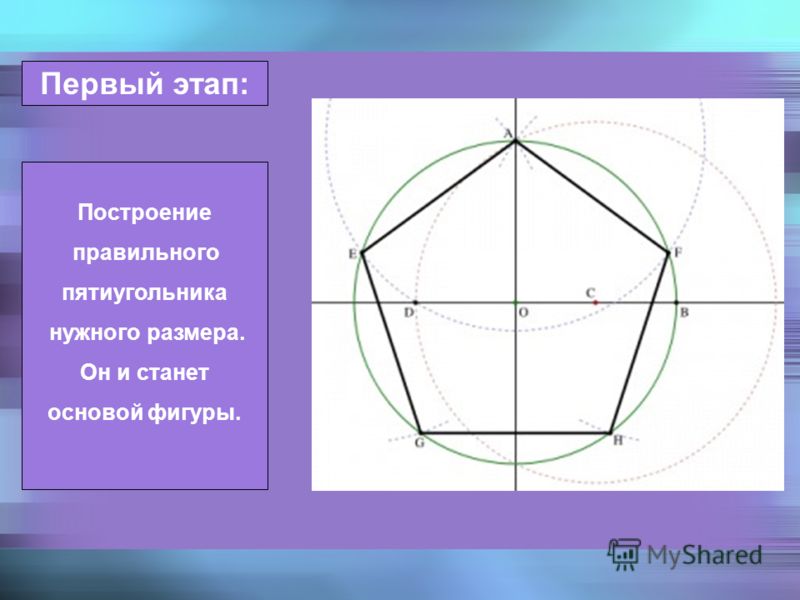

( Индекс первичной MathRoom )

Построение правильного Пентагона

Построение правильного Пентагона

1. Нарисуйте отрезок OB (длиной около 1 дюйма) в середине лист бумаги.Точка O будет одной вершиной пятиугольника.
2. Проведите серединный перпендикуляр CC ‘к OB так, чтобы отрезки CA и AC ‘имеют ту же длину, что и OB. Точка A — это середина OB а C и C ‘- концы серединного перпендикуляра. Вот как это сделать: нарисуйте достаточно круга с центром в точке O и пройдя через B и круг с центром в B, проходящий через O, чтобы увидеть два точки пересечения окружностей. Эти две точки — C и C ‘. Соедините их, чтобы получить отрезок CC ‘.
3. Нарисуйте круг S с центром в C, проходящий через O. Это будет круг, ограничивающий пятиугольник, который вы нарисуете.
4. Нарисуйте отрезок OC и нарисуйте достаточно круга с центром в O и проходя через A, чтобы увидеть, где он пересекает OC; позвонить в точка пересечения D.
5. Нарисуйте длинную линию L, перпендикулярную CD и проходящую через D.
6. Нарисуйте достаточно круга с центром в C и проходящим через C ‘, чтобы найти его пересечения E и F с L.
7. Нарисуйте точку пересечения E ‘окружности S с CE и пересечения F’. S и CF. Точки E ‘и F’ будут вершинами пятиугольника.
8. Нарисуйте достаточно круга с центром в E ‘, проходящего через O, чтобы найти точка пересечения G этой окружности и окружности S. Эта точка будет четвертой вершиной пятиугольник. Также нарисуйте достаточно круга, входящего в точку F ‘, проходящего через O найти точку пересечения H этой окружности и S. Эта точка будет последней вершиной.
9. Соедините пять вершин O, E ‘, G, H и F’, чтобы получить пятиугольник.

Если вы хотите шаг за шагом посмотреть, как выглядит конструкция, кликните сюда.

Если вы хотите увидеть сразу все девять шагов, кликните сюда.

Построение правильного восьмиугольника

Вот шаги, которые позволят вам построить правильный восьмиугольник.

1. Нарисуйте отрезок AB
2. Нарисуйте серединный перпендикуляр к AB и обозначьте середину C. сделайте этот шаг, используя шаг 2 процедуры построения пятиугольник.
3. Нарисуйте круг S с центром в C и проходящий через A (который также проходит через B). Обозначьте D и E точки, где этот круг пересекает перпендикулярная биссектриса, которую вы нарисовали на предыдущем шаге.
4. Нарисуйте достаточно кругов с центрами в B и D (с радиусом круг на предыдущем шаге), чтобы найти точку за пределами круга S, где пересекаются эти два круга. Проведите линию, проходящую через это точка пересечения и C и нарисуйте ее достаточно долго, чтобы отметить две точки где пересекает круг S.
5. Повторите этот шаг с точками A и D. Так будут отмечены еще два точки на окружности S.
6. Теперь у вас есть восемь точек на круге. Подключите их, чтобы получить восьмиугольник.

Если вы хотите шаг за шагом посмотреть, как выглядит конструкция, кликните сюда.