Вершки мера длины: Сторінку не знайдено – СКС™

Русская система мер. Единицы измерения

Главная Образование Русская система мер

Измерительные системы мер

1. Русская система мер
   — система мер, традиционно применявшихся на Руси и в Российской империи.
2. Метрическая система
   — общее название международной десятичной системы единиц, основанной на использовании метра и килограмма.
3. Международная система единиц, СИ (Systeme International, SI)
   — система единиц физических величин, современный вариант метрической системы.

 

---

Русская система мер

Русская система мер была стандартизирована на основе английских мер императорским указом 1835 года.
Были введены:

дюйм, линия, точка, фут. Ряд устаревших мер исключены.

Старорусские меры длины
1 миля	7 вёрст	≈ 7,47 км (Морская миля = 1,85 км)
1 верста	= 500 саженей	= 1066,8 м ≈ 1,07 км
1 сажень (косая)	≈ 2,5 м	Расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки — человек стоит буквой «Х»
1 сажень (казённая)	= 3 аршина = 7 футов = 12 пядей = 48 вершков = 84 дюйма	≈ 2,13 м (Маховая сажень, она же народная — расстояние от конца пальцев одной руки до конца пальцев другой при расставленных в стороны руках ≈ 1,5 м)
1 аршин	= 28 дюймов = 16 вершков	= 0,7112 м (В 1899 году «Положением о мерах и весах» аршин был узаконен в России в качестве основной меры длины)
1 фут	= 12 дюймов	= 30,48 cм ≈ 0,3 м
1 пядь с кувырком	≈ 27—31 см	Расстояние между концами большого пальца и указательного пальца с прибавкой двух суставов указательного пальца — «кувырок» выполнялся фиксированием конца указательного пальца на одной точке при измерении и перекладыванием пальца через ноготь на продолжение линии измерения
1 пядь большая	≈ 22—23 см	Расстояние между концами большого пальца и мизинца
1 четверть (малая пядь)	= 1/12 сажени = 1/4 аршина = 4 вершка = 7 дюймов	= 17,78 см ≈ 0,1778 м (От старорусского слова «пясть» — ладонь, кисть руки. Расстояние между концами растянутых пальцев руки — большого и указательного)
1 вершок	= 4 ногтя = 1/4 пяди = 1/16 аршина = 1,75 дюйма	= 44,45 мм = 4,445 см ≈ 0,044 м (Первоначально равнялся длине основной фаланги указательного пальца)
1 дюйм	= 10 линиям	= 2,54 см ≈ 0,0254 м
1 перст	≈ 20 мм
1 ноготь (нокоть)	≈ 11 мм
1 линия	= 10 точкам	≈ 2,54 мм Соответствует ширине линии, проводимой типовым карандашом
1 точка	= 1/100 дюйма = 1/10 линии	≈ 0,254 мм

Соотношение единиц длины с пропорциями тела человека

Старорусские меры веса
берковец	= 10 пудов	≈ 164 кг (От древнерусского названия старинного шведского торгового города Бьёрке до 1948 г. ), ныне Приморск — город в Ленинградской области.
пуд	= 40 фунтов	≈ 16,4 кг
безмен	= 1/16 пуда	≈ 1,02 кг
фунт	= 32 лота = 96 золотников	≈ 0,41 кг С 1747 года являлся эталонным весом.
лот	= 3 золотника	≈ 12,8 грамм
золотник	= 96 долей	≈ 4,27 грамм
доля	Самая мелкая старорусская единица измерения веса (массы)	= 0,0444 грамм
1 унция	аптекарская мера веса	≈ 29,860 грамм

 

Старорусские меры для жидкостей
бочка	40 вёдер	≈ 492 л Пивная бочка = 10 вёдер
корчага	= 2 ведра	≈ 25 л
ведро	= 4 четверти	≈ 12,3 л
четверть	= 1/4 ведра = 4 винные бутылки или 5 водочных бутылок	≈ 3,07 л
штоф (кружка)	= 1/10 ведра = 10 чарок	≈ 1,23 л
винная бутылка	= 1/16 ведра	≈ 0,77 л
водочная бутылка	= 1/20 ведра = 5 чарок	≈ 0,615 л
косушка	= 1/40 ведра = 1/2 водочной бутылки = 5 шкалика	= 0,31 л
четушка С введением метрической системы слово «четушка», потеряв смысл, преобразовалось «чекушку» («четвертинку» водки).	= 1/50 ведра = 2 шкалика	= 0,25 л
чарка	= 1/100 ведра = 2 шкалика	= 0,123 л
шкалик	= 1/200 ведра	≈ 0,062 л
В царской России в кабаках по закону водка из бочонка должна была сначала наливаться для правильности в казённую мерку, которую называли «крючок», а потом уже — в посуду. Существовало 4 вида таких мерок, различающихся размерами: штоф, полуштоф, косушка и шкалик. Они представляли собой металлические ёмкости с выгравированной государственной печатью, широкие снизу и узкие сверху. Они имели длинные ручки, с крючками на концах, чтобы их можно было вешать (отсюда их название — «крючок»).

Вершок :: Общие сведения: svetorusie — LiveJournal

Вершок – народная мера длины, равная длине верхней фаланги указательного пальца, и созданная на её основе официальная мера, равная ¹⁄₁₆ аршина, ¹⁄₄ пяди или чети (≈ 4,5 см). Метрологический термин вершок имел общерусское распространение и был обозначением самой малой меры в официальной русской метрологической системе до XVII века. В качестве долей вершка по памятникам письменности известны его половина, треть, четь, полчети. В XVIII веке вершок делится на более мелкие единицы – части и линии: вершок = 10 частям = 100 линиям.

Мера получила название по антропометрическому измерителю (вершок – верх перста). Попытки связать метрологическое значение слова вершок с другими его значениями такими как ‘небольшой излишек при насыпании зерна» или «маленькая часть, остающаяся поверх (сверх) чего-л.» неубедительны.

Термин «вершок» фиксируется в источниках относительно поздно. Так, если «локоть», «пядь», «верста» и «поприще» упоминаются в источниках, относящихся к XII веку, а сажень – к XI веку, то вершок впервые встречается лишь в документах XVI века. Одно из ранних упоминаний вершка в русских текстах содержится в «Домострое». Автор советует при пошиве одежды для молодых людей ткань «згибати вершка по два и по три на подоле и по краем и по швом и по рукавом», чтобы через несколько лет, когда молодой человек вырастет, загнутое отогнуть, и «опять платно хорошо станет лет на пять и на шесть».

По аршину, определённому англичанином Тассе в 1554 году, вершок равнялся 1¹¹⁄₁₆ английского дюйма, т.е. примерно 4,29 см. В «Торговой книге», составленной в конце XVI – начале XVII века, приводятся соотношения вершка с другими использовавшимися в то время единицами длины, из которых следует: 1 вершок = ¹⁄₄₈ сажени = ¹⁄₁₆ аршина = ³⁄₃₂ локтя. В XVII веке используются также дольные единицы вершка – «полвершки» и «четвертьвершки». В системе мер, сложившейся к концу XVII века, размер вершка в переводе на современные единицы составлял 4,5 см. Кроме официального, использовался также «народный вершок», равный приблизительно 3,5 см, его размер был связан с размером верха большого пальца. В XVIII веке вершок делился на ещё более маленькие единицы: часть составляла ¹⁄₁₀, а линия – ¹⁄₁₀₀ вершка. Позднее в связи с введением в России английских мелких мер эти единицы вышли из употребления.

В ходе осуществления реформ Петра I в связи с потребностями промышленности и торговли меры длины, сложившиеся ранее, были дополнены английскими мерами – футом и дюймом. После того как было установлено соотношение между русскими и английскими мерами (1 сажень = 7 футов) длина сажени уменьшилась приблизительно на 1%, соответственно изменился и размер вершка. Вершок при этом был приравнен к 1³⁄_{4 дюйма.}

11 октября 1835 года указом императора Николая I «О системе Российских мер и весов» соотношения единиц русской система мер длины с единицами длины английской системы были закреплены законодательно. Утверждённые соотношения имели вид:

1 сажень = 3 аршина = 7 английских футов = 84 дюйма = 48 вершков.

Таким образом, через другие единицы вершок стал выражаться следующим образом:

1 вершок = ¹⁄₄₈ сажени = ⁷⁄₄₈ фута = ¹⁄₁₆ аршина = 1,75 дюйма.

Сферы использования русских и английских мер различались.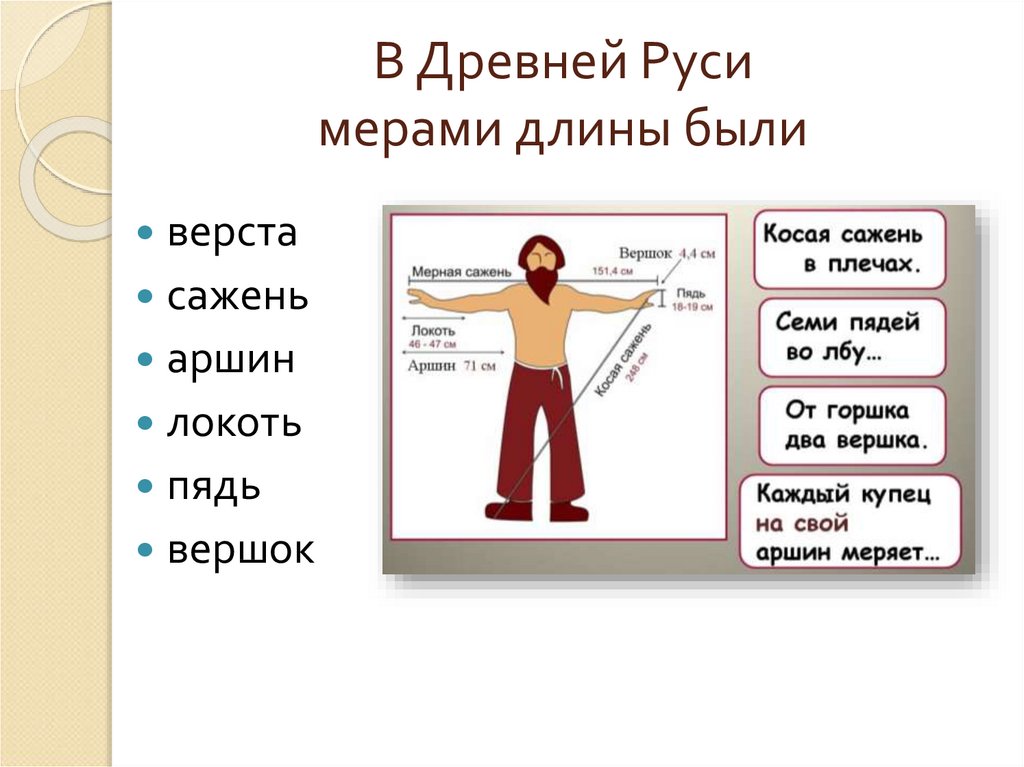 Так, в текстильной промышленности приоритет отдавался аршинам и вершкам, а в кораблестроении – футам и дюймам. Профессор О.Д. Хвольсон в своём докладе, сделанном на общем собрании членов Императорского Русского Технического Общества 18 ноября 1895 г., отмечал, что «в Москве считают большею частью вершками, в Петербурге же — дюймами…».

С метрологическим значением слова вершок связано его переносное употребление для обозначения «очень малого расстояния, длины или площади». Ср.: «По морю плыть, на вершок от смерти быть»; «У самого вершка земли нету»; «Девки на возрасте, стало быть от греха на вершок». Фразеологизм «от горшка два (три) вершка» мы употребляем до сих пор, когда говорим о человеке небольшого роста.

Для XIX века следует отметить странное для нас с точки зрения простых арифметических подсчётов употребление слова вершок при описании роста человека: «В нём [Головане] было, как в Петре Великом, пятнадцать вершков, сложение имел широкое, сухое и мускулистое», или: «Из числа всей ее челяди самым замечательным лицом был дворник Герасим, мужчина двенадцати вершков роста, сложенный богатырем и глухонемой от рожденья». Здесь писателями использован обычный для XIX века способ описания роста, когда упоминается только количество вершков свыше двух аршин, которые подразумевались сами собой, но не назывались, так как нормальный рост человека всегда был больше двух аршин. Такой приём при описании роста человека и лошадей отмечен позднейшими словарями русского языка: «Лошадь росту слишком трёх вершков (при двух аршинах)», «Ростом он был пяти вершков» (т.е. двух аршин и пяти вершков). В этой связи сказочный Конёк-горбунок «ростом только в три вершка» представлялся современникам П.П. Ершова не таким уж крошечным, а небольшой лошадкой ростом в 150 см, при обычном росте лошадей в 160-185 см (высота в холке).

Счёт роста на вершки для людей и лошадей применялся, прежде всего, в царской армии. См. в воспоминаниях графа А.А. Игнатьева «50 лет в строю»: «Дивизия эта долго сохраняла за собой название тяжёлой – не только из-за десятивершковых людей и шестивершковых лошадей, но и как воспоминание о той эпохе, когда кирасиры своей тяжёлой массой легко пробивали строй лёгкой кавалерии», или же: «При входе в манеж строился десяток новобранцев «1-го сорта», то есть ребят ростом в одиннадцать вершков и выше».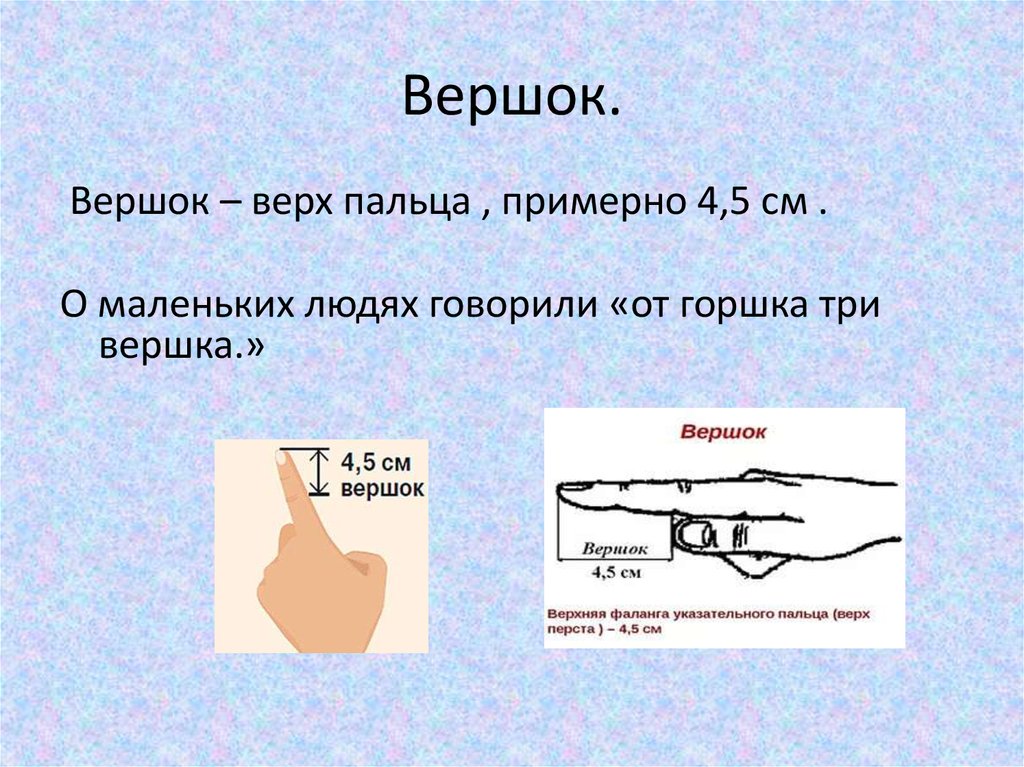

В наши дни такое употребление слова вершок забыто, в связи с чем возникают ошибочные написания при цитировании текстов XIX века. Так, в Словаре русского школьного жаргона XIX века О.А. Анищенко – в описании великовозрастных кадетов седьмого класса читаем: «Седьмовцы… восемнадцатилетние лентяи, восмидесятивершковые [следовало бы написать восьми-десятивершковые, т.е. рост кадетов был 175-186 см, а не три с половиной метра] верзилы, сидевшие в седьмом верхнем классе, творившие вместо учения разные безобразия и ожидавшие выпуска из корпуса в офицеры».

[ … ]

Старорусская единица измерения «вершок»

Вершок — что это такое? Вершок – это архаизм или историзм?

Значение слова «вершок» в толковом словаре. Почему вершок назвали вершком? Этимология слова «вершок».

История происхождения вершка. Чему был равен вершок в Древней Руси?

Лапоть, локоть, вершок — что меньше? Сколько это в метрах (сантиметрах)?

  Читайте также:
    – кто такой голбечник

Олимпиада по информатике 9 класс

           Вар-т 1            Вар-т 2            Вар-т 3            Вар-т 4

Задание 1.

N человек покупают билеты в четырех кассах.
Известно, что на обслуживание k-го человека требуется tk минут.
Распределите людей в 4 очереди таким образом, чтобы общее время, потраченное на покупку билетов, было наименьшим.

Задание 2.

Задан набор прямоугольников.
Из них на плоскости складывается пирамида по следующим правилам:
Каждый слой пирамиды состоит из одного прямоугольника.
Основание последующего прямоугольника полностью помещается на верхней стороне предыдущего прямоугольника.
Размеры прямоугольников заданы.
Какую самую высокую пирамиду можно сложить из этих прямоугольников?

Задание 3.

Древнерусская мера длины сажень состояла из трёх аршин.
Один аршин делился на четыре пяди. Одна пядь состояла из 4 вершков.
Купец привез на рынок рулон сукна длиной N вершков, но для уплаты пошлины ему нужно указать длину сукна в саженях, аршинах, пядях и вершках.
Помогите ему – переведите длину сукна, записанного в вершках в сажени, аршины, пяди и вершки. 9, – длину сукна в вершках.
Программа должна вывести 4 целых неотрицательных числа S, A, P, V – количество саженей, аршин, пядей и вершков, в сумме дающих ровно N вершков, при этом значение A должно быть меньше 3 (т. к. 3 аршина дают одну сажень), значение P должно быть меньше 4 (четыре пяди дают один аршин), значение V должно быть меньше 4 (четыре вершка дают одну пядь).

Задание 4.

На клеточном поле N x M расположены две жёсткие детали.
Деталь A накрывает в каждой строке несколько (не ноль) первых клеток,
деталь B — несколько (не ноль) последних; каждая клетка либо полностью накрыта одной из деталей, либо нет.

Деталь B начинают двигать влево, не поворачивая, пока она не упрётся в A хотя бы одной клеткой.
Определите, на сколько клеток будет сдвинута деталь B.

Входные данные

В первой строке входного файла INPUT.TXT записано два числа N и M — число строк и столбцов соответственно
(1 ≤ N, M ≤ 100).
Далее следуют N строк, задающих расположение деталей.
В каждой находится ровно M символов «A» (клетка, накрытая деталью A), «B» (накрытая деталью B)
или «.» (свободная клет-ка).

Выходные данные

В единственную строку выходного файла OUTPUT.TXT нужно вывести одно число — ответ на задачу.

Пример

№	INPUT.TXT	OUTPUT.TXT
1	4 6 AA.BBB A….B AAA..B A..BBB	1

Задание 5.

Вася записал ряд натуральных чисел в порядке возрастания:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23 и т.д.
Затем вычеркнул из него все числа, в которых имеется хотя бы две одинаковых цифры, и получил последовательность:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 23 и т.д.

Вам необходимо по заданному N найти N-ое по счету число в получившейся последовательности.

Входные данные

В единственной строке входного файла INPUT. TXT записано натуральное число N (1 ≤ N ≤ 10000).

Выходные данные
В единственную строку выходного файла OUTPUT.TXT нужно вывести N-ое по счету число без одинаковых цифр.

Пример

№	INPUT.TXT	OUTPUT.TXT
1	100	123

Задание 6.

Дед Иван с юности следит за своим газоном.
Газон можно считать плоскостью, на которой в каждой точке с целыми координатами растет один пучок травы.

В одно из воскресений Иван воспользовался газонокосилкой и постриг некоторый прямоугольный участок газона.
Стороны этого участка параллельны осям координат,
а две противоположные вершины расположены в точках (x1, y1) и (x2, y2).
Следует отметить, что пучки травы, находящиеся на границе этого прямоугольника, также были пострижены.

Довольный результатом Иван купил и установил на газоне дождевальную установку.
Она была размещена в точке с координатами (x3, y3) и имела радиус действия струи r.
Таким образом, установка начала поливать все пучки, расстояние от которых до точки (x3, y3) не превышало r.

Все было хорошо, но Ивана заинтересовал следующий вопрос:
сколько пучков травы оказалось и пострижено, и полито в это воскресенье?

Требуется написать программу, которая позволит дать ответ на вопрос Ивана.

Входные данные

Первая строка входного файла INPUT.TXT содержит четыре целых числа
x1, y1, x2, y2 (−100 000 ≤ x1 Во второй строке записаны три целых числа x3, y3, r (−100 000 ≤ x3, y3 ≤ 100 000; 1 ≤ r ≤ 100 000)

Выходные данные

В выходной файл OUTPUT.TXT необходимо вывести одно целое число – число пучков травы,
которые были и пострижены, и политы.

Пример

№	INPUT.TXT	OUTPUT.TXT
1	0 0 5 4 4 0 3	14

Задание 7.

Для проведения эксперимента надо выбрать из N имеющихся приборов только три.
Для этого выполняют следующую операцию — если в группе приборов больше трех,
то их нумеруют и выбирают одну из групп: с четными или нечетными номерами.
Операцию повторяют до тех пор, пока в группе не останется три или менее приборов.
Если их остается ровно три, то они и берутся для эксперимента.

Требуется написать программу, которая подсчитает количество способов такого выбора приборов.

Входные данные

В единственной строке входного файла INPUT.TXT записано число N (1

Выходные данные

В единственную строку выходного файла OUTPUT.TXT нужно вывести одно число — найденное количество способов выбора приборов.

Примеры

№	INPUT.TXT	OUTPUT.TXT
1	3	1
2	6	2

9
           Вар-т 1            Вар-т 2            Вар-т 3            Вар-т 4

Как читать линейку в дюймах и сантиметрах

Линейки — важный инструмент, но если вы боретесь с тем, как читать линейку, вы не одиноки. На линейке так много линий, что можно запутаться, чтобы понять, что они все означают.

В этом руководстве мы объясним, почему вы должны знать, как читать линейку, и дадим пошаговые инструкции, как читать линейку в дюймах и см. Мы также предоставим вам некоторые полезные ресурсы, которые вы можете использовать, чтобы продолжать оттачивать свои навыки чтения линейки.

 

Зачем нужно знать, как читать линейку

Умение читать линейку важно не только в школе, но и в повседневной жизни.

Например, если вы хотите сделать что-то из плотной бумаги, вам, скорее всего, понадобится линейка, чтобы отмерить необходимое количество материала. Или что, если вы хотите обрамить фотографию, которая у вас есть? В этом случае вам, возможно, придется измерить фотографию, чтобы увидеть, в какую рамку она поместится.

Правда в том, что в жизни бывает масса моментов, когда вам нужно уметь читать по линейке. И если вы не умеете читать линейку, то, скорее всего, вас ждут некоторые последствия. Например, что, если вы сделаете две части чего-то, что не подходит друг к другу, потому что одна из них короче или длиннее, чем должна была быть? Или что, если вы испортите научный эксперимент, потому что вы не точно прочитали размер куска веревки, которую вы разрезали?

Совершенно очевидно, что умение читать по линейке важно не только для оценок в школе, но и для повседневной жизни.

 

Как читать линейку: имперская или метрическая

Существует два типа линеек, которые вы можете использовать: дюймовая, или имперская, линейка, и сантиметровая, или метрическая, линейка.

Дюймы соответствуют имперской системе , которая является основной системой измерения, используемой в США и некоторых других странах.

Между тем, сантиметров являются частью метрической системы , которая используется во всем мире как в быту, так и в науке.

Хотя мы будем предоставлять изображения, которые вы можете использовать, чтобы следовать нашим инструкциям, мы рекомендуем взять с собой линейку или измерительную ленту, чтобы вы могли следить за ними в режиме реального времени.

 

 

Как читать линейку в дюймах

Начнем с того, как читать линейку в дюймах. Если вы американец, это измерение вы, вероятно, знаете лучше, чем сантиметры, которые иногда включают в вашу стандартную 12-дюймовую или 1-футовую линейку (мы рассмотрим, как читать линейку в сантиметрах в следующем разделе). раздел).

Вот изображение дюймовой линейки:

Сразу видно, что эта линейка использует дюймы, так как она разделена на 12 равноотстоящих областей (отмеченных 1-12), и мы знаем, что там 12 дюймов в футе (не обращайте внимания на см ниже).

Теперь обратите внимание на линии между каждым дюймом, некоторые из них длиннее, а некоторые короче, чем другие. Каждая из этих крошечных линий представляет долю дюйма. Всего имеется пяти линий разной длины.

Каждый дюйм разделен на 16 линий, что означает, что расстояние между каждой линией составляет 1/16 дюйма — это наименьшая длина, которую можно измерить линейкой. (Обратите внимание, что некоторые линейки уменьшаются только до линий 1/8 дюйма, а другие — до линий 1/32 дюйма.)

Дюйм — это самая большая единица измерения на линейке, представленная самой длинной линией. Каждая 1-дюймовая линия помечена числом, указывающим, какой дюйм находится на линейке (как показано на изображении выше).

Пример: Если бы вы измерили длину листа компьютерной бумаги, лист бумаги дошел бы до отметки 11 дюймов на линейке, что означает, что его длина составляет ровно 11 дюймов.

Второй по величине единицей на линейке является 1/2 дюйма, который представлен второй по длине линией. Обычно они не имеют маркировки, но могут быть на некоторых линейках (в этом случае вы увидите такие числа, как 1 1/2 дюйма, 2 1/2 дюйма и т. д.).

Линия 1/2 дюйма расположена посередине между каждым дюймом на линейке. Средняя точка между 7 и 8 дюймами, например, будет 7 1/2 (или 7,5) дюймов.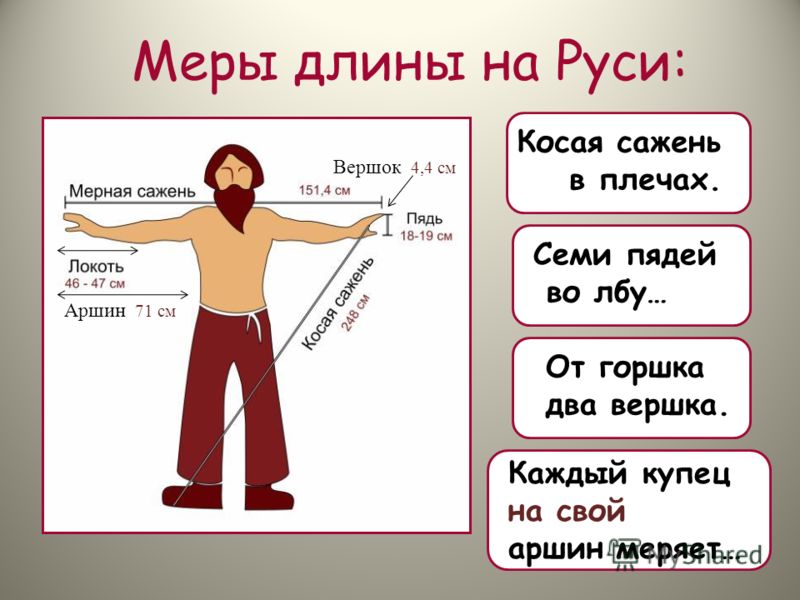

Пример: Если бы вы измерили ширину (а не длину) листа компьютерной бумаги, то он должен точно соответствовать линии 1/2 дюйма между 8 и 9 дюймами, что указывает на то, что ширина равна 8 1/2 (8,5) дюйма.

Третьи по величине линии на линейке — это линии 1/4 дюйма, которые появляются посередине между линиями 1/2 дюйма и целыми дюймовыми линиями:

Если бы вы считали 1/4 дюйма на линейке, вы бы увидели, что четвертая строка после 0 дюймов равна 1/4 дюйма, восьмая строка равна 2/4 (1/2) дюйма, а 12-я строка равна 3. /4 дюйма.

Пример: Допустим, вы измеряете кусок ткани, и линейка заканчивается на четвертой строке после отметки 10 дюймов. Это будет означать, что ткань имеет длину 10 1/4 (10,25) дюймов.

Далее идет 1/8 дюйма, вторая по величине единица линейки. Линии 1/8 находятся посередине между каждой линией 1/4 дюйма:

Если считать с шагом 1/8 дюйма, вы обнаружите, что вторая строка после 0 равна 1/8 дюйма, четвертая строка — 2/8 (1/4) дюйма, шестая строка — 3/8 дюйма. дюйма, восьмая строка 4/8 (2/4 или 1/2) дюйма, 10-я строка 5/8 дюйма, 12-я строка 6/8 (3/4) дюйма и 14-я строка 7/8 дюйма.

Пример: Допустим, вы решили измерить длину кукурузы в початке. Вы обнаружите, что ваша линейка подходит ко второй строке после 6-дюймовой отметки. Это будет означать, что кукуруза имеет длину 6 1/8 дюйма.

Наконец, наименьшая единица измерения на линейке — 1/16 дюйма. Эти крошечные линии, обозначающие 1/16 дюйма, располагаются между всеми линиями 1/8 дюйма:

Если вы посчитаете каждую линию в пределах первого дюйма линейки, вы получите следующие размеры:

• 1/16 дюйма
• 2/16 (1/8) дюйма
• 3/16 дюйма
• 4/16 (1/4) дюйма
• 5/16 дюйма
• 6/16 (3/8) дюйма
• 7/16 дюйма
• 8/16 (1/2) дюйма
• 9/16 дюйма
• 10/16 (5/8) дюйма
• 11/16 дюйма
• 12/16 (3/4) дюйма
• 13/16 дюймов
• 14/16 (7/8) дюйма
• 15/16 дюймов

Пример: Вы пытаетесь измерить длину указательного пальца. Линейка подходит к седьмой строке после 3 дюймов. Это будет означать, что ваш палец имеет длину 3 7/16 дюйма.

 

Практические вопросы по дюймовой линейке

1. Посмотрите на изображение выше. Какое измерение, в дюймах, он показывает?
2. Если ручка доходит до 14-й строки после 5 дюймов, то какой длины она?

 

Ответы

1. 11 3/4 дюйма
2. 5 7/8 дюйма (также допустимо: 5 14/16 дюйма)

 

 

Как читать линейку в сантиметрах

Теперь, когда мы узнали, как читать линейку в дюймах, давайте рассмотрим, как читать линейку в сантиметрах.

Это особенно важно знать, если вы изучаете науку (напомним, что наука обычно использует метрическую систему, а не имперскую). Умение читать линейку в сантиметрах также полезно для людей, которые предпочитают не работать с дробями (что необходимо делать с дюймами) и предпочитают работать с другими единицами измерения (в данном случае с миллиметрами).

Стандартная метрическая линейка имеет длину 30 см. Каждый сантиметр помечен номером, указывающим на измерение, к которому он относится. Вы можете увидеть дюймы на другой стороне вашей метрической линейки. В этом случае обратитесь к приведенным выше инструкциям, чтобы узнать, как читать линейку в дюймах.

Также имейте в виду, что  30 см не делает , а не прямым равным 12 дюймам, , хотя их часто помещают на одну и ту же линейку!

Итак, вот как выглядит типичная метрическая линейка:

Вы можете сказать, что это метрическая линейка, потому что она разделена на 30 равноотстоящих частей и на ней написано «см» (не обращайте внимания на дюймы ниже ).

Как и на дюймовой линейке, на метрической линейке вы увидите множество линий, некоторые из которых длиннее, а некоторые короче. Каждая линия представляет 1 миллиметр, что равно 1/10 или 0,1 см (так что 10 мм составляют 1 см).

Всегда будет 10 линий от одного сантиметра до следующего сантиметра. Всего на метрической линейке имеется три линии разной длины.

Самая длинная линия представляет наибольшую единицу на линейке: 1 см. Каждый сантиметр отмечен на линейке (1-30).

Пример: Вы берете линейку, чтобы измерить ширину ногтя. Линейка останавливается на отметке 1 см, что означает, что ширина вашего ногтя составляет ровно 1 см.

Линия средней длины на метрической линейке — это линия 1/2 (0,5) сантиметра, которая проходит посередине между каждым сантиметром (другими словами, это пятая линия после каждого целого сантиметра):

Итак например, если вы отсчитаете пять линий от 9 см, вы получите 9,5 см (или 95 мм).

Пример: Допустим, вы измеряете ширину своего смартфона, и она доходит до пятой линии через 4 см на линейке. Это будет означать, что телефон имеет ширину 4,5 см (45 мм).

Наименьшая единица, которую может измерить метрическая линейка, равна 1 мм или 0,1 см. Это самые маленькие линии на линейке, то есть те, которые проходят между целым сантиметром и 1/2 сантиметра:

Только в пределах первого сантиметра каждая строка от 0 будет равна следующему:

• 1 мм (0,1 см)
• 2 мм (0,2 см)
• 3 мм (0,3 см)
• 4 мм (0,4 см)
• 5 мм (0,5 или 1/2 см)
• 6 мм (0,6 см)
• 7 мм (0,7 см)
• 8 мм (0,8 см)
• 9 мм (0,9 см)
• 10 мм (1 см)

Пример: Вы измеряете длину пряди волос. Прядь доходит до девятой строки через 16 см по линейке. Это будет означать, что прядь имеет длину 16,9 см (это 16 см + 9 мм).

 

Практические вопросы по сантиметровой линейке

1. Посмотрите на изображение выше. Какое измерение в сантиметрах он показывает?
2. Вы измеряете очки от конца одной линзы до дальнего конца другой линзы. Ваша линейка достигает седьмой строки за 12 см. Какой длины очки?

 

Ответы

1. 24,1 см
2. 12,7 см (или 127 мм)

 

6 Дополнительные ресурсы для обучения чтению линейки

Если вам нужна дополнительная помощь в обучении чтению линейки в см или дюймах, видео и рабочие листы могут быть отличными ресурсами.

Вот два простых видео, которые помогут вам научиться читать на линейке:

 

Как читать линейку в дюймах

 

См Как читать линейку

 

Если вы предпочитаете проверить свои навыки чтения линейки с помощью практических вопросов, то это отличная идея: загрузить бесплатные рабочие листы для измерений с этих математических сайтов:

• K12 Math Worksheets
• DadsWorksheets. com
• Math-Aids.com
• ООО «ТехЭд»

Всех этих ресурсов, в дополнение к нескольким практическим вопросам, которые мы дали вам выше, должно быть достаточно, чтобы вы научились читать линейку в кратчайшие сроки!

 

Что дальше?

Есть вопросы о десятичных дробях и дробях? Наши опытные гиды научат вас преобразовывать десятичные дроби в дроби, а также складывать и вычитать дроби.

Метрические линейки обычно имеют только сантиметры и миллиметры. Но знаете ли вы, что есть еще более маленькая единица измерения, называемая нанометрами? Узнайте, как преобразовать нанометры в метры и другие единицы измерения с помощью нашего подробного руководства.

Вы когда-нибудь видели римские цифры, но не знали, как их прочитать? Ознакомьтесь с нашим подробным руководством, и вы будете на пути к пониманию этой древней системы счисления!

 

У вас есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!

Ханна Муниз

Об авторе

Ханна получила степень магистра японоведения в Мичиганском университете и степень бакалавра в Университете Южной Калифорнии. С 2013 по 2015 год преподавала английский язык в Японии по программе JET. Она увлечена образованием, писательством и путешествиями.

Как вы оцениваете измерения без линейки или рулетки?

По

Лесли Шеперд

Лесли Шепард

Лесли Шеперд — мастер миниатюр, которая делится своими знаниями о миниатюрах. Она имеет более чем 30-летний опыт преподавания этого узкоспециализированного ремесла. Лесли также является профессиональным создателем музейных моделей.

Узнайте больше о The Spruce Crafts’ Редакционный процесс

Обновлено 06.10.19

Иллюстрация: Ель / Элиза Дегармо

Есть много простых способов оценить размеры, используя части вашего тела или предметы, которые могут быть у вас под рукой. Это может пригодиться, когда вы делаете покупки, чтобы определить, подходит ли товар по размеру — например, обои или ткань с определенным размером рисунка. Это особенно полезно для энтузиастов масштабных моделей, таких как модели железнодорожников или коллекционеров кукольных домиков, которые всегда ищут интересные аксессуары для своего хобби.

Изучите длину некоторых обычных частей тела и обычных предметов и используйте их для оценки размеров предметов.

Общие измерения, основанные на вашем теле

Части вашего тела можно использовать для оценки многих распространенных единиц измерения. Очевидно, что люди различаются по размеру, поэтому лучше сначала измерить свои собственные части тела, чтобы понять, насколько ваши собственные пропорции близки к этим средним значениям.

• Один дюйм (2,5 см) — это примерное расстояние от верхней фаланги большого пальца до кончика большого пальца. Измерьте свой, чтобы увидеть, насколько он близок к 1 дюйму. В конце концов, у вас всегда должен быть под рукой большой палец для измерения предметов размером менее 6 дюймов (15 см)! В модельных миниатюрах, таких как стандартный масштаб кукольного домика (1:12), 1 дюйм равен примерно 1 футу.
• Четыре дюйма   (10 см),  или ширина одной ладони для измерения лошадей, примерно равна  ширине  ладоней большинства людей, измеренных поперек суставов пальцев (без большого пальца).
• Один ярд   (36 дюймов или 92 см)  примерно расстояние от носа до сустава указательного пальца (со сжатой в кулак) на вытянутой руке. Если вы часто используете это измерение, измерьте свою руку, чтобы увидеть, насколько это измерение близко к 1 ярду.
• Один метр (39 дюймов)  – это измерение, аналогичное приведенному выше ярду, но используйте руку с вытянутыми пальцами и измеряйте до кончиков пальцев. Это простой способ подсчитать ярды и метры шнура, ткани или ленты. Сравните длину своей руки с линейкой или измерительной лентой, чтобы узнать, насколько близко к 1 метру это расстояние для вас.
• Длина одного локтя, или расстояние от согнутого локтя до кончиков пальцев, для большинства людей составляет от 15 до 18 дюймов (от 35 до 48 см).
• Женский размер 9 футов (США и Канада) обычно имеет длину 10 дюймов (25 см). В Европе это 40-й размер, а в Великобритании — 6,5.

Измерения на основе офисных предметов

Обычные предметы, которые есть у вас в офисе или на домашнем столе, имеют стандартные размеры, которые можно использовать для оценки размеров других предметов.​

• Стандартная визитная карточка имеет размеры 3,5 дюйма в длину и 2 дюйма в высоту (9 см x 5 см).
• Стандартные кредитные и идентификационные карты  имеют размеры 3,4 дюйма в ширину и 2,1 дюйма в высоту (8,5 см x 5,4 см).
• Стандартный лист бумаги для принтера имеет размеры 8,5 x 11 дюймов.
• Деловые конверты имеют размер 4 дюйма x 9,5 дюйма.
• Стандартная канцелярская скрепка имеет длину 1 дюйм; большая скрепка 1,8 дюйма.

Использование монет и банкнот для измерения

Почти каждый носит в кармане несколько банкнот или монет, и знание их размеров может помочь вам оценить размеры других предметов.

• Банкнота США имеет размеры 2,6 дюйма в высоту и 6,2 дюйма в длину (6,6 см на 15,8 см).
• Канадские банкноты имеют размеры 6 дюймов в длину и 2,8 дюйма в высоту (15,2 см x 7 см).
• Монета номиналом 1 цент имеет диаметр 0,75 дюйма (2 см).
• Четверть имеет ширину чуть менее 1 дюйма (2,5 см).

Ель

Стандартные размеры мебели

Вы можете использовать эти стандартные размеры в качестве основы для оценки приблизительного размера более крупных предметов. И, преобразовав измерения, вы также можете использовать их при покупке предметов мебели или аксессуаров для модельных зданий или кукольных домиков. Ниже приведены размеры реальных предметов: например, в масштабе 1:12 шестифутовая (72-дюймовая) дверь будет иметь высоту 6 дюймов (15 см).

• Стандартные современные двери имеют высоту от 78 до 80 дюймов (от 198 до 203 см).
• Столешница столовой обычно находится на высоте 76 см от пола.
• Сиденье стула для столовой обычно находится на высоте от 38 до 43 см от пола.

Использование смартфона

Мало того, что сам физический телефон может служить единицей измерения, если вы посмотрите на его размеры, вы также можете обнаружить, что он предлагает приложения, которые обеспечивают фактическую шкалу линейки, которая позволяет вам измерять небольшие предметы, лежащие на лицевой стороне телефона.

единиц СИ – длина | НИСТ

Свяжитесь с нами

Метр (м) определяется путем взятия фиксированного числового значения скорости света в вакууме c, равного 299 792 458, выраженного в единицах м с ⁻¹ , где секунда определяется через ∆ν _Cs .

Счетчик когда-то определялся физическим артефактом — двумя отметками, нанесенными на платино-иридиевую пластину, вроде тех, что хранятся в музее NIST.

Из метра получают несколько других единиц измерения, таких как:

• единица скорости – метр в секунду (м/с). Скорость света в вакууме 299 792 458 метров в секунду.
• единицей ускорения является метр в секунду за секунду (м/с ² ).
• единица площади – квадратный метр (м ² ).
• единицей объема является кубический метр (м ³ ). Литр (1 кубический дециметр), хотя и не является единицей СИ, но принят к использованию вместе с СИ и обычно используется при измерении объема жидкости, но также используется при измерении газов и твердых веществ.

Часто задаваемые вопросы: Когда произошло переопределение дюйма в метрической системе?

В 1958 году конференция англоязычных стран согласилась унифицировать свои стандарты длины и массы и определить их с точки зрения метрических мер. В результате американский двор был укорочен, а имперский двор удлинён. Новые коэффициенты пересчета были объявлены в 1959 г. в уведомлении Федерального реестра 59-5442 (30 июня 1959 г.), в котором приводится определение стандартного дюйма: значение дюйма, полученное из значения ярда, действующего на 1 июля 19 г.59, в точности эквивалентен 25,4 мм .

Можно определить коэффициент преобразования:

Единицы длины
10 миллиметров (мм)	=	1 сантиметр (см)
10 см	=	1 дециметр (дм)
10 см	=	100 мм
10 дециметров	=	1 метр (м)
10 дециметров	=	1000 миллиметров
10 метров	=	1 декаметр (дамба)
10 декаметров	=	1 гектометр (гм)
10 декаметров	=	100 метров
10 гектометров	=	1 километр (км)
10 гектометров	=	1000 метров

Часто задаваемые вопросы: Как получить метрическую линейку?

Метрические линейки можно приобрести у многих розничных продавцов, которые можно идентифицировать с помощью поисковых запросов, таких как «метрическая линейка», «метрическая линейка» или «метрическая линейка». Пригодные для печати линейки, такие как сантиметровые линейки Color-Square, могут быть напечатаны в цвете на прозрачных листах для накладных работ, чтобы сделать недорогие метрические линейки.

Ресурсы для студентов и преподавателей

• Счетчик — будь то бесконечное расстояние до дома бабушки, отрезок ткани, расстояние до финиша легкоатлетического забега или расстояние между непостижимо маленькими транзисторами в компьютере. чип, длина — одна из самых привычных единиц измерения. (НИСТ)
• Национальный прототип счетчика № 27 (NIST)
• Использование метрической линейки. (Примечания к сварке, видео)
• Использование микрометра. (Университет Торонто)
• Использование штангенциркуля и микрометра. (Университет Кейптауна, факультет физики)
• Таблица шкалы вещей. (Министерство энергетики США)
• Изучите размер и масштаб ячеек с помощью интерактивной графики. (Университет Юты)
• Попрактикуйтесь в измерении длины в сантиметрах в упражнении «Квадраты и прямоугольники». (ПБС)
• Вычислите фокусное расстояние в этом практическом упражнении и изучите эту важную концепцию, которая используется в инструментах STEAM, таких как микроскопы, телескопы и камеры. (Оптическое общество)
• Развить понимание того, насколько на самом деле мал нанометр, с помощью задания Что такое нанометр? Во время урока учащиеся будут измерять обычные предметы в классе и переводить результаты в нанометры. (IEEE)
• Ознакомьтесь с эквивалентными метрическими измерениями длины в игре «Длина столбца». Нарисуйте линию, чтобы соединить одинаковые измерения. Смотрите внимательно, потому что у некоторых предметов нет совпадений! (Типичный учебный архив)
• Как это измеряется: калибровка рулеток. Внутри 60-метрового подземного туннеля ученые-измерители проверяют точность рулеток. (НИСТ, видео).
• Как убедиться, что рулетка точна. Узнайте, как лазерный интерферометр используется для точного измерения расстояний вдоль измерительной ленты. (НИСТ)
• На дистанции в Национальный день рулетки. Узнайте о значении рулеток, отмечаемых в Национальный день рулетки 14 июля  ^года  года. (НИСТ)
• Как измерить глубину океана. Ученые и исследователи могут использовать гидролокатор, радар и спутниковые методы для измерения глубины океана. Средняя глубина океана составляет 3,7 км, но самая глубокая из когда-либо зарегистрированных частей находится в Марианской впадине на глубине около 11 км. (НИСТ)
• Спроектируйте, спланируйте и начертите планировку сада в масштабе с помощью метрической линейки. (Калифорнийский университет в Беркли, Ноттингемский университет)
• Зона СИ. Исследуйте ресурсы, чтобы ознакомиться с единицами измерения площади, включая гектар.
• Том СИ. Изучите ресурсы, чтобы ознакомиться с единицами измерения объема, включая литр.
• Расчет длины окружности, площади и объема. Ознакомьтесь с методами, используемыми для вычисления длины окружности, площади и объема обычных предметов. (НИСТ)

Кредит: Дж.