Все формулы геометрии: Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.

Математические формулы по алгебре и геометрии для ЕГЭ

Как выучить все формулы по математике к ЕГЭ

Чтобы сдать ЕГЭ по математике, необходимо знать математические формулы из школьного курса алгебры и геометрии.

Для того, чтобы запомнить формулы школьной математики, желательно держать в течение всего года на видном месте шпаргалку с красиво написанными формулами. Таким образом подключается зрительная память и формулы лучше запоминаются.

Проверяйте себя время от времени: попробуйте написать все важные математические формулы по памяти, а затем проверьте. На самом деле, формул, которые надо выучить наизусть, не так много. И целого учебного года вполне достаточно, чтобы все выучить.

Многие алгебраические, геометрические, тригонометрические формулы можно быстро вывести прямо на экзамене, если Вы их забыли. Но на это придется потратить какое-то время. Поэтому преимущество получают те школьники, которые выучили формулы.
Зная математические формулы наизусть, можно гораздо быстрей решить сложные задачи по алгебре, тригонометрии и геометрии на ЕГЭ.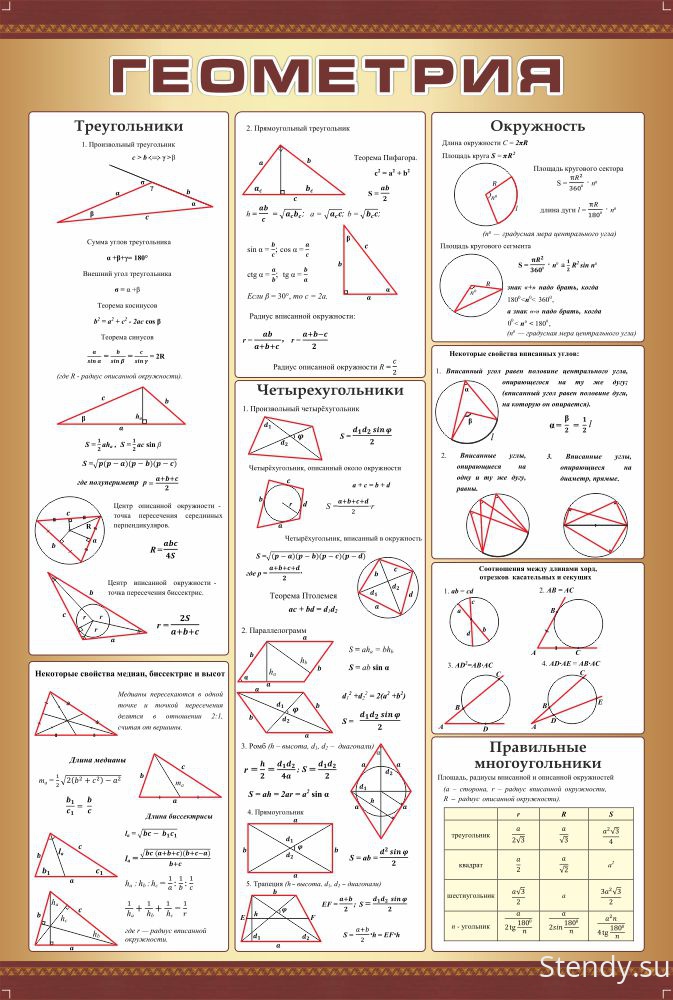

Мы собрали самые важные формулы из школьного курса математики, которые надо выучить для успешной сдачи ЕГЭ.

Математические формулы школьного курса алгебры

 

Степени и корни

Формулы сокращенного умножения

Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители

Логарифмические формулы

Формулы тригонометрии

 

Основные формулы тригонометрии

Тригонометрические уравнения

Значения тригонометрических функций

Формулы приведения

Сумма и разность углов

Формулы двойного и тройного аргумента

Формулы половинного аргумента

Сумма и разность тригонометрических функций

Произведение тригонометрических функций

Формулы дифференциального исчисления

Формулы векторной алгебры из школьного курса математики

Формулы арифметической и геометрической прогрессии

Геометрические формулы школьного курса математики для ЕГЭ

Планиметрия

Стереометрия

Выучить формулы по математике – это еще не все, что надо для успешной сдачи ЕГЭ. Опыт решения задач, знания правил оформления заданий на экзамене не менее важны. Приглашаем всех школьников 11-х классов на курсы подготовки к ЕГЭ ПАРАГРАФ. С нами Вы подготовитесь к ЕГЭ наиболее продуктивно.

Учите формулы по математике и сдавайте ЕГЭ на максимальные баллы!

Формулы

Дорогие друзья! Весь справочный материал вы найдете на страницах «Математика», «Алгебра» и «Геометрия» моего сайта. По многим разделам ( там, где кликабельные заголовки) имеется пояснительный материал с примерами.

Уважаемые родители! Если Вы ищите репетитора по математике для Вашего ребёнка, то это объявление для Вас. Предлагаю скайп-репетиторство: подготовка к ОГЭ, ЕГЭ, ликвидация пробелов в знаниях. Ваши выгоды очевидны:

1) Ваш ребенок находится дома, и Вы можете быть за него спокойны;

2) Занятия проходят в удобное для ребенка время, и Вы даже можете присутствовать на этих занятиях. Объясняю я просто и доступно на всем привычной школьной доске.

3) Другие важные преимущества скайп-занятий додумаете сами!

Напишите мне по адресу: [email protected] или сразу добавляйтесь ко мне в скайп, и мы обо всём договоримся. Цены доступные.

P.S. Возможны занятия в группах по 2-4 учащихся.

С уважением Татьяна Яковлевна Андрющенко.

 

Друзья! На этой странице я предлагаю вам получить все формулы математики (и алгебры и геометрии) за 7-11 классы. Разумеется, бесплатно. Пройдите по ссылке.

Трудно решать примеры и задачи, не имея под рукой формул. Так что получите, распечатайте и пользуйтесь на здоровье! Инструкция по распечатке сборника формул здесь! Воспользуйтесь ею, и Вы получите удобную книжечку. Желаю вам легко повторить и запомнить все формулы. Удачи!

Дорогие друзья! Готовитесь к ОГЭ или ЕГЭ? Вам в помощь «Справочник по геометрии 7-9».  Подробнее здесь.

 

 

 

 

Дорогие друзья! Если вас затрудняют задачи на проценты, то вам поможет книга «Как решать задачи на проценты».

Как её получить — смотрите здесь!

 

 

 

 

Дорогие друзья! По вашим просьбам я сделала подборку всех правил и формул по математике для 5 класса. Этот небольшой справочник будет полезен и детям и их родителям, ведь зная, что именно должен выучить учащийся в 5 классе, взрослым будет легче помочь и проконтролировать своего ребенка! А когда учебный год закончится, и учебники будут сданы в библиотеку — у вас останется мой справочник, а значит, и возможность летом все повторить и отлично подготовиться к 6 классу! Справочник  МАТЕМАТИКА 5. Переходите по ссылке здесь!

Дорогие друзья! Не секрет, что некоторые дети испытывают трудности при умножении и делении в столбик. Чаще всего это связано с недостаточным знанием таблицы умножения. Предлагаю подучить таблицу умножения с помощью лото.

 Посмотреть видео презентацию здесь. Скачать лото здесь.

Основные формулы | Олимпиадный Центр МатРИЦА

Оглавление:

Весь курс алгебры для ОГЭ в схемах и таблицах >>>

Весь курс геометрии для ОГЭ в схемах и таблицах >>>

Весь курс по реальной математике для ОГЭ >>>

Все графики функций >>>

Таблица умножения

К оглавлению…

Таблица квадратов двухзначных чисел

К оглавлению…

Формулы сокращенного умножения

К оглавлению…

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:

#Квадратное уравнение и формула разложения квадратного трехчлена на множители

К оглавлению…

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней.

В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

#Свойства степеней и корней

К оглавлению…

Основные свойства степеней:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:

Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

Арифметическая прогрессия

К оглавлению…

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

Геометрическая прогрессия

К оглавлению…

Формулы n-го члена геометрической прогрессии:

bn = b1 · q n-1

bn+1 =bn · q, где bn ≠ 0, q ≠ 0

q – знаменатель прогрессии

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Геометрия на плоскости (планиметрия)

К оглавлению…

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника: 

Площадь треугольника через две стороны и угол между ними:  

Площадь треугольника через сторону и высоту опущенную на неё: 

Полупериметр треугольника находится по следующей формуле: 

Формула Герона для площади треугольника: 

Площадь треугольника через радиус описанной окружности: 

Формула медианы: 

Свойство биссектрисы: 

Формулы биссектрисы: 

Основное свойство высот треугольника: 

Формула высоты: 

Еще одно полезное свойство высот треугольника: 

Теорема косинусов: 

Теорема синусов: 

Радиус окружности, вписанной в правильный треугольник: 

Радиус окружности, описанной около правильного треугольника: 

Площадь правильного треугольника: 

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты): 

Радиус окружности, вписанной в прямоугольный треугольник: 

Радиус окружности, описанной вокруг прямоугольного треугольника: 

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу): 

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника: 

Длина средней линии трапеции: 

Площадь трапеции: 

Площадь параллелограмма через сторону и высоту опущенную на неё: 

Площадь параллелограмма через две стороны и угол между ними: 

Площадь квадрата через длину его стороны: 

Площадь квадрата через длину его диагонали: 

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами): 

Площадь прямоугольника через две смежные стороны: 

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними: 

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т. е. в том числе для любых треугольников):  

Свойство касательных: 

Свойство хорды: 

Теорема о пропорциональных отрезках хорд: 

Теорема о касательной и секущей: 

Теорема о двух секущих: 

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу): 

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой): 

Свойство центральных углов и хорд: 

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

 

Формулы с логарифмами

К оглавлению…

Определение логарифма:

Определение логарифма можно записать и другим способом: 

Свойства логарифмов:

Логарифм произведения: 

Логарифм дроби: 

Вынесение степени за знак логарифма: 

Другие полезные свойства логарифмов:

Тригонометрия

К оглавлению…

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса: 

Определение косинуса: 

Определение тангенса: 

Определение котангенса: 

Основное тригонометрическое тождество: 

Простейшие следствия из основного тригонометрического тождества: 

Формулы двойного угла

Синус двойного угла: 

Косинус двойного угла: 

Тангенс двойного угла: 

Котангенс двойного угла: 

Тригонометрические формулы сложения

Синус суммы: 

Синус разности: 

Косинус суммы: 

Косинус разности: 

Тангенс суммы: 

Тангенс разности: 

Котангенс суммы: 

Котангенс разности: 

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов: 

Разность синусов: 

Сумма косинусов: 

Разность косинусов: 

Сумма тангенсов: 

Разность тангенсов: 

Сумма котангенсов: 

Разность котангенсов: 

Тригонометрические формулы преобразования произведения в сумму

Произведение синусов: 

Произведение синуса и косинуса: 

Произведение косинусов: 

Формулы понижения степени

Формула понижения степени для синуса: 

Формула понижения степени для косинуса: 

Формула понижения степени для тангенса: 

Формула понижения степени для котангенса: 

Формулы половинного угла

Формула половинного угла для тангенса: 

Формула половинного угла для котангенса: 

Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы:

Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения

К оглавлению…

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений в некоторых частных случаях:

Геометрия в пространстве (стереометрия)

К оглавлению…

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (трёхмерная Теорема Пифагора):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т. е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара: 

Площадь поверхности шара (площадь сферы): 

Координаты

К оглавлению…

Длина отрезка на координатной оси: 

Длина отрезка на координатной плоскости: 

Длина отрезка в трёхмерной системе координат: 

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы): 

Как успешно подготовиться к экзамену по математике?

Для того чтобы успешно подготовиться к ОГЭ или ЕГЭ по математике,  необходимо выполнить три важнейших условия:

1. Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к экзамену по математике, изучению теории и решению задач хотя бы по часу, но каждый день. Дело в том, что ОГЭ или ЕГЭ — это экзамены, где мало просто знать математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно, но только, решив тысячи задач.
2. Выучить все формулы и методы в математике! На самом деле, выполнить это тоже очень просто, необходимых формул по математике меньше 200. В алгебре и геометрии есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить. И, таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ОГЭ или ЕГЭ. После этого Вам останется подумать только над самыми сложными задачами.
3. Посетить все три этапа репетиционного тестирования (РТ) по математике в нашем Центре (ЦР). Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на РТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на реальном экзамене может показаться неподготовленному человеку очень непривычным.

Успешное и ответственное выполнение этих трех пунктов позволит Вам показать на экзамене отличный результат, максимальный из того на что Вы способны!

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно через контактную форму на данном сайте. В письме укажите предмет (математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

<<< Структура сайта подготовки к ОГЭ по математике

План подготовки к ОГЭ по математике >>>

Как запоминать формулы по математике

Голова идёт кругом от множества математических формул, которые необходимо знать. Зубрёжка и шпаргалки — удел слабых. А вот тем, кто хочет стать в математике сильнее, мы подскажем несколько советов, как запоминать формулы по математике так, чтобы они не выветрились из головы до контрольной, экзамена или ЦТ.

Понимай формулу

В школе учат читать формулы, потому что так ты запоминаешь их суть, а не просто сочетание символов. Возьмём простой пример:

Если ты будешь заучивать только последовательность переменных, рискуешь «потерять» всю формулу, когда забудешь символ или знак.

Задействуй все виды памяти

Читай формулы вслух, прописывай на листке по нескольку раз, пока не запомнишь. Задействуй все виды памяти, делая упор на ведущую. Визуальная и двигательная память вместе дают больший эффект. Конечно, потенциал для запоминания у каждого разный. Есть специальные методики, которые помогают тренировать память.

Вот ещё несколько советов, как запомнить формулы

Обязательно делай формулы наглядными: обводи формулу в рамку, пиши её другим цветом. Так будет легче найти в конспекте и запомнить. А лучше выписывай формулы в отдельный блокнот, структурируя их по темам. Помечай, в какого рода задачах та или иная формула пригодится, в чём её особенность. Заведи привычку пополнять список формул. Подобный «дневник наблюдений за формулами» поможет освежить в памяти важную информацию перед контрольной, экзаменом или ЦТ по математике.

Многие школьники ещё вот что делают: когда раздают проштампованные черновики, ты берёшь и сразу же записываешь на них важные формулы, которые тебе тяжело даются. За полчаса до ЦТ ты эти формулы зрительно запомнил, а потом быстренько написал. Это экономит время. Особенно такой лайфхак хорош в тригонометрии. Чем больше знаешь формул, тем лучше.

Дмитрий Судник, преподаватель математики в образовательном центре Адукар

Заучивание формул похоже на заучивание стихов: вызубрив только слова, прочесть стих выразительно не получится. А вот когда прочувствуешь содержание, научишься правильно расставлять паузы, произведение зазвучит и отложится в памяти надолго

Проверяй себя

Нужно постоянно возвращаться к выученному материалу, чтобы не забыть его. Попробуй метод «Две карточки», он подойдёт для запоминания формул приведения, сокращённого умножения, тригонометрических формул. Возьми две стопки карточек разного цвета, на одной напиши левую часть формулы, а на другой — правую. Раздели таким образом все формулы, что тебе нужно запомнить, затем перемешай обе стопки. Тяни по порядку карточку с левой частью формулы и подбирай её продолжение среди «правых» и наоборот.

Карточки хороши и в геометрии

Чтобы запомнить формулы по геометрии, заведи себе карточки по темам («Формулы площади», «Фомулы для треугольника», «Фомулы для квадрата» и т. д.) и записывай в них информацию следующим образом.

Можно фиксировать формулы в отдельном блокноте и всегда был под рукой — как тебе удобно

Будь на позитиве

Если ты учишь что-либо из-под палки, мозг сам желает избавиться от груза знаний. Воспринимай заучивание формул как хорошее упражнение для тренировки памяти. Да и настроение поднимается, когда вспоминаешь нужную формулу для решения. И конечно же, решай как можно больше тестов и задач для подготовки к контрольной, экзамену или ЦТ!

ЦТ по математике — это типовые задачи: чем больше тестов решаешь, тем выше шанс встретить что-то похожее на ЦТ. Невозможно подготовиться к ЦТ по одной задаче. Но когда ты прорешал 100 задач, то 101 задача не вызовет затруднений.

Дмитрий Судник, преподаватель математики в образовательном центре Адукар

***

Если материал был для тебя полезен, не забудь поставить «мне нравится» в наших соцсетях ВКонтакте, Instagram, Facebook, ASKfm и поделись постом с друзьями. А мы сделаем ещё больше материалов, которые пригодятся тебе для учёбы.

Перепечатка материалов с сайта adukar.by возможна только с письменного разрешения редакции. [email protected]

Все формулы по математике — Формулы под рукой

Не решается задачка? Наш сайт поможет тебе в учебе, подготовке к сложным экзаменам, контрольным, олимпиадам, сессиям, ЕГЭ.

ФОРМУЛЫ ПО АЛГЕБРЕ

ФОРМУЛЫ ПО ГЕОМЕТРИИ

ФОРМУЛЫ ПО ТРИГОНОМЕТРИИ

Обладатель премии Эйнштейна, известнейший британский исследователь в области теоретический физики Стивен Хокинг однажды рассказал, что получил должность профессора математики в Оксфордском университете, не имея специального образования. На тот момент за его плечами были лишь изрядно подзабытые школьные знания по математике. Царицу наук постигал «на ходу», читая студенческий учебник с опережением программы на две недели. Впоследствии студенты Хокинга вспоминали его занятия как исключительно познавательные и захватывающие!

Такие примеры вдохновляют, вселяют уверенность, что и каждый из нас может с таким же успехом освежить «хорошо забытое». А там и новый вектор развития появится.

Чтобы вспомнить (или освоить!) школьный материал было легче, предлагаем листать не страницы учебников и справочной литературы, а воспользоваться нашим сайтом, где удобная навигация и система поиска позволят быстро отыскать нужную формулу по предметам:

• арифметика;
• алгебра;
• геометрия;
• физика;
• химия.

От теории к практике

Бывает, что и материал знаком, да и формулы, теоремы и аксиомы по нужной теме — вот они, а задачка не поддается. Педагогический «диагноз»: нет опыта. Приобретается этот опыт при помощи решения типовых уравнений и задач. Предлагаем наиболее удачные и интуитивно понятные методики, которые уже помогли не одному ученику овладеть инструментарием точных наук!

Быстрее, выше, сильнее!

Возможно, сейчас ты и считаешь, что выучить все школьные формулы невозможно. Но на самом деле формул, необходимых для решения задач школьного уровня по математике, не более двухсот, а по физике — и того меньше! А это значит, что, заглядывая в наши справочники и освоив принципы решения типовых задач, можно постепенно запомнить все базовые формулы!

Какими бы сложными ни казались тебе задания твоих преподавателей сейчас, через какое-то время школьные, да и институтские стены могут показаться тебе тесными.

На нашем сайте собраны как часто используемые, так и гораздо более сложные формулы. Если захочешь знать больше, чем написано в школьном учебнике, начни с аксиомы — слов Марка Твена, который «никогда не позволял, чтобы школьные занятия мешали образованию!».

Подготовка к ЕГЭ и ОГЭ (справочник по математике для школьников — Геометрия

Основные фигуры планиметрии
	Фигуры, составляющие основу планиметрии
Углы
	Углы на плоскости
	Теорема Фалеса
	Углы, связанные с окружностью
		Вписанные и центральные углы
		Углы, образованные хордами, касательными и секущими
		Доказательства теорем об углах, связанных с окружностью
Параллельность прямых
	Признаки параллельности прямых
Треугольники
	Типы треугольников. Признаки равенства треугольников
		Типы треугольников
		Признаки равенства треугольников
		Признаки равенства прямоугольных треугольников
	Свойства и признаки равнобедренного треугольника
	Свойства прямоугольного треугольника
	Свойства сторон и углов треугольника
	Подобные треугольники. Признаки подобия треугольников
		Подобные треугольники
		Признаки подобия треугольников
		Признаки подобия прямоугольных треугольников
	Теорема Пифагора. Теорема косинусов
		Теорема Пифагора
		Теорема косинусов
	Биссектриса треугольника. Свойства биссектрисы. Вычисление длины биссектрисы
	Медиана треугольника. Свойства медианы. Вычисление длины медианы
	Высота треугольника. Задача Фаньяно
		Высота треугольника. Свойство высоты прямоугольного треугольника
		Расположение высот у треугольников различных типов
		Ортоцентр треугольника
		Расположение ортоцентров у треугольников различных типов
		Ортоцентрический треугольник
		Задача Фаньяно
	Средние линии треугольника
	Теорема Чевы
		Теорема Чевы 1
		Теорема Чевы 2
		Применения теоремы Чевы
	Теорема Менелая
	Окружность, описанная около треугольника. Треугольник, вписанный в окружность. Теорема синусов
		Серединный перпендикуляр к отрезку
		Окружность описанная около треугольника
		Свойства описанной около треугольника окружности. Теорема синусов
		Доказательства теорем о свойствах описанной около треугольника окружности
	Формулы для стороны, периметра и площади правильного треугольника
	Площадь треугольника
		Формулы для площади треугольника
		Вывод формул для площади произвольного треугольника
		Вывод формул для площади равностороннего (правильного) треугольника
		Вывод формул для площади прямоугольного треугольника
		Вывод формулы Герона для площади треугольника
	Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
		Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
		Формулы для радиуса окружности, вписанной в треугольник
		Вывод формул для радиуса окружности, вписанной в треугольник
	Вневписанные окружности
Четырехугольники
	Четырехугольники
		Типы четырехугольников
		Типы параллелограмов
		Типы трапеций
	Параллелограммы
		Свойства и признаки параллелограмма
		Свойства и признаки прямоугольника
		Свойства и признаки ромба
		Свойства и признаки квадрата
	Трапеции
		Основные определения и свойства трапеций
		Свойства и признаки равнобедренных трапеций
	Четырехугольники, вписанные в окружность. Теорема Птолемея
		Вписанные четырехугольники и их свойства
		Теорема Птолемея
	Описанные четырехугольники
	Средние линии четырехугольников
		Средняя линия трапеции
		Средние линии четырехугольников. Теорема Вариньона
	Формулы для стороны, периметра и площади квадрата
	Площади четырехугольников
		Формулы для площадей четырехугольников
		Вывод формул для площадей четырехугольников
		Вывод формулы Брахмагупты для площади вписанного четырехугольника
Многоугольники
	Многоугольники
		Определение многоугольника
		Диагонали n – угольника
		Внешний угол многоугольника
		Свойства углов треугольника
		Свойства углов многоугольника
		Свойства углов правильного n – угольника
		Доказательства теорем о свойствах углов многоугольника
	Правильные многоугольники
		Формулы для стороны, периметра и площади правильного n – угольника
		Формулы для стороны, периметра и площади правильного треугольника
		Формулы для стороны, периметра и площади правильного шестиугольника
		Формулы для стороны, периметра и площади квадрата
Окружность и круг
	Углы, связанные с окружностью
		Вписанные и центральные углы
		Углы, образованные хордами, касательными и секущими
		Доказательства теорем об углах, связанных с окружностью
	Отрезки и прямые, связанные с окружностью. Теорема о бабочке
		Отрезки и прямые, связанные с окружностью
		Свойства хорд и дуг окружности
		Теоремы о длинах хорд, касательных и секущих
		Доказательства теорем о длинах хорд, касательных и секущих
		Теорема о бабочке
	Две окружности на плоскости. Общие касательные к двум окружностям
		Взаимное расположение двух окружностей
		Общие касательные к двум окружностям
		Формулы для длин общих касательных и общей хорды
		Доказательства формул для длин общих касательных и общей хорды
	Длина окружности и ее дуг. Площадь круга и его частей
		Основные определения и свойства. Число π
		Формулы для площади круга
		Формулы для длины окружности и ее дуг
		Площадь круга
		Длина окружности
		Длина дуги
		Площадь сектора
		Площадь сегмента
	Окружность, описанная около треугольника. Треугольник, вписанный в окружность. Теорема синусов
		Серединный перпендикуляр к отрезку
		Окружность описанная около треугольника
		Свойства описанной около треугольника окружности. Теорема синусов
		Доказательства теорем о свойствах описанной около треугольника окружности
	Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
		Существование окружности, вписанной в треугольник
		Формулы для радиуса окружности, вписанной в треугольник
		Вывод формул для радиуса окружности, вписанной в треугольник
	Вневписанные окружности
	Четырехугольники, вписанные в окружность. Теорема Птолемея
		Вписанные четырехугольники и их свойства
		Теорема Птолемея
		Вывод формулы Брахмагупты для площади вписанного четырехугольника
	Описанные четырехугольники
Площади
	Площади четырехугольников
		Формулы для площадей четырехугольников
		Вывод формул для площадей четырехугольников
	Площадь треугольника
		Формулы для площади треугольника
		Вывод формул для площади произвольного треугольника
		Вывод формул для площади равностороннего (правильного) треугольника
		Вывод формул для площади прямоугольного треугольника
	Вывод формул Герона и Брахмагупты
		Вывод формулы Герона для площади треугольника
		Вывод формулы Брахмагупты для площади вписанного четырехугольника
Средние линии
	Средние линии
		Средние линии треугольника
		Средняя линия трапеции
		Средние линии четырехугольников. Теорема Вариньона
		Средние линии тетраэдра
Геометрические места точек на плоскости
	Геометрические места точек на плоскости
Преобразования плоскости
	Движения плоскости. Теорема Шаля. Афинные преобразования плоскости
		Преобразования плоскости
		Движения плоскости
		Теорема Шаля
		Афинные преобразования плоскости
		Классификация афинных преобразований плоскости

Справочник репетитора по математике — Колпаков Александр Николаевич

На этой странице будут размещены ссылки на исключительно математическую информацию. Одним из направлений развития сайта профессиональный репетитор по математике является представление учащимся теоретических сведений, полезных в работе над задачами. Не уходя с сайта можно найти ту или иную нужную формулу, теорему или правило. Большинство справочных материалов снабжены необходимыми комментариями и краткими объяснениями репетитора по математике. Некоторые страницы оформлены в виде шпаргалок. Остальные являются полноценными конспектами по отдельным темам.

На этой странице размещены только ссылки на тематические страницы. В них вы найдете найдете каталог графиков элементарных функций, базовые и дополнительные формулы школьного курса, алгоритмы решения типовых и конкурсных задач по математике, различные теоремы, аксиомы, свойства, схемы для равносильных переходов в уравнениях и неравенствах и многое другое. Я постараюсь оптимизировать информацию в виртуальном справочнике под потребности учеников разного уровня.

Краткий базовый перечень теоретических фактов будет предназначен для среднего и слабого ученика. Он будет содержать только те сведения, которые нужны для сдачи ГИА или ЕГЭ по математике не на самый высокий балл.Более развернутое содержание теории будет дано для сильного ученика. Отдельное место в справочнике займут теоремы по геометрии, не входящие ни в какие школьные программы.

Оглавление:

1.Алгебра

Графики основных функций и их свойства. Базовый уровень.

Тригонометрические формулы.

Обратные тригонометрические функции.

Свойства квадратных корней и корней n-ной степени.

Логарифмические формулы. Логарифмические уравнения и неравенства.

Производные математических функций. Определение, таблица основных производных и правила их вычисления.

Основные свойства функций.

Касательные, экстремумы, исследования функций.

Формулы сокращенного умножения и другие полезные алгебраические тождества.

Арифметическая и геометрическая прогрессия.

2. Математический анализ

Таблица интегралов (полезные неопределенные интегралы от основных функций).

Свойства и приемы вычисления неопределенных интегралов.

3.Геометрия

3.1) Планиметрия:

Формулы, теоремы и свойства элементов треугольников.

Четырехугольники. Основные теоремы, формулы и свойства.

Формулы, теоремы и свойства, связанные с окружностью.

Дополнительные теоремы планиметрии.

3.2) Стереометрия:
Аксиомы, определения, начальные свойства и теоремы по учебнику Атанасяна.

Многогранники:

Пирамида и ее элементы. Определение, виды пирамид, формулы объема и площади поверхности, свойств основания высоты, советы репетитору математики по работе с пирамидой.

Призма и ее элементы. Теоретические сведения о призмах: формулы и определения, совет репетитора по математике по выбору осей в методе координат.

Параллелепипеды:

Наклонный параллелепипед Определение, свойства и формулы. Задачи репетитора по математике на наклонный параллелепипед и советы преподавателям по работе с некоторыми его свойствами)

Прямой параллелепипед.

Прямоугольный параллелепипед. Определение, свойства, подборка любимых и часто используемых и репетитором по математике задач.

Тела вращения:
Шар, Конус, Усеченный конус, Цилиндр.

Метод координат в пространстве: формулы и объяснения репетитора.
Часть А: Справочная страница для подготовки к ЕГЭ по математике. Здесь Вы узнаете, как можно найти угол между прямыми, угол между прямой и плоскостью, угол между плоскостями, нормаль к плоскости, написать уравнение плоскости, узнаете формулу расстояния от точки до плоскости.

2. Математика 5 -6 класс

Простые и составные числа. Таблица простых чисел. Репетитор по математике дает пояснение терминам «простое число»,»составное число», изучаемых в курсе математики 6 класса. Приводится таблица простых чисел и основная теорема арифметики. Решето Эратосфена

Признаки делимости. Расширенный список признаков, необходимых для работы репетитора по математике в 6 классе с учащимися, которые хотя знать больше.

Специализированные страницы:

Приходится учитывать особенности чтения и поиска информации в интернете. Посетителей хотят получать к ней мгновенный доступ и в необходимом объеме. Для этого я решил дублировать теорию на отдельных страницах. Их лучше индексируют поисковые системы, на них удобнее ссылаться, а самое главное их можно сделать более подробными. Это полезнее как для учеников, так и для репетиторов по математике. Пока выбор невелик, но я собираюсь развиваться в этом направлении.

Ссылки:
Теорема синусов
Теорема косинусов
Площадь трапеции

Колпаков Александр Николаевич. Репетитор по математике в Москве. Строгино, м.Щукинская.

Получите список геометрических формул для 2D и 3D форм СПИСОК PDF Здесь

Формулы геометрии : Геометрия — это раздел математики, который занимается измерением, свойствами и взаимосвязями точек, линий, углов, поверхностей и твердых тел. Существует два типа геометрии — 2D-геометрия или плоская геометрия и 3D-геометрия или твердотельная геометрия . Плоские формы, такие как квадраты, круги и треугольники, являются частью плоской геометрии и называются 2D-фигурами. Эти формы имеют только два измерения: длину и ширину.

С другой стороны, твердые объекты, также известные как трехмерные объекты, имеют третье измерение высоты или глубины. Некоторыми примерами трехмерных фигур в твердотельной геометрии являются куб, кубоид, сфера и конус.

Также проверьте:

Геометрические формулы очень важны для решения всех математических задач, связанных как с плоской геометрией, так и с твердотельной геометрией. С помощью всех геометрических формул мы можем решать проблемы, связанные с длиной, периметром, площадью и объемом, а также площадью поверхности различных геометрических форм.Вы можете загрузить таблицу формул геометрии в формате PDF , представленную на этой странице, чтобы вычислить высоту, ширину, длину, радиус, периметр, площадь, площадь поверхности и объем 2D или 3D фигур.

Формулы геометрии для 2D и 3D фигур

Давайте посмотрим на таблицу формул геометрии для различных форм. Вы также можете скачать диаграмму геометрических формул в формате PDF ниже:

Все геометрические формулы
Форма	Формулы	Рисунок
Прямой треугольник	Теорема Пифагора: a 2 + b 2 = c 2 Площадь = ½ ab Периметр = a + b + √ (a 2 + b 2 )
Треугольник	Периметр, P = a + b + c Площадь, A = ½ bh Высота, h = 2 (A / b)
Прямоугольник	Периметр = 2 (длина + ширина) Площадь = лв Диагональ, d = √ (l 2 + w 2 )
Параллелограмм	Периметр, P = 2 (a + b) Площадь, A = bh Высота, h = A / b База, b = пк / ч
Трапеция	Площадь, A = ½ (a + b) h Высота, h = 2A / (a ​​+ b) База, b = 2 (пк / ч) — а
Круг	Окружность = 2πr Площадь = πr 2 Диаметр = 2r
Квадрат	Периметр, P = 4a Площадь, A = a 2 Диагональ, d = a√2 Сторона, a = √ A = d / 2√2
Дуга	Длина дуги, L = rθ Площадь, A = ½r 2 θ Здесь θ — центральный угол в радианах.
Куб	Площадь, A = 6a 2 Объем, V = a 3 Кромка, a = V ⅓ Диагональ пространства = a√3
Кубоид	Площадь поверхности, A = 2 (фунт + bh + hl) Объем, V = фунтов / ч Диагональ пространства, d = √ (l 2 + b 2 + h 2 )
Цилиндр	Общая площадь поверхности, A = 2πrh + 2πr 2 Площадь криволинейной поверхности, A c = 2πrh Объем, V = πr 2 ч Площадь основания, A b = πr 2 Радиус, r = √ (В / πh)
Конус	Общая площадь поверхности, A = πr (r + l) = πr [r + √ (h 2 + r 2 )] Площадь изогнутой поверхности, A c = πrl Объем, V = ⅓πr 2 ч Наклонная высота, l = √ (h 2 + r 2 ) Площадь основания, A b = πr 2
Сфера	Площадь поверхности, A = 4πr 2 Объем, V = ⁄₃πr 3 Диаметр = 2r

Загрузить — Формулы геометрии PDF

Проверьте другие важные математические статьи:

Решенные примеры формул основной геометрии

Здесь мы привели несколько примеров геометрических формул для класса 10 с решениями:

Вопрос 1 : Найдите площадь остроугольного треугольника с основанием 15 дюймов и высотой 8 дюймов.

Решение : A = (½) × b × h квадратных единиц
⇒ A = (½) × (15 дюймов) × (8 дюймов)
= (½) × (120 дюймов ² )
= 60 в ²

Вопрос 2 : Длина и ширина прямоугольной стены составляют 40 м и 30 м соответственно. Узнайте стоимость покраски стены, если ставка покраски 3 рупия за кв.м.

Решение : Длина стены = 40 м
Ширина стены = 30 м
Площадь стены = длина x ширина
= 40 м x 30 м
= 1200 кв.м

За 1 кв. М покраски стоит 3.
рупий Таким образом, за 1200 кв. М покраска стены будет = 3 x 1200 = 3600 рупий.

Вопрос 3 : Основание параллелограмма вдвое больше его высоты. Если его площадь составляет 243 см ² , найдите основание и высоту.

Решение : Пусть высота параллелограмма = h см
, тогда основание параллелограмма = 2h см
Площадь параллелограмма = 243 см ²
По формуле геометрии мы знаем, что площадь параллелограмма = основание × высота
Следовательно, 243 = 3h × h
⇒ 3 × h ² = 243
⇒ h ² = 81
⇒ h = 8 см
Следовательно, высота параллелограмма равна 8 см, а ширина — 3 × h
= 3 × 8
= 24 см

Вопрос 4 : Каковы длина окружности и площадь круга, если радиус равен 21 см?

Решение : Дано: Радиус, r = 21 см
Мы знаем, что длина окружности / периметра круга равна 2πr см.
Теперь подставляем значение радиуса, получаем
C = 2 × π × 5
= 2 × (22/7) x21 [∵ π = 22/7] = 132 см
Таким образом, длина окружности равна 132 см. .
Теперь площадь круга равна πr ² см ²
A = (22/7) × 21 × 21
= 1386
Следовательно, площадь = 1386 см ² .

Вопрос 5 : Размеры прямоугольного прямоугольника следующие:
Длина = 4,8 см
Ширина = 3,4 см
Высота = 7,2 см.
Найдите общую площадь поверхности и площадь боковой поверхности.

Решение: Общая площадь поверхности определяется как
TSA = 2 (lw + wh + hl)
= 2 ((4.8 × 3.4) + (3.4 × 7.2) + (7.2 × 4.8))
= 2 (16.32 + 24,48 + 34,56)
= 2 (75,36) см²
Следовательно, TSA кубовида = 150,72 см
Кроме того, площадь боковой поверхности = 2 h (l + w)
= 2 × 7,2 (4,8 + 3,4)
= 14,4 (8.2)
= 118,08
Следовательно, LSA кубоида = 118,08 см²

Проверьте свойства различных геометрических фигур:

Практические вопросы по геометрическим формулам

Давайте попрактикуемся в некоторых вопросах по важным формулам геометрии:

Вопрос 1 : Две стороны треугольника равны 7 и 13 сантиметрам.По периметру 27 сантиметров. Найдите третью сторону. Вопрос 2 : Если квадрат имеет площадь 49 футов², какова длина одной из его сторон? Какой периметр? Вопрос 3 : Если один угол прямоугольного треугольника равен 70 ° , каковы два других угла? Вопрос 4 : Если коробка имеет высоту 4 дюйма, длину 12 дюймов, объем 240 дюймов 3 , какова ширина коробки? Вопрос 5 : Каков диаметр круга площадью 16π? Какая у него окружность? Вопрос 6 : На следующем рисунке прямые m1 и m2 параллельны.Ответьте:

(i) Какова мера угла 1? (ii) Какова величина угла 5? (iii) Какова мера угла 4? Вопрос 7 : Найдите объем: (допустим π = 3,14)

Часто задаваемые вопросы, связанные с геометрическими формулами

Давайте посмотрим на некоторые из часто задаваемых вопросов, связанных с геометрическими формулами:

Q1: Какие 3 типа геометрии?

A: 3 типа геометрии:
(i) евклидова
(ii) сферическая
(iii) гиперболическая

Q2: Каковы основные геометрические формулы?

A: Основные геометрические формулы для площади, периметра, объема, длины, ширины, высоты, радиуса и диагонали.Вы можете скачать геометрические формулы в формате PDF с этой страницы.

Q3: Какова площадь и объем сферы?

A: Площадь поверхности сферы = 4πr ²
Объем сферы = ⁴⁄₃πr ³

Q4: Каков объем куба?

A: Объем куба равен a ³ , где a — длина стороны куба.

Q5: Где я могу скачать все геометрические формулы и теоремы в формате PDF?

A: Вы можете скачать полный список геометрических формул в формате PDF с этой страницы.

Теперь вам предоставлена ​​вся необходимая информация о формулах, важных для геометрии. Мы надеемся, что вы скачали шпаргалку по геометрическим формулам, доступную на этой странице. Практикуйте больше вопросов и овладевайте геометрией.

Студенты могут использовать NCERT Solutions для математики, предоставленные Embibe для подготовки к экзаменам.

Мы надеемся, что эта подробная статья о геометрических формулах и геометрических уравнениях вам поможет. Если у вас есть какие-либо вопросы по этой статье, свяжитесь с нами через раздел комментариев ниже, и мы свяжемся с вами как можно скорее.

1035 Просмотры

Формула геометрии

Добро пожаловать в область таблицы формул геометрии Math Salamanders.

Здесь вы найдете ряд различных формул геометрии для 2-х и 3-х фигур.

Здесь вы найдете нашу страницу поддержки о различных формулах геометрии, включая треугольники, круги, четырехугольники и многоугольники, а также трехмерные фигуры. Использование этих листов поможет вашему ребенку:

• знать разные геометрические формулы;
• применять ряд формул для решения проблем.

Все листы по математике в этом разделе соответствуют тестам по элементарной математике.

Для получения дополнительных формул геометрии треугольников, включая примеры, показывающие правила синуса и косинуса, используйте ссылку ниже.

Общая формула этого правила для n-стороннего правильного многоугольника:

Суммарные внутренние углы составляют (n-2) x 180 °

Каждый угол должен составлять 180 (n-2) ° / n

Взгляните на еще несколько наших рабочих листов, похожих на эти.

Здесь вы найдете ряд шпаргалок по геометрии, которые помогут вам ответить на ряд вопросов о геометрии.

Таблицы содержат информацию об углах, типах и свойствах двумерных и трехмерных фигур, а также общие формулы, связанные с двумерными и трехмерными фигурами.

На этой странице находятся:

• изображение обычных 2D и 3D фигур;
• свойства 2D и 3D форм;
• формул, включающих двумерные формы, такие как площадь и периметр, теорема Пифагора, законы тригонометрии и т. Д .;
• формула, включающая трехмерные фигуры об объеме и площади поверхности.

Использование листов в этом разделе поможет вам понять и ответить на ряд вопросов о геометрии.

Здесь вы найдете список различных геометрических фигур.

К каждой форме прилагается небольшое изображение и описание свойств. форма имеет и как она соотносится с другими формами.

На этой странице представлены следующие формы:

• треугольник
• четырехугольник
• правильные многоугольники
• неправильные многоугольники
• набор трехмерных фигур

Все печатные листы геометрии в этом разделе поддерживают Тесты по элементарной математике.

Здесь вы найдете наш ассортимент бесплатных сетей для трехмерных фигур.

Следующие печатные формы содержат сети распространенных трехмерных фигур. что ваш ребенок должен знать. Доступен каждый сетчатый лист как с язычками, так и без них для облегчения склеивания.

Использование этих листов поможет вашему ребенку:

• знать свойства различных 3D-форм;
• распознает различные 2D-формы внутри 3D-фигур;
• построить трехмерную фигуру из сетки;
• распознает трехмерные формы в разных ориентациях и размерах;
• испытайте удовольствие и чудо создания трехмерной формы из сети.

Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.

Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.

Уголки четырехугольные	Углы в четырехугольнике в сумме составляют 360 ° а + б + в + г = 360 °
Углы в прямоугольнике	Все углы в прямоугольнике прямые (равны 90 °).
Площадь и периметр прямоугольника	Площадь прямоугольника = а х б Периметр прямоугольника = 2a + 2b , где a и b — длины двух соседних сторон.
Углы в параллелограмме	Углы в параллелограмме противоположных угла равны (противоположные стороны также равны). Кроме того, поскольку 2a + 2b = 360 °, это означает, что a + b = 180 °.
Площадь параллелограмма	Площадь параллелограмма = b x h = bh , где b — длина основания, а h — высота перпендикуляра параллелограмма.
Окружность круга Окружность круга — это расстояние по всей окружности внешняя сторона круга или периметр круга.	Окружность круга = 2πr или πd где r — радиус круга, а d — диаметр круга.
Площадь круга	Площадь круга = πr 2 где r — радиус окружности.
Длина дуги окружности	Длина L дуги окружности составляет: где θ — угол (в градусах), а r — радиус.
Площадь дуги окружности	Площадь A дуги окружности: где θ — угол (в градусах), а r — радиус.
Треугольник по полукругу	Треугольник, нарисованный внутри круга, одна сторона которого проходит по диаметру, и две другие стороны встречаются в любой точке на краю круга. всегда будет под прямым углом. Треугольник всегда будет прямоугольным.
Кубики	Объем куба: = а х а х а = а 3 Площадь куба: = 6a 2 , где a — длина каждой стороны.
Кубоид	Объем кубоида: = длина x ширина x высота = lwh Площадь поверхности кубоида: = 2lw + 2wh + 2lh
Сфера	Объем шара: знак равно 4 / 3 πr 3 Площадь поверхности шара: = 4πr 2 где r — радиус сферы.
Цилиндр	Объем цилиндра = πr 2 ч Площадь открытого цилиндра: = 2πrh Площадь закрытого цилиндра: = 2πrh + 2πr 2 = 2πr (r + h) где r — радиус цилиндра, h — высота.
Конус	Объем конуса где r — радиус самой широкой части конуса, а h — высота конуса. Площадь конуса (включая основание): = πr 2 + πrs Площадь конуса (без основания): = πrs
Квадратная пирамида (квадратная пирамида)	Объем квадратной пирамиды Площадь квадратной пирамиды (включая основание): = b 2 + 2bs Площадь квадратной пирамиды (без основания): = 2bs , где b — длина одной стороны основания, h — вертикальная высота пирамиды, а s — наклонная высота одного из треугольников.
Пирамида (общая)	Объем пирамиды = 1 ⁄ 3 (площадь основания x высота) = 1 ⁄ 3 Ач где A — площадь основания, а h — высота. Эта формула работает для любой пирамиды с прямоугольным или треугольным основанием и треугольными сторонами.

Обзор геометрической формулы

| Purplemath

Purplemath

Существует множество геометрических формул, которые связывают высоту, ширину, длину, радиус и т. Д. С периметром, площадью, площадью поверхности или объемом и т. Д.Некоторые формулы довольно сложные, и вы их почти никогда не видите, не говоря уже о том, чтобы их использовать. Но есть несколько основных формул, которые вам действительно стоит запомнить, потому что ваш инструктор может ожидать, что вы их знаете.

Например, очень легко найти площадь A прямоугольника: это просто длина l , умноженная на ширину w :

MathHelp.com

«Прямоугольник» в приведенной выше формуле — это нижний индекс, означающий, что найденная область « A » является областью прямоугольника. Поскольку я собираюсь обсуждать формулу для различных форм площади, объема и т. Д., Я использую нижние индексы, чтобы прояснить форму, к которой относится конкретная формула (при использовании « A » для «площади», » SA «для» площади поверхности «,» P «для» периметра «и» V «для» объема «).Подстрочные символы такого рода могут быть полезным методом прояснения вашего смысла, поэтому постарайтесь держать это в памяти для возможного использования в будущем.

Если вы посмотрите на изображение прямоугольника и вспомните, что «периметр» означает «длину по внешней стороне», вы увидите, что периметр прямоугольника P представляет собой сумму верхней и нижней длины l и ширина слева и справа w :

Квадраты еще проще, потому что их длина и ширина идентичны.Площадь A и периметр P квадрата со стороной s определяются по формуле:

Вы должны знать формулу площади треугольника; его легко запомнить, и он может неожиданно всплывать посреди словесных задач. Учитывая размеры основания b и высоты h треугольника, площадь A треугольника равна:

Конечно, периметр P треугольника будет просто суммой длин трех сторон треугольника.

---

Вы должны знать формулу для окружности C и площади A окружности с учетом радиуса r :

(«π» — это число, приблизительно равное 3,14159 или дроби 22/7)

Помните, что радиус круга — это расстояние от центра до внешней стороны круга. Другими словами, радиус составляет половину диаметра. Если они дают вам длину диаметра, являющуюся длиной линии, проходящей через середину, проходящую через весь круг, то вам сначала нужно разделить это значение пополам, чтобы применить приведенные выше формулы.

---

Это все «плоские», двухмерные формы. Иногда вам придется иметь дело с объемными фигурами, например, кубиками или конусами. Для таких форм вы найдете площадь поверхности (если вы рисовали объект, это область, которую вам нужно было бы покрыть) и объем (внутреннее пространство, которое вы могли бы заполнить, если бы форма пустой).

Формула для объема V куба проста, так как длина, ширина и высота — все одно и то же значение s :

Формула для площади поверхности (площади, которую вы бы измерили, если бы вам нужно было закрасить внешнюю сторону куба) тоже довольно проста, поскольку все стороны имеют одинаковую квадратную площадь s ² .Имеется шесть сторон (верхняя, нижняя, левая, правая, передняя и задняя), поэтому площадь поверхности SA составляет:

Формулы немного усложняются для «прямоугольной призмы», технического термина, обозначающего кирпич. Объем V все еще довольно прост: длина умножена на ширину, умноженную на высоту:

.

Формула площади поверхности немного сложнее. (Постарайтесь следовать рассуждениям, которые я собираюсь использовать, потому что вы, вероятно, забудете формулу, но ее легко воссоздать, если вы просто потратите немного времени и подумаете над ней.) Верх и низ «кирпича» имеют одинаковую площадь: длина умножена на ширину. Левая и правая стороны кирпича имеют одинаковую площадь, равную ширине, умноженной на высоту. И передняя, ​​и задняя часть кирпича имеют одинаковую площадь: длина умножена на высоту. (Нарисуйте рисунок, обозначив размеры, если вы не уверены в этом.) Тогда формула для площади поверхности SA кирпича будет:

Цилиндры (похожие на трубки, но с крышками на концах) тоже иногда появляются.Объем цилиндра V прост: это площадь конца (которая является просто площадью круга), умноженная на высоту h :

Площадь поверхности SA — это площадь концов (которые представляют собой просто круги) плюс площадь стороны, которая равна длине окружности круга, умноженной на высоту h цилиндра:

В зависимости от класса, который вы посещаете, вам также может потребоваться формула для объема V конуса с радиусом основания r и высотой h :

…или объем V сферы (шара) радиусом r :

Вы можете заметить, что в вашем домашнем задании или классных упражнениях появляются другие формулы. Возможно, вам придется запомнить эти другие формулы (их много!), Поэтому обязательно посоветуйтесь со своим инструктором перед тестом, чтобы узнать, какие из них вы должны знать.

Некоторые инструкторы предоставляют все геометрические формулы, поэтому в вашем тесте будет список всего, что вам может понадобиться.Но не все инструкторы таковы, и вы не можете ожидать, что каждый инструктор, каждый отдел или «общие», общекорпоративные или другие стандартизированные тесты предоставят вам всю эту информацию. Спросите своих инструкторов об их правилах, но помните, что наступает момент (средняя школа? SAT? ACT? Колледж? «Реальная жизнь»?), В котором вы должны будете выучить хотя бы некоторые из этих основных формул. Начни запоминать прямо сейчас!

---

URL: https: // www.purplemath.com/modules/geoform.htm

Базовая геометрия: правила и формулы — видео и стенограмма урока

Точка, отрезок линии, луч и линия

Три Самолета

Двумерные формы

Двумерные объекты имеют только два измерения: длину и ширину.

Многоугольники — это двухмерные фигуры, состоящие из отрезков линий. Чтобы считаться многоугольником, набор линейных сегментов должен быть замкнут, то есть каждый линейный сегмент встречается с другим линейным сегментом. Из-за этого требования квадраты и треугольники считаются многоугольниками, а круг не является многоугольником.

Квадраты — это многоугольники, состоящие из четырех линейных сегментов, каждый из которых имеет одинаковую длину. Прямоугольники также состоят из четырех отрезков прямой, где два параллельных отрезка равны по длине, а два других параллельных отрезка равны. Треугольники — это многоугольники с тремя линейными сегментами, которые могут быть одинаковой длины, но не обязательно.

Периметр и площадь

Периметр — это обычно вычисляемое измерение с двумерными формами в геометрии, которое добавляет длину линейных сегментов многоугольника. Расчет периметра предназначен для различных приложений, в том числе для определения количества ограждений вокруг вашего двора.

Как показано, вычисления периметра по существу одинаковы для разных форм: длину каждого отдельного отрезка линии необходимо складывать вместе.Например, если одна сторона квадрата, a , имеет размер 12 дюймов, то, используя формулу для периметра квадрата, 4 a , p равно 4 умножить на 12, что равно 48 дюймам.

Формулы для определения периметра прямоугольника и треугольника также требуют нахождения суммы длин сторон:

Периметр прямоугольника = (2 * длина) + (2 * ширина)

Периметр прямоугольника треугольник = a + b + c

Формула периметра квадрата

Формула периметра прямоугольника

Формула периметра треугольника

Измерение периметра окружности называется окружностью .Окружность круга находится с использованием диаметра d (расстояние по кругу) или радиуса r (расстояние на полпути по кругу) и пи , которое является соотношением, используемым в геометрия, которая примерно равна 3,14.

Окружность, диаметр и радиус

Формула длины окружности круга

Вот пример того, как вычислить длину окружности.Чтобы найти длину окружности с радиусом r , равным 4 метрам, просто умножьте 4 на 2 и на пи (3,14). Окружность этого круга будет примерно 25,12 метра. Окружность = 4 * 2 * 3,14

Площадь — это мера поверхности объекта. Площадь квадрата, прямоугольника, треугольника и круга можно найти с помощью формул. Подсчет площади используется, например, когда люди хотят знать квадратные метры своих домов. 2 (l = длина стороны).Формула для определения площади прямоугольника: A = длина * ширина. При нахождении площади треугольника формула площадь = ½ основания * высота.

Формула для площади квадрата

Формула для площади прямоугольника

Формула площади треугольника

Формула для площади круга

В качестве примера, чтобы найти площадь треугольника с основанием b размером 2 см и высотой h 9 см, умножьте 1/2 на 2 и 9, чтобы получить площадь 9 см в квадрате. .2. Это означает использование 3,14 (для числа пи), умноженного на квадрат радиуса.

Трехмерные формы

В отличие от двухмерных объектов, трехмерные объекты имеют третье измерение, глубину, и поэтому не являются плоскими. Кубы, сферы и пирамиды являются примерами трехмерных объектов. Куб — это объект, состоящий из шести квадратных сторон. Сфера представляет собой объект в форме шара, каждая точка на поверхности которого находится на одинаковом расстоянии от центра шара.Цилиндр — это еще один трехмерный объект, такой как банка с двумя круглыми концами и изогнутыми сторонами.

Площадь и объем поверхности

При работе с трехмерными объектами формулы используются для определения площади и объема поверхности. Площадь поверхности аналогична периметру, но вместо суммирования длины отрезков линии складываются площади каждой из форм, составляющих трехмерный объект. Зная это, можно вывести формулы для этих трехмерных фигур.Например, площадь поверхности куба в 6 раз больше площади одного квадрата, потому что он состоит из 6 квадратов.

Площадь поверхности может быть полезна в реальной жизни при определении количества краски, необходимого для покрытия объекта. Просмотрите формулы для площади поверхности различных форм:

Формула для площади поверхности куба или прямоугольной призмы:

SA = 2lw + 2hw + 2lh. Формула для использования с цилиндром: SA = 2B + Ch (B = площадь основания, C = окружность).2).

Формула площади поверхности куба

Формула площади поверхности шара

Формула площади поверхности цилиндра

В качестве примера, чтобы найти площадь поверхности сферы с радиусом 3 фута, просто возведите радиус в квадрат и умножьте на 4 и на 3.14. Площадь поверхности составляет 113,04 футов в квадрате.

Объем — это объем пространства, занимаемого объектом. Для куба это означает нахождение площади одного квадрата и определение того, сколько вещей может поместиться внутри, если этот квадрат сложен столько же раз, сколько длина (или ширина). Итак, при решении для объема куба длину стороны можно умножить на себя в три раза, потому что ее длина, ширина и глубина равны.

Объем имеет много практических применений в реальной жизни, потому что он вычисляет, сколько может вместить объект.3). Вот пример определения объема сферы с радиусом сферы с радиусом 3 м. Начните с куба радиуса, чтобы получить квадрат 27 м. Затем умножьте 4/3 на Пи и 27, чтобы получить окончательный ответ 113,04 м в кубе.

И, наконец, чтобы рассчитать объем цилиндра, воспользуйтесь формулой V = Bh. (B = Площадь основания)

Формула объема куба

Формула объема шара

Формула объема цилиндра

Краткое содержание урока

Геометрия — это математический предмет, связанный с формами и пространством.Формулы можно использовать для определения периметра и площади двухмерных фигур , таких как многоугольников и кругов . Периметры измеряют длину внешней стороны двухмерного объекта, а область представляет собой пространство на поверхности двухмерной формы.

В геометрии формулы также могут использоваться для нахождения площади поверхности и объемов трехмерных форм , таких как кубов и цилиндров . Объем измеряет объем пространства, занимаемого трехмерным объектом. Площадь поверхности измеряет площадь всех сторон трехмерного объекта.

Формула площади и объема для геометрических фигур

пи (π) = 3,1415926535 …

9002 5

Формула периметра
Квадрат	4 × сторона
Прямоугольник	2 × (длина + ширина)
Параллелограмм	2 × (сторона1 + сторона2)
Треугольник	сторона1 + сторона2 + сторона3
Правильный n-полигон	n × сторона
Трапеция	высота × (base1 + base2) / 2
Trapezoid	base1 + base2 + height × [ csc (theta1) + csc (theta2)]
Окружность	2 × pi × радиус
Эллипс	4 × radius1 × E (k, pi / 2) E (k, pi / 2) — полный эллиптический интеграл второго рода k = (1 / radius1) × sqrt (radius1 2 — radius2 2 )
Формула площади
Квадрат	сторона 2
Прямоугольник	длина × ширина
Параллелограмм	основание × высота
Треугольник	основание × высота / 2
Правильный n-многоугольник	(1/4) × n × сторона 2 × кроватка (pi / n)
Трапеция	высота × (base1 + base2) / 2
Окружность	pi × радиус 2
Эллипс	пи × радиус1 × радиус2
Куб (поверхность)	6 × сторона 2
Сфера (поверхность)	4 × пи × радиус 2
Цилиндр ( вс r сторона стороны)	периметр круга × высота
	2 × pi × радиус × высота
Цилиндр (вся поверхность)	Области верхнего и нижнего кругов + Площадь стороны
	2 (пи × радиус 2 ) + 2 × пи × радиус × высота
Конус (поверхность)	пи × радиус × сторона
Тор (поверхность)	pi 2 × (радиус2 2 — радиус1 2 )
Формула объема
Куб	сторона 3
Прямоугольная призма	сторона1 × сторона2 × сторона3
Сфера	(4 / 3) × пи × радиус 3
Эллипсоид	(4/3) × пи × радиус1 × радиус2 × радиус3
Цилиндр	пи × радиус 2 × высота
Конус	(1/3) × пи × радиус 2 × высота
Пирамида	(1/3) × (площадь основания) × высота
Тор	(1/4) × pi 2 × (r1 + r2) × (r1 — r2) 2

Источник: Spiegel, Murray R.Математический справочник формул и таблиц.
Серия набросков Шаума по математике. McGraw-Hill Book Co., 1968.

Исчерпывающий список геометрических формул для печати

Геометрия — это большое развлечение, когда у вас есть все геометрические формулы на кончиках ваших пальцев. Эта статья ScienceStruck предоставляет полный список геометрических формул для печати.

Окружность круга можно объяснить следующим образом: если вы возьмете нить или веревку и изогнете ее так, чтобы образовать круг, тогда длина окружности будет равна длине выпрямленной струны.

Хотите написать для нас? Что ж, мы ищем хороших писателей, которые хотят распространять информацию. Свяжитесь с нами, и мы поговорим …

Давайте работать вместе!

Когда дело доходит до предмета геометрии, она в основном включает в себя природу форм, способы их определения и то, чему нас учат в отношении мира в целом. Изучение геометрии — это на самом деле познание сути всего, что существует на Земле, включая вас. Мы очерчиваем формулы в геометрии, которые довольно просто запомнить.* Щелкните в любом месте статьи, чтобы получить распечатку.

Двумерные фигуры (площадь и периметр)

Площадь: Площадь двумерной поверхности — это экстент, охватываемый ею, заключенный в границу. Периметр: Периметр — это длина линии, охватывающей поверхность. Это сумма всех сторон многоугольника. Периметр круга называется его окружностью.

Треугольники

1. Площадь треугольника, если указаны основание и высота: (см. Рис.1)

   A (△) = Площадь треугольника b = Основание h = Высота

2. Площадь треугольника, когда даны все 3 стороны: (см. Рис.2)

   A (△) = √ s (s-a) (s-b) (s-c) , где s — полупериметр, а a, b, c — стороны треугольника. Периметр треугольника = a + b + c Если s — полупериметр,

3. Когда известны 2 стороны и угол между ними (см. Рис.2)

   А (△) =	1	x	a	x	б	x	SinC
   	2

   А (△) =	1	x	б	x	с	x	SinA
   	2

   А (△) =	1	x	a	x	с	x	SinB
   	2

   Где, A △ = Площадь треугольника a, b, c — стороны, SinA, SinB, SinC = — синусы соответствующих углов между сторонами

4. Площадь треугольника при заданном радиусе (см. Рис.3) A = r x s, где r = внутренний радиус и s = полупериметр.
5. Площадь треугольника с заданным радиусом описанной окружности (см. Рис.4)

   , где a, b, c — стороны треугольника, а R — радиус описанной окружности

6. Площадь равностороннего треугольника (см. Рис.5)

   , где a — сторона равностороннего треугольника

7. Площадь равнобедренного треугольника (см. Рис.6)

   А (△) =	c	x	√ 4a 2 -c 2
   	4

   Где a — длина двух равных сторон, а c — длина третьей стороны.

8. Площадь прямоугольного треугольника (см. Рис.7) A (△) = ½ x (произведение перпендикулярных сторон)

Многоугольник:

Многоугольник — это замкнутая геометрическая фигура, имеющая на больше , чем 2 прямые стороны. Многоугольник с: 3 сторонами известен как треугольник, 4 стороны известны как четырехугольник, 5 сторон известны как пятиугольник, 6 сторон известны как шестиугольник, 7 сторон известны как семиугольник, 8 сторон известны как восьмиугольник, 9 сторон известен как девятиугольник, 10 сторон известен как десятиугольник.Для правильного многоугольника с n сторонами: Сумма всех внутренних углов = (n-2) x 180º Как найти значение одного угла правильного многоугольника, если задано количество его сторон?

Значение одного угла правильного многоугольника =	(n-2) x180º
	n

Значение внутреннего угла + значение внешнего угла = 180º Площадь правильного многоугольника = ½ x (периметр) x (перпендикулярно от центра к любой стороне) Периметр многоугольника = сумма всех сторон многоугольника.

Циклический многоугольник

Если все вершины многоугольника лежат на окружности, то этот многоугольник называется циклическим многоугольником.

Четырехугольники

Сумма всех 4 углов четырехугольника = 360º Площадь четырехугольника = ½ x (диагональ) x (сумма перпендикуляра из противоположных вершин) Площадь четырехугольника = ½ xd ₁ xd ₂ x sin θ где d ₁ и d ₂ — диагонали, а θ — угол между ними.

Параллелограмм

Площадь параллелограмма = основание x высота

Ромб

Площадь ромба = ½ x произведение диагоналей

Площадь

Площадь квадрата = сторона ² Площадь квадрата = ½ x (диагональ) ² Периметр = 4 стороны

Прямоугольник

Хотите написать для нас? Что ж, мы ищем хороших писателей, которые хотят распространять информацию.Свяжитесь с нами, и мы поговорим …

Давайте работать вместе!

Площадь прямоугольника = длина x ширина Периметр = 2 x (длина + ширина)

Трапеция

Площадь трапеции = ½ x (сумма параллельных сторон) x высота

Воздушный змей

Площадь воздушного змея = ½ x d ₁ x d ₂ , где d ₁ и d ₂ — диагонали

Циклический четырехугольник

Площадь вписанного четырехугольника = √ (s-a) (s-b) (s-c) (s-d), где s — полупериметр, а a, b, c, d — стороны вписанного четырехугольника

Круг

Площадь круга = π r ² Окружность круга = 2πr

Трехмерные фигуры (объем и площадь)

Объем: Объемные фигуры занимают некоторое пространство.Объем — это мера занимаемого ими пространства . Также можно сказать, что объем — это пространство , содержащееся в трехмерной фигуре. Площадь поверхности: Количество бумаги, необходимое для полного покрытия трехмерной фигуры, является ее площадью поверхности. Если фигура имеет криволинейные поверхности, ее площадь называется площадью криволинейной поверхности. Общая площадь поверхности — это сумма площади плоской поверхности и площади криволинейной поверхности. В следующей таблице: Диаг. обозначает диаграмму Vol. обозначает объем SA обозначает площадь поверхности LSA обозначает площадь боковой поверхности CSA обозначает площадь криволинейной поверхности TSA обозначает общую площадь поверхности

Периметр, площадь и объем

1.В периметр из многоугольник (или любая другая замкнутая кривая, например окружность) — это расстояние вокруг внешней стороны.

2. В область из простая замкнутая плоская кривая — это количество внутреннего пространства.

3. В объем из твердый 3 D shape — это количество перемещаемого им пространства.

Некоторые формулы для общих 2 -мерные плоские фигуры и 3 -мерные тела приведены ниже.Ответов один, два, или три измерения; периметр измеряется в линейные единицы , область измеряется в квадратные единицы , а также объем измеряется в кубические единицы .

Таблица 1 . Формулы периметра
Форма	Формула	Переменные
Квадратный	п знак равно 4 s	s длина стороны квадрата.
Прямоугольник	п знак равно 2 L + 2 W	L а также W — длины сторон прямоугольника (длина и ширина).
Треугольник	а + б + c	а , б , а также c — длины сторон.
	п знак равно а + б + а 2 + б 2	а а также б длины двух катетов треугольника
Круг		р это радиус и d это диаметр.

Таблица 2. Формулы площади
Форма	Формула	Переменные
Квадратный		s длина стороны квадрата.
Прямоугольник		L а также W — длины сторон прямоугольника (длина и ширина).
Треугольник	А знак равно 1 2 б час	б а также час основание и высота
Треугольник	А знак равно s ( s — а ) ( s — б ) ( s — c ) где s знак равно а + б + c 2	а , б , а также c длины сторон и s полупериметр
Параллелограмм		б длина основания и час это высота.
Трапеция	А знак равно б 1 + б 2 2 час	б 1 а также б 2 — длины параллельных сторон и час расстояние (высота) между параллелями.
Круг	А знак равно π р 2	р это радиус.

Таблица 3. Формулы объема
Форма	Формула	Переменные
Куб		s длина стороны.
Правая прямоугольная призма		L это длина, W это ширина и ЧАС это высота.
Призма или цилиндр		А площадь основания, час это высота.
Пирамида или конус		А площадь основания, час это высота.
Сфера		р это радиус.

.