Все формулы геометрия: Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.

Разное

Содержание

Основные формулы по геометрии — Математика — Теория, тесты, формулы и задачи

Знание формул по геометрии является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по геометрии, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении геометрических задач. На этой странице сайта представлены основные формулы по школьной геометрии.

Изучать основные формулы по школьной геометрии онлайн:

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.

Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

Планиметрия (Геометрия на плоскости) — Математика — Теория, тесты, формулы и задачи

Основные теоретические сведения

Треугольник

К оглавлению. ..

При решении задач по геометрии помимо всех геометрических формул и свойств, которые будут приведены ниже, нужно очень хорошо помнить основные формулы по тригонометрии. Укажем для начала несколько основных свойств различных типов углов:

Смежные углы в сумме равны 180 градусов.
Вертикальные углы равны между собой.

Теперь перейдем к свойствам треугольника. Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Запомните также, что сумма любых двух сторон треугольника всегда больше третьей стороны

. Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы (медиана — линия проведенная через некоторую вершину и середину противоположной стороны в треугольнике):

Свойства медиан:

Все три медианы пересекаются в одной точке.
Медианы делят треугольник на шесть треугольников одинаковой площади.
В точке пересечения медианы делятся в отношении 2:1, считая от вершин.

Свойство биссектрисы (биссектриса — линия, которая делит некоторый угол на два равных угла, т.е. пополам):

Важно знать:

Центр вписанной в треугольник окружности лежит на пересечении биссектрис (все три биссектрисы пересекаются в этой одной точке). Формулы биссектрисы:

Основное свойство высот треугольника (высота в треугольнике — линия проходящая через некоторую вершину треугольника перпендикулярно противоположной стороне):

Все три высоты в треугольнике пересекаются в одной точке. Положение точки пересечения определяется типом треугольника:

Если треугольник остроугольный, то точка пересечения высот находится внутри треугольника.
В прямоугольном треугольнике высоты пересекаются в вершине прямого угла.
Если треугольник тупоугольный, то точка пересечения высот находится за пределами треугольника.

Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов

Теорема синусов:

Центр окружности описанной около треугольника лежит на пересечении посерединных перпендикуляров. Все три посерединных перпендикуляра пересекаются в одной этой точке. Посерединный перпендикуляр — линия проведенная через середину стороны треугольника перпендикулярно ей.

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т.п.) пропорциональны. Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов. Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников. Отношение периметров подобных треугольников равно коэффициенту подобия. Отношение длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Признаки подобия треугольников:

По двум углам. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.

По двум сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.
По трём сторонам. Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.

Трапеция

К оглавлению…

Трапеция — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна. Длина средней линии трапеции:

Площадь трапеции:

Некоторые свойства трапеций:

Средняя линия трапеции параллельна основаниям.
Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
В трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон находятся на одной прямой.

Диагонали трапеции разбивают её на четыре треугольника. Треугольники, сторонами которых являются основания — подобны, а треугольники, сторонами которых являются боковые стороны — равновелики.
Если сумма углов при любом основании трапеции равна 90 градусов, то отрезок соединяющий середины оснований равен полуразности оснований.
У равнобедренной трапеции углы при любом основании равны.
У равнобедренной трапеции диагонали равны.
В равнобедренной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.

Параллелограмм

К оглавлению…

Параллелограмм — это четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Некоторые свойства параллелограмма:

Противоположные стороны параллелограмма равны.
Противоположные углы параллелограмма равны.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Сумма углов, прилежащих к одной стороне, равна 180 градусов.
Сумма всех углов параллелограмма равна 360 градусов.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.

Квадрат

К оглавлению…

Квадрат — четырёхугольник, у которого все стороны равны, а все углы равны по 90 градусов. Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Свойства квадрата – это все свойства параллелограмма, ромба и прямоугольника одновременно.

Ромб и прямоугольник

К оглавлению…

Ромб — это параллелограмм, у которого все стороны равны. Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Свойства ромба:

Ромб является параллелограммом. Его противолежащие стороны попарно параллельны.
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
Диагонали ромба являются биссектрисами его углов.

Прямоугольник — это параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника через две смежные стороны:

Свойства прямоугольника:

Диагонали прямоугольника равны.
Прямоугольник является параллелограммом — его противоположные стороны параллельны.
Стороны прямоугольника являются одновременно его высотами.
Квадрат диагонали прямоугольника равен сумме квадратов двух его не противоположных сторон (по теореме Пифагора).
Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру описанной окружности.

Произвольные фигуры

К оглавлению…

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т. е. в том числе для любых треугольников):

Обобщённая теорема Фалеса: Параллельные прямые отсекают на секущих пропорциональные отрезки.

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Многоугольники

К оглавлению…

Выпуклым многоугольником называется многоугольник, обладающий тем свойством, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Сумма внутренних углов плоского выпуклого n-угольника равна:

Число диагоналей всякого многоугольника равно (где: n – число сторон):

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны. Внутренний угол правильного многоугольника равен:

Центральный угол правильного n-угольника равен:

Площадь правильного многоугольника с числом сторон n, длиной стороны a, радиусом описанной окружности R, полупериметром p и радиусом вписанной окружности r, может быть рассчитана по следующим формулам:

Окружность

К оглавлению. ..

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

Планиметрия. Материалы для подготовки к ЕГЭ по Математике

Анна Малкова

На этой странице – всё, что необходимо для отличного освоения планиметрии и решения задачи 16 Профильного ЕГЭ по математике. В том числе – уникальные авторские материалы.

New: Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?

Знаете ли вы, что задание 16 Профильного ЕГЭ по математике в 2018 и 2019 годах было значительно проще, чем «параметры» или «экономическая» задача? Получается, те, кто не брался за планиметрию на ЕГЭ, добровольно отказались от трех первичных баллов, и кому-то не хватило их для поступления.

Да, мы знаем, что в школе планиметрией занимаются мало.

У нас даже статья есть о том, как там всё печально: Геометрия в школе: засада для абитуриента

Однако выучить геометрию и сдать ЕГЭ все равно надо. Как же это сделать: Вам поможет наша Программа по геометрии. Список необходимых фактов и теорем.

Учим определения, формулы и теоремы. Вспоминаем, что такое синус и что такое косинус острого угла в прямоугольном треугольнике. Учим определения и свойства биссектрисы, медианы и высоты треугольника. И 5 (да, 5) формул площади треугольника.

В общем, всё, что необходимо для решения заданий №3 и №6 первой части Профильного ЕГЭ по математике. До второй части и задачи 16 мы тоже дойдем!

Кратко – в нашем Справочнике.

Подробно – здесь:

Геометрия. Формулы площадей фигур

Синус, косинус и тангенс острого угла прямоугольного треугольника

Тригонометрический круг: вся тригонометрия на одном рисунке

Внешний угол треугольника. Синус и косинус внешнего угла

Высота в прямоугольном треугольнике

Сумма углов треугольника

Углы при параллельных прямых и секущей

Высоты, медианы, биссектрисы треугольника

Четырёхугольники

Параллелограмм

Прямоугольник

Ромб

Квадрат

Трапеция

Окружность. Центральный и вписанный угол

Касательная к окружности

Вписанные и описанные треугольники. Теорема синусов

Вписанные и описанные четырёхугольники

Правильный треугольник

Правильный шестиугольник

Обратите внимание на тему «Векторы»:

Векторы на ЕГЭ по математике

Задание 16 из второй части ЕГЭ состоит из пунктов (а) и (б). Пункт (а) — это доказательство. Как правило, доказать нужно не самый тривиальный факт, и нужно уметь это делать.

Вам помогут «домашние заготовки» — наши Полезные факты для решения задач по планиметрии (с доказательствами)

Докажите их все и проверьте, что у вас получилось. После этого вы сможете доказать любое утверждение, которое вам может встретиться на ЕГЭ в задаче 16.

Но это не всё. Знаете ли вы, что многие задачи 16 Профильного ЕГЭ строятся по одной из так называемых классических схем? И эти Классические схемы для решения задач по планиметрии (с доказательствами) надо знать.

А для тех, кому скучно на уроке, — два геометрических парадокса. Готовы ли вы поверить, что прямой угол равен тупому? И что катет равен гипотенузе? Попробуйте найти ошибку в этих «доказательствах».

Геометрический парадокс: Прямой угол равен тупому

Геометрический парадокс: Катет равен гипотенузе

Как оформить решение задачи №16 (планиметрия)? Смотри образец решения и оформления!

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 2, задача 16

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 4, задача 16

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 16

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 16

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 12, задача 16

Задача на доказательство. Планиметрия.

И несколько полезных советов:

1) Задачи ЕГЭ по планиметрии решаются без сложных формул. Все необходимые факты, определения и теоремы – на этой странице.

2) Часто пункт (а) задачи 16 Профильного ЕГЭ содержит подсказку для решения пункта (б).

3) Обратите внимание на теорему о секущей и касательной, а также на свойство биссектрисы. Их трудно найти в учебнике. А в задачах ЕГЭ они применяются постоянно.

4) Старшеклассники очень любят теорему Фалеса. Но на самом деле применяется она очень редко. Намного чаще применяются три признака подобия треугольников.

— По двум углам,

— По углу и двум прилежащим к нему сторонам,

— По трем пропорциональным сторонам.

5) Самое важное – правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Сначала – теория. Затем – доказательство полезных фактов и классических схем. И только после этого – задачи №16 Профильного ЕГЭ.

Справочник по геометрии : «Формулы по геометрии»

Справочник по геометрии 7-9

ОГЛАВЛЕНИЕ

стр.

1. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ. АКСИОМЫ ………………………………… 3

2. УГЛЫ. БИССЕКТРИСА УГЛА …………………………………………………. 4

3. ВИДЫ ТРЕУГОЛЬНИКОВ. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ

И УГЛАМИ ТРЕУГОЛЬНИКА …………………………………………………. .. 5

4. ПЛОЩАДЬ ТРЕУГОЛЬНИКА. СВОЙСТВА РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА ……..………………………………………………………………… 6

5. ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ. ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ ……………………………………………………………………. 7 6. ЗАМЕЧАТЕЛЬНЫЕ ЛИНИИ В ТРЕУГОЛЬНИКЕ ……………………………….. 8

7. ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. ОСНОВНЫЕ СООТНОШЕНИЯ ……. 9

8. СВОЙСТВА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА. ПРИЗНАКИ

РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ …………………………. 10

9. ЗНАЧЕНИЯ СИНУСА, КОСИНУСА И ТАНГЕНСА НЕКОТОРЫХ УГЛОВ. ЧЕТЫРЕХУГОЛЬНИКИ ……………………….……………………………………… 11

10. СВОЙСТВА И ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА ……………………… 12

11. ПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ ……………………………………… 13

12. ТРАПЕЦИЯ …………………………………………………………………….. 14

13. ОКРУЖНОСТЬ. ВПИСАННЫЙ УГОЛ ………………………………………. 15

14. СВОЙСТВА ОКРУЖНОСТИ И ЕЕ ЭЛЕМЕНТОВ ………………………….. 16

15. СВОЙСТВА КАСАТЕЛЬНЫХ И СЕКУЩИХ ………………………………… 17

16. ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ ……………………………. 18

17. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ ……………………………………….. 19

18. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ВЕКТОРЫ. ……………….. 20

Справочник по геометрии 7-9

ПАРАЛЛЕЛЬНОСТЬ

Прямые а и b пересечены секущей с

1 и 2;3 и4 – накрест лежащие углы

и 8; 3 и 5 — соответственные углы

2 и 7; 4 и 6 — соответственные углы

1 и 3;2 и 4 — односторонние углы

Признаки параллельности прямых

1=2а║b

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

1 =8 а║b

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

1 +3=а║b

Если при пересечении двух прямых секущей сумма односторонних углов равна 180º, то прямые параллельны.

а║b, а║сс║b а с║b

Свойства углов при параллельных прямых

а║b 1 =2

Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

а║b 1 = 8

Если две параллельные прямые пересечены секущей, то соответственные углы равны.

а║b 1 + 3=

Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна .

НЕКОТОРЫЕ АКСИОМЫ ПЛАНИМЕТРИИ

Через любые две различные точки проходит прямая, и притом только одна.

А а В а

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

а║b А а

УГЛЫ

Острый угол

меньше прямого угла

CDA<

Тупой угол

больше прямого угла

ab <

Прямой угол

hk =

Развернутый угол

AOM =

Смежные углы

Сумма смежных углов рав.

Вертикальные углы

Вертикальные углы равны.

БИССЕКТРИСА УГЛА

с – биссектриса ab

aс = сb

Луч с делит уголab пополам

Свойство биссектрисы

АМ = ВМ

Каждая точка биссектрисы

неразвернутого угла равноудалена от сторон угла.

ВИДЫ ТРЕУГОЛЬНИКОВ

Остроугольный

(все углы острые)

все стороны разной длины

две стороны равны

все стороны равны

Прямоугольный

(один из углов – прямой)

∠ А= В==60

Р = 3а, где

а — сторона,

Р— периметр

Тупоугольный

(один из углов – тупой)

СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА

Сумма углов треугольника равна 180 ̊.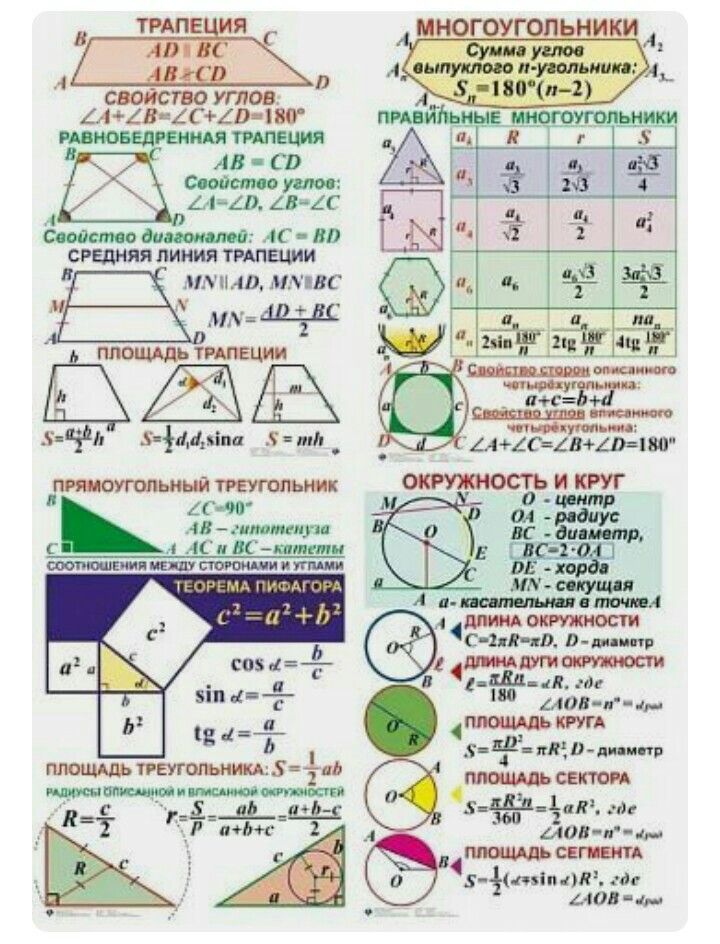

∠ А+ В+=180 ̊

Свойство внешнего угла: ∠ АСК = ∠ А + В

Неравенство треугольника

а < b+с b < а+с с < а+b

Каждая сторона треугольника меньше суммы двух других сторон.

а > b — с, где b>с

Теорема о соотношениях между сторонами и углами треугольника

b > с В >С и В >С b > с

В треугольнике против большей стороны лежит больший угол.

Против большего угла лежит большая сторона.

Теорема синусов

где адиус описанной окружности.

Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема косинусов

с² = а² + b² ― 2аb

а² = с² + b² ― 2 bс

b² = с² + а²― 2 ас

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

ПЛОЩАДЬ ТРЕУГОЛЬНИКА

Площадь треугольника равна половине произведения его стороны на высоту к этой стороне:

S =ah

Другие формулы:

S = ab = aс = сb

S = ,

где — полупериметр

S = r ,

где r— радиус вписанной в треугольник окружности

S = ,

где R – радиус описанной окружности

СВОЙСТВА РАВНОБЕДРЕНННОГО ТРЕУГОЛЬНИКА

В равнобедренном треугольнике углы при основании равны

А = С

АС – основание

АВ и ВС – боковые стороны

Биссектриса, проведенная к основанию, является медианой и высотой

ВК –биссектриса ВК – медиана ВК –высота

ВК – биссектриса

ВК – медиана

ВК — высота

РАВНЫЕ И ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

= , значит,

АВ = СВ = СА = С₁А₁

А = А₁ В = С = С_1.

подобен , значит, А = А₁ В = С = С₁

= =

По двум сторонам и углу между ними

АВ = СВ = В =

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

По двум углам

А = В =

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

По стороне и двум прилежащим углам

АС= А = С =

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

По двум сходственным сторонам и углу между ними

= А =

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

По трем сторонам

АВ = СВ = АС=

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

По трем сходственным сторонам

= =

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

ЗАМЕЧАТЕЛЬНЫЕ ЛИНИИ В ТРЕУГОЛЬНИКЕ

АМ – медиана АВС

точка М – середина ВС

Свойство медиан

СО:ОР = АО:ОМ = ВО:ОК = 2:1

Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1.

АМ = m

формула для вычисления медианы

АН – высота

АН — перпендикуляр, опущенный из

точки А на прямую ВС

Свойство высот

Высоты треугольника пересекаются в одной точке треугольника.

АЕ – биссектриса

2 (САЕ = ВАЕ)

Свойства биссектрисы треугольника

Биссектрисы треугольника пересекаются в одной точке (центре вписанной окружности).

Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

Прямая а – серединный перпендикуляр

О а ОС = ОВ а ВС

Свойство серединных перпендикуляров

Серединные перпендикуляры пересекаются в одной точке (центре описанной окружности)

MN – средняя линия

точка М — середина АВ, N – середина ВС

Свойство средней линии треугольника

MN АС; MN = АС

Средняя линия параллельна одной из сторон и равна её половине.

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК

Теорема Пифагора

c²=а² + b²

Квадрат гипотенузы равен сумме квадратов катетов.

Пропорциональные отрезки

h² =

а² =

b² =

С = 90⁰ А = α

с = АВ – гипотенуза

а = ВС – катет, противолежащий к α

b = АС – катет, прилежащий к углу α

СИНУС

Отношение противолежащего катета к гипотенузе

КОСИНУС

Отношение прилежащего катета к гипотенузе

ТАНГЕНС

Отношение противолежащего катета к прилежащему

КОТАНГЕНС

Отношение прилежащего катета к противолежащему

Свойства прямоугольного треугольника

А+ В = 90 ̊

Сумма острых углов в прямоугольном треугольнике равна 90 ̊

А = а = с

Катет прямоугольного треугольника, лежащий против угла в равен половине гипотенузы

а = с А =

Если катет равен половине гипотенузы, то угол, лежащий против этого катета,

равен 3

m = c = R

Медиана, проведенная к гипотенузе, равна её половине и является радиусом описанной окружности

Признаки равенства прямоугольных треугольников

По гипотенузе и катету

а = с =

По катету и прилежащему острому углу

А =А₁b =b₁

По катету и противолежащему острому углу

А =А₁ а = а₁

о гипотенузе и острому углу

А =А₁c = c₁

СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ

+ =1 – основное тригонометрическое тождество

формулы

приведения

(90 ̊– α) =

cos(90 ̊ – α) =

(180 ̊– α) =

cos(180 ̊– α) = –

ЗНАЧЕНИЯ СИНУСА, КОСИНУСА И ТАНГЕНСА НЕКОТОРЫХ УГЛОВ

ЧЕТЫРЕХУГОЛЬНИКИ

АВСD — четырехугольник

А +В +С +D = 360°

S =

АС, ВD — диагонали

ПАРАЛЛЕЛОГРАММ

ABCD- параллелограмм

AB CD

BC AD

Параллелограммом называется четырехугольник, у которого стороны попарно параллельны.

СВОЙСТВА И ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА

AB=CD; BC=AD

A=C; B=D

В параллелограмме противоположные стороны и противоположные углы равны

ACBD = O, AO = OC, BO = OD

Диагонали параллелограмма делятся точкой пересечения пополам.

А + В = 180⁰

В параллелограмме сумма углов, прилежащих к одной стороне, равна 180⁰

² +² = a² + b² + c² + d²

где = AC; = BD – диагонали;

a = AD; b = AB; c = BC;

d = CD – стороны

P = 2(a + b) – периметр параллелограмма,

где a = AD; b = AB

(ABCD; AB = CD)(ABCD-параллелограмм)

Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

(AB = CD; BC = AD)(ABCD-параллелограмм)

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм

(AO = OC; BO = OD,

где O = ACBD)(ABCD-параллелограмм)

Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм

ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА

S = ah,

где a = AD – основание

h = BH – высота

S = ab,

где а = AD, b = AB,

a =BAD

S =

S= 4

ЧАСТНЫЕ СЛУЧАИ ПАРАЛЛЕЛОГРАММА

ABCD – прямоугольник – это параллелограмм, у которого все углы прямые

A =B =C=D = 90°

Диагонали прямоугольника равны.

S =

S = – площадь

P = 2(a + b) — периметр

d₁² = a²+b²

где d₁, d₂ – диагонали,

а, b – стороны прямоугольника

ABCD – ромб – это параллелограмм,

у которого все стороны равны

AB = BC = CD = AD

1=2, 3=4,

Диагонали ромба взаимно перпендикулярны и делят его углы пополам

S =

S = — площадь

Р = 4а – периметр

² +² = 4a²

где d₁, d₂ — диагонали,

а – сторона ромба,

– угол ромба

ABCD – квадрат — это прямоугольник,

у которого все стороны равны

AB = BC = CD = AD

Диагонали квадрата равны,

взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

A=B=C=D =90°

S = a²– площадь

S =

S= ,

где r – радиус вписанной окружности

Р = 4а — периметр

= а

где d₁, d₂ — диагонали, а – сторона квадрата

ТРАПЕЦИЯ

ABCD — трапеция

AD = a, BC = b – основания

AB, CD – боковые стороны

BH = h — высота

ADBC;

MN – средняя линия трапеции,

где М – середина АВ

N – середина СD

MN BC; MN AD; MN=

Средняя линия трапеции параллельна

основаниям и равна их полусумме.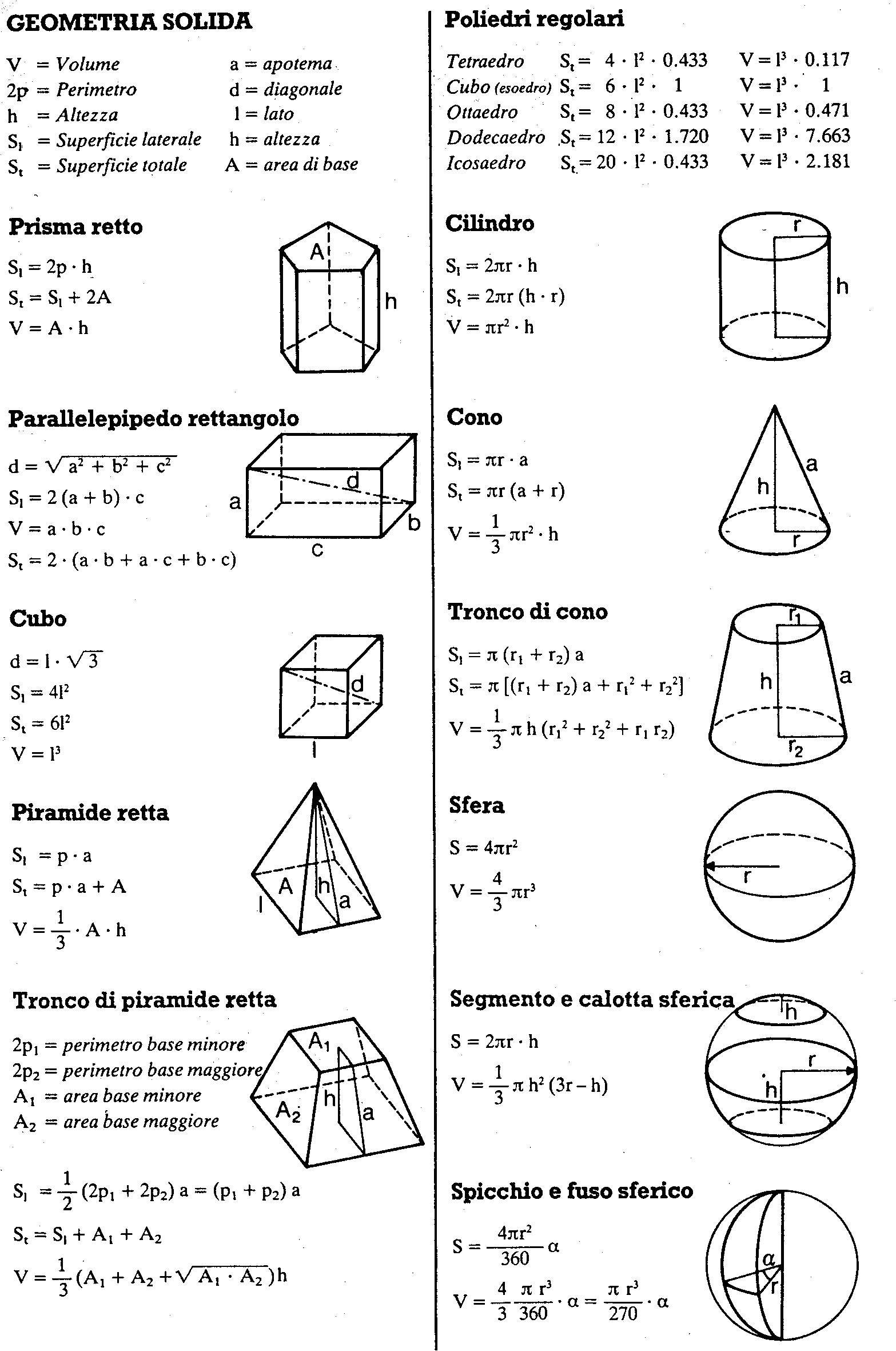

Трапеция прямоугольная,

если один из углов прямой

Трапеция равнобедренная,

если ее боковые стороны равны

В равнобедренной трапеции:

диагонали равны;
углы при основании равны;
середины сторон являются вершинами ромба.

Биссектрисы углов, прилежащих к боковой стороне, перпендикулярны

ОКРУЖНОСТЬ

Окр. (О; r)

т. О – центр окружности

OK = OB = OA = r – радиус

AB = d – диаметр

b – касательная

AC – хорда

MN — секущая

— дуга окружности

d = 2r

— длина окружности

L — длина дуги

— дуга окружности

АОВ — центральный угол

АОВ =

Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.

АСВ – вписанный угол

АСВ =

Вписанный угол измеряется половиной дуги, на которую опирается.

АСВ = , если меньше полуокружности

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на полуокружность – прямой.

ПЛОЩАДЬ Площадь круга

Площадь сектора

S =

СВОЙСТВА ОКРУЖНОСТИ И ЕЁ ЭЛЕМЕНТОВ

Свойство хорд

AB; CD – хорды

AB CD = M

AM · MB = CM · MD

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Свойство касательной

ОМ – радиус

а – касательная

М – точка касания

ОМ а

Основные формулы по геометрии и их свойства.

Основные формулы по геометрии и свойства

Радиус описанной окружности трапеции по сторонам и диагонали

a — боковые стороны трапеции

c — нижнее основание

b — верхнее основание d — диагональ

h – высота p = (a+d+c)/2

Радиус вписанной окружности в равнобочную трапецию

с — нижнее основание

b — верхнее основание

a — боковые стороны

h — высота

Найти радиус описанной окружности треугольника, формула

a, b, c — стороны треугольника

p — полупериметр, p= (a+b+c)/2

Найти радиус описанной окружности равностороннего треугольника по стороне

a — сторона треугольника

Формулы вычисления площади треугольника (если даны все стороны треугольника):

I формула Герона

p — полупериметр p=(a+b+c)|2

II формула Герона.

Формула расчета площади треугольника

h — высота треугольника

a — основание

Центральным называется угол с вершиной в центре окружности.
Центральный угол равен градусной мере дуги, на которую опирается. Поэтому углом в один радиан называется центральный угол, который опирается на дугу в один радиан.

Вписанным называется угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
Вписанный угол равен половине градусной меры дуги, на которую опирается.

Две различные точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности.

Дугою в один градус называется дуга окружности, длина которой равняется части его длины. Дугою в один радиан (1 рад) называется дуга окружности, длина которой равняется радиусу этой окружности.

Переход от градусной меры углов и дуг к радианной, и наоборот, осуществляется по формулам:

рад.

В частности:

рад.

Формула площади параллелограмма через сторону и высоту

a, b — стороны параллелограмма

H_b —высота на сторону b

H_a — высота на сторону a

Формула площади трапеции через основания и высоту

a — нижнее основание

b — верхнее основание

m — средняя линия

h — высота трапеции

2. Формула площади трапеции через четыре стороны

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

Формула площади трапеции, (S ):

Вычислить площадь ромба

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

Формулы площади ромба через диагонали и углы между сторонами ( S ):

a — сторона ромба h — высота

r — радиус вписанной окружности

Радиус вписанной окружности в шестиугольник

a — сторона шестиугольника

Радиус вписанной окружности в равнобедренный треугольник

a, b — стороны треугольника

Радиус вписанной окружности в равносторонний треугольник

a — сторона треугольника

Радиус вписанной окружности в треугольник

a, b, c — стороны треугольника

p — полупериметр, p=(a+b+c)/2

Радиус вписанной окружности в прямоугольный треугольник

Радиус вписанной окружности в ромб

r — радиус вписанной окружности

a — сторона ромба

D, d — диагонали

h — высота ромба

Радиус вписанной окружности в квадрат

a — сторона квадрата

Радиус вписанной окружности в равнобочную трапецию

с — нижнее основание

b — верхнее основание

a — боковые стороны

h — высота

Радиусы описанной окружности

Радиус описанной окружности правильного шестиугольника

a — сторона шестиугольника

d — диагональ шестиугольника

Найти радиус описанной окружности треугольника, формула

p= (a+b+c)/2

Найти радиус описанной окружности прямоугольного треугольника по катетам

Радиус описанной окружности прямоугольника по стороне

a, b — стороны прямоугольника

d — диагональ

Найти радиус описанной окружности около квадрата

Найти радиус описанной окружности равностороннего треугольника по стороне

найти радиус описанной окружности равнобедренного треугольника по сторонам

Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.

Плоские геометрические фигуры: свойства и основные формулы

В статье дается определение, основные свойства и формулы для следующих геометрических фигур:

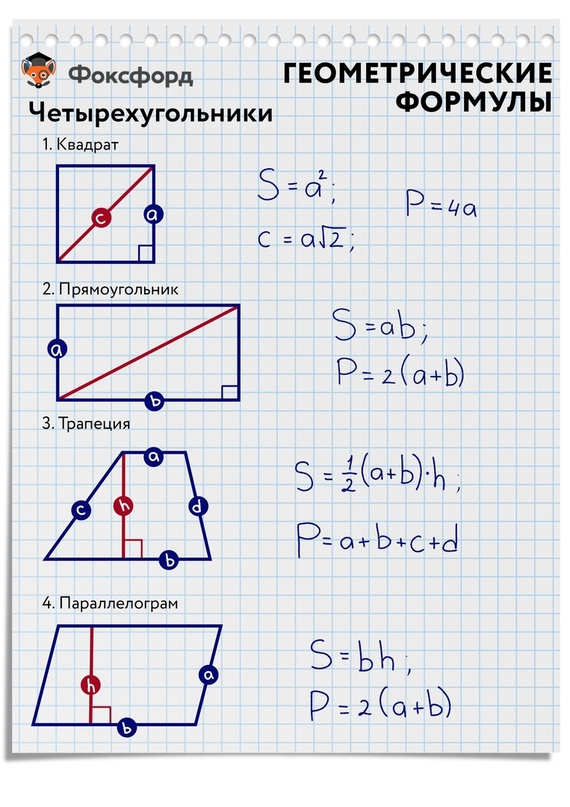
Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

Сумма углов четырёхугольника равна 360°
Не существует четырёхугольников, у которых все углы острые или все углы тупые.
Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.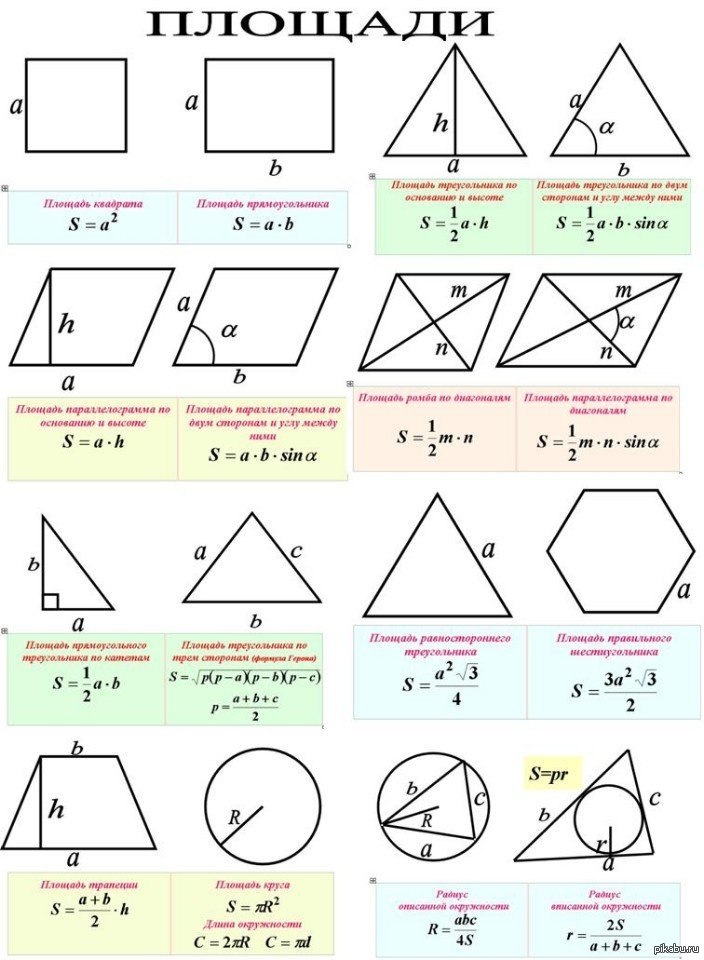

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Квадрат

Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a²или S=d²/2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

Все стороны равны, все углы равны и составляют 90°;
Диагонали квадрата равны и перпендикулярны;
У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
Квадрат является одновременно частным случаем ромба и прямоугольника.

Прямоугольник

Прямоугольник — четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a²+b²)/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a²+b²)/2 (теорема Пифагора)

где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a²+b²) – корень квадратный из (a²+b²).

Свойства:

Диагонали прямоугольника равны и делятся точкой пересечения пополам.
Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

Параллелограмм

Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁)²+(d₂)²=(a²+b²)*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
Площадь по двум сторонам и углу между ними: S=a*b*sin α
Площадь по двум диагоналям и углу между ними: S=(d₁*d₂)/2*sin γ

где a, b — длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).

Свойства:

У параллелограмма противоположные стороны равны и противоположные углы равны.
Сумма любых двух соседних углов параллелограмма равна 180°.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Каждая диагональ делит параллелограмм на два равных треугольника.
Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Ромб

Ромб — это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a² · sin α
Радиус окружности, вписанной в ромб: r=h/2 или r =(d₁*d₂)/4a

где a — длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба

Свойства:

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
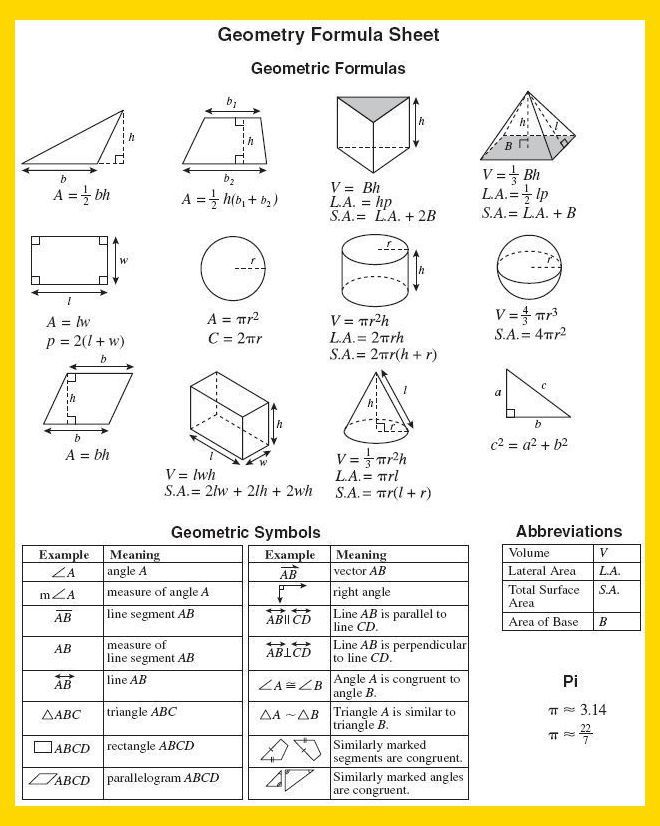
В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d₁*d₂/4a.

Трапеция

Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d₁, d₂ –диагонали,
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь по сторонам и углу между ними: S=(a*b)/2* sin γ
Площадь по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
Площадь по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c²=a²+b² (Теорема Пифагора)

где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
d₁, d₂ –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности

Свойства:

В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
Сумма углов треугольника равна 180°:
Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| <c<a+b
Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c²=a²+b² (Теорема Пифагора). В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Окружность

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

Радиус — отрезок, который соединяет центр окружности с любой её точкой.
Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
Диаметр — хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
Секущая — прямая, которая пересекает окружность в двух различных точках.

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r² или S = π*d²/4

где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

Список формул координатной геометрии (с PDF) для классов 9, 10 и 11

- БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
- КОНКУРСНЫЕ ЭКЗАМЕНА
  BNAT
  Классы
  Класс 1-3
  Класс 4-5
  Класс 6-10
  Класс 110003 CBSE
  Книги NCERT
  Книги NCERT для класса 5
  Книги NCERT, класс 6
  Книги NCERT для класса 7
  Книги NCERT для класса 8
  Книги NCERT для класса 9
  Книги NCERT для класса 10
  NCERT Книги для класса 11
  NCERT Книги для класса 12
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  9plar
  RS Aggarwal
  RS Aggarwal Решения класса 12
  RS Aggarwal Class 11 Solutions
  RS Aggarwal Решения класса 10
  Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  RD Sharma
  RD Sharma Class 6 Решения
  RD Sharma Class 7 Решения
  Решения RD Sharma класса 8
  Решения RD Sharma класса 9
  Решения RD Sharma класса 10
  Решения RD Sharma класса 11
  Решения RD Sharma Class 12
  PHYSICS
  Механика
  Оптика
  Термодинамика
  Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  MATHS
  Статистика
  Числа
  Числа Пифагора Тр Игонометрические функции
  Взаимосвязи и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Разделение фракций
  Microology
  FORMULAS
  Математические формулы
  Алгебраные формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  0003000
  000
  000 Калькуляторы по химии
  000
  000
  000 Образцы документов для класса 6
  Образцы документов CBSE для класса 7
  Образцы документов CBSE для класса 8
  Образцы документов CBSE для класса 9
  Образцы документов CBSE для класса 10
  Образцы документов CBSE для класса 1 1
  Образцы документов CBSE для класса 12
  Вопросники предыдущего года CBSE
  Вопросники предыдущего года CBSE, класс 10
  Вопросники предыдущего года CBSE, класс 12
  HC Verma Solutions
  HC Verma Solutions Класс 11 Физика
  HC Verma Solutions Класс 12 Физика
  Решения Лакмира Сингха
  Решения Лакмира Сингха класса 9
  Решения Лакмира Сингха класса 10
  Решения Лакмира Сингха класса 8
  9000BSE 9000 Класс
  2 6 Примечания CBSE
  Примечания CBSE класса 7
  Примечания
  Примечания CBSE класса 8
  Примечания CBSE класса 9
  Примечания CBSE класса 10
  Примечания CBSE класса 11
  Примечания 12 CBSE
  Примечания к редакции 9000 CBSE 9000 Примечания к редакции класса 9
  CBSE Примечания к редакции класса 10
  CBSE Примечания к редакции класса 11
  Примечания к редакции класса 12 CBSE
- Дополнительные вопросы CBSE
  Дополнительные вопросы по математике для класса 8 CBSE
  Дополнительные вопросы по науке для класса 8 CBSE
  Дополнительные вопросы по математике класса 9 CBSE
  Вопросы
  CBSE Class 10 Дополнительные вопросы по математике
  CBSE Class 10 Science Extra questions
- CBSE Class
  Class 3
  Class 4
  Class 5
  Class 6
  Class 7
  Class 8 Класс 9
  Класс 10
  Класс 11
  Класс 12
- Учебные решения
Решения NCERT
Решения NCERT для класса 11
Решения NCERT для класса 11 по физике
Решения NCERT для класса 11 Химия
Решения NCERT для биологии класса 11
Решение NCERT s Для класса 11 по математике
NCERT Solutions Class 11 Accountancy
NCERT Solutions Class 11 Business Studies
NCERT Solutions Class 11 Economics
NCERT Solutions Class 11 Statistics
NCERT Solutions Class 11 Commerce
NCERT Solutions for Class 12
Решения NCERT для физики класса 12
Решения NCERT для химии класса 12
Решения NCERT для биологии класса 12
Решения NCERT для математики класса 12
Решения NCERT, класс 12, бухгалтерия
Решения NCERT, класс 12, бизнес-исследования
NCERT Solutions Class 12 Economics
NCERT Solutions Class 12 Accountancy Part 1
NCERT Solutions Class 12 Accountancy Part 2
NCERT Solutions Class 12 Micro-Economics
NCERT Solutions Class 12 Commerce
NCERT Solutions Class 12 Macro-Economics
NCERT Solut Ионы Для класса 4
Решения NCERT для математики класса 4
Решения NCERT для класса 4 EVS
Решения NCERT для класса 5
Решения NCERT для математики класса 5
Решения NCERT для класса 5 EVS
Решения NCERT для класса 6
Решения NCERT для математики класса 6
Решения NCERT для науки класса 6
Решения NCERT для класса 6 по социальным наукам
Решения NCERT для класса 6 Английский язык
Решения NCERT для класса 7
Решения NCERT для математики класса 7
Решения NCERT для науки класса 7
Решения NCERT для социальных наук класса 7
Решения NCERT для класса 7 Английский язык
Решения NCERT для класса 8
Решения NCERT для математики класса 8
Решения NCERT для науки 8 класса
Решения NCERT для социальных наук 8 класса ce
Решения NCERT для класса 8 Английский
Решения NCERT для класса 9
Решения NCERT для класса 9 по социальным наукам
Решения NCERT для математики класса 9
Решения NCERT для математики класса 9 Глава 1
Решения NCERT для математики класса 9, глава 2
Решения NCERT
для математики класса 9, глава 3
Решения NCERT для математики класса 9, глава 4
Решения NCERT для математики класса 9, глава 5
Решения NCERT
для математики класса 9, глава 6
Решения NCERT для математики класса 9 Глава 7
Решения NCERT
для математики класса 9 Глава 8
Решения NCERT для математики класса 9 Глава 9
Решения NCERT для математики класса 9 Глава 10
Решения NCERT
для математики класса 9 Глава 11
Решения
NCERT для математики класса 9 Глава 12
Решения NCERT
для математики класса 9 Глава 13
NCER Решения T для математики класса 9 Глава 14
Решения NCERT для математики класса 9 Глава 15
Решения NCERT для науки класса 9
Решения NCERT для науки класса 9 Глава 1
Решения NCERT для науки класса 9 Глава 2
Решения NCERT для науки класса 9 Глава 3
Решения NCERT для науки класса 9 Глава 4
Решения NCERT для науки класса 9 Глава 5
Решения NCERT для науки класса 9 Глава 6
Решения NCERT для науки класса 9 Глава 7
Решения NCERT для науки класса 9 Глава 8
Решения NCERT для науки класса 9 Глава 9
Решения NCERT для науки класса 9 Глава 10
Решения NCERT для науки класса 9 Глава 12
Решения NCERT для науки класса 9 Глава 11

Формулы геометрии для класса 8 Математика Список формул геометрии

- БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
- КОНКУРСНЫЕ ЭКЗАМЕНА
  BNAT
  Классы
  Класс 1-3
  Класс 4-5
  Класс 6-10
  Класс 110003 CBSE
  Книги NCERT
  Книги NCERT для класса 5
  Книги NCERT, класс 6
  Книги NCERT для класса 7
  Книги NCERT для класса 8
  Книги NCERT для класса 9
  Книги NCERT для класса 10
  NCERT Книги для класса 11
  NCERT Книги для класса 12
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  9plar
  RS Aggarwal
  RS Aggarwal Решения класса 12
  RS Aggarwal Class 11 Solutions
  RS Aggarwal Решения класса 10
  Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  RD Sharma
  RD Sharma Class 6 Решения
  RD Sharma Class 7 Решения
  Решения RD Sharma класса 8
  Решения RD Sharma класса 9
  Решения RD Sharma класса 10
  Решения RD Sharma класса 11
  Решения RD Sharma Class 12
  PHYSICS
  Механика
  Оптика
  Термодинамика
  Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  MATHS
  Статистика
  Числа
  Числа Пифагора Тр Игонометрические функции
  Взаимосвязи и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Разделение фракций
  Microology
  FORMULAS
  Математические формулы
  Алгебраные формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  0003000
  000
  000 Калькуляторы по химии
  000
  000
  000 Образцы документов для класса 6
  Образцы документов CBSE для класса 7
  Образцы документов CBSE для класса 8
  Образцы документов CBSE для класса 9
  Образцы документов CBSE для класса 10
  Образцы документов CBSE для класса 1 1
  Образцы документов CBSE для класса 12
  Вопросники предыдущего года CBSE
  Вопросники предыдущего года CBSE, класс 10
  Вопросники предыдущего года CBSE, класс 12
  HC Verma Solutions
  HC Verma Solutions Класс 11 Физика
  HC Verma Solutions Класс 12 Физика
  Решения Лакмира Сингха
  Решения Лакмира Сингха класса 9
  Решения Лакмира Сингха класса 10
  Решения Лакмира Сингха класса 8
  9000BSE 9000 Класс
  2 6 Примечания CBSE
  Примечания CBSE класса 7
  Примечания
  Примечания CBSE класса 8
  Примечания CBSE класса 9
  Примечания CBSE класса 10
  Примечания CBSE класса 11
  Примечания 12 CBSE
  Примечания к редакции 9000 CBSE 9000 Примечания к редакции класса 9
  CBSE Примечания к редакции класса 10
  CBSE Примечания к редакции класса 11
  Примечания к редакции класса 12 CBSE
- Дополнительные вопросы CBSE
  Дополнительные вопросы по математике для класса 8 CBSE
  Дополнительные вопросы по науке для класса 8 CBSE
  Дополнительные вопросы по математике класса 9 CBSE
  Вопросы
  CBSE Class 10 Дополнительные вопросы по математике
  CBSE Class 10 Science Extra questions
- CBSE Class
  Class 3
  Class 4
  Class 5
  Class 6
  Class 7
  Class 8 Класс 9
  Класс 10
  Класс 11
  Класс 12
- Учебные решения
Решения NCERT
Решения NCERT для класса 11
Решения NCERT для класса 11 по физике
Решения NCERT для класса 11 Химия
Решения NCERT для биологии класса 11
Решение NCERT s Для класса 11 по математике
NCERT Solutions Class 11 Accountancy
NCERT Solutions Class 11 Business Studies
NCERT Solutions Class 11 Economics
NCERT Solutions Class 11 Statistics
NCERT Solutions Class 11 Commerce
NCERT Solutions for Class 12
Решения NCERT для физики класса 12
Решения NCERT для химии класса 12
Решения NCERT для биологии класса 12
Решения NCERT для математики класса 12
Решения NCERT, класс 12, бухгалтерия
Решения NCERT, класс 12, бизнес-исследования
NCERT Solutions Class 12 Economics
NCERT Solutions Class 12 Accountancy Part 1
NCERT Solutions Class 12 Accountancy Part 2
NCERT Solutions Class 12 Micro-Economics
NCERT Solutions Class 12 Commerce
NCERT Solutions Class 12 Macro-Economics
NCERT Solut Ионы Для класса 4
Решения NCERT для математики класса 4
Решения NCERT для класса 4 EVS
Решения NCERT для класса 5
Решения NCERT для математики класса 5
Решения NCERT для класса 5 EVS
Решения NCERT для класса 6
Решения NCERT для математики класса 6
Решения NCERT для науки класса 6
Решения NCERT для класса 6 по социальным наукам
Решения NCERT для класса 6 Английский язык
Решения NCERT для класса 7
Решения NCERT для математики класса 7
Решения NCERT для науки класса 7
Решения NCERT для социальных наук класса 7
Решения NCERT для класса 7 Английский язык
Решения NCERT для класса 8
Решения NCERT для математики класса 8
Решения NCERT для науки 8 класса
Решения NCERT для социальных наук 8 класса ce
Решения NCERT для класса 8 Английский
Решения NCERT для класса 9
Решения NCERT для класса 9 по социальным наукам
Решения NCERT для математики класса 9
Решения NCERT для математики класса 9 Глава 1
Решения NCERT для математики класса 9, глава 2
Решения NCERT
для математики класса 9, глава 3
Решения NCERT для математики класса 9, глава 4
Решения NCERT для математики класса 9, глава 5
Решения NCERT
для математики класса 9, глава 6
Решения NCERT для математики класса 9 Глава 7
Решения NCERT
для математики класса 9 Глава 8
Решения NCERT для математики класса 9 Глава 9
Решения NCERT для математики класса 9 Глава 10
Решения NCERT
для математики класса 9 Глава 11
Решения
NCERT для математики класса 9 Глава 12
Решения NCERT
для математики класса 9 Глава 13
NCER Решения T для математики класса 9 Глава 14
Решения NCERT для математики класса 9 Глава 15
Решения NCERT для науки класса 9
Решения NCERT для науки класса 9 Глава 1
Решения NCERT для науки класса 9 Глава 2
Решения NCERT для науки класса 9 Глава 3
Решения NCERT для науки класса 9 Глава 4
Решения NCERT для науки класса 9 Глава 5
Решения NCERT для науки класса 9 Глава 6
Решения NCERT для науки класса 9 Глава 7
Решения NCERT для науки класса 9 Глава 8
Решения NCERT для науки класса 9 Глава 9
Решения NCERT для науки класса 9 Глава 10
Решения NCERT для науки класса 9 Глава 12
Решения NCERT для науки класса 9 Глава 11
NCERT Solutions для Cla

Что такое Геометрия? Когда вы используете это в реальном мире?

Что такое геометрия? Когда вы используете это в реальном мире?

Геометрия — одна из классических дисциплин математики.Примерно перевод в переводе с греческого как «Измерение Земли», это связано со свойствами пространство и цифры. В первую очередь он разработан как практическое руководство для измерения длин, площадей и объемов, которые используются до сих пор. Евклид превратил изучение геометрии в аксиоматическую форму примерно в 3 веке До н.э., и эти аксиомы актуальны и по сей день. Важно Эволюция геометрии началась, когда Рене Декарт был смог создать концепцию аналитической геометрии.Из-за этого самолет цифры теперь можно представить аналитически, и это одна из движущих сил для развития математического анализа. Кроме того, рост перспектив дал подняться к проективной геометрии. В настоящее время современная геометрия тесно связана с физика, и является неотъемлемой частью новых физических концепций, таких как теория относительности и теории струн.

Самая основная форма геометрии — это так называемая евклидова геометрия. Здесь рассматриваются длины, площади и объемы. Окружности, радиусы и площади являются одним из понятий, касающихся длины и площади.Также объем Трехмерные объекты, такие как кубы, цилиндры, пирамиды и сферы, могут вычисляться с использованием геометрии. Раньше все касалось форм и размеров, но числа скоро перейдут в геометрию. Благодаря пифагорейцам, числа вводятся в геометрию в виде числовых значений длин и области. Числа используются далее, когда Декарт смог сформулировать понятие координат.

В реальной жизни геометрия имеет множество практических применений, начиная с самых простых. к самым передовым явлениям в жизни.Даже самая базовая концепция площади может иметь огромное значение для вашего повседневного бизнеса. Например, пробел это огромная проблема при планировании различных строительных проектов. Например, размер или площадь конкретного прибора или инструмента могут сильно повлиять на то, как он впишется в ваш дом или на рабочее место и может повлиять на то, как другие части вашего дома поместится вокруг него. Вот почему так важно учитывать областей, как вашего пространства, так и предмета, который вы собираетесь интегрировать там.Кроме того, геометрия играет важную роль в основных инженерных проектах. Например, используя понятие периметра, вы можете вычислить сумму материала (например, краски, материала для ограждений и т. д.), который необходимо использовать для ваш проект. А также дизайнерские профессии, такие как дизайн интерьера и архитектура. использует 3-х мерные фигуры. Доскональное знание геометрии поможет помочь им в определении правильного стиля (и, что более важно, оптимизировать его функция) конкретного дома, здания или транспортного средства.

Это некоторые из основных применений геометрии, но на этом все не заканчивается. Поскольку еще некоторые профессии используют геометрию для правильного выполнения своей работы. Например, компьютерное изображение, то, что сегодня используется для создания анимации, видеоигры, дизайн и тому подобное создаются с использованием геометрические понятия. Также при картографировании используется геометрия. Картирование — это очень важно элемент в таких профессиях, как геодезия, навигация и астрономия. Из от эскизов до расчета расстояний, они используют геометрию для выполнения своих работа.Кроме того, геометрические изображения приносят пользу в таких профессиях, как медицина. Такие технологии, как компьютерная томография и МРТ, используются как для диагностики, так и для хирургии. СПИД. Такие методы позволяют врачам выполнять свою работу лучше, безопаснее и проще.

Как видите, геометрия влияет на нас даже в самых элементарных деталях нашего жизни. Независимо от формы, он помогает нам понять конкретные явления. и это помогает нам повышать качество жизни.

Сайты для изучения геометрии

Энциклопедия центров треугольника
Евклида Доказательство теоремы Пифагора-
Основы геометрии
Геометрия Сфера
Интерактивная галерея Онлайн-геометрия
Геометрический Теория групп
Геометрия Формулы и факты
Геометрия в действии
Свалка геометрии
Математические кривые и поверхности

Площадь треугольника (координатная геометрия)
Площадь треугольника (координатная геометрия) — Math Open Reference
Зная координаты трех вершин треугольника ABC, площадь можно вычислить по формуле ниже.
Попробуй это Перетащите любую точку A, B, C. Площадь треугольника ABC непрерывно пересчитывается по приведенной выше формуле. Вы также можете перетащить исходную точку на (0,0).
Учитывая координаты трех вершин любого треугольника, площадь треугольника определяется как: где A _x и A _y — координаты x и y точки A и т. д.
Эта формула позволяет вычислить площадь треугольника, зная координаты всех трех вершины.Неважно, какие точки обозначены A, B или C, и он будет работать с любым треугольником, включая те, у которых некоторые или все координаты отрицательны.
Взглянув на приведенную выше формулу, вы увидите, что она заключена в две вертикальные полосы следующим образом: Две вертикальные полосы означают «абсолютное значение». Это означает, что он всегда положительный, даже если формула дала отрицательный результат. У полигонов никогда не может быть отрицательной области.
«Ручная работа» точки B
Если вы выполните этот расчет, но пропустите последний шаг, на котором вы берете абсолютное значение, результат может быть отрицательным.Если он отрицательный, это означает, что 2-я точка (B) находится слева от отрезка AC. Здесь мы имеем в виду «левый» в том смысле, что если бы вы стояли в точке A и смотрели на C, то B был бы слева от вас.
Если область равна нулю
Если площадь равна нулю, это означает, что три точки коллинеарен. Они лежат прямой линией и не образуют треугольника. Вы можете перетащить точки выше, чтобы создать это условие.
Вы также можете использовать Формулу Герона
Формула Герона позволяет вычислить площадь треугольника, если вам известны длины всех трех сторон.(См. Формулу Герона). В координатной геометрии мы можем найти расстояние между любыми двумя точками если мы знаем их координаты, и поэтому мы можем найти длины трех сторон треугольника, а затем подставить их в формулу Герона найти область.
Если одна сторона вертикальная или горизонтальная
В треугольнике выше сторона AC равна вертикальный (параллельно оси y). В этом случае легко использовать традиционный метод «половина основания, умноженная на высоту». См. Площадь треугольника — традиционный метод.
Здесь AC выбран в качестве базы и имеет длину 8, найденная вычитанием y-координат A и C. Аналогично, высота равна 11, найденная вычитанием x-координат B и A. Таким образом, площадь равна половине 8 умножить на 11 или 44.
Коробчатый метод
Вы также можете использовать метод коробки, который действительно работает для любого многоугольника. Подробнее об этом см. Площадь треугольника — прямоугольный метод (Координатная геометрия)
Что попробовать
На схеме вверху страницы перетащите точки A, B или C и обратите внимание, как при вычислении площади используются координаты.Попробуйте точки с отрицательными значениями x и y. Вы можете перетащить исходную точку, чтобы переместить оси.
Нажмите «скрыть детали». Перетащите треугольник к какой-нибудь новой случайной форме. Вычислите его площадь и нажмите «показать подробности», чтобы узнать, правильно ли вы поняли.
После вышесказанного оцените площадь, подсчитав квадраты сетки внутри треугольника. 2} $
НАПРАВЛЕНИЕ ТОЧЕК СОЕДИНЕНИЯ ЛИНИИ $ P_1 (x_1, y_1, z_1) $ И $ P_2 (x_2, y_2, z_2) $
$ l = \ cos \ alpha = \ frac {x_2-x_1} {d} $ , $ m = \ cos \ beta = \ frac {y_2-y_1} {d} $, $ n = \ cos \ gamma = \ frac {z_2-z_1} {d} $
где $ \ alpha, \ beta, \ gamma $ — это углы, которые линия $ P_1P_2 $ образует с положительными осями $ x, y, z $ соответственно, а $ d $ указано на рисунке выше.2}} $
УРАВНЕНИЯ ЛИНИИ, СОЕДИНЯЮЩЕЙ $ P_1 (x_1, y_1, z_1) $ И $ P_2 (x_2, y_2, z_2) $ В СТАНДАРТНОЙ ФОРМЕ
$ \ frac {x-x_1} {x_2-x_1} = \ frac {y -y_1} {y_2-y_1} = \ frac {z-z_1} {z_2-z_1} $ или $ \ frac {x-x_1} {l} = \ frac {y-y_1} {m} = \ frac {z -z_1} {n} $
Они также действительны, если $ l, m, n $ заменены на $ L, M, N $ соответственно.
УРАВНЕНИЯ ЛИНИИ, СОЕДИНЯЮЩЕЙ $ P_1 (x_1, y_1, z_1) $ И $ P_2 (x_2, y_2, z_2) $ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ
$ x = x_1 + lt, y = y_1 + mt, z = z_1 + nt $
Они также действительны, если $ l, m, n $ заменены на $ L, M, N $ соответственно.
УГОЛ $ \ phi $ МЕЖДУ ДВУМЯ ЛИНИЯМИ С НАПРАВЛЕНИЯМИ СОЗНАЧЕНИЯМИ $ l_1, m_1, n_1 $ И $ l_2, m_2, n_2 $
$ \ cos \ phi = l_1l_2 + m_1m_2 + n_1n_2 $
ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
$ Ax + By + Cz + D = 0 $ [$ A, B, C, D $ — константы]
УРАВНЕНИЕ ПЛОСКОСТИ ПРОХОДА ЧЕРЕЗ ТОЧКИ $ (x_1, y_1, z_1), (x_2, y_2, z_2), (x_3, y_3, z_3) $
$ \ begin {vmatrix} x-x_1 & y-y_1 & z-z_1 \\ x_2-x_1 & y_2-y_1 & z_2-z_1 \\ x_3-x_1 & y_3-y_1 & z_3-z_1 \ end {vmatrix} = 0 $
или
$ \ begin {vmatrix} y_2-y_1 & z_2-z_1 \\ y_3-y_1 & z_3-z_1 \ end {vmatrix} (x-x_1) $ $ + \ begin {vmatrix} z_2-z_1 & x_2-x_1 \\ z_3-z_1 & x_3-x_1 \ end {vmatrix} (y-y_1) $ $ + \ begin {vmatrix} x_2-x_1 & y_2-y_1 \\ x_3-x_1 & y_3-y_1 \ end {vmatrix} (z-z_1) = 0 $
УРАВНЕНИЕ ПЛОСКОСТИ В ФОРМЕ ПЕРЕСЕЧЕНИЯ
$ \ frac {x} {a} + \ frac {y} {b} + \ frac {z} {c} = 1 $
где $ a, b, c $ — точки пересечения по осям $ x, y, z $ соответственно.2}} $
где знак выбран так, чтобы расстояние было неотрицательным.
НОРМАЛЬНАЯ ФОРМА ДЛЯ УРАВНЕНИЯ ПЛОСКОСТИ
$ x \ cos \ alpha + y \ cos \ beta + z \ cos \ gamma = p $
где $ p = $ перпендикулярное расстояние от $ O $ до плоскости при $ P $ а $ \ alpha, \ beta, \ gamma $ — углы между $ OP $ и положительными осями $ x, y, z $.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ С ЧИСТЫМ ПЕРЕВОДОМ
$ \ left \ {\ begin {array} {lr} x = x ‘+ x_0 \\ y = y’ + y_0 \\ z = z ‘+ z_0 \ end {array} \верно.$ Или $ \ left \ {\ begin {array} {lr} x ‘= x-x_0 \\ y’ = y-y_0 \\ z ‘= z-z_0 \ end {array} \ right. $
где $ (x, y, z) $ — старые координаты [т.е. координаты относительно системы $ xyz $], $ (x ‘, y’, z ‘) $ — новые координаты [относительно системы $ x’y’z’ $] и $ (x_0, y_0, z_0) $ — координаты нового начала $ O ‘$ относительно старой системы координат $ xyz $.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ, СВЯЗАННОЕ С ЧИСТЫМ ВРАЩЕНИЕМ
$ \ left \ {\ begin {array} {lr} x = l_1x ‘+ l_2y’ + l_3z ‘\\ y = m_1x’ + m_2y ‘+ m_3z’ \\ z = n_1x ‘+ n_2y’ + n_3z ‘\ end {массив} \ право.$
или
$ \ left \ {\ begin {array} {lr} x ‘= l_1x + m_1y + n_1z \\ y’ = l_2x + m_2y + n_2z \\ z ‘= l_3x + m_3y + n_3z \ end {array} \ right. $
, где происхождение систем $ xyz $ и $ x’y’z ‘$ одинаково, а $ l_1, m_1, n_1; l_2, m_2, n_2; l_3, m_3, n_3 $ — направляющие косинусы осей $ x ‘, y’, z ‘$ относительно осей $ x, y, z $ соответственно.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ, ВКЛЮЧАЮЩЕЕ ПЕРЕВОД И ВРАЩЕНИЕ
$ \ left \ {\ begin {array} {lr} x = l_1x ‘+ l_2y’ + l_3z ‘+ x_0 \\ y = m_1x’ + m_2y ‘+ m_3z’ + y_0 \\ z = n_1x ‘+ n_2y’ + n_3z ‘+ z_0 \ end {array} \ right.$
или
$ \ left \ {\ begin {array} {lr} x ‘= l_1 (x-x_0) + m_1 (y-y_0) + n_1 (z-z_0) \\ y’ = l_2 (x-x_0) + m_2 (y-y_0) + n_2 (z-z_0) \\ z ‘= l_3 (x-x_0) + m_3 (y-y_0) + n_3 (z-z_0) \ end {array} \ right. $
, где $ O ‘$ системы $ x’y’z’ $ имеет координаты $ (x_0, y_0, z_0) $ относительно системы $ xyz $ и $ l_1, m_1, n_1; l_2, m_2, n_2; l_3, m_3, n_3 $ — направляющие косинусы осей $ x ‘, y’, z ‘$ относительно осей $ x, y, z $ соответственно.
ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ $ (r, \ theta, z) $
Точка $ P $ может располагаться по цилиндрическим координатам $ (r, \ theta, z) $, а также по прямоугольным координатам $ (x, y, z) $.
Преобразование между этими координатами:
$ \
Решение неравенств с помощью программы «Пошаговое решение математических задач»
Введите полиномиальное неравенство вместе с переменной, для которой необходимо решить, и нажмите кнопку «Решить».
В главе 2 мы установили правила решения уравнений с использованием чисел арифметики. Теперь, когда мы изучили операции с числами со знаком, мы будем использовать те же правила для решения уравнений, содержащих отрицательные числа.Мы также изучим методы решения и построения графиков неравенств с одним неизвестным.
РЕШЕНИЕ УРАВНЕНИЙ С ЗАПИСАННЫМИ ЧИСЛАМИ
ЗАДАЧИ
По завершении этого раздела вы сможете решать уравнения, содержащие числа со знаком.
Пример 1 Решите относительно x и проверьте: x + 5 = 3
Решение
Используя те же процедуры, что и в главе 2, мы вычитаем 5 из каждой части уравнения, получая
Пример 2 Решите относительно x и проверьте: — 3x = 12
Решение
Разделив каждую сторону на -3, получаем
Всегда проверяйте исходное уравнение.
Другой способ решения уравнения
3x — 4 = 7x + 8
— сначала вычесть 3x с обеих сторон, получив
-4 = 4x + 8,
, затем вычесть 8 с обеих сторон и получить
-12 = 4x .
Теперь разделите обе стороны на 4, получив
— 3 = x или x = — 3.
Сначала удалите круглые скобки. Затем выполните процедуру, описанную в главе 2.
ЛИТЕРАЛЬНЫЕ УРАВНЕНИЯ
ЗАДАЧИ
По завершении этого раздела вы сможете:
Определите буквальное уравнение.
Применяйте ранее изученные правила для решения буквальных уравнений.
Уравнение, состоящее из нескольких букв, иногда называют буквальным уравнением . Иногда бывает необходимо решить такое уравнение для одной из букв через другие. Пошаговая процедура, описанная и использованная в главе 2, остается действительной после удаления любых символов группировки.
Пример 1 Решите относительно c: 3 (x + c) — 4y = 2x — 5c
Решение
Сначала удалите скобки.
Здесь мы отмечаем, что, поскольку мы решаем для c, мы хотим получить c с одной стороны и все другие члены с другой стороны уравнения. Таким образом, получаем
Помните, что abx совпадает с 1abx.
Делим на коэффициент при x, который в данном случае равен ab.
Решите уравнение 2x + 2y — 9x + 9a, сначала вычтя 2.v из обеих частей. Сравните полученное решение с полученным в примере.
Иногда форму ответа можно изменить. В этом примере мы могли бы умножить числитель и знаменатель ответа на (- l) (это не меняет значения ответа) и получить
Преимущество этого последнего выражения перед первым в том, что в ответе не так много отрицательных знаков.
Умножение числителя и знаменателя дроби на одно и то же число — это использование фундаментального принципа дробей.
Наиболее часто используемые буквальные выражения — это формулы из геометрии, физики, бизнеса, электроники и т. Д.
Пример 4 — это формула площади трапеции. Решите для c.
Трапеция имеет две параллельные стороны и две непараллельные стороны. Параллельные стороны называются основаниями.
Удаление скобок не означает их просто стереть. Мы должны умножить каждый член в круглых скобках на коэффициент, стоящий перед скобками.
Менять форму ответа не обязательно, но вы должны уметь распознать правильный ответ, даже если форма не та.
Пример 5 — это формула, дающая проценты (I), полученные за период D дней, когда известны основная сумма (p) и годовая ставка (r). Найдите годовую ставку, когда известны сумма процентов, основная сумма и количество дней.
Решение
Задача требует решения для р.
Обратите внимание, что в этом примере r оставлено с правой стороны, и поэтому вычисление было проще. При желании мы можем переписать ответ по-другому.
ГРАФИЧЕСКИЕ НЕРАВЕНСТВА
ЗАДАЧИ
По завершении этого раздела вы сможете:
Используйте символ неравенства для обозначения относительного положения двух чисел на числовой прямой.
График неравенств на числовой прямой.
Мы уже обсуждали набор рациональных чисел как числа, которые могут быть выражены как отношение двух целых чисел.Существует также набор чисел, называемых иррациональными числами , , которые нельзя выразить как отношение целых чисел. В этот набор входят такие числа как и так далее. Набор, состоящий из рациональных и иррациональных чисел, называется действительных чисел.
Для любых двух действительных чисел a и b всегда можно заявить, что Часто нас интересует только то, равны ли два числа или нет, но бывают ситуации, когда мы также хотим представить относительный размер чисел, которые не равны. равный.
Символы представляют собой символы неравенства или отношения порядка и используются для отображения относительных размеров значений двух чисел. Обычно мы читаем символ как «больше чем». Например, a> b читается как «a больше, чем b». Обратите внимание: мы заявили, что обычно читаем
а

Какое положительное число можно добавить к 2, чтобы получить 5?

Проще говоря, это определение утверждает, что a меньше b, если мы должны что-то добавить к a, чтобы получить b.Конечно, «что-то» должно быть положительным.
Если вы думаете о числовой прямой, вы знаете, что добавление положительного числа эквивалентно перемещению вправо по числовой прямой. Это приводит к следующему альтернативному определению, которое может быть легче визуализировать.
Пример 1 3

Мы также можем написать 6> 3.
Пример 2 — 4

Мы также можем написать 0> — 4.
Пример 3 4> — 2, потому что 4 находится справа от -2 в числовой строке.

Пример 4 — 6

Математическое утверждение x
Вы понимаете, почему невозможно найти наибольшее число меньше трех?
На самом деле, назвать число x, которое является наибольшим числом меньше 3, невозможно. Однако это может быть указано в числовой строке.Для этого нам нужен символ, обозначающий значение такого оператора, как x
Символы (и) в числовой строке указывают на то, что конечная точка не включена в набор.
Пример 5 График x
Решение

Обратите внимание, что на графике есть стрелка, указывающая на то, что линия продолжается без конца влево.
На этом графике представлено каждое действительное число меньше 3.
Пример 6 График x> 4 на числовой прямой.
Решение

На этом графике представлено каждое действительное число больше 4.
Пример 7 График x> -5 на числовой прямой.
Решение

На этом графике представлены все действительные числа больше -5.
Пример 8 Постройте числовой график, показывающий, что x> — 1 и x
Решение

Выражение x> — 1 и x
На этом графике представлены все действительные числа от -1 до 5.
Пример 9 График — 3
Решение
Если мы хотим включить конечную точку в набор, мы используем другой символ:. Мы читаем эти символы как «равно или меньше» и «равно или больше».
Пример 10 x>; 4 указывает число 4 и все действительные числа справа от 4 в числовой строке.
Символы [и] в числовой строке указывают на то, что конечная точка включена в набор.
Вы обнаружите, что такое использование круглых и квадратных скобок согласуется с их использованием в будущих курсах математики.
На этом графике представлены число 1 и все действительные числа больше 1.
На этом графике представлено число 1 и все действительные числа, меньшие или равные — 3.
Пример 13 Напишите алгебраическое утверждение, представленное следующим графиком.
Пример 14 Напишите алгебраическое утверждение для следующего графа.
На этом графике представлены все действительные числа от -4 до 5 , включая -4 и 5.
Пример 15 Напишите алгебраическое выражение для следующего графика.
Этот график включает 4, но не -2.
Пример 16 График на числовой прямой.
Решение
В этом примере возникает небольшая проблема. Как мы можем указать на числовой строке? Если мы оценим суть дела, то другой человек может неправильно истолковать это утверждение. Не могли бы вы сказать, представляет ли эта точка или может быть? Поскольку цель графика — пояснение, всегда обозначает конечную точку.
Граф используется для передачи утверждения. Вы всегда должны называть нулевую точку, чтобы показать направление, а также конечную точку или точки, если быть точным.
УСТРАНЕНИЕ НЕРАВЕНСТВА
ЗАДАЧИ
По завершении этого раздела вы сможете решить неравенства с одним неизвестным.
Решение неравенств обычно включает те же основные правила, что и уравнения. Есть одно исключение, которое мы скоро обнаружим. Однако первое правило аналогично тому, что используется при решении уравнений.
Если к каждой стороне неравенства прибавить одинаковое количество, результаты будут неравными в том же порядке.
Пример 1 Если 5
Пример 2 Если 7
Мы можем использовать это правило для решения некоторых неравенств.

Основные формулы по геометрии — Математика — Теория, тесты, формулы и задачи

Изучать основные формулы по школьной геометрии онлайн:

Как успешно подготовиться к ЦТ по физике и математике?

Нашли ошибку?

Планиметрия (Геометрия на плоскости) — Математика — Теория, тесты, формулы и задачи

Оглавление:

Основные теоретические сведения

Треугольник

Трапеция

Параллелограмм

Квадрат

Ромб и прямоугольник

Произвольные фигуры

Многоугольники

Окружность

Планиметрия. Материалы для подготовки к ЕГЭ по Математике

Справочник по геометрии : «Формулы по геометрии»

Основные формулы по геометрии и их свойства.<img src='/800/600/http/anitos.ru/images/big_images/poleznye_formuly_geometriya_38071_medium.jpg' />

Найти радиус описанной окружности треугольника, формула

Найти радиус описанной окружности равностороннего треугольника по стороне

Формула расчета площади треугольника

Плоские геометрические фигуры: свойства и основные формулы

Четырёхугольник

Основные свойства:

Квадрат

Основные формулы:

Свойства:

Прямоугольник

Основные формулы:

Свойства:

Параллелограмм

Определения:

Основные формулы:

Свойства:

Ромб

Основные формулы:

Свойства:

Трапеция

Определения:

Основные формулы:

Свойства:

Треугольник

Определения:

Основные формулы:

Свойства:

Окружность

Определения:

Основные формулы:

Список формул координатной геометрии (с PDF) для классов 9, 10 и 11

Формулы геометрии для класса 8 Математика Список формул геометрии

Что такое Геометрия? Когда вы используете это в реальном мире?

Что такое геометрия? Когда вы используете это в реальном мире?

Сайты для изучения геометрии

Площадь треугольника (координатная геометрия)

«Ручная работа» точки B

Если область равна нулю

Вы также можете использовать Формулу Герона

Если одна сторона вертикальная или горизонтальная

Коробчатый метод

Что попробовать

Решение неравенств с помощью программы «Пошаговое решение математических задач»

РЕШЕНИЕ УРАВНЕНИЙ С ЗАПИСАННЫМИ ЧИСЛАМИ

ЗАДАЧИ

ЛИТЕРАЛЬНЫЕ УРАВНЕНИЯ

ЗАДАЧИ

ГРАФИЧЕСКИЕ НЕРАВЕНСТВА

ЗАДАЧИ

УСТРАНЕНИЕ НЕРАВЕНСТВА

ЗАДАЧИ

Добавить комментарий Отменить ответ

Основные формулы по геометрии и их свойства.