Многоугольники. Выпуклый многоугольник. Четырехугольник 8 класс онлайн-подготовка на Ростелеком Лицей
Многоугольники. Выпуклый многоугольник. Четырехугольник.
Треугольник – это частный случай многоугольника.
В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник – фигуру с пятью углами.
Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят к многоугольнику.
Иными словами, например, когда говорят о пятиугольнике А1А2А3А4А5, имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника.
Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).
Периметр многоугольника – сумма длин сторон многоугольника.
Отрезок, соединяющий любые две противоположные вершины, называется диагональю многоугольника.
Многоугольники делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на рисунке выше, является выпуклым, а на рисунке ниже – невыпуклым.
Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой.![]() Невыпуклыми являются все остальные многоугольники.
Невыпуклыми являются все остальные многоугольники.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны.
Существенное отличие четырехугольника от треугольника в том, что он может быть выпуклым или невыпуклым.
Очень важное различие, о котором знает каждый плотник, состоит в том, что треугольник – «жесткая» фигура, а четырехугольник (как и все остальные многоугольники) – «нежесткая».
У треугольника невозможно изменить его форму, не изменив длин сторон. При этом у любого четырехугольника можно изменить его форму, не меняя длины сторон. На практике это будет означать, что треугольник, сколоченный из трех дощечек, будет жестким, не будет сминаться даже при сильных воздействиях, а четырехугольник при достаточной нагрузке со стороны изменит свою форму.
Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольникаитеорема о сумме внешних углов выпуклого многоугольника.
Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).
Сумма углов n-угольника равна 180°·(n-2).
Математическая запись: ∠A1+∠A2+…+∠An=180°(n-2), где n – количество его углов (сторон).
Вспомним, что любой четырехугольник состоит из двух треугольников (достаточно провести диагональ). Но сумма углов каждого из них одинакова и равна 1800, значит, сумма углов четырехугольника 360 0.
Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).
∠1’+∠2’+…+∠n’=360°, где n – количество его углов (сторон), а ∠1′,…,∠n’ – внешние углы, по одному от каждой вершины.
Многоугольники — урок. Геометрия, 8 класс.
Ломаной называется фигура, которая состоит из точек и соединяющих их отрезков.
Точки называются вершинами ломаной, а отрезки — звеньями ломаной.
Виды ломаных
Ломаная называется замкнутой, если у неё концы совпадают.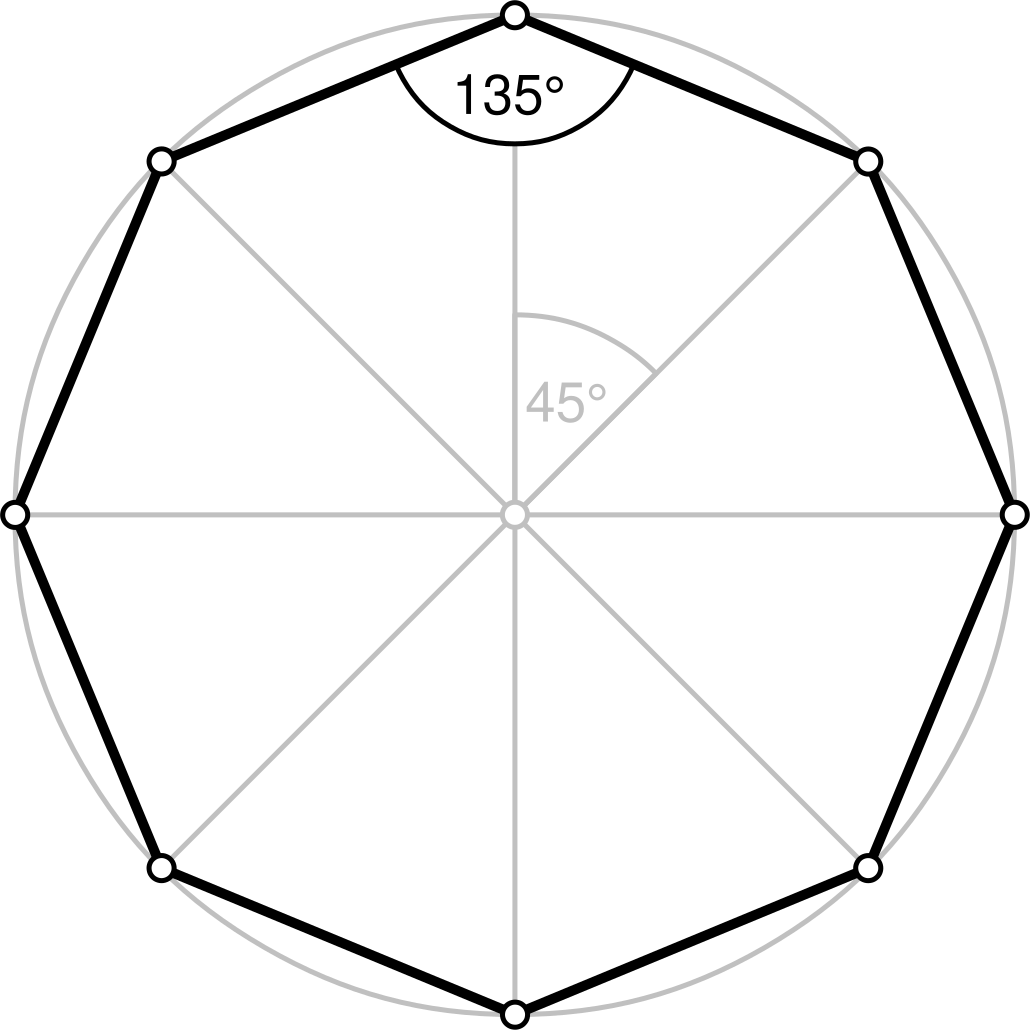
Если концы ломаной не совпадают, то она называется незамкнутой.
Ломаная называется простой, если она не имеет самопересечений. Обе ломаные выше являются простыми.
На следующем рисунке — ломаная с самопересечением.
Многоугольник
Многоугольник — это простая замкнутая ломаная линия и конечная часть
плоскости, которую она ограничивает.
Вершины ломаной линии называются вершинами многоугольника, а её звенья — сторонами многоугольника.
Отрезок, соединяющий две вершины, не лежащие на одной стороне, называется диагональю многоугольника.
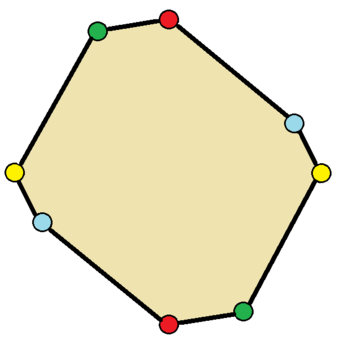
\(A\), \(B\), \(C\), \(D\), \(E\) — вершины;
\(AB\), \(BC\), \(CD\), \(DE\), \(AE\) — стороны;
\(AC\), \(AD\), \(BE\), \(BD\), \(CE\) — диагонали.
Многоугольник, у которого все углы меньше 180°, называется выпуклым многоугольником.
Пятиугольник \(ABCDE\) является выпуклым многоугольником.
Сумма углов выпуклого \(n\)-угольника
В общем случае многоугольник можно назвать \(n\)-угольником, это означает, что у данного многоугольника \(n\) сторон и \(n\) вершин.
Сумма углов выпуклого \(n\)-угольника равна 180°⋅n−2.
Любой выпуклый многоугольник можно разделить на треугольники. Количество треугольников на \(2\) меньше, чем количество сторон в многоугольнике.
Сумма внутренних углов любого треугольника равна 180°.
Поэтому сумма углов выпуклого \(n\)-угольника равна 180°⋅n−2.
Пример:
вычисли сумму внутренних углов выпуклого одиннадцатиугольника.
Можно нарисовать рисунок, но это не обязательно для решения задачи.
Используем формулу:
180°⋅n−2=180°⋅11−2=180°⋅9=1620°.
Многоугольник и его элементы. Выпуклые и невыпуклые многоугольники. Сумма углов выпуклого многоугольника
Конспект урока по геометрии
в 8 классе
«Многоугольник и его элементы. Выпуклые и невыпуклые многоугольники. Сумма углов выпуклого многоугольника»
Цели урока:
- Образовательные: изучение понятия многоугольник, его элементы; выпуклые и невыпуклые многоугольники; сумма углов выпуклого многоугольника.

- Развивающие: активизация познавательной деятельности учащихся через решение практических задач, умение выбирать правильное решение, лаконично излагать свои мысли, анализировать и делать выводы.
- Воспитательные: организация совместной деятельности, воспитание у учащихся интереса к предмету, доброжелательности, умения выслушивать ответы товарищей.
Тип урока: урок изучения нового материала
Оборудование:
Ход урок:
- Организационный момент
— Здравствуйте, дети! Проверьте, все ли, что нужно к уроку лежит у вас на партах? (тетрадь, ручка, дневник, линейка, карандаш)
— Садитесь!
2. Мотивация урока.
— Дорогие ребята!Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы те, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что геометрия – интересный и нужный предмет.
Французский писатель XIX столетия Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.
— Давайте последуем совету писателя на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.
3. Актуализация опорных знаний.
Какие геометрические фигуры нами уже изучены? (треугольники, четырехугольники, круг)
Каковы их элементы? (вершины, стороны, углы)
Фронтальный опрос:
- Какая фигура называется треугольником?
- Какая фигура называется четырехугольником? (Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков)
- Какие вершины четырехугольника называются соседними, какие противолежащими? (Вершины четырех угольника называются соседними вершинами, если они являются концами одной из его сторон.
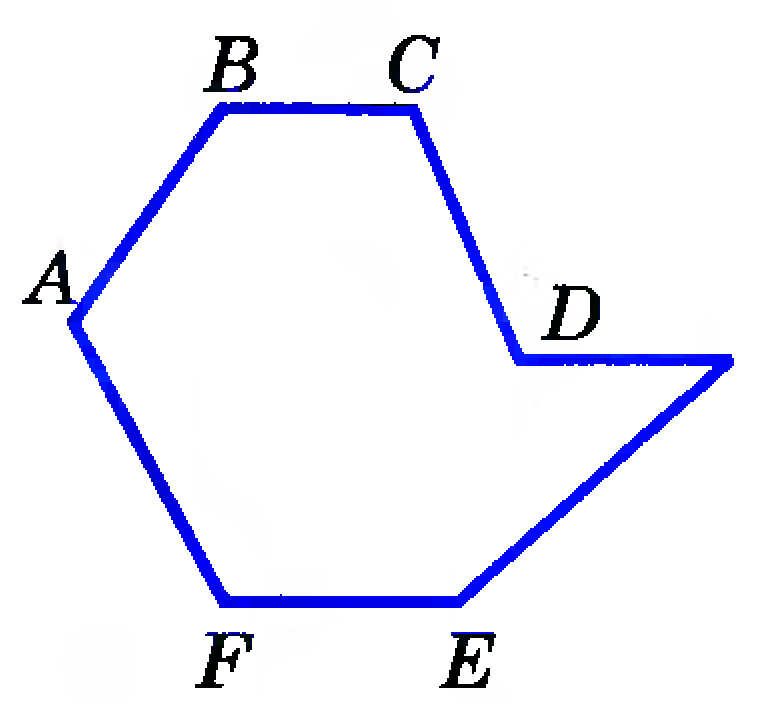 Вершины, не являющиеся соседними, называются противолежащими вершинами.)
Вершины, не являющиеся соседними, называются противолежащими вершинами.) - А какие вершины называются противоположными у треугольника?
- Что такое диагонали четырехугольника? (Диагональ — отрезок, соединяющий противоположные вершины)
- Какие стороны четырехугольника называются соседними? Какие стороны называются противолежащими? (Соседние стороны — стороны четырехугольника, выходящих из одной вершины. Противоположные стороны — стороны четырехугольника, которые не имеют общего конца.)
- А какие вершины называются противоположными у треугольника?
- Что такое периметр треугольника?
- А периметр четырехугольника? (сумма всех сторон четырехугольника.)
- Как проверить, можно ли из четырех данных отрезков построить четырехугольник?
- Чему равна сумма внутренних углов треугольника?
- А чему равна сумма внутренних углов четырехугольника? (Сумма углов любого четырехугольника равна 360)
- Могут ли все углы четырехугольника быть тупыми? острыми? прямыми? А в треугольника?
— Молодцы!
4. Изучение нового материала.
Изучение нового материала.
— Среди множества различных геометрических фигур на плоскости выделяется большое семейство МНОГОУГОЛЬНИКОВ.
Названия геометрических фигур имеют вполне определенный смысл. Присмотритесь внимательно к слову “многоугольник”, и скажите из каких частей оно состоит?
— Слово “многоугольник” указывает на то, что у всех фигур этого семейства “много углов”.
Подставьте в слово “многоугольник” вместо части “много” конкретное число, например 5. Что получили?
— Правильно! Вы получите ПЯТИУГОЛЬНИК. Или 6. Тогда – ШЕСТИУГОЛЬНИК. Заметьте, сколько углов, столько и сторон, поэтому эти фигуры вполне можно было бы назвать и многосторонниками.
— На рисунке геометрические фигуры. Используя рисунок, назовите эти фигуры.
(восьмиугольник, шестиугольник, пятиугольник, четырехугольник, треугольник)
— Каким наименьшим числом можно заменить “много” в многоугольнике? (Ответ: 3)
— Давайте попробуем определить, что такое ломаная? (Ло́маная— геометрическая фигура, состоящая из отрезков, последовательно соединенных своими концами. )
)
— Ребята, а если первая и последняя точки ломаной совпадают, то как называется такая ломаная (называется замкнутой)?
— Имея всю необходимую информацию, давайте попробуем сами сформулировать, что же такое многоугольник?
— Правильно! Фигура, ограниченная простой замкнутой ломаной, называется многоугольником.
- Вершины ломаной называются вершинами многоугольника,
- стороны ломаной — сторонами многоугольника,
- а углы, образованные соседними сторонами, — углами многоугольника.
- Точки многоугольника, не принадлежащие его сторонам, называются внутренними.
- Периметром многоугольника называется сумма длин всех его сторон.
- Многоугольник, у которого n углов называется n — угольником.
- Многоугольник называется выпуклым, если вместе с любыми двумя своими точками он содержит и соединяющий их отрезок.
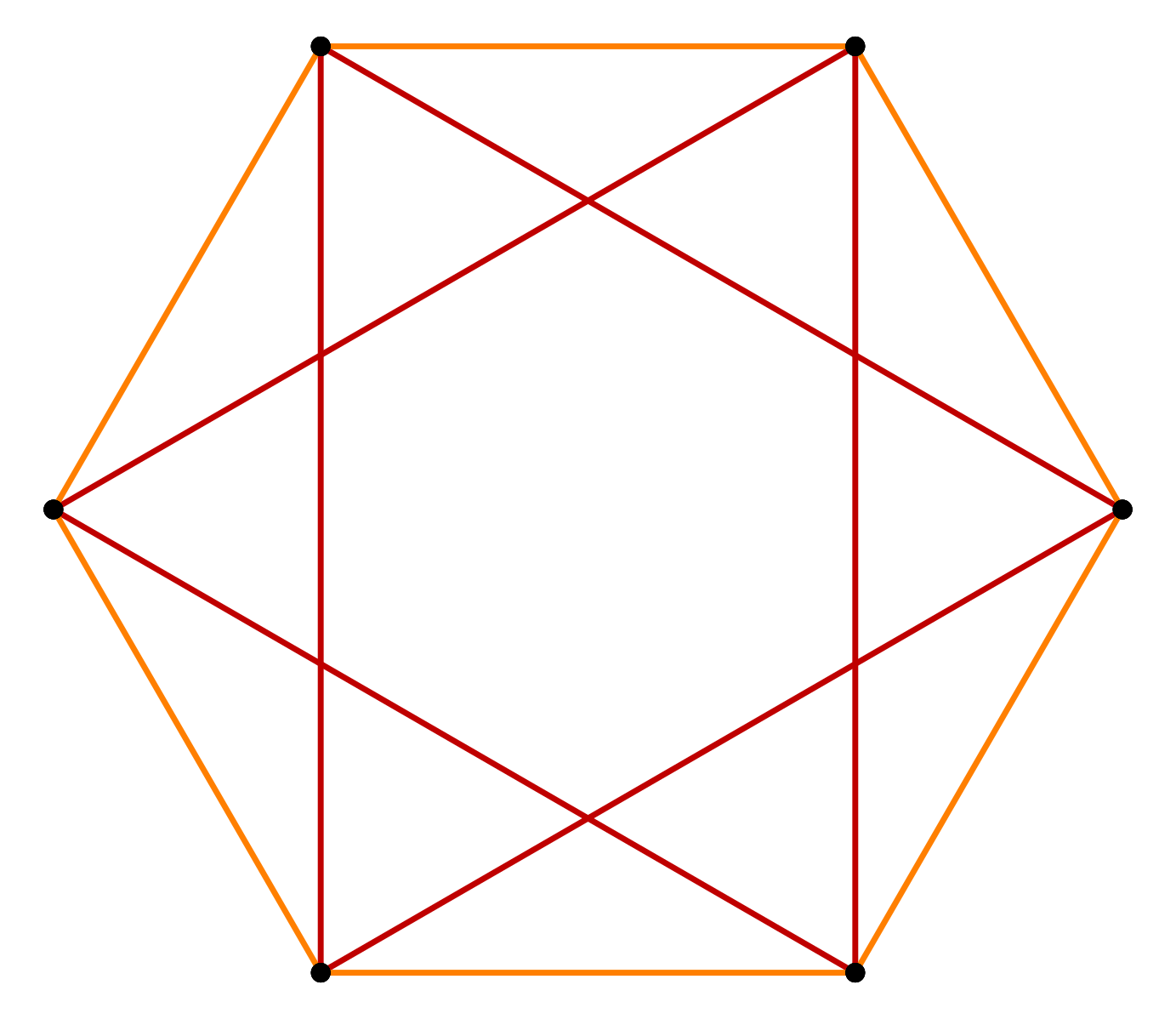
Любой треугольник выпуклый. Среди многоугольников, с числом углов большим трех, могут быть выпуклые и невыпуклые.
— В чем отличие данных многоугольников?
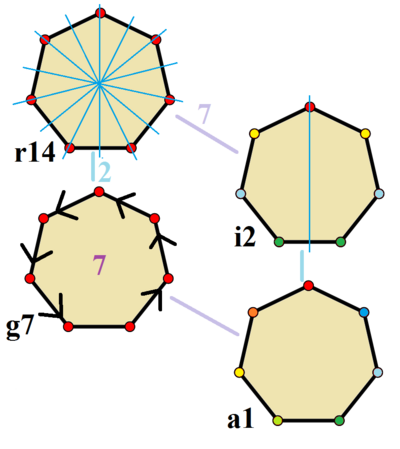
Диагональю многоугольника называется отрезок, соединяющий его несоседние вершины. Подсчет диагоналей
- Сколько диагоналей выходит с одной вершины четырехугольника, пятиугольника, шестиугольника?
- Давайте сравним их с количеством углов. Что мы видим?
- Какую формулу вы бы записали?
- Правильно, n-3.
- Давайте проверим, что это проходит и для треугольника. 3-3=0.
- А сколько вершин у n-угольника?
- Тогда, может нужно умножить количество углов n на количество диагоналей, которые выходят с одной вершины n-3?
- Хорошо! Но при этом мы посчитали каждую диагональ дважды.
 Как же исправить эту формулу?
Как же исправить эту формулу? - По этому, произведение n*(n-3) делят на два.
Диагоналей нет у треугольника на плоскости и у тетраэдра в пространстве, поскольку все вершины этих фигур попарно связаны сторонами (ребрами).
Количество диагоналей N у многоугольника легко вычислить по формуле:
N = n·(n – 3)/2, — запишем формулу в тетради, и выдилим ее.
где n — число вершин многоугольника. По этой формуле нетрудно найти, что
- у треугольника — 0 диагоналей
- у прямоугольника — 2 диагонали
- у пятиугольника — 5 диагоналей
- у шестиугольника — 9 диагоналей
- у восьмиугольника — 20 диагоналей
- у 12-угольника — 54 диагонали
- у 24-угольника — 252 диагонали
Исследовательская работа по группам
Каждая группа работает по учебно-исследовательской карте.
1.Задача.
Чему равна сумма углов выпуклого пятиугольника?
2. Проблема.
Проблема.
Как зависит сумма углов выпуклого n-угольника от числа углов
многоугольника и от числа треугольников, на которые он разбивается
диагоналями, проведенными из одной вершины?
3.Пробы.
1 проба-1800 2 проба-3600 3 проба-5400 4 проба-7200
n=3 n=4 n=5 n=6
— Что мы видим? (Количество треугольников (n-2)).
— Давайте заполним таблицу.
4.Таблица результатов.
Пробы | 1 | 2 | 3 | 4 |
Число углов | 3 | 4 | 5 | 6 |
Число треугольников | 1 | 2 | 3 | 4 |
Сумма углов | 1800 | 3600 | 5400 | 7200 |
— Так как, сумма углов одного треугольника – 180, то сумма углов выпуклого n-угольника равна 180° (n-2 )
Вывод: Формула для суммы внутренних углов n-угольника. 180° (n-2 ).
180° (n-2 ).
— Сумма внешних углов выпуклого многоугольника не зависит от числа сторон п- угольника и равна 360.
5. Закрепление нового материала.
Задача 253
— Сколько диагоналей можно провести из одной вершины выпуклого семиугольника? Найдите общее количество диагоналей выпуклого семиугольника. (можно провести 4 диагонали из одной вершины выпуклого семиугольника. Общее количество диагоналей выпуклого семиугольника – N=14: )
Задача 254
6. Итоги урока. Рефлексия.
- Что больше всего запомнилось на уроке?
- Что удивило?
- Что понравились больше всего?
- Каким ты хочешь увидеть следующий урок?
- Таким образом, мы самостоятельно вывели формулу для количества диагоналей многоугольника.
Домашнее задание: № 253, 254, 257 Вариант 2 с ваших сборников
Конспект урока по геометрии «Многоугольник. Выпуклый многоугольник»
МНОГОУГОЛЬНИК. ВЫПУКЛЫЙ МНОГОУГОЛЬНИК.
Цели: 1.ввести понятия многоугольника и выпуклого многоугольника и рассмотреть четырехугольник как частный вид многоугольника; научить объяснять, какая фигура называется многоугольником, и называть его элементы;
2. Коррекция слухового восприятия.
3. Воспитывание аккуратности при оформлении тетрадей.
Ход урока
I. Оргмомент.
Фонетическая разминка:
—геометрия
-многоугольник
-сторона
-вершина
-угол
-смежные стороны
II. Объяснение нового материала.
Объяснение нового материала.
1. Напомнить учащимся определение треугольника. Вспомнить элементы треугольника (сторона, вершина, угол).
2.
Что общего у этих геометрических фигур?
3. Вводится понятие многоугольника.
4. Рассматриваются элементы многоугольника (вершины, стороны, диагонали, углы).
5. Отмечается, что каждый многоугольник разделяет плоскость на две области: внутреннюю и внешнюю.
6. Дается понятие выпуклого многоугольника.
II. Закрепление изученного материала.
1. Ответить на вопросы (устно):
а)
б)
в)
г)
д)
е)
Какие фигуры, изображенные на доске, являются многоугольниками?
Учитель после обсуждения убирает те рисунки, на которых изображены фигуры, не являющиеся многоугольниками.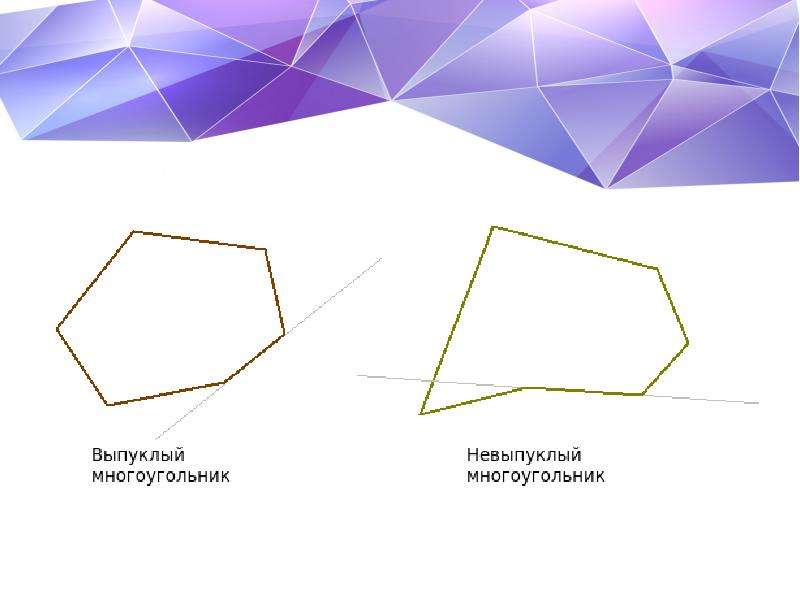
Какие многоугольники являются выпуклыми?
2. Задание для каждого ряда:
Начертите выпуклый семиугольник, восьмиугольник, девятиугольник и проведите все диагонали из какой-нибудь его вершины. Сколько получилось треугольников?
III. Решение задач №364(а,б), №365(а,б)
IV Физминутка. Упражнения для глаз.
1. Для разминки: плотно закройте глаза и с силой зажмурьтесь на несколько секунд. Откройте глаза и не моргайте секунд 5–10.
2. Горизонтальные движения глаз слева направо и наоборот.
3. Вертикальные движения глазами вверх-вниз.
4. Круговые движения глазами: по часовой стрелке и в противоположном направлении.
5. Движение глаз по диагонали. Сначала нужно скосить глаза в левый нижний угол, затем по прямой перевести взгляд вверх в правый угол. Аналогично в противоположном направлении.
6. Сведение глаз к носу. Для этого медленно поднесите палец к переносице, следя за его кончиком. Глаза легко «соединятся».
V. Итоги урока. Что нового узнали?
Назовите элементы многоугольника.
Д/з № 364(в), 365(б).
Материалы для проверки усвоения темы «правильные многоугольники» 2 1 проверочные тесты для учеников
2 Материалы для проверки усвоения темы «Правильные многоугольники»2.1 Проверочные тесты для учениковПервый вариант.
Закончить фразу.
Многоугольник называется правильным, если …
Какие из перечисленных многоугольников являются правильными? Выбрать и подчеркнуть.
равнобедренный треугольник;
квадрат;
ромб;
прямоугольник
Поставить знак «+» рядом с верным утверждением.
Окружность, вписанная в выпуклый многоугольник, и окружность, описанная около него, имеют один и тот же центр.
Вписанная и описанная окружности, правильного многоугольника имеют один и тот же центр.
4. Какая из предложенных формул выражает радиус вписанной в многоугольник окружности:
5. Точка О является центром правильного треугольника ABC. Чему равна его сторона, если радиус описанной окружности равен 6 см?
см;
см;
см;
см.
6. В окружность вписан правильный шестиугольник с периметром 18 см. Найти радиус окружности.
см;
3 см;
6 см;
см.
Второй вариант.
Какие из предложенных многоугольников являются правильными? Выбрать и подчеркнуть:
равносторонний треугольник;
параллелограмм;
равнобокая трапеция;
прямоугольник.
Закончить фразу.
Многоугольник называется описанным около окружности, если …
Поставить знак «+» рядом с верным утверждением.
Выпуклый многоугольник является вписанным в окружность и описанным около окружности.
Правильный выпуклый многоугольник является вписанным в окружность и описанным около окружности.
Какая из предложенных формул выражает радиус описанной окружности:
Треугольник DBC – правильный. Чему равна сторона треугольника, если радиус вписанной окружности равен 5 см?
см;
см;
10 см;
см.
Окружность вписана в правильный шестиугольник с периметром 183 см. Найти радиус окружности.
4,5 см;
9 см;
6 см;
см.
Вариант 1.
Закончить предложения: а) «Правильным многоугольником называется …»
б) «Угол правильного шестиугольника равен…»
2. Перечислите все известные вам формулы для сторон и площади правильного n-угольника.
3. Перечислите главные методические проблемы при изложении темы «Правильные многоугольники»
4. Отметить важные отличия при изложении материала «Выражение элементов треугольника через радиус вписанной или описанной окружностей» разными авторами.
Вариант 2.
Закончить предложения: а) «Выпуклый многоугольник называется правильным, если… »
б) «Угол правильного восьмиугольника равен…»
2. Перечислите все известные вам формулы для периметра и радиуса вписанной окружности правильного n-угольника.
3. Перечислите главные методические проблемы при изложении темы «Правильные многоугольники»
4. Отметить важные
отличия при изложении материала
«Построение правильных многоугольников»
разными авторами.
Отметить важные
отличия при изложении материала
«Построение правильных многоугольников»
разными авторами.
Класс: 10
Учебное пособие: Н.В.Гвоздович, Т.П.Кубеко «Геометрия, 10»
Цели:
1. Знать определения правильных многоугольников, уметь строить правильный четырёхугольник, шестиугольник, 2n-угольник.
2. Воспитывать аккуратность, эстетичность, умение оценивать результаты своего труда и труда одноклассников.
Тип урока – комбинированный.
Оборудование: плакат-правильные многоугольники; чертёжные принадлежности;
Ход урока.
1. Целеполагание.
На доске изображены рисунки,
получившиеся в результате комбинаций
правильных многоугольников. Какой, на
ваш взгляд, самый удачный рисунок? Где
можно использовать на практике подобные
комбинации многогранников? (Мoжно
оформить таким орнаментом потолочную
плитку или паркетный пол).
Возможно ли каждому из вас построить свой орнамент? Что для этого нужно уметь делать? (Уметь строить правильные многоугольники). Построение правильных многоугольников с целью создания своего орнамента – цель нашей работы сегодня.
2. Актуализация знаний.
Что называется правильным треугольником, четырёхугольником, n-угольником? (многоугольник с равными сторонами и углами – правильный).
Чему равна сумма углов в правильном треугольнике, четырёхугольнике, шестиугольнике, n-угольнике? (180º; 360º; 720º; 180º (n-2))
Чему равен каждый угол в правильном n-угольнике?
Как построить биссектрису угла, серединный перпендикуляр к отрезку с помощью циркуля и линейки? (Повторить построение, работая у доски, учащиеся – в тетрадях)
3. Изложение нового.
1) Можно около правильного
треугольника описать окружность. Сделаем
это. Центр окружности лежит в точке
пересечения серединных перпендикуляров
к сторонам треугольника.
Центр окружности лежит в точке
пересечения серединных перпендикуляров
к сторонам треугольника.
Соединим точки пересечения серединных перпендикуляров с окружностью?
Какой получился многоугольник? (правильный шестиугольник) Докажем это.
C
B D
А E
∆ АВС = ∆ ЕDС (по стороне и двум прилежащим к ней углам: АС = ЕС; В треугольниках АВС и ЕDС перпендикуляры – серединные, значит они – равнобедренные и А = С, С = Е, а т. к . АВС= СDЕ (на них опираются равные углы А и С в ∆ АСЕ), то равны и половины этих дуг, а значит, ВС = СD, и А = Е.
2) Измерим сторону получившегося шестиугольника и радиус окружности. Они приблизительно равны. Позднее мы докажем, что R=а .
3) Построим окружность, проведём
диаметр АС, проведём серединный
перпендикуляр к нему. Соединим точки
пересечения перпендикуляра и окружности.
Получившаяся фигура ABCD — квадрат. Докажем
это. (Углы, опирающиеся на диаметр —
прямые, стороны равны в силу равенства,
например, 4-х прямоугольных треугольников
по двум катетам).
Соединим точки
пересечения перпендикуляра и окружности.
Получившаяся фигура ABCD — квадрат. Докажем
это. (Углы, опирающиеся на диаметр —
прямые, стороны равны в силу равенства,
например, 4-х прямоугольных треугольников
по двум катетам).
4)Как построить правильный восьмиугольник? (Провести серединные перпендикуляры к сторонам квадрата и соединить их точки пересечения и окружности)
4.Закрепление.
Что необходимо для создания орнамента?
— Построить правильные многоугольники, зная, что R=а ;
— Восьмиугольник строится с помощью серединных перпендикуляров к сторонам квадрата, вписанного в окружность.
Построим вначале шаблоны правильных многоугольников и начнём построение орнамента.
Пример орнамента:
5.Задание на дом.
Закончить построение орнамента.
№384(а,б). (Н.В.Гвоздович)
(Н.В.Гвоздович)
Анализ урока.
Данный урок является первым уроком по теме «Правильные многоугольники», на нём вводятся термины, даётся их определения (многоугольник, правильный многоугольник).
Цели урока:
1. Знать определения правильных многоугольников, уметь строить правильный четырёхугольник, шестиугольник, 2n-угольник.
2. Воспитывать аккуратность, эстетичность, умение оценивать результаты своего труда и труда одноклассников.
Структура урока – традиционна. На этапе целеполагания мотивационной основой деятельности учащихся служит её практическая направленность (научится строить правильные многоугольники, чтобы создать красивый, оригинальный орнамент).
В устной работе первой части
урока запланировано решение задач,
направленных на активизацию мысли
ребят. Дети поставлены в условия, в
которых вынуждены анализировать,
сравнивать, делать выводы. Эта часть
урока направлена на повторение знаний,
необходимых для изучения нового
материала.
Эта часть
урока направлена на повторение знаний,
необходимых для изучения нового
материала.
На этапе изложения нового материала мотивационной основой работы учащихся служит доступный уровень сложности, а также наличие внутрипредметных связей (Построение серединного перпендикуляра к отрезку, построение треугольника) и межпредметных связей (с черчением).
На всех этапах урока учитываются психологические особенности познавательной деятельности учащихся. В связи с этим применяется наглядный материал (плакат с изображением правильных многоугольников, заготовленные орнаменты из правильных многоугольников, всё, что выполняют учащиеся в тетрадях, демонстрируется на доске с параллельными комментариями хода действий). Учащиеся применяют свой жизненный опыт, отвечая на вопрос, где используются комбинации правильных многоугольников.
Результатом работы на данном
уроке явились сделанные картонные
модели правильных многоугольников,
необходимые для выполнения домашней
работы – сделать макет, например, паркета
или потолочной плитки.
Класс: 10
Учебное пособие: В.В. Шлыков
1. Проверка д/з.
2. Математический диктант (на листочках; 10 – 15 минут).
1) Могут ли стороны выпуклого шестиугольника иметь длины:
1, 2, 3, 4, 5 и 14 см [Да] | 1, 2, 3, 4, 5 и 16 см [Нет]
2) Найдите сумму углов выпуклого
32 – угольника [5400] | 17 – угольника [2700]
3) Найдите количество сторон выпуклого многоугольника, сумма углов которого равна: 9000 [52] | 18000 [102]
4) Укажите общий вид выпуклых многоугольников, у которых все внешние углы:
тупые [остроугольные треугольники] | прямые [прямоугольники]
5) Укажите общий вид выпуклых многоугольников, у которых сумма внутренних углов
равна сумме внешних [четырехугольники]
| меньше суммы внешних [треугольники],
взятых по одному при каждой вершине.
6) Существует ли выпуклый многоугольник, у которого:
три острых и один прямой угол? [Нет]| три прямых и один острый угол? [Нет]
7) Существует ли выпуклый n – угольник, у которого:65 диагоналей? [Да, n = 13] | 27 диагоналей? [Да, n = 9]
3. Новый материал и устные упражнения.
Рис. 1
Определение. Многоугольник называется правильным, если у него равны все стороны и равны все углы.1) Примеры? [квадрат; равносторонний треугольник]
2) Существуют ли неправильные многоугольники с равными а) сторонами; б) углами? [Да; а) ромб; б) прямоугольник]
3) Каким свойством обладают внешние углы правильных многоугольников? [равны]
4) Дан правильный 2n
– угольник (см. рис. 1). Докажите, что если
его вершины соединить через одну, то
получится правильный n
– угольник [равенство треугольников].
5) Выведите формулы для вычисления величин внутреннего и внешнего углов правильного n – угольника [n = ; n = ]
6) Является ли какая — либо из этих последовательностей прогрессией? [Нет; вид формул]
7) Найдите количество сторон правильного n – угольника, если его внешний угол равен: а) 15; б) 75 [а) 24; б) не существует]
8) Найдите количество вершин правильного n – угольника, если его внутренний угол равен а) 172; б) 100 [а) 45; б) не существует]
9) Найдите количество углов правильного n – угольника, если сумма его трех внешних и пяти внутренний углов равна 756 [5n + 3n = 756 n = 5]
Домашнее задание: Выучите формулы
n и n;
докажите, что (n)
– возрастающая последовательность, а
(n)
– убывающая. Медиана АА1,
высота ВВ1 и биссектриса СС1 треугольника АВС пересекаются в одной
точке. Докажите, что длины a,
b и
c
соответствующих сторон треугольника
удовлетворяют равенству: (а2 + b2 – c2)(a
+ b)
= 2ab2.
Докажите, что длины a,
b и
c
соответствующих сторон треугольника
удовлетворяют равенству: (а2 + b2 – c2)(a
+ b)
= 2ab2.
К курсовой работе прилагается распечатанная статья из журнала «Квант» №12, которая будет интересна для проведения факультативных занятий по теме «Правильные многоугольники».
В этой статье разбираются три тесно связанные между собой вопроса.
1) Можно ли расположить правильный n-угольник на листе линованной бумаги — в прямую или косую клетку – так, чтобы его вершины попали в точки пересечения линий?
2) При каких углах α, соизмеримых с полным – то есть содержащих целое или рациональное число градусов, значения синуса, косинуса или тангенса α рациональны?
3) В какие положения может попасть центр правильного n-угольника, который разрешается перекатывать по плоскости?
2. 6 Динамические модели
6 Динамические моделиМодель «Правильный многоугольник»
Модель предназначена для изучения симметрии правильных многоугольников.
При загрузке модели на экране появляется правильный многоугольник (8-угольник) с центром в точке O, разбитый на равнобедренные треугольники с острым углом φn, количество которых равно числу вершин многоугольника. С помощью кнопок в нижней части экрана можно выбирать количество вершин многоугольника. Один из треугольников выделен серым цветом, вращая его курсором мыши вокруг точки O, можно наглядно наблюдать, что исходный многоугольник состоит из равнобедренных треугольников, получающихся из исходного поворотом вокруг центра (точки O) на определённый угол, равный 360o/n.
Кнопка «Сброс» в правом нижнем углу окна возвращает модель в исходное состояние.
Модель «Теорема о центре правильного многоугольника»
Модель предназначена для
иллюстрации доказательства теоремы о
центре правильного многоугольника.
Теорема. Если все стороны многоугольника равны друг другу и все его углы равны друг другу, то вокруг этого многоугольника можно описать окружность и в него можно вписать окружность. Центры этих окружностей совпадают.
Исходно в окне модели отображается
правильный пятиугольник ABCDE. Кнопки в
нижней части экрана позволяют менять
n- число вершин многоугольника. Точки
A, B — активны. «Клик» курсором мыши
на этих точках строит биссектрисы углов
A и B, которые пересекутся в некоторой
точке O. Точка O также активна. «Клик»
по этой точке соединяет ее отрезками
со всеми вершинами многоугольника
ABCDE. Покажем, что эти отрезки разобьют
многоугольник на равные друг другу
равнобедренные треугольники. Треугольник
OAB равнобедренный, так как его углы,
прилежащие к стороне AB равны (как половины
равных углов A и B многоугольника ABCDE).
Треугольник OBC равен треугольнику OAB
(BC=BA, сторона OB — общая, и угол OBA равняется
углу OBC, т.к. BO — биссектриса угла B). Потому
треугольник OBC тоже равнобедренный и
OB=OC, а угол OBC равен углу OCB. Значит угол
OCB равен половине угла C и луч OC — биссектриса
угла C. Повторяя эти рассуждения,
убеждаемся, что треугольники OCD, ODE и OEA
— равнобедренные треугольники, равные
треугольнику OAB. Поэтому окружность с
центром в точке O и радиусом OA описана
вокруг многоугольника ABCDE, а окружность
с центром O и радиусом OH (OH — высота
треугольника OAB) вписана в него.
Потому
треугольник OBC тоже равнобедренный и
OB=OC, а угол OBC равен углу OCB. Значит угол
OCB равен половине угла C и луч OC — биссектриса
угла C. Повторяя эти рассуждения,
убеждаемся, что треугольники OCD, ODE и OEA
— равнобедренные треугольники, равные
треугольнику OAB. Поэтому окружность с
центром в точке O и радиусом OA описана
вокруг многоугольника ABCDE, а окружность
с центром O и радиусом OH (OH — высота
треугольника OAB) вписана в него.
После «клика» по точке O треугольник OAB выделяется цветом, становится активным и способным вращаться вокруг своей вершины O. «Цепляя» этот треугольник курсором мыши и последовательно совмещая с другими треугольниками, можно убедиться в его равенстве с треугольниками: OBC, OCD и т.д. При этом в нижней части окна модели появляются кнопки, с помощью которых можно отображать и скрывать вписанную и описанную вокруг многоугольника окружности.
Кнопка «Сброс» в правом
нижнем углу окна возвращает модель в
исходное состояние.
Очень важной проблемой для учителя математики часто становится проблема заинтересованности учениками предметом. Тема «Правильные многоугольники» дает прекрасную возможность показать учащимся, что математика – это не «сухая» наука. Очень много научной и художественной литературы предлагают на своих страницах информацию из истории, которая обязательно должна стать интересной детям и, возможно, дать повод для дальнейшего углубленного изучения математики.
Дополнительный
материал, который можно использовать
как на уроках математики, так и на
дополнительных занятиях, приведен в
приложении к курсовой работе. Так же
будет очень эффективной организация
уроков математики совместно с уроками
мировой художественной культуры,
литературы, музыки и истории. Материал
может быть полезен для проведения
школьных конференций, олимпиад, конкурсов
и праздников.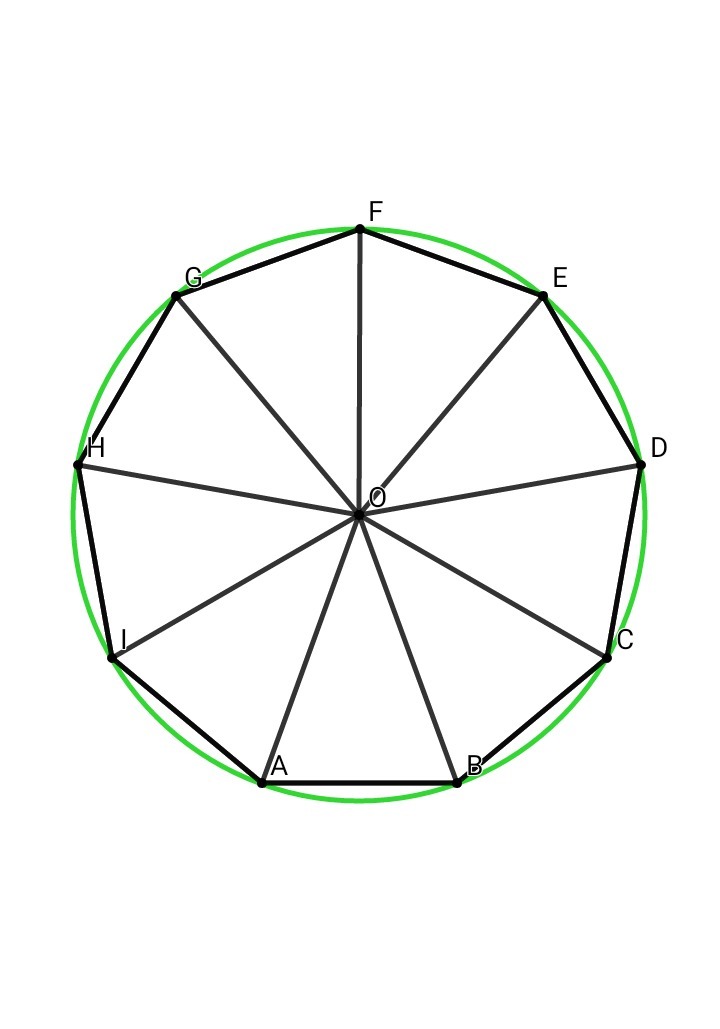
Таким образом, в курсовой работе проведен анализ учебных пособий разных авторов, в частности: В.В.Шлыков, Н.В.Гвоздович, Н.М Рогановский, Г.Н. Солтан. Существуют следующие методические проблемы при изучении данной темы:
1) проблема наглядности, т.е. данная тема требует большого количества иллюстраций, демонстраций графических построений, динамических моделей преобразований;
2) проблема рассмотрения большого количества разных типов задач в условиях ограниченности учебного времени и возможностей учебного пособия;
3) проблема заинтересованности учеников темой. Имеется очень много дополнительной литературы и интересных исторических сведений по теме, которые, если авторы не предлагают их в своих учебных пособиях, учитель должен преподносить на уроке , по возможности, в начале либо в процессе изучения темы.
4) проблема развития эстетического
вкуса и творческого мышления.
Также приведена подборка интересной исторической информации о правильных многоугольниках, которую можно предлагать ученикам на уроке и использовать в качестве пособия для проведения факультативных занятий.
Предлагаются примеры планов-конспектов уроков и самостоятельных работ, которые могут быть использованы студентами во время практики в школе.
К курсовой работе прилагается диск с разработанными презентацией и flash-программами по теме, с помощью которой можно проводить очень интересные уроки, соответствующие современным требованиям.
Список использованных источников1. Шлыков, В. В. Геометрия : учеб. пособие для 10-го кл. учреждений,
обеспечивающих получение общ. сред. образования, с рус. яз. обучения с 12-летним сроком обучения (базовый и повышенный уровни) / В. В. Шлыков. — 2-е изд. — Минск :Нар. асвета, 2007. — 174 с. : ил.
2. Гвоздович Н.В. Геометрия: учебное
пособие для 10 класса учреждений,
обеспечивающих получение общего среднего
образования, с русским языком обучения
с 12-летним сроком обучения(базовый и
повышенный уровни)/Н.В. Гвоздович,
Т.П.Кубеко.-Мн.: Нар. асвета, 2006.-125с. : ил.
Гвоздович Н.В. Геометрия: учебное
пособие для 10 класса учреждений,
обеспечивающих получение общего среднего
образования, с русским языком обучения
с 12-летним сроком обучения(базовый и
повышенный уровни)/Н.В. Гвоздович,
Т.П.Кубеко.-Мн.: Нар. асвета, 2006.-125с. : ил.
3.Геометрия: учеб.пособие для 10-го кл.общеобразовательных учреждений с бел.яз. обученияс 12-летним сроком обучения(углубл.уровень) / Н.М.Рогоновкий, А.М. Рогоновкая, Е.И.Тавгень; пер. с рус. яз. Л.Э. Гораниной. – Минск: Нар. асвета, 2007. – 335 с.: ил.
4. Рогановский Н.М. Геометрия: Учебник для 7-9-х кл. общеобразоват. шк. с углубл. изучением математики.-2-е изд.,перераб.-Мн.: Нар.асвета, 1997.-574 с.: ил.
5. Солтан Г. Н.Математика : Алгебра и геометрия : учеб. пособ. для 10-го кл.
учреждений,
обеспечивающих получение общ. сред.
образования, с рус. яз. обучения с
12-летним сроком обучения (базовый и
повыш. уровни) / Г. Н. Солтан, А. Е. Солтан;
под ред.Н. А. Лиходеда. — Минск : Нар.
асвета, 2006. — 303 с. : ил.
уровни) / Г. Н. Солтан, А. Е. Солтан;
под ред.Н. А. Лиходеда. — Минск : Нар.
асвета, 2006. — 303 с. : ил.
6. Геометрия: учебник для 7-9-х кл./ Л.С Атанасян, В.Ф Бутузов, С.Б. Кадомцев, Э.Г Позняк, И.И. Юдина.- 15-е изд., М.:»Просвещение», 2005.-340с.
7 Шарыгин И.Ф. Геометрия: учебник для 7-9-ч кл. общеобразоват.шк./И.Ф.Шарыгин.-8-е изд.-М.: Дрофа, 2007.-197с.: ил.
8. Журнал «Квант», 1973, № 8.
9. Журнал «Квант», 1974, №12.
10. Ковалев Ф.В. Золотое сечение в живописи. К.: Выш. школа, 1989.
Построение минимальных выпуклых оболочек / Хабр
Проведя небольшое научное исследование (проще говоря, выполнив поиск на сайте), обнаружил, что на хабре имеется всего две статьи с тегом
вычислительная геометрия, причем одна из них оказалась моей. Т.к. в последнее время я несколько заинтересовался этой тематикой, то решил продолжить тему алгоритмической геометрии рассмотрением задачи построения так называемых
минимальных выпуклых оболочек.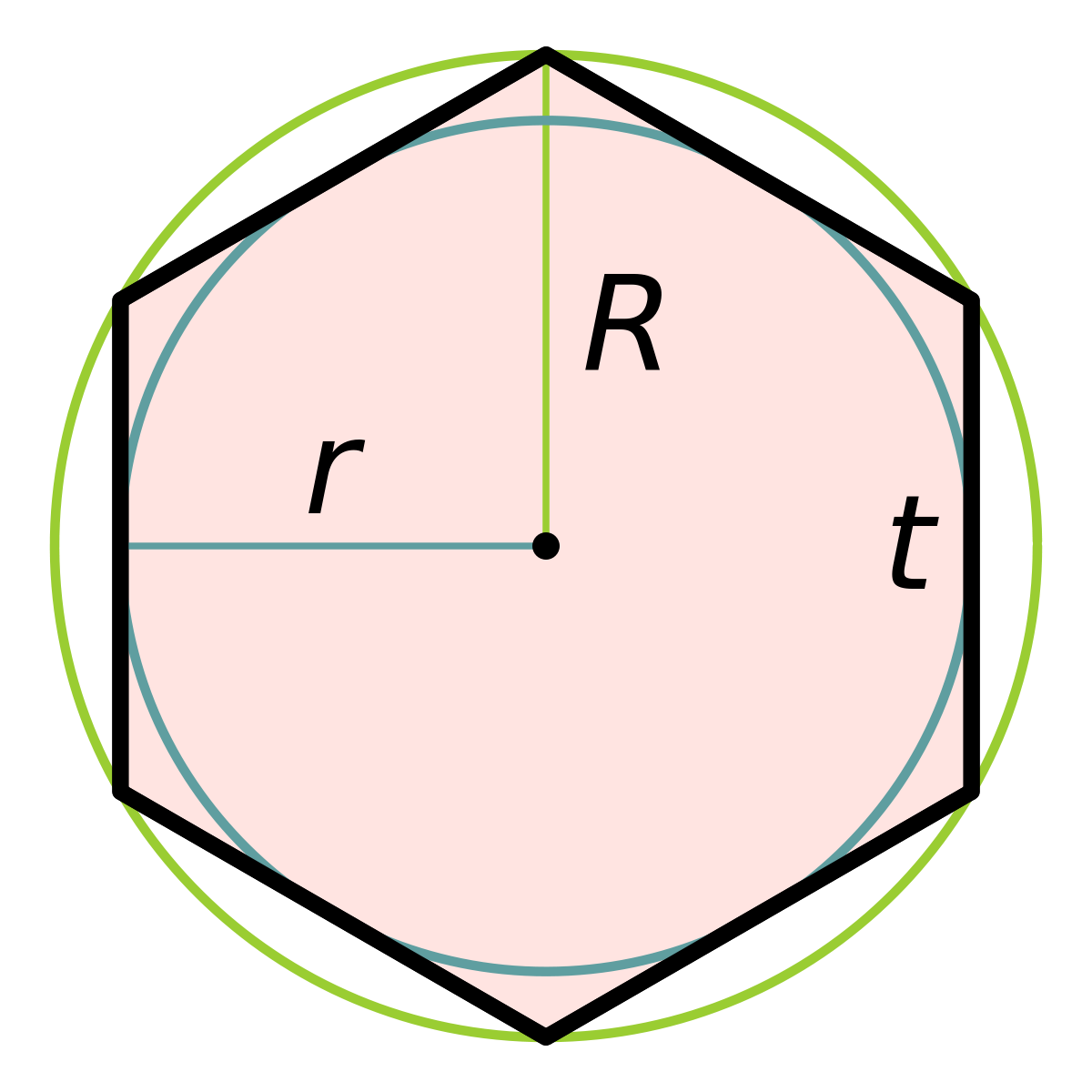 Хотя рисунок справа и дает проницательному хаброчитателю исчерпывающее объяснение того, что это такое, тем не менее под катом будут даны чуть более формальные определения и описаны два классических алгоритма построения минимальных выпуклых оболочек.
Хотя рисунок справа и дает проницательному хаброчитателю исчерпывающее объяснение того, что это такое, тем не менее под катом будут даны чуть более формальные определения и описаны два классических алгоритма построения минимальных выпуклых оболочек.
Пусть на
плоскостизадано конечное множество точек A.
Оболочкойэтого множества называется любая замкнутая линия H без самопересечений такая, что все точки из A лежат внутри этой кривой. Если кривая H является выпуклой (например, любая касательная к этой кривой не пересекает ее больше ни в одной точке), то соответствующая оболочка также называется
выпуклой. Наконец,
минимальной выпуклой оболочкой (далее кратко МВО) называется выпуклая оболочка минимальной длины (минимального периметра). Я не проверял (похоже, это можно доказать от противного), но кажется очевидным, что минимальная оболочка просто обязана быть выпуклой. Все введенные понятия иллюстрируются следующим рисунком.
Главной особенностью МВО множества точек A является то, что эта оболочка представляет собой выпуклый многоугольник, вершинами которого являются некоторые точки из A. Поэтому задача поиска МВО в конечном итоге сводится к отбору и упорядочиванию нужных точек из A. Упорядочивание является необходимым по той причине, что выходом алгоритма должен быть многоугольник, т.е. последовательность вершин. Наложим дополнительно условие на порядок расположения вершин — направление обхода многоугольника должно быть положительным (напомню, что положительным называется обход фигуры против часовой стрелки).
Задача построения МВО считается одной из самых простых задач вычислительной геометрии, для нее существует много различных алгоритмов. Ниже мы рассмотрим два таких алгоритма — Грэхема (Graham scan) и Джарвиса (Jarvis march). Их описание иллюстрируется кодом на Питоне. Обоим алгоритмам потребуется функция rotate, побробно описанная в предыдущем моем посте. Напомню, что эта функция определяет, с какой стороны от вектора AB находится точка C (положительное возвращаемое значение соответствует левой стороне, отрицательное — правой).
def rotate(A,B,C):
return (B[0]-A[0])*(C[1]-B[1])-(B[1]-A[1])*(C[0]-B[0])
Этот алгоритм является трехшаговым. На первом шаге ищется любая точка в A, гарантированно входящая в МВО. Нетрудно сообразить, что такой точкой будет, например, точка с наименьшей x-координатой (самая левая точка в A). Эту точку (будем называть ее стартовой) перемещаем в начало списка, вся дальнейшая работа будет производиться с оставшимися точками. По некоторым соображениям, исходный массив точек A нами меняться не будет, для всех манипуляций с точками будем использовать косвенную адресацию: заведем список P, в котором будут хранится
номераточек (их позиции в массиве A). Итак, первый шаг алгоритма заключается в том, чтобы первой точкой в P оказалась точка с наименьшей x-координатой. Код:
def grahamscan(A):
n = len(A) # число точек
P = range(n) # список номеров точек
for i in range(1,n):
if A[P[i]][0]<A[P[0]][0]: # если P[i]-ая точка лежит левее P[0]-ой точки
P[i], P[0] = P[0], P[i] # меняем местами номера этих точек
Второй шаг в алгоритме Грэхема — сортировка всех точек (кроме P[0]-ой), по степени их
левизныотносительно стартовой точки R=A
P[0]. Будем говорить, что B
Будем говорить, что B
Для выпонения такого упорядочивания можно применять любой алгоритм сортировки, основанный на попарном сравнении элементов, например, быструю сортировку. По некоторым причинам (главная из которых — корявость
*рук), я буду использовать сортировку вставками.
*я буду очень признателен тем, кто сможет мне объяснить, как применить в данном случае встроенную питоновскую сортировку…
Итак, сортировка вставками (не забываем про косвенную адресацию и про то, что нулевая точка не сортируется):
for i in range(2,n):
j = i
while j>1 and (rotate(A[P[0]],A[P[j-1]],A[P[j]])<0):
P[j], P[j-1] = P[j-1], P[j]
j -= 1
Результат сортировки можно проиллюстрировать следующим рисунком.
Если мы теперь соединим точки в полученном порядке, то получим многоугольник, который, однако, не является выпуклым.
Переходим к третьему действию. Все, что нам осталось сделать, так это срезать углы. Для этого нужно пройтись по всем вершинам и удалить те из них, в которых выполняется правый поворот (угол в такой вершине оказывается больше развернутого). Заводим стек S (реально список) и помещаем в него первые две вершины (они, опять же, гарантированно входят в МВО).
Для этого нужно пройтись по всем вершинам и удалить те из них, в которых выполняется правый поворот (угол в такой вершине оказывается больше развернутого). Заводим стек S (реально список) и помещаем в него первые две вершины (они, опять же, гарантированно входят в МВО).
S = [P[0],P[1]]
Затем просматриваем все остальные вершины, и отслеживаем направление поворота в них с точки зрения последних двух вершин в стеке S: если это направление отрицательно, то можно срезать угол удалением из стека последней вершины. Как только поворот оказывается положительным, срезание углов завершается, текущая вершина заносится в стек.
for i in range(2,n):
while rotate(A[S[-2]],A[S[-1]],A[P[i]])<0:
del S[-1] # pop(S)
S.append(P[i]) # push(S,P[i])
В итоге в стеке S (который теперь можно рассматривать, как список) оказывается искомая последовательность вершин, причем в нужной нам ориентации, определяющая МВО заданного множества точек A.
return S
Сложность первого и последнего шагов алгоритма является линейной по n (хотя в последнем случае имеется вложенный цикл, однако, каждая вершина внутри этого цикла ровно один раз заносится в стек, и не более одного раза оттуда удаляется), следовательно, сложность всего алгоритма определяется вторым шагом — сортировкой, именно поэтому сортировка вставкой оказывается не лучшим вариантом при больших n. Если ее заменить на быструю сортировку, то получим суммарную сложность алгоритма O(nlogn). Можно ли улучшить это время? Если алгоритм основан на попарном сравнении точек (как у нас), то доказано, что данная оценка в общем случае не улучшаема. С этой точки зрения алгоритм Грэхема оптимален. Тем не менее у него имеется не очень хорошая особенность — он не является адаптивным в том смысле, что не важно, сколько вершин в итоге войдет в МВО (три, пять, десять или n), все равно время будет линейно-логарифмическим. Такой адаптивностью обладает алгоритм Джарвиса, к рассмотрению которого мы плавно и переходим.
Полный код алгоритма Грэхема
def grahamscan(A):
n = len(A) # число точек
P = range(n) # список номеров точек
for i in range(1,n):
if A[P[i]][0]<A[P[0]][0]: # если P[i]-ая точка лежит левее P[0]-ой точки
P[i], P[0] = P[0], P[i] # меняем местами номера этих точек
for i in range(2,n): # сортировка вставкой
j = i
while j>1 and (rotate(A[P[0]],A[P[j-1]],A[P[j]])<0):
P[j], P[j-1] = P[j-1], P[j]
j -= 1
S = [P[0],P[1]] # создаем стек
for i in range(2,n):
while rotate(A[S[-2]],A[S[-1]],A[P[i]])<0:
del S[-1] # pop(S)
S.append(P[i]) # push(S,P[i])
return S
Алгоритм Джарвиса (другое название — алгоритм заворачивания подарков) концептуально устроен проще алгоритма Грэхема. Он является двухшаговым и не требует сортировки. Первый шаг точно такой же — нам нужна стартовая точка, которая гарантированно входит в МВО, берем самую левую точку из A.
def jarvismarch(A):
n = len(A)
P = range(n)
for i in range(1,n):
if A[P[i]][0]<A[P[0]][0]:
P[i], P[0] = P[0], P[i]
На втором шаге алгоритма строится МВО. Идея: делаем стартовую вершину текущей, ищем самую правую точку в A относительно текущей вершины, делаем ее текущей и т.д. Процесс завершается, когда текущей вновь окажется стартовая вершина. Как только точка попала в МВО, больше ее можно не учитывать. Поэтому заведем еще один список H, в котором в правильном порядке будут храниться вершины МВО. В этот список сразу же заносим стартовую вершину, а в списке P эту вершину переносим в конец (где мы ее в конце концов найдем и завершим алгоритм).
Идея: делаем стартовую вершину текущей, ищем самую правую точку в A относительно текущей вершины, делаем ее текущей и т.д. Процесс завершается, когда текущей вновь окажется стартовая вершина. Как только точка попала в МВО, больше ее можно не учитывать. Поэтому заведем еще один список H, в котором в правильном порядке будут храниться вершины МВО. В этот список сразу же заносим стартовую вершину, а в списке P эту вершину переносим в конец (где мы ее в конце концов найдем и завершим алгоритм).
H = [P[0]]
del P[0]
P.append(H[0])
Теперь организуем бесконечный цикл, на каждой итерации которого ищем самую левую точку из P относительно последней вершины в H. Если эта вершина стартовая, то прерываем цикл, если нет — то переносим найденную вершину из P в H. После завершения цикла в H находится искомая оболочка, которую мы и возвращаем в качестве результата.
while True:
right = 0
for i in range(1,len(P)):
if rotate(A[H[-1]],A[P[right]],A[P[i]])<0:
right = i
if P[right]==H[0]:
break
else:
H. append(P[right])
del P[right]
return H
append(P[right])
del P[right]
return H
Хм, мне удалось рассказать об алгоритме Джарвиса, не используя картинок. Следующий рисунок иллюстрирует все!
Оценим сложность алгоритма Джарвиса. Первый шаг линеен по n. Со вторым все интереснее. У нас имеется вложенный цикл, число внешних итераций равно числу вершин h в МВО, число внутренних итераций не превышает n. Следовательно, сложность всего алгоритма равна O(hn). Необычным в этой формуле является то, что сложность определяется не только длиной входных данных, но и длиной выхода (output-sensitive algorithm). А дальше как
точки лягут. В худшем случае все точки из A входят в МВО (т.е. A уже само по себе выпуклый многоугольник), тогда h=n и сложность подскакивает до квадратичной. В лучшем случае (при условии, что точки из A не лежат на одной прямой) h=3 и сложность становится линейной. Осталось заранее понять, какой у нас случай, что сделать не так просто (если у вас нет машины времени
**), можно только исходить из характера задачи — если точек много и они равномерно заполняют некоторую область, то (возможно) Джарвис будет быстрее, если же данные собраны на границе области, то быстрее будет Грэхем, как-то так…
**
Машина времени вообще полезная штука с точки зрения алгоритмов, любая задача, требующая триллиона лет вычислений, с ее помощью может быть решена практически мгновенно — запускаем программу, садимся в машину времени, «летим» в будущее, считываем результат, возвращаемся назад. Осталось придумать, как обеспечить бесперебойную работу компьютера на пару триллионов лет…Полный код алгоритма Джарвиса
Осталось придумать, как обеспечить бесперебойную работу компьютера на пару триллионов лет…Полный код алгоритма Джарвисаdef jarvismarch(A):
n = len(A)
P = range(n)
# start point
for i in range(1,n):
if A[P[i]][0]<A[P[0]][0]:
P[i], P[0] = P[0], P[i]
H = [P[0]]
del P[0]
P.append(H[0])
while True:
right = 0
for i in range(1,len(P)):
if rotate(A[H[-1]],A[P[right]],A[P[i]])<0:
right = i
if P[right]==H[0]:
break
else:
H.append(P[right])
del P[right]
return H
На мой взгляд, задача построения минимальных выпуклых оболочек — хороший способ войти в тему вычислительной геометрии, достаточно легко придумать свой собственный алгоритм (однако, наверняка это будет вариация алгоритма Джарвиса). Утверждается, что приложений у этой задачи много, большая их часть связана с распознаванием образов, кластеризацией и т.п. Кроме того, задача построения МВО используется в качестве вспомогательного средства при решении более сложных задач вычислительной геометрии. Да, стоит отметить, что у этой задачи имеется весьма интересное трехмерное обобщение.
Да, стоит отметить, что у этой задачи имеется весьма интересное трехмерное обобщение.
Спасибо всем за внимание!
Определение выпуклого треугольника. Чему равна сумма углов выпуклого многоугольника. Является ли параллелограмм выпуклым четырехугольником
Понятие многоугольника
Определение 1
Многоугольником называется геометрическая фигура в плоскости, которая состоит из попарно соединенных между собой отрезков, соседние из которых не лежат на одной прямой.
При этом отрезки называются сторонами многоугольника , а их концы — вершинами многоугольника .
Определение 2
$n$-угольником называется многоугольник, у которого $n$ вершин.
Виды многоугольников
Определение 3
Если многоугольник всегда будет лежать по одну сторону от любой прямой, проходящей через его стороны, то многоугольник называется выпуклым (рис. 1).
Рисунок 1. Выпуклый многоугольник
Определение 4
Если многоугольник лежит по разные стороны хотя бы одной прямой, проходящей через его стороны, то многоугольник называется невыпуклым (рис. 0\]
0\]
Теорема доказана.
На этом уроке мы приступим уже к новой теме и введем новое для нас понятие «многоугольник». Мы рассмотрим основные понятия, связанные с многоугольниками: стороны, вершины углы, выпуклость и невыпуклость. Затем докажем важнейшие факты, такие как теорема о сумме внутренних углов многоугольника, теорема о сумме внешних углов многоугольника. В итоге, мы вплотную подойдем к изучению частных случаев многоугольников, которые будут рассматриваться на дальнейших уроках.
Тема: Четырехугольники
Урок: Многоугольники
В курсе геометрии мы изучаем свойства геометрических фигур и уже рассмотрели простейшие из них: треугольники и окружности. При этом мы обсуждали и конкретные частные случаи этих фигур, такие как прямоугольные, равнобедренные и правильные треугольники. Теперь пришло время поговорить о более общих и сложных фигурах — многоугольниках .
С частным случаем многоугольников мы уже знакомы — это треугольник (см. Рис. 1).
Рис. 1).
Рис. 1. Треугольник
В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник (см. Рис. 2), т.е. фигуру с пятью углами.
Рис. 2. Пятиугольник. Выпуклый многоугольник
Определение. Многоугольник — фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки — сторонами . При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.
Определение. Правильный многоугольник — это выпуклый многоугольник, у которого все стороны и углы равны.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят к многоугольнику .
Иными словами, например, когда говорят о пятиугольнике , имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника, т.е. точка тоже относится к пятиугольнику (см. Рис. 2).
А ко внутренней области относятся и все точки, которые лежат внутри многоугольника, т.е. точка тоже относится к пятиугольнику (см. Рис. 2).
Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).
Определение. Периметр многоугольника — сумма длин сторон многоугольника.
Теперь надо познакомиться с видами многоугольников. Они делятся на выпуклые и невыпуклые . Например, многоугольник, изображенный на Рис. 2, является выпуклым, а на Рис. 3 невыпуклым.
Рис. 3. Невыпуклый многоугольник
Определение 1. Многоугольник называется выпуклым , если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой. Невыпуклыми являются все остальные многоугольники .
Легко представить, что при продлении любой стороны пятиугольника на Рис. 2 он весь окажется по одну сторону от этой прямой, т. е. он выпуклый. А вот при проведении прямой через в четырехугольнике на Рис. 3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
е. он выпуклый. А вот при проведении прямой через в четырехугольнике на Рис. 3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
Но существует и другое определение выпуклости многоугольника.
Определение 2. Многоугольник называется выпуклым , если при выборе любых двух его внутренних точек и при соединении их отрезком все точки отрезка являются также внутренними точками многоугольника.
Демонстрацию использования этого определения можно увидеть на примере построения отрезков на Рис. 2 и 3.
Определение. Диагональю многоугольника называется любой отрезок, соединяющий две не соседние его вершины.
Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольника и теорема о сумме внешних углов выпуклого многоугольника . Рассмотрим их.
Теорема. О сумме внутренних углов выпуклого многоугольника (n -угольника).
Где — количество его углов (сторон).
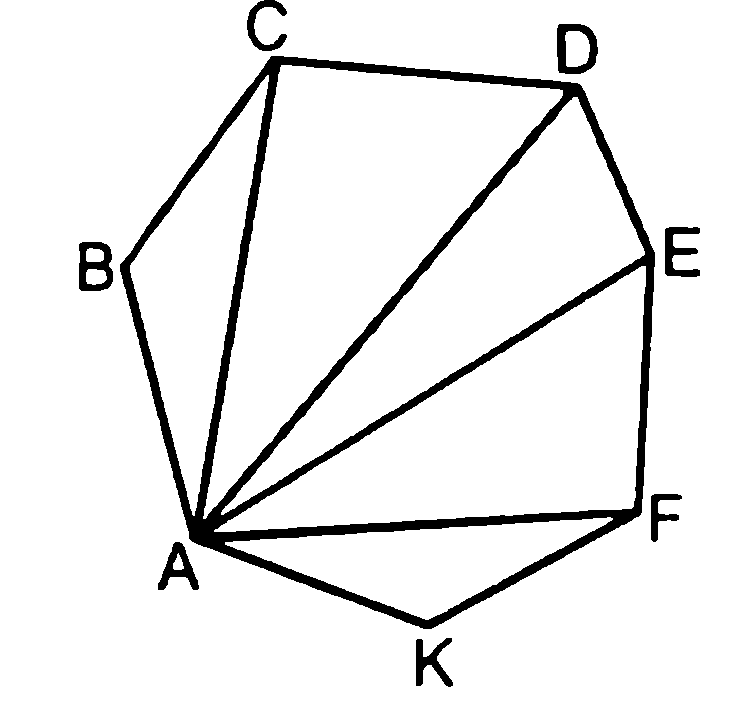
Доказательство 1. Изобразим на Рис. 4 выпуклый n-угольник.
Рис. 4. Выпуклый n-угольник
Из вершины проведем все возможные диагонали. Они делят n-угольник на треугольника, т.к. каждая из сторон многоугольника образует треугольник, кроме сторон, прилежащих к вершине . Легко видеть по рисунку, что сумма углов всех этих треугольников как раз будет равна сумме внутренних углов n-угольника. Поскольку сумма углов любого треугольника — , то сумма внутренних углов n-угольника:
Что и требовалось доказать.
Доказательство 2. Возможно и другое доказательство этой теоремы. Изобразим аналогичный n-угольник на Рис. 5 и соединим любую его внутреннюю точку со всеми вершинами.
Рис. 5.
Мы получили разбиение n-угольника на n треугольников (сколько сторон, столько и треугольников). Сумма всех их углов равна сумме внутренних углов многоугольника и сумме углов при внутренней точке, а это угол . Имеем:
Что и требовалось доказать.
Доказано.
По доказанной теореме видно, что сумма углов n-угольника зависит от количества его сторон (от n). Например, в треугольнике , а сумма углов . В четырехугольнике , а сумма углов — и т.д.
Теорема. О сумме внешних углов выпуклого многоугольника (n -угольника).
Где — количество его углов (сторон), а , …, — внешние углы.
Доказательство. Изобразим выпуклый n-угольник на Рис. 6 и обозначим его внутренние и внешние углы.
Рис. 6. Выпуклый n-угольник с обозначенными внешними углами
Т.к. внешний угол связан со внутренним как смежные, то и аналогично для остальных внешних углов. Тогда:
В ходе преобразований мы воспользовались уже доказанной теоремой о сумме внутренних углов n-угольника .
Доказано.
Из доказанной теоремы следует интересный факт, что сумма внешних углов выпуклого n-угольника равна от количества его углов (сторон). Кстати, в отличие от суммы внутренних углов.
Список литературы
- Александров А.
 Д. и др. Геометрия, 8 класс. — М.: Просвещение, 2006.
Д. и др. Геометрия, 8 класс. — М.: Просвещение, 2006. - Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. — М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. — М.: ВЕНТАНА-ГРАФ, 2009.
- Profmeter.com.ua ().
- Narod.ru ().
- Xvatit.com ().
Домашнее задание
Выпуклый четырехугольник — это фигура, состоящая из четырех сторон, соединенных между собой в вершинах, образующих вместе со сторонами четыре угла, при этом сам четырехугольник всегда находится в одной плоскости относительно прямой, на которой лежит одна из его сторон. Другими словами, вся фигура находится по одну сторону от любой из ее сторон.
Вконтакте
Как видно, определение довольно легко запоминающееся.
Основные свойства и виды
К выпуклым четырехугольникам можно отнести практически все известные нам фигуры, состоящие из четырех углов и сторон. Можно выделить следующие:
- параллелограмм;
- квадрат;
- прямоугольник;
- трапеция;
- ромб.

Все эти фигуры объединяет не только то, что они четырехугольные, но и то, что они еще и выпуклые. Достаточно просто рассмотреть схему:
На рисунке изображена выпуклая трапеция . Тут видно, что трапеция находится на одной плоскости или по одну сторону от отрезка . Если провести аналогичные действия, можно выяснить, что и в случае со всеми остальными сторонами трапеция является выпуклой.
Является ли параллелограмм выпуклым четырехугольником?
Выше показано изображение параллелограмма. Как видно из рисунка, параллелограмм также является выпуклым . Если посмотреть на фигуру относительно прямых, на которых лежат отрезки AB, BC, CD и AD, то становится понятно, что она всегда находится на одной плоскости от этих прямых. Основными же признаками параллелограмма является то, что его стороны попарно параллельны и равны так же, как и противоположные углы равны между собой.
Теперь, представьте себе квадрат или прямоугольник. По своим основным свойствам они являются еще и параллелограммами, то есть все их стороны расположены попарно параллельно. Только в случае с прямоугольником длина сторон может быть разной, а углы прямые (равные 90 градусам), квадрат — это прямоугольник, у которого все стороны равны и углы также прямые, а у параллелограмма длины сторон и углы могут быть разными.
Только в случае с прямоугольником длина сторон может быть разной, а углы прямые (равные 90 градусам), квадрат — это прямоугольник, у которого все стороны равны и углы также прямые, а у параллелограмма длины сторон и углы могут быть разными.
В итоге, сумма всех четырех углов четырехугольника должна быть равна 360 градусам . Легче всего это определить по прямоугольнику: все четыре угла прямоугольника прямые, то есть равны 90 градусам. Сумма этих 90-градусных углов дает 360 градусов, другими словами, если сложить 90 градусов 4 раза, получится необходимый результат.
Свойство диагоналей выпуклого четырехугольника
Диагонали выпуклого четырехугольника пересекаются . Действительно, это явление можно наблюдать визуально, достаточно взглянуть на рисунок:
На рисунке слева изображен невыпуклый четырехугольник или четырехсторонник. Как угодно. Как видно, диагонали не пересекаются, по крайней мере, не все. Справа изображен выпуклый четырехугольник. Тут уже наблюдается свойство диагоналей пересекаться.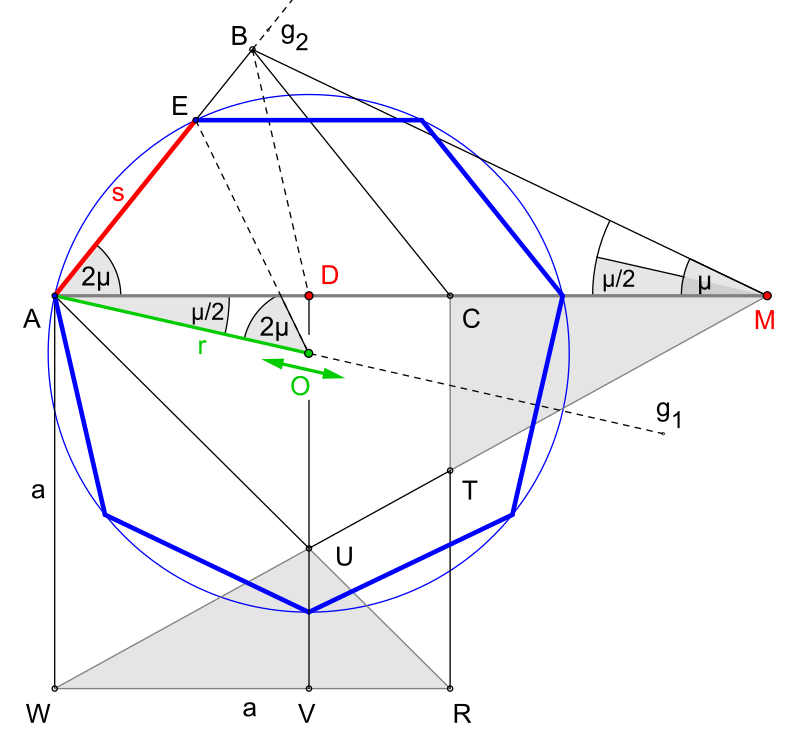 Это же свойство можно считать признаком выпуклости четырехугольника.
Это же свойство можно считать признаком выпуклости четырехугольника.
Другие свойства и признаки выпуклости четырехугольника
Конкретно по этому термину очень сложно назвать какие-то определенные свойства и признаки. Легче обособить по различным видам четырехугольников такого типа. Начать можно с параллелограмма. Мы уже знаем, что это четырехугольная фигура, стороны которой попарно параллельны и равны. При этом, сюда же включается свойство диагоналей параллелограмма пересекаться между собой, а также сам по себе признак выпуклости фигуры: параллелограмм находится всегда в одной плоскости и по одну сторону относительно любой из своих сторон.
Итак, известны основные признаки и свойства:
- сумма углов четырехугольника равна 360 градусам;
- диагонали фигур пересекаются в одной точке.
Прямоугольник . Эта фигура имеет все те же свойства и признаки, что и параллелограмм, но при этом все углы его равны 90 градусам. Отсюда и название — прямоугольник.
Квадрат, тот же параллелограмм , но углы его прямые как у прямоугольника. Из-за этого квадрат в редких случаях называют прямоугольником. Но главным отличительным признаком квадрата помимо уже перечисленных выше, является то, что все четыре его стороны равны.
Трапеция — очень интересная фигура . Это тоже четырехугольник и тоже выпуклый. В этой статье трапеция уже рассматривалась на примере рисунка. Понятно, что она тоже выпуклая. Главным отличием, а соответственно признаком трапеции является то, что ее стороны могут быть абсолютно не равны друг другу по длине, а также ее углы по значению. При этом фигура всегда остается на одной плоскости относительно любой из прямых, которая соединяет любые две ее вершины по образующим фигуру отрезкам.
Ромб — не менее интересная фигура . Отчасти ромбом можно считать квадрат. Признаком ромба является тот факт, что его диагонали не только пересекаются, но и делят углы ромба пополам, а сами диагонали пересекаются под прямым углом, то есть, они перпендикулярны. В случае, если длины сторон ромба равны, то диагонали тоже делятся пополам при пересечении.
Дельтоиды или выпуклые ромбоиды (ромбы) могут иметь разную длину сторон. Но при этом все равно сохраняются как основные свойства и признаки самого ромба, так и признаки и свойства выпуклости. То есть, мы можем наблюдать, что диагонали делят углы пополам и пересекаются под прямым углом.
Сегодняшней задачей было рассмотреть и понять, что такое выпуклые четырехугольники, какие они бывают и их основные признаки и свойства. Внимание! Стоит напомнить еще раз, что сумма углов выпуклого четырехугольника равна 360 градусам. Периметр фигур, например, равен сумме длин всех образующих фигуру отрезков. Формулы расчета периметра и площади четырехугольников будут рассмотрены в следующих статьях.
Виды выпуклых четырехугольников
Определение
Ломаной линией , или короче, ломаной , называется конечная последовательность отрезков, такая, что один из концов первого отрезка служит концом второго, другой конец второго отрезка служит концом третьего и т.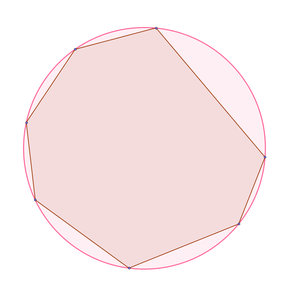 \circ$.
\circ$.
Доказательство
Пусть дан многоугольник $P$.
Проведем какую-нибудь прямую, не пересекающую его. Будем перемещать ее параллельно в сторону многоугольника. В некоторый момент мы впервые получим прямую $a$, имеющую с многоугольником $P$ хотя бы одну общую точку. От этой прямой многоугольник лежит по одну сторону (при этом некоторые его точки лежат на прямой $a$).
На прямой $a$ лежит хотя бы одна вершина многоугольника. В ней сходится две его стороны, расположенные по одну сторону от прямой $a$ (считая и тот случай, когда одна из них лежит на этой прямой). А значит, при этой вершине угол меньше развернутого.
Определение
Многоугольник называется выпуклым , если он лежит по одну сторону от каждой прямой, содержащей его сторону. Если многоугольник не является выпуклым, его называют невыпуклым .
Замечание
Выпуклый многоугольник является пересечением полуплоскостей, ограниченных прямыми, которые содержат стороны многоугольника. \circ$.
\circ$.
Докажем второе свойство
Возьмем любые две точки $A$ и $B$ выпуклого многоугольника $P$. Многоугольник $P$ является пересечением нескольких полуплоскостей. Отрезок $AB$ содержится в каждой из этих полуплоскостей. Поэтому он содержится и в многоугольнике $P$.
Определение
Диагональю многоугольника называется отрезок, соединяющий его несоседние вершины.
Теорема (о количестве диагоналей n-угольника)
Количество диагоналей выпуклого $n$-угольника вычисляется по формуле $\dfrac{n(n-3)}{2}$.
Доказательство
Из каждой вершины n-угольника можно провести $n-3$ диагонали (нельзя провести диагональ в соседние вершины и в саму эту вершину). Если посчитать все такие возможные отрезки, то их будет $n\cdot(n-3)$, так как вершин $n$. Но каждая диагональ будет посчитана дважды. Таким образом, количество диагоналей n-угольника равно $\dfrac{n(n-3)}{2}$.
Теорема (о сумме углов n-угольника)
Сумма углов выпуклого $n$-угольника равна $180^\circ(n-2)$. \circ$.
\circ$.
Плоская фигура, образованная замкнутым рядом прямолинейных отрезков, называется многоугольником. На рис.1 изображен шестиугольник ABCDEF . Точки А , В , С , D , Е , F — вершины многоугольника ; при них (углы многоугольника) обозначаются ∠A , ∠В , ∠С , …, ∠F . Отрезки: AC , AD , BE и т.д. — диагонали , АВ ; ВС , CD и т. д. — стороны многоугольника ; сумма длин сторон АВ + ВС + CD + … + FA называется периметром и обозначается р , а иногда 2р (тогда р — полупериметр ).
В элементарной геометрии рассматриваются только простые многоугольники, т. е. такие, контур которых не имеет самопересечений.
Многоугольники, контур которых имеет самопересечения, называются звездчатыми многоугольниками . На рис.2 изображен звездчатый многоугольник ABCDE .
рис.2
Если все диагонали многоугольника лежат внутри него, многоугольник называется выпуклым .
Шестиугольник на рис.1 выпуклый; пятиугольник на рис.3 невыпуклый (диагональ ЕС лежит вне многоугольника).
рис.3
Сумма внутренних углов во всяком выпуклом многоугольнике равна 180° (n-2 ), где n — число сторон многоугольника*.
* В учебниках геометрии это свойство высказывается обычно только для выпуклых многоугольников. Но оно справедливо для всех простых многоугольников. Но оно справедливо для всех простых многоугольников. Нужно заметить, что в невыпуклом многоугольнике один или несколько внутренних углов превышают 180°. Так, в невыпуклом пятиугольнике, изображенном на рис.3, два угла прямые, два угла имеют по 45°, а один содержит 270°. Суммаа углов составляет 180° (5-2)=540°.
Гептагон
Семиугольник — это многоугольник с семью сторонами (Гепта- означает семь). На рисунке ниже представлены несколько типов семиугольников.
Классификация Гептагон
Как и другие многоугольники, семиугольник может быть классифицирован как правильный или неправильный. Если все стороны и внутренние углы семиугольника равны, то это правильный семиугольник. В противном случае это неправильный семиугольник.
| Правильный семиугольник | Неправильный семиугольник |
|---|---|
| Все стороны и внутренние углы равны | Не все стороны и углы равны |
Семиугольники и другие многоугольники также могут быть классифицированы как выпуклые или вогнутые.Если все внутренние углы семиугольника меньше 180°, то он выпуклый. Если один или несколько внутренних углов больше 180 °, он вогнутый. Правильный семиугольник — это выпуклый семиугольник. Вогнутый семиугольник — это неправильный семиугольник.
| Выпуклый семиугольник | Вогнутый семиугольник |
|---|---|
| Все внутренние углы <180° | Один или несколько внутренних углов >180° |
Диагонали семиугольника
Диагональ — это отрезок, соединяющий две непоследовательные вершины. Всего в семиугольнике можно провести четырнадцать различных диагоналей. Следующий рисунок является примером.
Всего в семиугольнике можно провести четырнадцать различных диагоналей. Следующий рисунок является примером.
Из каждой из 7 вершин указанного выше семиугольника выходит 4 диагонали, что в сумме дает 14 диагоналей.
Внутренние углы семиугольника
Сумма внутренних углов семиугольника равна 900°.
Как показано на рисунке выше, можно провести четыре диагонали, чтобы разделить семиугольник на пять треугольников. Синие линии выше показывают только один способ разделить семиугольник на треугольники; есть другие.Сумма внутренних углов пяти треугольников равна сумме внутренних углов семиугольника. Поскольку сумма внутренних углов треугольника равна 180°, сумма внутренних углов семиугольника равна 5 × 180° = 900°.
Правильный семиугольник
Правильный семиугольник – это семиугольник, у которого все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую величину.
Углы правильного семиугольника
Поскольку все семь внутренних углов правильного семиугольника равны по размеру, каждый внутренний угол равен 900° ÷ 7 ≈ 128.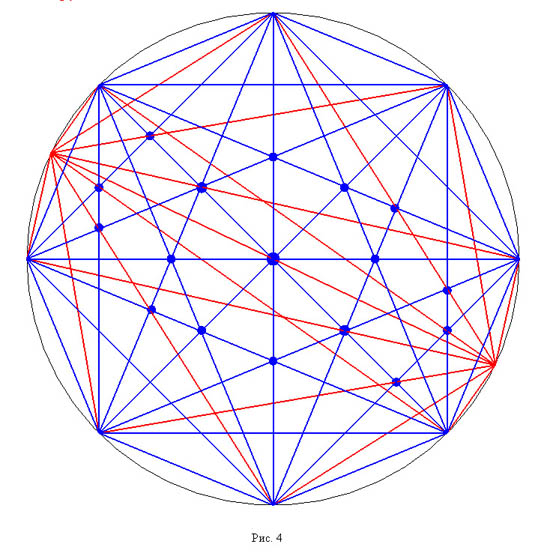 57°, как показано ниже.
57°, как показано ниже.
Каждый внешний угол правильного семиугольника имеет одинаковую меру, которая приблизительно равна 51,43°.
Симметрия в правильном семиугольнике
Правильный семиугольник имеет 7 линий симметрии и вращательную симметрию 7-го порядка, что означает, что его можно повернуть таким образом, что он будет выглядеть так же, как исходная форма, 7 раз на 360°.
| Линии симметрии | Вращательная симметрия |
|---|---|
| 7 линий симметрии | Семь 51.Угол поворота 43 градуса вокруг центра |
Полигонов — Heptagons
Свойства гептагонов, Углым внутренней части Heptagons
| 4 | |
|---|---|
| 5 | |
| 5 | 2|
| Сумма Углы внутренних углов HEPTAGAN: | |
| 0 | |
| 4 | Это изображение показывает процесс для шестиугольника | Использование тех же методов, что и для шестиугольников вправо (я позволю вам делай картинки). Итак, сумма внутренних углов семиугольника равна 900 градусов. |
Чтобы найти меру внутренних углов, мы знаем, что сумма всех углов равна 900 градусов (сверху)… И есть семь углов…
Итак, мера внутренний угол правильного семиугольника составляет около 128,57 градусов.
| 4 | 0 | 0 |
|---|---|---|
Для поиска меры центрального угла регулярного гептана , сделать круг в середине. .. Окружность составляет 360 градусов вокруг… Разделите это на семь углов… .. Окружность составляет 360 градусов вокруг… Разделите это на семь углов… Итак, мера центрального угла правильного семиугольника составляет около 51,43 градуса. |
Гептагон — определение, типы, свойства, формула
Гептагон — это двухмерная фигура с семью сторонами, семью вершинами и семью ребрами. Этот семиугольный многоугольник «семиугольник» состоит из двух слов «Гепта» и «Гония», что означает семь углов. Другое название семиугольника — септагон.
Что такое семиугольник?
Семиугольник — это многоугольник с семью сторонами, который имеет семь сторон, семь вершин и семь ребер. Они могут иметь одинаковые или разные размеры длины. Давайте посмотрим на приведенный ниже рисунок, на котором изображен семиугольник.
Типы формы семиугольника
Формы семиугольника можно разделить на категории на основе их сторон и углов.
а.) В зависимости от длины сторон семиугольники можно классифицировать следующим образом:
Правильный семиугольник: Правильный семиугольник — это треугольник с равными сторонами и равными углами.Сумма всех внутренних углов правильного семиугольника равна 900°. Величина каждого внутреннего угла правильного семиугольника равна 128,57°
.Неправильный семиугольник: Неправильный семиугольник — это такой, у которого стороны и углы разной величины. Величина каждого внутреннего угла неправильного семиугольника будет разной. Однако сумма всех внутренних углов неправильного семиугольника также равна 900°.
На следующих рисунках показаны правильный и неправильный семиугольник.
b.) На основании угловых величин семиугольники можно классифицировать следующим образом:
Выпуклый семиугольник: У выпуклого семиугольника все внутренние углы меньше 180°.
 Они могут быть правильными или неправильными семиугольниками. Все вершины выпуклого семиугольника направлены наружу.
Они могут быть правильными или неправильными семиугольниками. Все вершины выпуклого семиугольника направлены наружу.Вогнутый семиугольник: В вогнутом семиугольнике по крайней мере один из внутренних углов больше 180°.Они могут быть правильными или неправильными семиугольниками. В выпуклом семиугольнике хотя бы одна вершина указывает внутрь.
На следующих рисунках показаны выпуклый и вогнутый семиугольник.
Свойства Гептагона
Давайте рассмотрим некоторые важные свойства семиугольника следующим образом:
- Семиугольник имеет 7 сторон, 7 ребер и 7 вершин.
- Сумма внутренних углов семиугольника равна 900°.
- Величина каждого внутреннего угла правильного семиугольника равна 128,57°
- Сумма внешних углов семиугольника равна 360°
- Количество диагоналей, которые можно провести в семиугольнике, равно 14.
- Центральный угол правильного семиугольника приблизительно равен 51,43 градуса.

- Правильный семиугольник также известен как выпуклый семиугольник, так как все его внутренние углы меньше 180°
- Неправильный семиугольник имеет неравные стороны и углы разной величины.
Формула обычного семиугольника
Есть много формул, связанных с правильным семиугольником. Давайте разберемся, как найти периметр и площадь правильного семиугольника, используя формулы семиугольника.
Периметр семиугольника
Мы знаем, что у правильного семиугольника 7 сторон одинаковой длины. Следовательно, периметр правильного семиугольника равен 7 × длина стороны
.Следовательно, периметр правильного семиугольника со стороной «а» определяется как Периметр = 7а
Площадь семиугольника
Площадь семиугольника определяется как общая площадь, занимаемая многоугольником.Площадь правильного семиугольника со стороной «а» рассчитывается по формуле Площадь = (7a²/4) cot (π/7)
Эту формулу можно упростить и приблизительно записать как 3,634a², где «a» — длина стороны. Мы можем использовать это, чтобы вычислить площадь правильного семиугольника.
Мы можем использовать это, чтобы вычислить площадь правильного семиугольника.
Углы в семиугольнике
Семиугольник состоит из 7 внутренних и 7 внешних углов. Давайте прочитаем о внутренних и внешних углах семиугольника.
Внутренние углы правильного семиугольника
Сумма внутренних углов правильного многоугольника определяется по формуле внутреннего угла: (n — 2) × 180º, где n — количество сторон многоугольника.Таким образом, для семиугольника n = 7. Сумма внутренних углов правильного семиугольника = (7 — 2) × 180º = 900º. Таким образом, каждый внутренний угол правильного семиугольника = 900/7 = 128,57º
.Внешние углы правильного семиугольника
Согласно формуле суммы внешних углов сумма всех внешних углов правильного многоугольника равна 360º. Таким образом, сумма всех внешних углов правильного семиугольника равна 360º. Таким образом, каждый внешний угол правильного семиугольника = 360/7 = 51,43º
Ссылки по теме
Проверьте следующие ссылки, связанные с семиугольником.
Часто задаваемые вопросы о Heptagon
Что такое семиугольник в математике?
Семиугольник — это многоугольник с семью сторонами, который имеет 7 сторон, 7 вершин и 7 ребер. Длины сторон и меры углов семиугольника могут быть равны или не равны друг другу. Другое название семиугольника — септагон.
Что такое выпуклый семиугольник?
Выпуклый семиугольник — это такой, у которого все внутренние углы меньше 180°. Все вершины выпуклого семиугольника направлены наружу.
Как рассчитать диагонали семиугольника?
Диагонали семиугольника можно вычислить, нарисовав отрезки, соединяющие каждые две противоположные вершины, и посчитав их. Мы также можем рассчитать количество диагоналей, используя формулу n(n — 3)/2, где n — количество сторон многоугольника. Для семиугольника значение n равно 7. Таким образом, количество диагоналей можно рассчитать как 7 (7 — 3)/2 = 28/2 = 14,
.Сколько диагоналей у семиугольника?
Семиугольник имеет 14 диагоналей, которые можно рассчитать по формуле n(n — 3)/2, где n — количество сторон.
Чему равна сумма углов в семиугольнике?
Сумма внутренних углов семиугольника равна 900°, что можно рассчитать по формуле внутреннего угла правильного многоугольника (n — 2) × 180°, где n — количество сторон. Для семиугольника значение n равно 7. Таким образом, по формуле сумма внутренних углов будет равна 900°. Сумма внешних углов семиугольника равна 360°.
Как найти внутренние углы правильного семиугольника?
Каждый внутренний угол правильного семиугольника можно рассчитать, используя сумму внутренних углов семиугольника, которая равна 900°.Поскольку все углы правильного семиугольника равны, а внутренних углов в семиугольнике 7, величина каждого внутреннего угла будет равна 900°/7 = 128,57°
.Как найти периметр правильного семиугольника?
Периметр — это сумма всех сторон многоугольника. Поскольку у правильного семиугольника 7 сторон одинаковой длины, его периметр рассчитывается по формуле: периметр правильного семиугольника = 7 × длина стороны.
Сколько диагоналей имеет выпуклый многоугольник 7? – Кухня
Решенные примеры
| Название полигона | Количество сторон | Количество диагоналей |
|---|---|---|
| Четырехугольник | 4 | 2 |
| Пентагон | 5 | 5 |
| Шестигранник | 6 | 9 |
| Семиугольник | 7 | 14 |
Сколько диагоналей у выпуклого многоугольника?
Для выпуклого многоугольника с n сторонами имеется n вершин, и из каждой вершины можно провести n-3 диагонали, поэтому общее количество диагоналей, которые можно провести, равно n(n-3).
Сколько диагоналей у 8-стороннего выпуклого многоугольника?
Примера: квадрат (или любой четырехугольник) имеет 4(4−3)/2 = 4×1/2 = 2 диагонали. восьмиугольник имеет 8 (8−3) / 2 = 8 × 5/2 = 20 диагоналей. треугольник имеет 3 (3−3) / 2 = 3 × 0/2 = 0 диагоналей.
Сколько диагоналей в выпуклом семиугольнике?
Диагонали семиугольников Семиугольники имеют 14 диагоналей. Для выпуклых семиугольников все диагонали будут внутри фигуры.
Сколько диагоналей у семиугольника с 7 сторонами?
Гептагон — это многоугольник (замкнутая форма, состоящая из отрезков), состоящий из 7 сторон и 7 углов.Слово «гептагон» состоит из двух слов: «гепта» означает «семь» и «гон» означает стороны. В семиугольнике 14 диагоналей, и в данном семиугольнике сегменты синей линии представляют диагонали.
Чему равна сумма углов выпуклого многоугольника с числом сторон 7?
В этом вопросе n = 7, поэтому сумма углов равна: (7-2) × 180° = 5 × 180° = 900°.
Сколько диагоналей в многоугольнике с 12 сторонами?
В двенадцатиугольнике 54 диагонали. Эти диагонали можно рассчитать по формуле: 1/2 × n × (n-3), где n = количество сторон. В этом случае n = 12,
Эти диагонали можно рассчитать по формуле: 1/2 × n × (n-3), где n = количество сторон. В этом случае n = 12,
Сколько диагоналей в многоугольнике с 10 сторонами?
Сколько диагоналей правильного десятиугольника (10-стороннего многоугольника) не параллельны ни одной из сторон (AMC12)? В десятиугольнике (10 2) – 10 = 35 диагоналей. Каждая пара противоположных сторон имеет три диагонали, которые параллельны им, поэтому 5 * 3 = 15 диагоналей параллельны стороне.
Как называется семигранная фигура?
Семиугольник — это многоугольник с семью сторонами.Его также иногда называют септагоном, хотя это использование смешивает латинский префикс sept- (производный от septua-, что означает «семь») с греческим суффиксом -gon (от gonia, что означает «угол»), и поэтому не рекомендуется.
Что такое выпуклый семиугольник?
Если все внутренние углы семиугольника меньше 180°, то он выпуклый. Если один или несколько внутренних углов больше 180 °, он вогнутый.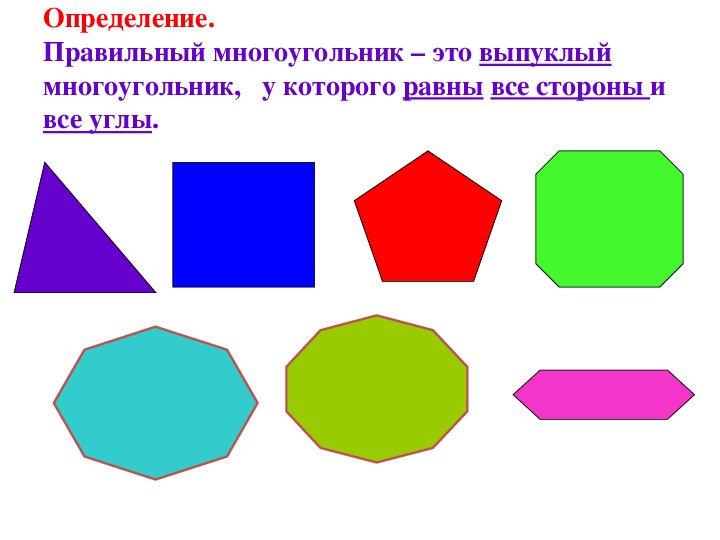 Правильный семиугольник — это выпуклый семиугольник.
Правильный семиугольник — это выпуклый семиугольник.
Что такое многоугольник семиугольника?
Семиугольник — это многоугольник с семью сторонами.Правильные семиугольники имеют семь равных сторон и семь равных углов.
Сколько сторон у семиугольника?
В геометрии семиугольник или септагон — это многоугольник с семью сторонами или 7-угольник.
Какой из следующих многоугольников является выпуклым?
Плоский многоугольник выпуклый, если он содержит все отрезки, соединяющие любую пару его точек. Так, например, правильный пятиугольник выпуклый (левый рисунок), а пятиугольник с выемками — нет (правый рисунок). Плоский многоугольник, который не является выпуклым, называется вогнутым многоугольником.
Без мозаики выпуклыми семиугольниками · Semidoc
09 мар 2018Четвертый пост серии GT CoA, см. здесь для ознакомления.
Доклад, связанный с этим постом, был сделан пользователем
Микаэль Рао о своем недавнем результате
о пятиугольных мозаиках. Эта тема обсуждалась во многих местах (см., например,
Журнал Кванта и это видео).
Этот пост будет посвящен другому аспекту: как насчет семиугольных мозаик?
Точнее, как показать, что нет замощения плоскости выпуклой
семиугольная плитка?
Эта тема обсуждалась во многих местах (см., например,
Журнал Кванта и это видео).
Этот пост будет посвящен другому аспекту: как насчет семиугольных мозаик?
Точнее, как показать, что нет замощения плоскости выпуклой
семиугольная плитка?
Сначала мы представляем простое эвристическое доказательство, которое дает интуитивное представление о том, почему это верно. а затем более подробное доказательство.В первом используется простая геометрия, во втором граф теоретический.
Пусть точка контакта будет местом, где встречаются три или более тайлов. Без потери В общем случае можно предположить, что тайлы сходятся только в вершинах, т. е. нет точка контакта внутри ребра, она всегда находится в конечной точке.
Как сумма внутренних углов $n$-угольника
составляет $(n-2)\times 180$ градусов, для семиугольника это $5\times 180=900$ градусов.
Средний градус $900/7\примерно 129$ градусов.Это означает, что в один
точки соприкосновения есть в среднем $360/129\около 2,8$ встречи семиугольников.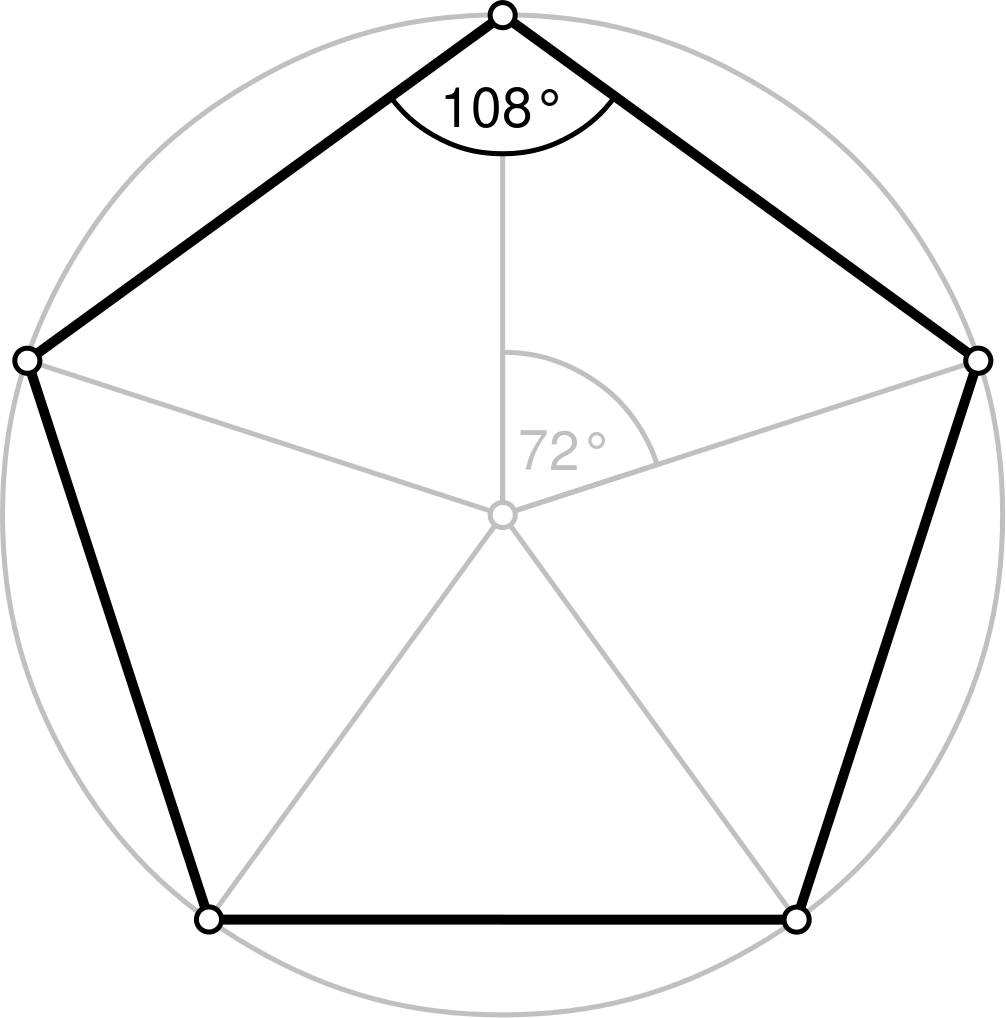 Это не имеет смысла, потому что в каждой точке контакта должно быть как минимум
три плитки.
Это не имеет смысла, потому что в каждой точке контакта должно быть как минимум
три плитки.
Первая попытка через степень
Возьмите бесконечную мозаику и нарисуйте следующий график. В середине каждого нарисуйте вершину, а между двумя вершинами, представляющими соседние плитки, нарисуйте край. Этот граф является бесконечным и плоским. Так как плитки выпуклые, то не менее семи различных плиток, примыкающих к ней, а затем минимальная степень вершина в графе равна семи.
Если вы привыкли к планарным графикам, то можете подумать, что этого достаточно для заключения.
Действительно, известно, что средняя степень панарных графов строго меньше
чем шесть
(см., например, здесь),
и следует противоречие. На самом деле этого недостаточно, потому что это среднее
верхняя граница степени выполняется только в конечном графе. В качестве контрпримера этому в
бесконечные графы, рассмотрим бесконечное регулярное дерево произвольно большой степени $d$ ;
это планарный граф со средней степенью $d$.
Формула Эйлера на двойственном
Граница степеней происходит из классического инструмента для плоских графов, Формула Эйлера. Он утверждает, что $|V|-|E|+|F|=2$ для конечных планарных графов, где $V$ — множество узлов, $E$ — множество ребер, а $F$ — множество граней. Проблема заключается в том, что он работает только для конечных графов. Мы рассмотрим достаточно большую часть бесконечный граф и использовать формулу Эйлера, чтобы доказать результат.
Вероятно, этого можно добиться в графе, который мы определили, но это более удобно на своем дуале.2$ строго внутри графа, называются внутренними узлами ($V_i$).
Мы дважды считаем ребра. Для каждого ребра, разделите его вдоль на два полуребра. Ясно, что полуребер $2|E|$. Также каждое лицо, кроме externalface представляет собой плитку, поэтому вносит семь полуребер. Количество полуребер внешней грани находится в $O(r)$. Таким образом, $2|E|=7|F|+O(r)$.
Теперь посчитаем углы (или внутренние углы) плитки. Каждая плитка имеет семь
углов, таким образом, это число равно $7|F|$.Поскольку каждый внутренний узел вносит свой вклад
не менее трех углов, $7|F|\geq 3|V_i|$.
Каждая плитка имеет семь
углов, таким образом, это число равно $7|F|$.Поскольку каждый внутренний узел вносит свой вклад
не менее трех углов, $7|F|\geq 3|V_i|$.
Теперь, используя $|V|=|V_i|+|V_b|$, затем $|E|=\frac{7}{2}|F|+O(r)$ и, наконец, $|F|\geq \frac{3}{7}|V_i|$ получается: $-\frac{15}{14}V_i+V_b-O(r)\geq 2$. Это невозможно, потому что $V_i$ имеет более высокий порядок величины, чем два других членов, таким образом, асимптотика должна стремиться к $-\infty$.
Спасибо Микаэлю Рао за обсуждения.
[PDF] Классификация полигонов — Скачать PDF бесплатно
Скачать классификацию полигонов…
Polygon ClassificationBill Zahner Lori Jordan
Скажите спасибо авторам Нажмите http://www.ck12.org/saythanks (регистрация не требуется)
Чтобы получить доступ к настраиваемой версии этой книги, а также к другому интерактивному контенту, посетите www.ck12.org
Фонд CK-12 — некоммерческая организация, миссия которой — снизить стоимость материалов для учебников для рынка K-12 как в США, так и во всем мире. Используя открытую, совместную и веб-модель компиляции, CK-12 является пионером и продвигает создание и распространение высококачественных адаптивных онлайн-учебников, которые можно смешивать, изменять и распечатывать (т.например, учебники FlexBook®). Copyright © 2015 CK-12 Foundation, www.ck12.org Названия «CK-12» и «CK12» и соответствующие логотипы, а также термины «FlexBook®» и «FlexBook Platform®» (совместно именуемые «Знаки CK-12») товарными знаками и знаками обслуживания Фонда CK-12 и защищены федеральными, государственными и международными законами. Любая форма воспроизведения этой книги в любом формате или на любом носителе, целиком или по частям, должна включать реферальную ссылку авторства http://www.ck12.org/saythanks (размещенную на видном месте) в дополнение к следующим условиям.Если не указано иное, весь Контент CK-12 (включая учебные материалы CK-12) предоставляется Пользователям в соответствии с лицензией Creative Commons Attribution-Non-Commercial 3.0 Unported (CC BY-NC 3.
Используя открытую, совместную и веб-модель компиляции, CK-12 является пионером и продвигает создание и распространение высококачественных адаптивных онлайн-учебников, которые можно смешивать, изменять и распечатывать (т.например, учебники FlexBook®). Copyright © 2015 CK-12 Foundation, www.ck12.org Названия «CK-12» и «CK12» и соответствующие логотипы, а также термины «FlexBook®» и «FlexBook Platform®» (совместно именуемые «Знаки CK-12») товарными знаками и знаками обслуживания Фонда CK-12 и защищены федеральными, государственными и международными законами. Любая форма воспроизведения этой книги в любом формате или на любом носителе, целиком или по частям, должна включать реферальную ссылку авторства http://www.ck12.org/saythanks (размещенную на видном месте) в дополнение к следующим условиям.Если не указано иное, весь Контент CK-12 (включая учебные материалы CK-12) предоставляется Пользователям в соответствии с лицензией Creative Commons Attribution-Non-Commercial 3.0 Unported (CC BY-NC 3.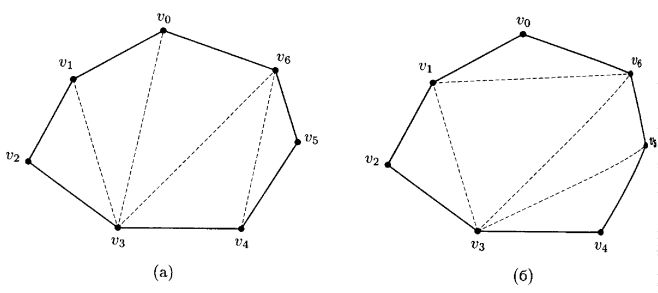 0) (http://creativecommons). .org/licenses/by-nc/3.0/), с изменениями и обновлениями Creative Commons время от времени («Лицензия CC»), которая включена в настоящий документ посредством этой ссылки. Полные условия можно найти по адресу http://www.ck12.org/about/terms-of-use. Напечатано: 1 июня 2015 г.
0) (http://creativecommons). .org/licenses/by-nc/3.0/), с изменениями и обновлениями Creative Commons время от времени («Лицензия CC»), которая включена в настоящий документ посредством этой ссылки. Полные условия можно найти по адресу http://www.ck12.org/about/terms-of-use. Напечатано: 1 июня 2015 г.
АВТОРЫ Билл Захнер Лори Джордан
www.ck12.org
ГЛАВА
Глава 1. Классификация многоугольников
1
Классификация многоугольников
Здесь вы узнаете, как классифицировать многоугольник на основе его сторон. Вы также узнаете, как определить, является ли многоугольник выпуклым или вогнутым. Что, если бы вам сказали, сколько сторон у многоугольника? Как бы вы описали многоугольник на основе этой информации? После завершения этой концепции вы сможете классифицировать многоугольник в соответствии с количеством его сторон. Смотреть это
МЕДИА Щелкните изображение слева или используйте указанный ниже URL.URL: http://www.ck12.org/flx/render/embeddedobject/136953
CK-12 Foundation: Chapter1PolygonClassificationA
МЕДИА Щелкните изображение слева или используйте указанный ниже URL. URL: http://www.ck12.org/flx/render/embeddedobject/1282
URL: http://www.ck12.org/flx/render/embeddedobject/1282
Джеймс Соуза: Руководство по классификации многоугольников
Многоугольник — это любая замкнутая плоская фигура, целиком состоящая из отрезков, пересекающихся в своих конечных точках. Многоугольники могут иметь любое количество сторон и углов, но стороны никогда не могут быть изогнутыми.Отрезки называются сторонами многоугольников, а точки, в которых отрезки пересекаются, называются вершинами. Самый простой способ определить многоугольник — найти замкнутую фигуру без изогнутых сторон. Многоугольники могут быть как выпуклыми, так и вогнутыми. Думайте о термине «вогнутый» как о пещере или «обрушении». У вогнутого многоугольника есть часть, которая «указывает внутрь» к середине фигуры. Все звезды представляют собой вогнутые многоугольники.
Выпуклый многоугольник не обладает этим свойством. 1
www.ck12.org
Диагонали — это отрезки, соединяющие вершины выпуклого многоугольника, не являющиеся его сторонами.
Все красные линии являются диагоналями. Этот пятиугольник имеет 5 диагоналей. Независимо от того, является ли многоугольник выпуклым или вогнутым, его всегда можно назвать по количеству сторон. См. диаграмму ниже.
Таблица 1.1:
2
2
многоугольника Треугольник
Количество сторон 3
Количество диагоналей 0
четырехугольник
4
2
Pentagon
5
5
Выпуклый пример
www .CK12.ORG
Глава 1. Полигон классификация
Таблица 1.1: (продолжение) Полигон Имя hexagon
Количество сторон 6
Количество диагоналей
Heptagon
7
14
Octagon
8
?
Нонагон
9
?
Декагон
10
?
11
?
Недесятиугольный десятиугольный
или
Выпуклый Пример
3
www.ck12.org
ТАБЛИЦА 1.1: (продолжение) Название многоугольника Додекагон
Количество сторон 12
Количество диагоналей ?
n−gon
n (где n > 12)
?
Выпуклая Пример
Пример A
Какая из фигур ниже является многоугольником?
Самый простой способ идентифицировать многоугольник — определить, какие фигуры не являются многоугольниками.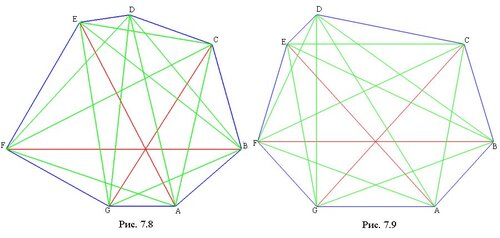 B и C имеют по крайней мере одну изогнутую сторону, поэтому они не могут быть многоугольниками. D имеет все прямые стороны, но одна из вершин не находится в конце соседней стороны, поэтому он также не является многоугольником.А — единственный многоугольник. Пример B
B и C имеют по крайней мере одну изогнутую сторону, поэтому они не могут быть многоугольниками. D имеет все прямые стороны, но одна из вершин не находится в конце соседней стороны, поэтому он также не является многоугольником.А — единственный многоугольник. Пример B
Определите, являются ли приведенные ниже формы выпуклыми или вогнутыми.
Чтобы определить, является ли многоугольник вогнутым, посмотрите на многоугольники и посмотрите, не «прогибается» ли какой-либо угол внутрь многоугольника. Первый многоугольник этого не делает, поэтому он выпуклый. У двух других есть, поэтому они вогнутые. Вы можете добавить сюда, что вогнутые многоугольники имеют по крайней мере одну диагональ вне фигуры. 4
www.ck12.org
Глава 1. Классификация многоугольников
Пример C
Какой из приведенных ниже рисунков не является многоугольником?
C — трехмерная фигура, поэтому она не лежит в одной плоскости, поэтому это не многоугольник.Посмотрите это видео, чтобы получить помощь с приведенными выше примерами.
МЕДИА Щелкните изображение слева или используйте указанный ниже URL. URL: http://www.ck12.org/flx/render/embeddedobject/136954
CK-12 Foundation: Chapter1PolygonClassificationB
Guided Practice
Назовите три приведенных ниже многоугольника по количеству сторон, а также если они выпуклые или вогнутые. .
Ответы: A. Эта фигура имеет шесть сторон и вогнута, поэтому это вогнутый шестиугольник. B. Эта фигура имеет пять сторон и выпукла, поэтому это выпуклый пятиугольник.C. Эта фигура имеет десять сторон и выпукла, поэтому это выпуклый десятиугольник.
Узнать больше
В задачах 1-6 назовите каждый многоугольник как можно подробнее. 5
www.cack12.org
1.
2.
3.
4.
5.
6. 7. Объясните, почему следующие цифры не являются многоугольниками:
6
www. ck12.org
8. 9. 10. 11. 12.
Глава 1. Классификация многоугольников
Сколько диагоналей можно провести из одной вершины пятиугольника? Нарисуйте набросок своего ответа. Сколько диагоналей можно провести из одной вершины восьмиугольника? Нарисуйте набросок своего ответа. Сколько диагоналей можно провести из одной вершины двенадцатиугольника? Используйте свои ответы с 8 по 10, чтобы выяснить, сколько диагоналей можно провести из одной вершины n-угольника? Определите общее количество диагоналей восьмиугольника, девятиугольника, десятиугольника, десятиугольника и додекагона. Вы видите закономерность? БОНУС: найдите уравнение общего числа диагоналей для n-угольника.
Для 13-17 определите, является ли утверждение ВСЕГДА истинным, ИНОГДА истинным или НИКОГДА верным.13. 14. 15. 16. 17.
Многоугольник должен быть заключен. Звезда – это вогнутый многоугольник. Четырехугольник — это квадрат. Из одной вершины многоугольника можно нарисовать (n − 1) треугольников. Десятиугольник — пятиконечная звезда.
В геометрии важно знать разницу между эскизом, чертежом и построением. Эскиз обычно рисуется от руки и помечается соответствующими отметками конгруэнтности или помечается размером. Он может или не может быть нарисован в масштабе. Чертеж выполняется с помощью линейки, транспортира или циркуля и должен быть выполнен в масштабе.Построение выполняется с использованием только циркуля и линейки и должно быть выполнено в масштабе. Для 18-21 нарисуйте, зарисуйте или постройте указанные фигуры. 18. 19. 20. 21.
Он может или не может быть нарисован в масштабе. Чертеж выполняется с помощью линейки, транспортира или циркуля и должен быть выполнен в масштабе.Построение выполняется с использованием только циркуля и линейки и должно быть выполнено в масштабе. Для 18-21 нарисуйте, зарисуйте или постройте указанные фигуры. 18. 19. 20. 21.
Нарисуйте выпуклый семиугольник, у которого две равные стороны и три равных угла. Нарисуйте не многоугольную фигуру. Начертите вогнутый пятиугольник, у которого ровно два прямых угла и по крайней мере две равные стороны. Нарисуйте равносторонний четырехугольник, который НЕ является квадратом.
7
1.18: Классификация многоугольников — K12 LibreTexts
Категории многоугольников на основе количества сторон, а также того, являются ли они вогнутыми или выпуклыми.
Полигоны
Многоугольник — это любая замкнутая двумерная фигура, полностью состоящая из отрезков, пересекающихся в своих концах. Многоугольники могут иметь любое количество сторон и углов, но стороны никогда не могут быть изогнутыми. Сегменты называются сторонами многоугольников, а точки, в которых сегменты пересекаются, называются вершинами .
Сегменты называются сторонами многоугольников, а точки, в которых сегменты пересекаются, называются вершинами .
Многоугольники могут быть выпуклыми или вогнутыми . Термин «вогнутый» относится к пещере, или многоугольник «прогибается».Все звезды представляют собой вогнутые многоугольники.
Рисунок \(\PageIndex{1}\)Выпуклый многоугольник не прогибается. Выпуклые многоугольники выглядят так:
Рисунок \(\PageIndex{2}\)Диагональ — это отрезок, не являющийся боковым, который соединяет две вершины выпуклого многоугольника.
Рисунок \(\PageIndex{3}\)Все сегменты красной линии являются диагоналями. Этот пятиугольник имеет 5 диагоналей.
Независимо от того, является многоугольник выпуклым или вогнутым, он всегда называется по количеству сторон. Исследуйте связь между количеством сторон выпуклого многоугольника и его диагоналями.Сможете заполнить таблицу?
Что, если бы вам сказали, сколько сторон у многоугольника? Как бы вы описали многоугольник на основе этой информации?
Пример \(\PageIndex{1}\)
Какая из фигур ниже является многоугольником?
Рисунок \(\PageIndex{15}\)Решение
Самый простой способ идентифицировать многоугольник — определить, какие фигуры являются , а не многоугольниками. B и C имеют по крайней мере одну изогнутую сторону, поэтому они не являются многоугольниками.D имеет все прямые стороны, но одна из вершин не находится в конце, поэтому это не многоугольник. А — единственный многоугольник.
B и C имеют по крайней мере одну изогнутую сторону, поэтому они не являются многоугольниками.D имеет все прямые стороны, но одна из вершин не находится в конце, поэтому это не многоугольник. А — единственный многоугольник.
Пример \(\PageIndex{2}\)
Определите, являются ли фигуры ниже выпуклыми или вогнутыми.
Рисунок \(\PageIndex{16}\)Решение
Чтобы определить, является ли многоугольник вогнутым, посмотрите на многоугольники и посмотрите, не «прогибается» ли какой-либо угол внутрь многоугольника. Первый многоугольник этого не делает, поэтому он выпуклый. У двух других есть, поэтому они вогнутые.
Пример \(\PageIndex{3}\)
Назовите три многоугольника ниже по количеству их сторон и по тому, является ли он выпуклым или вогнутым.
Рисунок \(\PageIndex{17}\)Решение
Розовый многоугольник представляет собой вогнутый шестиугольник (6 сторон).
Зеленый многоугольник выпуклый пятиугольник (5 сторон).
Желтый многоугольник представляет собой выпуклый десятиугольник (10 сторон).
Пример \(\PageIndex{4}\)
Нарисуйте многоугольник с 7 сторонами, также называемый семиугольником.Сколько диагоналей у семиугольника?
Рисунок \(\PageIndex{18}\)Решение
Сначала нарисуйте семиугольник. Проведя все диагонали и посчитав их, мы видим, что их 14.
Пример \(\PageIndex{5}\)
Правда или ложь: четырехугольник всегда квадрат.
Раствор
Ложь. Только четырехугольники с четырьмя равными сторонами и четырьмя прямыми углами будут квадратами. Существует много четырехугольников (таких как прямоугольники, воздушные змеи, параллелограммы, трапеции и т.), которые не обязательно являются квадратами.
Дополнительный ресурс
Видео: сумма внутренних углов многоугольника
Упражнения: Вопросы для обсуждения по классификации полигонов
Учебные пособия: Учебное пособие по многоугольникам
Практика: классифицировать многоугольники
Реальный мир: полигоны природы
.

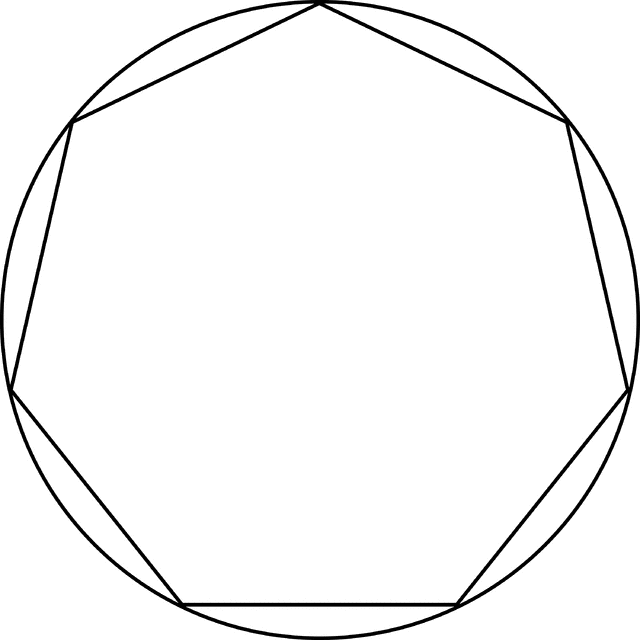
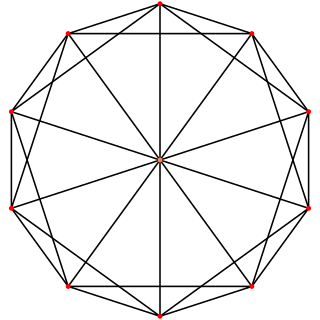 ..
..