Что такое многоугольник, выпуклый многоугольник, четырехугольник
В геометрии многоугольниками называют плоские замкнутые фигуры, состоящие из нескольких прямых отрезков. Суммарная длина всех сторон называется периметром.
Поговорим подробнее о видах многоугольников и их характеристиках.
Определение
Многоугольник — это замкнутая ломаная линия.
Многоугольник — это простое понятие: Если в замкнутой ломаной линии соседние стороны имеют общую точку и любые две стороны не являются продолжением друг друга, то фигура называется многоугольником.
При изучении темы, что такое многоугольники, применяются следующие термины:
- Вершины многоугольника.
- Стороны замкнутой ломаной.
- Углы, образованные между смежными сторонами.
- Отрезки между несмежными вершинами называются диагоналями.
- Сумма длин всех сторон фигуры является периметром.

- Внутренние углы между соседними сторонами. Число углов равно числу сторон и вершин.
Наименования данных фигур зависят от количества сторон:
- Треугольник – это 3 стороны.
- Четырехугольник имеет 4 стороны.
- Пятиугольник – это 5 сторон и пр.
Все фигуры имеют буквенные обозначения, необходимо правильно проставлять их при вершинах.
Например, обозначение пятиугольника ABCDE будет выглядеть так:
В этом пятиугольнике вершинами являются точки: A, B, C, D и E.
Отрезки: AB, BC, CD, DE и EA являются сторонами пятиугольника.
Виды многоугольников
Различают несколько видов этих фигур: выпуклые, вогнутые, правильные и неправильные.
Какие многоугольники называются выпуклыми и невыпуклыми (вогнутыми)? Чтобы определить, какой многоугольник называется выпуклым, достаточно знать его определение.
Если стороны, при продолжении до прямой линии, не пересекают плоскость, то это выпуклый многоугольник.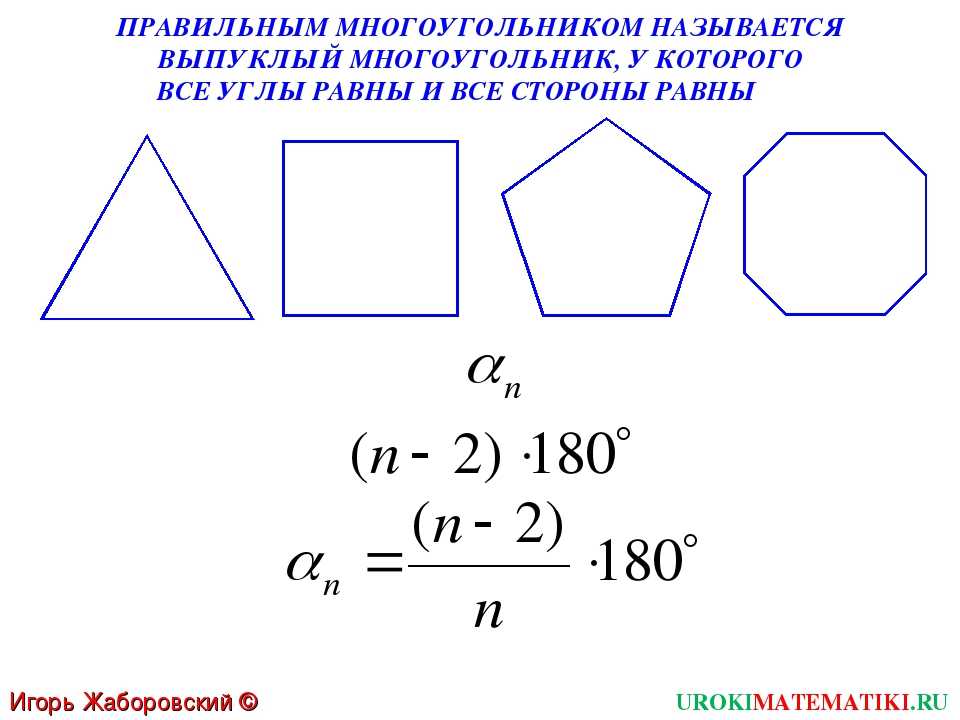
Определение невыпуклого многоугольника: если при продолжении сторон прямые линии пересекают плоскость фигуры, то она является вогнутой.
Что такое правильные многоугольники
Выпуклые многоугольники, у которых все стороны и все углы равны, называются правильными.
На рисунке показан правильный многоугольник.
Как найти периметр многоугольника и определить диагонали
Периметром многоугольника называется сумма длин его сторон.
Для четырехугольника ABCD периметр будет равен сумме его сторон: AB + BC + CD + DA.
Пример
Задание: Длина одной стороны четырехугольника ABCD равна 3 см. Требуется найти
периметр четырехугольника.
Решение: AB + BC + CD + DA = 3 + 3 + 3 + 3 = 12 см
Ответ: периметр четырехугольника ABCD равен 12 см.
Диагональю многоугольника является отрезок, который соединяет вершины противоположных углов.
Например, отрезок AD будет являться диагональю фигуры ABCDEF:
Свойство треугольников: если треугольник не имеет углов с общими сторонами, диагональ он иметь не может.
Если из вершин провести несколько диагоналей, то они разделят фигуру на несколько треугольников:
Количество треугольников будет на 2 меньше, чем число сторон:
Если t — количество треугольников, а n — количество сторон, то формула будет выглядеть так: t = n – 2.
Разделение многоугольника диагоналями на несколько треугольников помогает быстро найти площадь.
Чтобы найти площадь многоугольника, нужно разделить его на треугольники, затем найти их площадь и сложить полученные результаты.
Сумма углов выпуклого многоугольника
Научимся находить сумму углов выпуклого четырёхугольника, не только внешних, но и внутренних. Но сначала определим, какие углы называются внутренними углами выпуклого многоугольника.
Внутренним называется угол между смежными сторонами.
Например, ∠ABC является внутренним для ABCDEF.
Внешним называют угол между стороной фигуры и линейным продолжением близлежащего отрезка.
Например, ∠LBC является внешним углом для ABCDEF.
Правило: сумма углов выпуклого многоугольника всегда равно числу его сторон. Это определение относится ко всем углам.
Это значит, чтобы найти количество углов, достаточно посчитать количество всех его сторон. Значит сумма углов четырехугольника будет равна четырем.
Сумма внутренних углов
Правило для нахождения суммы углов гласит: чтобы найти сумму всех внутренних углов выпуклого многоугольника, нужно умножить уменьшенное на 2 количество его сторон на 180°.
Обозначения выглядят следующим образом:
- сумма углов – s;
- число сторон – n;
- два прямых угла (2 · 90 = 180°) – 2d.
Формула многоугольника для нахождения суммы углов: s = 2d · (n – 2).
Найти сумму углов также можно с помощью деления фигуры на треугольники. Она будет равна сумме углов всех треугольников (180° · n).
Пример:
Если у фигуры 4 треугольника, то сумму всех углов находим по следующей формуле: s = 2d (n — 2) = 180 · 4 = 720°.
Это означает, что сумма внутренних углов – это постоянная величина, которая зависит от количества его сторон.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Сумма внешних углов
Определение: Сумму всех внешних углов многоугольника находим по формуле: s = 4d.
Где:
- s — сумма внешних углов;
- 4d — четыре прямых угла (4 · 90 = 360°).
Сумма смежных (внутреннего и внешнего) углов, лежащих при вершине, равна 180° · (2d).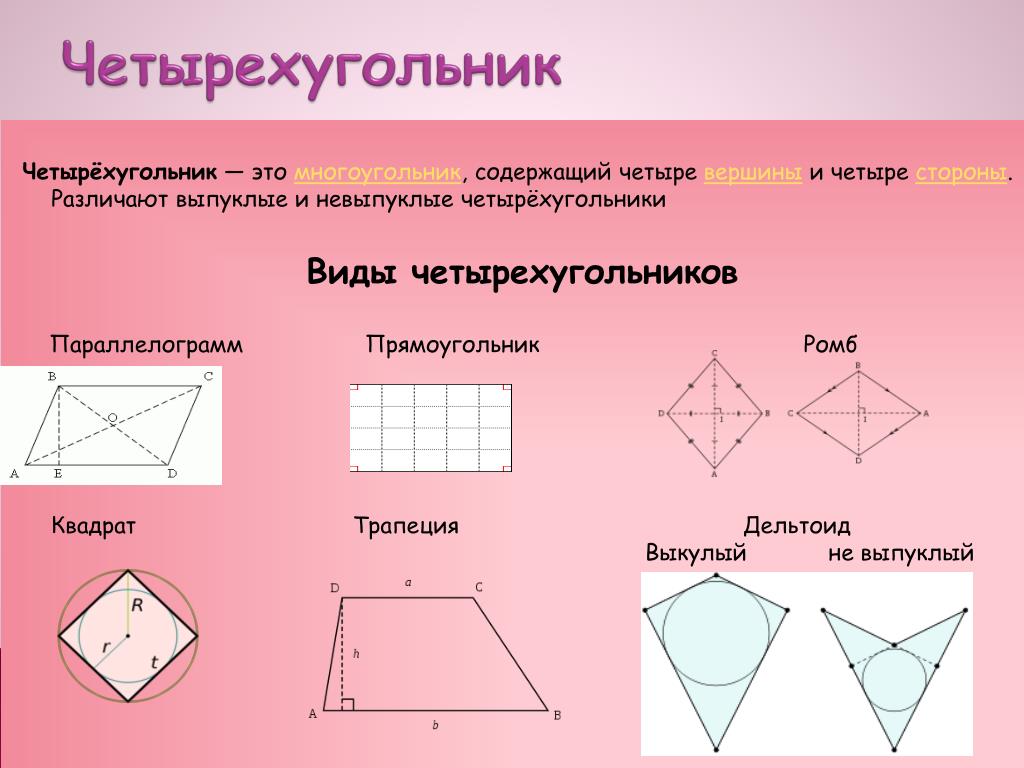
Например, ∠1 и ∠2:
Если имеется n вершин, то сумма внутренних и внешних и углов будет равна 2dn.
Пример
Задание: Найдите сумму углов выпуклого двенадцатиугольника.
Решение: Для выпуклого n-угольника сумма углов равна 180° (n -2).
Если имеется 12 вершин, то сумма всех углов будет рассчитываться следующим образом: 2 · 90 · (12 – 2) = 1800°.
Зная основные формулы и определения для многоугольников, можно легко справиться с любой задачей.
Построение минимальных выпуклых оболочек / Хабр
Проведя небольшое научное исследование (проще говоря, выполнив поиск на сайте), обнаружил, что на хабре имеется всего две статьи с тегом
вычислительная геометрия, причем одна из них оказалась моей. Т.к. в последнее время я несколько заинтересовался этой тематикой, то решил продолжить тему алгоритмической геометрии рассмотрением задачи построения так называемых минимальных выпуклых оболочек. Хотя рисунок справа и дает проницательному хаброчитателю исчерпывающее объяснение того, что это такое, тем не менее под катом будут даны чуть более формальные определения и описаны два классических алгоритма построения минимальных выпуклых оболочек.
Хотя рисунок справа и дает проницательному хаброчитателю исчерпывающее объяснение того, что это такое, тем не менее под катом будут даны чуть более формальные определения и описаны два классических алгоритма построения минимальных выпуклых оболочек.
Пусть на плоскости задано конечное множество точек A. Оболочкой этого множества называется любая замкнутая линия H без самопересечений такая, что все точки из A лежат внутри этой кривой. Если кривая H является выпуклой (например, любая касательная к этой кривой не пересекает ее больше ни в одной точке), то соответствующая оболочка также называется
Главной особенностью МВО множества точек A является то, что эта оболочка представляет собой выпуклый многоугольник, вершинами которого являются некоторые точки из A. Поэтому задача поиска МВО в конечном итоге сводится к отбору и упорядочиванию нужных точек из A. Упорядочивание является необходимым по той причине, что выходом алгоритма должен быть многоугольник, т.е. последовательность вершин. Наложим дополнительно условие на порядок расположения вершин — направление обхода многоугольника должно быть положительным (напомню, что положительным называется обход фигуры против часовой стрелки).
Задача построения МВО считается одной из самых простых задач вычислительной геометрии, для нее существует много различных алгоритмов. Ниже мы рассмотрим два таких алгоритма — Грэхема (Graham scan) и Джарвиса (Jarvis march). Их описание иллюстрируется кодом на Питоне. Обоим алгоритмам потребуется функция rotate, побробно описанная в предыдущем моем посте. Напомню, что эта функция определяет, с какой стороны от вектора AB находится точка C (положительное возвращаемое значение соответствует левой стороне, отрицательное — правой).
def rotate(A,B,C): return (B[0]-A[0])*(C[1]-B[1])-(B[1]-A[1])*(C[0]-B[0])
Этот алгоритм является трехшаговым. На первом шаге ищется любая точка в A, гарантированно входящая в МВО. Нетрудно сообразить, что такой точкой будет, например, точка с наименьшей x-координатой (самая левая точка в A). Эту точку (будем называть ее стартовой) перемещаем в начало списка, вся дальнейшая работа будет производиться с оставшимися точками. По некоторым соображениям, исходный массив точек A нами меняться не будет, для всех манипуляций с точками будем использовать косвенную адресацию: заведем список P, в котором будут хранится номера точек (их позиции в массиве A). Итак, первый шаг алгоритма заключается в том, чтобы первой точкой в P оказалась точка с наименьшей x-координатой. Код:
def grahamscan(A):
n = len(A) # число точек
P = range(n) # список номеров точек
for i in range(1,n):
if A[P[i]][0]<A[P[0]][0]: # если P[i]-ая точка лежит левее P[0]-ой точки
P[i], P[0] = P[0], P[i] # меняем местами номера этих точек
Второй шаг в алгоритме Грэхема — сортировка всех точек (кроме P[0]-ой), по степени их левизны относительно стартовой точки R=AP[0]. Будем говорить, что B<C, если точка С находится по левую сторону от вектора RB.
Будем говорить, что B<C, если точка С находится по левую сторону от вектора RB.
Для выпонения такого упорядочивания можно применять любой алгоритм сортировки, основанный на попарном сравнении элементов, например, быструю сортировку. По некоторым причинам (главная из которых — корявость* рук), я буду использовать сортировку вставками.
*я буду очень признателен тем, кто сможет мне объяснить, как применить в данном случае встроенную питоновскую сортировку…
Итак, сортировка вставками (не забываем про косвенную адресацию и про то, что нулевая точка не сортируется):
for i in range(2,n):
j = i
while j>1 and (rotate(A[P[0]],A[P[j-1]],A[P[j]])<0):
P[j], P[j-1] = P[j-1], P[j]
j -= 1
Результат сортировки можно проиллюстрировать следующим рисунком.
Если мы теперь соединим точки в полученном порядке, то получим многоугольник, который, однако, не является выпуклым.
Переходим к третьему действию. Все, что нам осталось сделать, так это срезать углы. Для этого нужно пройтись по всем вершинам и удалить те из них, в которых выполняется правый поворот (угол в такой вершине оказывается больше развернутого). Заводим стек S (реально список) и помещаем в него первые две вершины (они, опять же, гарантированно входят в МВО).
S = [P[0],P[1]]
Затем просматриваем все остальные вершины, и отслеживаем направление поворота в них с точки зрения последних двух вершин в стеке S: если это направление отрицательно, то можно срезать угол удалением из стека последней вершины. Как только поворот оказывается положительным, срезание углов завершается, текущая вершина заносится в стек.
for i in range(2,n):
while rotate(A[S[-2]],A[S[-1]],A[P[i]])<0:
del S[-1] # pop(S)
S.append(P[i]) # push(S,P[i])
В итоге в стеке S (который теперь можно рассматривать, как список) оказывается искомая последовательность вершин, причем в нужной нам ориентации, определяющая МВО заданного множества точек A.
return S
Сложность первого и последнего шагов алгоритма является линейной по n (хотя в последнем случае имеется вложенный цикл, однако, каждая вершина внутри этого цикла ровно один раз заносится в стек, и не более одного раза оттуда удаляется), следовательно, сложность всего алгоритма определяется вторым шагом — сортировкой, именно поэтому сортировка вставкой оказывается не лучшим вариантом при больших n. Если ее заменить на быструю сортировку, то получим суммарную сложность алгоритма O(nlogn). Можно ли улучшить это время? Если алгоритм основан на попарном сравнении точек (как у нас), то доказано, что данная оценка в общем случае не улучшаема. С этой точки зрения алгоритм Грэхема оптимален. Тем не менее у него имеется не очень хорошая особенность — он не является адаптивным в том смысле, что не важно, сколько вершин в итоге войдет в МВО (три, пять, десять или n), все равно время будет линейно-логарифмическим. Такой адаптивностью обладает алгоритм Джарвиса, к рассмотрению которого мы плавно и переходим.
Полный код алгоритма Грэхема
def grahamscan(A):
n = len(A) # число точек
P = range(n) # список номеров точек
for i in range(1,n):
if A[P[i]][0]<A[P[0]][0]: # если P[i]-ая точка лежит левее P[0]-ой точки
P[i], P[0] = P[0], P[i] # меняем местами номера этих точек
for i in range(2,n): # сортировка вставкой
j = i
while j>1 and (rotate(A[P[0]],A[P[j-1]],A[P[j]])<0):
P[j], P[j-1] = P[j-1], P[j]
j -= 1
S = [P[0],P[1]] # создаем стек
for i in range(2,n):
while rotate(A[S[-2]],A[S[-1]],A[P[i]])<0:
del S[-1] # pop(S)
S.append(P[i]) # push(S,P[i])
return S
Алгоритм Джарвиса (другое название — алгоритм заворачивания подарков) концептуально устроен проще алгоритма Грэхема. Он является двухшаговым и не требует сортировки. Первый шаг точно такой же — нам нужна стартовая точка, которая гарантированно входит в МВО, берем самую левую точку из A.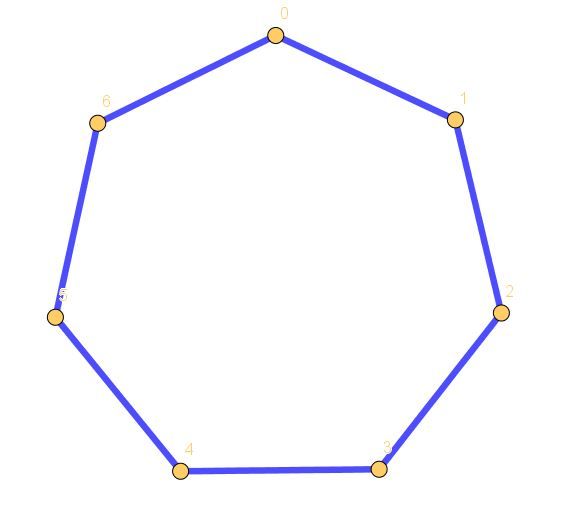
def jarvismarch(A):
n = len(A)
P = range(n)
for i in range(1,n):
if A[P[i]][0]<A[P[0]][0]:
P[i], P[0] = P[0], P[i]
На втором шаге алгоритма строится МВО. Идея: делаем стартовую вершину текущей, ищем самую правую точку в A относительно текущей вершины, делаем ее текущей и т.д. Процесс завершается, когда текущей вновь окажется стартовая вершина. Как только точка попала в МВО, больше ее можно не учитывать. Поэтому заведем еще один список H, в котором в правильном порядке будут храниться вершины МВО. В этот список сразу же заносим стартовую вершину, а в списке P эту вершину переносим в конец (где мы ее в конце концов найдем и завершим алгоритм).
H = [P[0]] del P[0] P.append(H[0])
Теперь организуем бесконечный цикл, на каждой итерации которого ищем самую левую точку из P относительно последней вершины в H. Если эта вершина стартовая, то прерываем цикл, если нет — то переносим найденную вершину из P в H.
while True:
right = 0
for i in range(1,len(P)):
if rotate(A[H[-1]],A[P[right]],A[P[i]])<0:
right = i
if P[right]==H[0]:
break
else:
H.append(P[right])
del P[right]
return H
Хм, мне удалось рассказать об алгоритме Джарвиса, не используя картинок. Следующий рисунок иллюстрирует все!
Оценим сложность алгоритма Джарвиса. Первый шаг линеен по n. Со вторым все интереснее. У нас имеется вложенный цикл, число внешних итераций равно числу вершин h в МВО, число внутренних итераций не превышает n. Следовательно, сложность всего алгоритма равна O(hn). Необычным в этой формуле является то, что сложность определяется не только длиной входных данных, но и длиной выхода (output-sensitive algorithm). А дальше как
точки лягут. В худшем случае все точки из A входят в МВО (т. е. A уже само по себе выпуклый многоугольник), тогда h=n и сложность подскакивает до квадратичной. В лучшем случае (при условии, что точки из A не лежат на одной прямой) h=3 и сложность становится линейной. Осталось заранее понять, какой у нас случай, что сделать не так просто (если у вас нет машины времени**), можно только исходить из характера задачи — если точек много и они равномерно заполняют некоторую область, то (возможно) Джарвис будет быстрее, если же данные собраны на границе области, то быстрее будет Грэхем, как-то так…
е. A уже само по себе выпуклый многоугольник), тогда h=n и сложность подскакивает до квадратичной. В лучшем случае (при условии, что точки из A не лежат на одной прямой) h=3 и сложность становится линейной. Осталось заранее понять, какой у нас случай, что сделать не так просто (если у вас нет машины времени**), можно только исходить из характера задачи — если точек много и они равномерно заполняют некоторую область, то (возможно) Джарвис будет быстрее, если же данные собраны на границе области, то быстрее будет Грэхем, как-то так…
**Машина времени вообще полезная штука с точки зрения алгоритмов, любая задача, требующая триллиона лет вычислений, с ее помощью может быть решена практически мгновенно — запускаем программу, садимся в машину времени, «летим» в будущее, считываем результат, возвращаемся назад. Осталось придумать, как обеспечить бесперебойную работу компьютера на пару триллионов лет…
Полный код алгоритма Джарвиса
def jarvismarch(A):
n = len(A)
P = range(n)
# start point
for i in range(1,n):
if A[P[i]][0]<A[P[0]][0]:
P[i], P[0] = P[0], P[i]
H = [P[0]]
del P[0]
P. append(H[0])
while True:
right = 0
for i in range(1,len(P)):
if rotate(A[H[-1]],A[P[right]],A[P[i]])<0:
right = i
if P[right]==H[0]:
break
else:
H.append(P[right])
del P[right]
return H
append(H[0])
while True:
right = 0
for i in range(1,len(P)):
if rotate(A[H[-1]],A[P[right]],A[P[i]])<0:
right = i
if P[right]==H[0]:
break
else:
H.append(P[right])
del P[right]
return H
На мой взгляд, задача построения минимальных выпуклых оболочек — хороший способ войти в тему вычислительной геометрии, достаточно легко придумать свой собственный алгоритм (однако, наверняка это будет вариация алгоритма Джарвиса). Утверждается, что приложений у этой задачи много, большая их часть связана с распознаванием образов, кластеризацией и т.п. Кроме того, задача построения МВО используется в качестве вспомогательного средства при решении более сложных задач вычислительной геометрии. Да, стоит отметить, что у этой задачи имеется весьма интересное трехмерное обобщение.
Спасибо всем за внимание!
Какие многоугольники образуют плоскость звезды
содержание
Каков многоугольник звезды?
В геометрии правильная многоугольная звезда — это равносторонний, равноугольный, самопересекающийся многоугольник.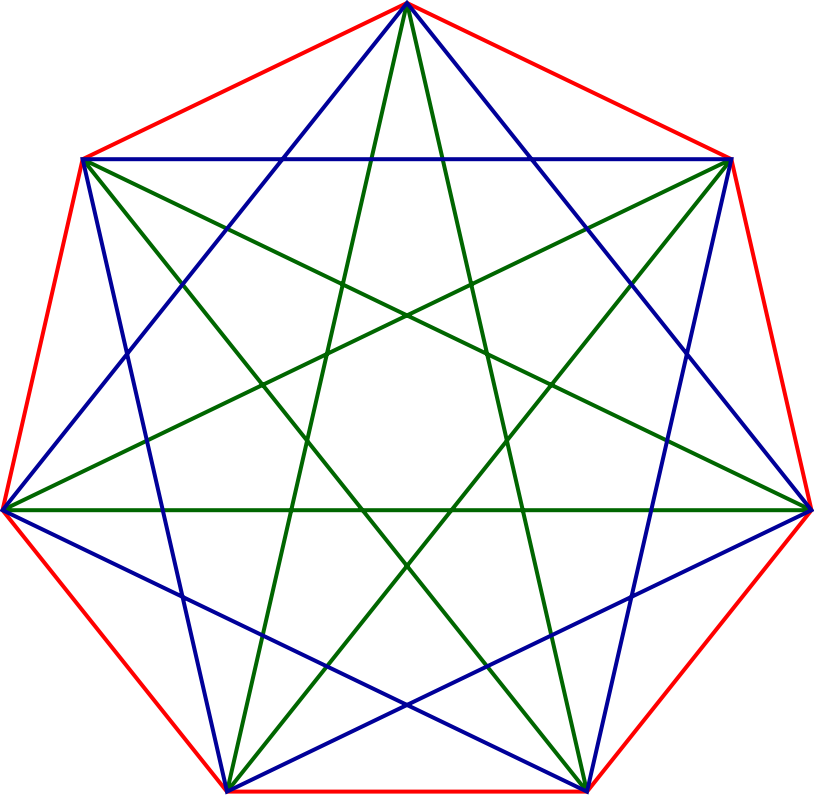
Какие многоугольники образуют сглаживание?
Таким образом, ваша развертка всегда представляет собой два конгруэнтных многоугольника и несколько параллелограммов, которые будут равны только в том случае, если основания призмы правильные. Способ расчета площади призмы, а также рабочие примеры можно найти здесь.
Сколько полигонов образуют развертку?
Развертка I) состоит только из многоугольников: треугольника и квадрата; Название пространственной геометрической формы, полученной по плану I, — пирамида с квадратным основанием, а по плану II — цилиндр.
Что такое звездчатые многоугольники?
Что такое звездчатые многоугольники? Звездные многоугольники — это именно то, что говорит само название, многоконечные звезды. Когда мы рисуем пятиконечную звезду традиционным способом, не отрывая карандаша от бумаги, у нас получается звездный правильный многоугольник (если удастся сделать все стороны и углы равными).
Как называются все многоугольники?
Поэтому по отношению к числу сторон многоугольникам можно давать следующие названия:
- 3 стороны → треугольник или трехугольник.

- 4 стороны → квадрат или четырехугольник.
- 5 сторон → пятиугольник или пятиугольник.
- 6 сторон → шестиугольник или шестигранник.
- 7 сторон → семиугольник или семиугольник.
- 8 сторон → восьмиугольник или восьмиугольник.
Почему звезда не многоугольник?
Ответ: Звезды — это многоугольники, которые, похоже, еще не определены формально. Можно только сказать, что это многоугольники, похожие на звезды; просто обычные звезды, изученной формы, с некоторой глубиной.
Как определить многоугольники?
Многоугольники представляют собой замкнутые плоские фигуры, образованные сторонами, которые, в свою очередь, являются отрезками прямых и не пересекаются ни в одной точке. Многоугольники — это замкнутые линии, образованные только непересекающимися отрезками.
Какая фигура представляет макет?
Трехмерная фигура, имеющая эту плоскость, представляет собой шестиугольную призму. Во-первых, нам нужно определить, что это за трехмерная фигура, и для этого мы проанализируем изображение.
Сколько полигонов?
Классификация полигонов
| имя | количество сторон | Внутренний угол (правильный многоугольник) |
|---|---|---|
| Гексагоно | 6 | 120 º |
| Семиугольник | 7 | 128,6 º |
| восьмиугольник | 8 | 135 º |
| энагон | 9 | 140 º |
Чем не полигон?
Что такое полигоны? Это плоские геометрические фигуры, состоящие только из одной замкнутой линии, а их стороны разделены прямыми линиями. Картина, например, представляет собой многоугольник, поскольку у него четыре стороны. Круг не является многоугольником, потому что он округлый и не имеет сторон.
Какие фигуры не являются многоугольниками?
Ответ: Да, есть замкнутые фигуры, не являющиеся многоугольниками. Чтобы замкнутую фигуру можно было классифицировать как многоугольник, она должна быть образована прямыми линиями, которые не пересекаются. Таким образом, если фигура имеет изогнутый сегмент, например, или пересекающиеся линии, она НЕ будет классифицироваться как многоугольник.
Чтобы замкнутую фигуру можно было классифицировать как многоугольник, она должна быть образована прямыми линиями, которые не пересекаются. Таким образом, если фигура имеет изогнутый сегмент, например, или пересекающиеся линии, она НЕ будет классифицироваться как многоугольник.
Сколько сторон у многоугольника?
По количеству сторон
| Ладос | имя |
|---|---|
| 4 | четырехугольник |
| 5 | пятиугольник |
| 6 | шестиугольник |
| 7 | семиугольник |
Каковы основные элементы многоугольника?
Элементами многоугольника являются:
- Вершина ⇨ Точка пересечения между двумя последовательными сторонами.
- Сторона ⇨ Отрезок, соединяющий две последовательные вершины.

- Диагональ ⇨ Отрезок, соединяющий две непоследовательные вершины.
- Внутренний угол ⇨ Внутренняя область, образованная двумя последовательными сторонами.
Что такое вогнутый и выпуклый многоугольник?
выпуклый и вогнутый многоугольник
Простые многоугольники называются выпуклыми, когда любая линия, соединяющая две точки, принадлежащие многоугольной области, будет полностью вставлена в эту область. В вогнутых многоугольниках этого не происходит.
Что такое правильные многоугольники?
Правильные многоугольники — это выпуклые многоугольники, которые являются равносторонними и равноугольными, то есть они имеют конгруэнтные стороны, а также углы с одинаковой мерой. Помните, что многоугольники являются выпуклыми, если любой отрезок, концы которого находятся внутри, полностью содержится внутри многоугольника.
Какие три типа многоугольников существуют?
типы полигонов
| количество сторон | имя |
|---|---|
| 3 | треугольник |
| 4 | четырехугольник |
| 5 | пятиугольник |
| 6 | Гексагоно |
Какое определение для полигонов?
Плоская фигура, ограниченная тремя отрезками (которые называются сторонами).
Какие многоугольники являются четырехугольниками?
Четырехугольник – это многоугольник с четырьмя сторонами, а главные четырехугольники: квадрат, прямоугольник, ромб, трапеция и трапеция.
Как определить звезду?
Звезды представляют собой большие сферы, образованные плазмой, нагретой до тысяч градусов. Его форма обусловлена гравитацией, направленной на ядро звезды. Звезды — это большие сферы плазмы, работающие за счет ядерного синтеза.
Что такое плоские фигуры?
Основными плоскими фигурами являются треугольник, круг, квадрат, прямоугольник, ромб и трапеция, и каждая из них имеет формулу вычисления площади. Стоит отметить, что область изучается в планиметрии, геометрии для двухмерных объектов.
Сколько сторон у пентаграммы?
Пентаграмма (от древнегреческого πεντάγραμμος, пентаграмма) — звезда, состоящая из пяти прямых линий с пятью точками.
Когда фигура считается многоугольником?
Многоугольники — это плоские и замкнутые фигуры, то есть ограниченные прямыми линиями. Многоугольники имеют в качестве элементов: стороны, вершины, углы и диагонали. Многоугольники — это плоские замкнутые геометрические фигуры, образованные отрезками прямых. Многоугольники делятся на две группы, выпуклые и невыпуклые.
Четырехугольники – это многоугольники, имеющие четыре стороны. Его специфические характеристики и свойства касаются сторон, углов и диагоналей.
Почему круг это многоугольник?
Окружность не является многоугольником, потому что многоугольники — это геометрические фигуры, стороны которых образованы отрезками прямых линий.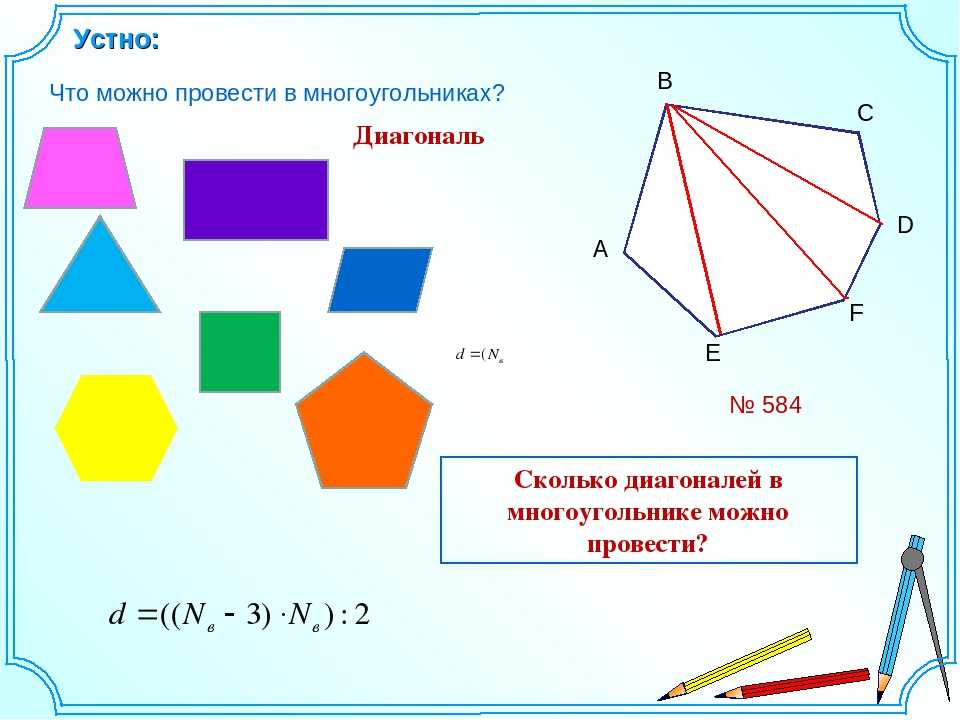
Что такое развертка в рисовании?
Развертка — это представление на плоскости, которое при складывании создает трехмерные формы. В развертке все поверхности модели рисуются на плоскости. Развертки выполняются сплошными линиями и пунктирными линиями.
Что такое планирование?
Планирование (или планирование) относится к действию и результату планирования (или планирования), то есть организации или организации чего-либо в соответствии с планом.
Какие квартиры имеют треугольные грани?
планирование пирамиды
Помните, что пирамида состоит из многоугольного основания, которым может быть любой многоугольник, и треугольных боковых граней. Таким образом, легко сделать вывод, что схема пирамиды имеет многоугольник и несколько треугольников.
Как называется многоугольник?
Многоугольники с четырьмя сторонами называются пятиугольниками, шестиугольниками и т. д. Также возможно классифицировать многоугольники по длине их сторон, а также по их углам.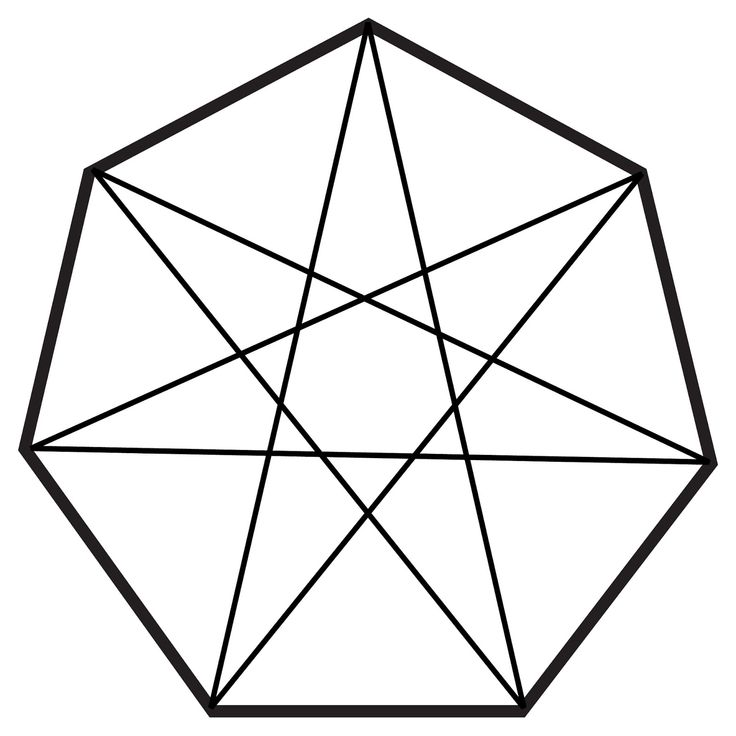 По отношению к сторонам многоугольник может быть правильным, если он имеет конгруэнтные стороны и углы, или неправильным.
По отношению к сторонам многоугольник может быть правильным, если он имеет конгруэнтные стороны и углы, или неправильным.
Как называются многоугольники, у которых три стороны?
декабрь 2022
| Ладос | имя |
|---|---|
| 3 | треугольник |
| 4 | четырехугольник |
| 5 | пятиугольник |
| 6 | шестиугольник |
Как называются полигоны с 1 по 20?
Классификация полигонов
| КОЛИЧЕСТВО СТОРОН (ИЛИ УГЛОВ) | ИМЯ ПОЛИГОНА | |
|---|---|---|
| 11 | без десятиугольника | декалатер |
| 12 | додекагон | додекалатер |
| 15 | пятиугольник | пентадекалатер |
| 20 | икосагон | икосалатеро |
Являются ли фигуры правильными многоугольниками?
Многоугольники называются правильными, если они выпуклые, имеют все стороны одинаковой длины и все внутренние углы равны.
Как отличить полигоны от не полигонов?
Ответ: Многоугольники — это замкнутые линии, образованные только отрезками прямых, которые не пересекаются. Другими словами, это плоские геометрические фигуры, образованные сторонами, которые, в свою очередь, представляют собой прямые отрезки, а не многоугольники, имеют разомкнутую форму или линии с перекрытием.
Сколько углов у многоугольника?
Сумма внутренних углов правильного многоугольника
| Ладос | углы | |
|---|---|---|
| четырехугольник | 4 | 4 |
| пятиугольник | 5 | 5 |
| Гексагоно | 6 | 6 |
| Семиугольник | 7 | 7 |
Какой многоугольник имеет две диагонали?
У треугольника диагонали равны нулю, у квадрата — две, у пятиугольника — пять, а у шестиугольника — девять.
Как называется многоугольник, у которого 35 диагоналей?
Десятиугольник: 35 диагоналей.
Что такое угол звезды?
Концы известной пятиконечной звезды расположены под углом 72 градуса. Линии, исходящие из них, сходятся на концах, направленных внутрь и имеющих угол 108 градусов.
Почему круг это многоугольник?
Окружность не является многоугольником, потому что многоугольники — это геометрические фигуры, стороны которых образованы отрезками прямых линий.
Какое имя мы можем дать многоугольнику в форме звезды на флаге Акко?
Ответ: Мы можем назвать его десятиугольником (десятиугольным многоугольником).
Сколько сторон у пятиконечной звезды?
Пентаграмма и звезда Давида
Она использовалась как символ различных религий и эзотерических учений, в то время как Звезда Давида визуально имеет шесть концов, что характерно для того, чтобы быть типичным символом еврейской культуры.
Вогнутый многоугольник Простой многоугольник Выпуклый многоугольник Выпуклый набор, многоугольник, угол, белый png
Вогнутый многоугольник Простой многоугольник Выпуклый многоугольник Выпуклый набор, многоугольник, угол, белый pngтеги
- угол,
- белый,
- прямоугольник,
- треугольник,
- симметрия,
- многоугольник,
- черный,
- степень,
- религия,
- точка В многоугольнике,
- простой многоугольник,
- квадрат,
- звезда многоугольник,
- точка,
- линия Art,
- область,
- черно-белый,
- вогнутый многоугольник,
- вогнутый набор,
- выпуклый многоугольник,
- выпуклый сет,
- геометрия,
- интерьер,
- внутренний угол,
- линия,
- википедия,
- png,
- прозрачный png,
- без фона,
- бесплатная загрузка
 15KB )
15KB )- Размер изображения
- 677x600px
- Размер файла
- 20.15KB
- MIME тип
- Image/png
изменить размер PNG
ширина(px)
высота(px)
Некоммерческое использование, DMCA Contact Us
- Звездный многоугольник Угол Круг восьмиугольник, многоугольник, белый, прямоугольник png 1024x1024px 29.65KB
- Правильный многоугольник Шестиугольник Внутренний угол Гептагон, шестигранник, угол, белый png 1024x1024px 16.14KB
- черная звезда искусства, пятиконечная звезда, черная звезда, угол, треугольник png
1200x1131px
17.
 34KB
34KB - Правильный многоугольник Пентагон Правильный многогранник Геометрия, шестиугольник, угол, белый png 1024x1024px 24.41KB
- Octagon Обычный многоугольник, шестигранник, угол, белый png 1024x1024px 9.05KB
- Шестигранник Форма Правильный многоугольник Геометрия, форма, синий, угол png 512x512px 14.87KB
- Шестигранник Правильный многоугольник Форма Геометрия, рисунок многоугольника, угол, белый png 600x600px 8.62KB
- Линия Симметрия Точка Геометрическая абстракция, Абстрактные геометрические линии, угол, белый png 7191x9530px 4.21MB
- org/ImageObject»> Линия Точка Симметрия, абстрактные геометрические линии, черные линии иллюстрации, угол, белый png 7612x12077px 3.34MB
- Треугольник Пенроуза Равносторонний треугольник Треугольник Серпинского Форма, треугольник, угол, треугольник png 706x611px 9.45KB
- Правильный многоугольник Hexagon Shape Geometry, шестиугольный, угол, белый png 2000x2000px 36.48KB
- Белые сияющие звезды, текстура, угол png 1500x1499px 382.98KB
- Перевод формы словаря шестиугольника многоугольника, шестиугольник, угол, белый png 512x512px 3.77KB
- ассорти с, геометрическая форма, геометрия, геометрический рисунок, угол, белый png
3433x3239px
333.
 84KB
84KB - Черно-белая точка угол, подвесная рама, квадратная белая подвесная рама крупным планом, кадр, белый png 1241x1650px 124.05KB
- Прямоугольный многоугольник, треугольник, угол, прямоугольник png 512x512px 2.69KB
- Правильный многоугольник Октагон Геометрия Внутренний угол, Угол, угол, белый png 1920x1920px 22.19KB
- Геометрическая форма Геометрия, геометрические фигуры, белый, треугольник png 800x800px 17.54KB
- Черно-белый узор, геометрические абстрактные перспективные блоки, синяя зеркальная иллюстрация, текстура, угол png
650x835px
95.
 79KB
79KB - Значок в форме звезды, красная звезда, иллюстрация красной звезды, угол, клипарт png 8715x8288px 513.09KB
- Угловая точка Черно-белый узор, Белые сияющие звезды, сияющая звезда, текстура, белый png 2000x1834px 685.3KB
- Северная Компас Роуз, угол, белый png 600x600px 16.48KB
- Hendecagon Правильный многоугольник Dodecagon Nonagon, форма, угол, белый png 1024x1024px 23.94KB
- Звездный многоугольник Геометрия, форма, угол, прямоугольник png 1024x1024px 38.04KB
- org/ImageObject»> иллюстрация черного восьмиугольника, гипотеза о сотах Шестиугольная черепица, шестиугольник, угол, белый png 1024x1024px 37.53KB
- Геометрия треугольника, красочный алмазный фон, серый и синий 3D, текстура, угол png 2078x2315px 974.48KB
- Форма Ромб Геометрия Параллелограмм Полигон, Ромб, угол, лицо png 600x600px 4.92KB
- Шестиугольник Bee Honeycomb, соты, угол, прямоугольник png 1920x1330px 184.99KB
- прямоугольная черная рамка, черно-белая линия угловых точек, симпатичные границы, белый, текст png 772x1115px 14.43KB
- Правильный многоугольник Пентагон Правильный многогранник Геометрия, геометрические неправильные фигуры, угол, белый png
1200x1200px
29.
 77KB
77KB - Черно-белая площадь, угол проекции тени бумаги, текстура, угол png 1200x700px 50.09KB
- Треугольник Черно-белый узор, синий треугольник технологии, черный рисунок, текстура, угол png 2409x2492px 177.2KB
- Черно-белая геометрия Геометрическая абстракция Pattern, Technology Triangle Cover, черно-серый шестиугольный скриншот, текстура, угол png 2430x2447px 258.18KB
- Сакральная геометрия Платонова сплошная Геометрическая форма, геометрическая, угол, прямоугольник png 512x512px 11.34KB
- Горошек белая точка, угол, угол, белый png
1600x1600px
18.
 64KB
64KB - Золотая рама, рама золотого цвета, кадр, угол png 1500x1500px 192.15KB
- Угловая диаграмма угломера степени, угол, шаблон, угол png 800x791px 99.04KB
- Значок в форме звезды, Голубая звезда, Голубая звезда, синий, угол png 8715x8288px 522.67KB
- Куб Трехмерное пространство Сплошная геометрия Шестигранник, белый куб, угол, белый png 2000x2000px 32.09KB
- Шаблон с шестигранником в форме восьмиугольника, шаблон, угол png 512x512px 2.04KB
- 65537-Гон регулярного многоугольника Угол 257-Гон, цирку, белый, текст png
1845x1845px
47.
 07KB
07KB - иллюстрация улья, шестиугольная черепица Правильный многоугольник Тесселяция Сотовая гипотеза, Сотовый рисунок, угол, белый png 512x512px 16.31KB
- Форма Шестиугольник Правильный многоугольник Геометрия, форма, угол, белый png 768x768px 16.22KB
- белая сердечная иллюстрация, Белый Симметрия Черный Угловой Образец, Белое Сердце s, текстура, угол png 600x557px 19.57KB
- Шестигранник Правильный многоугольник Форма Геометрия, форма, синий, угол png 512x512px 9.65KB
- Вращение в форме звезды, черная звезда, шаблон, угол png
512x512px
3.
 17KB
17KB - Шестигранник Правильный многоугольник Внутренний угол Геометрия, равносторонний шестиугольник, угол, белый png 1000x1000px 15.66KB
- шестиугольник, шестиугольник формы компьютерные иконки символ, шестиугольник, угол, прямоугольник png 512x512px 44.63KB
- Геометрия треугольника, геометрические фигуры, угол, чернила png 700x700px 36.63KB
- Квадрат прямоугольник Wiktionary четырехугольник, угол, угол, белый png 800x800px 3.79KB
Многоугольник и его элементы. Выпуклые и невыпуклые многоугольники. Сумма углов выпуклого многоугольника
Конспект урока по геометрии
в 8 классе
«Многоугольник и его элементы. Выпуклые и невыпуклые многоугольники. Сумма углов выпуклого многоугольника»
Выпуклые и невыпуклые многоугольники. Сумма углов выпуклого многоугольника»
Цели урока:
- Образовательные: изучение понятия многоугольник, его элементы; выпуклые и невыпуклые многоугольники; сумма углов выпуклого многоугольника.
- Развивающие: активизация познавательной деятельности учащихся через решение практических задач, умение выбирать правильное решение, лаконично излагать свои мысли, анализировать и делать выводы.
- Воспитательные: организация совместной деятельности, воспитание у учащихся интереса к предмету, доброжелательности, умения выслушивать ответы товарищей.
Тип урока: урок изучения нового материала
Оборудование:
Ход урок:
- Организационный момент
— Здравствуйте, дети! Проверьте, все ли, что нужно к уроку лежит у вас на партах? (тетрадь, ручка, дневник, линейка, карандаш)
— Садитесь!
2. Мотивация урока.
Мотивация урока.
— Дорогие ребята!Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы те, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что геометрия – интересный и нужный предмет.
Французский писатель XIX столетия Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.
— Давайте последуем совету писателя на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.
3. Актуализация опорных знаний.
Какие геометрические фигуры нами уже изучены? (треугольники, четырехугольники, круг)
Каковы их элементы? (вершины, стороны, углы)
Фронтальный опрос:
- Какая фигура называется треугольником?
- Какая фигура называется четырехугольником? (Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков)
- Какие вершины четырехугольника называются соседними, какие противолежащими? (Вершины четырех угольника называются соседними вершинами, если они являются концами одной из его сторон.
 Вершины, не являющиеся соседними, называются противолежащими вершинами.)
Вершины, не являющиеся соседними, называются противолежащими вершинами.) - А какие вершины называются противоположными у треугольника?
- Что такое диагонали четырехугольника? (Диагональ — отрезок, соединяющий противоположные вершины)
- Какие стороны четырехугольника называются соседними? Какие стороны называются противолежащими? (Соседние стороны — стороны четырехугольника, выходящих из одной вершины. Противоположные стороны — стороны четырехугольника, которые не имеют общего конца.)
- А какие вершины называются противоположными у треугольника?
- Что такое периметр треугольника?
- А периметр четырехугольника? (сумма всех сторон четырехугольника.)
- Как проверить, можно ли из четырех данных отрезков построить четырехугольник?
- Чему равна сумма внутренних углов треугольника?
- А чему равна сумма внутренних углов четырехугольника? (Сумма углов любого четырехугольника равна 360)
- Могут ли все углы четырехугольника быть тупыми? острыми? прямыми? А в треугольника?
— Молодцы!
4. Изучение нового материала.
Изучение нового материала.
— Среди множества различных геометрических фигур на плоскости выделяется большое семейство МНОГОУГОЛЬНИКОВ.
Названия геометрических фигур имеют вполне определенный смысл. Присмотритесь внимательно к слову “многоугольник”, и скажите из каких частей оно состоит?
— Слово “многоугольник” указывает на то, что у всех фигур этого семейства “много углов”.
Подставьте в слово “многоугольник” вместо части “много” конкретное число, например 5. Что получили?
— Правильно! Вы получите ПЯТИУГОЛЬНИК. Или 6. Тогда – ШЕСТИУГОЛЬНИК. Заметьте, сколько углов, столько и сторон, поэтому эти фигуры вполне можно было бы назвать и многосторонниками.
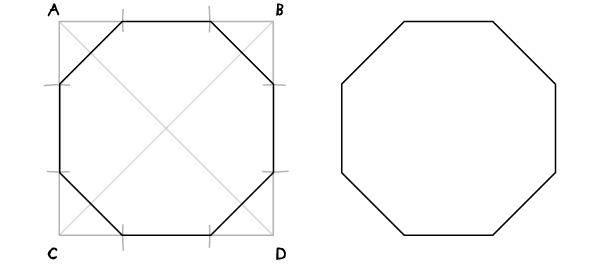
— На рисунке геометрические фигуры. Используя рисунок, назовите эти фигуры.
(восьмиугольник, шестиугольник, пятиугольник, четырехугольник, треугольник)
— Каким наименьшим числом можно заменить “много” в многоугольнике? (Ответ: 3)
— Давайте попробуем определить, что такое ломаная? (Ло́маная— геометрическая фигура, состоящая из отрезков, последовательно соединенных своими концами. )
)
— Ребята, а если первая и последняя точки ломаной совпадают, то как называется такая ломаная (называется замкнутой)?
— Имея всю необходимую информацию, давайте попробуем сами сформулировать, что же такое многоугольник?
— Правильно! Фигура, ограниченная простой замкнутой ломаной, называется многоугольником.
- Вершины ломаной называются вершинами многоугольника,
- стороны ломаной — сторонами многоугольника,
- а углы, образованные соседними сторонами, — углами многоугольника.
- Точки многоугольника, не принадлежащие его сторонам, называются внутренними.
- Периметром многоугольника называется сумма длин всех его сторон.
- Многоугольник, у которого n углов называется n — угольником.
- Многоугольник называется выпуклым, если вместе с любыми двумя своими точками он содержит и соединяющий их отрезок.

Любой треугольник выпуклый. Среди многоугольников, с числом углов большим трех, могут быть выпуклые и невыпуклые.
— В чем отличие данных многоугольников?
Диагональю многоугольника называется отрезок, соединяющий его несоседние вершины. Подсчет диагоналей
- Сколько диагоналей выходит с одной вершины четырехугольника, пятиугольника, шестиугольника?
- Давайте сравним их с количеством углов. Что мы видим?
- Какую формулу вы бы записали?
- Правильно, n-3.
- Давайте проверим, что это проходит и для треугольника. 3-3=0.
- А сколько вершин у n-угольника?
- Тогда, может нужно умножить количество углов n на количество диагоналей, которые выходят с одной вершины n-3?
- Хорошо! Но при этом мы посчитали каждую диагональ дважды.
 Как же исправить эту формулу?
Как же исправить эту формулу? - По этому, произведение n*(n-3) делят на два.
Диагоналей нет у треугольника на плоскости и у тетраэдра в пространстве, поскольку все вершины этих фигур попарно связаны сторонами (ребрами).
Количество диагоналей N у многоугольника легко вычислить по формуле:
N = n·(n – 3)/2, — запишем формулу в тетради, и выдилим ее.
где n — число вершин многоугольника. По этой формуле нетрудно найти, что
- у треугольника — 0 диагоналей
- у прямоугольника — 2 диагонали
- у пятиугольника — 5 диагоналей
- у шестиугольника — 9 диагоналей
- у восьмиугольника — 20 диагоналей
- у 12-угольника — 54 диагонали
- у 24-угольника — 252 диагонали
Исследовательская работа по группам
Каждая группа работает по учебно-исследовательской карте.
1.Задача.
Чему равна сумма углов выпуклого пятиугольника?
2. Проблема.
Проблема.
Как зависит сумма углов выпуклого n-угольника от числа углов
многоугольника и от числа треугольников, на которые он разбивается
диагоналями, проведенными из одной вершины?
3.Пробы.
1 проба-1800 2 проба-3600 3 проба-5400 4 проба-7200
n=3 n=4 n=5 n=6
— Что мы видим? (Количество треугольников (n-2)).
— Давайте заполним таблицу.
4.Таблица результатов.
Пробы | 1 | 2 | 3 | 4 |
Число углов | 3 | 4 | 5 | 6 |
Число треугольников | 1 | 2 | 3 | 4 |
Сумма углов | 1800 | 3600 | 5400 | 7200 |
— Так как, сумма углов одного треугольника – 180, то сумма углов выпуклого n-угольника равна 180° (n-2 )
Вывод: Формула для суммы внутренних углов n-угольника. 180° (n-2 ).
180° (n-2 ).
— Сумма внешних углов выпуклого многоугольника не зависит от числа сторон п- угольника и равна 360.
5. Закрепление нового материала.
Задача 253
— Сколько диагоналей можно провести из одной вершины выпуклого семиугольника? Найдите общее количество диагоналей выпуклого семиугольника. (можно провести 4 диагонали из одной вершины выпуклого семиугольника. Общее количество диагоналей выпуклого семиугольника – N=14: )
Задача 254
6. Итоги урока. Рефлексия.
- Что больше всего запомнилось на уроке?
- Что удивило?
- Что понравились больше всего?
- Каким ты хочешь увидеть следующий урок?
- Таким образом, мы самостоятельно вывели формулу для количества диагоналей многоугольника.
Домашнее задание: № 253, 254, 257 Вариант 2 с ваших сборников
16.
 Многоугольники | учебник для 7 класса «ГЕОМЕТРИЯ» 16. Многоугольники | учебник для 7 класса «ГЕОМЕТРИЯ» | Учебники по Геометрии
Многоугольники | учебник для 7 класса «ГЕОМЕТРИЯ» 16. Многоугольники | учебник для 7 класса «ГЕОМЕТРИЯ» | Учебники по Геометриитак то ЕНТ / Учебники по Геометрии / учебник для 7 класса «ГЕОМЕТРИЯ»
16. Многоугольники
Всякая простая замкнутая ломаная разбивает плоскость на две области — внутреннюю и внешнюю. На рисунке 16.1 внутренние области закрашены.
Фигура, образованная простой замкнутой ломаной и ограниченной ею внутренней областью, называется многоугольникам. Вершины ломаной сторонами, — углами многоугольник а. Точки многоугольника, не принадлежащие его сторонам, называются внутренними.
Периметром многоугольника называется сумма длин всех его сторон.
Многоугольники подразделяются на треугольники — многоугольники с тремя углами (рис. 16.1, а), четырёхугольники — многоугольники с четырьмя углами (рис. 16.1, б) и т. д. Многоугольник, у которого п углов называется п-угольником.
Многоугольник называется правильным, если у него все стороны равны и все углы равны (рис. 16.2).
Правильный четырёхугольник называется также квадратом.
Прямоугольникам называется четырёхугольник, у которого все углы прямые.
Многоугольник называется выпуклым, если вместе с любыми двумя своими точками он содержит и соединяющий их отрезок (рис. 16.3).
Любой треугольник выпуклый. Среди многоугольников с числом углов, большим трёх, могут быть выпуклые (рис. 16.4, а) и невыпуклые (рис. 16.4, б).
Многоугольники могут иметь и более сложную формы. Примеры таких многоугольников показаны на рисунке 16.5.
Диагональю многоугольника называется отрезок, соединяющий его несоседние вершины (рис. 16.6).
Ясно, что выпуклый многоугольник содержит все свои диагонали. Невыпуклый многоугольник может не содержать некоторые свои диагонали (рис. 16.6, б).
16.6, б).
Вопросы
1. На сколько частей разбивает плоскость простая замкнутая ломаная?
2. Какая фигура называется многоугольником? Что называется:
а) вершинами; б) сторонами; в) углами многоугольника?
3. Какие точки многоугольника называются внутренними?
4. Что называется периметром многоугольника?
5. Какой многоугольник называется «-угольником?
6. Какой многоугольник называется: а) правильным; 6) выпуклым?
7. Что называется диагональю многоугольника?
8. Какой многоугольник содержит все свои диагонали?
Задачи
1. Проверьте, что линия, изображённая на рисунке 16.7, является простой замкнутой ломаной. Выясните, какая из данных точек лежит:
а) внутри; 6) вне этой ломаной.
2. Укажите, какие из представленных на рисунке 16.8 фигур являются многоугольниками, а какие нет.
3. Укажите, какие из представленных на рисунке 16.9 фигур являются: а) выпуклыми многоугольниками; б) невыпуклыми многоугольниками.
4. Нарисуйте выпуклые и невыпуклые: а) четырёхугольник;
б) пятиугольник; в) шестиугольник. Используя линейку, найдите периметры этих многоугольников.
5. Нарисуйте правильные треугольник, четырёхугольник, пятиугольник и шестиугольник. Проверьте правильность нарисованных многоугольников с помощью линейки и транспортира.
6. Являются ли многоугольники, изображенные на рисунке 16.10, правильными?
7. На сколько треугольников делится выпуклый: а) четырёхугольник; 6) пятиугольник; в) шестиугольник своими диагоналями, проведёнными из одной вершины?
8. Сколько всего диагоналей имеет: а) четырёхугольник; б) пятиугольник; в) шестиугольник; г)* n-угольник?
Сколько всего диагоналей имеет: а) четырёхугольник; б) пятиугольник; в) шестиугольник; г)* n-угольник?
9. Может ли многоугольник иметь: а) одну диагональ; б) три диагонали; в) восемь диагоналей; г) десять диагоналей; д) двадцать диагоналей?
10. Существует ли многоугольник: а) число диагоналей которого равно числу его сторон; б) число диагоналей которого меньше числа его сторон; в) число диагоналей которого больше числа его сторон?
11. Выпуклый многоугольник имеет 14 диагоналей. Сколько у него сторон?
12*. На клетчатой бумаге изобразите какой-нибудь четырёхугольник, вершинами которого являются точки АД С и D (рис. 16.11). Сколько таких четырёхугольников?
13. Изобразите два треугольника так, чтобы их общей частью был: а) треугольник; б) четырёхугольник; в) пятиугольник; г) шестиугольник.
Гептагон | Определение, стороны, углы (правильные и неправильные)
Автор:
Malcolm McKinsey
Семиугольник – определение, форма, свойства, формулы
Определение
Семиугольник – это многоугольник с семью сторонами и семью углами. Термин «гептагон» происходит от греческих слов «гепта», что означает «семь», и «гон», что означает стороны. Семиугольник также известен как 7-угольник или септагон («септа» означает семь на латыни).
Гептагон Приведенные ниже свойства и формулы для нахождения периметра и площади применимы только к правильному семиугольнику.
Свойства
Свойства Гептагона- Имеет 7 сторон одинаковой длины; в семиугольнике ABCDEFG, AB = BC = CD = DE = EF = FG = GA
- Имеет 7 внутренних углов, каждый размером 128,57°; поэтому ∠ABC = ∠BCD = ∠CDE = ∠DEF = ∠EFG =∠FGA = ∠GAB
- Сумма всех семи внутренних углов равна 900°; поэтому ∠ABC + ∠BCD + ∠CDE + ∠DEF + ∠EFG +∠FGH + ∠GAB= 900°
- Имеет 7 внешних углов, каждый размером 51,43°
- Имеет 14 диагоналей; показаны как AC, AD, AE, AF, BD, BE, BF, BG, CE, CF, CG, DF, DG и EG
Формулы
Периметр
Формула для нахождения периметра семиугольника приведена ниже:
Формула периметра семиугольникаНайдите периметр правильного семиугольника, каждая сторона которого равна 20 см.
Решение:
Как известно,
Периметр (P) = 7a, здесь a = 22 см
= 7 x 22 см
= 154 см
Площадь
3 900 Формула площади
3 900 Гептагон приведен ниже:
Площадь Гептагона ФормулаПриведенное выше уравнение приблизительно равно
A = 3,634a 2 квадратных единиц, здесь cot π/7 = cot 25,71 = 2,0765
Найдите площадь правильного семиугольника, каждая сторона которого равна 7 см.
Решение:
Как известно,
Площадь (А) = 7/4 (а 2 койн π/7)
= 3,634 а 2 , здесь а = 7 6 6 3
9021 7) 2
= 3,634 (49)
= 178,06 см 2
Углы
Внутренний угол
Угол, образованный внутри семиугольника в его углах, когда отрезки соединяются встык.
Сумма внутренних углов
Общая мера всех внутренних углов, объединенных в семиугольнике. Формула приведена ниже:
Сумма внутренних углов = (n-2) x 180°, здесь n = количество сторон
В семиугольнике ABCDEFG n = 7
Таким образом,
Сумма внутренних углов = (7 -2) x 180°
= 900°
Один внутренний угол
Размер одного внутреннего угла можно получить, разделив сумму внутренних углов на количество стороны в семиугольнике. Формула приведена ниже:
Один внутренний угол = (n-2) x 180°/n, здесь n = количество сторон
В семиугольнике ABCDEFG n = 7
внутренние углы = (7-2) x 180°/7
= 128,57°
Внешний угол
Угол, образованный любой стороной семиугольника и продолжением примыкающей к нему стороны. Формула приведена ниже:
Формула приведена ниже:
Внешний угол = 360°/n, здесь n = количество сторон
= 51,43°
Типы
В зависимости от сторон, углов и вершин формы семиугольников подразделяются на следующие типы:
- Правильный семиугольник : имеет семь сторон одинаковой длины и семь внутренних углов, каждый размером 128,571° и внешний угол 51,43° каждый. Стороны правильного семиугольника встречаются друг с другом под углом 5π/7 радиан или [128(4/7) градусов]. Он имеет семь линий симметрии и вращательное равновесие седьмого порядка. Все правильные семиугольники выпуклы.
- Неправильный семиугольник : Не все стороны равны или все внутренние углы равны, но сумма всех семи внутренних углов равна 900°. Неправильный семиугольник может быть как выпуклым, так и вогнутым.
- Выпуклый семиугольник : все вершины направлены наружу. Ни один внутренний угол выпуклого семиугольника не превышает 180°, а все диагонали лежат внутри замкнутой фигуры.
 Выпуклый семиугольник может быть как правильным, так и неправильным.
Выпуклый семиугольник может быть как правильным, так и неправильным. - Вогнутый семиугольник : По крайней мере одна вершина направлена внутрь с внутренним углом больше 180°. Хотя бы одна диагональ лежит вне замкнутой фигуры. Таким образом, все вогнутые семиугольники неправильные.
Примеры из реальной жизни
- В настоящее время в Соединенном Королевстве есть две семиугольные монеты номиналом 50 и 20 пенсов, а барбадосский доллар также имеет семиугольную форму. Монета Замбии номиналом 1000 квач представляет собой настоящий семиугольник.
- Бразильская монета номиналом 25 центов имеет семиугольник, вписанный в диск монеты.
- В архитектуре семиугольные планы этажей встречаются в Мавзолее принца Эрнста в Штадтхагене, Германия.
- Некоторые другие искусственные объекты, такие как семиугольная призма, окно, часы, зеркало и газон.
- Некоторые полицейские партии в США имеют контур гептаграммы {7/2}.
- Форма некоторых кактусов.

- Полный граф K7 часто изображают в виде правильного семиугольника с двадцатью одним соединенным ребром.
Определение, типы, свойства, формула, примеры
Семиугольник — двумерная фигура с семью углами, семью вершинами и семью ребрами. Этот семиугольный многоугольник «семиугольник» состоит из двух слов «Гепта» и «Гония», что означает семь углов. Другое его название — септагон или 7-угольник. Семиугольник имеет четырнадцать диагоналей. Многоугольник — это замкнутая двумерная фигура, состоящая из прямых сторон, имеющих любое количество сторон. Простыми словами можно сказать, что семиугольник — это многоугольник с 7 сторонами.
В этой статье мы рассмотрим свойства и форму семиугольника. Мы обсудим его стороны, внутренние углы, диагонали и вершины. Мы решим несколько примеров, связанных с концепцией, для лучшего понимания.
| 1. | Что такое семиугольник? |
2. | Типы формы семиугольника |
| 3. | Свойства семиугольника |
| 4. | Формула обычного семиугольника |
| 5. | Углы семиугольника |
| 6. | Часто задаваемые вопросы о Heptagon |
Что такое семиугольник?
Семиугольник — это семиугольник с семью углами, семью вершинами и семью ребрами. Они могут иметь одинаковые или разные размеры длины. Это замкнутая фигура, а семиугольник, у которого все семь сторон равны, называется правильным семиугольником. Давайте посмотрим на приведенный ниже рисунок, на котором изображен семиугольник.
Стороны семиугольника
Семь сторон семиугольника представляют собой прямые ребра и могут иметь одинаковую или разную длину. Эти стороны встречаются друг с другом, но не пересекаются и не пересекаются. Стороны семиугольника встречаются в вершинах, образуя замкнутую семигранную фигуру.
Углы семиугольника
Семиугольник имеет семь внутренних углов, а сумма всех внутренних углов равна 900°. Некоторые углы фигуры могут быть тупыми или острыми. Сумма внешних углов семиугольника равна 360 °, и это справедливо как для правильных, так и для неправильных семиугольников.
Диагонали семиугольника
Семиугольник имеет четырнадцать диагоналей. Для выпуклого семиугольника диагонали лежат внутри фигуры, тогда как для вогнутого семиугольника по крайней мере одна диагональ лежит вне фигуры.
Типы формы семиугольника
Формы семиугольника можно разделить на категории в зависимости от их сторон и углов.
I) В зависимости от длины сторон семиугольники можно классифицировать следующим образом:
Обычный семиугольник: Правильный семиугольник — это тот, у которого равны стороны и углы. Сумма всех внутренних углов многоугольника равна (n — 2) × 180°, где n — количество сторон. Поскольку у семиугольника 7 сторон, сумма его внутренних углов равна (7 — 2) × 180° = 5 × 180° = 900°.
. Величина каждого внутреннего угла правильного семиугольника равна 900°/7 = 128,57°
Величина каждого внутреннего угла правильного семиугольника равна 900°/7 = 128,57°Неправильный семиугольник: Неправильный семиугольник — это такой, у которого стороны и углы разной величины. Величина каждого внутреннего угла неправильного семиугольника будет разной. Однако сумма всех внутренних углов неправильного семиугольника также равна 9.00°.
На следующих рисунках показаны правильный и неправильный семиугольник.
II) По величине угла семиугольники можно классифицировать следующим образом:
Выпуклый семиугольник: У выпуклого семиугольника все внутренние углы меньше 180°. Они могут быть правильными или неправильными семиугольниками. Все вершины выпуклого семиугольника направлены наружу.
Вогнутый семиугольник: В вогнутом семиугольнике по крайней мере один из внутренних углов больше 180°. Они могут быть правильными или неправильными семиугольниками.
 По крайней мере, одна вершина указывает внутрь вогнутого семиугольника.
По крайней мере, одна вершина указывает внутрь вогнутого семиугольника.
На следующих рисунках показаны выпуклый и вогнутый семиугольник.
Свойства Гептагона
Теперь, когда мы знаем основное значение семиугольника, давайте теперь рассмотрим некоторые важные свойства семиугольника следующим образом:
- Семиугольник имеет 7 сторон, 7 ребер и 7 вершин.
- Сумма внутренних углов семиугольника равна 900°.
- Значение каждого внутреннего угла правильного семиугольника равно 128,57°
- Сумма внешних углов семиугольника равна 360°
- Количество диагоналей, которые можно провести в семиугольнике, равно 14.
- Центральный угол правильного семиугольника приблизительно равен 51,43 градуса.
- Правильный семиугольник также известен как выпуклый семиугольник, так как все его внутренние углы меньше 180°
- Неправильный семиугольник имеет неравные стороны и углы разной величины.

Формула обычного семиугольника
Существует множество формул, связанных с правильным семиугольником. Давайте разберемся, как найти периметр и площадь правильного семиугольника, используя формулы семиугольника.
Периметр семиугольника
Мы знаем, что у правильного семиугольника 7 сторон одинаковой длины. Следовательно, периметр правильного семиугольника равен 7 × длина стороны. Следовательно, периметр правильного семиугольника со стороной «а» определяется как Периметр = 7a
Площадь семиугольника
Площадь семиугольника определяется как общее пространство, занимаемое многоугольником. Площадь правильного семиугольника со стороной «а» рассчитывается по формуле Площадь = (7a²/4) cot (π/7). Эту формулу можно упростить и приблизительно записать как 3,634а², где «а» — длина стороны. Мы можем использовать это, чтобы вычислить площадь правильного семиугольника.
Углы семиугольника
Семиугольник состоит из 7 внутренних и 7 внешних углов. Давайте прочитаем о внутренних и внешних углах семиугольника.
Давайте прочитаем о внутренних и внешних углах семиугольника.
Внутренние углы правильного семиугольника
Сумма внутренних углов правильного многоугольника определяется по формуле внутреннего угла (n — 2) × 180º, где n — количество сторон многоугольника. Таким образом, для семиугольника n = 7. Сумма внутренних углов правильного семиугольника = (7 — 2) × 180º = 900º. Таким образом, каждый внутренний угол правильного семиугольника = 900/7 = 128,57º
Внешние углы правильного семиугольника
Согласно формуле суммы внешних углов сумма всех внешних углов правильного многоугольника равна 360º . Таким образом, сумма всех внешних углов правильного семиугольника равна 360º. Таким образом, каждый внешний угол правильного семиугольника = 360/7 = 51,43º
Важные замечания о семиугольнике
- Семиугольник имеет 7 ребер, 7 внутренних углов и 7 вершин.
- Сумма внутренних углов семиугольника равна 900°, а сумма его внешних углов равна 360°.

- Семиугольник может быть двух видов — правильный и неправильный по сторонам.
Похожие статьи
- Многоугольники
- Шестигранник
- Внутренние уголки
Часто задаваемые вопросы о Heptagon
Что такое семиугольник в математике?
A семиугольник — это семиугольник с 7 сторонами, 7 вершинами и 7 ребрами. Длины сторон и меры углов семиугольника могут быть равны или не равны друг другу. Другое название семиугольника — септагон.
Что такое выпуклый семиугольник?
Выпуклый семиугольник — это такой, у которого все внутренние углы меньше 180°. Все вершины выпуклого семиугольника направлены наружу.
Как рассчитать диагонали семиугольника?
Диагонали семиугольника можно вычислить, нарисовав отрезки, соединяющие каждые две противоположные вершины, и посчитав их. Мы также можем рассчитать количество диагоналей, используя формулу n(n — 3)/2, где n — количество сторон многоугольника. Для семиугольника значение n равно 7. Таким образом, количество диагоналей можно рассчитать как 7(7 — 3)/2 = 28/2 = 14,9.0003
Для семиугольника значение n равно 7. Таким образом, количество диагоналей можно рассчитать как 7(7 — 3)/2 = 28/2 = 14,9.0003
Сколько диагоналей у семиугольника?
Семиугольник имеет 14 диагоналей, которые можно рассчитать по формуле n(n — 3)/2, где n — количество сторон.
Чему равна сумма углов в семиугольнике?
Сумма внутренних углов семиугольника равна 900°, что можно рассчитать по формуле внутреннего угла правильного многоугольника (n — 2) × 180°, где n — количество сторон. Для семиугольника значение n равно 7. Таким образом, по формуле сумма внутренних углов будет равна 900°. Сумма внешних углов семиугольника равна 360°.
Как найти внутренние углы правильного семиугольника?
Каждый внутренний угол правильного семиугольника можно рассчитать, используя сумму внутренних углов семиугольника, которая равна 900°. Поскольку все углы правильного семиугольника равны, а внутренних углов в семиугольнике 7, величина каждого внутреннего угла будет равна 900°/7 = 128,57°
Как найти периметр правильного семиугольника?
Периметр — это сумма всех сторон многоугольника. Поскольку у правильного семиугольника 7 сторон одинаковой длины, его периметр рассчитывается по формуле: периметр правильного семиугольника = 7 × длина стороны.
Поскольку у правильного семиугольника 7 сторон одинаковой длины, его периметр рассчитывается по формуле: периметр правильного семиугольника = 7 × длина стороны.
Как классифицировать семиугольники на основе сторон семиугольника?
Семиугольники можно разделить на правильные и неправильные семиугольники в зависимости от длины их сторон. Если все семь сторон имеют одинаковую длину, то такой семиугольник называется правильным. С другой стороны, если хотя бы одна сторона семиугольника имеет другую длину, то это неправильный семиугольник.
Какие бывают типы семиугольников?
Мы можем классифицировать семиугольники на основе сторон и углов. У нас есть в основном четыре типа семиугольников:
- Обычный семиугольник
- Неправильный семиугольник
- Вогнутый семиугольник
- Выпуклый семиугольник
Задача о счастливом конце | plus.maths.org
Задача со счастливым концом — одна из тех математических
вопросы, которые довольно легко объяснить, но до сих пор бросили вызов всем
пытается
ответь им. Некоторые из лучших математиков мира поставили свои
умы к этому, безрезультатно. Это касается точек
нарисованные на листе бумаги и фигуры, которые вы можете создать,
соединяя их.
Некоторые из лучших математиков мира поставили свои
умы к этому, безрезультатно. Это касается точек
нарисованные на листе бумаги и фигуры, которые вы можете создать,
соединяя их.
Давайте начнем с трех точек, нарисованных на листе бумаги, которые не все лежат на линия. Вы всегда можете соединить их, чтобы сформировать треугольник, у которого три точки являются углами:
Три точки на плоскости образуют треугольник (пока они не лежат на одной прямой).
Что произойдет, если у вас есть четыре точки (причем никакие три из них не лежат на одной линии)? Соединив их, вы можете создать четырехсторонняя фигура (называемая четырехугольником ), у которой четыре точки являются углами:
Некоторые четырехугольники.
Но в зависимости от того, как расположены точки, четырехугольник
может выглядеть немного странно (как центральный на изображении выше), содержащий вмятины и шипы и совсем не похожий на аккуратный и правильный
прямоугольник, который первым приходит на ум, когда мы думаем о четырехугольнике. цифры. Итак, давайте наложим еще одно ограничение. Посмотрим, сможем ли мы
нарисуйте выпуклый четырехугольник с нашими четырьмя точками, что
то есть такой, у которого все внутренние углы не превышают 180 градусов. Этот
гарантирует, что форма не содержит углов, которые «вдавлены внутрь»,
создание вмятины. Четырёхугольник внизу не выпуклый, а левый и правый на рисунке выше выпуклые.
цифры. Итак, давайте наложим еще одно ограничение. Посмотрим, сможем ли мы
нарисуйте выпуклый четырехугольник с нашими четырьмя точками, что
то есть такой, у которого все внутренние углы не превышают 180 градусов. Этот
гарантирует, что форма не содержит углов, которые «вдавлены внутрь»,
создание вмятины. Четырёхугольник внизу не выпуклый, а левый и правый на рисунке выше выпуклые.
Невыпуклый четырехугольник.
Некоторые простые примеры показывают, что при четырех точках вы не всегда можете рисовать выпуклый четырехугольник:
Имея четыре точки, не всегда возможно соединить их так, чтобы получился выпуклый четырехугольник.
Однако все меняется, когда вы добавляете еще одну точку. Когда у тебя есть пять точек, нарисованных на листе бумаги (при этом три из них не должны лежать на одной линии), всегда можно соединить четыре из чтобы они образовали выпуклый четырехугольник. Дополнительный балл дает вам только достаточно гибкости, чтобы сделать это. Вот несколько примеров (на самом деле вы можете нарисовать несколько разных выпуклых четырехугольников с одними и теми же пятью точками):
Имея пять точек (причем никакие три из них не лежат на одной прямой), вы всегда можете найти выпуклый четырехугольник, у которого четыре из них являются углами.
Этот результат был назван теоремой о счастливом конце математик Пауль Эрдёш, потому что два его друга, которые работали над ним, Джордж Секерес и Эстер Кляйн, в итоге получили женатый. Вы можете увидеть набросок доказательства этого результата ниже.
Добавление сторон
Очевидный следующий вопрос: сколько точек вам нужно убедитесь, что вы можете соединить пять из них, чтобы сформировать выпуклую пятиугольник (пятигранная фигура). Ответ 9(без трех из них, лежащих на одной линии). Вот два примера:
Имея девять точек (причем никакие три из них не лежат на одной прямой), вы всегда можете найти выпуклый пятиугольник, у которого пять из них являются углами.
Чтобы убедиться, что ты умеешь рисовать выпуклый шестиугольник (шесть сторон) нужно 17 точек. Вот пример:
Имея 17 точек (при этом никакие три из них не лежат на одной линии), вы всегда можете найти выпуклый шестиугольник, у которого шесть из них являются углами.
Сколько точек вам нужно, чтобы быть уверенным, что вы можете нарисовать выпуклый семиугольник (стороны), у которого эти точки являются углами? Ответ в том, что никто не знает. То же самое касается , , или любого количества сторон. Эрдёш и Секерес считали, что при заданном натуральном числе число точек, которое необходимо для того, чтобы соединить их и образовать многоугольник с выпуклыми сторонами, равно 9.0003
То же самое касается , , или любого количества сторон. Эрдёш и Секерес считали, что при заданном натуральном числе число точек, которое необходимо для того, чтобы соединить их и образовать многоугольник с выпуклыми сторонами, равно 9.0003
Результат верен для (треугольников), как в этом случае
Также работает для , и , как
и
Но верен ли результат для неизвестно. Эрдёш и Секереш смогли доказать, что количество точек, необходимое для получения выпуклого многоугольника, всегда не меньше, а также доказали его конечность: другими словами, нарисовав достаточное количество точек, вы можете быть уверены, что найдется многоугольник. внутри них есть многоугольник с выпуклыми сторонами. Что не было доказано, так это то, сколько достаточно.
Эрдёш и Секереш смогли доказать, что количество точек, необходимое для получения выпуклого многоугольника, всегда не меньше, а также доказали его конечность: другими словами, нарисовав достаточное количество точек, вы можете быть уверены, что найдется многоугольник. внутри них есть многоугольник с выпуклыми сторонами. Что не было доказано, так это то, сколько достаточно.
Задача о счастливом конце иллюстрирует интересное явление: если система достаточно велика (например, достаточно много точек), то вы можете надеяться найти в ней какой-то порядок (например, выпуклые фигуры), даже если система как все в беспорядке. Это явление изучается областью математики позвонил Рэмси теория . Вы можете узнать больше в Plus статья Друзья и незнакомцы .
Набросок доказательства теоремы о счастливом конце для
n=4 Предположим, у вас есть пять точек на плоскости. Давайте сначала предположим, что три из этих точек можно соединить, чтобы сформировать треугольник, содержащий две оставшиеся точки, назовем их и , внутри себя.
