Отношения хищник–жертва • Джеймс Трефил, энциклопедия «Двести законов мироздания»
200 законов мироздания > Науки о жизни
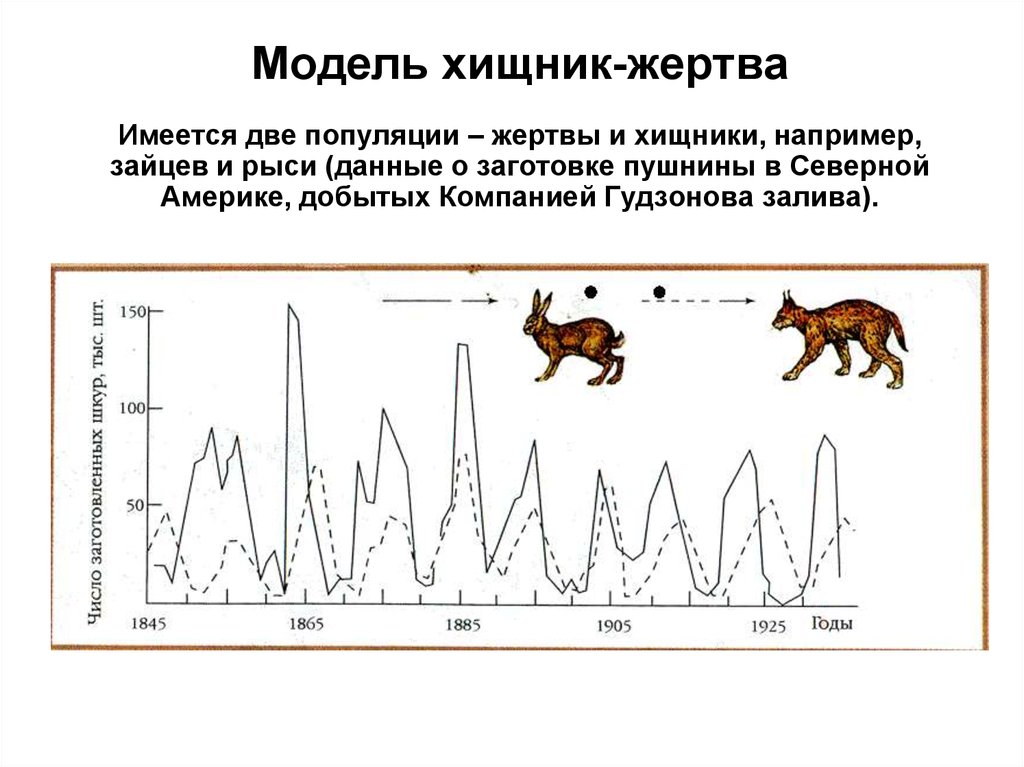
Отношения между хищниками и их жертвами развиваются циклически, являясь иллюстрацией нейтрального равновесия.
Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида (см. Экспоненциальный рост) показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва.
Итак, если число растительноядных жертв Н, а число плотоядных хищников С, то вероятность, что хищник встретится с травоядным, пропорциональна произведению
Другими словами, чем выше численность одного из видов, тем выше вероятность таких встреч. В отсутствие хищников популяция жертвы будет расти экспоненциально (по крайне мере вначале), а в отсутствие жертв популяция хищника сократится до нуля — либо из-за голода, либо в результате миграции. Теперь, если dH — изменение популяции растительноядных за время dt, а dC изменение популяции плотоядных за тот же интервал времени, то две популяции описываются уравнениями:dH/dt = rH – AHC и dC/dt = –qC + BHC
Здесь r — скорость роста численности травоядных в отсутствие хищников, а q — скорость сокращения численности плотоядных в отсутствие травоядных. Постоянные A и B — скорость, с которой встречи хищников с жертвами удаляют травоядных из популяции, и скорость, с которой эти встречи позволяют хищникам прибавлять численность своей популяции. Знак минус в первом уравнении показывает, что встречи сокращают популяцию жертвы, а знак плюс во втором говорит о том, что встречи увеличивают популяцию хищника.
Решение этих уравнений показывает, что обе популяции развиваются циклически. Если популяция травоядных увеличивается, вероятность встреч хищник—жертва возрастает, и, соответственно (после некоторой временной задержки), растет популяция хищников. Но рост популяции хищников приводит к сокращению популяции травоядных (также после некоторой задержки), что ведет к снижению численности потомства хищников, а это повышает число травоядных и так далее. Эти две популяции как бы танцуют вальс во времени — когда изменяется одна из них, за ней следом изменяется и другая.
4
Показать комментарии (4)
Свернуть комментарии (4)
grey 26.01.2007 21:51 Ответить
Поменяйте, пожайлуста, на графиках «хищники» с «жертвами».
А то все как-то ….
Ответить
tverd07 31.10.2007 15:27 Ответить
Амплитуда колебаний численности «жертв» в рамках модели и в реальности должна в несколько раз превышать таковую для «хищников»
Ответить
Написать комментарий
1798 | Экспоненциальный рост |
? | Зависимость количества видов от площади экосистемы |
около 1900 | Территориальность у животных |
1926 | Отношения хищник—жертва |
1934 | Принцип конкурентного исключения |
1966 | Теория оптимального фуражирования |
1970-е | Дифференциальное использование ресурсов |
1976 | Теорема о маргинальных значениях |
0000
Парадокс Зенона
1820
Открытие Эрстеда
Новостная рассылка
«Элементы» в соцсетях:
Модель «Хищник-жертва» на Node.
js / ХабрНедавно по сети прошел всплеск упоминаний игры Жизнь, в связи в основном с тем, что умер ее создатель.
Время сейчас такое, все стали интересоваться биологией, везде эти графики выживания, ну и у меня из закромов памяти вдруг выбралась интересная модель, по которой когда-то писал курсовую.
Модель похожа на Жизнь тем, что это такой же циклический процесс, на который можно смотреть как на огонь, бесконечно медитировать и размышлять о вечном.
Это — Хищник-жертва, вполне себе серьезная модель из прикладной математики (Predator-prey в англоязычном мире).
Суть процесса заключается в том, что в некотором лесу живет стадо оленей (в альтернативной версии — зайцев, но не суть), которые едят в волю и размножаются безудержно, и рано или поздно заполоняют всю территорию.
Однако в том же лесу есть еще и хищники, которые питаются этими оленями (волки, но для зайцев — обычно лисы).
Пара хищников, оказавшаяся в этом изобильном лесу, очень бодро размножается по экспоненте в соответствии с законом Мальтуса, но в какой-то момент ресурсы-олени начинают иссякать, волки — голодать и вымирать, экспонента стремительно летит вниз и там выживают только самые стойкие.
Загнанные было в угол олени поднимают головы, включают свою экспоненту и начинают доминировать над лесом, но пережившие пост волки на свежем мясе находят в себе силы на новую волну рождаемости… и так по кругу и до бесконечности.
Вот график (утащен с Википедии):
Математическая модель этого процесса была описана в начале 20ого века Лоткой и Вольтеррой и названа в их честь.
Почему эта модель существует уже сотню лет и все равно актуальна?
Основных причины две: она очень простая и описывает процесс достаточно реалистично.
У модели всего четыре параметра:
- альфа) скорость размножения оленей
- бета) скорость поедания оленей волками
- гамма) скорость вымирания голодных волков
- дельта) скорость размножения сытых волков
Модель содержит минимальную нелинейность и считается аналитически. При удачно подобранных параметрах она устойчива (ни олени, ни волки до конца не вымирают) и реалистично описывает динамику колебаний в популяциях.
За сто лет было много попыток сделать что-то более реалистичное — но любое повышение сложности ведет к нелинейной системе более высокого уровня и дальше все упирается в непробиваемые интегральные уравнения, которые решить можно только численными методами.
Есть еще один метод — просто запрограммировать этот процесс как игру.
На самом деле такой подход называется мультиагентным моделированием и вполне годится, чтобы сдать курсовую.
Выбираем технологию
Хочется, чтобы программа имела визуализацию, не только на машине автора, но у как можно большей аудитории, причем чтобы оно все само, при минимальных усилиях и все такое.
Логично, что решением будет запустить программу в браузере и, следовательно, писать ее придется на javascript.
Ну а чтобы не плодить зоопарк технологий, сервер тоже на нем напишем.
Стандартные шаги по установке node.js и всего необходимого описаны на Гитхабе.
Модель оленьего роста
Переходим к самому интересному — размножению.
Без хищников у нас мальтузианская модель в условиях ограниченных ресурсов (в мире математики описывается логистической функцией или уравнением Ферхюльста), ее теперь как-то надо применить к агентам.
Можно подобрать вероятностные коэффициенты к каждому оленю и все должно получиться.
Но чем хорошо агентное моделирование — можно задавать именно поведение, не ограничивая себя несколькими коэффициентами.
В общем, модель оленей жизни выглядит так:
- оленям необходимо двигаться. Олень, который не смог сдвинуться с места за единицу времени — погибает (а сдвинуться он не смог бы только потому, что все соседние клетки заняты его друзьями).
- дальше припишем оленям немного деликатности и поставим условие, что размножаться они могут, только если на соседних клетках никого нет.
breed(u) {
var spots = MapUtil.get_adj(u.point, this.W, this.H)
if (!spots || spots.length < 1)
return false
var free = spots.filter(p => !this.
GM.get(p))
if (free.length < spots.length)
return false
var spot = _.sample(spots)
if (!spot)
return false
var born = new Wild(u.kind)
born.move(spot)
this.add_wild(born)
this.born.push(born)
}
GM.get(p))
if (free.length < spots.length)
return false
var spot = _.sample(spots)
if (!spot)
return false
var born = new Wild(u.kind)
born.move(spot)
this.add_wild(born)
this.born.push(born)
}
Дальше сделаем легкий тестовый апп, который создает лесной мир 20×20, запускает в самый центр оленя, и прогоняет 100 циклов, каждый раз печатая статус в csv.
Получившийся csv-файл загоним в Google Spreadsheet и сгенерим график:
Вполне себе экспоненточка получается. Видим, что численность стабилизируется на 200+ оленей, это легко объяснить тем, что необходимость движения требует для оленя не менее двух клеток, а площадь всего леса — 400.
Максимальный прирост случается довольно рано — на 14-15 ходу, а последние 20 ходов численность стоит на месте с незначительнеми колебаниями.
В целом, что хочется подчеркнуть — простейшая агентная модель ведет себя очень реалистично, вполне похожа на логистическую кривую, разбавленную легким шумом.
Но мы сюда не столько за цифрами пришли, сколько за картинками на которые можно смотреть и расслабляться.
Итак, пришло время сделать страничку с картой и графиками, а прогон модели перенести на сервер.
Ставим express и socket.io, а рисовать будем прямо на html5 canvas (с js-движками я не знаком, да и задача не особо сложная).
Смотрим и нервничаем от того, как олени буквально заполоняют лес за считанные итерации, а потом ассимптотически флуктуируют вокруг максимума.
С одной стороны, это всего лишь модель, но кое-где это реальная проблема — достаточно погуглить deers overpopulation и удивиться обилию материала на эту тему.
Эта модель не учитывает деградацию леса, но на самом деле олени довольно жадные потребители — они выедают побеги, вытаптывают землю и в общем разрушают свои леса.
Что делать хозяину леса в таком случае?
Он покупает волков, вешает на каждого gps-датчик и молится, чтобы они не пропали.
Волки
Пора внедрить волка и в нашу модель.
Надо решить две вещи — как волк ест и размножается.
Охотиться просто, когда есть на кого — если в любой соседней клетке есть олень — просто едим его.
Если оленя нет, то можно выжить какой-то период времени.
Для начала положим, что есть волк может каждый ход, но если за два хода не удалось — на обочину эволюции.
С размножением вариантов побольше.
Для начала — уберем деликатность, пусть волки размножаются всегда когда есть свободное место.
И добавим ограничение — голодные волки не размножаются.
Первый блин
Дадим оленям немного размножиться и закинем волка в толпу:
Модель получилась, мягко говоря, неустойчивая — волки моментально выкосили всех оленей и быстренько сами вымерли.
Одно расстройство, никакого дзена.
Вторая попытка
Надо что-то менять.
Режет глаз, какими взрывными темпами плодятся волки.
Немного усложним им жизнь — поставим условие, что размножаться можно только, если на соседних клетках оленей больше чем волков.
var preys = spots.map(p => this.GM.get(p)).filter(u => u && u.kind == Wilds.DEER)
var preds = spots.map(p => this.GM.get(p)).filter(u => u && u.kind == Wilds.WOLF)
if (preys.length <= preds.length)
return false
И забросим волков, когда оленья популяция достигает максимума.
Эта попытка удалась намного лучше.
Баланс хищников и жертв постоянно в движении, оленья популяция сильно сократилась и теперь даже близко не подбирается к своему максимуму.
Однако случиться может всякое, и почти каждый раз происходит так, что волки умудряются вымереть, а олени вновь торжествующе заполоняют чащу.
Вот в этом прогоне волки продержались долго:
Третий круг
Придется закрутить гайки размножения еще сильней.
Поставим теперь условие: рядом должны быть олени, но не должно быть волков.
Такие вот нежные волки, не терпят конкуренции.
Система получается более устойчивой.
В сравнении с предыдущим графиком пики сглажены как у оленей, так и у волков.
В общем, понятно куда двигаться, чтобы получился такой же гладкий график как в Википедии.
В итоге приходим к банальному выводу — размножаться надо сознательно, а не по максимуму.
Звучит как реклама гедонизма, но можно и дальше понижать плодовитость волков в расчете «на повышение качества и продолжительности их жизни»…
Развертывание
В качестве эпилога — инструкция по развертыванию.
Она очень короткая:
1. Пишем простенький докер-файл:
FROM node:14 ADD https://github.com/tprlab/predator-prey/archive/master.zip / RUN unzip /master.zip WORKDIR /predator-prey-master RUN npm install EXPOSE 8081 CMD ["node", "server.js"]
2. docker build. -t predator-prey
3. docker run -p 8081:8081 predator-prey
Для самых ленивых я собрал и выложил образ на Docker Hub
Если не хочется возиться с докером — на странице репо (ссылка ниже) есть инструкция по установке с нуля.
Ссылки
- Модель Хищник-жертва
- Модель Лотки-Вольтерры
- Репо на Гитхабе
Математика отношений хищник-жертва · Границы для молодых умов
Аннотация
Некоторые животные охотятся на других животных, чтобы прокормить себя; этих животных называют хищниками. Животные, на которых охотятся и которых едят, называются добычей. Как вы думаете, что произошло бы, если бы хищник был введен в экосистему, где раньше жила добыча, не опасаясь охоты? Будет ли новый хищник есть всех животных-жертв, пока они не вымрут? На самом деле отношения между хищником и добычей намного интереснее. В этой статье мы покажем, как выглядят отношения «хищник-жертва» с течением времени, и объясним, как ученые могут делать прогнозы о будущих уровнях популяции, используя базовую математику, такую как сложение, вычитание и умножение.
Почему мы изучаем популяции животных?
Ученым необходимо собирать информацию, чтобы они могли понять, как защитить окружающую среду и животных, которые в ней живут. Ученые иногда используют математику для проверки своих теорий о животных или даже для того, чтобы предсказать будущее! Это называется математическим моделированием. Моделирование отношений между хищниками и добычей помогает ученым понять, как их популяции меняются с течением времени, и позволяет ученым узнать, когда животное может оказаться под угрозой исчезновения. Чтобы создать успешную математическую модель, нам нужно собрать данные из окружающей среды. В этой статье мы покажем, как некоторые базовые математические упражнения, такие как сложение, вычитание и умножение, можно использовать для моделирования отношений хищник-жертва, наблюдаемых в дикой природе.
Во-первых, нам нужны данные!
Хорошие модели начинаются с хороших данных. Чтобы смоделировать отношения хищник-жертва, мы будем использовать данные о популяции (записи о количестве животных), собранные компанией, которая охотилась как на хищников, так и на добычу из-за их меха в девятнадцатом и двадцатом веках. Компания Гудзонова залива ежегодно вела учет количества собранных ими шкур снежной рыси и зайца-беляка. На рис. 1 представлены данные компании по количеству шкурок зайца и рыси. Количество собранных шкур зайца или рыси говорит нам об уровне популяции каждого животного и может дать нам разумную картину взаимоотношений хищник-жертва. Данные показывают, что в некоторые годы, например 1927 года рысей (хищников) было больше, а зайцев (жертв) меньше, а в другие годы, например, в 1932 году, зайцев было больше, а рысей меньше.
- Рисунок 1 — (A) Количество собранных шкур зайца (в десятках тысяч) с течением времени.
- (B) Количество шкур рыси, собранных (в десятках тысяч) с течением времени, согласно данным компании Hudson Bay Company с 1895 по 1935 год 1 .
О чем говорят нам данные Гудзонова залива?
Рост и падение зарегистрированных популяций зайцев и рысей с течением времени предполагает, что между этими двумя животными существует связь, что имеет смысл, поскольку мы знаем, что рыси едят зайцев. Видите ли вы на рисунке 1, что популяции рысей и зайцев падают и растут примерно в одно и то же время? Чем больше рысей, тем больше они едят зайцев, что уменьшает их популяцию. Когда популяция зайцев невелика, это означает меньшее количество пищи для рысей и приводит к уменьшению популяции рысей. Когда популяция рысей уменьшается, популяция зайцев снова увеличивается, и цикл вверх-вниз продолжается. Если популяции хищников и жертв сбалансированы, то со временем они будут увеличиваться и уменьшаться, преследуя друг друга по кругу жизни. Математик задает вопрос: «Могу ли я объяснить это, используя сложение, вычитание и умножение; и могу ли я предсказать будущее население»
Объяснение связи с математическими моделями
Математики используют дифференциальные уравнения и данные для описания того, что они видят в мире. Отношения хищник-жертва были впервые описаны с помощью дифференциальных уравнений двумя учеными по имени Лотка [1] и Вольтерра [2]. Они хотели использовать математику, чтобы объяснить взлеты и падения, наблюдаемые в общих отношениях хищник-жертва.
Уравнения иногда могут выглядеть очень сложными, но все, что они представляют собой, — это способ описать, как и почему меняется популяция. Знаменитый математик Леонард Эйлер (1707–1783) показал, что дифференциальные уравнения можно просто записать в виде плюсов и минусов с небольшим умножением. Дифференциальные уравнения можно использовать для моделирования популяций рысей (хищников) и зайцев (добычи) с использованием данных компании Hudson Bay Company. Подгоняем исходные данные математическими методами [3], чтобы оценить значения скорости роста ( R Рост ) , Смертность ( R Смерть ) , Скорость съедения ( R Eute ) , и скорость продовольствия (R ) , и коэффициент продовольствия (R ) , и коэффициент продовольствия (R ) , и коэффициент пищи (R ) , и продовольственная скорость (R ) , и продовольственная. будет использоваться для прогнозирования популяций зайцев и рысей.
Моделирование популяции зайцев-беляков
При составлении уравнения математик думает о мире. Теперь давайте подумаем о том, что происходит с популяцией зайцев с течением времени. Если бы не было рысей, то популяция зайцев в будущем, Н F , будет равно текущей популяции зайцев, H C , плюс рождаемость и минус смертность. Мы называем это темпом роста, r рост . Количество рождений и смертей будет зависеть от того, сколько живо сейчас зайцев, поэтому умножаем r роста на H C (рис. 2А).
- Рисунок 2 — (A) Уравнения, используемые для прогнозирования будущей популяции зайцев, если бы не было рысей, что приводит к экспоненциальному росту.
- (Б) Уравнения, используемые для прогнозирования будущей популяции рысей, если бы не было зайцев, что привело к экспоненциальному сокращению. (C) Уравнения для популяций зайца и рыси при взаимодействии популяций друг с другом. Это приводит к колебаниям уровня популяции как зайцев, так и рысей.
Давайте воспользуемся данными Гудзонова залива, чтобы подставить числа в уравнение. когда данные начинаются с 1895 года, популяция зайцев составляет 85, поэтому мы примем H C = 85 зайцев. Скорость роста популяции зайцев r г г о ш т ч = 0,9 в год. Поскольку r рост положителен, мы ожидаем, что в будущем население будет расти. Это дает будущую популяцию зайцев H F в 1896 г.:
H F = H C + (r рост × H C ), H F = 85 + (5) × 8 161,5.
Мы прогнозируем, что будущая популяция зайцев составит 161,5 зайца. Если популяция продолжит расти так, как весь мир будет покрыт зайцами, что называется экспоненциальным ростом (рис. 2А).
Моделирование популяции снежной рыси
Давайте теперь рассмотрим, что происходит с популяцией рысей с течением времени. Если бы не было зайцев, у рысей не было бы еды, поэтому популяция рысей уменьшилась бы. Чтобы смоделировать это, мы используем вычитание. Будущее количество рысей (L F ) равно текущему количеству рысей (L C ) минус смертность, r d e a t h настоящее время, количество рысей (рис. 2B).
Популяция рысей в 1895 г. составляла 51 особь, и путем подгонки данных мы установили коэффициент смертности r смертей = 0,25. Теперь уравнение дает:
L F = L C — (r смерть × L C ),
L F = 51–(0,25 × 51) = 38,25.
Наши расчеты предсказывают, что будущая популяция рысей в 1896 году составит 38,25 особей. Это известно как экспоненциальное снижение, и если оно будет продолжаться, рысей не будет (рис. 2В).
Моделирование взаимодействия зайца и рыси
Сами по себе популяция зайцев увеличивается, а популяция рысей уменьшается. Что мы знаем о том, как эти популяции взаимодействуют друг с другом? Рыси поедают зайцев и таким образом сокращают популяцию зайцев; поэтому мы используем вычитание для моделирования этого. Нам нужен термин для скорости поедания, r съеденных , который зависит от текущей популяции рысей и зайцев, доступных как для еды, так и для того, чтобы быть съеденными. Итак, умножаем r съеденного на L C и H C .
По той же логике зайцы являются источником пищи для рысей, поэтому мы используем сложение в уравнении для рыси и умножаем текущую популяцию зайцев на текущую популяцию рысей, умноженную на норму корма, r пищевой (рис. 2С).
Значения H C = 85 зайцев, r роста = 0,9, L C = 51 рыси и r гибели = 0,25 остаются прежними. Из данных мы получаем норму еды r съеденных = 0,024 и норму еды r еды = 0,005. Подставляя эти числа в уравнение для предсказания будущей численности зайцев, получаем:
H F = H C + (r рост × H C ) – (r съел ×L C ×H C ),
H F = 85 + (0,9×85) – (0,024×85×51) = 59,24,
и уравнение для предсказания будущего Lynxes теперь дает:
L F = L C -(R Death × L C ) + (R Food × L C × H C ),
L 7 × H C ),
L 7 × H C ). F = 51–(0,25 × 51) + (0,005 × 51 × 85) = 59,925.
Наша модель (оба приведенных выше уравнения) предсказывает сокращение популяции зайцев и увеличение популяции рысей в 1896, как показано на рис. 3 зеленой и красной стрелками.
- Рисунок 3. Популяции зайцев и рысей, смоделированные с использованием уравнений и данных компании Гудзонова залива с 1895 по 1935 год.
- (A) Смоделированная популяция зайцев. (B) Смоделированная популяция рысей. Эти два графика показывают рост и падение, которые мы видели в реальных данных на рисунке 1. (C) Как меняется популяция рыси для разных популяций зайца. X — это средняя популяция рысей и зайцев, вокруг которой вращаются эти две популяции. Стрелками и цифрами указаны расчеты в тексте, начиная со 1895 по 1896 2 .
Чтобы предсказать, как население изменится в следующем, 1897 году, мы подставим наши значения H F и L F в H C и L C в новых уравнениях. Каждый раз, когда мы делаем это, мы получаем новые значения, и каждое значение является точкой для наших графиков на рисунке 3.
Визуализация отношений хищника и жертвы
популяций зайцев и рысей и сделать наши собственные данные, показывающие, как отношения хищник-жертва развиваются с течением времени (рис. 3).
Другой способ показать, как связаны два вида, состоит в том, чтобы построить график того, как популяция зайцев (ось x) и популяция рысей (ось y) изменяются по отношению друг к другу (рис. 3C). X в середине показывает среднюю популяцию зайца (39) и среднюю рысь (45), известную как точка равновесия. Популяции рысей и зайцев вращаются вокруг этого среднего значения по мере того, как популяции растут и падают, образуя круг жизни. Это немного похоже на орбиту Земли вокруг Солнца. Популяции постоянно меняются, что отражает их взлеты и падения с течением времени. В сбалансированной экосистеме, подобной смоделированной здесь, орбита остается стабильной; но если он начинает двигаться по спирали внутрь или наружу, это может быть ранним признаком перемен.
Одно из таких изменений произошло в 1995 году, когда в Йеллоустонский парк вновь завезли волков. Это привело к некоторым неожиданным результатам для окружающей экосистемы 3 . Основываясь на этих удивительных наблюдениях и математических расчетах, подобных тому, что мы показали здесь, Гудман и его коллеги разработали компьютерную игру для создания сбалансированной экосистемы 4 .
Модели не точны
Когда математики пытаются описать что-то сложное, они упрощают. Уравнения, которые мы показали, также должны упростить ситуацию. Упрощения означают, что прогнозы и симуляции не идеально соответствуют исходным данным. Вот некоторая информация, которую мы упустили из нашей модели:
- Существует более одного хищника зайца-беляка.
- Снежные рыси охотятся не только на зайцев-беляков; они также могут есть рыбу и белок.
- В нашей модели у зайцев-снегоступов не заканчивается еда, что не соответствует действительности зимой.
- А как насчет охотников за мехом, которые охотятся и на рысей, и на зайцев?
Чтобы уравнения работали во всех этих других ситуациях, нам пришлось бы включить дополнительные уравнения и больше плюсов и минусов. Если бы у нас были все данные, мы могли бы идеально смоделировать будущее. Даже с этими упрощениями математика по-прежнему хорошо моделирует популяции зайцев и рысей.
Как еще можно использовать эту модель?
Если в этой модели заменить слова «снежная рысь» на «акула» и «заяц-беляк» на «рыба», математика все равно будет работать с правильными данными [2]. Вы даже можете использовать те же уравнения и заменить слово «рысь» на «зомби» и «заяц» на «человек»! Отношения хищник-жертва могут быть расширены за пределы популяций животных и могут использоваться для моделирования того, как взаимодействуют компании, как происходят химические реакции и как распространяются вирусы. Вы можете прочитать больше о математике вирусов в другой статье Frontiers for Young Minds, нажав здесь [5].
Резюме
Чтобы разработать модели реального мира, математики должны начать с надежных данных. Это означает, что для ученых, защитников природы и даже охотников за мехом жизненно важно собирать информацию об окружающей их среде. Используя данные, мы можем определить закономерности в отношениях, а затем использовать математику, чтобы воссоздать эти закономерности и предсказать будущие данные, которые могут представлять и предсказывать будущее этих отношений. Эти прогнозы могут помочь нам поддерживать сбалансированные экосистемы. Надеюсь, из этой статьи вы поняли, что для моделирования и прогнозирования популяций хищника, его добычи и многого другого требуется лишь базовая математика сложения, вычитания и умножения — и немного умного мышления.
Глоссарий
Дифференциальные уравнения : ↑ Уравнения, которые описывают, как население меняется с течением времени, или описывают многие другие процессы, включая то, как летает вертолет, как планеты вращаются вокруг звезды или как кровь течет в наших венах.
Оценка : ↑ Значение, достаточно близкое к точному ответу, обычно создается на основе имеющихся у вас знаний о системе или путем предварительного расчета.
Скорость роста : ↑ Скорость роста — это увеличение популяции зайцев, если бы у них не было хищников. Его можно оценить по данным, используя число рождений за вычетом смертей.
Смертность : ↑ Смертность — это уменьшение популяции рысей с течением времени, если у них не было еды. Это число смертей минус число рождений.
Скорость поедания : ↑ Скорость поедания — это количество зайцев, добытых и съеденных рысью.
Скорость питания : ↑ Норма еды — это количество зайцев, которых рысь должна съесть, чтобы выжить.
Экспоненциальный рост : ↑ Устойчивый и быстрый рост.
Точка равновесия : ↑ Точка равновесия в двух популяциях. Когда система находится в равновесии, говорят, что она устойчива.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Благодарности
Работа выполнена при финансовой поддержке Ирландского исследовательского совета (GOIPG/2020/943).
Сноски
1. ↑ Ссылка на анимированную версию рисунка здесь.
2. ↑ Ссылка на анимированную версию рисунка здесь.
3. ↑ Смотреть: Sustainable Human 2014.
4. ↑ Играть здесь: https://ecobuildergame.org.
Каталожные номера
[1] ↑ Лотка, А. Дж. 1920. Аналитическая записка о некоторых ритмических отношениях в органических системах. Proc Natl Acad Sci USA. 6: 410–5.
[2] ↑ Volterra, V. 1926. Колебания численности вида, рассматриваемые математически. Природа . 118: 558–60.
[3] ↑ де Сильва, Б. М., Чемпион, К., Куад, М., Луазо, Дж. К., Куц, Дж. Н., и Брантон, С. Л. 2020. PySINDy: пакет python для разреженной идентификации нелинейной динамики по данным . Препринт arXiv архив: 2004.08424.
[4] ↑ Батлер, Дж. С., и Брейди, Р. М. 2020. Хищник: Кодекс добычи для молодых умов . Гитхаб. Доступно в Интернете по адресу: https://github.com/john-s-butler-dit/Predator-Prey-for-Young-Minds
.[5] ↑ Брукс, Х. З., Канджанасаратул, У., Курех, Ю. Х., и Мейсон. P. 2021. Детективы болезней: использование математики для прогнозирования распространения инфекционных заболеваний. Фронт Молодых Умов. 9:577741. doi: 10.3389/frym.2020.577741
Исследование взаимодействия хищник-жертва показывает, что больше еды не всегда означает больше потребления
Зимняя камбала (Pseudopleuronectes americanus) в заливе Наррагансетт. Это камбала, обитающая в прибрежных водах западного побережья Северной Атлантики от Лабрадора до Джорджии, хотя к югу от залива Делавэр она встречается реже. Питается донными животными. Фото: NOAA Fisheries
Ученые из Северо-восточного научного центра рыболовства разработали необычайно богатую картину того, кто кого ест на северо-востоке Соединенных Штатов. Выводы, опубликованные в Fish and Fisheries , подробно изучают особенности питания 17 видов рыб, хищников и их добычи.
Хищники делятся на 48 категорий размера хищников и 14 видов добычи. Хищниками среди рыб были атлантическая треска, атлантическая сельдь, пикша, гусиная рыба, минтай, акула, зимняя камбала и желтохвост-основатель. Среди видов добычи были кормовая рыба, кальмары, зоопланктон, креветкоподобные ракообразные, моллюски, офиуры, морские ежи и морские ежи.
«У нас есть крупнейший в мире непрерывный набор данных о пищевых привычках рыб в Северо-восточном научном центре рыболовства, и это позволило нам провести исследование такого масштаба и размаха», — сказал Брайан Смит, исследователь пищевых привычек в центре. и ведущий автор исследования. «Мы сосредоточились на общей и важной добыче многих хищных рыб, представляющих интерес, и, надеюсь, заполнили некоторые пробелы в информации, касающейся доступности добычи и хищничества».
Изображение
Атлантическая треска — донная рыба, то есть она живет у дна океана. Его добыча меняется по мере его роста. Фото: NOAA FisheriesХарактер питания внутри и среди разных групп рыб зависит от размера рыбы, численности или плотности добычи и других факторов. Исследователи, изучающие морские экосистемы, должны учитывать это хищничество в своих моделях. Однако в нескольких исследованиях одновременно рассматривались схемы питания различных групп хищных рыб — кормящихся рыбой, кормящихся планктоном и питающихся бентосом или донным кормом. В исследовании также рассматривалось, как эти группы взаимодействуют со своей добычей в толще воды.
Смит и его соавтор Лорел Смит протестировали три модели, используя данные о рыболовстве за десятилетия, в том числе данные о рационе и плотности добычи. Данные были собраны на северо-востоке континентального шельфа США во время бентических исследований в 1950-х и 1960-х годах, а также во время исследований экосистем, начиная с 1973 года. добыча доступна в окружающей среде
Среди результатов исследования: большая часть рыб реагировала на изменение численности добычи, меняя добычу или через «период обучения», когда целью была добыча в наибольшем количестве. Эта реакция помогает стабилизировать популяцию добычи и была распространена среди рыбоядных (рыбоедов). Это часто наблюдалось у хищников с менее специализированными привычками питания. Среди этих хищников были гусиные гуси и другие известные промысловые рыбы более крупных размеров.
Изображение
Кормовая рыба, атлантическая сельдь часто ходит стаями и питается планктоном. Фото: NOAA Fisheries Однако высокая плотность добычи беспозвоночных выявила уменьшение питания рыб, которые были планктоноядными и бентофагами — планктоном и донными кормами. Для этих рыб большее количество пищи не означало большего потребления. Исследователи обнаружили, что более плотная добыча может дезориентировать или сбивать с толку планктофагов, уменьшая их питание зоопланктоном. К планктофагам относятся атлантическая сельдь, атлантическая скумбрия, минтай меньшего размера, серебристый хек, акула и белый хек. Их пищевая реакция не часто учитывается при изучении морских экосистем.
Среди изученных бентофагов были атлантическая треска меньшего размера, красный хек и зимний скат, а также пикша всех размеров, морская дутыша, несколько камбал и несколько других видов. Эти рыбы поедали мелких донных беспозвоночных в виде мелких и средних рыб. Однако более крупные особи того же вида питались в основном рыбой и имели другое отношение хищник-жертва.
Результаты исследования дают представление о хищничестве и хищничестве промысловых видов во всей толще воды. Это поможет в моделировании экосистемы, поскольку хищничество необходимо учитывать как конкуренцию или как прямое удаление коммерчески и экологически важных видов добычи.