Резьба. Классификация резьбы. Изображение и обозначение резьбы на чертежах
Похожие презентации:
Основы архитектуры и строительных конструкций. Основы проектирования
Конструктивные схемы многоэтажных зданий
Стадии проектирования зданий. Маркировка строительных чертежей (лекция №2)
Правила выполнения архитектурно-строительных чертежей
ЕСКД. Общие правила оформления чертежей. (Лекция 1.1)
задачи на построение (геометрия 7 класс)
Выполненный вариант контрольной работы по разделу «Техническое черчение». (Приложение 3)
Параллельность в пространстве. (Графическая работа 2)
Строительное черчение. Графическое оформление и чтение строительных чертежей
Правила оформления чертежей ЕСКД. Форматы, масштабы, линии, шрифты
РЕЗЬБА.
КЛАССИФИКАЦИЯ РЕЗЬБЫ.
ИЗОБРАЖЕНИЕ И
ОБОЗНАЧЕНИЕ РЕЗЬБЫ НА
ЧЕРТЕЖАХ.
Девиз:
Использование в технике
винтовых поверхностей
(подсказано природой) – одно
из замечательных
достижений пытливой
человеческой мысли в

Резьба
винтовом
–
поверхность, образованная при
движении
плоского
контура
по
цилиндрической или конической поверхности.
В основе образования резьбы лежит принцип
получения винтовой линии.
Винтовая линия – это пространственная
кривая, которая может быть образована точкой,
совершающей движение по образующей какой-либо
поверхности вращения, при этом сама образующая
совершает вращательное движение вокруг оси.
Нарезание
резьбы
происходит,
когда
на
поверхности цилиндра винтовую линию описывает
резец, равномерно движущийся вдоль образующей
цилиндра,
который
вращается
скоростью вокруг своей оси.
с
постоянной
Примеры применения винтовой
линии
«Архимедов
винт» и рисунки
Леонардо да
Винчи
Эскизы приспособлений для
изготовления гаек и
винтов, выполненные
Леонардо да Винчи.
Токарно-копировальный станок А.К. Нартова 1712 г. в
стиле русского барокко (слева).
 Большой токарнокопировальный станок А.К. Нартова 1718-1729 г.г. в
Большой токарнокопировальный станок А.К. Нартова 1718-1729 г.г. встиле петровского барокко (справа).
Токарновинторезный
станок с
механизированным
суппортом и
набором сменных
зубчатых колёс
Дата изобретения:
1712 г.
Разработчик:
Нартов Андрей
Константинович
Станок А.К. Нартова
токарнокопировальный. 1729
г.
В этом станке
применены все лучшие
достижения Нартова,
доведенные до
совершенства.
РЕЗЬБА ПОДРАЗДЕЛЯЕТСЯ
по эксплуатационному назначению
Крепежная
Применяются в неподвижных
крепежных соединениях
(метрическая, дюймовая,
трубная).
Ходовая
Специальная
Параметры, а именно профиль,
шаг и диаметр, не
соответствуют стандартам.
Применяются в подвижных соединениях,
вращательного движения в поступательное
(грузовые винты домкратов, ходовые винты
металлорежущих станков и др.) (упорная,
трапецеидальная, прямоугольная, круглая).

РЕЗЬБА ПОДРАЗДЕЛЯЕТСЯ
по направлению винтовой линии
Правая
Левая
подъем винтовой линии на
видимой (передней) стороне идет
слева направо
подъем винтовой линии на
видимой (передней) стороне идет
справа налево
РЕЗЬБА ПОДРАЗДЕЛЯЕТСЯ
по форме поверхности
Цилиндрическая
резьба, образованная на цилиндрической
поверхности
Коническая
резьба, образованная на конической
поверхности
РЕЗЬБА ПОДРАЗДЕЛЯЕТСЯ
по числу заходов
Однозаходная
при перемещении по поверхности
одного плоского профиля
Многозаходная
при одновременном перемещении по
поверхности двух, трех и более плоских
профиля, равномерно расположенных по
окружности относительно друг друга
Однозаходная резьба
P
Ph = 3P
P
Ph = 2P
P
двухзаходная
трехзаходная
Многозаходная резьба
РЕЗЬБА ПОДРАЗДЕЛЯЕТСЯ
по расположению резьбы
Внешняя
резьба, нарезанная на наружной
поверхности
Внутренняя
резьба, нарезанная на внутренней
поверхности
РЕЗЬБА ПОДРАЗДЕЛЯЕТСЯ
по форме профиля
Треугольная
Трапецеидальная
Упорная
Прямоугольная
Круглая
С
т
а
н
д
а
р
т
н
ы
е
С
п
е
ц
и
а
л
ь
н
ы
е
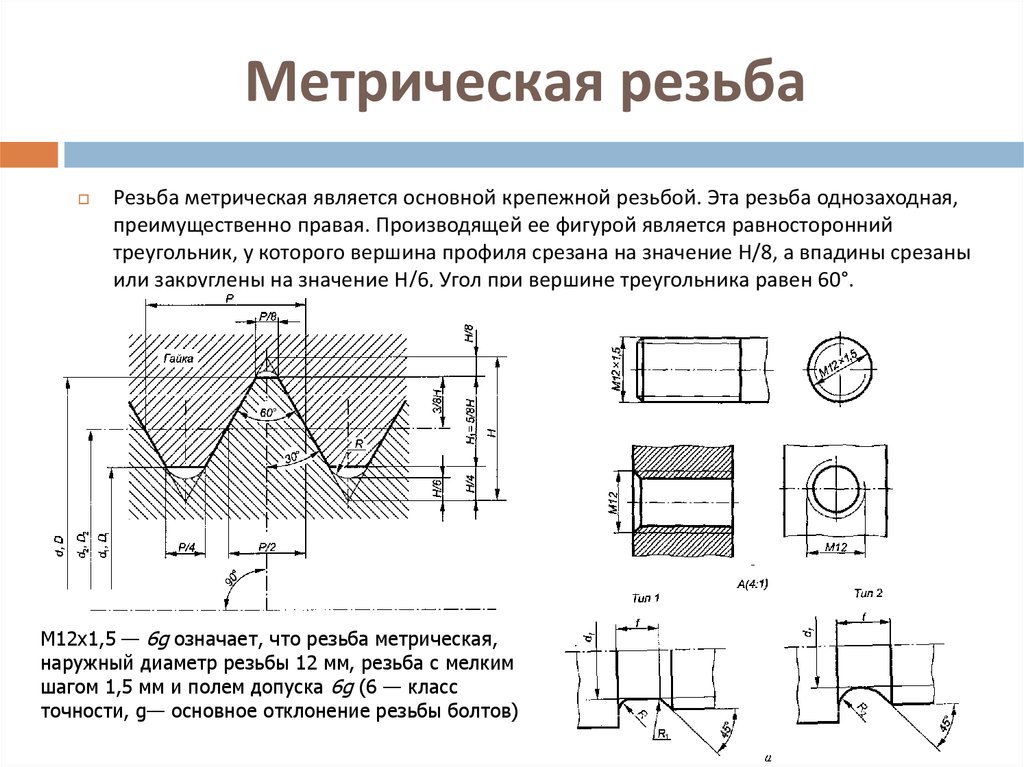
Метрическая резьба
(ГОСТ 9150 – 2002)
с углом профиля α = 60 ˚
Согласно ГОСТ 8724 – 2002
метрическая резьба делится на
два типа:
с крупным шагом – применяется
в соединениях, подвергающихся
ударным нагрузкам;
с мелким шагом – применяется в
соединениях стандартными
резьбовыми деталями (винты,

Трубная резьба
Цилиндрическая резьба
ГОСТ 6357 – 81 представляет собой
дюймовую резьбу с мелким шагом,
закругленными впадинами с углом α = 55 ˚
Коническая резьба
ГОСТ 6211 – 84 соответствует
закругленному профилю трубной
цилиндрической резьбы с углом α = 55 ˚
Конические резьбы применяют в трубных соединениях для получения
герметичности без специальных уплотняющих материалов (льняных нитей,
Трапецеидальная резьба (ГОСТ 9484 –
81).
Профиль – равнобочная трапеция с
углом
α = 30˚.
Трапецеидальная резьба применяется
для передачи осевых усилий и
движения в ходовых винтах.
Симметричный профиль резьбы
позволяет применять ее для
реверсивных винтовых механизмов.
Упорная резьба (ГОСТ 10177 –
82). Профиль – неравнобочная
трапеция с углом рабочей
стороны 3˚ и нерабочей – 30˚
Применяется в грузовых винтах для
передачи больших усилий,
действующих в одном направлении (в
мощных домкратах, прессах и т.
 д.).
д.).СПЕЦИАЛЬНЫЕ РЕЗЬБЫ
Прямоугольная и квадратные
резьбы
Применяются для передачи
осевых усилий в грузовых винтах и
движения в ходовых винтах.
Круглая резьба
Применяется в машиностроении
там, где имеются большие
динамические нагрузки или высокая
загрязненность.
КЛАССИФИКАЦИЯ РЕЗЬБЫ
резьба подразделяется
форме
поверхности
расположению
резьбы
направлению
винтовой
линии
числу
заходов
эксплуатационному
назначению
Внешняя
Крепежная
Внутренняя
Ходовая
Цилиндрическая
Коническая
Правая
форме
профиля
Специальная
Левая
Треугольная
Однозаходная
Многозаходная
Упорная
Прямоугольная
Круглая
Основные параметры резьбы
P
h
d – наружный диаметр
d1 – внутренний
диаметр
P – шаг резьбы
60˚ – угол профиля
h – глубина резьбы
L – длина резьбы
l – резьба полного
профиля
l1 – сбег резьбы
Последовательность получения резьбы в гнезде
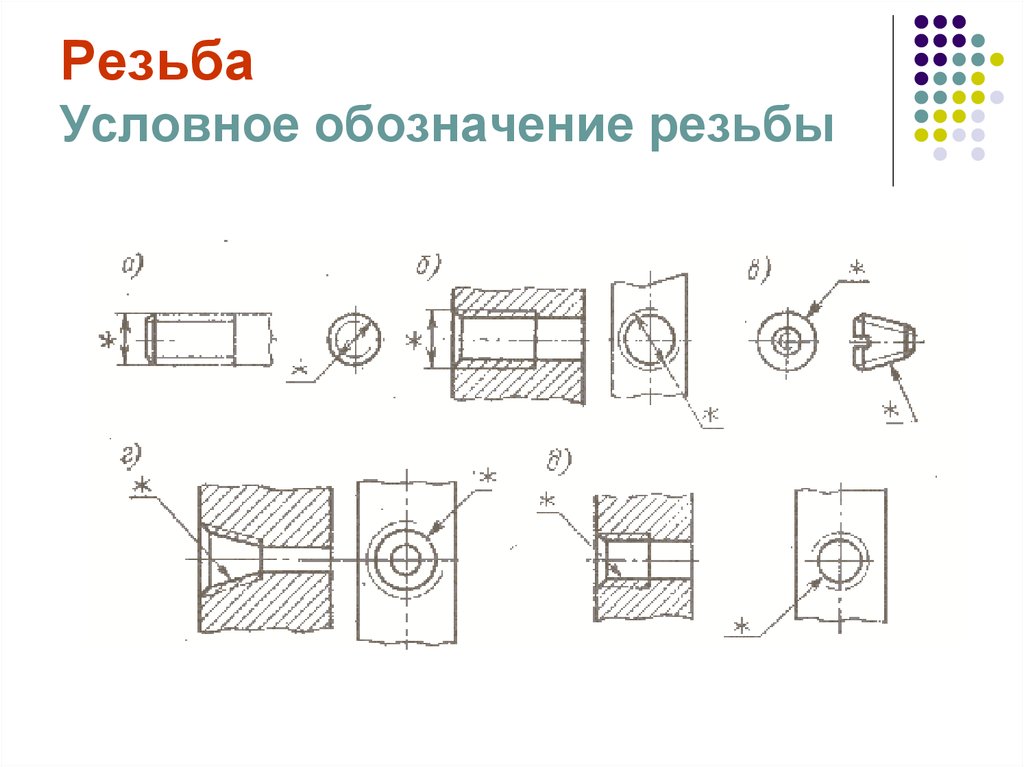
Изображение резьбы на
стержне:
натуральное и условное
Изображение резьбы в
отверстии (в разрезе):
натуральное и условное
А
А (5:1)
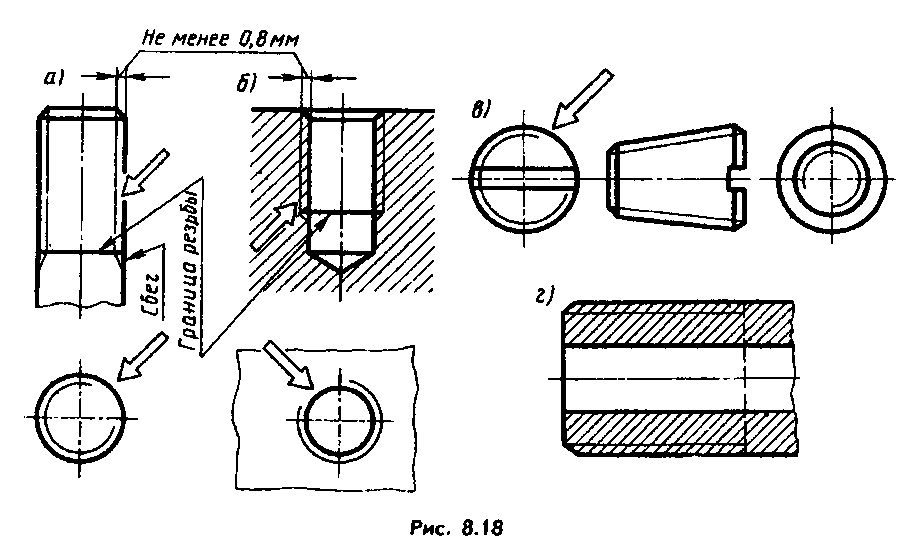
Изображение
сбега резьбы на
чертежах:
а) на стержне;
б) в отверстии.

Б
Б (5:1)
На выносных
элементах
изображены
формы сбегов
резьбы
Структура обозначения резьбы
1
2
˟
3
4
—
5
1. Условное обозначение типа (профиля) резьбы.
М
– метрическая,
G
– трубная цилиндрическая,
R
– трубная коническая,
Tr
– трапецеидальная,
S
– упорная,
Кр
– круглая.
2. Наружный диаметр резьбы (в мм или дюймах). В обозначении конической резьбы
указывается наружный диаметр в дюймах со знаком «»» [1″ = 24,5 мм].
3. Шаг резьбы или ход резьбы (в мм). Шаг резьбы указывается для метрической
(мелкий шаг), трапецеидальной и упорной резьбы.
Для многозаходных резьб в обозначении резьбы входит ход резьбы, а шаг
проставляется в скобках.
4. Направление винтовой линии. Направление винтовой линии указывается только
для левой резьбы (LH).
5. Поле допуска или класс точности резьбы. Обозначение поля допуска диаметра
резьбы состоит из цифры, показывающей степень точности, и буквы, обозначающей
основное отклонение.
Общая схема
обозначения
резьбы
Диаметры и шаги метрической
резьбы
(выдержка из ГОСТ 8724-2002
взаимозаменяемости Резьба
метрическая. Диаметры и шаги).
Примеры обозначения резьбы
Примеры обозначения резьбы
Ответить на вопросы:
1. Где применяют резьбовые соединения?
2. Что общего у плашки, метчика, резца, сверла?
English Русский Правила
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 5 из 5 Метрическая резьба является основным типом крепежной резьбы. Профиль резьбы установлен ГОСТ 9150–81 и представляет собой равносторонний треугольник с углом профиля α = 60°. Профиль резьбы на стержне отличается от профиля резьбы в отверстии величиной притупления его вершин и впадин. Основными параметрами метрической резьбы являются: номинальный диаметр – d(D) и шаг резьбы – Р, устанавливаемые ГОСТ 8724–81. На чертежах метрическая резьба обозначается буквой М, после которой пишется величина наружного диаметра резьбы, например М20, далее может быть указан мелкий шаг резьбы, например М20х1,5. Если после величины наружного диаметра не указывается величина шага резьбы, то это означает, что резьба имеет крупный шаг. Величина шага резьбы выбирается по ГОСТу (рис. 208). По ГОСТ 8724–81 каждому номинальному размеру резьбы с крупным шагом соответствует несколько мелких шагов. Трубная цилиндрическая резьба, ее профиль и условное обозначение. В соответствии с ГОСТ 6367–81 трубная цилиндрическая резьба имеет профиль дюймовой резьбы, т. е. равнобедренный треугольник с углом при вершине, равным 55° (см. табл.1.2.1). Резьба стандартизована для диаметров от 1/16 » до 6″ при числе шагов zот 28 до 11. Номинальный размер резьбы условно отнесен к внутреннему диаметру трубы (к величине условного прохода). Трубную резьбу применяют для соединения труб, а также тонкостенных деталей цилиндрической формы.трубная цилиндрическая резьба. Условное обозначение резьбы состоит из буквы G, обозначения размера резьбы, класса точности среднего диаметра (А или В). Для левой резьбы применяется условное обозначение LH. Например, G1½LH–В–40 длина свинчивания, указываемая при необходимости. Соединение внутренней трубной цилиндрической резьбы класса точности А с наружной трубной конической резьбой по ГОСТ 6211–81 обозначается следующим образом: например, G/Rp–1½–А. 19. Условное изображение резьбы на стержне и ее обозначение. Независимо от того, какой профиль имеет резьба, на чертежах она изображается следующим образом Изображение резьбы на стержне.
На виде спереди и слева наружный диаметр резьбы показывают сплошной основной линией, а внутренний — сплошной тонкой (рис. Условное изображение резьбы в отверстии и ее обозначение. В отверстии на виде спереди наружный и внутренний диаметры резьбы показывают штриховыми линиями (рис. 207, б). На виде слева не показывают фаску, а наружный диаметр резьбы проводят сплошной тонкой линией, разомкнутой на одну четверть окружности. При этом один конец дуги не доводят, а другой пересекает центровую линию на одинаковую величину. Внутренний диаметр резьбы проводят сплошной основной линией. Границу резьбы показывают штриховой линией. На разрезе резьбу в отверстии показывают следующим образом (рис. Схемы. Типы схем. Схема — это графический конструкторский документ, на котором показаны в виде условных изображений или обозначений составные части изделия и связи между ними. Схемы применяют при изучении принципа действия механизмов, машин, приборов, аппаратов, при их наладке и ремонте, монтаже трубопроводов и электрических сетей. (ГОСТ 2.102-68). Элемент схемы – составная часть схемы, которая выполняет определенную функцию в изделии и не может быть разделена на части, имеющие самостоятельное функциональное назначение. (резистор, трансформатор, насос и т.д.) Линии взаимосвязи – отрезок линии, указывающий на наличие связи между функциональными частями изделия. Устройство-совокупность элементов, представляющих единую конструкцию. Устройство может не иметь в изделий определенного функ. значения. ГОСТом 2.701-84 установлено 8 типов схем. Типы схем устанавливаются в зависимости от основного назначения схем. Обозначается арабскими цифрами: 1-структурная 2-функциональная 3-принципиальная полная 4-схема соединений 5-схема подключения 6-общая схема 7-схема расположения 0-объединенная схема Структурная схема определяет основные функ. части изделия, их назначения, их взаимосвязи. Разрабатывается на стадий проектирования, представляющей разработке схем других типов. Используется для общего ознакомления с изделием. Функциональные части изделия изображают на схеме в виде прямоугольников или других плоских фигур с вписанными в них обозначениями швов. Функ. схема поясняет определенные процессы, протекающие в отдельных цепях изделия или в изделий в целом. Используется для изучения принципов работы изделия, а также наладке, регулировке, контроля и ремонта изделия. Принципиальная схема – определяет полный состав элементов и связей между ними и дает представление о принципах изделия. Схема соединений(монтажные схемы) – показывает порядок составных частей изделия. Состав элементов изделия. Схема подключения – показывает внешние входные и выходные подключения изделия. Общая схема – определяет составные части комплекса и соединения его составных частей на месте эксплуатаций. Схема расположения – определяет относительное расположение составных частей изделия. Объединенная схема – содержит в виде совмещения на одном конструкторском документе 2 или более типов схем: схема соединения и схема подключения. Виды схем. Код схемы. ГОСТом 2.701-84 установлены 10 видов схем. Виды схем определяются в зависимости от видов элементов и связи, входящих в состав изделия. Обозначаются прописными буквами русского алфавита: Э-электрическая Г-гидравлическая П-пневмотическая Х-газовая, кроме пневматических К-кинематическая В-вакуумная Л-оптическая Е-схема деления С-коомбинированная Схема деления разрабатывают для определенного состава изделия. Коомбинированная – выполняют, если в состав входят элементы разных видов.
⇐ Предыдущая12345 Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 83; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Методы измерения резьбы на производстве и в домашних условиях — РИНКОМ
Методы измерения резьбы на производстве и в домашних условиях — РИНКОМГлавная
Статьи
Методы измерения резьбы на производстве и в домашних условиях Методы измерения резьбы на производстве и в домашних условиях
2 апреля 2021
Гирин Кирилл
измерить резьба
Содержание
- Какие дефекты можно выявить при контроле?
- Приборы для контроля резьбы
- Приборы активного контроля
- Измерение резьбы методом трех проволочек
- Измерение шага резьбы
- Измерение среднего диаметра резьбы
- Измерение наружного диаметра резьбы
- Измерение внутреннего диаметра резьбы
- Измерение профиля резьбы
- Где купить инструменты для измерения резьбы?
При измерении резьбы уточняют ее соответствие таким параметрам, как внутренний, наружный и средний диаметры, шаг и длина. С этой целью используют специальные и универсальные инструменты. Подходящий измерительный прибор выбирают с учетом типа резьбы и необходимой точности измерений. Первоначально контролируют средний диаметр, шаг и форму профиля, после этого — внутренний и внешний диаметры.
С этой целью используют специальные и универсальные инструменты. Подходящий измерительный прибор выбирают с учетом типа резьбы и необходимой точности измерений. Первоначально контролируют средний диаметр, шаг и форму профиля, после этого — внутренний и внешний диаметры.
Измерение резьбы выполняют с помощью разных инструментов
Есть два основных метода измерения резьбы:
- метод дифференцирования, когда каждый параметр проверяют отдельно;
- метод комплексной проверки, когда все параметры контролируют совместно бесшкальными инструментами.
Для измерения трубной и конической резьб обычно используют калибры, которые позволяют проверить размеры, форму и взаимное расположение поверхностей детали.
Какие дефекты можно выявить при контроле?
Контроль резьбовых поверхностей позволяет выявить следующие дефекты соединений.
Рваная нарезка. Дефект образуется, если диаметры отверстия и стержня отличаются от номинальных. Причиной также может стать недостаточная острота режущего инструмента. Предупредить проблему позволяет тщательный контроль всех диаметров и использование режущего инструмента нормальной степени заточки.
Дефект образуется, если диаметры отверстия и стержня отличаются от номинальных. Причиной также может стать недостаточная острота режущего инструмента. Предупредить проблему позволяет тщательный контроль всех диаметров и использование режущего инструмента нормальной степени заточки.
Тупая нарезка. Дефект проявляется, если номинальный диаметр меньше диаметра отверстия, но больше диаметра стержня. При нарезании профиль становится неполным. Избежать дефекта позволит точное измерение диаметров перед нарезкой резьбы.
Конусность резьбы. Дефект появляется, если режущий инструмент срезает лишний металл. Проблему решают, соотнося установленные размеры детали и инструмента.
Тугая нарезка. Если размерность детали не соблюдается, а инструмент имеет шероховатую резьбу, резание происходит с трудом. Дефект можно предупредить, предварительно измерив параметры заготовки и подобрав режущий инструмент оптимального размера.
Приборы для контроля резьбы
Для комплексного контроля и измерения наружных метрических резьб используют жесткие предельные калибры-кольца (ГОСТ 17763-72 и ГОСТ 17764-72), а также резьбовые скобы.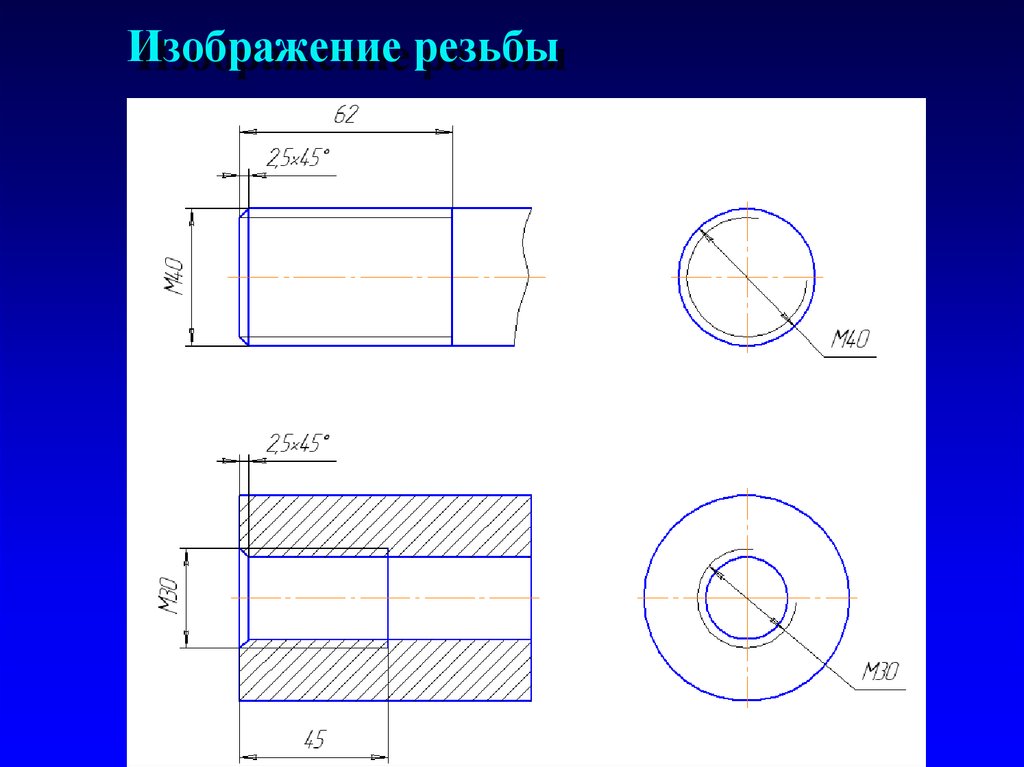 Внутренние резьбы контролируют резьбовыми калибрами-пробками (ГОСТ 17756-72 и ГОСТ 17759-72). При использовании резьбовых калибров-пробок и колец в качестве комплексного измерителя выступает проходной калибр. Непроходной калибр используют, чтобы измерить предельный размер среднего диаметра.
Внутренние резьбы контролируют резьбовыми калибрами-пробками (ГОСТ 17756-72 и ГОСТ 17759-72). При использовании резьбовых калибров-пробок и колец в качестве комплексного измерителя выступает проходной калибр. Непроходной калибр используют, чтобы измерить предельный размер среднего диаметра.
Калибр-кольцо М 1.1х0.25 6h ПР для комплексного контроля и измерения наружных метрических резьб
При поэлементном контроле наружный диаметр болта проверяют любым приборами, которые обычно применяются для контроля диаметра валов. А внутренний диаметр гайки — приспособлениями для контроля отверстий.
Для контроля среднего диаметра используют контактный и бесконтактный методы. Первый основан на применении вставок в микрометр или трех проволочек.
Измерение среднего диаметра вставками резьбового микрометра
Резьбовым микрометром со вставками проводят измерение среднего диаметра треугольной резьбы с углами профиля 60 и 55 градусов. Измерение проводят в пределах от 0 до 350 мм. Для каждого интервала в 25 мм используют или отдельный микрометр, или специальные сменные пятки.
Измерение проводят в пределах от 0 до 350 мм. Для каждого интервала в 25 мм используют или отдельный микрометр, или специальные сменные пятки.
Резьбовой микрометр МВМ-50 GRIFF со вставками для измерения среднего диаметра
Стандартный комплект включает две вставки: призматическую, которая ставится вместо пятки микрометра, и конусную, устанавливаемую в отверстие микрометрического винта.
Микрометр может оснащаться одним из пяти комплектов вставок, который выбирают в зависимости от шага проверяемой резьбы: 0,4–0,5; 0,6–0,8; 1–1,5; 1,75–2,5; 3–4,5 мм.
Контроль шага резьбы и угла профиля индикаторными измерительными приборами
Измерение шага резьбы и угла профиля производят, используя микроскопы и проекторы. При этом средний диаметр внутренней резьбы контролируют:
- индикаторными приборами с раздвижными полупробками;
- индикаторными приборами с раздвижными вставками;
- горизонтальными оптиметрами с помощью измерительных дуг с шаровыми измерительными наконечниками.

Измерять размеры деталей в ходе обработки удобно с помощью индикаторного приспособления. Благодаря особой конструкции упорной планки такое приспособление позволяет установить в удобном месте держатель индикатора. Приспособление универсально и может использоваться как при расточке, так и при обточке.
Индикаторное приспособление для активного контроля размеров при обработке на токарном станке
Применение индикаторов и установочных колец с номинальным размером обрабатываемого отверстия уменьшает время на предварительные операции и обеспечивает высокую точность измерения внутренних размеров резьбы.
При обработке отверстий резец настраивают по индикатору на снятие первой стружки с припуском 0,1–0,2 мм на сторону. После этого показания индикатора замеряют, а первую стружку снимают. Полученный размер отверстия замеряют индикаторным прибором, настроенным по установочному кольцу с номинальным размером отверстия.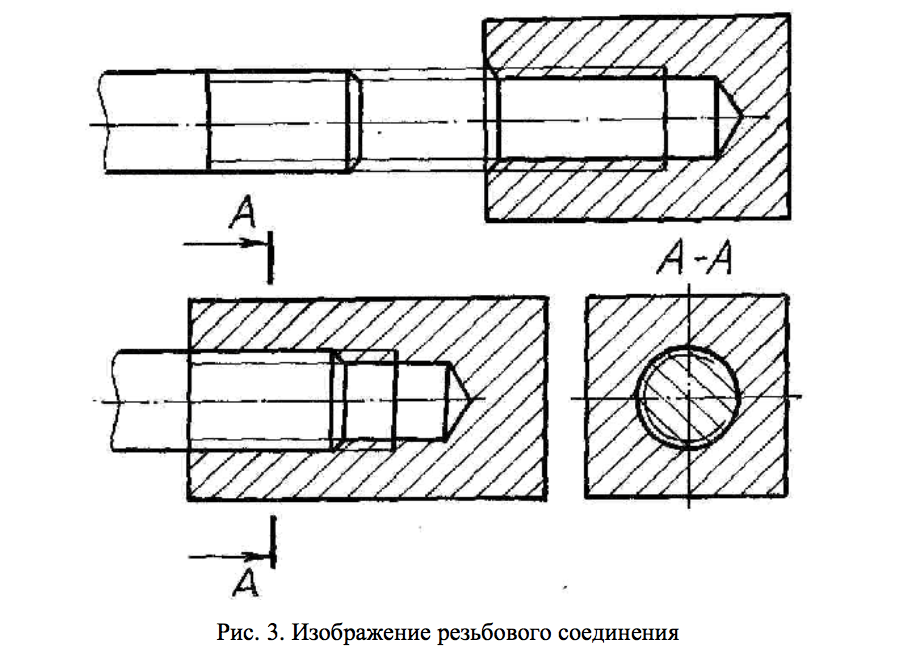 При настройке индикаторный прибор устанавливают на ноль.
При настройке индикаторный прибор устанавливают на ноль.
Измерив отверстие, уточняют, какой слой металла требуется снять, чтобы получить окончательный размер отверстия. Затем по индикатору резец устанавливают под расточку чистового отверстия. Этот способ измерения упрощает расточку отверстий по 2 и 3 классам точности.
Если партия деталей велика, удобнее вначале выполнить предварительную расточку всех изделий с припуском 0,3–0,5 мм на диаметр, а затем за один проход жестким резцом завершить чистовую расточку. Использование индикаторных приспособлений позволяет работать уверенно и с большой точностью. Однако индикатор не отменяет необходимости использования предельных калибров. Измерение резьбы калибром — обязательная процедура, которая требуется для окончательного контроля размера.
Приборы активного контроля
Один из самых прогрессивных методов измерения параметров резьбы считается активный. Он особенно востребован в условиях массового и крупносерийного производства. Устройства активного контроля позволяют автоматически контролировать ход технологического процесса и обеспечивают необходимую точность обработки.
Устройства активного контроля позволяют автоматически контролировать ход технологического процесса и обеспечивают необходимую точность обработки.
Устройства активного контроля обычно включают в конечный цикл обработки и по итогам проверки подают команду на наладку режущего инструмента. Есть и второй способ — проверять размеры изделия в ходе обработки, чтобы сразу контролировать величины перемещения, режимы резания и другие параметры. Приборы активного контроля такого типа используют на станках с числовым программным управлением.
Для автоматического контроля и наладки используют приборы контактного и бесконтактного действия. В первом случае наконечник прибора вступает в контакт с измеряемым изделием и может быть причиной погрешностей. Чтобы исключить такую возможность, наконечники приборов активного контроля изготавливают из твердых сплавов и алмазов.
Измерение резьбы методом трех проволочек
Для измерения среднего диаметра резьбы часто пользуются методом трех проволочек. Диаметр определяют, накладывая проволочки одного размера на впадины резьбовых соединений. Параметры получившейся конструкции измеряют микрометром. На итоговые результаты вычислений сильно влияет погрешность профиля. Чтобы устранить ее, проволочки накладывают на профиль таким образом, чтобы они соединялись на том уровне, где ширина впадин будет равна ширине выступов.
Диаметр определяют, накладывая проволочки одного размера на впадины резьбовых соединений. Параметры получившейся конструкции измеряют микрометром. На итоговые результаты вычислений сильно влияет погрешность профиля. Чтобы устранить ее, проволочки накладывают на профиль таким образом, чтобы они соединялись на том уровне, где ширина впадин будет равна ширине выступов.
Использование метода трех проволочек для измерения резьбы
При этом проволочки должны быть расположены таким образом:
- 1-я лежит на впадине с левой стороны;
- 2-я и 3-я на впадинах противоположной стороны.
Необходимо следить, чтобы во время измерения деталь не деформировалась, а проволочки не гнулись.
Размер всех трех проволочек, используемых для измерения среднего диаметра резьбы этим методом, выбирают по специальной таблице с учетом шага и угла профиля резьбы. Идеальным считают диаметр d = tg α /2c, где cs шаг, а α /2 угол профиля проверяемой резьбы.
Кроме среднего диаметра методом трех проволочек измеряют диаметр трапецеидальной резьбы.
Измерение шага резьбы
Для измерения шага резьбы используют штангенциркуль или линейку. Для этого определяют длину нескольких шагов и делят ее на количество шагов. Шаг внутренней и внешней резьбы определяют резьбомером. Каждая пластинка указывает на величину шага. При этом пластинки выбирают таким образом, чтобы зубья плотно входили в резьбу. Благодаря этому шаг совпадает с шагом на пластине.
Для измерения шага резьбы используют стандартные линейки с миллиметровыми и дюймовыми делениями и резьбомеры. Результаты вычисления шага линейкой неточные, так что главной задачей при замерах является нахождение количества витков, которые приходятся на единичный шаг резьбы. Допустим, если на 1 дюйм приходится 5 витков, шаг будет равен 1/5 дюйма. Чтобы было удобно, результаты в дюймах переводят в миллиметры.
Чтобы измерить шаг резьбы корректно, необходимо быть в курсе следующих хитростей:
- следует измерять не отдельные участки, а целую часть профиля детали;
- перед измерением необходимо подсчитать целое количество витков;
- шаг резьбы определяют после замера глубины и основных параметров резьбового соединения.

Итогом измерений будет усредненное значение шага. Погрешность в расчетах зависит от того, насколько правильно нарезана резьба на деталь.
Резьбомер предоставляет наиболее точные результаты измерений шага трубной и конической резьбы, поскольку он работает с самыми маленькими расстояниями. В конструкции предусмотрены пластины из сплавов железа. Каждая пластина имеет вырезы, равные профилю нарезки и ее шагу.
Для определения величины шага резьбомер прикладывают к детали. При этом необходимо следить, чтобы пластина была параллельна оси нарезки и совпадала по размеру с отверстием резьбы.
Измерение среднего диаметра резьбы
Для измерения среднего диаметра резьбы необходимо использовать резьбовой микрометр в комплекте с разными наконечниками (один с конусом, второй с вырезом). Предел измерения указывают обычно на самих средствах измерения. Так, маркировка М 3–5 обозначает, что комплект позволяет измерить резьбу с шагом 3; 3,5; 4; 4,5 и 5 мм.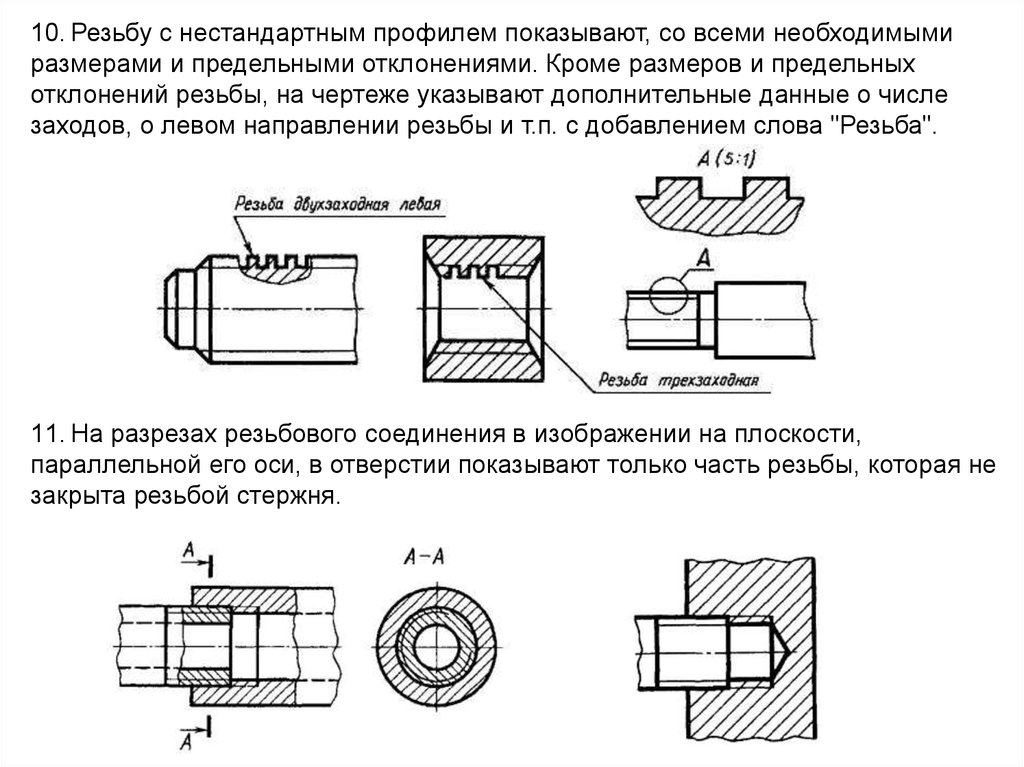
Вставки к резьбовому микрометру
Для измерения среднего диаметра резьбы пользуются микрометром. Сменные наконечники инструмента вставляются в отверстие винта и позволяют добиться максимально точных измерений.
Если в качестве результата достаточно усредненных значений, вместо микрометра допускается использовать кронциркуль. По конструкции он представляет собой шариковые наконечники, размеры которых должны совпадать с типом и шагом резьбового соединения. Чтобы узнать средний диаметр, наконечники кронциркуля необходимо выставить по резьбовому калибру. Затем процедуру повторяют с боковыми сторонами детали. Для оценки результатов измерений используют резьбовые скобы. А точность диаметра проверяют, сравнивая полученную резьбу с шаблоном.
Для контроля среднего диаметра резьбы, состоящей максимум из двух витков, пользуются методом двух проволочек. Измерение производят следующим образом: на противоположные выступы и впадины резьбы накладывают проволоки, диаметр которых совпадает с одной из табличных единиц. При этом расстояние между концами проволочек демонстрирует средний диаметр детали. Для каждого из классов точности создаются отдельные проволоки, соответствующие ГОСТ 2475-88. При выведении конечных чисел берут во внимание возможную погрешность, потому что метод двух проволочек не позволяет добиться точных значений.
При этом расстояние между концами проволочек демонстрирует средний диаметр детали. Для каждого из классов точности создаются отдельные проволоки, соответствующие ГОСТ 2475-88. При выведении конечных чисел берут во внимание возможную погрешность, потому что метод двух проволочек не позволяет добиться точных значений.
Еще один метод измерения среднего диаметра резьбы состоит в использовании микроскопа. Прибор прикладывают к боковой стороне профиля заготовки, а окуляры наводят на изображение профиля с каждой стороны, чтобы определить его размер. Значения, которые были получены в результате измерений, складывают и делят на количество сторон. Полученное среднее арифметическое — это и есть средний диаметр резьбового соединения.
Измерение наружного диаметра резьбы
Для измерения наружной резьбы используют микрометрические инструменты, основой конструкции которых служат микровинты. Контроль выполняют по такой схеме.
- Микровинты прикладывают к профилю резьбы.
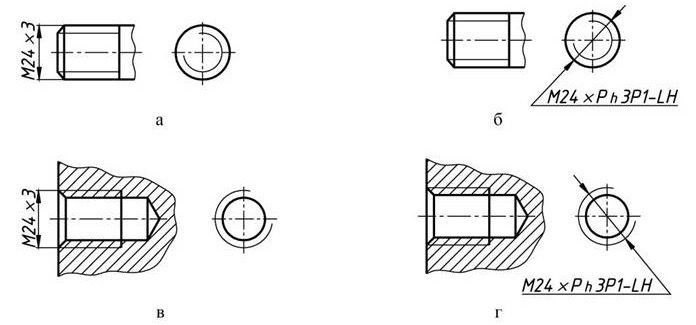 Положение инструмента корректируют, несколько раз вращая микрометр.
Положение инструмента корректируют, несколько раз вращая микрометр. - Записывают величину профиля нарезки для одной стороны. Значение рассчитывают, ориентируясь на цену деления на шкале микровинтов.
- Микрометр прикладывают к противоположному концу профиля и вычисляют его размер.
- Результат измерения наружного диаметр резьбы узнают, отняв от результата первого вычисления результат второго.
Измерение внутреннего диаметра резьбы
Измерение внутренней резьбы производят кронциркулем. Инструмент устанавливают на шаблонную деталь по резьбовому калибру, а затем сравнивают с исходным внутренним диаметром резьбового соединения. Для получения точных значений кронциркуль необходимо расположить под углом к измеряемой оси.
Также для измерения внутреннего диаметра резьбы можно использовать приборы для цилиндрической резьбы. Это связано с тем, что внутренний диаметр обладает гладкой поверхностью и идеально подходит для формы наконечников, используемых в этих инструментах. Полученные результаты проверяют, используя калибры-пробки.
Полученные результаты проверяют, используя калибры-пробки.
Измерение профиля резьбы
Для измерения профиля резьбы используют такой инструмент, как микроскоп, а контроль производят с помощью профилей. Процедура проводится в такой последовательности.
- Нормальным кольцом с резьбой измеряют внешний диаметр.
- На винт надевают кольцо, которое демонстрирует точность резьбы покачиванием.
- Диаметр координируют, пользуясь стандартной пробкой с резьбой. При этом ее выступающий гладкий конец одновременно служит инструментом для контроля диаметра резьбового отверстия.
Где купить инструменты для измерения резьбы?
Купить необходимые инструменты для измерения резьбы вы можете в интернет-магазине «Ринком». В наличии всегда есть:
- штангенциркули;
- щупы;
- микрометры;
- калибры.
Оформить заказ с доставкой по России вы можете прямо на сайте.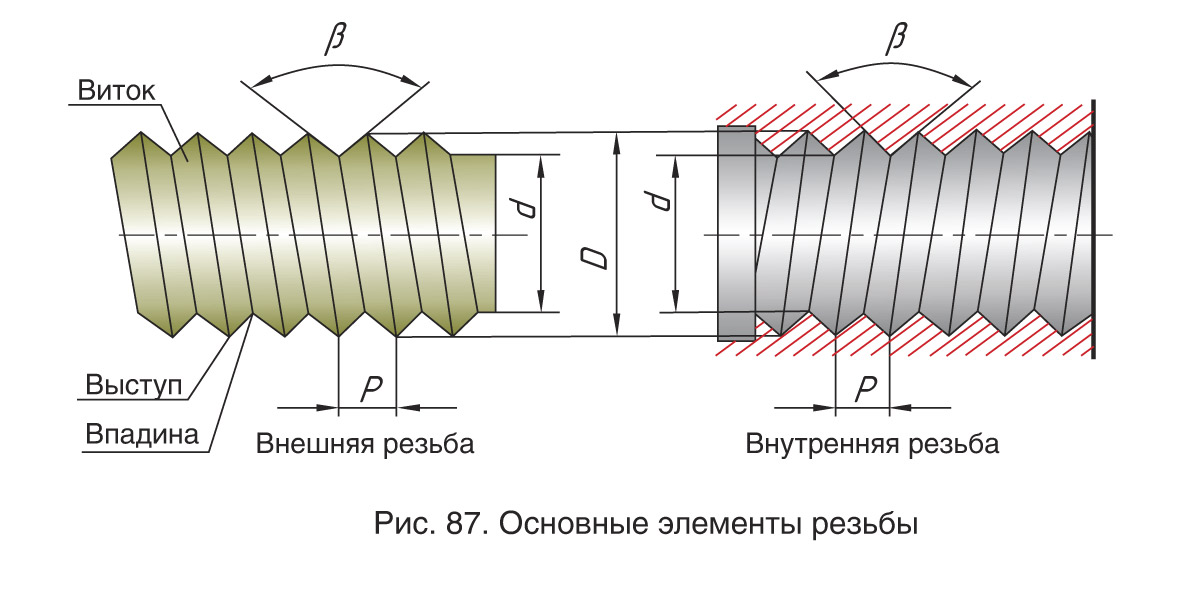 Возможно изготовление измерительного инструмента по вашим чертежам. Размер партии изделий не ограничен. я
Возможно изготовление измерительного инструмента по вашим чертежам. Размер партии изделий не ограничен. я
Больше полезной информации
Полезные обзоры и статьи
Все статьи
4 октября 2022
Фрезерование уступов и пазов
3 октября 2022
Клупп для нарезания резьбы
23 сентября 2022
Как пользоваться мультиметром
19 сентября 2022
Измерение кронциркулем
Все статьи
Подписывайтесь на нас
Присылаем скидки на инструмент и только полезную информацию!
Не нашли нужной позиции в каталоге?
Мы готовы изготовить и поставить уникальные виды инструмента специально под ваш заказ!
Заказать
Мы используем файлы cookie. Они помогают улучшить ваше взаимодействие с сайтом.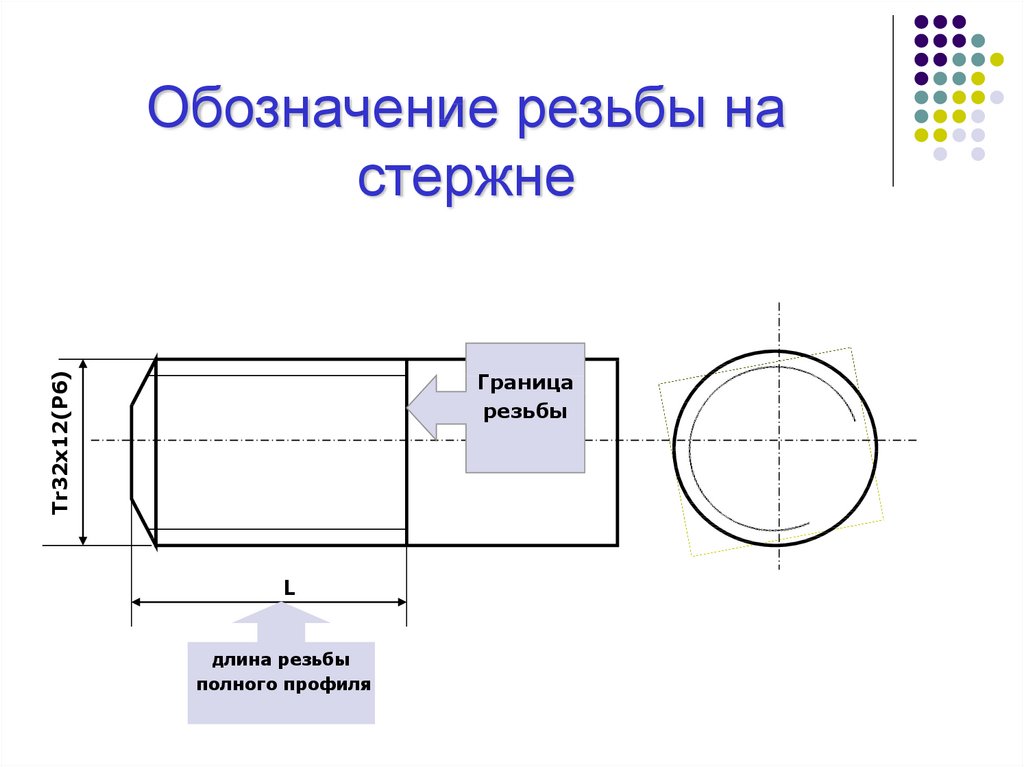
Принимаю
?>
Fastenerdata — ТАБЛИЦА РЕЗЬБЫ 10b
Похоже, в вашем браузере отключен JavaScript.
Для использования функций этого веб-сайта в вашем браузере должен быть включен JavaScript.
Детали резьбы резьбовых соединений с восемью таблицами и видео, показывающими производство резьбы со ссылкой на историю резьбы.
нажмите на изображения
Быстрое просмотр
Процесс проката нити Холодные формы потока, и не займает материал . Продолжительный. наружный диаметр между большим и малым диаметрами готовой резьбы вращают между плашками из закаленной стали, имеющими обратную форму резьбы.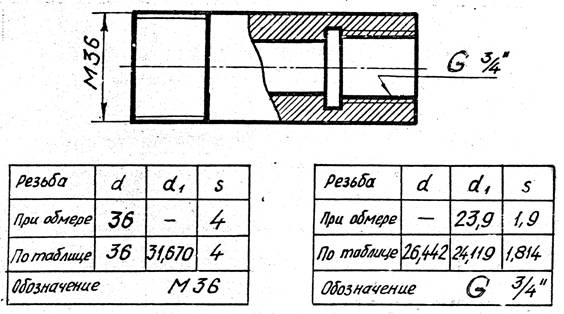
Нити матрицы проникают в поверхность заготовки, образуя основания резьбы, и смещают материал в радиальном направлении наружу, образуя гребни. Металл не удаляется и не тратится впустую, а вытесняется.
Повышенная прочность на растяжение, сопротивление сдвигу и сопротивление усталости
Зернистая структура нити не нарушена; вместо этого он преобразуется в непрерывные непрерывные линии, повторяющие контуры нити. Накатанные нити имеют повышенную устойчивость к зачистке, потому что такие разрушения вынуждены происходить поперек, а не по ходу потока зерна.
Резьба изготавливается с полированными корнями и боковыми поверхностями, без дефектов поверхности, которые могут оказаться исходными точками усталостного разрушения. Поверхностные слои нити, особенно у корней, испытывают напряжения сжатия. Эти сжимающие напряжения должны быть преодолены, прежде чем могут возникнуть растягивающие напряжения, вызывающие усталостное разрушение.
ОЧЕНЬ КОРОТКИЙ ВИДЕО НАКАТКИ РЕЗЬБЫ НА ДВУХ МАТРИЦАХ
ОЧЕНЬ КОРОТКИЙ ВИДЕО НАКАТКИ РЕЗЬБЫ НА ПЛОСКОЙ МАТРИЦЕ
История нитей Бессон во Франции приводил к тому, что изделия из вырезания винтов, которая будет использоваться на планках в 1569 году. В 1641 году была улучшена привольная резка, Англия. В 1760 году Джоб и Уильям Вятт продвинулись дальше в нарезании резьбы. Генри Крам запатентовал ту же машину Wyatt в США 76 лет спустя, в 1836 году. Карьера Генри Модслея началась в 1789 году в качестве кузнеца, который изготавливал механизмы для знаменитого слесаря Джозефа Брамы. Когда позже Генри Модслей основал свою собственную компанию, на его работу повлияла точность. В начале восемнадцатого века машины были примитивными, не было стандартных размеров, детали должны были проектироваться индивидуально, гайки и болты должны были подходить парами и не были взаимозаменяемыми. Генри Модсли был одним из первых, кто осознал важность стандартизации и взаимозаменяемости деталей машин. Его основным инженерным вкладом стал большой токарно-винторезный станок. Токарный станок Генри Модслея намного превосходил любого из своих предшественников и поэтому получил широкое распространение. Поэтому неудивительно, что Джозеф Уитворт выбрал произведения Модслея в качестве отправной точки для того, что должно было стать его очень успешной карьерой.
Генри Модсли был одним из первых, кто осознал важность стандартизации и взаимозаменяемости деталей машин. Его основным инженерным вкладом стал большой токарно-винторезный станок. Токарный станок Генри Модслея намного превосходил любого из своих предшественников и поэтому получил широкое распространение. Поэтому неудивительно, что Джозеф Уитворт выбрал произведения Модслея в качестве отправной точки для того, что должно было стать его очень успешной карьерой.
Джозеф Уитворт
Модслей взяла в ученики Джозефа Уитворта, который оказался исключительно талантливым. Затем он работал у Джозефа Клементса, где они пытались построить вычислительную машину Бэббиджа, первый компьютер, и, наконец, открыли для себя мастерскую по изготовлению инструментов.
Уитворт поставил перед собой задачу разработать стандарт для нитей. Он также собирал болты со всей Англии, отмечая, какие размеры оказались наиболее полезными, и результаты различных форм резьбы. В 1841 году он предложил в качестве стандарта форму резьбы с прилежащим углом 55°, а верхние и нижние части резьбы закруглены с радиусом, равным 0,1373 шага.
В 1841 году он предложил в качестве стандарта форму резьбы с прилежащим углом 55°, а верхние и нижние части резьбы закруглены с радиусом, равным 0,1373 шага.
Частично из-за огромного престижа, который Уитворт приобрел благодаря демонстрации своих машин на выставке Хрустального дворца в 1851 году, система Уитворта широко использовалась в Великобритании к 1860 году. Позже была выпущена вторая серия с более тонкой резьбой (BSF British Standard Fine). ) был добавлен.
Уильям Селлерс
Американцы столкнулись с теми же проблемами из-за отсутствия стандартизации резьбы, что и Британия. Вызов принял Уильям Селлерс из выдающейся семьи американских техников. В 1864 году комитет Института Франклина рекомендовал принять систему резьбы Селлера. Форма резьбы стала известна как «резьба Франклина» или, чаще, «резьба продавца», а позже как «стандартная резьба США». и Единая нить.
Основное различие между формой нитей Селлера и Витворта заключается в том, что верхние и нижние части нитей (гребни и корни) уплощены. Сплющенный корень был плохим выбором. Такие угловые конфигурации в металлическом концентрате напряжения и процесса производства в любом случае приводят к высоким напряжениям в корнях резьбы. Результат – трещины и сломанные крепления. Эта проблема была не так заметна во времена Продавца, корни резьбы в любом случае имеют тенденцию к закруглению , поскольку инструменты, из которых изготавливаются болты, изнашиваются. Круглые корни теперь являются нормой в США, а резьба описывается как UNRC, UNRF означает «R» для круглого корня.
Сплющенный корень был плохим выбором. Такие угловые конфигурации в металлическом концентрате напряжения и процесса производства в любом случае приводят к высоким напряжениям в корнях резьбы. Результат – трещины и сломанные крепления. Эта проблема была не так заметна во времена Продавца, корни резьбы в любом случае имеют тенденцию к закруглению , поскольку инструменты, из которых изготавливаются болты, изнашиваются. Круглые корни теперь являются нормой в США, а резьба описывается как UNRC, UNRF означает «R» для круглого корня.
Немцы, швейцарцы и французы разработали свои собственные формы метрической резьбы. Метрический мир в конечном итоге согласился, но не формализовал в 1898 году серию метрических резьб Systeme Internationale (SI) с углом резьбы 60 градусов.
Покрытия Комплект Ответственный отклонений Dimensal Data On Technical Implocal Domainain Damension и Technical Information. приобретенный через агентства по стандартизации, он был завершен и скомпилирован Fasterdata и предназначен только для ознакомления; при обнаружении несоответствий они могут быть изменены без предварительного уведомления. fasterdata не дает никаких гарантий или заявлений относительно точности и достоверности такой информации и данных, и, чтобы обеспечить вашу заинтересованность, мы предлагаем вам связаться с соответствующим органом по стандартизации для получения полной точности, мелких деталей и вспомогательной информации. крепежные данные поддерживаются платными рекламодателями, и все страницы могут содержать платный или спонсируемый контент
приобретенный через агентства по стандартизации, он был завершен и скомпилирован Fasterdata и предназначен только для ознакомления; при обнаружении несоответствий они могут быть изменены без предварительного уведомления. fasterdata не дает никаких гарантий или заявлений относительно точности и достоверности такой информации и данных, и, чтобы обеспечить вашу заинтересованность, мы предлагаем вам связаться с соответствующим органом по стандартизации для получения полной точности, мелких деталей и вспомогательной информации. крепежные данные поддерживаются платными рекламодателями, и все страницы могут содержать платный или спонсируемый контент
Крепеж
Резьба и крепеж |
Многие прецизионно обработанные детали бесполезны, пока они не собраны в
механические компоненты. Эти сборки требуют использования множества различных
виды крепежа. В этом блоке вы познакомитесь с различными типами
крепежных деталей и правильное их использование. Одна из самых основных задач
машинист — использование крепежных деталей. Резьбовые крепления берут на себя многие
различные формы и формы, но все они имеют одну общую черту — использование
нити. Хотя резьба используется для регулировки, измерение
применение инструментов и передача энергии, основное использование резьбы
является крепежным устройством.
Эти сборки требуют использования множества различных
виды крепежа. В этом блоке вы познакомитесь с различными типами
крепежных деталей и правильное их использование. Одна из самых основных задач
машинист — использование крепежных деталей. Резьбовые крепления берут на себя многие
различные формы и формы, но все они имеют одну общую черту — использование
нити. Хотя резьба используется для регулировки, измерение
применение инструментов и передача энергии, основное использование резьбы
является крепежным устройством.
Терминология резьбы
Некоторые из наиболее часто используемых терминов резьбы:
Угол резьбы — Угол резьбы является прилежащим углом между сторонами нити (рис. 1). Например, угол резьбы для унифицированных форм винтовой резьбы составляет 60 градусов.
Большой диаметр — обычно известный как внешний диаметр (рис.
2). На прямой винтовой резьбе наибольший диаметр равен наибольшему диаметру. резьбы на винте или гайке.
резьбы на винте или гайке.
Второстепенный диаметр — широко известен как диаметр корня (рис. 2). На прямой винтовой резьбе меньший диаметр — это наименьший диаметр резьбы. резьба на винте или гайке.
Количество витков — Относится к количеству витков на дюйм длина.
| Шаг -Расстояние от заданной точки на одном нить в соответствующую точку на следующей нити (рис. 1). | |
Рис. 2. Основные части потока
Шаг — расстояние, на которое резьба перемещается за один оборот. Ведущий и шаг одинарной резьбы одинаков. На двойном свинце резьбы, шаг в два раза больше. Двойная резьба имеет два захода. точки.
Резьбовые формы
Существует большое количество форм резьбы.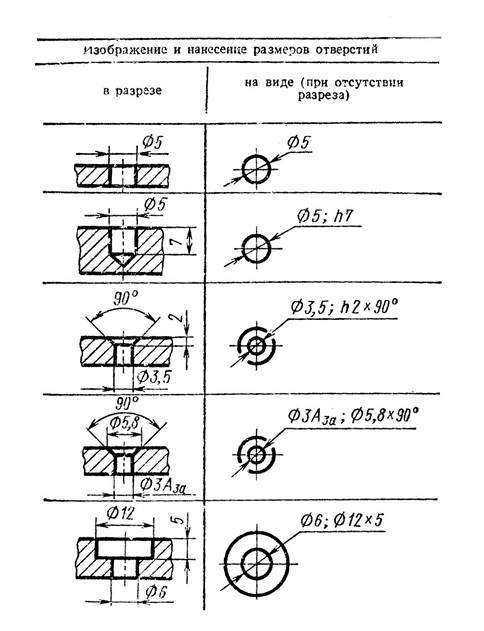 В более поздних подразделениях этого
конечно, вы изучите их более подробно, и у вас будет
возможность отрезать некоторые нити. Что касается крепежа, то мы
сосредоточится на унифицированной форме винтовой резьбы. Унифицированная форма резьбы
это попытка стандартизировать формы резьбы в США, Канаде,
и Великобритании. Унифицированные нити делятся на следующие серии:
В более поздних подразделениях этого
конечно, вы изучите их более подробно, и у вас будет
возможность отрезать некоторые нити. Что касается крепежа, то мы
сосредоточится на унифицированной форме винтовой резьбы. Унифицированная форма резьбы
это попытка стандартизировать формы резьбы в США, Канаде,
и Великобритании. Унифицированные нити делятся на следующие серии:
- UNC Unified National Coarse
- UNF Единый национальный штраф
- Унифицированный национальный специальный номер
UNS
Унифицированный грубый и унифицированный тонкий относятся к количеству витков на дюйм.
на застежках. Определенный диаметр болта или гайки будет иметь определенный
количество витков на дюйм длины. Например, дюймовый диаметр
унифицированный национальный крупный болт будет иметь 20 витков резьбы на дюйм длины.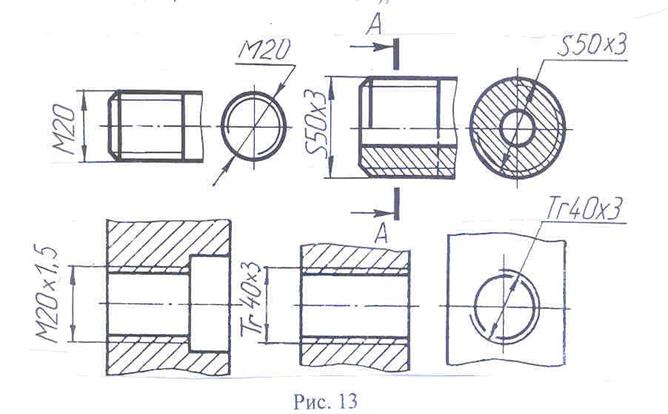 Этот
болт будет идентифицирован по следующим характеристикам:
Этот
болт будет идентифицирован по следующим характеристикам:
-20-УНК
— это основной диаметр, а 20 — количество витков на дюйм. Болт диаметром в дюйм с мелкой резьбой будет идентифицирован по следующие характеристики:
-28-УНФ
— это основной диаметр, а 28 — количество витков на
дюйм.
Точно так же идентифицируется унифицированная специальная серия. Дюймовый диаметр
Болт UNS может иметь 24 или 27 витков резьбы на дюйм.
Вы можете удивиться, зачем нужны резьбы серий UNC и UNF.
Вот некоторые основные области применения грубых и тонких нитей.
СЕРИЯ КРУПНОЙ РЕЗЬБЫ
Эта серия, UNC, наиболее часто используется в массовом производстве.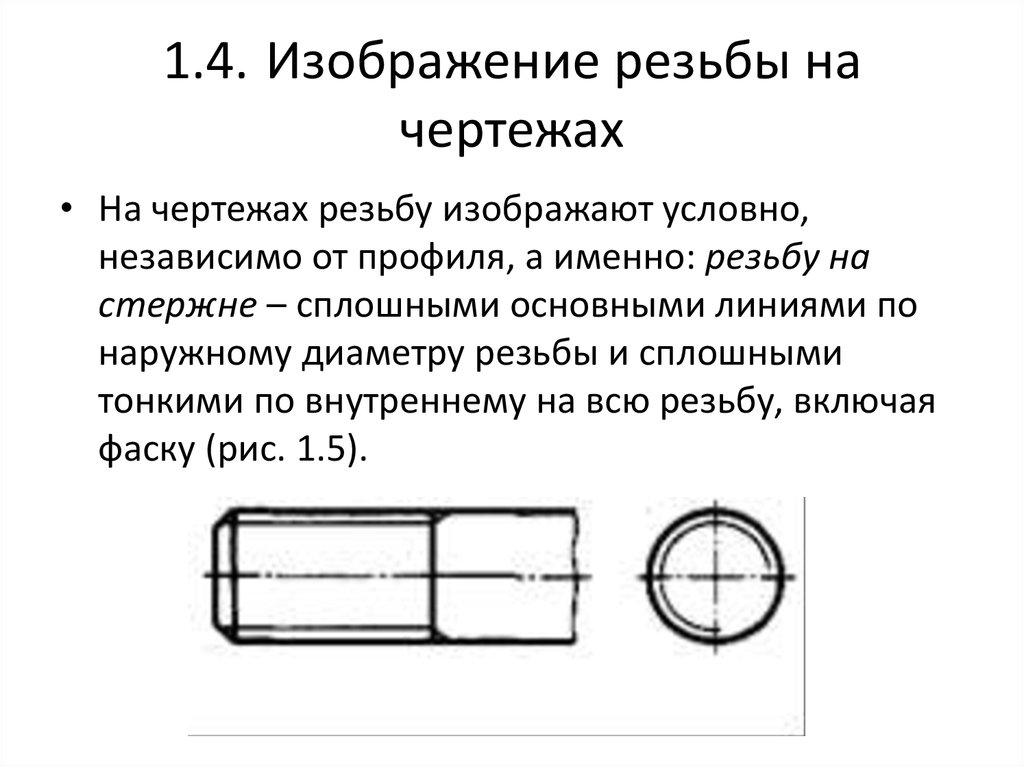 болтов, винтов, гаек и других общих крепежных изделий. это
также используется для нарезания резьбы в материалах с более низкой прочностью на растяжение (бронза,
латунь, алюминий и пластмассы) для получения наилучшей устойчивости к зачистке
внутренней резьбы. Он также используется для быстрой сборки или разборки,
или если возможны коррозия или легкое повреждение.
болтов, винтов, гаек и других общих крепежных изделий. это
также используется для нарезания резьбы в материалах с более низкой прочностью на растяжение (бронза,
латунь, алюминий и пластмассы) для получения наилучшей устойчивости к зачистке
внутренней резьбы. Он также используется для быстрой сборки или разборки,
или если возможны коррозия или легкое повреждение.
СЕРИЯ ТОНКОЙ РЕЗЬБЫ
Эта серия, UNF, при использовании на наружной резьбе имеет большую прочность на растяжение
площади напряжения, чем грубая резьба того же размера. Прекрасная серия будет
сопротивляться зачистке лучше, чем грубая резьба в местах, где
наружная и ответная внутренняя резьба подвергаются нагрузкам, равным или
больше, чем мощность винта или болта. Также используются тонкие нити.
там, где длина зацепления ограничена или где толщина стенки требует
тонкий шаг.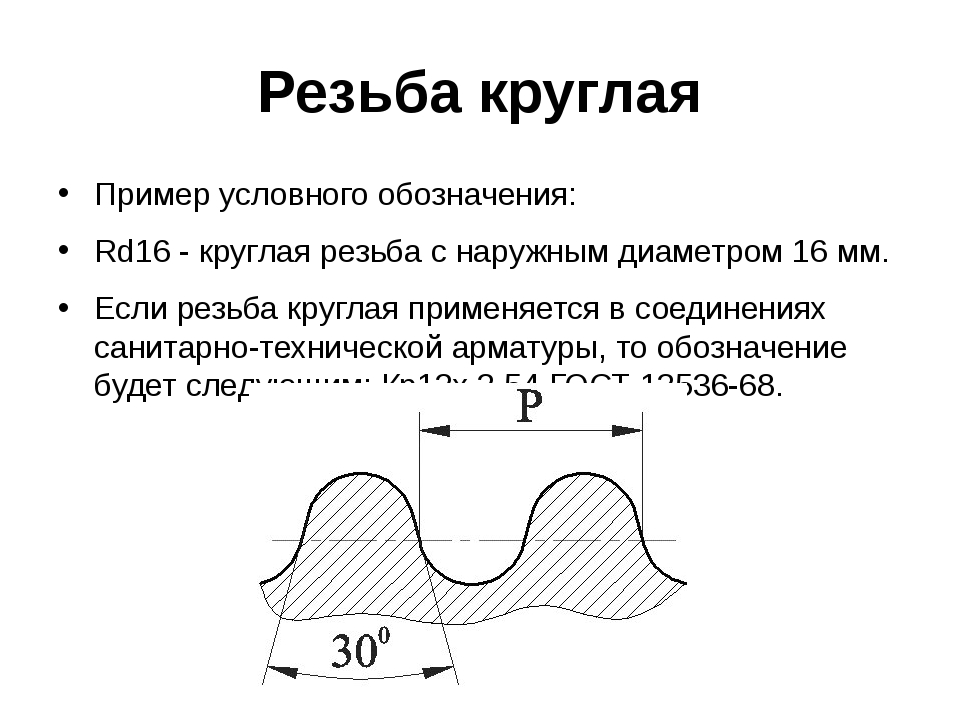
Рис. 3. Унифицированная таблица резьбы.
КЛАССЫ РЕЗЬБЫ
Некоторые потоковые приложения могут допускать незакрепленные потоки, в то время как другие требуют более плотного прилегания. Примером этого может быть головка двигателя. Головка двигателя вашего автомобиля или грузовика удерживается резьбовым креплением. называется шпилькой. Шпилька имеет резьбу на обоих концах. Один конец продет в блок двигателя. На другом конце используется гайка для затягивания цилиндра. глава. Когда головка снята, вы хотите, чтобы шпилька осталась в двигателе. блокировать. Этот конец требует более плотной посадки, чем конец шпильки, принимающий орех. Если посадка на гайке слишком тугая, шпилька будет отвинчиваться по мере того, как гайка снимается.
Унифицированные резьбовые посадки классифицируются как 1А, 2А, 3А… или 1В, 2В,
3B .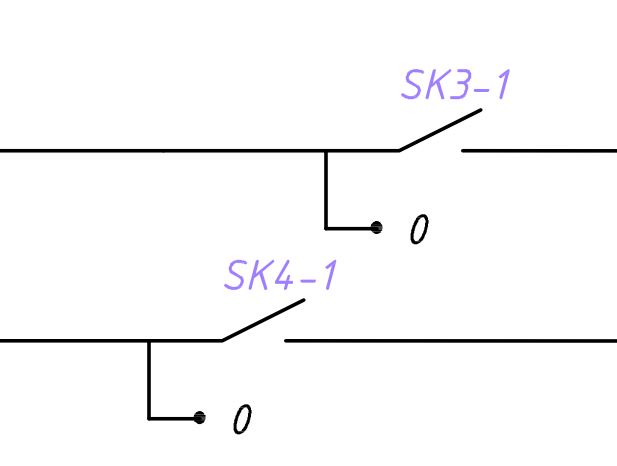 … A указывает на внешнюю резьбу. B указывает на внутреннюю
нить. Цифры обозначают класс пригодности. Чем меньше число, тем
более свободная посадка и наоборот. Посадки класса 2 используются на самых больших
процент резьбовых соединений. Чем плотнее посадка, тем ближе
допуска размеров резьбы и, следовательно, дороже
покупка. Типовое обозначение унифицированной формы резьбы с допуском посадки
будет:
… A указывает на внешнюю резьбу. B указывает на внутреннюю
нить. Цифры обозначают класс пригодности. Чем меньше число, тем
более свободная посадка и наоборот. Посадки класса 2 используются на самых больших
процент резьбовых соединений. Чем плотнее посадка, тем ближе
допуска размеров резьбы и, следовательно, дороже
покупка. Типовое обозначение унифицированной формы резьбы с допуском посадки
будет:
-28 УНФ 2А
В этом конкретном случае класс соответствия будет 2. Символ A указывает на внешнюю резьбу.
МЕТРИЧЕСКАЯ РЕЗЬБА
При ввозе и вывозе товаров, особенно в
автомобильная промышленность, метрическая резьба стала преобладающим типом резьбы
на многих видах оборудования. Форма метрической резьбы аналогична
унифицированная форма резьбы, основанная на угле резьбы 60 градусов.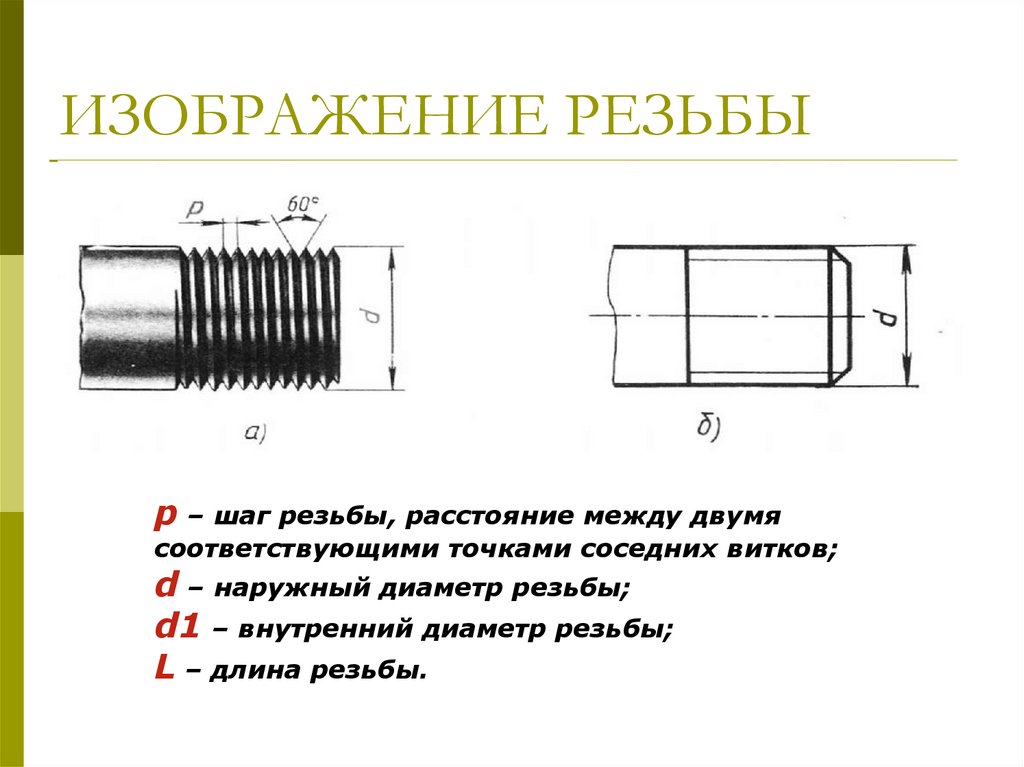 Серия метрической резьбы имеет следующий вид:
Серия метрической резьбы имеет следующий вид:
M10 X 1,5–6 г
Где М — основной диаметр в миллиметрах, а 1,5 — шаг. (расстояние от одной резьбы до следующей резьбы) в 1,5 миллиметра, 6 класс посадки, а буква «g» обозначает наружную резьбу. Этот внешний резьба будет иметь основной диаметр 10 миллиметров, шаг 1,5 миллиметров, и подойдет «средняя» резьба.
ИДЕНТИФИКАЦИЯ РЕЗЬБЫ
Общее определение болта – это «болт с наружной резьбой». крепеж, который вставляется через отверстия в сборке». затягивается гайкой (рис. 4). Винт – это резьба с наружной резьбой. крепеж, который вставляется в резьбовое отверстие и затягивается поворотом головка (рис. 4).
Рисунок 4.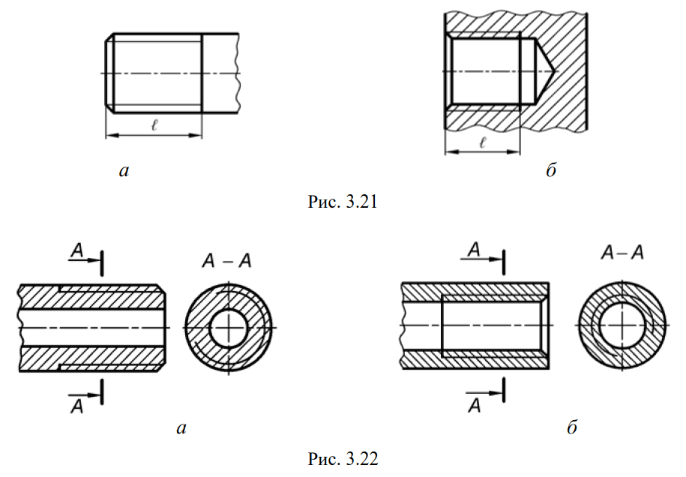 В резьбовом соединении используется винт.
отверстие, а болт используется с гайкой.
В резьбовом соединении используется винт.
отверстие, а болт используется с гайкой.
Из этих общих определений болт может стать винтом или наоборот может быть правдой. Это зависит от того, как они используются. Болты и винты – это самый распространенный резьбовой крепеж.
Прочность сборки во многом зависит от диаметра болт или резьбовое зацепление винта. Зацепление резьбы – это расстояние, на которое винт входит в резьбовое отверстие. Минимальная нить зацепление должно быть на расстоянии, равном используемому диаметру; предпочтительно ты хотелось бы иметь в 1-1/2 раза больше диаметра винта, ибо легче удалите сломанную шпильку, чем просверлите и нарежьте винт большего размера.
Машинные болты изготавливаются с шестигранной или квадратной головкой.
Диаметр корпуса, диаметр нерезьбовой части болта
ниже головы, как правило, немного больше номинального или стандартного
размер болта. Отверстие, которое должно принять болт, должно быть слегка просверлено
больше диаметра тела.
Отверстие, которое должно принять болт, должно быть слегка просверлено
больше диаметра тела.
Крепежные винты
Крепежный винт используется для общих сборочных работ. Он изготовлен серий как с мелкой, так и с крупной резьбой и оснащенных либо шлицевыми, либо утопленная голова.
Размеры крепежных винтов варьируются от № 0 (0,060) до дюйма (0,500) в диаметре, и бывают разной длины (рис. 5).
| A — Круглая головка | B — Овальная головка | C — Плоская головка |
| | |
Рис. | ||
| Болты с квадратным подголовком используются для крепления деревянных и металлических деталей. вместе. Болты с квадратным подголовком имеют круглую головку с квадратным телом под голова. Квадратная часть болта при втягивании в древесину удерживает его от проворачивания, пока вы затягиваете гайку (рис. 6). | Рисунок 6. Болт с квадратным подголовком |
Винты с головкой изготавливаются из различных
формы головки и используются там, где необходимы прецизионные болты или винты.
Винты с головкой изготавливаются с жесткими допусками и имеют обработанную
внешность. Винты с головкой под ключ могут иметь плоскую головку, круглую головку, цилиндрическую головку.
головки, торцевые головки и шестигранные головки (рис.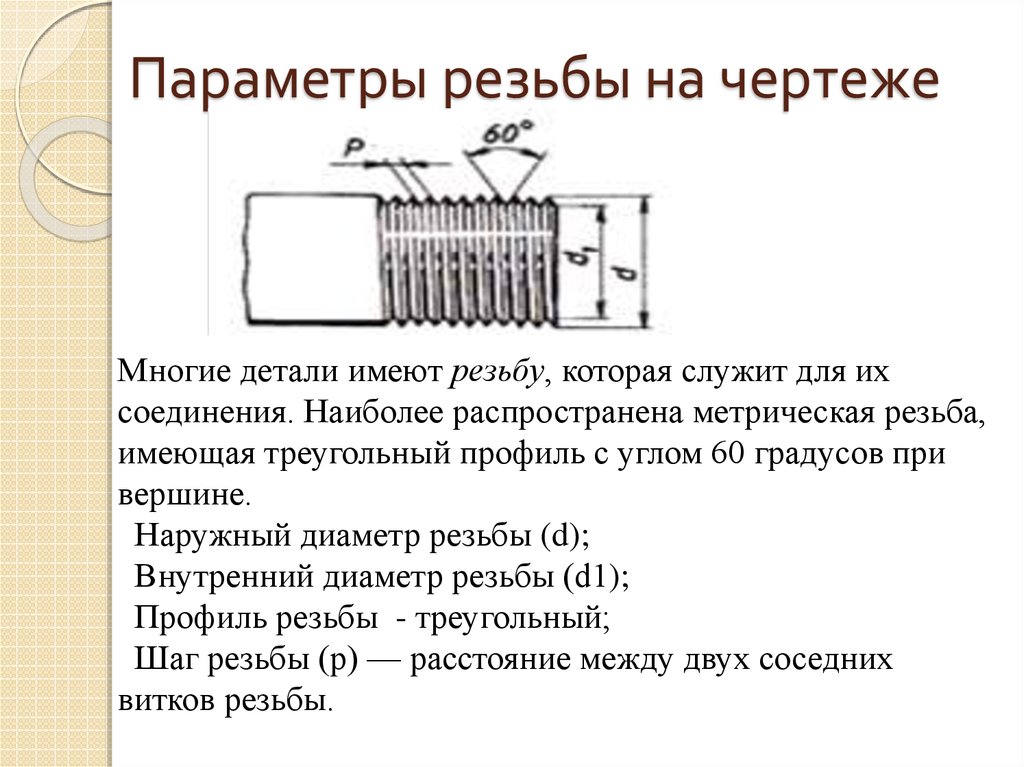 7). 7). |
| |||||||||
| Установочные винты используются для блокировки шкивов, колец или
валы на месте (Рисунок 8). Установочные винты с головкой под торцевой ключ обычно исчезают
ниже поверхности скрепляемой детали. Установочные винты с головкой под торцевой ключ
могут иметь шестигранные или шлицевые головки. |
Установочные винты имеют несколько разных точек (рис. 9).). Плоская головка винты используются там, где требуется минимальное вдавливание в деталь и где требуется частая регулировка. Они также используются для обеспечения Эффект стопорного винта при добавлении второго установочного винта для предотвращения вибрации свободный. Установочный винт с собачкой используется для удержания кольца на валу. Выравнивание всегда поддерживается с помощью установочного винта с собачкой, потому что вал просверливается с отверстием того же диаметра, что и вершина собачки. Чашка заостренный установочный винт обеспечит очень хорошее соединение, препятствующее скольжению.
| Конус | Собака | Плоский | Овальный |
| Рисунок 9 Точки установочные винты | |||
Марки болтов и коэффициенты крутящего момента
В некоторых случаях необходимо затянуть болты с нужным количеством
давления. В этих случаях производитель определенных продуктов будет
рекомендуют прикладывать определенное усилие зажима к тому или иному крепежному элементу.
Недостаточный крутящий момент обычно приводит к ослаблению деталей и
неисправность из-за несоосности. С другой стороны, чрезмерное затягивание может
вызвать напряжение или деформацию, что также может нарушить выравнивание узлов.
Способ затягивания креплений «армстронг» также может стать причиной
сломанные отливки, сломанные болты или растяжение крепежа.
В этих случаях производитель определенных продуктов будет
рекомендуют прикладывать определенное усилие зажима к тому или иному крепежному элементу.
Недостаточный крутящий момент обычно приводит к ослаблению деталей и
неисправность из-за несоосности. С другой стороны, чрезмерное затягивание может
вызвать напряжение или деформацию, что также может нарушить выравнивание узлов.
Способ затягивания креплений «армстронг» также может стать причиной
сломанные отливки, сломанные болты или растяжение крепежа.
обладает отличной эластичностью; способность, как пружина, растягиваться а затем вернуться к своей первоначальной форме. Любая застежка должна достигать своего пределы растяжения для проявления сжимающей силы. Но также как пружина, перетянутая застежка схватывается, теряет эластичность и не может вернуться к своей первоначальной форме. Правильная затяжка предотвратит это условие.
Во время финала иногда слышен хлопающий или щелкающий звук. затягивание застежки. Этот хлопающий звук указывает на то, что застежка
проходит набор. Когда используется новая застежка и выскакивает
случается, средство состоит в том, чтобы отпустить его и снова затянуть до надлежащего усилия
технические характеристики. Когда используется старая застежка, и вы слышите это
выскакивает, снимите крепеж и очистите болт и внутреннюю резьбу.
полностью. Безопаснее и экономичнее заменить старый.
застежка на новую.
затягивание застежки. Этот хлопающий звук указывает на то, что застежка
проходит набор. Когда используется новая застежка и выскакивает
случается, средство состоит в том, чтобы отпустить его и снова затянуть до надлежащего усилия
технические характеристики. Когда используется старая застежка, и вы слышите это
выскакивает, снимите крепеж и очистите болт и внутреннюю резьбу.
полностью. Безопаснее и экономичнее заменить старый.
застежка на новую.
Винт с головкой под ключ марки
Не менее важным, чем правильная затяжка, является выбор правильного
класс крепежа для работы. Марки болтов или болтов с головкой в
цифра 10 идентифицируются по маркировке на головках. Сорт
указывает на прочность крепления. Используйте таблицу производителей
в качестве руководства по правильному моменту затяжки крепежных деталей.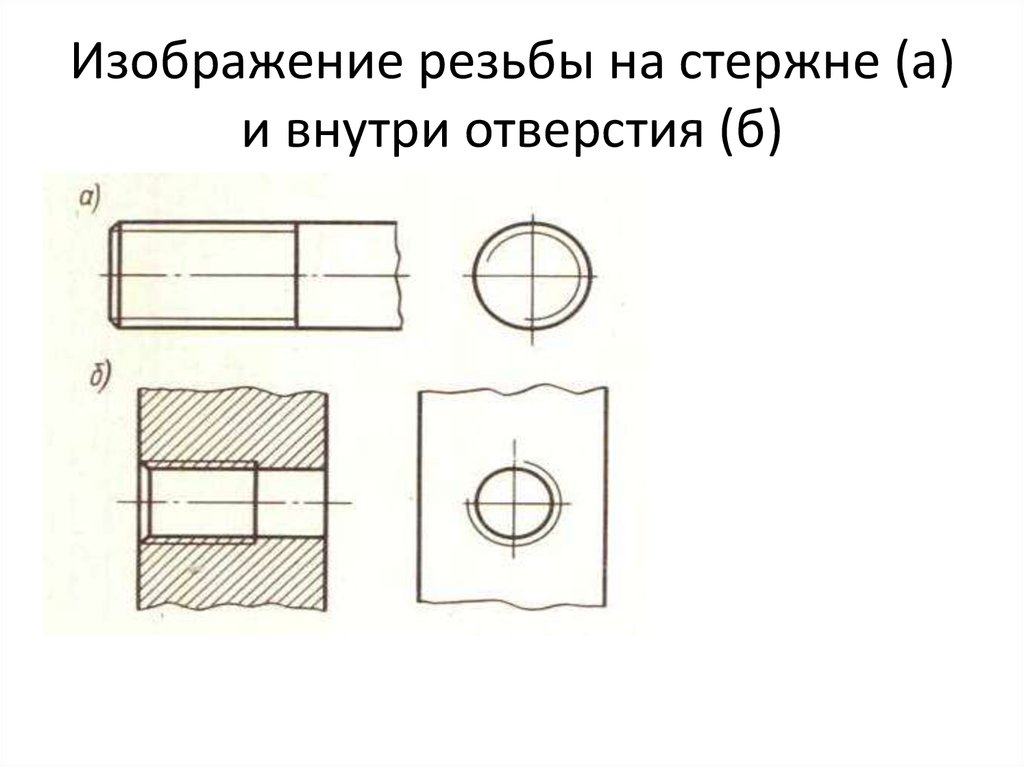 |
| |||||||||
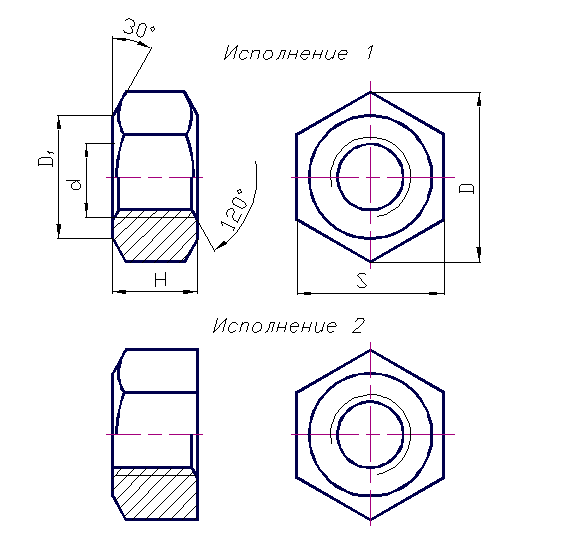
Гайки
Гайки имеют шестигранную или квадратную головку и используются с болтами с голова такой же формы. Они доступны в различных степенях отделки.
ОБЫЧНЫЙ не подвергается механической обработке (кроме резьбы).
ОБЫЧНЫЕ ПОЛУФАБРИКАТЫ подвергается механической обработке на опорной поверхности для обеспечения ровная ровная поверхность для стиральной машины.
ТЯЖЕЛЫЕ ПОЛУФАБРИКАТЫ имеет такую же отделку, что и полуфабрикаты;
однако корпус толще для большей прочности.
ЗУБЧАТЫЕ ГАЙКИ или ПРОРЕЗНЫЕ ГАЙКИ имеют фрезерованный паз поперек плоские, чтобы их можно было зафиксировать на месте с помощью шплинта или проволоки.
ЖЕЛУДЕВЫЕ ОРЕХИ используются, когда внешний вид имеет наибольшее значение или где выступающие нити должны быть защищены.
| КРЫШЕЧНЫЕ ГАЙКИ используются при частых регулировках или демонтаже. необходимо (Рисунок 11). | |
ШАЙБЫ
Шайбы используются для распределения зажимного усилия на большую площади и предотвращения загрязнения. Они также могут быть использованы для обеспечения большего опорная поверхность для головок болтов и гаек.
Стопорные шайбы
Стопорная шайба используется для предотвращения ослабления болта или гайки под
вибрация. Существует множество различных типов стопорных шайб. Некоторые из
более распространенные стопорные шайбы показаны на рис. 12. Существует множество различных типов стопорных шайб. Некоторые из
более распространенные стопорные шайбы показаны на рис. 12. |
| |||||||||
Крепежные устройства без резьбы
Крепежные изделия без резьбы составляют большую группу крепежных приспособлений.
Установочные штифты
Штифты изготовлены из обработанной легированной стали и используются в узлах
где детали должны быть точно расположены и удерживаться в абсолютном отношении к
друг друга (рис.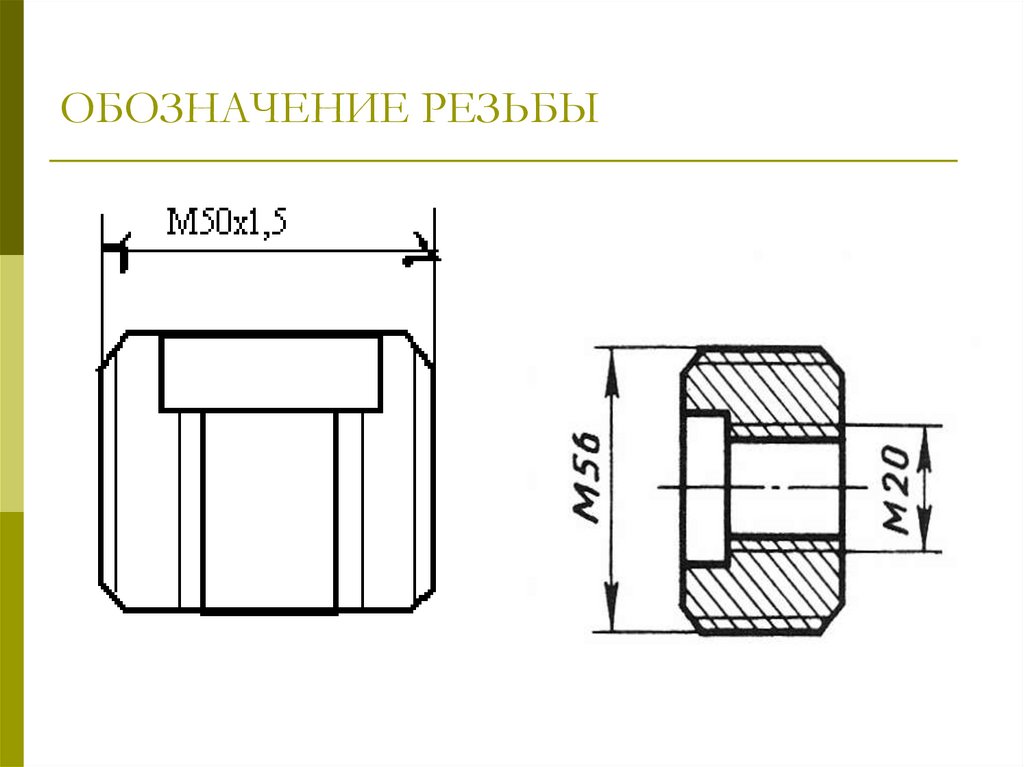 13). Они обеспечивают идеальное выравнивание и облегчают
более быстрая разборка и сборка деталей в точном соотношении. 13). Они обеспечивают идеальное выравнивание и облегчают
более быстрая разборка и сборка деталей в точном соотношении. | |
Шплинты
| Шплинты устанавливаются в отверстия, просверленные крест-накрест в валах для предотвращения соскальзывания или отключения деталей (Рисунок 14). | |
Стопорные кольца
Стопорные кольца представляют собой штампованные кольца, как внутренние, так и наружные, и
Используется для предотвращения соскальзывания или разъединения деталей. При сохранении большинства
Кольцам нужна канавка, чтобы зафиксировать их в нужном положении, некоторые типы самоблокирующиеся
и не требуют использования углубления.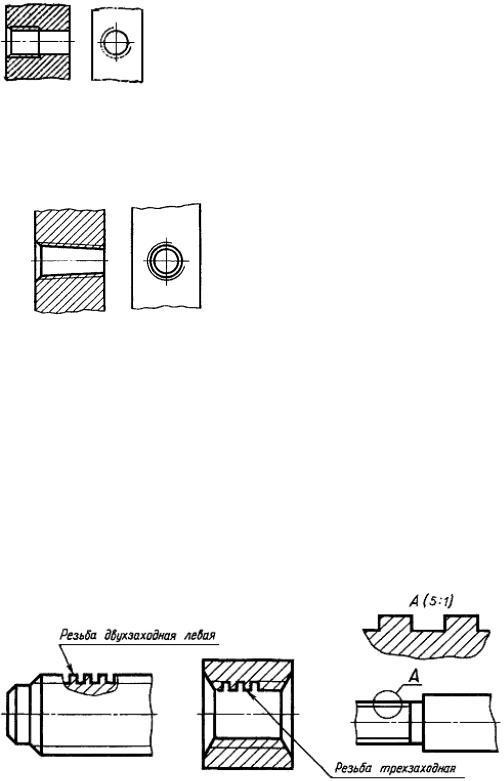
Ключи
Шпонка представляет собой небольшой кусок металла, частично вставленный в стержень и частично в ступице, чтобы предотвратить вращение шестерни или шкива на валу. Вот несколько разных типов ключей.
КВАДРАТНЫЕ КЛЮЧИ — Ширина обычно составляет одну четвертую диаметра вала. Один половина шпонки вставлена в вал, а другая половина вставлена в концентратор (рис. 16).
КЛЮЧ ОТ ГОЛОВКИ — За исключением головки, этот ключ идентичен квадратный ключ. Головка стрелы легко снимается (Рисунок 16).
КЛЮЧ PRATT & WHITNEY — Концы закруглены, и этот ключ установлен в прорезь на валу такой же формы (рис. 16).
КЛЮЧ ДЛЯ МАТЕРИАЛА — Ключ для деревянного дерева имеет полукруглую форму и входит в
ключница той же формы. Верхняя часть ключа входит в шпоночный паз в
ответная часть (рис. 16).
16).
Рис. 16 Ключи. A-Square, B-Gib Head, C-Pratt & Whitney,
Д-Вудрафф.
| Шпоночный паз | ключ |
Рисунок 17 Шпоночный паз прошивается в ступице детали. Ключница обработан в валу.
Модель расчета жесткости резьбового соединенияс учетом коэффициентов трения Для применения болтового соединения в машиностроении необходимо оценить жесткость резьбовых соединений. В работе создана расчетная модель распределения осевой силы и жесткости с учетом коэффициента трения резьбового соединения. Метод рассматривает резьбу как коническую консольную балку. Под действием осевой силы резьбы, с учетом трения, две консольные балки взаимодействуют, и балка деформируется, эти деформации включают деформацию изгиба, деформацию сдвига, деформацию наклона корня консольной балки, деформацию сдвига корня консольной балки, деформация радиального расширения и деформация радиальной усадки и т.
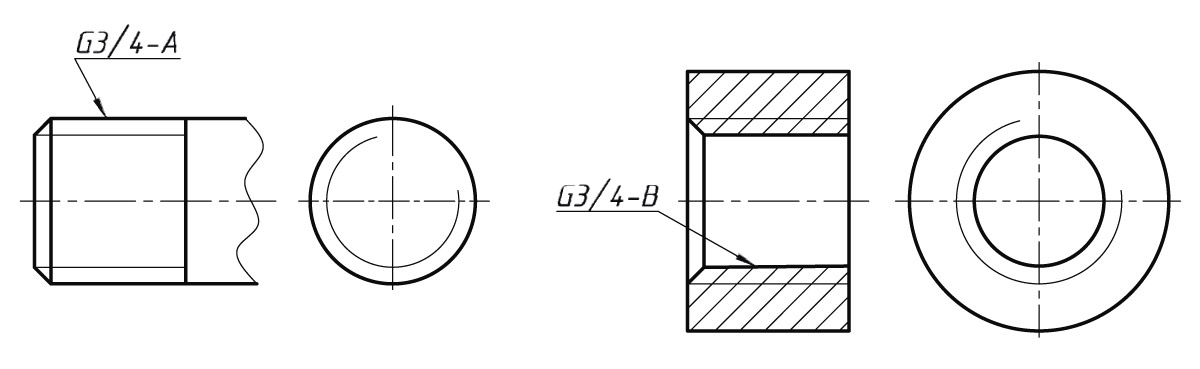 д.; рассчитать каждую деформацию резьбы соответственно и просуммировать их, то есть общую деформацию резьбы. В данной работе, с одной стороны, экспериментально измерялась жесткость резьбового соединения; с другой стороны, модели конечных элементов были созданы для расчета жесткости резьбы; результаты расчетов метода, описанного в данной статье, результаты испытаний и результаты анализа методом конечных элементов (МКЭ) сравнивались соответственно; результаты оказались в разумных пределах; таким образом, проверяется правильность расчета метода этой статьи.
д.; рассчитать каждую деформацию резьбы соответственно и просуммировать их, то есть общую деформацию резьбы. В данной работе, с одной стороны, экспериментально измерялась жесткость резьбового соединения; с другой стороны, модели конечных элементов были созданы для расчета жесткости резьбы; результаты расчетов метода, описанного в данной статье, результаты испытаний и результаты анализа методом конечных элементов (МКЭ) сравнивались соответственно; результаты оказались в разумных пределах; таким образом, проверяется правильность расчета метода этой статьи.1. Введение
Болты соединяют части оборудования в единое целое, которое используется для передачи силы, момента, крутящего момента или движения. Болтовое соединение широко используется в различных областях техники, таких как авиационные станки, прецизионные приборы и т. д. Точность резьбового соединения влияет на качество оборудования. Особенно для высококлассных станков с ЧПУ точность резьбового соединения очень высока. Поэтому важно изучить жесткость резьбового соединения для повышения точности устройства. Многие исследователи проводили исследования в этой области.
Поэтому важно изучить жесткость резьбового соединения для повышения точности устройства. Многие исследователи проводили исследования в этой области.
Дунмей Чжан и др. [1] предложили метод, который может вычислить жесткость зацепленного винта, и достоверность этого метода была подтверждена МКЭ и экспериментами. Маруяма и др. [2] использовали метод точечного согласования и МКЭ, основанный на экспериментальных результатах Боеника и предположениях, сделанных Фернлундом [3] при расчете распределения давления между соединительными пластинами. Моташ [4] предположил, что распределение давления на любой плоскости, перпендикулярной оси болта, имеет нулевой градиент при r = / 2 и r = , где также обращается в нуль. В основном они используют численные методы для расчета влияния различных параметров на жесткость болтовых соединений. Кенни Б., Паттерсон Э. А. [5] представили метод измерения деформации и напряжения резьбы. Кенни Б. [6] и соавт. рассмотрено распределение нагрузок и напряжений в резьбах крепления.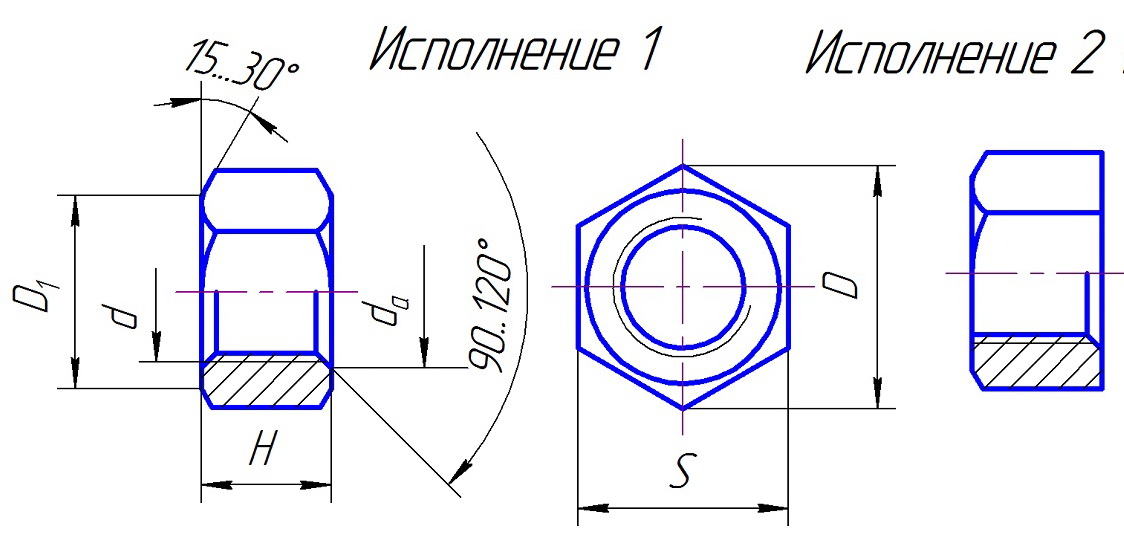 Миллер Д.Л. и соавт. [7] установили пружинную модель анализа силы резьбы и, в сочетании с математической теорией, проанализировали напряжение резьбы и сравнили его с результатами FEA и экспериментальными результатами, чтобы проверить правильность математической модели пружины. Ван В. и Маршек К. М. и соавт. [8] предложили улучшенную пружинную модель для анализа распределения нагрузки на резьбу, сравнили распределения нагрузки на эластичные нити и податливые резьбовые соединения и обсудили влияние линии текучести на распределение нагрузки. Вилеман и др. [9] выполнил двухмерный (2D) МКЭ для элементов жесткости соединения узлов. Де Агостинис М. и соавт. [10] изучали влияние смазки на характеристики трения резьбы или крутящий момент. Дарио Крокколо и др. В работах [11–13] изучалось влияние коэффициента зацепления (ER, а именно отношения длины резьбы к диаметру резьбы) на момент затяжки и развинчивания и коэффициент трения резьбовых соединений с использованием резьбовых запорных устройств средней прочности.
Миллер Д.Л. и соавт. [7] установили пружинную модель анализа силы резьбы и, в сочетании с математической теорией, проанализировали напряжение резьбы и сравнили его с результатами FEA и экспериментальными результатами, чтобы проверить правильность математической модели пружины. Ван В. и Маршек К. М. и соавт. [8] предложили улучшенную пружинную модель для анализа распределения нагрузки на резьбу, сравнили распределения нагрузки на эластичные нити и податливые резьбовые соединения и обсудили влияние линии текучести на распределение нагрузки. Вилеман и др. [9] выполнил двухмерный (2D) МКЭ для элементов жесткости соединения узлов. Де Агостинис М. и соавт. [10] изучали влияние смазки на характеристики трения резьбы или крутящий момент. Дарио Крокколо и др. В работах [11–13] изучалось влияние коэффициента зацепления (ER, а именно отношения длины резьбы к диаметру резьбы) на момент затяжки и развинчивания и коэффициент трения резьбовых соединений с использованием резьбовых запорных устройств средней прочности. Цзоу К. и соавт. [14, 15] изучали использование контактной механики для определения эффективного радиуса болтового соединения, а также изучали влияние смазки на трение и соотношение крутящий момент-растяжение в резьбовых соединениях. Нассар С.А. и соавт. В работах [16, 17] изучалось трение резьбы и момент трения резьбы в резьбовом соединении. Нассар С.А. и соавт. [18, 19] также исследовали влияние скорости затяжки и покрытия на соотношение крутящий момент-натяжение и характер износа в резьбовых соединениях, чтобы повысить надежность оценки зажимной нагрузки в болтовых соединениях. Копфер и др. [20] считают, что подходящие составы должны учитывать контактное давление и скорость скольжения; на основании этого вклад показывает экспериментальные примеры основных неопределенностей фрикционных свойств при затяжке с использованием различных комбинаций материалов (результаты сборочного стенда). Кенни Б. и др. [21] рассмотрели распределение нагрузки и напряжения в резьбе крепежных изделий. Шигли и др.
Цзоу К. и соавт. [14, 15] изучали использование контактной механики для определения эффективного радиуса болтового соединения, а также изучали влияние смазки на трение и соотношение крутящий момент-растяжение в резьбовых соединениях. Нассар С.А. и соавт. В работах [16, 17] изучалось трение резьбы и момент трения резьбы в резьбовом соединении. Нассар С.А. и соавт. [18, 19] также исследовали влияние скорости затяжки и покрытия на соотношение крутящий момент-натяжение и характер износа в резьбовых соединениях, чтобы повысить надежность оценки зажимной нагрузки в болтовых соединениях. Копфер и др. [20] считают, что подходящие составы должны учитывать контактное давление и скорость скольжения; на основании этого вклад показывает экспериментальные примеры основных неопределенностей фрикционных свойств при затяжке с использованием различных комбинаций материалов (результаты сборочного стенда). Кенни Б. и др. [21] рассмотрели распределение нагрузки и напряжения в резьбе крепежных изделий. Шигли и др.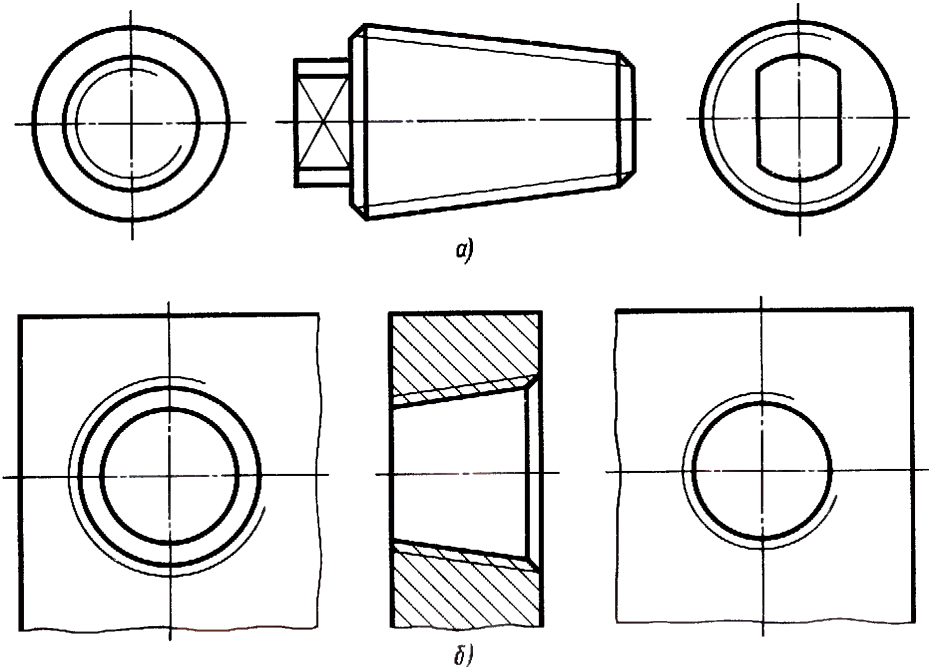 В [22] представлено аналитическое решение для жесткости стержня, основанное на работе Ленхоффа и Вистехаффа [23]. Нассер [24], Мусто и Конкле [25], Наврас [26] и Нассар и Аббаунд [27] также предложили математическую модель жесткости болтового соединения. Цинь и др. [28] создал аналитическую модель болтового соединения диска с барабаном и представил ее применение для динамического анализа шарнирного ротора. Лю и др. [29] провел экспериментальные и численные исследования болтовых соединений с аксиальным возбуждением.
В [22] представлено аналитическое решение для жесткости стержня, основанное на работе Ленхоффа и Вистехаффа [23]. Нассер [24], Мусто и Конкле [25], Наврас [26] и Нассар и Аббаунд [27] также предложили математическую модель жесткости болтового соединения. Цинь и др. [28] создал аналитическую модель болтового соединения диска с барабаном и представил ее применение для динамического анализа шарнирного ротора. Лю и др. [29] провел экспериментальные и численные исследования болтовых соединений с аксиальным возбуждением.
Есть также несколько авторов, которые, исходя из природы жесткости резьбы, с точки зрения деформации резьбы, создали математическую модель расчета распределения осевой силы резьбы. Метод Сопвича [30] и метод Ямамото [31] получили широкое признание. Метод Сопвича дал способ расчета осевого распределения усилий резьбовых соединений. Метод Ямамото позволяет не только рассчитать распределение осевой силы резьбы, но и рассчитать жесткость резьбового соединения. Предположение для метода Ямамото состоит в том, что нагрузка на единицу ширины вдоль направления спирали распределяется равномерно. Фактически, для трехмерной (3D) спиральной резьбы распределение нагрузки неравномерно. Поэтому, основываясь на методе Ямамото, Dongmei Zhang et al. [1] предлагают метод, который может вычислить жесткость зацепленного винта с учетом распределения нагрузки, и достоверность этого метода была подтверждена МКЭ и экспериментами. Метод Чжан Дунмея не учитывает влияние коэффициента трения контактной поверхности резьбы. Фактически коэффициент трения контактной поверхности резьбового соединения влияет на распределение осевой силы резьбы и жесткость резьбы. Поэтому мы предлагаем новый метод, который может более точно вычислить жесткость зацепленного винта, учитывая эффекты трения и распределения нагрузки. Точность метода подтверждена МКЭ и испытанием на растяжение болтов. Блок-схема статьи представлена на рисунке 2.9.0007
Фактически, для трехмерной (3D) спиральной резьбы распределение нагрузки неравномерно. Поэтому, основываясь на методе Ямамото, Dongmei Zhang et al. [1] предлагают метод, который может вычислить жесткость зацепленного винта с учетом распределения нагрузки, и достоверность этого метода была подтверждена МКЭ и экспериментами. Метод Чжан Дунмея не учитывает влияние коэффициента трения контактной поверхности резьбы. Фактически коэффициент трения контактной поверхности резьбового соединения влияет на распределение осевой силы резьбы и жесткость резьбы. Поэтому мы предлагаем новый метод, который может более точно вычислить жесткость зацепленного винта, учитывая эффекты трения и распределения нагрузки. Точность метода подтверждена МКЭ и испытанием на растяжение болтов. Блок-схема статьи представлена на рисунке 2.9.0007
2. Математическая модель
2.1. Распределение осевой нагрузки
Согласно Ямамото [31], резьба рассматривается как консольная балка, и нить деформируется под действием осевой силы и предварительной нагрузки. К этим деформациям относятся следующие (показаны на рисунке 3): деформация изгиба резьбы, деформация сдвига резьбы, деформация наклона корня резьбы, деформация сдвига корня резьбы, деформация удлинения в радиальном направлении или деформация радиальной усадки.
К этим деформациям относятся следующие (показаны на рисунке 3): деформация изгиба резьбы, деформация сдвига резьбы, деформация наклона корня резьбы, деформация сдвига корня резьбы, деформация удлинения в радиальном направлении или деформация радиальной усадки.
Для ISO резьба, осевая деформация резьбы при усилии осевой единицы ширины представляет собой деформацию изгиба резьбы, деформацию сдвига резьбы, деформацию наклона корня резьбы, деформацию сдвига корня резьбы и удлиненную деформацию в радиальном направлении (гайка) или радиальную усадочную деформацию (винт) , и вычислить эти деформации резьбы соответственно, а затем просуммировать их, то есть полную деформацию.
2.1.1. Деформация изгиба
В резьбовом соединении под действием нагрузки коэффициент трения контактных поверхностей равен μ , когда сила скольжения вдоль наклонной плоскости больше, чем сила трения вдоль наклонной плоскости, относительное скольжение происходит между двумя наклонными плоскостями, а сила осевой единицы ширины (показана на рисунке 3) равна ; если пренебречь влиянием угла подъема, сила на единицу ширины, перпендикулярная поверхности резьбы, может быть выражена как
y — составляющая силы направления соответственно и
Трение, создаваемое вдоль склона, равно w μ ; т. е.
е.
Сила w μ также разлагается на x -сила направления и y -сила направления, которые равны и , соответственно.
В единице ширины резьба рассматривается как прямоугольная консольная балка переменного сечения. Под действием указанной силы нить испытывает изгибную деформацию, и виртуальная работа, совершаемая изгибающим моментом на сечении балки, равна
В соответствии с принципом виртуальной работы прогиб (см. рис. 3(а)) балки, находящейся под нагрузкой, равен
где – изгибающий момент балки единичной нагрузки. — изгибающий момент балки под действием фактической нагрузки. I ( y ) — площадь момента инерции балки при . модуль Юнга материала. c — длина балки. Здесь предполагается, что силы действуют на средний диаметр резьбы.
Как показано на рис. 5, высота сечения балки на единицу ширины и момент инерции сечения могут быть выражены с помощью функции интерполяции.
где h — высота концевого сечения балки; b – ширина сечения балки; – отношение высоты корневого сечения балки к высоте концевого сечения балки; см. рисунок 5.
рисунок 5.
На рисунке 5 изгибающий момент балки связан с осевой составляющей y и w μ , и эти составляющие вызывают изгиб балки; поэтому аналитическое решение показывает, что изгибающий момент балки единичной ширины под действием силы трения и вертикальной нагрузки поверхности резьбы равен
Подставляя (10) и (9) в (8) и интегрируя, получаем аналитическое выражение прогиба (показанного на рис. 3(а)) консольной балки переменного сечения под нагрузкой, получаем
2.1. 2. Деформация сдвига
Предположим, что распределение напряжения сдвига на любом сечении распределено по параболе [31], а деформация (см. рис. 3(б)) под действием силы сдвига по ширине узла 1 равна
2.1. 3. Наклонная деформация корня резьбы
Под действием нагрузки на поверхность резьбы действует изгибающий момент, а основание резьбы наклоняется, как показано на рис. 3(в). Из-за наклона резьбы в месте действия поверхностной силы резьбы происходит осевое смещение, которое можно выразить как [31]
2.
 1.4. Деформация из-за радиального расширения и радиальной усадки
1.4. Деформация из-за радиального расширения и радиальной усадкиСогласно статическому анализу на резьбу действует радиальная сила (показана на рис. 4), а из литературы [31] известно, что радиальная деформация внутренней и внешней резьбы (показана на рис. 3(d)) и
2.1.5. Сдвиговая деформация корня
Если предположить, что напряжение сдвига в корневой части распределено равномерно, смещение точки в направлении, вызванном сдвиговой деформацией (показано на рис. 3(e)) такое же, как смещение нить по направлению; это смещение можно выразить как [31]
Для внутренней резьбы ISO соотношение между a, b, c и шагом равно (17) в (9), (10), (11), (12), (13 ), (14) и (16) получается соотношение
Для внутренней резьбы ISO отношение между a , b , c, и шагом составляет
Подставляя (24) в (9), (10), (11), (12), (13 ), (15) и (16) типа получается соотношение
. Складывая эти деформации по отдельности, можно получить суммарную деформацию (показанную на рис. 4) резьбы винта и резьбы гайки под действием силы .
4) резьбы винта и резьбы гайки под действием силы .
Единичная сила на единицу ширины осевого направления может быть выражена как
Под действием единичной силы осевой единицы ширины суммарная деформация наружной и внутренней резьбы равна
Для резьбовых соединений на оси нагрузки x F осевая деформация винтов и гаек может быть выражена как
Здесь длина вдоль винтового направления и отношение между осевой высотой и длина вдоль направления спирали может быть представлена следующей формулой в соответствии с геометрическим соотношением, показанным на рис. 6.
Здесь β — угол подъема резьбы, показанный на рис. 6, а затем
Предположим,
Здесь ( x ) и ( x ) представляют жесткость единицы осевой длины гайки и винта соответственно для единичной силы.
Суммарная осевая деформация резьбового соединения при обозначена как
Жесткость единичной осевой длины резьбового соединения выражается как
Как показано на рисунке 1(а), конструкция резьбового соединения включает корпус гайки и корпус шнека. Гайка закреплена, винт подвергается тяговому усилию, общая осевая сила равна , а осевая сила на резьбовом соединительном винте равна F ( х ). Если положение нижнего торца гайки является исходной точкой 0 и в этом положении осевая сила равна F ( x ), величину удлинения винта и сжатия гайки можно получить из следующего:
Гайка закреплена, винт подвергается тяговому усилию, общая осевая сила равна , а осевая сила на резьбовом соединительном винте равна F ( х ). Если положение нижнего торца гайки является исходной точкой 0 и в этом положении осевая сила равна F ( x ), величину удлинения винта и сжатия гайки можно получить из следующего:
, где ( x ) и ( x ) — площади вертикального поперечного сечения винтов и гаек в данном положении. и – соответственно модуль Юнга тела винта и модуль Юнга тела гайки. Найдите градиент смещения для выражения, которое соответственно выражается как
Здесь , и .
Как показано на рис. 1(а), на винт действует растягивающая сила , причем начало координат находится в нижней части гайки, а сила в точке x равна , а затем удлинение винта в точке x равно , а степень сжатия гайки в точке x равна . Связь между , , , и is (см. рис. 7 и 1(а)), а также частную производную от этой зависимости можно получить по следующей формуле:
Подставляя (45), (46), (47), и (48) в (49) и упрощая его
Пусть
Тогда
Из математических знаний уравнение является дифференциальным уравнением.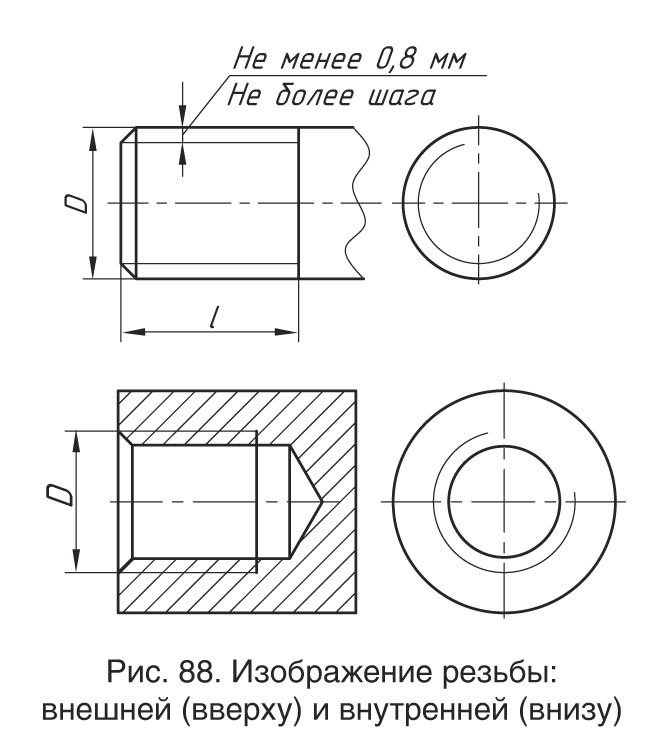 Общее решение уравнения может быть выражено как
Общее решение уравнения может быть выражено как
Как видно из рисунка 1, осевая сила на первой резьбе на поверхности соединения гайки и винта равна , а осевая сила на последней резьбе на нижней конец поверхности резьбового соединения гайки и винта равен 0; то есть граничное условие равно F ( x =0)= и F ( x = L )=0. Принимая эти граничные условия в уравнение, получим =-()/ и =, поэтому выражение осевой нагрузки резьбового соединения получаем как
Следовательно, плотность распределения осевой силы резьбового соединения по направлению можно выразить как
2.2. Жесткость резьбового соединения
Жесткость болтового соединения в осевом направлении равна осевому распределению усилия резьбового соединения, умноженному на единицу жесткости; то есть
Общая жесткость болтового соединения может быть выражена как
Подставляя (44) и (55) в (57), жесткость болтового соединения выражается как
3. Модель FEA
3D конечно-элементная модель (показан на рис. 10), и был выполнен МКЭ для анализа влияния различных параметров резьбы на жесткость резьбы. Эти параметры включают материал, длину резьбы, шаг и т. д.
10), и был выполнен МКЭ для анализа влияния различных параметров резьбы на жесткость резьбы. Эти параметры включают материал, длину резьбы, шаг и т. д.
Для анализа использовалась программа FEA ANSYS 14.0. В ходе анализа торец гайки был зафиксирован (показан на рис. 9).), исходное состояние модели показано на рис. 8, и к торцу винта было приложено осевое смещение. Затем осевая сила торца винта была извлечена. Осевая жесткость резьбового соединения рассчитывалась методом МКЭ. Первым задается коэффициент трения μ контактной поверхности резьбы. В МКЭ используется контактный алгоритм расширенного Лагранжа. На рисунках 11(а)–11(в) представлены кривые сходимости силы для МКЭ резьбовых соединений. Рисунки 12 (а)-12 (с) представляют собой эффект обратного размера сетки на осевой силы, полученной методом МКЭ. Из рисунков 12(a)–12(c) видно, что по мере уменьшения размера ячейки результирующая осевая сила постепенно уменьшается, но когда размер ячейки в определенной степени мал, результирующая осевая сила практически не уменьшится. Осевая сила в настоящее время является осевой силой, требуемой автором. При известных перемещениях и осевом усилии жесткость резьбового соединения можно рассчитать по формуле
Осевая сила в настоящее время является осевой силой, требуемой автором. При известных перемещениях и осевом усилии жесткость резьбового соединения можно рассчитать по формуле
4. Испытание резьбовых соединений на растяжение [1]
Для проверки эффективности данного бумажного метода использованы экспериментальные данные экспериментального устройства в [1]. В [1] для измерения характеристик нагрузки-деформации образцов используется электронная универсальная испытательная машина, причем испытуемый образец изготовлен из латуни. Значение натяжения можно считать с испытательной машины. Осевое отклонение резьбового соединения может быть представлено изменением смещения между двумя линиями, как показано на рисунке 14, которое можно измерить с помощью видеодатчика [1]. В [1] для получения максимально точных данных каждый размер резьбы находится в небольшом диапазоне деформации при испытании на растяжение, и каждый размер испытания на растяжение резьбы проводят 10 раз, а среднее значение равно рассчитываются как окончательные расчетные данные.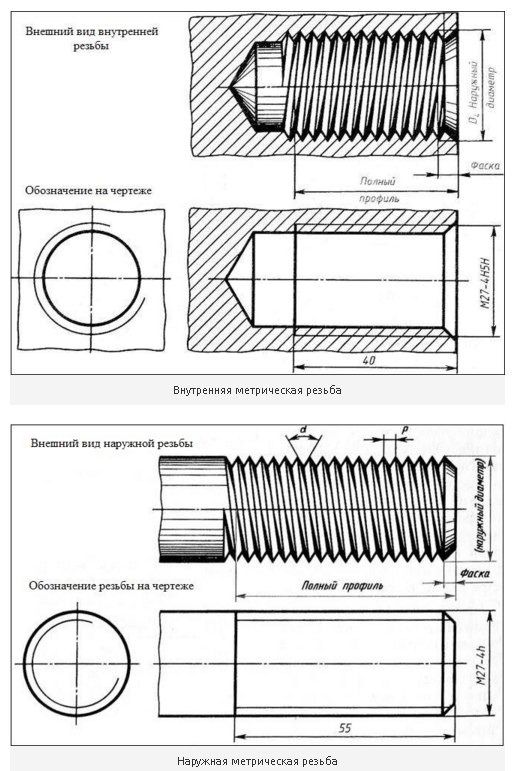 Некоторые образцы в эксперименте показаны на рис. 13.
Некоторые образцы в эксперименте показаны на рис. 13.
Формула расчета жесткости:
Для изготовления гаек и винтов используется латунь. Модуль Юнга латуни 107 ГПа, коэффициент Пуассона 0,32 [1].
5. Результаты и обсуждение
5.1. Жесткость резьбовых соединений
Croccolo, D. [12], Nassar SA [19] и Zou Q [32] изучали коэффициент трения резьбы. Согласно исследованию Zou Q и Nassar SA, в случае смазочного масла на поверхности резьбы коэффициент трения резьбового соединения сталь-сталь составляет 0,08, а коэффициент трения резьбового соединения алюминия-алюминия составляет 0,1.
Для проверки правильности результатов расчета теории, представленной в данной статье, для расчета экспериментального теста использовались различные резьбовые соединения.
В анализе конечных элементов и теоретических расчетах этой статьи модуль Юнга стали = = 200 ГПа, коэффициент Пуассона стали равен 0,3, а коэффициент трения [12, 19, 32] установлен равным 0,08.
Экспериментальные данные, данные МКЭ и данные метода Ямамото в таблицах 1 и 5 взяты из литературы [1]. Как видно из таблиц 1 и 5, все расчетные значения, полученные в данной работе, превышают экспериментальные результаты. Возможно, погрешность вызвана наличием небольшого количества загрязнений на поверхности резьбы и неизбежной частичной деформацией резьбы и проскальзыванием между резьбовыми контактными поверхностями. Результаты теоретических расчетов и результаты МКЭ в данной статье имеют небольшую погрешность.
В таблице 2 представлено влияние длины резьбы на жесткость. Видно, что при одном и том же номинальном диаметре М10, одном и том же шаге P =1,5 и одинаковом материале сталь, когда длина зацепления резьбы принимается равной 14 мм, 9 мм и 6 мм соответственно, Установлено, что чем больше длина зацепления резьбы, тем больше жесткость и чем меньше длина связи, тем меньше жесткость.
В МКЭ, методе данной статьи и методе Ямамото модуль Юнга алюминиевого сплава составляет E = 68,9 ГПа; Коэффициент Пуассона алюминиевого сплава равен 0,34.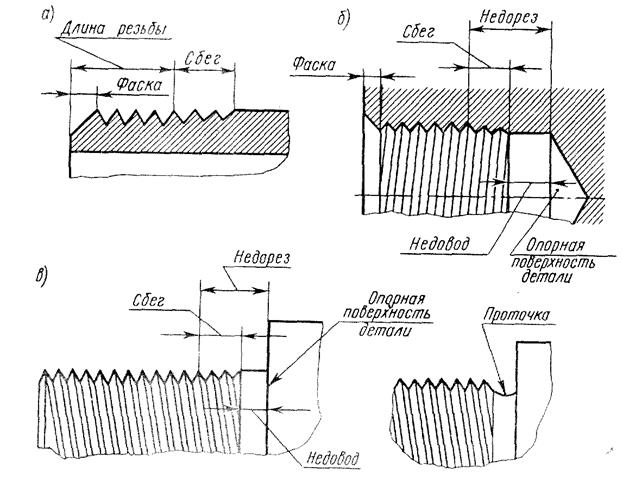 Коэффициент трения резьбового соединения сталь-сталь [12, 21, 22, 32] принимается равным 0,08, а коэффициент трения резьбового соединения алюминий-алюминий [12, 19, 32] принимается равным 0,1. В таблице 3 показано влияние различных материалов на жесткость резьбовых соединений. Два типа резьбовых соединений изготавливаются из двух разных материалов: стали и алюминиевых сплавов. Из таблицы видно, что при одном и том же шаге, одном и том же номинальном диаметре и одинаковой длине зацепления жесткость стального резьбового соединения больше, чем у алюминиевого материала.
Коэффициент трения резьбового соединения сталь-сталь [12, 21, 22, 32] принимается равным 0,08, а коэффициент трения резьбового соединения алюминий-алюминий [12, 19, 32] принимается равным 0,1. В таблице 3 показано влияние различных материалов на жесткость резьбовых соединений. Два типа резьбовых соединений изготавливаются из двух разных материалов: стали и алюминиевых сплавов. Из таблицы видно, что при одном и том же шаге, одном и том же номинальном диаметре и одинаковой длине зацепления жесткость стального резьбового соединения больше, чем у алюминиевого материала.
В таблице 4 также показано влияние различных шагов на жесткость резьбового соединения. Видно, что при одинаковой длине зацепления, том же материале и номинальном диаметре шаг составляет 1,5, 1,25 и 1 соответственно, и мы обнаруживаем, что чем меньше шаг, тем больше жесткость.
При использовании МКЭ для анализа влияния коэффициентов трения на жесткость резьбовых соединений спецификация резьбы составляет M6×1×6,1, а коэффициенты трения составляют 0,01, 0,05, 0,1, 0,2, 0,25 и 0,3. (как показано на рисунках 15–20)
(как показано на рисунках 15–20)
На рисунках 21 и 22 показаны результаты расчета жесткости. Размер резьбы М10×1,5×9 и М6×1×6,1, материал сталь, коэффициент Пуассона материала 0,3, модуль Юнга материала 200 ГПа, коэффициент трения поверхности резьбы принят равным 0,01, 0,05. , 0,1, 0,2, 0,25 и 0,3. Вычисленные с использованием теорий этой статьи, FEA и Yamamoto, соответственно, и из рисунков 21 и 22, мы можем видеть, что результаты FEA очень похожи на результаты теоретических расчетов этой статьи, тренд изменения жесткости с трением коэффициент одинаков и увеличивается с увеличением коэффициента трения, а результаты МКЭ хорошо согласуются с результатами МКЭ; однако теория Ямамото не учитывает влияние коэффициента трения на жесткость, и это явно неразумно.
5.2. Влияние коэффициента трения на распределение осевой силы
Возьмем размер резьбы M6×0,75×6,1, осевую нагрузку примем равной 100 Н, 350 Н и 550 Н соответственно, а коэффициенты трения примем равными 0, 0,3, 0,6 и 1, соответственно, для расчета распределения осевой силы резьбы.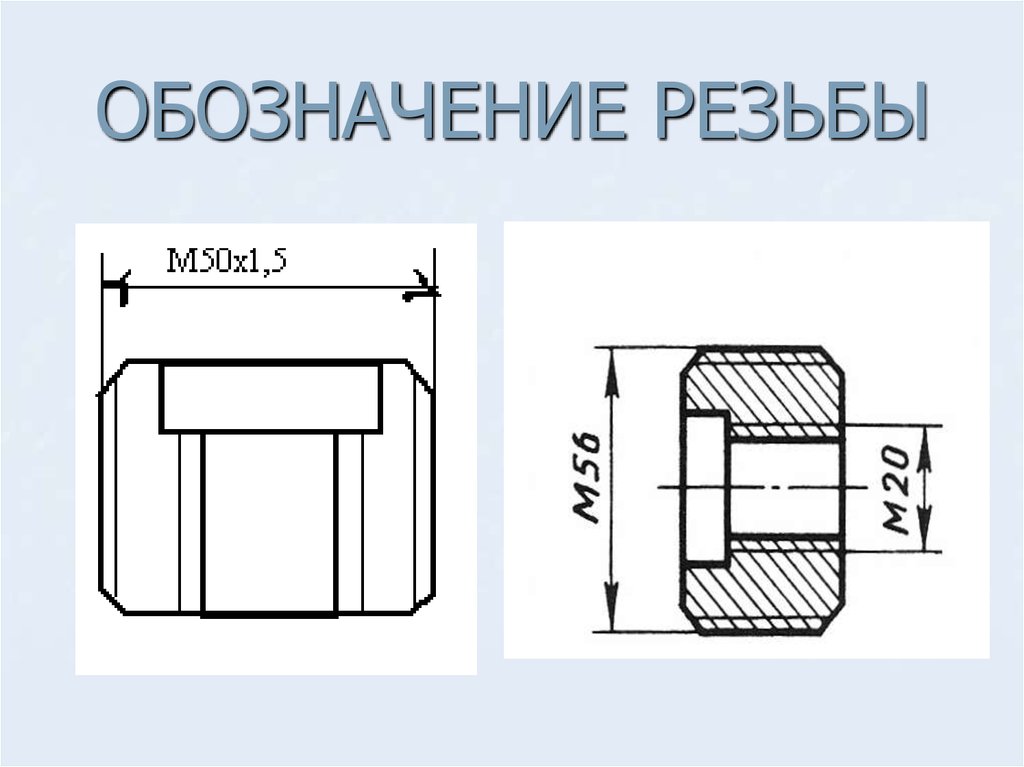 Как видно из рисунка 23, когда коэффициент трения равен 1, степень изгиба кривой наибольшая, когда коэффициент трения равен 0, степень изгиба кривой наименьшая, степень изгиба кривой больше, что указывает на то, что более неравномерная распределение осевой силы, тем меньше степень изгиба кривой, что указывает на более равномерное распределение осевой силы. Мы видим, что коэффициент трения поверхности резьбы влияет на распределение осевой силы.
Как видно из рисунка 23, когда коэффициент трения равен 1, степень изгиба кривой наибольшая, когда коэффициент трения равен 0, степень изгиба кривой наименьшая, степень изгиба кривой больше, что указывает на то, что более неравномерная распределение осевой силы, тем меньше степень изгиба кривой, что указывает на более равномерное распределение осевой силы. Мы видим, что коэффициент трения поверхности резьбы влияет на распределение осевой силы.
6. Заключение
В данном исследовании представлен новый метод расчета жесткости резьбы с учетом коэффициента трения и анализируется влияние геометрии резьбы и параметров материала на жесткость резьбы, а также анализируется влияние коэффициента трения на жесткость резьбы. и осевое распределение силы. (1) Результаты расчета жесткости нити, рассчитанные теоретическим методом расчета этого исследования, в основном согласуются с результатами FEA. Результаты, полученные тестом, меньше, чем расчетные результаты. Это связано с влиянием изготовления резьбы на экспериментальные результаты. (2) Жесткость резьбы тесно связана со свойствами материала, шагом и длиной резьбы. Мы можем получить более высокую жесткость, увеличив модуль Юнга материала, увеличив длину резьбы и уменьшив шаг. (3) Мы также можем увеличить коэффициент трения поверхности резьбового соединения, чтобы увеличить жесткость резьбового соединения, но мы обнаружили, что использование этого метода для увеличения жесткости резьбы ограничено. (4) Чтобы сделать распределение осевой нагрузки на резьбу равномерным, мы можем уменьшить коэффициент трения поверхности резьбы, но мы обнаружили, что использование этого метод улучшения распределения осевого усилия резьбы имеет ограниченную эффективность.
(2) Жесткость резьбы тесно связана со свойствами материала, шагом и длиной резьбы. Мы можем получить более высокую жесткость, увеличив модуль Юнга материала, увеличив длину резьбы и уменьшив шаг. (3) Мы также можем увеличить коэффициент трения поверхности резьбового соединения, чтобы увеличить жесткость резьбового соединения, но мы обнаружили, что использование этого метода для увеличения жесткости резьбы ограничено. (4) Чтобы сделать распределение осевой нагрузки на резьбу равномерным, мы можем уменьшить коэффициент трения поверхности резьбы, но мы обнаружили, что использование этого метод улучшения распределения осевого усилия резьбы имеет ограниченную эффективность.
Nomenclature
| : | Contact surface friction coefficient | ||
| : | Axial unit width force, N | ||
| : | Thread bending deformation, mm | ||
| : | Thread shear deformation , мм | ||
| : | Наклонная деформация корня резьбы, мм | ||
| : | Радиальная деформация растяжения или радиальная деформация усадки, мм | ||
| : | Деформация корня резьбы при сдвиге, мм | ||
| : | Изгибающий момент единичной силовой балки, Н•мм | ||
| : | 7 Изгибающий момент балки под фактической нагрузкой, Н• изгибающий момент балки, мм | ||
| : | Area moment of inertia, mm 4 | ||
| : | Young’s modulus of the screw material, N/mm 2 | ||
| : | Length of the beam, thread высота линии шага, мм | ||
| : | .|||
| : | Отношение высоты корневой части резьбы гайки к высоте сечения на среднем диаметре | ||
| : | Деформация радиальной усадки нити, мм | ||
| : | Радиальное направление. | : | Наружный диаметр цилиндра (гайки), мм |
| : | Рабочий диаметр резьбы, мм | ||
| : | Коэффициент Пуассона материала гайки3 901 60164 | ||
| P: | PINGE, MM | ||
| : | изгиб момент винтовой нити, n • MM | ||
| : | |||
| : | . Деформация резьбы при сдвиге резьбы, мм | ||
| : | Деформация наклона корня резьбы, мм | ||
| : | Деформация растяжения резьбы в радиальном направлении, мм | ||
| : | Деформация корня резьбы при сдвиге резьбы, мм | ||
| : | Изгибающий момент резьбы гайки, Н•мм | ||
| : | Деформация сдвига нити нити гайки, мм | ||
| : | Деформация наклона корня нити | MM||
7 г.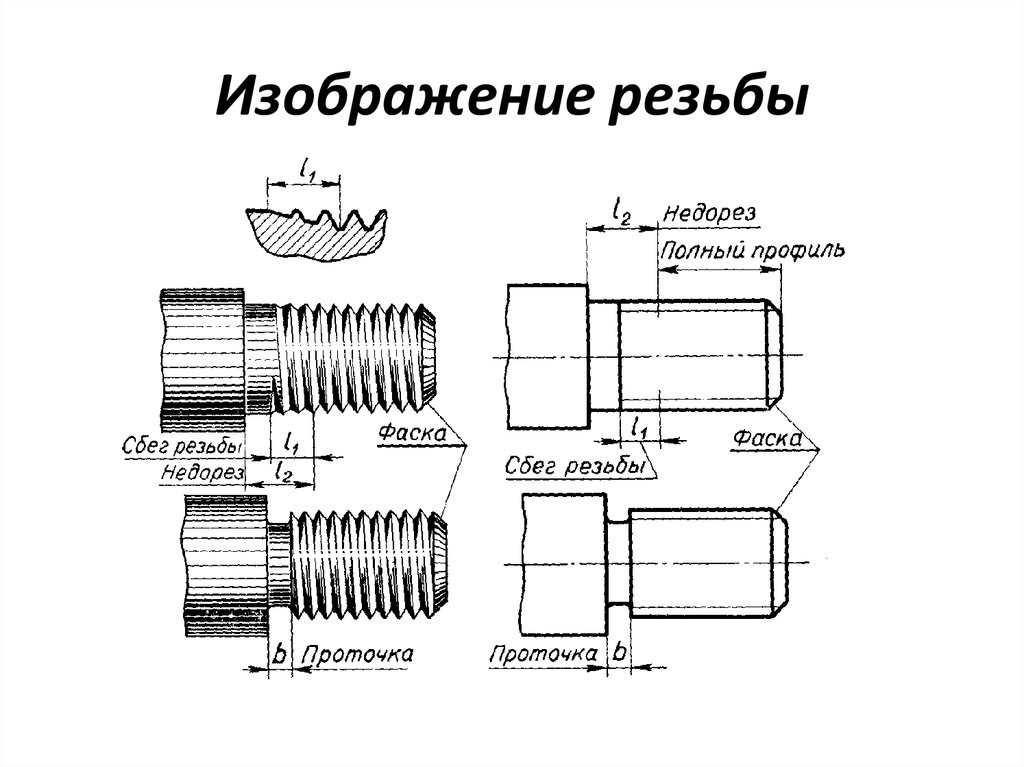 | |||
| : | Деформация сдвига корня резьбы гайки, мм | ||
| : | Единица усилия на единицу ширины в осевом направлении | ||
| Деформация наружная 5,5 мм резьбы | : | ||
| : | Суммарная деформация внутренней (гайки) резьбы, мм | ||
| : | Нагрузка где-то по оси абсцисс F, где осевая деформация резьбы, мм | ||
| : | Нагрузка где-то по оси абсцисс F, где осевая деформация резьбы гайки, мм | ||
| : | Длина по винтовой линии, мм | ||
| Угол подъема | |||
| резьба, град | |||
| (): | Жесткость узла осевой длины винта, Н/мм | ||
| (): | Жесткость узла осевой длины гайки, Н/мм 2 | ||
| : | Осевая суммарная деформация резьбового соединения, мм | ||
| : | Жесткость узла осевая длина резьбового соединения, Н/мм 2 | ||
| : Суммарная осевая нагрузка (осевая нагрузка) , Н | |||
| : | В положении осевая сила , величина удлинения винта | ||
| : | В положении осевая сила , величина сжатия гайки | ||
| : | Vertical cross-sectional areas of screw at the position, mm 2 | ||
| : | Vertical cross-sectional areas of nut at the position, mm 2 | ||
| : | Young’s modulus of the screw body, N/mm 2 | ||
| : | Young’s modulus of the nut body, N/mm 2 | ||
| : | Stiffness in the axial direction , N/mm | ||
| : | Overall stiffness of the threaded connection, N/mm | ||
| : | Axial displacement, mm | ||
| : | Total axial force, N | ||
| : | Axial tension load, N | ||
| : | Габаритная жесткость резьбового соединения, Н/мм | ||
| : | Осевая деформация резьбы, мм | ||
Доступность данных
Данные, использованные для поддержки результатов этого исследования, включены в статью.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Благодарности
Авторы хотели бы выразить благодарность Национальному фонду естественных наук Китая [Грант №. 51675422, 51475366 и 51475146] и Проект планирования науки и технологий провинции Шэньси [Грант №. 2016JM5074].
Ссылки
Д. Чжан, С. Гао и С. Сюй, «Новый метод расчета жесткости резьбового соединения», Достижения в области машиностроения , том. 8, нет. 12, 2016.
Посмотреть по адресу:
Google Scholar
К. Мураяма, И. Йошимото и Ю. Накано, «О жесткости пружинных соединений болтовых соединений», Труды Японского общества инженеров-механиков , об. 41, нет. 344, стр. 1289–1297, 1975.
Просмотр:
Сайт издателя | Google Scholar.
 соединений», Journal of Engineering for Industry , vol. 98, нет. 3, стр. 858–861, 1976.
соединений», Journal of Engineering for Industry , vol. 98, нет. 3, стр. 858–861, 1976.Посмотреть по адресу:
Сайт издателя | Google Scholar
Кенни Б. и Паттерсон Э. А. Распределение нагрузки и напряжения в резьбе, стр. 9.0750 Экспериментальная механика , том. 25, нет. 3, стр. 208–213, 1985.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Б. Кенни и Э. А. Паттерсон, «Распределение нагрузки и напряжения в резьбе крепежных изделий — обзор», Journal of the Mechanical Behavior of Materials , vol. 2, нет. 1–2, стр. 87–106, 1989.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. Л. Миллер, К. М. Маршек и М. Р. Наджи, «Определение распределения нагрузки в резьбовом соединении», Механизм и теория машин , том.
 18, нет. 6, стр. 421–430, 1983.
18, нет. 6, стр. 421–430, 1983.Посмотреть по адресу:
Сайт издателя | Google Scholar
В. Ван и К. М. Маршек, «Определение распределения нагрузки в резьбовом соединителе с податливой резьбой», Механизм и теория машин , том. 31, нет. 2, стр. 229–244, 1996.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж. Уайлман, М. Чоудхури и И. Грин, «Расчет жесткости стержня в болтовых соединениях», Журнал механического проектирования , том. 113, нет. 4, стр. 432–437, 1991.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Де Агостинис, С. Фини и Г. Олми, «Влияние смазки на фрикционные характеристики резьбовых соединений планетарных редукторов», Труды Института инженеров-механиков, часть C: журнал машиностроения , вып.
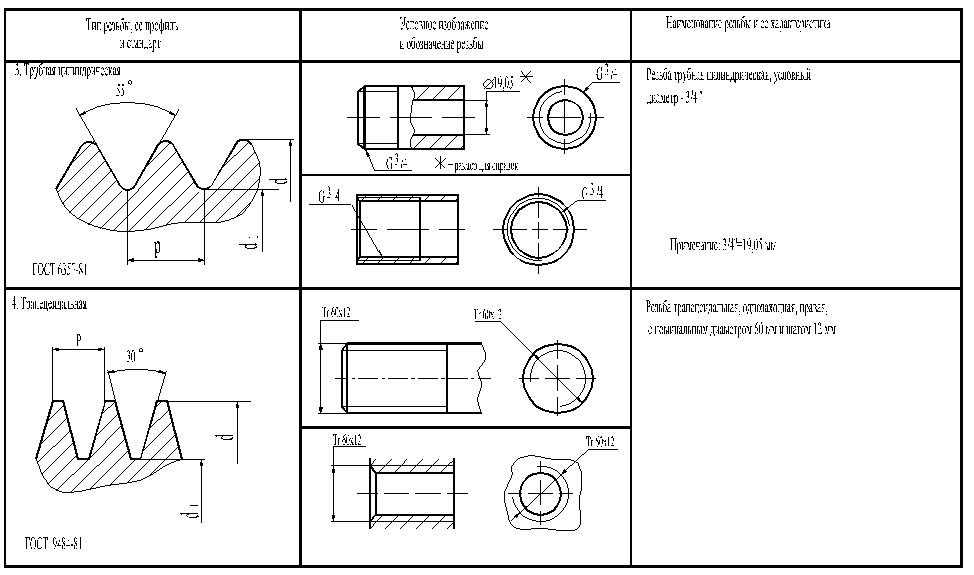 230, нет. 2016. Т. 15. С. 2553–2563.
230, нет. 2016. Т. 15. С. 2553–2563.Просмотр:
Сайт издателя | Google Scholar
Д. Крокколо, М. Де Агостинис, С. Фини и Г. Олми, «Трибологические свойства болтов в зависимости от различных покрытий и смазок винтов: экспериментальное исследование», Tribology International , vol. 107, стр. 199–205, 2017.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. Крокколо, М. Де Агостинис, С. Фини и Г. Олми, «Экспериментальное исследование реакции резьбового фиксатора с использованием различных материалов, размеров винтов и пропорций резьбы», International Journal of Adhesion and Adhesives , 2018.
Просмотр по адресу:
Google Scholar
Д. Крокколо, М. Де Агостинис и Н. Винченци, «Анализ отказов болтовых соединений: влияние коэффициентов трения на взаимосвязь между крутящим моментом и предварительным натягом», Engineering Failure Analysis , vol.
 18, нет. 1, стр. 364–373, 2011.
18, нет. 1, стр. 364–373, 2011.Посмотреть по адресу:
Сайт издателя | Google Scholar
Q. Zou, T.S. Sun, S.A. Nassar, G.C. Barber и A.K. Gumul, «Влияние смазки на трение и соотношение крутящего момента и напряжения в резьбовых соединениях», в Proceedings of the STLE/ASME International Joint Tribology Conference (IJTC ’06) , Сан-Антонио, Техас, США, октябрь 2006 г. Нассар, Г. К. Барбер, Х. Эль-Хиами и Д. Чжу, «Подход контактной механики к определению эффективного радиуса в болтовых соединениях», Journal of Tribology , vol. 127, нет. 1, стр. 30–36, 2005 г.
Посмотреть по адресу:
Сайт издателя | Академия Google
С. А. Нассар, П. Х. Матин и Г. К. Барбер, «Момент трения резьбы в болтовых соединениях», Журнал технологии сосудов под давлением , том. 127, нет. 4, стр. 387–393, 2005 г.

Посмотреть по адресу:
Сайт издателя | Google Scholar
С. А. Нассар, Х. Эль-Хиами, Г. К. Барбер, К. Цзоу и Т. С. Сун, «Экспериментальное исследование трения подшипников и резьбы в крепежных деталях», Journal of Tribology , vol. 127, нет. 2, стр. 263–272, 2005.
Просмотр:
Сайт издателя | Google Scholar
С. А. Нассар, Г. К. Барбер и Д. Цзо, «Момент трения подшипников в болтовых соединениях», Tribology Transactions , vol. 48, нет. 1, стр. 69–75, 2005 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С. Нассар А., С. Ганешмурти, Р. Ранганатан М. и др., «Влияние скорости затяжки на крутящий момент-натяжение и характер износа в болтовых соединениях», Journal of Pressure Vessel Technology , том.
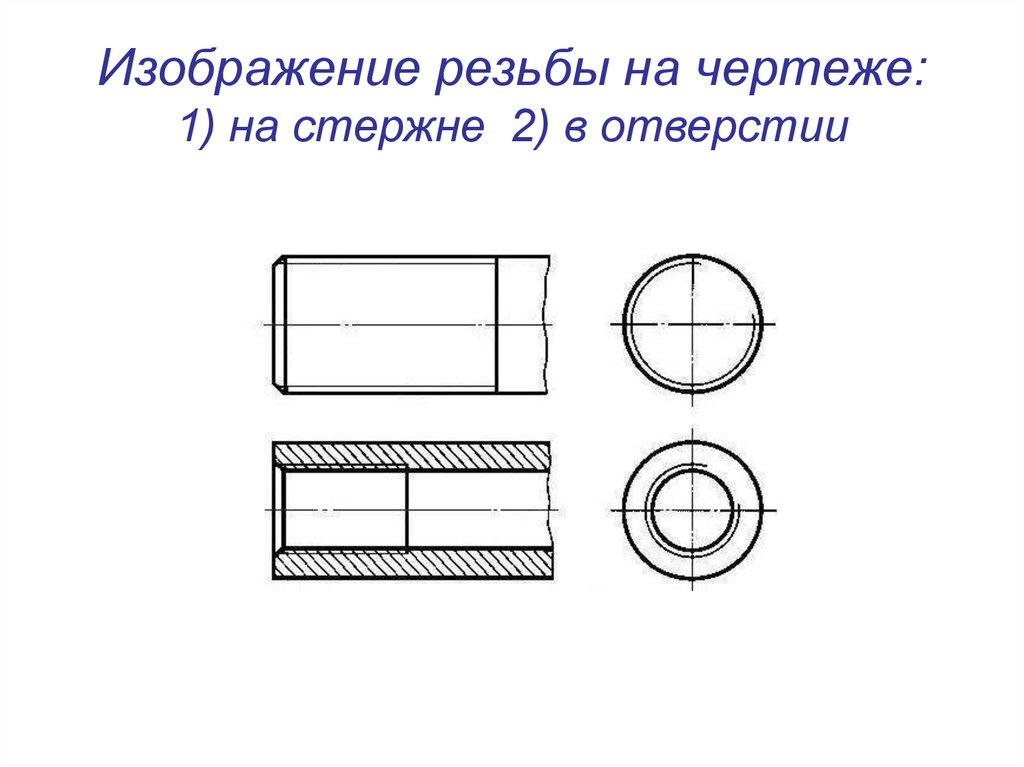 129, нет. 3, pp. 1669–1681, 2007.
129, нет. 3, pp. 1669–1681, 2007.Просмотр по адресу:
Google Scholar
H. Kopfer, C. Friedrich, M. De Agostinis, and D. Croccolo, «Характеристики трения в облегченной конструкции с фокусировкой на болтах соединения», в материалах Proceedings of the ASME International Machine Engineering Congress and Exposition (IMECE ’12) , стр. 839–846, ноябрь 2012 г. , «Распределение нагрузки и напряжения в резьбе крепежных изделий — обзор», Журнал механического поведения материалов , том. 2, нет. 1–2, стр. 87–105, 1989.
Посмотреть по адресу:
Сайт издателя | Google Scholar
J. E. Shigley, C. R. Mischke, and R. G. Budynas, Mechanical Engineering Design , McGraw-Hill, New York, NY, USA, 2004.
напряжения и деформации болтовых соединений», Журнал технологии сосудов под давлением, Труды ASME , том.
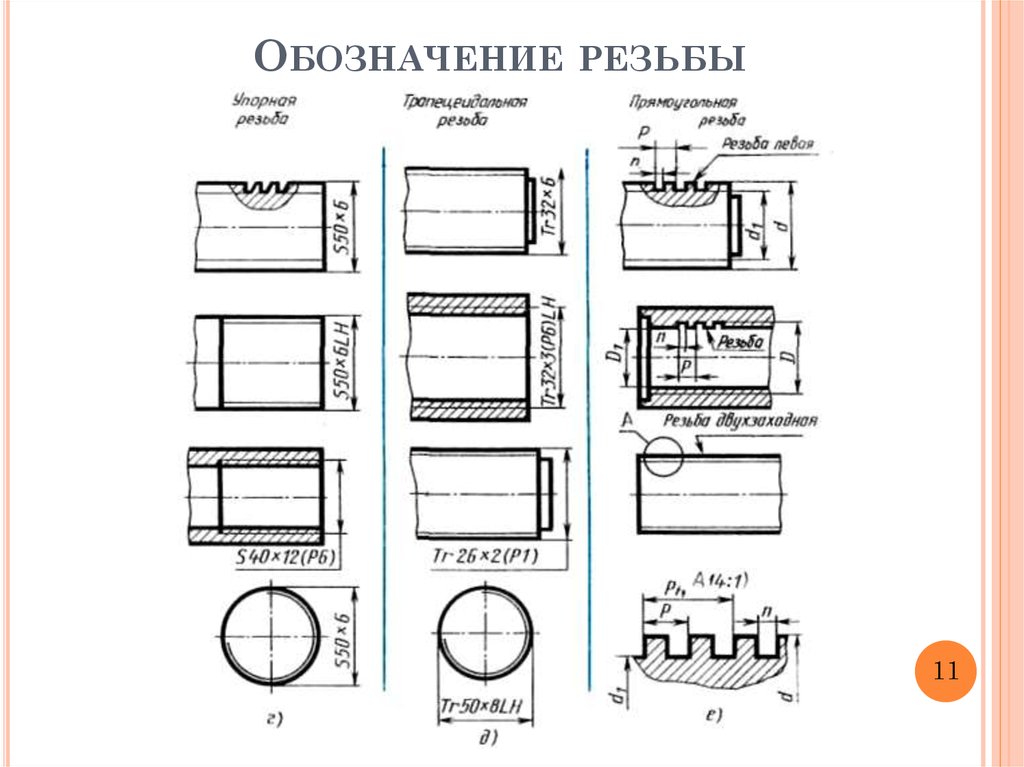 118, нет. 1, стр. 54–58, 1996.
118, нет. 1, стр. 54–58, 1996.Посмотреть по адресу:
Сайт издателя | Google Scholar
Н. С. Аль-Хунити, «Расчет жесткости стержня в болтовых соединениях с использованием анализа конечных элементов», Проектирование конструкций и машин на основе механики, , том. 33, нет. 3–4, стр. 331–342, 2005 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж. К. Мусто и Н. Р. Конкл, «Расчет жесткости стержня при расчете болтовых соединений», Журнал механического проектирования , том. 128, нет. 6, стр. 1357–1360, 2006.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Н. Хайдар, С. Обид и М. Джавад, «Математическое представление жесткости болтового соединения: новая предлагаемая модель», Journal of Mechanical Science and Technology , vol.
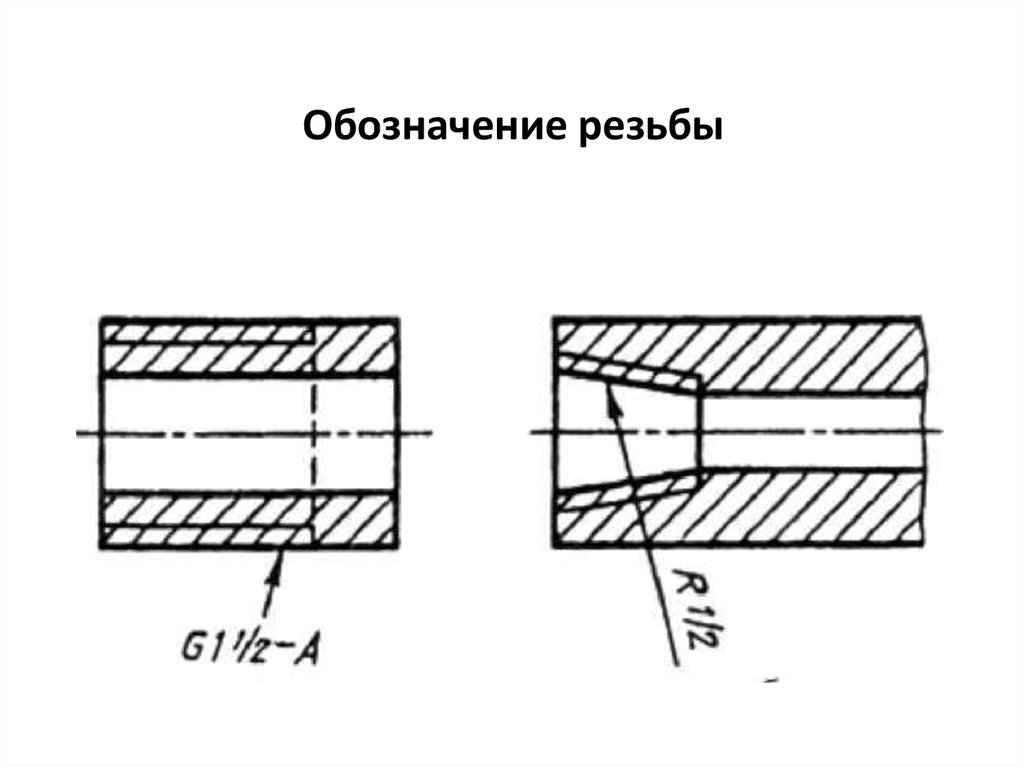 25, нет. 11, стр. 2827–2834, 2011.
25, нет. 11, стр. 2827–2834, 2011.Посмотреть по адресу:
Сайт издателя | Google Scholar
С. А. Нассар и А. Аббуд, «Улучшенная модель жесткости для болтовых соединений», Журнал механического проектирования , том. 131, нет. 12, ID статьи 121001, 2009 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
З. Ю. Цинь, К. К. Хан и Ф. Л. Чу, «Аналитическая модель болтовых соединений дискового барабана и ее применение к динамическому анализу шарнирного ротора», Труды Института инженеров-механиков, часть C: Журнал Машиностроение , том. 228, нет. 2014. Т. 4. С. 646–663.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж. Лю, Х. Оуян, Дж. Пэн и др., «Экспериментальные и численные исследования болтовых соединений, подвергаемых осевому возбуждению», Wear , vol.
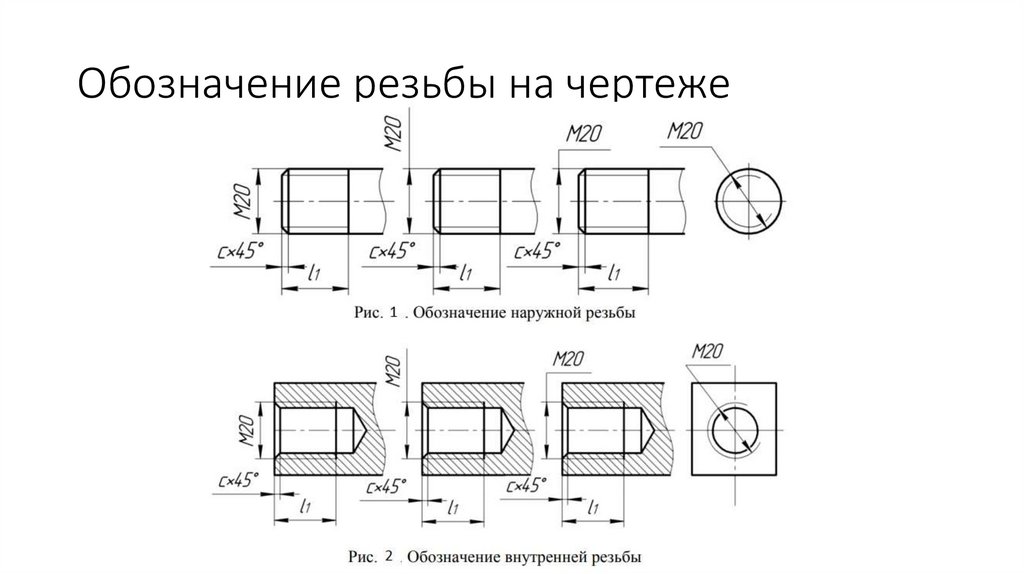


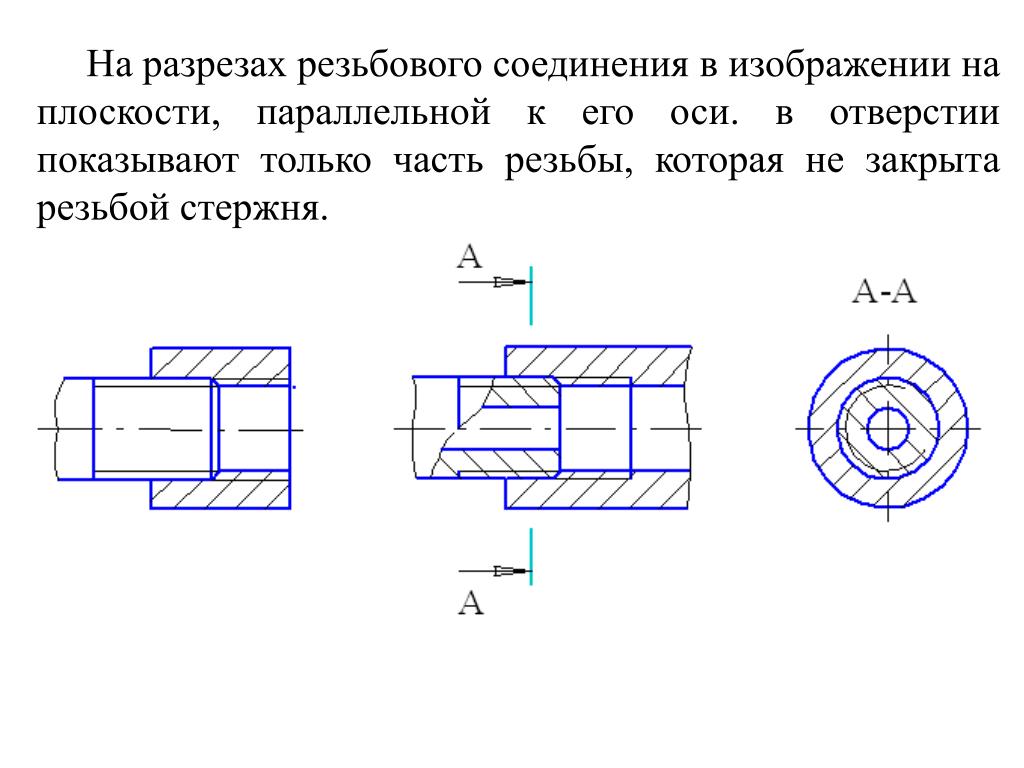 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 Резьбы с мелким шагом применяются в тонкостенных соединениях для увеличения их герметичности, для осуществления регулировки в приборах точной механики и оптики, с целью увеличения сопротивляемости деталей само отвинчиванию. В случае, если диаметры и шаги резьб не могут удовлетворить функциональным и конструктивным требованиям, введен СТ СЭВ 183–75 «Резьба метрическая для приборостроения». Если одному диаметру соответствует несколько значений шагов, то в первую очередь применяются большие шаги. Диаметры и шаги резьб, указанные в скобках, по возможности не применяются.
Резьбы с мелким шагом применяются в тонкостенных соединениях для увеличения их герметичности, для осуществления регулировки в приборах точной механики и оптики, с целью увеличения сопротивляемости деталей само отвинчиванию. В случае, если диаметры и шаги резьб не могут удовлетворить функциональным и конструктивным требованиям, введен СТ СЭВ 183–75 «Резьба метрическая для приборостроения». Если одному диаметру соответствует несколько значений шагов, то в первую очередь применяются большие шаги. Диаметры и шаги резьб, указанные в скобках, по возможности не применяются.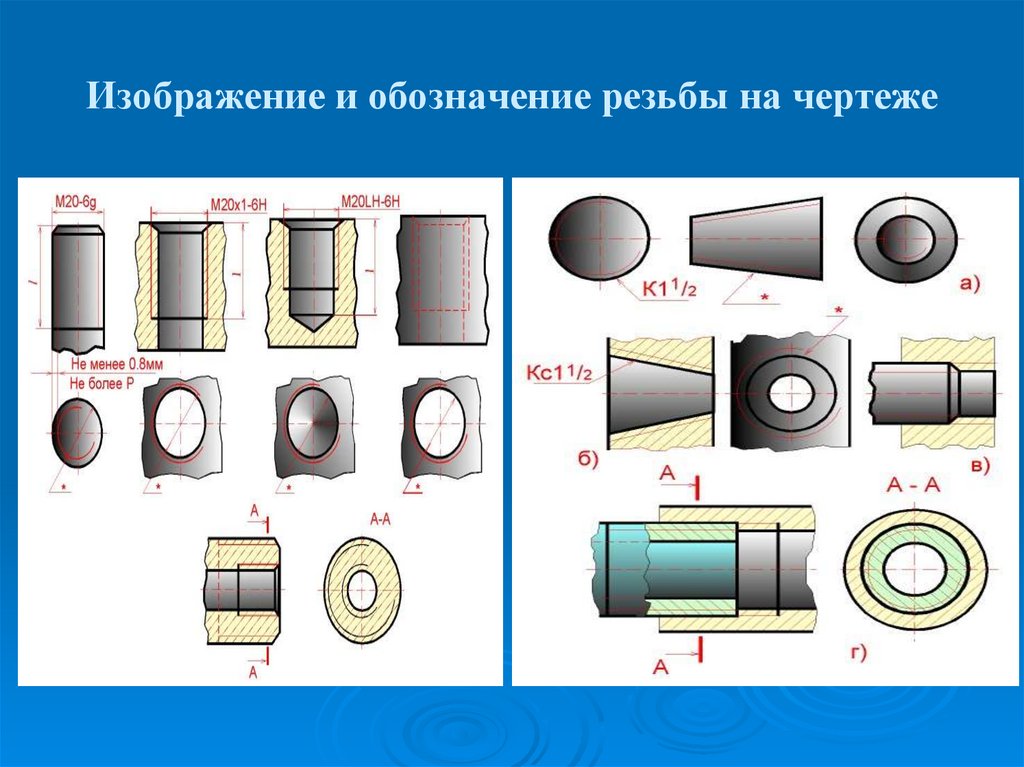 Так, резьба с номинальным диаметром 1 мм имеет диаметр условного прохода 25 мм, а наружный диаметр 33,249 мм.
Так, резьба с номинальным диаметром 1 мм имеет диаметр условного прохода 25 мм, а наружный диаметр 33,249 мм. 207, а). На виде слева не изображают фаску, чтобы иметь возможность нанести внутренний диаметр резьбы сплошной тонкой линией, разомкнутой на одну четверть диаметра окружности. Обратите внимание, что один конец дуги окружности не доводят до центровой приблизительно на 2 мм, а другой ее конец пересекает вторую центровую линию на такую же величину. Конец нарезанной части показывается сплошной основной линией.
207, а). На виде слева не изображают фаску, чтобы иметь возможность нанести внутренний диаметр резьбы сплошной тонкой линией, разомкнутой на одну четверть диаметра окружности. Обратите внимание, что один конец дуги окружности не доводят до центровой приблизительно на 2 мм, а другой ее конец пересекает вторую центровую линию на такую же величину. Конец нарезанной части показывается сплошной основной линией. 207, в). Наружный диаметр проводят сплошной тонкой линией, а внутренний — сплошной основной. Границу резьбы показывают сплошной основной линией.
207, в). Наружный диаметр проводят сплошной тонкой линией, а внутренний — сплошной основной. Границу резьбы показывают сплошной основной линией.
 Служит для разработки других конструкторских документов, монтажных схем, а также для изучения принципов работы изделия при наладке и эксплуатаций.
Служит для разработки других конструкторских документов, монтажных схем, а также для изучения принципов работы изделия при наладке и эксплуатаций.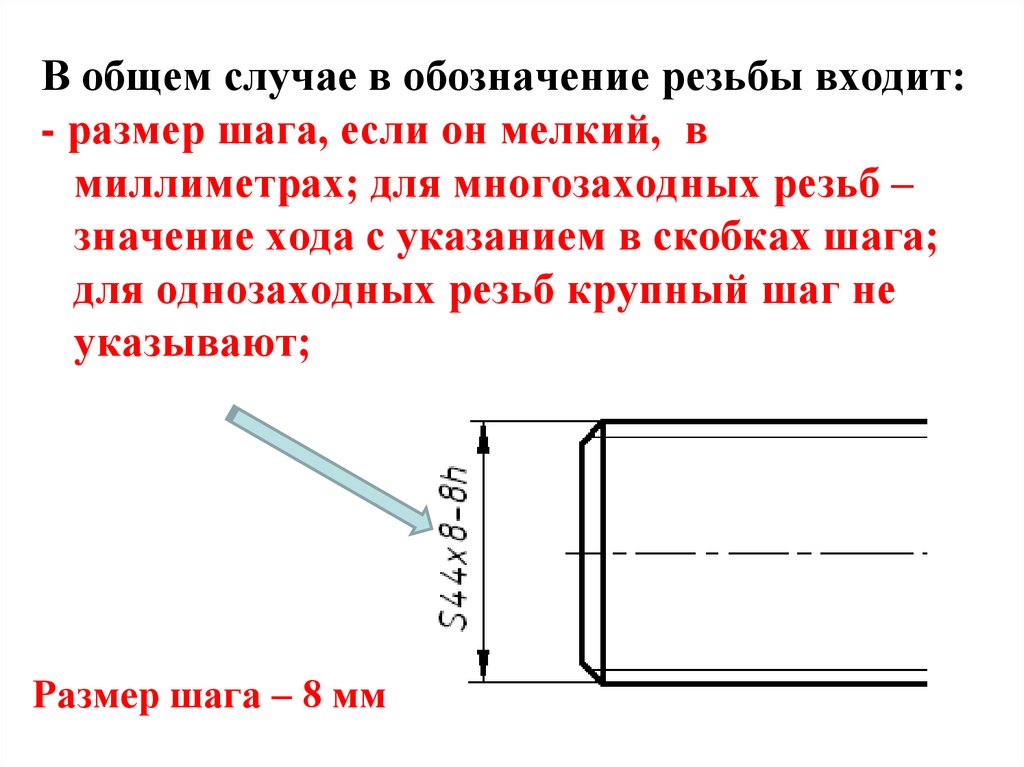
 Обратная связь — 161.97.168.212 (0.009 с.)
Обратная связь — 161.97.168.212 (0.009 с.)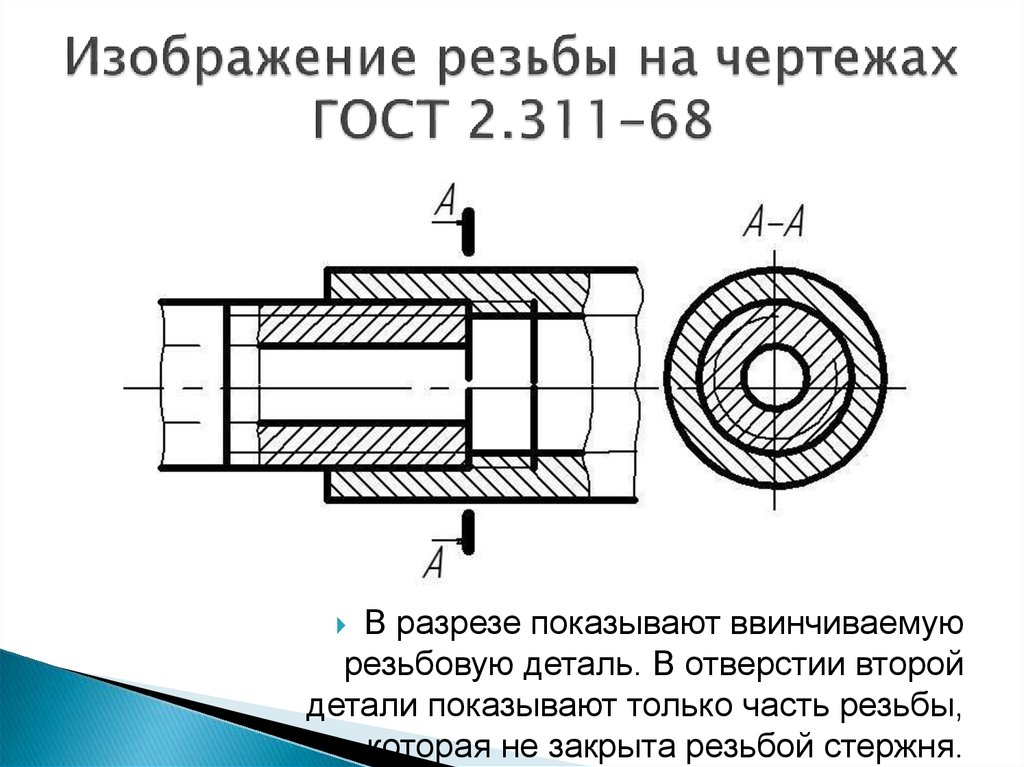 5. Машина
винты
5. Машина
винты 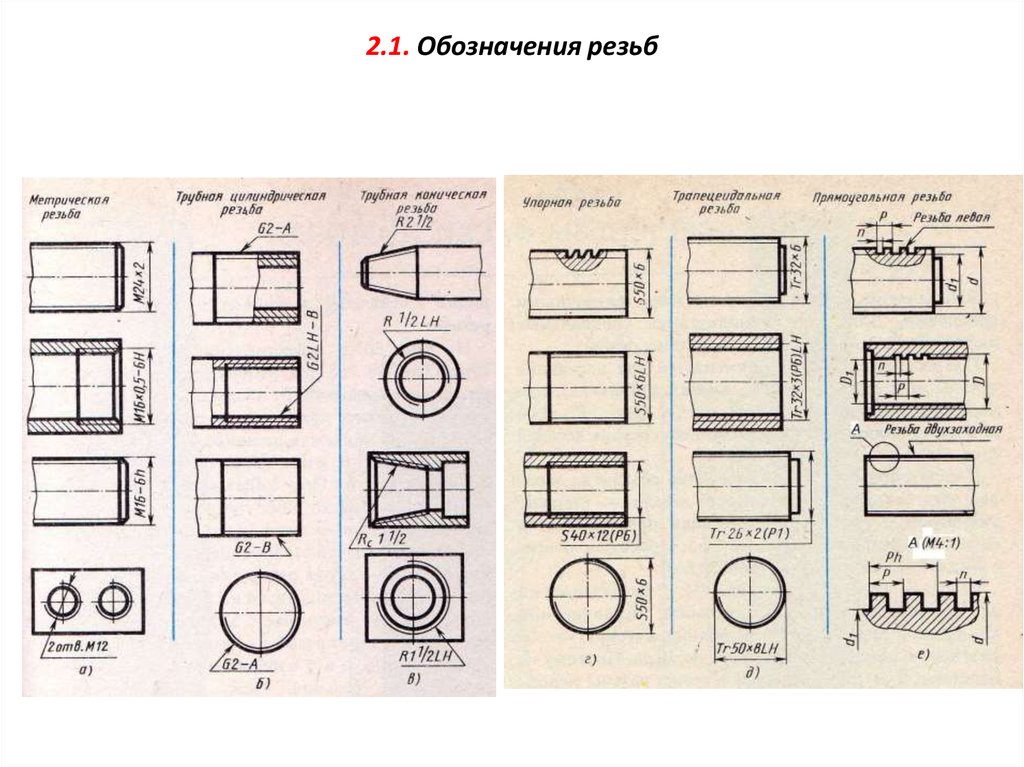 Отношение высоты корневой части резьбы к высоте сечения на среднем диаметре
Отношение высоты корневой части резьбы к высоте сечения на среднем диаметре