Длина стороны вписанного в окружность квадрата: Онлайн калькулятор длины стороны вписанного в круг квадрата. Как узнать длину стороны вписанного в круг квадрата.

Онлайн калькулятор длины стороны вписанного в круг квадрата. Как узнать длину стороны вписанного в круг квадрата.

При помощи нашего калькулятора вы легко сможете узнать длину стороны вписанного в круг квадрата.

Для того что бы найти длину стороны вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.

Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:

1. либо площадь круга, обозначаемая буквой S,
2. либо периметр круга, обозначаемый буквой P,
3. либо радиус круга, обозначаемый буквой R,
4. либо диаметр круга, обозначаемый буквой D.

Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой

c² = 2a²,
Таким образом

a = √c²/2

Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга

D = c

1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

D=2√S/π

2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

D=P/π

3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

D=2R

Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,

c=D

мы можем узнать длину сторон квадрата используя теорему Пифагора

a = √c²/2

Длина окружности, формула как найти длину окружности

Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Как найти длину окружности через диаметр

Хорда — это отрезок, который соединяет две точки окружности.

Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:

l=πd, где

π— число пи — математическая константа, примерно равная 3,14

d — диаметр окружности

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

l=2πr , где

π — число пи, примерно равное 3,14

r — радиус окружности

Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

где:

π — число пи, примерно равное 3,14

S — площадь круга

 

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник:

l=πd, где

π — число пи, примерно равное 3,14 

d — диагональ прямоугольника

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата: 

l=πa, где

π — математическая константа, примерно равная 3,14

a — сторона квадрата

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

где:

π — математическая константа, она примерно равна 3,14

a — первая сторона треугольника

b — вторая сторона треугольника

c — третья сторона треугольника

S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.

Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

где:

π — математическая константа, примерно равная 3,14

S — площадь треугольника

p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.

Формула вычисления длины окружности:

где:

π — математическая константа, примерно равная 3,14

a — сторона многоугольника

N — количество сторон многоугольника

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

l=πd

Подставляем туда известные переменные и получается, что длина окружности равна

l=πd=3,14·5=15,7(см)

Ответ: 15,7 (см)

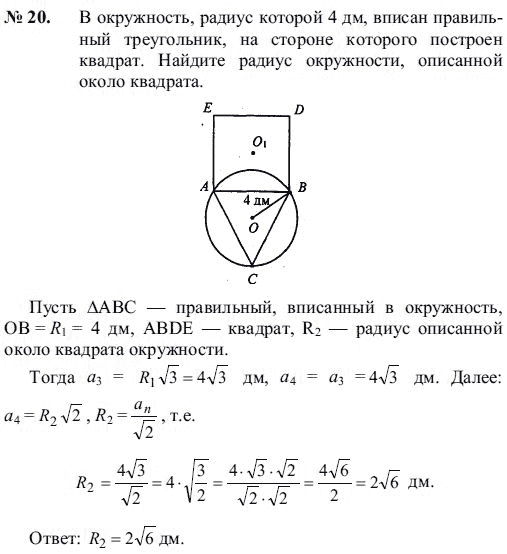
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм

Решение. Радиус окружности равен Подставим туда наши переменные и получим

Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.

Так и сделаем:

l=2πr=2·π·4≈2·3,14·4=25,12(дм)

Ответ: l=25,12(дм)
 

Квадрат вписанный в окружность формулы. Формула нахождения площади круга через радиус. Примеры решения задач

Круг – это видимая совокупность множества точек, которые находятся на одинаковом расстоянии от центра. 2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.

Вычислив значение длины диаметра круга, можно узнать и его радиус, после чего воспользоваться одной их формул определения площади круга.

Площадь сектора круга

Сектор – это часть круга, ограниченная 2 радиусами и дугой между ними. Чтобы узнать его площадь, нужно измерить угол сектора. После этого необходимо составить дробь, в числителе которой будет значение угла сектора, а в знаменателе – 360. Чтобы высчитать площадь сектора, значение, полученное в результате деления дроби, нужно умножить на площадь круга, вычисленную по одной из вышеперечисленных формул.

Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. У квадрата:

• все углы прямые, то есть, равны 90°;
• все стороны, как и углы, равны;
• диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.

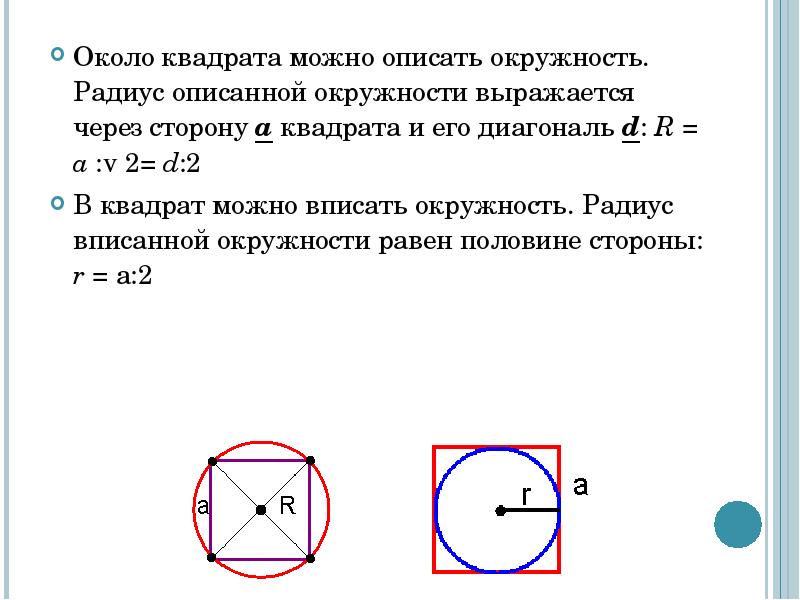
При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD , точку пресечения его диагоналей O . Как видно на рисунке 1, пересечение линий АС и ВD дают равнобедренный треугольник АОВ , в котором стороны АО =ОВ , углы ОАВ =АВО =45°, а угол АОВ =90°. Тогда радиусом вписанной окружности в квадрат будет не что иное, как высота ОЕ полученного равнобедренного треугольника АОВ .

Если предположить, что сторона квадрата равна у , то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:

Объяснение : в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ

. В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°. Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.

Для наглядности приведем численный пример нахождения величины радиуса вписанной окружности в квадрат со стороной равной 13 см. В данном случае значение вписанного радиуса будет равно:

Легко решить и обратную задачу. Предположим, что известен радиус вписанной окружности – 9 см, тогда анализируя пример нахождения величины радиуса вписанной окружности в квадрат, можно найти сторону квадрата:
Находим из этого уравнения неизвестное значение: .

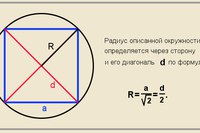
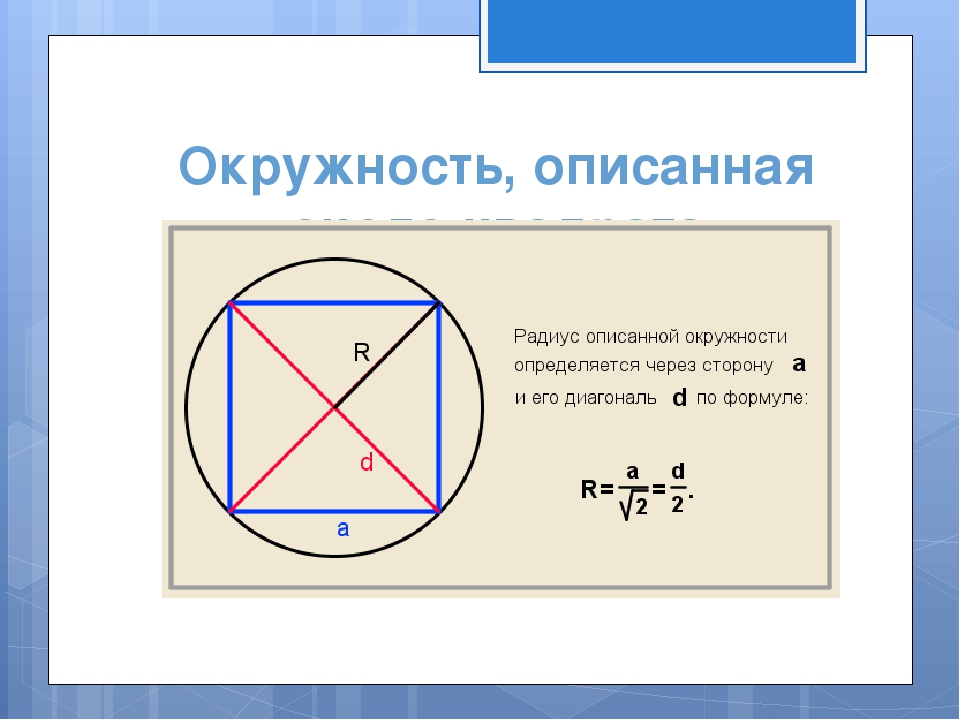
Вокруг квадрата также можно описать окружность. В этом случае каждая вершина фигуры будет касаться окружности. Следующая формула нахождения радиуса описанной окружности около квадрата будет находиться еще проще. В этом случае

R описанной окружности будет равен половине диагонали квадрата. В буквенном виде формула выглядит так (рисунок 2):

Объяснение : после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA .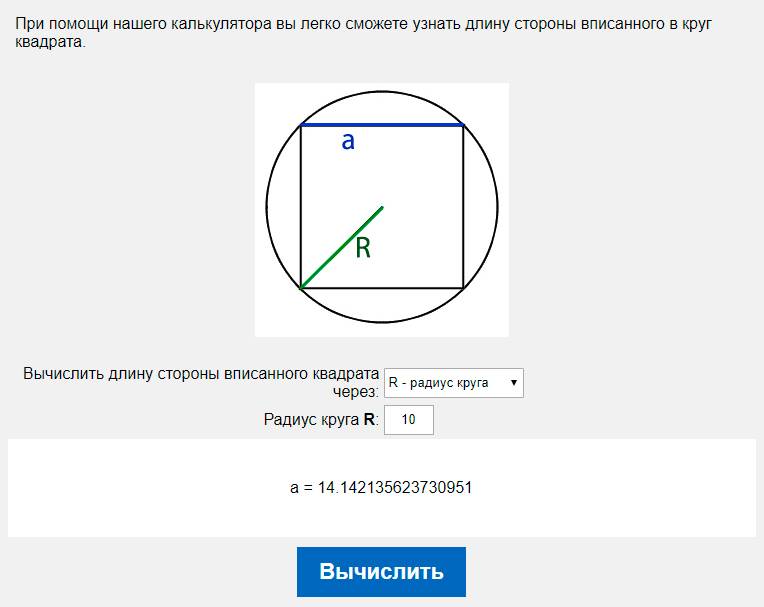 Рассмотрим один из них. В треугольнике CAD :

• угол CDA=90°;
• стороны AD =CD . Признак равнобедренного треугольника;
• угол DAC равен ACD . Они равны по 45°.

Чтобы найти в этом прямоугольном треугольнике гипотенузу АС , необходимо воспользоваться теоремой Пифагора:
, отсюда
Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид:

Поскольку AD =CD , а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:

Численный пример нахождения величины радиуса описанной окружности около квадрата будет таким.
Предположим, что диагональ квадрата равна , тогда:

Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.

Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.

Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.

Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.

Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.

Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.

Формула нахождения площади круга через радиус:

Примеры решения заданий по нахождению S-площади круга через R-радиус:

Задача: Найдите площадь окружности, если ее радиус равен 7 см.

Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².

Ответ: Площадь окружности равна 153,86 см².

Формула нахождения S-площади круга через D-диаметр:

Примеры решения заданий по нахождению S, если известен D:

————————————————————————————————————————-

Задача: Найдите S круга, если его D равен 10 см.

Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².

Ответ: Площадь плоской круглой фигуры равна 78,5 см².

Нахождение S круга, если известна длина окружности:

Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.

Рассмотрим решение на примере задачи:

———————————————————————————————————————-

Задача: Найдите площадь круга, если известна длина окружности L — 12 см.

Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.

Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².

Ответ: Площадь круга равна 11,46 см².

Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.

Формула нахождения площади круга, вписанного в квадрат:

Примеры решения задач по нахождению площади круга, вписанного в квадрат:

———————————————————————————————————————

Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.

Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².

Ответ: Площадь плоской круглой фигуры равна 28,26 см².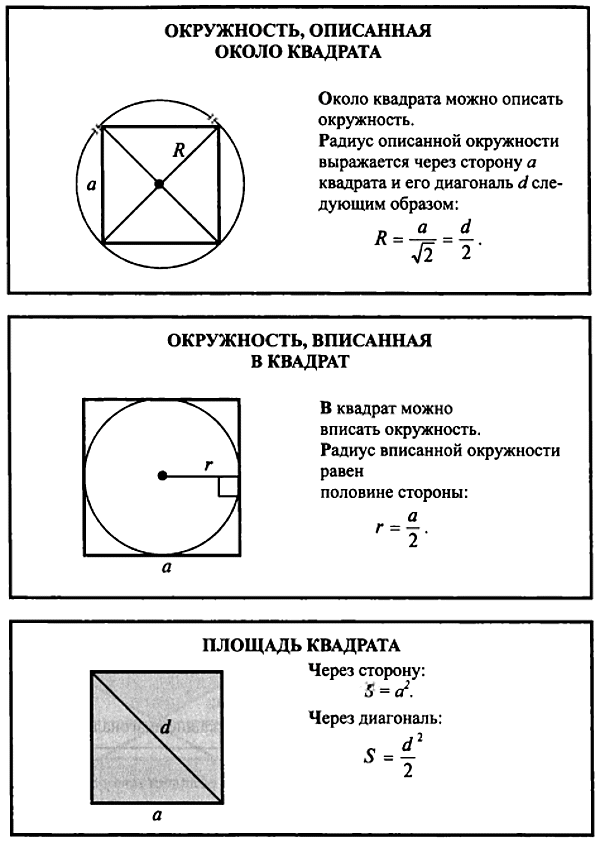

————————————————————————————————————————

Задача №2 : Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.

Решайте так : Сначала найдем R=a/2=4/2=2 см.

Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².

Ответ: Площадь плоской круглой фигуры равна 12,56 см².

Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.

Формула нахождения S круга, описанного около квадратной фигуры:

Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:

Задача

Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.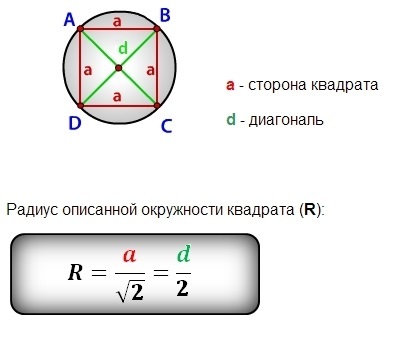

Формула нахождения площади круга, вписанного в равнобедренный треугольник:

Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².

Формула нахождения площади круга, вписанного в прямоугольный треугольник:

Примеры решения заданий:

Задача №1

Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²

Задача №2

Решение:

Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.

Задача №3

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач

Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.

Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:

Примеры решения задач:

Вот еще пример решения задачи с использованием формулы Герона.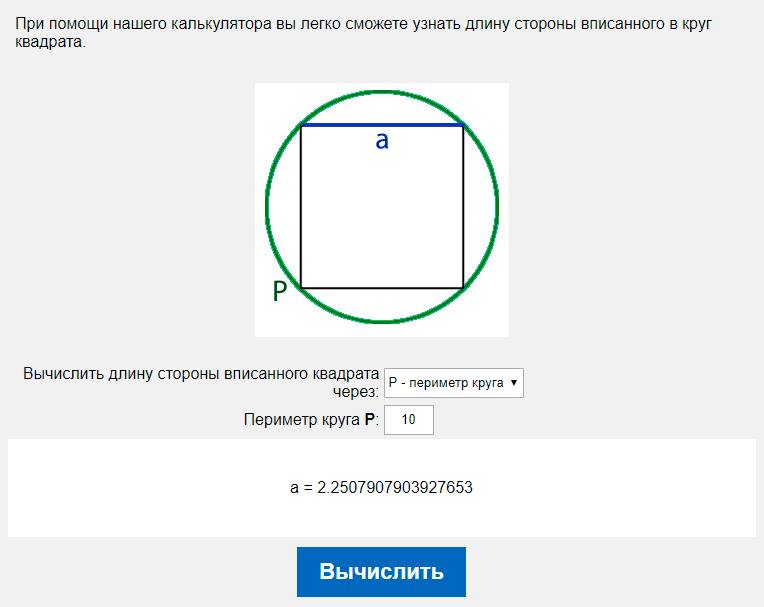

Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач

У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.

Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.

Для решения этой задачи нужно использовать такие формулы:

Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:

Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.

Примеры решения задач:

Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º.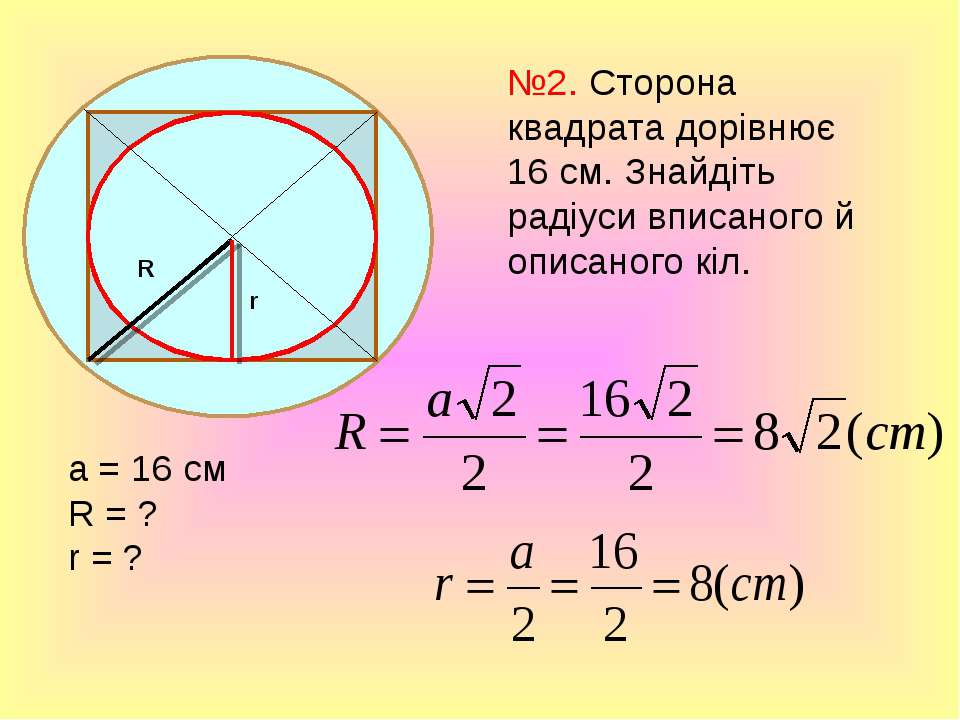 Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:

Примеры решения задач:

Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.

Ответ: Радиус равен 6.

В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.

Видео: Математика | Вычисление площадей круга и его частей

Кругом называется часть плоскости, ограниченная окружностью. Основным показателем и для окружности, и для круга является радиус. Если он задан, площадь круга можно вычислить по основной формуле S=πR2, где S – площадь круга, R – радиус окружности, ограничивающей круг, а π – константа, равная 3,14. В условиях задачи может быть дана длина окружности. Она равна L=2πR. В этом случае сначала необходимо вычислить радиус, разделив заданную величину L на 2π, то есть воспользоваться формулой R=L/2π.

По сторонам вписанного четырехугольника

В окружность, ограничивающую круг, может быть вписан четырехугольник, сумма противолежащих углов которого составляет 180°, то есть это квадрат или прямоугольник. В этом случае диаметр описанной вокруг четырехугольника окружности является одновременно диагональю. Если в условиях заданы размеры сторон четырехугольника, найти эту диагональ не составит особого труда, воспользовавшись теоремой Пифагора. Диагональ делит квадрат или прямоугольник на два прямоугольных треугольника, то есть является гипотенузой каждого из этих треугольников. Соответственно, найти ее можно, сложив квадраты сторон четырехугольника, то есть по формуле d2=a2+b2. Чтобы найти площадь круга, даже не нужно из полученного результата извлекать квадратный корень, поскольку R=d/2. Чтобы найти квадрат радиуса, достаточно квадрат диаметра разделить на 4.

По параметрам вписанного в окружность треугольника

Способ решения этого варианта задачи зависит от того, какой треугольник вписан и какие его параметры заданы. Если треугольник прямоугольны, алгоритм решения будет таким же, как для квадрата или , поскольку сторона, противолежащая прямому углу, всегда является диаметром описанной окружности. Если даны размеры катетов, возведите каждый из них в квадрат и найдите сумму, а затем полученный результат разделите на 4 и умножьте на число π. Если треугольник равносторонний, придется выполнить несколько дополнительных построений, чтобы в итоге получились прямоугольные треугольники, параметры которых вам известны. Например, в окружность с центром О вписан равносторонний треугольник АВС, сторона которого вам задана. Проведите высоты AN, ВM и СQ. Рассмотрите, например, прямоугольный треугольник AQO. Вам известна его гипотенуза AQ, которая равна половине стороны исходного треугольника, а также все углы, так что найти длину отрезка AQ, который одновременно является радиусом круга, площадь которого вам надо найти, можно по теореме синусов или косинусов.

Читайте статью, чтобы знать, как находить площадь квадрата разными способами.

Квадрат — это равносторонний прямоугольник. У данного правильного и плоского четырехугольника равенство во всех сторонах, углах и диагоналях. Из-за того что существует такое равенство, формула для вычисления площади и других характеристик, немного видоизменяется по сравнению с иными математическими фигурами. Но это не делает задачи слишком сложными. Давайте разберем все формулы и решения задач в этой статье.

Площадь S прямого и квадратного угольников вычисляется по формуле: a умножить на b . Но так как у квадрата полное равенство сторон, то его площадь будет равна: S=(a) во второй степени . Как узнать величину стороны квадрата, зная его площадь?

• Если известна площадь квадратного угольника, то сторону находим путем исчисления площади из-под квадратного корня.
• К примеру, площадь угольника равна 49, то чему равняется сторона?
• 49=(а) во второй степени . Решение: а=корень из 49=7. Ответ: 7 .

Если нужно найти сторону квадратного угольника, площадь которого состоит слишком длинного числа, тогда воспользуйтесь калькулятором. Наберите сначала число площади, а потом нажмите знак корня на клавиатуре калькулятора. Получившееся число и будет ответом.

В этом примере будем использовать теорему Пифагора. У квадрата все стороны равны, а диагональ d мы будем рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а . Теперь находим диагональ квадрата, если известна его площадь:

• Чтобы не расписывать всю теорему Пифагора будем решать по второму варианту: d=a√2, где а — это сторона квадрата.
• Итак, нам известна площадь квадрата, например, она равна 64. Значит одна сторона а=√64=8.
• Получается d=8√2 . Корень из 2 не получается целым числом, поэтому в ответе можно написать именно так: d=8√2 . Но, если хочется вычислить значение, тогда воспользуйтесь калькулятором: √2= 1,41421356237 и умножьте на 8, получается 11, 3137084 .

Важно: Обычно в математике не оставляют в ответе цифры с большим количеством чисел после запятой. Нужно округлять или оставить с корнем. Поэтому ответ на нахождение диагонали, если площадь равна 64 будет таким: d=8√2 .

Формула нахождения площади квадрата через диагональ простая:

Теперь напишем решение по нахождению площади квадрата через диагональ:

• Диагональ d=8.
• 8 в квадрате равняется 64.
• 64 разделить на 2 равно 32.
• Площадь квадрата равна 32.

Совет: У этой задачи есть еще одно решение через теорему Пифагора, но оно более сложное. Поэтому используйте решение, которое мы рассмотрели.

Периметр квадратного угольника P — это сумма всех сторон. Чтобы найти его площадь, зная его периметр, нужно сначала вычислить сторону квадратного угольника. Решение:

• Допустим периметр равен 24. Делим 24 на 4 стороны, получается 6 — это одна сторона.
• Теперь используем формулу нахождения площади, зная чему равна сторона квадратного угольника: S=а в квадрате, S=6 в квадрате=36 .
• Ответ: 36

Как видите, зная периметр квадрата, просто найти его площадь.

Радиус R — это половина диагонали квадрата, вписанного в окружность. Теперь можем найти диагональ по формуле: d=2*R . Далее находим площадь квадрата вписанного в окружность с заданным радиусом:

• Диагональ равна 2 умножить на радиус. Например радиус равен 5, тогда диагональ равна 2*5=10 .
• Выше было описано, как находить площадь квадрата, если известна диагональ: S=диагональ в квадрате разделить на 2. S=10*10 и разделить на 2=50.
• Ответ — 50 .

Эта задача немного сложнее, но тоже легко решаемая, если знать все формулы.

На картинке видно, что радиус вписанной окружности равен половине стороны. Сторона находится по формуле обратной той, которая изображена на картинке: а=2*r . Потом уже находим площадь квадрата описанного около окружности с заданным радиусом по формуле S=а в квадрате . Решение:

• Допустим, радиус равен 7. Сторона квадрата а равна 2*7=14.
• S=14 в квадрате=196 .

Если понять суть решения подобных задач, то можно решать их быстро и просто. Давайте рассмотрим еще несколько примеров.

Примеры решения задач на тему «Площадь квадрата»

Чтобы закрепить пройденный материал и запомнить все формулы, необходимо решить несколько примеров задач на тему «Площадь квадрата». Начинаем с простой задачи и движемся к решению более сложных: Примеры решения сложных задач на тему «Площадь квадрата»

Теперь вы знаете, как пользоваться формулой площади квадрата, а значит, вам любая задача под силу. Успехов в дальнейшем обучении!

Видео: Вычисление площади квадрата

Радиусы описанной и вписанной окружностей в квадрат

Окружность вписанная в квадрат

Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. У квадрата:

• все углы прямые, то есть, равны 90°;
• все стороны, как и углы, равны;
• диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.

При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD, точку пресечения его диагоналей O. Как видно на рисунке 1, пересечение линий АС и ВD дают равнобедренный треугольник АОВ, в котором стороны АО=ОВ, углы ОАВ=АВО=45°, а угол АОВ=90°. Тогда радиусом вписанной окружности в квадрат будет не что иное, как высота ОЕ полученного равнобедренного треугольника АОВ.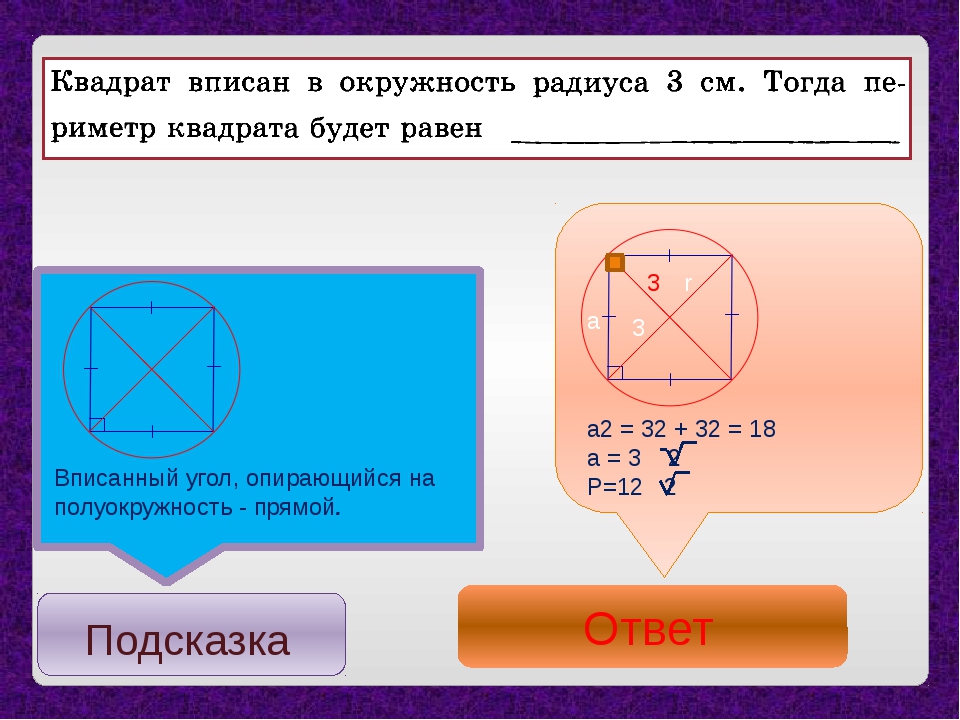

Если предположить, что сторона квадрата равна у, то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:

Объяснение: в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ. В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°. Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.

Для наглядности приведем численный пример нахождения величины радиуса вписанной окружности в квадрат со стороной равной 13 см. В данном случае значение вписанного радиуса будет равно:

Легко решить и обратную задачу. Предположим, что известен радиус вписанной окружности – 9 см, тогда анализируя пример нахождения величины радиуса вписанной окружности в квадрат, можно найти сторону квадрата:
Находим из этого уравнения неизвестное значение: .

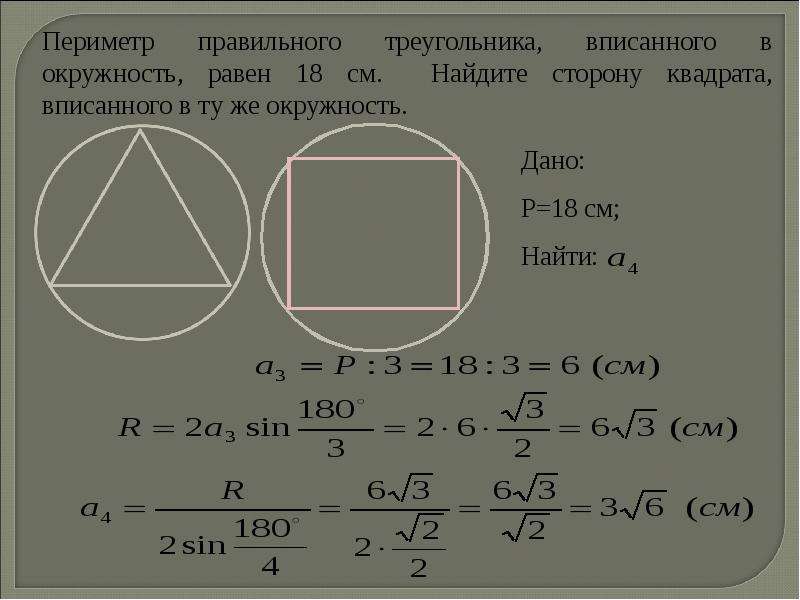
Окружность описанная около квадрата

Вокруг квадрата также можно описать окружность. В этом случае каждая вершина фигуры будет касаться окружности. Следующая формула нахождения радиуса описанной окружности около квадрата будет находиться еще проще. В этом случае R описанной окружности будет равен половине диагонали квадрата. В буквенном виде формула выглядит так (рисунок 2):

Объяснение: после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA. Рассмотрим один из них. В треугольнике CAD:

• угол CDA=90°;
• стороны AD=CD. Признак равнобедренного треугольника;
• угол DAC равен ACD. Они равны по 45°.

Чтобы найти в этом прямоугольном треугольнике гипотенузу АС, необходимо воспользоваться теоремой Пифагора:
, отсюда
Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид:

Поскольку AD=CD, а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:

Численный пример нахождения величины радиуса описанной окружности около квадрата будет таким.
Предположим, что диагональ квадрата равна , тогда:

Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.

Что больше: периметр квадрата или длина окружности?

Вот такая задача была предложена на экзамене ученикам старшей школы (не у нас, не знаю точно, где, страна англоязычная, видимо).

Пусть точка — середина стороны квадрата . Пусть окружность проходит через точки и , как показано на рисунке.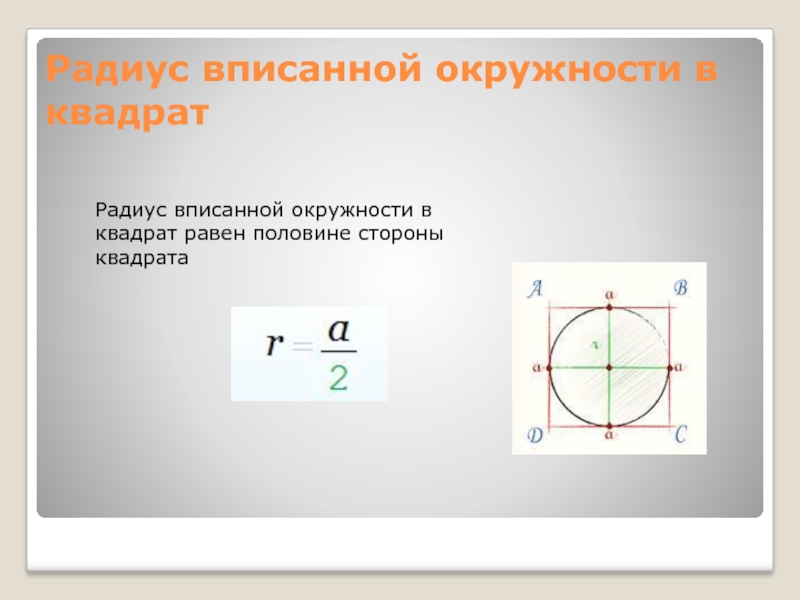 Что больше: периметр квадрата или длина окружности?

Конечно, есть несколько способов решения этой задачи. Один из них следующий: предположим, что длина стороны квадрата равна . Введем декартову прямоугольную систему координат. Зная координаты точек , и , выразим координаты центра окружности. Затем найдем радиус окружности. И наконец, с помощью найденного радиуса найдем длину окружности и сравним ее с периметром квадрата.

Проблема здесь в том, что предполагается, что предложенная задача очень простая. Она не предполагает знания школьником формулы центра окружности, проходящей через три данные точки. Возникает вопрос: существует ли простой путь решить задачу без знания каких-либо сложных геометрических формул?

Задача найдена здесь:

http://math.stackexchange.com/questions/1188845/does-the-square-or-the-circle-have-the-greater-perimeter-a-surprisingly-hard-pr?utm_campaign=snsdemo&utm_medium=twitter&utm_source=snsanalytics.

Там же в комментариях предлагается много вариантов ее решения. Однако ни один из них мне почему-то не понравился. Они или требуют некой догадки, которая может и не прийти в голову обычному школьнику, или слишком длинные.

Приведу мое решение. На всякий случай, скрываю его, вдруг кто-то захочет сам порешать?

Показать решение

Пусть сторона квадрата равна . Треугольник равнобедренный, длины его сторон равны

   

Очевидно, что площадь треугольника равна половине площади квадрата, т.е. .

Найдем радиус описанной вокруг этого треугольника окружности по формуле , где — стороны треугольника, — его площадь:

   

Осталось сравнить длину окружности и периметр квадрата . Поскольку , то периметр квадрата больше длины окружности.

Вопрос только в том, считается ли формула, выражающая радиус описанной окружности через стороны треугольника и его площадь сложной Почему-то мне кажется, наши школьники до сих пор ее знают. Может, конечно, я ошибаюсь…

Вы можете предлагать свои решения. Вдруг найдется еще более простое и короткое?

Как найти радиус окружности — Лайфхакер

Выбирайте формулу в зависимости от известных величин.

Через площадь круга

1. Разделите площадь круга на число пи.
2. Найдите корень из результата.

Иллюстрация: Лайфхакер

• R — искомый радиус окружности.
• S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
• π (пи) — константа, равная 3,14.

Сейчас читают 🔥

Через длину окружности

1. Умножьте число пи на два.
2. Разделите длину окружности на результат.

Иллюстрация: Лайфхакер

• R — искомый радиус окружности.
• P — длина окружности (периметр круга).
• π (пи) — константа, равная 3,14.

Через диаметр окружности

Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.

Иллюстрация: Лайфхакер

• R — искомый радиус окружности.
• D — диаметр.

Через диагональ вписанного прямоугольника

Диагональ прямоугольника является диаметром окружности, в которую он вписан.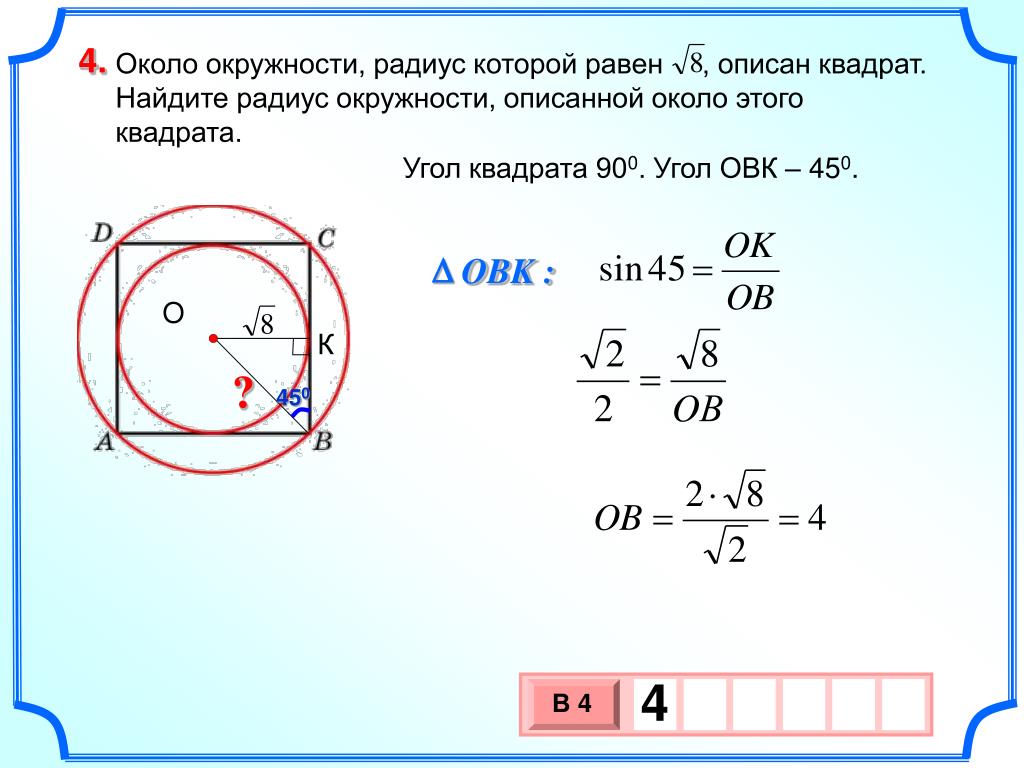 А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.

Иллюстрация: Лайфхакер

• R — искомый радиус окружности.
• d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
• a, b — стороны вписанного прямоугольника.

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

Иллюстрация: Лайфхакер

• r — искомый радиус окружности.
• a — сторона описанного квадрата.

Через стороны и площадь вписанного треугольника

1. Перемножьте три стороны треугольника.
2. Разделите результат на четыре площади треугольника.

Иллюстрация: Лайфхакер

Через площадь и полупериметр описанного треугольника

Разделите площадь описанного треугольника на его полупериметр.

Иллюстрация: Лайфхакер

• r — искомый радиус окружности.
• S — площадь треугольника.
• p — полупериметр треугольника (равен половине от суммы всех сторон).

Через площадь сектора и его центральный угол

1. Умножьте площадь сектора на 360 градусов.
2. Разделите результат на произведение пи и центрального угла.
3. Найдите корень из полученного числа.

Иллюстрация: Лайфхакер

• R — искомый радиус окружности.
• S — площадь сектора круга.
• α — центральный угол.
• π (пи) — константа, равная 3,14.

Через сторону вписанного правильного многоугольника

1. Разделите 180 градусов на количество сторон многоугольника.
2. Найдите синус полученного числа.
3. Умножьте результат на два.
4. Разделите сторону многоугольника на результат всех предыдущих действий.

Иллюстрация: Лайфхакер

• R — искомый радиус окружности.
• a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
• N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.

Читайте также 📐✂️📌

Как найти длину окружности? Ответ на webmath.ru

Остались вопросы?

Здесь вы найдете ответы.

Каким образом можно вычислить длину окружности при условии, что площадь круга (S) является известной величиной?

Площадь круга (S) рассчитывается путем умножения числа Пи на длину его радиуса (R), возведенную в квадратную степень (S = ПR²). Из указанного равенства можно выразить радиус:

R² = S/ П

Если избавиться от квадратной степени, то получится:

R = √(S/П)

Длина окружности (L) рассчитывается путем умножения числа Пи на длину радиуса, и последующего умножения на два полученного в результате числа:

L = 2ПR

Если R = √(S/П), то L = 2П*√(S/П)

Каким образом можно найти длину окружности, диаметр которой составляет 2 см?

Длина окружности (L) представляет собой число, которое получено в результате умножения числа Пи на диаметр данной окружности:

L = П*D

В конкретном случае:

L = 3,14*2 = 6,28 см.

Ответ: Длина окружности с диаметром 2 см составляет 6,28 см.

Дан квадрат, вокруг которого описана окружность. Ее длина составляет 12 Пи см. Как можно найти длину окружности, вписанной в этот же квадрат?

Известно, что длина окружности (L) рассчитывается путем умножения на два произведения числа Пи и длины ее радиуса (R). Формула выглядит так:

2ПиR

Из данной формулы можно выразить радиус

R = 12пи/2пи = 6 см

Радиус окружности, описанной около квадрата, равен 6 см.

Теперь можно вычислить сторону квадрата, вокруг которого описана данная окружность. Ее длина составляет R корней из 2:

а = 6 корней из 2.

Рассчитываем длину малого радиуса (r), который равен половине длины стороны квадрата:

r = а/2 = 6 корней из 2/2 = 3 корней из 2.

Длина окружности, вписанной в квадрат, рассчитывается по той же формуле:

L = 6 корней из 2 Пи.

Каким образом можно вычислить длину окружности, а также найти ее площадь, при условии, что радиус этой окружности равен 30 см?

Радиус окружности, равный 30 см, обозначается как R.

Площадь окружности можно найти, умножив число Пи на квадрат длины ее радиуса:

S = πR²

Подставим в формулу известные величины:

S = π*30² = 900π см. кв.

Длина окружности обозначается как С и рассчитывается путем умножения на 2 произведения числа Пи и ее радиуса:

C = 2πR

Снова подставляем в формулу величины, которые известны:

C = 2π*30 = 60π см

Ответ: Площадь окружности равна 900π см², а ее длина составляет 60π см.

Дана окружность, в которую вписан правильный треугольник. Его площадь составляет 12√3 см кв. Как можно вычислить длину окружности в данном случае?

По условию задачи известно, что треугольник является правильным, что означает равенство всех его трех сторон. 2 * √3 ÷ 4

Зная площадь, мы получаем возможность вычислить длину стороны а. Она будет равна ± √48. Учитывая то, что сторона не может быть отрицательной величиной, можно говорить о том, что сторона а равна √48.

После того как длина стороны стала известна, можно приступить к вычислению площади описанной и вписанной окружности. Для этого не достает еще одного элемента – длины радиуса.

Радиус описанной окружности (R) равен длине стороны треугольника, разделенной на √3:

R = √48 ÷ √3 = 4 см.

Радиус вписанной окружности (r) можно получить, разделив на 2 радиус описанной окружности:

r = 4/2 = 2 см.

Вычисленные длины радиусов вписанной и описанной окружностей позволяют определить ее длину ℓ, которая равна произведению числа Пи и радиуса окружности, умноженному на 2:

ℓ = 2πR

В нашем случае длина описанной окружности рассчитывается как:

ℓ= 2πR = 2π4 = 8π

Длина вписанной окружности будет составлять:

ℓ= 2πR = 2π2 = 4π

Известно, что радиус окружности равен 12 см.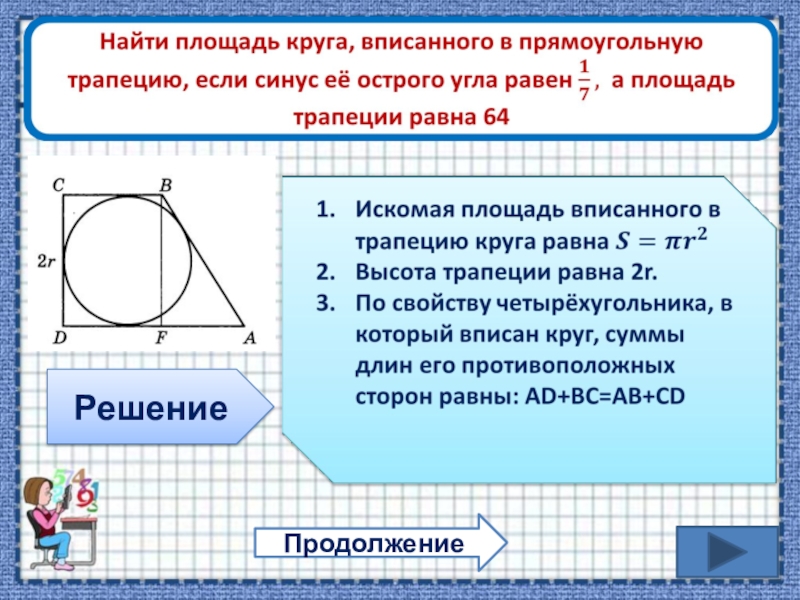 Как вычислить ее площадь и длину при Пи=3,14?

В условии задачи говорится о том, что радиус окружности R равен 12 см. Ее длина может быть вычислена посредством умножения на 2 произведения длины радиуса и числа Пи:

C=2πR

Известно, что число Пи – это константа, равная 3,14. Тогда длина окружности (С)высчитывается следующим образом:

C=2*3*12=72 см

Площадь окружности можно найти, умножив число Пи на длину ее радиуса, возведенную в квадратную степень:

S=πR²=3,14*12²=3,14*144=452,16 см кв.

Как можно вычислить радиус окружности и ее диаметр, если известно, что ее длина составляет 20 Пи см?

По условию задачи длина окружности равна 20 Пи см. Зная формулу, по которой вычисляется длина окружности, можно записать следующее равенство:

2Пи = 2ПиR

Можно сократить Пи в обеих частях записанного равенства, в результате чего получится, что:

2R = 20

Теперь высчитаем, чему равна длина радиуса окружности:

R = 20/2 = 10 см.

Длина диаметра равна длине радиуса, умноженной на 2:

D = R*2 = 10*2 = 20 cм.

Длина дуги окружности составляет 6Пи см, при этом ее градусная мера равна 120 градусов. Каким образом можно вычислить радиус окружности?

Полная градусная мера любой окружности равна 360 градусов. В случае, описанном в задании, градусная мера окружности составляет 120 градусов, что равно 1/3 части 360 градусов. Это позволяет сделать вывод о том, что длина окружности (L) может быть рассчитана следующим образом:

L = 6Пи * 3 = 18Пи

Формула, по которой вычисляется длина окружности, выглядит так:

L =2пR

Из данной формулы можно выразить радиус (R):

R = L/2Пи

В заданном случае длина радиуса будет равна:

18Пи/2Пи = 9 см.

Как на радиус окружности повлияет увеличение ее длины на 9,42 см?

Обозначим прежнюю длину окружности как L, а новую – как L₁. Тогда можно записать следующее равенство:

L₁ — L = 9,42 см

Прежний радиус окружности примем за R, а новый ее радиус, который получится в результате увеличения длины, обозначим как R₁. Для того чтобы вычислить ее значение, следует сначала записать формулу, по которой вычисляется прежняя длина данной окружности:

L = 2πR

Тогда формула для вычисления новой длины окружности будет иметь такой вид:

L + 9,42 = 2πR₁

Отнимем от новой длины старую, и в итоге получим:

2πR₁ — 2πR = 9,42 см.

Перенесем 2Пи из левой части равенства в правую:

R₁ — R = 9,42 : 2π = 1,5 см.

Ответ: В результате увеличения длины окружности на 9,42 см ее радиус станет больше на 1,5 см.

Как можно вычислить радиус окружности, вписанной в правильный треугольник, зная то, что площадь данного треугольника превышает площадь окружности на 27√3-9π?

Радиус окружности, которая вписана в правильный треугольник, обозначим r. Ее площадь (S) является произведением числа Пи и квадрата ее радиуса:

S = πr²

В случае треугольника, все стороны которого одинаковы, радиус вписанной в него окружности равен третьей части высоты, являющейся также и медианой.

Площадь правильного треугольника рассчитывается так:

Sтр = (1/2)*(2r/tg30)*3r = (1/2)*(2r√3)*3r = 3√3r².

Согласно условию задачи 3√3r² = πr² + 27√3 — 9π.

Перенесем πr² из левой части равенства в правую, изменив его знак на противоположный:

3√3r² — πr² = 27√3 — 9π

Вынесем в правой части равенства r² за скобки. То же самое сделаем с числом 9 в левой части равенства:

r²(3√3 — π) = 9(3√3 — π)

Сокращаем в обеих частях одинаковый множитель (3√3 — π) и получаем:

r² = 9

Таким образом, радиус окружности равен корню квадратному из 9:

r =3 см.

Дано две окружности, радиус одной из которых пятикратно превышает радиус другой.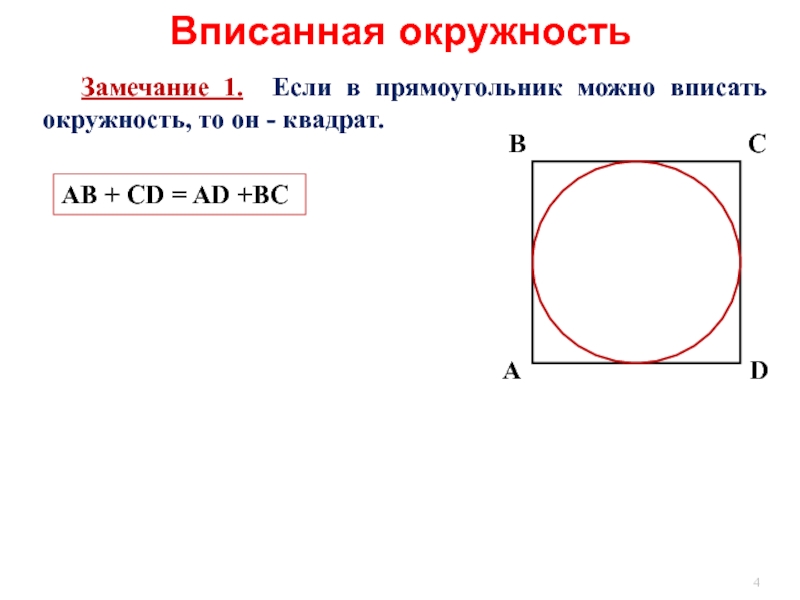 Каким образом вычислить радиус каждой из этих окружностей, если известно, что диаметр второй из окружностей на 240 мм меньше, чем диаметр первой?

Обозначим радиус второй окружности буквой х. В данном случае радиус первой окружности нужно обозначить как 5х. Известно, что разница между длинами диаметров двух окружностей равна 240 мм. На основании этого можно составить следующее равенство:

5х-х=240:2, что равно 4х=120

Теперь можно найти значение х:

х=120:4=30 мм.

Таким образом, радиус второй окружности равен 30 мм. Это позволяет вычислить радиус первой окружности, который в 5 раз больше радиуса второй из них:

30*5=150 мм.

Как можно высчитать радиус окружности, когда известна ее градусная мера и длина дуги?

Длина дуги обозначена как L. В качестве обозначения ее градусной меры используется α. Через R обозначена длина радиуса данной окружности. Формула расчета длины дуги выглядит так:

L = πR · α / 180°

Это же равенство может быть переписано следующим образом:

πR · α = L · 180°

Отсюда выведем радиус:

R = L · 180° / (π·α).

Как высчитать радиус окружности, длина дуги которой составляет 3,14 см, а ее градусная мера равна 18 градусам?

Длина окружности (L) равна произведению числа Пи и радиуса, которое умножено на 2:

L = 2Пиr

Согласно заданию, длина дуги равна 3,14, что равно значению константы Пи.

Дуга способна поместиться в длине окружности 2 пи r/пи =2 r раз

Подставив в равенство значения, которые известны, мы получим:

360:18=20 раз

Длина окружности будет равна:

3,14*20=20Пи

2Пиr = 20Пи

Сократим 2Пи в каждой из частей равенства и получим, что:

r=10 см.

Площадь круга составляет 169Пи см. Чему равна длина окружности в данном случае?

Для решения поставленной задачи следует записать формулу расчета площади круга:

S=πr2

Эта величина указана в задании, и составляет 169Пи. Это значит, что:

πr2 = 169π

Можно сократить одинаковый множитель Пи в обеих частях равенства:

r2= 169

r = √169 = 13 см.

Длина окружности обозначена С. Она считается по следующей формуле:

С = 2πr

Длина радиуса уже известна, и ее можно подставить в формулу расчета длины окружности:

С = 2* π*13 = 26π см.

В окружность вписан квадрат площадью 36 дм кв. Чему в этом случае будет равна площадь круга и длина окружности?

Известно, что площадь круга представляет собой величину, равную длине стороны этого квадрата, возведенной во вторую степень Sкв = а². Это значит, что в данном случае а² = 36 дм. Для того чтобы найти значение а, нужно извлечь квадратный корень из 36:

а = √36 = 6 дм.

Длина диагонали (d) квадрата считается по приведенной ниже формуле:

d = a√2 = 6√2 дм.

Радиус (R)окружности, которая описана около квадрата, равен половине длины ее диагонали:

R = d/2 = 3√2 дм.

Площадь круга можно посчитать, умножив число Пи на квадрат его радиуса:

S = πR² = π · (3√2)² = 18π дм. кв.

Длина окружности рассчитывается посредством умножения на два числа Пи, после чего полученное число умножается на длину радиуса окружности:

C = 2πR = 2π · 3√2 = 6√2π дм.

Длина окружности составляет 3,5 дм. Диаметр второй окружности равен 5/7 ее диаметра. Как вычислить длину второй окружности?

Ниже записана формула, которая используется для того, чтобы рассчитать длину окружности:

С = Пи*d,

где Пи – это константа, равная 3,14, а d – это диаметр окружности.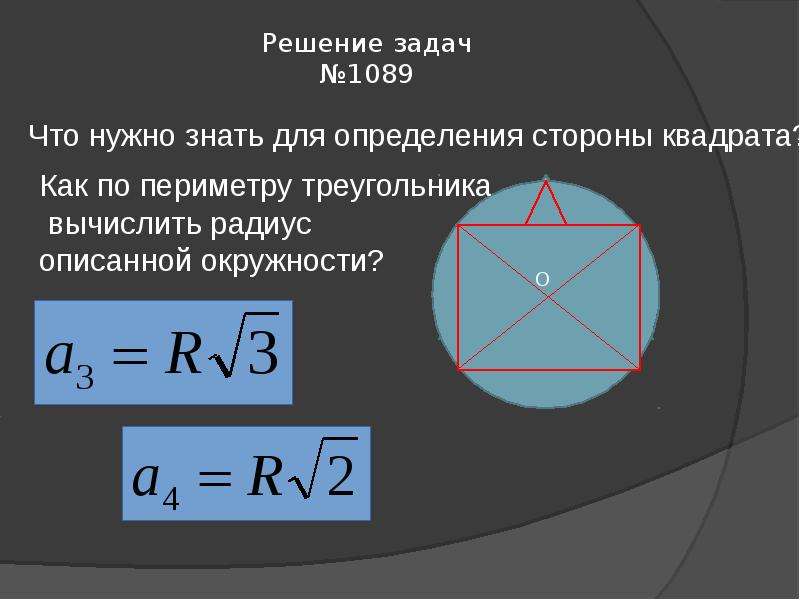

Отношение длины первой окружности к длине второй окружности равно отношению их диаметров:

C/C1 = d/d1

d1 = 5/7 d

В условии сказано, что длина первой окружности С = 3,5 дм. Таким образом:

C1 = 5/7 *C = 5/7 * 3,5 = 2,5 дм.

Длина радиуса окружности составляет 14 см. Какова будет ее длина при условии, что П=22/7?

Для того чтобы узнать длину окружности (C), следует воспользоваться формулой, предназначенной для ее расчета. Она выглядит так:

C = П*R*2

Если подставить в эту формулу величины, которые даны по условию задачи, то получим:

22/7*14*2=22/7*28/1=88 см.

Ответ: Длина окружности равна 88 см.

Какой будет длина окружности при условии, что ее половина составляет 25,5 см?

Длина окружности равна длине ее половины, умноженной на 2. Это значит, что в данном случае нужно умножить число 25,5, обозначающее половину длины окружности, на 2:

25,5*2 = 51 см.

Круг имеет площадь Пи м кв. Какова будет длина окружности данного круга?

Для вычисления длины окружности необходимо число Пи умножить на два и умножить на длину его радиуса (2πR). Для данной задачи это будет выглядеть следующим образом:

2π · 3√2 = 6√2π дм.

Для того чтобы посчитать площадь круга, необходимо умножить число Пи на радиус, взятый в квадрат (S = πR²). По условию задачи площадь круга равна Пи м кв. Это значит, что:

πR² = π

Из данного равенства можно выразить R

R — √π/π = 1

Зная длину радиуса, можно переходить к вычислению длины окружности (С):

C = 2πR = 2π x 1 = 2π

Ответ: Длина окружности равна 2π.

Какова формула длины окружности, при условии, что длина ее радиуса составляет R?

С целью вычисления длины окружности (С) используется приведенная ниже формула:

C=2πR

Ее составляющими является постоянное число Пи и радиус окружности (R), длину которой необходимо вычислить.

Какова формула расчета длины окружности, диаметр которой составляет 15 см?

Если длина диаметра окружности является известной величиной, то его нужно умножить на постоянное число Пи, равное 3,14, для того чтобы найти длину этой окружности. Формула выглядит так:

С = πD

В условии говорится, что диаметр окружности равен 15 см:

С = 3,14 * 15 = 47,1 cм.

Ответ: Длина окружности равна 47,1 см.

В результате деления длины окружности на величину ее диаметра получается число, приблизительно равное 22/7. Каким образом можно высчитать длину окружности с диаметром 10 см?

Для расчета длины окружности (С) нужно знать длину ее радиуса (R) или диаметра (d). Тогда могут быть использованы следующие формулы:

C = 2πR или C = πd

По условию задания d = 10 см, а π = 22/7. Тогда длина окружности будет равна:

C = πd = (22/7) * 10 = 220/7 ≈ 31,4 см.

В каком виде представлены формулы, которые используются для вычисления площади круга и длины окружности (через диаметр и через радиус)?

В случае, если длина диаметра (d) или длина радиуса (R) окружности известны, то эти величины можно использовать для нахождения длины окружности. При этом следует воспользоваться одной из формул:

С=πd или С=2πR.

Эти величины также помогут вычислить площадь круга. Формулы выглядят следующим образом:

S=πr² или S=π(d\2)².

Можно ли вычислить длину диаметра окружности, если известна только ее длина?

Нужно записать формулу расчета длины окружности, для того чтобы понять, существует ли взаимосвязь между этой величиной и диаметром окружности:

L = π·d

Очевидно, что длина окружности является результатом умножения числа Пи на длину ее диаметра.

Если длина окружности известна, то ее можно использовать для определения диаметра (d). Это можно сделать следующим образом:

d = L/π.

Во сколько раз длина окружности превышает ее диаметр, и в каком виде представлена формула ее расчета через диаметр?

Длину окружности (С) можно рассчитать через диаметр (d), если воспользоваться нижеприведенной формулой:

С = π*d

Это формула демонстрирует, что длина окружности больше длины ее диаметра в π раз. Именно отношение длины окружности к величине ее диаметра и является числом π.

Какова формула вычисления отношения длины окружности к величине, означающей ее диаметр?

Число π представляет собой константу, которая получается в результате деления длины окружности (С) на ее диаметр (d). В виде формулы это выглядит так:

π = С/d

Площадь круга составляет 185 см кв. Как вычислить 30% от длины окружности при заданных исходных?

Располагая информацией о том, что площадь круга равна произведению числа Пи и квадрата ее радиуса (S=πr²), можно через нее выразить радиус:

r² = S/π = 185/π

Избавляемся от квадратной степени:

r = √(185/π) см.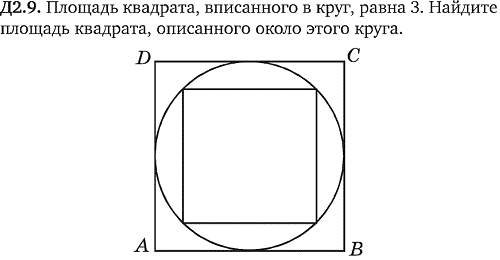

Следующим шагом в решении задачи станет вычисление длины окружности, которая находится путем умножения на 2 числа Пи и радиуса окружности:

С=2πr= C=2π√(185/π) = 2√(185π) см.

На последнем этапе находим 30%. Принимаем всю длину окружности за 100%:

2√(185π) — 100%

х — 30%

Тогда х можно найти следующим образом:

х=(30*2√(185π))/100 = 0,6√(185π) см.

Как выглядят формулы определения длины окружности через радиус и через диаметр? В какое количество раз длина диаметра окружности меньше ее длины?

Существует две формулы, которые предназначены для расчета длины окружности (С). Они отличаются друг от друга тем, что элементом одной из них является радиус (r), а другой – диаметр (D):

C=2Пr и C=ПD.

Для того чтобы понять, во сколько раз длина окружности превышает длину ее диаметра, нужно произвести деление этих величин:

С/D

В результате получается число Пи, которое является постоянным и имеет значение примерно 3,14.

Длина окружности, обозначаемая как L, может быть вычислена при условии, что известен ее диаметр (D). При этом следует воспользоваться формулой L = Пи*D. Можно ли использовать данную формулу с целью вычисления длины диаметра окружности, длина которой составляет 126 м. (число Пи считать равным 3)?

Формула расчета длины окружности (С) через диаметр (D) выглядит так:

С = Пи*D

Исходя из условий задания, это равенство может быть записано в следующем виде:

126=3*D

Отсюда можно выразить диаметр:

D=126:3=42 м.

кругов, вписанных в квадраты

Когда круг вписан в квадратный , диаметр стороны круга равна длине стороны квадрата.

Вы можете найти периметр и площадь квадрата, когда дана хотя бы одна мера круга или квадрата.

Для квадрата со стороной с , используются следующие формулы.

Периметр = 4 с

Площадь = с 2

Диагональ = с 2

Аналогичным образом можно найти длина окружности и площадь круга , когда дана хотя бы одна мера круга или квадрата.

Для окружности с радиусом р , используются следующие формулы.

Окружность = 2 π р

Площадь = π р 2

Пример 1:

Найдите периметр квадрата.

Когда круг вписан в квадрат, диаметр круга равен длине стороны квадрата.

Значит, длина стороны квадрата 6 см.

Периметр п квадрата со стороной с дан кем-то п знак равно 4 с .

Заменять 6 за с в п знак равно 4 с .

п знак равно 4 ( 6 ) знак равно 24

Периметр квадрата 24 см.

Пример 2:

Чему равна площадь круга, вписанного в квадрат площади 64 квадратные единицы?

Когда круг вписан в квадрат, длина каждой стороны квадрата равна диаметру круга. То есть диаметр вписанной окружности равен 8 единиц, поэтому радиус равен 4 единицы.

Площадь круга радиуса р единиц А знак равно π р 2 .

Заменять р знак равно 4 в формуле.

А знак равно π ( 4 ) 2 знак равно 16 π ≈ 50. 24

Следовательно, площадь вписанного круга примерно 50,24 квадратных единиц.

Квадрат, вписанный в круг

Когда квадрат вписан в круг, мы можем вывести формулы для всех его свойств — длины сторон, периметра, площади и длины диагоналей, используя только радиус круга.

И наоборот, мы можем найти радиус, диаметр, длину окружности и площадь круга, используя только сторону квадрата.

Проблема 1

Квадрат вписан в окружность радиусом ‘r’. Найдите формулы для длины стороны, длины диагонали, периметра и площади квадрата через r.

Стратегия

Ключевым моментом для решения этой задачи является то, что диагональ квадрата равна диаметру круга. Мы можем показать это, используя аргумент симметрии — квадрат симметричен относительно своей диагонали, поэтому диагональ должна проходить через центр круга.

Кроме того, мы знаем, что все внутренние углы квадрата прямые, равные 90°.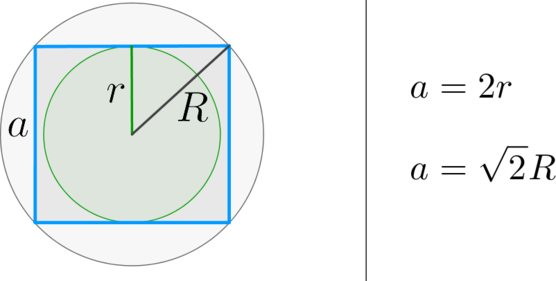 Поскольку эти углы вписаны в окружность, они измеряют половину центрального угла на той же дуге. Таким образом, центральный угол равен 180°, что означает диаметр.

Вооружившись этим знанием, длина диагонали квадрата равна просто 2r, каждая сторона измеряется r·√2 (теорема Пифагора, применяемая к треугольнику 45-45-90), тогда площадь равна 2r ² , а периметр равен 4·r·√2.

Теперь сделаем обратное, найдя свойства окружности по длине стороны вписанного квадрата.

Проблема 2

Квадрат со стороной а вписан в окружность. Найдите формулы для радиуса, диаметра, длины окружности и площади круга через а.

Стратегия

У нас уже есть ключевое понимание сверху — диаметр равен диагонали квадрата. Мы уже видели, как найти длину диагонали квадрата, считая от его стороны: это ·√2. Радиус равен половине диаметра, поэтому r=a·√2/2 или r=a/√2. Длина окружности равна 2·r·π, значит, это a·√2·π. А площадь равна π·r ² , значит, это π·a ² /2.

Теперь, когда мы сделали это, мы можем применить наши знания для решения различных задач «найти площадь заштрихованной фигуры», связанных с квадратом, вписанным в окружность, например:

Проблема 3

Квадрат со стороной а вписан в окружность. Найдите площадь заштрихованной фигуры.

Стратегия

Стратегия нахождения площади неправильной формы обычно заключается в том, чтобы посмотреть, можем ли мы выразить эту площадь как разность между площадями, образованными двумя или более правильными фигурами.

Здесь все очень просто — все 4 неправильные формы имеют одинаковый размер (из-за симметрии). Сумма их площадей равна разнице между площадью круга и площадью квадрата.

Таким образом, заштрихованная область A _{заштрихована} = (A _круг -A _{квадрат} )/4

Если у нас есть сторона квадрата, a, мы получаем A _{заштрихованное} =(A _круг -A _{квадрат} )/4=(π·a ² /2 -a ² )/4 =(π-2)·a ² /8.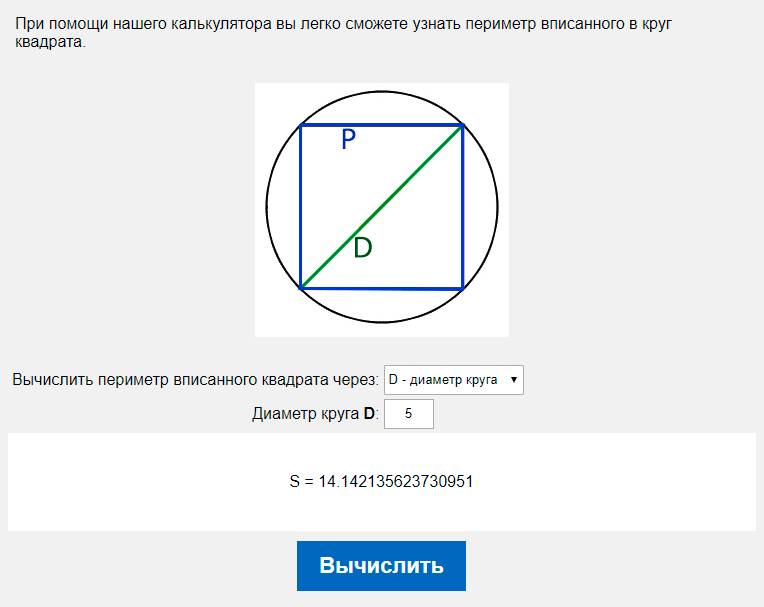 2)кв.(2)»в» = С#

#3″в»sqrt(2) = С#

#c = 3sqrt(2)» in»#

Теперь мы можем найти периметр квадрата и длину окружности.

Формула периметра квадрата:

#p = 4s#, где #s# — длина стороны квадрата.

Подстановка и вычисление #p# дает:

#p = 4 х 3 дюйма #

#p = 12 дюймов #

Формула длины окружности:

#c = 2pir#, где #r# — радиус окружности.

или

#c = dpi#, где #d# — диаметр круга. Помните: #d = 2r#

Подстановка и вычисление #c# дает:

#c = 3sqrt(2)pi» in»#

Тогда мы можем записать отношение длины окружности к периметру как:

#(3sqrt(2)pi» in»)/(12″ in») =>#

#(цвет(синий)(отменить(цвет(черный)(3)))sqrt(2)picolor(красный)(отменить(цвет(черный)(» in»))))/(цвет(синий)(отменить (цвет(черный)(12)))4цвет(красный)(отменить(цвет(черный)(«в»)))) =>#

#(sqrt(2)pi)/4#

SAT Математика: квадраты, вписанные в круги

Квадрат, который плотно вписывается в круг, — это , вписанный в круг . Углы квадрата будут касаться, но не пересекать границу круга, а диагональ квадрата будет равна диаметру круга. Кроме того, как и в случае с диагональю любого квадрата, она будет равна гипотенузе треугольника 45°-45°-90°. Вопросы GRE о квадратах, вписанных в круги, на самом деле являются вопросами о гипотенузе этого скрытого прямоугольного треугольника.

Вот пример задачи о вписанных квадратах.

Квадрат со стороной 4 вписан в окружность с центром О.Какова площадь круга?

Что еще можно сделать внутри qs jump ?

2500+ бесплатных

практических вопросов

Получите бесплатный доступ к более чем 2500 вопросам GMAT/GRE

30 минут

Подготовительные занятия

Посещайте бесплатные занятия по подготовке к GMAT/GRE каждый день

Виртуальные встречи один на один

Встречи

Бесплатные онлайн-встречи по запросу с приемной комиссией

1. 2π
2. 4π
3. 8π
4. 16π
5. 32π

Чтобы найти площадь круга, вам нужно найти радиус, который равен половине диаметра.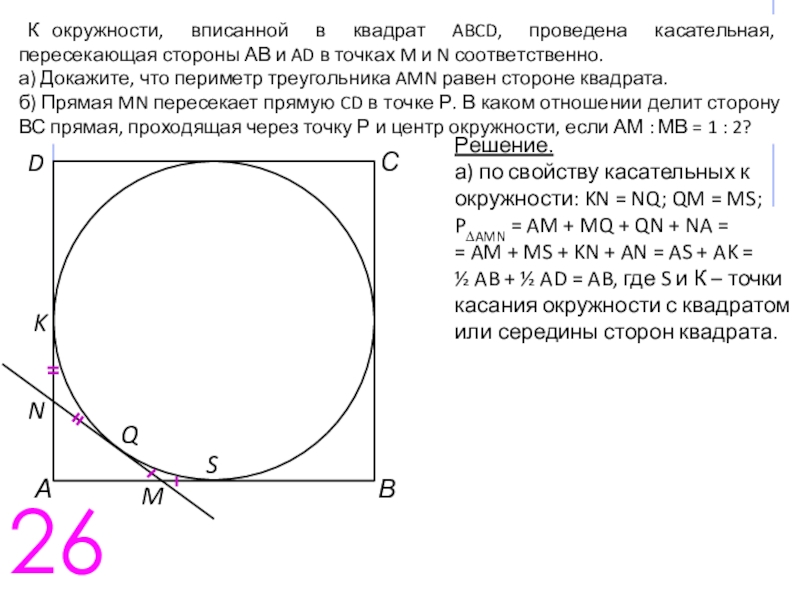 Нарисуйте фигуру, описанную в вопросе, и отметьте диагональ квадрата, а вместе с ней и диаметр круга.

Диаметр/диагональ делят вписанный квадрат на два прямоугольных треугольника, расположенных гипотенузой к гипотенузе. Оба треугольника имеют стороны 4 (поскольку у квадрата стороны 4) и внутренние углы 45 °, 45 ° и 90 °. Для любого из них вы можете найти гипотенузу, используя отношение сторон треугольника.

45°-45°-90° Соотношение треугольников
катет : катет : гипотенуза = s : s : s√2

Теперь разделите гипотенузу треугольника пополам, чтобы найти радиус окружности.

• д = с√2
• ⇒ д = 4√2
• г = d2
• ⇒ г = 2√2

Наконец, подставьте радиус круга в формулу площади.

Площадь круга = πr ²

• π(2√2) ²
• π(2 ² )(√2 ² )
• π(4)(2)
• 8π
• Таким образом, (С) верно.

Ищите скрытые треугольники в вопросах геометрии SAT. Если вы получите вопрос о квадрате, вписанном в круг, помните, что диагональ квадрата удваивается как гипотенуза треугольника 45°-45°-90°.Поиск этой гипотенузы, вероятно, будет ключом к ответу на вопрос.

Что еще можно сделать внутри qs jump ?

2500+ бесплатных

практических вопросов

Получите бесплатный доступ к более чем 2500 вопросам GMAT/GRE

30 минут

Подготовительные занятия

Посещайте бесплатные занятия по подготовке к GMAT/GRE каждый день

Виртуальные встречи один на один

Встречи

Бесплатные онлайн-встречи по запросу с приемной комиссией

#SAT Письмо и язык

#SAT Письмо и язык

#SAT Письмо и язык

Хотите больше математических советов, подобных этим? Посмотрите этот пост: SAT Math: перевод процентных вопросов. А пока попробуйте решить еще несколько практических задач.

1. Квадрат вписан в окружность. Площадь круга 50π. Чему равен периметр квадрата?
   1. 5
   2. 10
   3. 20
   4. 40
   5. 50
2. Квадрат вписан в окружность. Если площадь квадрата 36, какова длина окружности?
   1. 3π
   2. (3√2)π
   3. 6π
   4. (6√2)π
   5. 36π
3. Квадрат вписан в окружность.Если диаметр круга равен 4, какова площадь квадрата?
   1. 2
   2. 4
   3. 8
   4. 9
   5. 16

Ответы: 1. Д   2. Д   3. С

Как вписать квадрат в круг | Геометрия

шагов для вписания квадрата в круг

Шаг 1: Если диаметр или радиус круга известен, найдите длину диагонали квадрата, используя тот факт, что диаметр круга равен диагонали квадрата, или, что то же самое, радиус круг равен половине диагонали квадрата.2 {/экв}, где {экв}а {/экв} и {экв}б {/eq} — длины сторон квадрата, а {eq}c {/eq} — диагональ квадрата (гипотенуза прямоугольного треугольника). Диаметр круга равен диагонали квадрата.

Шаг 3: Используйте информацию из шагов 1 и 2, чтобы найти требуемое количество. Это может быть площадь круга или квадрата, длина окружности круга, периметр квадрата или другие измерения.

Словарь и уравнения для вписания квадрата в круг

Inscribed: Говорят, что квадрат вписан в круг, если все четыре его угла лежат на круге.2 {/экв}, где {экв}r {/eq} — радиус окружности. Периметр квадрата равен {eq}P = 4x {/экв}, где {экв}х {/eq} – длина стороны квадрата, а длина окружности – {eq}C = 2\pi r {/экв}, где {экв}r {/eq} — радиус окружности.

Мы будем использовать эти шаги, определения и уравнения, чтобы найти измерения, включающие квадрат, вписанный в круг, в следующих двух примерах.

Пример задачи 1. Как вписать квадрат в круг

На изображении ниже квадрат вписан в круг, а круг имеет радиус 2 дюйма.Найдите площадь и периметр квадрата.

Квадрат, вписанный в круг радиусом 2 дюйма

Шаг 1: Если диаметр или радиус круга известен, найдите длину диагонали квадрата, используя тот факт, что диаметр круга равен диагонали квадрата, или эквивалентно , радиус круга равен половине диагонали квадрата. 2 {/экв}, где {экв}а {/экв} и {экв}б {/eq} — длины сторон квадрата, а {eq}c {/eq} — диагональ квадрата (гипотенуза прямоугольного треугольника).

Поскольку мы знаем, что радиус равен {eq}r = 2 \text{ дюйма} {/eq} и радиус равен половине диагонали квадрата, мы можем найти диагональ квадрата, умножив радиус на 2. Таким образом, диагональ квадрата равна {eq}2\cdot 2 = 4 \text{ в .} {/экв}.

Теперь мы можем найти стороны квадрата по теореме Пифагора. Диагональ квадрата образует гипотенузу:

Прямоугольный треугольник

Поскольку у нас есть квадрат, две стороны прямоугольного треугольника должны быть равны, поэтому мы будем называть их {eq}x {/экв}.2 & = 8\\ \\ х& = \sqrt{8} \end{выравнивание} {/экв}

Это можно упростить, используя тот факт, что {eq}8 = 4\cdot 2 {/экв}.

{экв}\начало{выравнивание} х{}&=\sqrt{8}\\ \\ х& = \sqrt{4\cdot 2}\\ \\ х& = \sqrt{4}\cdot\sqrt{2}\\ \\ х& = 2\sqrt{2} \end{выравнивание} {/экв}

Таким образом, длина стороны квадрата {eq}x = 2\sqrt{2} \text{in. 2 {/экв}, где {экв}х {/eq} – длина стороны квадрата.2 {/eq} и периметр {eq}8\sqrt{2}\text{ дюймов}. {/экв}

Пример задачи 2. Как вписать квадрат в круг

На изображении ниже квадрат вписан в круг и имеет длину стороны 1 сантиметр. Найдите площадь и длину окружности.

Квадрат со сторонами длиной 1 см. вписанный в круг

Шаг 1: Если диаметр или радиус круга известен, найдите длину диагонали квадрата, используя тот факт, что диаметр круга равен диагонали квадрата, или эквивалентно , радиус круга равен половине диагонали квадрата.2 {/экв}, где {экв}а {/экв} и {экв}б {/eq} — длины сторон квадрата, а {eq}c {/eq} — диагональ квадрата (гипотенуза прямоугольного треугольника). Диаметр круга равен диагонали квадрата.

Стороны квадрата равны 1 см. и поэтому мы можем найти диагональ квадрата (которая также является диаметром круга), используя теорему Пифагора. 2\\ \\ \sqrt{2} & = с \end{выравнивание} {/экв}

Таким образом, диаметр круга равен {eq}d = \sqrt{2} \text{ см.2 {/eq} и окружность {eq}\pi\sqrt{2}\text{ см.} {/экв}

Получите доступ к тысячам практических вопросов и пояснений!

Длина стороны квадрата, вписанного в круг, равна 2. Чему равна площадь круга?

00:00 — 00:59	слон как вопрос решите длина квадрата вписанного в круг равна 2 какова площадь круга найдите площадь круга это длина а дана тогда начните гимнастику и вписанный в квадрат abc и d точка со мной тогда это диагональ квадрата ABCD AC это диаметр круга также это означает диагональ
01:00 — 01:59	равно диаметр круга ABC d равен диаметру контура для нахождения диаметра по теореме Пифагора, потому что угол b равен 90, потому что каждый угол квадрата равен 90 градусов. Навин Теорема Пифагора квадрат смерти равен перпендикулярному квадрату + b квадрат и здесь гипотенуза равна перпендикуляру то есть ab квадрат + b
02:00 — 02:59	то есть это он и дано что сторона этого прихода к нему означает ab равно BC равно c равно к КД равно потому что в плохо на Титане равно с двумя квадратными и с двумя и мы знаем что к клетке плюс за что равно МС квадрат равен ему новатех добавил к прототипу тогда выйдет только легко и квадратный корень из него и мы можем написать квадратный корень из 8 есть равно 2 в корень из 2 единиц это означает диаметр круга 2 в корень из 24 нахождение радиуса мы используем реле
03:00 — 03:59	между радиусом и диаметром то есть всегда равен диаметру, а диаметр равен 2.2 если получится это равно квадратному корню из 2 единиц нет с помощью этого мы можем найти площадь круга в радианах в это квадратный корень 2 корень тогда этот корень CA будет отменен и только вам много каждый умножается на и на тогда это придет к единице трубы
04:00 — 04:59	площадь круга до 5 если мы сравним нашу землю с отданной мы получим правильное спасибо

площадь квадрата — Примеры

Площадь квадрата определяется как количество квадратных единиц, необходимых для заполнения квадрата. Другими словами, когда мы хотим найти площадь квадрата, мы учитываем длину его стороны. Поскольку все стороны квадрата равны, его площадь равна произведению двух его сторон. Общепринятыми единицами измерения площади квадрата являются квадратные метры, квадратные футы, квадратные дюймы, квадратные сантиметры.

Площадь квадрата можно также рассчитать с помощью других измерений, таких как диагональ и периметр квадрата. Давайте попробуем понять больше о площади квадрата на этой странице.

Какова площадь квадрата?

Квадрат – это замкнутая двумерная фигура с четырьмя равными сторонами и четырьмя равными углами. Четыре стороны квадрата образуют четыре угла при вершинах. Сумма всех длин сторон квадрата — это его периметр, а общая площадь, занимаемая квадратом, — это площадь квадрата. Это четырехугольник со следующими свойствами.

• Противоположные стороны параллельны.
• Все четыре стороны равны.
• Все углы равны 90º.

Квадраты можно найти повсюду вокруг нас. Вот некоторые часто встречающиеся объекты, имеющие форму квадрата. Шахматная доска, часы, школьная доска, плитка — все это примеры квадрата.

Определение площади квадрата

Площадь квадрата – это мера занимаемой им площади или поверхности. Он равен произведению длин двух его сторон. Поскольку площадь квадрата равна произведению двух его сторон, единица измерения площади выражается в квадратных единицах.

Обратите внимание на зеленый квадрат, показанный ниже. Он занял 25 кв. Следовательно, площадь квадрата равна 25 квадратных единиц. Из рисунка видно, что длина каждой стороны равна 5 единицам. Следовательно, площадь квадрата равна произведению его сторон. Площадь квадрата = сторона × сторона = 5 × 5 = 25 квадратных единиц.

Площадь квадрата Формула

Формула площади квадрата с учетом сторон:

Площадь квадрата = Сторона × Сторона = S ²

Алгебраически площадь квадрата можно найти, возведя в квадрат число, представляющее меру стороны квадрата.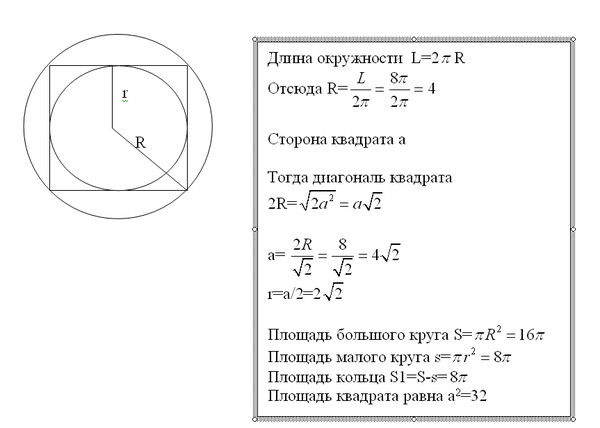 Теперь воспользуемся этой формулой, чтобы найти площадь квадрата со стороной 7 см. Мы знаем, что площадь квадрата = Сторона × Сторона. Подставляя длину стороны 7 см, 7 × 7 = 49. Следовательно, площадь данного квадрата равна 49 см ² .

Площадь квадрата также можно найти с помощью диагонали квадрата. Для нахождения площади квадрата по диагонали используется формула:

.

Площадь квадрата по диагоналям = Диагональ ² /2.

Давайте поймем вывод этой формулы с помощью следующего рисунка, где «d» — диагональ, а «s» — стороны квадрата.

Здесь сторона квадрата «s», а диагональ квадрата «d». Применяя теорему Пифагора, мы имеем d ² = s ² + s ² ; д ² = 2s ² ; д = √2с; с = d/√2. Теперь эта формула поможет нам найти площадь квадрата, используя диагональ. Площадь = s ² = (d/√2) ² = d ² /2. Следовательно, площадь квадрата равна d ² /2.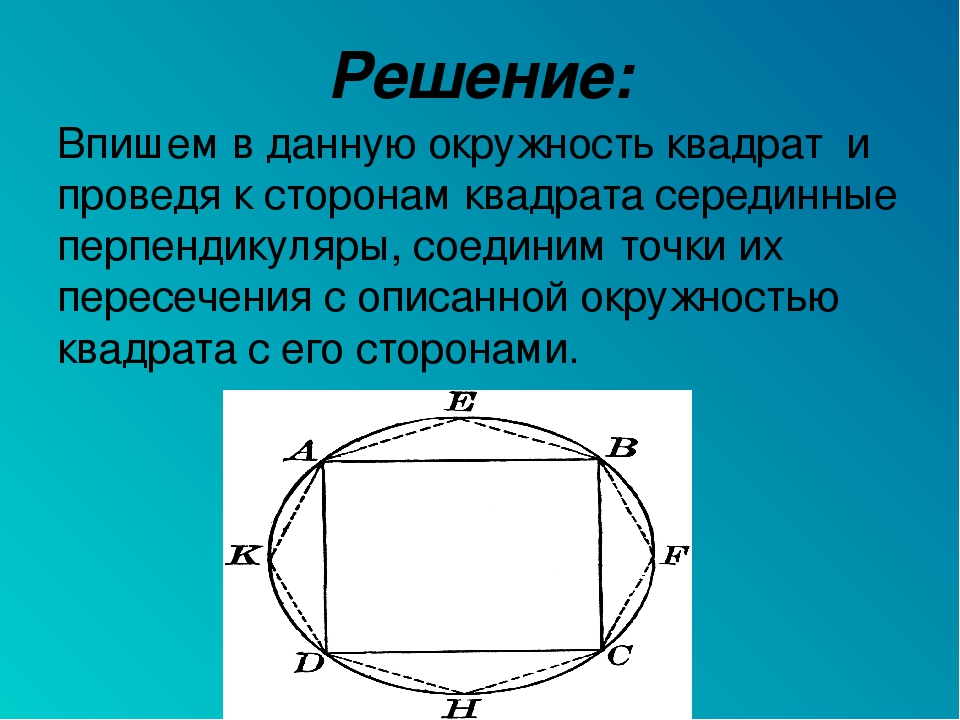

Как найти площадь квадрата?

В предыдущем разделе мы рассмотрели определение площади квадрата, а также формулу площади квадрата.В этом разделе давайте разберемся, как использовать формулу площади квадрата, чтобы найти ее площадь с помощью нескольких приложений или реальных примеров.

Найдите площадь квадрата, зная периметр квадрата

Пример: Найдите площадь квадратного парка с периметром 360 футов.
Решение:
Дано: Периметр квадратного парка = 360 футов
Мы это знаем,
Периметр квадрата = 4 × сторона
⇒ 4 × сторона = 360
⇒ сторона = 360/4
⇒ сторона = 90 футов
Площадь квадрата = сторона ²
Следовательно, Площадь квадратного парка = 90 ² = 90 × 90 = 8100 футов ²
Таким образом, площадь квадратного парка с периметром 360 футов составляет 8100 футов ² .

Найдите площадь квадрата, зная сторону квадрата

Пример: Найдите площадь квадратного парка со стороной 90 футов.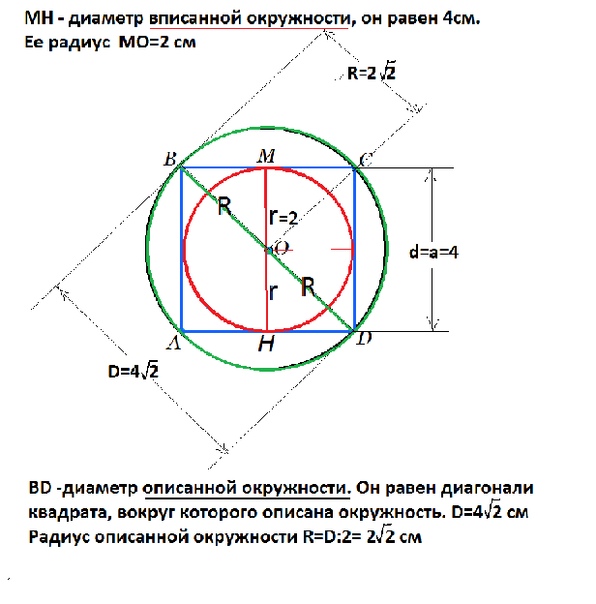
Решение:
Дано: сторона квадратного парка = 90 футов
Мы это знаем,
Площадь квадрата = ft ²
Следовательно, Площадь квадратного парка = 90 ² = 90 × 90 = 8100 футов ²
Таким образом, площадь квадратного парка со стороной 90 футов равна 8100 футов ²

Найдите площадь квадрата, зная диагональ квадрата

Пример: Найдите площадь квадратного парка с диагональю 14 футов.
Решение:
Дано: диагональ квадратного парка = 14 футов
Мы это знаем,
Формула площади квадрата при заданной диагонали = d ² / 2
Следовательно, площадь квадратного парка = (14 × 14)/2 = 98 футов ²
Таким образом, площадь квадратного парка с диагональю 14 м равна 98 футов ² .

Площадь квадратных наконечников:

Обратите внимание на следующие моменты, которые следует помнить при вычислении площади квадрата.

☛ Связанные статьи

Часто задаваемые вопросы о площади квадрата

Что такое площадь квадрата в геометрии?

В геометрии квадрат — это фигура с четырьмя равными сторонами. Площадь квадрата определяется как количество квадратных единиц, составляющих полный квадрат. Он рассчитывается по формуле площади квадрата Площадь = s × s = s ² в квадратных единицах.

Какая формула для нахождения площади квадрата?

Когда сторона квадрата известна, используется формула для нахождения площади квадрата со стороной s: Площадь = s × s = s ² .Когда дана диагональ ‘d’ квадрата, то формула, используемая для нахождения площади, такова: Площадь = d ² /2.

Как вычислить площадь квадрата?

Площадь квадрата рассчитывается по формуле: Площадь = s × s, где s — одна сторона квадрата. Поскольку площадь квадрата является двумерной величиной, она всегда выражается в квадратных единицах. Например, если мы хотим вычислить площадь квадрата со стороной 4 единицы, это будет: A = 4 × 4 = 16 единиц ² .Проверьте сейчас калькулятор площади квадрата для быстрых расчетов.

Что такое периметр и площадь квадратных формул?

Периметр квадрата представляет собой сумму четырех сторон квадрата, то есть P = 4 × Стороны. Она выражается в м, см, футах, дюймах.
Площадь квадрата = Площадь = s × s, где s — одна сторона квадрата. Дается в единицах м ² , см ² , футов ² , в ² .

Чек:

Как найти площадь квадрата по диагонали квадрата?

Площадь квадрата также можно найти, если известна его диагональ.В этом случае используется следующая формула: Площадь квадрата по диагоналям = Диагональ²/2. Например, диагональ квадрата равна 6 единицам, Площадь = 6²/2 = 36/2 = 18 квадратных единиц.

Как найти площадь квадрата по периметру квадрата?

Площадь квадрата можно вычислить, если известен периметр квадрата. Поскольку периметр квадрата: P = 4 × сторона, мы можем найти сторону квадрата ‘s’ = периметр/4. После получения стороны площадь квадрата можно вычислить по формуле: A = s × s.Например, если периметр квадрата равен 32 единицам, мы подставим это значение в формулу: P = 4 × сторона. 32 = 4 × стороны. Значит, сторона будет 8 единиц. Теперь мы можем вычислить площадь квадрата со стороной 8 единиц. Площадь = s × s = 8 × 8 = 64 кв.

Каковы единицы площади квадрата?

Поскольку площадь квадрата является двумерной фигурой, она всегда выражается в квадратных единицах. Общепринятыми единицами площади квадрата являются м ² , дюймы ² , см ² , футы ² .

Какова площадь квадрата, вписанного в круг?

Если квадрат вписан в круг, то диагональ квадрата равна диаметру круга. Итак, если диаметр круга дан, это значение можно использовать как диагональ квадрата, а площадь квадрата можно рассчитать по формуле: Площадь квадрата с использованием диагоналей = Диагональ²/2.