Формула прогиба балки: Расчет балки на прогиб: формулы и пример расчета

Разное

Содержание

Расчет металлической балки на прогиб: учимся составлять формулы

Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Что такое прогиб балки?

Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

ν-прогиб сечения C; θ-угол поворота сечения C.

Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет.

Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Метод начальных параметров

Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)

Под начальными параметрами понимаются уже известные перемещения:

в опорах прогибы равны нулю;
в жесткой заделке прогиб и угол поворота сечения равен нулю.

Учитывая эти хитрости, их называют еще граничными условиями, определяются перемещения в других частях балки.

Расчет прогибов балки

Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

Реакции опор

Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.

Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:

Система координат

Далее вводим систему координат, с началом в левой части балки (точка А):

Распределенная нагрузка

Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.

Если бы нагрузка была приложена вот таким способом:

То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение.

Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.

Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:

Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:

\[ { V }_{ A }=0\quad при\quad x=0 \]

\[ { V }_{ B }=0\quad при\quad x=8м \]

Записываем уравнение метода начальных параметров для сечения C:

\[ E{ I }_{ z }{ V }_{ C }=… \]

Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:

\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]

Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:

\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+… \]

Учет внешней нагрузки

И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. Здесь есть несколько особенностей:

Сосредоточенные силы и распределенные нагрузки, которые направленны вверх, то есть совпадают с направлением оси y, в уравнении записываются со знаком «плюс». Если они направленны наоборот, соответственно, со знаком «минус»:

Моменты, направленные по часовой стрелке – положительные, против часовой стрелки – отрицательные:

Все сосредоточенные моменты нужно умножать дробь:

\[ M\cdot \frac { { x }^{ 2 } }{ 2 } \]

Все сосредоточенные силы нужно умножать дробь:

\[ F\cdot \frac { { x }^{ 3 } }{ 6 } \]

Начало и конец распределенных нагрузок нужно умножать на дробь:

\[ q\cdot \frac { { x }^{ 4 } }{ 24 } \]

Откуда такие цифры и степени взялись? Все эти вещи вытекают при интегрировании дифференциального уравнения упругой линии балки, в методе начальных параметров все эти выводы опускаются, то есть он является как бы упрощенным и универсальным методом. { 4 } } =-2см \]

Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.

На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).

Прогибы балок | Блог Ярослава Указова

Как и в случае осевого нагружения, в изгибе будем допускать лишь малые деформации. Напомню, что для определения удлинений при растяжении за длину берётся исходная недеформированная длина, несмотря на тот факт, что при равномерном приложении нагрузки с каждым её увеличением увеличивается и исходная длина в каждый момент времени. То же самое и в изгибе – принимаем, что прогибы балки не влияют на её работу под нагрузкой и итоговая нагрузка прикладывается к недеформированной балке. На основе этого допущения выведем формулу для расчёта прогибов.

Имеющейся балочной теории достаточно лишь для того, чтобы определять прогибы для балок, где имеется участок чистого изгиба, на котором постоянен радиус кривизны.
Его можно определить из формулы:

Максимальный прогиб в таком случае определяется как высота сегмента окружности радиуса r.

Однако в общем случае изгиба имеется поперечная сила Q, и, как следствие этого, меняется изгибающий момент M. И если балка имеет постоянное сечение по длине, то тогда меняется и радиус кривизны.

Чем больше момент в сечении, тем меньше будет радиус кривизны.

Важно упомянуть, что при общем случае нагружения на балку будет действовать поперечная сила, которая также может оказывать влияние на прогибы. Хотя в длинных балках, где успевает «набежать» достаточно большой изгибающий момент, её влияние на прогибы становится крайне незначительным, в коротких балках обычно учитывают влияние сдвиговых деформаций, хотя и для их учёта требуется более сложная техника расчёта. В пределах данного курса мы ограничимся определением прогибов балок только от изгибающих моментов, действующих их сечениях.

Для того, чтобы при определении прогибов балок учитывать изменение изгибающего момента и, следовательно, радиусов кривизны, нужно получить зависимость кривизны кривой (а, следовательно, и момента M) от координаты x и y.

В курсе математического анализа даётся вывод формулы для кривизны плоской кривой:

Для заинтересованных ниже приводится вывод данной формулы.

Пусть имеется график функции y(x):

Отметим точку на графике m и проведём касательную к графику в этой точке. Угол между касательной и осью x обозначим как α:

На некотором расстоянии ∆s от точки m на графике обозначим точку m1, в которой также проведём касательную к графику. Угол между касательной и осью x обозначим как α–∆α:

Приращение по иксу – dx, приращение по игреку – dy:

С физической точки зрения кривизна – это:

Нужно избавиться от α и от s, выразив их через координаты y и x:

По определению производной:

Получим:

Рассмотрим второй множитель:

ds можно преобразовать по теореме Пифагора:

Подставим в итоговое выражение:

С геометрической точки зрения кривизна равняется:

Получившееся уравнение связывает радиус кривизны с координатами икс (сечение балки) и игрек (её прогиб).

Используя выведенные ранее зависимости, получим:

Это уравнение называют дифференциальным уравнением упругой оси. Оно нелинейно и пользоваться им для решения практических задач крайне неудобно. Однако можно заметить, что в отношении dy/dx (dy/dx – это наклон касательной к кривой в какой-либо точке) dy весьма мало для случаев малых прогибов относительно dx (малых – относительно длины балки). И уж тем более квадрат этого отношения стремится к нулю. Фактически, это обращает знаменатель в единицу и значительно упрощает выражение:

Удобнее записать так:

Для получения прогибов, это уравнение следует дважды проинтегрировать по dx.

Для наглядности рассмотрим пример. Пусть имеется шарнирно опёртая балка с равномерно распределённой нагрузкой:

На самом деле, такое нагружение справедливо для каждой шарнирно опёртой балки, ведь никто не отменял земную гравитацию. Ну и нам хотелось бы определить прогибы этой балки, как наибольший, так и в любой желаемой нами точке.

Для начала определим опорные реакции:

Чтобы определить прогибы, нам нужно знать модуль Юнга материала E, момент инерции сечения Iz (он не должен меняться по длине) и зависимость изгибающего момента по длине. Допустим, у нас есть свойства материала и характеристики сечения. Теперь нужно получить зависимость M(x).

Проинтегрируем по dx:

Здесь C – постоянная интегрирования. Её можно определить из граничных условий:

При x=0, прогиб балки y=0
При x=L, прогиб балки y=0

Данные граничные условия нельзя использовать в полученном выше уравнении, так как оно для углов поворота dy/dx, а необходимо уравнение прогибов y(x). Для получения уравнения прогибов проинтегрируем ещё раз по dx:

Здесь D – ещё одна постоянная интегрирования. Так как полученное уравнение является функцией прогибов балки, то можно использовать имеющиеся граничные условия.

Первое условие:

Второе условие:

Итого:

Уравнение для углов поворота:

Уравнение для прогибов:

Решим задачу отыскания места наибольшего прогиба и величину этого прогиба. В месте наибольшего прогиба производная функции прогиба будет равна нулю. Т.е. надо полученное выражение для dy/dx приравнять к нулю:

Уравнение имеет три корня:

Второй корень при какой бы то ни было длине балки L получается отрицательным; третий корень при какой бы то ни было длине L получается большим, чем длина балки. Остаётся только первый корень L/2, значит наибольший прогиб будет в середине пролёта, что для данного примера достаточно очевидно.

Место наибольшего прогиба также можно определить, построив непосредственно график функции прогибов. Это гораздо легче способа с решением кубического уравнения.

Для этого рассмотрим частный случай. Пусть:

Для построения графика функции прогибов воспользуемся программой MS Excel. Прежде чем это сделать, необходимо ещё раз проверить свои вычисления, так как при решении громоздких уравнений легко допустить ошибку, что может привести к ошибочным результатам.

После построения получим:

Из графика можно определить как место наибольшего прогиба, так и его величину, а также прогибы в любых интересующих точках.

Наибольший прогиб:

В качестве второго примера решим следующую задачу. Необходимо найти прогибы шарнирно опёртой балки при действии распределённой силы q и сосредоточенной силы P, если балка сделана из стали с модулем упругости E = 200 000 МПа, и имеет прямоугольное поперечное сечение с размерами B и H (размеры будут даны позже, сначала задача будет решена в общем виде).

Необходимо найти прогибы шарнирно опёртой балки при действии распределённой силы q и сосредоточенной силы P, если балка сделана из стали с модулем упругости 200 000 МПа, и имеет прямоугольное поперечное сечение с размерами B и H.

На балку действует два вида нагрузок: распределённая и сосредоточенная. Допустим, что последовательность приложения этих нагрузок не оказывает влияния на работу балки, т.е. результат действия суммы всех сил тот же, что и сумма результатов действия всех сил по отдельности. Это так называемый принцип независимости действия сил. Он вполне согласуется с тем, что происходит в реальности. Тогда данная задача распадается на три подзадачи:

Определение прогибов шарнирно-опёртой балки при распределённой нагрузке;
Определение прогибов шарнирно-опёртой балки при сосредоточенной нагрузке;
Суммирование прогибов.

Первая подзадача уже решена и уравнение прогибов имеет следующий вид:

Решим вторую подзадачу:

Опоры заменяются своими реакциями на балку:

Из уравнений статики получается, что:

В отличие от случая распределённой нагрузки, здесь имеется два участка, на которых функция изгибающего момента меняет свой вид.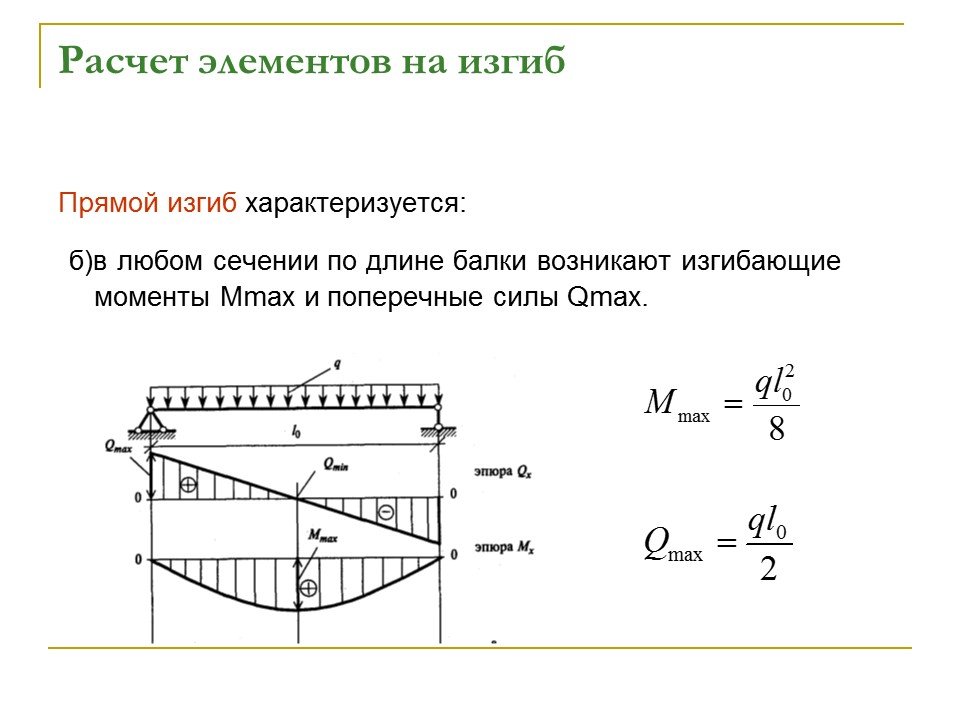

Первый участок:

Имея дифференциальное уравнение упругой оси

Получим:

Проинтегрируем по dx и получим уравнение углов поворота для первого участка:

Ещё раз проинтегрируем по dx и получим уравнение прогибов для первого участка:

Теперь рассмотрим второй участок:

Проинтегрируем по dx и получим уравнение углов поворота для второго участка:

Ещё раз проинтегрируем по dx и получим уравнение прогибов для второго участка:

Получилось четыре неизвестных постоянных интегрирования: C1, D1, C2, D2.

Для их определения имеются следующие граничные условия:

x=0, y=0 (первый участок)
x=a, dy/dx (1) = dy/dx (2) (для обоих участков)
x=a, y (1) = y (2) (для обоих участков)
x=L, y=0 (второй участок)

Для определения зависимости между соответственными постоянными интегрирования на обоих участках, используем условия, что угол поворота и прогиб в месте приложения силы P равны для обоих участков:

Для определения D используем условие x=0, y=0 для уравнения прогибов первого участка:

Для определения C используем условие x=L, y=0 для уравнения прогибов второго участка:

Итого получим:

При

Для построения графика прогибов зададимся значениями:

Момент инерции сечения относительно изгибаемой оси:

Для построения графиков прогибов использована программа MS Excel.

Прогибы балки от сосредоточенной нагрузки:

Прогибы балки от распределённой нагрузки:

Суммарные прогибы:

Применение принципа суперпозиции для решения задач (отыскания прогибов и т.д.) удобно лишь тогда, когда у вас уже имеются готовые решения для отдельных нагружений и остаётся только просуммировать результат. В остальном, в большинстве случаев бывает проще посчитать балку сразу с учётом всех нагрузок.

Полный расчет балки на прочность и жесткость

Задача

Произвести полный расчет на прочность и проверить жесткость статически определимой двутавровой двухопорной балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [σ]=160 МПа и [τ]=100 МПа, допустимый прогиб балки [f]=l/400

Рис. 1

Решение

Подготовка расчетной схемы к решению задачи:

Определение опорных реакций

Подробно, пример определения опорных реакций для балки рассмотрен здесь

А также в нашем коротком видеоуроке:

Из Σm_в=0

Из Σm_А=0

Построение эпюр Q и М

Подробный пример построения эпюр поперечных сил Q и изгибающих моментов M для балки

Видео про расчет значений Q и M для построения эпюр:

В пролете балки 0 ≤ z₂ ≤ l

Q_II= — R_B+ qz₂= -52+30∙z₂
Q_II(z=0)= -52 кН
Q_II(z=l)= -52+30∙4=68 кН

M_II=R_B∙z₂-qz₂²/2=52z₂-30∙z₂²/2
M_{II (z=0)}= 0
M_{II (z=l)}= -32 кНм

На консоли l ≤ z₁≤ (l+a)

Q_I= — R_B+ ql — R_A=-52+30∙4-108=-40 кН

M_I=R_B z₁-ql(z₁-l/2)+R_A(z₁-l)=52z₁-30∙4(z₁-4/2)+108(z₁-4)
M_{I (z=l)}= -32 кНм
M_{I (z=l+a)}= 0

По этим данным построены эпюры Q и М.

Короткое видео о том, как надо строить эпюры:

Так как М_mах = 45 кНм, то

W_x≥M_max / [σ] = 45∙10³ / 160∙10⁶= 0,281 м³= 281 см³.

О том, как подбирается сечение балки

По сортаменту выбираем двутавр № 24, для которого W_x = 289 см³, I_x= 3460 см⁴, S_max = 163 см³, h = 24 см, b_п = 11,5 см, t = 0,95 см, d = b_c = 0,56 см, h₀ = h-2t = 22,1 см.

Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения.

σ_max = M_max / W_x = 45∙10³ / 289∙10^-6= 156∙10⁶ Па = 156 МПа

Проверка сечения балки по касательным напряжениям

Так как Q_max = 68 кН, то

Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:

Построение эпюры нормальных напряжений

Построение эпюры касательных напряжений

В отношении главных напряжений неблагоприятным является сечение над левой опорой, в котором:

М = -32 кНм и Q = 68 кН.

Значение напряжений в различных точках по высоте двутавра сведены в таблицу 1

Таблица 1

Результаты расчета в примере

Проверка прочности балки по главным напряжениям

Наиболее опасной точкой в неблагоприятном сечении является точка 3. В этой точке σ₁=118 МПа и σ₃= -16 МПа. Проверяем прочность в этой точке по третьей гипотезе прочности согласно неравенству σ₁ — σ₃≤ [σ].

Так как 118 — ( -16) = 134 < 160, то выбранное сечение удовлетворяет условию прочности и по главным напряжениям.

Расчет перемещений сечений (прогибов балки)

Универсальные уравнения МНП для сечения z:

Опорные условия:

1) при z=0: y(z)=0, следовательно, y₀=0

2) при z=l: y(z)=0 находим θ₀

откуда θ₀= -8,48∙10^-3 радиан.

Прогиб в пролете при z=l/2=4/2=2 м.

Аналогично определяется прогиб на конце консоли при z = l + a =4+0,8 = 4,8 м.

Проверка жесткости балки

— пролетной части:

y_c=0,98 см < 1/400 = 400/400 = 1 см

— консольной части:

y_D=0,33 см < 2a/400 = 2∙80/400 = 0,4 см.

Следовательно, принятая двутавровая балка удовлетворяет требуемому условию жесткости.

Другие примеры решения задач >

Выполнение расчета прогиба деревянной балки

При действии нагрузки деревянные балки могут получать довольно большие прогибы, в результате которых нарушается их нормальная эксплуатация. Поэтому кроме расчетов по первой группе предельных состояний (прочность), необходимо выполнить расчет деревянных балок и по второй группе т. е.

по прогибам. Расчет деревянных балок на прогиб выполняется на действие нормативных нагрузок. Нормативную нагрузку получаем разделением расчетной нагрузки на коэффициент надежности по нагрузке.

Вычесление нормативной нагрузки выполнятся в сервисе расчет деревянных балокавтоматически. Нормальная эксплуатация балок возможна, в случае если расчетный прогиб деревянной балки не превышает прогиб, установленный нормами. Нормативными документами установлены конструктивные и эстетико-психологические требования.

1. Конструктивные требования к прогибам деревянных балок.

Представлены в СП64.13330.2011 “ДЕРЕВЯННЫЕ КОНСТРУКЦИИ” Таблица 19Элементы конструкцийПредельные прогибы в долях пролета, не более1 Балки междуэтажных перекрытий 2 Балки чердачных перекрытий 3 Покрытия (кроме ендов): а) прогоны, стропильные ноги б) балки консольные в) фермы, клееные балки (кроме консольных) г) плиты д) обрешетки, настилы 4 Несущие элементы ендов 5 Панели и элементы фахверха1/2501/2001/2001/1501/3001/250 1/1501/4001/250

1.

Эстетическо-психологические требования к прогибам деревянных балок.

Представлены в СП20.13330.2011 “НАГРУЗКИ И ВОЗДЕЙСТВИЯ” Приложение Е.2

Элементы конструкцийВертикальные предельные прогибы 2 Балки, фермы, ригели, прогоны, плиты, настилы (включая поперечные ребра плит и настилов):а) покрытий и перекрытий, открытых для обзора, при пролете l, м: l<1 l<3 l<6 l<12 l<24 1/1201/150 1/2001/2501/300В случае если балка скрыта (к примеру, под подшивным потолком) то соблюдение эстетико-психологических требований не является обязательным. В данном случае необходимо выполнить расчет прогибов балкина соблюдение только конструктивных требований по прогибам.

Чтобы построить деревянный дом необходимо провести расчёт несущей способности деревянной балки. Также особое значение в строительной терминологии имеет определение прогиба.

Без качественного математического анализа всех параметров просто невозможно построить дом из бруса. Именно поэтому перед тем как начать строительство крайне важно правильно рассчитать прогиб деревянных балок. Данные расчёты послужат залогом вашей уверенности в качестве и надёжности постройки.

Что нужно для того чтобы сделать правильный расчёт

Расчёт несущей способности и прогиба деревянных балок не такая простая задача, как может показаться на первый взгляд. Чтобы определить, сколько досок вам нужно, а также, какой у них должен быть размер необходимо потратить немало времени, или же вы просто можете воспользоваться нашим калькулятором.

Во-первых, нужно замерить пролёт, который вы собираетесь перекрыть деревянными балками.

Во-вторых, уделите повышенное внимание методу крепления. Крайне важно, насколько глубоко фиксирующие элементы будут заходить в стену. Только после этого вы сможете сделать расчёт несущей способности вместе с прогибом и ряда других не менее важных параметров.

Длина

Перед тем как рассчитать несущую способность и прогиб, нужно узнать длину каждой деревянной доски.

Данный параметр определяется длиной пролёта. Тем не менее это не всё. Вы должны провести расчёт с некоторым запасом.

Важно! Если деревянные балки заделываться в стены — это напрямую влияет на их длину и все дальнейшие расчёты.

При подсчёте особое значение имеет материал, из которого сделан дом. Если это кирпич, доски будут монтироваться внутрь гнёзд. Приблизительная глубина около 100—150 мм.

Когда речь идёт о деревянных постройках параметры согласно СНиПам сильно меняются. Теперь достаточно глубины в 70—90 мм. Естественно, что из-за этого также изменится конечная несущая способность.

Если в процессе монтажа применяются хомуты или кронштейны, то длина брёвен или досок соответствует проёму. Проще говоря, высчитайте расстояние от стены до стены и в итоге сможете узнать несущую способность всей конструкции.

Важно! При формировании ската крыши брёвна выносятся за стены на 30—50 сантиметров. Это нужно учесть при подсчёте способности конструкции противостоять нагрузкам.

К сожалению, далеко не всё зависит от фантазии архитектора, когда дело касается исключительно математики. Для обрезной доски максимальная длина шесть метров. В противном случае несущая способность уменьшается, а прогиб становится больше.

Само собой, что сейчас не редкость дома, у которых пролёт достигает 10—12 метров. В таком случае используется клееный брус.

Он может быть двутавровым или же прямоугольным. Также для большей надёжности можно использовать опоры. В их качестве идеально подходят дополнительные стены или колоны.

Совет! Многие строители при необходимости перекрыть длинный пролёт используют фермы.

Общая информация по методологии расчёта

В большинстве случаев в малоэтажном строительстве применяются однопролётные балки.

Они могут быть в виде брёвен, досок или брусьев. Длина элементов может варьироваться в большом диапазоне. В большинстве случаев она напрямую зависит от параметров строения, которые вы собираетесь возвести.

Внимание! Представленный в конце странички калькулятор расчета балок на прогиб позволит вам просчитать все значения с минимальными затратами времени. Чтобы воспользоваться программой, достаточно ввести базовые данные.

Роль несущих элементов в конструкции выполняют деревянные бруски, высота сечения которых составляет от 140 до 250 мм, толщина лежит в диапазоне 55—155 мм. Это наиболее часто используемые параметры при расчёте несущей способности деревянных балок.

Очень часто профессиональные строители для того чтобы усилить конструкцию используют перекрёстную схему монтажа балок. Именно эта методика даёт наилучший результат при минимальных затратах времени и материалов.

Если рассматривать длину оптимального пролёта при расчёте несущей способности деревянных балок, то лучше всего ограничить фантазию архитектора в диапазоне от двух с половиной до четырёх метров.

Внимание! Лучшим сечением для деревянных балок считается площадь, у которой высота и ширина соотносятся как 1,5 к 1.

Как рассчитать несущую способность и прогиб

Стоит признать, что за множество лет практики в строительном ремесле был выработан некий канон, который чаще всего используют для того, чтобы провести расчёт несущей способности:

M/W<=Rд

Расшифруем значение каждой переменной в формуле:

Буква Мвначале формулы указывает на изгибающий момент. Он исчисляется в кгс*м.Wобозначает момент сопротивления. Единицы измерения см3.

Расчёт прогиба деревянной балки является частью, представленной выше формулы. Буква Муказывает нам на данный показатель. Чтобы узнать параметр применяется следующая формула:

M=(ql2)/8

В формуле расчёта прогиба есть всего две переменных, но именно они в наибольшей степени определяют, какой в конечном итоге будет несущая способность деревянной балки:

Символ q показывает нагрузку, которую способна выдержать доска.В свою очередь буква l— это длина одной деревянной балки.

Внимание! Результат расчёт несущей способности и прогиба зависит от материала из которого сделана балка, а также от способа его обработки.

Насколько важно правильно рассчитать прогиб

Этот параметр крайне важен для прочности всей конструкции. Дело в том, что одной стойкости бруса недостаточно для долгой и надёжной службы, ведь со временем его прогиб под нагрузкой может увеличиваться.

Прогиб не просто портит эстетичный вид перекрытия. Если данный параметр превысит показатель в 1/250 от общей длины элемента перекрытия, то вероятность возникновения аварийной ситуации возрастёт в десятки раз.

Так зачем нужен калькулятор

Представленный ниже калькулятор позволит вам моментально просчитать прогиб, несущую способность и многие другие параметры без использования формул и подсчётов. Всего несколько секунд и данные по вашему будущему дому будут готовы.

В современном индивидуальном строительстве деревянные балки используются почти в каждом проекте. Найти постройку, в которой не используются деревянные перекрытия, практически невозможно. Деревянные балки применяются и для устройства полов, и в качестве несущих элементов, как опоры для межэтажных и чердачных перекрытий.

Формула расчета прогиба балки.

Известно, что деревянные балки, как и любые другие, могут прогибаться под воздействием различных нагрузок.

Эта величина — стрелка прогиба — зависит от материала, характера нагрузки и геометрических характеристик конструкции. Небольшой прогиб вполне допустим. Когда мы ходим, например, по деревянному настилу, то чувствуем, как пол слегка пружинит, однако если такие деформации незначительны, то нас это мало беспокоит.

Насколько можно допустить прогиб, определяется двумя факторами:

Прогиб не должен превышать расчетных допустимых значений.Прогиб не должен мешать эксплуатации здания.

Чтобы узнать, насколько будут деформироваться деревянные элементы в конкретном случае, нужно произвести расчеты на прочность и жесткость. Подробные и детальные расчеты такого рода — это работа инженеров-строителей, однако, имея навык математических вычислений и зная несколько формул из курса сопротивления материалов, вполне можно самостоятельно рассчитать деревянную балку.

Вспомогательная таблица для расчета количества балок.

Любая постройка должна быть прочной.

Именно поэтому балки перекрытия проверяют в первую очередь на прочность, чтобы конструкция могла выдерживать все необходимые нагрузки, не разрушаясь. Кроме прочности конструкция должна обладать жесткостью и устойчивостью. Величина прогиба является элементом расчета на жесткость.

Прочность и жесткость неразрывно связаны между собой. Вначале делают расчеты на прочность, а затем, используя полученные результаты, можно сделать расчет прогиба.

Чтобы правильно спроектировать собственный загородный дом, необязательно знать полный курс сопротивления материалов. Но углубляться в слишком подробные вычисления не стоит, как и просчитывать различные варианты конструкций.

Чтобы не ошибиться, лучше воспользоваться укрупненными расчетами, применяя простые схемы, а высчитывая нагрузки на несущие элементы, всегда делать небольшой запас в большую сторону.

Алгоритм вычисления прогиба

Рассмотрим упрощенную схему расчета, опуская некоторые специальные термины, и формулы для расчета двух основных случаев нагружения, принятых в строительстве.

Нужно выполнить следующие действия:

Составить расчетную схему и определить геометрические характеристики балки.Определить максимальную нагрузку на этот несущий элемент.При необходимости проверить брус на прочность по изгибающему моменту.Вычислить максимальный прогиб.

Расчетная схема балки и момент инерции

Расчетную схему сделать довольно просто. Нужно знать размеры и форму поперечного сечения элемента конструкции, способ опирания, а также пролет, то есть расстояние между опорами. Например, если вы укладываете опорные брусья перекрытия на несущие стены дома, а расстояние между стенами 4 м, то пролет будет l=4 м.

Деревянные балки рассчитывают как свободно опертые. Если это балка перекрытия, то принимается схема с равномерно распределенной нагрузкой q. В случае если нужно определить изгиб от сосредоточенной нагрузки (например, от небольшой печки, выложенной прямо на перекрытии), принимается схема с сосредоточенной нагрузкой F, равной весу, который будет давить на конструкцию. 3/48*E*J, где:

F — сила давления на брус, например, вес печи или другого тяжелого оборудования.

Модуль упругости Е для разных видов древесины различен, эта характеристика зависит не только от породы дерева, но и от вида бруса — цельные балки, клееный брус или оцилиндрованное бревно имеют различные модули упругости.

Подобные вычисления могут производиться с различными целями. Если вам нужно просто узнать, в каких пределах будут находиться деформации элементов конструкции, то после определения стрелки прогиба дело можно считать завершенным. Но если вас интересует, насколько полученные результаты соответствуют строительным нормам, то необходимо выполнить сравнение полученных результатов с цифрами, приведенными в соответствующих нормативных документах.

Балка является основным элементом несущей конструкции сооружения.

При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.

При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах.

Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно.Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

Виды балок

Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению.

Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.

Деревянные

Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

Для расчета максимального прогиба следует учитывать:

Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.Форма поперечного сечения и другие геометрические характеристики.Различные виды нагрузки на материал.

Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.

Конструкции из древесины хвойных пород

Стальные

Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:

электросварка;заклепки;болты, винты и другие виды резьбовых соединений.

Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.

Для проведения расчета балки на прогиб может помочь видео:

Прочность и жесткость балки

Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.

Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали.

Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.

Существует два основных метода расчета прочности и жесткости:

Простой. При использовании данного метода применяется увеличительный коэффициент.Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.

Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.

Расчет на жесткость

Для расчета прочности балки на изгиб применяется формула:

Где:

M – максимальный момент, который возникает в балке;

Wn,min– момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.

Ryявляется расчетным сопротивлением стали при изгибе. Зависит от вида стали.

γcпредставляет собой коэффициент условий работы, который является табличной величиной.

Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:

Составление расчетной схемы объекта.Расчет размеров балки и ее сечения.Вычисление максимальной нагрузки, которая воздействует на балку.Определение точки приложения максимальной нагрузки.Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.Вычисление значения жесткости или максимально прогиба балки.

Чтобы составить расчетную схему, потребуются такие данные:

Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.

Расчет моментов инерции и сопротивления сечения

Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:

Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.

Определение максимальной нагрузки и прогиба

Для точного определения прогиба балки, лучше всего применять данную формулу:

Где:

q является равномерно-распределенной нагрузкой;

E – модуль упругости, который является табличной величиной;

l – длина;

I – момент инерции сечения.

Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.

Особенности расчета на прогиб

Расчет на прогиб проводится обязательно для любых перекрытий.

Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.Варианты нагружения консольного стержня, который закреплен жестко.Действие на конструкцию сложной нагрузки.

Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.

Пример подсчета прогиба

Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов.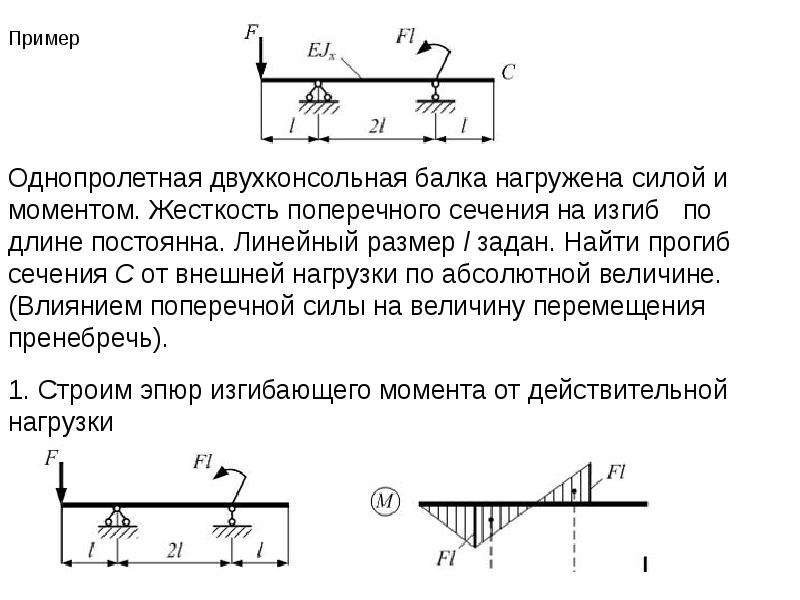 Данный расчет проводится для балки с такими характеристиками:

материал изготовления – древесина;плотность составляет 600 кг/м3;длина составляет 4 м;сечение материала составляет 150*200 мм;масса перекрывающих элементов составляет 60 кг/м²;максимальная нагрузка конструкции составляет 249 кг/м;упругость материала составляет 100 000 кгс/ м²;J равно 10 кг*м².

Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:

вес одного метра балки;вес м2 перекрытия;расстояние, которое оставляется между балками;временная нагрузка;нагрузка от перегородок на перекрытие.

Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.

Если подставить все эти значения в формулу, то получится:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].

Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.

Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко.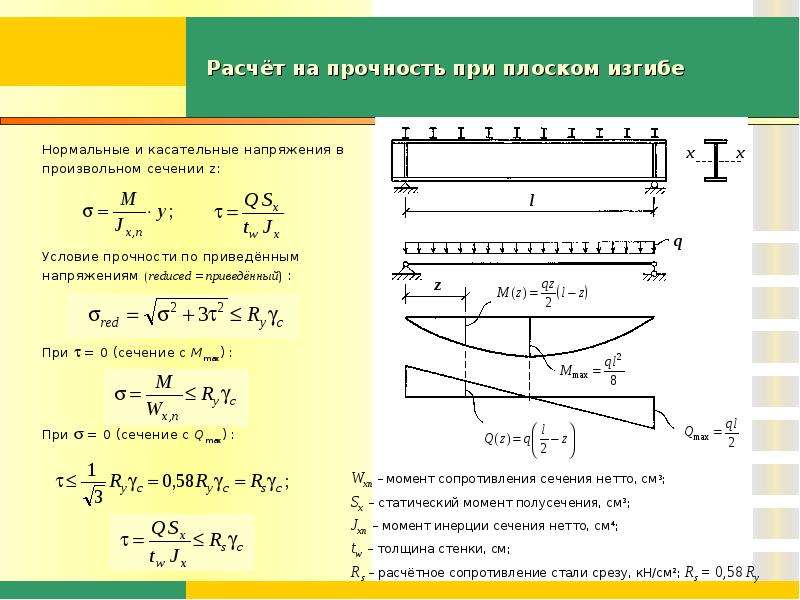 Достаточно знать необходимые формулы, а также высчитать величины.

Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид.

Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.

Источники:

rascheta.net
bouw.ru
1poderevu.ru
viascio.ru

формула, механизм и примеры вычисления прогиба по стандартам

Для строительства прочного, надежного и долговечного здания, нужно знать такой показатель, как прогиб балки (формула), то есть величину жесткости.

Данное направление изучается в таких науках (дисциплинах), как “Сопротивление материалов”, “Теория прочности”, “Механика строительная” и прочее.

Прочность и жесткость балки

Балки в доме

Современные строительные технологии, применяемые для просчета стройконструкций, называемых также стержневыми, по качествам прочности и жесткости дают уникальную возможность на первом же этапе проектировки вычислить величину прогиба.

Кроме этого, можно, опираясь на рассчитанные данные, составить заключение о вероятности использования строительной конструкции.

Какой вопрос позволяет решать указанная далее формула для расчета жесткости? Данные, полученные таким путем, говорят о самых больших изменениях в геометрии детали, что могут возникнуть в строительной конструкции.

Несмотря на некоторую бюрократизацию методик для вычисления прогиба, используются опытные формулы, а если воздействие реальных нагрузок отличается от идеальных или усредненных, вопрос решается введением дополнительных коэффициентов для запаса прочности. Понятия «жесткость» и «прочность» связаны и абсолютно неразделимы.

Хотя некоторые различия все-таки есть. Но только в том случае, если рассматривать данные показатели в автомашинах. В стройконструкциях главное нарушение конструкции объектов случается потому, что снижаются или нивелируются полностью вопросы, связанные с запасом прочности, вследствие чего здания нельзя эксплуатировать.

Деревянные балки из древесины хвойных пород

На сегодня в таких предметах изучения, как «Сопромат» и другие, приняты 2 метода для расчета прочности и жесткости:

Простой. При просчитывании показателей на основе этого метода используют увеличенный коэффициент.
Точный. Тут используются не только коэффициенты, показывающие запас прочности, но также осуществляется вычисление пограничного состояния (какую нагрузку может выдержать балка).

Как рассчитывать прогиб для балки дома

Чтобы просчитать, подходит ли конкретная балка для строительства дома, нужно знать такие показатели:

M – это тот максимальный момент, который возникает в балке, находящийся по эпюру моментов. Эпюр – это специальный чертеж с изображением пространственная фигура изображается на плоскости.
W _{n, m}_і_n – момент сопротивления сечения (его значение находят по таблице).
R_y – сопротивление, что оказывает материал, из которого изготовлен элемент конструкции дома, изгибаясь от нагрузки.
У_c – дополнительный показатель (его можно найти в одной из многочисленных таблиц строительных нормативов).

Формула для расчета прогиба представляет из себя неравенство следующего вида (формула № 1):

М / (W _{n, min}* R_y* У_c) ≤1

Чтобы правильно применить формулу, нужно действовать так:

Нарисовать схематично балку и ее будущее расположение под крышей дома. Чтобы верно изобразить на чертеже все части исследуемого объекта, нужно знать форму и линейные размеры балки, поперечного сечения, характер будущих нагрузок, материал, из которого балка изготовлена.
Записать ее точные размеры.
Рассчитать по указанной формуле, чему равно частное максимального момента балки к произведению остальных трех величин.
Сравнить полученный результат с единицей: если он меньше или равен 1, то вычисления дают положительный ответ.

Зная значение параметров рассматриваемой балки и сил, действующих на нее, сделав нехитрые вычисления, можно быстро справится с задачей вычисления допустимого прогиба балки дома.

Как вычислить вспомогательные величины

Для получения полной информации о значениях, необходимых для достижения конечной цели вычислений, нужно узнать, каков момент сопротивление сечения (формула № 2):

W_n_{(требуемое)} = М _мах/ (R_y* У_c)

Необходимо обязательно уитывать ориентирование рассматриваемого балочного сечения, так как с уменьшением моментов инерций жесткость балок снижается, чего допускать нельзя. Для выяснения максимального значения нагрузки f, которое может выдержать балка, надо вычислить его по такой формуле № 3:

f = (5 / 384) * [(q_n * L⁴) / (E * J)] £ [¦], где

L – продольный размер, в метрах
E – коэффициент, показывающий упругость (для каждого материала или сплава он будет разным)
J – момент инерции по сечению
q_n – это нагрузка, равномерно-распространенная, выражается в кг/м или в Н/м

Показатель J рассчитывается так:

J = b * h³/ 12

Обозначения:

b – диаметр сечений
h – вертикальный размер сечения

Примером для сечений, величиной 15 на 20 сантиметров:

J = 0,15 * (0,2)³/ 12 = 10 000 см⁴или 0,0001 м⁴

Кроме указанных расчетных или табличных величин, среди важных факторов, которые нужно учитывать при определении максимальных нагрузок, выделяют такие: статические (которые действуют постоянно, независимо от переменных внешних факторов), периодические (действие ветра, вибрации, ударов).

Пример подсчета прогиба

Прогиб балки (формула, пример расчета) вычисляется так. Допустим, есть балка, для которой нужно рассчитать прогиб, с такими параметрами:

Материал изготовления – дерево.
Плотность 600 кг/м³.
Длина балки L – 4 м, остальные размеры: 15 см х 20 см.
Масса перекрывающих элементов – 60 кг/м².
Максимальная нагрузка q равна 249 кг/м.
E (насколько упруго дерево) – 100 000 кгс/ м².
J балок – 10 кг*м².

Максимально допустимая нагрузка вычисляется с учетом веса не только балочной конструкции, но и перекрытия, а также опор.

Расчет на поперечный прогиб

Не лишним будет учесть тяжесть, которую будут оказывать люди или приборы, механизмы и другие тяжелые вещи, если вычисляется прогиб балок этажа дома. Нужны такие данные, как:

Сколько весит один пог. метр рассматриваемой балки.
Сколько весит каждый м² перекрытия.
Какова временная нагрузка на перекрытие.
Сколько составляет нагрузка от перегородок на 1 м² перекрытия.
Каков коэфф. k (это промежуток, оставляемый между балками).

Чтобы упростить пример расчетов, принимают масс перекрытия за 60 кг/м², нормальную непостоянную нагрузку на каждое перекрытие – 250 кг/м², нагрузки от перегородок равными 75 кг/м², тяжесть части деревянных балок – 18 кг/погонный метр. Когда расстояние между перекрытиями равно составляет 600 мм, тогда коэффициент k равен 0,6. Подставляем в формулу все эти значения:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Изгибающий момент нужно вычислить по формуле №3, учитывая все указанные выше данные. Получается:

f = (5 / 384) * [(q_n * L⁴) / (E * J)] = (5 / 384) * [(249 * 4⁴) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Это – показатель уровня прогиба во время воздействия максимальной нагрузки. Что именно он обозначает? Получается, что менее, чем на один сантиметр прогнется балка при указанной максимальной нагрузке. После этого нужно сравнить полученный результат с единицей: 0,83 меньше 1.

При расчетах деформации важных строящегося здания используют указанные выше простые формулы. Прогиб балки по формуле СНиП является универсальным способом вычисления жесткости балок и величины их прогибания.

Как посчитать балку на изгиб — на видео:

Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.

Пример расчета прогиба балки — Яхт клуб Ост-Вест

Прочность и жесткость балки

Деревянные балки из древесины хвойных пород

Простой. При просчитывании показателей на основе этого метода используют увеличенный коэффициент.
Точный. Тут используются не только коэффициенты, показывающие запас прочности, но также осуществляется вычисление пограничного состояния (какую нагрузку может выдержать балка).

Как рассчитывать прогиб для балки дома

Чтобы просчитать, подходит ли конкретная балка для строительства дома, нужно знать такие показатели:

M – это тот максимальный момент, который возникает в балке, находящийся по эпюру моментов. Эпюр – это специальный чертеж с изображением пространственная фигура изображается на плоскости.
W _{n, m}_і_n – момент сопротивления сечения (его значение находят по таблице).
R_y – сопротивление, что оказывает материал, из которого изготовлен элемент конструкции дома, изгибаясь от нагрузки.
У_c – дополнительный показатель (его можно найти в одной из многочисленных таблиц строительных нормативов).

Формула для расчета прогиба представляет из себя неравенство следующего вида (формула № 1):

Чтобы правильно применить формулу, нужно действовать так:

Нарисовать схематично балку и ее будущее расположение под крышей дома. Чтобы верно изобразить на чертеже все части исследуемого объекта, нужно знать форму и линейные размеры балки, поперечного сечения, характер будущих нагрузок, материал, из которого балка изготовлена.
Записать ее точные размеры.
Рассчитать по указанной формуле, чему равно частное максимального момента балки к произведению остальных трех величин.
Сравнить полученный результат с единицей: если он меньше или равен 1, то вычисления дают положительный ответ.

Как вычислить вспомогательные величины

f = (5 / 384) * [(q_n * L 4 ) / (E * J)] £ [¦], где

L – продольный размер, в метрах
E – коэффициент, показывающий упругость (для каждого материала или сплава он будет разным)
J – момент инерции по сечению
q_n – это нагрузка, равномерно-распространенная, выражается в кг/м или в Н/м

Показатель J рассчитывается так:

b – диаметр сечений
h – вертикальный размер сечения

Примером для сечений, величиной 15 на 20 сантиметров:

J = 0,15 * (0,2) 3 / 12 = 10 000 см 4 или 0,0001 м 4

Пример подсчета прогиба

Материал изготовления – дерево.
Плотность 600 кг/м 3 .
Длина балки L – 4 м, остальные размеры: 15 см х 20 см.
Масса перекрывающих элементов – 60 кг/м².
Максимальная нагрузка q равна 249 кг/м.
E (насколько упруго дерево) – 100 000 кгс/ м².
J балок – 10 кг*м².

Расчет на поперечный прогиб

Сколько весит один пог. метр рассматриваемой балки.
Сколько весит каждый м 2 перекрытия.
Какова временная нагрузка на перекрытие.
Сколько составляет нагрузка от перегородок на 1 м 2 перекрытия.
Каков коэфф. k (это промежуток, оставляемый между балками).

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Изгибающий момент нужно вычислить по формуле №3, учитывая все указанные выше данные. Получается:

f = (5 / 384) * [(q_n * L 4 ) / (E * J)] = (5 / 384) * [(249 * 4 4 ) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Как посчитать балку на изгиб — на видео:

Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.

Для заданной балки двутаврового сечения ( = 210 МПа, Е = 2 х 10 5 МПа) и нагрузок требуется;

1. Построить эпюры поперечных сил и изгибающих моментов;

2. Определить нормальные и касательные напряжения в сечениях с наибольшим моментом и поперечной силой на расстоянии h/4 от нейтральной оси;

3. Определить прогиб конца балки точки В.

При построении эпюр Q и М необходимо соблюдать правило знаков. Положительное направление сил показано на схеме.

1. Определяем опорные реакции

2. Методом сечений определяем ординаты поперечной силы в характерных сечениях. Для этого балку разбиваем на два участка. Границы участков – места изменения нагрузки. Построение эпюры начинаем с правого свободного конца балки.

Максимум изгибавшего момента находится в сечении, где поперечная сила равна нулю. Положение этого сечения определяем из условия:

3. Методом сечений определяем изгибающие моменты в характерных сечениях и строим эпюру моментов. Экстремум в т. х = 2 м.

Наиболее нагруженным сечением в балке является сечение А у заделки, где М_max = 120 кН м, Q_mах = – 80 кН.

4. Из условий прочности по нормальным напряжениям определяем требуемый момент сопротивления сечения.

По сортаменту ГОСТ 8509-72 принимаем двутавр № 33.

Максимальные напряжения в опасном сечении будут равны

5. Определяем нормальное напряжение в точке Е сечения на расстоянии h/4 = 8,25 см от нейтральной оси (рис. 4.9.).

Для определения касательного напряжения в точке Е вычислим статический момент отсеченной выше точки Е площади относительно центральной оси Х.

6. Определяем прогиб балки в точке В, используя универсальное уравнение прогибов

Для заданной консольной балки граничные условия будут: угол поворота сечения А ; прогиб сечения А

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 9825 – | 7406 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2.09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.

Способы выполнить расчет и проверку на прогиб

Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.

Просчитать прогиб конструкции можно несколькими способами:

Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.

Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.

Методика выполнения расчета на прогиб

Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.

Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.

В нашем случае балка:

Имеет прямоугольное сечение S=b*h , длина опирающейся части составляет L ;
Линейка нагружена силой Q , проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ , с прогибом относительно начального горизонтального положения, равным f ;
Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.

Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ , где Е – справочная величина, R — усилие, Δ — величина деформации тела.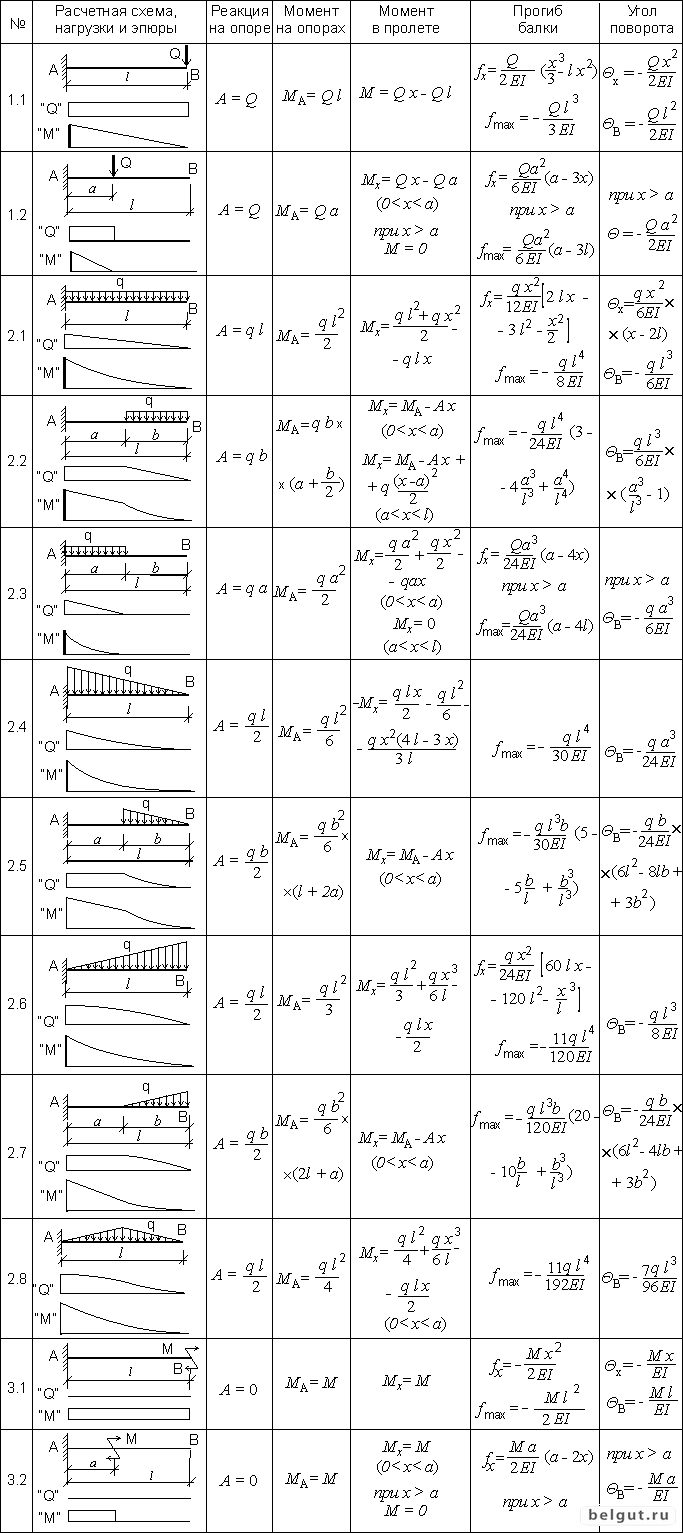

Вычисляем моменты инерции и сил

Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е) . Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е) .

Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.

Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е) .

Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил M_max = q*L*2/8 , соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е) . Величину b·h 2 /6 называют моментом инерции и обозначают W . В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.

Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L 2 /8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.

Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h 3 /12, где b и h – размеры сечения балки.

Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.

Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.

Формулы для практического использования

На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.

Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.

Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:

Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.

Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L 2 /(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.

Ответ прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.

Заключение

Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.

Составные балки и перемещения при изгибе (Лекция №21)

ПОНЯТИЕ О СОСТАВНЫХ БАЛКАХ

Работу составных балок проиллюстрируем на простом примере трехслойной балки прямоугольного поперечного сечения. Если слои между собой не связаны и силы трения между ними отсутствуют, то каждый из них деформируется как отдельная балка, имеющая свой нейтральный слой (рис. 1, а). Нагрузка между этими балками распределяется пропорционально их жесткостям при изгибе (в данном примере поровну). Это означает, что моменты инерции и моменты сопротивления трех независимо друг от друга деформирующихся балок должны быть просуммированы

Если скрепить балки сваркой, болтами или другим способом (рис. 1, б), то с точностью до пренебрежения податливостью наложенных связей сечение балки будет работать как монолитное с моментом инерции и моментом сопротивления, равным

Как видно, при переходе к монолитному сечению жесткость балки возрастает в девять раз, а прочностьв три раза. В инженерной практике наиболее распространены сварные двутавровые балки.

б)

а) несвязанная конструкция, б) связанная сварная конструкция
Рис.1. Расчетные схемы составных балок:

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ПРЯМОГО ИЗГИБА ПРИЗМАТИЧЕСКОГО СТЕРЖНЯ

Определено, что мерой деформации призматического стержня при прямом чистом изгибе является кривизна нейтрального слоя. Можно показать, что с достаточной для инженерных расчетов точностью этим тезисом можно пользоваться и в случае прямого поперечного изгиба стержня. Однако для практических целей кроме кривизны необходимо определить вертикальные перемещения центров тяжести отдельных поперечных сечений прогибов балки v, а иногда и углы поворота этих сечений (рис. 2). Вследствие гипотезы плоских сечений угол поворота сечения ( оказывается равным углу наклона касательной к изогнутой оси балки, который в силу малости

(1)

Тогда возникает геометрическая задача: составить уравнение для функции прогиба , зная закон изменения ее кривизны.

Рис.2. Расчетная схема определения перемещений при изгибе

Воспользуемся известным из дифференциальной геометрии выражением для кривизны в прямоугольных декартовых координатах:

(2)

Однако, учитывая, что в инженерной практике применяются достаточно жесткие балки, для которых наибольший прогиб f (рис.2) мал по сравнению с длиной (f / l << 1), а первая производная от прогиба имеет порядок

и, следовательно, величиной (dv / dz)²<<1, стоящей в знаменателе (2), можно пренебречь, выражение для кривизны упрощается

(3)

Тогда, подставив это выражение в полученную ранее связку кривизны и изгибающего мометна , условившись что ось Oy направлена вверх и согласовав знаки и М_х, приходим к дифференциальному уравнению прямого изгиба балки

(4)

известному также как дифференциальное уравнение упругой кривой.

Если учесть точное выражение для кривизны по формуле (2), то точное уравнение упругой кривой

является нелинейным дифференциальным уравнением. Поэтому линейное дифференциальное уравнение, описывающее малые прогибы балки, иногда называют линеаризованным уравнением упругой кривой.

Решение уравнения получаем путем двукратного почленного интегрирования. При первом интегрировании получаем выражение

(5)

которое с учетом , дает также закон изменения углов поворота поперечных сечений по длине балки. Повторным интегрированием получаем функцию прогиба

(6)

Постоянные интегрирования С и D должны быть найдены из граничных условий.

Во всех приведенных выше уравнениях функция изгибающего момента М_х(г) предполагалась известной, что возможно лишь для статически определимых балок. Простейшие варианты статически определимых однопролетных балок и соответствующие граничные условия показаны на рис. 3. Условия, накладываемые на прогиб и угол поворота сечения, получили название кинематических граничных условий. Как видно, для шарнирно опертой балки требуется, чтобы прогиб на опорах v(0) =v(l) =0, а для консольной балки прогиб и угол поворота сечения в заделке

Рис.3. Примеры граничных условий: а) двухопорная, б) консольная балки

Дифференциальное уравнение неприменимо для расчета статически неопределимых балок, так как содержит неизвестный изгибающий момент М_x появившийся в результате двукратного интегрирования уравнения четвертого порядка

(7)

В этом уравнении нагрузка q известна, поэтому его можно получить, учитывая, что

При интегрировании уравнения необходимо задать четыре граничных условия (по два на каждом конце балки) в том числе так называемые силовые граничные условия условия, накладываемые на силовые величины (изгибающий момент и поперечную силу), которые выражаются через производные от прогиба. Так как

а с учетом дифференциального соотношения Q_y=dM_x/dz, получаем

(8)

Вернемся к интегрированию уравнения второго порядка. Если имеется несколько участков, для которых правая часть уравнения исходного f(z)=M_x/EJ_x, содержит разные аналитические выражения, то интегрирование усложняется. На рис. 4 приведена эпюра М_x, содержащая п участков. Для каждого участка независимое интегрирование дает по две константы, а при п участках требуется определить 2n постоянных. Добавляя к двум граничным условиям на опорах 2(n1) условия непрерывности и гладкости упругой кривой на границе; смежных участков, заключающиеся в равенстве прогибов v и углов поворота сечений dv/dz на этих границах

получим 2п граничных условий, необходимых для нахождения постоянных интегрирования.

Рис.4. Расчетная схема балки, содержащая n углов

Рекомендую для практики решения дифференциальных уравнений второго порядка воспользоваться системой входных тестов Т-4, приведенных в ПРИЛОЖЕНИИ.

Дальше…

Отклонение луча

Балка — конструктивный элемент, способный выдерживать большие нагрузки при изгибе. В случае небольших прогибов форму балки можно описать линейным дифференциальным уравнением четвертого порядка.

Рассмотрим вывод этого уравнения. Для изгибающейся балки угол \ (d \ theta \) появляется между двумя соседними секциями, расположенными на расстоянии \ (dx \) (рисунок \ (1 \)).

Рис. 1.

Деформация \ (\ varepsilon \) в каждой точке пропорциональна координате \ (y, \), которая отсчитывается от нейтральной линии.Длина нейтральной линии не изменилась.

Из геометрии рисунка \ (1 \) следует, что

\ [\ varepsilon = \ frac {y} {R}, \]

где \ (R \) — радиус кривизны балки. 2}}} {2}} = {0.4}}} = q. \]

Это уравнение при соответствующих граничных условиях определяет прогиб нагруженной балки.

Решенные проблемы

Щелкните или коснитесь проблемы, чтобы увидеть решение.

Пример 1

Определите прогиб балки, жестко зажатой с обоих концов и нагруженной равномерно распределенной силой (рисунок \ (4 \)).

Пример 2

Тонкий цилиндрический вал длиной \ (L \) вращается с угловой скоростью \ (\ omega.\) На какой скорости \ (\ omega \) вал разрушается? Модуль упругости материала \ (E, \), масса вала \ (M, \) и радиус секции \ (a. \)

Прогиб балки — Приложение по прочности материалов для энергетики

Прогиб

Цели обучения

По завершении этой главы вы сможете вычислить:

Радиус кривизны отклоненной балки с использованием теоретических соотношений
Максимальный прогиб свободно опертой балки
Максимальный прогиб различных балок с использованием метода формул и приложений к учебнику

Упругие свойства материалов количественно оцениваются через их модуль упругости.Все материалы в той или иной степени эластичны, например сталь E ≈ 210 ГПа, чугун E ≈ 160 ГПа, алюминий E ≈ 70 ГПа, бетон E ≈ 40 ГПа. В реальных условиях балки, подверженные внешним нагрузкам, будут отклоняться пропорционально изгибающему моменту и обратно пропорционально их жесткости. Общая жесткость балки может быть выражена как E × I _c , где E можно рассматривать как жесткость материала, а I _c как поперечную или геометрическую жесткость.

Радиус закругления

Просмотрите вывод отклонения балки, подробно описанный в главе 10. В практических ситуациях деформация балки очень мала по сравнению с ее длиной, и в результате радиус кривизны относительно велик.

Этот радиус кривизны можно рассчитать с помощью

где:

E — модуль упругости (сопротивление, обусловленное свойствами материала)
I _c — момент инерции относительно центральной оси (сопротивление из-за геометрии сечения)
M — изгибающий момент на интересующем участке

Если балка нагружена таким образом, что изгибающий момент остается постоянным по сечению балки (горизонтальная линия на диаграмме BM), то прогиб представляет собой дугу окружности, а радиус кривизны постоянен.

Найдите минутку и проанализируйте приведенную выше формулу… увеличение жесткости балки (E × I _c) уменьшит прогиб (большое R), в то время как больший изгибающий момент приведет к меньшему радиусу кривизны (большему прогибу / провисанию).

Прогиб луча

Рассмотрим балку с простой опорой, как показано на схеме выше. Как только радиус кривизны найден, максимальный прогиб (в середине пролета) можно легко геометрически рассчитать следующим образом:

Формульный метод для простых случаев

Формула радиуса кривизны действительна только для случаев, когда изгибающий момент постоянен.В других случаях для определения отклонения балки используются геометрические методы или методы интеграции. Результаты этих вычислений, представленные в алгебраической форме, приведены в инженерной книге формул. Наиболее распространенные случаи описаны в Приложении F.

к учебнику.

При использовании стандартных формул необходимо сначала согласовать геометрию балки и нагрузку с одним из указанных случаев. Если вы имеете дело с более сложной нагрузкой, такой как точечные нагрузки, чрезмерно накладываемые на распределенную нагрузку, вы можете проанализировать две нагрузки по отдельности, а для полного прогиба просто добавьте составляющие.

Назначенные проблемы

Для каждой задачи определите максимальный прогиб с помощью уравнений балки и сравните со значением, найденным с использованием радиуса кривизны. {4} $$

Бесплатный калькулятор луча | ClearCalcs

Как использовать бесплатный калькулятор балки

Калькулятор балки ClearCalcs позволяет пользователю ввести геометрию и загрузку балки для анализа за несколько простых шагов.Затем он определяет изгибающий момент, диаграммы сдвига и прогиба, а также максимальные требования, используя мощный механизм анализа методом конечных элементов.

Регистрация учетной записи ClearCalcs откроет дополнительные расширенные функции для проектирования и анализа балок и множества других структурных элементов. ClearCalcs позволяет проектировать из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.

Лист разделен на три основных раздела:

«Ключевые свойства», где пользователь вводит геометрию выбранного сечения и опор балки.
«Нагрузки», где можно ввести распределенные, точечные и приложенные моментные нагрузки,
«Сводка», в котором отображаются основные выходные данные и диаграммы.

Раздел «Комментарии» также включен для того, чтобы пользователь мог оставить какие-либо конкретные примечания по дизайну. Щелчок по любой из меток ввода / свойства дает описательное справочное объяснение.

1. Свойства входных клавиш

Свойства балки и сечения задаются путем ввода непосредственно в поля ввода.

Длина балки — это общая длина балки, включая все пролеты балки, в мм или футах.

Модуль Юнга установлен на значение по умолчанию 200 000 МПа или 29 000 фунтов на квадратный дюйм для конструкционной стали, но может быть изменен пользователем.

Площадь поперечного сечения зависит от выбранного сечения балки и по умолчанию принимает значения для обычной стальной балки.

Второй момент области (или момент инерции) также зависит от выбранного сечения балки и снова по умолчанию соответствует свойствам обычной стальной балки.

Свойства E, A и Ix для других секций балки можно получить из библиотеки свойств секций ClearCalcs.Кроме того, вы можете создать свой собственный раздел, используя наш бесплатный калькулятор момента инерции.

Положение опор слева позволяет пользователю вводить любое количество опор и указывать их положение по длине балки. Тип опоры может быть закрепленным (фиксированный в перемещении, свободный поворот) или фиксированным (фиксированный как при перемещении, так и при повороте) и выбирается из раскрывающегося меню. Требуется минимум одна фиксированная опора или две штифтовые опоры.

Вычислитель балок также учитывает пролет консолей на каждом конце, поскольку положение первой опоры не обязательно должно быть равно 0 мм, а положение последней опоры не обязательно должно быть равно длине балки.

Реакции на каждой из опор автоматически обновляются по мере добавления, изменения или удаления опор в зависимости от указанной нагрузки.

2. Входные нагрузки

Калькулятор поддерживает различные типы нагрузок, которые можно применять в комбинации. Каждой загрузке может быть присвоено имя пользователем.

Знаковое обозначение, используемое для нагружения (показаны положительные значения):

Распределенные нагрузки указываются в единицах силы на единицу длины, кН / м или plf, вдоль балки и могут применяться между любыми двумя точками.В калькуляторе можно использовать два разных типа:

Равномерная нагрузка имеет постоянную величину по длине приложения. Следовательно, начальная и конечная величины, указанные пользователем, должны быть одинаковыми.

Линейные нагрузки имеют переменную величину по длине приложения. Различные начальные и конечные величины должны быть указаны пользователем, и они могут использоваться для представления треугольных или трапециевидных нагрузок.

Точечные нагрузки указываются в единицах силы, кН или тысячах фунтов, и площади, приложенной в дискретных точках вдоль балки.Например, они могут представлять реакции других элементов, соединенных с балкой. Пользователь вводит имя, величину и местоположение слева от луча.

В приведенном ниже примере диаграммы из сводного раздела показана двухпролетная неразрезная балка с линейно распределенной нагрузкой на заплату и точечной нагрузкой.

3. Итоговые результаты вычислений

После задания нагрузки и геометрии калькулятор автоматически использует механизм конечно-элементного анализа ClearCalcs для определения моментов, поперечных сил и прогибов.Максимальные значения каждого из них выводятся как «Требование момента» , «Требование сдвига» и «Отклонение» вместе с диаграммами по длине балки.

Положительные значения означают отклонение вниз, а отрицательные значения — отклонение вверх. Знаковое соглашение, используемое на диаграммах поперечной силы и изгибающего момента, следующее (показаны положительные значения):

Использование курсора для наведения курсора на любую точку на диаграммах изгибающего момента, поперечной силы или прогиба дает конкретные значения в этом месте вдоль балки.В приведенном ниже примере показаны выходные параметры для двухпролетной неразрезной балки с линейно распределенной коммутационной и точечной нагрузкой.

Лучшее руководство по определению прогиба в балках переменного поперечного сечения — опытный инженер

Таблицы балок дают информацию и предполагают, что прогиб расчет основан на постоянном сечении. Итак, что делать, если у нашей балки есть крест сечение, которое меняется по длине балки?

Чтобы определить величину отклонения в балка переменного сечения, необходимо интегрировать формулу прогиба балки с моментом инерции, являющимся переменной по отношению к длине и применить граничные условия.Луч Формула отклонения: v ’’ = M (x) / [E * I (x)].

Непрерывное или дискретное — Есть два типа секций балки: непрерывные и дискретные. Большинство балок представляют собой непрерывных балок и имеют либо постоянное сечение, либо сечение, которое постепенно изменяется по длине балки. Кровельные балки в больших стальных зданиях — отличный пример непрерывной переменной балки. Балка относительно короткая на концах и очень высокая посередине.

Дискретные балки балки которые имеют внезапные разрывы в разрезе.Вы не поверите, но иногда это проще для расчета, потому что дискретные участки обычно постоянны, что приводит к более легкий расчет.

Формула отклонения балки — универсальная формула, которая позволяет настраивать несколько нагрузок и балку разделы. Предупреждаю, что чем больше чем точнее должны быть ваши расчеты, тем сложнее будет выполнить математику. Упрощение здесь сэкономит много времени и усилия. Как упоминалось ранее, формула:

в ’’ = M (x) / [E * I (x)]

Где v ’’ — вторая производная отклонения ( ускорение прогиба), M — момент, который обычно является функцией положение по длине балки, x. E — модуль упругости, I — момент инерции поверхности луч. Все табличные балки будут считайте это постоянной величиной, и поэтому ни одна из формул прогиба может быть использован.

Теперь, когда мы проинтегрируем приведенное выше уравнение, мы будем выполнение неопределенного интеграла, что означает, что мы должны добавить константу, C _n, к многочлену каждый раз, когда мы интегрируем. Поскольку мы будем интегрировать уравнение два раза, мы получим две константы. Если у нас есть дискретный В этом случае у нас будет два или более уравнений.

Граничные условия — это требования, которым должна соответствовать формула отклонения балки, когда она находится в окончательном виде. Окончательная форма приходит только тогда, когда мы используем граничные условия для решения констант образованный неопределенным интегралом. 4.

Теперь мы определим момент и дважды проинтегрируем уравнение прогиба балки, каждый раз добавляя переменную для неопределенного интеграла. Я решил, что моя система координат (переменная x) начинается с основания. Это немного усложняет интегрирование, но переменные C ₁ и C ₂ будут уравновешиваться из-за граничных условий 1 и 2. Вы увидите через секунду.

Мне нужно выполнить интегрирование только для одного из разделов, а затем изменить I ₁ на I ₂ в уравнениях.Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.

Теперь, когда проблема определена, давайте установим граничные условия. Нам нужно, чтобы положение и наклон на фиксированном конце балки составляли 0 дюймов и 0 радиан. Также нам понадобятся еще два граничных условия на стыке сегментов. Наклон и положение в этом положении должны быть одинаковыми.

Решим граничные условия 1 и 2

Как упоминалось выше, я предвидел, что переменные C1 и C2 будет равно 0, когда я выберу, чтобы система координат начиналась с база.

Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.

Обратите внимание на чек, который я поставил в блок Find, чтобы чтобы мы могли проверить, что v ₁ = v ₂ и s ₁ = s ₂ на 50 дюймовЭто подтверждает что положение и наклон в этой точке будут непрерывными.

Следующим шагом является проверка результатов. Это делается в два этапа. Первый — построить каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены. Как видите, линии пересекаются и касаются друг друга на расстоянии 50 дюймов. Кроме того, v ₁ не имеет прогиба или наклона в основании.

Наконец, мы объединим два графика вместе, образуя окончательное уравнение для отклонения нашей консольной балки. 4.

Теперь определим момент и проинтегрируем уравнение отклонения балки дважды каждый раз, добавляя переменную. Я выбрал две системы координат. Координата x идет слева направо и координата y идет справа налево. Их связывает:

г = L-x

Я выбрал эту систему координат так, чтобы C ₂ и C ₄ будет сокращаться, когда мы решаем граничные условия 1 и 2. Это также упрощает математические вычисления. чрезвычайно.Вы увидите через секунду.

Мне нужно выполнить интегрирование только для одного из разделов, а затем изменить I ₁ на I ₂ и w ₁ на w ₂ в уравнениях. В уравнениях правого сечения я также заменю «y» на «x». Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.

Теперь, когда проблема определена, давайте установим граничные условия.Нам нужно, чтобы концы балки были отклонены на 0 дюймов (BC 1 и 2). Также нам понадобятся еще два граничных условия на стыке сегментов. Наклон и положение в этой позиции должны быть такими же, как и в месте соединения сегментов.

Решим граничные условия 1 и 2

Как упоминалось выше, я предвидел, что переменные C ₂ и C ₄ будет равно 0, если я выберу координату система запускается на базе.

Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.

Обратите внимание на чек, который я поставил в блок Find, чтобы чтобы мы могли проверить, что v ₁ = v ₂ и s ₁ = s ₂ при 200 дюйм. Это подтверждает что положение и наклон в этой точке будут непрерывными.

Ой, что случилось !? Линии определенно пересекаются на расстоянии 200 дюймов, и каждый конец имеет 0 дюймов прогиб, но они не касаются на пересечении. Я не только показываю силу график решения для точности, но также демонстрируя, что с помощью двух разные системы координат создают проблему. Согласно уравнениям склоны приближаются к месту расположения стык на равном по величине нисходящем склоне.Однако сделать эту работу одной из склонов на самом деле нужно подойти. Мы можем исправьте эту проблему, внеся одно небольшое изменение.

с ₁ = -s ₂

Давайте внесем это изменение и приступим к решению.

Да намного лучше! Наконец, мы объединим два графика вместе, образуя окончательное уравнение отклонения нашей консольной балки.

Как и ожидалось, более длинная и жесткая секция меньше прогибается.

Пример 3: Постоянно изменяющаяся неразрезная балка с простой опорой и постоянной распределенной нагрузкой.

Эта проблема состоит из стальной балки с простой опорой длиной 300 дюймов с распределенной нагрузкой 1000 фунтов / дюйм поперек балки. Сечение начинается на высоте 10 дюймов, линейно увеличивается к центру, где достигает высоты 24 дюйма. Затем он снова сужается до 10 дюймов.

Чтобы определить, как момент инерции изменяется по отношению к x, мы будем моделировать в Solidworks и делать сечения каждые 30 дюймов. Мы сведем эти данные в таблицу и подгоним к ним линию.

Вы, наверное, заметили, что я сделал таблицу только для значений от 0 до 150 дюймов. Это потому, что я собираюсь использовать симметрию, чтобы упростить эту сложную задачу. Мы можем использовать симметрию, потому что и нагрузка, и сечение балки симметричны относительно середины балки. Из-за симметрии нам нужно, чтобы конечная точка имела прогиб 0 дюймов, а наклон в середине балки был 0 градусов. Затем мы можем отразить это, чтобы получить непрерывное отклонение луча. В этом случае координата x будет идти слева направо.

Здесь вы можете видеть, что вычисленные значения I (x) точно соответствуют тому, что указано в таблице выше. Я назвал вторую производную от положения «а1» (ускорение). Как видите, верхняя и нижняя части имеют переменную «x», и интегрировать это будет очень весело. Итак, вам нужно знать обо мне одну вещь. У меня есть ограничения на то, что я не буду делать. Интеграция — одна из таких вещей. Вот почему у нас есть MathCAD!

Как видите, очень утомительная работа по интеграции была замалчена, и мы смогли напрямую решить для нашей границы условия.В уравнениях s (x) и v (x), на самом деле были натуральные бревна и каким-то образом появилась обратная касательная (не показано). Я до сих пор не жалею позволяя MathCAD делать всю работу.

Следующим шагом является проверка результатов. Это делается в два этапа. Первый — построить каждый сегмент по всей длине. Мы ищем, чтобы наши граничные условия были выполнены. Как видите, отклонение при x = 0 дюймов составляет 0 дюймов, а наклон кажется плоским при x = 150 дюймов.

Наконец, мы отразим графики вместе, образуя окончательное уравнение для отклонения нашей консольной балки.

Как видите, отклонение составляет 0 дюймов в конечных точках и имеет максимальное отклонение в центре.

Заключение

В этой статье рассматриваются три популярных варианта нагружения, когда балка имеет переменное поперечное сечение. Хотя это действительно связано с исчислением, часто это очень легко сделать вручную, потому что это многочлены. Если нет, то будьте благодарны за такие надежные программы, как MathCAD, которые сделают это за вас. Эта статья должна дать вам хорошее представление о процедуре, используемой для анализа подобных балок.Если ваша балка не загружена именно так, вы всегда можете найти расчет момента в таблице и интегрировать свое сердце.

Связанные

Метод наложения | Прогиб балки

Наклон или прогиб в любой точке балки равен результирующему наклону или прогибу в этой точке, вызванному каждой нагрузкой, действующей отдельно. 3} {360EI}

долл. США

Максимальный прогиб
$ \ delta = \ dfrac {2.2} {16EI}

долл. США

Уравнение прогиба ($ y $ положительно вниз)
$ EI \, y = \ dfrac {Mx} {6L} (L — x) (2L — x) $

Наклон и прогиб балки

Когда балка нагружается поперечными нагрузками, изгибающие моменты развиваются, что заставляет ось луча отклоняться от исходное положение без помех, как показано на следующем рисунке.

На рисунке выше невозмущенная ось консольной балки обозначена AB. а отклоненная форма — AB ‘.Отклоненная форма балки также известна как упругая кривая. Отклонение точки B от точки B ‘равно показано как отклонение δ _B и изменение наклона касательной в точке B показано как наклон θ _B.

Дифференциальное уравнение упругости Кривая была впервые дана Эйлером и записана как

, где E = модуль упругости эластичность материала балки

Я = момент инерции балки х-сечения

v = отклонение по оси y

x = расстояние от начала координат до точки отклонения

M = изгибающий момент на участке

Требуются расчеты прогиба для зданий, мосты и машины для удовлетворения некоторых критериев проектирования и контроля вибрации.

Существуют различные методы определения наклона и прогиб луча. Некоторые из них приведены ниже;

Метод интеграции / Метод Маколея
Площадь-моментный метод
Метод сопряженных пучков
Деформационно-энергетический метод (метод Кастильяно теоремы)
Виртуальный метод работы (Единичная нагрузка метод)

Воспользуйтесь нашим Калькулятор прогиба Простота использования калькулятор для различных нагрузок на балки

Калькулятор распределения моментов ^Новый для решения неопределенных балок с различными нагрузками

Расчет металлической балки на прогиб: учимся составлять формулы

Что такое прогиб балки?

Метод начальных параметров

Расчет прогибов балки

Реакции опор

Система координат

Распределенная нагрузка

Учет внешней нагрузки

Прогибы балок | Блог Ярослава Указова

Полный расчет балки на прочность и жесткость

Определение опорных реакций

Построение эпюр Q и М

Проверка сечения балки по касательным напряжениям

Проверка прочности балки по главным напряжениям

Расчет перемещений сечений (прогибов балки)

Проверка жесткости балки

Выполнение расчета прогиба деревянной балки

1. Конструктивные требования к прогибам деревянных балок.

1.

Что нужно для того чтобы сделать правильный расчёт

Длина

Общая информация по методологии расчёта

Как рассчитать несущую способность и прогиб

Насколько важно правильно рассчитать прогиб

Так зачем нужен калькулятор

Алгоритм вычисления прогиба

Расчетная схема балки и момент инерции

Виды балок

Деревянные

Стальные

Прочность и жесткость балки

Расчет на жесткость

Расчет моментов инерции и сопротивления сечения

Определение максимальной нагрузки и прогиба

Особенности расчета на прогиб

Пример подсчета прогиба

формула, механизм и примеры вычисления прогиба по стандартам

Прочность и жесткость балки

Как рассчитывать прогиб для балки дома

Как вычислить вспомогательные величины

Пример подсчета прогиба

Пример расчета прогиба балки — Яхт клуб Ост-Вест

Прочность и жесткость балки

Как рассчитывать прогиб для балки дома

Как вычислить вспомогательные величины

Пример подсчета прогиба

Способы выполнить расчет и проверку на прогиб

Методика выполнения расчета на прогиб

Вычисляем моменты инерции и сил

Формулы для практического использования

Заключение

Составные балки и перемещения при изгибе (Лекция №21)

Отклонение луча

Решенные проблемы

Пример 1

Пример 2

Прогиб балки — Приложение по прочности материалов для энергетики

Прогиб

Бесплатный калькулятор луча | ClearCalcs

Как использовать бесплатный калькулятор балки

1. Свойства входных клавиш

2. Входные нагрузки

3. Итоговые результаты вычислений

Лучшее руководство по определению прогиба в балках переменного поперечного сечения — опытный инженер

Метод наложения | Прогиб балки

Наклон и прогиб балки

Вы также можете выбрать из следующих ссылок решенных примеров, чтобы подготовиться к экзаменам, таким как GATE и GRE.

Добавить комментарий Отменить ответ