Формула расчет прогиба балки: Расчет балки на прогиб — формулы, параметры и примеры решения

Распределенная нагрузка на балку — формулы, условия и примеры расчета

Взаимодействия с деталями, отдельными элементами и конструкциями механизма задается с помощью нагрузок. В плоскости задается интенсивность взаимодействия конструкции по длине, а в пространстве – по её площади.

Распределённая нагрузка на балку задается площадью, обозначается буквой q и измеряется в [H/м³] для объемной конструкции, в [H/м²] — для площади, для линейной – в [H/м].

Продемонстрируем это на рисунке:

Нагрузку также можно заменить тягой, рассредоточенной по всей поверхности. Значение определяется по формуле:

Q = q ∗ AB⌈H⌉

здесь AB является тяжестью, q – интенсивностью, которая измеряется в [H/м].

Примечательно, что сила приложена к середине данного отрезка AB.

На данном рисунке представлен расчёт возрастающей нагрузки, которую можно заменить равнодействующей единицей, рассчитываемое по формуле:

Q = q_max ∗ AB/2

где q_max – максимальная интенсивность [Н/м].  

Q приложена к точке C, где AC равно: AC = 2/3 AB 

Рассматривая функцию q(x), представленную на рисунке:

можно высчитать значение эквивалентной силы по формуле:

Равномерно и неравномерно распределенная нагрузка на балку

Распределение сил, которые лежат в одной плоскости, задается равномерно распределенной тяжестью. Основным обозначением является интенсивность q — предельная тяга, несущая равнодействующую на единицу длины нагруженного участка АВ длиной а. 

Единицы измерения распределённой нагрузки [Н/м].

Её также можно заменить на величину Q, которая приложена в середину AB. 

Составим формулу: Q = q∗a

Неравномерно распределённую нагрузку чаще всего упрощают, приводя её к эквивалентной равномерно распределенной, чтобы упростить расчеты.

При построении также следует учитывать максимальный прогиб балки, её прочность, расчетную опорную реакцию и моментальную опору.

Пример решения задач с распределенной нагрузкой

Рассмотрим пример распределенной нагрузки на балку. Им может послужить тяга, благодаря которой происходит разрыв стальной стенки баллона с некоторым газом.

Для начала определяем результирующую давления в металлической трубе. Интенсивность равна q, радиус этого сектора трубы – R, ось симметрии Оx, а 2α – это центральный угол. Представим это на рисунке:

Выделим элемент сектора трубы ∆ϕ.

Затем определим единицу силы ∆Q. Она действует на плоскость дуги. Составим формулу:

Проекция результирующей тяги на ось Оx является:

Исходя из вышесказанного, можно найти проекцию этой же силы на ось Оy:

AB является хордой, которая стягивает дугу.

В нашей задаче сосуд – это ёмкость цилиндрической формы с высотой H, внутренним давлением P, действующим на стенки, и нагрузкой q = p [Н/м²].  

Разделим цилиндр вдоль его диаметра. 

Исходя из этого, равнодействующая результирующих сил определяется по формуле:

где d – это внутренний диаметр цилиндра, h — его высота. 

Формулу также можно записать следующим образом:

Итак, почему баллон имеет способность разрываться? На его стенки действуют значения S1, S2, S3 (площади), а также F, p (плотность), h (высота цилиндра) и R (его радиус). Рассчитаем их по формулам:

 

Изобразим баллон в момент разрыва:

Учтём a – толщину ёмкости. Таким образом напряжение, которое растягивает баллон, (усилия распространяются в том числе на крышку и дно цилиндра) равно:

Важную роль при решении практических задач также играет эпюра распределенной нагрузки – плоская фигура, которая ограничена графиком. Величина, действующая на балку, называется интенсивностью – силой, которая распространяется на единицы площади, объема или длины.

Расчет металлической балки на прогиб: учимся составлять формулы

Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Что такое прогиб балки?

Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

ν-прогиб сечения C; θ-угол поворота сечения C.

Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений.

Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Метод начальных параметров

Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)

Под начальными параметрами понимаются уже известные перемещения:

• в опорах прогибы равны нулю;
• в жесткой заделке прогиб и угол поворота сечения равен нулю.

Учитывая эти хитрости, их называют еще граничными условиями, определяются перемещения в других частях балки.

Расчет прогибов балки

Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

Реакции опор

Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.

Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:

Система координат

Далее вводим систему координат, с началом в левой части балки (точка А):

Распределенная нагрузка

Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат.

Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.

Если бы нагрузка была приложена вот таким способом:

То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.

Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:

Относительно системы координат записываем граничные условия.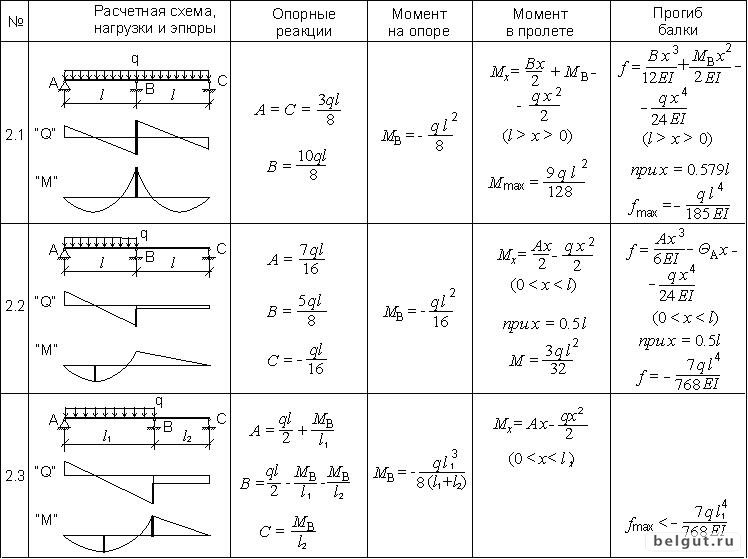 Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:

\[ { V }_{ A }=0\quad при\quad x=0 \]

\[ { V }_{ B }=0\quad при\quad x=8м \]

Записываем уравнение метода начальных параметров для сечения C:

\[ E{ I }_{ z }{ V }_{ C }=… \]

Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:

\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]

Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:

\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+… \]

Учет внешней нагрузки

И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. { 4 } } =-2см \]

Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.

На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).

Расчет балки на прогиб

Однопролетные балки на двух шарнирных опорах
1	Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке	Смотреть расчет
2	Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках	Смотреть расчет
3	Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке	Смотреть расчет
4	Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке	Смотреть расчет
5	Расчет балки на двух шарнирных опорах при действии изгибающего момента	Смотреть расчет
Балки с жестким защемлением на двух опорах
6	Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке	Смотреть расчет
7	Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках	Смотреть расчет
8	Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке	Смотреть расчет
9	Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке	Смотреть расчет
10	Расчет балки с жестким защемлением на опорах при действии изгибающего момента	Смотреть расчет
Балки с жестким защемлением на одной опоре (консольные)
11	Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке	Смотреть расчет
12	Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке	Смотреть расчет
13	Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке	Смотреть расчет
14	Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента	Смотреть расчет
Балки двухпролетные
15	Расчет двухпролетной с шарнирными опорами при одной сосредоточенной нагрузке	Смотреть
16	Расчет двухпролетной с шарнирными опорами при двух сосредоточенных нагрузках	Смотреть
17	Расчет двухпролетной с шарнирными опорами при одной равномерно-распределенной нагрузке	Смотреть
18	Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке	Смотреть
19	Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке	Смотреть

Основы сопромата, расчет прогиба балки

Cодержание:

Основы сопромата кратко.

1. Виды опор.

1.1. Шарнирные опоры.

Расчетная длина (пролет) балки.

1.2. Опорные связи шарнирно закрепленной балки.

1.3 Жесткое защемление на опорах.

1.4. Скользящие заделки.

2. Нагрузки (внешние силы).

3. Напряжения (внутренние силы).

4. Реакции опор.

5. Уравнения статического равновесия.

4.1. Определение опорных реакций.

6. Уравнения изгибающего момента.

7. Балка на двух шарнирных опорах.

8. Консольная балка.

9. Метод сечений.

10. Определение момента сопротивления.

11. Определение угла поворота.

12. Определение прогиба.

13. Определение угла поворота через прогиб.

14. Список использованной литературы.

Расчет прогиба балки не то, чтобы такой уж сложный, но для того, чтобы каждый раз не повторять одни и те же операции при расчете и этим максимально сократить время расчета, специалисты по сопромату уже давно вывели формулы для наиболее вероятных вариантов опор балок и нагрузок, действующих на балки. Достаточно только определиться с расчетной моделью балки и формула для расчета прогиба к Вашим услугам. Но аксиомы: «если хочешь, чтобы работа была сделана хорошо, сделай это сам» пока никто не отменял. Дело в том, что в разного рода справочниках и пособиях иногда бывают опечатки или ошибки, поэтому использовать готовые формулы не всегда есть хорошо.

11. Определение угла поворота.

(вернуться к основному содержанию)

Прогиб строительной конструкции, а в нашем случае балки — единственная величина, которую проще всего определить опытным путем и сложнее всего теоретическим. Когда мы прикладывали к линейке нагрузку (давили на нее пальцем или мощью своего интеллекта), то невооруженным глазом видели, что линейка прогибалась:

Рисунок 11.1. Перемещение центра тяжести поперечного сечения балки в центре балки и угол поворота продольной оси, проходящей через центр тяжести поперечного сечения, на одной из опор.

Если бы мы хотели определить величину прогиба опытным путем, то достаточно было бы измерить расстояние от стола, на котором лежат книги (на рисунке не показан) до верха или низа линейки, затем приложить нагрузку и измерить расстояние от стола до верха или низа линейки. Разница в расстояниях — это и есть искомый прогиб (на фотографии величина прогиба обозначена оранжевой линией):

Фотография 1.

Но попробуем прийти к тому же результату, следуя по тернистому пути теории сопромата.

Так как балка прогнулась (в хорошем значении этого слова), получается, что и продольная ось, проходящая через центры тяжести поперечных сечений всех точек балки, и до приложения нагрузки совпадавшая с осью х, сместилась. Это смещение центра тяжести поперечного сечения по оси у называется прогибом балки f. Кроме того, очевидно, что на опоре эта самая продольная ось теперь находится под некоторым углом θ к оси х, а в точке действия сосредоточенной нагрузки угол поворота = 0, так как нагрузка у нас приложена посредине и балка прогнулась симметрично. Угол поворота принято обозначать «θ«, а прогиб «f» (во многих справочниках по сопромату прогиб обозначается как «ν«, «w» или любыми другими литерами, но нам, как практикам, удобнее использовать обозначение «f«, принятое в СНиПах).

Как определить этот самый прогиб мы пока не знаем, но зато мы знаем, что нагрузка, действуя на балку, создает изгибающий момент. А изгибающий момент создает внутренние нормальные сжимающие и растягивающие напряжения в поперечных сечениях балки. Эти самые внутренние напряжения приводят к тому, что в верхней части балка сжимается, а в нижней растягивается, при этом длина балки по оси, проходящей через центры тяжести поперечных сечений остается такой же, в верхней части длина балки уменьшается, а в нижней части увеличивается, причем чем дальше расположены точки поперечных сечений от продольной оси, тем больше будет деформация. Определить эту самую деформацию мы можем используя еще одну характеристику материала — модуль упругости.

Если мы возьмем кусок бинтовой резины и попробуем его растянуть, то обнаружим, что резина растягивается очень легко, а выражаясь по научному деформируется на значительную величину при воздействии даже небольшой нагрузки. Если мы попробуем проделать то же самое с нашей линейкой, то растянуть ее даже на десятые доли миллиметра руками вряд ли получится, даже если прилагать к линейке нагрузку в десятки раз большую, чем к бинтовой резине. Это свойство любого материала описывается модулем Юнга, который часто называется просто модулем упругости. Физический смысл модуля Юнга при максимально допустимом загружении рассчитываемой конструкции примерно следующий: модуль Юнга показывает отношение нормальных напряжений, (которые при максимально допустимом загружении равны расчетному сопротивлению материала к относительной деформации при таком загружении:

E = R/Δ (11.1.1)

а это значит, что для работы материала в области упругих деформаций значение внутренних нормальных напряжений, действующих не абстрактно, а на вполне определенную площадь сечения, с учетом относительной деформации не должно превышать значения модуля упругости:

E ≥ N/ΔS (11. 1.2)

в нашем случае балка имеет прямоугольное сечение, поэтому S = b·h, где b — ширина балки, h — высота балки.

Измеряется модуль Юнга в Паскалях или кгс/м². Для абсолютного большинства строительных материалов модули упругости определены эмпирическим путем, узнать значение модуля для того или иного материала можно по справочнику или сводной таблице.

Определить величину деформации для поперечного сечения, к которому приложена равномерно распределенная нагрузка или сосредоточенная сила в центре тяжести поперечного сечения, очень просто. В таком сечении возникают нормальные сжимающие или растягивающие напряжения, равные по значению действующей силе, направленные противоположно и постоянные по всей высоте балки (согласно одной из аксиом теоретической механики):

Рисунок 507.10.1

и тогда определить относительную деформацию, если известны геометрические параметры балки (длина, ширина и высота) несложно, простейшие математические преобразования формулы (11. 1.2) дают следующий результат:

Δ = Q/(S·Е) (11.2.1) или Δ = q·h/(S·Е) (11.2.2)

Так как расчетное сопротивление показывает какую максимальную нагрузку можно приложить к определенной площади, то в данном случае мы можем рассматривать действие сосредоточенной нагрузки на всю площадь сечения нашей конструкции. В некоторых случаях важно определить деформации именно в точке приложения сосредоточенной нагрузки, но сейчас мы эти случаи не рассматриваем. Чтобы определить суммарную деформацию, нужно обе части уравнения умножить на длину балки:

Δl = Q·l/(b·h·Е) (11.2.3) или Δl = q·h·l/(b·h·Е) (11.2.4)

Но в рассматриваемом нами случае на поперечные сечения балки действует не сосредоточенная сила, приложенная к центру тяжести поперечного сечения, а изгибающий момент, который можно представить в виде следующей нагрузки:

Рисунок 149. 8.3 

При такой нагрузке максимальные внутренние напряжения и соответственно максимальные деформации будут происходить в самой верхней и в самой нижней части балки, а посредине никаких деформаций не будет. Равнодействующую для такой распределенной нагрузки и плечо действия сосредоточенной силы мы находили в предыдущей части (2), когда определяли момент сопротивления балки. Поэтому теперь без особого труда можем определить суммарную деформацию в самой верхней и в самой нижней части балки:

Δх = M·х/((h/3)·b·(h/2)·Е) (11.3.1)

или

Δх = M·х/(W·Е) (11.3.2)

так как W = b·h²/6 (10.6)

Эту же формулу мы можем получить и другим способом. Как мы знаем, момент сопротивления поперечного сечения балки должен удовлетворять следующему условию:

W ≥ М / R (10.3)

Если мы будем рассматривать эту зависимость как уравнение и заменим в этом уравнении значение R на ΔЕ, получим следующее уравнение:

W = М / ΔЕ (11. 4.1)

И тогда:

М = WΔЕ (11.4.2) a Δ = M/(W·Е) (11.4.5) и соответственно Δх = M·х/(W·Е) (11.3.2)

В результате деформации, которую мы только что определили, наша балка могла была бы выглядеть так:

Рисунок 11.2. Предполагаемая (для наглядности) деформация балки

то есть в результате деформаций самая верхняя и самая нижняя точки поперечного сечения сместятся на величину Δх. А это значит, что зная величину деформации и высоту балки, мы можем определить угол поворота θ поперечного сечения на опоре балки. Из школьного курса геометрии мы знаем, что отношение катетов прямоугольного треугольника (в нашем случае катеты Δх и h/2) равно тангенсу угла θ:

tgφ = Δх/(h/2) (11.5.1)

и тогда

tgφ = 2 M·х/(h·W·Е) (11.5.3)

Если вспомнить, что момент инерции — это момент сопротивления поперечного сечения, умноженный на расстояние от центра тяжести до крайней точки сечения или наоборот, момент сопротивления — это момент инерции, разделенный на расстояние от центра тяжести до крайней точки сечения:

W = I/(h/2) (10. 7) или I = W·h/2 (10.7.2)

то мы можем заменить момент сопротивления на момент инерции:

tgφ = M·х/(I·Е) (11.5.4)

хотя делать это было не обязательно, но таким образом мы получили формулу угла поворота почти такой, как она дается во всех учебниках и справочниках по сопромату. Главное отличие в том, что обычно речь идет о угле поворота, а не о тангенсе угла. И хотя при малых деформациях значения тангенса угла и угол сопоставимы, но тем не менее угол и тангенс угла — это разные вещи (впрочем в некоторых справочниках, например: Фесик С.П. «Справочник по сопротивлению материалов» Киев: Будiвельник. — 1982 переход от тангенса к углу упоминается, хотя и без достаточных на мой взгляд объяснений). Более того, если быть совсем уж точным, то таким способом мы определяем отношение продольной деформации к высоте балки

Рассчитываемые элементы далеко не всегда имеют прямоугольное сечение, как наша рассматриваемая линейка. В качестве балок и перемычек могут использоваться различные горячекатаные профили, тесанные и не тесанные бревна и вообще все, что угодно. Тем не менее понимание принципов расчета момента инерции позволяет определить момент инерции для поперечного сечения любой, даже очень сложной геометрической формы. В абсолютном большинстве случаев вычислять самому момент инерции нет необходимости, для металлических профилей сложного сечения (уголки, швеллера, двутавры и др.) момент инерции, как впрочем и момент сопротивления определяется по сортаменту. Для элементов круглого овального, треугольного сечения и некоторых других видов сечения определить момент инерции можно по соответствующей таблице.

Если рассматривать суммарную деформацию всей балки, т.е. по всей длине l, то очевидно, что суммарная деформация при наших нагрузках не может быть только с одной стороны балки, как показано на рисунке 11.3.а:

Рисунок 11. 3.

Так как к нашей балке нагрузка приложена посредине, в результате чего реакции на опорах, возникающие в результате действия нагрузки равны между собой и каждая равна половине приложенной нагрузки, то скорее при этих условиях суммарная деформация будет выглядеть так, как показано на рисунке 11.3.b и тогда в нашем конкретном случае угол наклона поперечного сечения на каждой из опор будет:

tgθ = M·х/(2IЕ) (11.5.5)

Пока мы определяли тангенс угла поворота простым графоаналитическим методом и в случае, когда нагрузка к балке приложена посредине, это у нас неплохо получилось. Но варианты приложения нагрузок к балке бывают всякие и хотя суммарная деформация всегда будет равна Δl, но угол наклона поперечных сечений на опорах может быть разным. Если мы присмотримся к формулам (11.5.4) и (11.5.5) повнимательнее, то увидим, что мы умножаем значение момента в некоторой точке на величину х, которая с точки зрения теоретической механики ни чем не отличается от понятия — «плечо действия силы».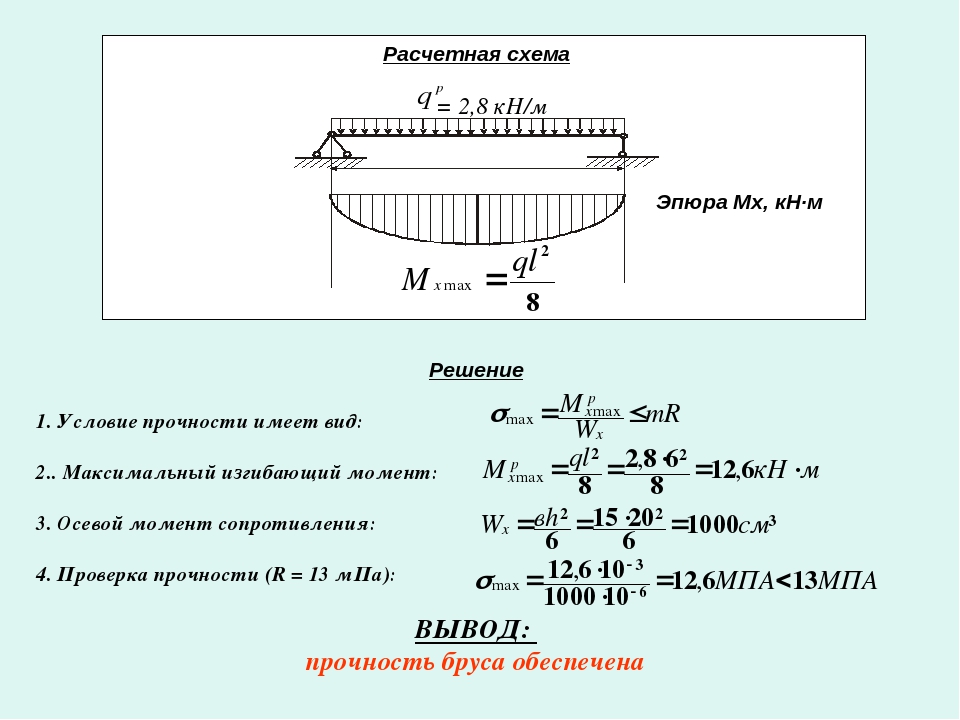 Получается, что для определения тангенса угла поворота мы должны умножить значение момента на плечо действия момента, и значит, понятие «плечо» можно применить не только к силе, но и к моменту. Когда мы использовали понятие плеча действия силы, открытое еще Архимедом, то мы и предполагали как далеко это может нас завести. Метод, показанный на рисунке 5.3, дал нам значение плеча момента = х/2. Теперь попробуем определить плечо момента другим способом (графоаналитический метод). Тут нам пригодятся эпюры, построенные для балки на шарнирных опорах:

               

          Рисунок 149.7.1                                                             Рисунок 149.7.2

Теория сопротивления материалов позволяет рассматривать внутренние нормальные напряжения, характеризуемые эпюрой «М» рисунка 149.7.1 для балки с постоянной жесткостью, как некую внешнюю фиктивную нагрузку. Тогда площадь эпюры «М» от начала балки до середины пролета — это фиктивная опорная реакция материала балки на равномерно изменяющуюся нагрузку. А фиктивный изгибающий момент — это площадь эпюры «М», умноженная на расстояние от центра тяжести эпюры «М» до рассматриваемой точки. Так как значение изгибающего момента посредине пролета составляет Ql/4, то площадь такой фигуры составит Ql/4(l/2)(1/2) = Ql²/16. А если это значение разделить на жесткость ЕI, то мы получим значение тангенса угла поворота.

Забегая наперед, определим значение прогиба. Расстояние от центра тяжести треугольной эпюры «М» до середины пролета равно l/6, тогда фиктивный изгибающий момент составит (Ql²/16)l/2 — (Ql²/16)l/6 = Ql³/48. Тогда прогиб f = Ql³/48EI. А так как эпюра моментов у нас расположена снизу балки, то такая фиктивная нагрузка будет в итоге давать отрицательное значение угла поворота и прогиба, что в общем-то логично, так как при таком действии нагрузки прогиб — смещение центра тяжести поперечного сечения будет происходить вниз по оси у.

Характерная особенность графоаналитического метода состоит в том, что количество вычислений можно еще сократить. Для этого нужно умножить площадь эпюры фиктивной нагрузки на расстояние от центра тяжести эпюры до начала координат, а не до рассматриваемой точки на оси. Например, для вышеприведенного случая (Ql²/16)l/3 = Ql³/48

При равномерно распределенной нагрузке эпюра моментов описывается квадратичной параболой, определить площадь такой фигуры и расстояние до центра тяжести сложнее, но для того нам и нужны знания по геометрии, чтобы можно было определить площадь любой фигуры и положение центра тяжести такой фигуры.

Таким образом получается, что для балки, на которую действует сосредоточенная нагрузка в середине балки при х=l/2:

tgθ = М·(x/2)/(ЕI) = ((Ql/4)·(l/4))/(ЕI) = Ql²/(16EI) (11.6.1)

То, что мы только что делали называется интегрированием, ведь если умножить значение значение эпюры «Q» (рисунок 149.7.1) на длину действия нагрузки, мы тем самым определим площадь прямоугольника со сторонами «Q» и х, при этом площадь данного прямоугольника равняется значению эпюры «М» в точке х.

Теоретически получается, что мы можем определить значение тангенса угла поворота, интегрируя одно из уравнений моментов, составленных для нашей балки. Максимальное значение тангенса угла поворота для балки на двух шарнирных опорах, на которую действует сосредоточенная нагрузка посредине (рисунок 149.7.1), будет при х=l/2

tgθ = ∫Mdx/(EI) = ∫Axdx/(EI)= Ax²/(2EI) = (Q/2)·(l/2)²/(2ЕI) = Ql²/(16EI) (11.6.2)

где А — это реакция опоры = Q/2

При распределенной нагрузке интегрирование уравнения моментов: q(l/2)·x — qx²/2 для левой части балки дает следующий результат:

tgθ = ∫Mdx/(EI) = q·(l/2)·(l/2)²/(2ЕI) -q·(l/2)³/(6ЕI) = ql³/(24EI) (11.6.3)

Тот же результат мы получим и при использовании графо-аналитического метода.

Когда мы определяли угол поворота, то для наглядности предположили, что балка деформировалась так, как показано на рисунке 5.2, потом так, как показано на рисунке 11.3.b, потом мы выяснили, что если бы второй опоры не было, то балка повернулась вокруг первой опоры, но в действительности вторая опора есть и потому так балка деформироваться (при нашей нагрузке на балку) не может. Так как на опоре нет никакого вращающего момента и соответственно никаких внутренних напряжений, способных изменить геометрическую форму балки, то геометрическая форма балки на опоре остается неизменной, а внутренние напряжения, увеличивающиеся по ходу балки, деформируют балку все сильнее и это приводит к тому, что балка поворачивается вокруг шарнирных опор и этот угол поворота равен углу наклона поперечного сечения θ (так как мы рассматриваем балку-параллелепипед):

Рисунок 11.4. Реальная деформация балки.

 

Если мы просто постоим эпюру углов поворота для балки со сосредоточенной нагрузкой посредине по уравнениям для левой и для правой части балки, то эпюра будет выглядеть так:

Рисунок 11. 5.

Данная эпюра была бы правильной только для балки, изображенной на рисунке 5.3.а. Очевидно, что в нашем случае эпюра так выглядеть не может и для построения правильной эпюры нужно учесть, что поперечные сечения балки имеют наклон на обоих опорах, причем наклон этот одинаковый по значению, но разный по направлению а наклон поперечного сечения балки посредине =0. Если мы опустим эпюру на Ql²/16EI, которое мы получаем при интегрировании уравнения моментов для левой части балки и которое показывает угол наклона поперечного сечения именно на опоре, то получим эпюру следующего вида:

Рисунок 11.6.

Данная эпюра абсолютно точно показывает, изменение угла поворота поперечных сечений, вдоль всей балки, а значение тангенса угла поворота на левой опоре балки не что иное, как некая постоянная С₁, которую мы получаем, если интегрирование выполнять корректно. И тогда уравнение угла поворота для балки при данной нагрузке на участке 0<x<0. 5l будет выглядеть так:

tgθ_х = — tgθ_A + Ax²/(2EI) (11.6.5)

Эпюра углов поворота для балки с распределенной нагрузкой визуально ни чем не отличается от эпюры углов поворота для балки со сосредоточенной нагрузкой, разница только в том, что эпюра углов поворота для балки с распределенной нагрузкой — это кубическая парабола. Уравнение угла поворота для балки с равномерно распределенной нагрузкой будет выглядеть так:

tgθ_х = — tgθ_A + Ax²/(2EI) — qx³/(6ЕI) (11.6.6)

По поводу знаков в данном уравнении. «-» означает, что рассматриваемый член уравнения как бы пытается повернуть балку против часовой стрелки относительно рассматриваемого поперечного сечения, а «+» — по часовой стрелке. Впрочем и по эпюре углов поворота видно, что значение tgθ_А должно быть отрицательным. Таким образом, если сечение имеет наклон по часовой стрелке относительно оси х, то оно будет отрицательным, а если против часовой стрелки — то положительным.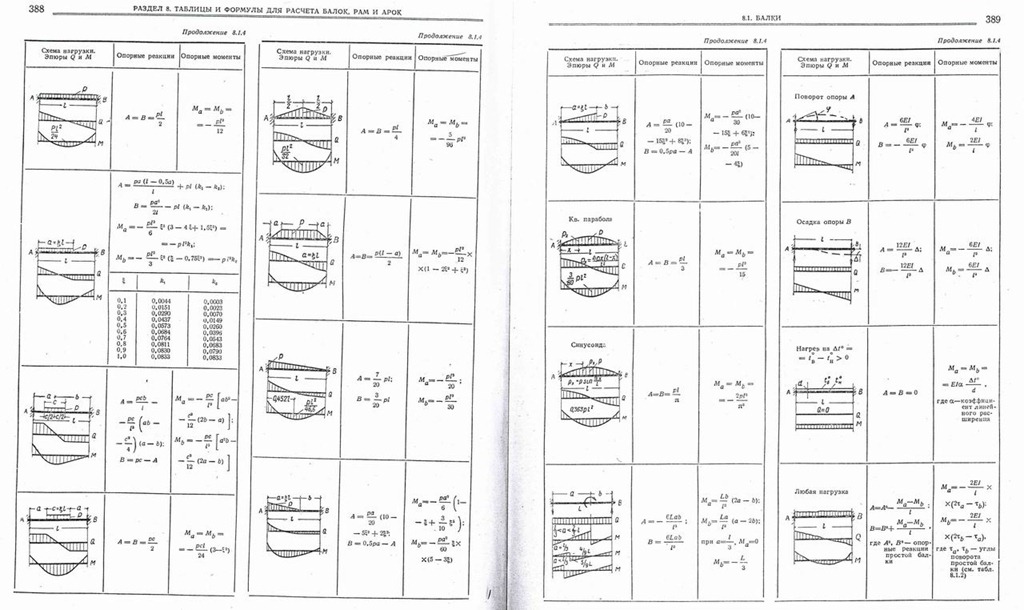

 

Ну и теперь самое главное, все эти разборки с углом поворота поперечного сечения нужны нам были для того, чтобы определить прогиб балки.

12. Определение прогиба.

(вернуться к основному содержанию)

Как мы видим из рисунка 11.4, треугольник с катетами h/2 и Δх является подобным треугольнику с катетом Х и вторым катетом, равным f+у, а это значит, что теперь мы можем определить значение прогиба:

tgθ = (f + y)/Х (12.1)

тогда

f + y = tgθ·X (12.2.1) или f + y = М·x·Х/(2ЕI) (12.2)

при малых значениях х значение у близко к 0, но в более дальних точках сечения значение у увеличивается. Значение у — это и есть влияние на величину прогиба наличия второй опоры. Отметим, что это значение у показывает разницу между реальным наклоном продольной оси балки и наклоном продольной оси балки, если бы балка просто поворачивалась вокруг опоры, и получается, что значение у зависит от изменения угла поворота. Кроме того, мы опять получили уравнение, в котором значение прогиба в некоторой точке зависит от тангенса угла поворота (12.2.1) и таким образом получается, что у угла поворота тоже есть «плечо действия». Например при у=f/2 (если присмотреться к левой части фотографии 1, то посредине балки это где-то так и будет) мы бы получили следующую формулу для определения прогиба:

f = М·x²/(3ЕI) (12.3.1)

Но мы не будем ничего предполагать, а воспользуемся интегрированием. Если мы проинтегрируем уравнение моментов для левой части балки, то получим значение у (эпюра для у показана бирюзовым цветом на фотографии 1):

у =∫∫∫(Q/2)dх = (Q/2)·(l/2)³/6EI = Ql³/(96EI) (12.3.2)

или площадь фиолетовой эпюры для левой части балки(рисунок 5.5), но нам нужна площадь голубой эпюры на левом участке балки (рисунок 5.6), которая в 2 раза больше площади фиолетовой эпюры.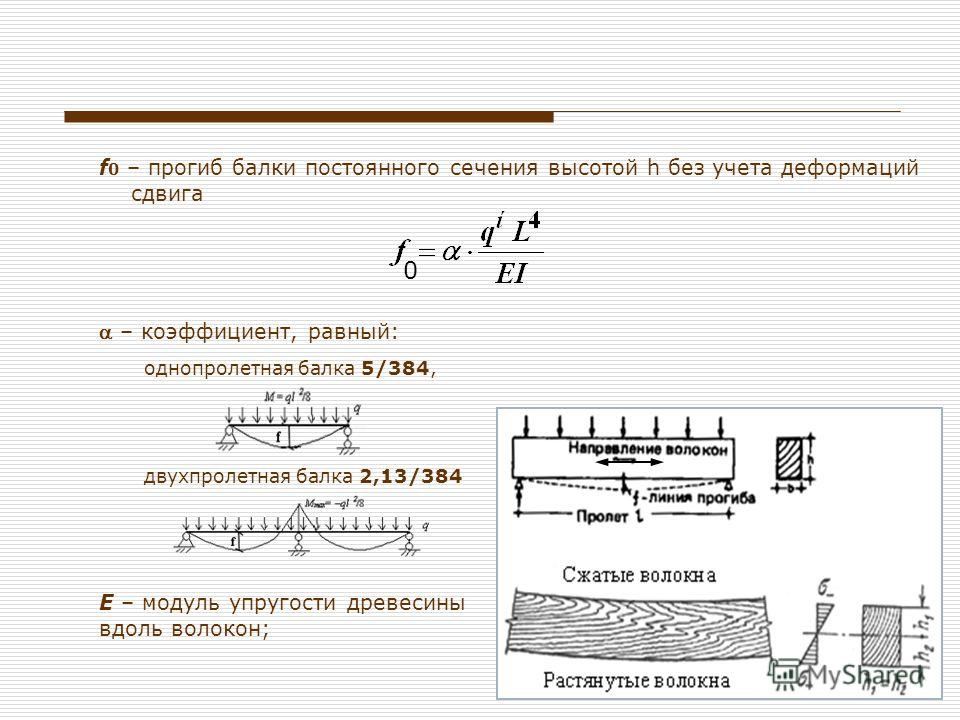 Таким образом:

f =2∫∫∫(Q/2)dх =2 (Q/2)·(l/2)³/6EI = Ql³/(48EI) (12.3.3)

Почему площадь голубой эпюры в 2 раза больше площади фиолетовой эпюры, объяснить очень легко. Площадь треугольника равна 1/2 от площади прямоугольника с теми же сторонами, площадь фигуры, описанной квадратной параболой, составляет 1/3 от площади прямоугольника с теми же сторонами. Если бы мы развернули фиолетовую эпюру, то получили бы прямоугольник, образованный голубой и фиолетовой эпюрами. Соответственно, если из площади прямоугольника вычесть 1/3, то мы получим 2/3. У этого логического ряда есть продолжение — площадь фигуры, описанной кубической параболой, составляет 1/4 от площади прямоугольника с теми же сторонами и так далее.

Мы можем найти значение прогиба и другим способом. Из рисунка 11.4 и формул (12.2) следует, что:

f_х = — tgθx + ∫tgθdx (12.3.4)

f_l/2 = — (Ql²/16EI) l/2 + (Ql³/96EI) = -(Ql³/48EI) (12.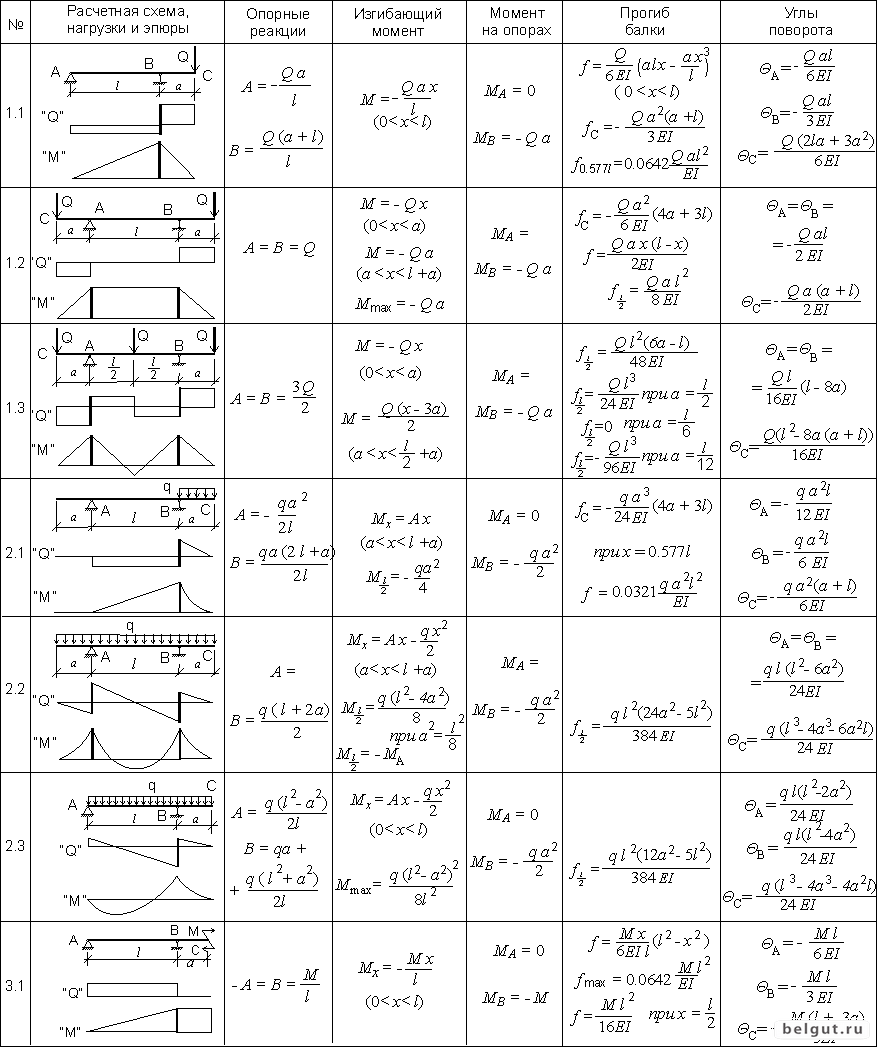 3.5)

В данном случае знак «-» показывает, что центр поперечного сечения балки переместится вниз по оси у относительно оси х. А теперь вернемся к фотографии 1. Под продольной осью балки изображена эпюра у, именно это значение в точке l/2 мы и вычли, решая уравнение (12.3.3).  Кроме того получается, что соотношение между f и у зависит от коэффициента предыдущего интегрирования, т.е. у = kf или f = y/k. Когда мы интегрировали уравнение сил, то получили коэффициент 1/2. Впрочем, такое же значение мы получили и тогда, когда определяли плечо действия момента. Если продолжить этот логический ряд, то получается, что при определении прогиба от распределенной нагрузки мы должны использовать коэффициент 1/3, то есть прогиб в середине балки мы можем вычислить по следующей формуле:

f= 2∫∫∫(ql/2)dx — 3∫∫∫∫qdх = (2(qlx³/6) — 3(qx⁴/24))/EI = 5ql⁴/(384EI) (12. 4.4)

или

f_х= — ∫tgθdx + ∫∫∫(ql/2)dx -∫∫∫∫qdх (12.4.5)

f_l/2 = (- ql³x/24 + (qlx³/6) — (qx⁴/24))/EI = — 5ql⁴/(384EI) (12.4.6)

В данном случае знак «-» означает, что центр тяжести поперечного сечения перемещается вниз по оси у.

Примечание: Предложенный метод определения прогиба несколько отличается от общепринятых, так как я старался сделать основной упор на наглядность.

Если определять прогиб графоаналитическим методом, то площадь фиктивной нагрузки — эпюры моментов, описываемой квадратной параболой, будет составлять (согласно таблице 378.1) (2ql²/(8·3))l/2 = ql³/24. А расстояние от центра тяжести эпюры до начала координат составляет 5/8, Тогда фиктивный момент равен (ql3/24)(5l/(8·2)) = 5ql⁴/384.

Конечно же, сосредоточенная нагрузка к балке может быть приложена и не посредине, распределенная нагрузка может быть не только равномерно распределенной и действовать не по всей длине балки, да и варианты крепления балки на опорах бывают разные. Но для того и существуют готовые формулы, чтобы ими пользоваться.

-Позвольте! — Скажете вы, — Все это хорошо, но как быть с касательными напряжениями? Ведь они действуют вдоль оси у и потому должны как-то влиять на прогиб!

Все верно. Касательные напряжения действительно влияют на прогиб, однако для балок с соотношением l/h > 10 это влияние очень незначительно и потому допустимо для определения прогиба пользоваться изложенным в данной статье методом.

Но это еще не все, как мы уже говорили, определить значение прогиба опытным путем достаточно просто по методу, описанному в самом начале статьи. Так так ничего лучшего под рукой не было, то я взял деревянную линейку, прообраз которой я так долго описывал (см. фотографию 1). Деревянная линейка имела размеры около 91.5 см, ширину b=4.96 см и высоту h=0.32 cм (высоту и ширину определял штангенциркулем). Затем я положил линейку на опоры, при этом расстояние между опорами составило около 90 см и таким образом получил балку с пролетом l=90 см. Под воздействием собственного веса линейка конечно же немного прогнулась, но столь малый прогиб меня не интересовал. Я измерил рулеткой (точность до 1 мм) расстояние от пола до низа линейки (77.65 см), затем приложил посредине условно сосредоточенную нагрузку (поместил посредине мерный стакан весом около 52 грамм с 250 граммами воды) и измерил расстояние от пола до низа линейки при нагрузке (75.5 см). Разница этих двух измерений и составила искомый прогиб. Таким образом величина прогиба определенного опытным путем составила 77.65 — 75.5 = 2.15 см. Осталось только найти модуль упругости для древесины, определить момент инерции для данного сечения и точно посчитать нагрузку. Модуль упругости Е для древесины = 10⁵ кгс/см², момент инерции прямоугольного сечения I_z = bh³/12 = 4.98·0.32³/12 = 0.01359872 см⁴, полная нагрузка — 0.302 кг.

Расчет прогиба по формуле дал: f = Ql³/(48EI) = 0.302·90³/(48·10⁵·0. 0136) = 3.37 см. Напомню, что прогиб, определенный опытным путем, составил: f = 2.15 см. Возможно следовало учесть влияние на прогиб первой производной функции — тангенса угла поворота? Ведь угол наклона, судя по фотографии, достаточно большой.

Проверяем: tgθ = Ql²/(16EI) = 0.302·90²/(16·10⁵·0.0136) = 0.11233. Тогда согласно формулы (542.12) f = 3.37/((1 + 0.112²)^3/2) = 3.307 см. Т.е. влияние конечно есть, но оно не превышает 2% или 0.63 мм. 

Результат меня сначала удивил, но потом объяснений для такого расхождения нашлось несколько, в частности в середине поперечное сечение линейки было не прямоугольным, так как линейка была деформирована от времени и воздействия воды, соответственно момент инерции для такого сечения больше чем, для прямоугольного, кроме того, линейка изготовлена не из сосны, а из более твердой породы древесины, для которой и модуль упругости следует принимать больше. Да и с научной точки зрения одного результата совершенно недостаточно, чтобы говорить о каких-либо закономерностях. После этого я проверил величину прогиба для деревянного бруска с моментом инерции I=2.02 см⁴, длиной более 2 м при пролете 2 м под нагрузкой 2 кг, приложенной посредине бруска и тогда значение прогиба, определенного теоретическим путем и опытным путем, совпало до десятых долей миллиметра. Конечно, можно было бы и дальше продолжать эксперименты, но так уж получилось, что до меня это уже сделали сотни других людей и получили на практике результаты, очень близкие к теоретическим. А если еще учесть, что идеально изотропные материалы бывают только в теории, то это очень хорошие результаты.

13. Определение угла поворота через прогиб.

(вернуться к основному содержанию)

Определить значение угла поворота для шарнирно опертой балки, на которую действует только изгибающий момент M на одной из опор, например на опоре А, казалось бы, проще простого:

tgθ_х = — tgθ_A + Мx/(EI) — Аx²/(2ЕI) (13. 1.1)

где А = М/l, (B = — M/l), но для этого нужно знать угол поворота на опоре А, а мы его не знаем, однако вычислить его помогает понимание того, что прогиб на опорах будет равен нулю и тогда:

f_A = tgθ_Bl — Bl³/(6EI) = 0; tgθ_B = — Ml³/(6l²EI) = — Ml/(6EI) (13.1.2)

f_B = tgθ_Al + Ml²/(2EI)- Al³/(6EI) = 0; tgθ_A = — Ml/(3EI) (13.1.3)

Как видим, угол поворота на опоре к которой приложен изгибающий момент, в два раза больше угла поворота на противоположной опоре, это очень важная закономерность, которая в дальнейшем нам очень пригодится.

Когда сосредоточенная нагрузка к балке приложена не по центру тяжести или распределенная нагрузка является неравномерной, то углы поворота на опорах определяются через прогиб, как в вышеприведенном примере. Другими словами — значения начальных параметров определяются в ходе решения дифференциальных уравнений.

Определение прогиба деревянной балки согласно СП 64.13330.2011

Конечно же, будь моя воля, я бы, перед тем как приводить формулу для определения прогиба изгибаемых элементов с учетом действия поперечных сил, сначала привел бы упрощенную формулу определения прогиба с соответствующим пояснением, что ей можно пользоваться для приблизительного определения прогиба при соотношениях высоты балки к длине h/l < 20.

Тем не менее, к разработке и составлению указанного Свода Правил я никакого отношения не имею, да и вообще до такого уровня просто еще не дорос. А потому считаю, что требования СП следует безусловно выполнять, а как именно это сделать, мы сейчас и узнаем.

Формула для определения прогиба с учетом действия поперечных сил, приведенная в СП, имеет следующий вид:

f = f_o[l + c(h/l)²]/k (544.1)

где f₀ — значение прогиба, определяемое без учета действия касательных напряжений, т. е. по упрощенной формуле. Формулы для определения прогиба статически определимых балок можно посмотреть здесь. Впрочем для определения прогиба некоторых видов статически неопределимых балок формулы также имеются.

с — коэффициент, учитывающий влияние поперечных сил на прогиб (о том, как определить этот коэффициент, мы поговорим чуть позже).

k — коэффициент, учитывающий возможное изменение высоты сечения по длине балки. При постоянной высоте k = 1.

При этом h — высота поперечного сечения балки, l — длина пролета балки.

Что лично мне не нравится в формуле (544.1)? Только одна маленькая деталь — наличие в квадратных скобках абсолютной величины — длины балки l.

На мой взгляд это делает данную формулу совершенно бессмысленной, так как определяя прогиб f₀, измеряемый хоть в метрах хоть в сантиметрах, и умножая его на длину, измеряемую в тех же метрах или сантиметрах, мы получим какую-то абстрактную величину, измеряемую то ли в м² то ли в см². Между тем прогиб всегда имеет линейную размерность, т.е. измеряется или в метрах или в сантиметрах.

Полагаю, что это просто опечатка и вместо длины l в формуле должна стоять единица — 1 (действительно 1 и l очень легко спутать). Кроме того, из общих положений теории сопротивления материалов следует, что в общем случае при учете влияния поперечных сил формула для определения прогиба (например, при действии сосредоточенной нагрузки на конце консольной балки) имеет следующий вид:

— f_l = Ql³(1 + λ)/3EI (536.13)

где

λ = k(1 + μ)h²/2l² (536.12)

И тогда коэффициент с это:

с = k(1 + μ)/2 (544.2) 

Мне кажется, что это является еще одним подтверждением того, что формула, приведенная в СП, как впрочем и в старом СНиПе, неправильная. А правильный вариант этой формулы должен иметь следующий вид:

f = f_o[1 + c(h/l)²]/k (544.1.2)

Тем не менее, как я уже говорил, я не являюсь ни составителем, ни разработчиком указанных нормативных документов, а потому мое мнение — это всего лишь мнение некоего частного лица, учитывать которое не обязательно.

Если у вас получается определить прогиб деревянной балки по приведенной в Своде Правил формуле, то — вперед! Не обращайте на мои сомнения внимания. Ну а для сомневающихся я бы все-таки предложил формулу (544.1.2). Осталось только выяснить, чему же равен коэффициент с.

Древесина не является изотропным материалом. Например значение модуля упругости древесины вдоль и поперек волокон отличается на порядок, чуть ли не на два, и потому для определения значения коэффициента с конечно же следует пользоваться не общими положениями теории сопротивления материалов, а рекомендациями СП.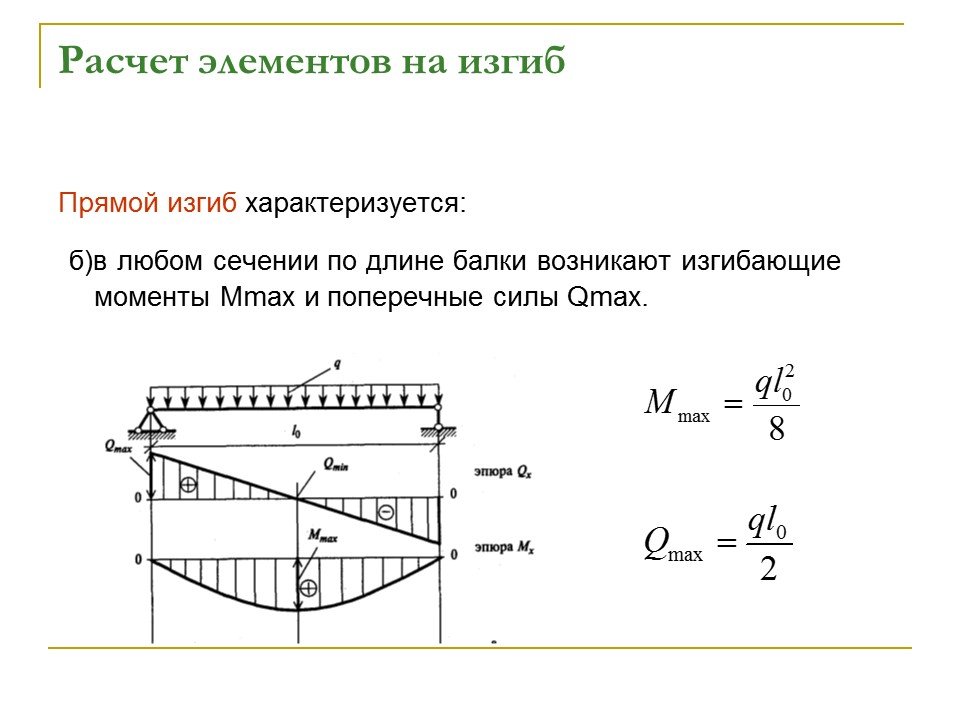

Так значение коэффициента с следует определять по таблице Е.3 обязательного приложения Е:

Таблица Е.3. Значения коэффициентов k и с для определения прогибов балок с учетом переменности сечений и деформаций сдвига

Тут может возникнуть дополнительный вопрос: а как определить значение коэффициента β, который присутствует чуть ли не во всех формулах данной таблицы?

СП на этот вопрос прямого ответа не дает, однако по контексту таблицы можно догадаться, что

β = h₀/h (544.3)

где h — максимальная высота балки (как правило посредине пролета), h₀ — высота балки в начале и(или) конце пролета.

Соответственно βh = h₀. Так же из приведенной таблицы становится понятным и то, почему при постоянной по всей длине балки высоте сечения, т. е. при β = 1, коэффициент, учитывающий возможное изменение высоты сечения балки, также равен единице —  k = 1.

Конечно же в представленной таблице Е.3 представлены далеко не все возможные случаи загружения балок. Как поступать в случаях, когда на балку действуют другие нагрузки, например несимметичные распределенные или сосредоточенные, в СП опять же не объясняется.

Я считаю, что в таких случаях действующие нагрузки следует привести к эквивалентным симметричным равномерно распределенным или сосредоточенным, но это опять же лишь мое личное мнение.

В целом прогиб, определяемый расчетом, должен быть не больше допустимого:

f ≤ f_д (544.4)

Значение допустимого прогиба определяется по таблице 19:

Таблица 19

Вот собственно и все, что мне хотелось сказать по поводу определения прогиба согласно требований СП 64.13330.2011 «Деревянные конструкции» (Актуализированная редакция СНиП II-25-80). Конкретные примеры определения прогиба деревянных балок приводятся отдельно.

Расчет прогиба балки на двух опорах

Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2.09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.

Способы выполнить расчет и проверку на прогиб

Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.

Просчитать прогиб конструкции можно несколькими способами:

• Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
• Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
• Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.

Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.

Методика выполнения расчета на прогиб

Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.

Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.

В нашем случае балка:

1. Имеет прямоугольное сечение S=b*h, длина опирающейся части составляет L;
2. Линейка нагружена силой Q, проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ, с прогибом относительно начального горизонтального положения, равным f;
3. Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.

Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ, где Е – справочная величина, R— усилие, Δ— величина деформации тела.

Вычисляем моменты инерции и сил

Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е). Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е).

Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.

Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е).

Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил M_max = q*L*2/8, соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е). Величину b·h²/6 называют моментом инерции и обозначают W. В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.

Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L²/8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.

Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h³/12, где b и h – размеры сечения балки.

Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.

Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.

Формулы для практического использования

На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.

Совет! В вопросе расчета предельного состояния балки по величине прогиба неоценимую услугу оказывают требования СНиПа. Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.

Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.

Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:

• Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
• По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
• По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.

Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L²/(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.

Ответ  прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.

Совет! Используйте в своих расчетах существующие ведомственные сборники различных проектных организаций, в которых в сжатом виде сведены все необходимые формулы для определения и расчета предельного нагруженного состояния.

Заключение

Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.

Что еще почитать по теме?

Автор статьи:

Сергей Новожилов — эксперт по кровельным материалам с 9-летним опытом практической работы в области инженерных решений в строительстве.

Понравилась статья? Поделись с друзьями в социальных сетях:

Facebook

Twitter

Вконтакте

Одноклассники

Google+

Отклонение луча: как рассчитать

В приложениях, связанных с перемещением, существует множество ситуаций, когда линейная направляющая или привод не полностью поддерживается по всей своей длине. В этих случаях прогиб (из-за собственного веса компонента и из-за приложенных нагрузок и сил) может повлиять на рабочие характеристики подшипников и вызвать плохую работу в виде преждевременного износа и заедания.

Изделия, которые могут быть смонтированы только с концевыми опорами, такими как линейные валы или узлы приводов, или в консольной ориентации, например телескопические подшипники, обычно имеют спецификацию на максимально допустимый прогиб. Важно проверить приложение и убедиться, что этот максимальный прогиб не превышен. К счастью, большинство линейных направляющих и приводов можно смоделировать как балки, а их отклонение можно рассчитать с помощью обычных уравнений отклонения балки.

Соображения, касающиеся материалов и конструкции

При расчете прогиба необходимо знать свойства направляющей или исполнительного механизма и условия приложенной нагрузки. Что касается направляющей или привода, важными критериями являются модуль упругости и планарный момент инерции компонента.Модуль упругости является мерой жесткости материала и обычно может быть найден в каталоге продукции. Момент инерции описывает сопротивление объекта изгибу и иногда предоставляется производителем компонента. Если момент инерции не указан, его можно разумно аппроксимировать, используя уравнение момента инерции для сплошного или полого цилиндра (для линейного круглого вала) или прямоугольника (телескопический подшипник или линейный привод).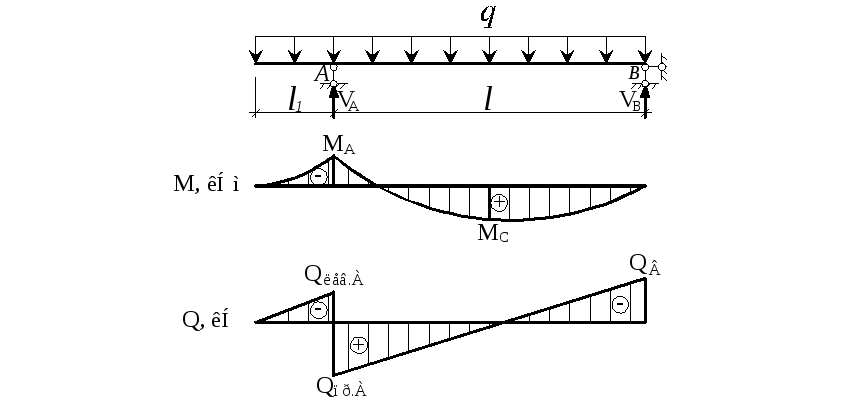

---

Модуль упругости, также известный как модуль Юнга или модуль упругости при растяжении, можно определить как отношение напряжения (силы на единицу площади) на оси к деформации (отношение деформации по длине) вдоль этой оси.

Планарный момент инерции (также называемый вторым моментом площади или моментом инерции площади) определяет, как точки области распределяются относительно произвольной плоскости и, следовательно, ее сопротивление изгибу.

---

С точки зрения применения и конструкции критериями, влияющими на прогиб балки, являются тип опоры на концах направляющей или привода, приложенная нагрузка и длина без опоры. Когда компонент является консольным, его можно смоделировать как фиксированную балку, а когда он поддерживается с обоих концов, он обычно может моделироваться как балка с простой опорой.Для консольных балок максимальное отклонение будет происходить, когда нагрузка находится на свободном конце балки, в то время как для балок с простой опорой максимальное отклонение будет иметь место, когда нагрузка находится в центре балки.

При определении общего отклонения имейте в виду, что будут иметь две нагрузки, , которые вызывают отклонение: вес направляющей или самого привода и приложенная нагрузка. Собственный вес компонента почти всегда можно смоделировать как равномерно распределенную нагрузку, оценивая приложенную нагрузку как точечную нагрузку в месте максимального прогиба (на свободном конце консольной балки или в центре балки с простой опорой) обычно обеспечивает наихудший сценарий полного прогиба.

Прогиб консольных балок

Телескопические подшипники часто являются консольными, и некоторые конфигурации декартовых роботов приводят к консольному приводу на оси Y или Z. В этом случае вес балки, который достаточно однороден по длине, вызывает максимальное отклонение на конце балки.

Изображение предоставлено: wikipedia.org

Этот прогиб рассчитывается как:

Где:

q = сила на единицу длины (Н / м, фунт-сила / дюйм)

L = длина без опоры (м, дюйм)

E = модуль упругости (Н / м ² , фунт-сила / дюйм ² )

I = планарный момент инерции (м ⁴ , дюйм ⁴ )

Для создания сценария наихудшего прогиба мы рассматриваем приложенную нагрузку как точечную нагрузку (F) на конце балки, и результирующий прогиб можно рассчитать как:

Сложив прогиб из-за равномерной нагрузки и прогиб из-за приложенной (точечной) нагрузки, получаем общий прогиб на конце балки:

Прогиб свободно опертых балок

Линейные валы и приводы часто закрепляются на концах, оставляя их длину без опоры, как у балки с простой опорой. Равномерная нагрузка на балку (собственный вес вала или привода) вызовет максимальный прогиб в центре балки, который можно рассчитать как:

Поскольку это балка с простой опорой, приложенная нагрузка может быть смоделирована как точечная нагрузка в центре балки для наихудшего сценария.

Изображение предоставлено: wikipedia.org

Прогиб из-за приложенной нагрузки в этом состоянии рассчитывается как:

Полный прогиб в центре балки:

Прогиб валов с двумя подшипниками

При использовании двух подшипников на балке с простой опорой, как это обычно бывает с круглыми направляющими вала, приложенная нагрузка распределяется между двумя подшипниками, и максимальное отклонение происходит в двух местах: в положении на каждом подшипнике , когда подшипниковый узел (иногда называемый кареткой или столом) находится в середине вала.

Изображение предоставлено: Thomson Linear

Расчет отклонения балки для этого условия:

Опять же, мы должны добавить прогиб из-за собственного веса балки плюс прогиб из-за приложенной нагрузки, чтобы получить общий прогиб:

---

Существуют дополнительные сценарии установки и нагрузки, которые могут возникнуть в некоторых приложениях, например, в приводе с фиксированной опорой на обоих концах. Но, как и в приведенных выше примерах, их можно оценить с помощью стандартных уравнений отклонения балки.Полный список сценариев опоры балки и уравнений отклонения можно найти на этой странице Корнельского университета.

Изображение предоставлено: wikipedia.org

Прогиб балки

от Расс Эллиотт Благодарности : Существует ряд стандартных работ, касающихся принципов отклонения балки. Особенно хорошее описание, на котором основаны приведенные здесь уравнения, содержится в книге Mechanics of Materials (четвертое издание SI) Дж. М. Гира и С. П. Тимошенко, Стэнли Торнса, ISBN 0 7487 3998 X.Для вывода уравнений следует обращаться к этой работе. Введение Прогиб пружинной балки зависит от ее длины, формы поперечного сечения, материала, к которому приложена отклоняющая сила и от того, как балка поддерживается. Уравнения, приведенные здесь, относятся к однородным, линейно упругим материалам, в которых вращение балки невелико. В следующих примерах, загружает только применяя в одной точке или отдельных точек рассматриваются — точка приложения силы F в диаграммах предназначена для обозначения модели локомотива hornblock (или буксы транспортного средства), способный перемещаться по вертикали в направляющей и действуя против силы пружинной балки, прикрепленной к локомотиву или основным шасси транспортного средства или переносимых ими.Доля общего веса, действующего на каждую ось локомотива или транспортного средства, будет зависеть от положения его центра тяжести по отношению к оси (или точек крепления уравновешивающих балок шасси, если они используются). Приложение для моделирования рожковых блоков локомотивов Как видно из уравнений, толщина материала ( h или d ) очень важна, и, следовательно, увеличивающиеся размеры в диапазоне доступных гитарных струн делают их очень привлекательными для использования в качестве пружинные балки. Существует также значительная разница в прогибе балки при заданной силе в зависимости от того, как она поддерживается и фиксируется, а также от того, поддерживается ли она только на одном конце или на обоих концах. Предполагается, что конструкция должна быть основана на заданном прогибе рогового блока, а затем определить, какая длина, толщина и стиль балки наиболее подходят для конкретной силы, которая должна восприниматься каждой осью. Для локомотивов, вес которых составляет от 4 до 6 граммов на тонну прототипа, массы, поддерживаемые каждым отдельным роговым блоком локомотива, вероятно, будут находиться в диапазоне от 30 до 60 граммов (что соответствует нагрузке прототипа от 14 до 20 тонн на тонну). ось). Выбор значения отклонения Для разумного мелкого пути в масштабе 4 мм рекомендуемое значение прогиба рогового блока, δ , при конечной нагрузке локомотива составляет 0,5 мм. Приведенная выше рекомендация, как известно, является чрезмерно упрощенным и, возможно, неверным предположением о том, каким должно быть расчетное значение прогиба, и вызвала серьезные споры. Любой опыт применения этой рекомендации в реальной практике моделирования шасси приветствуется — цель этой статьи — начало обсуждения, а не его заключение.Щелкните здесь для первоначального изучения вопросов по этому вопросу. Момент инерции, I Момент инерции прямоугольного сечения I = bh 3 ∕ 12 где h — размер в плоскости изгиба, то есть в оси, по которой действует изгибающий момент Момент инерции круглого сечения I = π r 4 ∕ 4 = π d 4 ∕ 64 , где r и d — радиус и диаметр соответственно Все приведенные ниже уравнения содержат I , момент инерции балки, который является константой, определяемой формой и толщиной поперечного сечения балки. Момент инерции не зависит от длины или материала балки. Здесь рассматриваются только прямоугольные и круглые цельные сечения. Пояснения к схемам и обозначениям прогибов На схемах показаны два типа опор: фиксированная и простая. На неподвижной опоре балка удерживается жестко, а угловой прогиб в точке крепления равен нулю. На простой опоре балка может скользить по опоре и вращаться в соответствии с силой, приложенной к балке. L = длина балки a = промежуточная длина балки δ = прогиб балки F = сила (т. Е. Доля веса локомотива, которому оказывает сопротивление букса) E = модуль Юнга I = момент инерции балки Уравнения и диаграммы прогиба Примечание к схемам и уравнениям .Приведенные здесь диаграммы были перевернуты по сравнению с их обычным описанием в учебниках, чтобы отразить их применение для моделей локомотивов и букс транспортных средств. Однако, хотя уравнения для отклонения были согласованы с их учебным представлением, нормальное соглашение о знаках (+ или -, чтобы указать отклонения по вертикальной оси y от базовой линии балки) было проигнорировано, поскольку мы здесь обеспокоены только с абсолютной величиной прогиба балки. Концевая нагрузка на консольную балку с одиночной неподвижной опорой δ = FL 3 ∕ 3 EI Это уравнение также следует использовать для отклонения уравнительной балки, вращающейся вокруг фиксированной оси и опирающейся на два рупорных блока по обе стороны от оси поворота. Двойные нагрузки на балку с двумя простыми опорами (примеры применения этой конфигурации) Это может быть применено для двух роговых блоков, прижимающихся к одной балке. Прогиб на расстоянии a от соседней опоры составляет: δ = Fa 2 (3 L — 4 a ) ∕ 6 EI Свисающая нагрузка на балку, ограниченная двумя простыми опорами δ = Fa 2 ( L + a ) ∕ 3 EI Промежуточная / центральная нагрузка на балку с одной фиксированной и одной простой опорой Прогиб на длине a от неподвижной опоры составляет: δ = Fa 3 ( L — a ) 2 (4 L — a ) ∕ 12 EIL 3 Для нагрузки в центре балки, подставив a = L ∕ 2 в вышеприведенное уравнение, прогиб будет: δ = 3. 5 FL 3 ∕ 384 EI Центровка нагрузки на балку с двумя неподвижными опорами δ = FL 3 ∕ 192 EI При нагрузке в центре отклонение на расстоянии a от фиксированной опоры (где a меньше чем или равно L ∕ 2 ): δ = Fa 2 (3 L — 4 a ) ∕ 48 EI Промежуточная нагрузка на балку с двумя неподвижными опорами Отклонение на расстоянии a от неподвижной опоры составляет: δ = 2 Fa 3 ( L — a ) 2 ∕ 3 EI (2 а + Д ) 2 Значения модуля Юнга, E Бериллий медный 124 ГПа 1 Латунь, твердость 70/30 117. 2 ГПа Латунь неуточненная от 96 до 110 ГПа Нейзильбер 132,5 ГПа (127 ГПа 1 ) Бронза фосфористая, 5%, твердая 131,8 ГПа Фосфорно-бронзовая (92% Cu / 8% Sn, или CuSn8) 111 ГПа 1 Сталь мягкая или инструментальная 212 ГПа Сталь мягкая, низкоуглеродистая 210 ГПа Сталь мягкая (закаленная) 201.4 ГПа Сталь нержавеющая 215,2 ГПа (190 ГПа 1 ) Сталь инструментальная (закаленная) 203,2 ГПа Следует отметить, что это теоретические значения. Типичное значение для стальной гитарной струны можно принять как 205 ГПа. Значения, указанные для фосфористой бронзы, различаются: кажется, что они будут зависеть от материала типа «пружинный» или «экстрапружинный» из фосфористой бронзы 92% Cu / 8% Sn. обычно используется в переключателях с защелкой. 1 Шигли, Отдел машиностроения, 1980, McGraw Hill Примечания к единицам и размерам 1 Па = 1 Н · м -2 = 10 -6 Н · мм -2 = 10 -6 кг · м · с -2 · мм -2 = 1 г · мм -1 · с -2 Чтобы получить силу F в приведенных выше уравнениях, массу нужно умножить на гравитационную постоянную г (9.81 м · с -2 , или, что нам удобнее, 9810 мм · с -2 ) Размеры модуля Юнга E составляют ML -1 T -2 Размеры усилия F составляют L 2 ML -1 T -2 = MLT -2 Размеры момента инерции I L 4 © Расс Эллиотт , впервые опубликовано 19 апреля 2000 г .; небольшая редакционная правка, август 2001 г .; уравнение для промежуточной нагрузки на балку с двумя фиксированными опорами исправлено, и уравнение прогиба для промежуточной / центральной нагрузки на балку с одной фиксированной и одной простой опорой повторно выражено, январь 2005 г .; График для свисающей нагрузки на балку, стесненную двумя простыми опорами, пересмотрено, 8 октября 2009 г .; Уравнение промежуточной нагрузки на балку с двумя неподвижными опорами исправлено, 30 декабря 2010 г.

ИНЖИНИРИНГ.com | Калькуляторы прогиба балки

Калькуляторы прогиба балки — сплошные прямоугольные балки, полые прямоугольные балки, сплошные круглые балки Введите значение и нажмите «Рассчитать». Будет показан результат

Расчет прогиба для сплошных прямоугольных балок Расчет прогиба для полых прямоугольных балок Расчет прогиба для сплошных круглых балок Расчет прогиба для круглых трубчатых балок

Расчет прогиба сплошных прямоугольных балок фунтов Введите свои значения: Длина: Дюймы Ширина: Дюймы Высота: Дюймы Сила: Материал: Результатов: Прогиб: Дюймы Изгибающее напряжение: PSI

Расчет прогиба полых прямоугольных балок фунтов Введите свои значения: Длина: Дюймы Ширина: Дюймы Высота: Дюймы Толщина стенки: Дюймы Сила: Материал: Результат: Прогиб: Дюймы Изгибающее напряжение: PSI

Расчет прогиба сплошных круглых балок фунтов Введите свои значения: Длина: Дюймы Диаметр: Дюймы Сила: Материал: Результатов: Прогиб: Дюймы Изгибающее напряжение: PSI

Расчет прогиба для круглых трубных балок фунтов стерлингов Введите свои значения: Длина: Дюймы Диаметр: Дюймы Толщина стенки: Дюймы Сила: Материал: Результат: Прогиб: Дюймы Изгибающее напряжение: PSI

Калькулятор прогиба балки

Калькулятор прогиба балки для расчета изгибающего момента, поперечной силы, напряжения изгиба, прогиба и наклон свободно поддерживаемой балки, консольной балки и неподвижной неподвижной балки.

КАЛЬКУЛЯТОРЫ КОМПРЕССИОННЫХ ЧЛЕНОВ
Калькулятор	Определение
	Расчет элементов сжатия (продольного изгиба)
ПРОСТО ОПОРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОБЕГА
	Балка с простой опорой и множественными точечными / распределенными нагрузками и моментами
	Балка с простой опорой и сосредоточенной нагрузкой в ​​любой точке
	Просто поддерживаемая балка с двумя Точечные нагрузки
	Балка с простой опорой и частично распределенной промежуточной нагрузкой

Легкий прогиб стальной балки

Верулам, инженер-строитель Том.70, No. 12, 16 июня 1992 г.

Легкое отклонение луча

Г-н А. Н. Бил из Лидса прислал нам записку, в которой предлагается простая процедура приблизительного ручного расчета прогибов стальных балок. Хотя его вклад оказался слишком длинным, чтобы быть включенным в Verulam полностью, его сокращенная версия может заинтересовать многих читателей. Г-н Бил отмечает, что, хотя расчет вручную изгибающих напряжений в балке обычно не является трудным, расчет прогибов может быть гораздо более трудоемким.Поскольку обычно нет необходимости знать прогиб с какой-либо большой степенью точности (в пределах 10%, вероятно, будет адекватным), предлагается следующий подход.

Пример балки с простой опорой, поддерживающей равномерную нагрузку, иллюстрирует подход.

Если мы возьмем формулу прогиба (Δ = 5WL³ / 384EI) и выразим ее через изгибающий момент (M = WL / 8), то получится Δ = 5ML³ / 48EI.

Теперь для стальной балки напряжение упругого изгиба fbt = M / Z, где Z = 2I / D, что дает fbt = MD / 2I.
(Z — модуль упругости, I — момент инерции, D — общая глубина сечения.)

Подставляя это в формулу отклонения, получаем Δ = 5 fbtL³ / 24ED. При E 210 кН / мм² это становится:

Δ (мм) = 0,992 фбтL² / д. . . (1)

Здесь fbt, L и D выражены в их обычных единицах измерения: Н / мм², м и мм соответственно.

Для всех практических целей формула

Δ = fbtL² / D. . . (2)

удобен в использовании, легко запоминается и отличается точностью до 1%.

Г-н Бил затем переходит к рассмотрению других распределений нагрузки, аналогичным образом связывая центральный прогиб Δ с экстремальным напряжением волокна fbt, получая результаты, показанные в первом столбце результатов таблицы 1. Во втором столбце приведены значения для балок с фиксированными концами , которые Г-н Бил предлагает использовать его для оценки прогибов непрерывных балок.

Наконец, г-н Бил показывает, как его методика может использоваться для сложных нагрузок, вычисляя отклонение нагруженной балки с простой опорой, как показано на рис. 1:

Рис.1

Центральный изгибающий момент, рассчитанный как 444,3 кНм.
Для сечения балки Z = 2474 см³, D = 539,5 мм, что дает

фут = 179,6 Н / мм².

Простое приблизительное отклонение с использованием ур. (2) это

ΔAPP = 179,6 x 7² / 539,5 = 16,3 мм = L / 429 OK.

Для более точной оценки, учитывая, что большая часть момента создается центральной точечной нагрузкой, мы могли бы взять коэффициент, более близкий к значению точечной нагрузки, равному 0.8 (скажем, 0,85), что дает

Δ = 0,85 фут x L² / D = 13,9 мм

Для сравнения, точный компьютерный анализ той же балки дал отклонение 13,8 мм.

Следовательно, для большинства практических целей нам нужно запомнить только четыре простые формулы для прогиба прямопертой или непрерывной стальной балки, как показано в таблице 2.

Эти формулы не только упрощают жизнь для простых равномерных и точечных нагрузок — они означают, что прогиб при более сложных схемах нагрузки может быть рассчитан без труда.Они также особенно подходят для проверки компьютерных изображений «обратной стороной конверта». Лучше всего то, что их легко запомнить.

Есть желающие?

Калькулятор прогиба балки и напряжения

На этой странице можно найти прогиб, а также максимальное напряжение. свободно опертой балки калькулятор всегда учитывает собственный вес балки и добавляет его к указанным вами нагрузкам. Выбирайте из австралийских стальных профилей, УНИВЕРСАЛЬНЫХ БАЛКОВ, ПАРАЛЛЕЛЬНЫХ ФЛАНЦЕВЫХ КАНАЛОВ, УНИВЕРСАЛЬНЫХ СТОЛБОВ и Z / C PURLINS.Также можно обнаружить отклонение луча правой стороны. Тип материала ограничивается сталью (модуль упругости 210 000 МПа), деревом и алюминием. Все входные значения должны быть метрическими.

Прогиб балки и максимальное напряжение балки.

Прогиб от собственного веса:
Прогиб от нагрузки:
Прогиб от продолжительной нагрузки:

Полный прогиб:

Максимальное напряжение:

3.91 мм
32,01 мм
7,14 мм

43.06 мм

156,48 МПа

Для выбора нестандартных размеров, ИСПОЛЬЗУЙТЕ ЗНАЧЕНИЯ НИЖЕ из раскрывающегося списка.
Оставьте значение толщины фланца (толщина стенки) пустым, чтобы указать твердое тело.
Единицы измерения должны быть в мм.

Диаграмма прогиба балки.

Ниже представлены неокругленные данные

Модуль упругости: 210000 (Н / мм ² )
Момент инерции: 271188 (мм ⁴ )
Перпендикулярное расстояние от нейтральной оси: 38 (мм)
Вес материала.Усилие на мм: 0,0273436 (Н / мм)
Материал: сталь
Сечение: 76X38X1,6 RHS
Сила нагрузки: 700 Н
Постоянная нагрузка Сила на мм: 0,05 Н / мм
Отклонение балки от собственного веса балки: 3,16995894 мм
Отклонение балки от силы в центре балки: 32,009364557265 мм
Прогиб от непрерывной нагрузки, поддерживаемой балкой: 7,1449474458181 мм
Полное отклонение этой балки с простой опорой : 43.