Как определить угол наклона уже готовой кровли
Расчет уклона кровли — обязательный этап проектирования дома. От угла наклона скатов зависят снеговая и ветровая нагрузки на крышу, которые через стены передаются на фундамент.
Но есть ситуации, когда необходимо узнать фактический уклон уже готовой кровли. Например, при реконструкции крыши с заменой кровельного материала более тяжелым или при установке солнечных панелей на скатах. Ниже — два способа, как определить угол наклона в этом случае.
Определить уклон ската можно либо с помощью специальных инструментов, либо воспользовавшись базовыми законами геометрии. Первый способ проще и точнее, второй доступен всегда — главное, чтобы была рулетка, а остальные инструменты не важны.
Инструментальный метод
Чтобы определить угол наклона кровли просто и быстро, используйте специальные измерительные инструменты:
- угломеры, которые измеряют угол между двумя «плечами» инструмента;
- уклономеры, которые показывают уклон кровли относительно гравитационного поля Земли.

Угломеры для расчета уклона кровли
Угломер — чрезвычайно простой, но эффективный инструмент. Он бывает механическим и электронным.
Механический угломер состоит из планок, которые соединены друг с другом с одного края, и шкалы между ними. Со второй стороны концы планок свободные и могут вращаться вокруг места соединения. Шкала показывает, на какой угол две части угломера повернуты друг относительно друга. Конструкция настолько простая, что, при необходимости, механический угломер можно даже сконструировать самостоятельно из двух линеек и транспортира.
Электронные угломеры по принципу работы точно такие же. Есть только одно отличие: шкала для определения угла между плечами инструмента заменена специальным датчиком, который считывает положение планок. Результат отображается на небольшом экране.
Механические угломеры — более надежный инструмент: нет риска, что откажет датчик или экран. Но с точки зрения удобства электронные устройства выигрывают.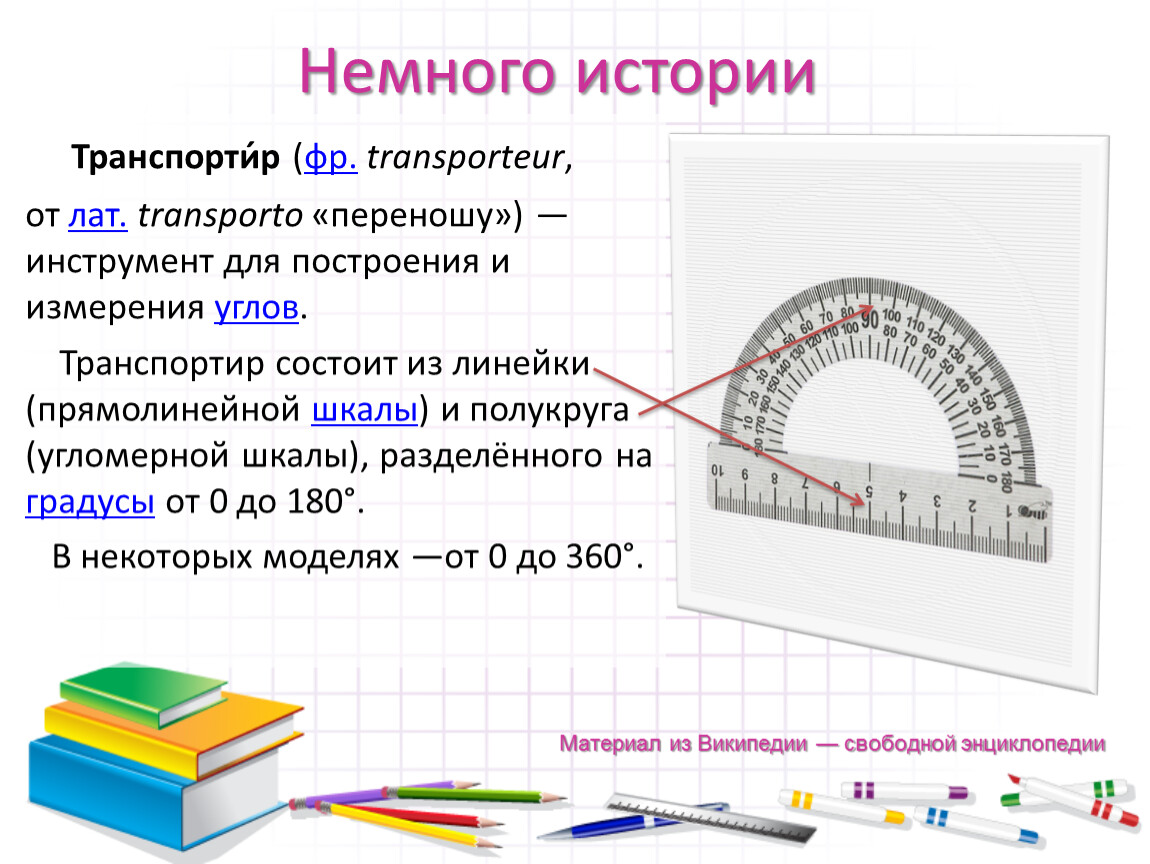
Как определить угол наклона кровли с помощью угломера:
- одну из планок плотно прижмите к стойке, подпирающей коньковую балку, или к самому коньку;
- вторую планку прижмите к нижней кромке стропильной ноги;
- запишите результат измерений и повторите их для разных стропил 8-10 раз;
- отбросьте результаты, которые сильно выбиваются из ряда измерений — слишком большие или слишком маленькие;
- для остальных вычислите среднее арифметическое — это и будет угол наклона кровли.
Учитывайте, что для расчета уклона кровли нужно обязательно делать не одно измерение, а несколько, иначе вы рискуете получить некорректные результаты. Приведем пример.
Допустим, вы сделали 10 измерений угломером и получили следующие результаты.
| Номер измерения | Угол, градусы |
| 1 | 25,3 |
| 2 | 28,1 |
| 3 | 25,8 |
| 4 | 25,4 |
| 5 | 27,5 |
| 6 | 25,1 |
| 7 | 25,3 |
| 8 | 30 |
| 9 | 25,5 |
| 10 | 25,2 |
Второе, пятое и восьмое измерение явно выбиваются из ряда, поэтому их нужно отбросить. Выполняем расчет уклона кровли только по семи измерениям: складываем их и делим на количество. В результате получаем среднее арифметическое — 25,37°. Если бы мы не отфильтровали измерения, то угол бы получился почти на градус больше — 26,32°. И это еще небольшая разница: измерение угла между разными парами стропил и стоек может дать результаты, отличающиеся на 5-7°, иногда даже больше.
Выполняем расчет уклона кровли только по семи измерениям: складываем их и делим на количество. В результате получаем среднее арифметическое — 25,37°. Если бы мы не отфильтровали измерения, то угол бы получился почти на градус больше — 26,32°. И это еще небольшая разница: измерение угла между разными парами стропил и стоек может дать результаты, отличающиеся на 5-7°, иногда даже больше.
Такая разница связана с качеством пиломатериалов, которые обычно используют для стропильной системы. Ее рекомендуют делать из калиброванного леса, то есть из досок, сечение которых примерно одинаковое по всей длине и равно эталонному. Для этого их пропускают через специальный станок — рейсмус, который срезает лишнее и доводит размеры досок до необходимых.
Но калибровка сильно повышает стоимость пиломатериалов, поэтому для большинства стропильных систем с целью экономии берут обычные, некалиброванные доски. Еще и часто недостаточно просушенные. А их ширина даже в сыром виде может отличаться на десятки миллиметров. Причем не у разных досок, а просто по длине одной.
Причем не у разных досок, а просто по длине одной.
В верхней части стропила выводят в плоскость — нужно же уложить кровельное покрытие, — а в нижней эта разница остается. Она и дает такую погрешность, из-за которой перед тем, как определить угол наклона кровли, нужно сделать множество измерений, чтобы получить более-менее точный результат.
Уклономеры для определения угла наклона ската
Уклономерами пользоваться еще проще, чем угломерами. В основе таких приборов специальные магнитные датчики — инклинометры. Они измеряют угол наклона поверхности, на которой установлены, относительно гравитационного поля Земли. Поэтому это более точный инструмент для расчета уклона кровли.
Чтобы определить угол наклона ската, достаточно просто поставить уклономер на кровельное покрытие или верхнюю кромку стропильной ноги. Независимо от качества пиломатериалов, сверху стропила с обрешеткой выводят в плоскость. Поэтому погрешность будет меньше — для получения точного результата нужно будет повторить измерения 3-4 раза.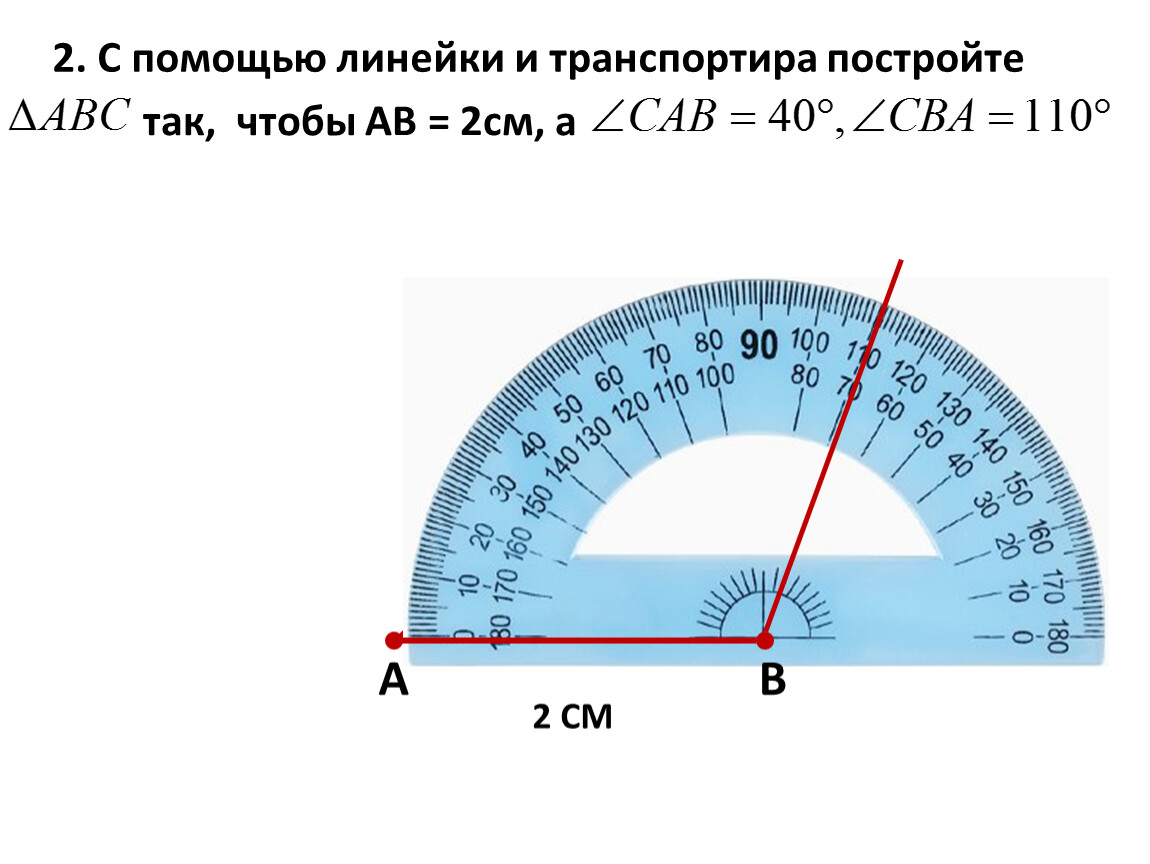
Если установить уклономер на кровельное покрытие нет возможности, его можно прижать к низу стропил. Но тогда измерения нужно будет делать по той же схеме, что и с угломером: 8-10 штук с отбрасыванием крайних значений и расчетом среднего.
Расчет уклона кровли по длине стропил
Угломер или уклономер — это специализированный инструмент, который не всегда есть под рукой, да и покупать его ради одного измерения нет смысла. Поэтому для расчета уклона кровли чаще пользуются базовыми законами геометрии.
Дело в том, что стропило, опорная стойка и перекрытие — это, по сути, стороны прямоугольного треугольника, где стропильная нога — гипотенуза. Следовательно, рассчитать уклон кровли можно по формуле:
α = (h/l)·100%
Здесь:
- α — угол наклона ската, %;
- h — высота крыши, включая коньковую балку, м;
- l — расстояние от середины опорной стойки до карнизного свеса ската, м.
Этот метод дает довольно точный результат, поскольку на него никак не влияют характеристики пиломатериалов. Но угол получается не в привычных градусах, а в процентах. Поэтому для дальнейших расчетов полученное значение нужно перевести.
Но угол получается не в привычных градусах, а в процентах. Поэтому для дальнейших расчетов полученное значение нужно перевести.
Как вычислить угол наклона в градусах? Сделать это можно двумя способами.
Первый способ подходит тем, у кого есть инженерный калькулятор и кто умеет с ним обращаться. Нужно посчитать арктангенс при делении высоты крыши на длину ската:
α = arctg(h/l)
Второй способ проще — нужно вычислить уклон в процентах с помощью следующей схемы.
Просто приложите линейку к схеме: один конец — к крайней точке справа, другой — к тому значению на вертикальной шкале, которое соответствует полученному вами углу наклона в процентах. Тогда место пересечения линейки со скругленной шкалой (транспортиром) покажет уклон в градусах.
Чтобы узнать уклон кровли, можно воспользоваться одним из двух методов:
- инструментальным — измерить его напрямую с помощью уклономера или угломера;
- расчетным — стропила, перекрытие и стойки образуют прямоугольный треугольник, поэтому угол можно рассчитать, разделив высоту крыши до конька на расстояние по полу от карнизного свеса до опор.
Расчетный метод даст уклон в процентах. Как рассчитать угол наклона в градусах? Взять арктангенс от соотношения или воспользоваться специальной схемой для перевода процентов в градусы.
Будьте в курсе!
Подпишитесь на новостную рассылкуопределение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Определение 1Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Определение 6Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол.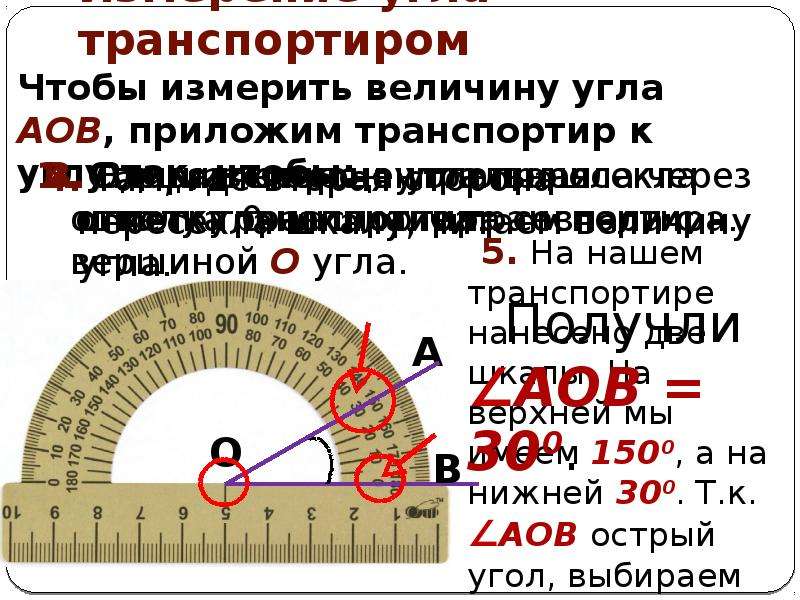 Ниже изображены неравные углы, не совмещенные при наложении.
Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Определение 8Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Определение 9Минутой называют одну шестидесятую часть градуса.
Определение 10Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:
1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .
Определение 11Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Как найти угол любого угла без инструментов
На прошлой неделе мы с мамой решили установить немного нового молдинга в ее гостиной, чтобы расширить уже существующую отделку и придать ей вид удлиненной короны. Это на самом деле великолепно, НО тем утром мы довольно быстро поняли, что наш угломер потерялся. Вместо того, чтобы тратить время на то, чтобы бежать в магазин за новым инструментом для определения угла, мы использовали несколько кусков дерева, чтобы измерить 2 угла в нашей комнате, которые не были стандартными.
Это на самом деле великолепно, НО тем утром мы довольно быстро поняли, что наш угломер потерялся. Вместо того, чтобы тратить время на то, чтобы бежать в магазин за новым инструментом для определения угла, мы использовали несколько кусков дерева, чтобы измерить 2 угла в нашей комнате, которые не были стандартными.
Я посмотрел этот небольшой трюк на YouTube, и он работал очень хорошо и был очень простым… но мне все же удалось раз или два облажаться. Не волнуйтесь, я покажу вам, как я облажался, чтобы вы не повторяли моих ошибок!
Поскольку инструкции, которые я нашел, были не такими надежными, как мне бы хотелось, я решил использовать свой новый опыт и написать здесь небольшое руководство по нахождению угла любого угла без инструментов (простой способ). Я надеюсь, что это помогает кому-то!
Начнем.
Расходные материалы:
- 2 куска дерева (одинаковой ширины)
- Карандаш
- Торцовочная пила (ручная, как та, что у нас есть)
- Торцовочная пила (электрическая, как та, которую мы хотим)
- Переносной рабочий стол Worx
- Зажимы
Прежде всего… если у вас угол меньше 90 градусов, вам нужно использовать один метод, а если ваш угол больше 90 градусов, вам понадобится немного другой метод. Поэтому убедитесь, что оба метода верны!
Поэтому убедитесь, что оба метода верны!
Как измерить угол, который меньше 90 градусов
Шаг 1: Маркировка обрезков древесины
Давайте сразу приступим к делу.
Для угла меньше 90 градусов мы начнем с размещения нашего первого куска дерева заподлицо со стеной слева. Убедитесь, что угол куска дерева находится в углу, который вы измеряете. Убедиться, что ваши куски дерева размещены точно, будет очень важно для получения точных измерений здесь.
После того, как первая часть будет прикреплена к стене, положите сверху вторую часть деревянного лома. Этот кусок должен быть на одном уровне с правой стороной стены, а его край должен находиться в углу. Выстраивание этих краев из угла в угол… именно в углу происходит все волшебство. Если эти 3 точки не сойдутся в углу, у вас не будет плотного прилегания.
Теперь возьмите карандаш и обведите нижнюю часть правой доски на нижней доске. Это даст вам линию, которая должна пересекаться с нижней частью вашего куска дерева. Эта нижняя точка (где линия касается нижней части дерева) является той частью измерения, которая вам нужна.
Эта нижняя точка (где линия касается нижней части дерева) является той частью измерения, которая вам нужна.
Чтобы найти угол, все, что вам нужно сделать, это поместить линейку на эту нижнюю отметку (где начерченная вами линия касается нижней части доски) и провести новую линию от этой отметки до верхнего угла обрезка древесины.
Видишь, как это выглядит? Нарисуйте эту линию красивой и темной… это угол, который вам нужен. Теперь отнесите кусок дерева к торцовочной пиле, чтобы определить линию разреза для вашего косого среза.
Шаг 2. Разрежьте свой лом
Давайте разрежем этого плохого мальчика! Теперь, когда у нас есть угол, отмеченный на куске дерева, следующая часть должна быть очень простой. Поместите древесину на торцовочную пилу и зажмите ее, если вам нужна дополнительная безопасность (это определенно полезно для ручной торцовочной пилы, которую я использую).
Затем отрегулируйте угол наклона торцовочной пилы до тех пор, пока лезвие пилы не совпадет с нарисованной вами линией разреза. Теперь вы можете прочитать угол вашего угла! Идите вперед и отрежьте этот угол… затем, оставив торцовочную пилу настроенной точно на тот угол, который вы только что обрезали, продолжайте и отпилите второй кусок дерева с той же настройкой.
Теперь вы можете прочитать угол вашего угла! Идите вперед и отрежьте этот угол… затем, оставив торцовочную пилу настроенной точно на тот угол, который вы только что обрезали, продолжайте и отпилите второй кусок дерева с той же настройкой.
Когда вы перевернете второй кусок дерева, у вас должны получиться два противоположных угла, которые идеально впишутся в ваш угол. Давай попробуем!
Шаг 3. Проверка угла
Я засунул внутрь два своих кусочка деревяшки и вуаля! Они подходят идеально!
Идеальный скошенный пропил в соответствии с моим точным измерением угла… и все это без инструмента. Конечно, это на двух кусках дерева, и это не очень поможет в долгосрочной перспективе, поэтому давайте вернемся к чертежной доске и вырежем наши настоящие куски лепнины.
Пришло время для настоящей сделки.
Шаг 4. Вырежьте молдинг
Теперь, когда вы знаете, под каким углом резать молдинг, пора собственно вырезать молдинг! Просто имейте в виду, что первый кусок будет точно под таким же углом, как и наш тестовый образец. Этот небольшой участок стены между карнизом и углом должен быть 90,5 дюйма, так что я отрежу свой первый угол с 9,5 дюймами молдинга с левой стороны.
Этот небольшой участок стены между карнизом и углом должен быть 90,5 дюйма, так что я отрежу свой первый угол с 9,5 дюймами молдинга с левой стороны.
Затем для следующего угла нам нужен целый кусок молдинга, так как это длинная стена.
Но вместо того, чтобы отрезать угол, идентичный первому, мы возьмем новый кусок молдинга и перевернем его так, чтобы верхняя часть была внизу, а нижняя часть молдинга была вверху. ТОГДА мы будем резать угол. Таким образом, когда мы закончим и повернем молдинг обратно, два угла будут противоположными и идеально совпадут.
Шаг 5: Установите молдинг!
Теперь, когда у вас есть идеальный угол, вы можете установить его на стену. Мне нравится использовать свой гвоздезабивной инструмент, чтобы прикрепить молдинг к стене… затем немного замазать под молдингом и покрасить, чтобы покрыть гвозди, и мы готовы к работе!
Я добавил несколько фотографий готовой отделки ниже, или вы можете ознакомиться с полным сообщением об установке, где я покажу вам, как именно расширить существующий молдинг короны здесь.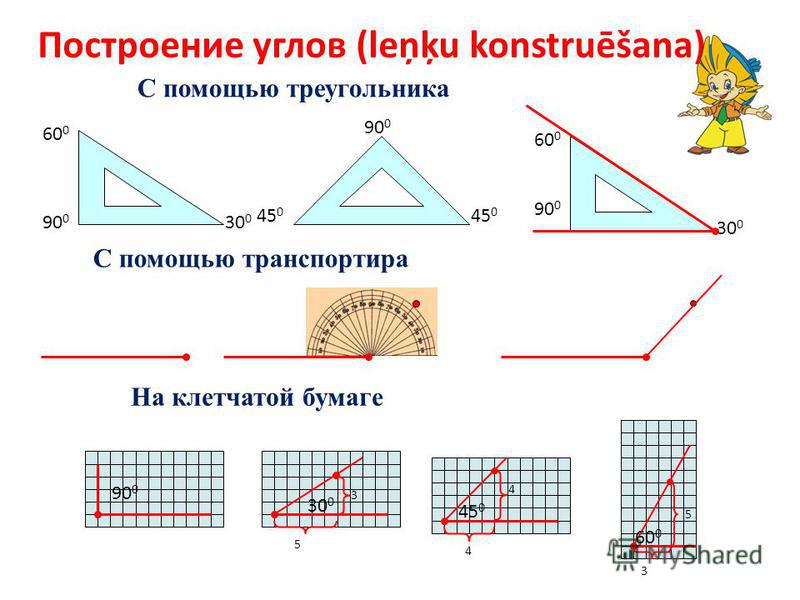
Как измерить угол больше 90 градусов
Шаг 1: Отметьте древесину
Если в вашей комнате есть оба типа углов, как у меня, то этот раздел покажется похожим с несколькими ключевыми деталями (в основном, как отметить ваш угол), но если у вас есть только больший угол, то давайте прыгать в этом.
Начните с размещения куска дерева вровень со стеной слева и за край угла. Нам нужно будет нарисовать эту расширенную часть обрезка дерева, поэтому оставьте достаточно места.
Затем возьмите второй кусок дерева и поместите его вровень со стеной справа… снова за угол и первый кусок дерева.
Отлично!
Теперь возьмите карандаш и аккуратно обведите обе стороны верхней части деревянного обрезка на нижней части.
На дереве должно остаться 2 линии. Теперь самое простое… возьмите линейку и нарисуйте линию, соединяющую два внутренних угла на куске дерева.
Карандашные метки, которые я использовал здесь, были немного трудноразличимы, поэтому я обвел их на своем компьютере для вас… розовая линия — это угол, который нам нужно нарисовать, соединяя внутренние углы. Это также тот ракурс, который мы ищем!
Это также тот ракурс, который мы ищем!
На данный момент мы можем полностью игнорировать серые линии… нам нужна только розовая линия. Эту среднюю линию мы собираемся вырезать торцовочной пилой.
Вот где я ошибся.
Когда я измерил и обрезал первый угол (тот, который меньше 90 градусов), мои два куска дерева оказались одинаковой ширины. ОДНАКО, когда я измерил свой больший угол, два куска дерева были менее удобной разной ширины.
О чем я ничего не думал, пока не обрезал свои углы, не завел их внутрь и они не работали.
Вот мой совет. Используйте два деревянных бруска одинаковой ширины. Различия в досках имеют огромное значение, и это действительно отбросит ваши измерения.
Просто взгляните на фото выше.
После небольшого панического приступа я взял две доски одинаковой ширины и заново измерил этот угол, точно по той же методике. Но даже несмотря на то, что техника такая же, посмотрите на разницу в старом ракурсе (где я использовал две доски разного размера) и новом ракурсе (используя доски одного размера).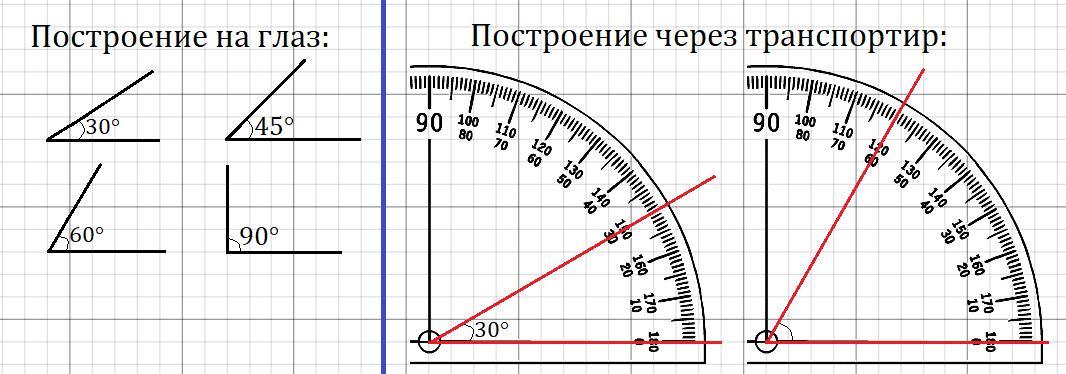 Вот такая разница в ракурсе!
Вот такая разница в ракурсе!
Вспышка новостей… белая линия, обозначающая старый угол? Это не работает. Он даже не приблизился к тому, чтобы завернуть за угол. Однако розовая линия… этот разрез сработал как волшебство.
Итак, вернемся к этому. На данный момент у нас есть отмеченная линия, и мы собираемся проверить ее, разрезав эту розовую линию на нашей торцовочной пиле.
Шаг 2. Разрежьте древесный лом
Готовы вырезать правильный угол? Поместите древесину на торцовочную пилу и зажмите ее, если вам нужна дополнительная безопасность (это определенно полезно для ручной торцовочной пилы, которую я использую).
Затем отрегулируйте угол наклона торцовочной пилы до тех пор, пока лезвие пилы не совпадет с нарисованной вами линией разреза. Теперь вы можете прочитать угол вашего угла! Идите вперед и отрежьте этот угол… затем, оставив торцовочную пилу настроенной точно на тот угол, который вы только что обрезали, продолжайте и отпилите второй кусок дерева с той же настройкой.
Когда вы перевернете второй кусок деревяшки, у вас должно получиться два противоположных угла, которые идеально подходят к вашему углу. Давай попробуем!
Шаг 3. Проверка угла
Я взял два своих кусочка дерева внутрь, и небеса словно разверзлись, и ангелы начали петь! Они идеально обогнули этот угол!
Скошенный срез (под правильным углом) идеально подходил для моего угла. И как только я начал действовать, мне даже не понадобился инструмент для измерения этого угла. Конечно, мы все еще используем обрезки древесины, так что давайте вернемся к чертежной доске и вырежем наши настоящие детали лепнины.
Пришло время для настоящей сделки.
Больше никаких ошибок.
Шаг 4. Вырежьте молдинг
Теперь, когда торцовочная пила настроена под идеальным углом, пришло время собственно вырезать молдинг! Просто имейте в виду, что первый кусок будет точно под таким же углом, как и наш тестовый образец. Этот участок стены между углом стены и углом, который мы измеряем, имеет длину 23,4 дюйма, поэтому нам нужен участок длиной 23,4 дюйма с вырезом под углом 45 градусов слева и нашим первым специализированным углом справа.
Затем для следующего угла нам понадобится еще меньший кусок с прямым краем справа, который будет упираться в этот карниз.
Но вместо того, чтобы отрезать угол, идентичный первому, мы возьмем новый кусок молдинга и перевернем его так, чтобы верхняя часть была внизу, а нижняя часть молдинга была вверху. ТОГДА мы будем резать угол. Таким образом, когда мы закончим и повернем молдинг обратно, два угла будут противоположными и идеально совпадут.
Шаг 5: Установите молдинг!
Теперь, когда у вас есть идеальный угол, вы можете установить его на стену (или мама может). Мне нравится использовать свой гвоздезабивной инструмент, чтобы прикрепить молдинг к стене… затем немного замазать под молдингом и покрасить, чтобы покрыть гвозди, и мы готовы к работе!
Я добавил несколько фотографий готовой отделки ниже, или вы можете ознакомиться с полным сообщением об установке, где я покажу вам, как именно расширить существующий молдинг короны здесь. А пока давайте проверим эти маленькие участки молдинга, как только они будут установлены и будут выглядеть идеально!
Насколько вам нравится законченный вид? И это было оооочень легко!
Теперь, когда я знаю эту маленькую хитрость, я буду использовать ее всякий раз, когда не смогу найти свой угловой инструмент. Что, кажется, все. в. время.
Что, кажется, все. в. время.
Может быть, мне стоит купить новый.
А пока, если вы хотите увидеть весь этот мини-преображение от начала до конца, вот вам сенсация!
Ознакомьтесь с моими советами о том, как быстро покрасить комнату, и посмотрите все фотографии этой комнаты до покраски (до покраски было… что-то).
Затем мы расширили лепнину для более мощного и впечатляющего эффекта лепки короны. Ознакомьтесь с моим руководством по расширению существующего молдинга короны здесь.
И последнее, но не менее важное: мы придали комнате фокус с трансформацией старинного камина. Вы можете увидеть все, как отреставрировать старинный камин здесь.
Хотите проверить оставшееся пространство?
Нажмите на любую из ссылок ниже, чтобы увидеть остальную часть «Преображение гостиной для мамы»!
Получите БЕСПЛАТНУЮ программу отслеживания цвета краски!
Готов к покраске?
Сделайте это проще простого с помощью нашего бесплатного трекера цвета краски! Никогда не забывайте цвет краски снова!
Имя
Адрес электронной почты
Мы используем это поле для обнаружения спам-ботов. Если вы заполните это, вы будете отмечены как спамер.
Если вы заполните это, вы будете отмечены как спамер.
Измерение углов
Измерение угловКонцепция угла
Понятие угла — одно из важнейших понятий геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов.Существуют две широко используемые единицы измерения углов. Более привычной единицей измерения являются градусы. Окружность разделена на 360 равных градусов, так что прямой угол равен 90°. Пока мы будем рассматривать только углы от 0° до 360°, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360° и отрицательные углы. Градусы могут быть далее разделены на минуты и секунды, но это разделение не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых 9. |
Части градуса теперь обычно указываются в десятичном виде. Например, семь с половиной градусов теперь обычно записывают как 7,5°.
Когда один угол рисуется на плоскости xy для анализа, мы рисуем его в стандартном положении с вершиной в начале координат (0,0), одна сторона угла вдоль x -ось, а другая сторона выше оси x .
Радиан
Другой распространенной единицей измерения углов являются радианы. Для этого измерения рассмотрим единичную окружность (окружность радиуса 1), центр которой является вершиной рассматриваемого угла. и Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах. Убедитесь, что вы знаете, какой режим использует ваш калькулятор. |
Краткая заметка об истории радианов
Хотя слово «радиан» было придумано Томасом Мьюиром и/или Джеймсом Томпсоном примерно в 1870 году, математики давно измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей книге « Элементов алгебры » прямо сказал, что нужно измерять углы длиной дуги, отсеченной на единичной окружности. Это было необходимо, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции знака и косинуса с показательной функцией.
где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается как отношение. Вместо того, чтобы взять единичную окружность с центром в вершине угла θ , возьмем любую окружность с центром в вершине угла. Тогда радианной мерой угла является отношение длины стягиваемой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, то мера радиана равна 1,5. Причина, по которой это определение работает, заключается в том, что длина стягиваемой дуги пропорциональна радиусу окружности. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше, с использованием единичного круга. Однако это альтернативное определение более полезно, так как его можно использовать для связи длин дуг с углами. Длина дуги равна радиусу r , умноженное на угол θ , где угол измеряется в радианах.
Однако это альтернативное определение более полезно, так как его можно использовать для связи длин дуг с углами. Длина дуги равна радиусу r , умноженное на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиусом r = 4 имеет длину 0,3 умножить на 4, то есть 1,2.
Радианы и площадь сектора
Сектором окружности называется та часть окружности, которая ограничена двумя радиусами и дугой окружности, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и угол θ между радиусами, если он измеряется в радианах. Поскольку площадь всего круга равна πr 2 , а сектор относится ко всему кругу как угол θ к 2 π , поэтомуУглы общие
Ниже приведена таблица общих углов как в градусах, так и в радианах. Обратите внимание, что измерение в радианах дается как π . . Его можно, конечно, представить в десятичном виде, но радианы часто появляются с коэффициентом π .
.
. Его можно, конечно, представить в десятичном виде, но радианы часто появляются с коэффициентом π .
.| Уголок | градусов | Радиан |
|---|---|---|
| 90° | № /2 | |
| 60° | № /3 | |
| 45° | № /4 | |
| 30° | № /6 |
Упражнения
Эдвин С. Кроули написал книгу «Тысяча упражнений в плоской и сферической тригонометрии», Пенсильванский университет, Филадельфия, 1914 г. Задачи этого краткого курса взяты из этого текста (но не все 1000 из них!) Он дал свои задачи с точностью до пяти знаков, поэтому учащимся пришлось поработать над их решением, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синусов-косинусов, тангенсов, логарифмов, логарифмических синусоидальных и логарифмических таблиц.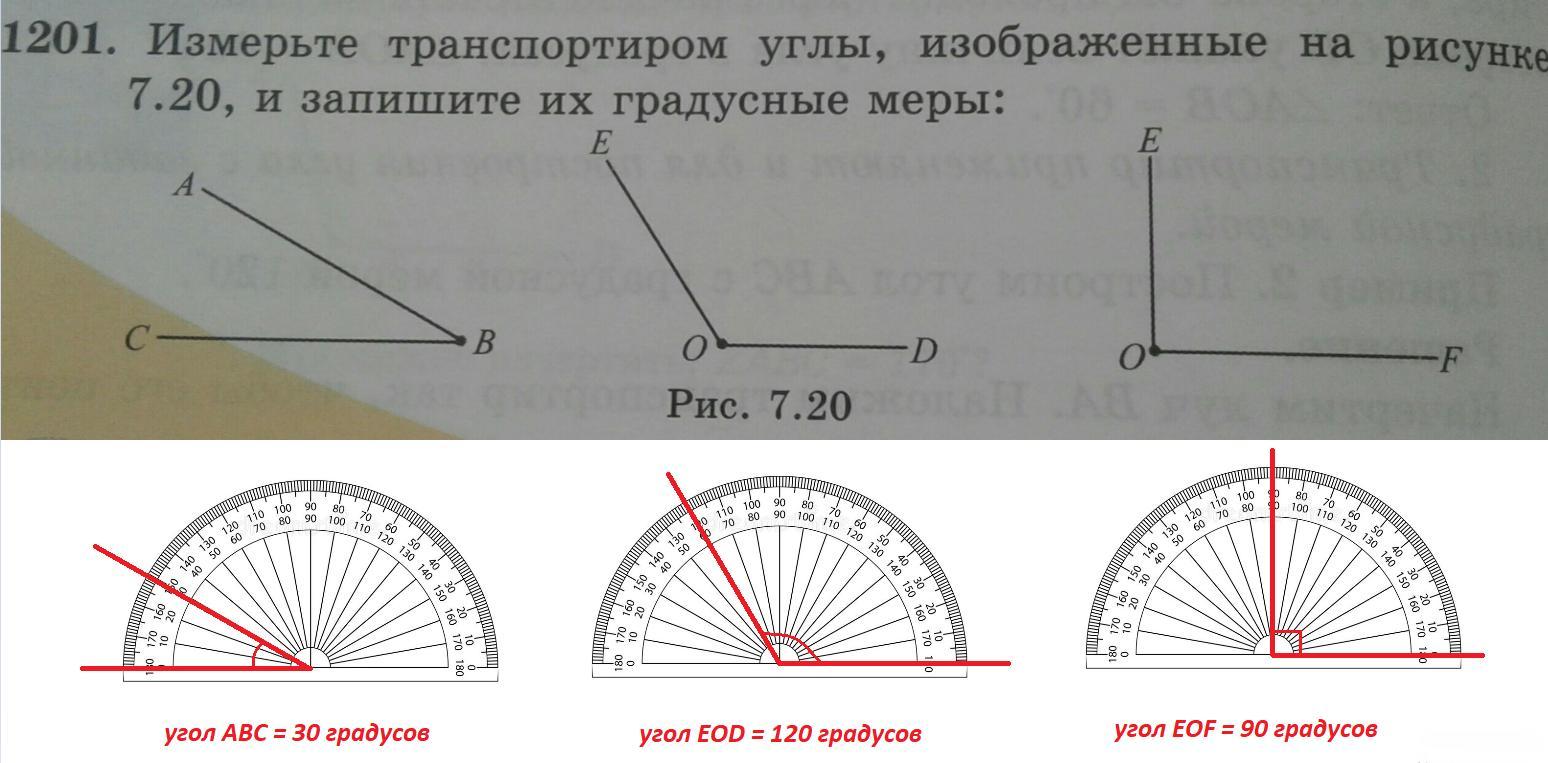 Теперь мы можем использовать калькуляторы! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.
Теперь мы можем использовать калькуляторы! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.Кроули использовал не десятичную запись для долей градуса, а минуты и секунды.
Каждый набор упражнений включает, во-первых, формулировки упражнений, во-вторых, несколько советов по решению упражнений и, в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов 28 минут, то есть 12° 28′.
(б). 36° 12′.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, найти длину стягивающей дуги.
(а). a = 0° 17′ 48″, r = 6,2935.
(б). a = 121° 6′ 18″, r = 0,2163.
4. Зная длину дуги l и радиус r, найти угол, опирающийся на центр.
(а). l = 0,16296, r = 12,587.
l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , на который она опирается в центре, найти радиус.
(а). a = 0° 44′ 30″, l = 0,032592.
(б). a = 60° 21′ 6″, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус равен 3200 футов.
7. Железнодорожная кривая образует дугу окружности 9 градусов 36,7 минут, радиус от центральной линии пути составляет 2100 футов. Если ширина колеи 5 футов, найдите разницу в длине двух рельсов с точностью до полдюйма.
9. Насколько изменится широта, если пройти на север одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину одной угловой минуты в футах по большому кругу Земли. Какова длина одной угловой секунды?
14. На окружности радиусом 5,782 метра длина дуги 1,742 метра. На какой угол он сужается в центре?
На окружности радиусом 5,782 метра длина дуги 1,742 метра. На какой угол он сужается в центре?
23. Известный воздушный шар диаметром 50 футов вытягивается из глаза под углом 8 1/2 минут. Как далеко это?
Советы
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘это 12 + 28/60, что равно 12,467°. Далее умножить на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите π и умножьте на 180. Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286°. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27° 17,16′.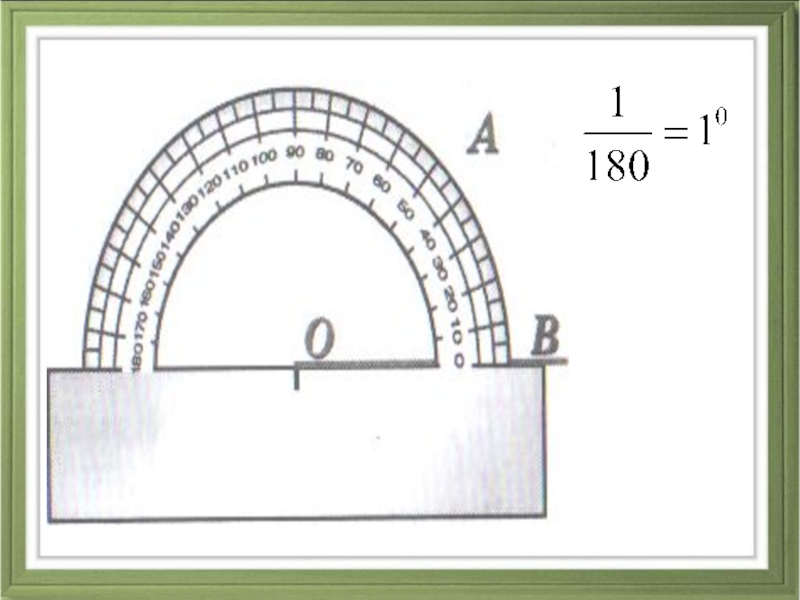 Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 примерно равно 10, поэтому угол можно также записать как 27° 17′ 10″.
Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 примерно равно 10, поэтому угол можно также записать как 27° 17′ 10″.
3. Чтобы найти длину дуги, сначала переведите угол в радианы. Для 3(a) 0°17’48» составляет 0,0051778 радиан. Затем умножьте на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Это можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умножить на радиус = длине дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусов в радианы. Таким образом, чтобы найти радиус 90 178 r, 90 179 сначала преобразуйте угол 90 178 a 90 179 в радианы, а затем разделите его на длину 90 178 l 90 179 дуги.
6. Длина дуги равна произведению радиуса на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешней направляющей равен 2102,5, а радиус внутренней направляющей равен 209.7.5.
9. У вас есть окружность радиусом 3956 миль и дуга этой окружности длиной 1 миля. Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрите, сможете ли вы узнать, каким Эратосфен считал радиус Земли еще в третьем веке до нашей эры.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус равен 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус. Радианы легко перевести в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности, в центре которой вы находитесь. (Это не совсем часть дуги, но довольно близко.) Эта дуга имеет длину 50 футов. Вы знаете угол, так каков радиус этого круга?
Ответы
1. (а). 0,2176. (б). 0,6318.
(а). 0,2176. (б). 0,6318.2. (а). 27° 17′ 10 дюймов (б). 14,56 ° = 14 °33,6′ = 14°33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296/12,587 = 0,012947 радиан = 0° 44′ 30″.
(б). 1,3672/1,2978 = 1,0535
радианы = 60,360° = 60° 21,6′ = 60° 21′ 35″.
5. (а). л/год = 0,032592/0,01294 = 2,518.
(б). л/год = 0,4572/1,0533 = 0,4340.
6. ra = (3200′) (0,20604) = 659,31′ = 659′ 4 дюйма.
7. Угол a = 0,16776 радиан. Разница в длинах есть 2102,5 a – 1997,5 a , что равно 5 a. Таким образом, ответ равен 0,84 фута, что с точностью до дюйма равно 10 дюймам.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448° = 0,8690′ = 52,14″.
10. Одна минута = 0,0002909 радиан. 1,15075 мили = 6076 футов. Поэтому одна секунда будет соответствовать 101,3 фута.
14. a = л/об = 1,742/5,782 = 0,3013 радиан = 17,26° = 17°16′.
23. Угол a равен 8,5′, что составляет 0,00247 радиана. Значит радиус равен r = л/год = 50/0,00247 = 20222′ = 3,83 мили, почти четыре мили.
О разрядах точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах. Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 исходная точка равна 12°28′, что имеет точность около четырех знаков, поэтому ответ 0,2176 также должен быть дан с точностью только до четырех знаков. (Обратите внимание, что начальные нули не учитываются при подсчете цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной. Другой пример см. в задаче 3(а). Данные равны 0°17’48» и 6,2935 с точностью до 4 и 5 знаков соответственно. Поэтому ответ следует давать только с точностью до 4 знаков, поскольку ответ не может быть более точным, чем наименее точные данные.


 0178 минут. Итак, семь с половиной градусов можно назвать 7 градусов и 30 минут, записав 7° 30′. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2° 5′ 30″. Деление градусов на минуты и угловые секунды аналогично делению часы в минуты и секунды времени.
0178 минут. Итак, семь с половиной градусов можно назвать 7 градусов и 30 минут, записав 7° 30′. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2° 5′ 30″. Деление градусов на минуты и угловые секунды аналогично делению часы в минуты и секунды времени. Тогда угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко конвертировать между измерением в градусах и измерением в радианах. Длина окружности всего круга 2 π , отсюда следует, что 360° равняется 2 π радиан. Следовательно,
Тогда угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко конвертировать между измерением в градусах и измерением в радианах. Длина окружности всего круга 2 π , отсюда следует, что 360° равняется 2 π радиан. Следовательно,