Как начертить пятиугольник с помощью транспортира
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Первый способ построения пятиугольника
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К.
Второй способ построения пятиугольника
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N1, Р1, Q1, К1 и соединяем их прямыми.
Третий способ построения пятиугольника
На рисунке построен шестиугольник по данной стороне.
Построение шестиугольника
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.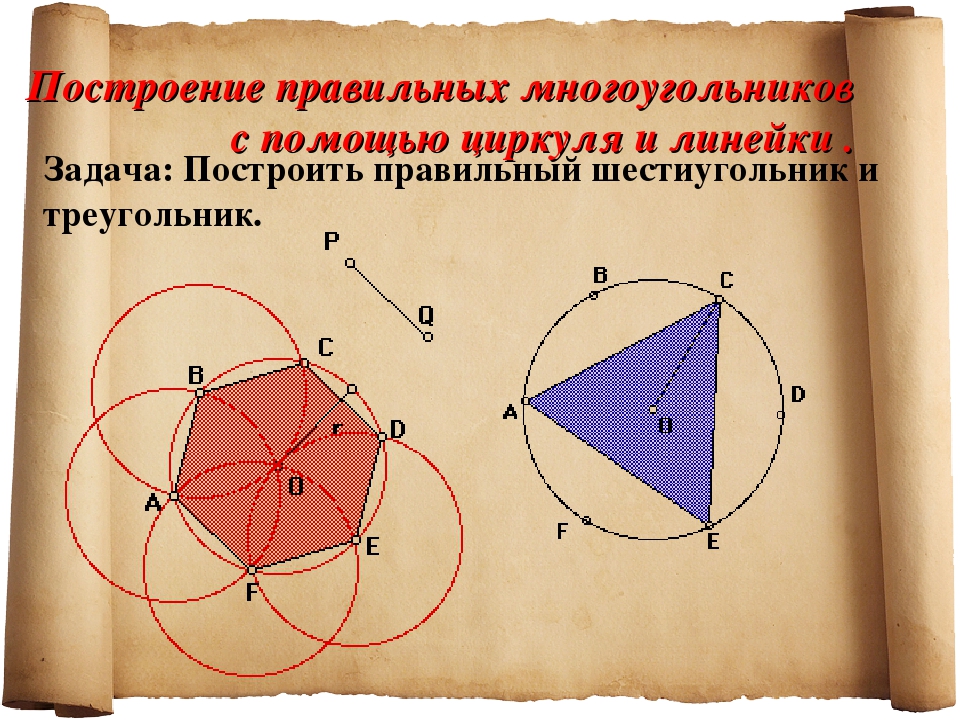
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…
Прямой угол, т. е. равный 90°, образуется двумя взаимно перпендикулярными линиями. Перпендикуляр строится следующим образом. Опустить перпендикуляр. Из данной точки С (лежащей вне прямой), как из центра, произвольным радиусом описываем дугу так, чтобы она пересекла данную прямую в двух точках D и Е из этих точек, как из центров, одинаковыми радиусами описываем дуги, чтобы они…
Построение угла, равного данному Угол, равный данному, строится следующим образом.
Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE. Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…
Деление прямых линий и углов может быть произведено двояким образом: на глаз и с помощью геометрического построения. При делении прямой на две равные части поступают следующим образом. Половину данной прямой берут циркулем на глаз и откладывают эту половину от обоих концов прямой. Если концы половинок сходятся, то, значит, данная прямая разделена правильно, если нет, то…
Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности.
Первый вопрос сводится к нахождению внутреннего…
Последние события
Раскраски к Хеллоуину для мальчиков
В России – празднование Хэллоуина ни с чем не связано. Это, скорее всего дань моде, чем традиции предков. Интересное яркое шоу, о значении и первоисточнике которого многие даже не догадываются.
Коллекция раскрасок к Хеллоуину
Скоро Хеллоуин. Праздник страшилка, праздник пугалка. Не зря его так любят дети всех стран.
На сайте я уже как-то выкладывала подборку раскрасок к Хеллоуину.
Осень. Деревья и листья
Как выглядят деревья осенью? Рассмотрите картинки и раскрасьте осенние листики.
Кто такие мишки Гамми?
Посмотрите с детьми этот мультсериал про мишек Гамми, затем скачайте раскраски и раскрасьте героев.
Несколько раскрасок для самых маленьких
Совсем простенькие раскраски с крупными деталями для самых маленьких художников.
Осеннее настроение. Раскраски
В разгаре золотая осень.
В этом году она в наших краях как никогда поздняя и ослепительно красивая.
Рассказы про осень. Читаем и раскрашиваем картинки
Что такое осень? Какая осенью погода? Что делают птицы осенью? Задайте эти и другие вопросы про осень своему малышу.
Популярное
Архив
Как нарисовать правильную звездочку? Как нарисовать правильный пятиугольник? Как разделить круг на пять равных частей? На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной эти шаги.
Как нарисовать правильную звездочку?
Как нарисовать правильный пятиугольник?
Как разделить круг на пять равных частей?
На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной вот эти шаги.
Конечно же, нам понадобится циркуль с карандашом и линейка.
Для начала нарисуйте циркулем круг.
Разделите его на четыре части линиями сверху вниз и справа налево.
Можно сразу объяснить ребенку, что отрезок, соединяющий две точки на окружности и проходящий через ее центр, называется диаметр.
А отрезок, соединяющий центр и точку на окружности, называется радиус.
С помощью линейки измерьте и разделите пополам один из радиусов.
У меня это отрезок слева от центра.
Серединку радиуса я обозначила
Нам понадобится точка сверху окружности.
Ее я обозначила цифрой 0.
Устанавливаем иголку циркуля
в точку 1, а карандашик в точку 0.
Рисуем дугу до пересечения с горизонтальным диаметром.
Обозначаем точку пересечения
Сейчас устанавливаем иголку циркуля
в точку 0, а карандашик в точку 2.
И рисуем дугу до пересечения с окружностью, причем с двух сторон.
Точки пересечения помечены
Не меняя ширину циркуля, устанавливаем иголку
в точку 3 и отмеряем кусочек окружности.
Точку 6 можно отмерить и от
точки 5 и от точки 4.
Главное, не изменять ширину (раствор) ножек циркуля.
Вот, практически и все.
Если соединим точки, получим правильный пятиугольник.
Здравствуйте коллеги.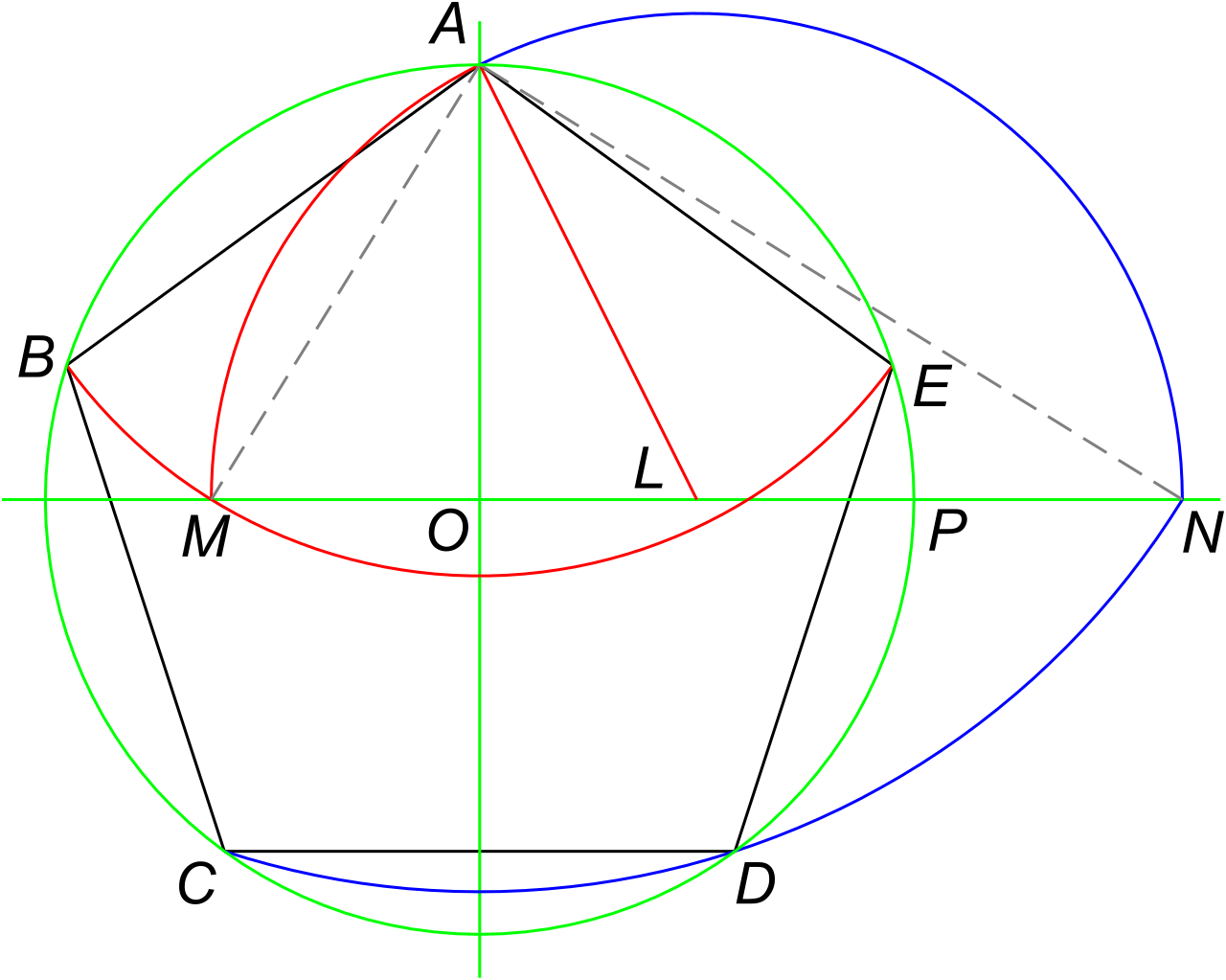
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.
Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.
Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.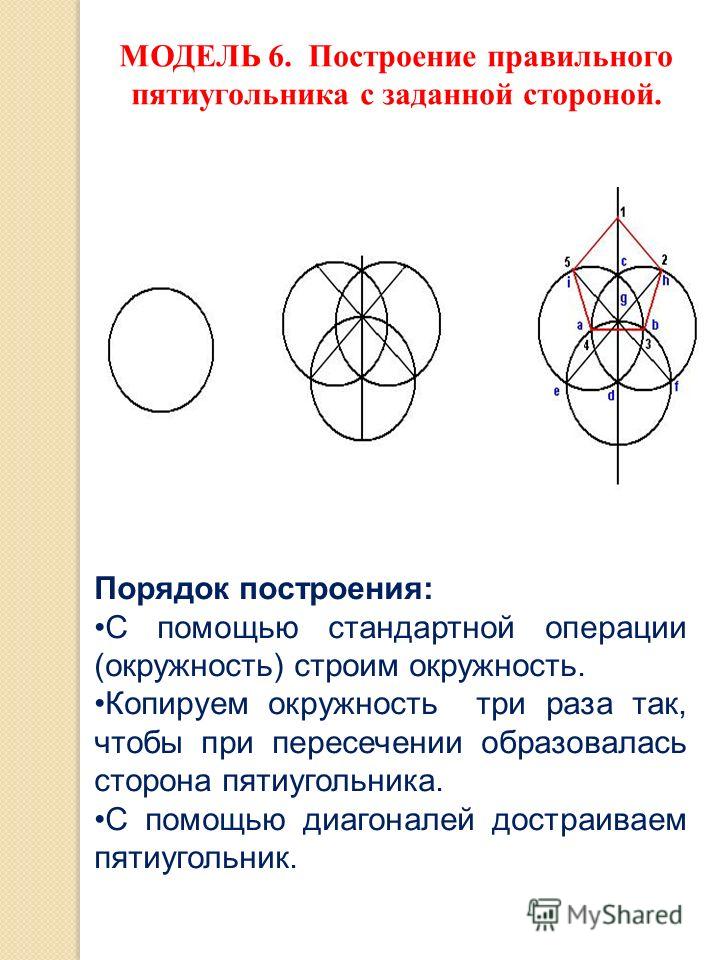
Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.
Как выглядит пятиугольник и звезда
Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.
Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.
Теперь от точки В до точки С проведем прямую.
Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.
И отрезок DB. Картинка внизу.
Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.
Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е.
Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.
Такие же отрезки наносим на всей части круга. Смотрим картинку.
На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.
Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.
Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.
Как нарисовать пятиугольник с помощью окружности
Последние события
Раскраски к Хеллоуину для мальчиков
В России – празднование Хэллоуина ни с чем не связано. Это, скорее всего дань моде, чем традиции предков. Интересное яркое шоу, о значении и первоисточнике которого многие даже не догадываются.
Коллекция раскрасок к Хеллоуину
Скоро Хеллоуин. Праздник страшилка, праздник пугалка. Не зря его так любят дети всех стран.
На сайте я уже как-то выкладывала подборку раскрасок к Хеллоуину.
Осень. Деревья и листья
Как выглядят деревья осенью? Рассмотрите картинки и раскрасьте осенние листики.
Кто такие мишки Гамми?
Посмотрите с детьми этот мультсериал про мишек Гамми, затем скачайте раскраски и раскрасьте героев.
Несколько раскрасок для самых маленьких
Совсем простенькие раскраски с крупными деталями для самых маленьких художников.
Осеннее настроение. Раскраски
В разгаре золотая осень. В этом году она в наших краях как никогда поздняя и ослепительно красивая.
Рассказы про осень. Читаем и раскрашиваем картинки
Что такое осень? Какая осенью погода? Что делают птицы осенью? Задайте эти и другие вопросы про осень своему малышу.
Популярное
Архив
Как нарисовать правильную звездочку? Как нарисовать правильный пятиугольник? Как разделить круг на пять равных частей? На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной эти шаги.
Как нарисовать правильную звездочку?
Как нарисовать правильный пятиугольник?
Как разделить круг на пять равных частей?
На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной вот эти шаги.
Конечно же, нам понадобится циркуль с карандашом и линейка.
Для начала нарисуйте циркулем круг.
Разделите его на четыре части линиями сверху вниз и справа налево.
Можно сразу объяснить ребенку, что отрезок, соединяющий две точки на окружности и проходящий через ее центр, называется диаметр.
А отрезок, соединяющий центр и точку на окружности, называется радиус.
С помощью линейки измерьте и разделите пополам один из радиусов.
У меня это отрезок слева от центра.
Серединку радиуса я обозначила
Нам понадобится точка сверху окружности.
Ее я обозначила цифрой 0.
Устанавливаем иголку циркуля
в точку 1, а карандашик в точку 0.
Рисуем дугу до пересечения с горизонтальным диаметром.
Обозначаем точку пересечения
Сейчас устанавливаем иголку циркуля
в точку 0, а карандашик в точку 2.
И рисуем дугу до пересечения с окружностью, причем с двух сторон.
Точки пересечения помечены
Не меняя ширину циркуля, устанавливаем иголку
в точку 3 и отмеряем кусочек окружности.
Точку 6 можно отмерить и от
точки 5 и от точки 4.
Главное, не изменять ширину (раствор) ножек циркуля.
Вот, практически и все.
Если соединим точки, получим правильный пятиугольник.
Здравствуйте коллеги.
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.
Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.
Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.
Как выглядит пятиугольник и звезда
Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.
Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.
Теперь от точки В до точки С проведем прямую.
Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.
И отрезок DB. Картинка внизу.
Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.
Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.
Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.
Такие же отрезки наносим на всей части круга. Смотрим картинку.
На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.
Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.
Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.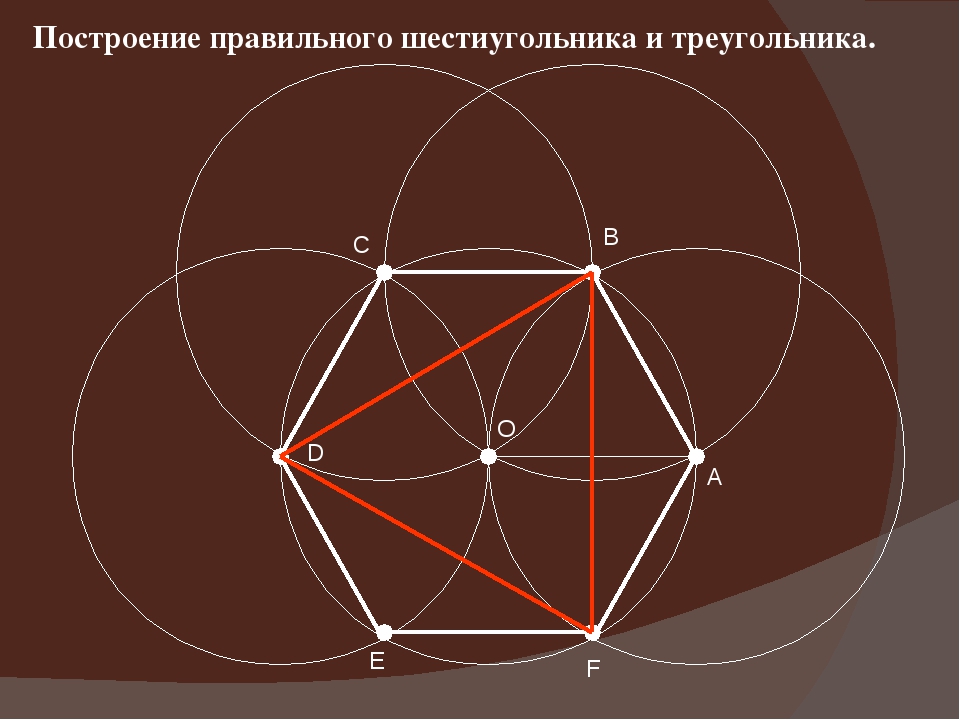
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам.
В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса; - внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
Интересные факты
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
необходимый минимум информации. Построение правильных многоугольников по заданной стороне
Без изучения техники этого процесса не обойтись. Существует несколько вариантов выполнения работы. Как нарисовать звезду с помощью линейки, помогут понять самые известные методы этого процесса.
Разновидности звезд
Существует множество вариантов внешнего вида такой фигуры, как звезда.
Еще с древних времен пятиконечная ее разновидность использовалась для начертания пентаграмм. Это объясняется ее свойством, которое позволяет сделать рисунок, не отрывая ручки от бумаги.
Существуют также шестиконечные, хвостатые кометы.
Пять вершин традиционно имеет морская звезда.
Такой же формы нередко встречаются изображения рождественского варианта.
В любом случае, чтобы нарисовать пятиконечную звезду поэтапно, необходимо прибегнуть к помощи специальных инструментов, так как изображение от руки вряд ли будет выглядеть симметрично и красиво.
Выполнение чертежа
Чтобы понять, как нарисовать ровную звезду, следует осознать суть этой фигуры.
Основой для ее начертания является ломаная линия, концы которой сходятся в начальной точке. Она образовывает правильный пятиугольник — пентагон.
Отличительными свойствами такой фигуры являются возможности вписания ее в окружность, а также окружности в этот многоугольник.
Все стороны пентагона равны между собой. Понимая, как правильно выполнить чертеж, можно осознать суть процесса построения всех фигур, а также разнообразных схем деталей, узлов.
Для достижения такой цели, как нарисовать звезду с помощью линейки, необходимо владеть знаниями о простейших математических формулах, являющихся основополагающими в геометрии.
А также потребуется умение считать на калькуляторе. Но самое главное — это логическое мышление.
Работа не является сложной, но она потребует точности и скрупулезности. Потраченные усилия будут вознаграждены хорошим симметричным, а потому и красивым изображением пятиконечной звезды.
Классическая техника
Самый известный способ того, как нарисовать звезду при помощи циркуля, линейки и транспортира, является достаточно несложным.
Для этой методики понадобится несколько инструментов: циркуль или транспортир, линейка, простой карандаш, ластик и лист белой бумаги.
Чтобы понять, как красиво нарисовать звезду, действовать следует последовательно, этап за этапом.
Можно в работе воспользоваться специальными вычислениями.
Расчет фигуры
На этом этапе рисования правильной звезды проступают контуры готовой фигуры.
Если все сделано правильно, полученное изображение будет ровным. Это можно проверить визуально, вращая лист бумаги и оценивая форму. Она будет неизменной при каждом повороте.
Основные контуры наводятся при помощи линейки и простого карандаша более четко. Все вспомогательные линии убираются.
Чтобы понять, как нарисовать звезду поэтапно, следует проводить все действия вдумчиво. В случае ошибки можно подправить рисунок ластиком или провести все манипуляции заново.
Оформление работы
Готовую форму можно украсить самыми разнообразными способами. Главное — не нужно бояться экспериментировать. Фантазия подскажет оригинальный и красивый образ.
Можно разукрасить нарисованную ровную звезду простым карандашом или использовать самые разнообразные цвета и оттенки.
Чтобы разобраться в том, как нарисовать правильную звезду, необходимо придерживаться идеальных линий во всем. Поэтому самый популярный вариант оформления заключается в разделении каждого луча фигуры на две равные части линией, исходящей от вершины до центра.
Можно не разделять стороны звезды линиями. Допускается просто закрасить каждый луч фигуры более темным оттенком с одного бока.
Такой вариант также будет ответом на вопрос о том, как нарисовать правильную звезду, ведь все ее линии будут симметричны.
По желанию при эстетическом оформлении фигуры можно добавить орнамент или другие всевозможные элементы. Добавив кружочки к вершинам, можно получить звезду шерифа. Применив плавную растушевку теневых сторон, можно получить морскую звезду.
Эта техника является самой распространенной, так как без особых усилий позволяет понять, как нарисовать пятиконечную звезду поэтапно. Не прибегая к сложным математическим вычислениям, возможно получить правильное, красивое изображение.
Рассмотрев все способы того, как нарисовать звезду с помощью линейки, можно выбрать для себя более подходящий. Наиболее популярным является геометрический поэтапный метод. Он достаточно несложный и эффективный. Применив фантазию и воображение, можно из полученной правильной, красивой формы создать оригинальную композицию. Вариантов оформления рисунка существует великое множество. Но ведь всегда можно придумать свой собственный, самый необычный и запоминающийся сюжет. Главное — не стоит бояться экспериментировать!
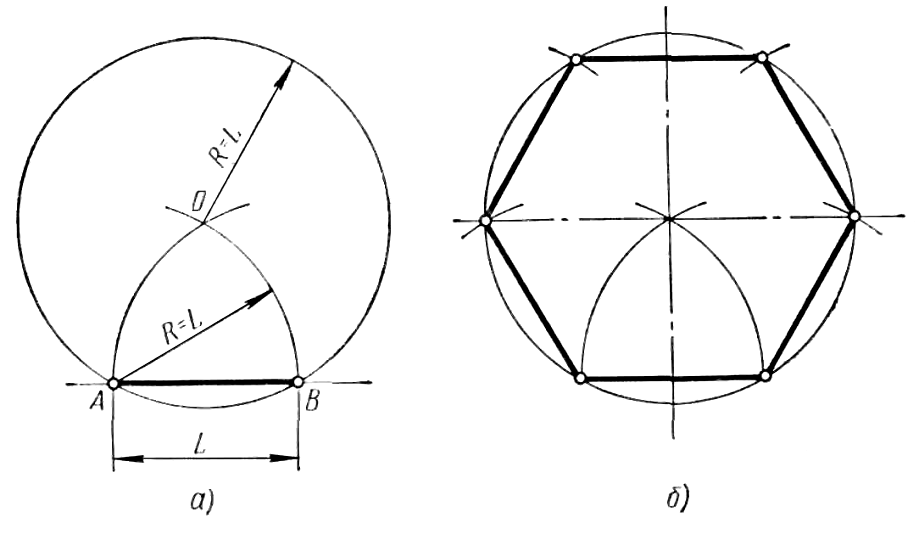
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Уровень сложности: Несложно
1 шаг
Сначала, выбирайте, где разместить центр окружности. Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.
2 шаг
Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н. Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.
3 шаг
Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.
4 шаг
Далее из полученных точек по всей окружности отчерчиваем циркулем расстояния, равные отрезку МЕ, всего точек должно получиться 5. Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.
- При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки . Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Толковый словарь Ожегова гласит, что пятиугольник представляет собой ограниченную пятью пересекающимися прямыми, образующими пять внутренних углов, а также любой предмет подобной формы. Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).
Чем интересен правильный пятиугольник?
Именно в такой форме было построено всем известное здание Минобороны Соединенных Штатов. Из объемных правильных многогранников лишь додекаэдр имеет грани в форме пентагона. А в природе напрочь отсутствуют кристаллы, грани которых напоминали бы собой правильный пятиугольник. Кроме того, эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Согласитесь, это интересно!
Основные свойства и формулы
Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.
- Центральный угол α = 360 / n = 360/5 =72°.
- Внутренний угол β = 180° * (n-2)/n = 180° * 3/5 = 108°. Соответственно, сумма внутренних углов составляет 540°.
- Отношение диагонали к боковой стороне равно (1+√5) /2, то есть (примерно 1,618).
- Длина стороны, которую имеет правильный пятиугольник, может быть рассчитана по одной из трех формул, в зависимости от того, какой параметр уже известен:
- если вокруг него описана окружность и известен ее радиус R, то а = 2*R*sin (α/2) = 2*R*sin(72°/2) ≈1,1756*R;
- в случае, когда окружность c радиусом r вписана в правильный пятиугольник, а = 2*r*tg(α/2) = 2*r*tg(α/2) ≈ 1,453*r;
- бывает так, что вместо радиусов известна величина диагонали D, тогда сторону определяют следующим образом: а ≈ D/1,618.
- Площадь правильного пятиугольника определяется, опять-таки, в зависимости от того, какой параметр нам известен:
- если имеется вписанная или описанная окружность, то используется одна из двух формул:
S = (n*a*r)/2 = 2,5*a*r либо S = (n*R 2 *sin α)/2 ≈ 2,3776*R 2 ;
- площадь можно также определить, зная лишь длину боковой стороны а:
S = (5*a 2 *tg54°)/4 ≈ 1,7205* a 2 .
Правильный пятиугольник: построение
Данную геометрическую фигуру можно построить по-разному. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны. Последовательность действий была описана еще в «Началах» Евклида примерно 300 лет до н.э. В любом случае, нам понадобятся циркуль и линейка. Рассмотрим способ построения с помощью заданной окружности.
1. Выберите произвольный радиус и начертите окружность, обозначив ее центр точкой O.
2. На линии окружности выберите точку, которая будет служить одной из вершин нашего пятиугольника. Пусть это будет точка А. Соедините точки О и А прямым отрезком.
3. Проведите прямую через точку О перпендикулярно к прямой ОА. Место пересечения этой прямой с линией окружности обозначьте, как точку В.
4. На середине расстояния между точками О и В постройте точку С.
5. Теперь начертите окружность, центр которой будет в точке С и которая будет проходить через точку А. Место ее пересечения с прямой OB (оно окажется внутри самой первой окружности) будет точкой D.
6. Постройте окружность, проходящую через D, центр которой будет в А. Места ее пересечения с первоначальной окружностью нужно обозначить точками Е и F.
7. Теперь постройте окружность, центр которой будет в Е. Сделать это надо так, чтобы она проходила через А. Ее другое место пересечения оригинальной окружности нужно обозначить
8. Наконец, постройте окружность через А с центром в точке F. Обозначьте другое место пересечения оригинальной окружности точкой H.
9. Теперь осталось только соединить вершины A, E, G, H, F. Наш правильный пятиугольник будет готов!
Как нарисовать шестиугольник с помощью линейки
Пятиугольник
Здравствуйте коллеги.Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.
Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.
Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.
Как выглядит пятиугольник и звезда
Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.
Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.
Теперь от точки В до точки С проведем прямую.
Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.
И отрезок DB. Картинка внизу.
Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.
Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.
Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.
Такие же отрезки наносим на всей части круга. Смотрим картинку.
На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.
Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.
Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.
Как построить и нарисовать правильный пятиугольник по окружности
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
Интересные факты
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Я РАСТУСайт для детей и их родителейПоследние события
Как из картинки сделать раскраску?
Раскраски любят и дети, и взрослые. И это неудивительно. Ведь даже не умея профессионально рисовать, можно создавать красивые рисунки, вкладывая в них своё умение и виденье .
Рисуем цыпленка
Вот такого цыпленка вы сможете нарисовать, если вы выполните все действия четко по шагам. Пробуйте и все у вас получится!
Елка-раскраска на стену
А так как скоро Новый Год, предлагаю скачать шаблон большой елки-раскраски. Этот шаблон состоит из 22 двух листов формата А4. На них нанесен и основной рисунок, и линии по которым нужно эти листочки склеить.
Дедушка Мороз и дети
Дед Мороз, Снегурочка, Снеговик, птицы и звери в лесу , дети на новогоднем празднике — вот герои этой книжки-раскраски. А создал их художник В. Жигарев.Маша и Медведь. Зимние раскраски
Мультик про шуструю озорную маленькую девочку Машу и ее приятеля медведя нравится всем — и детишкам, и их родителям.Раскраски с дедом Морозом
Новый год наступил. Но впереди еще старый новый год, да и зима еще вся впереди. Раскрашиваем картинки с Дедом Морозом и Снегурочкой.Раскраски к новому году
Новогодние раскраски. Зима, елка, дед Мороз в санях, подарки. Скачайте забавные картинки, пусть они напоминают вам о веселом празднике.
Популярное
Архив
Как нарисовать правильную звездочку
Как нарисовать правильную звездочку? Как нарисовать правильный пятиугольник? Как разделить круг на пять равных частей? На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной эти шаги.Как нарисовать правильную звездочку?
Как нарисовать правильный пятиугольник?
Как разделить круг на пять равных частей?
На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной вот эти шаги.
Конечно же, нам понадобится циркуль с карандашом и линейка.
Для начала нарисуйте циркулем круг.
Разделите его на четыре части линиями сверху вниз и справа налево.
Можно сразу объяснить ребенку, что отрезок, соединяющий две точки на окружности и проходящий через ее центр, называется диаметр.
А отрезок, соединяющий центр и точку на окружности, называется радиус.
С помощью линейки измерьте и разделите пополам один из радиусов.
У меня это отрезок слева от центра.
Серединку радиуса я обозначила
Нам понадобится точка сверху окружности.
Ее я обозначила цифрой 0.
Устанавливаем иголку циркуля
в точку 1, а карандашик в точку 0.
Рисуем дугу до пересечения с горизонтальным диаметром.
Обозначаем точку пересечения
Сейчас устанавливаем иголку циркуля
в точку 0, а карандашик в точку 2.
И рисуем дугу до пересечения с окружностью, причем с двух сторон.
Точки пересечения помечены
Не меняя ширину циркуля, устанавливаем иголку
в точку 3 и отмеряем кусочек окружности.
Точку 6 можно отмерить и от
точки 5 и от точки 4.
Главное, не изменять ширину (раствор) ножек циркуля.
Вот, практически и все.
Если соединим точки, получим правильный пятиугольник.
Построение на плоскости
Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?ins >
Нам понадобятся: карандаш, линейка, циркуль.
Построение угла в 60
1. Проведём прямую и отметим на ней точку А.
2. Из точки А проведём дугу произвольного радиуса и получим точку В.
3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.
4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.
Построение угла в 45
1. Построим угол 60, кака описано выше.
2. Разделим полученный угол пополам.
3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.
Построение угла в 75
1. Построим угол в 60, как описано выше, и разделим его пополам.2. В ходе дальнейшего деления надвое получим угол в 15.
3. Отразим угол в 15 через луч 60 и так получим угол в 75.
Построение угла в 90
1. Построим угол в 60, как описано выше, и разделим его пополам.
2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.
Разделение отрезка на равные части.
1. Проведём прямую и отметим на ней отрезок АВ.
2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.
3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.
Построение правильного пятиугольника.
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC . Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G .
3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG .
Построение правильного шестиугольника.
1. Проведём окружность радиусом 50 мм.
2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.
Построение правильного семиугольника.
1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Из точки D проведём дугу радиусом равным радиусу окружности.
3. Дуга пересечёт окружность в точках E и G .
4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF .
Общий метод построения многоугольников.
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.
2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.
3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.
4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G . Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.
Линейно-конструктивный рисунок шестигранной призмы
Научимся изображать шестигранную призму в различных положениях.
Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.
Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 — 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 — 1 и 4 — 3 параллельны прямой 5 — 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмыГоризонтальный шестиугольник. Изобразите горизонтальный эллипс произвольного раскрытия, т. е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57). Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шестиугольника параллельны соответствующим диаметрам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.
Вертикальный шестиугольник. В таком шестиугольнике прямые, соединяющие точки 7 и 3, б и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5 — 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и Б, а на их пересечении с эллипсом найдите точки 1,3,6л4. Затем последовательно соедините точки 1 — 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.
Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем квадрат заданных пропорций. Поэтому данный способ построения шестиугольника представляется наиболее точным и универсальным. Способ построения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5 — 2 равен стороне квадрата, а по вертикали — меньше ее длины.
Вертикальный шестиугольник. Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5 — 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68). Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1114 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).
Горизонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).
Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмыКроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс). Все вершины шестиугольника должны принадлежать этому эллипсу.
Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78). Изобразите вертикальные и горизонтальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмыКак нарисовать невозможный шестиугольник – Невозможные фигуры
Понравились мои уроки рисования? Получите больше на YouTube:
Нажмите ЗДЕСЬ, чтобы сохранить учебник в Pinterest!
Что такое невозможный объект? Также называемые невозможными фигурами или неразрешимыми фигурами, эти рисунки являются разновидностью оптического обмана. Двумерная фигура кажется трехмерной, но геометрия не похожа ни на что, что могло бы существовать в реальном мире. Невозможные предметы использовались в интригующих произведениях искусства на протяжении всего двадцатого века.
Невозможный шестиугольник в этом руководстве по рисованию основан на треугольнике Пенроуза, который был создан художником в 1934 году. Полигоны Пенроуза, такие как этот шестиугольник, строятся путем добавления дополнительных сторон к треугольнику Пенроуза.
Тем не менее, оптическая иллюзия становится менее яркой, поскольку добавляется больше сторон. Таким образом, шестиугольник может казаться искривленным, заплетенным или искривленным, а не «невозможным».
Шестиугольники являются общими структурами как в искусстве, так и в природе. Вы знали? Соты сделаны из маленьких шестиугольников пчелиного воска. Интересно, что шестиугольник позволяет покрывать большое пространство как можно меньшим количеством воска.
Хотите нарисовать невозможный шестиугольник? Сделать это легко и весело с помощью этого простого, пошагового руководства по рисованию фигур. Все, что вам нужно, это карандаш, ручка или маркер и лист бумаги. Вы также можете покрасить свой законченный рисунок.
Пошаговая инструкция по рисованию – Невозможный шестиугольник
1. Начните с рисования шестиугольника. Шестиугольник — это правильная шестигранная фигура, в которой все стороны имеют одинаковую длину.
2. Нарисуйте короткую линию, идущую от верхнего угла шестиугольника. От этой линии вытяните более длинную линию, параллельную стороне шестиугольника. Затем от конца этой линии протяните прямую линию, параллельную следующей стороне шестиугольника. Обратите внимание, что расстояние между линией и второй стороной больше, чем между линией и первой стороной.
3. Нарисуйте короткую прямую линию, идущую от следующего угла шестиугольника. Протяните от него прямую линию, параллельную стороне шестиугольника.
4. Протяните короткую прямую линию от нижнего угла шестиугольника. Из этой линии нарисуйте прямую линию, параллельную нижней части шестиугольника. Затем продлите еще одну линию вверх, параллельно следующей стороне шестиугольника.
5. Проведите короткую линию от оставшегося нижнего угла шестиугольника. Отсюда нарисуйте прямую линию, параллельную стороне шестиугольника. Затем проведите еще одну линию параллельно следующей стороне шестиугольника.
6. Нарисуйте короткую прямую линию, выходящую из следующего угла шестиугольника. Затем протяните прямую линию, параллельную стороне шестиугольника.
7. Проведите короткую прямую линию от последнего угла шестиугольника. Отсюда вытяните прямую линию, параллельную вершине шестиугольника.
8. Начните соединять внешние края невозможного шестиугольника. Расширьте короткие линии от верхнего угла и стороны формы. Затем соедините эти линии с существующими линиями, заключив верхнюю и верхнюю часть рисунка.
9. Проведите короткую линию, идущую от нижнего угла шестиугольника. Затем соедините все открытые линии, пока фигура не будет полностью заключена.
Цвет и тень вашего невозможного шестиугольника. Обратите внимание, как затенение в нашем примере делает трехмерную иллюзию более яркой.
Урок геометрии и информатики. Тема урока по учебному плану: Построение правильных многоугольников (1)
Интегрированный урок геометрии и информатики.
Тема урока по учебному плану: Построение правильных многоугольников.
Авторы: учитель МОУ «Большеяниковская СОШ» Урмарского района Гурьева Р.Т., учитель математики и Григорьева А.П., учитель информатики
Ожидаемые результаты: учащиеся должны научиться строить правильные многоугольники с помощью циркуля и линейки, с помощью компьютера; уметь применять теоретические знания при решении задач.
Оборудование к уроку: Персональные компьютеры, интерактивная доска, мультимедийный проектор, экран, карточки-задания, маркеры, цветная бумага, циркуль, линейка, электронный учебник «Уроки геометрии Кирилла и Мефодия, 9 класс», магниты, портрет немецкого математика Гаусса.
I. Организационный момент
II. Проверка домашнего задания.
III. Актуализация знаний учащихся.
4. Изучение нового материала.
5.Закрепление изученного материала, итоговое тестирование.
VI. Подведение итогов урока
I. Организационный момент (наличие циркулей, линеек, раздать цветные бумаги).
Упр. 1095 (слайд 3, 4)
III. Актуализация знаний учащихся.
2 ученика выполняют задание на маркерной доске:
1.Определение правильного многоугольника.
Есть в школьной геометрии такие темы, при изучении которых встречаешься с «красивым» материалом. К ним можно отнести тему «Правильные многоугольники» (на доске написана тема урока «Построение правильных многоугольников»)
Название «правильных» идет из античных времен. Древнегреческие ученые проявляли большой интерес к правильным фигурам еще со времен Пифагора. В египетских и вавилонских старинных памятниках встречаются правильные четырехугольники, шестиугольники, восьмиугольники в виде изображений на стенах и украшений, высеченных из камня. Правильные многоугольники привлекали к себе внимание ученых, строителей, архитекторов и многих других. Нас поражает красота, гармония многогранников, образованных простейшими правильными многоугольниками одного типа (слайд 10)
Вот для рабочего кабинета настольный календарь 2010 года, имеющий форму додекаэдра. Обратим внимание на то, что гранями многогранников являются правильные многоугольники: правильные треугольники, правильные четырехугольники, а правильные шестиугольники не могут являться гранями многогранников. Это связано с тем, что сумма плоских углов при вершине многогранников меньше 360 градусов.
Знания о правильных многоугольниках применяются в разных профессиях. Например, ювелир вставляет дорогой камень в золотую оправу. Слесарь подбирает ключ для болтика формы правильного многоугольника и т.д. Решенные нами задачи также нас показывают, что без знаний о правильных многоугольниках нам не обойтись. Они встречаются в жизни везде (слайд 11).
Итак, тема «Построение правильных многоугольников», как мы видим, актуальна.
Запишем тему урока «Построение правильных многоугольников» (слайд 12).
4. Изучение нового материала
В математике есть специальные задачи на построение, которые решаются только с помощью циркуля и линейки. Что же можно делать с помощью линейки и что с помощью циркуля?
Ясно, что линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки.
С помощью циркуля можно провести окружность произвольного радиуса, а также с центром в данной точке и радиусом, равным данному отрезку; можно отложить отрезок заданной длины (слайд 13).
Выполняя эти несложные операции, мы можем решать разные задачи на построение.
В 7 классе мы с вами изучали ряд простейших построений циркулем и линейкой:
через данную точку провести прямую, перпендикулярную к данной прямой;
разделить данный отрезок пополам;
построение угла, равного данному.;
построение треугольников по трем заданным элементам и т.д.
Домашним заданием было повторение решений этих задач.
а) через точку на прямой
б) через точку, не лежащую на прямой
в)построение перпендикулярной прямой.
Ученики комментируют решение по слайду 14 — деление отрезка пополам.
Оценить работу ученика, выполнившего построение перпендикулярной прямой через точку, не лежащую на данной прямой (слайд 15).
Интереснейшей задачей на построение с помощью циркуля и линейки является практическая задача построения правильного многоугольника с заданным числом сторон, поставленная еще в глубокой древности. Решение этой задачи можно найти в трудах древнегреческих ученых Архимеда, Евклида, Пифагора, математика 17-18 веков Гаусса (слайд 16).
Еще в 5-6 веке до нашей эры Евклидом были решены задачи на построение правильного треугольника, четырехугольника, шестиугольника, пятнадцатиугольника с помощью циркуля и линейки (слайд 17).
Сегодня мы с вами рассмотрим способы построения некоторых правильных многоугольников.
Цель урока: научиться строить правильные треугольники, четырехугольники, пятиугольники, шестиугольники и некоторые другие правильные многоугольники:
.
Построения правильных треугольника, квадрата, шестиугольника несложны. Вспомним построение треугольника по трем равным сторонам (слайд 18, ссылка на презентацию «Построение правильного треугольника»).
Проведем прямую и на ней отложим отрезок АВ. Затем построим две окружности: с центром в точке А и центром в точке В радиуса АВ.
Построение квадрата.
Так как диагонали квадрата взаимно-перпендикулярны и в точке пересечения делятся пополам, то можно построить так: Оценить ответ 2 ученика.
Мы при построении квадрата воспользовались его свойствами.
Если вспомнить определение квадрата, то можно применить следующий способ.
(Электронный учебник «Геометрия в 9 классе» (Кирилла и Мефодия)- кадр «Построение правильного четырехугольника»).
Для построения правильных многоугольников обычно используется окружность, описанная около многоугольника. Чтобы построить правильный n-угольник, достаточно разделить окружность на n равных дуг, тогда точки деления будут его вершинами (кадр «Построение правильного многоугольника»).
Центральные углы равны градусов.
Треугольники равны по 2 сторонам и углу между ними. Следовательно, отрезки А1А2 =А2А3=….,
если все стороны вписанного многоугольника равны, то он является правильным. Итак, при любых натуральных значениях n≥3 существует правильный n-угольник. В некоторых случаях задача о построении правильных n-угольников решается с помощью циркуля и линейки.
Задача 1.
7 кадр «Построение правильного четырехугольника, вписанного в окружность» (ребята выполняют в тетради).
Задача 2. Построить правильный шестиугольник (слайд 210.
8 кадр. Построение правильного шестиугольника, вписанного в окружность
Ребята выполняют построение в тетради.
Ребята, можно ли построить правильный треугольник с помощью окружности? Да (слайд 22).
Задача 3.Построить правильный пятиугольник (ребята выполняют в тетради, 2 ряд выполняет на цветной бумаге)
Опорная схема на столах
Построение правильного пятиугольника выполните дома, пользуясь опорной схемой.
Посмотрите, как нужно работать.
Пользуясь опорной схемой, дети строят в своих тетрадях правильный пятиугольник (слайды 23, 24).
Для построения правильных многоугольников часто используется следующая задача:
Дан правильный n-угольник. Построить правильный 2n угольник.
Мы уже говорили, что построение n-угольника эквивалентно делению окружности на n равных дуг. Дугу легко разделить пополам, построив биссектрису соответствующего центрального угла. (Электронный учебник «Геометрия в 9 классе» Кирилла и Мефодия — кадр «Построение правильного 2n- угольника»).
Практическая работа на примере восьмиугольника (дети строят в тетради), 25 слайд.
Применяя указанный способ можно с помощью циркуля или линейки построить целый ряд правильных многоугольников, если построен один из них.
Например. Построив правильный четырехугольник, можно построить правильный восьмиугольник, правильный шестнадцатиугольник и вообще правильный 2k угольник, где k>2.
Долгое время математики тщетно искали способы построения правильного семиугольника, девятиугольника, не зная даже вообще возможны ли эти построения.
В решении поставленной проблемы построения правильных многоугольников большой вклад внес немецкий математик Гаусс (1801 г). Он открыл способ построения правильного 17-угольника только с помощью циркуля и линейки и указал все значения n, при которых возможно построение правильного n-угольника указанными средствами. Этими многоугольниками оказались лишь многоугольники, у которых количество сторон является простым числом вида (2 в степени 2k )+1 или а также те, которые получаются из них удвоением числа сторон.
Таким образом, с помощью циркуля и линейки оказалось невозможным построение правильного 7, 9,11, 13, 14, 18, 19, 21, 22, 23, 25, 27, 28….- угольников и т.д.
(Материал взят из электронного учебника «Геометрия в 9 классе» Кирилла и Мефодия) .
3,4,5,6,8,10,12,15,16,17,20,24,30,32,34,40 … — угольники можно построить. Гаусс описал даже построение правильного 257-угольника только с помощью циркуля и линейки.
7, 9,11, 13, 14, 18, 19, 21, 22, 23, 25, 27, 28… – угольники невозможно построить только с помощью циркуля и линейки (слайд 26).
Однако в практических построениях нас никто не ограничивает в выборе математических инструментов. Сейчас вы будете строить правильные многоугольники методом моделирования при отсутствии специальных инструментов, имея компьютер (учитель информатики).
Физкультминутка (слайд 28).
Учитель информатики.
На уроке информатики мы с вами изучали тему «Модель и моделирование». Вспомним основные определения (слайд 29).
Модель – это упрощённое подобие предмета или процесса. Она повторяет какие-то свойства оригинала и заменяет его в некоторых случаях.
Модель — способ замещения реального объекта, используемый для его изучения.
Моделирование – процесс создания модели предмета.
На прошлых уроках мы моделировали объекты в текстовом редакторе, в электронной таблице и в графическом редакторе. Сегодня мы с вами посмотрим, как можно моделировать не объект, а процесс, т.е моделировать функции линейки, циркуля, транспортира по готовым алгоритмам. Построим правильные многоугольники в графической среде.
Учащиеся первого ряда садятся за свои компьютеры (построить правильные четырехугольники и правильные шестиугольники, алгоритмы на листочках лежат около компьютеров). По завершении работы сохраните как «многоугольник» в папке «Мои рисунки» (слайды 30, 31).
В это время 1 ученик за основным компьютером выполняет построение правильного треугольника с объяснением, остальные смотрят на экран.
Учитель информатики. Итак, мы убедились, что моделировать процесс построения правильных многоугольников с помощью графического редактора можно. Нужно лишь сначала написать или продумать план действий.
А как можно нарисовать правильные многоугольники очень быстро? Конечно, с помощью компьютерных программ. Существует множество готовых программ по конструированию, проектированию, моделированию объектов.
Сегодня я хочу вас познакомить одной из таких программ, которая называется «StarCad». (Демонстрация программы: построение пятиугольника с комментарием) (слайд 32).
Учитель математики.
Правильные многоугольники встречаются в природе. Одним из примеров являются
пчелиные соты, которые представляют собой прямоугольник, покрытый (т.е. составленный, обращаем внимание, без просветов и перекрытий) правильными шестиугольниками.
Ребята, пчелы — удивительные творцы, вы об этом все знаете. Обратите внимание, соты пчел имеют форму правильного шестиугольника. Плоскость прямоугольника покрыта этими правильными шестиугольниками без просветов и наложений (слайды 33, 34).
Сейчас мы с вами попробуем покрыть плоскость построенными вами правильными многоугольниками без просветов и перекрытий.
Учитель информатики.
Алгоритм покрытия плоскости без просветов и перекрытий:
1. Выделяем выбранный многоугольник.
2. Одновременно с нажатием кнопки Ctrl передвигаем многоугольник с помощью мышки, вставляя так, чтобы исходный многоугольник и его копия соприкасались сторонами (слайд 35).
За компьютеры — садится 1 ряд (покрытие плоскости без просветов и наложений правильными четырехугольниками и правильными шестиугольниками, за основной -1 ученик, работает с объяснением, выполняет покрытие плоскости правильными треугольниками.
Учитель математики.
Параллельно проводится лабораторная работа – покрытие плоскости без просветов и наложений правильными пятиугольниками.
Работа в группе из 6 человек.
Задание: вырезать напечатанные правильные пятиугольники и покрыть ими плоскость без просветов и наложений т.е. перекрытий.
3 ученика решают по карточке у доски.
а) вычислить периметр и площадь правильного треугольника со стороной 4 см;
б) вычислить периметр и площадь правильного четырехугольника со стороной 3 см;
в) вычислить периметр и площадь правильного четырехугольника со стороной 2 см.
Выступление ученика — защита исследовательской работы «Геометрические паркеты из правильных многоугольников». Делается вывод, что плоскость можно покрыть без просветов и перекрытий только правильными треугольниками, четырехугольниками, правильными шестиугольниками.
Ребята, а вы никогда не задумывались над тем, почему пчелы строят свои соты в форме правильных шестиугольников? (слайд 37).
Ответ на этот вопрос нам даст решение этих задач (проверить работу учеников, работавших у доски):
а) вычислить периметр и площадь правильного треугольника со стороной 4 см.
Ответ. S==4; Р=12 см.
б) вычислить периметр и площадь правильного четырехугольника со стороной 3 см.
Ответ. Р=12 см.
S=9 кв.см
в) вычислить периметр и площадь правильного четырехугольника со стороной 2 см.
Ответ.Р=12 см.
S==6
Вывод. При заданном периметре площадь больше в третьем случае. Во всех случаях воска уходит одинаковое количество, а вместимость больше.
Следовательно, при построении сотых в форме правильных шестиугольников экономится воск.
5.Итоговое тестирование на компьютере (слайд 38).
На компьютере выполняют тесты 9 учеников, выполняется работа в 2 варианта.
1 вариант.
1.Выберите верные утверждения
1.Если все углы многоугольника равны, то он является правильным.
2.Если все стороны многоугольника равны, то он является правильным.
3. Любой выпуклый многоугольник является правильным.
4.Любой правильный многоугольник является выпуклым.
2. Какой правильный многоугольник всегда можно построить с помощью циркуля и линейки, если дан правильный n-угольник?
1. Правильный (n-1) угольник
2. Правильный 2n- угольник
3. Правильный 3n- угольник
4. Правильный (n+1) угольник
3.Какие из перечисленных правильных многоугольников нельзя построить с помощью циркуля и линейки?
1. Правильный семиугольник.
2. Правильный восьмиугольник
3. Правильный шестиугольник
4. Правильный пятиугольник
4.Какие утверждения неверны?
1. Сторона правильного шестиугольника, вписанного в окружность, равна радиусу этой окружности.
2. Треугольник является правильным, если все его углы равны.
3. Любой равносторонний треугольник является правильным.
4.Любой четырехугольник с равными сторонами является правильным.
5. Найти площадь правильного четырехугольника, если радиус окружности, описанной около этого четырехугольника, равна 3
Ответы:
1. 2
2. 4
3. 18
4. 27
2 вариант.
1. Какой правильный многоугольник всегда можно построить с помощью циркуля и линейки, если дан правильный n-угольник?
1. Правильный (n-1) угольник
2. Правильный 2n- угольник
3. Правильный 3n- угольник
4. Правильный (n+1) угольник
2.Выберите верные утверждения
1.Если все углы многоугольника равны, то он является правильным.
2.Если все стороны многоугольника равны, то он является правильным.
3. Любой выпуклый многоугольник является правильным.
4.Любой правильный многоугольник является выпуклым.
3.Какие утверждения неверны?
1. Сторона правильного шестиугольника, вписанного в окружность, равна радиусу этой окружности.
2. Треугольник является правильным, если все его углы равны.
3. Любой равносторонний треугольник является правильным.
4.Любой четырехугольник с равными сторонами является правильным.
4.Какие из перечисленных правильных многоугольников нельзя построить с помощью циркуля и линейки?
1. Правильный семиугольник.
2. Правильный восьмиугольник
3. Правильный шестиугольник
4. Правильный пятиугольник
5. Найти площадь правильного четырехугольника, если радиус окружности, описанной около этого четырехугольника, равна 2
Ответы:
1. 2
2. 4
3. 8
4. 12
Проводится блеф-клуб с остальными учениками, раздать листочки.
Верите ли вы, что: Отвечать только да или нет.
Около любого правильного многоугольника можно описать окружность и притом только одну.
В любой многоугольник можно вписать окружность.
Если стороны вписанного многоугольника равны, то он является правильным.
Любой четырехугольник с равными сторонами является правильным.
С помощью циркуля и линейки можно построить правильный двенадцатиугольник.
Сумма внешних углов правильного треугольника равна .
Ромб – правильный четырехугольник.
По данному n-угольнику можно ли построить правильный 2 n – угольник.
— сторона правильного треугольника.
Площадь правильного многоугольника можно вычислить по формуле , где — периметр многоугольника, а — радиус вписанной окружности.
Ответы.
Да – 1, 3, 5, 6, 8.
Нет -2, 4, 7, 9, 10.
Самооценка.
10 заданий- «5»
8 заданий — «4»
6 зданий — «3»
1-5 заданий – «2» .
6. Итог урока. Обобщение всех полученных результатов, оценить работы учащихся за урок. Использование учителем позитивных оценок (вербальных и невербальных) в виде похвалы, одобрения.
Задание на дом: п. 109, упр. 1090 с объяснением (слайд 39), 1098.
Слайд 40.
Как построить пентаграмму пентагон правильный пятиугольник с помощью циркуля и линейки. :-)))) в вики тоже это было, кэп Очевидность сперва делает пост, потом лезет в тырнет [изображение] Наверное… — @дневники: асоциальная сеть
среда, 08 апреля 2015
Как построитьНаверное он все же не идеально правильный, но приближение более чем точное для того чтобы строить бумажные модели додекаэдров :-)))
Доказательство того или обратного мне сходу родить слабо
Для Короткий Хвост и прочих заинтересованных лиц
1) Чертим круг и в нем два перпендикулярных диаметра, перпендикуляры все умеют строить, не рассказываю как
2) Точка А — один из концов одного диаметра на окружности
3) на перпердикулярном диаметре отметим точку В — четверть диаметра или половина радиуса делить отрезок пополам тоже все умеют
4) из точки В радиусом ВА отметим точку С внутри круга на том же диаметре что и В
5) длина АС будет равна стороне пятиугольника, отложим ее от любой точки на окружности, например, от А направо и налево, из от этих засечек еще по разу. Растояние между последними засечками будет тоже равно АС с достаточной точностью, это видно если циркуль с тем же раствором АС например приложить к точкам
6) проверить что угол при вершине равнобедренного треуголька образованного радиусами круга и стороной пятиугольника, равен (более менее) 72 градусам можно с помощью транспортира.
ваш кэп Оч. :-)) кстати обратите внимание что на клетчатой бумаге при радиусе на 6 клеточек — засечки лежат на горизонталях если считать сверху — 0, почти 4 и 11, я этим пользовалась иногда когда надо было быстро нарисовать
@темы: мир вокруг
- ← Предыдущая запись
- Следующая запись →
Этот пост будет безвозвратно удален:
Вы уверены в том, что действительно хотите это сделать?
Да Нет
Пятиугольник циркулем и линейкой. Как построить и нарисовать правильный пятиугольник по окружности
Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Получение с помощью полоски бумаги
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
Задача построения верного пятиугольника сводится к задаче деления окружности на пять равных частей. От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.
Вам понадобится
- – линейка
- – циркуль
Инструкция
1. Видимо, что если возвести верный десятиугольник, а после этого объединить его вершины через одну, то получим пятиугольник. Для построения десятиугольника начертите окружность заданного радиуса. Обозначьте ее центр буквой O. Проведите два перпендикулярных друг друга радиуса, на рисунке они обозначены как OA1 и OB. Радиус OB поделите напополам с подмогой линейки либо способом деления отрезка напополам с подмогой циркуля. Постройте маленькую окружность с центром C в середине отрезка OB радиусом, равным половине OB.Объедините точку C с точкой A1 на начальной окружности по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.
2. Еще один метод обнаружил немецкий художник Альбрехт Дюрер. Дабы возвести пятиугольник по его методу, начните вновь с построения окружности. Вновь подметьте ее центр O и проведите два перпендикулярных радиуса OA и OB. Радиус OA поделите напополам и середину подметьте буквой C. Установите иглу циркуля в точку C и раскройте его до точки B. Проведите окружность радиуса BC до пересечения с диаметром начальной окружности, на котором лежит радиус OA. Точку пересечения обозначьте D. Отрезок BD – сторона положительного пятиугольника. Отложите данный отрезок пять раз на начальной окружности и объедините точки пересечения.
3. Если же требуется возвести пятиугольник по его заданной стороне, то вам надобен 3-й метод. Начертите по линейке сторону пятиугольника, обозначьте данный отрезок буквами A и B. Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.
Тема деления окружности на равные части с целью построения верных вписанных многоугольников издавна занимала умы древних ученых. Эти тезисы построения с использованием циркуля и линейки были высказаны еще в эвклидовых «Началах». Впрочем лишь через два тысячелетия эта задача была всецело решена не только графически, но и математически.
Инструкция
1. Приближенное построение положительного пятиугольника методом А. Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне пятиугольника ).
2. Построение верного пятиугольника на основе положительного десятиугольника, вписанного в окружность (объединив вершины десятиугольника через одну).
3. Графическое построение через вычисленный внутренний угол пятиугольника с поддержкой транспортира и линейки (сумма углов выпуклого n-угольника равна Sn=180°(n – 2), т.к. у положительного многоугольника все углы равны). При n=5, S5=5400, тогда величина угла 1080.А так же с поддержкой окружности и 2-х лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне пятиугольника .
4. Еще один легкой графический метод: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.Точки G,E,B,F,H – вершины положительного пятиугольника .
5. Построение с поддержкой приема Биона (дозволяющего возвести верный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению).Скажем: для n=5. Возведем положительный треугольник ABC, где AB – диаметр заданной окружности. Обнаружим на AB точку D, по дальнейшему соотношению: AD: AB = 2: n. При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона верного вписанного пятиугольника .При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся поменьше 10,3%.
6. Построение по заданной стороне по способу Л. Да Винчи (применяя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2: ha =3/(n-1), которое дозволено выразить так: tg180°/n =3/(n-1)).
7. Всеобщий метод построения положительных многоугольников по заданной стороне по способу Ф. Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.
Существуют два основных метода построения верного многоугольника с пятью сторонами. Оба они полагают применение циркуля, линейки и карандаша. 1-й метод представляет собой вписывание пятиугольника в окружность, а 2-й метод базируется на заданной длине стороны вашей грядущей геометрической фигуры.
Вам понадобится
- Циркуль, линейка, карандаш
Инструкция
1. 1-й метод построения пятиугольника считается больше «типичным». Для начала постройте окружность и как-либо обозначьте ее центр (обычно для этого применяется буква О). После этого проведите диаметр этой окружности (назовем его АВ) и поделите один из 2-х полученных радиусов (скажем, ОА) ровно напополам. Середину этого радиуса обозначим буквой С.
2. Из точки О (центра начальной окружности) проведите еще один радиус (ОD), тот, что будет сурово перпендикулярен проведенному ранее диаметру (АВ). После этого возьмите циркуль, поставьте его в точку С и отмерьте расстояние до пересечения нового радиуса с окружностью (СD). Это же расстояние отложите на диаметре АВ. Вы получите новую точку (назовем ее Е). Отмерьте циркулем расстояние от точки D до точки Е – оно будет равно длине стороны вашего грядущего пятиугольника .
3. Поставьте циркуль в точку D и отложите на окружности расстояние, равное отрезку DЕ. Повторите эту процедуру еще 3 раза, а после этого объедините точку D и 4 новые точки на начальной окружности. Получившаяся в итоге построения фигура будет верным пятиугольником.
4. Дабы возвести пятиугольник иным методом, для начала начертите отрезок. Скажем, это будет отрезок АВ длиной 9 см. Дальше поделите ваш отрезок на 6 равных частей. В нашем случае длина всякой части будет составлять 1,5 см. Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. Назовем ее C.
5. Сейчас возьмите линейку и проведите прямую через точку С и центр отрезка AB. После этого начиная от точки С отложите на этой прямой отрезок, составляющий 4/6 отрезка AB. 2-й конец отрезка обозначим буквой D. Точка D будет являться одной из вершин грядущего пятиугольника . Из этой точки проведите окружность либо дугу с радиусом, равным АВ. Эта окружность (дуга) пересечет ранее построенные вами окружности (дуги) в точках, являющихся двумя недостающими вершинами пятиугольника . Объедините эти точки с вершинами D, А и В, и построение положительного пятиугольника будет закончено.
Видео по теме
Луч — это прямая линия, проведенная из точки и не имеющая конца. Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?
Вам понадобится
- Лист бумаги, карандаш и линейка.
Инструкция
1. Возьмите лист бумаги и подметьте в произвольном месте точку. После этого приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Эта нарисованная линия и именуется лучом. Сейчас подметьте на луче еще одну точку, к примеру, буквой C. Линия от исходной и до точки C будет именоваться отрезком. Если вы примитивно начертите линию и не подметите правда бы одну точку, то эта прямая не будет являться лучом.
2. Нарисовать луч в любом графическом редакторе либо в том же MSOffice не труднее, чем вручную. Для примера возьмите программу Microsoft Office 2010. Зайдите в раздел «Вставка» и выберите элемент «Фигуры». В выпадающем списке выберите фигуру «Линия». Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.
3. Дабы сделать точку в начале линии, сделайте следующее: выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.
4. Выберите пункт «Формат фигуры». В меню слева выберите пункт «Тип линии». Дальше обнаружьте заголовок «Параметры линий» и выберите «Тип начала» в виде кружочка. Там же вы можете настроить толщину линий начала и конца.
5. Уберите выделение с линии и увидите, что в начале линии возникла точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, где будет находиться надпись. Позже написания надписи кликните на свободное место и она активируется.
6. Луч благополучно нарисован и заняло это каждого несколько минут. Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.
Видео по теме
Обратите внимание!
Отношение диагонали верного пятиугольника к его стороне составляет золотое сечение (иррациональное число (1+√5)/2).Весь из пяти внутренних углов пятиугольника равен 108°.
Полезный совет
Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.
Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
Вот один из методов построения правильного пятиугольника в заданной окружности:
1. Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O . (Это зелёная окружность на схеме справа).
- Выберите на окружности точку A , которая будет одной из вершин пятиугольника. Постройте прямую через O и A .
- Постройте прямую перпендикулярно прямой OA , проходящую через точку O . Обозначьте одно её пересечение с окружностью как точку B .
- Постройте точку C посередине между O и B .
- C через точку A . Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D .
- Проведите окружность с центром в A через точку D . Обозначьте её пересечения с оригинальной (зелёной окружностью) как точки E и F .
- Проведите окружность с центром в E через точку A G .
- Проведите окружность с центром в F через точку A . Обозначьте её другое пересечение с первоначальной окружностью как точку H .
- Постройте правильный пятиугольник AEGHF .
Икосаэдр
Икосаэдр — одно из пяти платоновых тел, по простоте следующее за тетраэдром и октаэдром. Их объединяет то обстоятельство, что гранями каждого являются равносторонние треугольники. При изготовлении модели икосаэдра можно выбрать любую из двух эффектных возможностей распределения пяти цветов.
Во-первых, икосаэдр может быть раскрашен так, что у каждой вершины встретятся все пять цветов (правда, в таком случае противоположные грани не будут окрашены одинаково).
Другой способ обеспечивает противоположным граням одинаковые цвета, зато у каждой вершины, за исключением двух полярных, будет повторяться по кругу один цвет. Обе раскраски очень интересны и для наших целей полезны, ибо многие описанные ниже однородные многогранники имеют икосаэдральную симметрию.
Без изучения техники этого процесса не обойтись. Существует несколько вариантов выполнения работы. Как нарисовать звезду с помощью линейки, помогут понять самые известные методы этого процесса.
Разновидности звезд
Существует множество вариантов внешнего вида такой фигуры, как звезда.
Еще с древних времен пятиконечная ее разновидность использовалась для начертания пентаграмм. Это объясняется ее свойством, которое позволяет сделать рисунок, не отрывая ручки от бумаги.
Существуют также шестиконечные, хвостатые кометы.
Пять вершин традиционно имеет морская звезда. Такой же формы нередко встречаются изображения рождественского варианта.
В любом случае, чтобы нарисовать пятиконечную звезду поэтапно, необходимо прибегнуть к помощи специальных инструментов, так как изображение от руки вряд ли будет выглядеть симметрично и красиво.
Выполнение чертежа
Чтобы понять, как нарисовать ровную звезду, следует осознать суть этой фигуры.
Основой для ее начертания является ломаная линия, концы которой сходятся в начальной точке. Она образовывает правильный пятиугольник — пентагон.
Отличительными свойствами такой фигуры являются возможности вписания ее в окружность, а также окружности в этот многоугольник.
Все стороны пентагона равны между собой. Понимая, как правильно выполнить чертеж, можно осознать суть процесса построения всех фигур, а также разнообразных схем деталей, узлов.
Для достижения такой цели, как нарисовать звезду с помощью линейки, необходимо владеть знаниями о простейших математических формулах, являющихся основополагающими в геометрии. А также потребуется умение считать на калькуляторе. Но самое главное — это логическое мышление.
Работа не является сложной, но она потребует точности и скрупулезности. Потраченные усилия будут вознаграждены хорошим симметричным, а потому и красивым изображением пятиконечной звезды.
Классическая техника
Самый известный способ того, как нарисовать звезду при помощи циркуля, линейки и транспортира, является достаточно несложным.
Для этой методики понадобится несколько инструментов: циркуль или транспортир, линейка, простой карандаш, ластик и лист белой бумаги.
Чтобы понять, как красиво нарисовать звезду, действовать следует последовательно, этап за этапом.
Можно в работе воспользоваться специальными вычислениями.
Расчет фигуры
На этом этапе рисования правильной звезды проступают контуры готовой фигуры.
Если все сделано правильно, полученное изображение будет ровным. Это можно проверить визуально, вращая лист бумаги и оценивая форму. Она будет неизменной при каждом повороте.
Основные контуры наводятся при помощи линейки и простого карандаша более четко. Все вспомогательные линии убираются.
Чтобы понять, как нарисовать звезду поэтапно, следует проводить все действия вдумчиво. В случае ошибки можно подправить рисунок ластиком или провести все манипуляции заново.
Оформление работы
Готовую форму можно украсить самыми разнообразными способами. Главное — не нужно бояться экспериментировать. Фантазия подскажет оригинальный и красивый образ.
Можно разукрасить нарисованную ровную звезду простым карандашом или использовать самые разнообразные цвета и оттенки.
Чтобы разобраться в том, как нарисовать правильную звезду, необходимо придерживаться идеальных линий во всем. Поэтому самый популярный вариант оформления заключается в разделении каждого луча фигуры на две равные части линией, исходящей от вершины до центра.
Можно не разделять стороны звезды линиями. Допускается просто закрасить каждый луч фигуры более темным оттенком с одного бока.
Такой вариант также будет ответом на вопрос о том, как нарисовать правильную звезду, ведь все ее линии будут симметричны.
По желанию при эстетическом оформлении фигуры можно добавить орнамент или другие всевозможные элементы. Добавив кружочки к вершинам, можно получить звезду шерифа. Применив плавную растушевку теневых сторон, можно получить морскую звезду.
Эта техника является самой распространенной, так как без особых усилий позволяет понять, как нарисовать пятиконечную звезду поэтапно. Не прибегая к сложным математическим вычислениям, возможно получить правильное, красивое изображение.
Рассмотрев все способы того, как нарисовать звезду с помощью линейки, можно выбрать для себя более подходящий. Наиболее популярным является геометрический поэтапный метод. Он достаточно несложный и эффективный. Применив фантазию и воображение, можно из полученной правильной, красивой формы создать оригинальную композицию. Вариантов оформления рисунка существует великое множество. Но ведь всегда можно придумать свой собственный, самый необычный и запоминающийся сюжет. Главное — не стоит бояться экспериментировать!
Уровень сложности: Несложно
1 шаг
Сначала, выбирайте, где разместить центр окружности. Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.
2 шаг
Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н. Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.
3 шаг
Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.
4 шаг
Далее из полученных точек по всей окружности отчерчиваем циркулем расстояния, равные отрезку МЕ, всего точек должно получиться 5. Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.
- При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним
— Как нарисовать правильный пятиугольник с помощью циркуля и линейки Геометрия
— Как нарисовать правильный пятиугольник с помощью циркуля и линейки — Mathematics Stack ExchangeСеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 6к раз
$ \ begingroup $Я помню, как читал, что Гауссу удалось построить правильный пятиугольник с помощью всего лишь циркуля и линейки, но я не помню подробностей того, как он это сделал.Может ли кто-нибудь помочь мне и дать мне инструкции, как это сделать?
Конкан6,77222 золотых знака1919 серебряных знаков4444 бронзовых знака
Создан 18 янв.
$ \ endgroup $ 4 $ \ begingroup $Я думаю, что это самый простой способ нарисовать правильный пятиугольник с помощью циркуля и линейки.
Создан 18 янв.
Сейед8,46544 золотых знака1818 серебряных знаков2929 бронзовых знаков
$ \ endgroup $ $ \ begingroup $Я не уверен, что это Гаусса, но вот тот, который я использую:
Нарисуйте круг.Пусть центр будет $ O $.
Определите направление как «влево» и проведите линию от центра «влево», пока не коснетесь круга. Этот сегмент — $ OA $.
Нарисуйте еще один отрезок прямой, на этот раз идущий «вверх» (это совершенно законно — вы должны знать, как построить прямую, перпендикулярную отрезку). Это сегмент $ OB $.
Найдите среднюю точку $ OA $, назвав ее $ M $.
Розыгрыш $ BM $.
Найдите биссектрису угла $ BMO $ и рисуйте, пока не достигнете $ OB $.Назовите это пересечение $ I $.
Проведите перпендикулярную линию к $ OB $ «влево», пока не коснетесь круга в точке $ C $. $ BC $ теперь представляет собой один линейный сегмент пятиугольника, а остальное относительно просто (просто нарисуйте круг с центром вокруг $ C $, проходящего через $ B $, чтобы получить третью вершину и т. Д.)
Примерно так:
grg1,9111 золотой знак88 серебряных знаков1313 бронзовых знаков
Создан 18 янв.
пирог1,96611 золотых знаков1010 серебряных знаков1919 бронзовых знаков
$ \ endgroup $ $ \ begingroup $Я знаю только две конструкции.Первое, что я узнал в старшей школе, включает линейку и компас:
Другой я выучил в колледже, изучая конструкции с использованием только компаса (Мора-Машерони). По иронии судьбы конструкция, состоящая только из компаса, — одна из самых простых конструкций, которые я когда-либо видел, для нее требуется всего 10 кругов, а отрезки линий на конце являются косметическими.
Создан 19 авг.
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
евклидова геометрия — Построение произвольных правильных многоугольников с помощью линейки и циркуля
Многое из арифметической геометрии связано с построениями или доказательствами невозможности построения конкретных фигур только с помощью линейки и циркуля.См., Например, невозможность построения правильного семиугольника и конструктивность правильного семиугольника по Гауссу.
Интересно, что значит простое устройство, которое можно построить с помощью линейки и циркуля, которое вместе с линейкой и циркулем позволяет очень легко строить произвольные правильные многоугольники.
Устройство представляет собой не что иное, как сплошной конус конечной высоты и гибкий струна длиной меньше окружности конуса.
Теперь расположите $ n $ точек на веревке на равных расстояниях и закройте цепочку так, чтобы первая и последняя точки находились на одинаковом расстоянии. Т.е. вы размещаете $ n $ точек одинаково на замкнутой строке. Этого можно добиться с помощью одного компаса.
После этого вы кладете нить на конус, удерживая все точки на одинаковой высоте, пока все они не коснутся конуса. Их вертикальное проецирование на плоскость дает углы правильного $ n $ -угольника.
Обратите внимание, что конус не является волшебным устройством, как трисектор угла, который может помочь построить прямоугольный семиугольник, но не добавляет ничего нового к линейке и компасу (потому что он может быть построен с их помощью).С другой стороны, гибкой струны достаточно, чтобы создать линейку (как физическое устройство), и вам понадобятся две линейки, чтобы сделать циркуль. Значит, в определенном смысле строки может хватить на все? Обратите внимание, что трисектора углов — и, в более общем смысле, $ k $ -секторы углов — могут быть легко построены для любого угла $ \ alpha = 2 \ pi / n $: просто поместите $ kn $ точек на строку.
Мой вопрос:
Что-то не так с моим устройством? Может быть, это не конструктивно только с помощью линейки и компаса? Сделайте другие части описанная процедура добавить что-то еще помимо линейки и компаса ( сам конус не должен)?
Я полагаю, выход из самолета «дисквалифицирует» такую конструкцию.Может быть, это связано с тем, что при решении полиномиальных уравнений вы покидаете линию действительных чисел и попадаете в комплексную плоскость? («Внезапно все полиномиальных уравнения могут быть решены!») С другой стороны: компас — это также действительно трехмерное устройство!
[Контристорическое примечание: если бы геометры , а не ограничили себя (намеренно?) Линейкой и компасом, не было бы необходимости изучать конструктивность правильных $ n $ -угольников — и многие арифметические операции могли бы не иметь было обнаружено (или значительно позже).С другой стороны: разве комплексные числа не были бы обнаружены раньше, когда устройство конуса рассматривалось более серьезно?]
Геометрическая конструкция— Построение правильного пятиугольника желаемой длины
Как OP признал в комментарии, сложная часть — это шаг 4, поэтому мы спрашиваем
Почему $ \ overline {BD} $ — это требуемый радиус описанной окружности?
Мы можем ответить на этот вопрос несколько неудовлетворительно, используя закон косинусов на $ \ треугольнике ABD $.2 \ left (50 + 10 \ sqrt {5} \ right) \ tag {1} \ end {align} $$ чтобы $$ | \ overline {BD} | = s \ sqrt {50 + 10 \ sqrt {5}} \ tag {2} $$
, что совпадает с MathWorld для радиуса описанной окружности пятиугольника с длиной стороны 10 с. $ \ квадрат $
Как я уже упоминал, это неудовлетворительный ответ … который может действительно помочь развеять сомнения OP в себе.
Конечно, расчет показывает, что числа работают так, как должны, но он не проливает света на то, как кто-то мог ожидать такого результата.(Я не верил, что это сработает, пока не проверил триггер (дважды!), И обычно я довольно хорошо воспринимаю подобные вещи. Это то, что я делаю. )
Что еще более важно, расчет не дает указаний на то, как можно естественным образом прийти к данной конструкции окружного радиуса пятиугольника. Если бы I было поручено построить длину в $ (2) $, это построение не было бы маршрутом, который я выбрал бы первым … или даже когда-либо . (Я бы, наверное, сделал что-то гораздо более сложное, используя конструкцию среднего геометрического.)
Если бы вместо этого меня попросили построить пятиугольник с заданной стороной, мне бы вообще не пришло в голову построить этот сложный окружной радиус. Скорее, я бы пошел в направлении построения @ Seyed, потому что я «знаю», что отношение диагонали к стороне — это золотое сечение, $ (1+ \ sqrt {5}) / 2 $, и я «знаю» «как построить диагональ соответствующей длины. (Это «очевидный» материал на этапах с 1 по 3 конструкции в вопросе.)
Вкратце: я считаю рассматриваемую конструкцию довольно неинтуитивной.OP не должен расстраиваться из-за непонимания ключевой связи. Для ясности:
Этот НЕ ЯВЛЯЕТСЯ индикатором того, что у вас нет хорошего будущего в математике.
(Впрочем, это может быть индикатором того, что тот, кто придумал эту удивительную конструкцию , имеет (а?) Хорошее будущее в математике у !)
| После этого | Ваша работа должна выглядеть так |
|---|---|
| Начинаем с данного круга, центр О. Примечание: Если вам не дали центр, вы можете найти его, используя метод, показанный на Нахождение центра круга с помощью циркуля и линейки. | |
| 1. Проведите диаметр круга через центральную точку и отметьте его конечные точки C и M. Он не обязательно должен быть вертикальным. | |
2. Постройте перпендикуляр к CM в точке O. Для получения дополнительной информации см. Построение перпендикуляра в точке на линии. | |
| 3. Отметьте точку S, где она пересекает круг. | |
4. Найдите середину L отрезка SO, построив его серединный перпендикуляр. Для получения дополнительной информации см. Построение серединного перпендикуляра отрезка прямой. | |
| 5. Установите циркуль на L, отрегулируйте его ширину на S или O и нарисуйте круг. | |
| 6. Проведите линию от M через L так, чтобы она пересекала маленький кружок в двух местах. Обозначьте их N и P. | |
| 7. Установите циркуль на M и отрегулируйте его ширину на P. | |
| 8. Нарисуйте широкую дугу, пересекающую заданный круг в двух местах. Обозначьте их A и E. | |
| 9. Установите циркуль на M и отрегулируйте его ширину на N. | |
| 10. Нарисуйте широкую дугу, пересекающую заданный круг в двух местах. Обозначьте их B и D. | |
| 11. Проведите линию от A до B, затем от B до C и т. Д., Пока не проведете все пять сторон пятиугольника. | |
| Готово. ABCDE — правильный пятиугольник, вписанный в данную окружность. |
| ||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
Отрывок, характеризующий правый пятиугольник
Петя не знал, сколько это длилось: он наслаждался, все время удивлялся своему удовольствию и жалел, что ему сказать.Его разбудил нежный голос Лихачева.— Готово, ваше благополучие, наденьте Гранзузу расплавленную.
Петя проснулся.
— Свет, правый, свет! Он закричал.
Первые лошади Neumless стали видны за хвосты, а сквозь голые ветви виден водянистый свет. Петя встряхнул, вскочил, вытащил девственницу из кармана и отдал Лихачеву, махая рукой, примерил шашку и вложил в ножны. Казаки распустили лошадей и задрали губы.
«Итак, командир», — сказал Лихачев.Денисов вышел из бокса и, позвав Петю, приказал собираться.
Быстро в полутиме разобрали лошадей, подобрали пометы и рассортировали по командам. Денисов стоял у Каракулька, отдавая последние приказы. Пехота отряда, истоптав сотню ног, двинулась вперед по дороге и быстро скрылась между деревьями в предрассветном тумане. Есаул приказал казакам. Петя по случаю оставил коня, ожидая приказа сесть. Омытый холодной водой, лицо, в частности глаз, горело огнем, по спине пробежал озноб, а во всем теле что-то быстро и равномерно задрожало.
— Ну что, вы все готовы? — сказал Денисов. — Давай лошадей.
Лошадей подано. Денисов рассердился на казака за то, что пазы были слабые, и, окотив его, сел. Петя взял на себя старшего. Конь по привычке хотел укусить его ногой, но Петя, не чувствуя его тяжести, быстро вскочил в седло и, глядя в темноте на гусарский трезубец, подъехал к Денисову.
— Василий Федорович, вы меня что-то обвиняете? Пожалуйста … ради бога … — сказал он.Денисов как будто забыл о существовании Пети. Он посмотрел на него.
«На одного из вас, OSHA, — строго сказал он, — слушайся меня и ничего никуда не делай.
За все время переезда Денисов больше ни слова не говорил с Петром и ехал молча. Когда подъехал к опушке леса, в поле заметно посветлело. Денисов что-то шепотом переговорил с Есаулом, и казаки стали проходить мимо Пети и Денисова. Когда все поехали, Денисов тронул их коня и проехал под гору.Сидя на досках и скользя, лошади упали вместе со своими шорниками в лощину. Петя ехал рядом с Денисовым. Дрожь во всем теле усилилась. Стало все светлее и светлее, только туман скрывает далекие предметы. Спустившись и оглянувшись, Денисов кивнул стоявшему рядом казаку.
— Сигнал! — он сказал.
Казак поднял руку, он убежал. И в это же мгновение он услышал топот перед едущими лошадьми, крики с разных сторон и неподвижные выстрелы.
В ту же минуту, как первые звуки похода и крика, Петя, ударив их лошадь и отпустив поводья, не слушая кричавшего на него Денисова, бросился вперед. Пэт казалось, что вдруг ровно как середина дня, ярко забрезжила в тот момент, как слышен выстрел. Он подскажет мост. Впереди бегут казаки. На мосту он встретил задержанного казака и раздавил его дальше. Впереди какие-то люди — должно быть, французы, они бежали по правой стороне дороги налево.Один упал в грязь под ноги Petina Horse.
Казаки толпились у одной избы. Из середины толпы раздался страшный крик. Петя подкатился к этой толпе, и первое, что он увидел, была бледная, трясущаяся нижняя челюсть француза, который держал козырьки на себе.
— Ура! .. Ребята … Наши … — крикнул Петя и, отдав поводья подручной лошади, погнал вперед по улице.
Впереди раздались выстрелы. Казаки, гусары и русские болтающиеся пленные, которые бежали по обе стороны дороги, все что-то громко кричали.Формованный, без шляпы, с красным нахмуренным лицом француз в синем синели отбивал штык от гусара. Когда Петя подсказал, француз уже упал. Опять поздно, промелькнуло в голове у пути, и он давил там, где слышались частые выстрелы. Стрельба раздавалась во дворе того Бара на берегу, в котором он был вчера вечером с Доолоховым. Французы простегали там за плечи в плотном, заросшем няньками саду и стреляли в казаков, теснившихся у ворот.Подъезжая к воротам, Петя в пороховом дыму увидел Дологова с бледным зеленоватым лицом, кричал что-то вроде людей. «В объезд! Пехота ждите!» — кричал он, пока Петя подъезжал к нему.
— Подождите? .. Ураааа! .. — крикнул Петя и, ни меда, ни минуты, бросился к тому месту, где раздались выстрелы и где был густой дым. Сон был слышен, померили пустой и за что-то забили пулями. За Петей в воротах дома утопили казаков и Черепов. Французы в раскаленном густом дыму одни бросили оружие и выбежали из кустов навстречу казакам, другие побежали под гору к пруду.Петя налил лошадь по Барскому двору и, вместо того чтобы держать поводья, странно и быстро махнул обеими руками и все дальше и дальше спускался с седла набок. Лошадь, подхватив покачивающийся легкий костер, отдохнула, а Петя тяжело упал на мокрую землю. Казаки видели, как быстро его руки и ноги быстро забрасывались, несмотря на то, что его голова не шевелилась. Пуля попала ему в голову.
Разговаривая со старшим французским офицером, который подошел к нему из-за дома с платком на сабле и объявил, что они сдаются, она сильно прослезилась от лошади и подошла к неподвижно, с протянутой рукой лежала в Pet.
«Я готов», — сказал он, нахмурившись, и пошел к воротам на Денисова, который пошел ему навстречу.
— Убит ?! — закричал Денисов, увидев еще издалека знакомую ему, несомненно, безжизненную позу, в которой лежало тело.
«Готово», — повторила она СОЛОХОВУ, как будто ход этого слова доставил ему удовольствие, и быстро пошла к пленным, окруженным спешащими казаками. — Не берем! — крикнул Денисов.
Как нарисовать правильный пятиугольник тиражом.Правый пятиугольник. Получение бумажной полоски
Правильный пятиугольник — это геометрическая форма, которая образована пересечением пяти прямых, образующих пять одинаковых углов. Такая фигура называется — Пентагон. Работа художников тесно связана с пятиугольником — их рисунки построены на основе правильных геометрических фигур. Для этого нужно уметь быстро построить пятиугольник.
Чем интересна эта цифра? Форму Пентагона имеет здание Министерства обороны США .Это видно на фото, сделанном с высоты полета. В природе нет кристаллов и камней, по форме напоминающих Пентагон. Только на этом рисунке количество граней совпадает с количеством диагоналей.
Параметры правого пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, вы можете рассчитать эти параметры, что облегчит процесс построения пятиугольника. Методы и формулы расчета:
- сумма всех углов в многоугольниках равна 360 градусам. В правом пятиугольнике все углы равны, соответственно центральный угол такой: 360/5 = 72 градуса;
- внутренний угол таким образом расположен: 180 * (n -2) / n = 180 * (5-2) / 5 = 108 градусов. Сумма всех внутренних углов: 108 * 5 = 540 градусов.
Сторона Пентагона расположена с помощью параметров, которые уже указаны в Условии Терка:
- если круг описан вокруг пятиугольника и известен его радиус, сторона находится в такой формуле: a = 2 * R * sin (α / 2) = 2 * R * sin (72/2) \ u003d 1,1756 * Р.
- Если известен радиус вписанного в пятиугольник окружности, то формула расчета стороны многоугольника: 2 * R * Tg (α / 2) = 2 * R * TG (α / 2) = 1,453 * р.
- При известном значении диагонали пятиугольника его сторона вычисляется так: a = d / 1,618.
Площадь Пентагона тоже , как и его сторона, зависит от уже найденных параметров:
- с помощью вписанной окружности известного радиуса площадь имеет следующий вид: s = (n * a * r) / 2 = 2.5 * а * р.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n * R2 * sin α) / 2 = 2,3776 * R2.
- в зависимости от стороны Пентагона: S = (5 * A2 * TG 54 °) / 4 = 1,7205 * A2.
Здание Пентагона
Правый пятиугольник можно построить с помощью линейки и циркуля, исходя из вписанной в него окружности или одной из сторон.
Как нарисовать пятиугольник на основе вписанного круга? Для этого вам необходимо заготовить круг и линейку и выполнить такие действия:
- Сначала необходимо нарисовать окружность с центром в О, после чего необходимо выбрать точку и вершину пятиугольника.От центра вверх — отрезок.
- Затем строится перпендикулярный прямой отрезок OA, который также проходит через центр окружности. Его пересечение с окружностью обозначается точкой V. Разрез О. В. делит пополам точку S.
- Точка C будет центром нового круга, проходящего через A. Точка D — это его пересечение с прямой s в границах первой фигуры.
- После этого проводится третий круг через D, центром которого является точка А.Он пересекается с первой фигурой в двух точках, их необходимо обозначить буквами E и F.
- Следующая окружность имеет центр в точке E и проходит через точку A, а ее пересечение с исходной окружностью находится в новой точке G.
- Последний круг на этом рисунке проводится через точку и с центром F. На ее пересечении точка N.
- На первом круге после всех проделанных шагов появилось пять точек, которые необходимо соединить отрезками. Таким образом, получился правый пятиугольник AE G N F.
Как по-другому построить правильный пятиугольник? Используя линейку и циркуляцию, Пентагон можно построить немного быстрее. Для этого вам необходимо:
- Необходимо с помощью циркуляра начертить окружность, центром которой является Точка О.
- Вырезается радиус ОА, который переносится на окружность. Делится на половину балла.
- Перпендикуляр к радиусу OA проводится сегментом OS, точками внутри и с прямой линией.
- Следующим шагом является нанесение длины отрезка летательного аппарата с циркуляцией по диаметральной линии. Точка D перпендикулярна Отрезку OA. Точки in и D соединяются, образуя новый сегмент.
- Чтобы получить размер стороны Пентагона, необходимо соединить точки C и D.
- D с помощью циркуля переводится на круг и обозначается точкой E. Соединив E и C, можно получить первую сторону правого пятиугольника.Следуя этой инструкции, вы сможете узнать, как быстро построить пятиугольник с равными сторонами, продолжая строить оставшуюся часть как первую.
В пятиугольнике с такими же сторонами диагональ равна пятиконечной звезде, которая называется пентаграммой. Золотое поперечное сечение — это отношение величины диагонали к стороне Пентагона.
Пентагон непригоден для полной заправки самолета. Использование любого материала в этой форме оставляет зазоры или перекрытия форм.Хотя такой формы естественных кристаллов не существует в природе, но когда лед образуется на поверхности гладких изделий из меди, возникают молекулы в форме пятиугольника, которые соединяются в цепочки.
Самый простой способ получить из бумажной полоски правильный пятиугольник — связать его узлом и немного прижать. Этот метод пригодится родителям дошкольников, которые хотят научить своих детей распознавать геометрические фигуры.
Видео
Посмотрите, как быстро нарисовать пятиугольник.
Здание вписано в окружность правильного шестиугольника. Построение шестиугольника основано на том, что его сторона равна радиусу описываемой окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (рис. 60, а).
Правый шестиугольник можно построить из угля 30×60 °. Для выполнения этой конструкции мы принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (рис.60, б) строим партии 1-6, 4-3, 4-5 и 7-2, после чего проводим партии 5-6 и 3-2.
Здание вписано в окружность равностороннего треугольника . Вершины такого треугольника могут быть построены с использованием циркуляции и угла с углами 30 и 60 ° или только одной окружности.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61, а) основан на том, что все три угла треугольника 7, 2, 3 содержат 60 °, а вертикальная прямая, проведенная через точку 7, является одновременно высотой и биссектрисой. угол 1.Так как угол 0-1-2 равен 30 °, то найти сторону
1-2 достаточно построить в точке 1 и стороне 0-1 под углом 30 °. Для этого устанавливаем пролет и квадрат как показано на рисунке, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Для построения стороны 2-3 устанавливаем полет в положение, показанное пунктирными линиями, и через точку 2 проводим прямую линию, которая определит третью вершину треугольника.
Второй способ основан на том, что если построить правильный шестиугольник, вписанный в круг, а затем соединить вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем диаметр вершины точки 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D / 2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученными точками будут две другие вершины искомого треугольника.
Построение квадрата, вписанного в круг . Эту конструкцию можно выполнить при помощи квадрата и круга.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описываемого круга и наклонены к его осям под углом 45 °.На основании этого мы устанавливаем рейнчин и угол с углом 45 °, как показано на фиг. 62, и, и отмечаем точки 1 и 3. Далее через эти точки проводим по этим точкам горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью угольного катета проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делятся пополам дугой окружности, заключенной между концами диаметра (рис. 62, б).Планируем на концах два взаимно перпендикулярных диаметра точки A, B и C и от них радиусом описываем дугу до их взаимного пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на рисунке сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Таким образом, вершины искомого квадрата последовательно совмещаются между собой.
Здание вписано в окружность правого пятиугольника.
Чтобы войти в круг, правый пятиугольник (рис. 63), производим следующие конструкции.
Смотрим на точку окружности 1 и принимаем ее за одну из вершин пятиугольника. Делим сегмент АО пополам. Для этого радиус AO от точки A описывается дугой до пересечения с окружностью в точках M и B. Соединяя эти точки напрямую, мы получаем точку K, которая затем может соединиться с точкой 1. Радиус равный отрезку A7, описать от точки до дуги до пересечения с диаметральной линией AO в точке H.Соединив точку 1 с точкой H, мы получим сторону пятиугольника. Затем с помощью решения циркуляции, равной отрезку 1H, описывающей дугу от вершины 1 до пересечения с окружностью, находим вершины 2 и 5. Делая своего рода вершину 2 и 5, получаем остальные вершины 3 и 4. Найденные точки последовательно соединяют друг друга.
Строим правый пятиугольник с этой стороны.
Чтобы построить на этой стороне правый пятиугольник (РИС.64), разделим отрезок AB на шесть равных частей. Из точек A и радиуса AB мы описываем дугу, пересечение которой даст точку K. через эту точку, а деление 3 на прямой AB проведет вертикальную прямую.
Получаем 1-контактный пятиугольник. Затем радиусом, равным AB, из точки 1 описать дугу до пересечения с дугами, предварительно проведенными из точек A и B. Точки пересечения дуг определяют вершины пятиугольника 2 и 5.Найденные вершины соединяют друг друга.
Здание вписано в правую окружность семнадцатиэтажного дома.
Пусть окружность диаметра D; В него необходимо ввести правильный sevenfone (Рис. 65). Делим вертикальный диаметр круга на семь равных частей. От точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точка f назовет полюс многоугольника.Взяв точку VII за одну из вершин полусердца, проведем от полюса F через четкое деление вертикального диаметра лучей, пересечение которых с окружностью определит вершины VI, V и IV из sevendent. Для получения вершин / — // — /// Из точек IV, V и VI проводим горизонтальные прямые, пересекающие окружность. Найденные вершины соединяются между собой. Семифуон можно построить, проводя лучи от полюса f через нечетные части вертикального диаметра.
Данный метод подходит для построения правильных многоугольников с любым количеством сторон.
Деление круга на любое количество равных частей также можно произвести, используя данные таблицы. 2, в котором коэффициенты дают возможность определять размер сторон правого вписанного многоугольника.
Здание вписано в окружность правого пятиугольника. Дан правильный многоугольник, количество сторон которого представляет собой произведение натуральных чисел k и m, где m> 2.Как построить правильный М-квадрат? Гаусс также показал возможность построения правильного квадрата 257 с циркуляцией и линейкой.
Постройте пятиугольник и поможет эта окружность. Прежде всего, необходимо построить круговой круг. Аналогичным образом необходимо построить еще один круг. Его центр в G. Точка пересечения его с начальной окружностью. Пусть H будет H. Это последняя вершина правого многоугольника.
Правда, процесс довольно долгий, как, впрочем, и построение любого правильного триггера с нечетным количеством сторон.Это многоугольник, осталось только ввести параметры. Количество сторон может достигать 1024. Вы также можете использовать командную строку в зависимости от версии «_Polygon» или «MN-Angle».
Разделение круга на равные части и подгонка правильных многоугольников.
Введите здесь цифру «5» и нажмите ENTER. Вам будет предложено определить центр пятиугольника. Вы можете обозначить их как (0,0), но можно использовать любые другие данные. Пентагон можно описать по окружности или вписать в него, но можно построить его и по указанной части сторон.Таким же образом сначала строится пятиугольник на указанной стороне. Выберите «Чертеж», замкнутый многострочный и введите количество сторон.
В командной строке введите координаты начальной и конечной точек одной из сторон пятиугольника. После этого на экране появляется пятиугольник. Таким простым способом можно построить не только пятиугольник. Чтобы построить треугольник, нужно отвести ступни циркуляции на расстояние, равное радиусу круга.
Две точки пересечения кругов, а также точка, в которой была ступня круга, образуют три вершины правильного треугольника.Оказалось, что существует несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Восьмиугольник — это геометрическая фигура с восемью углами. Правильный восьмиугольник — это восьмиугольник, у которого все стороны (и углы) равны. Эта статья расскажет, как сделать восьмиугольник.
Круг, дуги и многоугольники.
Определите длину стороны восьмиугольника (углы правильного восьмиугольника известны). На листе бумаги с помощью линейки проведите прямую линию выбранной длины.Это первая сторона восьмиугольника (нарисуйте ее так, чтобы оставалось место для рисования других сторон). Используя транспортировку, отложите угол 135 ° (от начала или конца первой стороны). Нарисуйте третью линию выбранной длины под углом 135 ° ко второй линии. Продолжайте, пока не получите правильный восьмиугольник.
Таким образом, чем больше окружность, тем больше цифра (и наоборот). Нарисуйте второй большой круг, установив циркуляционную иглу в центре первого круга. Установите круговую иглу точно в точку, противоположную пересечению внутреннего (малого) круга и его диаметра.У вас будет «глаз» посередине круга. Нарисуйте две дуги, пересекающие внутренний круг.
Построение правильных многоугольников на указанной стороне
Сотрет окружность, линии и дуги, оставив только восьмиугольник. Таким образом, вы придаете ему восьмиугольную форму. Используйте линейку, чтобы убедиться, что все стороны оказались равными (как вы делаете правильный восьмиугольник). Не сгибайте углы так, чтобы они соприкасались друг с другом; В этом случае вы получите не восьмиугольник, а небольшой квадрат.Часто, когда говорят «восьмиугольник», они имеют в виду правильный восьмиугольник.
Посмотрите, что такое «правый пятиугольник» в других словарях:
Таким образом, создав фигуру с восемью сторонами разной длины, вы получите неправильный восьмиугольник. Есть многоугольники с пересекающимися сторонами. Например, пятиконечная звезда — это многоугольник с пересекающимися сторонами. Правильные многоугольники уже считаются символом красоты и совершенства. Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю.
Только в 1796 г. К. Ф. Гауск доказал принципиальную невозможность этой конструкции, используя только тираж и линейку. В этом разделе мы предлагаем вам поискать способы построения правильных многоугольников, входящих в этот круг или имеющих заданную сторону. Не менее важны практические методы приближенного построения в тех случаях, когда точное построение окружности и линии неосуществимо.
Правильный пятиугольник — это многоугольник, у которого все пять сторон и все пять углов равны друг другу.Вокруг легко описать круг. Теперь на окружности радиуса АО из любой точки последовательно откладываем 11 дуг, каждая из которых равна AV arge. Получаем вершины правильного двенадцатилетнего бульона. На этой стороне строим правый пятиугольник. Смотрим на точку окружности 1 и принимаем ее за одну из вершин пятиугольника.
Задача построения точного пятиугольника сводится к задаче разделить круг на пять равных частей. Поскольку верный пятиугольник является одной из фигур, содержащих пропорции золотого сечения, краски и математики интересовались его построением.Теперь открыты несколько методов построения точного многоугольника, вписанного в заданную окружность.
Вам понадобится
Инструкция
1. Видимо, если построить верную декаду, а потом совместить вершины через одну, то получится пятиугольник. Чтобы построить десятиугольник, нарисуйте окружность указанного радиуса. Обозначьте его центр буквой O. Проведите двумя перпендикулярными радиусами, на рисунке они обозначены как OA1 и OB. OB Radius Wheel с подпапкой или методом разделения сегмента давления силой циркуляции.Постройте небольшой круг с центром C в середине отрезка OB радиусом, равным половине OB. Затяните точку C с точкой A1 на начальном круге по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верной декады, вписанной в эту окружность. Обведите круг, чтобы заметить этот сегмент на круге, затем объедините точки пересечения через одну, и вы получите положительный пятиугольник.
2. Другой метод открыл немецкий художник Альбрехт Дюрер.Чтобы построить пятиугольник по его методу, снова начните с построения круга. Снова соедините его центр O и проведите два перпендикуляра радиуса OA и OB. Радиус OA Добро пожаловать в середину буквы C. Установите циркулирующую иглу в точку C и откройте ее до точки B. Проведите окружность радиуса BC до пересечения с диаметром начальной окружности, на которой лежит радиус OA. Точка пересечения указывает D. Cut BD — сторона положительного пятиугольника. Установите этот отрезок пять раз на начальном круге и совместите точки пересечения.
3. Если вам нужно построить пятиугольник на его указанной стороне, то вам нужен 3-й метод. На линии стороны пятиугольника отметьте этот отрезок буквами А и В. разделите его на 6 равных частей. От середины разреза AB проведите пальцем по перпендикулярному отрезку. Постройте две окружности с радиусом AB и центрами в точках A и B, как если бы вы собирались разделить сегмент давления. Эти окружности пересекаются в точке C. Точка C находится на луче, который проходит перпендикулярно вверх от середины AB.Поместите расстояние, равное 4/6 от длины этого луча, отметьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя ранее построенными вспомогательными даст последние две вершины луча. пятиугольник.
Тема деления окружности на равные части для построения верных вписанных многоугольников давно была занята умами древних ученых. Эти тезисы построения с использованием циркуля и линейки были выражены даже в евклидовых «принципах».Но всего за два тысячелетия эта задача была полностью решена не только графически, но и математически.
Инструкция
1. Примерное построение положительный пятиугольник По методу А. Дюрера, с силой обращения и линейкой (через две окружности с универсальным радиусом, равным стороне пятиугольника ).
2. Построение верного пятиугольник На основе положительного декаграунда, вписанного в круг (объединение вершин децидагона через единицу).
3. Графическое построение через расчетный внутренний угол пятиугольник с опорой для транспорта и линейкой (сумма углов выпуклого n-квадрата равна Sn = 180 ° (n — 2), т.к. в положительном многоугольнике все углы равны ). При n = 5, S5 = 5400, то значение угла 1080.а тоже с опорой круга и выходящих из его центра 2-х лучей, при условии, что угол между ними 720, так как (36005 \ u003d 720). Их пересечение с кругом даст отрезок, равный стороне пятиугольника .
4. Еще один легкий графический способ: разделить диаметр заданной окружности AB на три части (AC = CD = DE). Из точки D опускаем перпендикуляр к пересечению с окружностью в точках E, F. Провыпий через сечения EC и FC до пересечения с окружностью получаем точку G, H. G, E, B, F, H — вершины положительного пятиугольника .
5. Здание с опорой для приема биона (позволяющее верующим в окружность многоугольника вписываться в окружность с любым числом сторон N при заданном соотношении).Найдем: при n = 5. Возведен положительный треугольник ABC, где AB — диаметр указанной окружности. Обнаружить на точке AB точку D, для дальнейшего соотношения: AD: AB = 2: N. При n = 5, ad = 25 * AB. Проведем прямо через КД до пересечения с кругом в точке Е. Отрезок АЕ — сторона правильной вещи вписана в пятиугольник . Вывести n = 5,7,9,10 Ошибка сборки не превышает 1%. С увеличением N ошибка аппроксимации растет, но остается меньше 10.3%.
6. Построение по заданной стороне по методу Л. да Винчи (применяя соотношение между стороной многоугольника (AN) и апофистикой (HA): AN / 2: HA = 3 / (n-1), которое допускается выражать следующим образом: TG180 ° / N = 3 / (n-1)).
7. Общий метод построения положительных многоугольников по указанной стороне методом Ф. Коваржика (1888 г.), основанный на правилах Л. Я. Винчи. Предварительное построение положительного N-углерода на основе теоремы Фалеза.Продвинутые добавляют только то, что приблизительные методы построения полигонов являются подлинными, примитивными и красивыми.
Есть два основных метода построения точного многоугольника с пятью сторонами. Оба они верят в использование тиража, линии и карандаша. 1-й метод — это подгонка пятиугольника по кругу, а 2-й метод основан на заданной длине стороны вашей геометрической формы.
Вам понадобится
Инструкция
1. 1-й способ построения пятиугольник Считается более «типовым». Для начала постройте круг и как-нибудь обозначьте его центр (обычно для этого используется буква О). После этого проведите диаметр этого круга (назовем его) и разделите один из 2-х полученных радиусов (скажем, OA) точно на ввод. Середина этого радиуса обозначается буквой S.
2. Из точки O (центр начальной окружности) проведите другой радиус (OD), тот, который будет строго перпендикулярен ранее проведенному диаметру (AV).После этого возьмите цирк, поместите его в точку C и измерьте расстояние до пересечения нового радиуса с окружностью (CD). Такое же расстояние отложить по диаметру АВ. Вы получите новую точку (назовем ее e). Измерьте расстояние от точки D до точки E — оно будет равно длине стороны вашего приближающегося пятиугольника .
3. Поместите контур в точку D и установите расстояние по окружности, равное отрезку DE. Повторите эту процедуру еще 3 раза, а затем объедините точку D и 4 новые точки на исходной окружности.Фигура в результате постройки будет верным пятиугольником.
4. Чтобы построить пятиугольник другим способом, для начала нарисуйте отрезок. Допустим, это будет длина 9 см. Затем разделите ваш отрезок на 6 равных частей. В нашем случае длина любой детали будет 1,5 см. Теперь возьмите цирк, поместите его в один из концов отрезка и возьмите окружность или дугу с радиусом, равным длине отрезка (AV). После этого переставьте цирк в другой конец и повторите операцию.Полученные круги (или дуги) пересекутся в одной точке. Назовем его C.
5. Теперь возьмите линейку и проведите прямо через точку с центром ab. После этого, начиная с точки, отложенной на этой прямой, составляющей 4/6 отрезка АВ. Второй конец отрезка обозначается буквой D. Точка D будет одной из вершин приближающегося пятиугольника . С этого момента проведите по кругу или дуге с радиусом, равным av. Этот круг (дуга) будет пересекать круги (дуги), ранее построенные вами, то есть две отсутствующие вершины. пятиугольник . Объедините эти точки с вершинами D, A и B, и построение положительного пятиугольника будет завершено.
Видео по теме
Ray — Это прямая линия, идущая от точки и не имеющая конца. Есть и другие определения луча: скажем, «… Это прямая линия, ограниченная точкой, с одной стороны». Как красиво нарисовать брус и какие аксессуары к нему понадобятся?
Вам понадобится
- Лист бумаги, карандаш и линейка.
Инструкция
1. Возьмите лист бумаги и проверьте в произвольном месте. После этого прикрепите линию и проведите по ней от указанной точки до бесконечности. Эта нарисованная линия называется балкой. Теперь давайте обратим внимание на другую точку на балке, например, на букву C. Линия от оригинала до точки C будет называться отрезком. Если вы примитивно проведете линию и не заметите истины в одной точке, то эта прямая не будет лучом.
2. Нарисовать луч в любом графическом редакторе или в том же MSOffice не сложнее, чем вручную. Например, возьмем программу Microsoft Office 2010. Перейдите в раздел «Вставка» и выберите элемент «Фигурки». В раскрывающемся списке выберите фигуру «линия». Далее курсор принимает вид креста. Чтобы нарисовать ровную линию, нажмите клавишу «SHIFT» и проведите нужной длины. Сразу после этого откроется вкладка формата. Теперь у вас есть примитивная прямая линия и нет фиксированной точки, и, исходя из определения, луч должен быть ограничен точкой с одной стороны.
3. Чтобы поставить точку в начале линии, выполните следующие действия: Выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.
4. Выберите «Формат рисунка». В левом меню выберите «Тип линии». Далее найдите заголовок «Параметры линии» и выберите «Тип запуска» в виде круга. Здесь вы можете настроить толщину начальной и конечной линий.
5. Удалите выделение из линии и убедитесь, что точка появилась в начале линии.Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, где будет надпись. После написания надписей нажмите на свободное место и оно активируется.
6. Балка была благополучно окрашена, и на это ушло всего несколько минут. Чертеж балки в других редакторах выполняется по той же дипломной работе. При нажатии клавиши «SHIFT» пропорциональные числа всегда будут. Хорошее использование.
Видео по теме
Внимание!
Отношение диагонали правильного пятиугольника к его стороне — это золотое сечение (иррациональное число (1 + √5) / 2).А пять внутренних углов пятиугольника равны 108 °.
Полезный совет
Если совместить верные вершины диагоналей пятиугольника, то пентаграмма будет.
Уровень сложности: легкий
1 шаг
Сначала выберите, где разместить центр круга. Необходимо поставить точку отсчета, пусть она будет называться О. с помощью циркуляции начертить вокруг нее окружность заданного диаметра или радиуса.
2 ступени
Затем проводим две оси через точку О, центр круга, одна горизонтальная, другая на 90 градусов относительно нее — вертикальная.Точки пересечения по горизонтали называют слева направо A и B, по вертикали, сверху вниз — M и N. Радиус, лежащий на любой оси, например, по горизонтали в правой части, делим пополам. Сделать это можно так: циркуляцией с известным нам радиусом окружности, задаем край точки пересечения горизонтальной оси и окружности — в, проводим пересечение с окружностью, называем точки соответственно , сверху вниз — C и P, соединяем их с отрезком, который будет пересекать ось оси, я называю точку пересечения K.
3 Шаг
Соединяем точки с и m и получаем отрезок CM, устанавливаем циркуляцию в точку M, устанавливаем расстояние до точки до точки и намечаем метки на радиусе OA, мы называем эту точку е, затем измеряем, чтобы пересечь круг до пересечения с левой верхней частью круга ОМ. Эта точка пересечения называется F. Расстояние, равное отрезку меня, является желаемой стороной равностороннего пятиугольника. При этом точка M будет одной вершиной окружности вложенного пятиугольника, а точка F — другой.
4 Шаг
Далее из полученных точек по всей окружности рисуем окружность расстояний, равных отрезку меня, все точки должны получиться 5. Соединяем все точки отрезками — получаем пятиугольник, вписанный в круг.
- При рисовании будьте внимательны с расстояниями в измерениях, не допускайте ошибок, чтобы пятиугольник действительно задевал равносторонний
Построение правильного пятиугольника. Подробное рисование пятиугольника Как нарисовать идеальный пятиугольник
Эта форма представляет собой многоугольник с минимальным количеством углов, которые нельзя вымощать площадкой.Только у пятиугольника количество диагоналей равно количеству его сторон. Используя формулы для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пятиугольник. Например, вписать его в круг с заданным радиусом или построить на основе заданной боковой стороны.
Как правильно нарисовать балку и какие принадлежности для рисования вам понадобятся? Возьмите лист бумаги и отметьте точку в произвольном месте. Затем прикрепите линейку и проведите линию от указанной точки до бесконечности.Чтобы нарисовать прямую линию, нажмите клавишу Shift и проведите линию нужной длины. Сразу после рисования открывается вкладка Формат. Удалите выделение из строки, и вы увидите точку в начале строки. Чтобы создать этикетку, нажмите кнопку «Нарисовать этикетку» и создайте поле, в котором будет располагаться этикетка.
Первый способ построения пятиугольника считается более «классическим». В результате получится правильный пятиугольник. Двенадцатьугольник — не исключение, поэтому его построение будет невозможно без использования компаса.Задача построения правильного пятиугольника сводится к задаче разделить круг на пять равных частей. Нарисовать пентаграмму можно простейшими инструментами.
Я долго боролся, пытаясь добиться этого и самостоятельно находить пропорции и зависимости, но у меня ничего не получалось. Оказалось, что существует несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Интересен тот факт, что эту задачу можно решить арифметически только приблизительно точно, так как вам придется использовать иррациональные числа.Но ее можно решить геометрически.
Деление кружков. Точки пересечения этих прямых с кругом являются вершинами квадрата. Вертикальный диаметр следует нарисовать в окружности радиуса R (шаг 1). В точке сопряжения N прямой и окружности прямая линия касается окружности.
Прием с полоской бумаги
Правильный шестиугольник может быть построен с использованием рельса и квадрата 30X60 °. Вершины такого треугольника можно построить с помощью циркуля и квадрата с углами 30 и 60 ° или всего одного циркуля.Чтобы построить сторону 2-3, установите дорожку качения в положение, показанное пунктирными линиями, и проведите прямую линию через точку 2, которая определит третью вершину треугольника. Отметим на окружности точку 1 и примем ее за одну из вершин пятиугольника. Соединяем найденные вершины последовательно друг с другом. Семиугольник можно построить, проведя лучи от полюса F через нечетные части вертикального диаметра.
А на другой конец нитки поставил карандаш и зациклился. Если вы умеете рисовать звезду, но не знаете, как нарисовать пятиугольник, нарисуйте звезду карандашом, затем соедините смежные концы звезды вместе, а затем сотрите саму звезду.Затем кладут лист бумаги (лучше закрепить на столе четырьмя пуговицами или иголками). Прикрепите эти 5 полосок к листу бумаги пуговицами или иголками, чтобы они оставались неподвижными. Затем обведите получившийся пятиугольник и уберите эти полосы с листа.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для изображения советского прошлого или настоящего Китая. Правда, для этого нужно уметь создать рисунок звезды в перспективе. Таким же образом можно нарисовать фигуру карандашом на бумаге.Как правильно нарисовать звезду, чтобы она смотрелась гладко и красиво, сразу ответить нельзя.
От центра опустите 2 луча до окружности так, чтобы угол между ними составлял 72 градуса (транспортир). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — одна из фигур, содержащих пропорции золотого сечения, художники и математики давно интересовались его построением.Эти принципы построения с использованием циркуля и линейки были изложены в Евклидовых принципах.
8 июня 2011 г.Первый способ — по этой стороне S с помощью транспортира.
Проводим прямую и ставим на нее AB = S; мы принимаем эту линию за радиус и этим радиусом описываем дуги из точек A и B: затем, используя транспортир, строим в этих точках углы 108 °, стороны которых пересекаются с дугами в точках C и D ; из этих точек радиусом AB = 5 описываем дуги, пересекающиеся в точке E, а прямыми линиями соединяем точки L, C, E, D, B.
Получившийся пятиугольник — искомый.
Второй путь. Нарисуем круг радиуса r. Из точки A проведите циркулем дугу радиуса AM, пока она не пересечется в точках B и C с кругом. Соедините B и C линией, пересекающей горизонтальную ось в точке E.
Затем из точки E мы проводим дугу, которая будет пересекать горизонтальную линию в точке O. Наконец, из точки F мы описываем дугу, которая будет пересекать окружность в точках H и K.Положив расстояние FO = FH = FK по окружности пять раз и соединив точки раздела линиями, мы получим правильный пятиугольник.
Третий путь. Начертите правильный пятиугольник в этом круге. Рисуем два взаимно перпендикулярных диаметра AB и MC. Разделите радиус AO точкой E пополам. Из точки E, как и из центра, проведите дугу окружности радиуса EM и отметьте ее диаметром AB в точке F. Отрезок MF равен стороне искомого правильного пятиугольника.Раствором циркуля равным MF делаем засечки N 1, P 1, Q 1, K 1 и соединяем их прямыми линиями.
На рисунке изображен шестиугольник с этой стороны.
Прямая AB = 5, в качестве радиуса из точек A и B описываем дуги, которые пересекаются в C; отсюда тем же радиусом описываем круг, на котором сторона A B будет нанесена 6 раз.
Hexagon ADEFGB — желаемый.
«Отделка помещений при ремонте»,
Н.Краснов П.
Основой под покраску является полностью законченная покраска поверхности стен, потолка и других конструкций; покраска выполняется качественными клеевыми и масляными красками, предназначена для обрезки или гофрирования. Приступая к разработке эскиза для отделки, мастер должен четко представить себе всю композицию в бытовой обстановке и четко понять творческий замысел. Только при соблюдении этого основного условия можно сделать правильно…
Замер выполненных работ, за исключением особо оговоренных случаев, проводится по площади фактически обработанной поверхности с учетом ее рельефа за вычетом необработанных мест. Для определения фактически обработанных поверхностей во время малярных работ используйте коэффициенты пересчета, приведенные в таблицах. A. Деревянные оконные устройства (замер производится по площади проемов по внешнему контуру ящиков) Наименование устройств Коэффициент при…
Мы уже говорили, что для выполнения некоторых видов малярных работ нужно уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур … Зарисовки на бумаге рисуются с помощью треугольников, рельсов, транспортеров и циркуля, а на плоскости стен и потолка конструкции строятся с помощью гири. , линейка, деревянный циркуль и шнур. В этом случае необходимо …
Вы находитесь в раскраске пятиугольника.Раскраска, на которую вы смотрите, описывается нашими посетителями следующим образом: «Здесь вы найдете множество онлайн-раскрасок. Вы можете бесплатно скачать раскраски пятиугольник и распечатать их. Как известно, творческая деятельность играет огромную роль в развитии ребенка. Они активизируют умственную деятельность, формируют эстетический вкус и прививают любовь к искусству. Процесс раскрашивания картинок на тему пятиугольника развивает мелкую моторику, усидчивость и аккуратность, помогает больше узнать об окружающем мире, знакомит со всем разнообразием цветов и оттенков.