Как начертить пятиугольник в окружности с помощью циркуля поэтапно: Как построить пятиугольник с помощью циркуля

Как построить пятиугольник в круге

Содержание

• Параметры правильного пятиугольника
• Построение пентагона
• Интересные факты
• Видео
• Содержание
• Свойства [ править | править код ]
• Построение [ править | править код ]
• Получение с помощью полоски бумаги [ править | править код ]
• В природе [ править | править код ]
• Как выглядит пятиугольник и звезда

Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон.

Только в этой фигуре количество граней совпадает с числом диагоналей.

Параметры правильного пятиугольника

Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:

• сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
• внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

• если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
• Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
• При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:

• с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
• описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
• в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

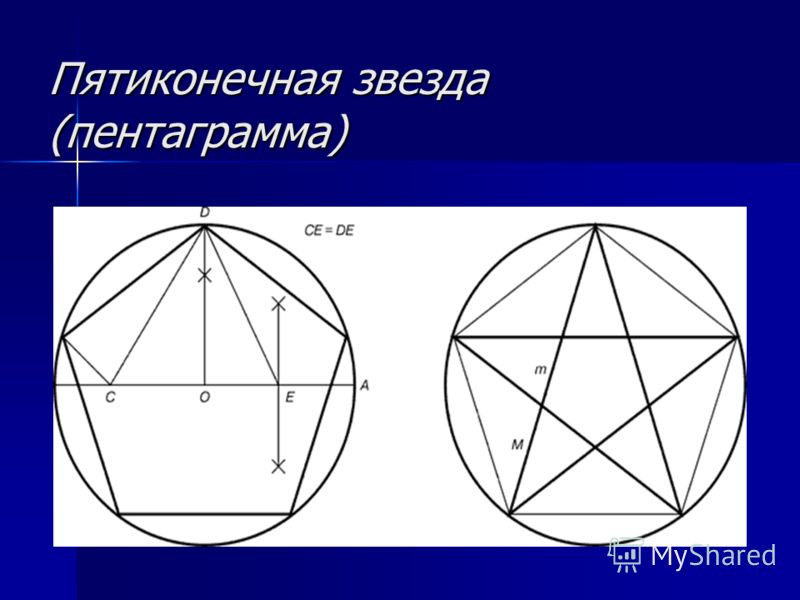
1. Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
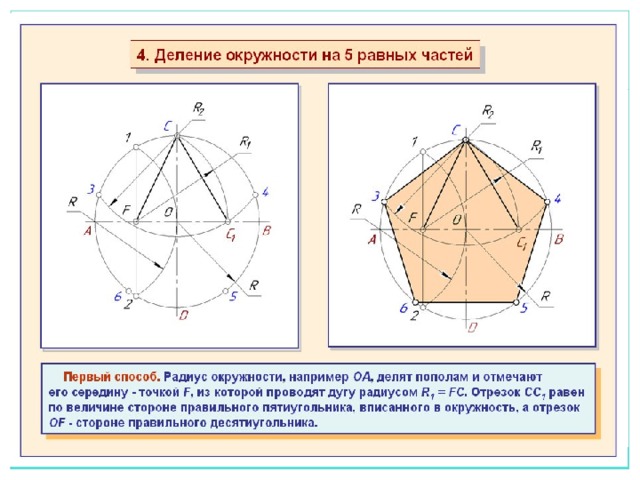
2. Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
3. Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
4. После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
5. Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
6. Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
7. На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

1. Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
2. Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
3. Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
4. Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
5. Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
6. D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

Интересные факты

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.

Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

Видео

Посмотрите, как можно быстро начертить пятиугольник.

Пятиугольник
Правильный пятиугольник
Тип	Правильный многоугольник
Рёбра	5
Символ Шлефли
Диаграмма Коксетера — Дынкина
Вид симметрии	Диэдрическая группа (D5)
Площадь	t 2 25 + 10 5 4 = <displaystyle <frac <sqrt <25+10<sqrt <5>>>>><4>>=> 5 R 2 4 5 + 5 2 ; <displaystyle <frac <5R^<2>><4>><sqrt <frac <5+<sqrt <5>>><2>>>;> 2>
Внутренний угол	108°
Свойства
выпуклый, вписанный, Равносторонний, равноугольный [en] , изотоксальный
Медиафайлы на Викискладе

Правильный пятиугольник (или пентагон от греч. <circ >><2>>t=<frac <sqrt <5+2<sqrt <5>>>><2>>tapprox 1<,>539t>

• Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
• Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу 1 + 5 2 <displaystyle <frac <1+<sqrt <5>>><2>>>.

Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

R>

• Радиус вписанной окружности:

r = 5 5 + 2 5 10 t ≈ 0,688 191 t <displaystyle r=<frac <<sqrt <5>><sqrt <5+2<sqrt <5>>>>><10>>tapprox 0<,>688191

t>

• Радиус описанной окружности:

R = 1 0 5 + 5 10 t = ( 5 − 1 ) r ≈ 0,850 651 t ≈ 1,236 07 r <displaystyle R=<frac <<sqrt <1>>0<sqrt <5+<sqrt <5>>>>><10>>t=(<sqrt <5>>-1)

r>

• Диагональ:

d = Φ 5 R = 5 + 1 2 t ≈ 1,902 R ≈ 1,618 t <displaystyle d=<sqrt <Phi <sqrt <5>>>>R=<frac <<sqrt <5>>+1><2>>tapprox 1<,>902

t>

• Площадь:

S = 5 5 + 2 5 4 t 2 ≈ 1,720 48 t 2 <displaystyle S=<frac <<sqrt <5>><sqrt <5+2<sqrt <5>>>>><4>>t^<2>approx 1<,>72048

t^<2>>

• Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. 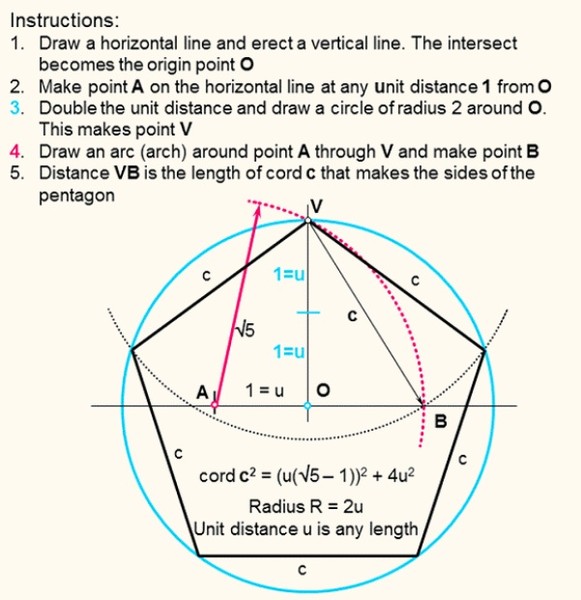<4>=3Phi +2=<frac <3<sqrt <5>>+7><2>>approx 6<,>8541>где Φ <displaystyle Phi >— отношение золотого сечения.

  Построение [ править | править код ]

  Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

  Вот один из методов построения правильного пятиугольника в заданной окружности:

  1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
  2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
  3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
  4. Постройте точку C посередине между O и B.
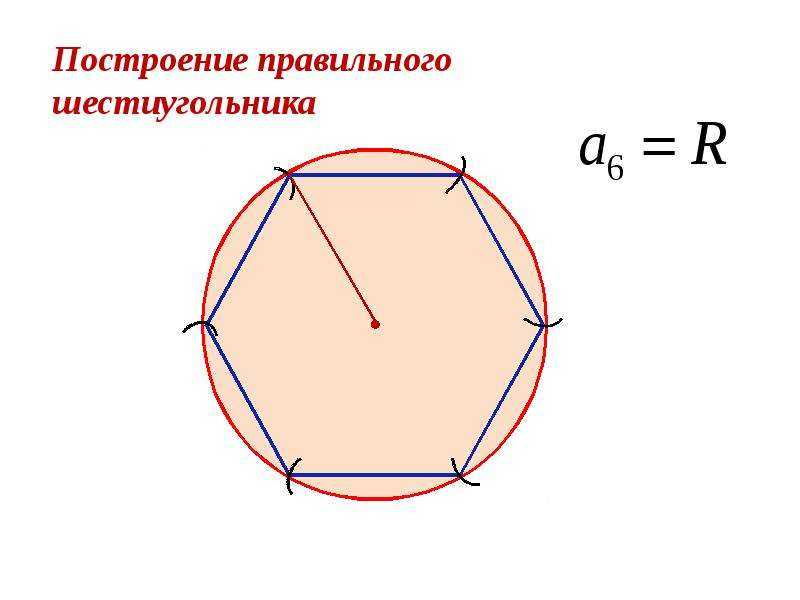
  5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
  6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
  7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
  8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
  9. Постройте правильный пятиугольник AEGHF.

  Получение с помощью полоски бумаги [ править | править код ]

  Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

  В природе [ править | править код ]

  Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры. [1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.

  Иглокожие, например морские звёзды, обладают пентасимметрией.

  Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как мушмула германская.

  Здравствуйте коллеги.
  Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.

  Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.

  Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.

  Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.

  Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:

  Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.

  Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.

  Как выглядит пятиугольник и звезда

  Внизу на фото разберем, как нарисовать звезду поэтапно.
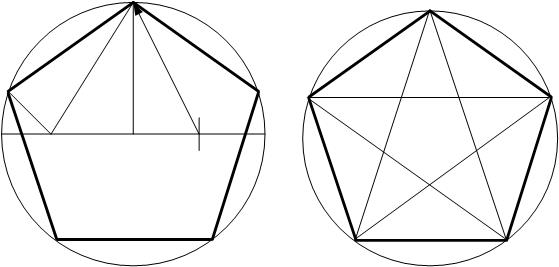
  Для начала рисуем окружность с центром О.

  Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.

  
  Теперь от точки В до точки С проведем прямую.

  Отложим расстояние отрезка ВС на диаметральной линии окружности. 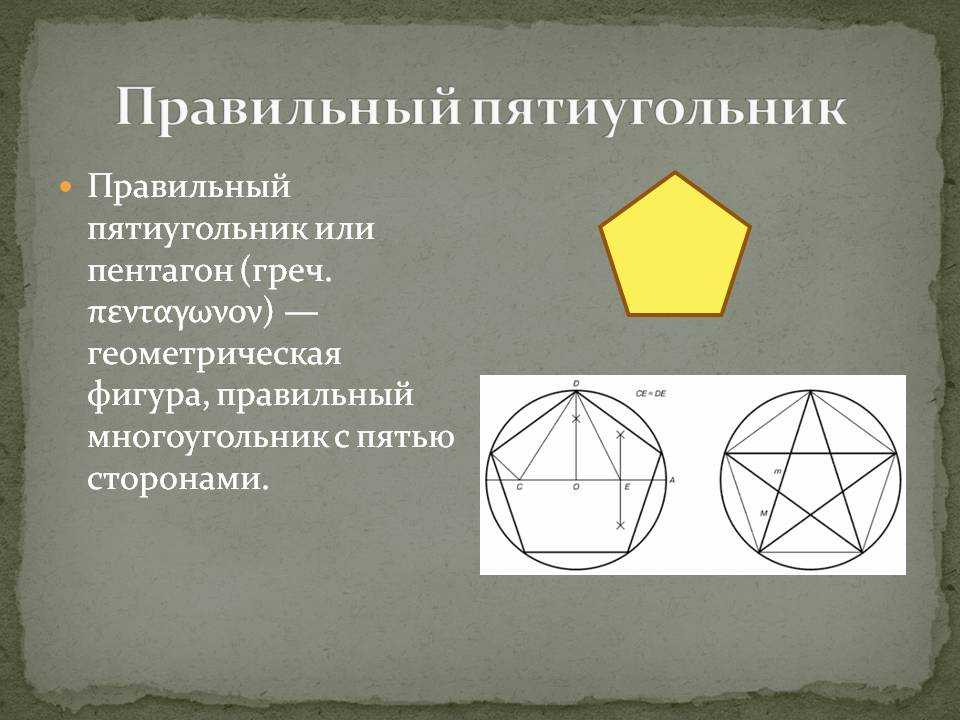Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.

  
  И отрезок DB. Картинка внизу.

  Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.

  
  Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.

  
  Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.

  Такие же отрезки наносим на всей части круга. Смотрим картинку.

  
  На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.

  Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.

  Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.

  Как построить и нарисовать правильный пятиугольник по вписанной и описанной окружности

  Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. 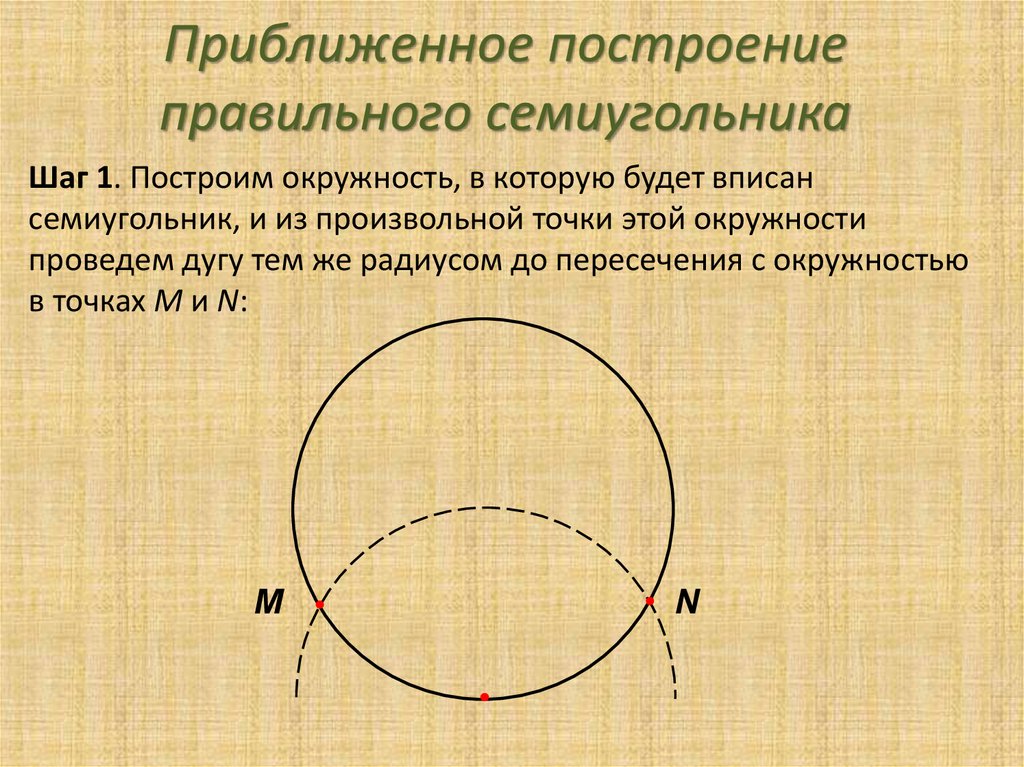Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

  Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

  Параметры правильного пятиугольника

  Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона.

  Способы и формулы расчетов:
  • сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
  • внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

  Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

  • если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
  • Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
  • При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

  Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:

  • с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
  • описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
  • в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

  Деление окружности на равные части и вписывание правильных многоугольников.

  

  Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Можно обозначить их как (0,0), но могут быть и любые другие данные. Пятиугольник может быть описанным вокруг окружности или вписанным в нее, но можно построить его и по заданному размеру стороны. Пятиугольник по заданной стороне сначала строится точно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон.

  В командной строке наберите координаты начальной и конечной точек одной из сторон пятиугольника. После этого пятиугольник появится на экране. Таким нехитрым способом можно построить не только пятиугольник. Для того чтобы построить треугольник, необходимо разведите ножки циркуля на расстояние, равное радиусу окружности.

  Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. 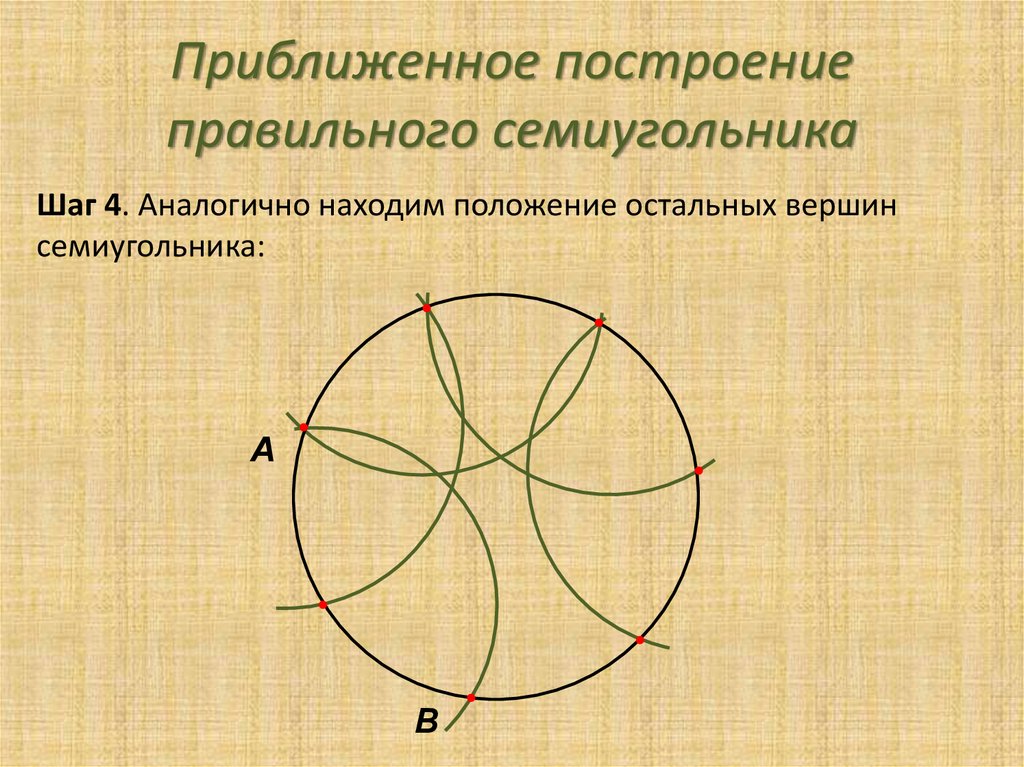Восьмиугольник — это геометрическая фигура с восемью углами. Правильный восьмиугольник – это восьмиугольник, у которого все стороны (и углы) равны. Эта статья расскажет вам, как сделать восьмиугольник.

  Построение пентагона

  Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

  Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

  1. Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
  2. Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
  3. Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
  4. После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
  5. Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
  6. Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
  7. На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

  Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

  1. Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
  2. Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
  3. Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
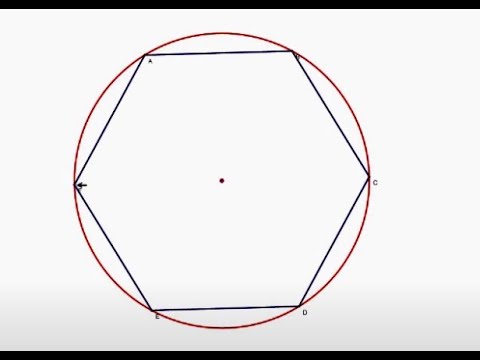
  4. Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
  5. Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
  6. D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

  Как выглядит пятиугольник и звезда

  Внизу на фото разберем, как нарисовать звезду поэтапно. Для начала рисуем окружность с центром О.

  Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.

  
  Теперь от точки В до точки С проведем прямую.

  Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.

  
  И отрезок DB. Картинка внизу.

  Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.

  
  Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.

  
  Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.

  Такие же отрезки наносим на всей части круга. Смотрим картинку.

  Интересные факты

  В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

  Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.

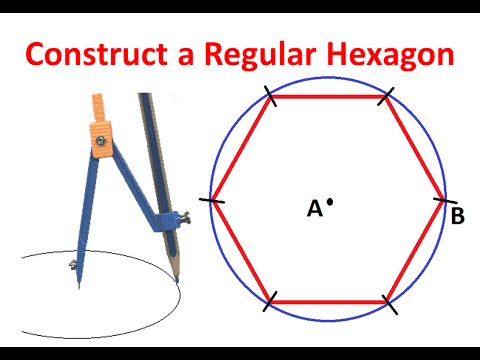
  Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

  Окружность, дуги и многоугольники.

  Определите длину стороны восьмиугольника (углы правильного восьмиугольника известны). На листе бумаги при помощи линейки нарисуйте прямую линию выбранной длины. Это первая сторона восьмиугольника (нарисуйте ее так, чтобы оставить место для рисования других сторон). Используя транспортир, отложите угол в 135o (от начала или конца первой стороны). Нарисуйте третью линию выбранной длины под углом в 135o ко второй линии. Продолжайте до тех пор, пока у вас не получится правильный восьмиугольник.

  Таким образом, чем больше окружность, тем больше фигура (и наоборот). Нарисуйте вторую большую окружность, установив иглу циркуля в центре первой окружности. Установите иглу циркуля в прямо противоположной точке пересечения внутренней (малой) окружности и ее диаметра. У вас получится «глаз» в середине окружности. Нарисуйте две дуги, пересекающие внутреннюю окружность.

  Видео

  Посмотрите, как можно быстро начертить пятиугольник.

  Правильный пятиугольник
  

  Смотреть что такое «Правильный пятиугольник» в других словарях:

  Таким образом, создав фигуру с восемью сторонами разной длины, вы получите неправильный восьмиугольник. Существуют многоугольники с пересекающимися сторонами. Например, пятиконечная звезда является многоугольником с пересекающимися сторонами. Правильные многоугольники уже в глубокой древности считались символом красоты и совершенства. Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю.

  Лишь в 1796 г. К. Ф. Гаусc доказал принципиальную невозможность этого построения с помощью только циркуля и линейки. В настоящем параграфе мы предлагаем вам самим поискать способы построения правильных многоугольников, вписанных в данную окружность или имеющих заданную сторону. Не менее важное практическое значение имеют методы приближенного построения в тех случаях, когда точное построение циркулем и линейкой неосуществимо.

  Правильный пятиугольник — это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Теперь на окружности радиуса AО от любой точки последовательно отложим 11 дуг, каждая из которых равна дуге АВ. Получим вершины правильного двенадцатиугольника. Построение правильного пятиугольника по данной его стороне. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника.

  Задача построения верного пятиугольника сводится к задаче деления окружности на пять равных частей. От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.

  Вам понадобится

  • – линейка
  • – циркуль

  Инструкция

  1.

  Видимо, что если возвести верный десятиугольник, а после этого объединить его вершины через одну, то получим пятиугольник. Для построения десятиугольника начертите окружность заданного радиуса. Обозначьте ее центр буквой O. Проведите два перпендикулярных друг друга радиуса, на рисунке они обозначены как OA1 и OB. Радиус OB поделите напополам с подмогой линейки либо способом деления отрезка напополам с подмогой циркуля. Постройте маленькую окружность с центром C в середине отрезка OB радиусом, равным половине OB.Объедините точку C с точкой A1 на начальной окружности по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.

  2.

  Еще один метод обнаружил немецкий художник Альбрехт Дюрер. Дабы возвести пятиугольник по его методу, начните вновь с построения окружности. Вновь подметьте ее центр O и проведите два перпендикулярных радиуса OA и OB. Радиус OA поделите напополам и середину подметьте буквой C. Установите иглу циркуля в точку C и раскройте его до точки B. Проведите окружность радиуса BC до пересечения с диаметром начальной окружности, на котором лежит радиус OA. Точку пересечения обозначьте D. Отрезок BD – сторона положительного пятиугольника. Отложите данный отрезок пять раз на начальной окружности и объедините точки пересечения.

  3.

  Если же требуется возвести пятиугольник по его заданной стороне, то вам надобен 3-й метод. Начертите по линейке сторону пятиугольника, обозначьте данный отрезок буквами A и B. Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. 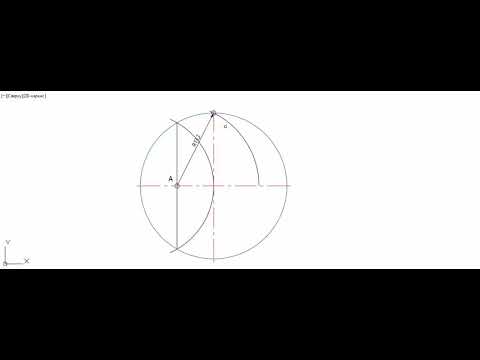Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.

  Тема деления окружности на равные части с целью построения верных вписанных многоугольников издавна занимала умы древних ученых. Эти тезисы построения с использованием циркуля и линейки были высказаны еще в эвклидовых «Началах». Впрочем лишь через два тысячелетия эта задача была всецело решена не только графически, но и математически.

  Инструкция

  1.

  Приближенное построение положительного
  пятиугольника
  методом А. Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне
  пятиугольника
  ).

  2.

  Построение верного
  пятиугольника
  на основе положительного десятиугольника, вписанного в окружность (объединив вершины десятиугольника через одну).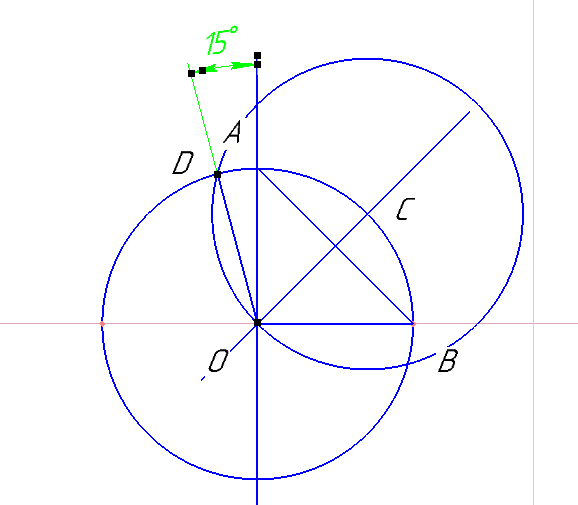

  3.

  Графическое построение через вычисленный внутренний угол
  пятиугольника
  с поддержкой транспортира и линейки (сумма углов выпуклого n-угольника равна Sn=180°(n – 2), т.к. у положительного многоугольника все углы равны). При n=5, S5=5400, тогда величина угла 1080.А так же с поддержкой окружности и 2-х лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне
  пятиугольника
  .

  4.

  Еще один легкой графический метод: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.Точки G,E,B,F,H – вершины положительного
  пятиугольника
  .

  5.

  Построение с поддержкой приема Биона (дозволяющего возвести верный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению). 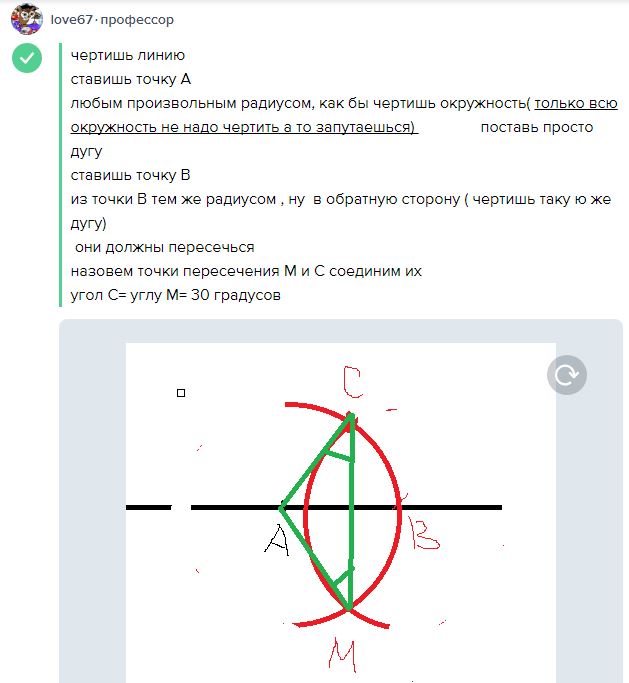Скажем: для n=5. Возведем положительный треугольник ABC, где AB – диаметр заданной окружности. Обнаружим на AB точку D, по дальнейшему соотношению: AD: AB = 2: n. При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона верного вписанного
  пятиугольника
  .При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся поменьше 10,3%.

  6.

  Построение по заданной стороне по способу Л. Да Винчи (применяя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2: ha =3/(n-1), которое дозволено выразить так: tg180°/n =3/(n-1)).

  7.

  Всеобщий метод построения положительных многоугольников по заданной стороне по способу Ф. Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.

  Существуют два основных метода построения верного многоугольника с пятью сторонами. Оба они полагают применение циркуля, линейки и карандаша. 1-й метод представляет собой вписывание пятиугольника

  в окружность, а 2-й метод базируется на заданной длине стороны вашей грядущей геометрической фигуры.

  Вам понадобится

  • Циркуль, линейка, карандаш

  Инструкция

  1.

  1-й метод построения
  пятиугольника
  считается больше «типичным». Для начала постройте окружность и как-либо обозначьте ее центр (обычно для этого применяется буква О). После этого проведите диаметр этой окружности (назовем его АВ) и поделите один из 2-х полученных радиусов (скажем, ОА) ровно напополам. Середину этого радиуса обозначим буквой С.

  2.

  Из точки О (центра начальной окружности) проведите еще один радиус (ОD), тот, что будет сурово перпендикулярен проведенному ранее диаметру (АВ). После этого возьмите циркуль, поставьте его в точку С и отмерьте расстояние до пересечения нового радиуса с окружностью (СD). 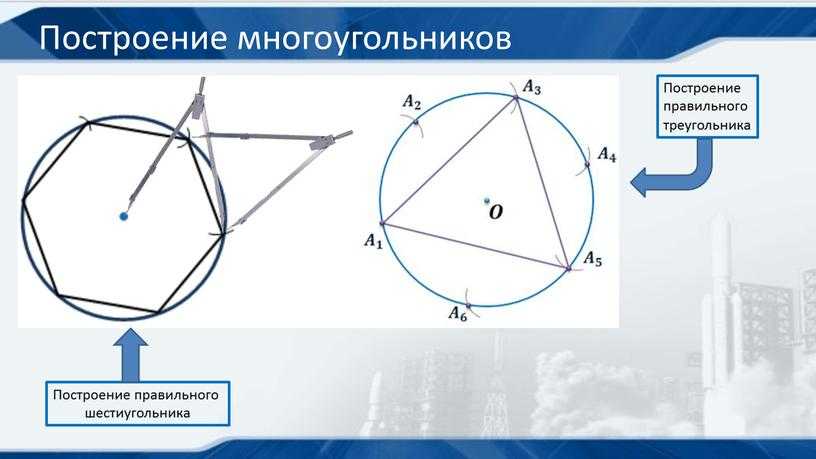Это же расстояние отложите на диаметре АВ. Вы получите новую точку (назовем ее Е). Отмерьте циркулем расстояние от точки D до точки Е – оно будет равно длине стороны вашего грядущего
  пятиугольника
  .

  3.

  Поставьте циркуль в точку D и отложите на окружности расстояние, равное отрезку DЕ. Повторите эту процедуру еще 3 раза, а после этого объедините точку D и 4 новые точки на начальной окружности. Получившаяся в итоге построения фигура будет верным пятиугольником.

  4.

  Дабы возвести пятиугольник иным методом, для начала начертите отрезок. Скажем, это будет отрезок АВ длиной 9 см. Дальше поделите ваш отрезок на 6 равных частей. В нашем случае длина всякой части будет составлять 1,5 см. Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. 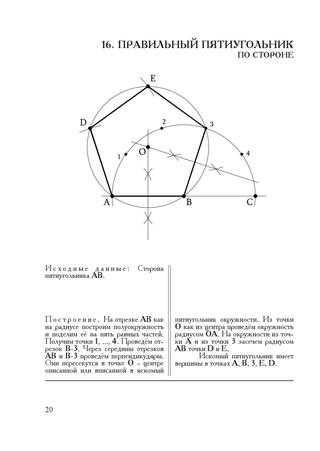Назовем ее C.

  5.

  Сейчас возьмите линейку и проведите прямую через точку С и центр отрезка AB. После этого начиная от точки С отложите на этой прямой отрезок, составляющий 4/6 отрезка AB. 2-й конец отрезка обозначим буквой D. Точка D будет являться одной из вершин грядущего
  пятиугольника
  . Из этой точки проведите окружность либо дугу с радиусом, равным АВ. Эта окружность (дуга) пересечет ранее построенные вами окружности (дуги) в точках, являющихся двумя недостающими вершинами
  пятиугольника
  . Объедините эти точки с вершинами D, А и В, и построение положительного
  пятиугольника
  будет закончено.

  Видео по теме

  Луч —

  это прямая линия, проведенная из точки и не имеющая конца. Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?

  Вам понадобится

  • Лист бумаги, карандаш и линейка.

  Инструкция

  1.

  Возьмите лист бумаги и подметьте в произвольном месте точку. После этого приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Эта нарисованная линия и именуется лучом. Сейчас подметьте на луче еще одну точку, к примеру, буквой C. Линия от исходной и до точки C будет именоваться отрезком. Если вы примитивно начертите линию и не подметите правда бы одну точку, то эта прямая не будет являться лучом.

  2.

  Нарисовать луч в любом графическом редакторе либо в том же MSOffice не труднее, чем вручную. Для примера возьмите программу Microsoft Office 2010. Зайдите в раздел «Вставка» и выберите элемент «Фигуры». В выпадающем списке выберите фигуру «Линия». Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.

  3.

  Дабы сделать точку в начале линии, сделайте следующее: выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.

  4.

  Выберите пункт «Формат фигуры». В меню слева выберите пункт «Тип линии». Дальше обнаружьте заголовок «Параметры линий» и выберите «Тип начала» в виде кружочка. Там же вы можете настроить толщину линий начала и конца.

  5.

  Уберите выделение с линии и увидите, что в начале линии возникла точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, где будет находиться надпись. Позже написания надписи кликните на свободное место и она активируется.

  6.

  Луч благополучно нарисован и заняло это каждого несколько минут. Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.

  Видео по теме

  Обратите внимание!

  Отношение диагонали верного пятиугольника к его стороне составляет золотое сечение (иррациональное число (1+√5)/2). 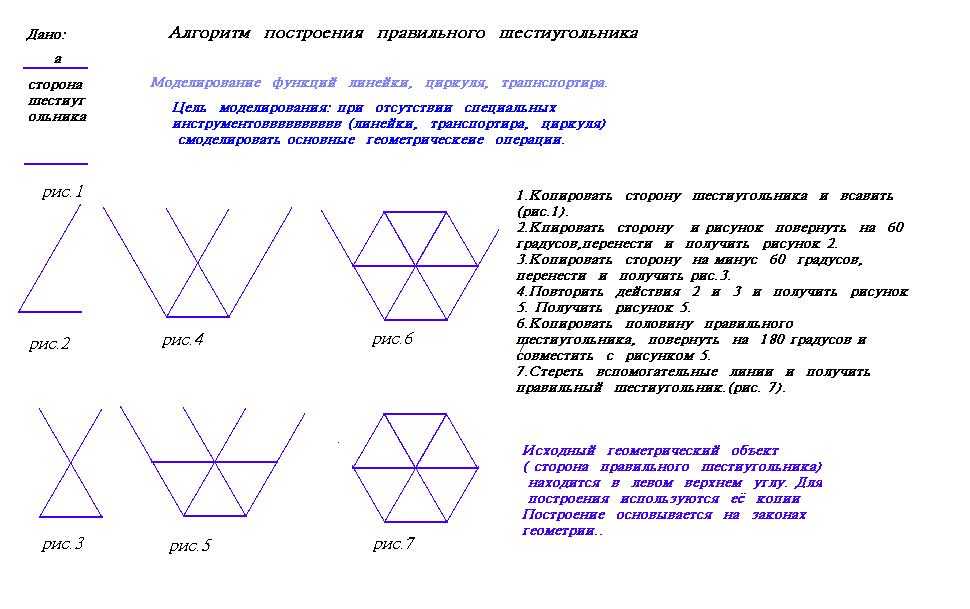Весь из пяти внутренних углов пятиугольника равен 108°.

  Полезный совет

  Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.

  Уровень сложности: Несложно

  1 шаг

  Сначала, выбирайте, где разместить центр окружности. Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.

  2 шаг

  Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н. Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.

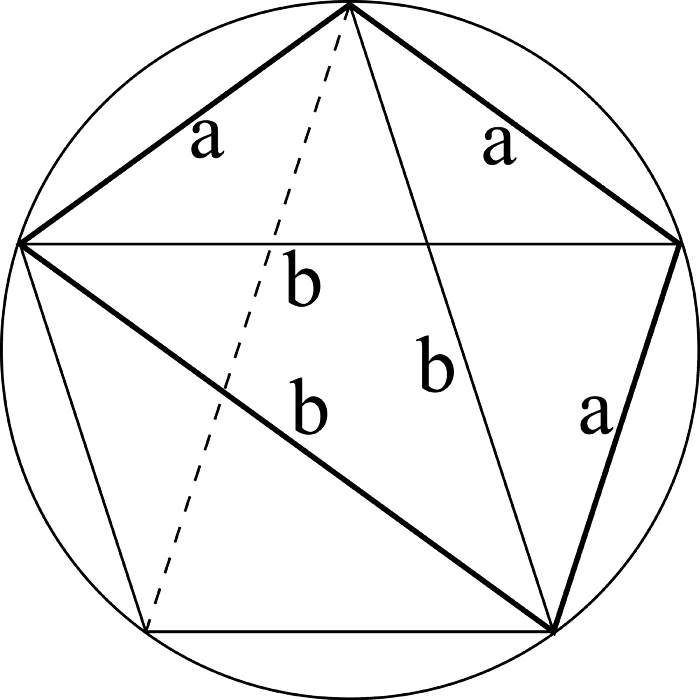
  3 шаг

  Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.

  Я РАСТУСайт для детей и их родителей

  Последние события

  Раскраски к Хеллоуину для мальчиков

  В России – празднование Хэллоуина ни с чем не связано. Это, скорее всего дань моде, чем традиции предков. Интересное яркое шоу, о значении и первоисточнике которого многие даже не догадываются.

  Коллекция раскрасок к Хеллоуину

  Скоро Хеллоуин. Праздник страшилка, праздник пугалка. Не зря его так любят дети всех стран.

  На сайте я уже как-то выкладывала подборку раскрасок к Хеллоуину.

  Осень. Деревья и листья

  Как выглядят деревья осенью? Рассмотрите картинки и раскрасьте осенние листики.

  Кто такие мишки Гамми?

  Посмотрите с детьми этот мультсериал про мишек Гамми, затем скачайте раскраски и раскрасьте героев.

  Несколько раскрасок для самых маленьких

  Совсем простенькие раскраски с крупными деталями для самых маленьких художников.

  Осеннее настроение. Раскраски

  В разгаре золотая осень. В этом году она в наших краях как никогда поздняя и ослепительно красивая.

  Рассказы про осень. Читаем и раскрашиваем картинки

  Что такое осень? Какая осенью погода? Что делают птицы осенью? Задайте эти и другие вопросы про осень своему малышу.

  Популярное

  Архив

  От теории к практике

  Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. 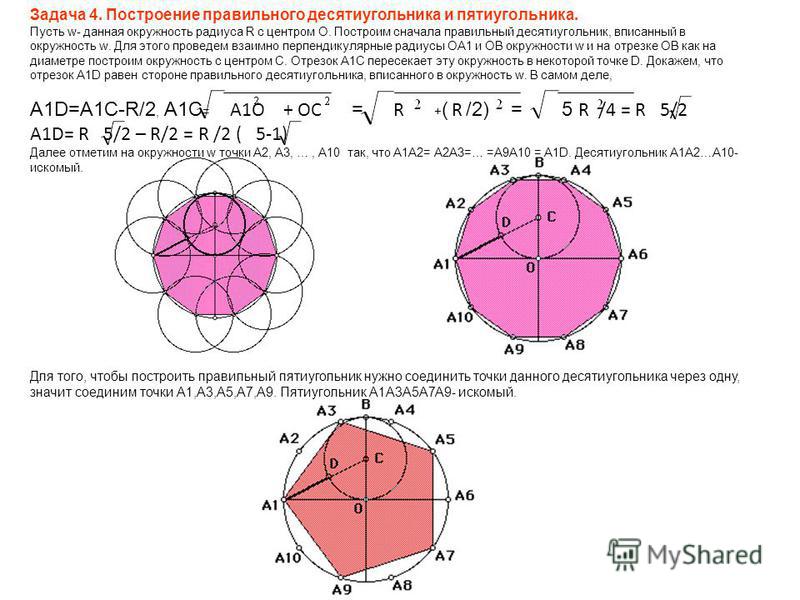Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.

  Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:

  Выпускается и бетонная плитка для мощения.

  Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.

  Свойства простые и интересные

  Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

  Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

  1. диаметр описанной окружности;
  2. диаметр вписанной окружности;
  3. площадь;
  4. периметр.

  Описанная окружность и возможность построения

  Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

  Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

  После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

  R=а.

  Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

  Ну а площадь этой окружности будет стандартная:

  S=πR²

  Вписанная окружность

  Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

  Высота равностороннего треугольника вычисляется просто:

  h²=а²-(а/2)²= а²3/4, h=а(√3)/2

  А поскольку R=a и r=h, то получается, что

  r=R(√3)/2.

  Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

  Ее площадь будет составлять:

  S=3πa²/4,

  то есть три четверти от описанной.

  Периметр и площадь

  С периметром все ясно, это сумма длин сторон:

  P=6а, или P=6R

  А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

  S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

  S=3R²(√3)/2

  Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

  Занимательные построения

  В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

  Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

  1. Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
  2. Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
  3. Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.

  Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

  1. Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
  2. Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
  3. Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
  4. Углы новообразованного шестиугольника равняются 360-120-60-60=120°.

  Как нарисовать звезду карандашом с помощью линейки и циркуля: поэтапное описание

  Для рисования звезды нужны следующие предметы: лист бумаги формата A4, карандаш, ластик, линейка. Для черчения точных отрезков можно использовать циркуль и транспортир.

  Если циркуль отсутствует, то можно потренироваться на компьютере, воспользовавшись графическим модулем MS Word. В этой компьютерной программе можно создавать различные геометрические фигуры.

  Содержание:

  Как начертить пятиконечную звезду

  На уроке изобразительного искусства иногда требуется нарисовать правильную пятиконечную звезду.

  Как же начертить эту сложную геометрическую фигуру, чтобы получилось красиво? Существует несколько способов нарисовать идеальную звездочку: при помощи циркуля, без циркуля или просто по клеточкам в тетради.

  Инструкция для рисования звезды с циркулем

  Для получения рисунка с идеальной звездой поэтапно строится правильный пятиугольник в соответствии со следующими шагами:

  • рисуется основной круг диаметром 6 см с центром в точке O;
  • через центр окружности проводятся две стартовые линии –отрезки, перпендикулярные друг к другу;
  • правая точка пересечения горизонтального отрезка с кругом – точка A;
  • верхняя точка пересечения вертикальной линии с кругом – т. B;
  • радиус круга равен OA = OB = 3 см;
  • середина OA обозначается как т. C;
  • иголка циркуля ставится в т. C и строится дополнительный круг с радиусом CB, пересекающий основную окружность в т. B и горизонтальную линию в т. D;
  • затем циркуль переносится на т. B и по радиусу BD рисуется новый круг, пересекающий первоначальную окружность в т. E и т. F;
  • далее циркуль ставится в т. E и наносится копия нового круга, который пересекает основную окружность в т. B и т. G;
  • циркуль помещается в т. F и чертится новый круг, пересекающий первоначальную окружность в т. B и т. H;
  • правильный пятиугольник BFHGE – на чертеже;
  • противоположные вершины полученного пятиугольника соединяются линиями и образуется изображение звездочки.

  Вспомогательные линии стираются при помощи ластика. На картинке – звезда.

  Рисование звездочки без циркуля

  Звезду с длиной 5 см можно начертить при помощи линейки и карандаша, зная расположение вершин правильного пятиугольника.

  Для того чтобы определить, где будут вершины этого многоугольника, выполняются следующие шаги:

  • проводится первый горизонтальный отрезок длиной 5 см,
  • отмечается середина этого отрезка,
  • под этой линией чертится параллельный отрезок на расстоянии 3,2 см = (5/1,549) см,
  • концы верхнего отрезка будут средними вершинами пятиугольного многоугольника,
  • концы нижнего отрезка будут нижними вершинами пятиугольной фигуры,
  • верхняя точка пятиугольника отмечается на расстоянии 1,9 см = (5/2,59) см от первого отрезка,
  • нужный пятиугольник создан.

  Противолежащие вершины многоугольной фигуры соединяются линиями и картинка со звездой готова.

  Детская звездочка

  Используя вышеперечисленные схемы прорисовки контуров идеальной звезды, можно создать смешную звездочку для малышей.

  Нарисованную звездочку можно прикрепить на стену детской комнаты.

  Для создания цветной иллюстрации можно использовать акварельные краски, маркеры, гуашь, фломастеры или цветные карандаши.

  Этапы создания звездочки для ребенка:

  • сначала создается набросок или эскиз. Для этого, слабо нажимая на карандаш, проводится вертикальная линия,
  • из центра вертикального отрезка просто отмечаются примерные направления верхних и нижних лучиков,
  • далее кончик карандаша ставится с отступом от центра фигуры, в середину промежутка между вершинами и рисуются закругленные полоски для каждого луча, похожие на лепестки ромашки,
  • вспомогательные линии удаляются ластиком,
  • в центре звездочки добавляются два полуовала для создания щек, над ними – две дуги для глазков. Внутри дуг чертятся малые дуги для создания зрачков,
  • под щечками добавляется улыбка.

  Полученный эскиз раскрашивается цветными карандашами или красками.

  Использование тетради в клетку для рисования звездочек

  Используя тетрадные листы в клетку, можно нарисовать оригинальные звезды интересных и забавных форм.

  Пошаговое рисование звезд по клеткам:

  1. создается верхний лучик. Он будет шириной семь колонок по горизонтали и высотой шесть строчек по вертикали;
  2. в первой строчке, обводится четвертая по счету клетка, а во второй строке – третья и пятая ячейки;
  3. в третьей и четвертой строках выделяются 2 прямоугольника, содержащие соответственно две клетки второй и шестой колонок;
  4. в пятом и шестом рядах повторяются контуры еще двух прямоугольников, состоящих из двух клеток первой и седьмой колонок;
  5. создается правая часть звездочки. Для этого в седьмой строке создается прямоугольник, объединяющий шесть ячеек из колонок с 8 по 13. Далее последовательно обводятся клетки, идущие лесенкой в левом направлении, от 8 до 11 строки. Это второй лучик;
  6. рисуются два прямоугольника с двумя клетками и один прямоугольник с тремя клетками, направленные в правую сторону. Далее, смещаясь влево, обводится прямоугольник с двумя ячейками, одна клеточка, 2 объединенные клетки и четырехугольник с тремя клетками. Третий лучик нарисован;
  7. левая часть звездочки – зеркальное отображение ее правой части;
  8. глазки делаются из 2 прямоугольников с тремя клетками;
  9.  улыбающийся ротик создается из прямоугольника с двумя клетками, двух ячеек по краям ротика строкой выше;
  10. можно начинать раскрашивать контур звездочки, ротик и глазки;
  11. цвет звездочки можно сделать желтым.

  Получилась красивая звездочка.

  Выводы

  Звездочки можно создавать при помощи линеек, карандашей, красок, циркуля. Созданные рисунки звездочек можно использовать в качестве шаблонов, чтобы быстро тиражировать одинаковые формы фигур.

  Это удобно при оформлении праздничных интерьеров, детских комнат, а также для украшения стен и окон, при изготовлении сувениров и подарков, для использования в качестве учебного пособия при объяснении урока.

  На примере рисования звезд показывается, как создаются многоугольники идеальной формы. Это помогает закрепить теоретические материалы по математике на практике, а также способствует формированию творческих способностей учеников средней школы.

  Фото нарисованной звезды

  Как нарисовать звезду в майнкрафте

  Если поставлена задача нарисовать ровную и красивую пятиконечную звезду, без изучения техники этого процесса не обойтись. Существует несколько вариантов выполнения работы. Как нарисовать звезду с помощью линейки, помогут понять самые известные методы этого процесса.

  Существует множество вариантов внешнего вида такой фигуры, как звезда.

  Еще с древних времен пятиконечная ее разновидность использовалась для начертания пентаграмм. Это объясняется ее свойством, которое позволяет сделать рисунок, не отрывая ручки от бумаги.

  Существуют также шестиконечные, восьмиконечные звезды, семиконечные хвостатые кометы.

  Пять вершин традиционно имеет морская звезда. Такой же формы нередко встречаются изображения рождественского варианта.

  В любом случае, чтобы нарисовать пятиконечную звезду поэтапно, необходимо прибегнуть к помощи специальных инструментов, так как изображение от руки вряд ли будет выглядеть симметрично и красиво.

  Чтобы понять, как нарисовать ровную звезду, следует осознать суть этой фигуры.

  Основой для ее начертания является ломаная линия, концы которой сходятся в начальной точке. Она образовывает правильный пятиугольник — пентагон.

  Отличительными свойствами такой фигуры являются возможности вписания ее в окружность, а также окружности в этот многоугольник.

  Все стороны пентагона равны между собой. Понимая, как правильно выполнить чертеж, можно осознать суть процесса построения всех фигур, а также разнообразных схем деталей, узлов.

  Для достижения такой цели, как нарисовать звезду с помощью линейки, необходимо владеть знаниями о простейших математических формулах, являющихся основополагающими в геометрии. А также потребуется умение считать на калькуляторе. Но самое главное – это логическое мышление.

  Работа не является сложной, но она потребует точности и скрупулезности. Потраченные усилия будут вознаграждены хорошим симметричным, а потому и красивым изображением пятиконечной звезды.

  Самый известный способ того, как нарисовать звезду при помощи циркуля, линейки и транспортира, является достаточно несложным.

  Для этой методики понадобится несколько инструментов: циркуль или транспортир, линейка, простой карандаш, ластик и лист белой бумаги.

  Чтобы понять, как красиво нарисовать звезду, действовать следует последовательно, этап за этапом.

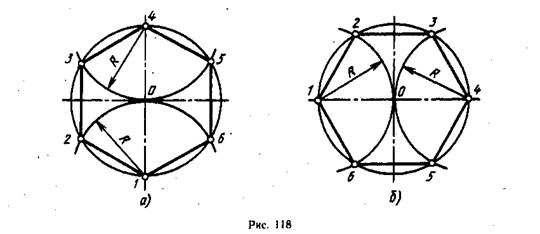
  Можно в работе воспользоваться специальными вычислениями.

  Приступая к рисованию красивой звезды, круг следует поделить на 5 равных частей. Угол каждой будет составлять 72 градуса. Тяжело высчитанные идеально показатели нанести на круг вручную.

  Поэтому необходимо построить правильный пятиугольник. Для этого используют систему «золотых чисел» прямоугольного треугольника с катетами 1 и 2, а гипотенузой, равной квадратному корню из 5.

  В решении можно отталкиваться от вычислений радиуса основной окружности или длины сторон пентагона. В последнем варианте верхние точки лучей звезды станут располагаться на одинаковых промежутках вершин пятиугольника.

  Арифметически поставленная задача решается неточно (присутствуют определенные округления результатов), что объясняется методикой использования иррациональных чисел. Поэтому геометрически начертить правильную, симметричную звезду все же проще.

  Задумываясь над тем, как нарисовать звезду с помощью линейки, следует, прежде всего, начертить окружность. 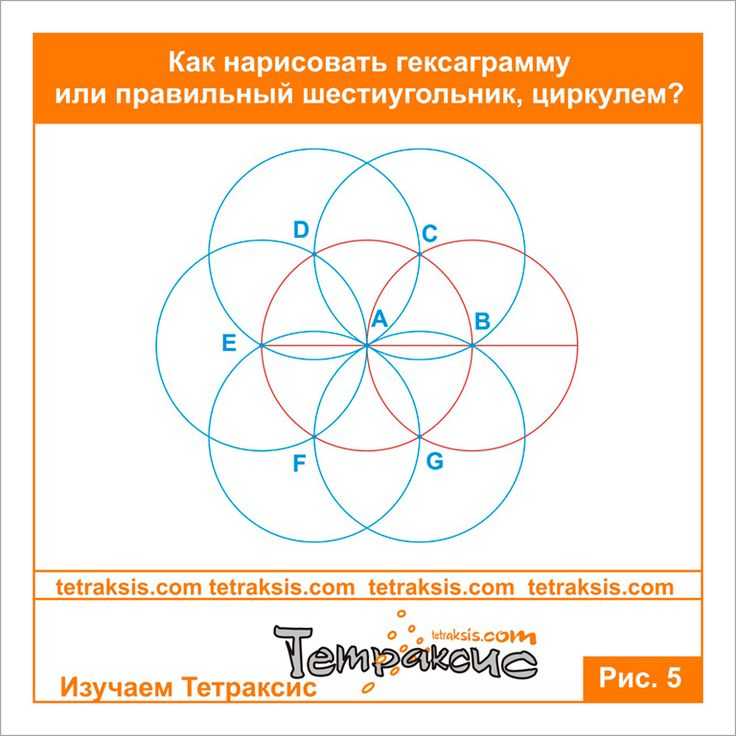Ее допускается выполнить при помощи циркуля, транспортира или же обычной чашки. Приложив ее верхний обод к листу бумаги, его край нужно обвести карандашом.

  Этот контур необходимо проводить очень тонко, так как он впоследствии будет убираться ластиком.

  Рисуя звезду поэтапно, следует разделить окружность на 5 равных частей. Это можно осуществить при помощи главного правила геометрии.

  Диаметр окружности измеряется при помощи линейки. Полученная величина умножается на 6,28. Итоговый результат и станет расстоянием, используемым для обозначения вершин звезды.

  Все точки равномерно нанести на окружность, используя рассчитанное значение.

  Чтобы понять, как нарисовать звезду поэтапно, следует выполнять все действия по четко рассчитанным величинам, не округляя их. Иначе работа получится недостаточно правильная и эстетичная.

  Вершины, размеченные ранее, соединяются друг с другом.

  Для обеспечения объемности фигуры необходимо нарисовать основные грани. Для этого все точки острых углов соединяют с противоположными им тупыми углами.

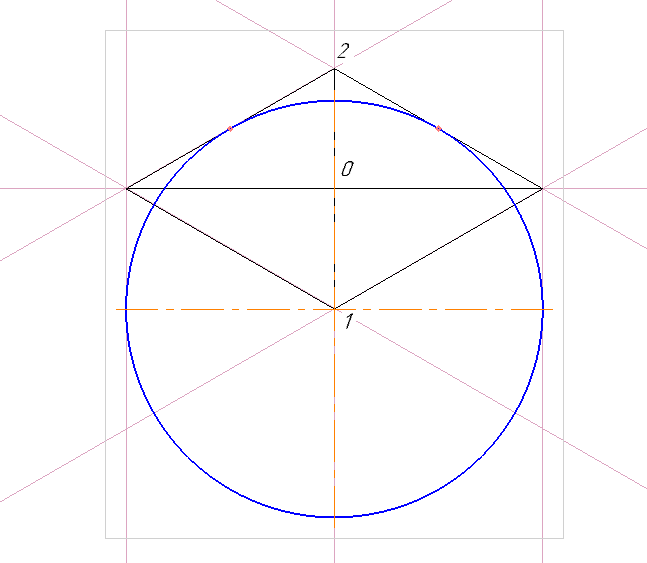
  На этом этапе рисования правильной звезды проступают контуры готовой фигуры.

  Если все сделано правильно, полученное изображение будет ровным. Это можно проверить визуально, вращая лист бумаги и оценивая форму. Она будет неизменной при каждом повороте.

  Основные контуры наводятся при помощи линейки и простого карандаша более четко. Все вспомогательные линии убираются.

  Чтобы понять, как нарисовать звезду поэтапно, следует проводить все действия вдумчиво. В случае ошибки можно подправить рисунок ластиком или провести все манипуляции заново.

  Готовую форму можно украсить самыми разнообразными способами. Главное — не нужно бояться экспериментировать. Фантазия подскажет оригинальный и красивый образ.

  Можно разукрасить нарисованную ровную звезду простым карандашом или использовать самые разнообразные цвета и оттенки.

  Чтобы разобраться в том, как нарисовать правильную звезду, необходимо придерживаться идеальных линий во всем. Поэтому самый популярный вариант оформления заключается в разделении каждого луча фигуры на две равные части линией, исходящей от вершины до центра.

  Далее одна сторона штрихуется темным оттенком, а вторая — более светлым. Можно также использовать только простой карандаш. Штриховка будет в этом случае с одной стороны каждого луча.

  Можно не разделять стороны звезды линиями. Допускается просто закрасить каждый луч фигуры более темным оттенком с одного бока.

  Такой вариант также будет ответом на вопрос о том, как нарисовать правильную звезду, ведь все ее линии будут симметричны.

  По желанию при эстетическом оформлении фигуры можно добавить орнамент или другие всевозможные элементы. Добавив кружочки к вершинам, можно получить звезду шерифа. Применив плавную растушевку теневых сторон, можно получить морскую звезду.

  Эта техника является самой распространенной, так как без особых усилий позволяет понять, как нарисовать пятиконечную звезду поэтапно. Не прибегая к сложным математическим вычислениям, возможно получить правильное, красивое изображение.

  Рассмотрев все способы того, как нарисовать звезду с помощью линейки, можно выбрать для себя более подходящий. 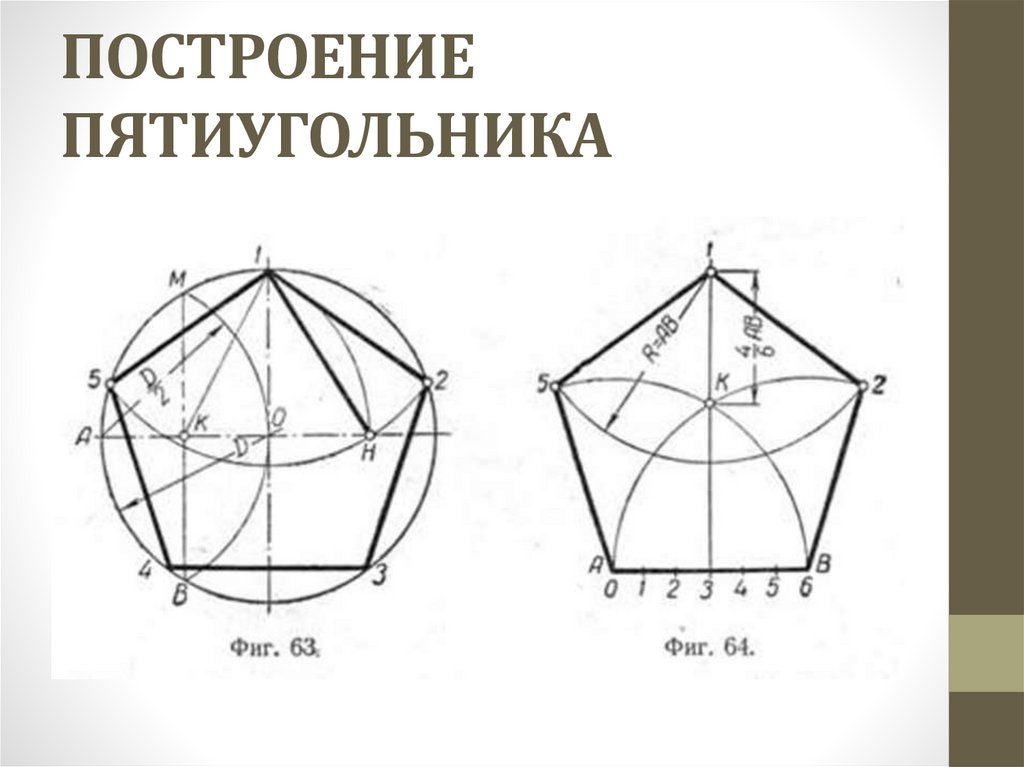Наиболее популярным является геометрический поэтапный метод. Он достаточно несложный и эффективный. Применив фантазию и воображение, можно из полученной правильной, красивой формы создать оригинальную композицию. Вариантов оформления рисунка существует великое множество. Но ведь всегда можно придумать свой собственный, самый необычный и запоминающийся сюжет. Главное — не стоит бояться экспериментировать!

  
  
  
  
  
  

  Такая фигура как пятиконечная звезда имеет множество значений в разных культурах. Упоминания об этом символе встречаются и в Европе, и на Ближнем Востоке, и даже в далекой Африке. В язычестве она обозначает единение четырех стихий и человеческого начала, в исламе (вместе с полумесяцем) — символизирует пророка Мухаммеда. А в ХХ веке именно красная пятиконечная звезда стала символом коммунизма. Сейчас же звездочки можно встретить и просто как декоративный символ — их вешают на новогоднюю елку, делают поделки, рисуют на стенах домов. И если вы тоже хотите научиться тому, как нарисовать звезду, вам в этом поможет поэтапная инструкция.

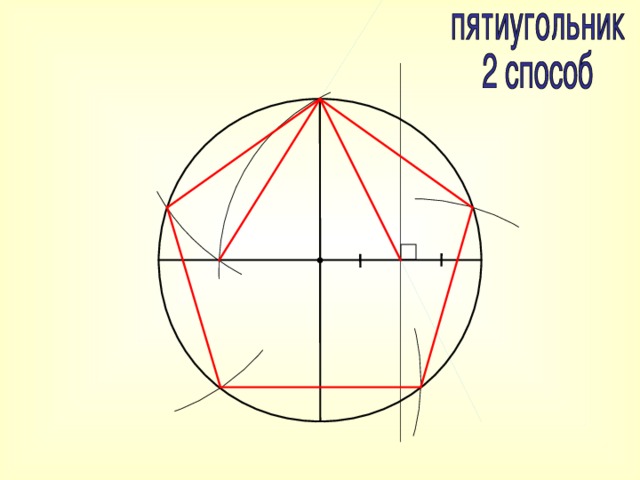
  Если вы хотите научиться тому, как нарисовать звезду пятиконечную, то действовать надо следующим образом:

  Первым делом рисуем ровную вертикальную линию — ось симметрии.

  От ее верхней точки рисуем две диагональные линии так, чтобы угол, образованный ими, делился осью симметрии на две равные части.

  Затем изображаем две параллельные горизонтальные линии.

  На основе этих вспомогательных осей рисуем три верхних луча.

  Затем делаем два нижних луча. Важно, чтобы все они были одинаковой длины.

  Стираем все вспомогательные контуры.

  Все, теперь наша картинка полностью готова!

  Если в прошлом разделе мы научились тому, как нарисовать звезду поэтапно, то сейчас немного усложним задачу — добавим фигуре объема. Не волнуйтесь, это совсем не сложно.

  Вначале рисуем три линии — вертикальную и две диагональные. Должно получится что-то вроде разделенного пополам равнобедренного треугольника.

  Затем нарисуйте еще один треугольник, на этот раз с тупым углом и направленной вниз вершиной.

  Осталось только дополнить два нижних луча при помощи двух диагональных линии. Общие контуры готовы.

  Теперь еще двумя диагональными, сходящимися в центре линиями делим нижние лучи пополам.

  Проделываем то же самое с двумя верхними лучами.

  Добавим еще 4 сходящиеся к центру короткие линии.

  Затем уберем все лишние контуры.

  Время поработать с цветом. Мы выбрали синий и голубой, но можно подобрать любой оттенок. Важно лишь помнить об одном правиле: темные и светлые участки должны чередоваться. Тогда фигура будет выглядеть объемной.

  На этом все, рисунок завершен.

  Вы наверняка видели, что геометрические тела очень часто рисуют внутри круга. И неспроста, ведь так изобразить ровную фигуру гораздо проще. В этом вы сможете убедиться сами, если решите научиться тому, как нарисовать звезду карандашом.

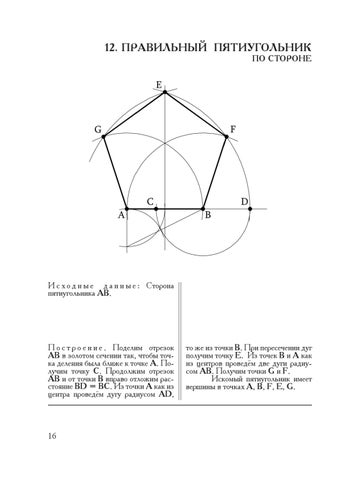
  Первым делом изобразим окружность. Чтобы все получилось ровно, лучше сделать это при помощи циркуля. Затем отметим пять точек на равноудаленном друг от друга расстоянии.

  Каждую точку соединим с двумя другими, не являющимися соседними.

  Теперь наведем основной контур маркером или фломастером.

  И сотрем все лишнее.

  Теперь звезда готова — мы справились!

  Если вы хотите узнать, как правильно нарисовать звезду, то есть один очень простой и быстрый способ. Правда, для этого нужно уметь рисовать пятиугольники. Или иметь в распоряжении готовый.

  На первом этапе рисуем пятиугольник.

  На втором — соединяем его вершины так, чтобы одна точка была соединена с двумя противолежащими.

  Если вы только начинаете свой путь в изобразительном искусстве и хотите научиться тому, как ровно нарисовать звезду, то делать это надо так:

  Затем левую крайнюю точку поперечной планки соединяем с нижним концом правой диагональной линии.

  Повторяем то же самое относительно другой стороны.

  После этого раскрашиваем получившуюся фигуру в желтый цвет. При желании можно выбрать и другой оттенок.

  На этом рисунок можно считать полностью завершенным.

  Вначале изобразим обычную пятиконечную звезду. Не страшно, если линии будут немного неровными.

  Потом наметим точку в левом нижнем углу и проведем к ней от лучей четыре плавно изгибающиеся линии. Чем-то эти линии будут напоминать часть зонтика — его спицы расположены похожим образом.

  Затем следует навести все контуры черным фломастером.

  Теперь добавим поперечных штрихов — они будут обозначать движение, придавать рисунку динамичность.

  Все, наш рисунок готов.

  • Как нарисовать звезду циркулем
  • Как нарисовать ровную звезду
  • Как делать звездочки
  • Лист бумаги, циркуль, линейка, карандаш
  • Как нарисовать звезду
  • как рисовать знаменитостей
  • как ровно нарисовать звезду
  • линейка;
  • карандаш;
  • циркуль;
  • транспортир.

  Построение пятиконечной звезды сводится к построению правильного пятиугольника с последующим соединением его вершин друг с другом последовательно через одну. Для того чтобы построить правильный пятиугольник необходимо разбить окружность на пять равных частей.
  Постройте произвольную окружность при помощи циркуля. Обозначьте ее центр точкой O.

  Отметьте на окружности точку A и при помощи линейки начертите отрезок ОА. Теперь необходимо разделить отрезок OA пополам, для этого из точки А проведите дугу радиусом ОА до пересечения ее с окружностью в двух точках M и N. Постройте отрезок MN. Точка Е, в которой MN пересекает OA, будет делить отрезок OA пополам.

  Восстановите перпендикуляр OD к радиусу ОА и соедините точку D и E. Сделайте засечку B на диаметре OA из точки E радиусом ED.

  Как нарисовать треугольник на листе чтобы вырезать. Как нарисовать несуществующий объемный треугольник поэтапно.

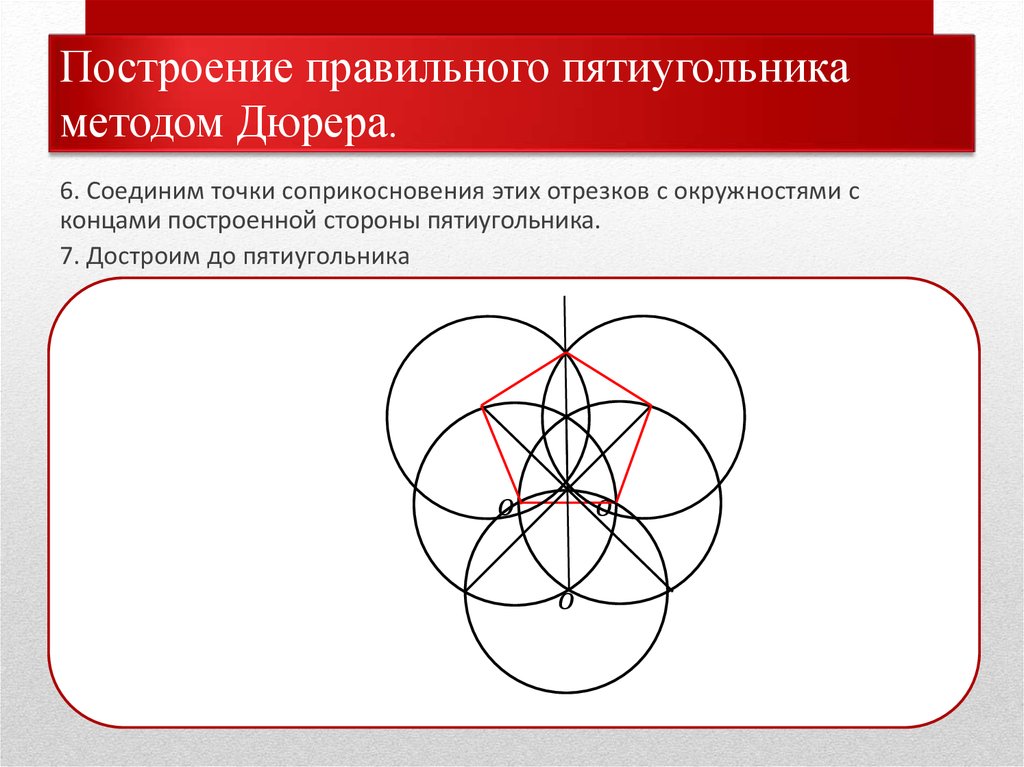  Построение остроугольного треугольника

  Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.

  Как рисовать треугольник с равными сторонами?

  Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.

  Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.

  Варианты создания фигуры

  Обязательно используйте линейку и один из представленных ниже способов:

  1. Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. 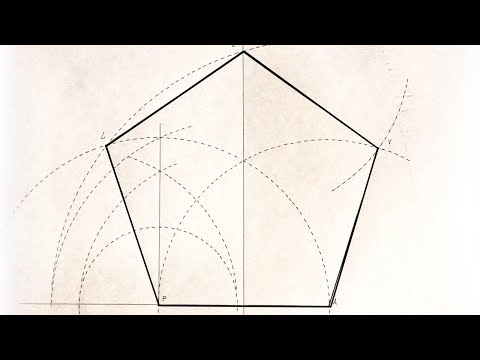Удостоверьтесь, что достаточно места для рисования всех трех сторон!
  2. Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии — это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
  3. Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.

  Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.

  Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).

  Как нарисовать равнобедренный треугольник:

  1. Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
  2. Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
  3. Учитывая базовые и смежные углы — необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
  4. Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.

  Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.

  Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта — расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.

  С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект — должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.

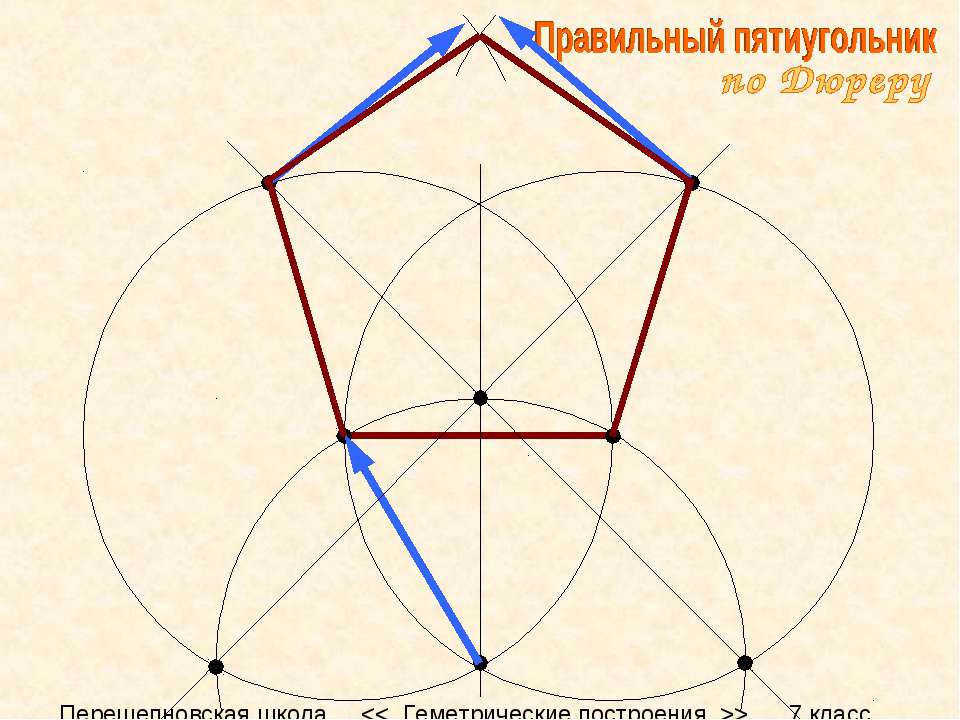
  Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу — это четверть пути по окружности.

  Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.

  Подведем итоги

  Как начертить треугольник?

  Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.

  Треугольники бывают

  • разносторонние;
  • равнобедренные;
  • равносторонние;
  • прямоугольные;
  • тупоугольные;
  • остроугольные;
  • вписанные в окружность;
  • описанные вокруг окружности.

  Построение равностороннего треугольника

  Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.

  1. С помощью линейки начертите одну из сторон, заданной длины.
  2. Измерьте ее длину с помощью циркуля.
  3. Поместите острие циркуля в один из концов отрезка и проведите окружность.
  4. Переставьте острие в другой конец отрезка и проведите окружность.
  5. У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.

  Построение равнобедренного треугольника

  Данный тип треугольников можно построить по основанию и боковым сторонам.

  Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:

  1. С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
  2. Циркулем измеряем необходимую длину боковой стороны.
  3. Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
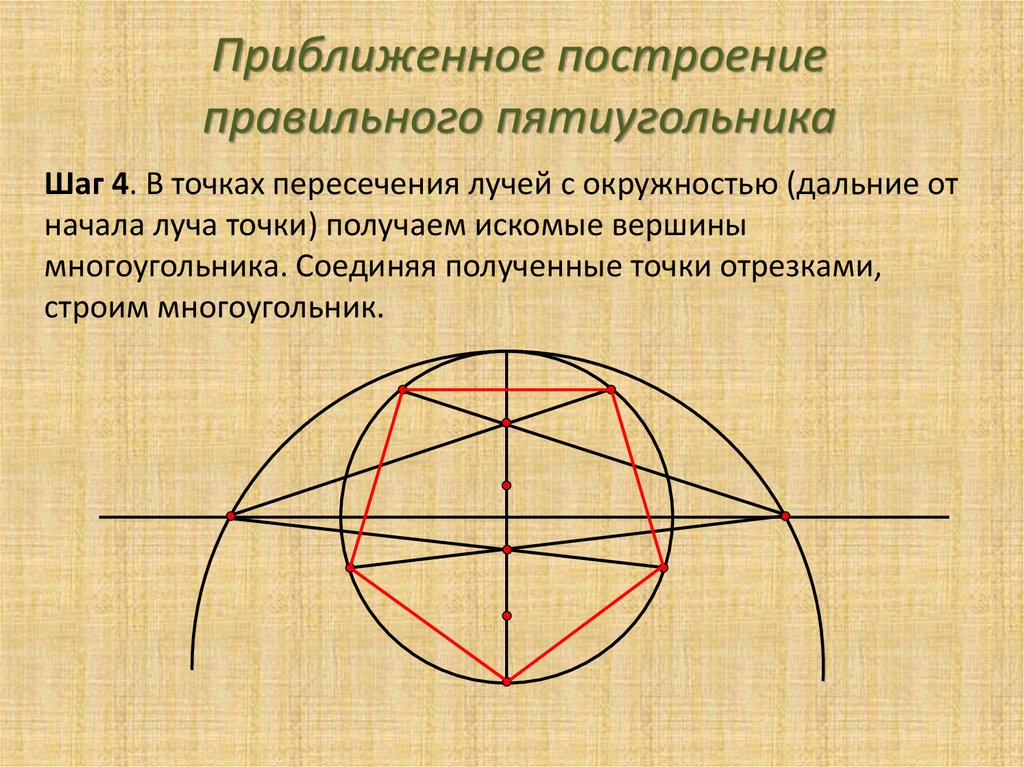
  4. Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.

  Построение прямоугольного треугольника

  Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.

  Построение тупоугольного треугольника по углу и двум прилегающим сторонам

  Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:

  1. С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
  2. Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
  3. Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.

  Построение остроугольного треугольника

  Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.

  1. Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
  2. Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.

  Вписанный треугольник

  Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:

  У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.

  Чертим описанный треугольник

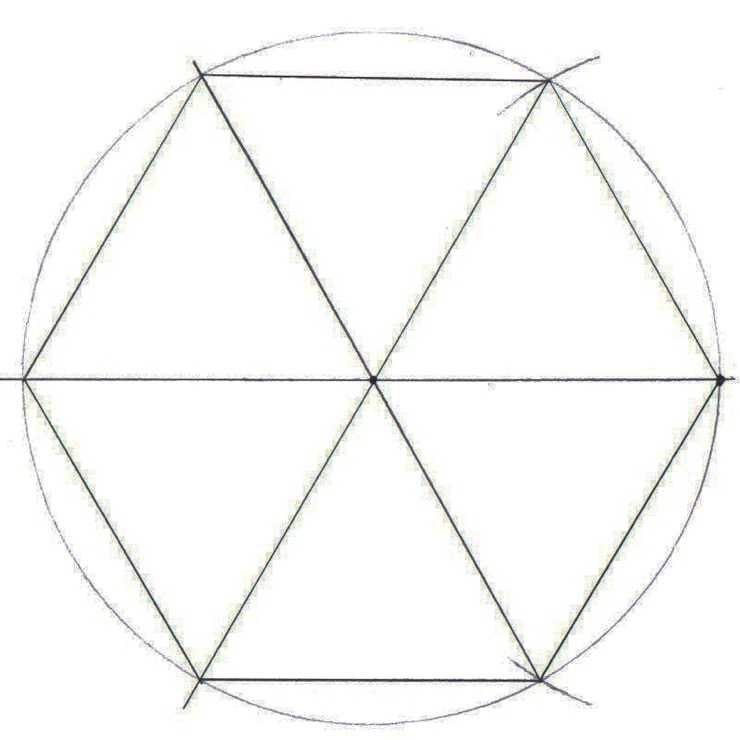
  Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:

  Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

  Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего прово­дим стороны 5-6 и 3-2.

  Построение вписанного в окружность равностороннего треуголь­ника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

  Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

  Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны

  1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

  Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

  Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. 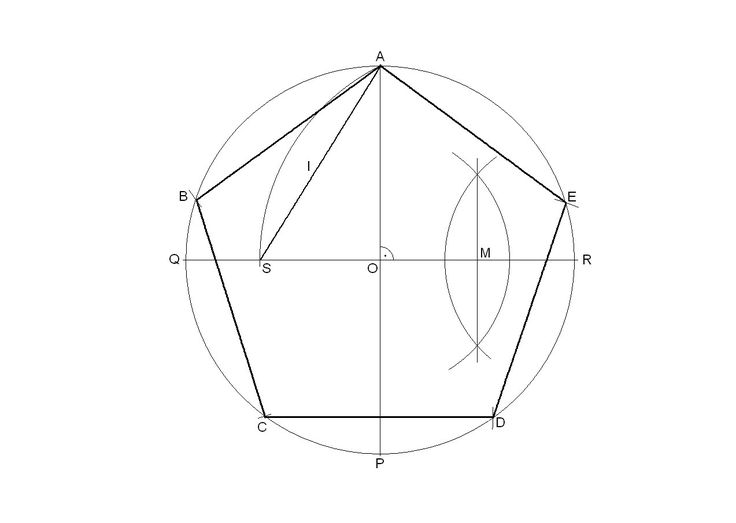Полученные точки будут двумя другими вер­шинами искомого треугольника.

  Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.

  Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.

  Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

  Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. 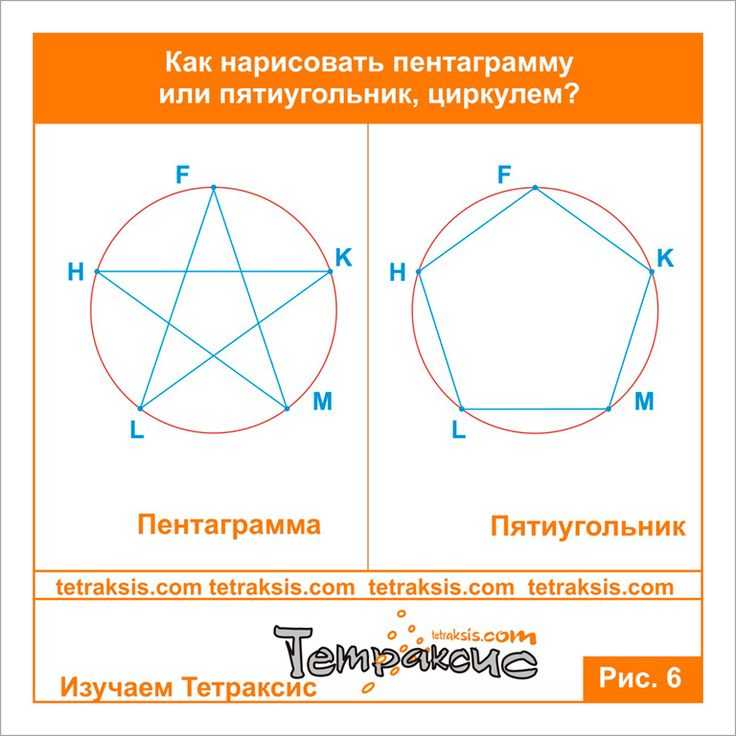Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

  Построение вписанного в окружность правильного пятиугольника.

  Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

  Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

  Построение правильного пятиугольника по данной его стороне.

  Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

  Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

  Построение вписанного в окружность правильного семиугольника.

  Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

  Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

  Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

  Сегодня мы расскажем вам, как легко прослыть художником среди своих друзей или показать девушке, какой ты весь разносторонний (о, они это любят!). 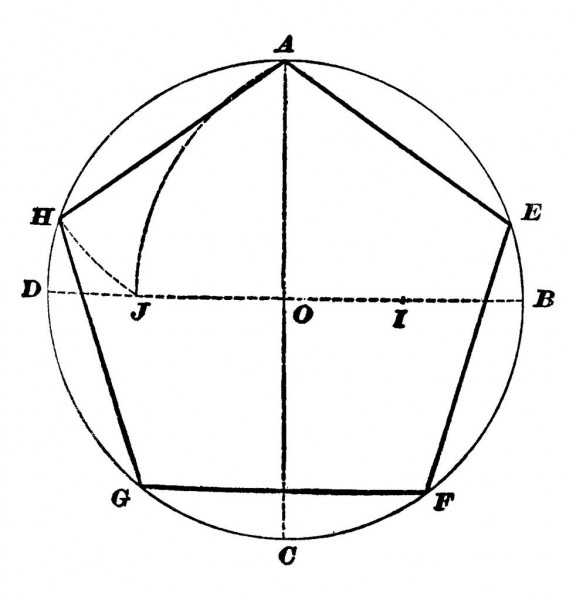Итак начнем!

  Нам понадобится: 50 грамм для храбрости, 2 карандаша (один жесткий, другой мягкий), лист бумаги, линейка и ластик. Да начнется магия!

  Шаг 1.

  Рисуем обычный треугольник – он не должен являть собой венец геометрической мысли: просто соедини три линии.

  Шаг 2.

  Теперь нарисуй внутри линии, прямо как у нас. Старайся сделаить их одной ширины, ты ж не рукожоп, как мы!

  Шаг 3.

  Нарисовал? Молодец! Теперь нарисуй еще, как мы показали. Мы знаем, ты устал, но скоро все закончится.

  Шаг 4.

  Спили вершины треугольника как на рисунке.

  Шаг 5.

  Теперь обведи все линии, которые выделили мы, жирным карандашом, пером или гелевой ручкой. Или маркером. Или фломастером. Может надо бутерброд забацать?

  Шаг 6.

  Сотри все ненужное. Мы близко к цели, видишь?

  Шаг 7.

  Тут мы обратились к богам Олимпа и они нарисовали нам тени. Ты рисуй сам.

  Шаг 8.

  

  Теперь можно вырезать наше творение лезвием или ножницами и ломать хрупкие разумы своих друзей. Этот треугольник входит в число фигур, которые геометрически не имеют право на существование или по по-другому “несуществующие фигуры”.

  Надеемся, тебе понравилось, ибо мы старались и крали этот урок рисования несуществующего треугольника поэтапно. И теперь тебе лучше нарисовать героев

  Нарисуем треугольник 3D с оптической иллюзией поэтапно.

  Сначала рисуем обыкновенный равносторонний треугольник карандашом. Внутри него, параллельно каждой из сторон, проводим по линии на равном расстоянии так, что внутри треугольника получается еще один треугольник.

  Вновь проводим параллельные линии, отступив на то же расстояние и рисуя еще один меньший треугольник внутри первых двух.

  Жирно проводим контур по периметру сторон большого треугольника, обводя его стороны, но срезая острые углы.

  Проводим еще один контур из двух прямых, повторяющих одну сторону среднего и одну сторону меньшего треугольников внутри большого, как показано на рисунке.

  Проводим еще по контуру, — две прямые, повторяя стороны треугольников, как на рисунке.

  И еще раз делаем те же действия, с другими сторонами, — обводим жирным контуром две прямые, как на рисунке.

  Лишние линии убираем. Вот получился 3D треугольник, пока не закрашенный.

  Заштриховываем стороны треугольника, придавая изображению объемность. Рисунок готов, треугольник 3D иллюзия .

  Посмотрим видео, как рисовать оптическую иллюзию треугольник 3D.

  Нарисовать треугольную иллюзию несложно, особенно если есть пошаговая инструкция. Понадобится карандаш, бумага и желательно линейка, с ней будет аккуратнее рисунок. По шагам повторить все действия, а потом затенить с помощью растушевки нужные места.

  Как нарисовать треугольник … Да, при этом не простой, а очень сложный с множеством треугольников внутри. Чтобы все его грани проглядывались, а на бумаге он выглядел реалистичным и четким.

  Для этого нам потребуется:

  • карандаш,
  • стерка,
  • лист бумаги,
  • пошаговая интсрукция.

  Процесс рисования:

  • сперва изобразить треугольник,
  • затем все его грани, начиная с внешней,
  • заштриховать участки свето-тени, чтобы придать объем фигуре,
  • при необходимости разукрасить объект.

  Получается необычайная фигура с множеством завихрений. Смотрится немного завораживающе, так как разум пытается продлить все линии и уловить суть.

  Видео-инструкция, как нарисовать треугольник на бумаге:

  Треугольник Пенроуза или невозможные фигуры. Был придуман в 1953 году художником Оскаром Реутерсвардом. Первый треугольник был сделан из кубиков.

  Уникальность этого объекта в том, что посмотрев на прямые палки под определнным углом можно четко увидеть треугольник. Как например вот на этом памятнике.

  Пятиконечная звезда. Как нарисовать ее быстро и просто

  Пятиконечная звезда – наиболее почитаемый символ у всех народов мира во все времена. Ее изображения обнаружены у самых истоков цивилизации, когда еще не была изобретена письменность.

  Съдържание

  • Видео: Как нарисовать звезду поэтапно.Как нарисовать пятиконечную звезду
  • Как нарисовать пятиконечную звезду, не отрывая карандаш от бумаги
  • Как нарисовать звезду, используя линейку и транспортир
  • Как нарисовать звезду с помощью циркуля и транспортира
  • Видео: sacred geometry: how to draw a five pointed star
  • Как нарисовать звезду с помощью циркуля и линейки
  • Видео: Геометрия — Построение пятиугольника и звезды

  Самое первое изображение пятиконечной звезды, найденное археологами, датируется 3500 годом до нашей эры. Она была запечатлена на глиняной табличке, найденной при раскопках шумерского города Урук.

  Символ звезды пользовался популярностью в Древнем Египте и Вавилоне. Его почитали древние римляне и греки, считая пятиконечную звезду символом круговорота в природе. Пять углов звезды греки ассоциировали с пятью элементами, из которых сотворен наш мир, – землей, водой, воздухом, огнем и эфиром.

  Пятиконечная звезда является атрибутом гербов и флагов многих современных государств и присутствует на воинских знаках различия.

  А вот нарисовать эту незамысловатую фигуру не так просто, как может показаться на первый взгляд.

  Видео: Как нарисовать звезду поэтапно.Как нарисовать пятиконечную звезду

  Как нарисовать пятиконечную звезду, не отрывая карандаш от бумаги

  Великий греческий мыслитель и математик Пифагор называл пятиконечную звезду математическим совершенством. Действительно, эту сложную фигуру можно нарисовать одной ломаной линией, не отрывая карандаша от листа бумаги и вернувшись в конце в ту же отправную точку, с которой был начат рисунок.

  Вот такая она, сложная и простая на первый взгляд фигура – пятиконечная звезда. Как нарисовать ее одной ломаной линией, видно из рисунка.

  Как нарисовать звезду, используя линейку и транспортир

  Теперь узнаем, как нарисовать правильную пятиконечную звезду. Из измерительных приборов понадобятся линейка и транспортир.

  Чтобы получилась звезда, нужно провести отрезки одинаковой длины таким образом, чтобы внутренние углы между всеми пятью вершинами фигуры были равны 36°. Практически это осуществляется следующим образом – чертится угол в 36°, от его вершины отмеряются отрезки одинаковой длины, и от их конечных точек проводятся новые прямые под углом 36°.

  Можно также подойти к решению задачи немного иным способом, нарисовав равносторонний пятиугольник с вершинами углов в 106°, а затем соединив отрезками его противолежащие углы.

  
  
  

  Если вы соблюдете все условия, у вас в конечном счете получится красивая пятиконечная звезда. Как нарисовать ее более простым способом, читайте далее.

  Как нарисовать звезду с помощью циркуля и транспортира

  Теперь вам понадобятся циркуль и транспортир. Так как в окружности 360°, то в 1/5 ее части – 72° (360 : 5 = 72). Приступаем к построению.

  Начертите с помощью циркуля окружность. Отметьте на ней отправную точку – вершину звезды и середину окружности. Возьмите транспортир, совместите его центр с центром окружности, и по всей длине окружности отметьте рисками будущие точки вершин звезды через каждые 72°.

  Видео: Sacred Geometry: How to draw a five pointed star

  Останется соединить их прямыми, и получится красивая пятиконечная звезда. Как нарисовать ее, если под рукой не окажется транспортира? Без него можно обойтись, из инструментов понадобится лишь линейка и циркуль.

  Как нарисовать звезду с помощью циркуля и линейки

  Как нарисовать пятиконечную звезду циркулем? Рассмотрим вариант 1.

  Чертим окружность. Измеряем ее диаметр с помощью линейки. Производим несложные математические действия: умножаем диаметр окружности на коэффициент 0,58779. Полученный результат – необходимая длина хорды (прямой, соединяющей 2 точки кривой линии, а в нашем случае – окружности), с помощью которой мы сможем разделить окружность на 5 равных частей.

  Например, диаметр окружности равен 7 см. Умножаем 7 х 0,58779 = 4,11453, округляем до десятых (так как нарисовать на бумаге отрезок более точной длины не представляется возможным), получим 4,1 см. Это и будет нужная длина хорды.

  Видео: Геометрия — Построение пятиугольника и звезды

  Осталось раздвинуть и зафиксировать ножки циркуля на данную величину, и можно делать насечки на окружности. Когда вы их соедините, получится пятиконечная звезда.

  Как нарисовать фигуру другим способом? Рассмотрим вариант 2.

  Для начала начертим правильный пятиугольник, вписанный в окружность. Как нарисовать правильную пятиконечную звезду на его основе, показано на рисунке 2.

  Начертите циркулем окружность. Условно обозначим ее центр как О. Через точку О проведите прямую – диаметр нашей окружности. Прочертите радиус этой окружности таким образом, чтобы он был перпендикулярен диаметру. Точку пересечения радиуса с окружностью обозначим как V. Слева от точки О отложите расстояние, равное половине длины радиуса этой окружности, обозначьте его точкой А. Из точки А через точку V проведите полуокружность до пересечения с линией диаметра (на рисунке она выделена красным цветом) и обозначьте ее точкой В. Длина отрезка VB и будет длиной хорды, с помощью которой окружность разделится на 5 равных частей. Останется лишь соединить полученные точки в виде звезды.

  Споделяне в социалните мрежи:

  
  

  сроден

  • Визит в «школу монстров», или как нарисовать «монстер хай»
  • Урок изобразительного искусства: как нарисовать павлина
  • Как нарисовать летучую мышь красиво?
  • Знаете ли вы, как нарисовать жука?
  • Как нарисовать вечный огонь: пошаговая инструкция
  • Узнайте несколько способов о том, как нарисовать космос акварелью
  • Как нарисовать «май литл пони»? Рассмотрим несколько способов
  • Уроки рисования. Как нарисовать косичку простым карандашом
  • Как нарисовать леопарда карандашом? Поэтапно рассмотрим простой способ
  • Как нарисовать татуировку поэтапно карандашом
  • Как нарисовать звезду с помощью линейки быстро?
  • Как поэтапно нарисовать русалку карандашом: идеи и советы
  • Знак качества ссср на товарах и его история
  • Завораживающее зрелище, или почему звезды мерцают?
  • Кассиопея — созвездие, увековечившее героев античного мира
  • Звезда антарес — красный исполин, сердце скорпиона, соперник марса
  • Как найти полярную звезду на звездном небе. В каком созвездии находится полярная звезда
  • Альдебаран (звезда). Альдебаран в созвездии тельца
  • Солнце — ближайшая звезда к земле
  • Самая яркая звезда: вакансия свободна
  • Сверхновая звезда – смерть или начало новой жизни?

  Рисование с помощью компаса: шаги по рисованию и полезные советы

  LearnPracticeDownload

   

  Компас — это инструмент, используемый для рисования кругов. Размер кругов зависит от радиуса круга, нарисованного с помощью компаса. При рисовании круга всегда предпочтительнее рисовать с помощью циркуля, так как это помогает точно построить круг. В этом уроке мы научимся рисовать с помощью компаса и подробнее об инструменте компасе.

  1.	Что означает компас?
  2.	Части компаса
  2.	Рисование с помощью компаса
  3.	Решенные примеры на чертеже компаса
  4.	Практические вопросы по рисованию компаса
  5.	Часто задаваемые вопросы о рисовании компаса

  Что означает компас?

  Слово «компас» буквально означает «окружать», что, другими словами, также называется «обходить». Компас — это инструмент, который обычно представляет собой металлический или пластиковый инструмент для рисования V-образной формы. Он в основном состоит из двух подвижных рычагов, которые шарнирно соединены друг с другом. Он используется для рисования кругов или частей кругов, называемых дугами. Компас также называют парой компасов. Типы чертежного компаса включают в себя лучевой компас, разметочный компас, разделитель со свободной ножкой и пропорциональный компас. Циркуль используется в математике для рисования и черчения для создания дуг, окружностей или других геометрических фигур, которые можно определить путем измерения пересекающихся отрезков. Его можно использовать для деления прямых и углов пополам, поиска середины, помощи в решении задач по геометрии, а также для измерения расстояний или более точных расстояний на картах.

  Детали компаса

  Как у циркуля есть две руки, одна рука держит карандаш, а другая рука имеет заостренный конец. Компас предназначен для того, чтобы пользователи могли держать его между большим и указательным пальцами. Имея в виду то же самое, длина ручки чертежного компаса составляет около 1,25 сантиметра. Руки компаса. Расстояние между стрелками компаса регулируется. Если мы раздвинем стрелки компаса, легче построить окружность или дугу большего радиуса. На одном конце есть зажим для удержания карандаша, а на другом конце есть острый конец, который удерживает инструмент на поверхности для рисования во время движения карандаша.

  Петля

  Ручка компаса. Держим его между указательным и большим пальцами. Обычно для рисования круга используется только одна рука. Компас поворачивается поворотом между указательным и большим пальцами.

  Стрелка компаса

  Это точка, расположенная в центре круга. Кончик карандаша поворачивается вокруг этой точки. Зазор между стрелкой компаса и кончиком карандаша равен радиусу окружности. Он устанавливается с помощью линейки. Зазор можно изменить, изменив угол между лучами компаса.

  Держатель для карандаша

  В этом месте крепко зажат острый карандаш. Кончик карандаша выравнивается по отношению к стрелке компаса путем сближения кончика карандаша и стрелки компаса. Как только их кончики совпадут, можно использовать компас для построения кругов.

  Рисование с помощью компаса

  С помощью компаса можно строить окружности, дуги, биссектрисы, биссектрисы углов и определять середины. Шаги, чтобы нарисовать круг с помощью компаса:

  • Шаг 1: Выберите размер дуги или окружности, которую необходимо нарисовать.
  • Шаг 2: Мы помещаем острие компаса в центр намеченной окружности или дуги.
  • Шаг 3: Нажмите на иглу, поверните ручку в верхней части компаса, чтобы нарисовать окружность или дугу, и перетащите карандаш вокруг центра, чтобы нарисовать кривую.
  • Шаг 4: Рисуется круг. При необходимости вы можете отметить его центральную точку, радиус или диаметр.

  Полезные советы

  • Просто убедитесь, что петля в верхней части компаса затянута, чтобы он не скользил.
  • Не давите на карандаш, но затяните фиксацию карандаша, иначе ширина круга изменится.
  • Следите за тем, чтобы стержень карандаша совпадал со стрелкой компаса.
  • Циркуль для рисования может рисовать круги на любом конкретном материале (дерево, металл, пластик и т.д.). Все, что вам нужно сделать, это поставить иглу на поверхность/страницу, на которой должен быть нарисован круг, зафиксировать ее и повернуть другую руку вокруг, сохраняя тот же угол на шарнире.

  Темы, связанные с рисованием компаса

  • Геометрическое построение
  • Создание кругов
  • Базовые треугольные конструкции
  • Усовершенствованные треугольные конструкции
  • Сущность геометрических построений
  • Построение биссектрисы угла

   

   

  1. Пример 1:  Как Хэлси сможет точно нарисовать круг диаметром 7 дюймов с отмеченной центральной точкой?
     Решение:  Хэсли, безусловно, может выбрать любые круглые объекты и обвести их или даже использовать веревку, но для получения точных результатов ей следует воспользоваться компасом. Следовательно, она будет использовать циркуль для построения круга.

  2. Пример 2: Эшли хочет узнать, можно ли построить отрезок длиной 4 единицы с помощью линейки и циркуля. Джеймс дал ей следующие шаги для рисования:

     Шаг 1: Нарисуйте линию любой длины и отметьте точку A на линии, которая является начальной точкой отрезка линии.

     Шаг 2: Используйте линейку и поместите указатель компаса на 4 единицы отдельно от грифеля карандаша.

     Шаг 3. Поместите стрелку компаса в точку A. Отметьте дугу на линии острием карандаша.

     Шаг 4: Отметьте точку пересечения дуги и прямой, назовите ее B.

     Шаг 5: AB — искомый отрезок линии, имеющий длину = 4 единицы.

     Давайте выполним эти шаги и изучим!

     Решение: Чертеж компаса для отрезка длиной 4 единицы показан как:

  3. Пример 3:  Фред увлекается геометрией. Он рисовал круги с помощью циркуля для создания различных художественных рисунков. Он столкнулся с проблемами, когда ее учитель попросил его построить круг известного радиуса, скажем, 5 единиц. Давайте поможем ему нарисовать круг радиусом 5 единиц.
     Решение:  Чтобы нарисовать круг известного радиуса, нужны циркуль и линейка. Рисунок компаса для круга выполняется с помощью следующих шагов:

     Шаг 1: Откройте компас, измерьте длину 5 единиц с помощью линейки.

     Шаг 2: Отметьте точку О, используйте ее как центр круга.

     Шаг 3: Наведите указатель на эту точку, точка O.

     Шаг 4: Поверните циркуль, проведите карандашом вокруг центра, чтобы сделать полный круг.

     Попробуйте сделать это в одном экземпляре.

  перейти к слайдуперейти к слайдуперейти к слайду

   

   

  Есть вопросы по основным математическим понятиям?

  Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.

  Забронировать бесплатный пробный урок

   

   

  перейти к слайдуперейти к слайдуперейти к слайду

   

   

  Часто задаваемые вопросы о рисовании компаса

  Как нарисовать круг без компаса?

  Мы можем использовать круглые предметы, такие как браслеты или веревки, чтобы нарисовать круг без компаса.

  Для чего нужен компас?

  Циркуль — это инструмент, который используется для построения геометрических фигур, таких как окружности, дуги, биссектрисы и биссектрисы углов. Его также можно использовать для определения средних точек, решения задач на основе геометрии и для измерения точных расстояний на карте.

  Какой инструмент можно использовать для рисования угла 90 градусов?

  Для построения угла в 90 градусов можно использовать циркуль и линейку или транспортир.

  Как правильно пользоваться компасом при рисовании?

  Следим за соблюдением следующих пунктов:

  • Нам нужно затянуть шарнир в верхней части компаса, чтобы он не соскальзывал.
  • Держатель для карандаша плотный, так что он не должен скользить, но не оказывайте никакого давления на карандаш, иначе ширина круга изменится.
  • Грифель карандаша должен быть совмещен со стрелкой компаса.

  Как пользоваться компасом?

  Мы используем циркуль для рисования, выполнив следующие шаги:

  • Шаг 1: Выберите размер дуги или окружности, которую нужно нарисовать.
  • Шаг 2: Поместите острие компаса в центр намеченной окружности или дуги.
  • Шаг 3: Нажмите на иглу, поверните ручку в верхней части компаса, чтобы нарисовать окружность или дугу, и проведите карандашом вокруг центра.

  Какие бывают чертежные циркуль?

  Существует четыре типа компасов для рисования:

  • Биммер
  • Писцовый компас
  • Разделитель ножек
  • Пропорциональный компас

  Скачать БЕСПЛАТНЫЕ учебные материалы

  Рабочие листы по геометрии

  Рабочие листы по математике и
  наглядный учебный план

  Как нарисовать шестиугольник: с помощью компаса и рисованной

  Понравился этот урок?

  Научитесь рисовать шестиугольник двумя способами. Постройте точный шестиугольник с помощью циркуля или научитесь рисовать шестиугольник из шести треугольников вручную.

  Как нарисовать шестиугольник: используя компас и рисунок от руки — пошаговое руководство по рисованию показанное изображение

  Первый способ нарисовать шестиугольник — это построить его точно с помощью циркуля и линейки. Таким образом, мы получаем геометрически совершенный шестиугольник.

  Наш второй шестиугольник нарисован вручную и составлен из шести треугольников одинаковой формы. Это простая техника рисования шестиугольника правильной формы от руки.

  Время рисования: около

  Вам понадобится: карандаш, фломастер, цветные карандаши, ластик и бумага для рисования или альбом для рисования

  Это любимые предметы, которые мы используем для рисунков на Let’s Draw That, которые мы любим и рекомендуем:

  Набор карандашей Staedtler Mars Lumograph с ластиком и точилкойКупить на AmazonНабор карандашей и маркеров Staedtler Mars Lumograph с ластиком и точилкойКупить на AmazonDerwent Inktense Watercolor PencilsКупить на AmazonMoleskine SketchbookКупить на Amazon на Amazon

  Отказ от ответственности: LetsDrawThat. com участвует в программе Amazon Associates. Если вы покупаете продукт, используя ссылку на нашем веб-сайте, мы получаем небольшую комиссию без каких-либо дополнительных затрат для вас. Это один из способов, как вы можете поддержать этот сайт.

  Любишь рисовать? Никогда не пропустите учебник!

  Как нарисовать шестиугольник с помощью циркуля

  Наш первый метод рисования шестиугольника использует циркуль и линейку для точного построения – мы получаем геометрически совершенную форму. Все стороны шестиугольника имеют одинаковую длину — ровно половину диаметра окружности, в которую он вписан. Это позволяет легко регулярно разбивать окружность и отмечать нужные точки на окружности с помощью циркуля. Давайте углубимся в это.

  Рисунок шестиугольника с помощью циркуля

  Шаг 1: Нарисуйте окружность

  Этап рисования: Нарисуйте окружность

  Сначала нарисуйте крест – две направляющие одинаковой длины, пересекающиеся под прямым углом (90 градусов). Они станут основой нашей конструкции.

  Затем возьмите циркуль и нарисуйте круг из центра, где пересекаются две линии.

  Если вы хотите построить шестиугольник с заданной длиной стороны, радиус окружности, т. е. отверстие вашего компаса, представляет собой заданную длину стороны завершенного шестиугольника.

  Шаг 2: Отметьте два верхних угла

  Шаг рисования: Отметьте два верхних угла

  Далее мы отметим два верхних угла. Оставьте свой компас настроенным на тот же радиус и нарисуйте полукруг от верхнего пересечения нашего круга и вертикальной поперечной линии.

  Если вы хотите стереть все эти вспомогательные линии позже, просто отметьте места, где полукруг пересекается с кругом.

  Мы нарисовали здесь полный полукруг только для того, чтобы показать тот факт, что мы по-прежнему рисуем с тем же радиусом, и сделать объяснение более очевидным.

  Шаг 3: Повторите и отметьте два нижних угла

  Шаг рисования: Повторите и отметьте два нижних угла

  Повторим и нарисуем полукруг точно такого же радиуса от нижнего пересечения нашего круга и вертикальной поперечной линии. Это отмечает оставшиеся две точки нашего шестиугольника в нижней половине круга.

  Опять же, не стесняйтесь просто отмечать точки, а не рисовать полный полукруг.

  Шаг 4: Соедините отмеченные точки, чтобы нарисовать шестиугольник

  Шаг рисования: Соедините отмеченные точки, чтобы нарисовать шестиугольник

  На этом рисунке мы выделили шесть пересекающихся точек, которые образуют углы нашего шестиугольника.

  Осталось соединить их все прямыми линиями, и мы построили идеальный правильный шестиугольник.

  Наслаждаетесь геометрией? Вот вам еще один технический чертеж:

  Как нарисовать шестиугольник с помощью циркуля: готовый рисунок

  Как нарисовать шестиугольник с помощью циркуля: завершенный идеальный шестиугольник

  Как нарисовать шестиугольник с помощью циркуля: завершенный правильный шестиугольник

  Вот полный геометрически совершенный шестиугольник.

  Если вы хотите, чтобы шестиугольник располагался плоской стороной, а не стоял на углу, вы можете использовать ту же технику. Просто нарисуйте полукруги слева и справа, а не верхнее и нижнее пересечение креста и круга.

  И, наконец, если у вас нет компаса под рукой: вы можете подойти довольно близко, используя что-нибудь круглое, например, верхнюю часть стакана, чтобы нарисовать круги. Просто постарайтесь, чтобы верхний и нижний полукруги встретились как можно ближе к центру полного круга.

  Теперь вы изучили простой способ рисования шестиугольника с помощью циркуля, чтобы построить правильный шестиугольник.

  Как нарисовать шестиугольник от руки (без циркуля)

  В правильном шестиугольнике длина от центра до любого угла шестиугольника равна длине любой стороны. Из-за этого правильный шестиугольник можно представить как состоящий из шести равносторонних треугольников — треугольников, все три стороны которых имеют одинаковую длину. Давайте используем эти знания, чтобы научиться рисовать шестиугольник от руки.

  Рисование шестиугольника вручную

  Шаг 1: Нарисуйте треугольник

  Шаг рисования: Нарисуйте треугольник

  Итак, давайте нарисуем первый треугольник. Как уже упоминалось, все три стороны имеют одинаковую длину. Внутренний угол равностороннего треугольника равен 60 градусов. Это делает наш треугольник красивой и симметричной формой пирамиды.

  Шаг 2: Добавьте еще два перевернутых треугольника

  Шаг рисования: Добавьте еще два перевернутых треугольника

  Затем мы добавим еще два треугольника того же размера и формы. Они будут нарисованы вверх ногами, по одному с каждой стороны нашего начального треугольника.

  Вероятно, самый простой способ — провести горизонтальную линию через вершину начального треугольника. Затем вытяните стороны, пока они не встретятся с горизонтальной линией.

  Попробуйте отзеркалить треугольники как можно ближе к оригиналу – размер и все углы.

  Шаг 3: И еще два треугольника наверху

  Шаг рисования: И еще два треугольника наверху

  Давайте добавим еще два треугольника – теперь вы становитесь профессионалом в рисовании равносторонних треугольников.

  Эти двое стоят спиной к плоской стороне, снова вершинами вверх, как и наш первый треугольник.

  Их можно нарисовать, продлив боковые линии нашего первого треугольника за центр шестиугольника. Затем нарисуйте внешние стороны. Опять же, постарайтесь отразить нижние треугольники как можно точнее.

  Как видите, после того, как я нарисовал внешние стороны, мне пришлось немного подкорректировать внутренние. Теперь верхние точки моих треугольников хорошо совпадают с зеркальными треугольниками в нижней половине шестиугольника.

  Шаг 4: Заполните шестиугольник

  Шаг рисования: Заполните шестиугольник

  Ну, это самое простое. Чтобы закрыть последний треугольник, мы просто добавляем простую линию вверху. На этом рисунок шестиугольника завершен.

  Вот еще одна фигура, которую нужно построить дальше:

  Как нарисовать шестиугольник от руки: законченный рисунок

  Завершенный нарисованный от руки шестиугольник

  Завершенный нарисованный от руки шестиугольник

  Наконец, давайте наметим наш шестиугольник. Вы можете стереть направляющие треугольника, если планируете использовать свой шестиугольник в каком-либо дальнейшем рисунке.

  Как видите, хоть форма и не такая идеальная, как та, что была построена с помощью компаса, мы все равно нарисовали довольно правильную шестиугольную форму просто от руки.

  А если тебе хочется попрактиковаться в своих шестиугольниках на каком-нибудь реальном рисунке, как насчет того, чтобы нарисовать черепаху? Весь панцирь черепахи сделан из шестиугольников!

  Понравился этот урок? Поделись весельем с другими:

  Любишь рисовать? Никогда не пропустите учебник!

  Получайте уведомления, когда на Let’s Draw That публикуется новый учебник! (2-4 раза в месяц)

  	Рисуем лица тыкв на Хэллоуин

  Как нарисовать куб: 3 разных способа и перспективы

  Понравился этот урок? Поделись весельем с друзьями:

  Построение правильных многоугольников 2022 — Бесплатные математические задания

  Мы знаем, что a  правильный многоугольник   — это многоугольник, у которого   имеет все стороны равной длины и все внутренние углы. В этом уроке мы научимся строить их с помощью циркуля и линейки.

  Равносторонний треугольник

  Начнем с построения первого правильного многоугольника, равностороннего треугольника.

  Пример. Построить треугольник, зная длину стороны $a$.

  Сначала мы создаем эскиз. Это не обязательно должно быть точным, но это даст нам представление о том, с чего начать.

  Нарисуем луч с конечной точкой $A$, которая будет первой вершиной треугольника. Берем линейку и устанавливаем ширину компаса равной длине заданной стороны $a$. Затем поместите стрелку компаса в точку $A$ и начертите дугу. Убедитесь, что дуга пересекается с ранее нарисованным лучом. Точка пересечения дуги и луча — это наша вторая вершина, $B$. Не меняя ширины компаса, повторяем предыдущий шаг. Разница лишь в том, что мы ставим стрелку компаса в точку $B$ и делаем дугу, которая пересекается с первой. Мы видим, что дуги пересекаются в двух точках, что дает нам две последние вершины, $C$ и $C’$. Теперь у нас есть два треугольника, $\bigtriangleup ABC$ и $\bigtriangleup ABC’$. Треугольники конгруэнтны из-за теоремы SSS, поэтому мы говорим, что у нас есть только одно решение.

  Расширенный:  

  Мы использовали луч, чтобы получить точки $A$ и $B$, но если бы мы использовали линию, мы получили бы еще одну вершину $B’$ по другую сторону от $A $. Следуя шагам, описанным выше, мы получили бы еще два треугольника, всего четыре. Все четыре из них конгруэнтны, и мы рассматриваем их как одно решение проблемы.

  Пример. Построить треугольник, зная радиус описанной окружности.

  Сначала сделаем окружность $c(O, r)$ и один диаметр $\overline{AA’}$. Затем делаем окружность $c(A’, |OA’|)$. Точки пересечения окружностей $c(O,r)$ и $c(A’, |OA’|)$ — это $B$ и $C$, две оставшиеся вершины нашего треугольника.

   

  Квадрат

  Пример. Построить квадрат, зная сторону $a$.

  Сначала делаем набросок, чтобы знать расположение точек и сторон.

  Мы начнем с создания линии и точки $A$. Затем берем длину стороны $a$ в ширину компаса и делаем дугу, которая пересекается с линией, которую мы нарисовали первой. Пересечение — это точка $B$, наша вторая вершина. Теперь нам нужно построить линию, перпендикулярную $AB$, с точкой пересечения $B$. Мы делаем это, потому что хотим создать угол $\measuredangle ABC = 9{\circ}$.

  Теперь у нас есть перпендикулярная линия, и мы знаем, что вершина $C$ будет на ней. Возьмем длину стороны $a$ на ширину компаса и проведем дугу, которая пересекается с перпендикуляром – точка пересечения и есть наша вершина $C$. Осталось построить вершину $D$. Мы делаем это, создавая две дуги окружностей $c(A,a)$ и $c(C,a)$. Их пересечение является конечной вершиной, вершиной $D$.

  * Здесь мы построили только один квадрат, но мы могли бы построить четыре из них, следуя тому же процессу, что и при построении равностороннего треугольника.

  Пример. Как построить квадрат, если известен радиус описанной окружности?

  Сначала нарисуем точку $O$ и окружность $c(O, r)$. Выберите начальную точку $A$ в любом месте круга. Теперь проведем диаметр от $A$ до $O$. Пусть точкой пересечения диаметра и окружности будет точка $C$. Прямая $AB$ — это одна из диагоналей квадрата, который мы хотим построить. Как получить другой? Мы знаем, что диагонали в квадрате перпендикулярны, поэтому проводим перпендикуляр к диаметру $AC$. Убедитесь, что точкой пересечения является точка $O$. Теперь точками пересечения перпендикуляра и окружности $c(O,r)$ являются точки $B$ и $C$, наши две последние вершины.

   

  Правильный пятиугольник

  Сначала рисуем эскиз от руки. Он не должен быть идеальным, так как это не наша окончательная конструкция, мы просто будем использовать его для строгания.

  Пример. Построить правильный пятиугольник, зная сторону $a$.

  Создайте луч с точкой $B$ в конце, а затем постройте точку $A$ так, чтобы $|AB|=a$. Мы хотим создать биссектрису $|AB|$. Возьмите циркуль и убедитесь, что ширина компаса равна длине стороны $a$ (ВАЖНО!). Наденьте иглу на $B$ и сделайте две дуги окружности $c(B, a)$. Повторите шаг для дуг $c(A,a)$. Дуги пересекаются в точках $K$ и $L$. Соедините их, чтобы получить среднюю точку между $A$ и $B$, точку $M$. Опять же, оставьте радиус компаса равным $a$, поместите стрелку компаса на $M$ и нарисуйте дугу, которая пересекает биссектрису, образуя точку $N$. Теперь настройте компас на длину $AN$. Вставьте иглу в $A$ и проведите дугу, которая пересекается с лучом, который мы сделали в начале, что даст нам точку $P$.

  Расстояние от $M$ до $P$ очень важно, оно даст нам остальные вершины. Сделайте радиус компаса равным расстоянию между $M$ и $P$. Поместите иглу на $B$ и сделайте дугу, которая пересекается с одной из дуг, которые мы сделали, чтобы получить среднюю точку. Сделайте вторую дугу, которая пересекает биссектрису. Пересечениями будут точки $E$ и $D$ соответственно. Чтобы получить вершину $C$, мы поместим иглу в $A$ и повторим процесс.

  Пример. Постройте правильный пятиугольник, зная радиус описанной окружности.

  Постройте окружность $c(O, r)$ и два перпендикулярных диаметра, $\overline{AA’}$ и $\overline{PP’}$ . Теперь построим биссектрису отрезка $\overline{OP}$, точкой пересечения будет точка $M$. В качестве ширины компаса возьмите длину между $A$ и $M$ и поместите стрелку компаса на $M$, чтобы создать дугу, которая пересекается с $\overline{PP’}$. Пересечение $N$.

  Расстояние от $A$ до $N$ равно длине стороны $a$ правильного пятиугольника. Теперь, когда мы знаем длину $a$, нам нужно построить вершины. Пусть $D$ будет нашей первой вершиной.

  Сначала мы открываем циркуль на длину $a$ и ставим стрелку компаса на $A$. Теперь создадим дугу, пересекающуюся с окружностью $c(O,r|)$, что даст нам вершину $B$. Не меняя ширины циркуля, мы ставим стрелку на $B$ и делаем то же самое, чтобы получить вершину $A$, и так далее. Этот процесс даст нам оставшиеся $4$ вершины.

  Правильный шестиугольник

   

  Пример. Построить правильный шестиугольник, зная сторону $a$.

  Правильный шестиугольник можно разбить на $6$ равносторонних треугольников со стороной $a$. Вершина $O$ является центром вписанной и описанной окружностей, а $|AO|=|BO|=|CO|=|DO|=|EO|=|FO|$. Сначала мы строим $\bigtriangleup ABO$, следуя процедуре, которую мы использовали при построении равностороннего треугольника. Нарисуем $c(O, |AO|)$. Так как $O$ — центр описанной окружности, мы знаем, что вершины шестиугольника будут лежать на окружности. Теперь мы просто возьмем длину $a$ в ширину компаса и сделаем $4$ дуги на окружности.

  Не меняя ширины циркуля, ставим стрелку компаса на $B$, делаем дугу, которая пересекается с окружностью $c(O, |AO|)$, давая нам вершину $C$. Затем мы помещаем иглу в $C$ и делаем то же самое, чтобы получить вершину $D$, и так далее. Этот процесс даст нам последние $4$ вершины. Не имеет значения, начинаем ли мы с $A$ и делаем это по часовой стрелке или от $B$, как мы сделали здесь, результат будет одинаковым.

  Важно помнить:  В правильном шестиугольнике $\bigtriangleup ABO$ равносторонний треугольник, а это значит, что длина радиуса описанной окружности и длина стороны всегда равны.

   

  Пример. Построить правильный шестиугольник, зная радиус описанной окружности.

  Это еще проще. Мы просто рисуем окружность $c(O, r)$ и выбираем на ней начальную точку, пусть это будет точка $A$. В правильном шестиугольнике мы знаем, что радиус описанной окружности равен стороне многоугольника, что означает $r=|AO|=|AB|$. Теперь, когда у нас есть сторона правильного шестиугольника, мы строим оставшиеся $5$ вершин, как в предыдущем примере.

   

   

  Правильный восьмиугольник

  Пример. Как построить правильный восьмиугольник, если известен радиус описанной окружности?

  Сначала мы строим квадрат внутри данного круга с его диагоналями, следуя описанному выше процессу. Затем строим биссектрисы $\измеренного угла AOB, \измеренного угла BOC, \измеренного угла COD$ и $\измеренного угла DOA$. Биссектрисы пересекаются с описанными окружностями, что дает нам $4$ новых точек: $E, F, G$ и $H$. Эти точки являются оставшимися вершинами восьмиугольника.

   

  Правильный десятиугольник

  Пример. Как построить правильный десятиугольник, если известен радиус описанной окружности?

  Сначала мы строим правильный пятиугольник внутри заданного круга, следуя процессу, описанному в построении пятиугольника. Затем каждую вершину соединяем с центром описанной окружности, чтобы разделить пятиугольник на $5$ конгруэнтных треугольников. Следующим шагом является построение биссектрисы $\измеряемого угла AOB, \измеряемого угла BOC, \измеряемого угла COD,\измеряемого угла DOE$ и $\измеряемого угла EOA$.

  Биссектрисы пересекаются с описанными окружностями, что дает нам $5$ новых точек,  $F, G, H, I$ и $J$. Эти точки являются оставшимися вершинами десятиугольника.

  Правильный додекагон

  Пример. Как построить правильный двенадцатиугольник, если известен радиус описанной окружности?

  Как и в предыдущих двух примерах, мы можем построить правильный двенадцатиугольник из правильного шестиугольника. Биссектрисы центральных углов шестиугольника дают нам оставшиеся вершины двенадцатиугольника.

  Творческий проект для классов K-8

  ---

  Планы уроков
  

  • Задача «3N+1»
  • Задача с Всероссийской олимпиады по математике
  • Доказательство теоремы Пифагора с использованием подобных треугольников
  • Головоломка с номером 1089
  • Дополнительная плата
  • Прибавление в детском саду и первом классе
  • Арифметическое чудо из 1899 года
  • Старый купец и четверо его детей
  • Древний узел
  • Анимации на TI
  • Районы и границы
  • Площадь и периметр
  • Средний балл за тест
  • Мяч в коробке
  • Банан
  • Бочки, бочонки и другие фигурные контейнеры
  • Большие числа АКА Зерна риса на шахматной доске
  • Блочные дома
  • Сборка собачьей будки в масштабе
  • Сборка каркасной коробки в соответствии со спецификациями
  • Свечи
  • Корзины для конфет
  • Вместимость
  • Наутилус с камерой
  • Проверка, является ли число простым
  • Коробка с китайским календарем
  • Аккорды по кругу
  • Круг, квадрат и треугольник
  • Часы и время
  • Монеты
  • Раскрашивание линий в шестиугольнике
  • Разноцветные треугольники
  • Конгруэнтные треугольники
  • Счет
  • Счетная доска для юных учащихся
  • Счет до 100
  • Биговка бумаги по изгибам
  • Кубики
  • Куб со срезанным краем
  • Кулинарные полоски
  • Вырезание прямоугольника
  • Вырезание треугольника
  • Разрезание треугольника на две части равной площади и равного периметра
  • Вырезание равностороннего треугольника
  • Резка многогранников
  • Вывод формулы площади треугольника
  • Диагональ квадрата
  • Разделение квадрата
  • Деление с остатком на ТИ-108: два экземпляра
  • Собаки, кошки и мыши
  • Точка за точкой
  • Удвоение и деление пополам
  • Рисование прямоугольника
  • Рисование простой фигуры по словесным инструкциям
  • Рисование треугольников
  • Легкие квадраты
  • Яичная дилемма (Часть 1)
  • Возведение в степень
  • Факторинг
  • Необычные конверты
  • Нахождение дроби между двумя дробями
  • Пятиконечная трехмерная звезда
  • Подбрасывание монет
  • Сложенный бумажный цветок с шестью лепестками
  • Четыре жука
  • Четыре карты
  • Четыре кубика
  • От одного миллиарда до нуля
  • От одного до одного триллиона
  • Игра кругов и звезд
  • Игра в десятки
  • Гигантская энчилада
  • Шляпа для Хэллоуина
  • Орел или решка?
  • Шестиугольная головоломка
  • Как калькулятор вычисляет квадратный корень числа?
  • Сколько пентамино?
  • Как измерить угол без транспортира
  • Как преобразовать прямоугольник в другой прямоугольник
  • Гиперболы и эллипсы
  • Вписанный треугольник
  • Проценты
  • Юлекурв АКА Валентинка Корзина
  • Воздушные змеи
  • Дырявая крыша
  • Ушастые твари
  • Волшебные бобы
  • Волшебный складной кубик
  • Магический квадрат
  • Создание животных путем вырезания многоугольников
  • Изготовление блоков из четырех кубиков
  • Изготовление коробок
  • Изготовление эвольвенты
  • Лабиринт
  • Мини-слот-машина
  • Луны
  • Больше задач «точка-точка»
  • Больше старых словесных задач
  • Умножения «Сделано по Адаму Райсу»
  • Натан подбрасывает монету 20 раз
  • Игра в числа с кубиками
  • Одна треть
  • Парадокс средних
  • Разделение квадрата
  • Пазлы Пентагона
  • Алгебра телефонных номеров
  • Копилка
  • Игра с формами
  • Powerball 55
  • Красивая подарочная коробка
  • Тыквы
  • Пазл с камешками
  • Пирамида на четверти
  • Пирамида кубов
  • Пирамида из мрамора
  • Четырехугольники
  • Правильные многоугольники с равными площадями
  • Связанные проблемы
  • Прямоугольный треугольник
  • Последовательности составных чисел: конкурс
  • Формы чисел
  • Формы чисел с использованием треугольников
  • Шесть пирамид
  • Шестнадцать квадратных дюймов
  • Печать Соломона
  • Сортировочная игра
  • Спираль (марки К-4)
  • Спираль (5-8 классы)
  • Спираль Теодора на калькуляторе ТИ-83/84
  • Квадратные и кубические единицы
  • Квадрат в треугольнике
  • Соломенные многогранники
  • Алгоритм вычитания
  • Вычитание со счетчиками
  • Сумма двух квадратов
  • Выживший на шестиугольном острове
  • Татами
  • Чайные коробки
  • Преобразование температуры
  • Мозаика круга
  • Задача о лестнице и ящике
  • Контейнеры для сыра «Смеющаяся корова»
  • Практическая ценность доказательств
  • Три четверти
  • Круглая головоломка из трех частей
  • Бросание одного кубика
  • От треугольника до квадрата: Шарнирное рассечение
  • Превращение прямоугольника в квадрат путем рассечения
  • Двенадцать простых фигур
  • Двадцать четыре кубика
  • Две старые проблемы
  • Два брата-пастуха
  • Понимание длинного деления
  • Необычные контейнеры
  • Что дальше?
  • Что это за прямоугольник?
  • Инь Ян

  Как нарисовать 5-конечную звезду с помощью компаса

  Чтобы отпраздновать зимнее солнцестояние в этом году и уникальное соединение Сатурна и Юпитера, я создал этот точечный рисунок звезды. По сути, это набор пятиконечных звезд, нарисованных тысячами точек. Я тоже провел 3 часа мастер-класс по пунктирному и геометрическому искусству и буду повторять его время от времени, так что дайте мне знать, если вы хотите провести еще один. С помощью циркуля и линейки легко нарисовать идеальную пятиконечную звезду. Вот два метода с пошаговыми инструкциями о том, как нарисовать 5-конечную звезду.

  **** Этот пост может содержать партнерские ссылки. Для получения дополнительной информации, пожалуйста, прочитайте мой отказ от ответственности. ****

   

  Я использовал перо Sakura Micron Pigma Pen с размером острия всего 0,5 мм, чтобы нарисовать изображение выше, но вы также можете рассмотреть более тонкий вариант, чтобы нарисовать более сложный рисунок даже больше точек.

   

  Два способа рисования пятиконечной звезды

  Как вы увидите, простую пятиконечную звезду можно нарисовать как с транспортиром, так и без него. В рисовании без транспортира есть элегантность, которую я люблю, но попробуйте их оба и посмотрите, какой из них вам больше нравится. Однако, если вы хотите попробовать что-то более сложное, ознакомьтесь с моим учебным пособием по узору «Звезда и крест».

  Список оборудования

  Вот что вам понадобится, чтобы нарисовать пятиконечную звезду. Обратите внимание, что для первого метода вам не понадобится транспортир.

  • Geometry compass
  • Pencil
  • Protractor
  • Ruler
  • Rubber/Eraser
  • White paper
  • Smudge-proof fineliner pen

  D ifficulty: Easy

  How to draw a 5 point star с циркулем и линейкой

  1. Нарисуйте круг в центре листа бумаги.

  2. Проведите прямую линию через центр круга.

   

  3. Сделайте компас немного шире исходного круга и поместите точку компаса там, где линия пересекается с нижней частью круга (отмечена черным крестиком). Нарисуйте две короткие дуги, как показано ниже.

   

  4. Сделайте то же самое с другой стороны круга, чтобы дуги пересеклись.

   

  5. Нарисуйте линию, соединяющую два креста.

   

  6. Поместите острие компаса в центр круга и нарисуйте еще две дуги, как показано ниже.

   

  7. Поместите острие компаса на пересечение горизонтальной линии с левой стороной круга и нарисуйте дополнительные дуги, которые пересекаются с двумя предыдущими.

   

  8. Соедините два только что созданных креста второй вертикальной линией. Эта линия проходит параллельно исходной вертикальной линии.

   

  9. Поместите острие компаса на пересечение двух только что нарисованных линий и нарисуйте окружность, проходящую через центр исходной окружности (как показано ниже).

   

  10. Теперь поместите острие компаса на пересечение вертикальной линии, проходящей через центр большего круга и нижний край этого круга. Нарисуйте арочный полукруг, который касается края маленького круга.

   

  11. Удерживая стрелку компаса на том же месте, нарисуйте вторую арку, касающуюся другой стороны меньшего круга.

   

  12. Пересечения, отмеченные зелеными крестиками ниже, должны быть равномерно распределены вокруг вашего исходного круга и являются пятью точками вашей звезды.

   

  13. Оставаясь карандашом, соедините точку 1 с 2, точку 2 с 3, точку 3 с 4 и точку 5 обратно с точкой 1. значение во многих культурах с древних времен.

   

  14. Держите пентаграмму карандашом, и вы можете использовать ее, чтобы нарисовать контур вашей пятиконечной звезды тушью.

   

   

  Как нарисовать пятиконечную звезду с помощью циркуля и транспортира

  Хотя мне нравится элегантность рисования геометрических фигур с помощью циркуля и линейки, если вы хотите нарисовать более сложную звезду, возможно, вам будет проще использовать следующий метод.

  Вы можете просто разделить 360 градусов на 5, что даст вам 72 градуса, и отметьте с помощью транспортира 5 равных делений вашего круга – 72, 144 (72 x 2), 216 (72 x 3) и 288 (72 x 5) градусов.

  Как и ранее, соедините точки 1 с 2, 3 с 4, 4 с 5 и 5 с 1.

  Как и прежде, вы можете нарисовать внешние линии пентаграммы, чтобы получить идеальную пятиконечную звезду.

   

  Что такое Рождественская звезда?

  В этот день зимнего солнцестояния, 21 декабря, две крупнейшие планеты Юпитер и Сатурн оказались ближе друг к другу в небе, чем в течение 800 лет. Ходили слухи, что они будут настолько близки, что будут похожи на одну яркую звезду. Об этом ведутся споры, но будут они или нет, зависит от того, где вы находитесь, насколько хорошее у вас зрение и погодные условия. Если у вас плохое зрение, вы вполне можете увидеть их как одну яркую звезду, и из-за времени года неудивительно, что люди называют ее Рождественской звездой. Прошлой ночью там, где я живу, было пасмурно, и лучшая ночь для наблюдения за звездами во время этого соединения может оказаться в канун Рождества.

  Так какой же была оригинальная Рождественская Звезда? Некоторые считают, что необычно большая яркая звезда, о которой говорится в Библии и появившаяся при рождении Иисуса, была соединением планет. Но это лишь одна из множества теорий. Мы точно не знаем ни года рождения Иисуса, ни даже времени года.

   

  Видеть звезды!

  Бесконечное множество рисунков, которые можно создать, начиная с этой простой звезды и используя такие техники, как ткачество или пунктир. Скоро появятся новые уроки блога.

  Подпишитесь на мой информационный бюллетень , чтобы быть в курсе всех моих новостей и новых классов, включая мой недавно запущенный онлайн-семинар по звездам и зернистости!

   

  Рисунок компаса. Как нарисовать компас шаг за шагом

  Компас — это простой, но невероятно полезный навигационный инструмент. Эти полезные маленькие гаджеты всегда направят вас на север, и это поможет вам всегда найти дорогу.

  Они также стали символом направления и приключений в жизни, и может быть очень весело научиться рисовать компас, чтобы вы могли создавать интересные дизайны.

  Это руководство покажет вам, как нарисовать один из этих удивительных инструментов самостоятельно!

  Наше пошаговое руководство по рисованию компаса поможет вам не заблудиться в своем путешествии по рисованию!

  О чем эта запись в блоге

  • Как нарисовать компас — приступим!
    • Шаг 1
    • Шаг 2 – Затем нарисуйте некоторые внутренние детали компаса
    • Шаг 3 – Теперь начните лицевую сторону компаса
    • Шаг 4 – Затем нарисуйте еще несколько деталей для лица
    • Шаг 5. Теперь вы можете закончить окончательные детали вашего рисунка компаса
    • Шаг 6. Завершите рисунок компаса каким-либо цветом
    • Ваш рисунок компаса готов!

  Шаг 1

  Для этого первого шага нашего руководства по рисованию компаса мы будем делать его простым. Все, что мы сейчас будем делать, это нарисовать идеальный круг, который послужит контуром компаса.

  Есть несколько способов нарисовать идеальный круг. Самый простой способ — использовать компас для рисования (который сильно отличается от компаса, который вы сейчас рисуете!)

  Эти простые инструменты для рисования значительно упрощают рисование круга с помощью ручки или карандаша. Вы также можете обвести что-то круглое и плоское, если у вас нет под рукой циркуля.

  Что бы вы ни выбрали, вы готовы продолжить!

  Шаг 2 – Затем нарисуйте некоторые внутренние детали компаса

  На этом втором этапе рисования вашего компаса мы добавим некоторые детали к внутренним частям компаса.

  На этом шаге вы захотите использовать любой метод, который вы использовали для рисования внешнего круга компаса, так как мы будем рисовать еще несколько кругов внутри него.

  Для этого просто нарисуйте еще один круг внутри первого и близко к контуру. Затем нарисуйте еще один внутри этого, еще ближе, чем раньше.

  Наконец, мы добавим маленькую округлую фигуру поверх компаса.

  Шаг 3 – Теперь начнем с лица компаса

  Компас не был бы очень полезен без направлений на лице, поэтому мы нарисуем некоторые из этих деталей на этом шаге нашего руководства по рисованию. компас.

  Сначала нарисуйте букву N в верхней части компаса с крошечным треугольником над ней. Затем нарисуйте боковую букву W слева и боковую букву Е справа.

  Наконец, закончите буквой S внизу. Каждая из этих букв также будет иметь крошечный треугольник между ними и контуром лица.

  Затем, используя закругленные линии, вы можете нарисовать острые формы, которые сформируют стрелки компаса, как показано на образце.

  Затем вокруг этих рук можно добавить несколько мелких деталей, прежде чем переходить к шагу 4.

  Шаг 4 – Затем нарисуйте еще несколько деталей для лица.

  Основные части вашего компаса завершены, поэтому в следующих шагах мы добавим несколько мелких деталей.

  В этой части мы добавим множество маленьких прямых линий по внутреннему периметру циферблата компаса.

  Сейчас они будут идти только по левой стороне, и эти линии помогают более точно ориентироваться на реальном компасе.

  Если вы хотите быть точным, вы можете подсчитать, сколько их на нашем эталонном изображении, и попытаться воспроизвести его для своего собственного изображения.

  Шаг 5 – Теперь вы можете закончить последние детали вашего рисунка компаса

  Мы будем завершать последние детали на этом шаге нашего руководства о том, как нарисовать компас.

  Эта часть должна быть довольно простой, так как все, что вам нужно сделать, это повторить то, что вы сделали на предыдущем шаге, только с другой стороны.

  Как только вы закончите эти маленькие линии, вы будете готовы к последнему шагу! Однако, прежде чем двигаться дальше, вы также можете добавить некоторые собственные штрихи.

  Возможно, вы могли бы нарисовать причудливую цепочку, на которой будет висеть компас, или поставить его поверх карты, чтобы по-настоящему завершить навигационную тему.

  Вы также можете нарисовать на компасе несколько гравировок или изменить некоторые детали.

  Это всего лишь несколько деталей, на которые вы могли бы обратить внимание, так что не забудьте повеселиться и поэкспериментировать, завершая эту картинку для последнего шага!

  Шаг 6 – Завершите рисунок компаса, используя цвет

  На этом шестом и последнем этапе рисования компаса вы можете повеселиться, добавив к нему несколько цветов!

  В нашем примере мы использовали более приглушенные оттенки серого и красного для компаса, но эти цвета являются всего лишь предложением.

  Вы можете использовать немного золотисто-желтого цвета, чтобы он выглядел как бронза, или использовать различные цвета, чтобы он выглядел так, как будто он сделан из разных материалов.

  Вы также можете изменить материалы и художественные инструменты, которые вы используете для компаса, так как использование различных материалов может быть отличным способом добиться любого тона, который вы хотите для рисунка.

  Это ваш шанс показать, насколько вы креативны, поэтому нам не терпится увидеть, какие цвета и материалы вы используете, чтобы закончить свой удивительный рисунок!

  Ваш компас готов!

  Вы дошли до конца этого руководства по тому, как нарисовать компас , и вы должны очень гордиться своим невероятным произведением искусства!

  Мы надеемся, что это руководство показало вам, что рисовать одним из этих полезных инструментов может быть намного проще и веселее, чем вы могли себе представить.

  Теперь вы можете показать нам, как, по вашему мнению, должен быть закончен этот рисунок, и есть так много деталей и цветов, которые вы можете использовать для этого. Обязательно повеселитесь и посмотрите, что вы можете придумать!

  Это руководство, которое вы только что закончили, является одним из многих, которые есть на нашем веб-сайте для вас! Обязательно заходите к нам почаще, чтобы насладиться многочисленными руководствами, которые мы часто загружаем.