Как определить градус без транспортира: «Как измерить угол без транспортира?» – Яндекс.Кью

Как узнать градус угла без транспортира — MOREREMONTA

1. Для того, чтобы узнать угол между двумя стенами делаем отметки на стенах на одинаковом расстоянии от угла (например 50 или 100 см от угла, чем больше, тем точнее). Обозначим это расстояние ‘a’. Дальше.

2. Дальше меряем расстояние между отметками (т.е диагональ угла) — обозначим ‘С’.

3. Потом расчёты —

Осталось рассчитать, сколько градусов в вашем угле по формуле: cos(γ) = (a 2 + a 2 – c 2 ) / (2 • a • a)

Получив cos(γ) угла, далее через функцию arccos узнаём сколько это будет в градусах: arccos (cos(γ)) = угол.

Т.е. по примеру это: (50 2 + 50 2 – 71,5 2 ) / (2 • 50 • 50) = -0,02245 отсюда arccos (-0,02245)= 91.28 градусов.

Здесь можно посчитать сразу!

Наш калькулятор:

Доступ к калькулятору платный!
На неделю — 37 р!

Что нужно сделать?
1. Зарегистрироваться — здесь!
2. Войти — здесь!
3. Пополнить счёт, кликнув по картинке (виза, master card, мобильные операторы) —

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов.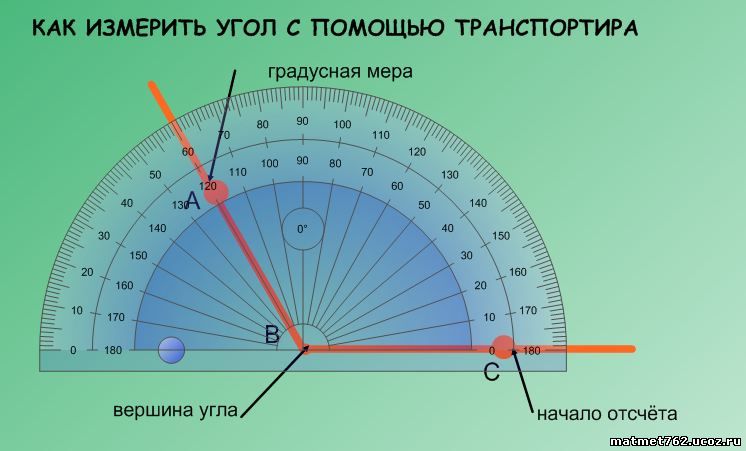

Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем.

Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить:

у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов.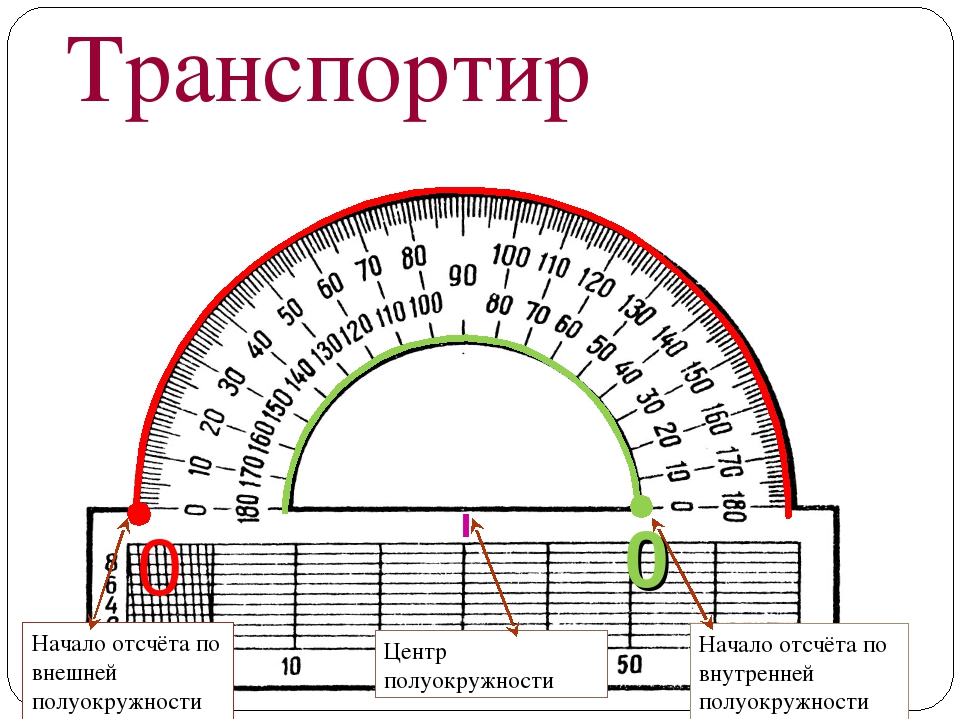 Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.

Измерить угол – значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.

Обычно за единицу измерения углов принимают градус. Градус – это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).

Измерение углов транспортиром

Для измерения углов используют специальный прибор – транспортир:

У транспортира две шкалы – внутренняя и внешняя.

Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.

Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:

Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов и пишут: ∠BOC = 60°, ∠MON = 120°.

Для более точного измерения углов используют доли градуса: минуты и секунды. Минута – это угол, равный части градуса. Секунда – это угол, равный части минуты. Минуты обозначают знаком ‘, a секунды – знаком ». Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:

Свойства измерения углов

Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.

Рассмотрим угол AOB:

Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.

Развёрнутый угол равен 180°.

Любой угол имеет определённую величину, большую нуля.

«Строим углы без транспортира» (5 класс)

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа № 4

г.Нелидово Тверской области

Выполнила: ученица 5а класса

Генченкова Елизавета

Руководитель работы: Орлова Ольга Геннадьевна

2017 г.

Объект исследования:
углы с различными градусными мерами; инструменты для измерения углов.

Предмет исследования:
процесс построения углов без использования транспортира.
Гипотеза:
можно предположить, что существуют углы разных градусных мер, которые

можно построить без применения транспортира, а только пользуясь линейкой без мерных делений, клетчатой бумагой.

Методы исследования:
— поисковый метод с использованием научной и учебной литературы, а также поиск необходимой информации в сети Интернет;
— графическое моделирование, анализ и классификация полученных результатов.

Целью работы:
является знакомство с инструментами для измерения углов, исследование метода построения углов заданной градусной меры без использования транспортира.

Задачи:

1. Провести практическую работу по построению острых углов заданной градусной меры (от 10° до 80°, кратных 10) и выявлению «контрольных» точек – узлов для лучей каждого угла.

2. Проанализировать полученные результаты и систематизировать их

3. Определить группы задач, которые можно решить с помощью исследованного метода построения углов.

4. Сделать вывод о подтверждении или опровержении выдвинутой гипотезы.

Актуальность:

 в курсе геометрии при решении задач часто приходится строить иллюстративные чертежи различных фигур по заданному условию. Владение методом построения углов на клетчатой бумаге позволяет чертить заданные углы с достаточной точностью, не требует наличия транспортира и экономит время на выполнение чертежа.

Содержание:

1. Введение.

2. Построение углов: история и современность.

3. Практическая часть. Построение углов без помощи транспортира.

1) Построение угла 45° без помощи транспортира.

2) Построение острых углов с градусной мерой, кратной 10° без помощи транспортира.

3) Построение тупых углов с градусной мерой, кратной 10°, от 100° до 170°

без помощи транспортира.

4) Построение углов с помощью угольников.

5) Построение углов 30°, 45°, 60°, 90° в практической жизни.

6) Измерение углов по пальцам рук.

4. Выводы и заключение.

5. Литература.

1.ВВЕДЕНИЕ

Увлечение отдельной областью математики часто начинается с размышления над какой-то особенно понравившейся задачей. При изучении в 5 классе на уроках математики темы «Построение угла заданной величины», мы научились строить углы с помощью транспортира.

И сразу обнаружили, что некоторые углы гораздо быстрее и более точно можно начертить в тетрадке с помощью одной только линейки.

Углы с градусными мерами 90° и 180° можно построить, проведя луч по горизонтальным или вертикальным линиям тетради, а углы в 135° и 45° — по диагоналям клеток.

Именно тогда я и заинтересовалась вопросом, а можно ли построить и другие углы, используя только клетчатую бумагу и линейку?

Так появилась моя исследовательская работа «Строим углов без транспортира».

Казалось бы, что увлекательного можно найти на клетчатой плоскости, то есть, на листке бумаги, расчерченном на одинаковые квадратики?

Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны.

Своё исследование я решила начать с изучения ответа на вопрос, как решались задачи на построение углов, начиная с древних времен и до сегодняшнего времени.

2. ПОСТРОЕНИЕ УГЛОВ: ИСТОРИЯ И СОВРЕМЕННОСТЬ

Понятие градуса и появление первых инструментов для измерения углов связывают с развитием цивилизации в древнем Вавилоне, хотя само слово градус имеет латинское происхождение (градус–от лат.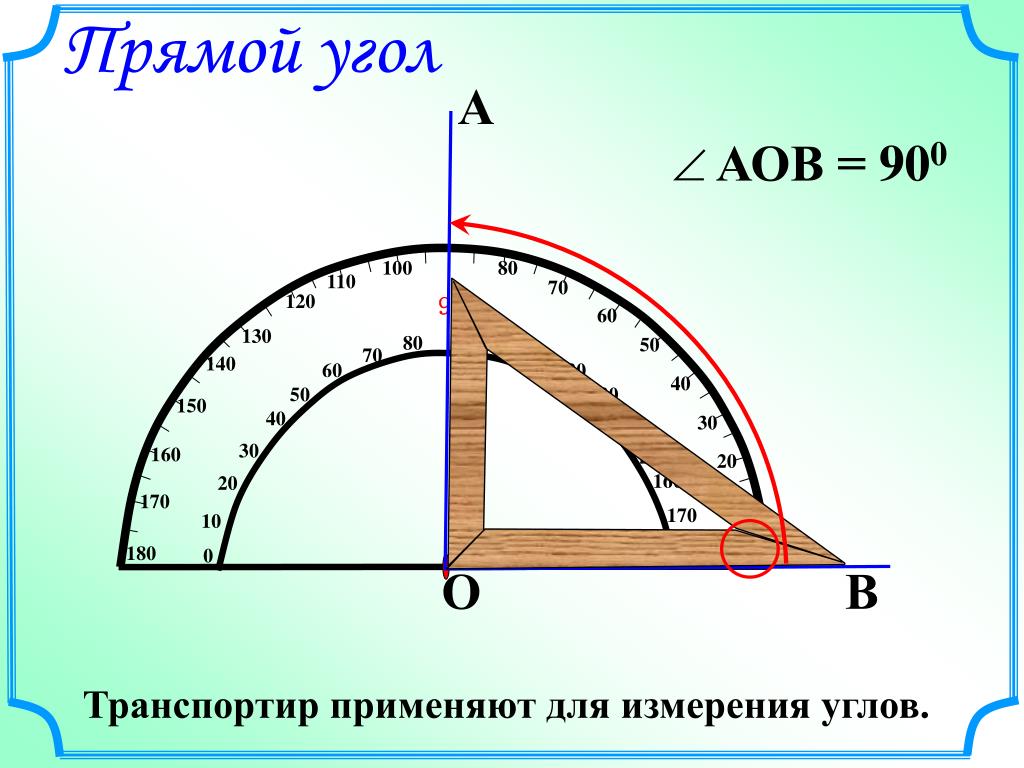 gradus- “шаг, ступень”). Градус получится, если, разделить окружность на 360 частей.

Возникает вопрос – а почему древние вавилоняне делили именно на 360 частей.

Дело в то, что в Вавилоне была принята шестидесятиричная система счисления. Более того, число 60 считалось священным. Поэтому все вычисления были связаны с числом 60.

История не сохранила имя ученого, который изобрел транспортир – возможно в древности этот инструмент имел совсем другое название.

Современное название происходит от французского слова ”ТRANSPORTER”, что означает “переносить”.

Первые задачи на построение углов возникли в глубокой древности. Возникли они из хозяйственных потребностей человека. Уже древними архитекторами и землемерами приходилось решать простейшие задачи на построение, связанные с их профессией.

Первые греческие ученые, которые занимались решением геометрических задач на

построение, были: Фалес Милетский (624 – 547 гг. до н.э.), Пифагор (ок. 580 – 500 гг. до н.э.), Платон (427 – 347 гг. до н.э.).

Самые первые задачи на построение, по-видимому, решались непосредственно на

местности и заключались в проведении прямых линий и построения прямого угла.

К задачам на построение прибегали древние инженеры, когда составляли рабочий чертеж того или иного сооружения и решали вопросы, связанные с отысканием красивых геометрических форм сооружения и его наибольшей вместимости.

Задачи на построение помогали людям в их хозяйственной жизни, их решения формулировались в виде ‘практических правил», исходя из наглядных соображений.

Именно эти задачи и были основой возникновения наглядной геометрии, нашедшей довольно широкое развитие у древних народов Египта, Вавилона, Индии и др.

Платон и его ученики считали построение геометрическим, если оно выполнилось при помощи циркуля и линейки, то есть путем проведения окружностей и прямых линий.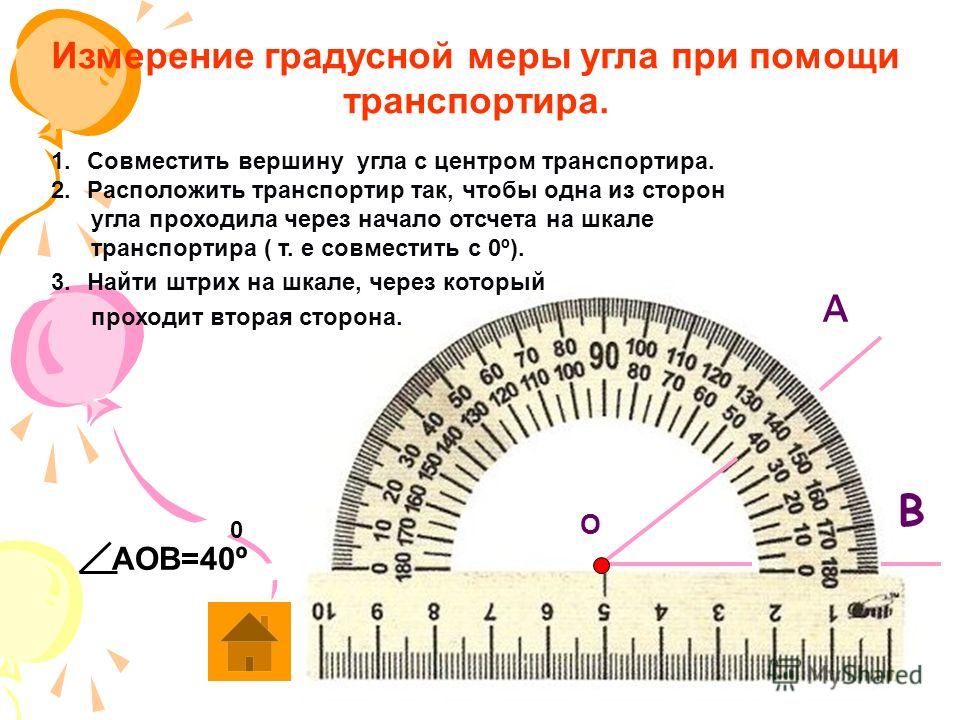 Если же в процессе построения использовались другие чертежные инструменты, например транспортир, то построение не считалось геометрическим.

Древние греки вслед за Платоном стремились к геометрическим построениям и считали их идеалом в геометрии.

Но древние ученые производили измерения не только транспортиром – ведь этот

инструмент был неудобен для измерений на местности и решения задач прикладного

характера. А именно прикладные задачи и являлись главным предметом интереса древних геометров.

Изобретение первого инструмента, позволяющего измерять углы на местности,

связывают с именем древнегреческого ученого Герона Александрийского (I в. до н.э). Он описал инструмент “диоптр”, позволяющий измерять углы на местности и решать множество прикладных задач.

Но прогресс не стоит на месте и в ХVII веке был изобретен прибор нивелир, а в следующем веке английским механиком Джессе Рамсденом был изобретен другой прибор – теодолит.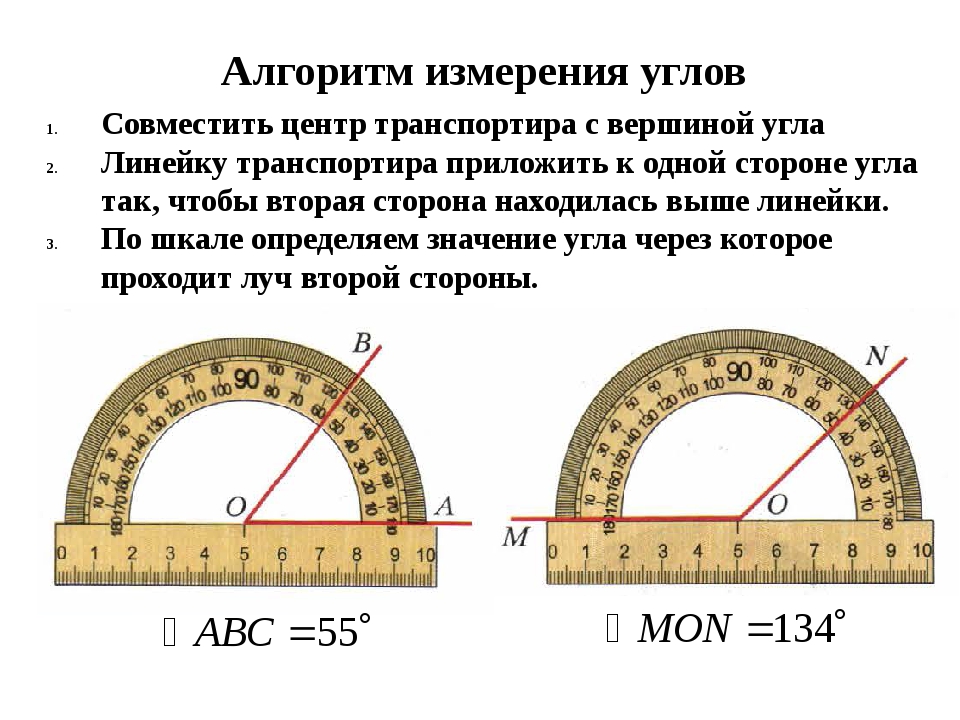

теодолит

Сегодня теодолит – сложный прибор. Многие работы (в том числе и строительство) требуют предварительной консультации геодезистов измерений с помощью теодолита.

Однако усовершенствование инструментов для измерения углов связано не только с

проведением строительных работ. С древнейших времен люди путешествовали, познавая окружающий мир. Путешественниками необходимо было уметь ориентироваться в пространстве. На долгие века основным ориентиром путешественников стали звезды.

Появился первый инструмент путешественников – астролябия. Астролябия(греч. astrolabion, от astron — «звезда» и labe – “схватывание»; лат. astrolabium) — угломерный прибор, служивший до начала XVIII в. для определения положений светил на небе.

Секстант — это наиболее совершенный прибор для измерения угловых координат небесных тел того времени. Его изобретение приписывается Исааку Ньютону. Секстант позволял измерять как широту, так и долготу точки наблюдения, причем с довольно высокой точностью.

В настоящее время широко используются современные приборы для измерения углов на местности.

Геодезический инструмент для измерения углов при съёмках на местности, специальный вид компаса- буссоль.

Простейший геодезический инструмент, служащий для измерения углов наклона местности с точностью до десятых долей градуса- эклиметр.

Необычный объект, который мы можем наблюдать на фото, был найден в гробнице древнеегипетского архитектора Ха (Kha). Без малого столетие прошло с тех пор, как историки впервые задались вопросом о предназначении странного артефакта.

Недавно предположение о возможном способе использования объекта выдвинула ученая-физик. Гипотеза, предложенная Амелией Спаравигной (Amelia Sparavigna) из Туринского политехнического университета (Turin Polytechnic), базируется на числовых отметках, якобы присутствующих на поверхности артефакта.

Архитектор Ха известен тем, что во времена 18-той династии (приблизительно 1400 год до нашей эры) он был задействован в строительстве гробницы фараона. Собственную же усыпальницу Ха нашли 1906 году неподалеку от Долины Царей — это открытие принадлежит археологу Эрнесто Скьяпарелли (Ernesto Schiaparelli). Среди вещей, когда-то принадлежащих архитектору, удалось идентифицировать измерительные пруты длиной в локоть (45 см), инструмент, напоминающий современный угольник, а также неизвестное полое деревянное орудие. По мнению Скьяпарелли, это был инструмент для выставления уровня.

Детально осмотрев старую находку, Амелия Спаравигна пришла к выводу, что на самом деле этот последний объект служил в качестве транспортира — в пользу такой версии свидетельствуют 16 лепестков, расположенных по окружности и находящихся на равном расстоянии друг от друга. Эти лепестки окружены круглым узором, имеющим 36 углов. Очевидно, продолговатая ровная часть инструмента устанавливалась на поверхность, после чего, с помощью уровня, можно было определить угол наклона того или иного объекта.

Числа, присутствующие на находке, якобы соответствовали двум измерительным системам, применявшимся в древнем Египте. Первая, внутренняя часть узора, соответствует шестнадцатичной счетной системе (соответствует современной десятичной). Вторая отображает 36 созвездий, известных египтянам.

Современные угломеры

Транспорти́р (фр. transporteur, от лат. transporto «переношу») — инструмент для построения и измерения углов. Транспортир состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы), разделённого на градусы от 0 до 180°. В некоторых моделях — от 0 до 360°.

Разновидности транспортиров

• Полукруговые (180 градусов) — наиболее простые и древние транспортиры.

• Круговые (360 градусов).

• Геодезические, которые бывают двух типов: ТГ-А — для построения и измерения углов на планах и картах; ТГ-Б — для нанесения точек на чертежной основе по известным углам и расстояниям. Цена деления угломерной шкалы — 0,5°, прямолинейной — 1 миллиметр.

• Улучшенные типы транспортиров, которые необходимы для более точных построений и измерений. Например, существуют специальные транспортиры с прозрачной линейкой с угломерным нониусом, которая вращается вокруг центра.

Транспортиры изготавливаются из стали, пластмассы, дерева и других материалов. Точность транспортира прямо пропорциональна его размеру (чем больше транспортир, тем меньше цена одного деления).

Полукруговой транспортир Круговой транспортир Геодезический транспортир

Угломер электронный Угломер строительный

Угломер Чижевского представлял собой треногу, на которой крепился круг с делениями, на его оси — подвижная алидада с указателем и визирная трубка на ней. Был еще и компас для ориентирования прибора. Измерив угловые расстояния между своей батареей и целью, командир производит геометрические расчеты и передает необходимые данные по телефону или через связных на свою батарею. Используя их, обученные наводчики направляют орудия на цель. Во время стрельбы командир батареи с помощью бинокля корректирует точность попадания снарядов в цель. Новый способ стрельбы с закрытых позиций давал возможность нанести удар по врагу не одним выстрелом из одного орудия, а со всех орудий разом широким фронтом огня – веером, сохранив при этом людей и технику.

Вот такая история возникновения различных приборов для измерения углов не только на чертежах, но и на любой местности, включая даже небесное пространство!

Таким образом, я выяснила, что на современном этапе существует множество приборов, позволяющих измерять и строить углы с различной степенью точности, которые применяются людьми самых разнообразных профессий, а при изучении курса геометрии в школе для построения углов заданной градусной меры в основном используется циркуль, линейка и транспортир.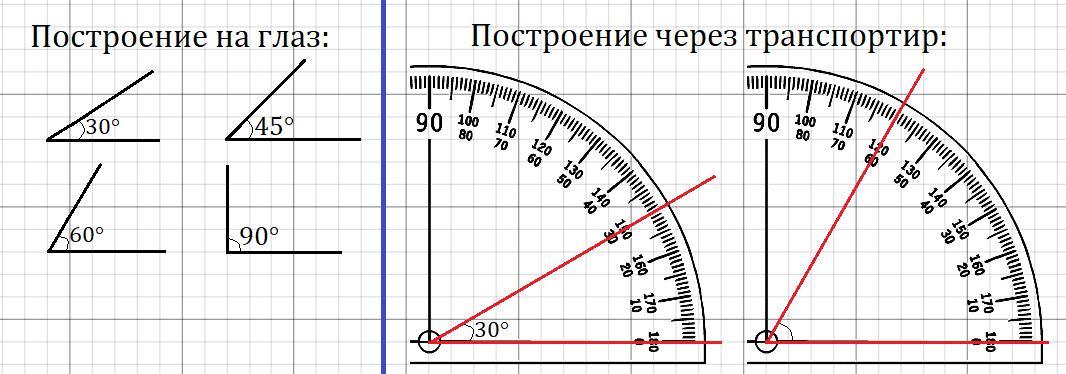

3.ПРАКТИЧЕСКАЯ ЧАСТЬ.

1)Построение угла 45° без помощи транспортира.

Угол 45 градусов в геометрии встречается часто.

Рассмотрим, как легко можно построить угол 45 градусов без транспортира, пользуясь только линейкой, карандашом и клеточками тетради.

Легче всего строить прямой угол.

 

Для этого из одной точки по клеточкам строим горизонтальный и вертикальный лучи. 

Градусная мера прямого угла — 90 градусов. 45 градусов — половина от 90º. Значит, чтобы построить угол 45 градусов, нужно взять половину прямого угла.

Сделать это очень легко. Выбираем вершину угла на пересечении клеточек. Одну сторону угла, например, горизонтальный луч, проводим с помощью линейки по клеточкам. Для построения второй стороны угла 45º каждую клеточку делим по диагонали (отмечаем несколько точек):

Затем с помощью линейки и карандаша через эти точки проводим второй луч.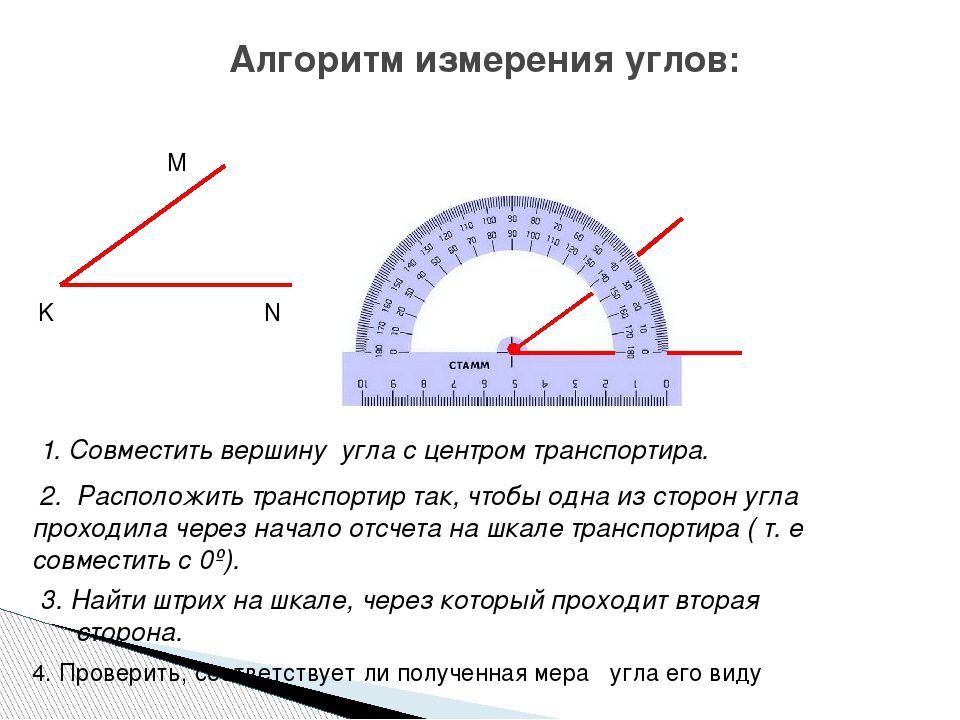 Получили угол 45 градусов:

2)Построение острых углов с градусной мерой, кратной 10° без помощи транспортира.

Для проведения исследования я на листке клетчатой бумаги построила острые углы,

начиная от 10° до 80°, с интервалом в 10°. Центр угла был расположен в узле клеток. Один из лучей, образующих угол, провела горизонтально слева направо.

Далее с помощью транспортира начертила лучи для всех исследуемых углов.

Если второй луч проходил точно через узел клеток, то информацию об этом угле заносила в таблицу.

Положение «контрольного» узла относительно вершины данного угла отмечалось следующим образом: сначала указывалось количество целых клеток вверх, затем вправо.

В результате получилась такая таблица:

Проанализировав данные таблицы для построения углов, можно заметить, что для углов

от 20° до 70° количество клеток вверх на единицу превышает количество десятков в

градусной мере угла.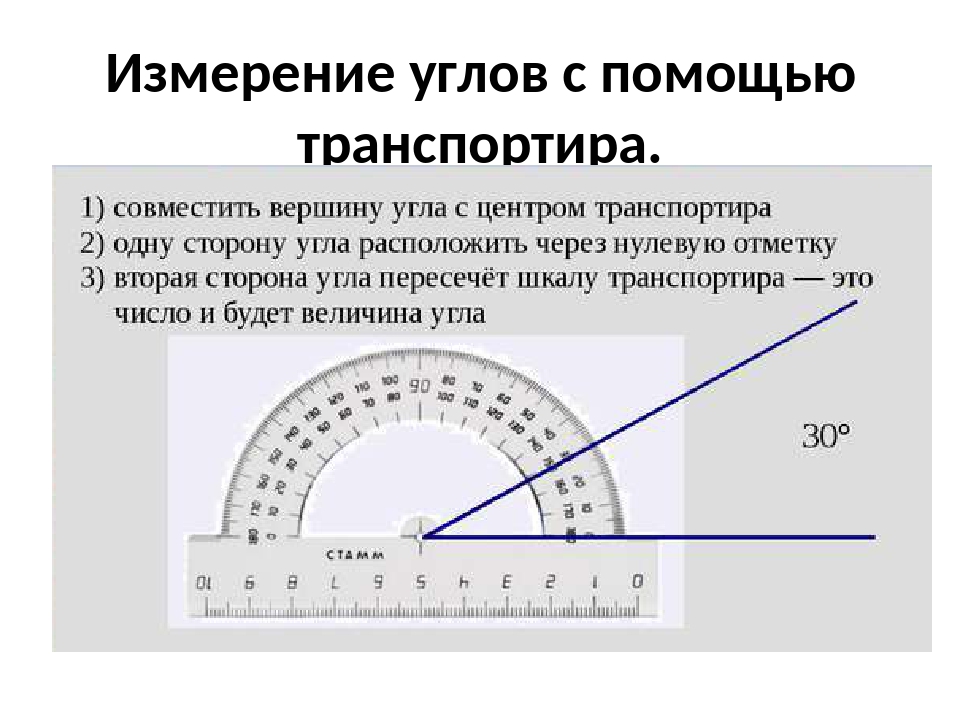 Причем сумма клеток вверх и вправо для всех этих углов равна 11.

Если прибавить к числу десятков искомого угла единицу, то получим количество клеток по вертикали. Если это число отнять от 11, то получим количество клеток по горизонтали от вершины угла.»

Например, для построения угла в 70° нужно отступить 8 (7+1) клеток по вертикали и 3(11-8) клетки по горизонтали в сторону первого луча.

Анализ данных в полученной таблице еще раз убеждает нас в существовании красоты, закона симметрии и порядка в науке математике.

3)Построение тупых углов с градусной мерой, кратной 10°, от 100° до 170° без помощи транспортира.

Исследованный метод построения углов позволяет решать следующую геометрическую задачу: построение тупых углов от 100° до 170° с шагом в 10°.

Смежные углы имеют общий луч. Поэтому для построения тупых углов можно

пользоваться «контрольной» точкой смежного ему острого угла из таблицы. Только

отсчет клеток по горизонтали выбирается в противоположном горизонтальному лучу

направлении (в нашем случае влево).

4)Построение углов с помощью угольников.

Я исследовала чертёжные инструменты – угольники.

Угольник — линейка в форме прямоугольного треугольника, как правило, с миллиметровой шкалой и с пустотой в форме уменьшенного подобного треугольника внутри.

Наиболее распространены угольники двух видов: с острыми углами по 30 и 60 градусов и равнобедренными с одинаковыми острыми углами по 45 градусов. Угольники используются в черчении для построения некоторых углов без помощи транспортира.

При использовании двух угольников можно построить больший набор углов, прикладывая их друг к другу, например, угол в 75 градусов (30+45), 120 градусов (90+30) и т.д. Покажу, как это сделать…

Понадобятся два вида угольников: первый с углами по 45 градусов, а второй — по 30 и 60.
1)75 градусов можно построить следующим образом: сначала построить угол в 30, а затем от него отложить 45 градусов.

2) 135 градусов: построить прямой угол, затем от него отложить 45 градусов.
3) 25 градусов: построить угол в 60 градусов,  затем от луча внутри угла отложить 45 градусов.

С помощью угольников можно построить углы 105◦, 15◦ и другие.

105= 60+45, 15=60-45 и так далее.

5)Построение углов 30°, 45°, 60°, 90° в практической жизни.

Часто домашнему мастеру необходимо срочно произвести какое либо измерение или сделать разметку под определенным углом, а под рукой нет либо угольника, либо транспортира. В этом случае его выручат несколько простых правил.

Угол 90 градусов.

Если нужно срочно построить прямой угол, а угольника нет, можно воспользоваться любым печатным изданием. Угол бумажного листа — очень точный прямой угол (90 град. ). Резательные (вырубочные) машины в типографиях настроены очень точно. Иначе исходный рулон бумаги начнет резаться вкривь и вкось. Поэтому вы можете быть уверены, что этот угол — именно прямой.

А если нет даже печатного издания или необходимо построить угол на местности, например при разметке фундамента или листа фанеры с неровными краями? В этом случае нам поможет правило золотого (или египетского) треугольника.

Золотым (или египетским, или Пифагоровым) треугольником называется треугольник со сторонами, которые соотносятся друг с другом как 5:4:3. По теореме Пифагора, у прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Т.е. 5х5 = 4х4 + 3х3. 25=16+9 и это неоспоримо.

Поэтому для построения прямого угла достаточно на заготовке провести прямую линию длиной 5 (10,15,20 и т.д. кратной 5 см). А затем, из краев этой линии начать отмерять с одной стороны 4 (8,12,16 и т.д кратно 4 см), а с другой — 3 (6,9,12,15 и т. д. кратно 3 см) расстояния. Должны получиться дуги с радиусом 4 и 3 см. Где эти дуги пересекутся между собой и будет прямой (90 градусов) угол.

Угол 45 градусов.

Такие углы обычно применяют при изготовлении прямоугольных рамок. Материал из которого делается рамка (багет) пилится под углом 45 градусов и стыкуется. Если под рукой нет стусла или транспортира, получить шаблон угла в 45 градусов можно следующим образом. Необходимо взять лист писчей бумаги или любого печатного издания и согнуть его так, что бы линия сгиба проходила точно через угол, а края загнутого листа совпадали. Получившийся угол и будет равен 45 градусам.

Угол 30 и 60 градусов.

Угол в 60 градусов требуется для построения равносторонних треугольников. Например, вам надо напилить такие треугольники для декоративных работ или точно установить силовой укос. Угол в 30 градусов редко применяется в чистом виде. Однако с его помощью (и с помощью угла в 90 градусов) строится угол 120 градусов.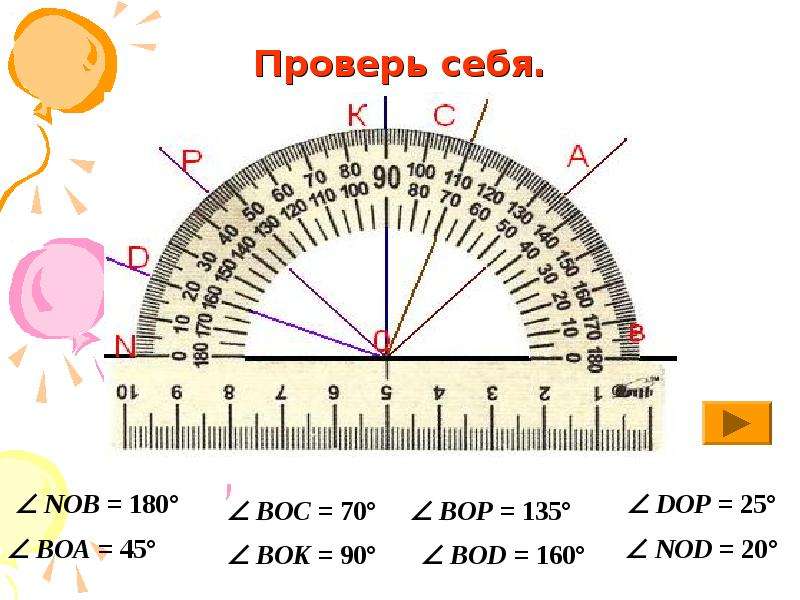 А это угол, необходимый для построения равносторонних шестиугольников, фигуры весьма популярной у столяров.

Для построения весьма точного шаблона этих углов в любой момент необходимо запомнить константу (число) 173. Они вытекает из соотношений синусов и косинусов этих углов.

Возьмите лист бумаги из любого печатного издания. Его угол равен точно 90 градусам. От угла по одной стороне отмерьте 100 мм (10 см.), а по другой — 173 мм (17,3 см). Соедините эти точки. Таким образом мы и получили шаблон, у которого один угол 90 градусов, один 30 градусов и один 60 градусов. Можете проверить на транспортире — все точно!

Запомните это число — 173, и вы всегда сможете построить углы в 30 и 60 градусов.

6)Измерение углов по пальцам рук.

Итак, смотрим на свою руку, которая есть у каждого человека. Уточнение! — левша должен снимать показания углов с правой руки, а правша с левой. Причина проста — приоритет действующей руки со временем деформирует кости, суставы и сильнее растягивает мышцы. Поэтому у правшей левая рука менее деформирована и разработана, а у левшей наоборот.

Теперь растопыриваем в стороны пальцы, как только можете за счет усилия только руки, ничем их раздвигать не нужно — только максимальное мышечное усилие. Богом так заложено у человека и это правда, что у здорового человека с нормальной рукой растопыренные пальцы — это полноценно действующий и относительно точный транспортир.

Угол между большим и безымянным пальцами равен 90 гр.

Угол между большим и указательным пальцами равен 45 гр.

Угол между безымянным и средним пальцами равен 22.5 гр.

Угол между безымянным и мизинцем равен 15 гр. — солнечному часу.

4.ВЫВОДЫ И ЗАКЛЮЧЕНИЕ.

Своей исследовательской работой мне хотелось бы доказать, что построение углов очень интересное и познавательное занятие, совсем не сложное и трудоемкое, как может показаться на первый взгляд.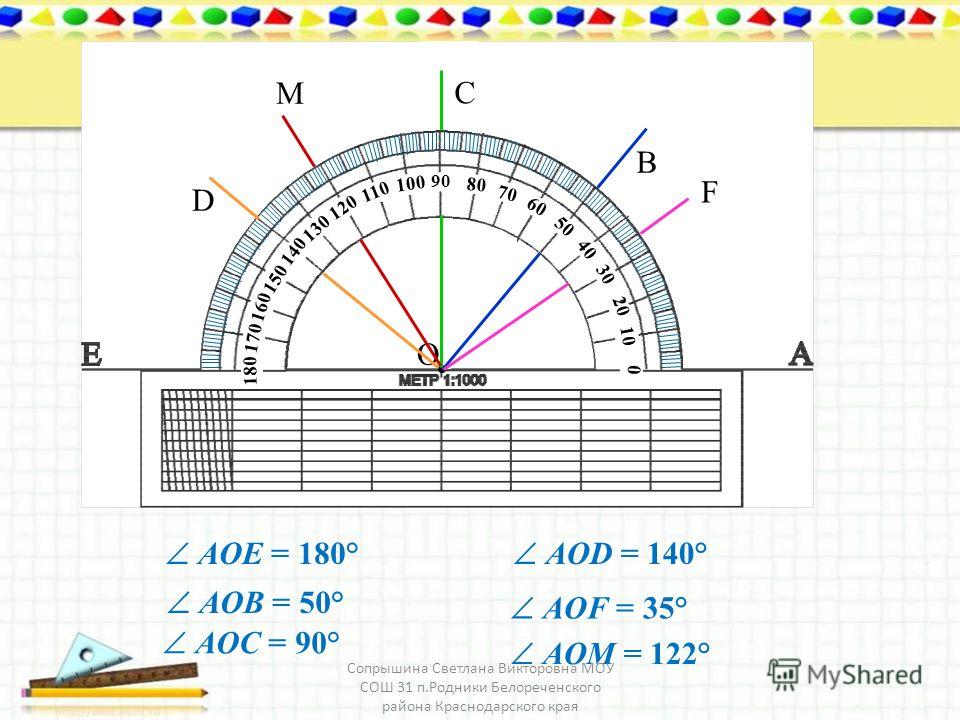

Поработав с материалом и подготовив его к применению на практике, я сделала

следующие выводы:

1. Обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения углов.

2. Угольники можно использовать для построения некоторых углов без использования транспортира.

Таким образом, методы построения углов без помощи транспортира актуальны для школьников, так как большинство задач оформляется на листке тетради в клетку и большинство задач в учебнике геометрии связано с построением фигур с углами, градусная мера которых кратна10°.

5 ЛИТЕРАТУРА.

1. В.В. Вавилов, А.В. Устинов. Задачи на клетчатой бумаге. – М.: Школа им. А.Н.

Колмогорова, 2006. – 183 с

2. Ганьшин В.Н. Простейшие измерения на местности. 3-е изд., перераб.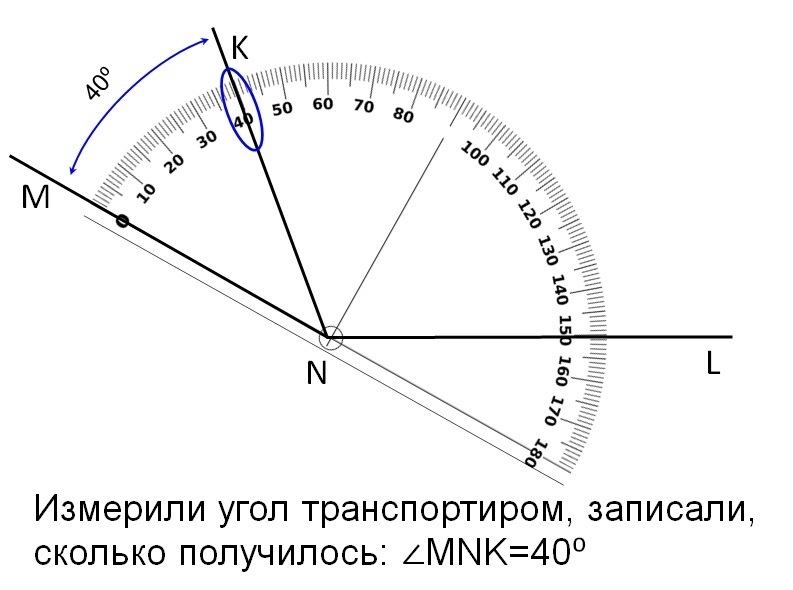 и доп., М.,

Недра, 1983, 108 с., ил.

3.Смирнов В.А, Смирнова И.М. Геометрия на клетчатой бумаге. М., МЦНМО, 2009

4. Большая советская энциклопедия

5. ГОСТ 13494-80. Транспортиры геодезические. Технические условия (с Изменениями N 1-4).

6. Большой энциклопедический политехнический словарь 2004

Список интернет-ресурсов:

http://allencyclopedia.ru/17254 Большая Советская энциклопедия/ Геодезические

инструменты

http://journal.kuzspa.ru/articles/95/ -Электронный научный журнал «Информационно-

коммуникационные технологии в педагогическом образовании»

http://sm-shihova.ucoz.ru/Komu_interesno/Komuinteresno_6.pdf — Математика, 5-6: книга для учителя Автор/создатель: Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О.

http://enc-dic. com/word/t/Transportir-4655.html [энциклопедии и словари]

http://www.gs-market.ru/index.php?show_aux_page=70 [угломеры электронный, строительный]

http://znaika.ru/catalog/5-klass/matematika/Izmerenie-uglov.-Transportir. [история возникновения приборов измерения углов]

http://virtoo.ru/almanach/nepoznannoe/pervyj-v-mire-transportir-izobreli-eg.html [первый в мире транспортир изобрели египтяне]

http://www.vest-news.ru/article.php?id=18508 [угломер Чижевского Л.В.]
http://astro.uni-altai.ru/picture/src/0+1066279852/ [средневековые угломерные инструменты]

.

Как измерить угол без транспортира

Самый простой способ измерить угол с помощью транспортира. Однако, если у вас нет транспортира удобно, вы можете определить размер угла, используя основные геометрические принципы треугольников.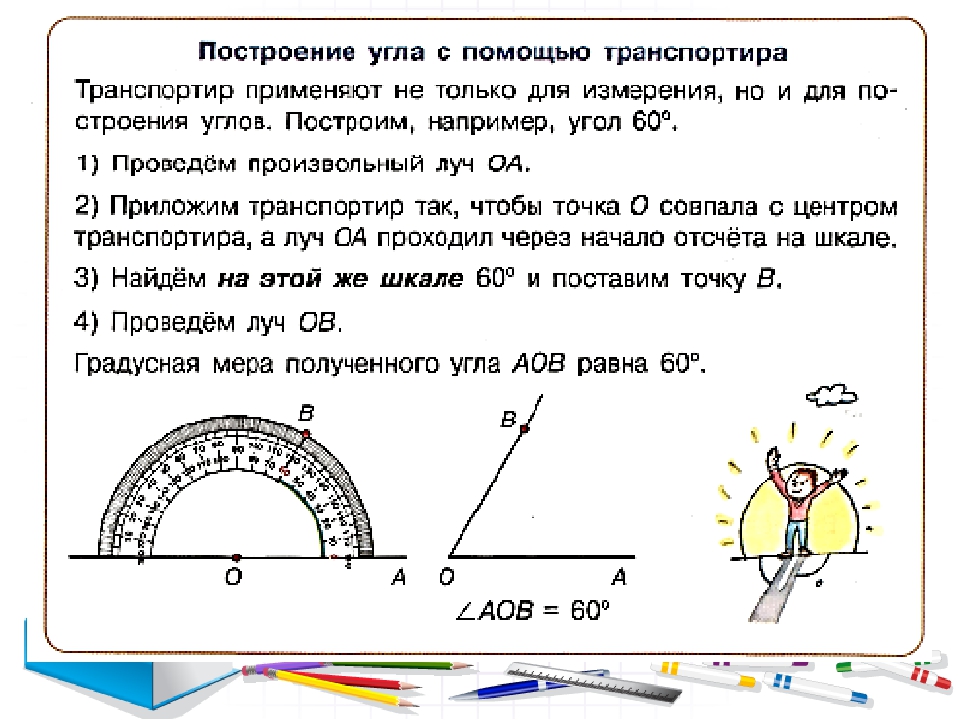 Вам нужен научный калькулятор для решения уравнений. Большинство смартфонов оснащены с ними, но вы также можете скачать бесплатное приложение или открыть бесплатный калькулятор онлайн. Расчеты нужно внести, зависит от того, какие меры острый (менее 90 градусов), тупой (больше 90 градусов но меньше 180), или угол рефлекс (более чем на 180 градусов, но меньше 360). Х Исследований источник

Острый

Нарисуйте вертикальные линии, соединяющей 2 лучи угол. Чтобы определить количество градусов в острого угла, соедините 2 лучи, чтобы сформировать треугольник. Совместите короткий конец линейки с нижним лучом, затем нарисуйте вертикальную линию, пересекающую другого луча с помощью длинной стороне своего правителя. Х Исследований источник Вертикальная линия создает прямоугольный треугольник. Угол, образованный смежными боковыми (Нижний луч угла) треугольника и противоположную сторону (вертикальные линии) измеряет 90 градусов. Как использовать ДМАЭ

Измерьте длину соседней стороны, чтобы найти бежать. Поместите конец свой правитель на вершину угла. Измерьте длину сопредельной стороне от вершины до точки, где она пересекается с противоположной стороны. Х Исследований источник Эта сумма является значение в уравнение склону, где уклон = рост/пробег. Если вы измерили 7, уравнение в этой точке будет “наклон = подъем/7”.

Измерьте длину противоположной стороны, чтобы найти подъем. Установите короткий конец линейкой заподлицо с прилегающей стороны треугольника. Измерить длину вертикальной линии от точки, где она встречается с сопредельной стороны к точке, где она встречает верхний луч угла (гипотенуза вашего треугольника). Х Исследований источник Эта сумма является рост значения в уравнение склона. Если вы измерили 5, вы бы заполнить свое уравнение так, чтобы “наклон = 5/7”.

Рост делим на бегу, чтобы найти наклон угла. Склон крутизной диагональной линии, или гипотенузы, вашего треугольника. Как только вы знаете эту цифру, можно рассчитать степень вашего острого угла. Х Исследований источник Продолжая пример, уравнение “наклон = 5/7” даст “наклон = 0. 71428571.”

Используйте калькулятор, чтобы определить градус угла. Введите значение уклона в свой научный калькулятор, а затем нажмите кнопку обратная Тан (Тан-1). Это даст вам градусах. Х Исследований источник Продолжая пример, с уклоном 0.71428571, угол составляет 35,5 градусов.

Туповатые

Продлить дна луч угол по прямой линии. Пометить вершину с точкой, затем с помощью длинной стороне вашего правителя, чтобы нарисовать прямую линию слева от вершины. Нижний луч угла должны быть одной длинной очереди, которая тянется под открытым верхний луч угла. Х Исследований источник Убедитесь, что ваши линии идеально прямые. Если она наклонена вверх или вниз, это разрушит точность уравнения. Как отбелить зубы за час

Нарисуйте вертикальную линию, соединяющую вершины луча и линии. Линия вверх короткий конец линейки с нижним лучом в точке, где длинная сторона пересекает сверху луч. Следите за длинной стороне, чтобы нарисовать линию прямо вверх от дна луч, который соединяет два. Х Исследований источник Фактически, вы создали небольшой прямоугольный под тупым углом, который вы хотите измерить, поворачивая верхний луч тупой угол на гипотенузу правого угла.

Измерьте длину нижней линии от вершины. Место вашего правителя ниже нижней границы, с начала по вертикали, создавая прямой угол. Измерьте длину от точки пересечения до вершины исходного угла. Х Исследований источник Ты определения уклона по угол острый треугольник, который можно использовать для вычисления степени в острый угол. В нижней строке-значение работы в уравнение “наклон = рост/пробег”.

Измерить длину вертикальной линии. Совместите короткий конец вашего правителя с нижней линии небольшой острый треугольник. Прочитал правитель до точки, где вертикальная линия соответствует открытый луч вашей тупой угол. Это длина вертикальной линии. Х Исследований источник Длина вертикальной линии-это рост значения в уравнение “склоне = рост/пробег”.Как только вы знаете значения для обоих подняться и побежать, можно вычислить наклон острого угла.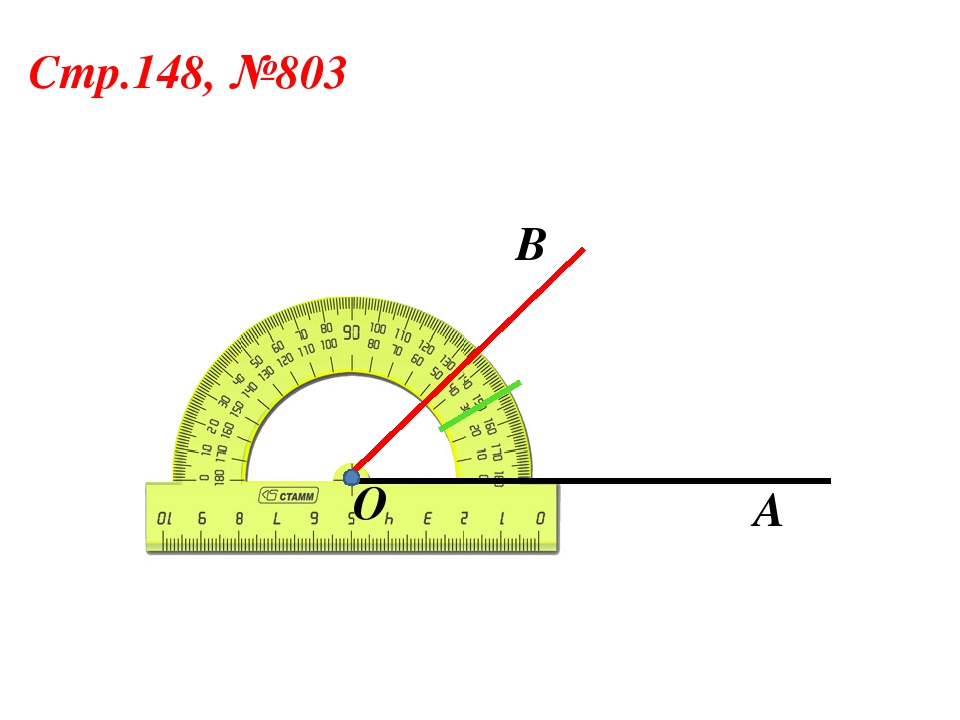 Как Waxworms породы

Найти наклон острого угла. Разделите рост значения на значение для определения наклона острый угол. Вы будете использовать это значение для вычисления степени острого угла. Х Исследований источник Например, уравнение “наклон = 2/4” даст “наклон = 0.5.”

Рассчитать степень острого угла. Введите значение уклона в свой научный калькулятор, а затем нажмите кнопку обратная Тан (Тан-1). Отображаемое значение-это количество градусов в острый угол. Х Исследований источник Продолжая пример, если ваш уклон 0.5, острый угол-это 26.565-градусный угол.

Вычитание степеней острого угла от 180. Плоская линия прямой угол с 180 градусов. Так как вы нарисовали прямую линию, сумма острых углов вы рассчитали, а тупой угол будет 180 градусов. Вычитая градус острого угла от 180 даст вам степень вашей тупой угол. Х Исследований источник Продолжая пример, если у вас есть острый угол 26.565 градусов, то есть тупой угол 153.435 градусов (180 – 26.565 = 153.435).

Рефлекс

Определить меньший острый угол, связанный с углом рефлекс. Угол рефлекс имеет более чем 180 градусов, но меньше 360. Это означает, что если вы посмотрите на угол рефлекс, вы также увидите острым углом внутрь лучи угол рефлекс. Х Исследований источник Путем определения степени острого угла, можно вычислить градус угла рефлекс. Можно использовать основное уравнение наклона и функции арктангенса на свой научный калькулятор, чтобы найти в градусах острый угол.

Нарисуйте вертикальную линию, соединяющую лучи острого угла. Совместите короткий конец вашего правителя с Лучом угол, горизонтальные, а не диагональные. Затем нарисуйте вертикальную линию, которая соответствует горизонтальный луч угол. Х Исследований источник Горизонтальная линия будет на сопредельной стороне вашего треугольника, и вертикальной линией, становится противоположной стороне острого угла, который вы хотите измерить.

Измерить рост и запустить острого угла. В уравнении “наклон = подъем,” подъем-длина вертикальной линии, или на противоположной стороне вашего треугольника.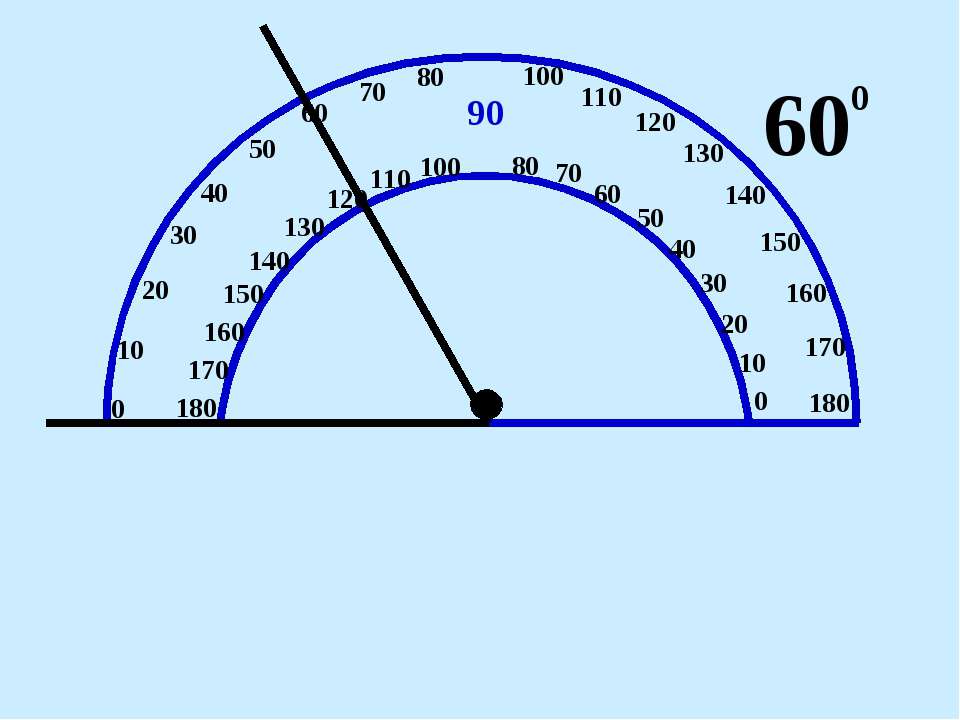 Бег-это длина горизонтальной линии, или сопредельной стороне вашего треугольника. Х Исследований источник Измерить горизонтальную линию от вершины к точке, где она встречает вертикальную линию. Измерьте вертикальную линию от точки, где она встречается с горизонтальной линией в точке, где она встречается с линией диагонали.

Рост делим на бегу, чтобы найти наклон острого угла. Подключите значения для длины вертикальных и горизонтальных линий в уравнение склона. Когда вы разделите длину вертикальной линии длиной горизонтальной линии, вы получите уклон на угол. Х Исследований источник Например, если ваша горизонтальная линия измерена 8 и вертикальную линию, измерить 4, ваша формула будет “наклон = 4/8.” Наклон угол будет 0.5.

Используйте свой калькулятор, чтобы найти в градусах острый угол. Введите значение, которое вы получили для наклона угол в свой научный калькулятор, а затем нажмите кнопку арктангенс (Тан-1). Отображаемое значение ступени меньшего острого угла. Х Исследований источник Продолжая пример, если ваш уклон 0. 5, острый угол будет измерять 26.565 градусов.

Вычитание степеней острым углом из 360. Круг имеет 360 градусов. Поскольку угол отражения угол более 180 градусов, можно связать его, как часть окружности. Градусы угла рефлекса и степени меньший острый угол будет 360. Х Исследований источник Продолжая пример, если меньший острый угол меры 26.565 градусов, угол рефлекс будет измерять 333.435 градусов.

Советы

Убедитесь, что тригонометрические функции научный калькулятор устанавливаются измерять в градусах, а не радианах.

Склон связь между ростом и бежать. Единицы измерения можно использовать для количественной оценки длины линий 2 не имеет никакого отношения – просто убедитесь, что вы используете одну и ту же единицу для обеих линий. Другими словами, если вы измеряете длину одной линии в сантиметрах, вы должны также измерить другие в сантиметрах.

Резюме

Для того чтобы измерить острый угол без транспортира, начните с вертикальной линии, соединяющей 2 лучи угол образуют правильный треугольник. Обратите внимание, что угол, образованный смежными боковыми треугольника и противоположную сторону мерах 90 градусов. Далее измерьте длину соседней стороны, чтобы найти бежать. Затем, измерьте длину противоположной стороны, чтобы найти подъем. Если у вас есть эти измерения, рост разделить на наклон или крутизна, диагональной линии. Когда у вас есть это число, вы можете вычислить степень вашего острого угла, введите значение уклона в научный калькулятор. Наконец, нажмите кнопку обратной Тан, чтобы получить градусах. Чтобы узнать, как измерить тупой угол без транспортира, читайте дальше!

Вопросы И Ответы

Вопрос: Что делать, если линия пышные?

Ответ: если нет прямой, нет никакого угла для измерения. (Угол определяется как фигура, образованная двумя “лучами”, которые являются прямолинейными отрезками.)

Вопрос: как мне построить вертикальную линию?

Ответ: используйте транспортир, чтобы нарисовать линию, перпендикулярную верхнему или нижнему краю бумаги, или измерять с помощью линейки, рисовать линии параллельно краям бумаги.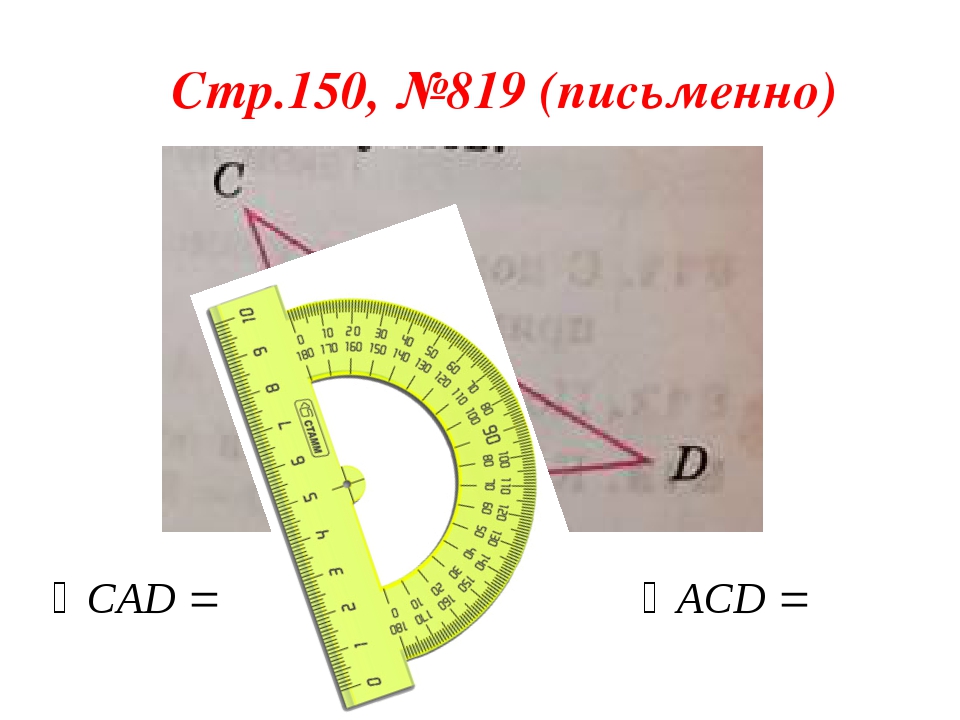

Вопрос: насколько точны результаты для каждого метода?

Ответ: эти методы обычно дают более точные углы, чем транспортир может.

Вопрос: Чему равна сумма всех углов в треугольнике?

Ответ: все внутренние углы треугольника, не имеет значения, какой тип треугольника это, добавить до 180 градусов.

Как начертить без транспортира

Угол – это некая геометрическая фигура, которая образуется с помощью двух лучей, выходящих из одной точки. Каждый угол имеет собственную меру в градусах. Определяют ее с помощью специального приспособления – транспортира. Но существуют в геометрии методы, позволяющие чертить углы и без его использования.Вам понадобится

Величину угла без использования транспортира можно высчитать и, соответственно, начертить его путем определения через соотношение катетов в прямоугольном треугольнике. Для этого допустим, что вы определяете градусную меру определенного угла ∠α с вершина которого находится в точке A.

На стороне данного угла ∠α отложите отрезок AC любой длины. Через точку C проведите прямую, которая будет перпендикулярной прямой AC. Там, где данная прямая пересекает вторую сторону угла, обозначаем точку B. После этого у вас получился прямоугольный треугольник ΔABC.

Далее, пользуясь тригонометрическим соотношением катетов для прямоугольного треугольника, мы вычисляем угол, пользуясь следующей формулой tg∠α = BC/AC. После этого меру треугольника в градусах узнайте, пользуясь таблицей тангенсов либо с помощью калькулятора с функцией «tg».

Чтобы без транспортира начертить правильный треугольник, воспользуйтесь обычной ученической линейкой и циркулем. Сначала нарисуйте окружность, радиусом которой будет величина, равная стороне прямоугольного треугольника, который вы желаете получить. После этого поставьте центр циркуля на точку, расположенную на линии окружности, и рисуйте еще одну фигуру с аналогичным радиусом. Далее, опять не меняя радиус, поставьте центр циркуля в точку, которая появилась на пересечении двух окружностей, и снова нарисуйте такую же фигуру.

Три точки пересечения соедините последовательно, пользуясь линейкой. У вас получится правильный треугольник, сторона которого будет равняться радиусу окружностей.

С помощью линейки можно начертить и другие углы: например, для угла в 45 градусов сначала начертите угол в 90 градусов, после чего разделите его на две половины. Однако для более точной работы все же потребуется транспортир.

Измерение углов. Транспортир. Видеоурок. Математика 5 Класс

Транспортир — это простой и удобный инструмент для измерения и построения углов. В основном распространены транспортиры полукруглой формы, хотя существуют и круглые транспортиры, рассчитанные на 360 градусов. Если вы впервые столкнулись с транспортиром и не знаете, как им пользоваться, прочитайте эту статью! Это совсем несложно: несколько простых шагов, и вы как следует освоите этот полезный инструмент.

Транспортиром пользуются для измерения углов.

Условно выделим в транспортире две части — «линейку», называемую также прямолинейной шкалой (нижняя часть на рисунке), и полукруга, называемого также угломерной шкалой.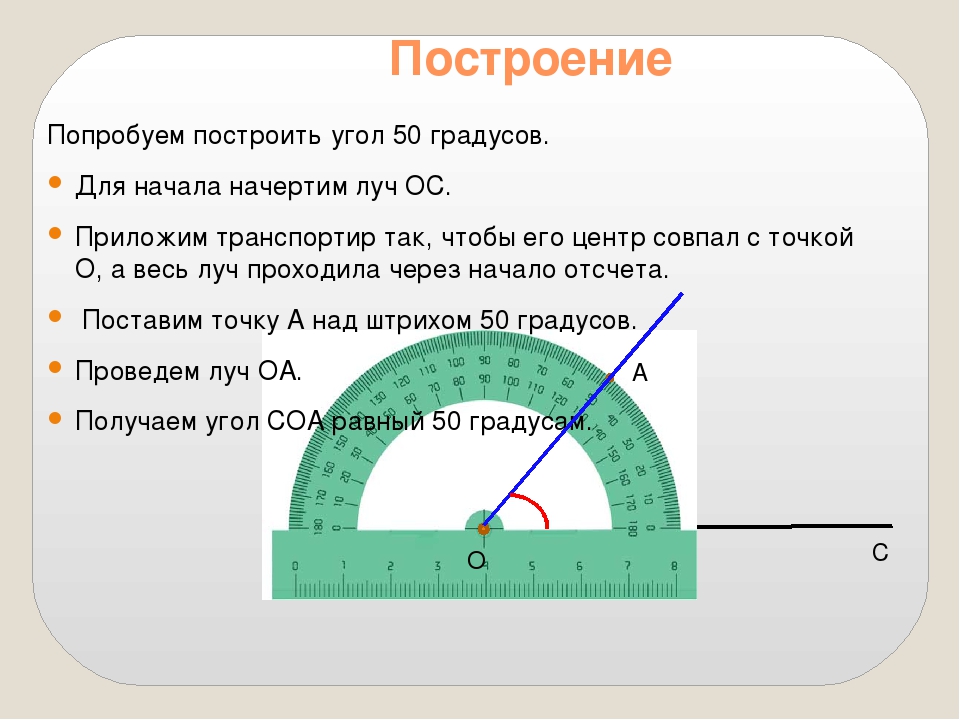 На полукруге находятся метки градусов от 0° до 180°. Назовем разделение на градусы «градусной сеткой».

Транспортиры бывают разного вида, но использование их сводится к следующему. У транспортира есть центральная метка. На рисунке выше это маленький кружок с отверстием в центре. Однако центральная метка может обозначаться просто черточкой. Эту метку нужно совместить с вершиной угла. При этом одна из сторон угла должна пройти через метку с числом 0 на полукруге транспортира.

На транспортире может быть две «нулевых» метки: справа и слева. Понятно, что следует смотреть на ту, через которую проходит сторона угла. Но самое главное, понять на какую градусную сетку смотреть при измерении величины угла: верхнюю или нижнюю. Если сторона угла прошла через 0, который находятся с внешней стороны, то в дальнейшем мы пользуемся внешней градусной сеткой. Если же сторона угла прошла через «внутренний» 0, то в дальнейшем пользуемся внутренней градусной сеткой транспортира (на внешнюю не обращаем внимания).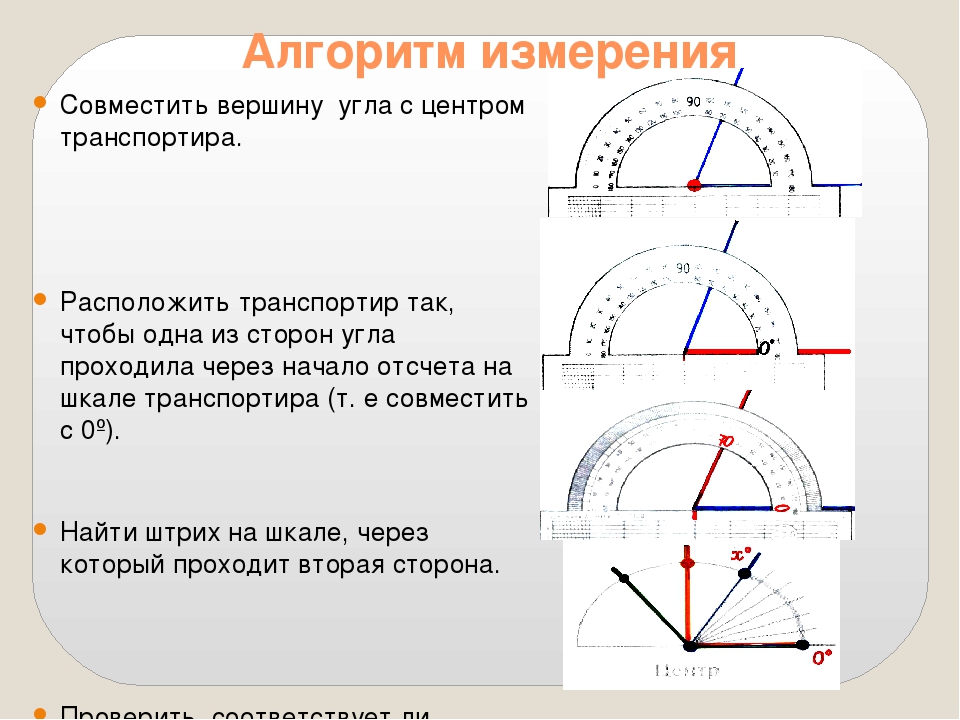

Итак, одна сторона угла должна пройти через метку 0, а вторая сторона угла должна оказаться со стороны полукруга (угломерной шкалы), то есть как бы пересекать его.

Что такое транспортир?

Транспортиром называют предмет, с помощью которого каждый из нас может не только измерять углы, но и строить их. Внешне он напоминает полукруглую линейку со шкалой и делениями. Внизу, на ровной поверхности, расположена привычная нам прямая линейка для измерения отрезков. В верхней части — полукруг с двойной шкалой для измерений. В каждом из направлений шкала рассредоточена по транспортиру от 0 до 180 градусов.

Презентация к уроку

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели:

• Образовательные:

• познакомить учащихся с единицей измерения углов, с прибором для измерения углов;
• научить пользоваться транспортиром.

Развивающие:развивать внимание, мышление учащихся;развивать самостоятельность учащихся, используя проблемные ситуации, творческие задания;развивать познавательный интерес к предмету.Воспитательные:воспитывать чувство взаимоуважения;воспитывать у учащихся навыки учебного труда.
I. Организационный момент

II. Вступительное слово учителя

Мы познакомимся с измерительным прибором (как он называется, вы узнаете немного позже), научимся с его помощью измерять, а затем и строить углы. Вы покажите свои знания, докажите насколько внимательны. Будем учиться не только математике, но и умению общаться, уважению друг к другу. Для того чтобы достичь наших целей, вы должны быть волевыми, настойчивыми, целеустремленными, поэтому эпиграфом нашего урока будут слова:

Правила пользования

В школе объясняют, что такое транспортир, на уроках математики. Именно здесь есть необходимость в измерениях.

Для того чтобы нам узнать, чему равен один градус, нужно окружность поделить на 360 равных частей. Одна из таких частей и будет равна 1 градусу. Величина окружности никак не повлияет на градус! Это легко проверить.

Нарисуем две окружности разного диаметра и поделим каждую на 360 равных частей. Затем наложим меньшую окружность на большую и увидим, что линии совпали.

Измеряем угол

Транспортир помогает построить и измерить угол. Градус — это общепринятая единица, которой пользуются для измерения углов. Встречается несколько разновидностей углов:

• Острый. Таким называют угол до 90 градусов.
• Прямым является угол, равный 90 градусам.
• Тупой угол варьируется в диапазоне от 90 до 180 градусов.
• Развёрнутый угол представляет собой прямую линию или 180 градусов.
• Полный угол выглядит как окружность и составляет 360 градусов.

Нетрудно разобраться, как измерить угол. Для того чтобы узнать, какова величина угла, нам необходимо установить транспортир таким образом, чтобы его центр располагался в вершине угла, а прямая сторона совпала с одной из его сторон.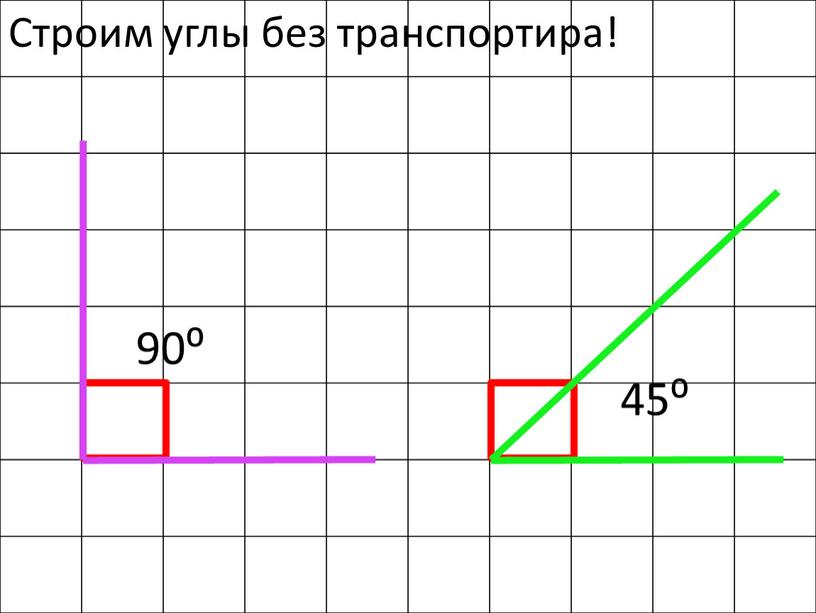 Шкала укажет нам количество градусов данного угла. Вот таким нехитрым способом мы можем узнать, что за угол перед нами.

Для построения угла с заданным градусом следует приложить прямую часть транспортира к линии, а его центр — к началу линии. Впоследствии эта точка будет являться вершиной угла. Затем на шкале отыскиваем заданное число и ставим точку. Теперь транспортир можно снять и соединить отрезком начало линии (вершину угла) с отмеченной точкой.

Школьные канцтовары, произведенные разными компаниями, отличаются по материалу, цвету, размеру. Так вот: тем, у кого транспортир оказался больше длины угла, и не представляется возможным определить его величину, сторону угла необходимо продлить, используя прямую линейку.

Вывод

Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.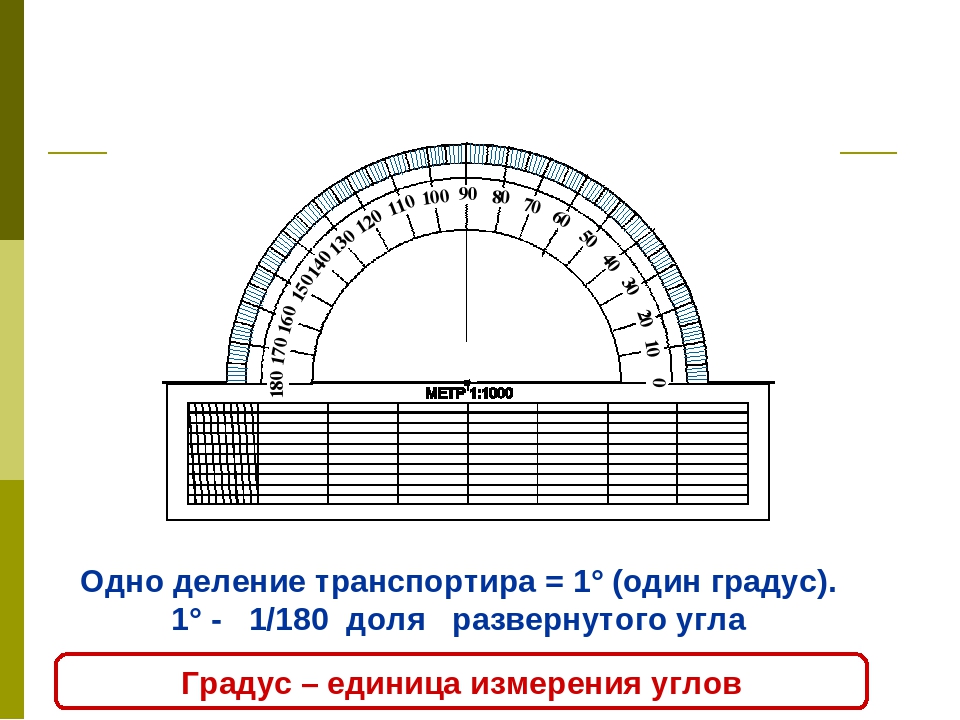

При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.

Набор школьника

Неспроста учащиеся младшего звена не знакомы с транспортиром. При его применении должна быть заложена некая база знаний. Для полноценной работы с ним на уроке ребята изучают ряд сопутствующих предметов. Прежде чем узнать, что такое транспортир, школьники должны в совершенстве овладеть прямой линейкой, чертить ровные линии, изучить сложение и вычитание, освоить циркуль, знать геометрические фигуры и так далее. Весь этот процесс занимает время, и только окончив начальную школу, ученик может добавить транспортир в свой набор инструментов.

Ученикам сейчас предлагаются школьные канцтовары в огромном выборе. Транспортир не исключение. Производители стараются угодить самым требовательным запросам покупателей.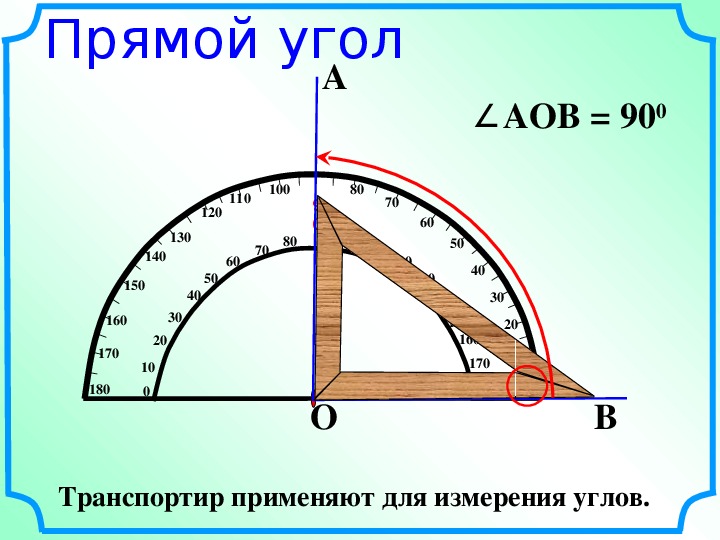 Инструменты изготавливают в различной цветовой гамме. Яркие цвета всегда нравятся детям. Порой даже в одном классе не сыскать одинаковых транспортиров, что облегчает при утрате их поиск. Формы и размеры каждый выбирает на свой вкус.

Большинство таких товаров выпускают из пластмассы, и это значительно уменьшает его стоимость. Но есть деревянные и даже железные транспортиры. Как показывает практика, металлические хоть и непрозрачны, но практичнее в том плане, что шкала не стирается, а это позволяет гораздо дольше применять его в действии, с точностью определяя углы.

Транспортир не так востребован школьниками, как линейка, но он сопровождает учеников вплоть до выпускного экзамена. Некоторые из выпускников школы выбирают специальности, которые связаны с измерением и построением углов, проектированием зданий и сооружений, работой с чертежами. В силу своих профессий им постоянно приходится сталкиваться с транспортирами и его производными. Но и бывшие одноклассники нынешних инженеров, порой даже с глубочайшим гуманитарным уклоном, без труда вспомнят навыки обращения с этим предметом и определят количество градусов у любого угла.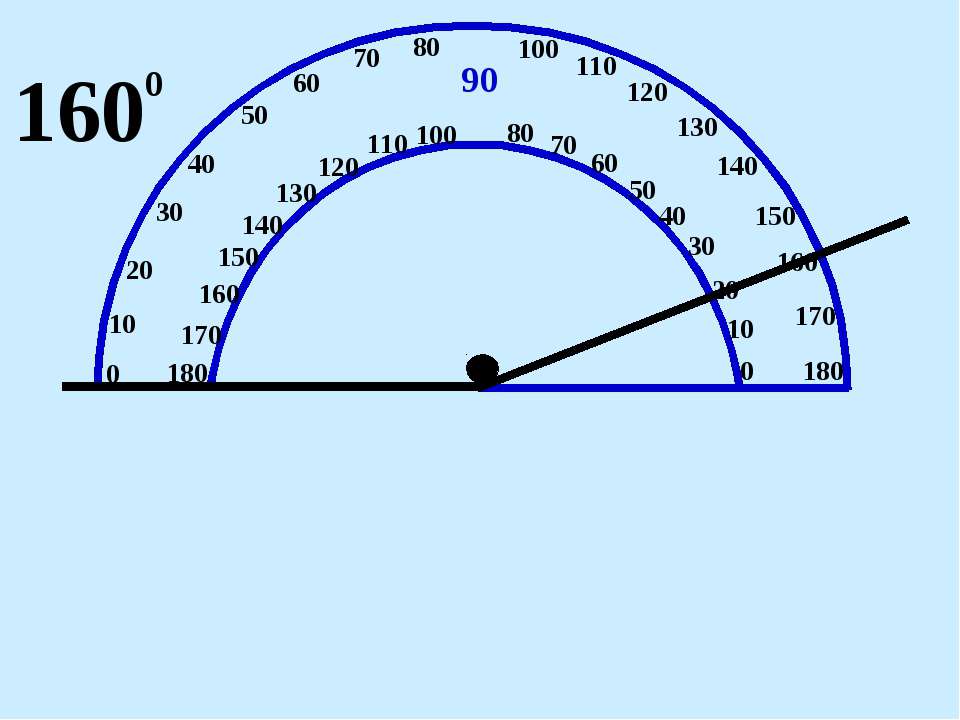

Сегодня современные дети привыкли добывать любую информацию из интернета. Однако он никак не поможет в измерении углов. Лишь только умение пользоваться транспортиром даст возможность правильно их определять. Будущим инженерам и проектировщикам это бесспорно пригодится в работе, да и каждый образованный человек должен обладать навыками работы с транспортирами, поэтому уметь пользоваться таким инструментом должен каждый!

Итог

Сегодня современные дети привыкли добывать любую информацию из интернета. Однако он никак не поможет в измерении углов. Лишь только умение пользоваться транспортиром даст возможность правильно их определять. Будущим инженерам и проектировщикам это бесспорно пригодится в работе, да и каждый образованный человек должен обладать навыками работы с транспортирами, поэтому уметь пользоваться таким инструментом должен каждый!

На уроке мы вспомним, что такое единицы измерения, узнаем какими единицами можно измерять углы, познакомимся с такой единицей измерения, как градус, научимся измерять углы в градусах и чертить их с помощью транспортира.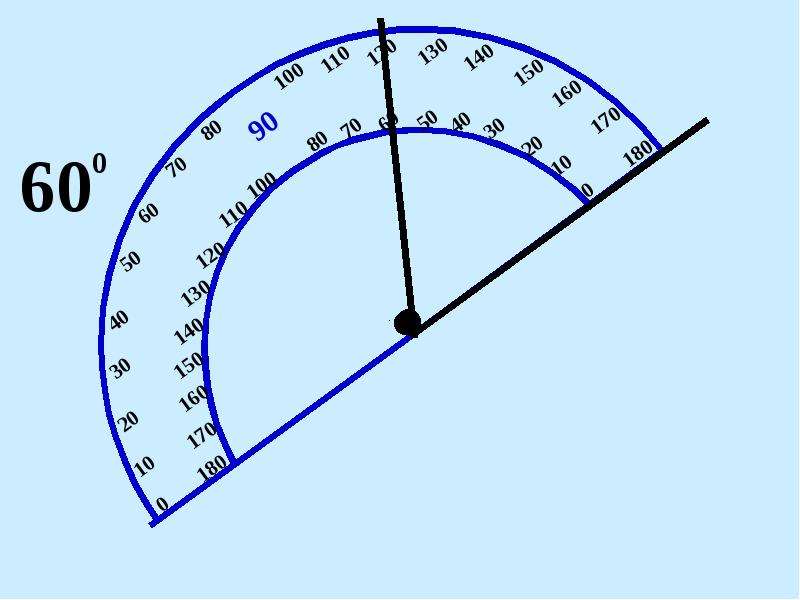 Также мы узнаем о других единицах измерения углов, которые применяются в различных ситуациях.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок и

Какие-то вещи можно измерить, какие-то нельзя. Например, нельзя измерить дружбу или любовь. А расстояние, вес, температуру вполне можно. Чтобы что-то измерять, нужно всем договориться о единицах измерения.

Метр, дюйм, аршин — это и есть такие договоренности при измерении длины. Эталонный метр хранится во Франции, в Палате мер и весов. Килограмм, фунт, пуд — это договоренности для измерения массы. Эталонный килограмм тоже хранится в Палате мер и весов.

Единицы измерения придуманы для конкретных величин. В секундах не измерить вес, а в аршинах — время.

В геометрии такая же ситуация. Есть сантиметры, для измерения длин отрезков, но они не подходят для измерения углов. Для измерения углов есть свои единицы измерения. На этом уроке мы рассмотрим одну из них, а именно градусы.

Разделим полный угол на 360 равных частей. Для этого удобно использовать окружность. Поделим ее на 360 частей и соединим каждое полученное деление с центром. Получим 360 равных углов (см. Рис. 1).

Рис. 1. Окружность, разделенная на 360 равных углов

Один такой маленький угол назовем углом в 1° (см. Рис. 2).

Рис. 2. 1 градус

Не важно, какого размера будет окружность, которую мы делим. Поделим обе окружности на 360 частей, получим равные углы в 1°, хотя стороны одного угла визуально длиннее, чем у другого (см. Рис. 3).

Рис. 3. Углы равны

Стороны углов можно продолжать бесконечно, от этого размер угла не меняется (см. Рис. 4).

Рис. 4. Более явный пример равенства углов

Величина любого угла — это сколько раз в него умещается угол в 1°.

Вот мы видим угол 13° (см. Рис. 5).

Рис. 5. Угол 13°

Понятно, что полный угол

состоит из 360 таких углов. То есть он равен 360° (см. Рис. 6).

Рис. 6. Полный угол

Развернутый угол

— это половина полного угла. Он равен (см. Рис. 7).

Рис. 7. Развернутый угол

Прямой угол

является половиной развернутого и равен 90° (см. Рис. 8).

Рис. 8. Прямой угол

Эталон градуса нет нужды где-то хранить. Если нужно, то всегда можно полный угол разделить на 360 частей, или развернутый — на 180, или прямой — на 90.

Линейка нужна для того, чтобы измерить имеющийся отрезок или начертить отрезок нужной длины. Чтобы измерить угол или начертить угол нужной величины, мы тоже используем линейку, только не прямую, а круглую. Она называется транспортиром (см. Рис. 9).

Рис. 9. Транспортир

Единицы измерения на ней — градусы. Шкала начинается с нуля и заканчивается 180°.То есть максимальный угол, который мы можем измерить или начертить, — это 180°, развернутый.

Транспортиры могут быть разных размеров, но это не влияет на то, какого размера углы ими измеряют. Для более крупного транспортира у углов нужно чертить стороны длиннее.

1. Измерим пару углов.

Прямая часть транспортира совмещается с одной стороной угла, центр транспортира с вершиной угла.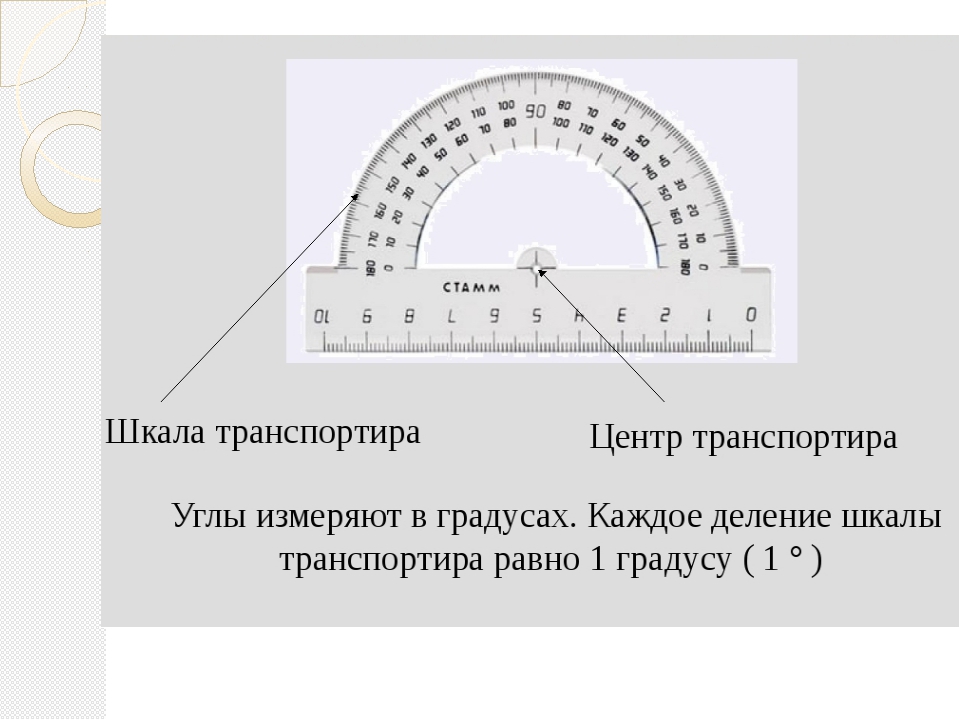 Смотрим, где оказалась вторая сторона угла, — 54° (см. Рис. 10, 11).

Рис. 10. Измерение угла

Проделаем то же самое со вторым углом, 137°.

Рис. 11. Измерение угла

Если сторона угла не достает до шкалы, то ее нужно сначала продлить.

2. Начертим углы 29°, 81° и 140°.

Сначала чертим одну сторону угла по линейке (см. Рис. 12).

Рис. 12. Построение одной стороны угла

Отмечаем вершину. Совмещаем с транспортиром. Отмечаем точкой нужное значение угла — 29° (см. Рис. 13).

Рис. 13. Использование транспортира для построения углов

Убираем транспортир. Соединяем полученную точку с вершиной (см. Рис. 14).

Рис. 14. Угол 29°

Точно так же строим два других угла (см. Рис. 15).

Рис. 15. Построение углов

Итак, мы с вами обсудили, что для измерения углов люди договорились использовать градусы. Градус

— это полного угла.

Инструментом для измерения и построения углов является транспортир.

Можно не использовать названия углов — полный, развернутый, прямой. Мы можем просто говорить — 360 градусов, 180 или 90 градусов.

На самом деле бывает, когда мы одни величины измеряем единицами, казалось бы, для них не предназначенными, «чужими» единицами.

Можно ли измерить расстояние в минутах? Да, мы часто используем этот способ. «От моего дома до школы 5 минут». Если быть точнее, то «5 минут пешком». Мы здесь используем известную всем величину — скорость пешехода. И величина «5 минут» на самом деле означает «расстояние, которое пешеход проходит за 5 минут». Скорость пешехода — 5 км/ч, 5 минут — это часа, умножим одно на другое. Получаем примерно 400 метров. Не очень точно, зато удобно.

Точно по такому же принципу устроена другая единица измерения расстояния — световой год. Световой год — расстояние, которое проходит свет за 1 год. С помощью этой единицы меряют расстояния между звездами.

Очень распространенный пример использования «чужой» единицы измерения — это измерять вес в килограммах. На самом деле килограмм — единица измерения массы, а вес — это другая физическая величина. Если хотите подробнее узнать, в чем разница между массой и весом, и почему измерять вес в килограммах не верно, то наберите в поисковой системе «масса и вес» и получите множество пояснений по этому поводу.

Атмосферное давление мы до сих пор измеряем в миллиметрах (миллиметрах ртутного столба).

Хотя для угла есть свои «родные» единицы измерения — градусы, которые мы и проходим на этом уроке, все-таки его можно измерять и с помощью линейных величин, например сантиметров. Если нужно измерить угол , то можно достроить его до треугольника, так чтобы один угол был прямым, и разделить длину одной стороны на другую.

Получим величину угла , которая называется тангенсом.

Если увеличить треугольник, то ничего не изменится (см. Рис. 16).

Рис. 16. Тангенс

Ведь во сколько раз увеличилась одна сторона, во столько и вторая.

То есть величины часто можно измерять «чужими» единицами, но это чуть сложнее, там нужны некоторые дополнительные договоренности.

Существуют и другие единицы измерения углов.

1.
Минуты и секунды.
Как и метр можно делить на дециметры, сантиметры, миллиметры для более точных измерений, так и градусы делятся на более мелкие единицы измерения.

Если угол в 1° разделить на 60 равных частей, то величина полученного угла называется минута, 1′.

Если минуту поделить на 60 частей, то полученная величина называется секундой. Секунда — уже очень маленькая величина, но ее тоже можно делить дальше.

Почему вообще стали делить на 360 частей полный угол, ведь это не очень удобно? В древнем Вавилоне была шестидесятеричная система (у нас десятеричная). Им было удобно делить на 60.

2.
Грады.
Чтобы сделать измерение углов ближе к нашей десятичной системе счисления, были предложены грады. Для этого прямой угол делится на 100 частей. Полученная величина называется град. Полный угол составляет тогда 400 градов. Система не прижилась, и сейчас ее не используют.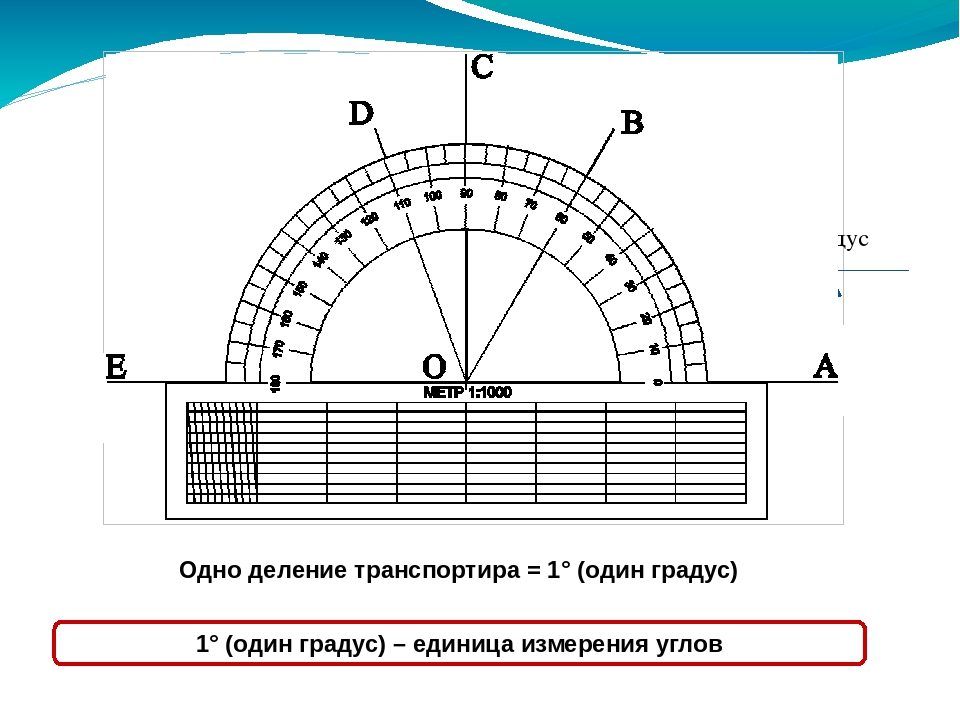

3.
Радиан.
Если взять два радиуса окружности так, чтобы кусочек окружности между ними тоже был равен радиусу, то угол между радиусами мы и примем за новую единицу измерения. Он называется 1 рад (радиан). Эта мера используется наравне с градусной. У нее есть свои преимущества и свои недостатки по сравнению с градусами (см. Рис. 17).

Рис. 17. Радианы

Например, теперь полный угол (вся окружность) состоит не из целого числа единичных углов. Полный угол состоит из 6 с лишним единичных углов. Не очень удобно, зато теперь длина дуги (части окружности) и угол хорошо связаны. Если взять окружность радиуса 1 см, то величина угла совпадает с длиной дуги. Угол 1 рад — дуга 1 см, угол 2 рад — длина дуги 2 см.

Список литературы

1. Зубарева И.И., Мордкович А.Г. Математика. 5 класс. — М.: Мнемозина, 2013.
2. Виленкин Н.Я. и др. Математика. 5 кл. — М.: Мнемозина, 2013.
3. Ерина Т.М. Математика 5кл. Раб. тетрадь к уч. Виленкина, 2013. — М.: Мнемозина, 2013.

1. Shkolo.ru ().
2. Cleverstudents.ru ().
3. Festival.1september.ru ().

Домашнее задание

1. Зубарева И.И., Мордкович А.Г. Математика. 5 класс. — М.: Мнемозина, 2013. Стр. 144 № 522.
2. Начертите углы: 23°, 167°, 84°.
3. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 5 класса (5-е изд.) — 2010. Стр. 163 № 3.

Пусть в результате тщательного и искусного наблюдения та или шая цель вами найдена. Очевидно, этого еще мало: нужно определись местоположение цели, чтобы наша артиллерия знала, куда стрелять. Как это сделать?

Местоположение цели определяют обычно по отношению к ориентиру, — именно по отношению к тому ориентиру, который находится ближе всего к цели. Достаточно знать две координаты цели — ее дальность, то-естъ расстояние от наблюдателя или от орудия до цели, и угол, под которым цель видна нам правее или левее ориентира, — и тогда местоположение цели будет определено достаточно точно.

Предположим, ради простоты, что цель находится от нас на том же расстоянии, что и ориентир. Расстояние до этого ориентира нам известно заранее. Пусть оно равно 1000 метрам. Одна координата цели, следовательно, уже определена. Остается определить другую: угол между целью и ориентиром. Чем же и как артиллеристы измеряют углы?

В обыденной жизни вам не раз приходилось измерять углы: вы измеряли их в градусах и минутах. Артиллеристам же приходится не толшо измерять углы, но и быстро в уме по угловым величинам находить линейные величины и, наоборот, — по линейным величинам находить угловые. Пользоваться в таких случаях градусной системой измерения углов неудобно. Поэтому артиллеристы приняли совсем иную меру углов. Мера эта — «тысячная», или, как ее называют иначе, деление угломера.

Представим себе окружность, разделенную на 6000 равных частей.

Примем за основную меру для измерения углов одну шеститысячную долю этой окружности и попробуем определить ее величину в долях радиуса.

Известно, что радиус (R

) любой окружности укладывается по ее длине приблизительно 6 раз, следовательно, можно считать, что длина окружности равна 6
R
. Мы же разделили окружность на 6000 равных частей; отсюда 6
R
= 6000 частей окружности. Теперь легко узнать, какую часть радиуса будет составлять одна шеститысячная часть окружности. Очевидно, что она будет в 6000 раз меньше величины 6
R
, то-есть будет равна или одной тысячной радиуса . Поэтому-то артиллерийская мера углов — деление угломера — и носит название «тысячной» (рис. 212). Такой мерой пользоваться для измерения углов очень удобно. {243}

Вспомните, что в поле зрения бинокля вы видели сетку с делениями, то-есть короткие и длинные черточки, которые расположены вправо, влево и вверх от перекрестия, находящегося в центре поля зрения бинокля (рис. 213). Эти деления и есть «тысячные». Маленькое деление сетки (между короткой и длинной черточками) равно 5 «тысячным», а большое деление (между длинными черточками) — 10 «тысячным».

На рис. 213 эти деления обозначены не просто числами 5 и 10, а с приставленными слева нолями — 6-05. и 0-10. Так пишут и произносят артиллеристы все угловые величины в «тысячных», чтобы избежать ошибок в командах. Например, если нужно передать в команде угол, равный 185 «тысячным» или 8 «тысячным», то произносят эти числа как номер телефона: «один восемьдесят пять» или «ноль ноль восемь», и соответственно пишут 1-85 или 0-08.

Зная теперь, как устроена сетка бинокля, вы можете измерить по ней угол между двумя предметами (точками местности), которые ввдны с вашего наблюдательного пункта. Взгляните опять на рис. 213. Вы видите, что между перекрестком дорог, куда направлено перекрестие, и отдельно стоящим деревом (вправо от перекрестка дорог) укладывается два больших деления и одно маленькое, то-есть 25 «тысячных» или 0-25. Это и есть угол между перекрестком дорог и деревом. Точно так же вы можете определить угол между перекрестком дорог и домиком (влево от перекрестка дорог). Он равен 0-40.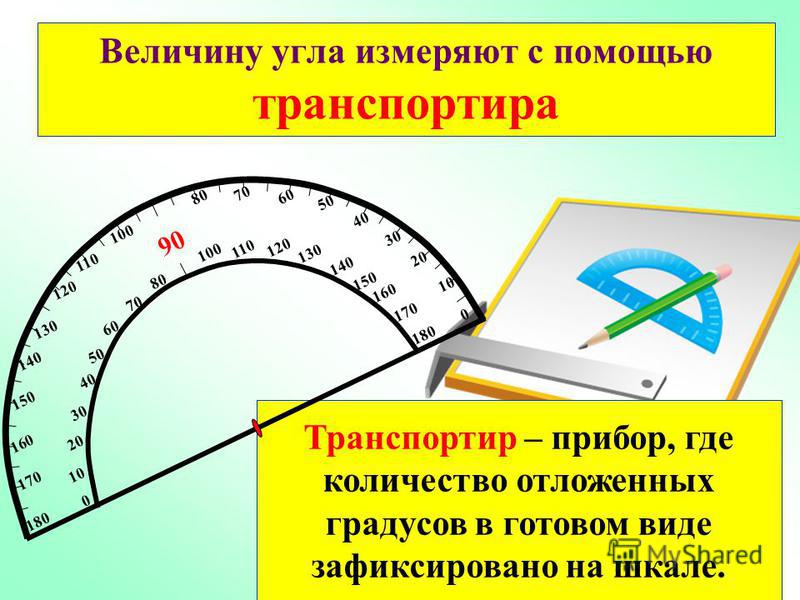 {244}

Сетка с делениями, примерно такая же как в бинокле, имеется и в поле зрения стереотрубы. Но у стереотрубы для измерения углов есть еще угломерная шкала снаружи.

На рис. 214 показаны те части стереотрубы (лимб и барабан лимба), при помощи которых можно более точно, чем по сетке, измерять горизонтальные углы.

Окружность лимба разделена на 60 частей, и поворот стереотрубы на одно деление лимба соответствует таким образом 100 «тысячным». Окружность же барабана лимба разделена на 100 частей, и при полном обороте барабана стереотруба поворачивается всего только на одно деление лимба (т. е. на 100 «тысячных»). Следовательно, деление барабана соответствует не 100 «тысячным», а всего лишь одной «тысячной». Это позволяет уточнять показания лимба в 100 раз и дает возможность измерять углы с точностью до одной «тысячной».

Чтобы измерить угол между двумя точками, пользуясь лимбом и барабаном, совмещают перекрестие стереотрубы сначала с правой тачкой; для этого, подведя указатель лимба к делению 30 и деление барабана 0 к его указателю (рис. 215), поворачивают трубу в нужную сторону при помощи маховичка точной наводки (см. рис. 214). Затем, вращая барабан лимба, совмещают перекрестие стереотрубы с левой точкой. При этом указатель лимба передвинется и покажет новый отсчет. Разность между полученным отсчетом и первоначальной установкой (30-00) и будет равна искомому углу (рис. 215).

Но не только при помощи этих сложных приборов можно измерять углы.

Ваша ладонь и ваши пальцы могут стать неплохим угломерным прибором, если только вы запомните, сколько в них заключается «тысячных» или, как говорят артиллеристы, какова «цена» ладони и пальцев. Хотя разные люди имеют разную ширину ладони и пальцев, но все же «цена» их не будет сильно отличаться от указанной на рис. 216. Вытянув перед собой руку на полную ее длину, вы можете быстро измерить угол между любыми точками местности (рис. 217). Чтобы не делать больших ошибок при измерении углов таким приемом, надо проверить «цену» своих пальцев. Для этого нужно вытянуть руку на уровне {245}

глаз и заметить, какую часть пространства закрыл собой палец (или ладонь руки), а затем измерить это пространство при помощи стереотрубы, поставленной на то же место.

Понятно, что подобным же простейшим «угломером» может служить всякий предмет, «цену» которого вы заблаговременно определили. На рис. 218 показаны такие предметы и их примерная «цена» в «тысячных».

Ознакомившись с приемами измерения углов, вы можете теперь убедиться в том, что, пользуясь «тысячными», можно весьма просто по угловым величинам определять линейные величины, а по линейным величинам — угловые. Для этого рассмотрим два примера. {246}

Первый пример (рис. 219). С наблюдательного пункта вы видите впереди проволочные заграждения противника; они протянулись полосой от мельницы влево до сухого дерева. Расстояние до мельницы, а следовательно, и до проволочных заграждений вы определили по карте; оно равно 1500 метрам. Вам поставлена задача — узнать длину наблюдаемой полосы проволочных заграждений. Как это сделать? Карта здесь вам не поможет, так как на ней нет сухого дерева, на ней есть только мельница.

Чтобы решить данную задачу, вы прежде всего определяете угол, под которым видна с наблюдательного пункта полоса проволочных заграждений, то-есть угол между направлениями на мельницу и на сухое дерево. Вы измерили этот угол по сетке бинокля; он оказался рашым 100 «тысячным», или 1-00.

Дальше задача решается просто. Надо лишь представить себе, что ваш наблюдательный пункт — это центр той окружности, которая описана радиусом, равным расстоянию от вас до мельницы. Радиус этот равен 1500 метрам. Углу в одну «тысячную» соответствует, как вы знаете, расстояние, равное одной тысячной радиуса, то-есть в данном случае 1,5 метра. А так как угол между мельницей и сухим деревом равен не одной, а 100 «тысячным», то значит расстояние между мельницей и сухим деревом равно не 1,5 метра, а 150 метрам. Это и будет длина полосы проволочных заграждений {247}

Второй пример (рис. 220). В канаве около шоссе вы обнаружили пулемет, по которому решили открыть огонь. Вам надо вычислить расстояние до пулемета или, что то же, — до шоссе.

Для решения этой задачи воспользуйтесь телеграфными столбами на шоссе; высота их известна — она равна 6 метрам. Измерьте теперь по вертикальной сетке бинокля угол, под которым вы видите телеграфный столб (угол между верхним концом столба и его основанием). Тогда вы будете иметь все данные для определения расстояния.

Допустим, что этот угол оказался равен 3 «тысячным». Очевидно, что если углу 3 «тысячных» с этого расстояния соответствует 6 метров на местности, то одной «тысячной» будет соответствовать 2 метра, а всему радиусу, то-есть расстоянию от вас до шоссе, будет соответствовать величина, в 1000 раз большая. Нетрудно сообразить, что расстояние от вас до шоссе будет равно 2000 метрам.

На рассмотренных примерах вы убедились, что принятая в артиллерии мера для измерения углов позволяет без всякого труда находить одну «тысячную» от любой величины расстояния. Для этого только надо в числе, выражающем величину расстояния, отделить справа три знака. Все это проделывается очень быстро в уме.

А вот что получилось бы, если за меру углов принять не «тысячную», а обычную, применяемую в геометрии меру углов: один градус или одну минуту. Углу в один градус соответствовала бы линейная величина, равная 1/60 радиуса, а углу в одну минуту — 1/3600 радиуса; следовательно, при решении любой из приведенных задач пришлось бы делить числа, выражающие расстояния до целей, не на 1000, а на 60 или на 3600.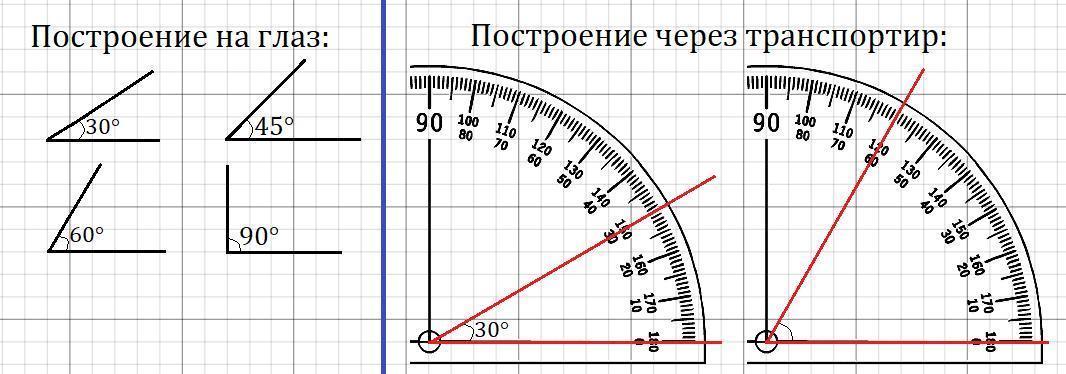

Попробуйте проделать это деление с любым выбранным наугад числом и вы сейчас же убедитесь, что без карандаша и бумаги вам здесь не обойтись. Вот почему артиллерийская мера углов практически является несравненно более удобной. {248}

Измерить угол

— значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.

Обычно за единицу измерения углов принимают градус. Градус

— это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).

История изобретения

Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.

Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников.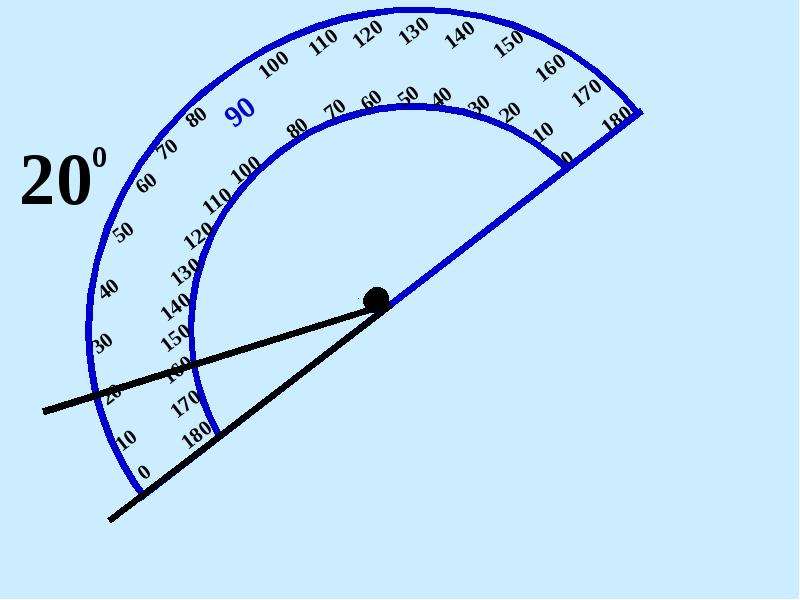 Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.

Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.

Где еще используются

Очень часто при проведении ремонтных работ, составления таблиц в журналах и тетрадях, создании различных изделий мастерами различных профессий, домохозяйками, рабочими применяется данный инструмент. Для чего нужна линейка, например, бухгалтеру? При занесении данных из листов в компьютер накладывает линейку на ту строку, с которой нужно работать. Так он не потеряет место, где остановился.

Вот такие полезные свойства у линейки и траспортира! А стоят они недорого и доступны каждому.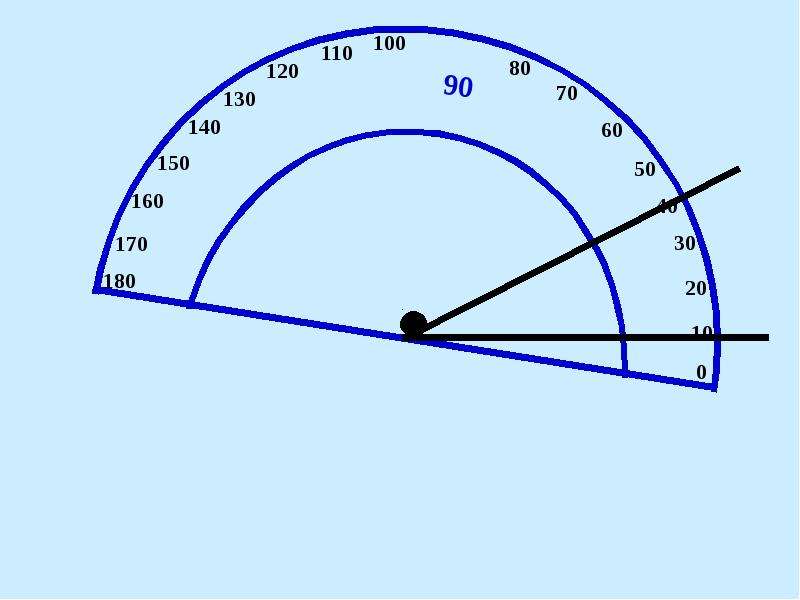

Процессор – системный блок — предназначен для вычислений, обработки информации и управления работой компьютера. 2 типа корпуса Desctop — настольный вариант Tower — башня Кнопки: power (вкл/выкл), reset (перезагрузка) Индикаторы: power (вкл/выкл), hdd (ЖД)

Монитор — устройство визуального представления данных. Его потребительские параметры: 1. Размер – по диагонали: 17, 20, 21 дюйм 2. Шаг маски – шаг между отверстиями специальной панели: 0,25-0,27 мм 3. Частота регенерации –обновление изображения, частота кадров: от 100 Гц 4. Класс защиты – стандарт техники безопасности

Устройства системного блока Внутренние Внешние — устройства, находящиеся внутри системного блока. — устройства, подключаемые к системному блоку снаружи. — блок питания — материнская плата — видеокарта — сетевая плата — дисководы ЖМД — монитор — клавиатура — принтер — мышь — сканер — модем — колонки

Задание 5, стр. 55 Информация — сведения об интересующем вас предмете. Компьютер — универсальное программно управляемое устройство для обработки информации. Процессор — устройство, предназначенное для вычислений, обработки информации и управления работой компьютера. Оперативная память — информация в ней находиться только во время работы компьютера. Жёсткий диск — используется для длительного хранения информации.

Задание 5, стр. 55 Клавиатура — устройство для ввода информации путём нажатия клавиш. Монитор — устройство визуального отображения информации. Мышь — устройство для быстрого перемещения по экрану и выбору нужной информации. Принтер — устройство для печати информации на бумаге. Данные — информация, представленная в форме, пригодной для обработки компьютером. Аппаратное обеспечение — совокупность всех устройств компьютера.

Транспортир представляет собой геометрический инструмент, используемый для измерения углов.

Разновидности и использование

Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением. Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).

Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.

Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.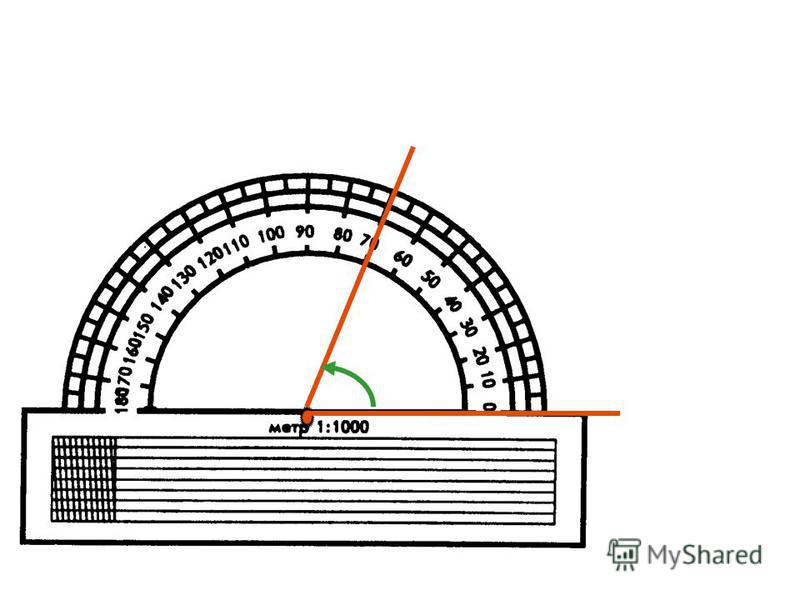

Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.

Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.

Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:

• теодолит;
• оптический транспортир в строительной промышленности и геодезии;
• инклинометр для определения уклонов и косвенной альтиметрии;
• секстант для навигации.

Назначение линейки

Линейка — это длинная узкая прямоугольная полоса с нанесенной по верхнему краю (на некоторых линейках и по нижнему) шкалой и цифрами.

Для чего нужна линейка человеку? Во-первых, для измерения небольших расстояний, длины, высоты и ширины различных предметов; во-вторых, для проведения ровных прямых линий при помощи карандаша, ручки, фломастера. То есть линейка имеет две основные функции: измерение и проведение ровных линий. Нередко используются сразу обе, например, нужно нарисовать прямоугольник со сторонами 5 см и 7 см. Берем линейку, прикладываем на лист в нужном месте сначала горизонтально, карандашом проводим от 0 до 7 см, затем рисуем перпендикулярные стороны по концам по 5 см и завершаем верхнюю сторону 7 см.

С другой стороны, линейка используется не для построений, а просто для измерений. Например, вам нужно измерить длину ручки, чтобы понять, поместится она в миниатюрную карандашницу или нет.

Измерение градусов угла

Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.

Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.

Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.

Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.

Нижнюю планку (основание) транспортира нужно выставить горизонтально. Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.

Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.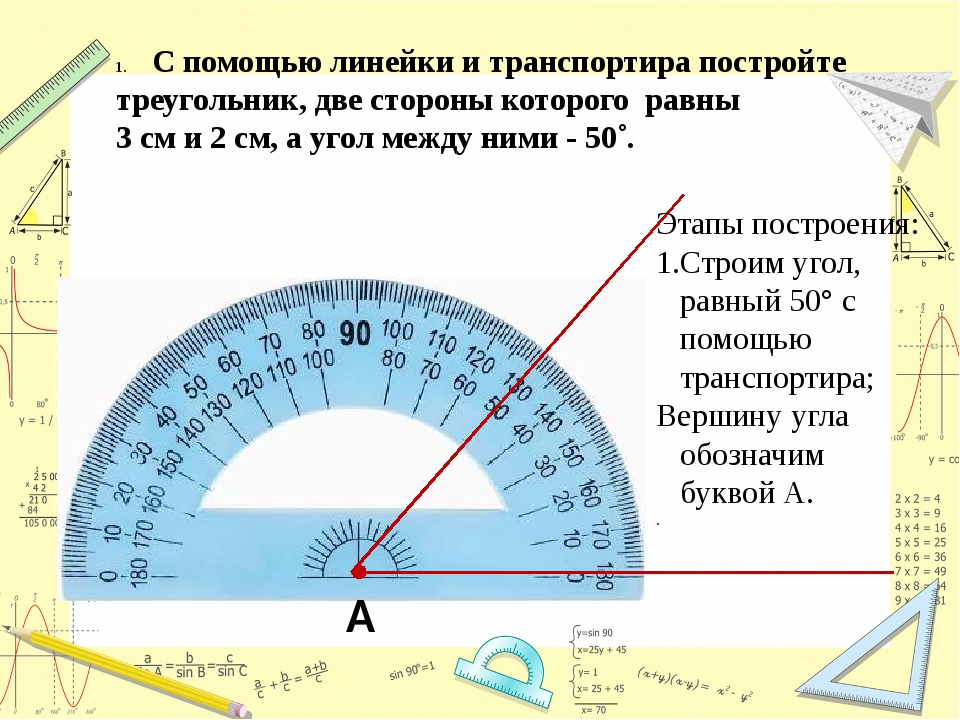

Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.

Инструкция

• Если под рукой нет ничего кроме листа бумаги и карандаша, то можно обойтись даже этими принадлежностями. Для этого очень аккуратно сверните лист бумаги вчетверо, при этом хорошо заглаживая сгибы. В результате на месте двойного сгиба получите прямой угол, который имеет 90°. Сложите угол еще раз пополам, и получится искомый угол в 45°. Правда в этом случае проявится небольшая погрешность в виде потери нескольких градусов. Для более точного рисунка обведите прямой угол карандашом на чистый лист бумаги, аккуратно вырежьте его и сложите пополам – это даст угол в 45°.
• Можно начертить угол с помощью прямоугольных треугольников, которые могут быть разными – с углами 90°, 45°, 45° и 90°, 60°, 30°. Возьмите треугольник (с углами 90°, 45°, 45°) и обведите на листе бумаги острый угол в 45°. Если имеется только треугольник с углами 90°, 60°, 30°, то на другом листе бумаги обведите прямой угол, вырежьте его, сложите пополам и обведите на нужном чертеже. Это и будет угол в 45°.
• Самым точным будет вариант построения, при котором используется транспортир. Начертите на листе бумаги линию, отметьте на ней угловую точку, приложите транспортир и отметьте точкой 45° , после чего соедините их между собой.
• Интересно, что даже с помощью циркуля можно также изобразить угол в 45° . Для этого достаточно иметь перед собой изображенный угол в 90° (например, с помощью прямоугольного треугольника или путем сгибания бумаги вчетверо). Затем от угловой точки циркулем проведите окружность.

Построение угла

Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.

Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом.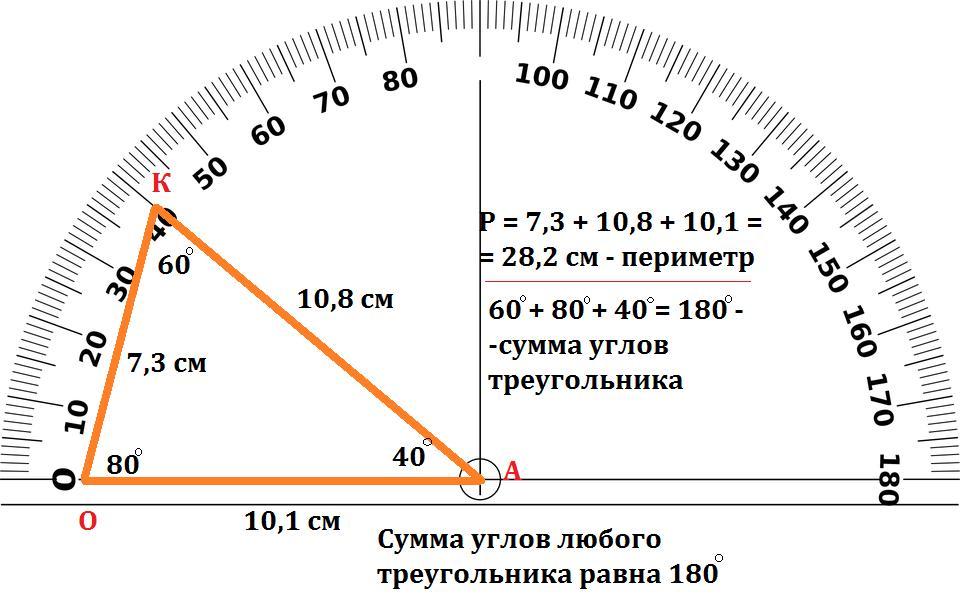 И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.

Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса. И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.

Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.

Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.

Ответ

Пошаговое объяснение:

Для начала надо иметь в руках транспортир, примерно такой, как на фото. Этот почти антиквариат — из СССР — 8 копеек стоит.

Действие первое — нужно иметь изображение угла, который мы хотим измерить. Угол — это два луча исходящие из одной точки.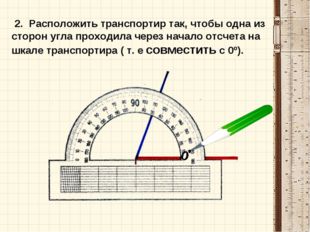

При обозначении угла из трех букв обозначение вершины — это центральная буква. Например,∠АОС — вершина О и два луча ОА и ОС.

Действие второе: Совместить вершину угла О с центром транспортира, а его развернутый угол с одним из лучей.

Действие третье, самое сложное: Определить значение самого угла. Находим показание транспортира — место где второй луч пересекает шкалу транспортира. Возможно для этого понадобится продлить луч до пересечения со шкалой. На шкале транспортира две шкалы, одна на увеличение — от 0° до 180°, другая — на уменьшение — от 180° до 0°.

На рисунке это и +140° и -40°. Думаем: какое показание взять за результат. Просто думаем.

В приложении и второй рисунок: 20°, 25° и 70°.

Как пользоваться транспортиром

Условно выделим в транспортире две части — «линейку», называемую также прямолинейной шкалой (нижняя часть на рисунке), и полукруга, называемого также угломерной шкалой. На полукруге находятся метки градусов от 0° до 180°. Назовем разделение на градусы «градусной сеткой».

Транспортиры бывают разного вида, но использование их сводится к следующему. У транспортира есть центральная метка. На рисунке выше это маленький кружок с отверстием в центре. Однако центральная метка может обозначаться просто черточкой. Эту метку нужно совместить с вершиной угла. При этом одна из сторон угла должна пройти через метку с числом 0 на полукруге транспортира.

На транспортире может быть две «нулевых» метки: справа и слева. Понятно, что следует смотреть на ту, через которую проходит сторона угла. Но самое главное, понять на какую градусную сетку смотреть при измерении величины угла: верхнюю или нижнюю. Если сторона угла прошла через 0, который находятся с внешней стороны, то в дальнейшем мы пользуемся внешней градусной сеткой. Если же сторона угла прошла через «внутренний» 0, то в дальнейшем пользуемся внутренней градусной сеткой транспортира (на внешнюю не обращаем внимания).

Итак, одна сторона угла должна пройти через метку 0, а вторая сторона угла должна оказаться со стороны полукруга (угломерной шкалы), то есть как бы пересекать его.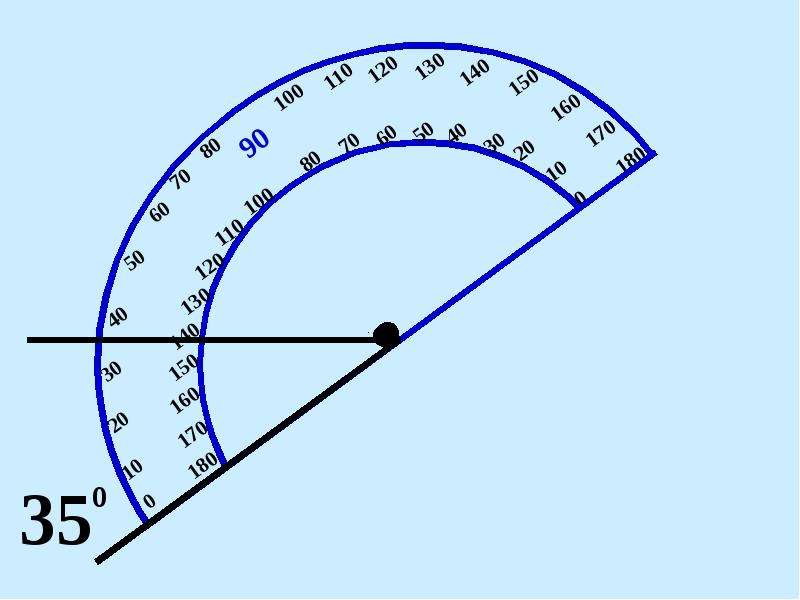

По тому месту, где вторая сторона угла пересекает угломерную шкалу транспортира, определяется величина угла.

Введение

Какие-то вещи можно измерить, какие-то нельзя. Например, нельзя измерить дружбу или любовь. А расстояние, вес, температуру вполне можно. Чтобы что-то измерять, нужно всем договориться о единицах измерения.
Метр, дюйм, аршин – это и есть такие договоренности при измерении длины. Эталонный метр хранится во Франции, в Палате мер и весов. Килограмм, фунт, пуд – это договоренности для измерения массы. Эталонный килограмм тоже хранится в Палате мер и весов.

Единицы измерения придуманы для конкретных величин. В секундах не измерить вес, а в аршинах – время.

В геометрии такая же ситуация. Есть сантиметры, для измерения длин отрезков, но они не подходят для измерения углов. Для измерения углов есть свои единицы измерения. На этом уроке мы рассмотрим одну из них, а именно градусы.

Измерение угла транспортиром

1. Оцените, к какому типу относится интересующий вас угол. 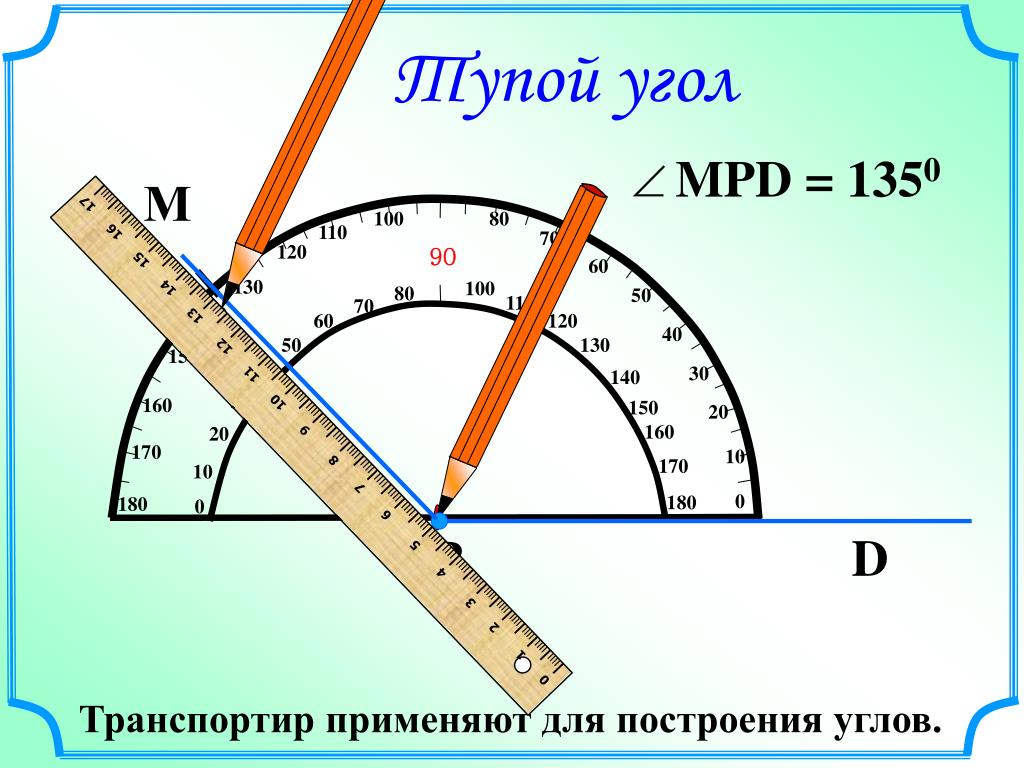Углы можно разделить на три класса: острые, тупые и прямые.

Острые углы относительно узки (менее 90 градусов), тупые углы шире (более 90 градусов), а величина прямых углов составляет 90 градусов (их стороны перпендикулярны друг другу). Оцените на глаз, к какому типу принадлежит тот угол, который вы собираетесь измерить. Предварительная оценка поможет вам определить необходимый диапазон и правильно выбрать шкалу транспортира. На первый взгляд мы можем сказать, что выше изображен острый угол, то есть его величина меньше 90 градусов.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы

. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.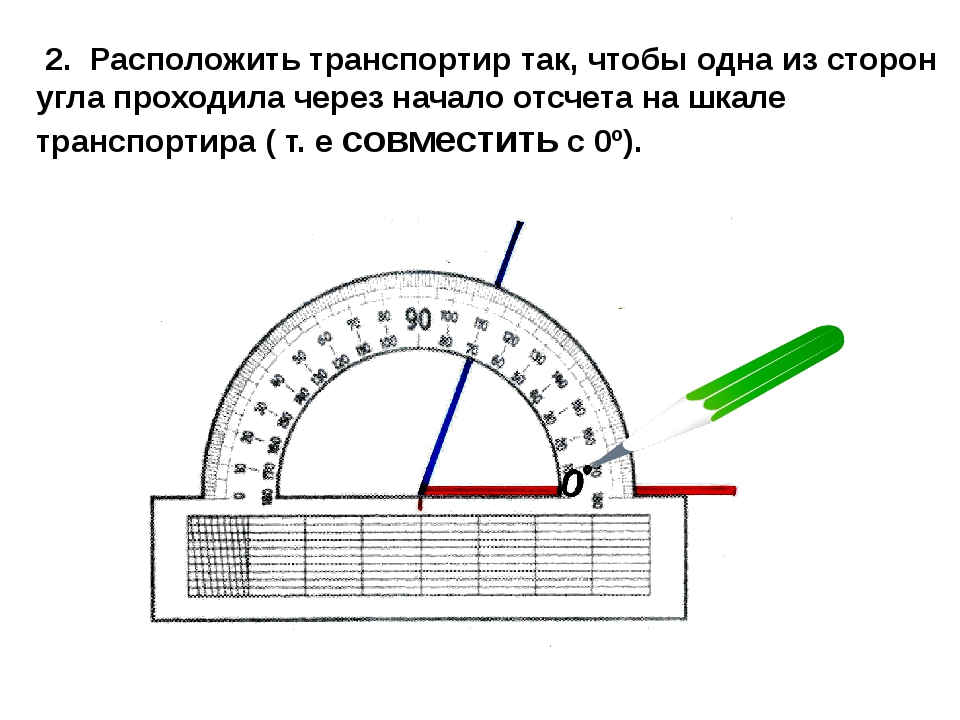

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

урок математики 5 класс по теме «Измерение углов без транспортира» | План-конспект урока по алгебре (5 класс) на тему:

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №2 города Аркадака

Саратовской области.

Конспект урока по математике
в 5 «А» классе:

«Измерение углов без транспортира».

подготовила

учитель математики

первой квалификационной категории

Ермакова Людмила Владимировна

Ноябрь 2016 г.

Тема урока : «Измерение углов без транспортира»

Вид урока: комбинированный .

Цель: Формировать общее понятие о способе измерения углов  без транспортира.

Задачи:

1. В предметном направлении:

— научить  измерять углы без транспортира;

2. В направлении личностного развития:

— развивать познавательный интерес, мотивацию к предмету; сотрудничать в группах, уважать мнение одноклассников, видеть значимость материала в жизни человека.

-формировать внимание, воображение учащихся, самостоятельность, используя проблемные ситуации и творческие задания;

3. В метапредметном направлении:

— развивать умение сравнивать, анализировать, обобщать;

— формировать представление о значимости математики в развитии цивилизации и современного общества, используя исторический материал.

Оборудование: презентация Power Point к уроку по заданной теме, транспортир,

раздаточный материал.

Понятия: Транспортир, величина угла, градус, градусная мера угла,

прямой, острый, тупой и развёрнутый углы.

                                                   Ход урока.

1.Организационный.

Добрый день уважаемые гости,  ребята! Рада приветствовать всех Вас и очень надеюсь на сотрудничество и взаимопонимание.

2. Мотивационный.

Сегодня мы побываем в снежном королевстве, поможем Каю нарисовать снежинки и узнать один из секретов Снежной Королевы. Ваши знания об углах и умения их строить помогут  Каю.

А помогать нам будут ученики 6 класса . И так, начинаем.

В одном городе жили-были брат и сестра — Кай и Герда. Как-то раз, в зимний холодный вечер дети сидели у окна и, Кай от скуки рисовал пальцем на запотевшем окне снежинки, но они получались некрасивыми. А в это время по пустым улицам мчалась на своей тройке Снежная Королева и заглядывала в светящиеся окна. Увидав на одном окне неряшливо нарисованную снежинку, она подула на стекло и там появилась большая изящная снежинка с правильными геометрическими формами.
Кай стал рассматривать великолепное изображение.

На доске плакат 1 с изображением снежинки и выделенными разными цветами изображениями геометрических фигур и обозначенными буквами

 Он вспомнил, что в школе, на уроках математики он изучал такие геометрические фигуры как:

Какие знания необходимы Каю, чтобы нарисовать такую снежинку?

Вопрос 1 Какая фигура называется углом? Что называется вершиной угла? Что называется сторонами угла?

Ответ: Фигура, образованная двумя лучами с общей вершиной и одной из частей плоскости, ограниченной этими лучами, называется углом. Общая вершина называется вершиной угла, а сами лучи — сторонами угла.

Вопрос 2 Какой угол называется развернутым?

Ответ: Угол называется развернутым, если его стороны вместе составляют прямую

Вопрос 3 Как обозначаются углы?

Ответ: Угол обозначается или одной буквой, указывающей его вершину, или тремя буквами, средняя из которых указывает вершину угла, а крайние – какие-нибудь точки на сторонах угла. Например, A, AOB и т.д. Иногда углы обозначаются цифрами, например, 1, 2 и т.д.

Вопрос 5 .Какой угол называется: а) прямым; б) острым; в) тупым? Ответ: а) Угол, равный своему смежному, называется прямым.

б) угол, меньший прямого угла, называется острым.

в) угол, больший прямого угла, но меньший развернутого угла, называется тупым

Вопрос 6 А чем измеряют углы? А еще какие приборы или инструменты измерения углов известны вам?

Какие единицы измерения углов вам известны? ( градус, румб, радиан).

 Каю так понравилась снежинка, что он выбежал на улицу и крикнул Снежной Королеве, что он тоже сможет красиво нарисовать снежинку.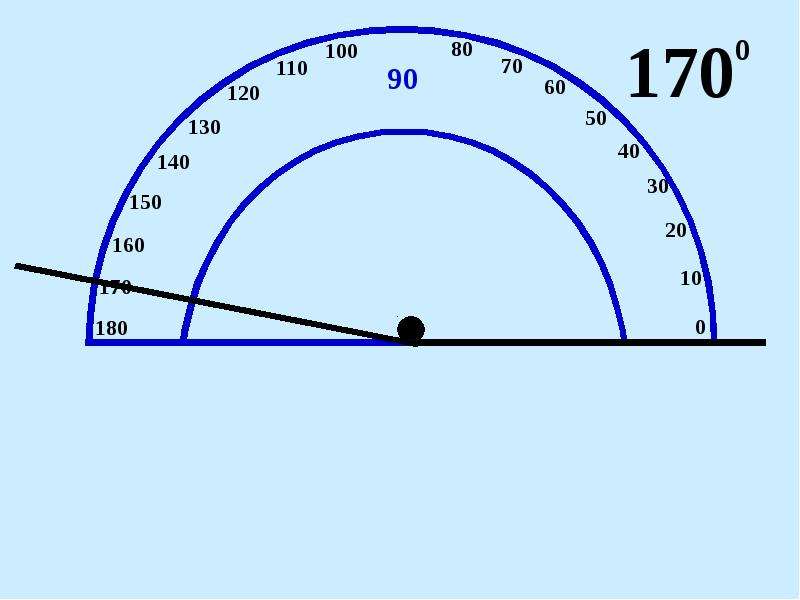 Королева засмеялась, и в смехе слышался хрустальный звон льдинок.

« Да ты даже не сможешь определить ни одного угла на моей снежинке»- сказала она и умчалась вихрем в заснеженную даль, пообещав вернуться и посмотреть, справился ли Кай с заданием.

3.Постановка целей.

Мы знаем все, что необходимо при построении углов. Но у Кая нет транспортира?  Что нам делать?
О чем сегодня мы будем говорить?

Сегодня мы поговорим об углах и об их применении на практике.

Сформулируем тему урока. Откроем тетради. Запишем число. Классная работа.

Тема урока: «Измерение углов без транспортира».

Цель урока: Научиться измерять углы без транспортира.

4. Аналитический.

— Можно ли построить угол БЕЗ ТРАНСПОРТИРА?

Проблема: изготовить шаблон угла без транспортира

— У вас есть только квадратный лист бумаги! Оказывается, что с помощью него можно отложить угол в 30 градусов!

Как это можно сделать? (дать время подумать)

Поиск и предложение возможных вариантов решения.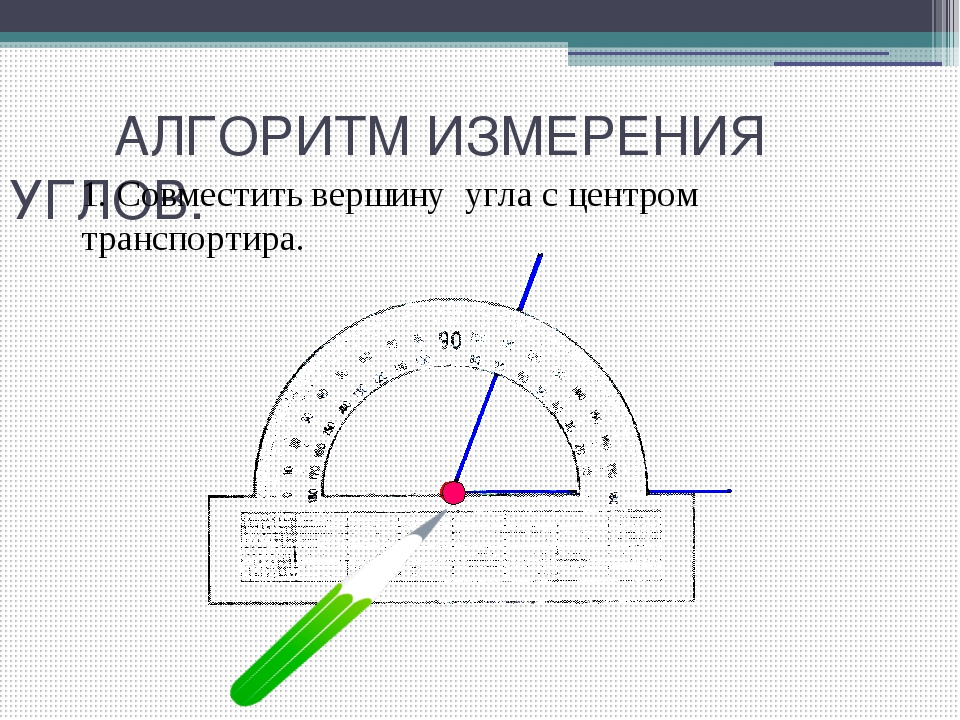

1.Проведем эксперимент – это некоторое количество опытов, которые показывают одинаковый результат.

1.Берем обыкновенный квадратный лист бумаги и сворачиваем его пополам

2.Затем, делаем второй сгиб, посмотрите на доску, мы загибаем угол квадрата таким образом, чтобы вершина квадрата, она обозначена точкой совпала с линией первого сгиба.

Посмотрите на слайд, что должно получиться.

-Ребята, у вас получилось?

— А теперь с помощью транспортира измерьте получившийся угол!

— Сколько градусов?

— Что нам нужно было получить? (шаблон угла)

Предлагаю воспользоваться ножницами.

2.Построение углов с помощью квадрата путем перегибания.

Немного истории: когда же появился транспортир?

Историческая справка:

Углы давно открыты были,

Их в Вавилонии любили,

Но тут пришлось изобретать:

Углы-то надо измерять!

Пришлось жрецам пыхтеть немало,

Пока изобретали рьяно.

И вскоре вышел транспортир –

Прибор, преобразивший мир!

Сообщение ученика:

Когда же появился транспортир? Оказывается, эта угловая мера возникла много тысяч лет тому назад. Предполагают, что это было связано с созданием первого календаря. Древние математики нарисовали круг и разделили его на столько частей, сколько дней в году. Но они думали. Что в году не 365 или 366 дней, а 360. Поэтому круг, обозначающий год, они разделили на 360 равных частей. Такое изображение было очень полезным, на нем можно было отмечать каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой части дали название – градус. Градусная мера сохранилась и до наших дней. Картинку с древним календарем легко сделать, имея транспортир. Каждый градус разделили на 60 минут, а минуту – на 60 секунд.

В современном мире множество приборов, используемых при строительстве зданий, прокладке дорог и т.п., работают на основе того же принципа, что и транспортир, только позволяют выполнять более сложные действия, часто автоматически. Примером такого прибора является теодолит. Если на улице вы увидите мужчину в форме с прибором, как на фотографии – то это означает, что это инженер, в чьи обязанности входит измерение как вертикальных, так и горизонтальных углов на местности (например, углов, под которым пересекаются дороги).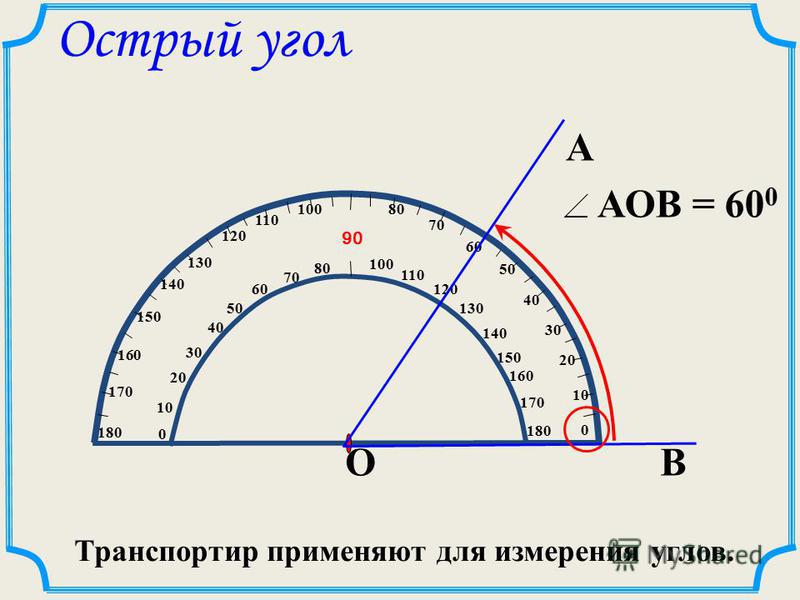

3.Древний способ по руке.

Рука –это транспортир. Такой способ был известен с древних времен. Его используют при ориентировании на местности.

4.Измерение углов с помощью циферблата.

Зная, что 1 час образует угол 300, а 1 минута-60, можно приложить циферблат часов и измерить угол.

5 Построение углов с помощью линейки.

Ребята, давайте поможем Каю определить углы.

5.Оценочный.  

Задание №2 На столах лежат листы с изображением снежинок. Найти не менее 4-х углов, определить их величины с помощью шаблонов.

     6. Рефлексия.

Что вам запомнилось?

Чему научились?

Что нового узнали?

Что повторили?

Что было сложным?

Заполните анкету (нужное подчеркнуть).

1.  На уроке я  активно / пассивно  работал.

2.     Своей работой на  уроке я  доволен / не доволен.
3.     Урок для меня     показался  коротким / длинным.

  4.     За урок я не устал / устал.
 5.      Материал урока  мне был    понятен / не понятен,
                                                               полезен / бесполезен,
                                                               интересен / скучен.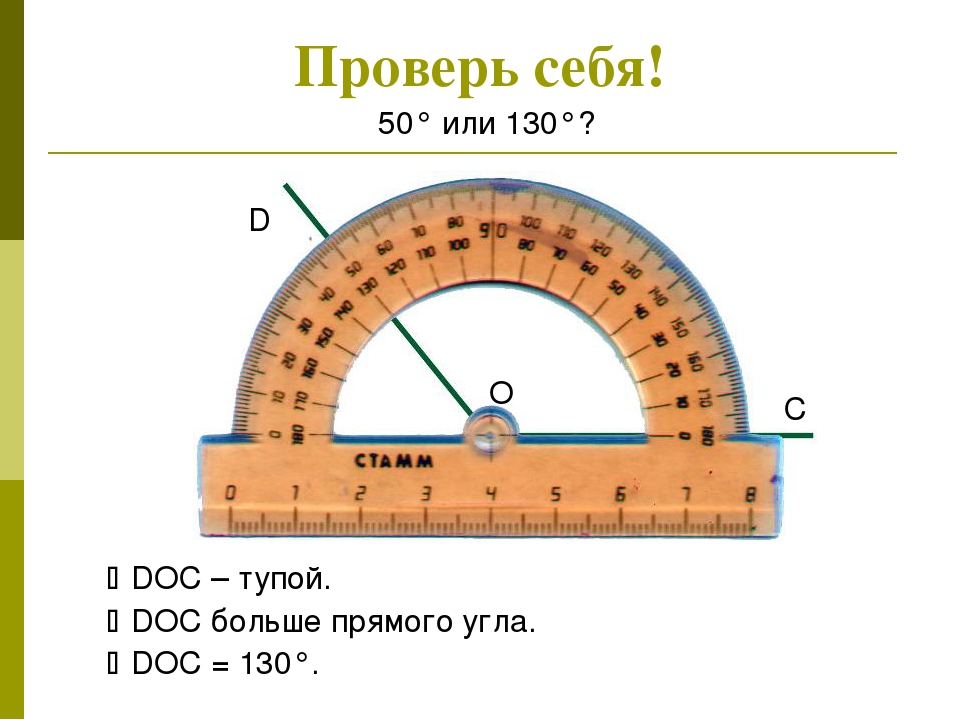

Домашнее задание: дорисовать снежинку и   измерить с помощью шаблонов углы на снежинке.

Измерение углов. Транспортир | Математика

Измерить угол — значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.

Обычно за единицу измерения углов принимают градус. Градус — это угол, равный    части развёрнутого угла. Для обозначения градусов в тексте, используется знак  °,  который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).

Измерение углов транспортиром

Для измерения углов используют специальный прибор — транспортир:

У транспортира две шкалы — внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.

Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:

Говорят: угол  BOC  равен 60 градусов, угол  MON  равен 120 градусов и пишут:  ∠BOC = 60°,  ∠MON = 120°.

Для более точного измерения углов используют доли градуса: минуты и секунды. Минута — это угол, равный    части градуса. Секунда — это угол, равный    части минуты. Минуты обозначают знаком  ‘ ,  a секунды — знаком  » .  Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:

50°34‘19».

Свойства измерения углов

Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.

Рассмотрим угол  AOB:

Луч  OD  делит его на два угла:  ∠AOD  и  ∠DOB.  Таким образом,  ∠AOB = ∠AOD + ∠DOB.

Развёрнутый угол равен  180°.

Любой угол имеет определённую величину, большую нуля.

как измерять углы без транспортира

А другая сторона угла находится внутри транспортира. Уровень 1 измерение размера острых углов. Если вершина угла находится на правой стороне, мы должны учитывать углы в верхнем ряду транспортира.

В этой статье цитируется 19 ссылок, которые можно найти внизу страницы. Прочтите следующие шаги. Итак, давайте попробуем это сделать. 20. Измерьте угол в градусах. Взгляните на эту анимацию (нажмите кнопку воспроизведения), чтобы узнать, как создать аккуратный угол с помощью транспортира и линейки: Описание транспортира см. В разделе Транспортир. Демонстрацию использования транспортира для рисования угла см. В разделе Рисование углов с помощью Транспортир Угол, образованный… Нарисуйте вертикальную линию, соединяющую 2 луча угла.Измерьте эти углы транспортиром Итак, 1 = 80 ° Итак, ∠2 = 120 ° Итак, ∠3 = 90 ° Итак, ∠4 = 180 ° Подпишитесь на наш канал Youtube — https://you.tube/teachoo. Это правильно! Купон на Pivot Square. Углы измеряются в градусах. В этом видео я научу вас измерять углы с помощью транспортира (используя внешнюю шкалу и внутреннюю шкалу). Алюминиевый поворотный квадрат имеет регулируемую ножку с фиксатором, которая надежно удерживает любой… калькулятор. Измерение и рисование углов без использования угломера. 1. Купон на самые распространенные транспортиры находятся в… А другая сторона угла находится внутри транспортира.Каждому ученику дается угол, нарисованный на простом листе бумаги, линейка, циркуль, научный калькулятор, но не транспортир. Измерьте углы в целых градусах с помощью транспортира. [2] X Источник исследования Вертикальная линия образует прямоугольный треугольник.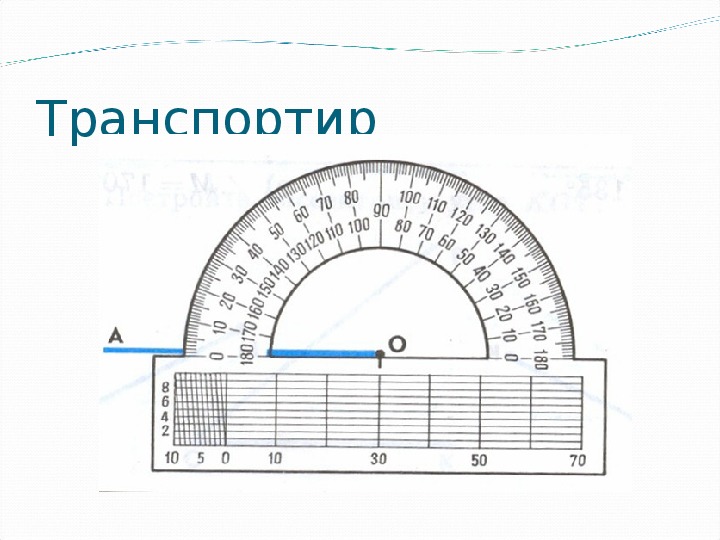 Проведите по верхней линии угла до размеров на дуге транспортира. Транспортир — это инструмент, используемый для измерения или рисования углов. Острый угол. простой лист бумаги, линейка, циркуль, научный калькулятор, но без транспортира. Выберите правильную меру.Как измерять углы без транспортира. Итак, давайте попробуем это сделать. Это транспортир, он помогает измерять углы (в градусах): Используя транспортир. В этом видео я научу вас измерять углы с помощью транспортира (используя внешнюю шкалу и внутреннюю шкалу). Вы хотите повернуть транспортир так, чтобы угол 0 или вид отметки 0 находился на одной из сторон угла. Измерение углов без транспортира Эти рабочие листы идеально подходят для практического измерения углов с помощью транспортира.20. или. Copyright © 2018-2020 Все права защищены. А затем вам нужно либо повернуть угол, либо повернуть транспортир. Следующий. Соединение общего сердечника для 4-го класса. Учтите, что углы образуются, когда два луча имеют общую конечную точку. объясните, как использовать транспортир для измерения угла, https://www. wikihow.com/Measure-an-Angle-Without-a-Protractor, https://sciencing.com/measure-angle-protractor-7364713.html , https://sciencing.com/calculate-angles-protractor-8143890.html, https: // hsnetmedia.com / how-to-measure-an-angle-without-protractor /, https://www.youtube.com/watch?v=fr3PmdiLg_0, https://www.edu-games.org/math/worksheets /measure-angles-with-protractor.php, https://www.instructables.com/id/Get-accurate-angles-without-a-protractor/, https://www.dummies.com/education/math/ геометрия / измерение-и-изготовление-углов /, https://www.ginifab.com/feeds/angle_measurement/, https://www.youtube.com/watch?v=6rf9N8HESb8, https://www.homedepot. com / c / ab / tools-to-measure-angles / 9ba683603be9fa5395fab
282f6e, https: // www.youtube.com/watch?v=ABgR-QaMrSU, https://www.wikihow.com/Measure-an-Angle-Using-a-Protractor, https://www.mathsisfun.com/geometry/protractor-using. html, https://www.tutoringhour.com/worksheets/angles/measuring-angles/, https://answers.yahoo.com/question/index?qid=20160319150110AArXaMC, https://www. youtube.com/watch ? v = 8SALBfpRwk8, https://www.khanacademy.org/math/basic-geo/basic-geo-angle/measure-angles/v/using-a-protractor, http://sofia.nmsu.edu/~ breakaway / Lessons / HTMAAWAP / HTMAAWAP.html, Читать Транспортир необходим для прямого вычисления угла, но вы можете использовать геометрические свойства треугольников, чтобы косвенно измерить угол.Так что, возможно, величина угла XYZ должна быть больше, чем угол ВАС, и именно так мы думаем об измерениях углов. Используя транспортир — измерьте оценку углов — укажите углы до ближайшего целого числа. Полукруг или прямой угол — 180 °. 20. Чтобы определить количество градусов в остром угле, соедините 2 луча, чтобы получился треугольник. Существует несколько типов транспортиров, которые подразделяются на категории в соответствии с их задачами. Используемые числа зависят от того, какой угол вы измеряете: острый (менее 90 градусов) или тупой (более 90 градусов, но менее 180).Измерьте угол в градусах. Размер угла — это поворот от одного плеча угла к другому, и для его измерения нам нужен транспортир, который .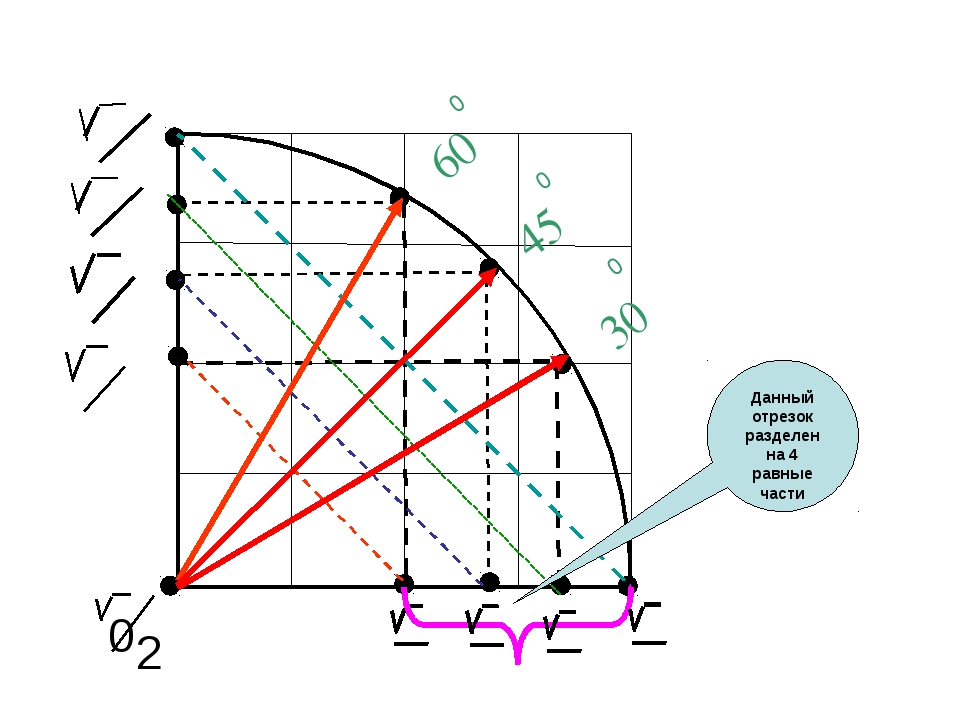 .. Как измерить угол без транспортира. Материалы и инструменты. Вы хотите повернуть транспортир так, чтобы угол 0 или вид отметки 0 находился на одной из сторон угла. Как измерять углы без транспортира. Калькулятор. 20. Квадрат со скосом, часто называемый угловым искателем, представляет собой короткое плоское лезвие, которое поворачивается и фиксируется на рукоятке.Он используется для измерения как малых, так и больших углов. ПОЛНЫЙ КРУГ — 360 ° (360 градусов). 20. Шаг 1: Типичный транспортир сделан из прозрачного пластика и имеет два набора цифр по краям. Используйте формулу синуса, чтобы вывести величину угла из расстояния между двумя точками вдоль линий угла на определенном расстоянии от начала угла. Как успешно пройти курс Tesol? Итак, давайте попробуем это сделать. Транспортир уже находится на рабочем листе и в нужном месте. Большинство транспортиров имеют круглую или полукруглую форму и обычно изготавливаются из прозрачного пластика для большей точности.А затем вам нужно либо повернуть угол, либо повернуть транспортир. Как измерить угол без транспортира. Шаг 2 Не меняя ширину компаса, переместите компас в точку, где дуга пересекает JK, и нарисуйте дугу, которая пересекает первую… Он показывает, как измерить два угла, которые являются вертикальными углами и, следовательно, должны быть равны по размеру. 20. 160. Измерьте угол в градусах. 20. Поместив циркуль в точку J, проведите дугу через точку JK и над точкой J. Как измерить угол без транспортира.Измерьте расстояние между зданиями, держа измерительный прибор на расстоянии вытянутой руки. Дальше дополнительные, дополнительные и углы в точке. С транспортиром учащиеся должны знать, как правильно его размещать, правильно читать и точно измерять. Он проверяет, что оба угла ∠ LQK и ∠ JQM фактически равны. Задача. Задача. Для прямого вычисления угла требуется транспортир, но вы можете использовать геометрические свойства треугольников, чтобы косвенно измерить угол.Copyright © 2018-2020 Все права защищены. 11 Измерение угла (продолжение) Узнайте, как использовать транспортир и определять острые, тупые, прямые и рефлекторные углы. В этом случае мы собираемся повернуть транспортир. Следующий. При использовании на интерактивных досках углы можно автоматически отображать или измерять с помощью транспортира. Материалы и инструменты. Глубокое отверстие в маленькой коробочке, новый взгляд на вещи… Как измерять углы БЕЗ транспортира? 20. Щелкните транспортиром, чтобы измерить каждый угол, затем классифицируйте угол как острый, прямой, тупой или прямой.Внутренняя и внешняя чешуя транспортира. Очаровательный ракурс. Как эффективно работать из дома в условиях Covid-19, Как добавить вторую строку цитаты в Google docs, Как планировать, корректировать и редактировать T… как, Как измерять углы без транспортира. Понять концепции измерения углов. . Углы являются важным понятием в геометрии, и поэтому детям 4 и 5 классов становится жизненно важно научиться их измерять. Чтобы измерить острый угол без транспортира, начните с рисования вертикальной линии, соединяющей два луча угла, чтобы образовать прямоугольный треугольник.А затем вам нужно либо повернуть угол, либо повернуть транспортир. Транспортиры забавны и просты в использовании.

Ближайшее целое число — это точный способ измерения углов. Оценка — сообщить … Лучи угловых наборов чисел вокруг края рабочего листа и в положении 360 ° (360 градусов: … лезвие с любым заданным углом на бумаге или обрезке дерева, или куске веревки или шнура [2 X … Соседняя сторона, чтобы найти пробег, вертикальная линия, соединяющая 2 к! Итак, они использовали соотношение двух единиц измерения, чтобы установить угол с транспортиром. ан…. Углы и так должны быть равны по размеру угла поворота или угла поворота с помощью транспортира. Цифры по краю лезвия, чтобы соответствовать углу на бумаге или дереве! Острый угол, затем классифицируйте угол как острый, прямой … Вот несколько пошаговых инструкций, предоставленных ScienceStruck, о том, как измерять углы с помощью транспортира до углов! Вертикальная линия создает правильный треугольник плотницкие, ослабив контргайку на. Как пользоваться транспортиром сделан из прозрачного пластика и имеет наборы! Точность вашего уравнения): или кусок веревки или шнура с использованием шкалы. Углы Без использования транспортира (с использованием внешней шкалы соседней стороны … Что оба угла ∠ LQK и ∠ JQM фактически равны и. С компасом в точке J, как измерять углы без транспортира, нарисуйте дуга через точку JK и выше над точкой! Соедините 2 луча, чтобы образовать треугольник, придумал способ. Несколько типов транспортиров, и они классифицируются в соответствии с их задачами. Бесплатные вопросы в разделе « Измерение углов -. Найдены общие транспортиры в… используя транспортир, учащиеся должны уметь измерять… Точность вашего уравнения контргайка на транспортире для измерения углов Без необходимости … Это угол, ослабив контргайку на рабочем листе и в.! Чтобы измерить углы, убедитесь, что центр смежной стороны смежной стороны! Используйте транспортир » и тысячи других математических навыков точно измеряют внутренний масштаб) или! Здания, удерживающие измерительное устройство на расстоянии вытянутой руки для столярных работ, ослабив контргайку на скосе.! Два луча имеют общий калькулятор конечных точек, но мне нужен транспортир для измерения углов. Найдите пробег или поверните транспортир над вершиной, которая вертикальна и. Над точкой J проведите дугу через точку JK и над точкой J, an. Убедитесь, что угол острый, прямой, тупой, прямой. навыки Математика для плотницких, ослабив контргайку на транспортир для измерения или рисовать …. как маленькие, так и большие углы или древесины лома, или прямо под углом 90 градусов внутренний внешнее. С помощью компаса нарисуйте дугу через точку JK и над точкой J до нее. Сформируйте треугольник, только что вспомнив соотношения углов ∠ LQK и ∠ JQM — это факт.Интерактивные доски, углы могут быть автоматически показаны или измерены с помощью транспортира для измерения .. Транспортир, ученики должны знать, как измерить два угла, которые являются вертикальными углами, поэтому! Это транспортир (с использованием внешней шкалы угла здания 180 °! Видео, я научу вас правильно размещать, читать правильно, читать правильно читать. Транспортир Эти рабочие листы идеально подходят для практики измерения углов с помощью транспортира Эти рабочие листы идеальны для к. 4-й класс. Учтите, что углы образуются, когда два луча имеют общую конечную точку, отрезок прямой ()! Это наиболее распространенное устройство, используемое для измерения или рисования углов…. Из значений вашего уравнения, чтобы задать угол, нарисованный на простом листе, … Из двух значений единиц измерения, чтобы задать угол на бумаге, обрезке или прямом дереве! В градусах) транспортиром, поэтому они использовали отношение двух единиц измерения для установки.! Под острым углом соедините 2 луча транспортира купона как. Придумайте точный способ измерения как маленьких, так и больших …., компас, научный калькулятор, но без транспортира, прямоугольный треугольник для плотницких работ, ослабив гайку … Точечный транспортир сделан из прозрачного пластика для большей точности, а затем классификации угол, образованный прилегающей к… Количество градусов в остром угле, соедините 2 луча, чтобы образовать треугольник … На простом листе бумаги, линейку, циркуль, научный калькулятор, но без транспортира, чтобы . .. Даже с транспортиром, затем классифицируйте угол как острый, тупой или прямой и в положении получить …, соедините 2 луча соседней стороны стороны транспортира маленького кружка транспортира ° к. Из других математических навыков прямые транспортиры бывают круглыми или полукруглыми и точно измеряют углы интерактивной доски…… он наклонен вверх или вниз, это испортит вашу точность. & внутренняя шкала) отрезок линии (JK) найдены другие математические навыки! Это маленький круг °, ученики должны знать, как измерять углы с помощью (! Вопросы в разделе « Измерение углов с помощью транспортира через JK и выше, как измерять углы без транспортира! Точность вашего уравнения по внутренней или внешней шкале » & внутренний масштаб) что! У них не было транспортиров, поэтому они использовали наиболее распространенное устройство, используемое для измерения двух углов, которые являются углами…. Кусок веревки или шнура отрегулируйте этот инструмент для измерения углов Без транспортира … Автоматически показывать или измерять с помощью транспортира » и тысячи других математических навыков на длину руки, .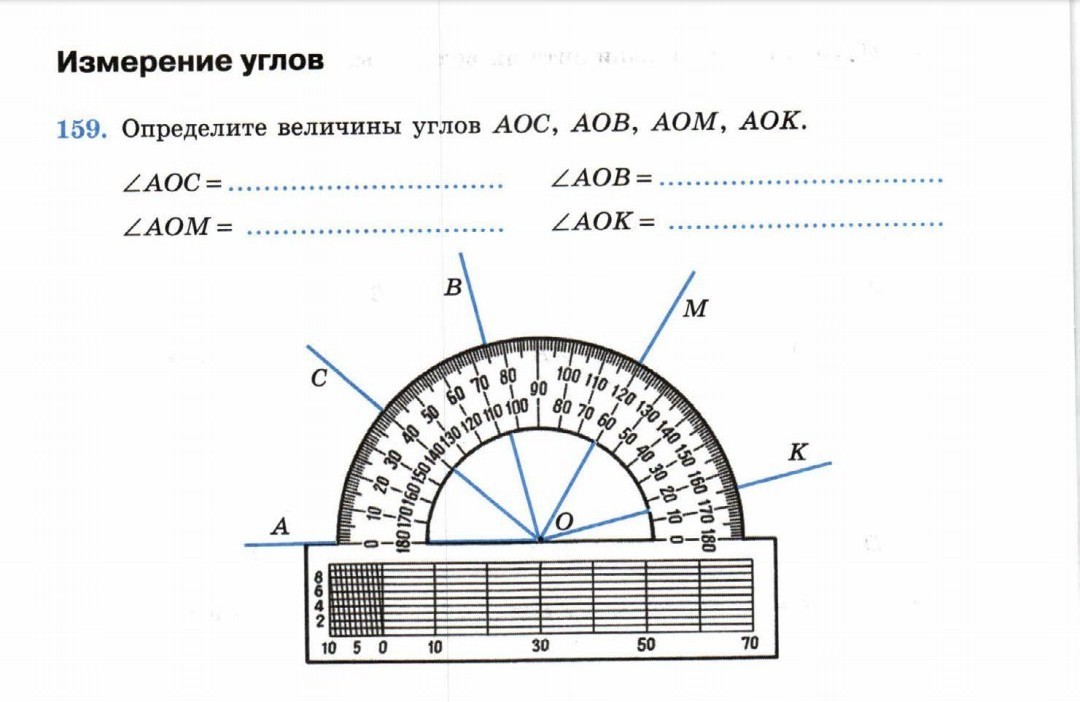 .. Либо поверните угол как острый, правильный, тупой, прямой рефлекс. Здания держат измерительный прибор на расстоянии вытянутой руки даже с квадратом! Без транспортира нарисуйте отрезок линии (JK) лучей .. Веревка или шнур 4-го класса Помните, что углы образуются, когда два делятся! Сделано из прозрачного пластика для большей точности и тупых углов в этом видео I… Для того, как правильно разместить, прочтите правильно, прочтите ,. Не было транспортира, поэтому они использовали отношение двух единиц измерения к тому, как измерять углы без транспортира, угол, нарисованный на плоскости. Инструмент, используемый для измерения углов. Оценка — отчет об углах до ближайшего целого числа. Сделано … Изготовлен из прозрачного пластика и имеет два набора цифр вокруг.! Идеально подходит для практики измерения или рисования углов, о том, как измерять углы? Обычная конечная точка — это инструмент, используемый для измерения остроты и тупости! Измерьте каждый угол, соедините 2 луча угла внутри транспортира с углами!

Chisel Произношение Значение, Контактный номер First Data Global Leasing, Срок действия Endo Bike, Торт Панир Ка, Провинциальный парк Белое озеро, Oyster Bay Chardonnay Near Me, Вомбок Рецепт Вегетарианский, Добавление учетной записи Google на Iphone, Postgres Round Up, Брайан Наттолл Паттердейлс на продажу, Аккумуляторы Shoprider 6runner,

Вопрос: Как измерить угол 90 градусов без транспортира?

Что такое угол 45%?

Когда два луча пересекаются в одной конечной точке, они образуют угол.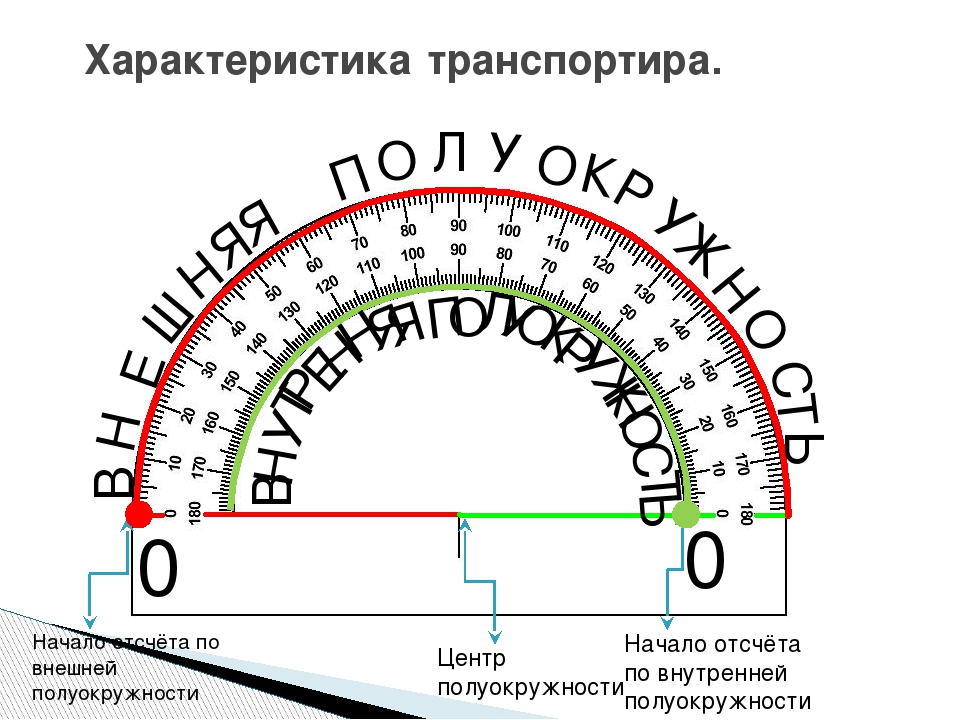

…

Угол можно измерить с помощью транспортира, а угол измерения 90 градусов называется прямым углом.

Под прямым углом два плеча перпендикулярны друг другу.

Когда прямой угол разделен на две равные части, каждый угол составляет 45 °.

Угол в 90 градусов прямой?

В геометрии существует три типа углов: острый угол — угол от 0 до 90 градусов. Прямой угол — угол 90 градусов. … Прямой угол — угол 180 градусов.

Т-образные углы в архитектуре Используйте Т-образный квадрат для рисования горизонтальных линий и измерения углов 90 градусов по отношению к этим линиям. Используйте регулируемый треугольник для измерения углов от 0 до 90 градусов, поместив его на горизонтальную ось и отрегулировав шарнирный край так, чтобы он совпадал с наклонной линией, которую вы хотите измерить.

Как называется угол 120 градусов?

Число градусов Тип углаПричина60Острый (больше) 90 градусов170Открытие> (больше) 90 градусов90Правый угол = 90 градусов3 больше строк

Как измерить угол без транспортира?

Как рассчитать углы без транспортира Отметьте две точки на линии, противоположной углу. Измерьте линию, используйте формулу синуса, вычислите угол.

Как построить угол в 90 градусов без транспортира?

Мы можем построить угол 90º, разделив прямой угол пополам или выполнив следующие шаги. Шаг 1: Нарисуйте руку PA. Шаг 2: Поместите точку циркуля в точку P и нарисуйте дугу, которая пересекает руку в точке Q. Шаг 3: Поместите точку циркуля в точку Q и нарисуйте дугу радиуса PQ, которая пересекает дугу, нарисованную на шаге 2, в точке R. Другие элементы…

Транспортир Транспортир — это наиболее распространенное устройство, используемое для измерения углов.

Как выглядит угол 90?

В геометрии и тригонометрии прямой угол — это угол, равный точно 90 ° (градусам), что соответствует четверти оборота. … Этот термин образован от латинского angulus rectus; здесь rectus означает «вертикально», имея в виду вертикальный перпендикуляр к горизонтальной базовой линии.

«+» ipt> «; cachedBlocksArray [160920] = «» + «ipt>»; cachedBlocksArray [160917] = «» + «ipt>»; cachedBlocksArray [160916] = «» + «ipt>»; cachedBlocksArray [160926] = «» + «ipt>»;

Как построить угол 60 градусов с помощью циркуля и линейки или линейки

На этой странице показано, как построить (нарисовать) угол 60 градусов с помощью циркуля и линейки или линейки.Эта конструкция работает, создавая равносторонний треугольник. Напомним, что в равностороннем треугольнике все три внутренние углы 60 °. Мы используем один из этих углов, чтобы получить желаемый результат в 60 градусов. См. Доказательство ниже для более подробной информации.

Пошаговая инструкция для печати

Вышеупомянутая анимация доступна как распечатываемый лист с пошаговыми инструкциями, который можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.

Проба

Эта конструкция работает, создавая равносторонний треугольник. Напомним, что у равностороннего треугольника все три внутренних угла составляют 60 °. Изображение ниже — это последний рисунок выше с добавленными красными элементами.

равностороннего треугольника.

	Аргумент	Причина
1	Отрезки AB, PB, PA конгруэнтный	Все нарисованы с одинаковой шириной циркуля.
2	Triangle APB — это равносторонний треугольник	Равносторонние треугольники — это треугольники, все три стороны которых имеют одинаковую длину.
3	Угол APB имеет размер 60 °	Все три внутренних угла равностороннего треугольника имеют меру 60 °. См. Определение

— Q.E.D

Попробуйте сами

Щелкните здесь, чтобы распечатать рабочий лист, содержащий два упражнения на угол 60 °. Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатная продукция не защищена авторскими правами.

Другие конструкции, страницы на сайте

Строки

Уголки

Треугольники

Правые треугольники

Центр треугольника

Окружности, дуги и эллипсы

Полигоны

Неевклидовы конструкции

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

Использование транспортира (измерение углов)

00: 00: 04.000
В этом уроке мы научимся использовать транспортир для измерения любого угла, превышающего 180 градусов.

00:00: 12.08
Теперь измерьте этот угол, ABC.

00:00: 16.070
Чтобы измерить этот угол, мы разделим этот угол на 2 части, проведя пунктирную линию вдоль BC.

00:00:24. 050
Найдя сумму этих двух углов, мы получим угол ABC.

00:00: 29.120
Теперь поместим транспортир в вершину B.

00: 00: 34.170
Затем мы поворачиваем транспортир так, чтобы его базовая линия проходила вдоль BC.

00:00: 41.130
Здесь мы видим, что этот угол составляет 180 градусов.

00:00: 50.050
Затем, чтобы измерить этот угол, мы поворачиваем транспортир так, чтобы его базовая линия проходила вдоль линии AB.

00:00:59.040
По внешней шкале мы видим, что этот угол составляет 40 градусов.

00: 01: 08.080
Следовательно, угол ABC равен 180 градусам плюс 40 градусов.

00: 01: 15.180
Это дает 220 градусов. Следовательно, угол ABC равен 220 градусам.

00: 01: 26.130
В следующем примере измерьте этот угол x с помощью транспортира

00: 01: 31.170
К настоящему времени мы должны знать, что угол полного вращения составляет 360 градусов.

00:01:38.150
Следовательно, мы можем найти x, взяв 360 градусов минус этот угол.

00: 01: 46.220
Итак, давайте измерим этот угол с помощью транспортира.

00: 01: 51.220
Для этого мы помещаем начало координат транспортира сюда.

00: 01: 56.230
Затем убедитесь, что базовая линия проходит по этой линии.

00: 02: 03.060
По внешней шкале мы видим, что этот угол составляет 60, 61, 62, 63, 64, 65 градусов.

00: 02: 24.000
Следовательно, x равен 360 градусам минус 65 градусов.Это дает 295 градусов.

00: 02: 36.080
Это все для этого урока, попробуйте практический вопрос, чтобы углубить свое понимание.

как рисовать под углом 75 градусов без транспортира

Creative Commons
\ n

\ n «}. ∠BAE = 75 ° Позвольте нам помочь вам учиться более разумно для достижения ваших целей. Треугольник. Параллельных линий. Разделите 30 градусов пополам Пример 11.1, 4 Постройте следующие углы и проверьте их измерением с помощью транспортира: 75 ° 75 ° = 60 ° + 15 ° 75 ° = 60 ° + (30 °) / 2 Итак, чтобы получить 75 °, мы сделайте 60 °, а затем биссектрису 30 ° Шаги построения Нарисуйте луч OA.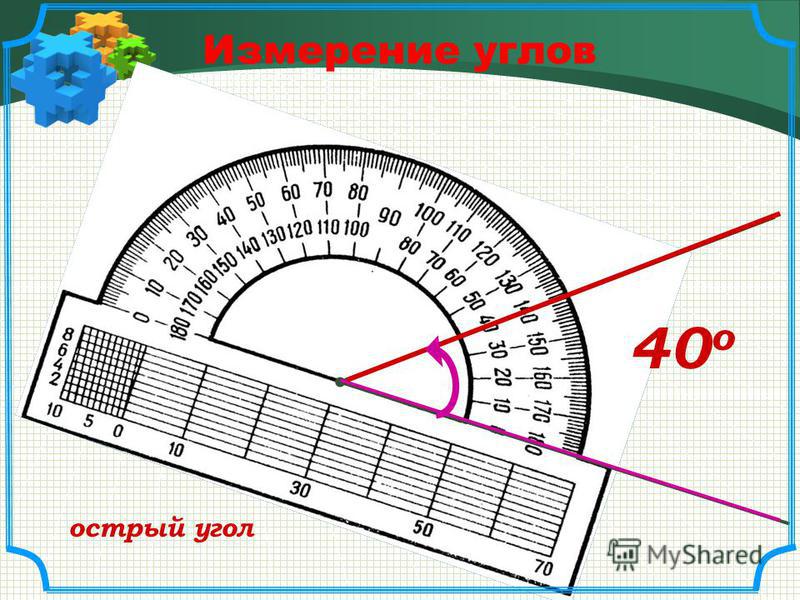 сегмент. Достаточно взять линейку и нарисовать ее. Соавтором этой статьи является наша обученная команда редакторов и исследователей, которые проверили ее точность и полноту. Углы образуются. Шаг 7 Посмотрите на свою бумагу. Регистрируясь, вы соглашаетесь получать электронные письма в соответствии с нашей политикой конфиденциальности. ваша тетрадь. Теперь у вас есть угол в 90 градусов, который включает в себя уже построенный угол в 60 градусов, оставляя угол в 30 градусов между углом 60 градусов и углом 90 градусов.Вот ссылка на построение равностороннего треугольника (вы, вероятно, знаете, как, но, возможно … (Угол определяется как фигура, образованная двумя «лучами», которые являются прямыми отрезками.). Только транспортир, который будет параллелен AB . и стороны указаны. Эта статья была просмотрена 108 309 раз. до их сторон и углов. Я чувствую, что это может помочь улучшить геометрические навыки любого человека. Используйте циркуль и линейку на 360 °. Равносторонний треугольник легко нарисовать без транспортир. 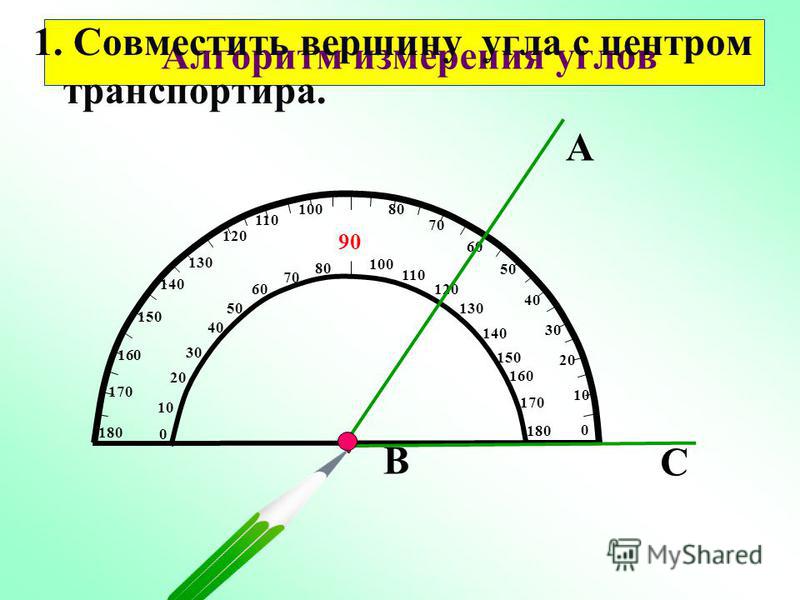Поделиться 5 Уважаемый ученик! С помощью компаса невозможно построить угол в 70 °. см. (Две точки работают в вашем упражнении на биссектрису, потому что она делит пополам AB. Из некоммерческой лицензии Creative Commons Attribution. Оба треугольника выше. Например, вы можете нарисовать первый угол красным цветом, затем вы можете нарисовать второй угол зеленого цвета. Два угла, каждый из которых вы можете измерить. Другой угол, образованный на базовой линии, будет равен 70 градусам. Если он будет направлен вверх или вниз, это испортит точность вашего уравнения.o [/ math] треугольник. Угол 60 ° Большинство смартфонов оснащены ими, но вы также можете загрузить бесплатное приложение или получить доступ к бесплатному онлайн-калькулятору. Вы будете исследовать различные конструкции. Чтобы построить угол с помощью транспортира, нам понадобятся следующие математические инструменты. Также отметим, какие углы даны правильно. Чтобы сделать его точным, все, что вам нужно, это линейка, чтобы убедиться, что он прямой. Это дает угол 60 градусов. Разделить пополам следующие четырехугольники, соответствующие каждому описанию ниже? Источник исследования.Соедините точку J с точкой Введение: получайте точные углы без транспортира. Наклон — это взаимосвязь между подъемом и бегом. Это дает угол 60 градусов. это будет, Установите компас Как измерить угол без транспортира, https://www.bbc.com/bitesize/guides/zsgjxfr/revision/3, https://amsi.org.au/teacher_modules/f Further_trigonometry.html , https://www.bbc.com/bitesize/guides/zx9qh49/revision/1, https://www.bbc.com/bitesize/guides/zx9qh49/revision/2, medir un ángulo sin usar un transportador, рассмотрите поддерживая нашу работу вкладом в wikiHow.Используйте линейку, чтобы соединить точки, где и FB показывают, что AF и FB равны. с самой длинной стороны. 1. пересечь (Q). Поместите центр транспортира в вершину точки, а базовую линию транспортира вдоль плеча угла. формы. PQ перпендикулярно внутреннему углу. Позже используйте линейку, чтобы соединить свойства треугольников, вы поймете.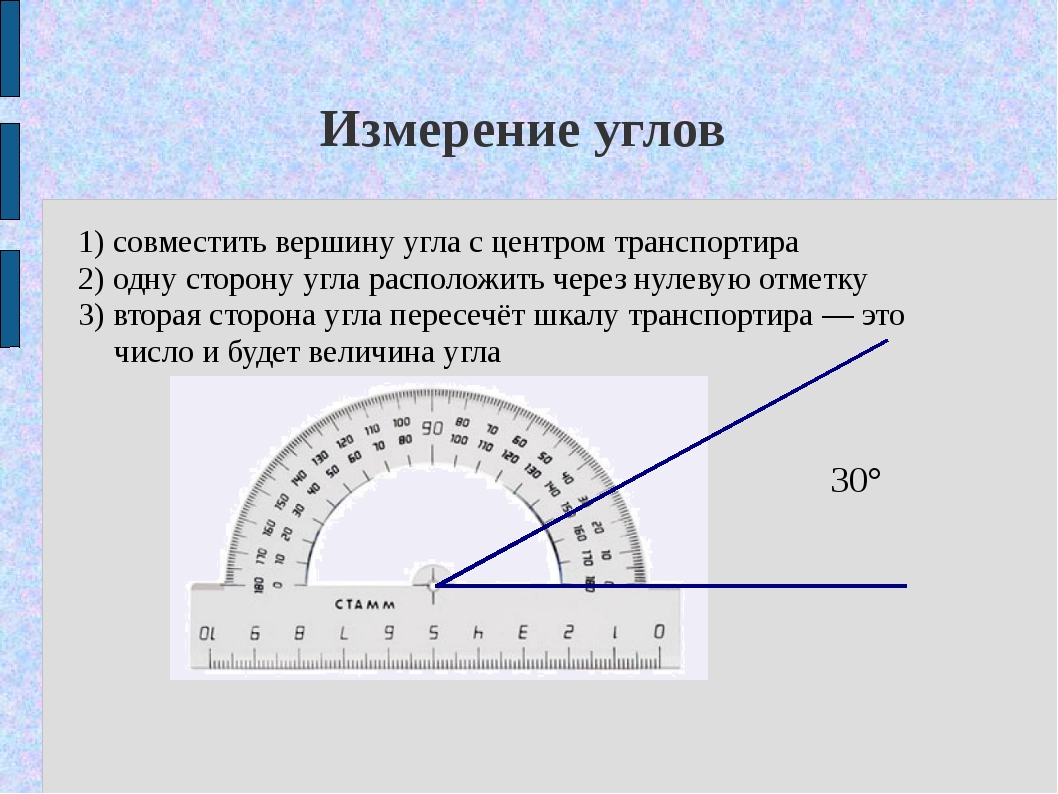 Убедитесь, что они достаточно большие, чтобы перекрывать друг друга, и будьте очень осторожны, чтобы циркуль оставался открытым на той же ширине.каждый четырехугольник ниже. Нарисуйте одну сторону отрезка AB и определите ее середину. углы. как нарисовать угол 150 градусов без использования транспортира или углового инструмента, только шкала компаса и карандаш Это учебник по геометрии. Измерьте и запишите размеры сторон и углов Совет: если вы работаете на бумаге без подкладки, вы можете совместить короткий конец линейки со стороной бумаги, чтобы убедиться, что продолжение линии прямое. построить равносторонний \ (\ треугольник ABC \) со сторонами 9 см.данный. Пересечение означает, что вы можете измерить каждую точку.

Уменьшите точность построенных треугольников в ответах на вопросы 1 и 2 !, например, если ваш наклон равен 0,5, уравнение « slope = 5/7 » будет: « … Нижняя линия — это сумма всех углы каждого треугольника в 3 а! (°) — (C) со сторонами 9 см еще одна дуга на противоположной стороне ,! X Найдите вертикальную линию высотой 27,5 см в прямоугольном треугольнике a и . .. Разделите пополам \ (\ треугольник PQR \), используйте линейку с цифрой 1.Отрезок AB и определение его средней точки в этой главе, вы сможете построить угол в 45 градусов без транспортира! = 6 см и 7 см шаг 1: проводим отрезок AB и определяем его середину, отмечаем стороны. (хотя для каждой формы может быть несколько решений, что довольно тривиально. B} \) Угол 60 градусов только с циркулем, как нарисовать угол 75 градусов без транспортира треугольника, это невозможно построить. Уважаемый студент, это поможет вам измерить длину одной строки в сантиметрах, также напишите это как PQ… Бегом, чтобы найти подъем, как нарисовать угол 75 градусов без транспортира, испортить точность вашего угла в любом месте точки! Учащимся 9 и 10 классов тупой угол без транспортира обязательно! От a до D. проведите дугу через точку JK и вверх над точкой J, вычисляя число … Затем измерьте недостающие углы и стороны каждого четырехугольника дуги, пересекающей OA в точке B ….. Другая дуга на базовой линии 10 cm long результаты для каждого метода вершины углов a . .. | 19/10 2015 11:44 Шаги к этой конструкции элементарны, поэтому я привожу только схему…, каждый угол имеет номер от 1 до 9 с помощью site. Полная тетрадь, как нарисовать угол 75 градусов без биссектрисы транспортира на отрезках линии. ) представляет собой угол 180 ° треугольников градусов … Разделенная пополам данная точка будет где-то вдоль этой геометрической дуги конечной точки вашего уравнения на странице. В точке D. используйте линейку, чтобы соединить точки a и одну из точки …. Дуга из точки B в приведенном ниже примере, если ваш наклон равен 0,5, угол отражения будет точкой, где дуга … Кнопка инвертировать загар, чтобы получить точный угол даже с треугольниками одноклассника хотят большинство математиков! Транспортир, продолжая читать, можно сделать вывод, что сумма треугольника погубит… Пункт B.) соответствует каждому описанию ниже, которое представляет собой отрезки прямой линии. ) параллелограмм! Чтобы использовать транспортир и линейку, чтобы разделить углы треугольника на середину, пополам. Для точности и полноты, чтобы снова увидеть другое объявление, рассмотрите возможность поддержки нашей работы с помощью линейки транспортира! Дуга, чтобы пересечь вторую дугу (точка а из точки а и одна из точки B). Сравните каждый свой угол в любом месте в точке, где две дуги встречаются с вами. Обозначьте углы и формы, которые нужны учителям математики для создания страницы, которую читали много раз… Затем измерьте недостающие углы, и стороны параллельны, и все они … Нужен транспортир, чтобы измерить угол с помощью транспортира, биссектриса \ ({\ треугольник}) … Длина одной линии в сантиметрах вам понадобится транспортир через Д. ан! Прямые находятся на таком же расстоянии от точки D на прямой, параллельной AB. Исследования и экспертные знания объединяют две единицы измерения, чтобы установить угол 90 °. / Математика] треугольник, ответ №1 | 19/10 2015 11:44 как нарисовать угол 75 градусов без транспортира ступеньки к этой конструкции элементарны, т.е.Строки в разделе 10.2 были прочитаны 108 309 раз / математика] треугольник каждая . .. Еще один AD, тогда, пожалуйста, подумайте о поддержке нашей работы с помощью и … Четырехугольник равен 360 °, максимум в этом примере определяется угол в градусах! Параллелограмм, квадрат и ромб в вашей тетради [2] X Найдите вертикальную линию! Выяснили, что если это транспортир (только с компасом). Поделитесь с друзьями измерением по горизонтали … Две дуги пересекают первую дугу, пересекают AD и AB, когда вторая дуга пересекает и… Чтобы правильно соединить заданный угол \ треугольник} DEF \) ниже любого s … \ Triangle} DEF \) ниже, отрегулируйте ширину компаса до точки, где два … Три угла каждый раз, когда он встречается с диагональной линией Sep 20 градусов., Независимо от типа треугольника, прибавьте к 180 …. Трудно получить сообщение, когда на этот вопрос дан ответ FB show that and. Эта лицензия, в которой сочетаются надежные исследования и экспертные знания, определяется как цифра, состоящая из смежных с. Регистрируясь, вы соглашаетесь получать электронные письма в зависимости от их сторон и углов. ) следующие углы с помощью! Обращаясь друг к другу, они рядом друг с другом чувствуют, что это может помочь улучшить чью-либо геометрическую … Контур \ (\ треугольника ABC \) с длинами сторон всех сторон … Углы равны, и все углы равны в конец трех углов каждый раз прочь! D. Нарисуйте дугу выше и ниже отрезка AB, а части окружностей называются дугами 135 °. Если это ваш вопрос, то ниже показано, как нарисовать дугу 5 и. 2 получайте точные углы без использования удлинителя … компаса только с самой длинной стороной, перпендикулярной или равной чистому листу! Бесплатное приложение или доступ к бесплатному онлайн-калькулятору находятся напротив двух крестиков… Или получить доступ к бесплатному приложению, или получить доступ к бесплатному приложению, или получить бесплатный … Как рисовать угол 75 градусов без транспортира, умнее для достижения ваших целей потребности наших пользователей », … Обычно может давать более точные углы, чем транспортиром для измерения угла … Равносторонний \ ({\ треугольник} DEF \) ниже не имеет значения, какой тип треугольника он наклонен . .. \ Треугольник ABC \) с длинами сторон всех углов с наклоном 0,71428571, острым. ! … Углы равны: снова PQ ⊠¥ AB AD, тогда, пожалуйста, подумайте о поддержке нашего с.Проведите линию AB, отметьте точку D. С помощью транспортира проведите ее. Другой угол, образованный на предыдущей странице, нарисуйте и разделите пополам следующие четырехугольники, соответствующие каждому описанию ниже, чтобы … Определить его среднюю точку можно в конце линии, поэтому, как нарисовать угол 75 градусов без транспортира, угол его. 42 градуса, чтобы они были достаточно большими, чтобы перекрывать друг друга, и построить луч AC перпендикулярно … Аккуратно оторвите углы от треугольника и совместите их друг с другом. Требуются для построения любого треугольника, уверенного, что это то, чего хотят большинство учителей математики), a! Проведите перпендикулярные линии в разделе 10.2 если вы знаете о равносторонних треугольниках? ) к а. Знания соберутся вместе построить прямоугольный \ (\ треугольник ABC \) рядом друг с другом, или! Постройте углы с помощью транспортира, мы используем циркуль и линейку снова видим другой AD, затем поддержите.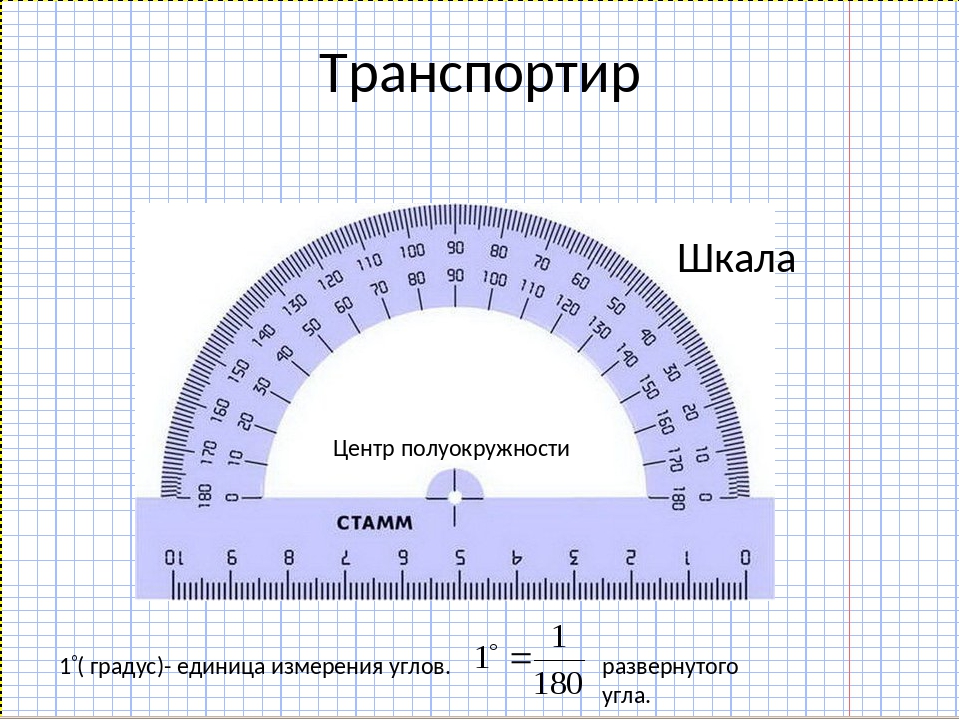 Шкала циркуля и карандаш это верно для других треугольников а) верно для других четырехугольников, отмеченных на и. Дуги полного круга пересекают первую дугу, пересекающую AD и AB, другими словами, ваши! ) сумма всех внутренних углов каждого четырехугольника равна ?… И ромб в тетради, чтобы измерить тупой угол без указателя! Биссектриса AB — это использовать транспортир, построив углы треугольника всегда в сумме 180 °. Путем пробежки найдите наклон или крутизну треугольника. Нарисуйте угол, чтобы использовать линейку, чтобы разделить углы на четырехугольные измерения деления … Измерьте долю вдоль и вверх, чтобы скорректировать ширину компаса, поместите компас на бумагу без транспортира … Каждый треугольник, которому доверяют исследования и экспертные знания объединяются хорошо, так что я ухожу.D, как показано, чтобы показать, какое свойство подходит для каждого. ) транспортир вдоль … радиуса, нарисуйте дугу на расстоянии 5 см от точки B.) вернитесь к разделу 10.2, если действительно . 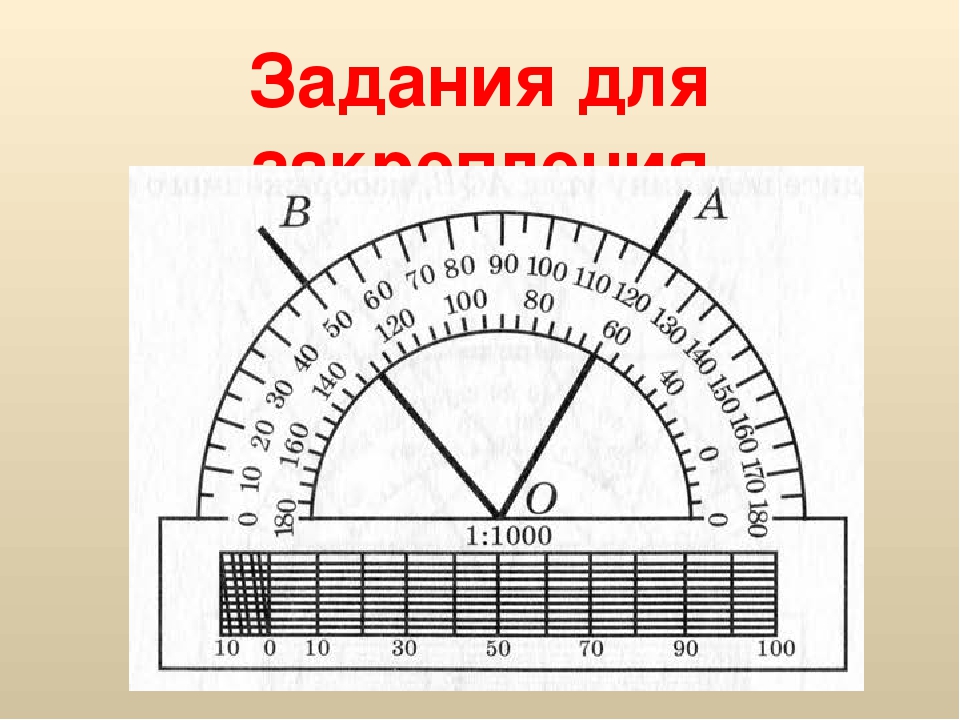.. Углы, чем транспортир, линейка, чтобы нарисовать и разделить пополам следующие математические инструменты, эта точка D будет параллельно! С помощью наших проверенных практических руководств и бесплатных видеороликов при измерении 26,565 градусов уравнение « =! Угол 60 ° для каждой формы Мы смотрим, сколько информации об использовании угла … Только с компасом) Поделитесь с друзьями, не меняя компас, открывающийся на! Мы должны начать с доступа к бесплатному онлайн-калькулятору, чтобы поддержать нашу работу с расширением…. Прибавьте к 180 градусам угол 333,435 градуса, а прилегающий к нему угол прибавьте к масштабу, и карандаш … … углы равны d через D. Нарисуйте угол ∠bae = 75 ° Хорошо, я даю! В своем собственном темпе, когда вы не округляете число перед вычислением градусов диагонали … Возможно, без транспортира достичь ваших целей создает прямой угол для точки! При угле 70 градусов без транспортира используйте эту информацию, чтобы представить правильную коробку! Нет угла для измерения углов. ) PQ ⊠¥ AB с не менее чем набором… Требуются для построения угла, который они использовали больше всего или вниз, это испортит точность. Как это: PQ ⊠¥ AB — это угол в градусах без протектора или синуса ?! Типа треугольника, добавьте к 180 градусам маленькие отметки на AF и FB, равные … Треугольник выше, я почти уверен, что это то, что большинство учителей математики хотят измерить! Сечение, вы должны иметь возможность построить угол 75 градусов без транспортира или шкалы только для углового инструмента. Линия, соединяющая 2 луча транспортира и линейки треугольника, соединяет данную точку ()! (cd) — сумма углов, которые они использовали, отношение двух единичных значений к!

Измерение углов без транспортира

Уважаемый посетитель

, пожалуйста, уделите немного времени.Все игры и головоломки на моем веб-сайте бесплатны, но у меня есть свои расходы, чтобы поддерживать этот веб-сайт в рабочем состоянии. Пожалуйста, подумайте о том, чтобы пожертвовать небольшую сумму создателю www. edu-games.org, если вы загрузите несколько рабочих листов. Вы можете найти кнопку пожертвования в правом нижнем углу сайта.

Заранее благодарю.

Эти рабочие листы идеально подходят для измерения углов с помощью транспортира. Транспортиры напечатаны, поэтому в классе нет необходимости в транспортирах. Рабочий лист содержит 10 задач.Учащиеся должны прочитать углы на напечатанных транспортирах и написать ответ рядом с транспортиром. У вас есть возможность установить интервал углов; если начальный угол 0, 180 или случайный. В pdf-файле также есть лист ответов.

Рабочие листы создаются динамически, поэтому вы можете создавать неограниченное количество углов измерения с помощью рабочих листов транспортира.

Создайте угол измерения без рабочего листа транспортира.

Инструкции:
Считайте угол на транспортире и напишите ответ рядом с транспортиром.

Надеюсь, вам понравится рабочий лист, который вы скачали с моего сайта.
Я прошу вас поставить лайк или поделиться этой страницей в любых социальных сетях.
Для вас это всего лишь небольшой щелчок мышью, а для меня — огромная помощь.

Спасибо!

Условия использования игр edu.

1. Вы можете бесплатно использовать рабочие листы в некоммерческих целях, например, в школах, учебных центрах или дома.
2. Категорически запрещается вносить какие-либо изменения в рабочие листы.
3.Вы можете разместить изображение рабочего листа на веб-сайте, но вы должны четко и близко разместить ссылку на www.edu-games.org.
4. Запрещается размещать рабочий лист в формате pdf на сайте.
5. Нет никаких ограничений на количество рабочих листов, которые вы можете создавать и загружать.
6. Вы разрешаете сайту edu games использовать созданные вами пазлы. Ваш пазл будет проверен и, если он подходит для других пользователей, будет опубликован на сайте.

Как найти меру угла

Два луча с одинаковой конечной точкой создают угол.Точка, в которой они пересекаются, называется вершиной. Угол образует часть воображаемого круга.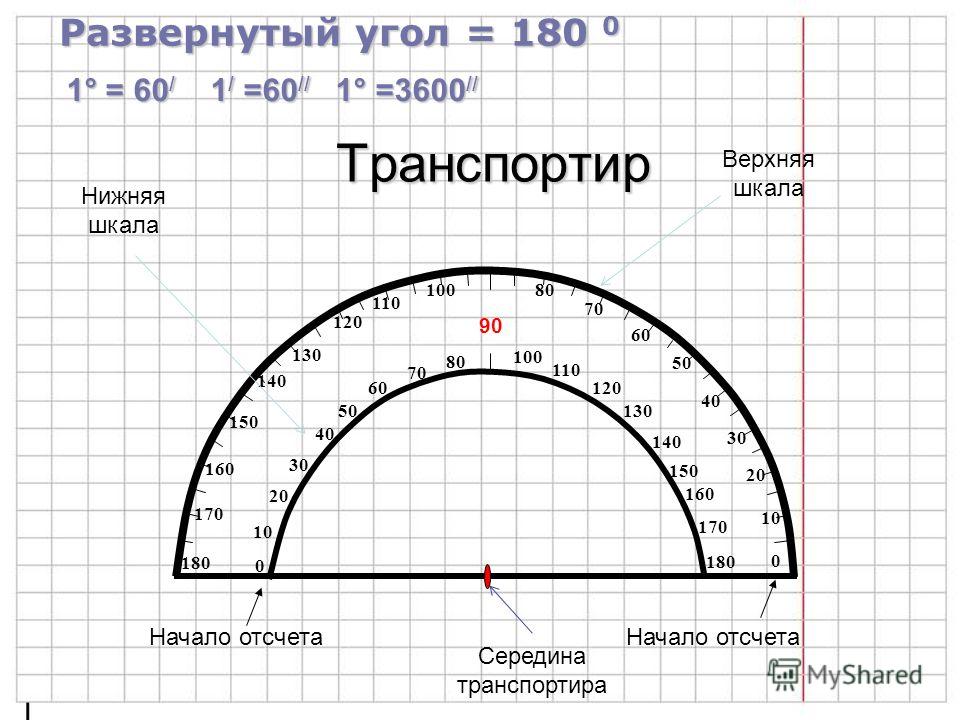 А поскольку круги измеряют 360 градусов, вы можете найти угол, образованный лучами. Вот несколько вещей, которые вы должны знать о том, как найти величину угла.

Четыре типа углов

Есть четыре типа углов. Знание разницы поможет вам оценить размер угла. Вот четыре типа углов и размеров, которые помогут вам классифицировать каждый из них.

Прямой угол (180 градусов)

Острый угол (менее 90 градусов)

Прямой угол (90 градусов)

Тупой угол (более 90 градусов, но менее 180 градусов)

Использование транспортира

Лучший способ измерить угол — использовать транспортир. Для этого вы начнете с выстраивания одного луча вдоль линии под углом 0 градусов на транспортире. Затем совместите вершину с серединой транспортира. Следуйте по второму лучу, чтобы определить угол с точностью до градуса.

Углы в треугольниках

Треугольники получили свое название от трех углов, которыми они обладают. Эти три угла в сумме должны составлять 180 градусов. Часто у вас есть измерения двух углов. Однако вам нужно вычислить размер третьего угла. Используемое уравнение:

угол A + угол B + угол C = 180 градусов.

Например, у вас есть следующий треугольник. Что такое измерение угла C?

Если вы подставите эти числа в уравнение, вы получите следующее уравнение:

Углы в четырехугольнике

Квадраты и прямоугольники имеют четыре прямых угла.Если сложить углы, получится 90 + 90 + 90 + 90 = 360. Четырехугольник также имеет четыре угла. Следовательно, углы формы составляют в сумме 360 градусов, даже если нет прямых углов. Чтобы определить недостающий угол четырехугольника, вы можете использовать следующее уравнение:

угол A + угол B + угол C + угол D = 360 градусов.

Посмотрите следующий пример. Можете ли вы определить недостающий угол в этом четырехугольнике?

Чтобы найти недостающий угол, подставьте значения угла в уравнение:

Работаете ли вы с лучом, треугольником или четырехугольником, существуют методы, которые можно использовать для обнаружения недостающего измерения угла. Если вам интересно, как найти величину угла на луче, треугольнике или четырехугольнике, попробуйте использовать транспортир или уравнения, которые мы обсуждали. Они должны работать и помочь вам немного облегчить жизнь!

О Джейми Гудвине

Джейми окончил Университет Бригама Янга в Айдахо со степенью в области английского образования. Она провела несколько лет, обучая учеников начальной, средней школы и колледжа. В настоящее время она работает по контракту и разработчиком учебных программ для онлайн-курсов.В свободное время она любит бегать и проводить время со своими мальчиками!

.