Построить пятиугольник правильный: Построение пятиугольника подробно. — Чертежик

2.1. Построение плоских фигур в прямоугольной диметрии

На рис. 10 изображены некоторые плоские фигуры в прямоугольных диметрических проекциях. Построение их аналогично изометрическим проекциям, лишь по направлению оси Y требуется уменьшение размеров в 2 раза.

На рис. 11 изображён в горизонтальной плоскости правильный пятиугольник АВСDЕ. Координатные оси проходят через центр описанной окружности. Через вершины А и С проведена горизонтальная прямая, параллельная оси Х, пересекающая ось Y в точке М.

Пример построения прямоугольной диметрии пятиугольника в плоскости XОY:

Проводим аксонометрические оси Х и Y. На оси Y в обе стороны от точки О откладываем отрезки, равные половине величины отрезков ОМ, ОВ и ОN. Через полученные точки М и N проводят прямые, параллельные оси Х, и откладывают на них соответственно натуральные величины стороны пятиугольника ЕD и вспомогательной прямой АС. Полученные пять вершин пятиугольника соединяют между собой.

На рис. 10 изображены диметрические проекции плоских фигур, расположенных параллельно горизонтальной, фронтальной и профильной плоскостям проекций.

Рис. 10. Диметрическое изображение плоских фигур

а) на чертеже; б) на плоскости H; в) на плоскости V; г) на плоскости W.

На рис. 11 изображено проецирование в диметрии окружностей, расположенных в плоскостях, параллельных плоскостям проекций. Согласно ранее сформулированного положения для эллипса, расположенного в горизонтальной плоскости, большая ось направлена перпендикулярно к оси Z, а малая совпадает с осьюZ. Для эллипса, расположенного во фронтальной плоскости, большая ось направлена перпендикулярно к оси Y, а малая совпадает с осью Y и т.д. В отличие от изометрического изображения эллипсов в различных плоскостях, в диметрии размеры эллипсов одинаковы лишь в горизонтальной (Н) и профильной (W) плоскостях. Во фронтальной плоскости проекции малая ось эллипса выполняется большей, чем в двух других (0,95dпротив 0,35d).

Правило определения главных осей эллипса: большая ось эллипса располагается перпендикулярно к той аксонометрической оси, которая отсутствует в данной плоскости, а малая ось совпадает с направлением этой оси.

Рис. 11 Проецирование окружностей в диметрии на гранях куба

а. Порядок выполнения овала на плоскости, параллельной горизонтальной и профильной плоскостям проекций (рис. 12, а).

1. Проводим из точки О большие полуоси овала ОА= ОВ (АВ = 1,06d), где d – заданный диаметр окружности.

2. Из точки О проводим малые полуоси овала ОС = ОD. Малая ось овала СD = 0,35d.

3. Из точки О на малых полуосях овала откладываем отрезок ОЕ = ОЕ₁=АВ (на рис. 12,а отрезок ОЕ₁ не показан) равный 1,06d.

4. Проводим дуги окружностей радиусом R= ЕС= Е₁D из точек Е и Е₁.

5. Из точек А и В на больших полуосях овала откладываем отрезки АК= ВК₁= 1/2 ОС.

6. Из точек К и К₁ проводим дуги окружностей радиусом r = АК= ВК_1.

б. Порядок построения овала на плоскости, параллельной фронтальной плоскости проекций (рис. 12, б).

1. Из точки О проводим окружность радиусом r = ОК₁= 0,1d, (где d — заданный диаметр окружности) и оси овала АВ и СD. АВ  Y, СD  АВ, АВ = 1,06d, СD = 0,95d.

2. Из точки Е проводим дугу окружности радиусом R= ЕС. Аналогичное построение из точки Е₁.

3. Из точки К₁ проводим дугу окружности радиусом R₁= АК₁= КВ, полученное изображение является на плоскости V овалом.

а) б)

Рис. 12. Построение овалов в диметрической проекции:

а) в плоскости Н и W; б) в плоскости V

Как нарисовать правильный пятиугольник с шестигранной симметрией?

Следующая процедура используется для построения правильного пятиугольника:
Шаг 1
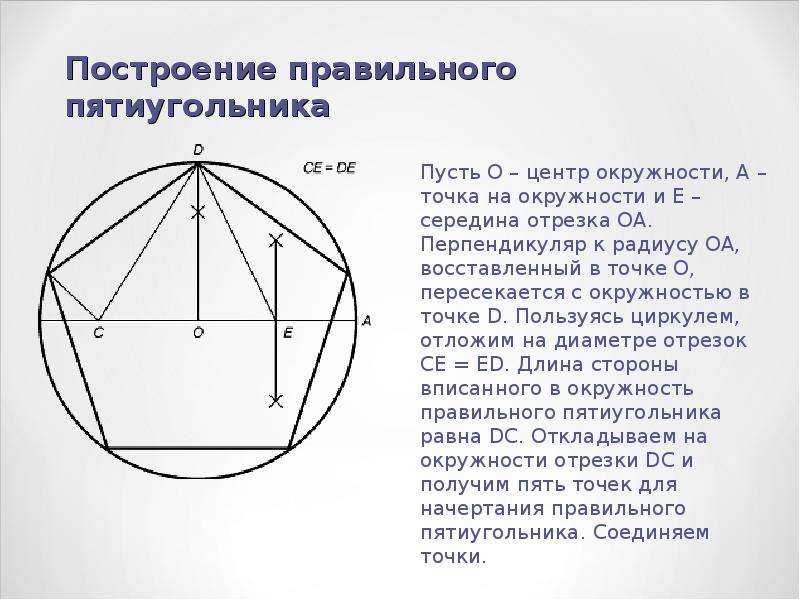
Нарисуйте окружность с центром O.
Шаг 2
Произвольно выберите точку на окружности и назовите ее A. Эта точка станет единицей вершин Пентагона. Нарисуйте прямую, проходящую через точку A и центр O.
Шаг 3
Постройте прямую, перпендикулярную прямой OA и проходящую через центр окружности O. Назовите одну из сторон, с которой эта линия пересекает окружность, как Б
Шаг 4
Установите середину линии OB, назовите ее точкой C и нарисуйте окружность с центром в C и проходящей через точку A, как показано: Отметьте точку, где окружность пересекается с линией OB внутри исходной окружности, как точку D.
Шаг 5
Нарисуйте окружность с центром в точке A и проходящей через точку D. Отметьте точки пересечения окружности с исходной окружностью как точки E и F.
Шаг 6
Нарисуйте еще одну окружность с центром в точке E и проходит через точку A. Назовите точку, где окружность пересекается с исходной окружностью, как G
Шаг 7
Нарисуйте последнюю окружность с центром в точке F и проходящую через точку A. Назовите точку пересечения с исходной окружностью точкой H.
Шаг 8
Теперь постройте правильный пятиугольник AEGHF Многоугольник, отмеченный бордовая линия представляет собой правильный пятиугольник с точками A, E, G, H и F в качестве вершин.
Процесс построения пятиугольника чертовски сложен, но его довольно легко освоить. Как только вы построили первый круг, который пересекается с первоначальным кругом, который был построен, ваша работа будет наполовину сделана.
Для того, чтобы освоить весь процесс, вам, конечно, нужно пройти его два или три раза, практикуя его, чтобы по-настоящему понять его.
Помните, что каждый внутренний угол пятиугольника равен 108˚, и вы можете проверить это, если ваша конструкция была правильной.
Построение правильного шестиугольника
Давайте теперь посмотрим на построение правильного шестиугольника с помощью линейки и циркуля. Как мы уже говорили ранее, правильный шестиугольник обладает идеальной симметрией и, таким образом, является одним из самых простых многоугольников для построения. Ниже описана процедура построения правильного шестиугольника с помощью линейки и циркуля:
Шаг 1
Постройте круг с центром О и нарисуйте его диаметр.
Шаг 2
Не изменяя ширины циркуля, поместите его острие в каждую из точек пересечения диаметра с окружностью и начертите дуги, как показано
Шаг 3
Теперь соедините все точки пересечения дуг и диаметра с круг как показано:
Бордовая линия на рисунке представляет собой правильный шестиугольник. Если ваш рисунок был достаточно точен, вы поймете, что все стороны равны по длине, а также равны по размеру все внутренние углы.

Что такое Пентагон? Определение, типы, свойства, примеры

Что такое пятиугольник?

Двухмерный многоугольник с пятью сторонами и пятью углами называется пятиугольником.

«Пента» означает «пять», а «гон» переводится как «углы» на греческом языке, и, следовательно, если мы объединим оба слова «пента + угольник», мы получим слово «пятиугольник».

Родственные игры

Как выглядит Пентагон?

Вот как выглядит пятисторонняя фигура: 

Связанные листы

Части пятиугольника

1. Сторона: Это один из пяти отрезков, образующих эту фигуру. Всего у этой фигуры пять сторон. На изображении отрезок «а» показывает одну из 5 сторон пятиугольника.
2. Вершина: Это точка, где встречаются две стороны фигуры. Проще говоря, он также известен как угол. Например, когда вы посмотрите на страницу своей тетради, вы обнаружите, что она имеет четыре угла или четыре вершины, которые образуют 9угол 0°. На изображении выше A, B, C D и E — пять вершин этой формы.
3. Диагональ: Это линия, соединяющая две несмежные вершины. Когда вы соединяете любые два несмежных угла или вершины 2D-фигуры с помощью прямой линии, эта прямая линия называется диагональю. Диагональ представлена ​​буквой «d» на изображении для справки.
4. Внутренний угол : Угол, образованный двумя смежными сторонами фигуры внутри. Когда две прямые линии встречаются или пересекаются, они образуют два типа углов в замкнутой двумерной фигуре. Угол, лежащий внутри фигуры, называется внутренним углом. Углы, отмеченные зеленым цветом на изображении ниже, показывают внутренние углы.

5. Внешний угол : Угол, образованный двумя смежными сторонами формы снаружи. Внешний угол — это мера угла на конкретной вершине, но снаружи. Углы, отмеченные синим цветом на изображении выше, показывают внешние углы.

Типы пятиугольников

Пятиугольники можно разделить на четыре типа в зависимости от их сторон, углов и вершин.

• Обычный
• Нестандартный
• Выпуклая
• Вогнутая

Правильные и неправильные пятиугольники

Если все пять сторон равны по длине и все пять углов имеют одинаковую меру, то фигура называется правильной. Когда сторона и углы не равны, он называется неправильным. Чтобы лучше понять это, если вы посмотрите на правильный пятиугольник с любой стороны, он всегда будет выглядеть одинаково, поскольку он симметричен. Но неправильный может выглядеть по-разному со всех сторон или углов, поскольку у него разные длины сторон и углы.

Выпуклые и вогнутые пятиугольники

Выпуклый пятиугольник — это пятиугольник, у которого все вершины направлены наружу. Вогнутая форма относится к фигуре, у которой хотя бы одна вершина направлена ​​внутрь.

 Другими словами, вогнутый пятиугольник будет иметь чашеобразную форму между некоторыми сторонами, а выпуклый не будет иметь такой формы, так как все его вершины направлены наружу.

Свойства пятиугольника 

• Эта фигура должна иметь пять сторон, образующих замкнутую двумерную фигуру. (Замкнутая фигура — это фигура, у которой все стороны встречаются друг с другом, образуя вершины.)

• Пятиугольник имеет пять диагоналей, соединяющих пять вершин с противоположными вершинами.

• В правильном пятиугольнике каждый внутренний угол равен 108°, а каждый внешний угол равен 72°.

• Сумма всех пяти внутренних углов любого пятиугольника равна 540°.

Пентагон Примеры из жизни

• Футбол : Футбол состоит из нескольких черно-белых пятен пятиугольной формы.
• Бамия : В следующий раз, когда будете есть бамию, внимательно посмотрите на внутреннее сечение, так как оно имеет пятиугольную форму.
• Пентагон здание : Штаб-квартира Министерства обороны США в Вашингтоне, округ Колумбия, представляет собой пятиугольное здание под названием Пентагон.

Площадь пятиугольника

Площадь этой фигуры равна общему пространству внутри ее пяти сторон. Чтобы найти область, мы должны сначала определить ее тип и информацию, которую мы имеем о ней.

Площадь правильного пятиугольника: 

Правильный пятиугольник образует пять подобных треугольников.

Площадь правильного пятиугольника = 5 × площадь треугольника pothem sq unit

Апофема — это перпендикулярная линия, проведенная из центра многоугольника к одной из его сторон. Он также известен как радиус формы.

Площадь неправильного пятиугольника

Чтобы найти площадь неправильного пятиугольника, разделите его на меньшие многоугольники. Сумма всех площадей меньших многоугольников дает общую площадь фигуры.

Периметр пятиугольника

Общая длина пяти сторон правильного или неправильного многоугольника называется его периметром.

Периметр пятиугольника = (сторона 1 + сторона 2 + сторона 3 + сторона 4 + сторона 5) единиц

Периметр правильной пятиугольной фигуры равен (5 x сторона) единицам, если все стороны одинаковы измерение.

Забавные факты

Знаете ли вы, что можно сделать простой пятиугольник из полоски бумаги?

Шаг 01 : Возьмите длинную полоску бумаги. Вы можете выбрать свой любимый цвет.

Шаг 02: Теперь сделайте из бумаги узелок, похожий на крендель. Посмотрите на изображение и следуйте инструкциям.

Шаг 03: Удерживая бумагу плоской, затяните узел мягкими руками. Будьте осторожны, чтобы не порвать его.

Шаг 04: Теперь, если есть лишняя бумага, отогните ее или обрежьте.

Шаг 05: Вуаля! Теперь он готов. Вы можете проверить, все ли стороны имеют одинаковую длину и все углы имеют одинаковую меру.

Заключение

Пятиугольники широко используются архитекторами и встречаются повсюду в мире природы. Они также очень часто используются в фундаментальной геометрии. Чтобы изучать принципы геометрии в увлекательной игровой форме, ознакомьтесь с обучающими играми, курсами и рабочими листами SplashLearn для детей.

Решенные примеры

1. Нил измеряет правильный пятиугольник и находит, что его сторона равна 8 футам, а длина апофемы 6 футов . Как он найдет его площадь?

Решение:

Данный вопрос

Апофема = 6 футов

Сторона = 8 футов

Площадь правильного пятиугольника = ½ × периметр × апофема 9 0033

= ½ × 5 × 8 × 6

= ½ × 240

= 120 квадратных футов

Следовательно, площадь = 120 футов

2

2.  Если правильный пятиугольник имеет длину стороны 10 см и апофему 5 см, найдите его площадь.

Решение: Дано,

Длина стороны = 10 см

Длина апофемы = 5 см

Площадь правильного пятиугольника = ½ × периметр × апофема

= 1⁄2 × 5 x 10 × 5

Площадь = 125 см ²

3. Если периметр правильного пятиугольника равен 200 см, какова длина каждой стороны?

Решение :
Периметр правильного пятиугольника = 200 см
5 × сторона = 200
Сторона = 200/5
Сторона = 40 см

Длина каждой стороны 40 см.

Практические задачи

1

Сколько параллельных сторон может быть в правильном пятиугольнике?

1

5

3

Правильный ответ: 0
Правильный пятиугольник не имеет параллельных сторон. Неправильный может иметь две (одна пара) или четыре (две пары) параллельных сторон.

2

Длина стороны периметра 6 см. Чему равен периметр пятиугольника?

30 см

33 см

36 см

40 см

Правильный ответ: 30 см
Периметр пятиугольника = длина стороны пятиугольника x 5
Данная длина стороны равна 6 см.

3

Если периметр правильного пятиугольника равен 250 см, какова будет длина каждой стороны?

50 см

60 см

30 см

90 см

Правильный ответ: 50 см
Периметр правильного пятиугольника = 250 см
5 × сторона = 250 90 004 Сторона = 250/5
Сторона = 50 см

4

На сколько треугольников можно разделить пятиугольник?

5

3

4

6

Правильный ответ: 3
Пятиугольник можно разделить на 3 треугольника.

5

Если мера четырех внутренних углов неправильного пятиугольника равна 135, 78, 119 и 117°, то какова мера его пятого внутреннего угла?

90

91

60

45

Правильный ответ: 91
Сумма всех внутренних углов пятиугольника равна 540°.
Отсюда $135 + 78 + 119 + 117 + X$ = $540$ (X — неизвестный угол)
$X$ = $540$ – $449$ = $91°$

6

Какова площадь пятиугольника, сторона которого 9 см, а апофема 10 см?

340 см²

225 см²

235 см²

210 см²

Правильный ответ: 225 см²
Периметр пятиугольника = длина стороны x 5
Пери метр = 9 x 5 = 45 см
Площадь пятиугольника = 1/ 2 × п × а
Площадь = ½ x 45 x 10
Площадь = 225 см²

Часто задаваемые вопросы

Является ли пятиугольник также параллелограммом?

Нет, пятиугольник — это пятиугольник, а у параллелограмма только четыре стороны.