Шестиугольник вписать в окружность: Радиус вписанной окружности в шестиугольник

чему равна сторона и периметр

Содержание:

• Что такое правильный шестиугольник
• Основные свойства правильного шестиугольника
• Нахождение радиуса вписанной окружности
  • Классическая формула для нахождения радиуса вписанной окружности правильного многоугольника
• Периметр правильного шестиугольника

Содержание

• Что такое правильный шестиугольник
• Основные свойства правильного шестиугольника
• Нахождение радиуса вписанной окружности
  • Классическая формула для нахождения радиуса вписанной окружности правильного многоугольника
• Периметр правильного шестиугольника

Что такое правильный шестиугольник

Правильный шестиугольник или гексагон — выпуклый шестиугольник, у которого все стороны и углы равны.

Сумма всех углов n–угольника равна 180°(n−2). Каждый угол правильного n–угольника равен \(α_n=\frac{\left(n-2\right)}n180°\). Следовательно углы правильного шестиугольника равны \(\frac{\left(6-2\right)}6180°=120°\).

Основные свойства правильного шестиугольника

1. У гексагона все внутренние углы равны между собой.
2. Каждый внутренний угол правильного шестиугольника равен 120°.
3. Все стороны гексагона равны между собой.
4. Радиус окружности, описанной около правильного шестиугольника, равен его стороне.
5. Большая диагональ правильного шестиугольника равна диаметру описанной около него окружности или сумме двух его сторон.
6. Меньшая диагональ правильного шестиугольника в \(\sqrt3\) раз больше его стороны.
7. Меньшая диагональ правильного шестиугольника и две его противолежащие стороны перпендикулярны друг другу.
8. Меньшая диагональ правильного шестиугольника равна удвоенному радиусу вписанной в него окружности.
9. Правильный шестиугольник замещает плоскость, это значит заполняет ее без пробелов и наложений.
10. Диагонали правильного шестиугольника пересекаются в одной точке и делят его на 6 равных равносторонних треугольников. Высота этих треугольников равна радиусу вписанной в правильный шестиугольник окружности.
11. При поворотах относительно центра на угол, кратный 60°, правильный шестиугольник переходит в себя.
12. Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями — прямоугольный. Гипотенузой такого треугольника является большая диагональ. Его острые углы равны 30° и 60°.

У изображенного правильного шестиугольника ∠А=∠В=∠С=∠D=∠Е=∠F=120°. Стороны равны между собой АВ=ВС=СD=DE=EF=FA. Точка О — центр пересечения диагоналей. Большая диагональ AD=2АВ. Меньшая диагональ \(СА=\sqrt3·АВ\).

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления).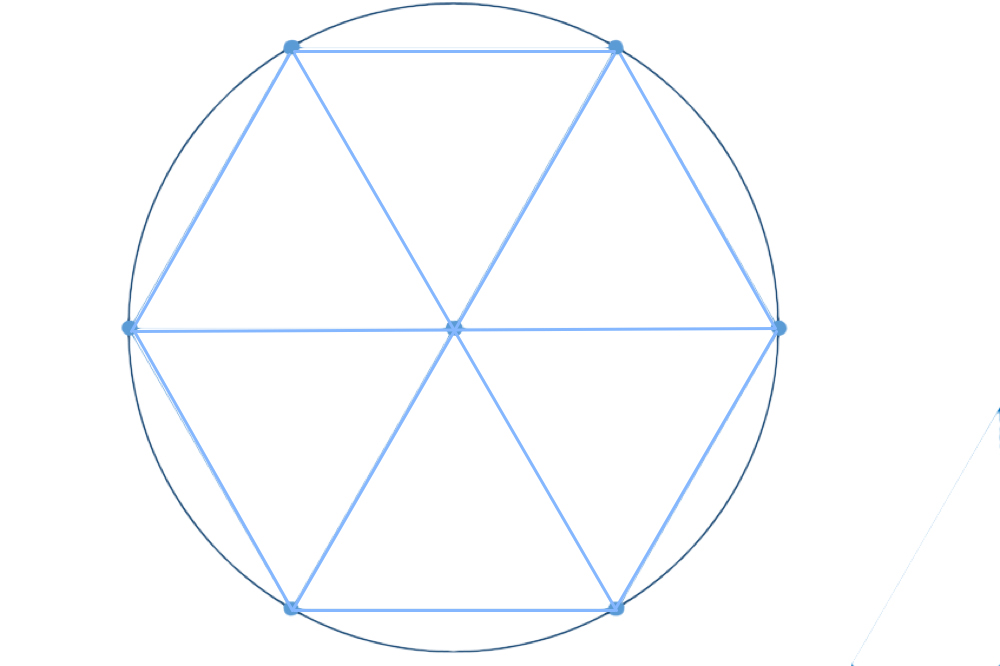

0=\frac1{\sqrt3}\), то \(r=\frac{\sqrt3}2·a\). То есть, получаем формулу, найденную выше.

Периметр правильного шестиугольника

Если известен радиус вписанной окружности, то периметр правильного шестиугольника можно найти по формуле:

Формула 3

\(Р=4\sqrt3r\)

где Р — периметр правильного шестиугольника,

r — радиус вписанной в него окружности.

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Комбинации с окружностью — что это, определение и ответ

Около выпуклого многоугольника можно описать окружность или в него можно вписать окружность.

Вписанная в многоугольник окружность – это окружность, лежащая внутри многоугольника, касающаяся всех его сторон.

Описанная около многоугольника окружность – это окружность, на которой лежат все вершины многоугольника.

ТРЕУГОЛЬНИК

ВПИСАННАЯ ОКРУЖНОСТЬ

1. В каждый треугольник можно вписать окружность и при том только одну.

2. Центром вписанной окружности является точка пересечения биссектрис.

3. Радиус вписанной в треугольник окружности равен площади треугольника, деленной на полупериметр: \(r = \frac{S}{p},\ где\ p = \frac{a + b + c}{2}\)

4. Радиус окружности, вписанной в прямоугольный треугольник с катетами а, b и гипотенузой с, равен:

\(r = \frac{a + b\ –\ c}{2}\)

ОПИСАННАЯ ОКРУЖНОСТЬ

1. Около каждого треугольника можно описать окружность и при том только одну.

2. Центром вписанной окружности является точка пересечения серединных перпендикуляров.

3. Радиус описанной около треугольника окружности равен произведению сторон треугольника, деленному на четыре его площади:

\(R = \frac{\text{abc}}{4S}\)

РАСПОЛОЖЕНИЕ ЦЕНТРА ОПИСАННОЙ ОКРУЖНОСТИ В ЗАВИСИМОСТИ ОТ ВИДА ТРЕУГОЛЬНИКА:

1. Остроугольный

Центр описанной окружности лежит внутри треугольника.

2. Прямоугольный

Центр описанной окружности лежит на середине гипотенузы треугольника.

3. Тупоугольный

Центр описанной окружности лежит вне треугольника.

ЧЕТЫРЁХУГОЛЬНИК

ВПИСАННАЯ ОКРУЖНОСТЬ

В четырёхугольник можно вписать окружность, если суммы его противоположных сторон равны.

Суммы противоположных сторон равны, в частности, у следующих фигур:

1. Квадрат (как параллелограмм с равными сторонами)

\(r = \frac{h}{2} = \frac{a}{2}\)

2. Ромб (как параллелограмм с равными сторонами)

\(r = \frac{h}{2}\)

3. Трапеция (если сумма длин оснований равна сумме длин боковых сторон)

\(r = \frac{h}{2}\)

ОПИСАННАЯ ОКРУЖНОСТЬ

Около четырёхугольника можно описать окружность, если сумма его противоположных углов равна 180⁰.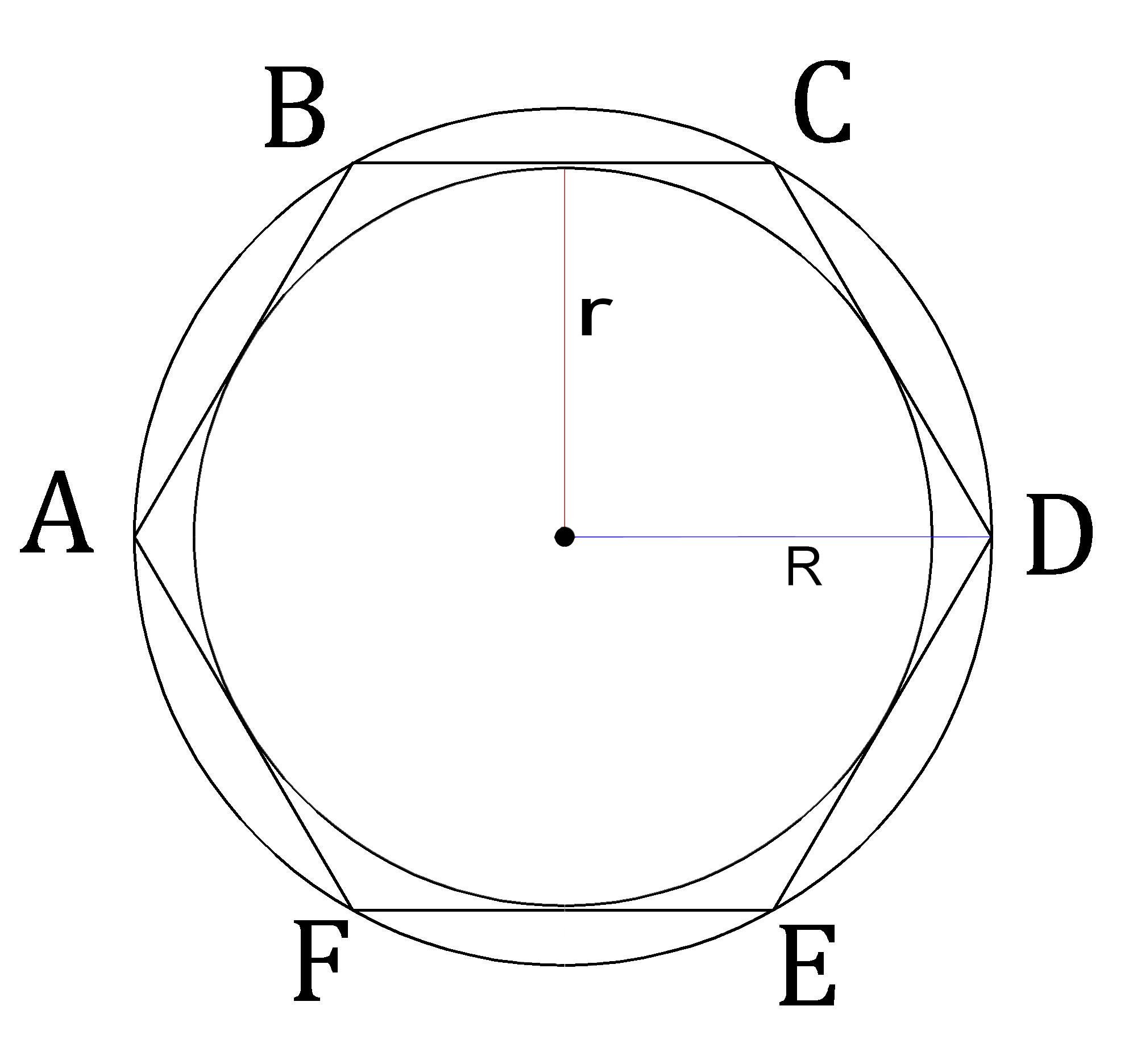 {2}}}{2}\)

3. Равнобедренная трапеция

ПРАВИЛЬНЫЙ ШЕСТИУГОЛЬНИК

Любой правильный шестиугольник можно вписать в окружность и описать около нее, т.к. все его углы и стороны соответственно равны.

Радиусы вписанной и описанной окружностей правильного шестиугольника совпадают.

ВПИСАННАЯ ОКРУЖНОСТЬ

Радиус вписанной окружности равен половине высоты:

\(r = \frac{h}{2}\)

При этом высота правильного шестиугольника равна двум высотам правильного многоугольника со стороной a:

\(h = 2\frac{a\sqrt{3}}{2}\)

Тогда через сторону шестиугольника радиус вписанной окружности равен:

\(r = \frac{a\sqrt{3}}{2}\)

ОПИСАННАЯ ОКРУЖНОСТЬ

Радиус описанной окружности равен стороне правильного шестиугольника (как сторона правильного треугольника, из которых состоит правильный шестиугольник):

\(R = a\)

Построить вписанный шестиугольник – GeoGebra

Автор:

Хрустальный жилет

Тема:

Конструкции

Чертежи 90 016 геометрических фигур создаются с помощью измерительных инструментов, таких как линейка и транспортир.

Конструкции  – это методы создания этих фигур без использования измерительных инструментов. Как правило, в конструкциях используются только карандаш, линейка и циркуль. Эскизы создаются без использования какого-либо из этих инструментов. Этапы строительства Вместо использования линейки для измерения можно использовать циркуль для создания двух равных сегментов, копию. Шаг 1: Используйте кнопку «Окружность: центр и радиус», чтобы нарисовать окружность с центром А. Щелкните, чтобы создать центр А, и перетащите, чтобы создать радиус окружности. Отпустите кнопку мыши, когда ваш круг станет таким большим, как вам нравится. Шаг 2: Используйте кнопку «Точка на объекте», чтобы создать точку на круге A. Щелкните правой кнопкой мыши точку и выберите «Показать метку» и назовите ее точкой B. Шаг 3: Выберите кнопку «компас» (круг).

Выберите точки A и B , чтобы определить размер круга, который также представляет собой длину линии. Затем выберите (выберите) точку B , чтобы указать программе создать окружность с центральной точкой B, также известную как окружность B или ⊙B. Шаг 4: С помощью кнопки «Пересечение» создайте точки пересечения между окружностью A и окружностью B, выбрав окружность A и окружность B. Шаг 5: Нажмите кнопку «компас» (круг). Выберите точки B и D , чтобы определить размер круга, который также представляет собой длину линии. Затем выберите (выберите) точку D , чтобы указать программе создать окружность с центральной точкой D. Шаг 6 : С помощью кнопки «Пересечение» создайте точки пересечения между окружностью A и окружностью D, выбрав окружность A и окружность D. Шаг 7: Нажмите кнопку «компас» (круг). Выберите точки D и E

, чтобы определить размер круга, который также представляет собой длину линии. Затем выберите (выберите) точку E , чтобы указать программе создать окружность с центральной точкой E. Шаг 8: С помощью кнопки «Пересечение» создайте точки пересечения между окружностью A и окружностью E, выбрав окружность A и окружность E. Шаг 9: Выберите кнопку «компас» (круг). Выберите точки E и H , чтобы определить размер круга, который также представляет собой длину линии. Затем выберите (выберите) точку H , чтобы указать программе создать окружность с центральной точкой H. Шаг 10: Используя кнопку «Пересечение», создайте точки пересечения между окружностью A и окружностью H, выбрав окружность A и окружность H. Шаг 11: Используя кнопку «Многоугольник», нажмите на точку B, а затем на каждую точку на круге A, двигаясь по часовой стрелке, закончив, снова нажав на точку B.

Шаг 12: Используйте инструмент «Расстояние или длина», чтобы измерить длину сегментов вашего шестиугольника, выбрав каждый из них. Измерения должны быть равными. Шаг 13: Используйте инструмент «ABC» для напиши свое имя Шаг 14: Сделайте скриншот своей работы ниже.

вписанный шестиугольник в круг｜TikTok Search

Войдите, чтобы следить за создателями, ставить лайки видео и просматривать комментарии.

drchristisdell

11

mathigon

8

profomarmath

2223

mrsespejom

9 0076 23

zuitabuka1

19

calliechalks

643

schoolonl

1377

zakslab

132

tan_creativity01

126

sami_math01

280

antonioparlati

93.2K

y.b.upcycle

9993

mathslessonsmalta

20.8K

Infinititser_123

11

edu.oho

𝒪🦩

22,6 тыс. подписчиков

not.checking.

till.022

Входящие

170 подписчиков

joray_07

9 0132 Джорай 9Входящие 14 1556 подписчиков

naooizz

*ੈ✩‧₊ 𝓀𝒶𝓎 ₊˚⊹♡

4667 подписчиков

13doctorwhoo

901 32 닥터후(Доктор Кто)

5 миллионов подписчиков

inbox_85

INBOX

3599 подписчиков

inbox.i

Входящие!

10,2 тыс. подписчиков

notchecinbox 9Входящие 131

1307 просмотров

inhelogonne

536 просмотров

circusclownsintraining

84 просмотров

inscribedhexagon

371 просмотров

hisokaingeneral

12,6 тыс. просмотров

inheloogon

1163 просмотров

goodwinscircuschain

179просмотров

inhelogon😂😂

157 просмотров

Inscribed (Inscryption Song)

Genichris

01:00

Hexagone

Renaud

01:00

Touch in the Night (радиоверсия) )

Silent Circle

01:00

Circle in the Sand — 7″ Mix

Белинда Карлайл

01:00

Ходить по кругу

Отличительные друзья

01:00

Прикосновение в ночи

Безмолвный круг

01:00

В кругу

Критический конфликт

01:00

Touch in the Night 3000 — Неизданный альбом Редактировать

Silent Circle

01:00

6 Inch (feat.