Прогиб от сосредоточенной нагрузки: Расчет балки на прогиб

Расчет балки на прогиб

вернуться в раздел РАСЧЕТЫ КМ И КЖ

Здесь представлены формулы расчета для нахождения значений изгибающих моментов и прогибов для различных балок.

Однопролетные балки на двух шарнирных опорах
1	Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке	Смотреть расчет
2	Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках	Смотреть расчет
3	Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке	Смотреть расчет
4	Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке	Смотреть расчет
5	Расчет балки на двух шарнирных опорах при действии изгибающего момента	Смотреть расчет
Балки с жестким защемлением на двух опорах
6	Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке	Смотреть расчет
7	Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках	Смотреть расчет
8	Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке	Смотреть расчет
9	Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке	Смотреть расчет
10	Расчет балки с жестким защемлением на опорах при действии изгибающего момента	Смотреть расчет
Балки с жестким защемлением на одной опоре (консольные)
11	Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке	Смотреть расчет
12	Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке	Смотреть расчет
13	Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке	Смотреть расчет
14	Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента	Смотреть расчет
Балки двухпролетные
15	Расчет двухпролетной с шарнирными опорами при одной сосредоточенной нагрузке	Смотреть
16	Расчет двухпролетной с шарнирными опорами при двух сосредоточенных нагрузках	Смотреть
17	Расчет двухпролетной с шарнирными опорами при одной равномерно-распределенной нагрузке	Смотреть
18	Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке	Смотреть
19	Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке	Смотреть

 

 

 

Теория рядов

Теория рядов

Теория рядов. Воробьев Н. Н. 4 изд., перераб. и доп., Наука, Главная редакция физико-математической литературы, М., 1979, — 408 с. В книге излагаются основы теории числовых рядов и функциональных рядов, в том числе степенных рядов и рядов Фурье. Первая часть курса составлена в точном соответствии с разделом «Ряды» программы по высшей математике для инженерно-технических специальностей высших учебных заведений. Ее можно использовать не только как учебное пособие для слушателей курса лекций, но и при самостоятельной работе над предметом. Вторая часть представляет собой цикл очерков, посвященных более глубоким вопросам теории рядов, Оглавление ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ Часть I ГЛАВА 1. ПРОГРЕССИИ § 2. Геометрические прогрессии § 3. Бесконечные прогрессии; их сходимость и расходимость § 4. Элементарные преобразования прогрессий § 5. Функциональные прогрессии: область сходимости; равномерная сходимость § 6. Почленное интегрирование прогрессий § 7. Почленное дифференцирование прогрессий § 8. Прогрессии с комплексными членами ГЛАВА 2. ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ. ОСНОВНЫЕ ТЕОРЕМЫ О СХОДИМОСТИ § 2. Определение числового ряда и его сходимости § 3. Остаток ряда § 4. Принцип сходимости Коши § 5. Критерий Коши сходимости рядов § 6. Необходимый признак сходимости ряда § 7. Желательность систематической теории § 8. Свойства сходящихся рядов, подобные свойствам сумм § 9. Дальнейшие свойства рядов ГЛАВА 3. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ § 1. Признаки сходимости рядов § 2. Признаки сравнения § 3. Интегральный признак сходимости Маклорена — Коши § 4. Применения интегрального признака сходимости § 5. Сравнительная оценка различных признаков сходимости § 6. Признак сходимости Даламбера § 7. Признак сходимости Коши § 8. Чувствительность признаков сходимости Даламбера и Коши ГЛАВА 4. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ § 2. Абсолютная сходимость и расходимость § 3. Возможность переставлять члены в абсолютно сходящихся рядах § 4. Условно сходящиеся знакопеременные ряды § 5. Умножение абсолютно сходящихся рядов § 6. Признак сходимости Лейбница § 7. Существенность условий признака сходимости Лейбница ГЛАВА 5. ФУНКЦИОНАЛЬНЫЕ РЯДЫ § 2. Область сходимости функционального ряда § 3. Сходимость последовательности функций. Основные определения § 4. Предел последовательности непрерывных функций § 5. Переход к пределу под знаком интеграла § 6. Переход к пределу под знаком производной § 7. Определение равномерной сходимости функционального ряда и признак Вейерштрасса § 8. Непрерывность суммы равномерно сходящегося ряда с непрерывными членами § 9. Почленное интегрирование функциональных рядов § 10. Почленное дифференцирование функциональных рядов ГЛАВА 6. СТЕПЕННЫЕ РЯДЫ. ОБЩИЕ ВОПРОСЫ § 2. Теорема Абеля § 3. Круг сходимости ряда § 4. Вещественный степенной ряд и его интервал сходимости § 5. Равномерная сходимость ряда в круге его сходимости § 6. Вещественные ряды § 7. Комплексные ряды § 8. Разложение функций в степенные ряды § 9. Формула Тейлора § 10. Ряды Тейлора и Маклорена ГЛАВА 7. СТЕПЕННЫЕ РЯДЫ. ПРИМЕРЫ И ПРИЛОЖЕНИЯ § 2. Разложения в ряды Маклорена гиперболических функций ch x и sh x § 3. Разложения в ряды Маклорена тригонометрических функций cos x и sin x § 4. Показательная функция с комплексным значением показателя § 5. Формулы Эйлера § 6. Тригонометрические функции от комплексного значения аргумента § 7. Гиперболические функции от комплексного значения аргумента § 8. Вычисление значений функций при помощи ряда Маклорена § 9. Биномиальный ряд § 10. Приложения биномиального ряда § 11. Разложение в ряд Маклорена логарифмической функции § 12. Приближенное вычисление определенных интегралов при помощи степенных рядов § 13. Приближенное интегрирование дифференциальных уравнений при помощи степенных рядов ГЛАВА 8. ОРТОГОНАЛЬНЫЕ И ОРТОНОРМАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ § 2. Векторы и функции § 3. Нормированные и ортогональные функции § 4. Нормированные и ортогональные системы функций § 5. Нормировка систем функций § 6. Разложение по системам функций ГЛАВА 9. РЯДЫ ФУРЬЕ § 1. Ряды и коэффициенты Фурье § 2. Условия Дирихле и теорема о разложении функции в ряд Фурье § 3. Разложение периодических функций в ряд Фурье § 4. Физическое истолкование разложения функции в тригонометрический ряд Фурье § 5. Разложение функции f(x) = x § 6. Сдвиг сегмента разложения § 7. Изменение длины сегмента разложения § 8. Четные и нечетные функции § 9. Разложение четной функции в ряд Фурье § 10. Разложение нечетной функции в ряд Фурье § 11. Разложение ряд Фурье функций на сегменте от 0 до пи § 12. Комплексная форма записи ряда Фурье § 13. Разложение в комплексный ряд Фурье § 14. Характер сходимости рядов Фурье ГЛАВА 10. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ С ЗАКРЕПЛЕННЫМИ КОНЦАМИ § 2. Начальные и граничные условия § 3. Метод разделения переменных § 4. Использование граничных условий. Собственные функции и собственные значения § 5. Использование начальных условий ГЛАВА 11. ИНТЕГРАЛ ФУРЬЕ § 1. Представление функций интегралом Фурье § 2. Простейшие достаточные условия представимости функции интегралом Фурье § 3. Интеграл Фурье для четных функций § 4. Интеграл Фурье для нечетных функций § 5. Комплексная форма интеграла Фурье § 6. Понятие о преобразовании Фурье § 7. Косинус-преобразование Фурье § 8. Синус-преобразование Фурье § 9. Спектральная функция Часть II § 1. Признак сходимости Куммера § 2. Признак сходимости Раабе § 3. Признак сходимости Бертрана § 4. Признак сходимости Гаусса § 5. Сходимость знакопеременных рядов § 6. Признак сходимости Дирихле ГЛАВА 13. ДВОЙНЫЕ РЯДЫ § 1. Определение двойного ряда § 2. Сходимость двойных рядов § 3. Критерии сходимости двойных рядов. Теорема Маркова § 4. 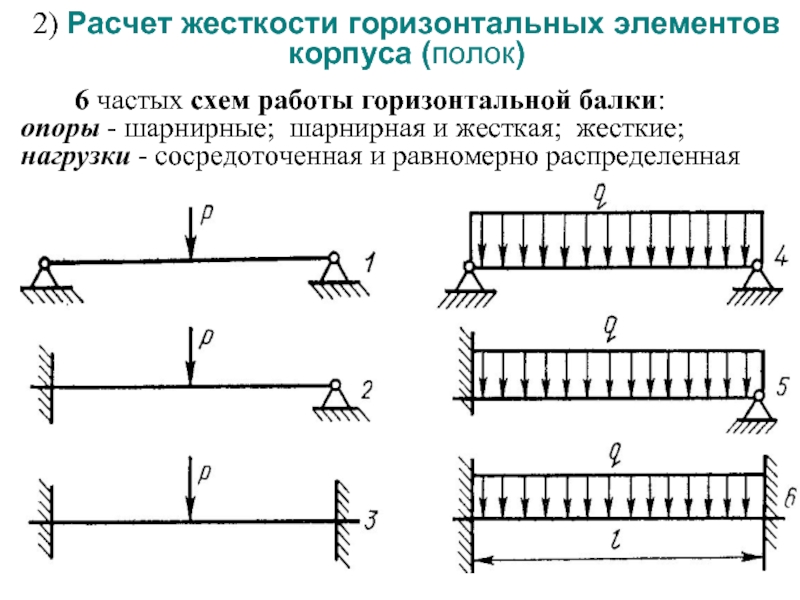Свойства двойных рядов и признаки сходимости § 5. Абсолютная сходимость двойных рядов § 6. Двойные функциональные ряды § 7. Двойные степенные ряды § 8. Разложение функций двух переменных в двойные ряды Тейлора и Маклорена § 9. Ортогональные и ортонормальные системы функций от двух переменных § 10. Двойные ряды Фурье ГЛАВА 14. СУММИРОВАНИЕ СХОДЯЩИХСЯ РЯДОВ § 2. Линейные преобразования рядов § 3. Теорема Абеля и почленное дифференцирование и интегрирование рядов § 4. Последовательности разностей § 5. Преобразование рядов по Эйлеру § 6. Преобразование рядов по Куммеру ГЛАВА 15. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ § 1. Расходящиеся геометрические прогрессии § 2. Суммирующие функции § 3. Суммирование по Пуассону — Абелю § 4. Линейность и регулярность суммирования по Пуассону — Абелю § 5. Суммируемость рядов по Пуассону — Абелю и их абсолютная сходимость § 6. Теорема Таубера § 7. Суммирование по Чезаро § 8. Соотношение между сходимостью по Чезаро и по Пуассону — Абелю § 9. Суммирование по Эйлеру ГЛАВА 16. СХОДИМОСТЬ РЯДОВ ФУРЬЕ § 2. Исследование двух интегралов § 3. Исследование одного класса интегралов § 4. Доказательство теоремы Дирихле § 5. Теорема Фурье § 6. Коэффициенты Фурье разрывных функций § 7. Скорость сходимости рядов Фурье § 8. Улучшение сходимости рядов Фурье по методу выделения особенностей § 9. О равномерной сходимости рядов Фурье § 10. Неравномерная сходимость последовательностей непрерывных функций § 11. Поведение рядов Фурье функций в точках их разрыва. Явление Гиббса § 12. Экстремальное свойство сумм Фурье § 13. Суммирование рядов Фурье по Чезаро. Теорема Фейера § 14. Равенство Парсеваля § 15. Теорема Вейерштрасса ГЛАВА 17. ПРИМЕНЕНИЕ РЯДОВ ФУРЬЕ В ТЕОРИИ ИЗГИБА БАЛОК § 2. Изгиб балки § 3. Свободно опертая балка § 4. Первая возможность ограничиться двукратным дифференцированием § 5. Случай сосредоточенной нагрузки § 6. Прогиб балки от распределенной нагрузки § 7. Прогиб от сосредоточенного момента § 8. Статически неопределимая балка § 9. Сложный изгиб балки § 10. Балка на упругом основании § 11. Вторая возможность ограничиться двукратным дифференцированием. Потенциальная энергия изгиба балки § 12. Потенциальная энергия изгиба балки в случае нескольких нагрузок § 13. Функции прогиба с ортогональными вторыми производными § 14. Свободно опертая нагруженная балка § 15. Работа продольных сил при сложном изгибе балки § 16. Общий случай изгиба балки § 17. Общий случай изгиба свободно опертой балки § 18. Изгиб симметрично нагруженной балки, жестко заделанной по концам § 19. Функция прогиба симметрично загруженной балки с жестко заделанными концами

Таблицы отклонения балки | МеханиКальк

ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.

---

В таблицах ниже приведены уравнения для прогиба, наклона, сдвига и момента вдоль прямых балок для различных условий на концах и нагрузок. Вы можете найти исчерпывающие таблицы в таких справочниках, как Gere, Lindeburg и Shigley. Однако приведенные ниже таблицы охватывают большинство распространенных случаев.

Для получения информации об отклонении балки см. наш справочник по напряжениям и отклонениям в балках.

Консольные балки

Консоль, торцевая нагрузка		@ х = L @ х = L В = +F М = -F (L — х) M макс. = −FL @ х = 0
Консоль, промежуточная нагрузка		(0 ≤ х ≤ а) (а ≤ х ≤ L) @ х = L (0 ≤ х ≤ а) (а ≤ х ≤ L) В = +F (0 ≤ х ≤ а) В = 0 (а ≤ х ≤ L) М = -F (а — х) (0 ≤ х ≤ а) М = 0 (а ≤ х ≤ L)
Консоль, равномерно распределенная нагрузка		@ х = L @ х = L V = +w (L − x) В макс. = +wL @ х = 0 М = -w (L — x) 2 / 2 M макс. = −wL 2 / 2 @ х = 0
Консоль, треугольная распределенная нагрузка		@ х = L @ х = L В макс. = +w 1 л / 2 @ х = 0 M макс. = −w 1 L 2 / 6 @ х = 0
Консоль, Конечный момент		@ х = L @ х = L М = -М 0

Просто поддерживаемые балки

Просто поддерживаемые, промежуточная нагрузка		(0 ≤ х ≤ а) Для a ≥ b: @ (0 ≤ х ≤ а) @ х = 0 @ х = L В 1 = +Fb / L (0 ≤ х ≤ а) В 2 = −Fa / L (а ≤ х ≤ L) M макс = +Fab / L @ х = а
Простая опора, центральная нагрузка		(0 ≤ х ≤ L/2) @ х = L/2 (0 ≤ х ≤ L/2) @ х = 0 @ х = L В 1 = +F / 2 (0 ≤ х ≤ L/2) В 2 = −F / 2 (L/2 ≤ x ≤ L) M макс. = FL / 4 @ х = L/2
Просто поддерживаемый, 2 нагрузки на равном расстоянии от опор		(0 ≤ х ≤ а) ( а ≤ х ≤ L — а ) @ х = L/2 (0 ≤ х ≤ а) ( а ≤ х ≤ L — а ) @ х = 0 @ х = L В 1 = +F (0 ≤ х ≤ а) В 2 = −F ( L — а ≤ x ≤ L ) M макс. = Fa ( а ≤ х ≤ L — а )
Простая опора, равномерная распределенная нагрузка		@ х = L/2 @ х = 0 @ х = L V = w (L/2 − x) В 1 = +wL / 2 @ х = 0 В 2 = −wL / 2 @ х = L M макс. = wL 2 / 8 @ х = L/2
Простая опора, момент на каждой опоре		@ х = L/2 @ х = 0 @ х = L М = М 0
Простая опора, момент в одну опору		@ x = L (1 − √3/3) @ х = 0 @ х = L В = −М 0 / л М макс. = М 0 @ х = 0
Простая опора, центральный момент		(0 ≤ х ≤ L/2) (0 ≤ х ≤ L/2) @ х = 0 @ х = L В = +M 0 / L М = М 0 х/л (0 ≤ х ≤ L/2) М макс. = М 0 / 2 @ х = L/2

Фиксированные-Фиксированные балки

Фиксированные-Фиксированные, центральная нагрузка		(0 ≤ х ≤ L/2) @ х = L/2 В 1 = +F / 2 (0 ≤ х ≤ L/2) В 2 = −F / 2 (L/2 ≤ x ≤ L) М = F (4x — L) / 8 (0 ≤ х ≤ L/2) M 1 = M 3 = −FL / 8 @ х = 0 и х = L М 2 = +FL / 8 @ х = L/2
Фиксированная-фиксированная, равномерная распределенная нагрузка		@ х = L/2 V = w (L/2 − x) В 1 = +wL / 2 @ х = 0 В 2 = −wL / 2 @ х = L М = w (6Lx — 6x 2 — L 2 ) / 12 M 1 = M 3 = −wL 2 / 12 @ х = 0 и х = L M 2 = шл 2 / 24 @ х = L/2

---

Ознакомьтесь с нашим калькулятором луча, основанным на методологии, описанной здесь.

• Расчет напряжений и прогибов в прямых балках
• Построение диаграмм сдвига и моментов
• Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил

---

1. Будинас-Нисбетт, «Машиностроение Шигли», 8-е изд.
2. Гир, Джеймс М., «Механика материалов», 6-е изд.
3. Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена PE», 13-е изд.

---

Формула прогиба балок с диаграммами для всех условий .

15.05.2021 19.07.2020 Вики

, когда есть вертикальное смещение в любой точке нагруженной балки, говорят, что это отклонение балок . Максимальный прогиб балок происходит там, где уклон равен нулю.

Наклон луча определяется как угол между отклоненным лучом и фактическим лучом в той же точке.

Общие и стандартные уравнения для прогиба балок приведены ниже: = Модуль Юнга,
I = Момент инерции .

Продукт E.I известен как жесткость на изгиб .

Существует много типов балок, и для этих различных типов балок или случаев формула не будет одинаковой. Он должен быть изменен в зависимости от случая или типа луча. Теперь давайте рассмотрим следующие случаи.

1. Свободно опертая балка с центральной точечной нагрузкой:

Свободно опертая балка AB длиной l несет точечную нагрузку в центре балки на уровне C. отклонение в точка C будет:

2. Свободно опертая балка с внецентренной точечной нагрузкой:

Свободно опертая балка AB длиной 9099 4 л несет эксцентричную точечную нагрузку на C , как показано на рис. Отклонение балки определяется следующим образом:

Поскольку b > a , поэтому максимальное отклонение происходит в CB , а расстояние от B определяется как:

а максимальное отклонение определяется выражением :

3. Свободно опертая балка с равномерно распределенной нагрузкой :

Свободно опертая балка AB при равномерно распределенной нагрузке w /единица длины показана на рисунке ,

Максимальный прогиб происходит в средней точке C и определяется как:

90 995 4. Просто поддерживаемая балка с Постепенно меняющаяся нагрузка:

Свободно опертая балка из AB длиной l , несущая постепенно изменяющуюся нагрузку от нуля на B до w/единицы длины на A , показана на рисунке ниже. ,

Максимальное отклонение балки происходит, когда x = 0,519 l и его значение определяется как:

5. Консольная балка с точечной нагрузкой на свободном конце:

Консоль балка АВ длиной l , несущая на свободном конце точечную нагрузку, показана на рис. Прогиб в любом сечении х на расстоянии х от свободного конца определяется как:

Максимальный прогиб происходит на свободном конце (когда x = 0,) и его значение определяется выражением

6. Консольная балка с равномерно распределенной нагрузкой:

90 011

Консоль балка AB длиной l , несущая равномерно распределенную нагрузку на единицу длины, показана на рис. Прогиб в любом сечении х на расстоянии х от В определяется выражением

Максимальное отклонение происходит на свободном конце (когда x = 0), а его значение определяется

, когда консоль частично загружается, как показано на рис. расстояние от фиксированного конца) определяется как:

и максимальное отклонение происходит на B , значение которого определяется как

7. Консольная балка с постепенно меняющейся нагрузкой:

Консольная балка AB длиной 909 94 л с постепенно меняющейся нагрузкой от нуля до B на единицу длины при A показан на рис. Прогиб в любом сечении х на расстоянии х от В определяется как

Максимальный прогиб происходит на свободном конце (при х = 0) и его значение определяется как

8. Неподвижная балка, несущая центральную точечную нагрузку:

Неподвижная балка AB длиной l , несущая точечную нагрузку в центре балки C , как показано на рис. Максимальное отклонение балки происходит при C , а его значение определяется как

9. Неподвижная балка, несущая внецентренную нагрузку:

Фиксированная балка AB длиной л с эксцентриком загрузить в C , как показано на рис. Прогиб в любом сечении х на расстоянии х от А определяется как

Максимальное расстояние возникает, когда

90 002 Отсюда Максимальное отклонение луча,

и прогиб под нагрузкой при C ,

10.