Ребро (геометрия)
Ребро в геометрии — отрезок, соединяющий две вершины многоугольника или многогранника (в размерностях 3 и выше)[1]. В многоугольниках ребро является отрезком, лежащим на границе[2] и чаще называется стороной многоугольника. В трёхмерных многогранниках и в многогранниках большей размерности ребро — это отрезок, общий для двух граней[3]. Отрезок, соединяющий две вершины и проходящий через внутренние или внешние точки, ребром не является и называется диагональю.
Три ребра AB, BC и CA, каждое из которых соединяет две вершины треугольника. | Многоугольник, ограниченный рёбрами (в данном случае — квадрат, имеющий 4 ребра). |
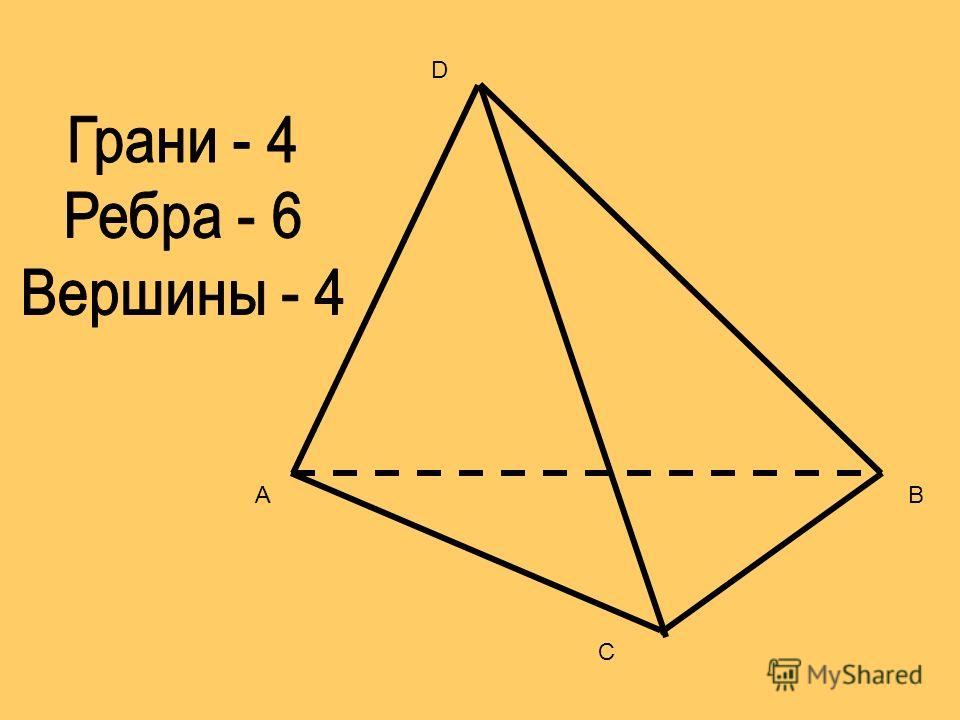
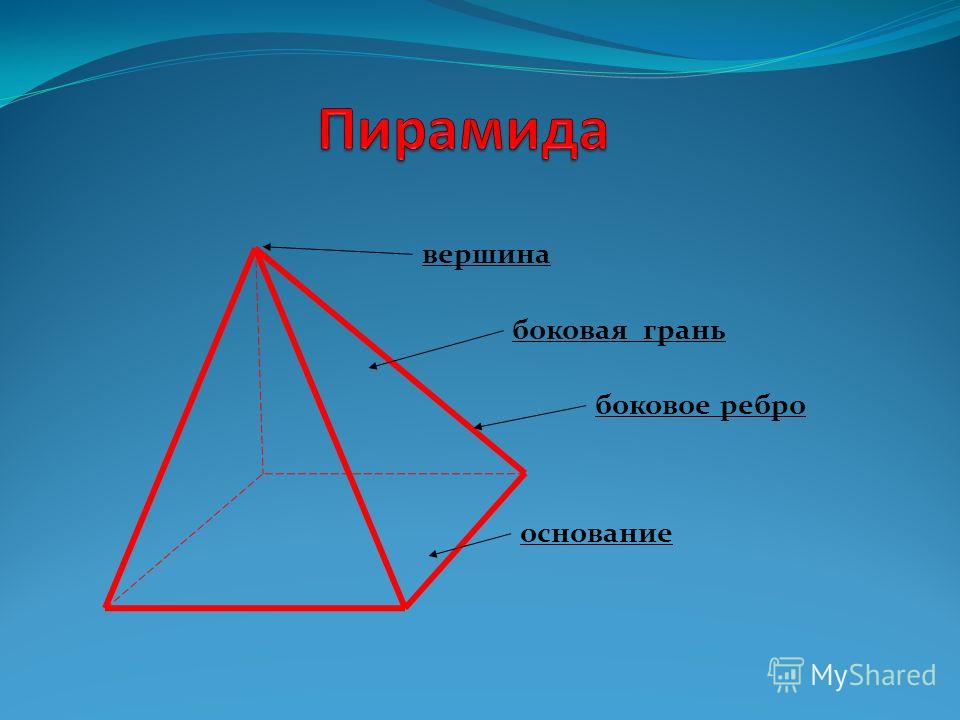
Каждое ребро является общим для двух граней многогранника, в данном случае, куба. | Любое ребро является общим для трёх и более граней четырёхмерного многогранника, как видно на этой проекции тессеракта.  |
У этого термина существуют и другие значения, см. Ребро.
Содержание
- 1 Связь с рёбрами графа
- 2 Число рёбер в многограннике
- 3 Инцидентность другим граням
- 4 Альтернативная терминология
- 5 См. также
- 6 Примечания
- 7 Литература
- 8 Ссылки
Связь с рёбрами графа
Любой многогранник может быть представлен его рёберным скелетом[en], то есть графом, вершинами которого служат геометрические вершины многогранника, а рёбра графа соответствуют геометрическим рёбрам[4]. И обратно, графы, являющиеся скелетами трёхмерных многогранников по теореме Штайница — то же самое, что вершинно k-связные планарные графы[5].
Число рёбер в многограннике
Любая поверхность выпуклого многогранника имеет эйлерову характеристику
- V−E+F=2,{\displaystyle V-E+F=2,}
где V{\displaystyle V}
— число вершин, E{\displaystyle E}
— число рёбер, а F{\displaystyle F}
— число граней.
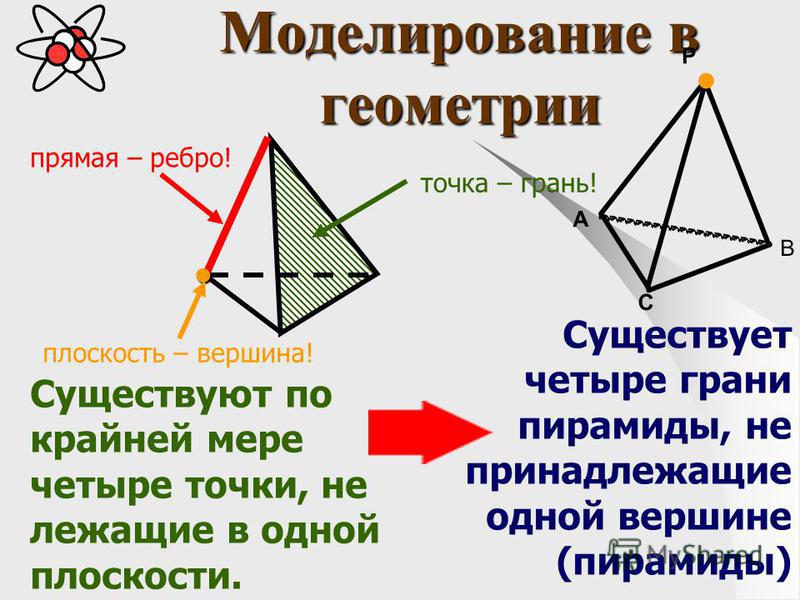Это равенство известно как формула Эйлера. Таким образом, число рёбер на 2 меньше суммы числа вершин и граней. Например, куб имеет 8 вершин и 6 граней, а потому (по формуле) 12 рёбер.Инцидентность другим граням
В многоугольнике в каждой вершине сходятся два ребра (стороны). По теореме Балинского по меньшей мере d{\displaystyle d}
рёбер сходятся в каждой вершине d{\displaystyle d}
-мерного выпуклого многогранника[6]. Аналогично, в трёхмерном многограннике в точности две двумерные грани имеют общее ребро[7], в то время как в многогранниках более высоких размерностей общее ребро могут иметь три и более двумерных граней.
Альтернативная терминология
В теории выпуклых многогранников высоких размерностей (свыше 3) фасета (сторона d{\displaystyle d}
-мерного многогранника) — это (d−1){\displaystyle (d-1)}
-мерная грань.
Таким образом, рёбра (стороны) многоугольника являются также фасетами (для трёхмерных многогранников фасетами будут грани)[8].См. также
- Продолжение стороны[en]
Примечания
- ↑ Ziegler, 1995, с. 51, Definition 2.1.
- ↑ Weisstein, Eric W. «Polygon Edge.» From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/PolygonEdge.html
- ↑ Weisstein, Eric W. «Polytope Edge.» From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/PolytopeEdge.html
- ↑ Senechal, 2013, с. 81.
- ↑ Pisanski, Randić, 2000, с. 174–194.
- ↑ Balinski, 1961, с. 431–434.
- ↑ Wenninger, 1974, с. 1.
- ↑ Seidel, 1986, с. 404–413.
Литература
- Günter M. Ziegler. Lectures on Polytopes. — Springer, 1995. — Т. 152. — (Graduate Texts in Mathematics).
- M. L. Balinski. On the graph structure of convex polyhedra in n-space // Pacific Journal of Mathematics. 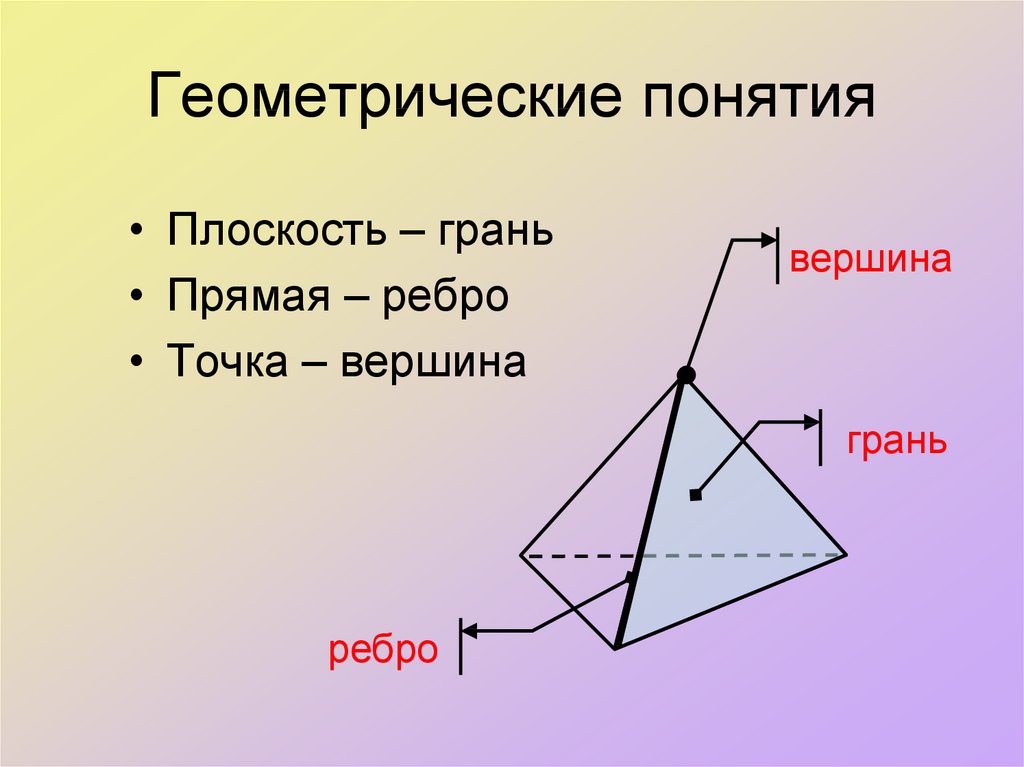— 1961. — Vol. 11. — Вып. 2. — doi:10.2140/pjm.1961.11.431.
- Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — ISBN 9780521098595.
- Marjorie Senechal. Shaping Space: Exploring Polyhedra in Nature, Art, and the Geometrical Imagination. — Springer, 2013. — ISBN 9780387927145.
- Tomaž Pisanski, Milan Randić. Geometry at work / Catherine A. Gorini. — Washington, DC: Math. Assoc. America, 2000. — Т. 53. — (MAA Notes).. См., в частности, теорему 3, стр. 176.
- Raimund Seidel. Proceedings of the Eighteenth Annual ACM Symposium on Theory of Computing (STOC ’86). — 1986. — doi:10.1145/12130.12172.
Ссылки
- Olshevsky, George. «». Glossary for Hyperspace. Архивировано с оригинала 4 февраля 2007.
- Weisstein, Eric W. Polygonal edge (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Polyhedral edge (англ.) на сайте Wolfram MathWorld.
Ребро, геометрия, Ребро, геометрии, отрезок, соединяющий, две, вершины, многоугольника, или, многогранника, размерностях, выше, многоугольниках, ребро, является, отрезком, лежащим, на, границе, чаще, называется, стороной, многоугольника, трёхмерных, многогранн.
Rebro v geometrii otrezok soedinyayushij dve vershiny mnogougolnika ili mnogogrannika v razmernostyah 3 i vyshe 1 V mnogougolnikah rebro yavlyaetsya otrezkom lezhashim na granice 2 i chashe nazyvaetsya storonoj mnogougolnika V tryohmernyh mnogogrannikah i v mnogogrannikah bolshej razmernosti rebro eto otrezok obshij dlya dvuh granej 3 Otrezok soedinyayushij dve vershiny i prohodyashij cherez vnutrennie ili vneshnie tochki rebrom ne yavlyaetsya i nazyvaetsya diagonalyu Tri rebra AB BC i CA kazhdoe iz kotoryh soedinyaet dve vershiny treugolnika Mnogougolnik ogranichennyj ryobrami v dannom sluchae kvadrat imeyushij 4 rebra Kazhdoe rebro yavlyaetsya obshim dlya dvuh granej mnogogrannika v dannom sluchae kuba Lyuboe rebro yavlyaetsya obshim dlya tryoh i bolee granej chetyryohmernogo mnogogrannika kak vidno na etoj proekcii tesserakta U etogo termina sushestvuyut i drugie znacheniya sm Rebro Soderzhanie 1 Svyaz s ryobrami grafa 2 Chislo ryober v mnogogrannike 3 Incidentnost drugim granyam 4 Alternativnaya terminologiya 5 Sm takzhe 6 Primechaniya 7 Literatura 8 SsylkiSvyaz s ryobrami grafa PravitLyuboj mnogogrannik mozhet byt predstavlen ego ryobernym skeletom en to est grafom vershinami kotorogo sluzhat geometricheskie vershiny mnogogrannika a ryobra grafa sootvetstvuyut geometricheskim ryobram 4 I obratno grafy yavlyayushiesya skeletami tryohmernyh mnogogrannikov po teoreme Shtajnica to zhe samoe chto vershinno k svyaznye planarnye grafy 5 Chislo ryober v mnogogrannike PravitLyubaya poverhnost vypuklogo mnogogrannika imeet ejlerovu harakteristiku V E F 2 displaystyle V E F 2 gde V displaystyle V chislo vershin E displaystyle E chislo ryober a F displaystyle F chislo granej Eto ravenstvo izvestno kak formula Ejlera Takim obrazom chislo ryober na 2 menshe summy chisla vershin i granej Naprimer kub imeet 8 vershin i 6 granej a potomu po formule 12 ryober Incidentnost drugim granyam PravitV mnogougolnike v kazhdoj vershine shodyatsya dva rebra storony Po teoreme Balinskogo po menshej mere d displaystyle d ryober shodyatsya v kazhdoj vershine d displaystyle d mernogo vypuklogo mnogogrannika 6 Analogichno v tryohmernom mnogogrannike v tochnosti dve dvumernye grani imeyut obshee rebro 7 v to vremya kak v mnogogrannikah bolee vysokih razmernostej obshee rebro mogut imet tri i bolee dvumernyh granej Alternativnaya terminologiya PravitV teorii vypuklyh mnogogrannikov vysokih razmernostej svyshe 3 faseta storona d displaystyle d mernogo mnogogrannika eto d 1 displaystyle d 1 mernaya gran Takim obrazom ryobra storony mnogougolnika yavlyayutsya takzhe fasetami dlya tryohmernyh mnogogrannikov fasetami budut grani 8 Sm takzhe PravitProdolzhenie storony en Primechaniya Pravit Ziegler 1995 s 51 Definition 2 1 Weisstein Eric W Polygon Edge From MathWorld A Wolfram Web Resource http mathworld wolfram com PolygonEdge html Weisstein Eric W Polytope Edge From MathWorld A Wolfram Web Resource http mathworld wolfram com PolytopeEdge html Senechal 2013 s 81 Pisanski Randic 2000 s 174 194 Balinski 1961 s 431 434 Wenninger 1974 s 1 Seidel 1986 s 404 413 Literatura PravitGunter M Ziegler Lectures on Polytopes Springer 1995 T 152 Graduate Texts in Mathematics M L Balinski On the graph structure of convex polyhedra in n space Pacific Journal of Mathematics 1961 Vol 11 Vyp 2 doi 10 2140 pjm 1961 11 431 Magnus J Wenninger Polyhedron Models Cambridge University Press 1974 ISBN 9780521098595 Marjorie Senechal Shaping Space Exploring Polyhedra in Nature Art and the Geometrical Imagination Springer 2013 ISBN 9780387927145 Tomaz Pisanski Milan Randic Geometry at work Catherine A Gorini Washington DC Math Assoc America 2000 T 53 MAA Notes Sm v chastnosti teoremu 3 str 176 Raimund Seidel Proceedings of the Eighteenth Annual ACM Symposium on Theory of Computing STOC 86 1986 doi 10 1145 12130 12172 Ssylki PravitOlshevsky George Edge Glossary for Hyperspace Arhivirovano s originala 4 fevralya 2007 Weisstein Eric W Polygonal edge angl na sajte Wolfram MathWorld Weisstein Eric W Polyhedral edge angl na sajte Wolfram MathWorld Dlya uluchsheniya etoj stati zhelatelno Proverit kachestvo perevoda s inostrannogo yazyka Ispravit statyu soglasno stilisticheskim pravilam Vikipedii Pozhalujsta posle ispravleniya problemy isklyuchite eyo iz spiska parametrov Posle ustraneniya vseh nedostatkov etot shablon mozhet byt udalyon lyubym uchastnikom Istochnik https ru wikipedia org w index php title Rebro geometriya amp oldid 90449747, Википедия, чтение, книга, библиотека, поиск, нажмите,истории
, книги, статьи, wikipedia, учить, информация, история, секс, порно, скачать, скачать, sex, seks, porn, porno, скачать, бесплатно, скачать бесплатно, mp3, видео, mp4, 3gp, jpg, jpeg, gif, png, картинка, музыка, песня, фильм, игра, игры
Это равенство известно как формула Эйлера. Таким образом, число рёбер на 2 меньше суммы числа вершин и граней. Например, куб имеет 8 вершин и 6 граней, а потому (по формуле) 12 рёбер.
Таким образом, рёбра (стороны) многоугольника являются также фасетами (для трёхмерных многогранников фасетами будут грани)[8].
— 1961. — Vol. 11. — Вып. 2. — doi:10.2140/pjm.1961.11.431.
Rebro v geometrii otrezok soedinyayushij dve vershiny mnogougolnika ili mnogogrannika v razmernostyah 3 i vyshe 1 V mnogougolnikah rebro yavlyaetsya otrezkom lezhashim na granice 2 i chashe nazyvaetsya storonoj mnogougolnika V tryohmernyh mnogogrannikah i v mnogogrannikah bolshej razmernosti rebro eto otrezok obshij dlya dvuh granej 3 Otrezok soedinyayushij dve vershiny i prohodyashij cherez vnutrennie ili vneshnie tochki rebrom ne yavlyaetsya i nazyvaetsya diagonalyu Tri rebra AB BC i CA kazhdoe iz kotoryh soedinyaet dve vershiny treugolnika Mnogougolnik ogranichennyj ryobrami v dannom sluchae kvadrat imeyushij 4 rebra Kazhdoe rebro yavlyaetsya obshim dlya dvuh granej mnogogrannika v dannom sluchae kuba Lyuboe rebro yavlyaetsya obshim dlya tryoh i bolee granej chetyryohmernogo mnogogrannika kak vidno na etoj proekcii tesserakta U etogo termina sushestvuyut i drugie znacheniya sm Rebro Soderzhanie 1 Svyaz s ryobrami grafa 2 Chislo ryober v mnogogrannike 3 Incidentnost drugim granyam 4 Alternativnaya terminologiya 5 Sm takzhe 6 Primechaniya 7 Literatura 8 SsylkiSvyaz s ryobrami grafa PravitLyuboj mnogogrannik mozhet byt predstavlen ego ryobernym skeletom en to est grafom vershinami kotorogo sluzhat geometricheskie vershiny mnogogrannika a ryobra grafa sootvetstvuyut geometricheskim ryobram 4 I obratno grafy yavlyayushiesya skeletami tryohmernyh mnogogrannikov po teoreme Shtajnica to zhe samoe chto vershinno k svyaznye planarnye grafy 5 Chislo ryober v mnogogrannike PravitLyubaya poverhnost vypuklogo mnogogrannika imeet ejlerovu harakteristiku V E F 2 displaystyle V E F 2 gde V displaystyle V chislo vershin E displaystyle E chislo ryober a F displaystyle F chislo granej Eto ravenstvo izvestno kak formula Ejlera Takim obrazom chislo ryober na 2 menshe summy chisla vershin i granej Naprimer kub imeet 8 vershin i 6 granej a potomu po formule 12 ryober Incidentnost drugim granyam PravitV mnogougolnike v kazhdoj vershine shodyatsya dva rebra storony Po teoreme Balinskogo po menshej mere d displaystyle d ryober shodyatsya v kazhdoj vershine d displaystyle d mernogo vypuklogo mnogogrannika 6 Analogichno v tryohmernom mnogogrannike v tochnosti dve dvumernye grani imeyut obshee rebro 7 v to vremya kak v mnogogrannikah bolee vysokih razmernostej obshee rebro mogut imet tri i bolee dvumernyh granej Alternativnaya terminologiya PravitV teorii vypuklyh mnogogrannikov vysokih razmernostej svyshe 3 faseta storona d displaystyle d mernogo mnogogrannika eto d 1 displaystyle d 1 mernaya gran Takim obrazom ryobra storony mnogougolnika yavlyayutsya takzhe fasetami dlya tryohmernyh mnogogrannikov fasetami budut grani 8 Sm takzhe PravitProdolzhenie storony en Primechaniya Pravit Ziegler 1995 s 51 Definition 2 1 Weisstein Eric W Polygon Edge From MathWorld A Wolfram Web Resource http mathworld wolfram com PolygonEdge html Weisstein Eric W Polytope Edge From MathWorld A Wolfram Web Resource http mathworld wolfram com PolytopeEdge html Senechal 2013 s 81 Pisanski Randic 2000 s 174 194 Balinski 1961 s 431 434 Wenninger 1974 s 1 Seidel 1986 s 404 413 Literatura PravitGunter M Ziegler Lectures on Polytopes Springer 1995 T 152 Graduate Texts in Mathematics M L Balinski On the graph structure of convex polyhedra in n space Pacific Journal of Mathematics 1961 Vol 11 Vyp 2 doi 10 2140 pjm 1961 11 431 Magnus J Wenninger Polyhedron Models Cambridge University Press 1974 ISBN 9780521098595 Marjorie Senechal Shaping Space Exploring Polyhedra in Nature Art and the Geometrical Imagination Springer 2013 ISBN 9780387927145 Tomaz Pisanski Milan Randic Geometry at work Catherine A Gorini Washington DC Math Assoc America 2000 T 53 MAA Notes Sm v chastnosti teoremu 3 str 176 Raimund Seidel Proceedings of the Eighteenth Annual ACM Symposium on Theory of Computing STOC 86 1986 doi 10 1145 12130 12172 Ssylki PravitOlshevsky George Edge Glossary for Hyperspace Arhivirovano s originala 4 fevralya 2007 Weisstein Eric W Polygonal edge angl na sajte Wolfram MathWorld Weisstein Eric W Polyhedral edge angl na sajte Wolfram MathWorld Dlya uluchsheniya etoj stati zhelatelno Proverit kachestvo perevoda s inostrannogo yazyka Ispravit statyu soglasno stilisticheskim pravilam Vikipedii Pozhalujsta posle ispravleniya problemy isklyuchite eyo iz spiska parametrov Posle ustraneniya vseh nedostatkov etot shablon mozhet byt udalyon lyubym uchastnikom Istochnik https ru wikipedia org w index php title Rebro geometriya amp oldid 90449747, Википедия, чтение, книга, библиотека, поиск, нажмите,Параметры проверки геометрии — 2016
Перед выполнением проверки геометрии можно задать различные параметры проверки.
К ним относятся:
| Короткие кромки | К коротким кромкам относятся все кромки малой длины. Короткое ребро Чтобы проверить наличие коротких кромок, выберите Несущественная геометрия и Короткие кромки, затем установите Длину кромки. Если длина кромки менее заданной, то такую кромку называют короткой. |
| Малые грани | Малые грани — это грани, в которых:
Два конца цилиндра определены как малые грани. Чтобы выявить наличие малых граней, выберите Несущественная геометрия и Малые грани, затем задайте максимальную длину ребра в поле Длины всех кромок. Все грани, имеющие длину ребер менее заданной, являются малыми. |
| Вытянутые грани | Вытянутые грани — это грани с высоким форматным соотношением (отношение длины к ширине). Грань является вытянутой, если ее площадь меньше минимальной площади W*((P/2)-W), где W — ширина, заданная пользователем, а P — периметр грани.
Вытянутая грань
Чтобы проверить расщепленных граней, выберите Несущественная геометрия и Поверхность среза, затем установите Ширину грани. Все грани, которые по площади меньше минимальной, являются вытянутыми. |
| Острые кромки | Острыми называют такие ребра, которые расположены между двумя смежными гранями, образующими острый угол. Если острые кромки попадают в сетку при моделировании методом конечных элементов, то указанная сетка в непосредственной близости от острых кромок может оказаться чрезмерно плотной.Острое ребро Чтобы выявить наличие острых кромок, выберите Острые углы и Острые кромки и задайте Угол грани. Если величина угла между двумя смежными гранями меньше заданной, то общее ребро таких граней называют острым |
| Острые вершины | Острыми называют вершины, которые образованы двумя смежными кромками, составляющими острый угол. В точке пересечения острых ребер, как правило, образуется острая вершина. Острые вершины Чтобы выявить наличие острых вершин, выберите Острые углы и Острые вершины и задайте Угол кромки. |
| Прерывистые грани | Чтобы проверить наличие прерывистых граней, выберите Прерывистая геометрия и Грани. Все грани в детали, для которых геометрия поверхностей, расположенная на заднем плане, имеет позиционный разрыв или разрыв кривизны геометрии поверхности, называются прерывистыми. Позиционный разрыв или разрыв кривизны поверхности может возникать при импортировании детали. |
| Прерывистые кромки | Чтобы проверить наличие прерывистых ребер, выберите Прерывистая геометрия и Кромки. Все кромки в детали, для которых геометрия кривизны, расположенная на заднем плане, имеет позиционный разрыв или разрыв кривизны геометрии поверхности, называются прерывистыми. |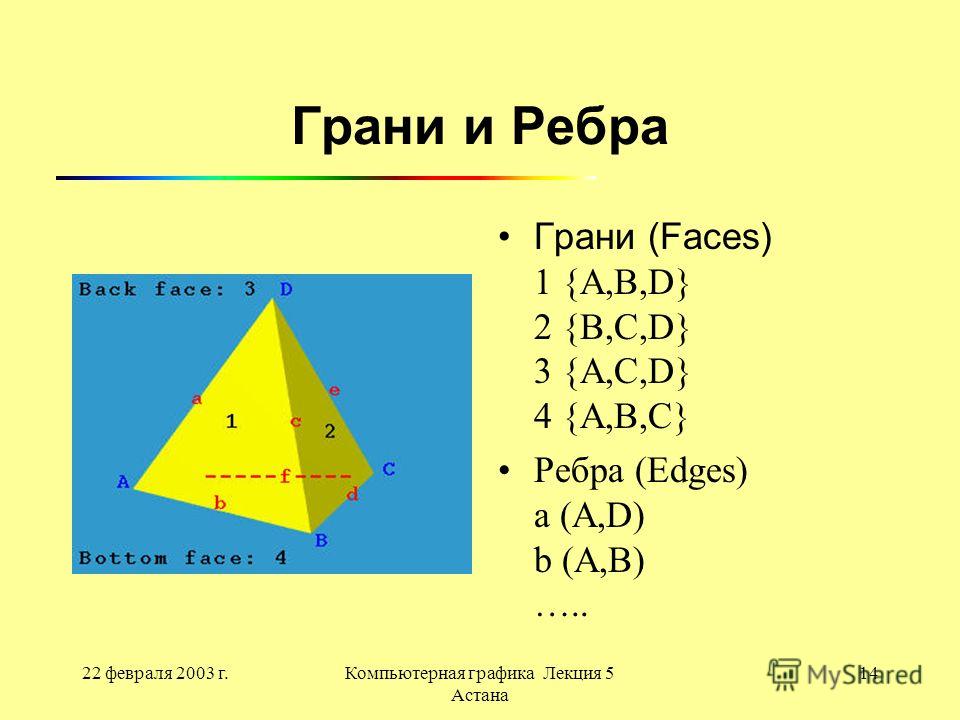
Если две смежные кромки пересекаются под углом, величина которого менее заданной, то вершина в точке пересечения этих кромок называется острой.
Желательно […] базовые формы a n d геометрия кромки o f te n невозможно […] с вращающимися инструментами. kavofr.com kavofr.com | Fo rm as b sic as y geometras m arg ina les d es […] muchas veces no se pueden conseguir con tools rotatorios. kavofr.com kavofr.com | ||||||||||||||||||||||||||||||||||||||||||||||||||||
SketchUp может неправильно обрабатывать […] некоторые виды инв al i d геометрия кромок w h en разбор вредоносного файла . sketchup. sketchup.google.com | SketchUp не обрабатывается […] correctamen te determi nad as geometras de aristas no vl id as[…]анализ и архив. sketchup.google.com sketchup.google.com | ||||||||||||||||||||||||||||||||||||||||||||||||||||
Зажим ножа […] Техника и сокращение TI N G Геометрия края : C UT Ting Angle 27 Weinig.D Weinig.de . | Tcnica d e suj eci n y geometra d e l de desprendimiento de 27 Estndar weinig.de weinig.de | ||||||||||||||||||||||||||||||||||||||||||||||||||||
Определить разрез ti n g геометрия кромки u s в 900. lutz-blades.com lutz-blades.com | Утилис ла […] siguiente matri z para d efinir las f ormas de filo . lutz-blades.com lutz-blades.com | ||||||||||||||||||||||||||||||||||||||||||||||||||||
Высококачественное покрытие […] разреза ti n g геометрия кромки e n ab les выдающийся […]производительность. wikus.com wikus.com | Ла Альта Калидад дель […] recubrie nt o en el filo de cort e разрешение […] исключительные выдачи. wikus.com wikus.com | ||||||||||||||||||||||||||||||||||||||||||||||||||||
Техника зажима ножа и разрез ti n g геометрия кромки weinig. weinig.de | Tcnica d e suje cin y geometra de las cuc
|
google.com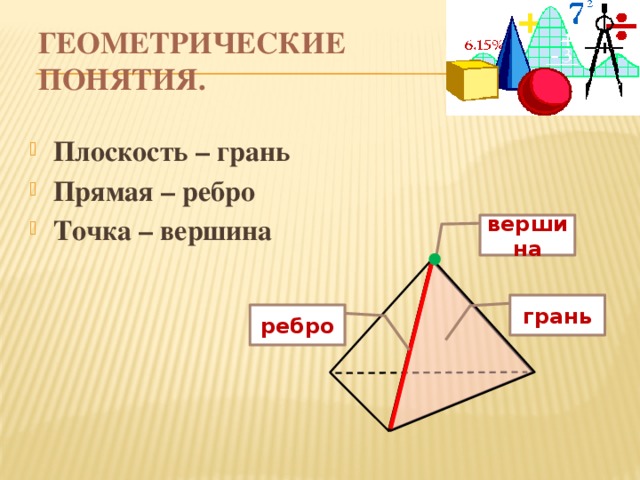
10 g следующую матрицу
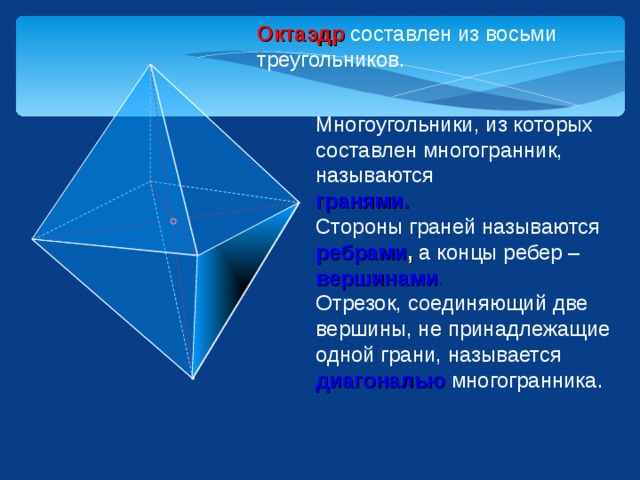de
de
..]
Жесткий бетон
es