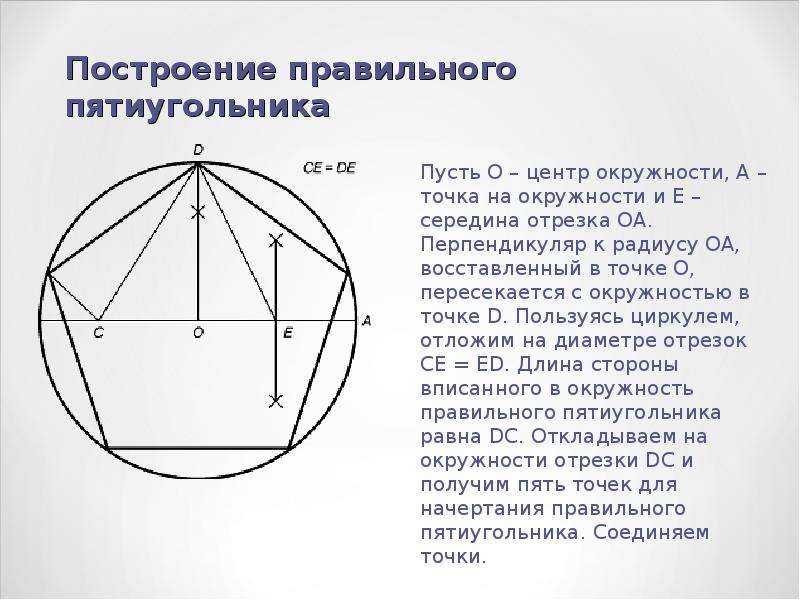
Как начертить пятиугольник с равными сторонами. Правильный пятиугольник
Построение вписанного в окружность правильного пятиугольника. Дан правильный многоугольник, число сторон которого представляет собой произведение натуральных чисел k и m, где m>2. Как построить правильный m-угольник? Гаусс показал также возможность построения правильного 257-угольника с помощью циркуля и линейки.
Построить пятиугольник и поможет именно эта окружность. В первую очередь необходимо построить циркулем окружность. Аналогичным образом необходимо построить еще один круг. Центр его в G. Точка пересечения его с первоначальной окружностью пусть будет H. Это последняя вершина правильного многоугольника.
Правда, процесс это достаточно длительный, как, впрочем, и построение любого правильного многоугльника с нечетным количеством сторон. Она и представляет собой многоугольник, остается только ввести параметры. Число сторон может достигать 1024. Можно использовать и командную строку, в зависимости от версии набрав « _polygon» или «мн. -угол».
-угол».
Деление окружности на равные части и вписывание правильных многоугольников.
Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Можно обозначить их как (0,0), но могут быть и любые другие данные. Пятиугольник может быть описанным вокруг окружности или вписанным в нее, но можно построить его и по заданному размеру стороны. Пятиугольник по заданной стороне сначала строится точно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон.
В командной строке наберите координаты начальной и конечной точек одной из сторон пятиугольника. После этого пятиугольник появится на экране. Таким нехитрым способом можно построить не только пятиугольник. Для того чтобы построить треугольник, необходимо разведите ножки циркуля на расстояние, равное радиусу окружности.
Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Восьмиугольник — это геометрическая фигура с восемью углами. Правильный восьмиугольник – это восьмиугольник, у которого все стороны (и углы) равны. Эта статья расскажет вам, как сделать восьмиугольник.
Восьмиугольник — это геометрическая фигура с восемью углами. Правильный восьмиугольник – это восьмиугольник, у которого все стороны (и углы) равны. Эта статья расскажет вам, как сделать восьмиугольник.
Окружность, дуги и многоугольники.
Определите длину стороны восьмиугольника (углы правильного восьмиугольника известны). На листе бумаги при помощи линейки нарисуйте прямую линию выбранной длины. Это первая сторона восьмиугольника (нарисуйте ее так, чтобы оставить место для рисования других сторон). Используя транспортир, отложите угол в 135o (от начала или конца первой стороны). Нарисуйте третью линию выбранной длины под углом в 135o ко второй линии. Продолжайте до тех пор, пока у вас не получится правильный восьмиугольник.
Таким образом, чем больше окружность, тем больше фигура (и наоборот). Нарисуйте вторую большую окружность, установив иглу циркуля в центре первой окружности. Установите иглу циркуля в прямо противоположной точке пересечения внутренней (малой) окружности и ее диаметра. У вас получится «глаз» в середине окружности. Нарисуйте две дуги, пересекающие внутреннюю окружность.
У вас получится «глаз» в середине окружности. Нарисуйте две дуги, пересекающие внутреннюю окружность.
Построение правильных многоугольников по заданной стороне
Сотрите окружности, линии и дуги, оставив только восьмиугольник. Таким образом, вы придадите ему восьмиугольную форму. Используйте линейку, чтобы убедиться, что все стороны получились равными (так как вы делаете правильный восьмиугольник). Не загибайте углы так, чтобы они соприкасались друг с другом; в этом случае вы получите не восьмиугольник, а небольшой квадрат. Зачастую, когда говорят «восьмиугольник», имеют в виду правильный восьмиугольник.
Смотреть что такое «Правильный пятиугольник» в других словарях:
Таким образом, создав фигуру с восемью сторонами разной длины, вы получите неправильный восьмиугольник. Существуют многоугольники с пересекающимися сторонами. Например, пятиконечная звезда является многоугольником с пересекающимися сторонами. Правильные многоугольники уже в глубокой древности считались символом красоты и совершенства.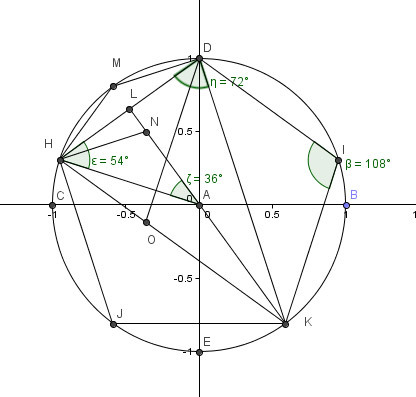 Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю.
Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю.
Лишь в 1796 г. К. Ф. Гаусc доказал принципиальную невозможность этого построения с помощью только циркуля и линейки. В настоящем параграфе мы предлагаем вам самим поискать способы построения правильных многоугольников, вписанных в данную окружность или имеющих заданную сторону. Не менее важное практическое значение имеют методы приближенного построения в тех случаях, когда точное построение циркулем и линейкой неосуществимо.
Правильный пятиугольник — это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Теперь на окружности радиуса AО от любой точки последовательно отложим 11 дуг, каждая из которых равна дуге АВ. Получим вершины правильного двенадцатиугольника. Построение правильного пятиугольника по данной его стороне. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника.
Если под руками нет циркуля, то можно нарисовать простую звезду с пятью лучами затем просто соединить эти лучи. как видим на картинке ниже получается абсолютно правильный пятиугольник.
как видим на картинке ниже получается абсолютно правильный пятиугольник.
Математика сложная наука и у нее много своих секретиков, некоторые из них весьма забавны. Если вы увлекаетесь такими вещами советую найти книгу Забавная математика.
Окружность можно нарисовать не только при помощи циркуля. Можно, например, использовать карандаш и нитку. Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.
Внутри окружности рисуем крестьян от центра: вертикальная линия и горизонтальная линия. Точка пересечения вертикальной линии и окружности будет вершиной пятиугольника (точка 1). Теперь правую половину горизонтальной линии делим пополам (точка 2). Измеряем расстояние от этой точки до вершины пятиугольника и этот отрезок откладывает влево от точки 2 (точка 3). При помощи нитки и карандаша проводим от точки 1 радиусом до точки 3 дугу, пересекающую первую окружность слева и справа — точки пересечения будут вершинами пятиугольника. Обозначим их точка 4 и 5.
При помощи нитки и карандаша проводим от точки 1 радиусом до точки 3 дугу, пересекающую первую окружность слева и справа — точки пересечения будут вершинами пятиугольника. Обозначим их точка 4 и 5.
Теперь от точки 4 делаем дугу, пересекающую окружность в нижней части, радиусом равной длине от точки 1 до 4 — это будет точкой 6. Точно так же и от точки 5 — обозначим точкой 7.
Остатся соединить наш пятиугольник с вершинами 1, 5, 7, 6, 4.
Я знаю как построить простой пятиугольник с помощью циркуля: Строим окружность, отмечаем пять точек, соединяем их. Можно построить пятиугольник с равными сторонами, для этого нам еще понадобится транспортир. Просто те же самые 5 точек ставим по транспортиру. Для этого отмечаем углы по 72 градуса. После чего также соединяем отрезками и получаем нужную нам фигуру.
Зеленую окружность можно чертить произвольным радиусом. В эту окружность будем вписывать правильный пятиугольник. Без циркуля начертить точно окружность нельзя, но это не обязательно. Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.
Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.
Адептам черного искусства: что бы просто, красиво и быстро нарисовать пятиугольник, следует начертить правильную, гармоничную основу для пентаграммы (пятиконечная звезда) и соединить окончания лучей этой звезды посредством прямых, ровных линий. Если все было сделано верно — соединительная черта вокруг основы и будет искомым пятиугольником.
(на рисунке — завершенная, но незаполненная пентаграмма)
Для тех, кто неуверен в правильности начертания пентаграммы: возьмите за основу витрувианского человека Да Винчи (см.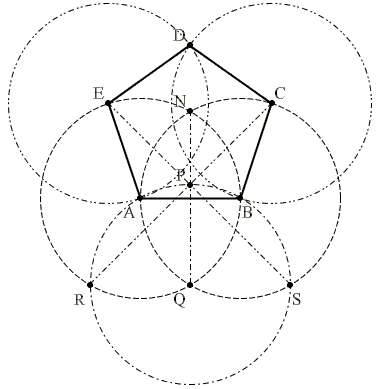
Если нужен пятиугольник — тыкаете произвольным образом 5 точке и их внешний контур будет пятиугольником.
Если нужен правильный пятиугольник, то без математического циркуля это построение совершить невозможно, поскольку без него нельзя провести два одинаковых, но не параллельных отрезка. Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю.
Сначала надо надо начертить круг, потом направляющие, потом второй пунктирный круг, находим верхнюю точку, потом отмеряем два угла верхние, от них чертим нижние. Заметьте, радиус циркуля один и тот же при всем построении.
Вс зависит от того, какой пятиугольник вам необходим. Если любой, то ставите пять точек и соединяете их между собой(естествено точки ставим не по прямой линии). А если нужен пятиугольник правильно формы, возьмите любые пять по длине(полосок бумаги, спичек, карандашей и т.п), выложите пятиугольник и обчертите его.
Пятиугольник можно начертить, к примеру, из звезды. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите.
Второй способ. Вырежьте полосочку из бумаги, длиной, равной желаемой стороне пятиугольника, а шириной узкой, допустим 0.5 — 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.
Затем положите лист бумаги (лучше его закрепить на столе при помощи четырх кнопок или иголочек). Затем наложите эти 5 полосочек на листок так, чтобы они образовали пятиугольник. Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Если нет циркуля и нужно построить пятиугольник, то я могу посоветовать следующее. Я и сама так строила. Можно начертить правильную пятиконечную звезду. И после этого, чтобы получить пятиугольник, просто нужно соединить все вершины звезды.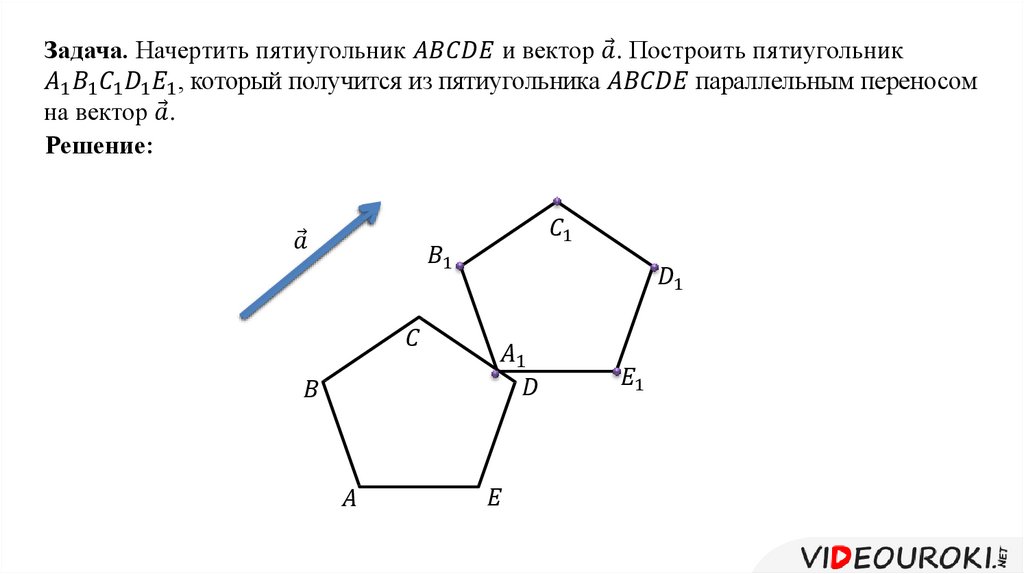 Вот так и получится пятиугольник. Вот что мы получим
Вот так и получится пятиугольник. Вот что мы получим
Ровными чрными линии мы соединили вершины звезды и получили пятиугольник.
Задача построения верного пятиугольника сводится к задаче деления окружности на пять равных частей. От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.
Вам понадобится
- – линейка
- – циркуль
Инструкция
1. Видимо, что если возвести верный десятиугольник, а после этого объединить его вершины через одну, то получим пятиугольник. Для построения десятиугольника начертите окружность заданного радиуса. Обозначьте ее центр буквой O. Проведите два перпендикулярных друг друга радиуса, на рисунке они обозначены как OA1 и OB. Радиус OB поделите напополам с подмогой линейки либо способом деления отрезка напополам с подмогой циркуля.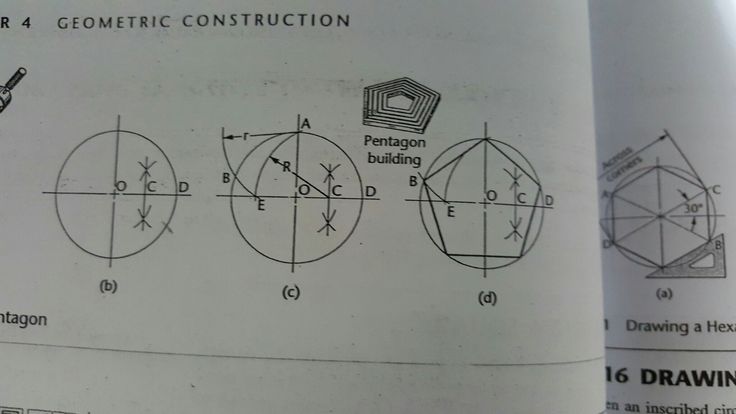 Постройте маленькую окружность с центром C в середине отрезка OB радиусом, равным половине OB.Объедините точку C с точкой A1 на начальной окружности по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.
Постройте маленькую окружность с центром C в середине отрезка OB радиусом, равным половине OB.Объедините точку C с точкой A1 на начальной окружности по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.
2. Еще один метод обнаружил немецкий художник Альбрехт Дюрер. Дабы возвести пятиугольник по его методу, начните вновь с построения окружности. Вновь подметьте ее центр O и проведите два перпендикулярных радиуса OA и OB. Радиус OA поделите напополам и середину подметьте буквой C. Установите иглу циркуля в точку C и раскройте его до точки B. Проведите окружность радиуса BC до пересечения с диаметром начальной окружности, на котором лежит радиус OA. Точку пересечения обозначьте D. Отрезок BD – сторона положительного пятиугольника. Отложите данный отрезок пять раз на начальной окружности и объедините точки пересечения.
3. Если же требуется возвести пятиугольник по его заданной стороне, то вам надобен 3-й метод. Начертите по линейке сторону пятиугольника, обозначьте данный отрезок буквами A и B. Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.
Тема деления окружности на равные части с целью построения верных вписанных многоугольников издавна занимала умы древних ученых. Эти тезисы построения с использованием циркуля и линейки были высказаны еще в эвклидовых «Началах».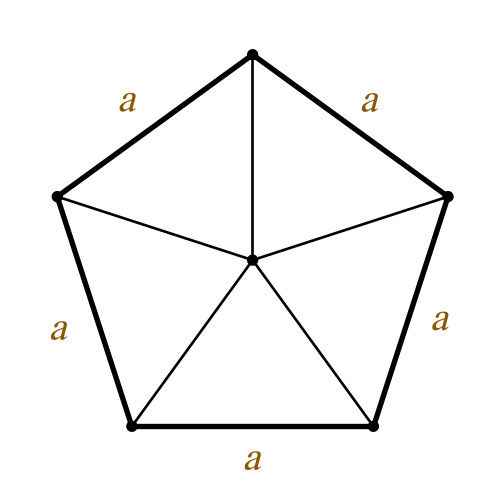 Впрочем лишь через два тысячелетия эта задача была всецело решена не только графически, но и математически.
Впрочем лишь через два тысячелетия эта задача была всецело решена не только графически, но и математически.
Инструкция
1. Приближенное построение положительного пятиугольника методом А. Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне пятиугольника ).
2. Построение верного пятиугольника на основе положительного десятиугольника, вписанного в окружность (объединив вершины десятиугольника через одну).
3. Графическое построение через вычисленный внутренний угол пятиугольника с поддержкой транспортира и линейки (сумма углов выпуклого n-угольника равна Sn=180°(n – 2), т.к. у положительного многоугольника все углы равны). При n=5, S5=5400, тогда величина угла 1080.А так же с поддержкой окружности и 2-х лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне пятиугольника .
4. Еще один легкой графический метод: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.Точки G,E,B,F,H – вершины положительного пятиугольника .
5. Построение с поддержкой приема Биона (дозволяющего возвести верный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению).Скажем: для n=5. Возведем положительный треугольник ABC, где AB – диаметр заданной окружности. Обнаружим на AB точку D, по дальнейшему соотношению: AD: AB = 2: n. При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона верного вписанного пятиугольника .При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся поменьше 10,3%.
6. Построение по заданной стороне по способу Л.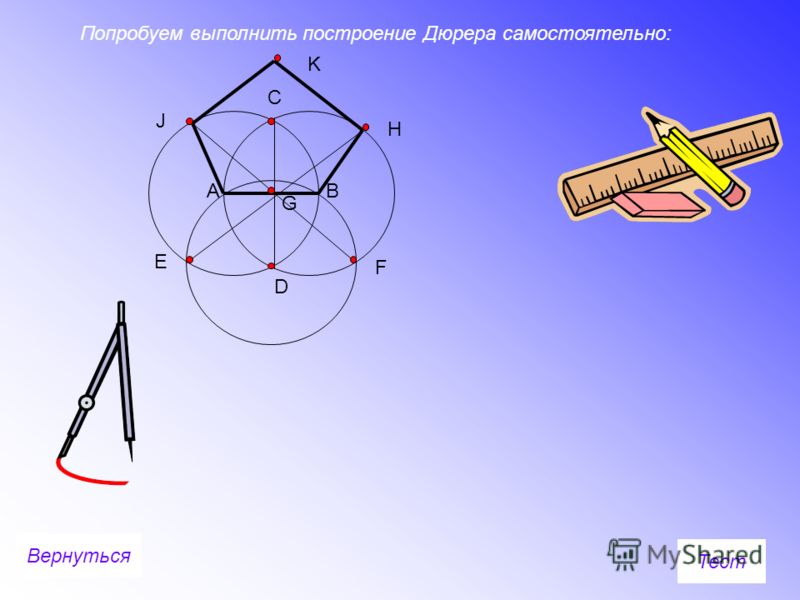 Да Винчи (применяя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2: ha =3/(n-1), которое дозволено выразить так: tg180°/n =3/(n-1)).
Да Винчи (применяя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2: ha =3/(n-1), которое дозволено выразить так: tg180°/n =3/(n-1)).
7. Всеобщий метод построения положительных многоугольников по заданной стороне по способу Ф. Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.
Существуют два основных метода построения верного многоугольника с пятью сторонами. Оба они полагают применение циркуля, линейки и карандаша. 1-й метод представляет собой вписывание пятиугольника в окружность, а 2-й метод базируется на заданной длине стороны вашей грядущей геометрической фигуры.
Вам понадобится
- Циркуль, линейка, карандаш
Инструкция
1. 1-й метод построения пятиугольника считается больше «типичным». Для начала постройте окружность и как-либо обозначьте ее центр (обычно для этого применяется буква О). После этого проведите диаметр этой окружности (назовем его АВ) и поделите один из 2-х полученных радиусов (скажем, ОА) ровно напополам. Середину этого радиуса обозначим буквой С.
Для начала постройте окружность и как-либо обозначьте ее центр (обычно для этого применяется буква О). После этого проведите диаметр этой окружности (назовем его АВ) и поделите один из 2-х полученных радиусов (скажем, ОА) ровно напополам. Середину этого радиуса обозначим буквой С.
2. Из точки О (центра начальной окружности) проведите еще один радиус (ОD), тот, что будет сурово перпендикулярен проведенному ранее диаметру (АВ). После этого возьмите циркуль, поставьте его в точку С и отмерьте расстояние до пересечения нового радиуса с окружностью (СD). Это же расстояние отложите на диаметре АВ. Вы получите новую точку (назовем ее Е). Отмерьте циркулем расстояние от точки D до точки Е – оно будет равно длине стороны вашего грядущего пятиугольника .
3. Поставьте циркуль в точку D и отложите на окружности расстояние, равное отрезку DЕ. Повторите эту процедуру еще 3 раза, а после этого объедините точку D и 4 новые точки на начальной окружности. Получившаяся в итоге построения фигура будет верным пятиугольником.
4. Дабы возвести пятиугольник иным методом, для начала начертите отрезок. Скажем, это будет отрезок АВ длиной 9 см. Дальше поделите ваш отрезок на 6 равных частей. В нашем случае длина всякой части будет составлять 1,5 см. Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. Назовем ее C.
5. Сейчас возьмите линейку и проведите прямую через точку С и центр отрезка AB. После этого начиная от точки С отложите на этой прямой отрезок, составляющий 4/6 отрезка AB. 2-й конец отрезка обозначим буквой D. Точка D будет являться одной из вершин грядущего пятиугольника . Из этой точки проведите окружность либо дугу с радиусом, равным АВ. Эта окружность (дуга) пересечет ранее построенные вами окружности (дуги) в точках, являющихся двумя недостающими вершинами пятиугольника .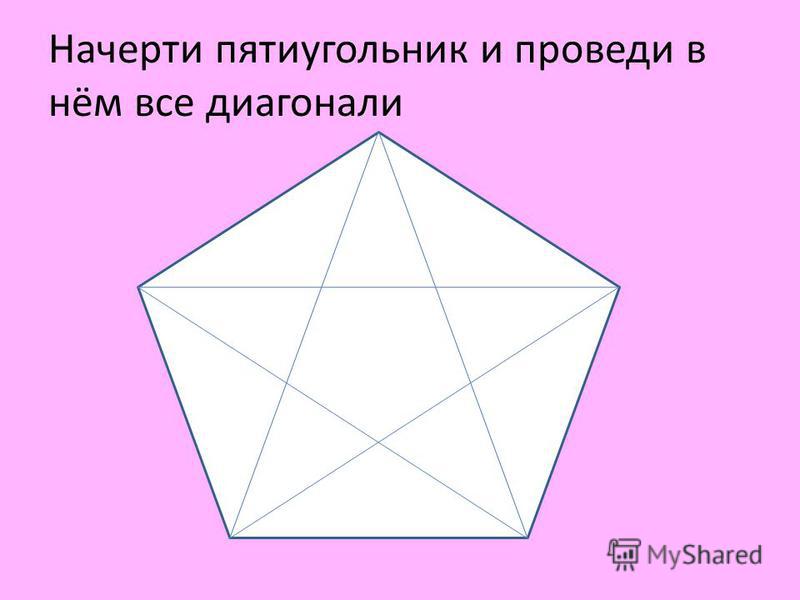 Объедините эти точки с вершинами D, А и В, и построение положительного пятиугольника будет закончено.
Объедините эти точки с вершинами D, А и В, и построение положительного пятиугольника будет закончено.
Видео по теме
Луч — это прямая линия, проведенная из точки и не имеющая конца. Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?
Вам понадобится
- Лист бумаги, карандаш и линейка.
Инструкция
1. Возьмите лист бумаги и подметьте в произвольном месте точку. После этого приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Эта нарисованная линия и именуется лучом. Сейчас подметьте на луче еще одну точку, к примеру, буквой C. Линия от исходной и до точки C будет именоваться отрезком. Если вы примитивно начертите линию и не подметите правда бы одну точку, то эта прямая не будет являться лучом.
2. Нарисовать луч в любом графическом редакторе либо в том же MSOffice не труднее, чем вручную. Для примера возьмите программу Microsoft Office 2010. Зайдите в раздел «Вставка» и выберите элемент «Фигуры». В выпадающем списке выберите фигуру «Линия». Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.
Для примера возьмите программу Microsoft Office 2010. Зайдите в раздел «Вставка» и выберите элемент «Фигуры». В выпадающем списке выберите фигуру «Линия». Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.
3. Дабы сделать точку в начале линии, сделайте следующее: выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.
4. Выберите пункт «Формат фигуры». В меню слева выберите пункт «Тип линии». Дальше обнаружьте заголовок «Параметры линий» и выберите «Тип начала» в виде кружочка. Там же вы можете настроить толщину линий начала и конца.
5. Уберите выделение с линии и увидите, что в начале линии возникла точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, где будет находиться надпись.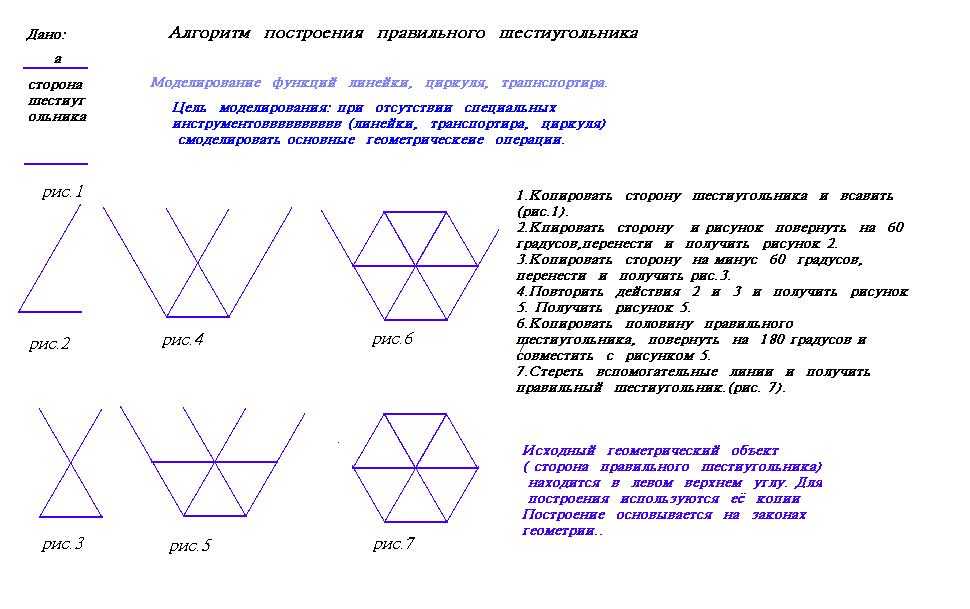 Позже написания надписи кликните на свободное место и она активируется.
Позже написания надписи кликните на свободное место и она активируется.
6. Луч благополучно нарисован и заняло это каждого несколько минут. Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.
Видео по теме
Обратите внимание!
Отношение диагонали верного пятиугольника к его стороне составляет золотое сечение (иррациональное число (1+√5)/2).Весь из пяти внутренних углов пятиугольника равен 108°.
Полезный совет
Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.
Положительный пятиугольник – это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Возвести пятиугольник и поможет именно эта окружность.
Инструкция
1. В первую очередь нужно возвести циркулем окружность. Центр окружности пускай совпадает с точкой O. Проведите оси симметрии перпендикулярные друг другу. В точке пересечения одной из этих осей с окружностью поставьте точку V. Эта точка будет вершиной грядущего пятиугольник а. В точке пересечения иной оси с окружностью расположите точку D.
Центр окружности пускай совпадает с точкой O. Проведите оси симметрии перпендикулярные друг другу. В точке пересечения одной из этих осей с окружностью поставьте точку V. Эта точка будет вершиной грядущего пятиугольник а. В точке пересечения иной оси с окружностью расположите точку D.
2. На отрезке OD обнаружьте середину и подметьте в ней точку А. Позже этого надобно возвести циркулем окружность с центром в этой точке. Помимо того, она должна проходить через точку V, то есть, радиусом CV. Точку пересечения оси симметрии и этой окружности обозначьте за В.
3. Позже этого при помощи циркуля проведите окружность такого же радиуса, поставив иголку в точку V. Пересечение этой окружности с изначальной обозначьте как точку F. Эта точка станет 2-й вершиной грядущего верного пятиугольник а.
4. Сейчас необходимо провести такую же окружность через точку Е, но с центром в F. Пересечение только что проведенной окружности с изначальной обозначьте как точку G. Эта точка так же станет еще одной из вершин пятиугольник а. Аналогичным образом нужно возвести еще один круг. Центр его в G. Точка пересечения его с изначальной окружностью пускай будет H. Это последняя вершина верного многоугольника.
Эта точка так же станет еще одной из вершин пятиугольник а. Аналогичным образом нужно возвести еще один круг. Центр его в G. Точка пересечения его с изначальной окружностью пускай будет H. Это последняя вершина верного многоугольника.
5. У вас должно получиться пять вершин. Остается их легко объединить по линейке. В итоге всех этих операций вы получите вписанный в окружность положительный пятиугольник .
Построение положительных пятиугольников дозволено с поддержкой циркуля и линейки. Правда, процесс это довольно долгий, как, однако, и построение всякого положительного многоугльника с нечетным числом сторон. Современные компьютерные программы разрешают сделать это за несколько секунд.
Вам понадобится
- – компьютер с программой AutoCAD.
Инструкция
1. Обнаружьте в программе AutoCAD верхнее меню, а в нем — вкладку «Основная». Нажмите на нее левой клавишей мыши. Появится панель «Рисование».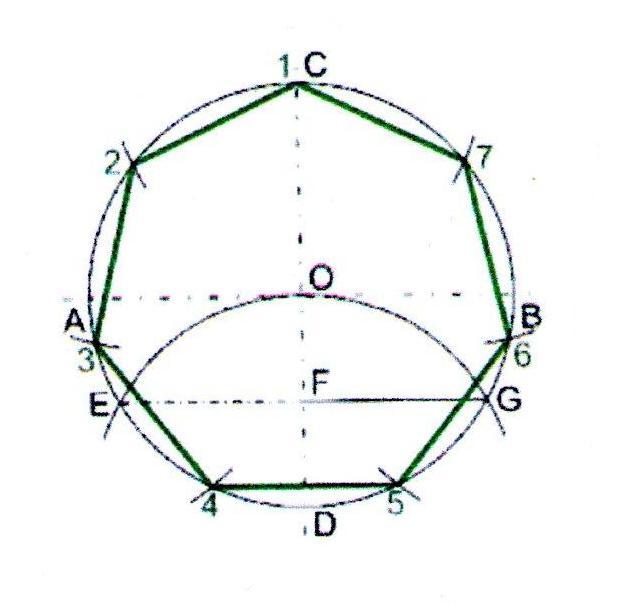 Появятся различные типы линий. Выберите замкнутую полилинию. Она и представляет собой многоугольник, остается только ввести параметры. AutoCAD. Дозволяет рисовать самые различные правильне многоугольники. Число сторон может добиваться 1024. Дозволено применять и командную строку, в зависимости от версии набрав « _polygon» либо «мн.-угол».
Появятся различные типы линий. Выберите замкнутую полилинию. Она и представляет собой многоугольник, остается только ввести параметры. AutoCAD. Дозволяет рисовать самые различные правильне многоугольники. Число сторон может добиваться 1024. Дозволено применять и командную строку, в зависимости от версии набрав « _polygon» либо «мн.-угол».
2. Вне зависимости от того, пользуетесь ли вы командной строкой либо контекстными меню, на экране у вас появится окошко, в которое предлагается ввести число сторон. Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Вбейте в появившееся окошко координаты. Дозволено обозначить их как (0,0), но могут быть и всякие другие данные.
3. Выберите необходимый метод построения. . AutoCAD предлагает три варианта. Пятиугольник может быть описанным вокруг окружности либо вписанным в нее, но дозволено возвести его и по заданному размеру стороны. Выберите надобный вариант и нажмите на ввод. В случае необходимости задайте радиус окружности и тоже нажмите enter.
4. Пятиугольник по заданной стороне вначале строится верно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон. Правой клавишей мыши вызовите контекстное меню. Нажмите команду «edge” либо «сторона”. В командной строке наберите координаты исходной и финальной точек одной из сторон пятиугольника. Позже этого пятиугольник появится на экране.
5. Все операции дозволено исполнять с поддержкой командной строки. Скажем, для построения пятиугольника по стороне в русскоязычной версии программы введите букву «с». В англоязычной версии это будет «_e”. Дабы возвести вписанный либо описанный пятиугольник, введите позже определения числа сторон буквы «о» либо «в» (либо же английские “_с” либо “_i”)
Видео по теме
Видео по теме
Полезный совет
Таким нехитрым методом дозволено возвести не только пятиугольник. Для того дабы возвести треугольник, нужно разведите ножки циркуля на расстояние, равное радиусу окружности.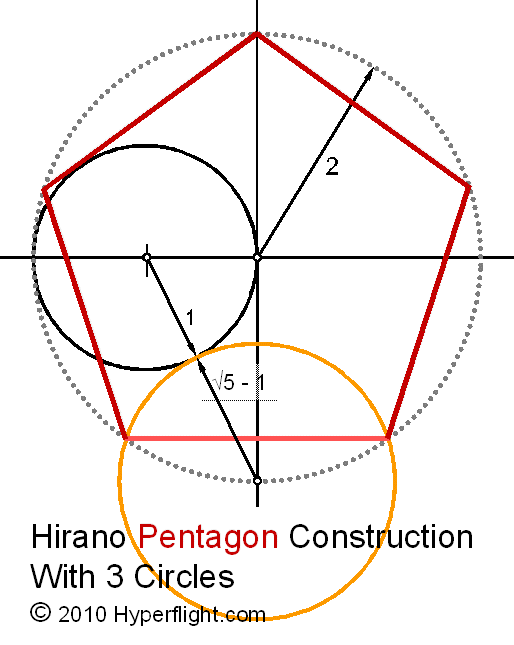 После этого в всякую точку установите иглу. Проведите тонкую вспомогательную окружность. Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины положительного треугольника.
После этого в всякую точку установите иглу. Проведите тонкую вспомогательную окружность. Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины положительного треугольника.
Правильный пятиугольник — это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Построить пятиугольник и поможет именно эта окружность.
Инструкция
В первую очередь необходимо построить циркулем окружность. Центр окружности пусть совпадает с точкой O. Проведите оси симметрии перпендикулярные друг другу. В точке пересечения одной из этих осей с окружностью поставьте точку V. Эта точка будет вершиной будущего пятиугольник а. В точке пересечения другой оси с окружностью расположите точку D.
На отрезке OD найдите середину и отметьте в ней точку А. После этого нужно построить циркулем окружность с центром в этой точке. Кроме того, она должна проходить через точку V, то есть, радиусом CV.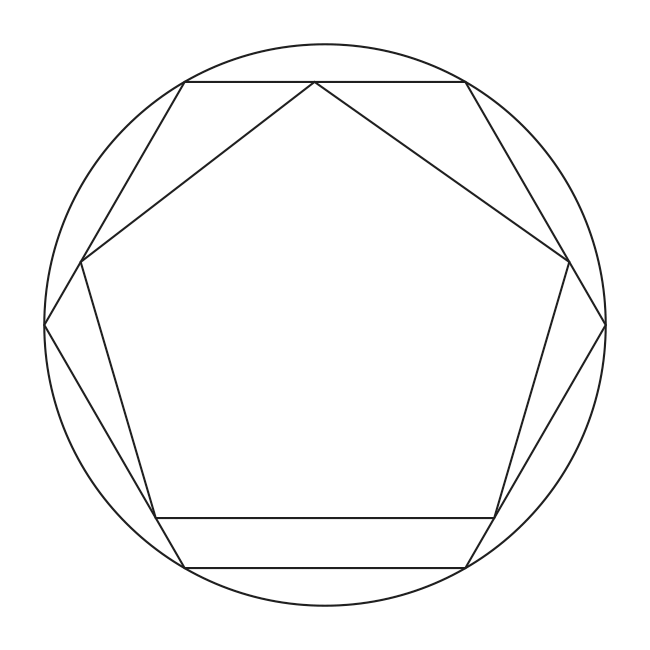 Точку пересечения оси симметрии и этой окружности обозначьте за В.
Точку пересечения оси симметрии и этой окружности обозначьте за В.
После этого при помощи циркуля проведите окружность такого же радиуса, поставив иголку в точку V. Пересечение этой окружности с первоначальной обозначьте как точку F. Эта точка станет второй вершиной будущего правильного пятиугольник а.
Теперь нужно провести такую же окружность через точку Е, но с центром в F. Пересечение только что проведенной окружности с первоначальной обозначьте как точку G. Эта точка так же станет еще одной из вершин пятиугольник а. Аналогичным образом необходимо построить еще один круг. Центр его в G. Точка пересечения его с первоначальной окружностью пусть будет H. Это последняя вершина правильного многоугольника.
У вас должно получиться пять вершин. Остается их просто соединить по линейке. В результате всех этих операций вы получите вписанный в окружность правильный пятиугольник .
Построение правильных пятиугольников можно с помощью циркуля и линейки. Правда, процесс это достаточно длительный, как, впрочем, и построение любого правильного многоугльника с нечетным количеством сторон. Современные компьютерные программы позволяют сделать это за несколько секунд.
Правда, процесс это достаточно длительный, как, впрочем, и построение любого правильного многоугльника с нечетным количеством сторон. Современные компьютерные программы позволяют сделать это за несколько секунд.
Вам понадобится
- — компьютер с программой AutoCAD.
Инструкция
Найдите в программе AutoCAD верхнее меню, а в нем — вкладку «Главная». Нажмите на нее левой клавишей мыши. Появится панель «Рисование». Появятся разные типы линий. Выберите замкнутую полилинию. Она и представляет собой многоугольник, остается только ввести параметры. AutoCAD. Позволяет рисовать самые разные правильне многоугольники. Число сторон может достигать 1024. Можно использовать и командную строку, в зависимости от версии набрав « _polygon» или «мн.-угол».
Вне зависимости от того, пользуетесь ли вы командной строкой или контекстными меню, на экране у вас появится окошко, в которое предлагается ввести количество сторон. Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Вбейте в появившееся окошко координаты. Можно обозначить их как (0,0), но могут быть и любые другие данные.
Вбейте в появившееся окошко координаты. Можно обозначить их как (0,0), но могут быть и любые другие данные.
Выберите нужный способ построения. . AutoCAD предлагает три варианта. Пятиугольник может быть описанным вокруг окружности или вписанным в нее, но можно построить его и по заданному размеру стороны. Выберите нужный вариант и нажмите на ввод. В случае необходимости задайте радиус окружности и тоже нажмите enter.
Пятиугольник по заданной стороне сначала строится точно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон. Правой клавишей мыши вызовите контекстное меню. Нажмите команду «edge” или «сторона”. В командной строке наберите координаты начальной и конечной точек одной из сторон пятиугольника. После этого пятиугольник появится на экране.
Все операции можно выполнять с помощью командной строки. Например, для построения пятиугольника по стороне в русскоязычной версии программы введите букву «с». В англоязычной версии это будет «_e”. Чтобы построить вписанный или описанный пятиугольник, введите после определения количества сторон буквы «о» или «в» (либо же английские «_с» или «_i»)
Таким нехитрым способом можно построить не только пятиугольник.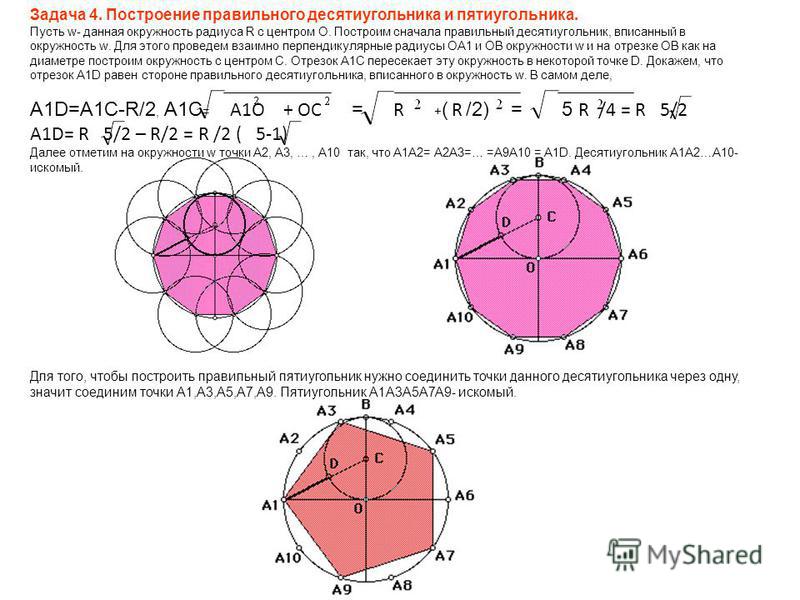 Для того чтобы построить треугольник, необходимо разведите ножки циркуля на расстояние, равное радиусу окружности. Затем в любую точку установите иглу. Проведите тонкую вспомогательную окружность. Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника.
Для того чтобы построить треугольник, необходимо разведите ножки циркуля на расстояние, равное радиусу окружности. Затем в любую точку установите иглу. Проведите тонкую вспомогательную окружность. Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника.
Построение пятиугольника подробно. Построение правильного пятиугольника Правильный пятиугольник рисунок
Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира.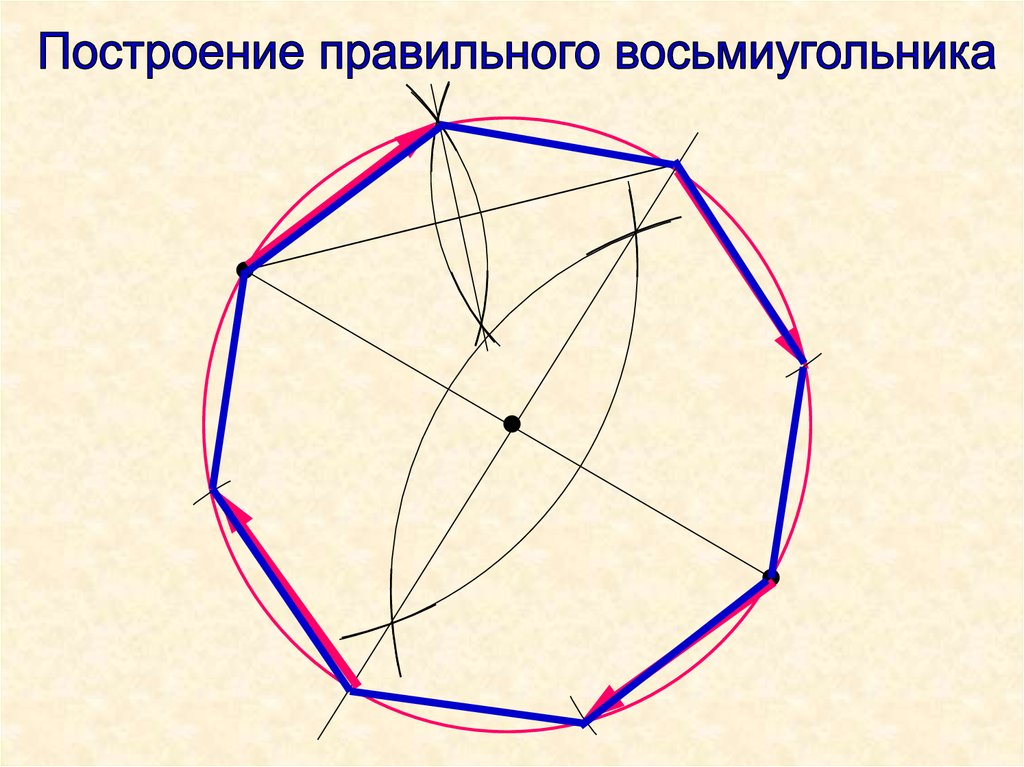 Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
Вы находитесь в категории раскраски пятиугольник. Раскраска которую вы рассматриваете описана нашими посетителями следующим образом «» Тут вы найдете множество раскрасок онлайн. Вы можете скачать раскраски пятиугольник и так же распечатать их бесплатно. Как известно творческие занятия играют огромную роль в развитии ребенка. Они активизируют умственную деятельность, формируют эстетический вкус и прививают любовь к искусству. Процесс раскрашивания картинок на тему пятиугольник развивает мелкую моторику, усидчивость и аккуратность, помогает узнать больше об окружающем мире, знакомит со всем разнообразием цветов и оттенков. Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать.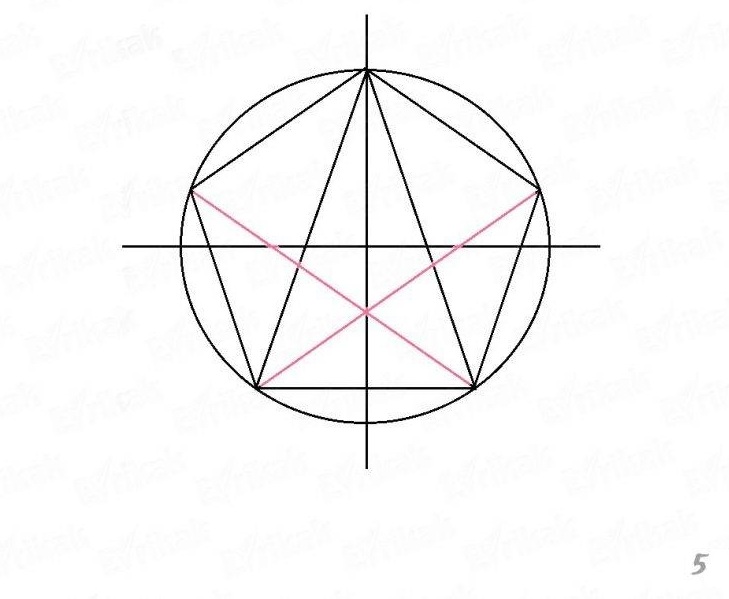 Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания.
8 июня 2011
Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания.
8 июня 2011
Первый способ — по данной стороне S с помощью транспортира.
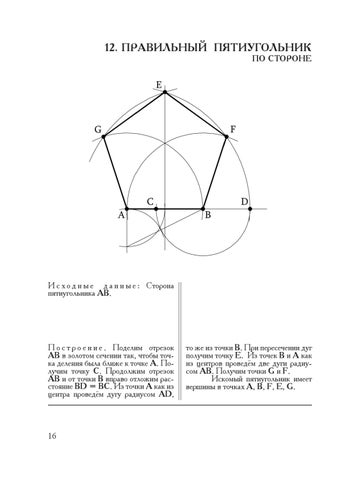
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К.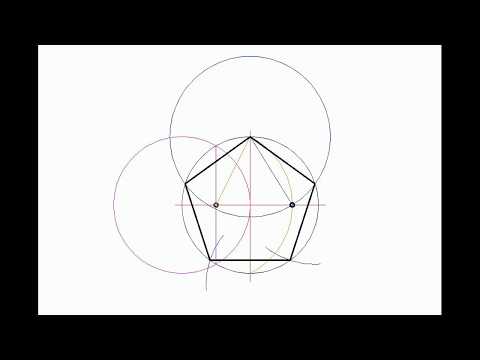 Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.
На рисунке построен шестиугольник по данной стороне.
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц.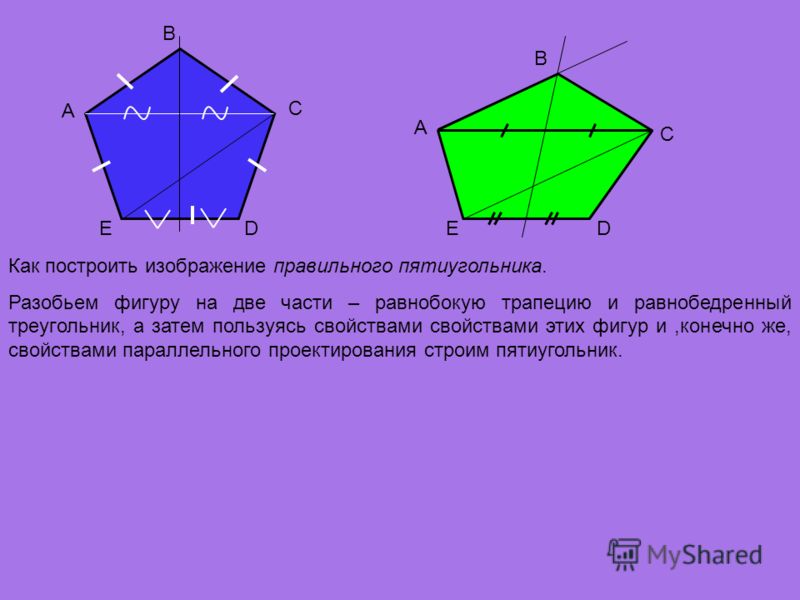 Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…
Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…
При этом надо…
Правильный шестиугольник как построить без циркуля
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
- Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана.
 R и r – радиусы описанной и вписанной окружности.
R и r – радиусы описанной и вписанной окружности. - Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Вам понадобится
- Циркуль, линейка, карандаш, лист бумаги.
Инструкция
1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.
3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.
Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.
Вам понадобится
- Карандаш, лист бумаги, линейка
Инструкция
1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.
2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.
2.
Видео по теме
Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.
Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.
Вам понадобится
- Карандаш, линейка, лист бумаги.
Инструкция
1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)
2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)
Видео по теме
Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой.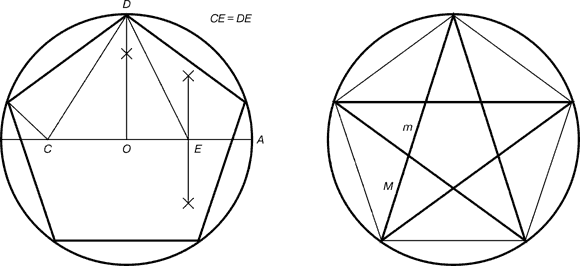 Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.
Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.
Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.
Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен ?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.
Вам понадобится
- транспортир, угольник, циркуль, линейка
Инструкция
1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир.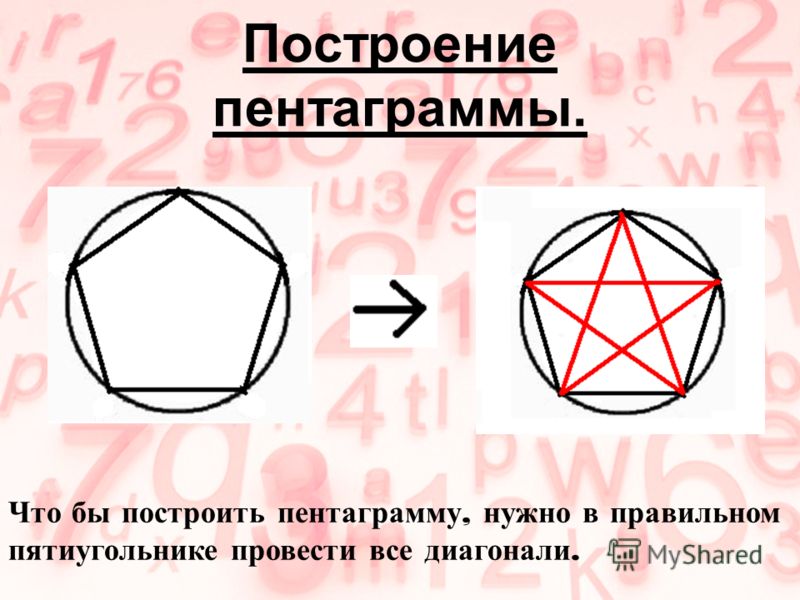 Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.
Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.
2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.
3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.
4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.
Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.
5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен ?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.
Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.
6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной ?*R/6, мы также получим угол в 30 градусов.
Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.
Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.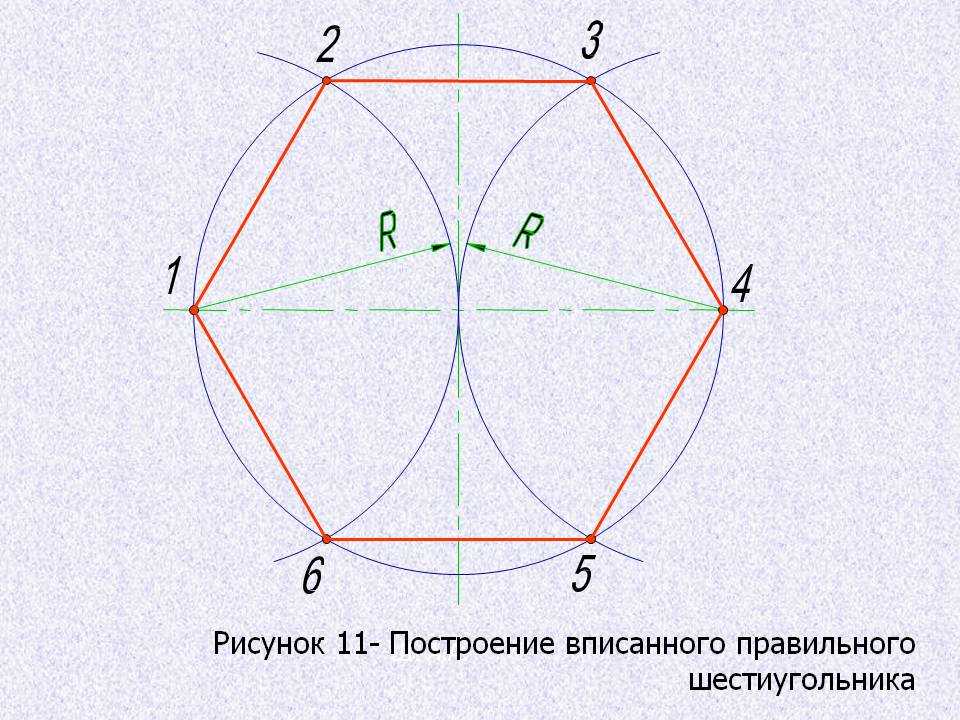
Вам понадобится
Инструкция
1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.
2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.
4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений.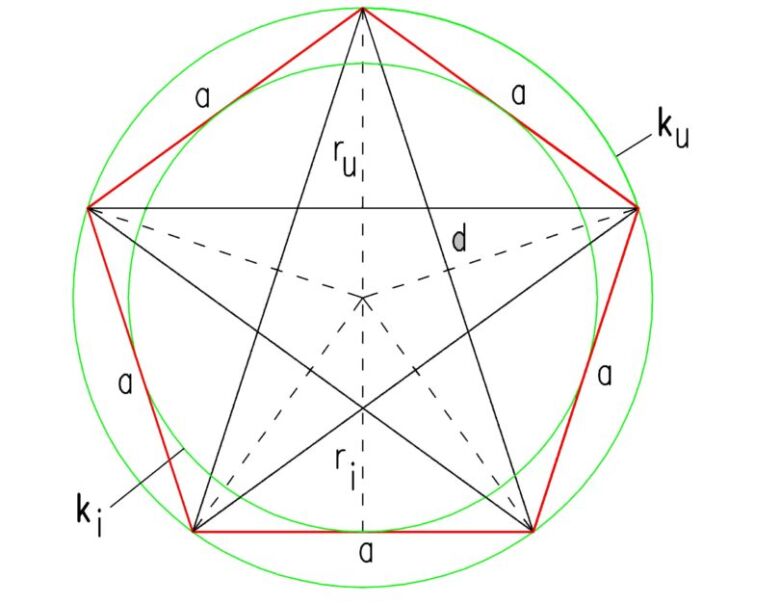 Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.
Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.
5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.
7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).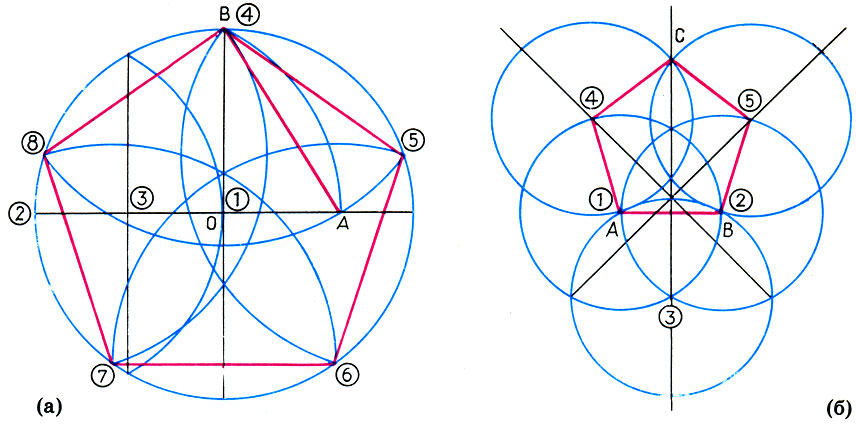
Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.
При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.
Инструкция
1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.
2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.
А дозволено обозначать углы греческими буквами, скажем, α, β, γ.
3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.
4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.
5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.
Он должен быть равен отрезку ВС. Получите точку L.
6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.
Видео по теме
Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.
Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.
В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Первый способ построения пятиугольника
Второй способ. Проведем окружность радиусом r.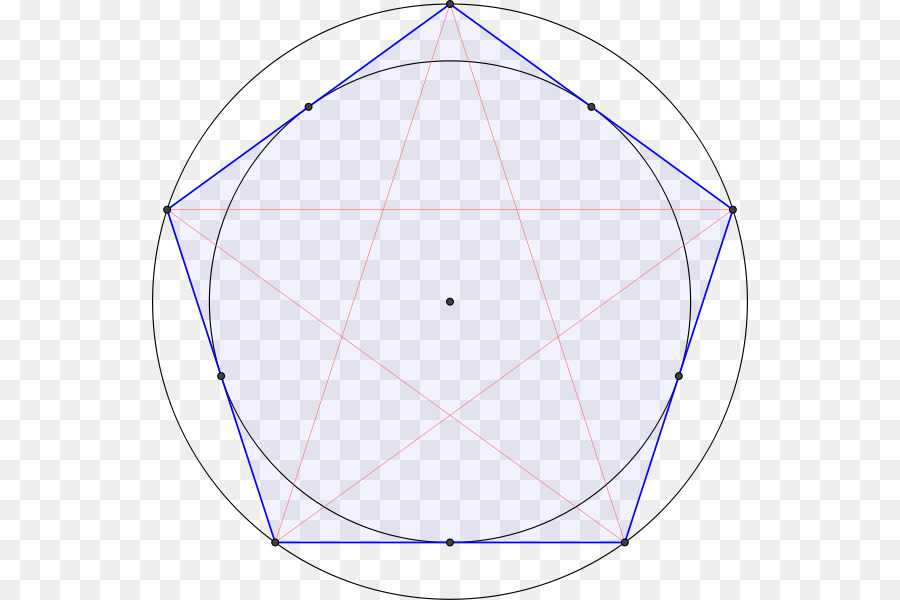 Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Второй способ построения пятиугольника
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N1, Р1, Q1, К1 и соединяем их прямыми.
Третий способ построения пятиугольника
На рисунке построен шестиугольник по данной стороне.
Построение шестиугольника
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…
Прямой угол, т. е. равный 90°, образуется двумя взаимно перпендикулярными линиями. Перпендикуляр строится следующим образом. Опустить перпендикуляр. Из данной точки С (лежащей вне прямой), как из центра, произвольным радиусом описываем дугу так, чтобы она пересекла данную прямую в двух точках D и Е из этих точек, как из центров, одинаковыми радиусами описываем дуги, чтобы они…
Построение угла, равного данному Угол, равный данному, строится следующим образом.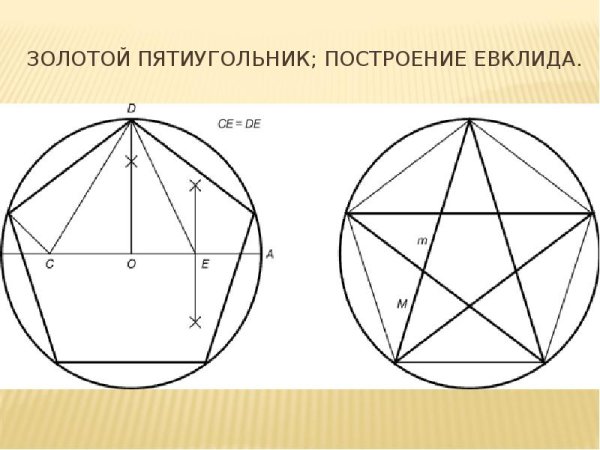 Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE. Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…
Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE. Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…
Деление прямых линий и углов может быть произведено двояким образом: на глаз и с помощью геометрического построения. При делении прямой на две равные части поступают следующим образом. Половину данной прямой берут циркулем на глаз и откладывают эту половину от обоих концов прямой. Если концы половинок сходятся, то, значит, данная прямая разделена правильно, если нет, то…
Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности. Первый вопрос сводится к нахождению внутреннего…
Первый вопрос сводится к нахождению внутреннего…
Страница не найдена — Фонд Наффилда
Страница не найдена — Фонд НаффилдаСтраница, которую вы ищете, не может быть найдена. Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.
Поиск проектов, новостей, воздействия, событий
Поиск
Образование 640 Когнитивные и некогнитивные навыки 32curriculum и субъект.Образование и навыки после 16 лет 93Начальное образование 128Q-Step 26Эффективность школы 45Среднее образование 153Специальные образовательные потребности и инвалидность 53Проблемы системного образования 97Правосудие 230Доступ к правосудию 36Административное правосудие 23Гражданское правосудие 21Судебный опыт и доказательства 18Уголовное право 22Домашнее насилие 5Равенство и права человека 2Семейное правосудие и 130Частное право закон о социальном обеспечении 9Молодежное правосудие 21Благополучие 759Искусственный интеллект 3Помощь при смерти 1Дополненная реальность 0Преимущества 52Обязанности по уходу 27Сообщества и социальная сплоченность 63Страна рождения 24COVID-19327Прогнозирование преступности 2Данные для общественного блага 27Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 47Инвалидность 13Экономика, государственные расходы и услуги 177Этническая принадлежность 47Семья и семейная динамика 115Гендер 42Глобальное неравенство в отношении здоровья и нуждающиеся дети 73Психическое здоровье 90Заболевания опорно-двигательного аппарата 11Пенсии 16Физическое здоровье 43Бедность и уровень жизни 107Производительность и инновации 6Общественное здравоохранение 150Социальные сети 2Социоэкономика старения 24Социоэкономика раннего взросления 40Спортивная наука 1Злоупотребление психоактивными веществами 11Налоги 47Доверие к демократии 65Оценка данных 5
ProjectsNewsEventsImpactOpinionPublicationsSeriesReportsEducation 640Cognitive and non-cognitive skills 32Curriculum and subject choice 30Early years 161Education workforce 74Educational assessment 28Higher education 91Language and literacy 78Lifelong learning 14Nuffield Research Placements 23Numeracy 83Parenting 73Pedagogy 19Post-16 education and skills 93Primary education 128Q-Step 26School effectiveness 45Secondary education 153Special educational needs и инвалидность 53Системные проблемы образования 97justice 230 к правосудию 36 Административное правосудие 23Civil юстиции 21 Корт.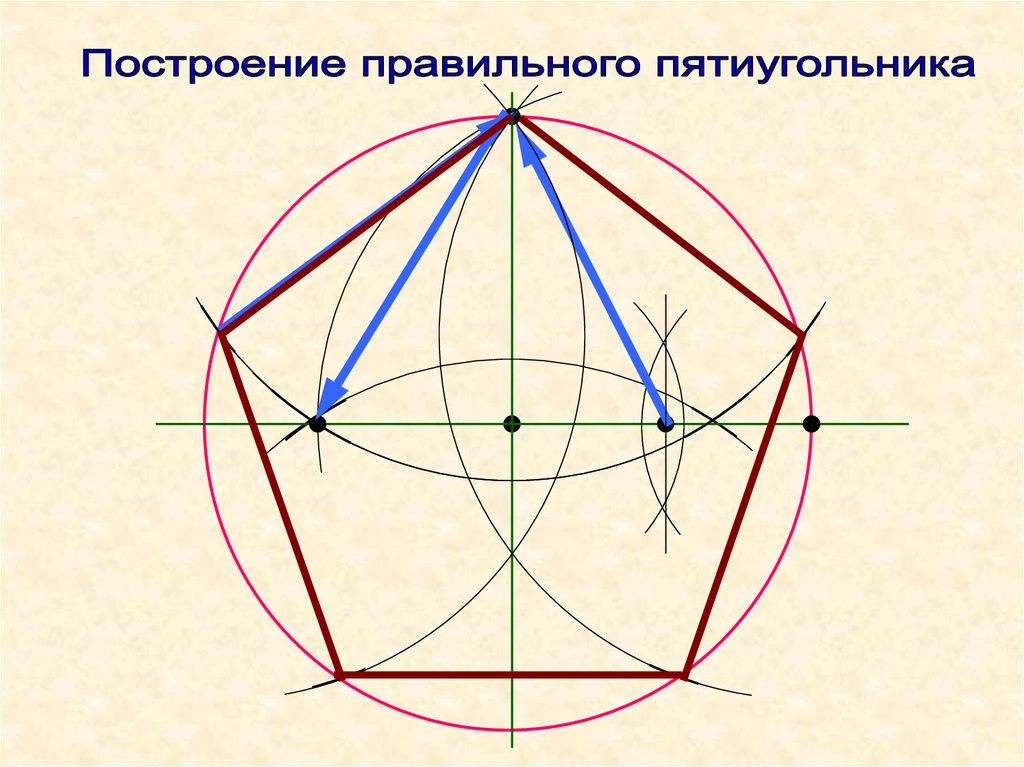 Опыт и доказательства 18 КРИМИНАЛЬНОЕ ПРАВДОВОСТИ 22DOMESTIC ЗНАЧЕНИЕ 5 ЭКСПОЛИНА И ПРАВАМИ 16 СВЯЗАНСКОГО ПРАВИТЕЛЬСТВА 130 ПРИВАТ И ПРОМЕМОЙ ЗАКОН 2SOCIAL WELFARE LAWERINGALESTERITIONS 24SMARIFAIFARIAL IDSIDIDARIDAINGARID ВСЕГДА 27-й. СООТВЕТСТВЕННАЯ ИЛИДЕР. 19 327Прогнозирование преступности 2Данные для общественного блага 27Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 47Инвалидность 13Экономика, государственные расходы и услуги 177Этническая принадлежность 47Семья и семейная динамика 115Гендер 42Глобальное неравенство в отношении здоровья дети и нуждающиеся дети 73Психическое здоровье 90Заболевания опорно-двигательного аппарата 11Пенсии 16Физическое здоровье 43Бедность и уровень жизни 107Производительность и инновации 6Общественное здравоохранение 150Социальные сети 2Социоэкономика старения 24Социоэкономика раннего взросления 40Спортивная наука 1Злоупотребление психоактивными веществами 11Налоги 47Доверие к демократии 65Оценка данных 5
Опыт и доказательства 18 КРИМИНАЛЬНОЕ ПРАВДОВОСТИ 22DOMESTIC ЗНАЧЕНИЕ 5 ЭКСПОЛИНА И ПРАВАМИ 16 СВЯЗАНСКОГО ПРАВИТЕЛЬСТВА 130 ПРИВАТ И ПРОМЕМОЙ ЗАКОН 2SOCIAL WELFARE LAWERINGALESTERITIONS 24SMARIFAIFARIAL IDSIDIDARIDAINGARID ВСЕГДА 27-й. СООТВЕТСТВЕННАЯ ИЛИДЕР. 19 327Прогнозирование преступности 2Данные для общественного блага 27Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 47Инвалидность 13Экономика, государственные расходы и услуги 177Этническая принадлежность 47Семья и семейная динамика 115Гендер 42Глобальное неравенство в отношении здоровья дети и нуждающиеся дети 73Психическое здоровье 90Заболевания опорно-двигательного аппарата 11Пенсии 16Физическое здоровье 43Бедность и уровень жизни 107Производительность и инновации 6Общественное здравоохранение 150Социальные сети 2Социоэкономика старения 24Социоэкономика раннего взросления 40Спортивная наука 1Злоупотребление психоактивными веществами 11Налоги 47Доверие к демократии 65Оценка данных 5
Ознакомьтесь с нашими проектами
Благосостояние | 2022 – 2023
Пересмотр политики на рынке труда для будущего работы
Посмотреть проект
Образование | 2022 – 2023
Перевод в школу Северной Ирландии без экзаменов в 2021 году
Посмотреть проект
Образование | 2022 – 2023
Повышение успеваемости учащихся с ООП и инвалидностью
Посмотреть проект
Новый
Правосудие | 2022 – 2024
Child First: изучение сотрудничества детей в системе правосудия по делам несовершеннолетних
Посмотреть проект
Новый
Образование | 2022 – 2024
Опыт дополнительного образования детей от 14 до 16 лет в Англии
Посмотреть проект
Новый
Благосостояние | 2022 – 2024
Связь между когнитивными нарушениями и эксплуатацией в Англии
Посмотреть проект
Новый
Благосостояние | 2022 – 2023
Влияние автоматического зачисления на пенсию и COVID-19по сохранению поведения
Посмотреть проект
Новый
Правосудие | 2022 – 2024
Административная справедливость в цифровом государстве всеобщего благосостояния
Посмотреть проект
Новый
Благосостояние | 2022 – 2024
Жизнь детей в переменчивых местах
Посмотреть проект
Новый
Благосостояние | 2022 – 2023
Влияние автоматического зачисления на пенсию и COVID-19 на сберегательное поведение
Посмотреть проект
Новый
Образование | 2022 – 2024
Долгосрочное влияние пособия на содержание образования
Посмотреть проект
Новый
Образование | 2023 – 2025
Помогают ли субтитры на одном языке детям научиться читать?
Посмотреть проект
Новый
Благосостояние | 2022 – 2024
Связь между когнитивными нарушениями и эксплуатацией в Англии
Посмотреть проект
Новый
Образование | 2022 – 2024
Опыт дополнительного образования детей от 14 до 16 лет в Англии
Посмотреть проект
Новый
Правосудие | 2022 – 2024
Child First: изучение сотрудничества детей в системе правосудия по делам несовершеннолетних
Посмотреть проект
Образование | 2022 – 2023
Повышение успеваемости учащихся с ООП и инвалидностью
Посмотреть проект
Образование | 2022 – 2023
Перевод в школу Северной Ирландии без экзаменов в 2021 году
Посмотреть проект
Образование | 2022 – 2023
Практика преподавания начальных наук, опыт и достижения учащихся
Посмотреть проект
Новый
Образование | 2022 – 2024
Долгосрочное влияние пособия на содержание образования
Посмотреть проект
Новый
Образование | 2023 – 2025
Помогают ли субтитры на одном языке детям научиться читать?
Посмотреть проект
Новый
Благосостояние | 2022 – 2024
Связь между когнитивными нарушениями и эксплуатацией в Англии
Посмотреть проект
Новый
Правосудие | 2022 – 2024
Child First: изучение сотрудничества детей в системе правосудия по делам несовершеннолетних
Посмотреть проект
В процессе
Образование | 2022 – 2023
Движение и рассказывание историй для приемных детей
Посмотреть проект
В процессе
Образование | 2022 – 2024
Исследовательское обучение языку и грамотности: рандомизированное контрольное исследование
Посмотреть проект
В процессе
2022 – 2025
Разработка классов математики с учетом языка
Посмотреть проект
В процессе
Благосостояние | 2022 – 2024
Сельские активы: взгляды на политику и практику децентрализованных стран
Посмотреть проект
В процессе
Благосостояние | 2022 – 2024
Интеграция на основе природы: соединение сообществ с природой/в природе
Посмотреть проект
Сообщено
Образование | 2020 – 2022
Этические принципы, лежащие в основе совместного производства с молодежью
Посмотреть проект
Сообщено
Образование | 2020 – 2022
Могут ли математические приложения повысить ценность обучения?
Посмотреть проект
Сообщено
Благосостояние | 2020 – 2022
Реалии COVID: малообеспеченные семьи во время пандемии
Посмотреть проект
Сообщено
Благосостояние | 2020 – 2020
Как население Великобритании получает информацию о COVID-19
Посмотреть проект
Сообщено
Образование | 2019 – 2020
Систематический обзор дипломов и путей трудоустройства
Посмотреть проект
Сообщено
Образование | Благосостояние | 2020 – 2020
Измерение разрыва в уровне образования в 16-19 лет
Посмотреть проект
Сообщено
Образование | 2019 – 2022
«Неуправляемые» школы: может ли решение Ofsted помешать устойчивому улучшению?
Посмотреть проект
Сообщено
Образование | 2014 – 2015
Исследовательская программа Nuffield Languages Inquiry и Nuffield Languages Program
Посмотреть проект
Сообщено
Образование | 2003 – 2003
Nuffield Review of 14-19 Education and Training
Посмотреть проект
Увидеть всеПоследние
Последние
7.
 1: Правильные многоугольники — Математика LibreTexts
1: Правильные многоугольники — Математика LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 34152
- Генри Африк
- CUNY Нью-Йоркский технологический колледж через Нью-Йоркский городской технологический колледж в CUNY Academic Works
Правильный многоугольник — это многоугольник, у которого все стороны равны и все углы равны. Примерами правильного многоугольника являются равносторонний треугольник (3 стороны), квадрат (4 стороны), правильный пятиугольник (5 сторон), и правильный шестиугольник (6 сторон). Углы правильного многоугольника легко найти с помощью методов раздела 1.5.
Рисунок \(\PageIndex{1}\): примеры правильных многоугольников.
Предположим, мы проводим биссектрису каждого угла правильного многоугольника. Мы обнаружим, что все эти биссектрисы пересекаются в одной точке (рис. \(\PageIndex{2}\)).
Рисунок \(\PageIndex{2}\): Биссектрисы правильного многоугольника пересекаются в одной точке \(O\). \(O\) называется центром правильного многоугольника.Теорема \(\PageIndex{1}\)
Биссектрисы каждого угла правильного многоугольника пересекаются в одной точке. Эта точка называется 9.0330 центр правильного многоугольника.
На рисунке \(\PageIndex{2}\). \(O\) — центр каждого правильного многоугольника. Отрезок биссектрисы каждого угла от центра до вершины называется радиусом . Например, \(OA, OB, OC, OD\) и \(OE\) — это пять радиусов правильного пятиугольника \(ABCDE\).
Теорема \(\PageIndex{2}\)
Радиусы правильного многоугольника делят многоугольник на конгруэнтные равнобедренные треугольники. Все радиусы равны.
На рисунке \(\PageIndex{3}\) радиусы \(OA, OB, OC, OD\) и \(OE\) делят правильный пятиугольник на пять равнобедренных треугольников с \(OA = OB =OC = OD = ОЕ\).
 9{\circ}\).
9{\circ}\).Теорема \(\PageIndex{1}\) и Теорема \(\PageIndex{2}\) кажутся верными интуитивно, но мы проверяем их формальным доказательством:
Доказательство теоремы \(\PageIndex{1}\) и теоремы \(\PageIndex{2}\): Мы докажем эти теоремы для правильного пятиугольника. Доказательство для других правильных многоугольников аналогично.
Нарисуйте биссектрисы углов \(\угол A\) и \(\угол B\), как показано на рисунке \(\PageIndex{4}\), и назовите их точку пересечения \(O\). Мы покажем, что \(OC, OD\) и \(OE\) являются биссектрисами углов \(\угол C\), \(\угол D\) и \(\угол E\) соответственно.
\(\угол EAB = \угол ABC\), так как углы правильного пятиугольника равны. \(\угол 1 = \угол 2 = \dfrac{1}{2}\) из \(\угол EAB = \dfrac{1}{2}\) из \(\угол ABC = \угол 3 = \угол 4\), так как \(OA\) и \(OB\) являются биссектрисами углов.
Рисунок \(\PageIndex{4}\): начертите биссектрисы углов \(\угол A\) и \(\угол B\) и назовите их точку пересечения \(O\).Рисунок \(\PageIndex{5 }\).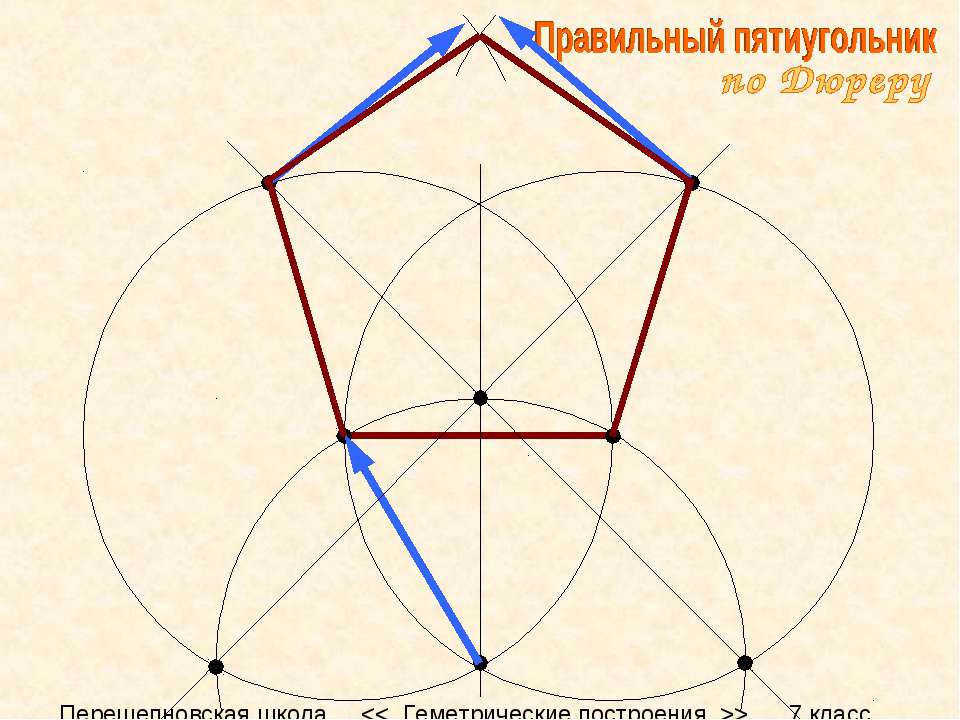 Нарисуйте \(ОС\).
Нарисуйте \(ОС\).Нарисуйте \(OC\) (Рисунок \(\PageIndex{5}\)). \(AB = BC\), так как стороны правильного пятиугольника равны. Поэтому \(\треугольник AOB \cong \треугольник COB\) через \(SAS = SAS\). Поэтому \(\угол 5 = \угол 2 = \dfrac{1}{2}\) из \(\угол EAB = \dfrac{1}{2}\) из \(\угол BCD\). Таким образом, \(OC\) — это биссектриса угла \(\угол BCD\).
Точно так же мы можем показать \(\треугольник BOC \cong \треугольник DOC\), \(\треугольник COD \cong \треугольник EOD\), \(\треугольник DOE \cong \треугольник AOE\) и что \(OD\) и \(OE\) — биссектрисы угла. Все треугольники равнобедренные, так как их углы при основании равны. Это завершает доказательство.
Отрезок, проведенный из центра перпендикулярно сторонам правильного многоугольника, называется апофемой (см. рисунок \(PageIndex{6}\)).
Рисунок \(\PageIndex{6}\): Апофемы правильного пятиугольника.Теорема \(\PageIndex{1}\)
Все апофемы правильного многоугольника равны. Они делят стороны правильного многоугольника пополам.

- Доказательство
Все апофемы равны, потому что они являются высотами конгруэнтных равнобедренных треугольников, образованных радиусами (см. Теорему \(\PageIndex{2}\)), Каждая апофема делит равнобедренный треугольник на два конгруэнтных прямоугольных треугольника, Следовательно, каждая апофема делит пополам сторона многоугольника, что мы и хотели доказать. 9{\ circ}} & = & {\ dfrac {a} {10}} \\ {(10) 1,3764} & = & {\ dfrac {a} {10} (10)} \\ {13,764} & = & {a} \\ {13.8} & = & {a} \end{массив}\)
Ответ: 13.8
Апофема правильного многоугольника важна, потому что она используется для нахождения площади:
Теорема \(\PageIndex{4}\)
Площадь правильного многоугольника равна половине произведения апофемы на периметр.
\[A = \dfrac{1}{2} a P\]
- Доказательство
- Рисунок \(PageIndex{9}\). Площадь \(\треугольника AOB\) равна \(\dfrac{1}{2}\) as, где \(s\) — сторона пятиугольника.
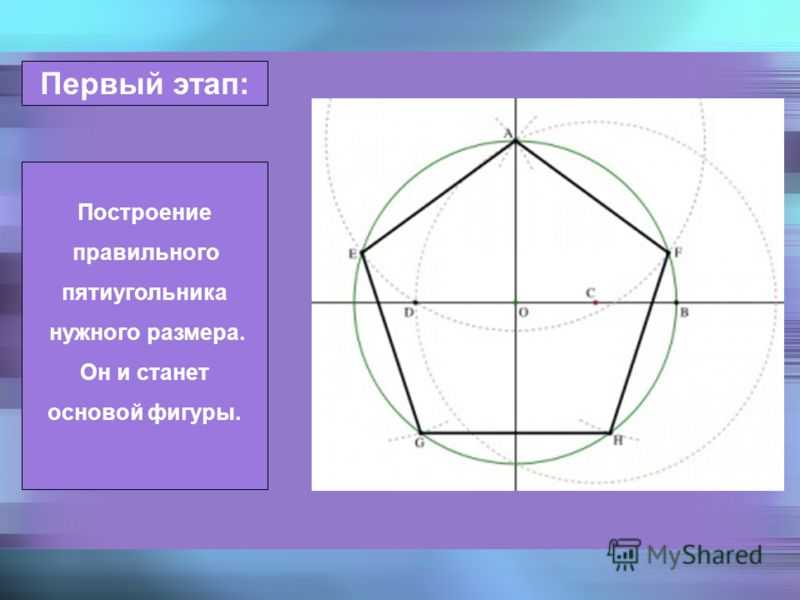
Докажем теорему для правильного пятиугольника. Доказательство для других правильных многоугольников аналогично.
Радиусы правильного пятиугольника делят правильный пятиугольник на пять конгруэнтных треугольников. Площадь каждого треугольника равна \(\dfrac{1}{2}\) as, где \(s\) – сторона пятиугольника (рис. \(PageIndex{9}\)). Следовательно, площадь пятиугольника = 5(\dfrac{1}{2} as) = \dfrac{1}{2} a (5s) = \dfrac{1}{2}aP\), что является формулой, которую мы хотел доказать.
Пример \(\PageIndex{3}\)
Найдите площадь правильного пятиугольника со стороной 20 с точностью до десятых.
Решение
Из примера \(\PageIndex{2}\) мы знаем \(a = 13,764\). Периметр \(P = (5)(20) = 100\). Следовательно, \(A = \dfrac{1}{2} aP = \dfrac{1}{2} (13,764)(100) = \dfrac{1}{2} (1376,4) = 688,2\).
Ответ: 688,2
Чтобы найти периметр правильного многоугольника, нам нужно всего лишь умножить длину стороны на количество сторон.
 Например, пятиугольник на рисунке \(\PageIndex{8}\) имеет периметр \(P = 5(20)=100\). Однако также полезно иметь формулу для периметра, когда только 9{\circ}}{n}\) близко к числу \(\pi\). Мы вернемся к этому вопросу, когда будем обсуждать длину окружности в разделе 7.5.
Например, пятиугольник на рисунке \(\PageIndex{8}\) имеет периметр \(P = 5(20)=100\). Однако также полезно иметь формулу для периметра, когда только 9{\circ}}{n}\) близко к числу \(\pi\). Мы вернемся к этому вопросу, когда будем обсуждать длину окружности в разделе 7.5.Пример \(\PageIndex{4}\) (повторяется)
Найдите периметр правильного пятиугольника с радиусом Hi, равным 10, с точностью до десятых.
Решение
Из таблицы
\[ \begin{align*} P &= 5.8780\ r \\[4pt] &= 5.8780(10) \\[4pt] &= 58.78 \\[4pt] &= 58.8 \end{align*}.\]
Ответ 9{\ circ}} & = & {\ dfrac {a} {10}} \\ {(10).8090} & = & {\ dfrac {a} {10}(10)} \\ {8,090} & = & {a} \end{array}\)
Из примера \(\PageIndex{4}\), \(P = 58,78\). Следовательно, по теореме \(\PageIndex{4}\)
\(A = \dfrac{1}{2} a P = \dfrac{1}{2} (8.09) (58.78) = \dfrac{1 {2} (475,5302) = 237,7651 = 237,8.\)
Ответ : \(а = 8,1, Р = 237,8\).
Историческая справка
В 1936 году археологи раскопали группу древних вавилонских таблиц, содержащих формулы площадей правильных многоугольников с тремя, четырьмя, пятью, шестью и семью сторонами.
 Имеются свидетельства того, что правильные многоугольники широко использовались в архитектуре и проектах и другие древние цивилизации. Классическая задача греческой математики состояла в том, чтобы построить правильный многоугольник, используя только линейку и циркуль. Правильные многоугольники обычно изучались по отношению к окружностям. Как мы увидим далее в этой главе, формулы площади и периметра круга можно вывести из соответствующих формул для правильных многоугольников. 9{\ Circ} \) и Radius \ (r \) обычных многоугольников:
Имеются свидетельства того, что правильные многоугольники широко использовались в архитектуре и проектах и другие древние цивилизации. Классическая задача греческой математики состояла в том, чтобы построить правильный многоугольник, используя только линейку и циркуль. Правильные многоугольники обычно изучались по отношению к окружностям. Как мы увидим далее в этой главе, формулы площади и периметра круга можно вывести из соответствующих формул для правильных многоугольников. 9{\ Circ} \) и Radius \ (r \) обычных многоугольников:1.
2.
3.
4.
5.
6.
7 — 18. Найдите апофему, периметр и площадь с точностью до десятых:
7. правильный пятиугольник со стороной 40.
8. правильный пятиугольник со стороной 16.
9. правильный шестиугольник со стороной 20.
10. правильный шестигранник со стороной 16.
11. правильный десятиугольник (десятиугольник) со стороной 20.
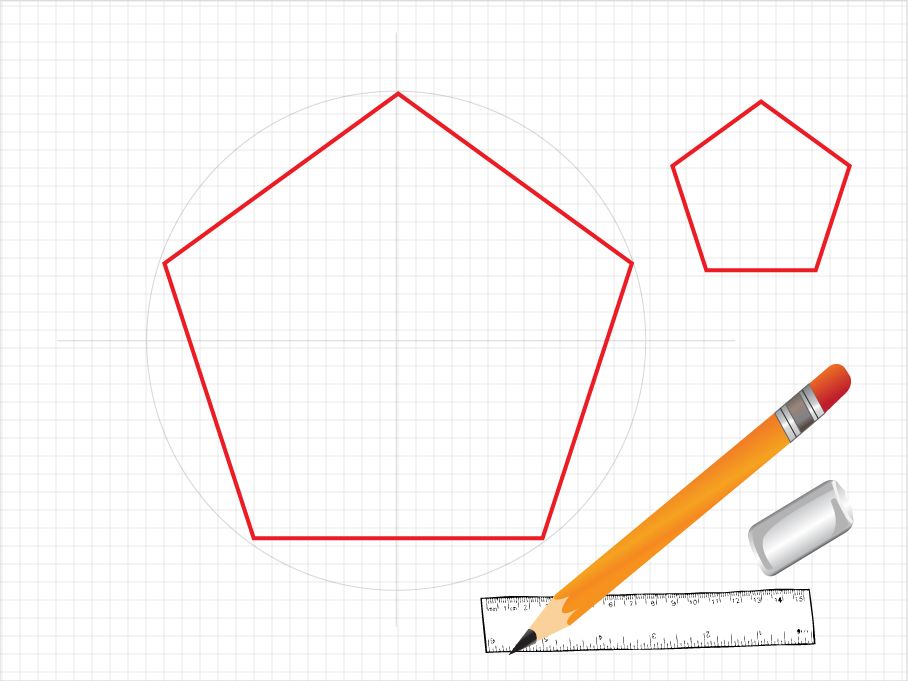
12. правильный девятиугольник (девятиугольник) со стороной 20.
13. правильный пятиугольник радиусом 20.
14. правильный пятиугольник радиусом 5 .
Эта страница под названием 7.1: Правильные многоугольники распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Генри Африком (Нью-Йоркский технологический колледж в CUNY Academic Works) через исходный контент, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Генри Африк
- Лицензия
- СС BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- апофема
- радиус
- обычный шестигранник
- правильный пятиугольник
- правильных многоугольника
- источник@https://academicworks.
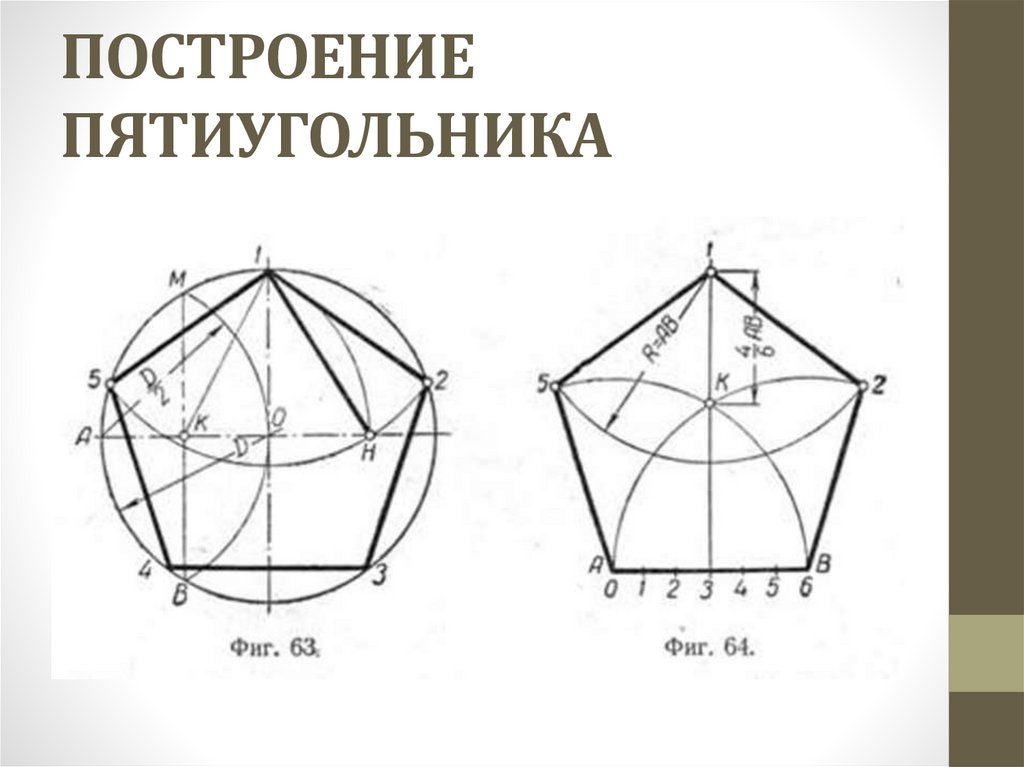 cuny.edu/ny_oers/44
cuny.edu/ny_oers/44
Построение правильных многоугольников — технический чертеж. Построение правильных многоугольников Нарисуйте восьмиугольник с помощью циркуля
Построение правильного шестиугольника, вписанного в окружность. Построение шестиугольника основано на том, что его сторона равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (рис. 60, а).
Правильный шестиугольник можно построить из Т-угольника и квадрата 30X60°. Для выполнения этого построения возьмем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (рис. 60, б), построим стороны 1-6, 4-3, 4-5 и 7-2, после чего нарисуйте стороны 5-6 и 3-2.
Построение равностороннего треугольника, вписанного в окружность . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами 30 и 60° или только одного циркуля.

Рассмотрим два способа построения равностороннего треугольника, вписанного в окружность.
Первый способ (рис. 61, а) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная линия, проведенная через точку 7, является одновременно и высотой, и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить угол 30° в точке 1 и стороне 0-1. Для этого установите Т-угольник и угольник, как показано на рисунке, проведите линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, установите Т-образный квадрат в положение, показанное пунктирными линиями, и проведите прямую линию через точку 2, которая определит третью вершину треугольника.
Второй способ основан на том, что если построить правильный шестиугольник, вписанный в окружность, а затем соединить его вершины через единицу, то получится равносторонний треугольник.
Для построения треугольника (рис.
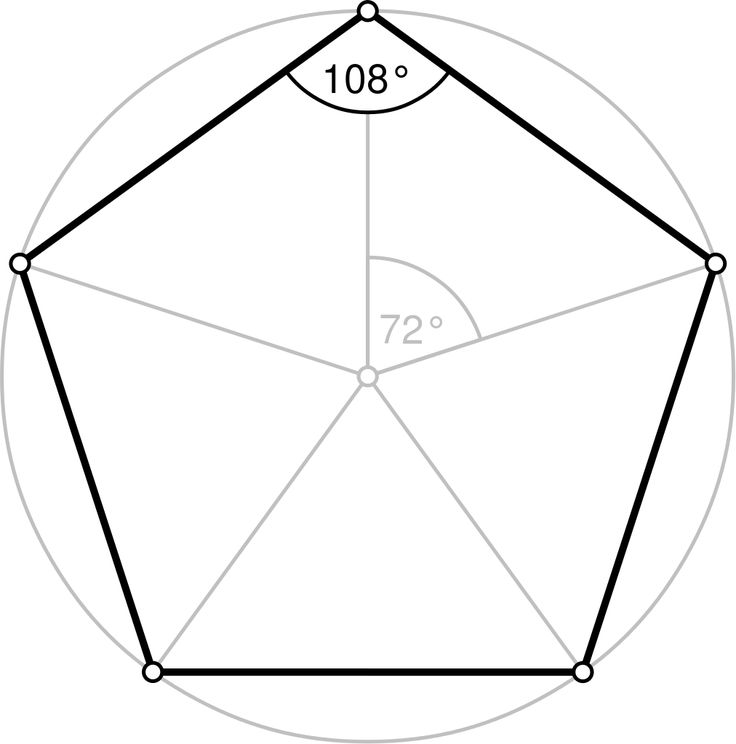 61, б) отмечаем на диаметре вершину 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
61, б) отмечаем на диаметре вершину 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.Построение квадрата, вписанного в круг . Это построение можно сделать с помощью угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанной окружности и наклонены к ее осям под углом 45°. Исходя из этого, устанавливаем Т-образный угольник и угольник с углами 45°, как показано на рис. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим горизонтальные стороны угольника 4- 1 и 3-2 с помощью Т-угольника. Затем с помощью Т-угольника по катету квадрата рисуем вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключенные между концами диаметра (рис. 62, б). Отмечаем точки А, В и С на концах двух взаимно перпендикулярных диаметров и от них радиусом у описываем дуги до их пересечения.
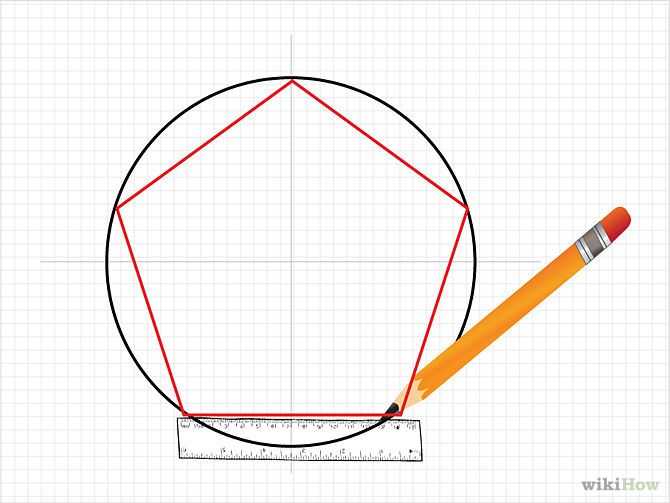
Далее через точки пересечения дуг проводим вспомогательные линии, отмеченные на рисунке сплошными линиями. Их точки пересечения с окружностью будут определять вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяются последовательно друг с другом.
Построение правильного пятиугольника, вписанного в окружность.
Для вписания правильного пятиугольника в окружность (рис. 63) проведем следующие построения.
Отмечаем на окружности точку 1 и принимаем ее за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках М и В. Соединив эти точки прямой, получим точку К, которую затем соединим с точкой 1. С радиусом, равным отрезку А7, описываем дугу от точки К до пересечения с диаметральной линией АО в точке Н. Соединив точку 1 с точкой Н, получим сторону пятиугольника. Затем при апертуре, равной отрезку 1Н, описав дугу от вершины 1 до пересечения с окружностью, находим вершины 2 и 5.
 Сделав из вершин 2 и 5 засечки с тем же апертурой, получим оставшиеся вершины 3 и 4. Соединяем найденные точки последовательно друг с другом.
Сделав из вершин 2 и 5 засечки с тем же апертурой, получим оставшиеся вершины 3 и 4. Соединяем найденные точки последовательно друг с другом.Построение правильного пятиугольника по стороне.
Чтобы построить правильный пятиугольник по заданной стороне (рис. 64), разделим отрезок АВ на шесть равных частей. Из точек А и В радиусом АВ описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой АВ проводим вертикальную линию.
Получаем точку 1-вершины пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, проведенными ранее из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Соединяем найденные вершины последовательно друг с другом.
Построение правильного семиугольника, вписанного в окружность.
Пусть дан круг диаметром D; в него нужно вписать правильный семиугольник (рис. 65). Разделите вертикальный диаметр круга на семь равных частей.
 Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точка F называется полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проведем лучи от полюса F через четные деления вертикального диаметра, пересечение которых с окружностью определит вершины VI, V и IV семиугольника. Для получения вершин /-//-// из точек IV, V и VI проводим горизонтальные линии до пересечения с окружностью. Соединяем найденные вершины последовательно друг с другом. Семиугольник можно построить, проводя лучи от полюса F и через нечетные деления вертикального диаметра.
Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точка F называется полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проведем лучи от полюса F через четные деления вертикального диаметра, пересечение которых с окружностью определит вершины VI, V и IV семиугольника. Для получения вершин /-//-// из точек IV, V и VI проводим горизонтальные линии до пересечения с окружностью. Соединяем найденные вершины последовательно друг с другом. Семиугольник можно построить, проводя лучи от полюса F и через нечетные деления вертикального диаметра.Описанный выше метод подходит для построения правильных многоугольников с любым количеством сторон.
Деление окружности на любое количество равных частей можно произвести и по данным табл. 2, где приведены коэффициенты, позволяющие определить размеры сторон правильных вписанных многоугольников.
В рисовании часто требуется построить положительные многоугольники.
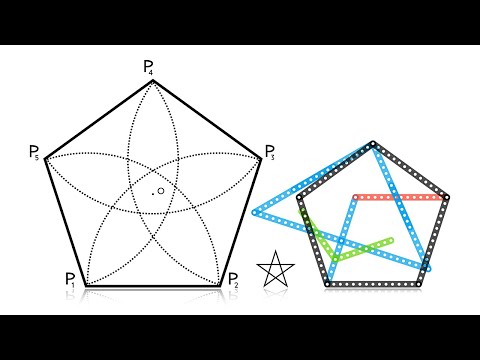 Итак, допустим, положительных восьмиугольника используются на дорожных знаках.
Итак, допустим, положительных восьмиугольника используются на дорожных знаках.Вам понадобится
- — компасы
- — линейка
- — карандаш
Инструкция
1. Пусть задан отрезок, равный длине стороны искомого восьмиугольника. Требуется построить настоящий восьмиугольник. Первым шагом является построение равнобедренного треугольника на заданном отрезке, используя отрезок в качестве основания. Для этого сначала постройте квадрат со стороной, равной отрезку, проведите в нем диагонали. Теперь постройте биссектрисы углов по диагоналям (на рисунке биссектрисы обозначены синим цветом), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу круг, описанный вокруг правильного восьмиугольника.
2. Построить окружность с центром в вершине треугольника. Радиус окружности равен стороне треугольника. Теперь разведите компас на расстояние, равное величине данного отрезка.
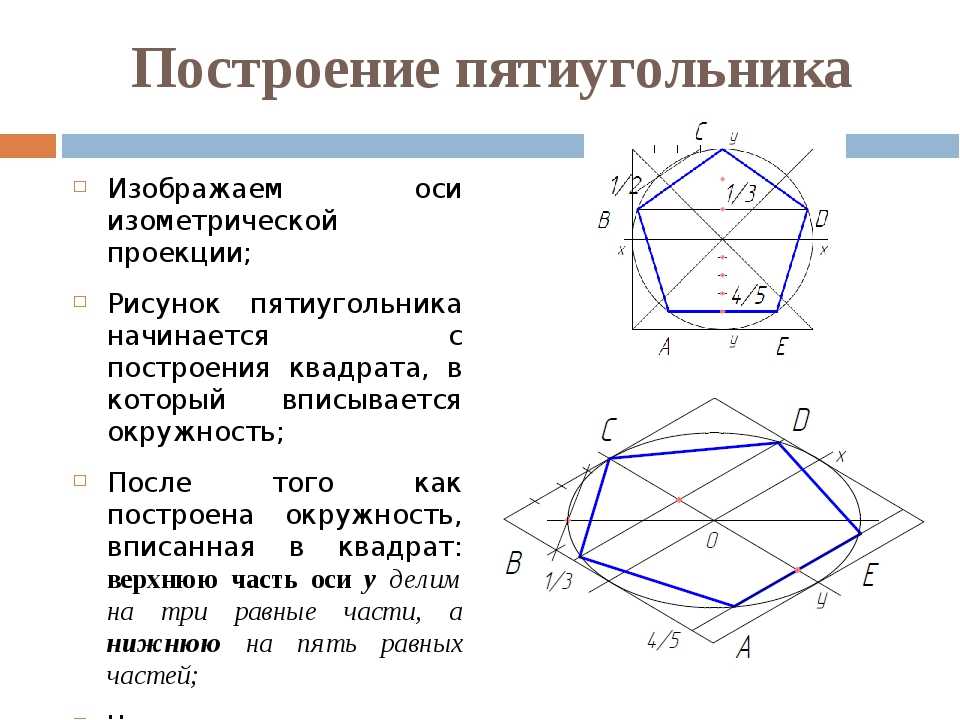 Отложите это расстояние по кругу, начиная с каждого конца отрезка. Объедините все полученные точки в восьмиугольник.
Отложите это расстояние по кругу, начиная с каждого конца отрезка. Объедините все полученные точки в восьмиугольник.3. Если дана окружность, в которую следует вписать восьмиугольник, то построения будут еще проще. Постройте две центральные линии, перпендикулярные друг другу, проходящие через центр круга. На пересечении оси и окружности получится четыре вершины будущего восьмиугольника. Осталось разделить расстояние между этими точками на дуге окружности пополам, чтобы получить еще четыре вершины.
Верный треугольник — такой, у которого все стороны имеют одинаковую длину. Основываясь на этом определении, построение треугольника , аналогичного многообразию , но является простой задачей.
Вам понадобится
- Линейка, лист линованной бумаги, карандаш
Инструкция
1. Возьмите лист чистой бумаги, разлинованный в клеточку, линейку и отметьте на бумаге три точки так, чтобы они находились на одинаковом расстоянии друг от друга (рис.
 1)
1)2. С помощью линейки последовательно совместите точки, отмеченные на листе, одну за другой, как показано на рисунке 2.
Внимание!
В прямоугольном (равностороннем) треугольнике все углы равны 60 градусов.Полезный совет
Равносторонний треугольник также является равнобедренным треугольником. Если треугольник равнобедренный, то это означает, что 2 из 3 его сторон равны, а третья сторона считается основанием. Каждый положительный треугольник равнобедренный, а обратное неверно.Октагон — это, по сути, два квадрата, смещенные друг относительно друга на 45° и объединенные в вершинах сплошной линией. И поэтому, чтобы положительно изобразить такую геометрическую фигуру, нужно нарисовать квадрат или круг твердым карандашом, по правилам, с которыми выполнять последующие действия. Изложение ориентировано на длину стороны, равную 20 см. Итак, при компоновке чертежа учитывайте, чтобы вертикальные и горизонтальные линии длиной 20 см уместились на листе бумаги.

Вам понадобится
- Линейка, прямоугольный треугольник, транспортир, карандаш, циркуль, лист бумаги
Инструкция
1. Способ 1. Проведите снизу горизонтальную линию длиной 20 см. После этого с одной стороны проведите транспортиром прямой угол, тот, что равен 90°. То же самое можно сделать с опорой на прямоугольный треугольник. Проведите вертикальную линию и проведите 20 см. Те же манипуляции проделайте с другой стороны. Соедините две полученные точки горизонтальной линией. В результате получается геометрическая фигура – квадрат.
2. Чтобы построить 2-й (сдвинутый) квадрат, вам нужен центр фигуры. Для этого разделите каждую сторону квадрата на 2 части. Соедините сначала 2 точки параллельных верхней и нижней сторон, а затем точки сторон. Проведите 2 прямые линии через центр квадрата перпендикулярно друг другу. Начиная от центра, отмерьте по новым прямым линиям 10 см, в результате получится 4 прямые линии.
 Объедините полученные 4 крайние точки друг с другом, в результате чего получится 2-й квадрат. Теперь совместите любую точку из 8 полученных углов друг с другом. Таким образом, будет нарисован восьмиугольник.
Объедините полученные 4 крайние точки друг с другом, в результате чего получится 2-й квадрат. Теперь совместите любую точку из 8 полученных углов друг с другом. Таким образом, будет нарисован восьмиугольник.3. Способ 2. Для этого потребуются циркуль, линейка и транспортир. Из центра листа с помощью циркуля начертите окружность диаметром 20 см (радиус 10 см). Проведите прямую линию через центральную точку. После этого проведите вторую линию перпендикулярно ей. То же самое можно сделать с помощью транспортира или прямоугольного треугольника. В результате круг будет разделен на 4 равные части. Затем разделите каждую из секций еще на 2 части. Для этого также допускается использовать транспортир, размером 45° или с прямоугольным треугольником, тот, который присоединяет острый угол 45° и проводит лучи. Отмерьте 10 см от центра по любой прямой линии. В итоге у вас получится 8 «лучей», которые вы совместите друг с другом. В результате получается восьмиугольник.
4.
 Способ 3. Для этого таким же образом нарисуйте круг, проведите линию через середину. После этого возьмите транспортир, положите его в центр и измерьте углы, учитывая, что каждый участок восьмиугольника имеет в центре угол 45°. Позже на полученных лучах отмерьте длину 10 см и соедините их между собой. Октагон готов.
Способ 3. Для этого таким же образом нарисуйте круг, проведите линию через середину. После этого возьмите транспортир, положите его в центр и измерьте углы, учитывая, что каждый участок восьмиугольника имеет в центре угол 45°. Позже на полученных лучах отмерьте длину 10 см и соедините их между собой. Октагон готов.Полезный совет
Сделайте рисунок твердым карандашом, боковые линии на котором после этого будет легко удалитьНастоящий восьмиугольник — это геометрическая фигура, в которой каждый угол равен 135°, а все стороны равны друг другу. Эта фигура часто используется в архитектуре, например, при построении колонн, а также при изготовлении дорожного знака СТОП. Как нарисовать положительный восьмиугольник?
Вам потребуется
- — альбомный лист;
- — карандаш;
- — линейка;
- — компас;
- — ластик.
Инструкция
1. Сначала нарисуйте квадрат.
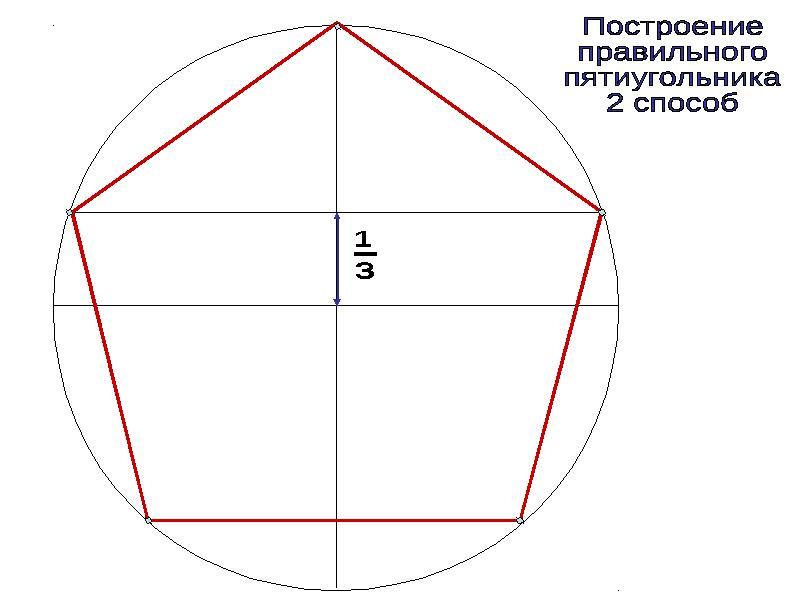 После этого нарисуйте круг так, чтобы квадрат оказался внутри круга. Теперь проведите две осевые срединные линии квадрата — горизонтальную и вертикальную до пересечения с кругом. Совместите точки пересечения осей с окружностью и точки касания описанной окружности с квадратом с прямыми отрезками. Таким образом, получаются стороны настоящего восьмиугольника.
После этого нарисуйте круг так, чтобы квадрат оказался внутри круга. Теперь проведите две осевые срединные линии квадрата — горизонтальную и вертикальную до пересечения с кругом. Совместите точки пересечения осей с окружностью и точки касания описанной окружности с квадратом с прямыми отрезками. Таким образом, получаются стороны настоящего восьмиугольника.2. Нарисуйте настоящий восьмиугольник другим способом. Сначала нарисуйте круг. После этого проведите горизонтальную линию через его центр. Отметьте точку пересечения крайней правой границы круга с горизонталью. Эта точка будет центром другой окружности с радиусом, равным предыдущей фигуре.
3. Проведите вертикальную линию через точки пересечения 2-го круга с первым. Поместите ножку циркуля на пересечение вертикали и горизонтали и нарисуйте маленький круг с радиусом, равным расстоянию от центра маленького круга до центра исходного круга.
4. Проведите прямую через две точки — центр исходного круга и точку пересечения вертикали и маленького круга.
 Продолжайте его до пересечения с границей исходной фигуры. Это будет вершина восьмиугольника. Циркулем отметьте еще одну точку, начертив окружность с центром в точке пересечения крайней правой границы исходной окружности с горизонтальной линией и радиусом, равным расстоянию от центра до ближайшей вершины восьмиугольника.
Продолжайте его до пересечения с границей исходной фигуры. Это будет вершина восьмиугольника. Циркулем отметьте еще одну точку, начертив окружность с центром в точке пересечения крайней правой границы исходной окружности с горизонтальной линией и радиусом, равным расстоянию от центра до ближайшей вершины восьмиугольника.5. Проведите прямую через две точки — центр исходной окружности и последнюю вновь образованную точку. Продолжайте прямую линию, пока она не пересечется с границами исходной формы.
6. Совместить с прямыми отрезками пошагово: точку пересечения горизонтали с правой границей исходной фигуры, затем по часовой стрелке все образовавшиеся точки, включая точки пересечения осей с исходной окружностью.
Видео по теме
Куклин Алексей
Работа носит реферативный характер с элементами исследовательской деятельности. В нем обсуждаются различные способы построения правильных n-угольников. В работе содержится подробный ответ на вопрос, всегда ли можно построить n-угольник с помощью циркуля и линейки.
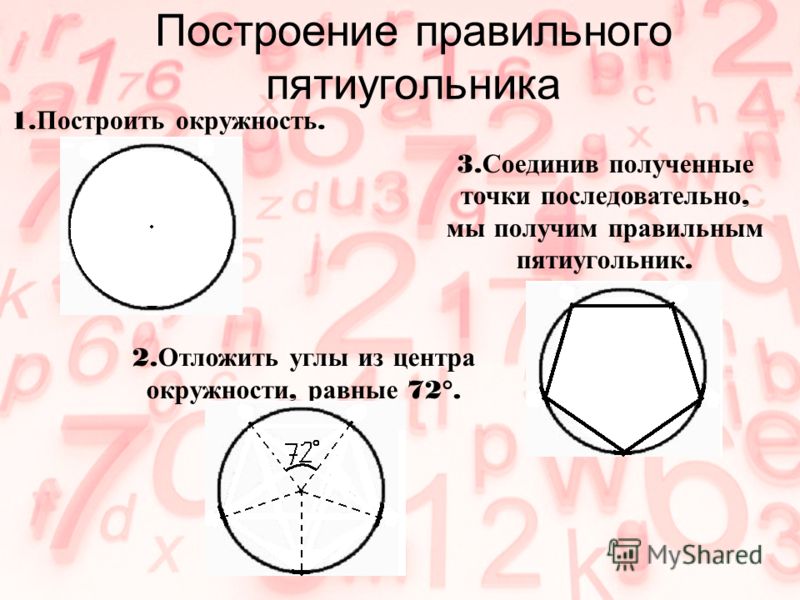 К работе прилагается презентация, которую можно найти на этом мини-сайте.
К работе прилагается презентация, которую можно найти на этом мини-сайте.Скачать:
Предварительный просмотр:
Чтобы использовать предварительный просмотр, создайте себе учетную запись Google (аккаунт) и войдите в систему: https://accounts.google.com
Предпросмотр:
https://accounts.google.com
Подписи к слайдам:
Построение правильных многоугольников Работу выполнил: учащийся 9 «Б» МБОУ СОШ № 10 Куклин Алексей
Правильные многоугольники Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны. Перейти к примерам Выпуклый многоугольник — это многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его смежные вершины.
Назад Правильные многоугольники
Основоположниками раздела математики о правильных многоугольниках были древнегреческие ученые. Одними из них были Архимед и Евклид.
Доказательство существования правильного n-угольника Если n (количество углов многоугольника) больше 2, то такой многоугольник существует.
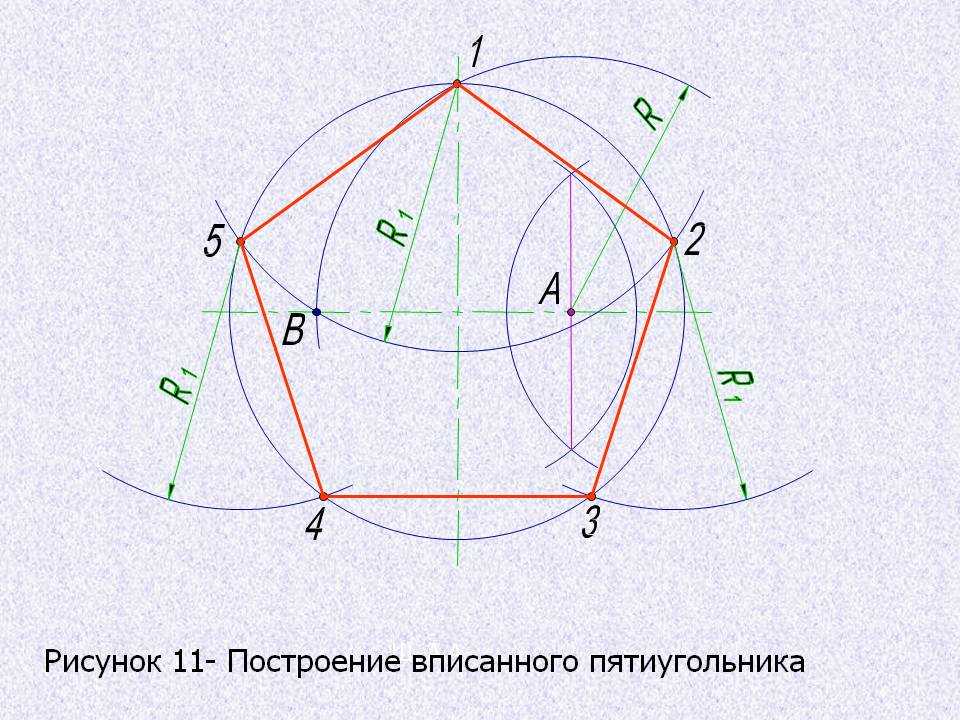 Попробуем построить 8-угольник и доказать это. Доказательство
Попробуем построить 8-угольник и доказать это. ДоказательствоВозьмем окружность произвольного радиуса с центром в точке О. Разделим ее на определенное количество равных дуг, в нашем случае 8. Для этого проведем радиусы так, чтобы получилось 8 дуг, а угол между двумя ближайшими радиусы были равны 360°: количество сторон (в нашем случае случае 8), соответственно каждый угол будет равен 45°.
3. Получить очки A1, A2, A3, A4, A5, A6, A7, A8. Соединяем их по очереди и получаем правильный восьмиугольник. Назад
Построение правильного многоугольника по стороне с помощью поворота Правильный многоугольник можно построить, зная его углы. Мы знаем, что сумма углов выпуклого n-угольника равна 180°(n — 2). Отсюда можно вычислить угол многоугольника, разделив сумму на n. Angles Building
Прямой угол: 3-угольник равен 60° 4-угольник равен 90° 5-угольник равен 108° 6-угольник равен 120° 8-угольник равен 135° 9-угольник равен 140° 10-угольник равен 144° 12-угольник равен 150° Градусная мера углов правильных треугольников Назад
Предварительный просмотр:
Для использования предварительного просмотра презентаций создайте учетную запись Google (аккаунт) и войдите в систему: https ://accounts.
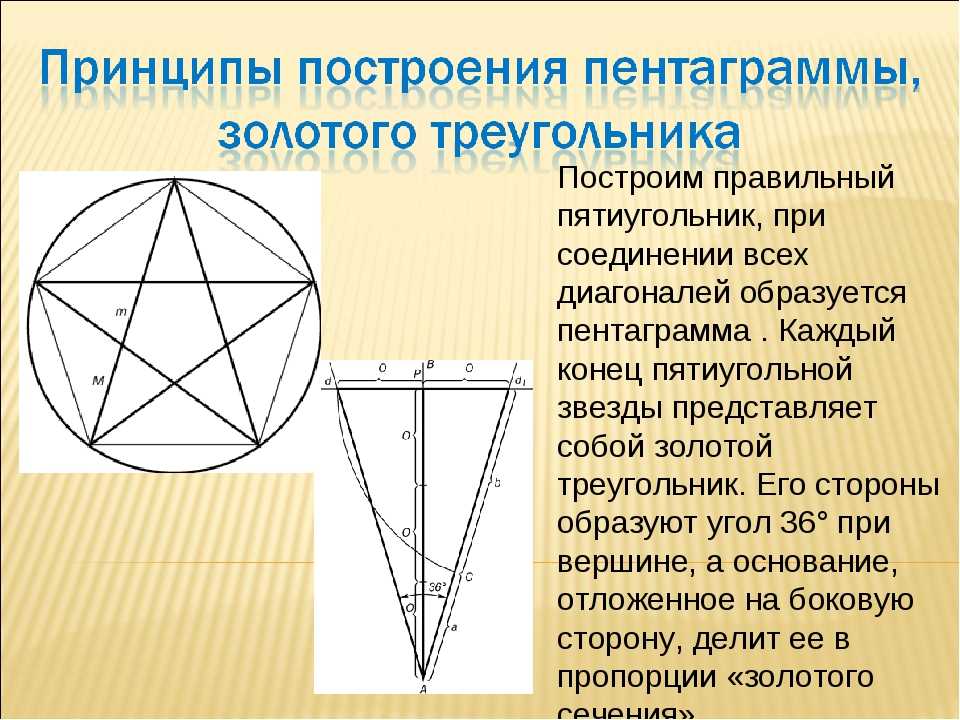 google.com
google.comПодписи к слайдам:
В 1796 году один из величайших математиков всех времен Карл Фридрих Гаусс показал возможность построения правильных n-угольников, если выполняется равенство, где n — количество углов, а k — любое натуральное число. Таким образом, оказалось, что в пределах 30 можно разделить круг на 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30 равных частей. В 1836 году Ванзель доказал, что правильные многоугольники, не удовлетворяющие этому равенству, нельзя построить с помощью линейки и циркуля. Теорема Гаусса
Построение треугольника Построим окружность с центром в точке О. Построим еще одну окружность такого же радиуса, проходящую через точку О.
3. Соединим центры окружностей и одну из точек их пересечения, получив правильную полигон. Назад Рисуем треугольник
Построение шестиугольника 1. Построим окружность с центром в точке О. 2. Проведем прямую через центр окружности. 3. Нарисуйте дугу окружности того же радиуса с центром в точке пересечения прямой с окружностью до пересечения с окружностью.
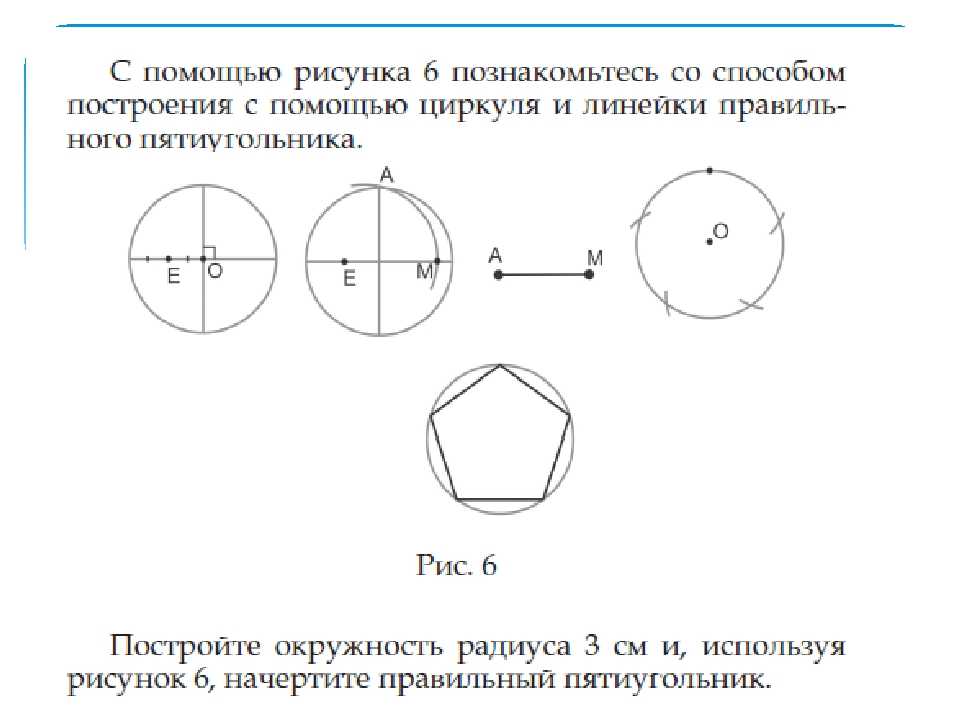
4. Проведите прямые через центр исходной окружности и точки пересечения дуги с этой окружностью. 5. Соединяем точки пересечения всех линий с исходной окружностью и получаем правильный шестиугольник. Построение шестиугольника
Построение четырехугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Из точек, в которых диаметры касаются окружности, проводим другие окружности заданного радиуса до их пересечения (окружности).
Построение четырехугольника 4. Проведите прямые через точки пересечения окружностей. 5. Соединяем точки пересечения прямых и окружности и получаем правильный четырехугольник.
Построение восьмиугольника Можно построить любой правильный многоугольник, у которого в 2 раза больше углов, чем у заданного. Давайте построим восьмиугольник, используя четырехугольник. Соедините противоположные вершины четырехугольника. Проведем биссектрисы углов, образованных пересекающимися диагоналями.
4. Соедините точки, лежащие на окружности, получив правильный восьмиугольник.
 Построение восьмиугольника
Построение восьмиугольникаПредварительный просмотр:
Чтобы использовать предварительный просмотр презентаций, создайте учетную запись Google (аккаунт) и войдите в нее: https://accounts.google.com
Подписи к слайдам:
Построение десятиугольника Давайте построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Разделите радиус окружности пополам и из полученной точки начертите на ней окружность, проходящую через точку О.
Построение десятиугольника 4. Проведите отрезок от центра маленького круга до точки, где большой круг касается своего радиуса. 5. Из точки соприкосновения большого круга и его радиуса начертите круг так, чтобы он соприкасался с малым.
Построение десятиугольника 6. Из точек пересечения большого и получившегося кругов проводим круги построенные в прошлый раз и так будем рисовать до соприкосновения соседних кругов. 7. Соедините точки и получите десятиугольник.
Построение пятиугольника Чтобы построить правильный пятиугольник, нужно соединить не все точки по очереди, а через одну, при построении правильного десятиугольника.