Помогите решить / разобраться (М)
| Maximmmm |
|
||
|
20/01/21 |
|
||
|
|
|||
| kotenok gav |
|
||
|
21/05/16 |
|
||
|
|
|||
| StepV |
|
||
|
23/05/20 |
|
||
|
|
|||
| Maximmmm |
|
||
|
20/01/21 |
|
||
|
|
|||
Вроде понял. Если провести отрезок EC, то в треугольнике EAC | arseniiv |
|
|||
27/04/09 |
|
|||
|
|
||||
01.2021, 20:31 
| StepV |
|
||
|
23/05/20 |
|
||
|
|
|||
| arseniiv |
|
|||
27/04/09 |
|
|||
|
|
||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 |
[ Сообщений: 7 ] |
Модераторы: Модераторы Математики, Супермодераторы
Вершина — шестиугольник — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Болты с шестигранной головкой ( ГОСТ 7805 — 70. |
Вершины шестиугольника являются проекциями ребер шестигранной головки болта. По ним строят проекцию ребер на главном виде. [2]
Через вершины шестиугольника abcdef проведем вертикальные линии, отложим на них по 40 мм ( высоту призмы) и полученные точки А, В, С, D, Е и F соединим прямыми. Этим заканчивается построение прямоугольной диметрии призмы. Невидимые ребра призмы bd и cd и стороны нижнего основания ab, be, cd выполним штриховыми линиями. [3]
В вершинах шестиугольника ABCDEF ( см. рис. 33) закон пластического течения допускает любую линейную комбинацию ( с положительными коэффициентами) режимов течения, соответствующих примыкающим сторонам. [4]
Поместим в вершины шестиугольника единичные массы; пусть О — центр масс полученной системы точек. [5]
Из каждой вершины шестиугольника восставим перпендикуляры к основанию картины, которые пересекутся с ним в точках О2, О3, Оь О5, Ов, От.
Затем с помощью масштаба глубины определим перспективу каждой вершины. Высоту ребер призмы определим по масштабу высоты.
[6]
Если шесть вершин шестиугольника лежат, чередуясь, на двух прямых, то три пары противоположных сторон пересекаются в коллннеарных точках. Если шесть сторон шестиугольника проходят, чередуясь, через две точки, то три его диагонали конкурентны ( [19], стр. [7]
Проводим из вершин шестиугольника линии связи — получаем проекции ребер и боковых граней головки болта. [8]
Атомы углерода занимают вершины правильных плоских шестиугольников со стороной 1 42 А. Такое плоское расположение соответствует р2 — гибридизации ( см. стр. Каждый атом углерода связан со своими соседями двумя простыми и одной двойной связью. Однако я-электроны двойной связи распределены равномерно между тремя 0-связями ( так же как в ионах NO и COg; см. стр. Поверхности расположены таким образом, что каждый атом находится выше и ниже центра шестиугольника соседних плоскостей.
Расстояние между параллельными плоскостями кристалла равно 3 4 А; это доказывает, что атомы различных плоскостей взаимно притягиваются вандерваальсовыми силами. У графита плоскость спайности параллельна атомным плоскостям.
[9]
Полученные таким образом вершины шестиугольника и есть геометрическое представление искомых корней. [10]
После построения всех вершин шестиугольника в аксонометрии они соединены между собой отрезками прямых. [11]
Лягушка прыгает по вершинам шестиугольника ABCDEF, каждый перемещаясь в одну из соседних вершин. [12]
Атомы располагаются в вершинах шестиугольников. [13]
Говорят, что две вершины шестиугольника являются смежными, чередующимися или противоположными в зависимости от того, разделяются они одной стороной, двумя или тремя сторонами. Таким образом, в шестиугольнике ABCDEF вершины F и В смежны с вершиной А, вершины Е и С — чередующиеся с вершиной А и вершина D противоположна вершине А.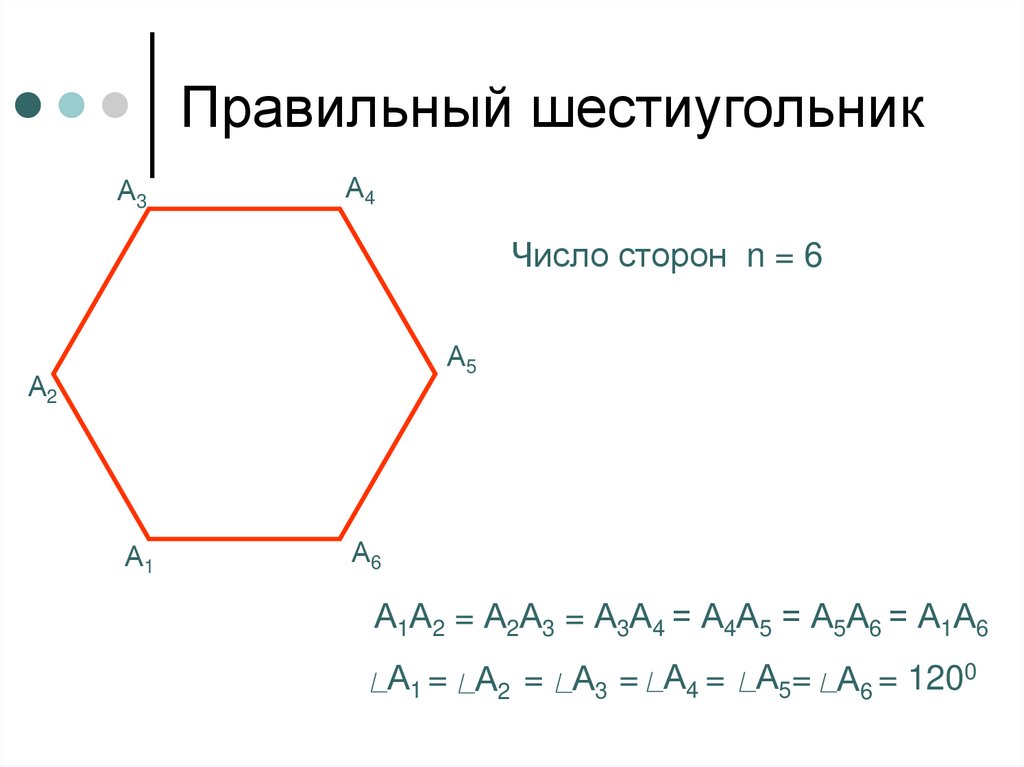
Отрезок, соединяющий две противоположные вершины, называется диагональю.
[14]
Если пять из шести вершин шестиугольника лежат на окружности и три пары противоположных сторон пересекаются в трех коллинеарных точках, то и шестая вершина лежит на той же окружности. [15]
Страницы: 1 2 3 4
Шестиугольник— Polytope Wiki
Шестиугольник — это многоугольник с 6 сторонами. Правильный шестиугольник имеет равные стороны и равные углы.
Префикс объединения в BSA — h-, как и в haco.
Правильный шестиугольник — один из трех правильных многоугольников, которыми можно замостить плоскость, два других — равносторонний треугольник и квадрат. Его мозаика называется шестиугольной мозаикой, и у нее есть 3 шестиугольника в вершине.
Шестиугольник обладает тем редким свойством, что его радиус описанной окружности равен длине его ребра. Другими известными многогранниками, удовлетворяющими этому свойству, являются кубооктаэдр (а также все расширенные симплексы), тессеракт и икоситетрахорон.
Благодаря этому правильный шестиугольник можно точно разложить на 6 равносторонних треугольников.
Шестиугольник и пятиугольник — единственные правильные многоугольники, имеющие ровно одну звездчатую форму. Это также многоугольник с наибольшим количеством сторон, не имеющий несоставной звёздчатой формы. Другие многоугольники без несоставных звёздочек (вообще без звёздочек) — это треугольник и квадрат. Это также единственный правильный многоугольник, состоящий только из составных звездочек.
Также может быть построен как равномерное усечение равностороннего треугольника. Он почти всегда имеет эту симметрию, когда появляется в многомерных однородных многогранниках.
Правильный шестиугольник — это пермутоэдр 3-го порядка.
Содержимое
- 1 Наименование
- 2 Координаты вершины
- 3 Представительства
- 4 варианта
- 4.1 Другие косые шестигранники
- 5 звездчатых тел
- 6 Внешние ссылки
Название шестиугольник происходит от древнегреческого ἕξ (6) и γωνία (угол), что означает количество вершин.
Другие названия включают:
- hig , аббревиатура в стиле Bowers, сокращение от «шестиугольник»
- Усеченный треугольник
Координаты правильного шестиугольника с единичной длиной ребра с центром в начале координат:
- (± 1,0), {\ Displaystyle \ влево (\ pm1, \, 0 \ вправо),}
- (± 12, ± 32). {\ displaystyle \ left (\ pm \ frac12, \, \ pm \ frac {\ sqrt3} {2} \ right).}
Правильный шестиугольник может быть представлен следующими диаграммами Кокстера:
- x6o (обычный)
- x3x (симметрия A 2 , обычно дитригон)
- ho3oh&#zx (A 2 , обычно триамбус)
- xu ho&#zx (прямоугольная симметрия)
- xux&#xt (осевой край вперед)
- ohho&#xt (осевая вершина вперед)
Два основных варианта шестиугольника имеют треугольную симметрию: дитригон с двумя чередующимися длинами сторон и равными углами и двойной триамб с двумя чередующимися углами и равными сторонами.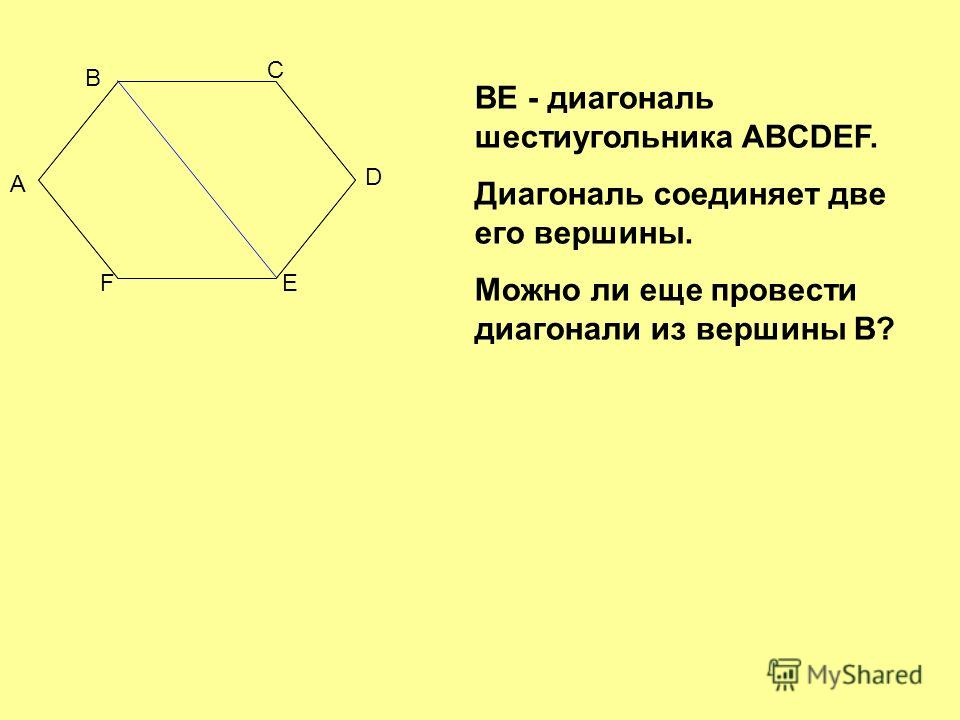
Существуют и другие менее регулярные вариации с хиральной треугольной, прямоугольной, зеркальной, инверсионной или нулевой симметрией.
Несоставной самопересекающийся шестиугольник можно назвать уникурсальной гексаграммой.
Другие косые шестиугольники[edit | править код]
Шестиугольник — один из пяти правильных шестиугольников в евклидовом пространстве, остальные четыре — наклонные:
| Наименование | Расширенный символ Шлефли | Размеры |
|---|---|---|
| шестигранник | {61}{\displaystyle \left\{\dfrac{6}{1}\right\}} | 2 |
| шестигранно-треугольная катушка | {61,2} {\ Displaystyle \ влево \ {\ dfrac {6} {1,2} \ вправо \}} | 4 |
| косой шестигранник | {61,3}{\displaystyle \left\{\dfrac{6}{1,3}\right\}} | 3 |
| косой треугольник | {62,3}{\displaystyle \left\{\dfrac{6}{2,3}\right\}} | 3 |
| Косая шестигранно-треугольная катушка | {61,2,3}{\displaystyle \left\{\dfrac{6}{1,2,3}\right\}} | 5 |
Гексаграмма (соединение двух треугольников) — единственная звездчатая форма шестиугольника.
- Бауэрс, Джонатан. «Правильные многоугольники и другие двумерные формы».
- Клитцинг, Ричард. «Полигоны»
- участников Википедии. «Шестиугольник».
- Участники Hi.gher.Space Wiki. «Шестиугольник».
- Хартли, Майкл. «{6}*12».
Как найти площадь шестиугольника
Пояснение:Есть несколько способов найти площадь шестиугольника.
- В правильном шестиугольнике разбейте фигуру на треугольники.
- Найдите площадь одного треугольника.
- Умножьте это значение на шесть.
В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.
Правильные шестиугольники:
Правильные шестиугольники представляют собой интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:
В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.
Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.
На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:
Мы также знаем следующее:
Теперь давайте посмотрим на каждый из треугольников в шестиугольнике.
Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.
Каждый угол в треугольнике равен . Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два треугольника.
Найдем длину этого треугольника. Помните, что в треугольниках длины сторон треугольников находятся в следующем соотношении:
.
Теперь мы можем проанализировать, используя замещающую переменную для длины стороны, .
Мы знаем размеры основания и высоты и можем найти его площадь.
Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.
Мы нашли площадь правильного шестиугольника с длиной стороны, . Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.
Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. е. ) и апофему (т.е. ), которая представляет собой длину линии, проведенной из центра многоугольника к прямому углу любой стороны. Это обозначено переменной на следующем рисунке:
Альтернативный метод:
Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:
, и является апофемой.